1 Introduction

The evolution of the universe has been proceeding while the temperature decreases. During the vacuum phase transition in the early stage of the universe, various topological defects such as domain walls, cosmic strings and monopoles may have generated [1, 2]. These topological objects formed due to a breakdown of local or global gauge symmetries. A global monopole is a spherically symmetric topological defect arose in the phase transition of a system composed of a self-coupling triplet of a scalar field whose original global O(3) symmetry is spontaneously broken to U(1) [3]. There should exist a kind of massive sources that swallow global monopoles and the metric of the source has a solid deficit angle [4]. According to the fact of the accelerated expansion of the universe, the theory of f(R) gravity as a kind of modified gravity theory was put forward by Buchdahl [5] and has been applied to explain the accelerated-inflation problem instead of adding dark energy or dark matter [6,7,8]. The f(R) gravity generalizes the general relativity and certainly the generalization should appear in the description of the background around the gravitational objects. With the expansion of the analytical function of the Ricci scalar under the weak field approximation, the gravitational field of a global monopole in the modified gravity theory has been explored [9]. It was also found that the presence of the parameter because of the modification of gravity is indispensable in providing stable circular orbits for particles [10]. The metric outside a massive object with f(R) global monopole was obtained [9, 10]. Certainly the components of this kind of metric contain the terms subject to the global monopoles and f(R) issue. The numerous investigations have been paid for the black holes shown with this type of metric. We considered the gravitational lensing of the massive f(R) global monopole in the strong field limit [11, 12]. We also calculate the thermodynamic quantities of this kind of the black hole to examine the black hole’s stability [13]. We derived the gray-body factor for scalar fields in the Schwarzschild spacetime with f(R) global monopole [14]. The timelike naked singularities of the black hole were probed [15]. The Hawking radiations of the f(R) global monopole black hole was studied based on the Heisenberg uncertainty principle or generalized uncertainty principle respectively [16, 17]. Recently, the absorption and scattering of a black hole with f(R) global monopole have been investigated [18].

The instability of black holes based on the thermodynamics is of great concern. As a kind of thermodynamic instability, the fragmentation instability was evaluated under non-perturbation [19]. The evolutions of black holes are thought to be driven by the second law of thermodynamics and whether the evolution could happen depends on the sign of the entropy difference of the black holes [19]. For a black hole, we derive its entropy. The isolated black hole is thought to be split and we also derive the total entropy of the broken black holes [19]. If the final entropy is smaller than the initial one, the black hole will exist as a whole, or the black hole will break into parts [19]. The fragmentation scheme has been utilized to explore the final fates of a serious of black holes such as the rotating anti-de Sitter black holes [20], black holes with a Gauss–Bonnet term [21] and charged anti-de Sitter black holes [22].

In the research on black holes, it is impossible to neglect the gravitational effect, so the terms associated with the Newtonian constant would be added in the Heisenberg uncertainty principle [23,24,25,26,27,28,29]. The generalized uncertainty principle (GUP) with the additional terms can be used to cure the divergence from states density near the black hole horizon and relate the entropy of black hole to a minimal length as quantum gravity scale [30,31,32,33]. The influence from the GUP modifying the black hole horizon and definitely changing the black hole entropy further was considered in terms of the radiation from black holes [30,31,32,33].

It is significant to analyze the fragmentation instability of a Schwarzschild black hole with global monopole under GUP within the frame of f(R) gravity. There must exist the gravitational sources that contain global monopoles in the spacetime governed by f(R) theory as mentioned above. At the same time the GUP corrects the horizons subject to the entropies. In the process of our research on the entropy of a massive source involving the global monopoles in the accelerated universe, we should not neglect the influences from global monopole, f(R) approach and GUP. To the best of our knowledge, few efforts have been made contributing to the study of the fragmentation of a black hole with f(R) global monopole under GUP. We are going to investigate the possibility that the f(R) global monopole-contained black hole breaks into two sections by means of the technique from Ref. [19]. We proceed by the same derivation and calculation on entropies of the same black holes under the GUP. We compare the entropy of the initial black hole with that of the final system composed of two fragmented black holes to find how the black hole entropy changes. The sign of the entropy difference will decide whether the fragmentation will happen under the second law of thermodynamics. We wonder how the f(R) gravity and GUP have influence on the fragmentation of the black holes. The results will appear in the end.

2 The fragmentation of a black hole with a f(R) global monopole

We plan to discuss the entropy of black hole with global monopole in the f(R) gravity. The spherically symmetric metric of the source was found [9, 10]:

$$\begin{aligned} \mathrm{d}s^{2}=A(r)\mathrm{d}t^{2}-B(r)\mathrm{d}r^{2}-r^2(\mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\varphi ^{2}) \end{aligned}$$
(1)

where

$$\begin{aligned} A(r)=B^{-1}(r)=1-8\pi G\eta ^{2}-\frac{2GM}{r}-\psi _{0}(r) \end{aligned}$$
(2)

and G is the Newtonian constant. As a monopole parameter, \(\eta \) is of the order \(10^{16}\) GeV in a typical grand unified theory, leading to \(8\pi G\eta ^{2}\approx 10^{-5}\) [2,3,4]. M is the mass parameter. The factor \(\psi _{0}\) reflects the extension of Einstein’s general relativity. According to \(A(r)=0\) from the metric (1), the smaller root is chosen to be an event horizon,

$$\begin{aligned} r_{H}= & {} r_{H}(M, \eta ^{2}, \psi _{0})\nonumber \\= & {} \frac{(1-8\pi G\eta ^{2})-\sqrt{(1-8\pi G\eta ^{2})^{2}-8GM\psi _{0}}}{2\psi _{0}} \end{aligned}$$
(3)

and the larger one is thought of as a cosmological horizon like

$$\begin{aligned} r_{C}=\frac{(1-8\pi G\eta ^{2})+\sqrt{(1-8\pi G\eta ^{2})^{2}-8GM\psi _{0}}}{2\psi _{0}}. \end{aligned}$$
(4)

It is obvious that the cosmological horizon will disappear if the modified parameter \(\psi _{0}\) is equal to 0. According to Refs. [34,35,36], the Bekenstein–Hawking entropy of black hole is proportional to the horizon area,

$$\begin{aligned} S=\frac{1}{4}A_{H} \end{aligned}$$
(5)

where

$$\begin{aligned} A_{H}=4\pi r_{H}^{2}. \end{aligned}$$
(6)

The thermodynamic argument for the fragmentation of a black hole claimed that the black hole entropy must increase during the process in view of the second law of thermodynamics [19]. Here we assume that the black hole with f(R) global monopole splits into two parts with the same kind of monopole. Within the fragmentation, the original black hole can be thought of as the initial state and the final state consists of two black holes under the conservation of mass. Before the splitting, the entropy of the initial state can be obtained from Eq. (5),

$$\begin{aligned} S_{i}=\pi r_{H}^{2}(M, \eta ^{2}, \psi _{0}). \end{aligned}$$
(7)

After fragmentation, the entropy for the final state is

$$\begin{aligned} S_{f}=\pi r_{H}^{2}(\varepsilon _{M}M, \eta ^{2}, \psi _{0})+\pi r_{H}^{2}((1-\varepsilon _{M})M, \eta ^{2}, \psi _{0})\nonumber \\ \end{aligned}$$
(8)

where \(r_{H}(\varepsilon _{M}M, \eta ^{2}, \psi _{0})\) and \(r_{H}((1-\varepsilon _{M})M, \eta ^{2}, \psi _{0})\) are the horizons of the fragmented black holes with masses \(\varepsilon _{M}M\) and \((1-\varepsilon _{M})M\), respectively, from Eq. (3). Following the same procedure as of Ref. [22], we define the mass ratio and its region \(0\le \varepsilon _{M}\le 1\). We obtain the entropy difference by substituting the event horizon (3) into the entropies (7) and (8) with various masses like \(\varepsilon _{M}M\) and \((1-\varepsilon _{M})M\),

$$\begin{aligned}&\triangle S=S_{f}-S_{i}\nonumber \\&\quad =\pi \left\{ \left[ \frac{(1-8\pi G\eta ^{2})-\sqrt{(1-8\pi G\eta ^{2})^{2}-8\varepsilon _{M}GM\psi _{0}}}{2\psi _{0}}\right] ^{2}\right. \nonumber \\&\qquad +\left[ \frac{(1-8\pi G\eta ^{2})-\sqrt{(1-8\pi G\eta ^{2})^{2}-8(1-\varepsilon _{M})GM\psi _{0}}}{2\psi _{0}}\right] ^{2}\nonumber \\&\left. \qquad -\left[ \frac{(1-8\pi G\eta ^{2})-\sqrt{(1-8\pi G\eta ^{2})^{2}-8GM\psi _{0}}}{2\psi _{0}}\right] ^{2}\right\} . \end{aligned}$$
(9)

If the deviation from the general relativity is ignored, the difference will be recovered to be

$$\begin{aligned} \lim _{\psi _{0}\longrightarrow 0}\triangle S=-2\pi \frac{(2GM)^{2}}{(1-8\pi G\eta ^{2})^{2}}\varepsilon _{M}(1-\varepsilon _{M})<0. \end{aligned}$$
(10)

The division of the isolated black hole cannot happen spontaneously, because this process makes the entropy decrease based on the second law of thermodynamics [19]. The negative nature of the difference above shows that the black holes are stable instead of rupturing in the case of general relativity although the weaker influence from a global monopole appears. The influence from the term \(8\pi G\eta ^{2}\) relating to the monopole can be neglected because its order is infinitely small. In fact the existence of the term \(8\pi G\eta ^{2}\) cannot change the sign of the difference.

As functions of the mass ratio \(\varepsilon _{M}\) with positive \(\psi _{0}\), the shapes of the entropy difference subject to the generalization of general relativity are plotted in Fig. 1. The greater the magnitude of \(\psi _{0}\) is, the larger the absolute value of the difference is. \(\triangle S\) expressed in Eq. (9) remains negative with \(\psi _{0}>0\), which means that the black holes keep stable instead of breaking up within the frame of generalized general relativity, no matter whether the sources contain global monopoles.

Fig. 1
figure 1

The solid, dotted, dashed curves of the dependence of entropy difference \(\triangle S\) on \(\varepsilon _{M}\) in units of \(\pi (GM)^{2}\) for \(\psi _{0}=0.05, 0.1, 0.12\), respectively, without GUP

Full size image

3 The fragmentation of black hole with f(R) global monopole under the generalized uncertainty principle

The discussion of the fragmentation of a black hole with f(R) global monopole is performed in the context of GUP. The Heisenberg uncertainty principle can be generalized within the microphysics regime as [25, 29,30,31,32,33, 37,38,39,40,41,42,43,44,45,46]

$$\begin{aligned} \bigtriangleup x\bigtriangleup p\ge \frac{\hbar }{2}\left[ 1-\frac{\alpha l_{p}}{\hbar }\bigtriangleup p+\left( \frac{\beta l_{p}}{\hbar }\right) ^{2}\bigtriangleup p^{2}\right] \end{aligned}$$
(11)

and

$$\begin{aligned} y_{-}\le y\le y_{+} \end{aligned}$$
(12)

where

$$\begin{aligned} y_{\pm }= & {} \left( \frac{l_{p}}{\hbar }\bigtriangleup p\right) _{\pm }=\frac{1}{2\beta ^{2}}\left( \alpha +\frac{2\bigtriangleup x}{l_{p}}\right) \nonumber \\&\quad \pm \frac{1}{2\beta ^{2}}\left( \alpha +\frac{2\bigtriangleup x}{l_{p}}\right) \sqrt{1-\left( \frac{2\beta }{\alpha +\frac{2\bigtriangleup x}{l_{p}}}\right) ^{2}}. \end{aligned}$$
(13)

The subscript ± corresponds to the sign ± of the term in the second line in Eq. (13). Here \(\alpha \) and \(\beta \) are dimensionless positive parameters modifying Heisenberg’s inequality. The Planck length is expressed as \(l_{p}=\sqrt{\frac{\hbar G}{c^{2}}}\) with velocity of light in the vacuum c. The terms with the Planck length having something to do with the Newtonian constant G provide the inequality with the gravitational effects. Following the procedure of Ref. [30,31,32,33, 47, 48], we choose

$$\begin{aligned} \triangle p'= & {} \frac{\hbar }{l_{p}}y_{-}=\frac{\hbar }{l_{p}}\left[ \frac{1}{2\beta ^{2}}\left( \alpha +\frac{2\bigtriangleup x}{l_{p}}\right) \right. \nonumber \\&\left. -\frac{1}{2\beta ^{2}}\left( \alpha +\frac{2\bigtriangleup x}{l_{p}}\right) \sqrt{1-\left( \frac{2\beta }{\alpha +\frac{2\bigtriangleup x}{l_{p}}}\right) ^{2}}\right] . \end{aligned}$$
(14)

From Eq. (14), the approximate expression for the uncertainty in the momentum is [47, 48],

$$\begin{aligned} \triangle p'\approx \frac{\hbar }{\alpha l_{p}+2\triangle x}. \end{aligned}$$
(15)

According to the combination of the GUP and the approximation (15), we estimate the black hole horizon amended by the gravitation with the original horizon of black hole as the lower bound on the region like \(\triangle x=2r_{H}\) [30,31,32,33, 47, 48],

$$\begin{aligned} r'_{H}=r_{H}\left[ 1+\frac{(\beta l_{p})^{2}}{4r_{H}(\alpha l_{p}+4r_{H})}\right] . \end{aligned}$$
(16)

From Eq. (16) the correction to the horizon includes \(\alpha \) and \(\beta \). It is interesting that no gravitational effect will act on the black hole horizon with the disappearance of the \(\beta \)-term in the GUP no matter whether the other term with \(\alpha \) exists or not. The nonvanishing \(\beta \) can keep the correction. The term \((\beta l_{p})^{2}\) determines the net effect from the correction, so we can discuss the black hole entropy with different values of \(\beta \), while we set \(\alpha \) to a definite magnitude. Under GUP, the corrected horizons of black holes certainly lead to the corrected entropy difference,

$$\begin{aligned} \triangle S'=S'_{f}-S'_{i} \end{aligned}$$
(17)

where

$$\begin{aligned} S'_{i}= & {} \pi r'^{2}_{H}(M, \eta ^{2}, \psi _{0}) ,\end{aligned}$$
(18)
$$\begin{aligned} S'_{f}= & {} \pi r'^{2}_{H}(\varepsilon _{M}M, \eta ^{2}, \psi _{0})+\pi r'^{2}_{H}((1-\varepsilon _{M})M, \eta ^{2}, \psi _{0}).\nonumber \\ \end{aligned}$$
(19)

We can use Eq. (16) to obtain the corrected radii \(r'_{H}(M, \eta ^{2}, \psi _{0})\), \(r'_{H}(\varepsilon _{M}M, \eta ^{2}, \psi _{0})\) and \(r'_{H}((1-\varepsilon _{M})M, \eta ^{2}, \psi _{0})\) as follows:

$$\begin{aligned}&r'_{H}(M, \eta ^{2}, \psi _{0})=r_{H}(M, \eta ^{2}, \psi _{0})\nonumber \\&\qquad +\,\frac{(\beta l_{p})^{2}}{4(\alpha l_{p})+16r_{H}(M, \eta ^{2}, \psi _{0})} , \end{aligned}$$
(20)
$$\begin{aligned}&r'_{H}(\varepsilon _{M}M, \eta ^{2}, \psi _{0})=r'_{H}(M, \eta ^{2}, \psi _{0})|_{M\longrightarrow \varepsilon _{M}M} , \end{aligned}$$
(21)
$$\begin{aligned}&r'_{H}((1-\varepsilon _{M})M, \eta ^{2}, \psi _{0})=r'_{H}(M, \eta ^{2}, \psi _{0})|_{M\longrightarrow (1-\varepsilon _{M})M}.\nonumber \\ \end{aligned}$$
(22)

Here \(r'_{H}(M, \eta ^{2}, \psi _{0})\) stands for the GUP-limited horizon of the initial black hole and \(r'_{H}(\varepsilon _{M}M, \eta ^{2}, \psi _{0})\) and \(r'_{H}((1-\varepsilon _{M})M, \eta ^{2}, \psi _{0})\) are the horizon radii of the separated black holes belonging to the final state, respectively, under GUP.

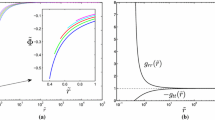
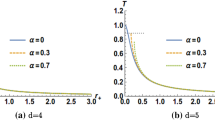
We should consider the fragmentation of an f(R) global monopole black hole under the GUP and that the entropy of an isolated system cannot decrease in any spontaneous process [19, 49]. The nature of the entropy difference during the evolution of the black hole helps us to determine whether the black hole will split. According to that monopoles probably formed in the process of the vacuum phase transition early in the universe and the fact that the universe expands faster, mentioned above, the gravitational sources involving f(R) global monopoles exist inevitably. It should be pointed out that some kinds of black holes are special cases of the gravitational sources. The black holes are limited by the GUP because of the requirement of a minimal length of the order of the Planck length. At first we ignore the correction to general relativity and show the entropy difference as a function of the ratio \(\varepsilon _{M}\) graphically in Fig. 2. It is found that there may be two roots \(\varepsilon _{M0}\) and \(1-\varepsilon _{M0}\) from \(\triangle S'=0\). If \(\varepsilon _{M}<\varepsilon _{M0}\) or \(\varepsilon _{M}>1-\varepsilon _{M0}\), then \(\triangle S'>0\), which means that the black hole will break into two parts under the GUP. The farther the inequality deviates from the Heisenberg uncertainty principle, the larger the value of \(\triangle S'\) is. Figure 3 indicates how the generalization of general relativity affects the entropy difference \(\triangle S'\) within the frame of GUP. The generalization will adjust the distribution of the masses for the portions of black hole. The larger \(\psi _{0}\) makes \(\varepsilon _{M0}\) smaller, meaning that the black hole is divided into two sources, a tiny one and the other a huge as regards their masses. We sum up the results from Figs. 2 and 3 to exhibit the relation among \(\varepsilon _{N0}\), \(\psi _{0}\) and \(\beta \) in Fig. 4. The appearance of GUP must lead to the black holes swallowing f(R) global monopoles to be divided. The weaker \(\beta \)-term in GUP and the stronger modification on standard general relativity cause the black hole to become a system with one part with extremely small mass and the other one with extremely large mass. Here we fix the value of \(\alpha \) for simplicity during our discussion.

Fig. 2
figure 2

The solid, dotted, dashed curves of the dependence of entropy difference \(\triangle S'\) on \(\varepsilon _{M}\) in units of \(\pi (GM)^{2}\) for \((\beta l_{p})^{2}=2, 6, 10\), respectively, with \(\psi _{0}=0\) and \(\alpha l_{p}=1\) for simplicity

Full size image
Fig. 3
figure 3

The solid, dotted, dashed curves of the dependence of entropy difference \(\triangle S'\) on \(\varepsilon _{M}\) in units of \(\pi (GM)^{2}\) for \(\psi _{0}=0.03, 0.02, 0.01\), respectively, with \((\beta l_{p})^{2}=5\) and \(\alpha l_{p}=1\) for simplicity

Full size image
Fig. 4
figure 4

The solid, dashed, dot curves of the relations between \(\varepsilon _{M0}\) and \(B=l_{p}\beta \) for \(\psi _{0}=0.01, 0.02, 0.03\), respectively, while \(\alpha l_{p}=1\) for simplicity

Full size image

4 Conclusion

We discuss the fragmentation instability of a black hole with the f(R) global monopole under the GUP. The influence that the global monopoles bring about is too small to be considered. At first we employ the approach of the non-perturbative fragmentation from Ref. [19] to compare the entropy of the initial f(R) global monopole black hole limited by the standard Heisenberg inequality with the sum of those of two fragmented ones. According to the second law of thermodynamics, only fragmentation of a black hole with a nonnegative nature of the entropy difference can happen. The sign of the entropy difference depends on whether the traditional principle of indeterminacy has been revised. Under the original indeterminate principle, the nature of the entropy difference will remain negative no matter whether general relativity has been modified. When the GUP is introduced, the entropy of initial black hole will be smaller than that of the final system consisting of two fragmented black holes. The more manifest the deviation from the Heisenberg certainty principle is, the smaller the difference of the masses for the two fragmented black holes is. In this case the more considerable correction of f(R) just regulates the division of the mass of initial black hole, resulting in one fragmented black hole mass being tiny and other being huge. Our results show the influences from the global monopole, modified general relativity and the generalized uncertainty principle on Schwarzschild black hole fragmentation.