Abstract
An alternative left–right model of quarks and leptons, where the \(SU(2)_R\) lepton doublet \((\nu ,l)_R\) is replaced with \((n,l)_R\) so that \(n_R\) is not the Dirac mass partner of \(\nu _L\), has been known since 1987. Previous versions assumed a global \(U(1)_S\) symmetry to allow n to be identified as a dark-matter fermion. We propose here a gauge extension by the addition of extra fermions to render the model free of gauge anomalies, and just one singlet scalar to break \(U(1)_S\). This results in two layers of dark matter, one hidden behind the other.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The alternative left–right model [1] of 1987 was inspired by the \(E_6\) decomposition to the standard \(SU(3)_C \times SU(2)_L \times U(1)_Y\) gauge symmetry through an \(SU(2)_R\), which does not have the conventional assignments of quarks and leptons. Instead of \((u,d)_R\) and \((\nu ,l)_R\) as doublets under \(SU(2)_R\), a new quark h and a new lepton n per family are added so that \((u,h)_R\) and \((n,e)_R\) are the \(SU(2)_R\) doublets, and \(h_L\), \(d_R\), \(n_L\), \(\nu _R\) are singlets.
This structure allows for the absence of tree-level flavor-changing neutral currents (unavoidable in the conventional model), as well as the existence of dark matter. The key new ingredient is a \(U(1)_S\) symmetry, which breaks together with \(SU(2)_R\), such that a residual global \(S'\) symmetry remains for the stabilization of dark matter. Previously [2,3,4], this \(U(1)_S\) was assumed to be global. We show in this paper how it may be promoted to a gauge symmetry. To accomplish this, new fermions are added to render the model free of gauge anomalies. The resulting theory has an automatic discrete \(Z_2\) symmetry which is unbroken as well as the global \(S'\), which is now broken to \(Z_3\). Hence dark matter has two components [5]. They are identified as one Dirac fermion (nontrivial under both \(Z_2\) and \(Z_3\)) and one complex scalar (nontrivial under \(Z_3\)).
In Sect. 2 we make a digression to the historical perspective which motivated this study. In Sect. 3 our model is described, with a complete list of its particle content. In Sect. 4 the gauge sector is shown in detail. In Sect. 5 the fermions are discussed with details of how they obtain masses. In Sect. 6 we deal with the scalars and show how the desirable pattern of symetry breaking is obtained. In Sect. 7 we discuss the present phenomenological constraints on the new \(Z'\) bosons and would-be dark-matter candidates. In Sect. 8 we show an example of two viable dark-matter candidates, both in terms of relic abundance and direct detection. In Sect. 9 we conclude.
2 Motivation and historical perspective
This section is for those who are unfamiliar with, but interested in the historical perspective which motivated our study. In the beginning, the idea of an \(SU(2)_L \times SU(2)_R\) electroweak extension of the standard model (SM), which is based only on \(SU(2)_L\), was very attractive, because it restores left–right symmetry to the interactions of the quarks and leptons. In the conventional approach, \((u,d)_{iL}\) are \(SU(2)_L\) doublets and \((u,d)_{jR}\) are \(SU(2)_R\) doublets. To allow them to have masses, a scalar bidoublet
is needed, so that \(\bar{u}_{iL} u_{jR}\) couple to \(\delta _1^0\) and \(\bar{d}_{iL} d_{jR}\) couple to \(\delta _2^0\), thereby obtaining masses from the vacuum expectation values of the two neutral scalars. However, because of the peculiarity of SU(2) doublets, the bidoublet
transforms identically as \(\Delta \). Hence \(\delta _2\) contributes to the u mass matrix, and \(\delta _1\) contributes to the d mass matrix. In other words, each quark sector gets its masses from two different Higgs particles. This means that flavor changing neutral currents (FCNC) are unavoidable at tree level through neutral Higgs exchange. This is a very strong constraint on the masses of these particles, of order 10–100 TeV. As such they are not likely to be observable at the Large Hadron Collider (LHC). On the general issue of FCNC, they are, of course, present in the SM, but only at the loop level, and they are known to be small and consistent with experimental data. In any extension of the SM, they may occur at tree level, and if so the scalar particles in question are required to be very heavy and out of reach of the LHC. It is thus a valid question to ask whether a model beyond the SM may be constructed with the absence of tree-level FCNC, so that it may have new scalars which are light enough to be discovered in addition to the SM Higgs boson of 125 GeV.
To distinguish \(\tilde{\Delta }\) from \(\Delta \), an extra symmetry is needed. This is what happens in supersymmetry, but then the u quark mass matrix must be proportional to the d quark mass matrix, which disagrees with data. The solution to this conundrum was pointed out 30 years ago [1]. It was discovered in the context of superstring-inspired \(E_6\) models, but applicable to the \(SU(2)_L \times SU(2)_R\) case [2, 3]. The idea is to add another quark h to each family which has the same charge as d, i.e. \(-1/3\). Both \(h_L\) and \(h_R\) are singlets in the SM, but they are distinguished from \(d_L\) and \(d_R\) in their \(SU(2)_R\) assignments, i.e.
To forbid the term \(\bar{h}_L d_R\), a global \(U(1)_S\) symmetry is added which also distinguishes \(\Delta \) from \(\tilde{\Delta }\). In this way, the d mass comes from an \(SU(2)_L\) Higgs doublet, the h mass comes from an \(SU(2)_R\) Higgs doublet, and the u mass comes from only \(\delta _1^0\) whereas \(\delta _2^0\) has no vacuum expectation value. Thus the model is guaranteed the absence of tree-level FCNC. It was realized a few years ago [2, 3] that this extra \(U(1)_S\) also serves the purpose of a dark symmetry, because even though it is broken, the combination \(T_{3R} + S\) or \(T_{3R} - S\) may remain unbroken and protects the condition \(\langle \delta _2^0 \rangle = 0\). In other words, the symmetry which allows us to solve the FCNC conundrum has now been connected to that of dark matter. Contrast this with most models of dark matter, where the existence of the dark symmetry is completely ad hoc, and unrelated to any other symmetry of the original model. This we believe is a good motivation for studying alternative left–right models. The logical next step is to ask the question whether it is possible for this \(U(1)_S\) to be gauged. What follows is a simple example of how it can be done and the resulting consequences.
3 Model
The particle content of our model is given in Table 1.
Without \(U(1)_S\) as a gauge symmetry, the model is free of anomalies without the addition of the \(\psi \) and \(\chi \) fermions. In the presence of gauge \(U(1)_S\), the additional anomaly-free conditions are all satisfied by the addition of the \(\psi \) and \(\chi \) fermions. The \([SU(3)_C]^2 U(1)_S\) anomaly is canceled between \((u,h)_R\) and \(h_L\); the \([SU(2)_L]^2 U(1)_S\) anomaly is zero because \((u,d)_L\) and \((\nu ,l)_L\) do not transform under \(U(1)_S\); the \([SU(2)_R]^2 U(1)_S\) and \([SU(2)_R]^2 U(1)_X\) anomalies are both canceled by summing over \((u,h)_R\), \((n,l)_R\), \((\psi _1^0,\psi _1^-)_R\), and \((\psi _2^+,\psi _2^0)_R\); the addition of \(\chi _R^\pm \) renders the \([U(1)_X]^2 U(1)_S\), \(U(1)_X [U(1)_S]^2\), \([U(1)_X]^3\), and \(U(1)_X\) anomalies zero; and the further addition of \(\chi ^0_{1R}\) and \(\chi ^0_{2R}\) kills both the \([U(1)_S]^3\) and the \(U(1)_S\) anomalies, i.e.
The scalar \(SU(2)_L \times SU(2)_R\) bidoublet is given by
with \(SU(2)_L\) transforming vertically and \(SU(2)_R\) horizontally. Under \(T_{3R} + S\), the neutral scalars \(\phi _R^0\) and \(\eta _2^0\) are zero, so that their vacuum expectation values do not break \(T_{3R} + S\), which remains as a global symmetry. However, \(\langle \sigma \rangle \ne 0\) does break \(T_{3R} + S\) and gives masses to \(\psi ^0_{1R} \psi ^0_{2R} - \psi ^-_{1R} \psi ^+_{2R}\), \(\chi ^+_R \chi ^-_R\), and \(\chi ^0_{1R} \chi ^0_{2R}\). These exotic fermions all have half-integral charges [6] under \(T_{3R} + S\) and only communicate with the others with integral charges through \(W_R^\pm \), \(\sqrt{2} Re(\phi ^0_R)\), \(\zeta \), and the two extra neutral gauge bosons beyond the Z. Some explicit Yukawa terms are
This dichotomy of particle content results in an additional unbroken symmetry of the Lagrangian, i.e. discrete \(Z_2\) under which the exotic fermions are odd. Hence dark matter has two layers: those with nonzero \(T_{3R} + S\) and even \(Z_2\), i.e. \(n, h, W_R^\pm , \phi ^\pm _R, \eta _1^\pm , \eta _1^0, \bar{\eta }_1^0\), \(\zeta \), and the underlying exotic fermions with odd \(Z_2\). Without \(\zeta \), a global \(S'\) symmetry remains. With \(\zeta \), because of the \(\zeta ^3 \sigma ^*\) and \(\chi ^0_{1R} \chi ^0_{1R} \zeta \) terms, the \(S'\) symmetry breaks to \(Z_3\).
Let
then the \(SU(3)_C \times SU(2)_L \times SU(2)_R \times U(1)_X \times U(1)_S\) gauge symmetry is broken to \(SU(3)_C \times U(1)_Q\) with \(S'\), which becomes \(Z_3\), as shown in Table 2 with \(\omega ^3 = 1\). The discrete \(Z_2\) symmetry is unbroken. Note that the global \(S'\) assignments for the exotic fermions are not \(T_{3R} + S\) because of \(v_S\), which breaks the gauge \(U(1)_S\) by 3 units.
4 Gauge sector
Consider now the masses of the gauge bosons. The charged ones, \(W_L^\pm \) and \(W_R^\pm \), do not mix because of \(S'(Z_3)\), as in the original alternative left–right models. Their masses are given by
Since \(Q = I_{3L} + I_{3R} + X\), the photon is given by
where \(e^{-2} = g_L^{-2} + g_R^{-2} + g_X^{-2}\). Let
where \(g_Y^{-2} = g_R^{-2} + g_X^{-2}\), then the \(3 \times 3\) mass-squared matrix spanning \((Z,Z',S)\) has the entries:
Their neutral-current interactions are given by
where \(g_Z^2 = g_L^2 + g_Y^2\) and \(\sin ^2 \theta _W = g_Y^2/g_Z^2\).
In the limit \(v^2_{1,2}<< v^2_R, v^2_S\), the mass-squared matrix spanning \((Z',S)\) may be simplified if we assume
and let
then
with mass eigenvalues given by
In addition to the assumption of Eq. (18), let us take for example
then \(\sin \theta _D = 1/\sqrt{10}\) and \(\cos \theta _D = 3/\sqrt{10}\). Assuming also that \(g_R = g_L\), we obtain
The resulting gauge interactions of \(D_{1,2}\) are given by
Since \(D_2\) is \(\sqrt{3}\) times heavier than \(D_1\) in this example, the latter would be produced first in pp collisions at the Large Hadron Collider (LHC).
5 Fermion sector
All fermions obtain masses through the four vacuum expectation values of Eq. (6) except \(\nu _R\), which is allowed to have an invariant Majorana mass. This means that neutrino masses may be small from the usual canonical seesaw mechanism. The various Yukawa terms for the quark and lepton masses are
These terms show explicitly that the assignments of Tables 1 and 2 are satisfied.
As for the exotic \(\psi \) and \(\chi \) fermions, they have masses from the Yukawa terms of Eqs. (4) and (5), as well as from
As a result, two neutral Dirac fermions are formed from the matrix linking \(\chi ^0_{1R}\) and \(\psi ^0_{1R}\) to \(\chi ^0_{2R}\) and \(\psi ^0_{2R}\). Let us call the lighter of these two Dirac fermions \(\chi _0\), then it is one component of dark matter of our model. The other will be the scalar \(\zeta \), to be discussed later. Note that \(\chi _0\) communicates with \(\zeta \) through the allowed \(\chi ^0_{1R} \chi ^0_{1R} \zeta \) interaction. Note also that the allowed Yukawa terms
enable the dark fermions h and n to decay into \(\zeta \).
6 Scalar sector
Consider the most general scalar potential consisting of \(\Phi _{L,R}\), \(\eta \), and \(\sigma \). Let
then
Note that
The minimum of V satisfies the conditions
The \(4 \times 4\) mass-squared matrix spanning \(\sqrt{2}Im(\phi _L^0,\eta _2^0, \phi _R^0,\sigma )\) is then given by
and that spanning \(\sqrt{2}Re(\phi _L^0,\eta _2^0,\phi _R^0,\sigma )\) is
Hence there are three zero eigenvalues in \(\mathcal{M}^2_I\) with one nonzero eigenvalue \(-\mu _3[v_1 v_2/v_R + v_R (v_1^2+v_2^2)/v_1v_2]\) corresponding to the eigenstate \((-v_1^{-1},v_2^{-1},v_R^{-1},0)/\sqrt{v_1^{-2}+v_2^{-2}+v_R^{-2}}\). In \(\mathcal{M}^2_R\), the linear combination \(H = (v_1,v_2,0,0)/\sqrt{v_1^2+v_2^2}\), is the standard-model Higgs boson, with
The other three scalar bosons are much heavier, with suppressed mixing to H, which may all be assumed to be small enough to avoid the constraints from dark-matter direct-search experiments. The addition of the scalar \(\zeta \) introduces two important new terms:
The first term breaks global \(S'\) to \(Z_3\), and the second term mixes \(\zeta \) with \(\eta _1^0\) through \(v_2\). We assume the latter to be negligible, so that the physical dark scalar is mostly \(\zeta \).
7 Present phenomenological constraints
Many of the new particles of this model interact with those of the standard model. The most important ones are the neutral \(D_{1,2}\) gauge bosons, which may be produced at the LHC through their couplings to u and d quarks, and decay to charged leptons (\(e^-e^+\) and \(\mu ^-\mu ^+\)). As noted previously, in our chosen example, \(D_1\) is the lighter of the two. Hence current search limits for a \(Z'\) boson are applicable [7, 8]. The \(c_{u,d}\) coefficients used in the data analysis are
where B is the branching fraction of \(Z'\) to \(e^-e^+\) and \(\mu ^-\mu ^+\). Assuming that \(D_1\) decays to all the particles listed in Table 2, except for the scalars which become the longitudinal components of the various gauge bosons, we find \(B = 1.2 \times 10^{-2}\). Based on the 2016 LHC 13 TeV data set from ATLAS [9], this translates to a bound of about 4 TeV on the \(D_1\) mass.
The would-be dark-matter candidate n is a Dirac fermion which couples to \(D_{1,2}\), which also couples to quarks. Hence severe limits exist on the masses of \(D_{1,2}\) from underground direct-search experiments as well. The annihilation cross section of n through \(D_{1,2}\) would then be too small, so that its relic abundance would be too big for it to be a dark-matter candidate. Its annihilation at rest through s-channel scalar exchange is p-wave suppressed and does not help, barring of course any accidental resonance enhancement. As for the t-channel diagrams, they also turn out to be too small. Suggestions of previous studies [2, 3] where n is chosen as dark matter are now ruled out.
8 Dark sector
Dark matter is envisioned to have two components. One is a Dirac fermion \(\chi _0\), which is a mixture of the four neutral fermions of odd \(Z_2\), and the other is a complex scalar boson which is mostly \(\zeta \), with the added assumption that \(m_{\chi _0}\) is significantly greater than \(m_\zeta \). The annihilation \(\chi _0 \bar{\chi }_0 \rightarrow \zeta \zeta ^*\) determines the relic abundance of \(\chi _0\), and the annihilation \(\zeta \zeta ^* \rightarrow H H\), where H is the standard-model Higgs boson, determines that of \(\zeta \). The direct \(\zeta \zeta ^* H\) coupling is assumed small to avoid the severe constraint in direct-search experiments.
Let the interaction of \(\zeta \) with \(\chi _0\) be \(f_0 \zeta \chi _{0R} \chi _{0R} + H.c.\), then the annihilation cross section of \(\chi _0 \bar{\chi }_0\) to \(\zeta \zeta ^*\) times relative velocity is given by
This determines the relic abundance of \(\chi _0\).
As the Universe cools below \(m_{\chi _0}\), \(\chi _0\) decouples from the thermal bath. We assume that \(m_\zeta \) is much below \(m_{\chi _0}\) so that \(\chi _0\) is essentialy frozen out at \(m_\zeta \). The relic abundance of \(\zeta \) is then mostly determined by \(\zeta \zeta ^* \rightarrow HH\). Let the effective interaction strength of \(\zeta \zeta ^*\) with HH be \(\lambda _0\), then the annihilation cross section of \(\zeta \zeta ^*\) to HH times relative velocity is given by
Note that \(\lambda _0\) is the sum over several interactions. The quartic coupling \(\lambda _{\zeta H}\) is assumed negligible, to suppress the trilinear \(\zeta \zeta ^* H\) coupling which contributes to the elastic \(\zeta \) scattering cross section off nuclei. However, the trilinear couplings \(\zeta \zeta ^* Re(\phi _R^0)\) and \(Re(\phi _R^0) H H\) are proportional to \(v_R\), and the trilinear couplings \(\zeta \zeta ^* Re(\sigma )\) and \(Re(\sigma ) H H\) are proportional to \(v_S\). Hence their effective contributions to \(\lambda _0\) are proportional to \(v_R^2/m^2[\sqrt{2}Re(\phi _R^0)]\) and \(v_S^2/m^2[\sqrt{2} Re(\sigma )]\), which are not suppressed. Whereas there are other possible contributions to Eqs. (44) and (45), we assume that the \(f_0\) and \(\lambda _0\) interactions are in fact dominant.
As a rough estimate, we will assume that
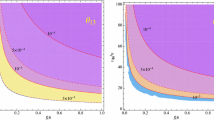
to satisfy the condition of dark-matter relic abundance [10] of the Universe. For given values of \(m_\zeta \) and \(m_{\chi _0}\), the parameters \(\lambda _0\) and \(f_0\) are thus constrained. We show in Fig. 1 the plots of \(\lambda _0\) versus \(f_0\) for \(m_\zeta = 150\) GeV and various values of \(m_{\chi _0}\). Since \(m_\zeta \) is fixed at 150 GeV, \(\lambda _0\) is also fixed for a given fraction of \(\Omega _\zeta /\Omega _{DM}\). To adjust for the rest of dark matter, \(f_0\) must then vary as a function of \(m_{\chi _0}\) according to Eq. (44).
As for direct detection, both \(\chi _0\) and \(\zeta \) have possible interactions with quarks through the gauge bosons \(D_{1,2}\) and the standard-model Higgs boson H. They are suppressed by making the \(D_{1,2}\) masses heavy, and the H couplings to \(\chi _0\) and \(\zeta \) small. In our example with \(m_\zeta = 150\) GeV, let us choose \(m_{\chi _0} = 500\) Gev and the relic abundances of both to be equal. From Fig. 1, these choices translate to \(\lambda _0 = 0.12\) and \(f_0 = 0.56\).
Consider first the \(D_{1,2}\) interactions. Using Eq. (26), we obtain
The effective \(\zeta \) elastic scattering cross section through \(D_{1,2}\) is then completely determined as a function of the \(D_1\) mass (because \(M_{D_2} = \sqrt{3} M_{D_1}\) in our example), i.e.
Using the most recent XENON result [11] at \(m_\zeta = 150\) GeV for which \(\sigma < 2 \times 10^{-46}~\mathrm{cm}^2\) and Eq. (25), we obtain \(v_R > 35\) TeV which translates to \(M_{D_1} > 18\) TeV, and \(M_{W_R} > 16\) TeV. These are a few percent more restrictive than the most recent LUX result [12].
The \(\bar{\chi _0} \gamma _\mu \chi _0\) couplings to \(D_{1,2}\) depend on the \(2 \times 2\) mass matrix linking \((\chi _1,\psi _1)\) to \((\chi _2,\psi _2)\), which has two mixing angles and two mass eigenvalues, the smaller one being \(m_{\chi _0}\). By adjusting these parameters, it is possible to make the effective \(\chi _0\) interaction to any particular nucleus through \(D_{1,2}\) negligibly small. Hence there is no useful limit on the \(D_1\) mass in this case. Note that the amplitude cancellation here is through \(D_{1,2}\) and not necessarily through u and d quarks (which are not adjustable in this model), as would be necessary in models with only one vector mediator.
Direct search also constrains the coupling of the Higgs boson to \(\zeta \) (through a possible trilinear \(\lambda _{\zeta H} \sqrt{2} v_H \zeta ^* \zeta \) interaction) or \(\chi _0\) (through an effective Yukawa coupling \(\epsilon \) from H mixing with \(\sigma _R\) and \(\phi _R^0\)). Let their effective interactions with quarks through H exchange be given by
where \(f_q = m_q/\sqrt{2}v_H = m_q/(246~\mathrm{GeV})\). The spin-independent direct-detection cross section per nucleon in the former is given by
where \(\mu _{\zeta } = m_\zeta M_A/(m_\zeta + M_A)\) is the reduced mass of the dark matter, and [13]
with [14]
For \(m_\zeta = 150\) GeV, we have
Using \(A=131\), \(Z=54\), and \(M_A=130.9\) atomic mass units for the XENON experiment [11], and twice the most recent bound of \(2 \times 10^{-46}~\mathrm{cm}^2\) (at \(m_\zeta = 150\) GeV) because \(\zeta \) is assumed to account for only half of the dark matter) at this mass, we find
As noted earlier, this is negligible for considering the annihilation cross section of \(\zeta \) to H.
For the H contribution to the \(\chi _0\) elastic cross section off nuclei, we replace \(m_\zeta \) with \(m_{\chi _0} = 500\) GeV in Eq. (51) and \(\lambda _{\zeta H}/2 m_\zeta \) with \(\epsilon /\sqrt{2}v_H\) in Eq. (52). Using the experimental data at 500 GeV, we obtain the bound.
From the above discussion, it is clear that it is possible for future improvements in direct-search experiments to yield positive results within the framework of our model.
9 Conclusion and outlook
In the context of the alternative left–right model, a new gauge \(U(1)_S\) symmetry has been proposed to stabilize dark matter. This is accomplished by the addition of a few new fermions to cancel all the gauge anomalies, as shown in Table 1. As a result of this particle content, an automatic unbroken \(Z_2\) symmetry exists on top of \(U(1)_S\), which is broken to a conserved residual \(Z_3\) symmetry. Thus dark matter has two components. One is the Dirac fermion \(\chi _0 \sim (\omega ,-)\) and the other the complex scalar \(\zeta \sim (\omega ,+)\) under \(Z_3 \times Z_2\). We have shown how they may account for the relic abundance of dark matter in the Universe, and satisfy present experimental search bounds.
Whereas we have no specific prediction for discovery in direct-search experiments, our model will be able to accommodate any positive result in the future, just like many other existing proposals. To single out our model, many additional details must also be confirmed. Foremost are the new gauge bosons \(D_{1,2}\). Whereas the LHC bound is about 4 TeV, the direct-search bound is much higher, provided that \(\zeta \) is a significant fraction of dark matter. If \(\chi _0\) dominates instead, the adjustment of free parameters of our model can lower this bound to below 4 TeV. In that case, future \(D_{1,2}\) observations are still possible at the LHC as more data become available.
Another is the exotic h quark which is easily produced if kinematically allowed. It would decay to d and \(\zeta \) through the direct \(\bar{d}_R h_L \zeta \) coupling of Eq. (29). Assuming that this branching fraction is 100%, the search at the LHC for 2 jets plus missing energy puts a limit on \(m_h\) of about 1.0 TeV, as reported by the CMS Collaboration [15] based on the \(\sqrt{s} = 13\) TeV data at the LHC with an integrated luminosity of 35.9 fb\(^{-1}\) for a single scalar quark.
If the \(\bar{d}_R h_L \zeta \) coupling is very small, then h may also decay significantly to u and a virtual \(W_R^-\), with \(W_R^-\) becoming \(\bar{n} l^-\), and \(\bar{n}\) becoming \(\bar{\nu } \zeta ^*\). This has no analog in the usual searches for supersymmetry or the fourth family because \(W_R\) is heavy (\(> 16\) TeV). To be specific, the final states of 2 jets plus \(l_1^- l_2^+\) plus missing energy should be searched for. As more data are accumulated at the LHC, such events may become observable.
References
E. Ma, Phys. Rev. D 36, 274 (1987)
S. Khalil, H.-S. Lee, E. Ma, Phys. Rev. D 79, 041701(R) (2009)
S. Khalil, H.-S. Lee, E. Ma, Phys. Rev. D 81, 051702(R) (2010)
S. Bhattacharya, E. Ma, D. Wegman, Eur. Phys. J. C 74, 2902 (2014)
Q.-H. Cao, E. Ma, J. Wudka, C.-P. Yuan, arXiv:0711.3881 [hep-ph]
C. Kownacki, E. Ma, Phys. Lett. B 760, 59 (2016)
G. Aad et al., ATLAS Collaboration, Phys. Rev. D 90, 052005 (2014)
S. Khachatryan et al., CMS Collaboration, JHEP 1504, 025 (2015)
M. Aaboud et al., ATLAS Collaboration, JHEP 1710, 182 (2017)
G. Steigman, B. Dasgupta, J.F. Beacom, Phys. Rev. D 86, 023506 (2012)
E. Aprile et al., XENON Collaboration, Phys. Rev. Lett. 119, 181301 (2017)
D.S. Akerib et al., LUX Collaboration, Phys. Rev. Lett. 118, 021303 (2017)
G. Belanger, F. Boudjema, A. Pukhov, A. Semenov, Comput. Phys. Commun. 180, 747 (2009)
S. Durr et al., Phys. Rev. Lett. 116, 172001 (2016)
A.M. Sirunyan et al., CMS Collaboration, Eur. Phys. J. C 77, 710 (2017)
Acknowledgements
This work was supported in part by the U. S. Department of Energy Grant No. DE-SC0008541.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Kownacki, C., Ma, E., Pollard, N. et al. Dark Gauge U(1) symmetry for an alternative left–right model. Eur. Phys. J. C 78, 148 (2018). https://doi.org/10.1140/epjc/s10052-018-5630-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-5630-6