NLO QCD predictions for $Z+\gamma$ + jets production with Sherpa

Abstract

We present precise predictions for prompt photon production in association with a Z boson and jets. They are obtained within the Sherpa framework as a consistently merged inclusive sample. Leptonic decays of the Z boson are fully included in the calculation with all off-shell effects. Virtual matrix elements are provided by OpenLoops and parton-shower effects are simulated with a dipole parton shower. Thanks to the NLO QCD corrections included not only for inclusive $Z\gamma$ production but also for the $Z\gamma$ + 1-jet process we find significantly reduced systematic uncertainties and very good agreement with experimental measurements at $\sqrt{s}=8\,\mathrm {TeV}$. Predictions at $\sqrt{s}=13\,\mathrm {TeV}$ are displayed including a study of theoretical uncertainties. In view of an application of these simulations within LHC experiments, we discuss in detail the necessary combination with a simulation of the Z + jets final state. In addition to a corresponding prescription we introduce recommended cross checks to avoid common pitfalls during the overlap removal between the two samples.

1 Introduction

The production of a Z boson is one of the standard candle processes at hadron colliders like the LHC. The massive boson is often produced in association with photons, which are typically low-energetic or collinear with charged final state particles. Cases where one of the photons happens to be well-isolated and high-energetic can be regarded as an individual important final state, $Z\gamma$ production.

$Z\gamma$ production plays an important role both as a signal and as a background process at the LHC. The absence of couplings of the photon to the uncharged Z boson in the Standard Model can be probed by measurements in this channel, resulting in differential cross sections and limits on anomalous couplings from LEP experiments [1,2,3,4], Tevatron experiments [5,6,7], and by ATLAS [8,9,10] and CMS [11,12,13,14].

The $Z\gamma$ process also constitutes an irreducible background in the search for the Higgs boson [15] or new massive gauge bosons decaying to $Z\gamma$ [16, 17] or in more inclusive searches in final states containing a photon and missing transverse momentum [18,19,20,21].

Theoretical predictions for $Z\gamma$ production can be divided into on-shell and off-shell calculations. Results for on-shell $Z\gamma$ production leave out the decays of the Z boson or include them only in a narrow-width or pole approximation. Beyond the leading-order results [22], the first on-shell higher-order calculations included NLO QCD [23,24,25] and, more recently, also NNLO QCD corrections [26]. In reality, the Z boson is unstable and is thus never produced as an on-shell final-state particle. Recent calculations take this finite width into account and provide predictions for the off-shell  $\ell \ell \gamma$ final state. The most accurate off-shell predictions contain NNLO QCD [27, 28] and NLO EW corrections [29].

Experimental analyses at the LHC rely heavily on theoretical predictions for their signal and background processes. Fixed-order predictions as listed above can provide such an input only to some extent. While they describe the dominant features of the given final state objects at the parton level, they are not made to simulate a realistic behaviour of the hadronic final state. Monte-Carlo event generator programs on the other hand combine fixed-order predictions and an approximate all-order resummation of QCD corrections to enable a full simulation at the hadron level. Different approaches and programs are available, but the simulation currently in use in LHC experiments for $Z\gamma$ production is generated with leading-order multi-leg generators using approaches like CKKW(-L) or MLM merging [30,31,32,33,34,35,36]. For the related process of $W\gamma$ production, an implementation of a NLO QCD calculation of the inclusive process matched to a parton shower exists within the Powheg framework [37].

This article applies a NLO-accurate multi-leg merging formalism to the processes of $Z\gamma$ and $Z\gamma$+jet production¹ for the first time. After a review of the relevant methods in Sect. 2 we present our computational setup and results comparing LO and NLO-accurate merged predictions to each other and to experimental data in Sect. 3. A special aspect relevant for the application of multi-jet merged $Z\gamma$ samples in experimental analyses is a combination of $Z\gamma$+jets and Z+jets. Recommended techniques and cross checks for such a combination are implemented and discussed in Sect. 4.

Fig. 1

Possible cluster configurations for an $ll\gamma +j$ configuration for the exclusive clustering. Grey blobs symbolize the final core process. If $\mu _1 < \mu _{\mathrm {core}}$ this would be an ordered configuration, otherwise the clustering will stop

Fig. 2

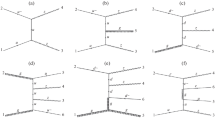
Possible cluster configurations for an $ll\gamma +j$ configuration (see Fig. 1 ) for the inclusive clustering. Grey blobs symbolize the final core process. Instead of stopping at the $Z\gamma j$ process in the case of not finding a suited QCD configuration, this algorithm then allows the clustering of non-QCD particles

2 Methods

2.1 Matching and merging with Sherpa at NLO

To obtain NLO-accurate multi-jet-merged predictions the “MEPS@NLO” formalism [38] is applied to $Z\gamma$ production within the Sherpa framework. It combines two essential ingredients, NLO + parton-shower matching and multi-jet merging, which are briefly summarised in the following.

For the combination of NLO-accurate matrix-element calculations with a parton shower (PS), a matching procedure to avoid double counting of the QCD emission effects at $\mathcal {O}(\alpha _s)$ is needed. Here, the prescription proposed in [39, 40] is applied, both to $pp\rightarrow Z\gamma$ and $pp\rightarrow Z\gamma$ + jet simulations. It is based on the original MC@NLO method [41] but extends it to a fully colour-correct formulation also in the limit of soft emissions.

Both simulations and further PS emissions are then consistently merged into one inclusive $pp\rightarrow Z\gamma +0$,1j@NLO sample using the “MEPS@NLO” method [38]. Shower emissions above a pre-defined separation criterion, $Q_\text {CUT}$, are vetoed in the lower multiplicity contribution, and Sudakov factors are applied where appropriate such as to make this contribution exclusive and allow the combination with a higher jet multiplicity. This applies not only to the emissions from the parton shower but to all contributions of the NLO-matched emission, including the hard remainder (“$\mathbb {H}$ events”). In the application of the Sudakov factors care has to be taken to remove the $\mathcal {O}(\alpha _s)$ contribution which is already present in the NLO(-matched) emission.

Beyond the processes simulated at NLO accuracy, higher-multiplicity processes can be added to the simulation at LO accuracy to improve the modelling of high jet multiplicities beyond the parton-shower approximation.

Similar to merging methods at LO, an appropriate scale choice for the evaluation of multi-jet configurations is obtained by statistically identifying a parton-shower history in the matrix-element final state. To that end, the parton shower is run in reverse mode, i.e. the closest parton pair is identified according to the shower splitting probabilities and then recombined using the kinematical properties of the shower. When applied recursively, this clustering results in a core process, e.g. $pp\rightarrow Z\gamma$, and in an ordered history of shower emissions. The factorisation scale is then determined by a typical momentum transfer within the core process (core scale), and the renormalisation scale is calculated from the n identified branchings to resemble $\alpha _s^n(\mu _R)=\prod _{i=1}^n\alpha _s(k_{\perp ,i})$, where $k_{\perp ,i}$ is a suitably scaled relative transverse momentum encountered in the ith splitting. If the clustering algorithm is restricted to splitting functions active in the shower (“exclusive clustering”) it stops if no possible ordered shower history can be reconstructed. Thus, for events with very hard QCD emissions, the core process can also contain jets and contribute to the renormalisation scale accordingly.

By contrast, the clustering applied by default (“inclusive clustering”) may include electroweak combinations to preserve the ordering in the history, even though electroweak splitting functions are not enabled in the shower.

An example configuration which demonstrates the different treatment in the inclusive and the exclusive clustering algorithm is shown in Figs. 1 and 2. The possible core processes will become relevant for the discussion of different scale choices later in this work.

2.2 Soft photon resummation with YFS

The YFS-algorithm [42] describes a possibility to resum soft logarithmically enhanced photon radiation to all orders in a process-independent manner. This algorithm is implemented in Sherpa for both, leptonic decays of W/Z bosons and hadron decays. Details of this implementation are given in [43] and briefly summarised here. The decay width for a decay of a particle i with mass M into a final state f, corrected for the radiation of $n_\mathrm {R}$ real and $n_\mathrm {V}$ virtual photons, reads

$$\begin{aligned} \begin{aligned} 2M \Gamma&= \sum \limits _{n_\mathrm {R}=0}^{\infty } \int \mathrm {d} \tilde{\Phi } \left| \sum \limits _{n_\mathrm {V}}^{\infty } \mathcal {M}_{n_\mathrm {R}}^{n_\mathrm {V}+ \frac{1}{2}n_\mathrm {R}} \right| ^2. \end{aligned} \end{aligned}$$

(1)

Here, $\mathcal {M}_{n_\mathrm {R}}^{n_\mathrm {V}+ \tfrac{1}{2}n_\mathrm {R}}$ describes a decay matrix element with additional $n_\mathrm {R}$ real and $n_\mathrm {V}$ virtual photons and $\tilde{\Phi }$ denotes the corresponding phase space. As shown in [42], the soft limits of all these (virtual and real) matrix elements can be resummed and factorised out. The corresponding infrared divergences cancel order by order and result in the finite YFS form factor $Y(\mathrm {\Omega })$. $Y(\mathrm {\Omega })$ includes the soft limits of all virtual and real contributions. However, only the divergent part of the real contributions is retained and separated by the symbolic cut-off $\mathrm {\Omega }$ from the non-divergent one. Equation (1) can then be approximated with

$$\begin{aligned} 2M\Gamma = \sum \limits _{n_{\gamma }} \frac{1}{n_{\gamma }} \int \mathrm {d} \Phi e^{Y(\mathrm {\Omega })} \prod \limits _{i=1}^{n_{\gamma }} S(k_i) \Theta (k_i, \mathrm {\Omega }) \beta _0^0 \mathcal C. \end{aligned}$$

(2)

The eikonals S(k) include all contributions for the emission of a real photon with momentum k. Since the divergent, real part is already included in $Y(\mathrm {\Omega })$, these eikonals will only be integrated in the non-divergent phase space. The number of additional, resolved photons is denoted with $n_{\gamma }$, while $\beta _0^0$ is the undressed matrix element without any real or virtual photons and $\Phi$ the corresponding phase space. The YFS algorithm can in principle be improved order by order with exact, process dependent real and virtual matrix elements. These possible corrections are incorporated in the factor $\mathcal C$, which is equal to one in the case of no corrections. In Sherpa, higher-order corrections are available either in an approximative way using collinear splitting kernels or as exact matrix elements. The first option is independent of the process whereas the second one is limited to a few cases, including the decay of a vector boson into two fermions.

It is worth noting that in a Monte Carlo code photons radiated by YFS are—in contrast to e.g. QED showers—unordered.

2.3 Isolated photons

Matching theoretical predictions with experimental measurements including isolated photons has turned out to be a non-trivial problem when going beyond leading order in QCD. It is no longer possible to isolate the photon completely from all kind of hadronic activity since this would constrain the phase space of soft gluon radiation and destroy the cancellation of infrared singularities. As a consequence, many experiments allow a small fraction of hadronic energy within the isolation cone. However, this relaxed cone criterion requires special attention when calculating theoretical cross sections. An observable constructed with such an isolation criterion includes a divergence when the photon gets collinear to a massless quark. This divergence is of QED origin and does not cancel within the perturbative QCD calculation. In principle there are two common ways to solve this problem, either by absorbing the divergences into fragmentation functions or by using a smooth isolation criterion. Such a smooth isolation criterion has been proposed in [44] and is also used in this paper. This criterion suppresses the divergent collinear contribution by limiting the maximal transverse energy $E_\perp ^{\mathrm {max}}$ close to the photon axis,

$$\begin{aligned} E_\perp ^{\mathrm {max}} \le \epsilon p_\perp ^{\gamma } \left( \frac{1-\cos (r)}{1-\cos (R)} \right) ^n . \end{aligned}$$

(3)

Here, $p_\perp ^{\gamma }$ is the transverse momentum of the photon and $\epsilon$, n and R are parameters which define the final shape of the smooth cone. $E_\perp ^{\mathrm {max}}$ is defined as the sum of the transverse energies of all partons present at matrix-element level within a cone of radius r around the photon axis. The condition in Eq. (3) has to be fulfilled for all cones with

$$\begin{aligned} r=\sqrt{(\mathrm {\Delta }\eta )^2 + (\mathrm {\Delta }\phi )^2} < R \end{aligned}$$

(4)

and ensures that $E_\perp ^{\mathrm {max}}$ converges smoothly to zero for $r \rightarrow 0$.

3 NLO-accurate multi-jet predictions for $Z\gamma$ production

3.1 Setup

All results in this publication are obtained with the Monte Carlo event generator Sherpa [45] using merged calculations. Version 2.2.2 of the program was upgraded in the context of this work to enable the $Z\gamma$ process and to generically improve the stability of the on-the-fly assessment of systematic uncertainties.

Two process setups will be compared in the following:

MEPS@NLO:

$pp \rightarrow e^+ e^- \gamma \,+\, 0,1\mathrm {jets@NLO} + 2,3\mathrm {jets@LO}$,

MEPS@LO:

$pp \rightarrow e^+ e^- \gamma + 0,1,2,3\mathrm {jets@LO}$.

Therein, jet refers to an additional parton in the matrix element and LO/NLO denotes the accuracy of the corresponding multiplicity.

The matrix elements are calculated by the internal matrix-element generators Amegic++ [46] and Comix [47]. Virtual diagrams are calculated by OpenLoops 1.3.1 [48], using CutTools [49] and OneLoop [50]. In all MEPS@NLO setups Amegic++ is used only for Born-like processes. All real-subtracted contributions and the leading-order diagrams of higher multiplicity are calculated by Comix. The merging cut $Q_\mathrm {CUT}$ is set to 30$\,\mathrm {GeV}$.

Where not explicitly stated otherwise, scales are determined by the inclusive clustering algorithm described in Sect. 2.1 (STRICT_METS). The core scale is calculated according to the core process as

$$\begin{aligned} \mu ^2_\text {core}={\left\{ \begin{array}{ll} m^2_{Z} &{}\quad \text {for } Z,\\ m^2_{Z\gamma } &{}\quad \text {for } Z\gamma ,\\ \tfrac{1}{4}m^2_{\perp ,Z/\gamma } &{}\quad \text {for } Z/\gamma +\text {jet},\\ \tfrac{1}{4}\tfrac{-1}{1/\hat{s}+1/\hat{t}+1/\hat{u}} &{} \quad \text {for jet + jet},\\ \tfrac{1}{4}\bigl (m_{\perp ,Z\gamma } ~ + &{} \\ \sum _{\text {jets}} m_{\perp ,\text {jet}} \bigr )^2 &{}\quad \text {for unordered } Z\gamma +\text {jets}.\\ \end{array}\right. } \end{aligned}$$

(5)

This corresponds to the default core scale implementation in Sherpa 2.2.

The electroweak couplings are evaluated using a mixed scheme as recommended in [51]. First, all couplings are calculated using the $G_\mu$ scheme. In this scheme, the coupling constant is evaluated as a function of the Fermi constant $G_\mu$ and the masses of W and Z,

$$\begin{aligned} \alpha _{G_\mu } = \frac{\sqrt{2}}{\pi } G_\mu M_W^2 \left( 1 - \frac{M_W^2}{M_Z^2}\right) . \end{aligned}$$

(6)

This behaviour effectively resums contributions which arise when evolving the electroweak coupling to the electroweak scale and is a common choice for processes involving heavy W or Z bosons. However, in the $V\gamma$ processes an additional external—i.e. on-shell—photon is present. Taking this into account one electroweak coupling should be evaluated at $\alpha (0)$. This is achieved by a global reweighting with $k=\alpha (0) / \alpha _{G_\mu }$.

Fig. 3

Merging cut variation for $e^+ e^- \gamma + 0,1\mathrm {j@NLO} + 2,3\mathrm {j@LO}$ at 13$\,\mathrm {TeV}$. The splitting scales are determined without any additional phase space cuts, the generation cuts at matrix-element level are $p_\perp ^\gamma > 15$ $\,\mathrm {GeV}$, mass$(e^+,e^- )>40$ $\,\mathrm {GeV}$, $\mathrm {\Delta } R (\gamma , e^{\pm })>0.4$ and an smooth isolation cone with $R=0.1, n=2, \epsilon =0.1$. The phase space cuts used for the $E_\perp ^\gamma$ spectrum are defined in Sect. 3.2. The error bars describe statistical fluctuations

Unstable particles are described using the complex mass scheme [52, 53]. Following [29], on-shell masses and widths are converted to pole values and result in

$$\begin{aligned} \begin{aligned} M_W=80.3580\,\,\mathrm {GeV}, \quad \Gamma _W=2.0843\,\,\mathrm {GeV}, \\ M_Z=91.1535\,\,\mathrm {GeV}, \quad \Gamma _Z=2.4943\,\,\mathrm {GeV}. \end{aligned} \end{aligned}$$

(7)

These values are used for all calculations.

As parton distribution functions NNPDF3.0 [54] sets are used, taking the NLO set for MEPS@LO calculations and the NNLO set for MEPS@NLO. The running of $\alpha _\mathrm {s}$ and its value at $M_\mathrm {Z}$ are thereby set according to these PDF sets, resulting in $\alpha _\mathrm {s}(M_\mathrm {Z})=0.118$ and a running at two(three) loop order when using the NLO(NNLO) sets. YFS is set active and includes matrix-element corrections for further photon emissions.

For the event generation, all parton-level cuts are set to be more inclusive than the respective analysis cuts. As described in Sect. 2.3, it is not possible to use the experimental isolation criterion; instead the smooth cone criterion is used and validated for two different sets of parameters.

When comparing to experimental data the simulation is performed including the default multiple interactions [55, 56] and hadronisation models [57]. The final state analyses are done within the Rivet framework [58].

3.2 Predictions for $\sqrt{s}=$13$\,\mathrm {TeV}$

3.2.1 Merging cut variation

Using the ME + PS merging method defined in Sect. 2.1 a new parameter is introduced, the merging cut $Q_{\mathrm {CUT}}$. It separates the different phase space regions for the parton shower and higher-multiplicity matrix elements. Since this parameter is unphysical, physical observables should be independent of its exact value as long it is chosen in a reasonable range.

An interesting observable for checking this behaviour are the splitting scales as defined by the $k_\perp$-algorithm [59]. All final state partons² are clustered to jets according to this algorithm. The splitting scale $d_\mathrm {(n-1)(n)}$ is then defined as the jet measure which describes the cluster step of a n-parton final state to a $(n-1)$ final state. Following this, $d_{01}$ gives the $p_\perp$ of the hardest jet and $d_{12}$ either describes the production of a second jet or the second splitting of the first jet in the case there is only one.

In the context of matching and merging, jets can emerge either from higher-multiplicity matrix elements or from the parton shower. Since the $k_\perp$ algorithm uses a jet measure which is very similar to the jet criterion used by the merging algorithm, its splitting scales are very sensitive observables to study the interplay between LO/NLO matrix elements and partonic showers.

In Fig. 3, these differential jet rates are evaluated for the first two splittings while varying the merging cut between 20 and 40$\,\mathrm {GeV}$. Figure 3a shows the hardest splitting scale. This jet rate is sensitive to the transition from the zero-jet NLO matrix element³ with a shower emission at $Q_\mathrm {emission} < Q_\mathrm {CUT}$ to a one-jet NLO matrix element with $Q_\mathrm {emission} > Q_\mathrm {CUT}$.

By contrast, in Fig. 3b the subleading splitting scale is shown. This splitting probes the transition from the one-jet NLO matrix element with an unresolved emission to a LO matrix element with two resolved jets.

In both cases the uncertainties coming from the merging cut variation are less than 10%. As mentioned above these splitting scales are shown since they are expected to be very sensitive to $Q_\mathrm {CUT}$. Indeed, other observables have a much smaller merging cut uncertainty. The $E_\perp ^\gamma$ spectrum is given in Fig. 3c, here the merging cut variation is found to be completely negligible in contrast to the scale uncertainties studied in Sect. 3.2.3.

Fig. 4

Comparison of different scale choices for a $pp\rightarrow e^+ e^- \gamma + 0,1j$@NLO + 2, 3j@LO setup. The prediction labelled “inclusive” uses the inclusive clustering algorithm with the core scale defined in Eq. (5). The remaining predictions use the exclusive clustering algorithm: “scale 1” and “scale 2” correspond to the core scales defined in Eq. (8) and Eq. (9), respectively, while “scale 3” uses the default core scale described in Eq. (5) for the $Z\gamma$ core process

3.2.2 QCD core scale choice

After validating the stability of the MEPS@NLO method, here and in the next section the scale choices and variations will be discussed for a centre of mass energy of 13 $\,\mathrm {TeV}$. As before, all predictions are performed at shower level, meaning that hadronisation and multiple interactions are switched off explicitly. All phase space cuts for the 13 $\,\mathrm {TeV}$ analysis are summarised in Table 1.

Table 1 This table summarizes all cuts which define the differential cross section analysis for 13$\,\mathrm {TeV}$. The leading photon has to be isolated from all other particles by fulfilling the requirement $\sum _{\mathrm {\Delta }R<0.4} E < \epsilon _{\mathrm {iso}}E^{\gamma }$ where the sum includes all particles which have an angular distance of 0.4 or less to the photon axis. In addition, the photon is required to not come from a hadron decay. The leptons are dressed with all photons not coming from a hadron decay and within $\mathrm {\Delta }R < 0.1$

Different scale choices have been employed for $V\gamma$ production in the literature. Two of them are

$$\begin{aligned} \mu = \sqrt{{M_\mathrm {V}}^2 + {p_\perp ^\gamma }^2} \end{aligned}$$

(8)

and

$$\begin{aligned} \mu = \sqrt{0.5 \left( {M_\mathrm {V}}^2 + {p_\perp ^\gamma }^2 + {(p^{e^+}+ p^{e^-})_\perp }^2 \right) }. \end{aligned}$$

(9)

The former was used for the NNLO-QCD calculation of $V+\gamma$ in [27], the latter is inspired by [60] and was used e.g. in the NLO QCD+EW calculation [61] in a slightly modified manner.

Since this is a merged calculation it is not possible to use these scale definitions directly. However, the STRICT_METS scale setter also allows one to use custom scales for the core process. In order to use this possibility, the clustering has to be restricted such that it results in a $Z\gamma$ core process. This can be enforced by using the exclusive cluster mode which exactly reconstructs a possible shower history using QCD splittings only (see Sect. 2.1).

Altogether, four different scale choices are compared. The first one is inclusive, it uses the default settings of Sherpa as described in Sect. 3.1. By contrast, the three remaining setups make use of the exclusive cluster mode and use different core scales as defined in Fig. 4.

In Fig. 4 the differential $E_\perp ^\gamma$ distribution and the $p_\perp$ spectrum of the leading jet are compared for the four different scale schemes.

In the $E_\perp ^\gamma$ spectrum all scale choices are in good agreement and differ by not more than 10%. Switching from the default to the exclusive clustering algorithm does not make a large difference for this observable. This also holds for all other observables which where measured by ATLAS and are discussed later on in Sect. 3.3, those measurements do not allow us to discriminate between the different scale choices.

By contrast, the difference is much higher when looking at the $p_\perp$ spectrum of the leading jet. Here, all scale and cluster choices are in good agreement for low $p_\perp$ but differ as soon as $p_\perp$ exceeds 100$\,\mathrm {GeV}$. At large values at order of 1000$\,\mathrm {GeV}$ the difference reaches almost a factor of 2. There, the highest cross section corresponds to the core scale defined in Eq. (8) in combination with the exclusive cluster model, whereas the lowest cross section is given by the default settings. This is not surprising since such a high $p_\perp$ region probes configurations where the jet is harder than the typical scale of this process, e.g. the Z mass. Such configurations are unordered in terms of the parton-shower evolution variable and are thus very sensitive to the clustering definition. If here a $pp \rightarrow Z \gamma + n ~\mathrm {partons}$ core process is determined but the core scale is evaluated solely based on Z and $\gamma$, this scale will underestimate the physical scale and thus overestimate the strong couplings, resulting in a larger cross section.

However, based on the available information, there is no clear way to decide which cluster / scale settings are best suited for this process and the inclusive cluster settings are retained. Measuring the leading jet $p_\perp$ distribution in $Z\gamma$ events could greatly help to improve this situation.

Fig. 5

13$\,\mathrm {TeV}$ predictions for $E_\mathrm {T, inclusive}^\gamma$

Fig. 6

13$\,\mathrm {TeV}$ predictions for $m_{e^+ e^- \gamma }$

3.2.3 Scale and PDF variation uncertainties

In addition to the core scale variations studied above, independent variations of the $\mu _\mathrm {R}$ and $\mu _\mathrm {F}$ scales are performed. All replicas of the NNPDF set are used to estimate the PDF uncertainty. These variations are performed using on-the-fly weights [62] and include only contributions from the matrix elements but not from the shower.

All figures are structured as follows. Each figure has three ratio plots. The main plot and the first ratio plot point out the difference between MEPS@NLO and MEPS@LO. Here, the MEPS@NLO prediction is chosen as reference. By contrast, the additional subplots show the size of all performed scale variations for each method as a ratio with respect to the corresponding nominal prediction.

Figures 5 and 6 show predictions for $E_\perp ^\gamma$ and $M_{ll\gamma }$. The corrections between MEPS@LO and MEPS@NLO are almost flat at a level of 20%. As expected, the scale uncertainties are reduced when moving from MEPS@LO to MEPS@NLO. The factorisation scale dependency vanishes almost completely for $p_\perp ^\gamma \lesssim 60\,\mathrm {GeV}$ and $m_{ll\gamma }$ close to the Z peak, compared to 10% in the MEPS@LO case. The renormalisation scale uncertainty is reduced by roughly a factor of 2 for both observables, it shrinks from 20 to 10% for high $E_\perp ^\gamma$.

Figure 7 shows $H_\perp$, which is defined as the sum of the transverse momenta of all jets fulfilling the conditions defined in Table 1, $H_\perp = \sum _\mathrm {jets} p_\perp ^\mathrm {jet}$.

Fig. 7

13$\,\mathrm {TeV}$ predictions for $H_\perp =\sum _{\mathrm {jets}}p_\perp ^\mathrm {jet}$

Fig. 8

13$\,\mathrm {TeV}$ predictions for $p_\perp ^\mathrm {leading jet}$

Fig. 9

13$\,\mathrm {TeV}$ predictions for the jet multiplicity distribution

Here both the factorisation and the renormalisation scale uncertainties are reduced significantly for small $H_\perp$ but have almost the same size if $H_\perp$ exceeds $200\,\mathrm {GeV}$. The leading jet $p_\perp$ is depicted in Fig. 8 and shows a very similar behaviour. Again the renormalisation scale uncertainty is reduced from 15 to 5% for low $p_\perp ^\mathrm {jet}$ but does not change for values from 200$\,\mathrm {GeV}$ onwards. Finally, Fig. 9 shows the jet multiplicity. In the zero-jet bin the factorisation scale dominates when using MEPS@LO, this uncertainty vanishes almost completely when moving to MEPS@NLO. However, the one-jet bin is dominated by the renormalisation scale uncertainty. This uncertainty is reduced from 20 to 10% when moving to MEPS@NLO.

All of these observables only show minor improvements in the multi-jet regions. This is not surprising since observables which are sensitive to a high number of hard jets are hardly improved by the MEPS@NLO applied here. Only the zero- and one-jet matrix elements are calculated at next-to-leading order but the two- and three-jet calculations still have leading-order accuracy. Both $H_\perp$ and $p_\perp ^\mathrm {jet}$ are dominated at large values by multi-jet configurations and are thus described at leading-order accuracy only. This effect is reflected by the ratio between the MEPS@NLO and the MEPS@LO method, too. At low values of $H_\perp$ and $p_\perp ^\mathrm {jet}$ it amounts to 0.7 but increases to one for larger values.

3.3 Comparison with $\sqrt{s}=$8$\,\mathrm {TeV}$ measurements

Both, the stability and the reduction of the perturbative uncertainties have been demonstrated in the 13 $\,\mathrm {TeV}$ results in the last section. Now, the focus is on the comparison with recent experimental data and a study of the interplay between the smooth isolation criterion with the experimental one.

This section relies on a measurement of the ATLAS collaboration at 8$\,\mathrm {TeV}$[10], using 20.3 fb$^{-1}$ of data. In this measurement, final states with $ll\gamma$ and up to three jets are studied. Here, the focus lies on the $e^+ e^- \gamma + \mathrm {jets}$ final state. All cuts which define the extended, differential fiducial cross section are summarised in Table 2.

The first topic to be studied is the isolation criterion used by this analysis. As described in Sect. 2.3 our prediction uses the smooth cone isolation criterion. By contrast, the experimental isolation is based on anti-$k_\perp$-jets with $\mathrm {\Delta }R=0.4$. These jets include all particles except neutrinos and muons and are not required to fulfill the cuts described in Table 2. A photon is defined as isolated if either the nearest jet has an angular distance $\mathrm {\Delta }R>0.4$ to the photon axis or this jet’s transverse energy $E_\perp ^\mathrm {jet}$ fulfils

$$\begin{aligned} \frac{E_\perp ^\mathrm {jet} - E_\perp ^\gamma }{E_\perp ^\gamma } = \epsilon _\mathrm {exp} < \epsilon _\mathrm {max}. \end{aligned}$$

(10)

Table 2 This table summarizes all cuts which define the extended, fiducial cross section in the measurement [10]. Leptons are dressed with all photons having an angular distance of $\mathrm {\Delta }R<0.1$

Even if one assumes that both the final jet $E_\perp$ and its direction are in perfect agreement with the closest parton $E_\perp$ at matrix-element level, this criterion differs from the one used in our calculation and described in Sect. 2.3 when going to lower angular distances.

As a consequence, two different parameter sets for the smooth isolation criterion are compared. The first set is based on the 2013 Les Houches report [51] which recommends the usage of the smooth isolation criterion for fixed-order calculations if the parameters are matched to the experiment. Following this, the parameters are $R=0.4$, $n=1$ and $\epsilon =0.5$. However, since this is not a fixed-order calculation, the smooth isolation criterion is used only at matrix-element level and in the subsequent final state analysis the experimental cut has to be passed additionally.

Fig. 10

Comparison of two different parameter sets using the smooth isolation criterion at a centre of mass energy of 8$\,\mathrm {TeV}$

Fig. 11

$E_\perp ^\gamma$ spectrum measured by ATLAS in $pp\rightarrow e^+e^- \gamma$ at 8$\,\mathrm {TeV}$, compared for MEPS@LO and MEPS@NLO

Fig. 12

$m_{ll\gamma }$ measured by ATLAS in $pp\rightarrow e^+e^- \gamma$ at 8$\,\mathrm {TeV}$, compared for MEPS@LO and MEPS@NLO

The second parameter set is thus chosen more inclusively in R, here $R=0.1$, $n=2$ and $\epsilon =0.1$. Such a setup also reflects the requirement that experiments want to generate event samples to be as universal as possible, usable not only as signal process but also as background for many other measurements.

In Fig. 10 both these parameter sets are compared with the $E_\perp ^\gamma$ spectrum measured by ATLAS. Both predictions are in good agreement with the data but the more inclusive set gives a slightly higher cross section. This is most obvious in a $p_\perp ^\gamma$ region of around 70$\,\mathrm {GeV}$, there the difference reaches almost 10%. Although it is expected that the first set with $R=0.4$ may miss some contributions due to the smoothing of the cone, it is not guaranteed that the second set gives a more accurate prediction. A more inclusive parton-level isolation always allows configurations which come closer to the collinear, non-perturbative region. This region cannot be described without fragmentation functions or QED parton-shower matching [63]. However, this is not expected to happen if the angular distance is large enough and thus the inclusive parameter set is used in the following.

All measured observables are shown in Figs. 11, 12. The plots are structured in the same way as in Sect. 3.2.3. Both methods, MEPS@LO and MEPS@NLO, are compared to the data and directly to each other. In the main plot and the first ratio plot both the MEPS@LO and the MEPS@NLO predictions are compared to the measured data. In addition, two further ratio plots show the impact of the described perturbative variations. In contrast to the first ratio plot the respective nominal prediction is chosen as reference here since this simplifies a direct comparison of both methods.

Fig. 13

Jet multiplicity measured by ATLAS in $pp\rightarrow e^+e^- \gamma$ at 8$\,\mathrm {TeV}$, compared for MEPS@LO and MEPS@NLO

In almost all observables the MEPS@NLO prediction is in excellent agreement with the data. A small deviation is found in the invariant mass prediction with zero jets in a region around 250 GeV. The MEPS@NLO differential cross sections are about 20% larger with respect to the MEPS@LO results at small scales. At large scales the difference gets smaller since the contribution of the additional LO jets is increasing.

As already seen in the 13 $\,\mathrm {TeV}$ section, the uncertainties estimated by the scale variations are reduced when moving from MEPS@LO to MEPS@NLO. At MEPS@LO, for lower values of $E_\perp ^\gamma$ and $m_{ee\gamma }$ the factorisation scale is the dominant source of uncertainty and reaches up to 10%. This is reflected in the zero jet bin of Fig. 13, too. By contrast, in the MEPS@NLO case this uncertainty is removed almost completely. At higher values of $E_\perp ^\gamma$ or $m_{ee\gamma }$ the renormalisation scale uncertainty takes over in all inclusive observables and reaches values of 10–20 % in the MEPS@LO case. This uncertainty is reduced for MEPS@NLO to 5–10% in both large $E_\perp ^\gamma$ and the lower jet multiplicity bins. Both, the size of the corrections and their uncertainties behave very similarly between 8 and 13 $\,\mathrm {TeV}$.

In contrast to the 13 $\,\mathrm {TeV}$ section, here an additional comparison with an inclusive $Z\gamma$ NLO calculation matched to the parton shower is performed. The MC@NLO method [41] as implemented in Sherpa [39] is used with the same settings as for MEPS@NLO but the NLO PDF set. The most significant difference between the multileg-merged and NLO-matched methods can be seen in the jet multiplicity distribution, shown in Fig. 13. In the MC@NLO simulation the two- and three-jet bins are only generated by the parton shower which cannot describe hard jet production properly. The same situation holds for large $E_\perp ^\gamma$, as a hard photon is likely to be produced in conjunction with several hard jets.

4 Interplay with Z+jets production and QED final state radiation

4.1 Motivation

When predictions for $V\gamma$ production are used in experimental searches to determine background contributions, they have to be combined with predictions for V + jets production in several cases. A jet from the V + jets sample can be misidentified as a photon at the detector level and thus contribute to the $V\gamma$ event selection. Another example is a selection requiring multiple leptons, if the photon is misidentified as an electron.

At the same time the two types of MC samples are not exactly complementary: the simulation of QED final state radiation (FSR) from the leptons in the V + jets sample generates a fragmentation contribution also contained in the FSR-like diagrams of the $V\gamma$ process. It is obvious that this overlap has to be removed before the samples can be used for background estimation.

This combination of V and $V\gamma$ samples can be achieved by means of a QED merging as introduced in [63]. However, due to the smallness of the corresponding QED Sudakov suppression, it is not necessary to use an elaborate implementation of such a QED merging within MEPS@NLO samples. Instead, it suffices to define a more simple overlap removal prescription for the case discussed in this publication.

This overlap removal is a conceptually straightforward requirement, which is complicated by two facts. The QED FSR photons in the V+jets simulation are produced at the hadron level and can thus not simply be subjected to parton-level cuts matching the ones in the $V\gamma$ simulation. Furthermore the photon cuts in a multi-jet merged sample of $V\gamma$+jets require an isolation of the photon with respect to partons from the multi-jet matrix elements. This constraint has to be respected when defining the complementary cuts for the V+jets sample.

An implementation of such an overlap removal at the event generation level is discussed in this section using the example of $V=Z$.

4.2 Implementation of overlap removal

In order to combine Z and $Z\gamma$ events⁴ the phase space is split into two regions. The $Z\gamma$ process includes photons directly in the matrix elements. The phase space of this region should be as large as possible but is limited since the matrix elements diverge when the photon is soft or collinear either to a massless lepton or quark.⁵ By contrast, photons generated by YFS in Z events do not have these limitations, but cannot describe initial state radiation which usually gives most of the contribution to hard photons.

In principle, the phase space slicing is defined by three components. First, a $p_\perp ^{\gamma }$ cut, secondly a lepton photon isolation and finally a photon–hadron isolation. These cuts exclude a region where collinear or soft divergences are present and no fixed-order calculation in QCD is possible. Thus, an $Z\gamma$ event has to pass all these cuts while a Z event has to fail at least one of them.

In case of $Z\gamma$ events, there are already cuts at matrix-element level present and it would be desirable to use them directly for the overlap removal. Unfortunately, this is not possible since the generation of additional final state photons via YFS happens technically after the parton shower. The shower can shift the kinematics of all particles, thus cutting once before and once after the shower would result in a mismatch. As a consequence, the slicing cuts are applied to both Z and $Z\gamma$ events at hadron level.

Hadron-level cuts are not supported by Sherpa out-of-the-box. For this study, a support for custom modules was implemented which makes it possible to veto events at the hadron level very flexibly. This feature will be available within the next Sherpa release.

Fig. 14

Demonstration of multiple-photon effects in $Z\gamma$ events using two kinds of photon selections as described in the text. The only analysis cut is $p_\perp ^\gamma >10~\,\mathrm {GeV}$. The generation cuts are $p_\perp ^\gamma >4\,\mathrm {GeV}$, $\mathrm {\Delta }R(\mathrm {lepton},\gamma )>0.05$ and an isolation cut with $R=0.1$, $n=2$ and $\epsilon =0.1$

Special care has to be taken when selecting the photon and leptons which take part in the slicing procedure. Non-prompt leptons and photons can easily be produced by the decay of hadrons and there is no requirement that these additional particles are softer than the particles coming directly from the hard interaction or the YFS algorithm. However, it has to be guaranteed that all divergences which are present at matrix-element level are covered by the slicing cuts since otherwise the result would still depend on the matrix-element level cuts.

As a consequence, the hardest photon which does not come from a hadron decay is used for the definition of the slicing variables. The photon–lepton isolation is applied only to prompt leptons. For the hadronic isolation all particles excluding the prompt leptons and the photon are taken into account.

Table 3 This table summarizes all cuts which define the phase space region which is used for testing the introduced overlap removal procedure

It should be noted that it cannot be guaranteed that this photon selection indeed chooses the direct photon from the matrix element and not any further photon from final state radiation. The latter ones are not ordered in $p_\perp$ and selecting one of them would introduce a dependency on the generation cut. This behaviour was studied in the $p_\perp ^\gamma$ spectrum of $Z\gamma$ events including additional final state radiation. Two kinds of photon selections are compared. In the first approach always the hardest photon is chosen, no matter whether it stems from the direct production or from additional FSR. The second method uses $\mathrm {\Delta }R$ matched photons to identify the final state photon which is closest to the original matrix-element photon in angular space. Both spectra are shown in Fig. 14 and agree at the percent level, thus any bias on the overlap-removed result due to the photon choice will be negligible.

In the following, isolated photons are required to fulfill $p_\perp >10\,\mathrm {GeV}$, a photon–lepton isolation of $\mathrm {\Delta }R > 0.4$ and the hadronic isolation using a smooth cone isolation with $R=0.4$, $n=1$ and $\epsilon =0.5$.

4.3 Results

The validation of the overlap removal algorithm proceeds with analyses in three different phase space regions. Both the $Z\gamma$ and the Z prediction should not be altered by the overlap removal in their regions of validity. The first condition is checked using the $Z\gamma$ analysis introduced in Sect. 3.2. It covers the explicit $Z\gamma$ phase space and defines region i. By contrast, the Z phase space is probed by the default inclusive Z analysis provided by Rivet. Here, a reconstructed Z boson with an invariant mass between 65 and 115$\,\mathrm {GeV}$ is required. The leptons are dressed with all photons having an angular distance of 0.2 or smaller. These cuts define the phase space region ii.

In addition, a special region iii is defined where final state radiation contributions via YFS are supposed to give similar contributions as the direct production from matrix elements. Having such a region it is directly possible to study the interplay between both components of the overlap removal and compare their sum with a pure YFS or direct sample.

Table 4 Slicing parameters which are used for validation of the overlap removal procedure. These cuts are applied according to the procedure defined in Sect. 4.2

Fig. 15

Comparison of the overlap removal procedure (OR) with a pure $Z\gamma$ and a pure Z sample in the $Z\gamma$ control region (region i)

Fig. 16

Comparison of the overlap removal procedure (OR) with a pure $Z\gamma$ and a pure Z sample in the inclusive Z control region (region ii)

Fig. 17

Comparison of the overlap removal procedure (OR) with a pure $Z\gamma$ and a pure Z sample in a final state radiation dominated test region (region iii). $\mathrm {\Delta }R_{\gamma e^\pm }$ refers to the angular distance between the photon and the closest electron/positron

Fig. 18

Comparison of the overlap removal procedure (OR) with a pure $Z\gamma$ and a pure Z sample for further observables in a final state radiation dominated test region (region iii)

A region dominated by final state radiation is defined by requiring the lepton pair to have an invariant mass below the Z peak, $30\,\mathrm {GeV}< m^{ll} < 87\,\mathrm {GeV}$. An event is accepted, if both leading leptons have electron flavour but opposite charge. As photon candidate the leading photon ($p_\perp ^\gamma > 5\,\mathrm {GeV}$) is chosen, it has to be isolated from the selected leptons by requiring $\mathrm {\Delta }R^{\gamma , e^\pm } > 0.05$. In addition, the total energy of all remaining particles (excluding the selected leptons) in a cone with $\mathrm {\Delta }R<0.4$ around the photon axis has to be less than $0.5 \cdot E_\perp ^\gamma$. Details of all analyses are summarised in Table 3. All cuts and observables are implemented as a user module using the Rivet framework.

A comparison is performed using four sets of separately generated event samples; pure $Z\gamma$, pure Z, sliced Z and sliced $Z\gamma$. The latter two are summed up to give the total prediction after overlap removal. YFS is set active for all samples.

For event generation, the matrix-element level cuts are selected to be more inclusive than the analysis cuts. For the generation of the sliced direct part, the matrix level cuts are additionally chosen to be more inclusive than the phase space slicing parameters. All events are generated with $Q_\mathrm {CUT}=30$ $\,\mathrm {GeV}$ and up to three jets at leading-order accuracy.⁶ The slicing parameters which are used for this test are summarised in Table 4.

In Fig. 15, the inclusive jet multiplicity and the inclusive $E_\perp ^\gamma$ spectrum for the $Z\gamma$ phase space (region i) are shown. In these and all further plots the inclusive Z, the direct $Z\gamma$ and the summed overlap-removed predictions are shown, together with the corresponding components in the overlap removal. For better readability the statistical uncertainties of the latter have been omitted.

Here, the overlap removal result is in very good agreement with the pure $Z\gamma$ prediction in both plots. The dominating contribution is the $Z\gamma$ component, giving about 90% of the cross section for low $p_\perp$ and almost 100% if $p_\perp$ exceeds 80$\,\mathrm {GeV}$.

By contrast, the inclusive Z phase space (region ii) is dominated by the Z component. The Z mass and Z $p_\perp$ distributions are shown in Fig. 16. The overlap removal result is in excellent agreement with the pure Z prediction. The only region of phase space where the direct component of the overlap removal is sizeable is the low mass region of less than 85$\,\mathrm {GeV}$, there the direct component gives around 10% of the cross section.

Despite the good agreement between overlap removal and the respective reference, one might want to construct the overlap removal to require only the $Z\gamma$ component when looking at $Z\gamma$ analyses. This would require one to take into account the analysis cuts for slicing the phase space and is thus not possible in a generic sample. An overlap-removed contribution with inclusive Z production allows more flexibility as needed in general purpose experiments.

Finally, in Figs. 17 and 18 some observables of the FSR dominated phase space (region iii) are shown. In this region neither the pure Z nor the pure $Z\gamma$ predictions are guaranteed to give an accurate result. The former one includes only final state radiation and will therefore miss contributions especially in the high $E_\perp$ region. By contrast, the latter one includes all contributions at a fixed order but may fail to describe the region where the photon is soft or very close to the lepton. Thus, both these predictions can only be interpreted as lower and upper bounds for the overlap removal in the context of this validation.

In Fig. 17, different $E_\perp ^\gamma$ spectra are shown. The first subplot covers the whole phase space, while the two remaining ones cover only the regions where the photon is either very close to ($0.05<\mathrm {\Delta }R<0.5$) or separated from ($0.5< \mathrm {\Delta }R<3$) the closest lepton. While in the inclusive plot the two components of the overlap removal procedure give a very similar contribution if $E_\perp ^\gamma$ exceeds the slicing cut, the two remaining plots reveal the nature of the overlap removal procedure much better. Whereas the low $\mathrm {\Delta }R$ region is entirely dominated by the Z component, the high $\mathrm {\Delta }R$ region is dominated by the $Z\gamma$ component as soon as the cut-off is exceeded.

Figure 18 shows the azimuthal angle between the photon and its closest lepton and the invariant mass of the photon and both leptons. Both observables show an interesting behaviour. As expected, the cross section of the combined overlap removal result always interpolates between the cross section of the pure $Z\gamma$ and the pure Z sample. When looking at the azimuthal distance, the Z component dominates at lower and the $Z\gamma$ component at higher values, while both components are equal in a large region of phase space. The invariant mass spectrum is dominated at lower values ($<105$ $\,\mathrm {GeV}$) by the Z component and at higher values by $Z\gamma$.

5 Conclusions

Precise Standard Model predictions for $Z\gamma$ + jets production are crucial for the search for new particles or anomalous couplings in measurements of this final state at the LHC.

With the presented simulation within the Sherpa framework using the MEPS@NLO algorithm we provide a simulation which is at the same time precise and realistic: NLO QCD corrections for the $Z\gamma$ and $Z\gamma$ + jet processes are included and reduce the uncertainties in relevant observables significantly. At the same time, the matching and merging with the parton shower allows a realistic simulation of the full final state at the hadron level, and the inclusion of all off-shell effects allows one to place realistic experimental cuts on the prompt leptons without approximations.

Comparing to data from experimental measurements at $\sqrt{s}=8\,\mathrm {TeV}$ we find very good agreement. On that basis we make predictions at $\sqrt{s}=13\,\mathrm {TeV}$ and identify the dominant theoretical uncertainties and the phase space regions affected by them.

To further the application of these precise $Z\gamma$+jets predictions in experiments we also demonstrate how they can be combined with event generator predictions for Z+jets including final-state photon radiation. As a validation we introduce a number of cross checks based on different phase space regions which can be repeated for any specific application of such samples in the experiments.