1 Introduction

The proposed International Linear Collider (ILC) [1] which could collide \(e^+\) and \(e^-\) at a centre-of-mass energy of several hundred GeV, if built, would serve as an instrument for precision measurements of various parameters underlying particle physics and the dedicated study has published a five-volume Technical Design Report (for the physics part, see Ref. [2], and for the detector, see Ref. [3]). The purpose of the ILC, and indeed of other proposed high energy \(e^+e^-\) colliders, such as the Compact Linear Collider (CLIC) [4, 5] the Future Circular Collider (FCC-ee) [6, 7] and the Circular Electron Positron Collider (CEPC) [8] is to study the properties of the Standard Model (SM) at high precision in order to validate its predictions as well as to find deviations, if any, and to discover particles and interactions that lie Beyond the Standard Model (BSM). Deviations from SM predictions would arise because of virtual loop effects of particles too heavy to be produced, or indeed due to new interactions which would give rise to terms in the low-energy effective action modifying interaction vertices. Amplitudes from such vertices could interfere with SM amplitudes and produce deviations from its predictions, and could possibly give rise to correlations that are forbidden by the symmetries of the SM when SM particles are observed in the detectors with high-precision measurements of their kinematic and other properties. A dedicated study of the benefits of a strong beam polarization program, of one or both beams, as well as of the benefits of transverse and longitudinal beam polarization, has also been carried out some years ago in the context of the ILC [9]. An important new compendium of physics at the ILC is the review in Ref. [10].

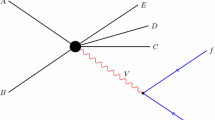
A useful approach that has been applied in the context of BSM physics searches at \(e^+e^-\) colliders relies on the classification of new physics in terms of its space-time transformation properties using, e.g., one-particle [11] inclusive distributions \(e^+ e^-\rightarrow h(p) X\), where h denotes a particle that is detected, and p is its momentum. The new physics is lumped into ‘structure functions’ that are inspired by analysis used in deep-inelastic scattering. It has also been extended in the context of a two-particle inclusive process [12] \(e^+ e^-\rightarrow h_1(p_1) h_2(p_2) X\), where \(h_1\) and \(h_2\) denote two particles that are detected, and \(p_1\) and \(p_2\) are their respective momenta, and the process is called the basic process (I). The two-particle inclusive process is depicted in Fig. 1, while the one-particle process can be considered a special case where only one of the particles is detected and the other is included in X.

Fig. 1
figure 1

The basic process (I)

Full size image
Fig. 2
figure 2

The basic process (II)

Full size image

This approach is model independent and is based only on Lorentz covariance for deriving the most general form of one-particle and two-particle kinematic distributions. It was found that the two-particle case provides more information than the single-particle case as discussed in detail in Ref. [12], and, in principle, this could be extended to an n-particle inclusive framework, with a rapid rise in complexity. Our formalism is restricted to envisaging new physics only through an s-channel exchange, i.e., that (i) the SM contribution is assumed to be through the tree-level exchange of a virtual photon and a virtual Z, and that (ii) the BSM effects could arise through the exchange of a new particle like a new gauge boson \(Z'\), or through the exchange of Z, but a with a BSM vertex or a SM loop producing the final state in question, or through a new scalar or tensor exchange in the s channel. Our work above is an extension of the work of Dass and Ross [13, 14], which had been performed in the context of \(\gamma \) contributing to the s-channel production, probing the then undiscovered neutral current. As discussed extensively in Refs. [11, 12], our work in practice is the inclusion of Z in the s-channel, in addition to \(\gamma \), and where now it is BSM physics that we intend to fingerprint. Moreover, the results can be applied to a more general situation where the interference need not be between SM and BSM amplitudes, but any two amplitudes, one of which is characterized by the exchange of a spin-1 particle, and the other characterized by scalar, pseudo-scalar, vector, axial-vector or tensor interactions.

Many studies of such manifestations of BSM physics rely on the measurement of an exclusive final state for which there are definite predictions in the SM, and/or definite predictions within the framework of effective Lagrangians, or effective BSM vertices. An early work in this regard in the context of the ILC is Ref. [15], where it was shown that transverse polarization plays a key role in uncovering CP violation due to BSM physics due to scalar (S), pseudo-scalar (P) and tensor (T) type interactions, when no spins are measured. This work was inspired partly by even earlier work done for LEP energies; see Ref. [16].

The question then arises as to how one may be able to probe BSM physics further with one-particle inclusive distributions, in the event that its spin has been measured. Keeping in mind that spin measurement is actually performed by further decays of the particle in question, such a scenario is really a quasi-one-particle inclusive process. Nevertheless, the availability of a second final-state momentum vector as in the two-particle inclusive case is what renders it a more powerful probe. On the other hand, a single-particle inclusive measurement with the measurement of spin of the particle along a specific quantization axis may provide a second vector and thereby play an important role in uncovering BSM physics. Whereas in Ref. [14], the possibility of measuring the spin of the particle in a one-particle inclusive measurement \(e^+ e^-\rightarrow h(p,s) X\), where h and s denote the SM particle that are detected, and h and s are its momentum and spin respectively, has been considered, it had not been considered in Ref. [12]. This is called the basic process (II) and is depicted in Fig. 2.

We also note here that in the recent past, numerous investigations have been made in the context of exclusive processes at the ILC, where it has been shown that the measurement of the final-state spin can also be an excellent probe of BSM physics. We had considered specific exclusive processes and had concluded that many types of BSM interactions reveal themselves only when the spin of one of the final-state particles is resolved. For instance, in order to separately resolve BSM contributions from scalar and tensor type couplings in \(e^+e^-\) collisions with transversely polarized beams, one has to resolve the spin of the top quark in \(t \overline{t}~\)production [17, 18].Footnote 1 Early work on the necessity to resolve the final-state spins in the context of \(\tau ^+\tau ^-\) production at significantly lower energies to probe the presence of anomalously large magnetic moments and possible electric dipole moments of the \(\tau \)-lepton are Refs. [22, 23]. (For a general and interesting discussion see Ref. [24].) In the present work, for purposes of illustration, we introduce these sources of BSM physics to provide a concrete framework wherein we can make some remarks about the resulting structure functions derivable from such an exclusive process.

It is usual practice to study the dependence of a process on the spin of a produced particle by restricting to a single spin-quantization axis, typically, the momentum direction of the particle. In this case, what is accessible is the probability of production of the particle with a definite helicity. However, this corresponds to only the diagonal element of the spin density matrix. In order to study the full spin structure of amplitudes, one needs also off-diagonal elements of the spin density matrix, or equivalently, the polarization information for two other mutually orthogonal spin-quantization axes. This approach has been advocated earlier, for example, in Refs. [25, 26] in the context of top-pair production at an \(e^+e^-\) collider and in [27] for single-top production at the Large Hadron Collider. Single-top production itself is an interesting process in itself; for a review, see Ref. [28]. Single-top production at CLIC has been studied in Ref. [29].

Keeping in mind these considerations, for the purposes of this work we confine ourselves to an inclusive, massive spin-1/2 fermion, where we now employ the three suitably chosen axes explicitly. We note here that the considerations of Ref. [14] remained general in the choice of the spin-quantization axis. In the present work, we present results for the three different quantization axes. In practice, this is made possible by the fact that the two types of processes are closely related: the single-particle inclusive process with spin measurement is closely related to the two-particle inclusive process with suitable identification of vectors entering the definition of the structure functions. Thus, by employing the standard techniques as in Ref. [11,12,13,14] we can proceed with the analysis of the single-particle inclusive measurement with spin resolution. As in our earlier work, significant new features arise due to the presence of the axial-vector coupling of the Z to the electron, a feature missing in a vector theory like QED, as in the considerations of Ref. [14], and an extensive discussion can be provided on the features of the correlations for the three specific quantization axes. In all considerations of the top-quark spin resolution at the LHC as Ref. [27] or at the ILC, as well as in \(\tau -\hbox {spin}\) reconstruction as in the work discussed here, it can only be done from the distributions of its decay products and typically taken in the rest frame of the top quark, by looking at the angular distribution of a decay product about the quantization axis. This, of course, is independent of the environment in which the top quark is produced, whether it is in a hadron collider or an \(e^+e^-\) collider, and whether or not in the hadron collider it is pair or singly produced. Analogous considerations apply also to the \(\tau \)-lepton. For reviews of approaches to these issues, see Refs. [30,31,32,33,34].

As in the past, once a general discussion is provided for an inclusive final state, it may be readily applied to exclusive final states as well, thereby providing a framework for discussing several processes of interest. The expectations from our general model-independent analysis are compared for some specific processes with the results obtained earlier for those processes. Our approach would thus be useful to derive general results for newer processes which fall within the framework described above. Thus, what is presented here is the result of a detailed calculation for each individual process.

We also note that many of the considerations that have been spelled out for the ILC also apply to the other planned facilities, namely CLIC, FCee and CEPC.

The structure of this paper is as follows: In the next section we include some preliminaries about the inclusive process, the kinematics and a discussion of the choice of spin-quantization axes. In Sect. 3 we present a computation of the spin–momentum correlations resulting from the presence of structure functions that characterize the new physics. Our results here are presented in the form of results arising from the computation of a trace that encodes the leptonic tensor as well as the new physics encoded in a tensor constructed out of the momenta of the observed final-state particles (which is known as a ‘hadronic’ tensor, for historical reasons, since the term arose at a time when the final state consisted largely of hadrons). These tables provide the analog, for the SM and new physics, of what was provided by Dass and Ross [14] for QED and neutral currents. In Sect. 4 we discuss the CP and T properties of correlations for different classes of inclusive and exclusive final states. We provide a discussion of the polarization dependence of the correlations in different cases. In Sect. 5 we will specialize to specific examples of processes, into which our approach can give significant insight. In Sect. 6 we present our conclusions and discuss prospects for extension of the present framework to account for classes of BSM interactions not presently covered.

2 The process and kinematics

We consider the two-particle inclusive process and the one-particle spin-resolved process

$$\begin{aligned} e^-(p_-) + e^+(p_+) \rightarrow h(p,s) X, \end{aligned}$$
(1)

where h is the final-state particles whose momentum p and spin s are measured, X is an inclusive state. The process is assumed to occur through an s-channel exchange of a photon and a Z in the SM, and through a new current whose coupling to \(e^+e^-\) can be of the type V, A, or S, P, or T. Since we will deal with a general case without specifying the nature or couplings of h, we do not attempt to write the amplitude for the process (1). We will only obtain the general form, for each case of the new coupling, of the contribution to the angular distribution of h from the interference of the SM amplitude with the new-physics amplitude. It might be clarified here that even though we use the term “inclusive”, implying that no measurement is made on the state X, in practice it may be that the state X is restricted to a concrete one-particle or two-particle state which is detected. In such a case the sum is not over all possible states X. Nevertheless, the momenta of the few particles in the state X are assumed to be integrated over, so that there is a gain in statistics as compared to a completely exclusive measurement. The angular distributions we calculate hold also for such a case, except that structure functions would depend on the states included in X.

Fig. 3
figure 3

Representation of the momentum and spin vectors in the laboratory frame. The left panel depicts the electron and positron momenta, respectively, \(\vec p_-\) and \(\vec p_+\), their respective transverse spin vectors \(\vec s_-\) and \(\vec s_+\), which lie along the positive and negative x-axis, respectively, the momentum \(\vec p\) of the detected particle and the spin-quantization axis that is denoted by \(\vec s\). The right panel depicts the three different spin-quantization axes \(\vec s\), \(\vec n\) and \(\vec t\) defined in the text. In both panels, the axes \(x'\) and \(y'\) denote axes obtained by rotation of the x and y axes about the z axes through an angle \(\phi \)

Full size image

The following symbols have been used by us in various stages of the computations and we present here a comprehensive list of these definitions. We define \(q=p_-+p_+\), \(\vec K\equiv (\vec {p}_- - \vec {p}_+)/2= E \hat{z}\), where \(\hat{z}\) is a unit vector in the z-direction, E is the beam energy, and \(\vec {s}_\pm \) lie in the x-y plane.

We now turn to the important question of the choice of three linearly independent vectors which will define the quantization axes. Although the decay distributions of the top quark are correlated to the spin in the top-quark rest frame, our choice of vectors is in the laboratory, or \(e^+e^-\) c.m. frame. It is assumed that all the kinematic information would be available which would allow one to construct any quantity of interest for the event sample. In particular, it may be noted that this choice would suffice for the full analysis of the top-quark polarization for which the SM would have definite predictions, and it could also be used in other contexts, such as anomalous couplings, or any kind of BSM physics.

In the \(e^+e^-\) center-of-mass frame, the spin vectors have components given by

$$\begin{aligned}&s^\mu \equiv \frac{1}{m} ( | \vec p |, E_p {\hat{p}} ),\end{aligned}$$
(2)
$$\begin{aligned}&n^\mu \equiv \frac{1}{2E\sin \theta }( 0, {\hat{p}} \times (\vec p_- - \vec p_+) ),\end{aligned}$$
(3)
$$\begin{aligned}&t^\mu \equiv ( 0, - {\hat{p}} \times \vec n ), \end{aligned}$$
(4)

where \(P = \vert \vec p \vert \) and \(E_p = \sqrt{P^2 + m^2}\). In covariant notation,

$$\begin{aligned} n_\mu\equiv & {} \frac{1}{\sqrt{q^2(4 (p\cdot p_-)( p\cdot p_+) - m^2 q^2)}}\epsilon _{\mu \nu \alpha \beta } p^\nu (p_-+p_+)^\alpha (p_+-p_-)^\beta , \nonumber \\\end{aligned}$$
(5)
$$\begin{aligned} t_\mu\equiv & {} \frac{1}{\sqrt{q^2(4 (p\cdot p_-)( p\cdot p_+) - m^2 q^2)}} \left[ \displaystyle \frac{ p\cdot (p_- - p_+)q^2}{\sqrt{(p\cdot q)^2 - m^2 q^2}} p_\mu \right. \nonumber \\&+\, \sqrt{(p\cdot q)^2 - m^2q^2} \, (p_- - p_+)_\mu \nonumber \\&\left. +\, \displaystyle \frac{p\cdot q\,p\cdot (p_+ - p_-)}{\sqrt{(p\cdot q)^2 - m^2 q^2}} (p_- + p_+)_\mu \right] . \end{aligned}$$
(6)

Note that \(\theta \) is the angle of h with respect to the beam direction, and \(\phi \) is the azimuthal angle where the x-axis is chosen as the direction of the transverse polarization of the \(e^+\) and \(e^-\) beams. Note that the symbol h(p, s) is a generic symbol, where the spin s could stand for the measurement of the spin along any one of the three quantization axes of choice.

The three-vectors \(\vec n\) and \(\vec t\) in the laboratory frame are actually quite simple:

$$\begin{aligned} \vec {n} \equiv (\sin \phi , - \cos \phi , 0) \end{aligned}$$
(7)

and

$$\begin{aligned} \vec {t} \equiv ( - \cos \theta \cos \phi , -\cos \theta \sin \phi , \sin \theta ). \end{aligned}$$
(8)

\(\vec n\) is along a direction perpendicular to both the momentum \(\vec p\) of h and the beam direction; see for example Ref. [35]. On the other hand, \(\vec t\) is in the plane of the beam direction and \(\vec p\), though perpendicular to the latter. For ease of visualization, we have represented the vectors in Fig. 3.

As in the past, we calculate the relevant factor in the interference between the standard model currents with the BSM currents as

$$\begin{aligned}&{\mathrm{Tr}}\left[ \left( 1-\gamma _5 h_++ \gamma _5 s /_+\right) p /_+\gamma _\mu \left( g_V^e-g_A^e \gamma _5\right) \right. \nonumber \\&\quad \left. \left( 1+\gamma _5 h_-+\gamma _5 s /_-\right) p /_-\Gamma _i\right] H^{i\mu }. \end{aligned}$$
(9)

Here \(g_V^e, g_A^e\) are the vector and axial-vector couplings of the photon or Z to the electron current, and \(\Gamma _i\) is the corresponding coupling to the new-physics current, \(h_{\pm }\) are the helicities (in units of \(\frac{1}{2}\)) of \(e^{\pm }\), and \(s_{\pm }\) are, respectively, their transverse polarizations. For ease of comparison, we have sought to stay with the notation of Refs. [13, 14], with some exceptions which we spell out when necessary. We should, of course, add the contributions coming from photon exchange and Z exchange, with the appropriate propagator factors. However, we give here the results for Z exchange, from which the case of photon exchange can be deduced as a special case. The tensor \(H^{i\mu }\) stands for the interference between the couplings of the final state to the SM current and the new-physics current, summed over final-state polarizations, and over the phase space of the unobserved particles X. It is only a function of the momenta q, p and s (or n or t). The implied summation over i corresponds to a sum over the forms V, A, S, P, T, together with any Lorentz indices that these may entail.

3 Computation of correlations

We now determine the forms of the matrices \(\Gamma _i\) and the tensors \(H^{i\mu }\) in the various cases, using only Lorentz covariance properties. Our additional currents are as in Refs. [13, 14], except for the sign of \(g_A\) in the following. We explicitly note that in our convention is \(\epsilon ^{0123}=+1\). We set the electron mass to zero. Consider now the three cases where the BSM physics could be of the scalar and pseudo-scalar type, vector and axial-vector type or tensor type. Note that, in each case, \(H^{i\mu }\) can be independent of the spin vector (s, n or t), or linearly dependent on the spin vector. The linear dependence can arise either from the spin vector entering the tensor structure or from a simple multiplicative factor \(q\cdot s\) (\(q\cdot n\), \(q\cdot t\) being zero in the center-of-mass frame). We explicitly include the tensors which involve the spin vector. But we do not show the spin vector entering through a factor of \(q\cdot s\), as this would have the same distribution as the spin-independent tensor. It is thus understood that, in what follows, each spin-independent structure function, say F, should be actually replaced by \(F + F' (q\cdot s)\), where \(F'\) is another structure function.

1. Scalar and pseudo-scalar case

In this case, there is no free Lorentz index for the leptonic coupling. Consequently, we can write it as

$$\begin{aligned} \Gamma = g_S + i g_P \gamma _5. \end{aligned}$$
(10)

The tensor \(H^{i\mu }\) for this case has only one index, viz., \(\mu \). Hence the most general form for \(H^S_\mu \) isFootnote 2:

$$\begin{aligned} H^{S}_\mu = r_\mu F^r, \end{aligned}$$
(11)

where r is chosen from p, and the spin vectors s, n and t, corresponding, respectively, to longitudinal polarization, transverse polarization perpendicular to the production plane, and transverse polarization in the production plane. Here \(F^r\) denotes the relevant structure functions we encounter and is a function of invariants \(q^2\) and \(p\cdot q\). In fact, all the structure functions introduced in the above, as well as those to be introduced in the following, are functions of the same Lorentz invariants \(q^2\) and \(p\cdot q\). The dependence of the functions on \(q^2\) and \(p\cdot q\) encodes the dynamics of the BSM interactions. In particular, they would contain propagators and form factors occurring in the BSM amplitudes. It may be noted that these definitions can result in an unconventional phase for the spin vectors, and will have implications to our analysis of spin–momentum distributions and their properties implied by the CPT theorem: it would imply that relative to the momentum the spin vectors would have required an additional factor of i in the definition of the structure functions in the usual correspondence between \(\hbox {CPT}=-1\) distributions and the appearance of imaginary parts of these structure functions [36]. (For another useful review, see Ref. [37].)

2. Vector and axial-vector case

The leptonic coupling for this case can be written as

$$\begin{aligned} \Gamma _\nu = \gamma _\nu (g_V - g_A \gamma _5). \end{aligned}$$
(12)

Note that we differ from Dass and Ross [13, 14] in the sign of the \(g_A\) term, in order to be in line with the convention for the standard neutral current coupling of the SM, which was established well after the work in Refs. [13, 14]. The tensor H for this case has two indices and can be written as

$$\begin{aligned} H^V_{\mu \nu }= & {} -g_{\mu \nu } W_1 + {1\over 2}\left( r_\mu w_\nu +r_\nu w_\mu \right) W_2^{rw} \nonumber \\&+ \,\epsilon _{\mu \nu \alpha \beta }u^{\alpha }v^\beta W_3^{uv} +{1\over 2}\left( p_{\mu } n_{\nu } - p_{\nu } n_{\mu }\right) W_4 \end{aligned}$$
(13)

where \(W_1, W_2^{rw}, W_3^{uv}, W_4\) are invariant functions, and r, w can be chosen from p, s, n and t, and u, v can be chosen from p, q, s, n and t, with the condition that the tensor be at most linear in the spin vector. As compared to the one-particle exclusive case, there is an additional tensor structure with structure function \(W_4\), which requires two vectors, being antisymmetric. The only non-zero contribution is in the case when two vectors are p and n.

3. Tensor case

In the tensor case, the leptonic coupling is

$$\begin{aligned} \Gamma _{\rho \tau } = g_T \sigma _{\rho \tau }. \end{aligned}$$
(14)

The tensor H for this case can be written in terms of the four invariant functions \(F_1\), \(F_2\), \(PF_1\), \(PF_2\) as

$$\begin{aligned} H^T_{\mu \rho \tau }= & {} (r_\rho u_\tau - r_\tau u_\rho ) w_\mu F_1^{ruw} + ( g_{\rho \mu } u_\tau - g_{\tau \mu } u_\rho ) F_2^u \nonumber \\&+\, \epsilon _{\rho \tau \alpha \beta } r^\alpha u^\beta w_\mu PF_1^{ruw} + \epsilon _{\rho \tau \mu \alpha } u^\alpha PF_2^u, \end{aligned}$$
(15)

where w is chosen from p, s, n and t, r from p and q, and u from p, q, s, n and t. These choices of the vectors for r, w and u give a complete set of independent tensors. The use of vectors other than covered by the choices would result in tensors which are combinations of the tensors described by Eq. (15). Details can be found in [14].

We next substitute the leptonic vertices \(\Gamma \) and the respective tensors \(H^i\) in (9), and evaluate the trace in each case. We present the results in Tables 1, 2, 3 and 4. The structure functions accompanying the tensors which depend on spin (i.e. contain one of the vectors \(\vec s\), \(\vec n\) and \(\vec t\)), would occur in the spin-dependent differential cross section with a factor \(\lambda _s\), \(\lambda _n\) or \(\lambda _t\), each taking the value \(+1\) or \(-1\), denoting the spin projection along the respective spin vector \(\vec s\), \(\vec n\) or \(\vec t\).

A superscript T on a vector is used to denote its component transverse with respect to the \(e^+e^-\) beam directions. For example, \(\vec {r}^T= \vec {r}- \vec {r}\cdot \hat{z}\,\hat{z}\), and similarly for other vectors. Tables 1, 2, 3 and 4 are, respectively, for cases of scalar-pseudo-scalar, vector-axial-vector, real and imaginary parts of tensor couplings, respectively.

Since our present case is that of a single particle being measured, there is only one momentum p. However, there is one more vector, viz. the spin vector. These are the three possible spin-quantization axes given by \(s^\mu ,\, n^\mu \) and \(t^\mu \) and a full evaluation of the resulting correlations is given in Tables 1, 2, 3 and 4.

Table 1 Correlations due to structure functions for scalar and pseudo-scalar BSM physics from the interference of the SM amplitude with the BSM physics. An overall factor of 8 has been suppressed to be consistent with published results, Refs. [11, 12]. Note the symmetry of the correlations under the simultaneous interchange of \(\hbox {Im}\leftrightarrow \hbox {Re}\), \(g_V^e \leftrightarrow g_A^e\)
Full size table
Table 2 As in Table 1, for vector and axial-vector couplings
Full size table
Table 3 As in Table 1 for real parts of the tensor couplings
Full size table
Table 4 As in Table 1 for imaginary parts of the tensor couplings
Full size table

In the absence of any further assumptions of the theory, it is not possible to draw very pointed conclusions. However, we can still very often deduce some useful points related to what measurements are not possible even under the very minimal assumptions made by us. Examining the tables, one can make the following observations. Many of the observations we have here are similar to the case of one- and two-particle inclusive measurements without spin resolution [11, 12]. These may be summarized as follows in bullet form:

  • In the case of S, P and T couplings, all the entries in the corresponding tables vanish for unpolarized beams, or for longitudinally polarized beams.

  • Thus at least one beam has to be transversely polarized to see the interference.

  • In the case of V and A couplings, both beams have to be transversely polarized, or the effect of polarization vanishes. It is interesting to note that all the correlations in the latter case are symmetric under the interchange of \(\vec s_+\) and \(\vec s_-\).

  • In the case of S, P and T to observe terms which correspond to combinations like \((h_-\vec s_+\, \pm \, h_+\vec s_-)\), it is necessary to have one beam longitudinally polarized, and the other transversely polarized.

  • It is only the coupling \(g_V^e\) which accompanies the imaginary part of the structure functions in the case of S, P couplings, and \(g_A^e\) in the case of T couplings. Likewise, \(g_A^e\) and \(g_V^e\) occur with the real parts in these respective cases.

  • In the case of vector and axial-vector BSM interactions the structure functions without final-state spin measurement which contribute when polarization is included are the same as the ones which contribute when beams are unpolarized, provided absorptive parts are neglected. We assume here that the final-state particles which are observed are themselves eigenstates of CP, in which case, the imaginary parts of the structure functions contain absorptive parts of the BSM amplitudes. In other words, no qualitatively new information is contained in the polarized distributions if we neglect the imaginary parts of the structure functions and do not make a final-state spin measurement. However, this situation is changed when structure functions dependent on final-state spin are included.

  • Most BSM interactions are chirality conserving in the limit of massless electrons, and can therefore be cast in the form of vector and axial-vector couplings. Thus, in a large class of contexts and theories, it is possible to conclude that polarization does not give qualitatively new information, unless absorptive parts are involved. Again, the inclusion of spin measurement of the one-particle inclusive state changes this situation.

  • It is possible to conclude that polarization can be used to get information on absorptive parts of structure functions of BSM interactions, which cannot be obtained with only unpolarized beams, and the final-state spin resolution can be used to obtain information even on the dispersive parts.Footnote 3

  • In our case, if absorptive parts are included, there is a contribution from \({\mathrm{Im}}~W_3^{uv}\). Again, in this case, it possible to predict the differential cross section for the polarized case, if the unpolarized cross section is known.

  • On the other hand, we see that \({\mathrm{Im}}~W_2^{pp}\) contributes only for transversely polarized beams. Thus, to observe these structure functions, it is imperative to have transverse polarization of both beams.

  • A further point to notice about the contributions of \({\mathrm{Im}}~W_2^{rw}\) is that if \(g_V^e = g_V\) and \(g_A^e = g_A\), the contribution vanishes. In other words, if the new-physics contribution corresponds to the exchange of the same gauge boson as the SM contribution, so that the coupling at the \(e^+e^-\) vertex is the same, even though the final state may be produced through a new vertex, the contribution to the distribution is zero. Thus, in the case of a neutral final state, where the SM contribution through a virtual photon vanishes at tree level, the observation of \({\mathrm{Im}}~W_2^{rw}\) through transverse polarization could be used to determine the absorptive part of a loop contribution arising from \(\gamma \) exchange. In the case of a charged-particle final state for which both Z and \(\gamma \) contribute, such a contribution would be sensitive to loop effects arising in both these exchanges.

The features mentioned here capture the main reasons for enhancing BSM physics in the presence of beam polarization, which is the essence of the studies of Refs. [9, 11, 12].

4 CP and T properties of correlations

It is important to characterize the C, P and T properties of the various terms in the correlations, which would in turn depend on the corresponding properties of the structure functions which occur in them.

In this context we recall that a similar analysis was done for the one-particle inclusive case treated in [11]. In that case, we deduced the important result that when the final state consists of a particle and its antiparticle, it is not possible to have any CP-odd term in the case of V and A BSM interactions. This deduction depended on the property that in the center-of-mass frame, the particle and antiparticle three-momenta are equal and opposite. In the case of two-particle inclusive distributions, even if the two particles observed are conjugates of each other, their momenta are not constrained. Thus it is possible to have CP-odd correlations even in the V, A case. In this section, we present an extension of those analyses to the case at hand, which is the one-particle inclusive case with spin-resolution. It may be noted that the work of [11] is the simplest possible realization of this framework. The present work is a highly non-trivial extension of the work therein, and it is based on the introduction of not just one, but three different spin-quantization axes. It is not possible to anticipate the results of this analysis and thus the present work is an important extension. Furthermore, it brings into the focus the requirement of a dedicated spin analysis of final-state particles at future \(e^+e^-\) colliders.

We now come to a more systematic analysis. We consider two important cases, one when the particle h in the final state in \(e^+e^-\rightarrow h X\) is its own conjugate, and the other when it is not. We treat these two cases separately.

4.1 Case A: \(h^c = h\)

Since in this case, the particle h is required to be its own conjugate, and is a spin-half particle, it would be a Majorana fermion, and therefore uncharged. Then, if h is light (e.g., a Majorana neutrino), it would escape detection leading to missing energy and momentum, and the state X would have to include a pair of charged particles to make possible a measurement of this state. On the other hand, if h is heavy (e.g., a heavy Majorana neutrino or a neutralino in a supersymmetric theory), it would decay making it possible to measure it spin with the help of its decay products.

We first examine the case of scalar and pseudo-scalar interactions. When the spin of h is not measured, the distributions in the first two rows of Table 1 being even under CP would be present if the structure function \(F^p\) does not violate CP. On the other hand, the distributions in the third and fourth rows of Table 1, if seen, would measure possible CP violation in \(F^p\).

If the spin of h is measured, we have to keep in mind that the spin-dependent structure functions are multiplied by a factor \(\lambda \) depending on the spin-quantization axis. When the spin-quantization axis is along its momentum direction, the dependence of distributions on the CP properties of \(F^s\) is opposite in sign as for \(F^p\), since the spin projection along the momentum (which we denote by \(\lambda _s\)) and the spin itself have opposite P properties. Since the distributions are identical in the two cases, except for an additional factor of \(E_p/(Pm)\) in the former case, the distribution with spin measurement corresponds to CP opposite to that in the case without spin measurement.

Since under naive time reversal T momentum and spin have the same behavior, viz., change of sign, the CPT property will follow the CP property. We remind the reader that T here denotes naive time reversal, i.e., reversal of the spin and momenta vectors, as opposed to genuine time reversal, in which initial and final states are also interchanged.

The distributions in the case when the spin-quantization axis is \(\vec n\) are very similar, and the additional factor in this case is \({\mathrm{cosecant}}\;\, \theta /P\). However, in this case, the roles of the real and imaginary parts of the structure functions are reversed, and the distributions have an interchange \(g_V^e \leftrightarrow g_A^e\) relative to the ones for \(F^p\) or \(F^s\). This has great significance, because numerically \(g_V^e<< g_A^e\). Thus, the distributions which occur with a certain \(F^p\) or \(F^s\) will have widely different numerical value as compared to those occurring with the \(F^n\) of the same magnitude. Moreover, the vector \(\vec n\) as chosen has exactly opposite C, P and T properties as compared to \(\vec s\). Correspondingly, \(\lambda _n\) has also opposite C, P and T properties as compared to \(\lambda _s\).

In the case of the spin-quantization axis of h being \(\vec t\), the distributions for \(F^t\) are related to those of \(F^p\) by a factor \(\cot \theta /P\). This changes the CP property of the distribution, since \(\cot \theta \) is odd under CP. In addition, as \(\vec t\) has C opposite to that of \(\vec p\), \(\lambda _t\) has \(\hbox {C}=-1\), whereas its P and T properties are the same as those of \(\lambda _s\), resulting in \(\hbox {CP}=+1\), and \(T=+1\). Thus, the CP properties of the distributions for \(F^t\) remain opposite to those for the distributions for \(F^p\).

To see how a study of the CP properties would be affected by the experimental configuration, consider the case when the \(e^-\) and \(e^+\) beams have only transverse polarization, and whose directions are oppositely directed. This would be a natural scenario in the case of circular colliders, where the \(e^-\) and \(e^+\) polarizations, because of synchrotron radiation via the well-known Sokolov–Ternov effect, are directed perpendicular to the plane of the trajectories of the particles, and antiparallel to each other. In this case, \(\vec s_- = - \vec s_+\). Then CP-odd distributions arise in the case of spin-independent structure function \(F^p\) for scalar couplings, and for spin-dependent structure functions \(F^s\), \(F^n\) and \(F^t\) for pseudo-scalar couplings.

In the case of vector and axial-vector couplings, if the spin of h is not measured, CP violation can be found in distributions associated with \(\hbox {Im}(g_VW_3^{pq}\)) and \(\hbox {Im}(g_AW_3^{pq}\)) because the factor \(\cos \theta \) occurring there is odd under CP. This CP violation results from absorptive parts of the structure function \(W_3^{pq}\) and is consistent with [11]: the observation of CP violation in the case when the spin of h is not measured requires either an absorptive part to be present, or the use of transverse beam polarization. We find that this is not true when the spin of h is observed because then there are more possibilities of observing CP violation, again because of the CP-odd factor \(\cos \theta \) (or \(\cot \theta \)) as in the distributions associated with \(W_2^{pt}\), or because \(\lambda _s\) or \(\lambda _n\) is odd under CP, as in the case of \(W_2^{ps}\), \(W_2^{pn}\) and \(W_4^{pn}\). Thus, even in the absence of absorptive parts, CP violation is observable even without transverse beam polarization for the structure function \(W_4^{pn}\). An example of a suggestion for measurement of CP violation in neutralino production using the spin of the neutralino along the direction \(\vec n\) normal to the production plane can be found in [38, 39]. Another feature seen is a CP-violating contribution associated with the structure function \(W_2^{pn}\) which survives only in the presence of transverse beam polarization, but with an entirely different kinematic dependence compared with any other structure function.

In the tensor case, when spin is not observed, all F-type structure functions are CP even and all PF-type ones are CP odd. Of the spin-dependent structure functions, all F-type structure functions with one superscript s, n or t are CP odd, whereas all PF-type structure functions with one such superscript are CP even.

Again, if we restrict ourselves to the configuration where \(\vec s_+ = - \vec s_-\), the surviving CP-odd terms of the ones just listed are only those of the type \(F_2^{s,n,t}\) and \(PF^{pqp}\).

It is interesting to notice that, with T as usual denoting naive time reversal, the distributions which correspond to \(\hbox {CPT}=+1\) and \(\hbox {CPT}=-1\) arise from the two opposite cases where the structure function does not have an absorptive part and where it does have an absorptive part. This follows from the CPT theorem. If the phases in the definitions of the structure functions are chosen appropriately, the former would be associated with the real part of the structure function and the latter with the imaginary part.

4.2 Case B: \(h^c \ne h\)

In the case when h is not self-conjugate, the most interesting case would be the one where \(X \equiv h^c\), i.e., when only h and \(h^c\) are pair produced. In that case, ascribing the momentum \(p^c\) to \(h^c\), we can write \(\vec p = \frac{1}{2} (\vec p - \vec p^c )\) in the c.m. frame, so that under CP, P is invariant, as also \(\cos \theta \).

Looking at Tables 1, 3 and 4, it is clear that in the case of scalar, pseudo-scalar and tensor interactions, when spin of h is not measured, the only CP-odd correlations are those which have a combination \((\vec {s}_+-\vec {s}_-)\), which is C odd and P even, or the combination \((h_-\vec {s}_+\, +\, h_+\vec {s}_-)\), which is C even and P odd. Thus, for the configuration \(\vec s_+ = -\vec s_-\), only CP-odd correlations survive. In the scalar and pseudo-scalar case, the CP-odd correlation is present for all structure functions with a pseudo-scalar coupling to leptons.

In the case of vector and axial-vector couplings, there are no CP-odd correlations.

If the spin of h is measured, one cannot make definite statements about CP properties, because the spin of \(h^c\) is not measured.

Some more interesting situations are possible in this situation: When h is not self-conjugate, and when h and \(h^c\) are not pair produced, one can draw conclusions about the CP properties only by comparing the distributions for an inclusive process with final state \(h +X\) with those for the final state \(h^c + X\). We can construct special combinations \(\Delta \sigma ^\pm \) corresponding to the sum and difference of the partial cross sections \(\Delta \sigma \) and \(\Delta \bar{\sigma }\) for production of h and \(h^c\), respectively. We could then make statements of the CP properties of \(\Delta \sigma ^\pm \) for various structure functions. A general discussion in this case is somewhat complicated. However, in the case we restrict ourselves to only tree-level contributions, then, by unitarity, the effective Lagrangian can be taken to be Hermitian and also avoiding complications arising from absorptive parts generated by loops. Then the couplings and structure functions contributing to \(\Delta \sigma \) would be complex conjugates of those contributing to \(\Delta \bar{\sigma }\). Thus, only the real parts of the couplings would contribute to \(\Delta \sigma ^+\) and only the imaginary part to \(\Delta \sigma ^-\). It would not be possible to make such a clear-cut separation if loop effects are included. In this scenario, it would be possible for terms in the distribution which would be CP even in the earlier case of \(h=h^c\) to be CP odd in the combination \(\Delta \sigma ^-\). This combination would occur with only imaginary parts of the couplings. On the other hand, terms which were CP odd in the case \(h=h^c\) would be CP odd in the combination \(\Delta \sigma ^+\), and real parts of couplings would contribute to it.

5 Implications for specific processes

In this section we discuss the implications of our framework to specific processes. As in the preceding section, since we are specifically interested in the possibility of CP-violating signatures, we need to separately consider the cases of self-conjugate and non-self-conjugate exclusive final states.

5.1 Case A: \(h^c=h\)

The two important cases we consider here are the production of a pair of heavy neutrinos in a left–right symmetric model [40] and a pair of neutralinos in a supersymmetric model [38, 39] at electron–positron colliders, both of which can occur in an appropriate extension of the SM.

5.1.1 Heavy neutrino production

Since in many theoretical scenarios neutrinos are massive Majorana fermions, our formalism will be applicable to inclusive neutrino production in most theoretical models. Moreover, many theories incorporate CP violation, which may be relevant for baryogenesis through leptogenesis. The neutrino needs to be heavy, so that it decays in the detector so that its polarization would be measurable. The neutrino may be accompanied by another neutrino or some other inclusive state. Since the process does not occur in the SM, we will apply our formalism to the interference of two amplitudes for the production, one of which would be through the s-channel exchange of the Z boson, non-vanishing only for a \(e^-_Le^+_R\) or \(e^-_Re^+_L\) combination of initial states, and the other, may be through s-, t-, or u-channel exchanges of massive particles. Since the cases we consider correspond to unpolarized beams, the interfering second amplitude would also have to have the same initial helicity combinations, viz., \(e^-_Le^+_R\) or \(e^-_Re^+_L\), giving essentially the same results as would a vector-axial-vector interaction. Consequently, we can anticipate the resulting distributions from Table 2. If the spin of the final state is not measured, the relevant rows in Table 2 which incorporate CP violation correspond to the combinations \(\hbox {Im}(g_VW_3^{pq}\)) and \(\hbox {Im}(g_AW_3^{pq}\)). In either case, the factor \(\cos \theta \) leads to a forward–backward asymmetry, which is discussed in [40].

It is conceivable that with polarized beams, and/or by studying the polarization of the neutrinos, more information can be obtained on the structure of a possible theory of Majorana neutrinos. While our tables can be used as an indication of what correlations may be useful, the corresponding structure functions would have to be worked out in the specific model being tested.

5.1.2 Neutralino production

Neutralinos are Majorana fermions and are relevant to supersymmetric extensions of the SM. Again, neutralino production is not a SM process, we again consider the interference of two amplitudes for the production, one through the s-channel exchange of the Z boson, and the other through t-, or u-channel exchanges of massive charged sleptons. In the absence of beam polarization, the terms corresponding to \(W_4^{pn}\) would indicate CP violation, which corresponds to neutralino polarization in a plane normal to the production plane, and is discussed in [38]. In [39] a CP-odd forward–backward asymmetry with transverse beam polarization and without the neutralino spin being measured is also presented. Our formalism misses this term because it arises on account of t- and u-channel contributions in the neutralino pair-production process, whereas we consider only s-channel processes.

Of related interest is the discussion in Ref. [41] where the production of Dirac and Majorana particles in fermion–antifermion annihilation is considered in some generality. The main results relate to the symmetry or antisymmetry of the cross section and the polarization of the observed final state when the \(e^+e^-\) beams are unpolarized or longitudinally polarized. These correspond to \(V, \,A\) type of interactions (\(S,\, P\) and T interactions requiring transverse beam polarization in order for them to be observable). Also, in the case of Dirac fermions, the results require observation of the spins of both the fermion and the antifermion. Hence we cannot make a comparison with the corresponding results, as our formalism concerns only spin measurement of one final-state fermion. In the case of Majorana fermions we have found agreement with the symmetry properties in all cases studied in their case, with the exception of the symmetry property of polarization in one of the form factors we consider, viz., \(\hbox {Re}(W_2^{pt}\)).

5.2 Case B: \(h^c\ne h\)

In the case when the produced particle h is not self-conjugate, the simplest possibility is that h is produced in association with \(h^c\), its conjugate particle. We will restrict ourselves to this possibility, as a larger inclusive state is complicated as regards discussion in specific detail.

We would like to emphasize that ours is a model-independent approach, and we would like to elicit general features in our formalism. We do not include here predictions from individual models for our structure functions. Nevertheless, we outline an intermediate step in such a calculation in the case of the \(hh^c\) final state.

Here there are two possibilities, one when the particle h is a particle in the SM spectrum, and the other when h is new particle in an extension of the SM. Examples of the former are when h is a charged massive particle, like the top quark or the tau lepton. As for extensions of the SM, cases often studied in the literature are production of excitations of quarks or leptons, charginos in supersymmetric theories, production of heavy quarks or leptons in a model with extra generations or an extended gauge group, and production of Kaluza–Klein partners of SM fermions in extra-dimension theories. In all these cases, corresponding to a number of different underlying theories, a unified model-independent approach can be used. There are two possibilities which we consider.

A. Loop-level BSM contribution to \(\gamma hh^c\) and \(Z h h^c\) vertices

In this case, the amplitudes for \(hh^c\) production through s-channel \(\gamma \) exchange and through s-channel Z exchange are parametrized in a general way in terms of vector, axial-vector and tensor couplings, with coefficients which are momentum-dependent form factors. Thus, the structure functions appearing in our formalism, corresponding to the interference between SM \(\gamma \) and Z exchange contributions with an indirect loop-level BSM contribution, are represented, still in a relatively model-independent way, in terms of form factors. The assumption made is that the BSM contribution appears in the loop contribution to \(\gamma hh^c\) and \(Z h h^c\) vertices.

This approach can include models mentioned above, for some of which form factors have been calculated in the past [42,43,44,45,46].

B. BSM contribution through effective \(e^+e^-hh^c\) interactions

This case includes contributions which do not take place through \(\gamma hh^c\) and \(Z h h^c\) vertices. Without explicit details of the production mechanism, the BSM contribution can be represented as general contact \(e^+e^-hh^c\) interactions, which would include all tensor contributions in a model-independent way. Again, the interference between the SM contribution and the BSM contact interaction contribution would result in the structure functions that we use in our analysis. The structure functions could be calculated in terms of the contact interaction form factors. Contact interactions in this context have been studied in [47,48,49].

The issue of the spin resolution has been studied in the context of \(t\bar{t}\) production in the presence of BSM physics due to an effective Lagrangian characterized exclusively by its Lorentz signature. In Ref. [17, 18] it was shown that the availability of helicity amplitudes for both the initial- and the final-state particles allows one to obtain distributions and to construct suitable asymmetries to probe BSM physics in a manner that was not possible when the helicity was unresolved, in contrast to the work in Ref. [15]. Furthermore, it was also demonstrated that a correspondence could be made between the one-particle inclusive distribution and the related relevant structure functions to the parameters of the effective Lagrangian of the exclusive process [11]. This work was further extended to a scenario of measurements of the spin in the so-called beam-line and off-diagonal bases to enhance the sensitivity to BSM physics [18], where these bases were discussed in the context of \(t\bar{t}\) production in some detail in Ref. [50].

We now study these cases in some more detail.

5.2.1 Loop-level BSM contribution to \(\gamma hh^c\) and \(Z h h^c\) vertices

In this section we study the process \(e^+ e^- \rightarrow f \overline{f}\), where f is a quark or a lepton, a process which will dominate at the ILC. We also look at further decays of the final-state fermions when they are heavy and the momentum correlations amongst these as probes of BSM interactions. We concentrate on CP-odd correlations which indicate CP violation and are therefore important to study. However, these are by no means the only interesting correlations. CP-even correlations could be used to study new CP-conserving interactions like magnetic dipole moments.

Early work in this regard was the study by Couture [22, 23] of \(e^+e^-\rightarrow \tau ^+\tau ^-\) in the presence of dipole moments.Footnote 4 Couture has studied in detail the spin–spin correlations in \(\tau ^+\tau ^-\) production and studied the effects of possible electric and magnetic dipole moments on these, but at energies where the presence of Z boson can be safely neglected. It turns out that many important effects show up only in the presence of the Z boson due to its parity violating properties, and at energies comparable or significantly larger than its mass. Here we consider the process in the full electro-weak theory, but with a sum over the spin of the \(\bar{f}\), giving rise therefore to a one-particle inclusive type distribution with spin resolution, wherein the effective structure functions are actually known in terms of the dipole strengths.

Consider the process \(e^-(p_-)e^+(p_+) \rightarrow f(p)\bar{f}(\bar{p})\), in the presence of anomalous magnetic dipole couplings \(\kappa _\gamma \) and \(\kappa _Z\) and electric dipole couplings \(d_\gamma \) and \(d_Z\) of the spin-half fermion f to \(\gamma \) and Z, respectively. The effective Lagrangian of the dipole couplings (\(V \equiv \gamma , Z\)) is given by

$$\begin{aligned} \mathcal{L}_\mathrm{dipole} = \frac{i}{2m_f} \sum _{V=\gamma ,Z} \left( \partial _\nu V_\alpha - \partial _\alpha V_\nu \right) \bar{f} \sigma ^{\nu \alpha } (\kappa _V + i d_V \gamma _5) f.\nonumber \\ \end{aligned}$$
(16)

The interference term between the amplitude in the SM model and the amplitude with the anomalous couplings, summed over the spins of \(\bar{f}\), for the contribution of one vector boson V (\(\gamma \) or Z) is

(17)

Here s is the spin four-vector of the fermion f, and it would represent the helicity four-vector. The calculation above is a generic one, and as a result the vector s can also be replaced by the vectors n and t to get the results for the cases when the spin-quantization axes are in transverse directions. Comparing this expression with Eqs. (9) and (13), we can immediately identify the various structure functions listed in Eq. (13) for the present exclusive case. For this purpose, one has also to consider the s-dependent terms above with s replaced by n or t. Moreover, some terms in Eq. (17) above do not find a place in Eq. (13). To understand this, we note that the terms with the factors \(\epsilon ^{\alpha \beta \gamma \mu }p_\alpha q_\beta s_\gamma \) and \(\epsilon ^{\alpha \beta \gamma \nu }p_\alpha q_\beta s_\gamma \) are vanishing, since in these, q has only the time component, and the space components of p and s are proportional to each other. When s in these \(\epsilon \) tensors is replaced by n, \(\epsilon ^{\alpha \beta \gamma \mu }p_\alpha q_\beta n_\gamma \) reduces, apart from a scalar factor, to the transverse spin vector \(t^\mu \), giving a term present in Eq. (13). Similarly, \(\epsilon ^{\alpha \beta \gamma \mu }p_\alpha q_\beta t_\gamma \) is proportional to \(n^\mu \).

As stated earlier, since the spin of \(\bar{f}\) is not measured, it is not possible to get correlations which are explicitly even or odd under CP. However, it is clear that both the CP-even dipole couplings \(\kappa _V\) and the CP-odd dipole couplings \(d_V\) can be measured from a measurement of the structure functions through correlations listed in Table 2.

In the case of the photon, for which \(g_A^f\) = 0, the electric dipole coupling \(d_\gamma ^f\) appears only in the structure functions \(W_2\), and \(W_4\), and then only in their imaginary parts. However, as observed earlier, in the case of Im \(W_2\), the coupling constant combination multiplying the final distribution is \(g_V^fg_A^e - g_A^f g_V^e\), which for the case of photon couplings is 0, as both \(g_A^e\) and \(g_A^f\) vanish. Hence the only possibility of measurement of the photon electric dipole coupling is through \(W^4\). In that case, both the longitudinal polarization of the beams and measurement of the transverse polarization of the final-state fermion are required.

As for the dipole coupling of f to the Z, the fact that the vector coupling \(g_V^e\) of the electron to the Z is numerically small (\(g_V^e/g_A^e \approx 0.08\)) would play a role in deciding the approximate nature of the distributions. In the case the f is a charged lepton like \(\tau \), the corresponding vector coupling \(g_V^f\) to the Z is also small. In that case, neglecting vector couplings of the e and \(\tau \), an examination of Eq. (17) and Table 2 reveals that the measurement of the weak dipole moment would require longitudinal polarization of the \(e^-\) or \(e^+\) beam, preferably both beam longitudinally polarized with helicities of opposite sign. These observations are in accordance with early work that pointed out that availability of beam polarization would significantly enhance the sensitivity to the measurement of dipole moments [51, 52] which generalized the results for unpolarized beams; see Ref. [53].

5.2.2 BSM physics with effective operators in \(e^+e^-\rightarrow f\bar{f}\)

In [18] we had obtained kinematic distributions for the process \(e^+e^-\rightarrow t\bar{t}\) (which would be applicable in general to any inclusive state \(f\bar{f}\) with a heavy fermion f) with transversely polarized beams and when the polarization of the top quark in the final state is measured. In that work, four-fermion contact interactions were used, following the work of Grzadkowski [54]. It would seem natural that the present formalism could be applied to that exclusive process as a special case. It was observed in [18] that the distributions obtained by explicit evaluation of the amplitudes were consistent with those predicted by appropriate structures in our formalism. In the course of these investigations we find, on closer examination, that with the restrictions of hermiticity on the couplings of the contact interactions, the structure functions for the scalar, pseudo-scalar and tensor interactions turn out to be vanishing. Therefore, it may appear that there is some kind of incompatibility between the current framework and exclusive processes with scalar or tensor contact interactions. Furthermore, although we did find schematic evidence that they can be mapped one to another, the two schemes are actually distinct. The presence of a ‘current’ of the present framework when related to the adopted contact interaction framework imposes too stringent a requirement between the various couplings thereby leading to the vanishing of the structure functions.

In the case of vector and axial-vector interactions, however, the formalism is compatible with even contact interactions. It is thus possible to predict the distributions in this case using our formalism. This case was not treated in [18].

One could also compare the results coming from more complicated exclusive states that could arise in popular extensions such as techni-pion models, for the process \(e^+e^-\rightarrow t \bar{t}\pi _t\) [55]. Other general considerations of discrete symmetry in processes involving top and b-quarks in the SM as well as in the MSSM, without spin resolution, may be found in Refs. [56,57,58] to cite a few examples.

It may be fruitful to point out that our aim is to establish a model-independent approach. As such, it is not intended to take up specific models. Nevertheless, we have taken up some explicit categories of final states, both as inclusive states and exclusive states, and with that categorization, we have tried to construct general amplitudes characterized by form factors. Thus, within our model-independent approach, we have been as explicit as possible and have tried to illustrate the power of the approach. The work here is meant to be a set of consistency checks on specific BSM models, and not meant to be a full-fledged substitute to important and popular extensions of the SM.

6 Summary and discussion

We now present a summary of the motivation, the approach and the main results in this work and provide a discussion of these results.

The motivation for our work comes from the planned high energy and high performance \(e^+e^-\) machines that are now being considered seriously at very high levels for construction. While there are several technical differences between the various machines under discussion in terms of their physical layout, technology and detector and accelerator aspects between the ILC, CLIC, FCee and CEPC, the underlying physics that is sought to be probed is the same. These machines are expected to provide a clear environment and high statistics environment to study SM particles and their properties at high precision in the light of LHC discoveries. A great deal of work has been carried out to study the feasibility of improving the degree of polarization both for the electron and the positron beams. It is therefore highly likely that longitudinally polarized beams will be commissioned at linear colliders. It is also possible to create transverse polarization out of longitudinally polarized beams using spin rotators. Less work has been done for feasibility studies for longitudinally polarized beams at a circular collider. Whereas such studies are desirable from the stand point of accelerator science, the essential features of the physics with polarized beams remain the same for linear and circular colliders.

In order to build a serious case for high-precision SM and BSM studies, all valid approaches much be studied as diligently as possible. Our work is an important model-independent effort in this direction, in order to provide a no-frills approach to the study of fingerprinting BSM physics at these machines.

A model-independent approach to the study of possible BSM physics is to represent such effects in terms of the most general vertices allowed by Lorentz invariance and gauge invariance in the case of various exclusive processes. It may be worth emphasizing that BSM models are characterized by alterations to effective vertices arising in higher orders from the integrating out of more massive states of the theory, which would make specific predictions for the structure functions of the inclusive framework. While we have provided some illustrations of such a correspondence, our framework has the advantage of model independence, which also is its most important distinguishing feature.

An even more general approach, which is the one pursued here, is one where only one SM particle is observed, and the effects of all interactions are represented, assuming Lorentz invariance, in terms of the vectors on hand. These are primarily momenta of the colliding particles in \(e^+e^-\) collisions, the polarizations of the incoming particles, the momentum and the spin of the observed particle.

We now itemize the important points of this work.

  • In this work, we have started out by considering the most general terms that can occur in the interference between SM and BSM physics and construct vertices involving vectors on hand, namely the momenta and the directions of transverse polarization of the incoming particles and the momenta and spin-quantization axes of the observed spin-1/2 particle, consistent with Lorentz covariance. Thus, we have computed the spin and momentum correlations, expressed as angular distributions, in \(e^+e^-\) collisions arising from the interference between the virtual \(\gamma \) and Z exchange SM amplitudes and BSM amplitudes characterized by their Lorentz signatures, with the unknown physics encoded into structure functions for a one-particle inclusive measurement with spin resolution. Transverse and longitudinal beam polarizations are explicitly included.

  • The generalization of simple one-particle to two-particle inclusive measurement was also done some years ago, since the availability of a second vector gives rise to greater possibilities for structure functions. The availability of a second vector in the form of the spin-quantization direction in turns gives rise to more intriguing possibilities which is the subject of this work. Whereas it is natural to assume the direction of the motion of the detected particle as the quantization axis, the full reconstruction of the density matrix of a spin-1/2 particle requires three mutually orthogonal directions. We have employed three mutually orthogonal directions as quantization axes corresponding to longitudinal, normal and transverse directions in the plane of production.

  • A large number of structure functions have to be introduced, which are taken to be complex, with definite implications for their properties under the discrete symmetries of C, P and T for the dispersive (real) and absorptive (imaginary) parties, as dictated by the CPT theorem. The spin-quantization axes themselves can be expressed in terms of the momentum vectors at hand, and they allow us to express the results for the spin–momentum correlations and spin–spin correlations in terms of economical tables, namely Tables 1, 2, 3 and 4. While we present the results for the general couplings \(g_A^e\) and \(g_V^e\) directly applicable to Z, those case for the photon are obtained by simply setting \(g_V^e=e\) and \(g_A^e = 0\).

  • Some salient features of the entries in the tables were the following.

    • Indeed, as in the case of the one- and two-particle inclusive study with no spin resolution, with S, P and T type couplings, transverse polarization of at least one of the beams is needed to uncover their presence at leading order, or a hybrid of longitudinal and transverse polarization. In the case of imaginary parts of S and P type structure functions, the result is accompanied by \(g_V^e\) while in the case of T type structure functions it is accompanied by \(g_A^e\). In the case of the real parts, the vector and axial-vector couplings will have to be swapped, in accordance with the symmetry of the tables under the simultaneous swap of vector and axial-vector couplings, and of real and imaginary parts of the structure functions.

    • The structure functions corresponding to V and A type BSM interactions lead to correlations that have distinctly different properties. In particular, without final-state spin resolution beam polarization does not lead to any qualitatively different information when the imaginary parts are disregarded. However, when spin resolution is included, this is no longer true, which is an important finding of the present investigation. In other words, the appearance of specific structure functions and combinations of initial beam polarizations which render some spin structure functions as being observable only with beam polarization is noteworthy.

    • Analogously, absorptive parts of structure functions with spin resolution are qualitatively different from those without spin, which was not pointed out earlier. Thus beam polarization is crucial for uncovering interactions which cannot be done with unpolarized beams. Our analysis of the correlations also shows that there are special circumstances under which contributions may vanish as in the case of a new vector boson, which would imply equality of the vector- and axial-vector couplings of the electron and the observed particle, and new interactions would be visible only through loop effects.

  • As a sequel to the thorough analysis of the general results found in Tables 1, 2, 3 and 4, we have presented a discussion of the nature of the correlations and the deductions that can be made on their polarization dependence. We have also discussed the CP and CPT properties of certain structure functions. This was based on a systematic analysis under the rubric of (a) \(h^c=h\), and (b) \(h^c\ne h\). The main features of this analysis may be summarized as follows.

    • As one can see from the study without final-state spin being resolved, when \(h^c=h\) (Majorana fermions), CP violation cannot be observed in the absence of transverse beam polarization. However, when final spin is measured, CP violation can indeed be observed without transverse polarization of the beams. Thus, in the absence of absorptive parts, CP violation is observable even without transverse beam polarization for the structure function \(W_4^{pn}\), which corresponds to spin measurement of the final-state particle along the direction of \(\vec n\), perpendicular to the production plane. A realization of this possibility can be found in [38]. It is possible that some other suggestions of different possibilities of CP-violating distributions discussed here will find realization in other practical situations.

    • For the case when the unobserved state X is just \(h^c\), that is, h and \(h^c\) are pair produced, in the case of scalar, pseudo-scalar and tensor interactions, and when the spin of h is not measured, the only CP-odd correlations are those which have a combination \((\vec {s}_+-\vec {s}_-)\), which is C odd and P even, or the combination \((h_-\vec {s}_+\, +\, h_+\vec {s}_-)\), which is C even and P odd. Thus, for the configuration \(\vec s_+ = -\vec s_-\), only CP-odd correlations survive. In the scalar and pseudo-scalar case, the CP-odd correlation is present for all structure functions with a pseudo-scalar coupling to leptons. In the case of vector and axial-vector couplings, there are no CP-odd correlations.

    • For the case of \(h^c\ne h\), interesting results that could be obtained when h and \(h^c\) are pair produced do not directly apply to the case when only one of them is produced. It is not possible to make definite statements for the case h and \(h^c\) are produced when the spin of h is measured, because CP would relate the spin of h to the spin of \(h^c\) and the latter is not measured. It is possible to envisage that one has samples separately with hX and \(h^c X\) and construct suitable asymmetries to uncover CP violation.

  • We have provided a discussion of the possible ways in which our work can be related to prior studies of exclusive fermion pair production. In particular, for purposes of illustration, we have considered the process in the presence of electric and magnetic dipole moments and evaluate the effective structure functions. Their computation proves to be a useful illustration of the framework. The cases of self-conjugate fermions and otherwise have also been discussed.

  • We have also examined our prior analysis of BSM physics in the form of certain four-fermion effective operators with spin resolution in the present framework. We find that in the scalar, pseudo-scalar and tensor cases, our formalism cannot be used without change to the case of contact interaction framework that had been adopted, which proves to be too restrictive and leads to vanishing structure functions. A sufficiently general inclusive framework that is not based on ‘currents’ and is more general is yet to be developed and may prove to be useful for the study where the observed particle is a boson, in contrast to the present framework where the observed particle is taken to be a fermion.

  • The precise modification of the present framework to other spin bases (as for example beam-line and off-diagonal bases considered in the past) is yet to be analyzed and is work for the future, and so is an extension to spin–spin correlations in a two-particle inclusive state.

  • In contrast to specific models that go into BSM physics with exclusive final states, our present work remains very general and model independent, and it could provide the simplest possible framework to study BSM physics to look for signals independent of assumptions of what lies at higher energy scales. Sufficiently precise data when gathered can be used to study if the structure functions so measured respect constraints that would be implied by specific extensions of the SM in exclusive particle production.

Many of the considerations that have been spelled out for the ILC also apply to the other planned facilities, namely CLIC, FCee and CEPC. In particular, our work would also call for dedicated studies of the advantages of beam polarization at these facilities, real-life estimates of beam polarization for transverse and longitudinal polarizations that could result for these configurations, and the impact of these on detector design and accelerator design.

We also suggest that specific studies of such inclusive processes be implemented also at the level of detector simulations and event generators to study how departures from ideal detection can influence the outcome of the concepts put forward here.