Exact one-loop results for $l_i \rightarrow l_j\gamma$ in 3-3-1 models

Abstract

We investigate the decays $l_i\rightarrow l_j \gamma$, with $l_i=e,\mu ,\tau$ in a general class of 3-3-1 models with heavy exotic leptons with arbitrary electric charges. We present full and exact analytical results keeping external lepton masses. As a by product, we perform numerical comparisons between exact results and approximate ones where the external lepton masses are neglected. As expected, we found that branching fractions can reach the current experimental limits if mixings and mass differences of the exotic leptons are large enough. We also found unexpectedly that, depending on the parameter values, there can be huge destructive interference between the gauge and Higgs contributions when the gauge bosons connecting the Standard Model leptons to the exotic leptons are light enough. This mechanism should be taken into account when using experimental constraints on the branching fractions to exclude the parameter space of the model.

1 Introduction

The discovery of flavor neutrino oscillations (see Ref. [1] and the references therein) proves that neutrinos are massive. This leads to an important consequence that the lepton-flavor number violating decay $\mu \rightarrow e \gamma$ is non-vanishing, being proportional to the neutrino masses and the mixing matrix. Assuming tiny neutrino masses satisfying current experimental constraints [1], extension of the Standard Model (SM) with right-handed neutrinos predicts that the branching ratio is $\text {Br} \approx 10^{-55}$, which will be called the SM contribution from now on. Meanwhile, the current experimental limits read [1]

$$\begin{aligned}&\text {Br}(\mu ^- \rightarrow e^-\gamma )< 4.2\times 10^{-13},\nonumber \\&\text {Br}(\tau ^- \rightarrow e^-\gamma )< 3.3\times 10^{-8},\nonumber \\&\text {Br}(\tau ^- \rightarrow \mu ^-\gamma ) < 4.4\times 10^{-8}. \end{aligned}$$

(1)

From theoretical side, the processes $l_i \rightarrow l_j \gamma$ are loop induced. Given that the SM contribution is strongly suppressed, they can be good places to look for new physics. In this paper, we consider a simple extension of the SM using the local gauge group of $SU(3)_C\otimes SU(3)_L\otimes U(1)_X$ (3-3-1) with new exotic leptons. The word exotic here means that they can have arbitrary electric charges and arbitrary masses. In this model, the electron (and similarly for muon and tauon) together with a neutrino and a new exotic lepton are in a triplet (or anti-triplet) representation of $SU(3)_L$. In this work, we calculate both neutrino and exotic-lepton contributions, with special attention to the latter because the former is numerically suppressed as mentioned above.

We remark that 3-3-1 model is an active field of research and has a long history; see Ref. [2] and the references therein. In this work, we choose a general class of 3-3-1 models, which are similar to the models presented in Refs. [2,3,4] where new heavy leptons are introduced. However, there is an important difference: instead of fixing the electric charges of the new leptons to specific values being 0, $+\,1$ or $-\,1$, we let them be arbitrary. We will then study the dependence of the $l_i \rightarrow l_j \gamma$ branching fractions on this arbitrary charge. That class of 3-3-1 models has been studied in many works; see e.g. [5, 6]. If we replace the new leptons with charge-conjugated partners of the SM leptons, we will have different 3-3-1 models with lepton-number violation; see e.g. Refs. [7,8,9,10,11]. The decays $l_i \rightarrow l_j \gamma$ in these models have been discussed in Refs. [12, 13]; see also the recent review [14] and the references therein. We do not discuss these types of models in this work, but rather focus on the case with exotic leptons.

In the general class of 3-3-1 models here considered, there is one important parameter usually called $\beta$, which together with X, the new charge corresponding to the group $U(1)_X$, define the electric-charge operator. The electric charges of new particles therefore depend on $\beta$. It has been known and widely accepted that $\beta$ is one of the most important parameters to classify 3-3-1 models.

Recently, new efforts were made using 3-3-1 models to understand tensions between experimental measurements and the SM results in B physics; see e.g. [15, 16]. Motivated by this work, we want to use 3-3-1 models to understand the $l_i \rightarrow l_j \gamma$ decays. Since the new leptons are assumed to be heavy, we expect large branching fractions. However, this is not totally obvious, because there are two contributions from gauge and Higgs sectors. Does a destructive interference effect occur?

The aim of this paper is manifold. First, we calculate the full and exact result for $l_i \rightarrow l_j \gamma$ partial decay widths for a general class of 3-3-1 models with arbitrary $\beta$. As a by product, we will perform numerical comparisons between the exact results (i.e. external lepton masses are kept) and approximate ones where external lepton masses are neglected. We note that approximate results have been almost exclusively used in the literature for the SM and many other models. We found this uncomfortable because the neutrino masses, which are much smaller than the lepton masses, are kept. We therefore want to know to what accuracy the approximate results valid, using the SM with arbitrary neutrino masses to answer this. As far as we know, this important point has never been addressed in the literature. We will also perform numerical studies for 3-3-1 model to see whether destructive interference effects occur and to see the dependence on $\beta$, gauge boson and Higss masses. To the best of our knowledge, this is the first study of $l_i \rightarrow l_j \gamma$ in 3-3-1 models with exotic leptons.

The paper is organized as follows. In the next section, we review the model and calculate the Feynman rules needed for $l_i \rightarrow l_j \gamma$ decays. We then summarize the main calculation steps and present analytical results in Sect. 3. Numerical results are discussed in Sect. 4. In Sect. 4.1 we perform comparisons between the approximate and exact results for the neutrino contribution. In Sect. 4.2 we present results for the exotic-lepton contribution. Conclusions are in Sect. 5. Finally, we provide Appendices A and B to complete the results of Sect. 3.

2 3-3-1 model with arbitrary $\beta$

One important condition we require is that the 3-3-1 model has to match the SM at the energy of the EW scale, about$250{\,\text {GeV}}$. This means that the $SU(3)_L$ symmetry is valid at a higher energy scale and is spontaneously broken down to the $SU(2)_L$ symmetry using the Brout–Englert–Higgs mechanism. In order to match the fermion representation of the SM, the simplest choice is to assign fermions into triplets and anti-triplets of the $SU(3)_L$ group. However, this requires new fermions. In general, the electric charges of these new fermions are unkown. They, however, cannot be totally arbitrary because of the symmetry and of the matching condition with the SM. In most general terms, the electric-charge operator can be written as

$$\begin{aligned} Q = T_3 + \beta T_8 + X \mathbb {1}, \end{aligned}$$

(2)

where we have introduced the SU(3) generators $T_3$, $T_8$. Thus, the charge operator Q depends on two parameters $\beta$ and X. With this information, we can write down the lepton representation as follows. Left-handed leptons are assigned to anti-triplets and right-handed leptons to singlets:

$$\begin{aligned}&L'_{aL}=\left( \begin{array}{c} e'_a \\ -\nu '_{a} \\ E'_a \\ \end{array} \right) _L \sim \left( 3^*~, -\frac{1}{2}+\frac{\beta }{2\sqrt{3}}\right) , \quad a=1,2,3,\nonumber \\&e'_{aR}\sim \left( 1~, -1\right) , \quad \nu '_{aR}\sim \left( ~1~, 0\right) ,\nonumber \\&E'_{aR} \sim \left( ~1~, -\frac{1}{2}+\frac{\sqrt{3}\beta }{2}\right) . \end{aligned}$$

(3)

The model includes three RH neutrinos $\nu '_{aR}$ and exotic leptons $E'^a_{L,R}$ which are much heavier than the normal leptons. The prime denotes flavor states to be distinguished with mass eigenstates introduced later. The numbers in the parentheses are to label the representation of $SU(3)_L\otimes U(1)_X$ group. For singlets, we have $Q=X$ and hence the electric charges of the new leptons can be read off from the above information. The quark sector is not specified here since it is irrelevant to our present work.

We now discuss gauge and Higgs interactions. There are totally nine EW gauge bosons, included in the following covariant derivative:

$$\begin{aligned} D_{\mu }\equiv \partial _{\mu }-i g T^a W^a_{\mu }-i g_X X T^9X_{\mu }, \end{aligned}$$

(4)

where $T^9=\mathbb {1}/\sqrt{6}$, g and $g_X$ are coupling constants corresponding to the two groups $SU(3)_L$ and $U(1)_X$, respectively. The matrix $W^aT^a$, where $T^a =\lambda _a/2$ corresponding to a triplet representation, can be written as

$$\begin{aligned} W^a_{\mu }T^a=\frac{1}{2}\left( \begin{array}{ccc} W^3_{\mu }+\frac{1}{\sqrt{3}} W^8_{\mu }&{} \sqrt{2}W^+_{\mu } &{} \sqrt{2}Y^{+A}_{\mu } \\ \sqrt{2}W^-_{\mu } &{} -W^3_{\mu }+\frac{1}{\sqrt{3}} W^8_{\mu } &{} \sqrt{2}V^{+B}_{\mu } \\ \sqrt{2}Y^{-A}_{\mu }&{} \sqrt{2}V^{-B}_{\mu } &{}-\frac{2}{\sqrt{3}} W^8_{\mu }\\ \end{array} \right) , \nonumber \\ \end{aligned}$$

(5)

where we have defined the mass eigenstates of the charged gauge bosons as

$$\begin{aligned} W^{\pm }_{\mu }=\frac{1}{\sqrt{2}}\left( W^1_{\mu }\mp i W^2_{\mu }\right) ,\nonumber \\ Y^{\pm A}_{\mu }=\frac{1}{\sqrt{2}}\left( W^4_{\mu }\mp i W^5_{\mu }\right) ,\nonumber \\ V^{\pm B}_{\mu }=\frac{1}{\sqrt{2}}\left( W^6_{\mu }\mp i W^7_{\mu }\right) . \end{aligned}$$

(6)

From Eq. (2), the electric charges of the gauge bosons are calculated as

$$\begin{aligned} A=\frac{1}{2}+\beta \frac{\sqrt{3}}{2}, \quad B=-\frac{1}{2}+\beta \frac{\sqrt{3}}{2}. \end{aligned}$$

(7)

We note that B is also the electric charge of the new leptons $E_a$.

To generate masses for gauge bosons and fermions, we need three scalar triplets. They are defined as

$$\begin{aligned}&\chi =\left( \begin{array}{c} \chi ^{+A} \\ \chi ^{+B} \\ \chi ^0 \\ \end{array} \right) \sim \left( 3~, \frac{\beta }{\sqrt{3}}\right) , \nonumber \\&\rho =\left( \begin{array}{c} \rho ^+ \\ \rho ^0 \\ \rho ^{-B} \\ \end{array} \right) \sim \left( 3~, \frac{1}{2}-\frac{\beta }{2\sqrt{3}}\right) \nonumber \\&\eta =\left( \begin{array}{c} \eta ^0 \\ \eta ^- \\ \eta ^{-A} \\ \end{array} \right) \sim \left( 3~, -\frac{1}{2}-\frac{\beta }{2\sqrt{3}}\right) , \end{aligned}$$

(8)

where A, B denote electric charges as defined in Eq. (7). These Higgses develop vacuum expectation values (VEVs) defined as

$$\begin{aligned}&\langle \chi \rangle =\frac{1}{\sqrt{2}}\left( \begin{array}{c} 0 \\ 0 \\ u \\ \end{array} \right) , \quad \langle \rho \rangle =\frac{1}{\sqrt{2}}\left( \begin{array}{c} 0 \\ v \\ 0 \\ \end{array} \right) ,\nonumber \\&\langle \eta \rangle = \frac{1}{\sqrt{2}}\left( \begin{array}{c} v' \\ 0 \\ 0 \\ \end{array} \right) . \end{aligned}$$

(9)

The symmetry breaking happens in two steps: $SU(3)_L\otimes U(1)_X\xrightarrow {u} SU(2)_L\otimes U(1)_Y\xrightarrow {v,v'} U(1)_Q$. It is therefore reasonable to assume that $u > v,v'$. After the first step, five gauge bosons will be massive and the remaining four massless gauge bosons can be identified with the before-symmetry-breaking SM gauge bosons. This leads to the following matching condition for the couplings:

$$\begin{aligned} g_2 = g,\quad g_1 = g_X\frac{g}{\sqrt{6g^2 + \beta ^2 g_X^2}}, \end{aligned}$$

(10)

where $g_2$ and $g_1$ are the two couplings of the SM corresponding to $SU(2)_L$ and $U(1)_Y$, respectively. From this we get the following important equation, which helps to constrain $\beta$:

$$\begin{aligned} \frac{g_X^2}{g^2} = \frac{6s_W^2}{1-(1+\beta ^2)s_W^2}, \end{aligned}$$

(11)

where the Weinberg mixing angle is defined as $t_W = \tan \theta _W = g_1/g_2$ and we denote $s_W = \sin \theta _W$. Putting in the value of $s_W$, we get approximately

$$\begin{aligned} |\beta | \le \sqrt{3}, \end{aligned}$$

(12)

which will be used in the numerical analysis.

The masses of the charged gauge bosons are

$$\begin{aligned} m^2_{Y^{\pm A}}= & {} \frac{g^2}{4}(u^2+v^{\prime 2}),\quad m^2_{V^{\pm B}}=\frac{g^2}{4}(u^2+v^2),\nonumber \\ m^2_{W^\pm }= & {} \frac{g^2}{4}(v^2 + v^{\prime 2}). \end{aligned}$$

(13)

We now discuss the mixings of leptons. In general, the mixing between a SM lepton and a new lepton is allowed if they have the same electric charge. However, since we consider a general class of models with arbitrary $\beta$, this mixing effect will be neglected. This is justified because we will assume that the new leptons are much heavier than the SM leptons. Therefore, only generation mixings as in the SM are allowed. The Yukawa Lagrangian related to these mixings reads

$$\begin{aligned} \mathcal {L}^\text {yuk}_{\mathrm {lepton}}= & {} -Y^e_{ab} \overline{L'}_{aL} \eta ^*e'_{bR}- Y^\nu _{ab} \overline{L'}_{aL} \rho ^*\nu '_{bR} \nonumber \\&- Y^E_{ab} \overline{L'}_{aL} \chi ^*E'_{bR}+\mathrm {h.c.}, \end{aligned}$$

(14)

where $a,b=e,\mu ,\tau$ are family indices. The corresponding mass terms are:

$$\begin{aligned} \mathcal {L}^\text {mass}_{\mathrm {lepton}}= & {} -\frac{Y^e_{ab}v'}{\sqrt{2}} \overline{e'}_{aL}e'_{bR}+\frac{Y^\nu _{ab}v}{\sqrt{2}} \overline{\nu '}_{aL} \nu '_{bR}\nonumber \\&- \frac{Y^E_{ab}u}{\sqrt{2}} \overline{E'}_{aL} E'_{bR}+\mathrm {h.c.}. \end{aligned}$$

(15)

From now on we will work in the basis where the SM charged leptons are in their mass eigenstates. This can always be done without loss of generality. We can therefore set $Y^e_{ab}$ to be diagonal and $e' = e$ in Eqs. (14,15). The transformations from the flavor states to mass eigenstates are defined as

$$\begin{aligned} \nu '_{aL}= & {} U^L_{ab} \nu _{bL}, \quad \nu '_{aR} = U^R_{ab} \nu _{bR},\nonumber \\ E'_{aL}= & {} V^L_{ab} E_{bL}, \quad E'_{aR} = V^R_{ab} E_{bR}, \end{aligned}$$

(16)

where $U^{L,R}$ and $V^{L,R}$ are $3\times 3$ unitary matrices for the neutrinos and new leptons, respectively. The matrix $V^L$, included in the vertices of the SM charged leptons and the new leptons, is similar to the matrix $U^L=U_\text {PMNS}$.

For the Higgs sector, we assume $A,B \ne 0, \pm 1$, so that only the following mixings of scalar fields with the same electric charge are allowed: $(\chi _{A},~\eta _{A})$, $(\chi _{B},~\rho _{B})$, $(\rho ^+,\eta ^+)$ and $(\chi ^0,~\rho ^0,~ \eta ^0)$. The neutral components are expanded as

$$\begin{aligned}&\chi ^0=\frac{1}{\sqrt{2}} \left( u+\xi _{\chi }+i \zeta _{\chi }\right) , \quad \langle \xi _{\chi }\rangle =\langle \zeta _{\chi }\rangle =0, \nonumber \\&\rho ^0=\frac{1}{\sqrt{2}} \left( v+\xi _{\rho }+i \zeta _{\rho }\right) , \quad \langle \xi _{\rho }\rangle =\langle \zeta _{\rho }\rangle =0, \nonumber \\&\eta ^0=\frac{1}{\sqrt{2}} \left( v'+\xi _{\eta }+i \zeta _{\eta }\right) , \quad \langle \xi _{\eta }\rangle =\langle \zeta _{\eta }\rangle =0. \end{aligned}$$

(17)

The ratios between VEVs are used to define three mixing angles:

$$\begin{aligned} s^2_{v'v}= & {} \sin ^2\beta _{v'v}= \frac{v'^2}{v^2+v'^2}, \; s^2_{vu}=\sin ^2\beta _{vu}= \frac{v^2}{u^2+v^2}, \;\nonumber \\ s^2_{v'u}= & {} \sin ^2\beta _{v'u}= \frac{v'^2}{v'^2+u^2}. \end{aligned}$$

(18)

We will also use the following notation: $t_{v'v}=s_{v'v}/c_{v'v}$, $t_{v'u}=s_{v'u}/c_{v'u}$.

The scalar potential is

$$\begin{aligned} V_{\mathrm {h}}= & {} \mu _1^2 \eta ^{\dagger }\eta +\mu _2^2\rho ^{\dagger }\rho +\mu _3^2\chi ^{\dagger }\chi +\lambda _1 \left( \eta ^{\dagger }\eta \right) ^2 +\lambda _2\left( \rho ^{\dagger }\rho \right) ^2 \nonumber \\&+\lambda _3\left( \chi ^{\dagger }\chi \right) ^2\nonumber \\&+ \lambda _{12}(\eta ^{\dagger }\eta )(\rho ^{\dagger }\rho ) +\lambda _{13}(\eta ^{\dagger }\eta )(\chi ^{\dagger }\chi ) +\lambda _{23}(\rho ^{\dagger }\rho )(\chi ^{\dagger }\chi )\nonumber \\&+\tilde{\lambda }_{12} (\eta ^{\dagger }\rho )(\rho ^{\dagger }\eta ) +\tilde{\lambda }_{13} (\eta ^{\dagger }\chi )(\chi ^{\dagger }\eta ) +\tilde{\lambda }_{23} (\rho ^{\dagger }\chi )(\chi ^{\dagger }\rho )\nonumber \\&+\sqrt{2} f\left( \epsilon _{ijk}\eta ^i\rho ^j\chi ^k +\mathrm {h.c.} \right) . \end{aligned}$$

(19)

With the above notation, the mass eigenstates are

$$\begin{aligned} \left( \begin{array}{c} \phi ^{\pm }_W \\ H^{\pm } \\ \end{array} \right)= & {} \left( \begin{array}{cc} c_{v'v} &{} -s_{v'v} \\ s_{v'v} &{} c_{v'v} \\ \end{array} \right) \left( \begin{array}{c} \rho ^{\pm } \\ \eta ^{\pm } \\ \end{array} \right) , \end{aligned}$$

(20)

$$\begin{aligned} \left( \begin{array}{c} \phi ^{ \pm A}_Y \\ H^{\pm A} \\ \end{array} \right)= & {} \left( \begin{array}{cc} s_{v'u} &{} -c_{v'u} \\ c_{v'u} &{} s_{v'u} \\ \end{array} \right) \left( \begin{array}{c} \eta ^{\pm A} \\ \chi ^{\pm A} \\ \end{array} \right) , \end{aligned}$$

(21)

$$\begin{aligned} \left( \begin{array}{c} \phi ^{\pm B}_V \\ H^{\pm B} \\ \end{array} \right)= & {} \left( \begin{array}{cc} s_{vu} &{} -c_{vu} \\ c_{vu} &{} s_{vu} \\ \end{array} \right) \left( \begin{array}{c} \rho ^{\pm B} \\ \chi ^{\pm B} \\ \end{array} \right) , \end{aligned}$$

(22)

where $\phi _W^\pm$, $\phi ^{ \pm A}_Y$ and $\phi ^{\pm B}_V$ are the Goldstone bosons of $W^\pm$, $Y^{\pm A}$ and $V^{\pm B}$, respectively. The masses of the charged Higgs bosons are

$$\begin{aligned}&m^2_{H^{\pm }}=(v^2 + v^{\prime 2})\left( \frac{-fu}{v'v}+\frac{1}{2}\tilde{\lambda }_{12}\right) ,\nonumber \\&m^2_{H^{\pm A}}=(u^2+v^{\prime 2})\left( \frac{-fv}{v'u}+\frac{1}{2}\tilde{\lambda }_{13}\right) ,\nonumber \\&m^2_{H^{\pm B}}=(u^2+v^2)\left( \frac{-fv'}{uv}+\frac{1}{2}\tilde{\lambda }_{23}\right) . \end{aligned}$$

(23)

The neutral Higgs bosons are not involved in our calculation; hence they have been ignored. In total, there are six charged Higgs bosons, one neutral pseudoscalar Higgs and three neutral scalar Higgses. Bosonic particles with electric charges of $\pm B$ are not involved in the present calculation. Nevertheless, their masses and mixing angles are provided above for the sake of completeness.

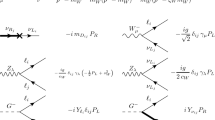
From the above information we can obtain all vertices needed for the calculation of $l_i \rightarrow l_j \gamma$ decays. They are listed in Table 1.

Table 1 Vertices and couplings for $l_i\rightarrow l_j\gamma$ decays in the 3-3-1 model with arbitrary $\beta$ and new leptons. All momenta are defined as incoming. The photon field is denoted as $A^\mu$, $a,b = 1,2,3$ are family indices and $\Gamma _{\lambda \mu \nu }(p_1,p_2,p_3)=(p_1-p_2)_\nu g_{ \lambda \mu } + (p_2-p_3)_\lambda g_{\mu \nu }+(p_3-p_1)_\mu g_{ \nu \lambda }$. Other notations are defined in the text

3 Analytical results

Equipped with the above Feynman rules, we can proceed to calculate the partial decay width of $l_1 \rightarrow l_2 \gamma$ using standard techniques of one-loop calculation. We have done this in a careful way, with at least two independent calculations, and paid special attention to the relative sign between the gauge and Higgs contributions. This relative sign is very important because, as we will see in the numerical results, the interference term can be positive or negative.

In the literature, the calculation of $l_1 \rightarrow l_2 \gamma$ is usually done by neglecting the external lepton masses. As stated in the introduction, we found this uneasy because the neutrino masses, which are much smaller than the lepton masses, are kept. We therefore want to check the validity of this approximation. To achieve this we have to keep the external lepton masses.

We have calculated the partial decay width of $l_1 \rightarrow l_2 \gamma$ from scratch without approximation. In the following we summarize the key points and present exact analytical results. Results for the SM case are obtained as a special case and are discussed in Sect. 4.1.

We consider the process

$$\begin{aligned} l_1(p_1) \rightarrow l_2(p_2) + \gamma (q), \end{aligned}$$

(24)

where $p_1 = p_2+q$ and the helicity indices have been omitted for simplicity. The amplitude reads

$$\begin{aligned} \mathcal {M} = \epsilon ^\lambda (q) \bar{u}_1(p_1)\Gamma _\lambda u_2(p_2), \end{aligned}$$

(25)

where $\epsilon ^\lambda$ is the photon’s polarization vector, $\Gamma _\lambda$ are $4\times 4$ matrices depending on the gamma matrices, external momenta and coupling constants. After requiring the general conditions that the spinors obey the Dirac equations, $q^\mu \epsilon _\mu =0$, and $q^\lambda \bar{u}_1(p_1)\Gamma _\lambda u_2(p_2) = 0$, we can prove that the amplitude depends on only two form factors as

$$\begin{aligned} \mathcal {M}= & {} 2(p_1\cdot \epsilon ) \left[ C_L\bar{u}_2(p_2)P_Lu_1(p_1)+C_R\bar{u}_2(p_2)P_Ru_1(p_1)\right] \nonumber \\&- (m_1C_R + m_2C_L) \bar{u}_2(p_2)/\!\!\!\epsilon P_L u_1(p_1) \nonumber \\&- (m_1C_L + m_2C_R)\bar{u}_2(p_2)/\!\!\!\epsilon P_R u_1(p_1), \end{aligned}$$

(26)

where $C_{L,R}$ are called form factors, $P_L = (1-\gamma _5)/2$, $P_R = (1+\gamma _5)/2$. The partial decay width is then written as

$$\begin{aligned} \Gamma (l_1\rightarrow l_2\gamma )= \frac{(m^2_1-m^2_2)^3}{16\pi m^3_1}\left( |C_L|^2+|C_R|^2\right) . \end{aligned}$$

(27)

This result is well known and has been given in e.g. Ref. [17].

Since we assume that the exotic leptons are much heavier than the SM leptons, the branching fractions of the dominant decays of $l_1 \rightarrow l_2 \bar{\nu }_2 \nu _1$ in the 3-3-1 model are the same as those of the SM. Using the well-known tree-level result of $\Gamma (l_1 \rightarrow l_2 \bar{\nu }_2 \nu _1) = G_F^2 m_1^5/(192\pi ^3)$ (see e.g. [18]), where $G_F$ is the Fermi coupling constant, we write the branching fraction as

$$\begin{aligned} \text {Br}(l_1 \rightarrow l_2 \gamma ) = \frac{12\pi ^2}{G_F^2}\left( |D_L|^2+|D_R|^2\right) \text {Br}(l_1 \rightarrow l_2 \bar{\nu }_2 \nu _1),\nonumber \\ \end{aligned}$$

(28)

where $G_F=g^2/(4\sqrt{2}m^2_W)$ and we have defined $C_{L,R} = m_1 D_{L,R}$ and the approximation $m_2 \ll m_1$ has been used for the first factor, but not for $D_{L,R}$. For later numerical analysis we will use $\text {Br}(\mu \rightarrow e \bar{\nu }_e \nu _\mu ) = 100\%$, $\text {Br}(\tau \rightarrow e \bar{\nu }_e \nu _\tau ) = 17.82\%$ and $\text {Br}(\tau \rightarrow \mu \bar{\nu }_\mu \nu _\tau ) = 17.39\%$ as given in Ref. [1]. It is noted that $D_L\propto \mathcal {O}(m_2/m_1)$ (since only a left-handed electron can participate in $SU(3)_L$ interactions) and $D_R\propto \mathcal {O}(1)$, and hence, in the approximation $m_2 \ll m_1$, we have $\text {Br}(l_1 \rightarrow l_2 \gamma ) \propto |D_R|^2$. This point is important to understand the approximate results discussed in the next sections.

Fig. 1

Representative Feynman diagrams contributing to $l_1\rightarrow l_2 \gamma$ decays. There are two groups: the neutrino contribution (a,d) and the exotic-lepton contribution (b,c,e,f)

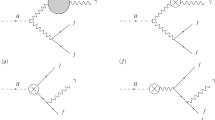
The next step is to calculate $D_{L,R}$ for the 3-3-1 model with arbitrary beta presented in the previous section. Representative Feynman diagrams are shown in Fig. 1. Using the Feynman rules in Table 1 and summing over all possible Feynman diagrams, we obtain the following results:

$$\begin{aligned} D_{L,R}=D_{L,R}^{\nu W}+D_{L,R}^{\nu H^+}+D_{L,R}^{E Y}+D_{L,R}^{E H^A}, \end{aligned}$$

(29)

where

$$\begin{aligned} D_R^{\nu W} =&-\frac{ieg^2}{32\pi ^{2}m_W^2}\sum _{a=1}^3 U_{i_1 a}^{L \star }U_{i_2 a}^{L}\nonumber \\&\times \left( 2m^2_W g_1^{\nu _a WW} + m^2_{\nu _a}g_2^{\nu _a WW} + m^2_2g_3^{\nu _a WW} \right) ,\nonumber \\ D_L^{\nu W} =&-\frac{ieg^2m_2}{32\pi ^{2}m_W^2m_1}\sum _{a=1}^3 U_{i_1 a}^{L \star }U_{i_2 a}^{L}\nonumber \\&\times \left( 2m_W^2g_4^{\nu _a WW} +m^2_{\nu _a}g_5^{\nu _a WW} +m_1^2g_6^{\nu _a WW} \right) ,\nonumber \\ D_R^{\nu H^+} =&-\frac{ieg^2}{32\pi ^{2}m_W^2}\sum _{a=1}^3 U_{i_1 a}^{L \star }U_{i_2 a}^{L}\nonumber \\&\times \left( m^2_{\nu _a}t^2_{v'v}h_1^{\nu _a H^+H^+} + \frac{m^2_2}{t^2_{v'v}}h_2^{\nu _a H^+H^+} + m^2_{\nu _a}h_3^{\nu _a H^+H^+} \right) ,\nonumber \\ D_L^{\nu H^+} =&-\frac{ieg^2m_2}{32\pi ^{2}m_W^2m_1}\sum _{a=1}^3 U_{i_1 a}^{L \star }U_{i_2 a}^{L}\nonumber \\&\times \left( \frac{m^2_1}{t^2_{v'v}}h_1^{\nu _a H^+H^+} + m^2_{\nu _a}t^2_{v'v}h_2^{\nu _a H^+H^+} + m^2_{\nu _a}h_3^{\nu _a H^+H^+} \right) ,\nonumber \\ D_R^{E Y} =&-\frac{ieg^2}{32\pi ^{2}m_Y^2}\sum _{a=1}^3 V_{i_1 a}^{L \star }V_{i_2 a}^{L}\nonumber \\&\times \left[ A\left( 2m^2_Y g_1^{E_a YY} + m^2_{E_a}g_2^{E_a YY} + m^2_2g_3^{E_a YY} \right) \right. \nonumber \\&+\left. B\left( 2m^2_Y g_7^{YE_aE_a} + m^2_{E_a} g_8^{YE_aE_a} + m^2_2 g_9^{YE_aE_a}\right) \right] ,\nonumber \\ D_L^{E Y} =&-\frac{ieg^2m_2}{32\pi ^{2}m_Y^2m_1}\sum _{a=1}^3 V_{i_1 a}^{L \star }V_{i_2 a}^{L}\nonumber \\&\times \left[ A\left( 2m_Y^2g_4^{E_a YY} +m^2_{E_a}g_5^{E_a YY} +m_1^2g_6^{E_a YY} \right) \right. \nonumber \\&+\left. B\left( 2m^2_Y g_{10}^{YE_aE_a}+m^2_{E_a} g_{11}^{YE_aE_a}+m^2_1 g_{12}^{YE_aE_a}\right) \right] ,\nonumber \\ D_R^{E H^A} =&-\frac{ieg^2}{32\pi ^{2}m_Y^2}\sum _{a=1}^3 V_{i_1 a}^{L \star }V_{i_2 a}^{L}\nonumber \\&\times \left[ A\left( m^2_{E_a}t^2_{v'u}h_1^{E_a H^AH^A} + \frac{m^2_2}{t^2_{v'u}}h_2^{E_a H^AH^A} + m^2_{E_a}h_3^{E_a H^AH^A} \right) \right. \nonumber \\&+\left. B\left( m^2_{E_a}t^2_{v'u}h_4^{H^AE_aE_a} + \frac{m^2_2}{t^2_{v'u}}h_5^{H^AE_aE_a} + m^2_{E_a}h_6^{H^AE_aE_a} \right) \right] ,\nonumber \\ D_L^{E H^A} =&-\frac{ieg^2m_2}{32\pi ^{2}m_Y^2m_1}\sum _{a=1}^3 V_{i_1 a}^{L \star }V_{i_2 a}^{L}\nonumber \\&\times \left[ A\left( \frac{m^2_1}{t^2_{v'u}}h_1^{E_a H^AH^A} + m^2_{E_a}t^2_{v'u}h_2^{E_a H^AH^A} + m^2_{E_a}h_3^{E_a H^AH^A} \right) \right. \nonumber \\&+\left. B\left( \frac{m^2_1}{t^2_{v'u}}h_4^{H^AE_aE_a} + m^2_{E_a}t^2_{v'u}h_5^{H^AE_aE_a} + m^2_{E_a}h_6^{H^AE_aE_a} \right) \right] , \end{aligned}$$

(30)

where the loop functions $h_i$ and $g_i$ are simple linear combinations of Passarino–Veltman one-loop 3-point functions as given in Appendix A. The above writing is inspired by Lavoura [17]. Our results have been checked by three different calculations using (i) the unitary gauge, (ii)the ’t Hooft–Feynman gauge, and (iii) the general formulas of Ref. [17]. We have classified the results into neutrino and exotic-lepton groups. Each of these groups includes Higgs and gauge contributions. In the ’t Hooft–Feynman gauge, the gauge contribution includes gauge–gauge, Goldstone–gauge and Goldstone–Goldstone diagrams. We have used FORM [19, 20] to calculate the amplitudes.

The results can be further simplified if $m_{E_a} \ll m_Y$ and $m_{E_a} \ll m_{H^A}$ with $a=1,2,3$ as presented in Appendix B.

Finally, we make an important remark on the dependence on coupling constants. From Eq. (30) we have $D_{L,R}\propto eg^2$. Using Eq. (28) and noticing that $G_F=g^2/(4\sqrt{2}m^2_W)$, we get $\text {Br}(l_1 \rightarrow l_2 \gamma ) \propto e^2$, being independent of g or $s_W$. Clearly, the coupling constant $e=\sqrt{4\pi \alpha }$ should be calculated in the low-energy limit for the processes at hand. Therefore, we will use $\alpha (0)$ as input parameter in our numerical analyses.

4 Numerical results

Input parameters are specified as follows. We use, according to Ref. [1],

$$\begin{aligned}&\alpha (0) = 1/137.035999679,\quad m_W = 80.385 {\,\text {GeV}},\nonumber \\&m_e = 0.5109989461 {\,\text {MeV}}, \quad m_{\mu } = 105.6583745 {\,\text {MeV}}, \nonumber \\&m_{\tau } = 1776.86 {\,\text {MeV}},\nonumber \\&\Delta m^2_{21}=7.53\times 10^{-5} {\,\text {eV}}^{2}, \quad \Delta m^2_{32}=2.45\times 10^{-3} {\,\text {eV}}^2,\nonumber \\&\sin ^2(\theta _{12})=0.307, \quad \sin ^2(\theta _{13}) = 0.021, \quad \sin ^2(\theta _{23}) = 0.51.\nonumber \\ \end{aligned}$$

(31)

The neutrino mixing matrix is assumed to be real and is calculated from the above mixing angles as

$$\begin{aligned} U^L = \left( \begin{array}{ccc} c_{12}c_{13} &{} s_{12}c_{13} &{} s_{13} \\ -s_{12}c_{23}-c_{12}s_{23}s_{13} &{} c_{12}c_{23} - s_{12}s_{23}s_{13} &{} s_{23}c_{13}\\ s_{12}s_{23} - c_{12}c_{23}s_{13} &{} -c_{12}s_{23} - s_{12}c_{23}s_{13} &{} c_{23}c_{13} \end{array} \right) ,\nonumber \\ \end{aligned}$$

(32)

where $c_{ij}=\cos \theta _{ij}$, $s_{ij}=\sin \theta _{ij}$ with $i,j=1,2,3$.

4.1 Neutrino contribution: approximate vs. exact

The approximate results calculated by neglecting the external lepton masses have been exclusively used in the literature. However, the justification is not totally obvious to us because the neutrino masses, which are much smaller than the lepton masses, are kept. We therefore here present compact formulas for the exact results (i.e. $m_1$ and $m_2$ kept) and perform a numerical comparison with the approximate ones.

The SM result includes only the W contribution and is given by $D_{L,R}^{\nu W}$. Using the formulas in Appendix A we write the result in terms of scalar one-loop integrals $A_0$, $B_0$ and $C_0$, which are also calculated in Appendix A. We obtain

$$\begin{aligned} D_R^{\nu W}=&-\frac{ieg^2}{64\pi ^{2}m_W^4 t_1 (t_1-t_2)^2}\sum _{a=1}^3 U_{i_1 a}^{L \star }U_{i_2 a}^{L} \{(t_1-t_2)\nonumber \\&(t_{a}-t_1+2)[A_{0}(m^2_W) - A_{0}(m^2_{\nu _a})]\nonumber \\&+m^2_W \left[ t_{a}^2(2t_1-t_2)-t_{a}(2t_1^2-2t_1+t_2)+t_1^2\right. \nonumber \\&\left. (4+t_2)-5t_1t_2-4t_1+2t_2\right] B^{(1)}_{0}\nonumber \\&-m^2_W t_1 \left[ t_{a}^2-t_{a}(t_1+t_2-1)\right. \nonumber \\&\left. + t_1t_2-4t_2+3t_1-2\right] B^{(2)}_{0}\nonumber \\&-2m^4_W t_1 (t_1-t_2)(t_{a}+t_2-2t_1+2)C_0\nonumber \\&-m^2_W t_1 (t_1-t_2) (t_{a}-t_2+2)\},\nonumber \\ D_L^{\nu W}=&-\frac{ieg^2m_2}{64\pi ^{2}m_W^4 m_1 t_{2}(t_{1}-t_{2})^2}\sum _{a=1}^3 U_{i_1 a}^{L \star }U_{i_2 a}^{L} \{(t_{2}-t_{1})\nonumber \\&(t_{a}-t_{2}+2)[A_{0}(m^2_W) - A_{0}(m^2_{\nu _a})]\nonumber \\&+m^2_W \left[ t_{a}^2(2t_2-t_1)-t_{a}(2t_2^2-2t_2+t_1)\right. \nonumber \\&\left. +t_2^2(4+t_1)-5t_1t_2-4t_2+2t_1\right] B_0^{(2)}\nonumber \\&-m^2_W t_{2} \left[ t_{a}^2-t_{a} (t_{1}+t_{2}-1)+ t_{1}t_{2}-4t_{1}+3 t_{2}-2\right] B_0^{(1)}\nonumber \\&- 2 m^4_W t_{2} (t_{2}-t_{1})(t_{a}+t_1-2t_2+2)C_0\nonumber \\&- m^2_W t_{2} (t_{2}-t_{1}) (t_{a}-t_{1}+2) \}, \end{aligned}$$

(33)

where $t_i=m^2_i/m^2_W$, $t_a=m^2_{\nu _a}/m^2_W$, $B_0^{(i)}=B_0(m^2_i,m^2_W,m^2_{\nu _a})$ with $i=1,2$ and $C_0=C_0(m^2_1,0,m^2_2,m^2_{\nu _a},m^2_W,m^2_W)$.

In the limit of $m_1=m_2=0$ we have $D_L=0$ and

$$\begin{aligned} D_R^\text {appr}= & {} \frac{ieg^2}{128\pi ^{2}m^2_W}\sum _{a=1}^3 U_{i_1 a}^{L \star }U_{i_2 a}^{L}\nonumber \\&\times \left[ \frac{10-43 t_{a}+78 t_{a}^2 -49 t_{a}^3+18 t_{a}^3 \log (t_{a}) +4 t_{a}^4}{3 (t_{a}-1)^4} \right] .\nonumber \\ \end{aligned}$$

(34)

This result was first obtained in Ref. [21] and has been widely used for any values of neutrino masses. We may wonder whether this is justified for the case of $m_{\nu _a}\ll m_1$ or $m_{\nu _a}\approx m_1$. This is the reason we perform a numerical comparison here between the exact result and the approximate one with $m_1=m_2=0$ for many values of $m_{\nu _1}$ from zero to$10^{16}{\,\text {GeV}}$. The motivation is of purely mathematical nature and we ignore the physical constraints on the neutrino masses here. The results are shown in Table 2 and Fig. 2. We have used Eq. (28) to calculate the branching fractions for both cases. We see that the difference is less than permil level for $\mu \rightarrow e \gamma$ and $\tau \rightarrow e \gamma$ and is at the permil level for $\tau \rightarrow \mu \gamma$. This result is independent of neutrino masses.

Table 2 Exact (i.e. $m_1$ and $m_2$ are kept in $D_{L,R}$) and approximate (i.e. $m_1=m_2=0$) branching fractions of $l_1 \rightarrow l_2 \gamma$ at various hypothetical values of $m_{\nu _1}$. Other two neutrino masses are fixed at tiny values calculated using $m_{\nu _1}=0$ and the current known values of $\Delta m^2_{21}$ and $\Delta m^2_{32}$ specified in the text, namely$m_{\nu _2}\approx 8.678\times 10^{-3}{\,\text {eV}}$ and$m_{\nu _3}\approx 5.025\times 10^{-2}{\,\text {eV}}$. The neutrino mixing matrix is assumed being real and is calculated from three known mixing angles $\theta _{12}$, $\theta _{13}$ and $\theta _{23}$ as given in the text. For the sake of comparison we set $\text {Br}(l_1\rightarrow l_2\bar{\nu }_2\nu _1)=1$ for all three channels. The difference between exact and approximate results is defined as: $\text {diff}=(\text {appr}-\text {exact})/\text {exact}$

Fig. 2

Exact branching fraction (left) and difference between exact and approximate results (right) as functions of $m_{\nu _1}$, which we deliberately chose from very small to very large values. All input parameters and definitions are as in the caption of Table 2

We now take into account the charged Higgs contribution. There are two additional parameters $t_{v'v}$ and $m_{H^\pm }$ (see the $D_{L,R}^{\nu H^+}$ terms in Eq. (30)). We have calculated the difference between the exact and approximate results for four cases of $t_{v'v}=1/50$ or 50 (we choose these exotic values so that the effect of $t_{v'v}$ is large) and $m_{H^\pm }=70$ or$700{\,\text {GeV}}$. The result is very similar to the SM case: the difference is below permil level for $\mu \rightarrow e \gamma$ and $\tau \rightarrow e \gamma$ and is at the permil level for $\tau \rightarrow \mu \gamma$. For the absolute value of $\text {Br}(\mu \rightarrow e \gamma )$ the result is $5\times 10^{-49}$ for $t_{v'v}=50$ and$m_{H^\pm }=70{\,\text {GeV}}$ and getting smaller for lower values of $t_{v'v}$ and/or higher values of $m_{H^\pm }$.

We make a technical remark here. Due to the huge hierarchy among the neutrino, charged leptons and W boson masses, the numerical calculation of the exact result is non-trivial because of numerical cancellation. To obtain the $\mu \rightarrow e \gamma$ results in Table 2 we have used Mathematica 9 with at least 62 precision digits for$m_{\nu _1}=10^{-13}{\,\text {GeV}}$ and about 180 precision digits for$m_{\nu _1}=10^{16}{\,\text {GeV}}$.

4.2 Exotic-lepton contribution

In this numerical study we investigate the exotic-lepton contribution, to see how large the branching fractions can reach, what can be the dominant effects and dependence on the parameter $\beta$, $m_Y$ and $m_{H^A}$. We will also show the gauge–Higgs interference effects.

In the previous section we have shown that the neutrino contribution is well below the current experimental limit. We will therefore neglect the neutrino contribution including interference effects with exotic leptons in the following. The external lepton masses will be neglected as justified in Sect. 4.1.

In the following we choose a benchmark point, which is a typical scenario where the $SU(3)_L$ symmetry-breaking energy scale is much larger than the SM energy scale, i.e. $m_{Y^A} \gg m_W$. If not otherwise stated, the value is chosen as

$$\begin{aligned} m_{Y^A} = 2{\,\text {TeV}}. \end{aligned}$$

(35)

From Eq. (18) we have

$$\begin{aligned} 1 + \text {ct}^2_{v'u} = \frac{m^2_{Y^A}}{m^2_W}\left( 1 + \text {ct}^2_{v'v}\right) , \end{aligned}$$

(36)

where $\text {ct}_{v'u} = 1/t_{v'u} = u/v'$, $\text {ct}_{v'v} = 1/t_{v'v} = v/v'$. For the case of $m_{Y^A} \gg m_W$, we get

$$\begin{aligned} \text {ct}^2_{v'u} \approx \frac{m^2_{Y^A}}{m^2_W}\left( 1 + \text {ct}^2_{v'v}\right) \gg 1. \end{aligned}$$

(37)

This means that the terms proportional to $t_{v'u}$ in $D_R^{E H^A}$ in Eq. (30) can be safely neglected and the branching fractions are almost independent of $t_{v'v}$. We note that terms proportional to $\text {ct}_{v'u}$ are suppressed because they are also proportional to the external lepton masses. We will therefore set $t_{v'v} = 1$ in the following. As a side note, for the choice of $v' = v$ there is another good justification: it makes the parameter $\rho = m^2_W/(m^2_Z \cos ^2\theta _W)$ with $\theta _W$ being the weak-mixing angle close to unity, as pointed out in Ref. [22] where the same scalar potential is used.

Other parameters related to the exotic leptons are unknown. We choose, as an example, the following default values for the remaining input parameters:

$$\begin{aligned} \beta&= 1/\sqrt{3}, \quad m_{H^{A}} = 3{\,\text {TeV}}, \nonumber \\ m_{E_1}&= 700{\,\text {GeV}}, \quad m_{E_2} = 800{\,\text {GeV}}, \quad m_{E_3} = 1{\,\text {TeV}}, \nonumber \\ \theta _{12}^{E}&= \pi /6, \quad \theta _{13}^{E} = \pi /3, \quad \theta _{23}^{E} = \pi /4. \end{aligned}$$

(38)

The mixing matrix $V^L$ is calculated from three mixing angles $\theta _{12}^{E}$, $\theta _{13}^{E}$, and $\theta _{23}^{E}$ as in the case of neutrinos. The values of the exotic-lepton masses are chosen within the unitary bound of $m_{E_i} < 16m_{Y^A}$ as derived from the partial wave unitarity of the $E_i \bar{E}_i \rightarrow E_i \bar{E}_i$ scattering [23].

Table 3 Summary of lower bounds on $m_{Z'}$ for 3-3-1 models with exotic leptons obtained using ATLAS or CMS data at 7 and$8{\,\text {TeV}}$. Exotic fermion contributions to the $Z'$ total width are neglected, except for Ref. [24] where$m_F = 1{\,\text {TeV}}$ is assumed for all exotic fermions. In the last column we have derived the bound on $m_{Y^A}$ using the relation $m_{Y^A} \approx m_{Z'}\sqrt{3[1-(1+\beta ^2)s^2_W]}/(2c_W)$ obtained using $v,v'\ll u$ approximation [6] and $s^2_W = 0.231$

Table 4 Branching fractions of $l_1 \rightarrow l_2 \gamma$ at various values of $\beta$, $m_{Y^A}$. Other parameters are fixed as given in the text

Fig. 3

Density plot of $\mu \rightarrow e\gamma$ branching fraction as a function of $\beta$ and $m_Y$ (left) and of $\beta$ and $m_{H^A}$ (right). Other parameters are fixed as given in the text

Fig. 4

$l_i\rightarrow l_j\gamma$ branching fractions as functions of $m_Y$ (left column) and of $m_{H^A}$ (right column) for various values of $\beta$: 0 (top row), $1/\sqrt{3}$ (middle row) and $\sqrt{3}$ (bottom row). Other parameters are fixed as given in the text

A few remarks on the above default input-parameter choice are appropriate here. Concerning gauge bosons, the best ATLAS/CMS limits for 3-3-1 models with exotic leptons are summarized in Table 3. We note that, in almost all cases, the contributions from exotic leptons to the $Z'$ total width are neglected, except for the case of Ref. [24] where$m_F = 1{\,\text {TeV}}$ is assumed for all exotic fermions. When those contributions are properly taken into account, the bound on $m_{Z'}$ will get weaker, because the branching fractions of $Z'\rightarrow l^+ l^-$ with $l=e,\mu$ will decrease. Therefore, the default choice in Eq. (35) may be acceptable. However, one should keep in mind that, strictly speaking, the ATLAS/CMS bound on $m_{Z'}$ is unknown for our present numerical analysis, because it depends on the masses and electric charges of the exotic fermions (i.e. leptons and quarks) which have not been properly taken into account. We will therefore relax the constraint on $m_{Y^A}$, varying it from 0.5 to$3{\,\text {TeV}}$ for some plots. In this context, it is noted that, using LEP II data, the authors of Ref. [15] obtained$m_{Z'}\gtrapprox 1{\,\text {TeV}}$ for $\beta = \pm 1/\sqrt{3}$, $2/\sqrt{3}$, leading to$m_{Y^A}\gtrapprox 0.7{\,\text {TeV}}$. Phenomenological constraints on the masses of exotic Higgs bosons $H^A$ and of the exotic leptons and their mixing angles are much more difficult to obtain and do not exist to the best of our knowledge.

With those difficulties in mind, we decided to choose the above default input parameters in a fairly random way following a few general principles: (i) $u \gg v,v'$ (i.e. the $SU(3)_L$ breaking scale is much larger than that of $SU(2)_L$), (ii) the exotic leptons are heavy and satisfy the unitary bound, (iii) and their mixing angles are large. We note that the choice of heavy masses are in agreement with the negative results of collider searches for physics beyond the SM. Large mixing angles are motivated by the PMNS matrix of the neutrino sector and the fact that we want to have large branching fractions close to the experimental limits.

In the following tables and plots, if not otherwise stated, the above default values are used. Differently from Sect. 4.1, we will use the true values of $\text {Br}(l_1 \rightarrow l_2 \bar{\nu }_2\nu _1)$ as given in the text below Eq. (28) so that one can compare the results in this section with current experimental limits.

Fig. 5

Branching fraction of $\mu \rightarrow e\gamma$ as a function of $m_Y$ (left) and of $\beta$ (right). Gauge (blue), Higgs (brown) and interference (red) contributions are also separately shown. Total branching fractions are the black lines. Other parameters are fixed as given in the text

In Table 4 we present the $l_1 \rightarrow l_2 \gamma$ branching fractions for various values of $\beta$, $m_{Y^A}$. We observe the following features: the branching fractions are smallest at $\beta = 0$ and increase with $|\beta |$. The results exhibit a clear asymmetry under the transformation of $\beta \rightarrow -\beta$, or in other words, they depend on the sign of $\beta$. The right table shows a strong dependence on $m_{Y^A}$. As expected, the branching fractions are large when $m_{Y^A}$ is small. With the choice of exotic-lepton masses and mixing angles as given in Eq. (38), the branching fraction is largest for $\mu \rightarrow e \gamma$ and smallest for $\tau \rightarrow \mu \gamma$. With this setup, we see that the branching fractions of $\tau \rightarrow e \gamma$ and $\tau \rightarrow \mu \gamma$ all satisfy the current experimental constraints for all values of $\beta$ and $m_{Y^A}$ in Table 4. For the decay of $\mu \rightarrow e \gamma$, only the cases of $\beta = 0$ or$m_{Y^A}=3{\,\text {TeV}}$ are below the experimental limit of $4.2\times 10^{-13}$.

We now focus on the decay $\mu \rightarrow e \gamma$ and discuss two density plots to see the dependence on $\beta$, $m_{Y}$ and $m_{H^A}$. In Fig. 3 we show the density plot of $\text {Br}(\mu \rightarrow e \gamma )$ as a function of $\beta$ and $m_Y$ (left) and of $\beta$ and $m_{H^A}$ (right). We observe from the left plot, consistently with Table 4, the branching fraction are smallest when $\beta$ is around zero or when $m_{Y}$ is large. From the right plot, we see a similar dependence on $\beta$, but the dependence on $m_{H^A}$ is much weaker than on $m_{Y}$. From those two plots, we conclude that large branching fraction occurs at large $|\beta |$, small $m_Y$ and small $m_{H^A}$.

In a series of six plots in Fig. 4 we would like to show again the dependence on $\beta$, $m_Y$ and $m_{H^A}$, but with two-dimensional plots this time and for all three decays. We see clearly that the case of $\beta = 0$ is special and different from the other cases of $\beta = 1/\sqrt{3}, \sqrt{3}$. For $\beta = 0$, the branching fractions of all three decays have a deep minimum when $m_Y$ or $m_{H^A}$ reach special values. The minimum positions are at low energies and are different for different decays, suggesting that they depend on the mixing angles. Together with Fig. 3 we conclude that a deep minimum occurs when $|\beta |$ is small enough. This has a very important phenomenological consequence: for small values of $|\beta |$, branching fraction can be very small even at small values of $m_Y$ and $m_{H^A}$. This means that, contrary to naive expectation, there can be small values of $m_Y$ and $m_{H^A}$ escaping the exclusion limit obtained using the experimental constraints on $\text {Br}(l_i \rightarrow l_j \gamma )$, if $|\beta |$ is small enough.

To understand the minimum occurring when $\beta$ is around zero we have to study the dependence of the branching fraction on $\beta$. This is shown in Fig. 5 (right). On the left plot we display again the dependence on $m_Y$ for the special case of $\beta = 0$. This time, differently from Fig. 4 (top-left), we focus on the low-energy region of$m_Y \in [0.5,1]{\,\text {TeV}}$ and gauge, Higgs and interference contributions are also plotted. The left plot shows that the interference is strongly destructive and there is a spectacular cancellation between the sum of gauge and Higgs contributions and the interference term, leaving a very small branching ratio. The $\beta$ dependence plot also shows a negative interference effect when $\beta \in [0.035:0.26]$ for our default choice of input parameters. The insert in Fig. 5 (right) shows that the interference line crosses the zero branching fraction line when the gauge contribution (blue line) vanishes and when the Higgs term (brown line) vanishes. One should note that the gauge or Higgs contributions are non-negative. Overall, Fig. 5 shows that destructive interference effect tends to occur when $|\beta |$ and $m_Y$ are small.

5 Conclusions

In this paper, we have provided full and exact analytical results for the $l_i \rightarrow l_j \gamma$ partial decay widths for a general class of 3-3-1 models with exotic leptons and with arbitrary $\beta$. As a by product, we performed numerical comparisons between exact results (i.e. external lepton masses are kept) and approximate ones where $m_i = m_j = 0$. We conclude that, for either extremely light neutrinos or very heavy leptons, the difference between exact and approximate results is less than permil level for $\mu \rightarrow e \gamma$ and $\tau \rightarrow e \gamma$ and is at the permil level for $\tau \rightarrow \mu \gamma$. Therefore, unsurprisingly, approximation results widely used in the literature are excellently justified.

Concerning the exotic-lepton contribution, we found huge destructive interference between the gauge and Higgs contributions. This can happen when $|\beta |$ and $m_Y$ are small enough. This has an interesting consequence: the branching fractions can be small even for small $m_Y$. Therefore, this destructive interference mechanism must be taken into account when using experimental constraints on $\text {Br}(l_i \rightarrow l_j \gamma )$ to exclude parameter space. This in particular means that if one takes into account only the gauge contribution then the results can be completely off. It is likely that this destructive interference mechanism also occurs in $b \rightarrow s\gamma$ and other similar processes.

Besides, we found that the gauge and Higgs contributions can be of similar size. Dependences on $\beta$, $m_Y$ and $m_{H^A}$ have been shown. We observe that the branching fractions are very sensitive to $\beta$ and $m_Y$. They also depend on $m_{H^A}$, but to a lesser extent. The dependence on $\beta$ is interesting: the branching fractions are largest for $|\beta |=\sqrt{3}$ and smallest around zero.

Appendices

Appendix A: One-loop integrals

In this appendix we provide all loop functions introduced in Eq. (30). We have

$$\begin{aligned} h_1^{LHH}&=C_{1}([p_i^2],m_L^2,m_H^2,m_H^2) +C_{11}(\cdots ) +C_{12}(\cdots ),\nonumber \\ h_2^{LHH}&=C_{2}([p_i^2],m_L^2,m_H^2,m_H^2) +C_{22}(\cdots ) +C_{12}(\cdots ),\nonumber \\ h_3^{LHH}&=-C_{0}([p_i^2],m_L^2,m_H^2,m_H^2) -C_{1}(\cdots ) -C_{2}(\cdots ),\nonumber \\ h_4^{HLL}&=C_1([p_i^2],m_H^2,m_L^2,m_L^2)+C_{11}(\cdots )+C_{12}(\cdots ),\nonumber \\ h_5^{HLL}&=C_2([p_i^2],m_H^2,m_L^2,m_L^2)+C_{22}(\cdots )+C_{12}(\cdots ),\nonumber \\ h_6^{HLL}&=C_1([p_i^2],m_H^2,m_L^2,m_L^2)+C_{2}(\cdots ),\nonumber \\ g_1^{LGG}&=-C_{2}([p_i^2],m_L^2,m_G^2,m_G^2)+C_{11}(\cdots )+C_{12}(\cdots ),\nonumber \\ g_2^{LGG}&=C_0([p_i^2],m_L^2,m_G^2,m_G^2)+2C_{1}(\cdots )+C_{2}(\cdots )\nonumber \\&\quad +C_{11}(\cdots )+C_{12}(\cdots ),\nonumber \\ g_3^{LGG}&=C_{2}([p_i^2],m_L^2,m_G^2,m_G^2)+C_{22}(\cdots )+C_{12}(\cdots ),\nonumber \\ g_4^{LGG}&=-C_{1}([p_i^2],m_L^2,m_G^2,m_G^2)+C_{22}(\cdots )+C_{12}(\cdots ),\nonumber \\ g_5^{LGG}&=C_{0}([p_i^2],m_L^2,m_G^2,m_G^2)+C_{1}(\cdots )+2C_{2}(\cdots )\nonumber \\&\quad +C_{22}(\cdots )+C_{12}(\cdots )),\nonumber \\ g_6^{LGG}&=C_{1}([p_i^2],m_L^2,m_G^2,m_G^2)+C_{11}(\cdots )+C_{12}(\cdots ),\nonumber \\ g_7^{GLL}&=C_0([p_i^2],m_G^2,m_L^2,m_L^2)+2C_{1}(\cdots )+C_{2}(\cdots )\nonumber \\&\quad +C_{11}(\cdots )+C_{12}(\cdots ),\nonumber \\ g_8^{GLL}&=-C_2([p_i^2],m_G^2,m_L^2,m_L^2)+C_{11}(\cdots )+C_{12}(\cdots ),\nonumber \\ g_9^{GLL}&=C_2([p_i^2],m_G^2,m_L^2,m_L^2)+C_{22}(\cdots )+C_{12}(\cdots ),\nonumber \\ g_{10}^{GLL}&=C_0([p_i^2],m_G^2,m_L^2,m_L^2)+C_{1}(\cdots )+2C_{2}(\cdots )\nonumber \\&\quad +C_{22}(\cdots )+C_{12}(\cdots ),\nonumber \\ g_{11}^{GLL}&=-C_1([p_i^2],m_G^2,m_L^2,m_L^2)+C_{22}(\cdots )+C_{12}(\cdots ),\nonumber \\ g_{12}^{GLL}&=C_1([p_i^2],m_G^2,m_L^2,m_L^2)+C_{11}(\cdots )+C_{12}(\cdots ), \end{aligned}$$

(A1)

where $[p_i^2]=m_1^2,0,m_2^2$ related to external momenta and occurring in all functions, the notation $(\cdots )$ means that the same list of arguments as in the first term should be used. The masses of particles in the loop are written explicitly in the argument list and there is an one-to-one correspondence between those masses and the upper index of the $h_i$ (h stands for Higgs) and $g_i$ (g for gauge) functions.

Using Passarino–Veltman techniques [27], the results for $C_{i\ldots }([p_i^2],m^2_F,m^2_B,m^2_B)$ read

$$\begin{aligned} C_1&= \frac{(m^2_1+m^2_2) \text {B}_0^{(1)}}{(m^2_1-m^2_2)^2}-\frac{2 m^2_2 \text {B}_0^{(2)}}{(m^2_1-m^2_2)^2}-\frac{\text {B}_0^{(0)}}{m^2_1-m^2_2} +\frac{k_2 \text {C}_0}{m^2_1-m^2_2},\nonumber \\ C_2&= \frac{(m^2_1+m^2_2) \text {B}_0^{(2)}}{(m^2_1-m^2_2)^2}-\frac{2 m^2_1 \text {B}_0^{(1)}}{(m^2_1-m^2_2)^2}+\frac{\text {B}_0^{(0)}}{m^2_1-m^2_2}-\frac{k_1 \text {C}_0}{m^2_1-m^2_2},\nonumber \\ C_{11}&= \frac{\left[ k_1(3m^4_1-m^4_2 + 4m^2_1 m^2_2)-4m^6_1+4m^4_2m^2_1\right] \text {B}_0^{(1)}}{2 m^2_1 (m^2_1-m^2_2)^3}\nonumber \\&\quad -\frac{3 m^2_2 k_2 \text {B}_0^{(2)}}{(m^2_1-m^2_2)^3}-\frac{[k_1+k_2+2(m^2_2-m^2_1)]\text {B}_0^{(0)}}{2 (m^2_1-m^2_2)^2}\nonumber \\&\quad +\frac{\left( k_2^2+2m^2_B m^2_2\right) \text {C}_0}{(m^2_1-m^2_2)^2}\nonumber \\&\quad -\frac{(m^2_1+m^2_2) [\text {A}_0(m^2_B)-\text {A}_0(m^2_F)]}{2 m^2_1 (m^2_1-m^2_2)^2} +\frac{m^2_2}{(m^2_1-m^2_2)^2},\nonumber \\ C_{22}&= \frac{\left[ k_2(-3m^4_2+m^4_1-4m^2_1m^2_2)+4m^6_2-4m^4_1m^2_2\right] \text {B}_0^{(2)}}{2 m^2_2 (m^2_1-m^2_2)^3}\nonumber \\&\quad +\frac{3 m^2_1 k_1 \text {B}_0^{(1)}}{(m^2_1-m^2_2)^3}-\frac{[k_1+k_2+2(m^2_1-m^2_2)]\text {B}_0^{(0)}}{2 (m^2_1-m^2_2)^2}\nonumber \\&\quad +\frac{\left( k_1^2+2m^2_B m^2_1\right) \text {C}_0}{(m^2_1-m^2_2)^2}\nonumber \\&\quad -\frac{(m^2_1+m^2_2) [\text {A}_0(m^2_B)-\text {A}_0(m^2_F)]}{2 m^2_2 (m^2_1-m^2_2)^2} +\frac{m^2_1}{(m^2_1-m^2_2)^2},\nonumber \\ C_{12}&= -\frac{\left[ k_2(5m^2_1+m^2_2)+m^4_1-m^4_2 \right] \text {B}_0^{(1)}}{2 (m^2_1-m^2_2)^3}\nonumber \\&\quad +\frac{\left[ k_1(5m^2_2+m^2_1)+m^4_2-m^4_1\right] \text {B}_0^{(2)}}{2 (m^2_1-m^2_2)^3}\nonumber \\&\quad +\frac{(2 m^2_B-2 m^2_F+m^2_1+m^2_2)\text {B}_0^{(0)}}{2 (m^2_1-m^2_2)^2}\nonumber \\&\quad -\frac{\left[ k_1k_2+m^2_B(m^2_1+m^2_2)\right] \text {C}_0}{(m^2_1-m^2_2)^2}\nonumber \\&\quad +\frac{[\text {A}_0(m^2_B)-\text {A}_0(m^2_F)]}{(m^2_1-m^2_2)^2} -\frac{m^2_1+m^2_2}{2 (m^2_1-m^2_2)^2}, \end{aligned}$$

(A2)

where $B_0^{(0)}=B_{0}(0,m^2_B,m^2_B)$, $B_0^{(i)}=B_{0}(m^2_i,m^2_B,m^2_F)$, and $k_i = m^2_B - m^2_F + m^2_i$ with $i=1,2$.

The Passarino–Veltman functions in Eq. (A1) and Eq. (A2) are defined from the standard one-loop functions as

$$\begin{aligned}&A_{0}(m^2)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\int \frac{d^D k}{k^2-m^2+i\epsilon },\nonumber \\&B_{0}(p^2,m^2_F,m^2_B)=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\nonumber \\&\quad \times \int \frac{d^D k}{(k^2-m_F^2+i\epsilon )\left[ (k+p)^2-m_{B}^2+i\epsilon \right] },\nonumber \\&C_{0,\mu ,\mu \nu }=\frac{(2\pi \mu )^{4-D}}{i\pi ^2}\nonumber \\&\quad \times \int \frac{d^D k (1,k_\mu ,k_\mu k_\nu )}{(k^2-m_F^2+i\epsilon )\left[ (k+p_1)^2-m_{B}^2+i\epsilon \right] \left[ (k+p_2)^2-m_B^2+i\epsilon \right] },\nonumber \\&C_\mu = p_{1\mu }C_1 +p_{2\mu }C_2,\nonumber \\&C_{\mu \nu } = g_{\mu \nu }C_{00} + p_{1\mu }p_{1\nu }C_{11} +p_{2\mu }p_{2\nu }C_{22}+ (p_{1\mu }p_{2\nu }+p_{2\mu }p_{1\nu })C_{12}, \end{aligned}$$

(A3)

where $\mu$ is an arbitrary mass parameter introduced via dimensional regularization [28].

The scalar functions $A_0$, $B_0$, $C_0$ can be calculated using the techniques of [29]. We have

$$\begin{aligned} A_{0}(m^2)&= m^2\left( C_{UV} - \log (m^2) + 1\right) ,\nonumber \\ B_{0}(0,m^2,m^2)&=C_{UV} - \log (m^2),\nonumber \\ B_{0}(p^2,m^2_B,m^2_F)&=C_{UV} - \log (m^2_B) + 2 \nonumber \\&\quad - \sum _{\sigma =\pm }(1-\frac{1}{x_\sigma })\log \left( 1-x_\sigma \right) ,\nonumber \\ C_{0}(p^2_1,0,p^2_2,m^2_F,m^2_B,m^2_B)&= \frac{1}{p^2_1-p^2_2}\sum _{i=1}^{2}\sum _{\sigma =\pm }(-1)^{i}\text {Li}_2(y_{i\sigma }), \end{aligned}$$

(A4)

where $C_{UV}=2/(4-D)-\gamma _E + \log (4\pi \mu ^2)$ with $\gamma _E$ being Euler’s constant and $x_\sigma$ and $y_{i\sigma }$ are the roots of the following equations:

$$\begin{aligned}&m^2_B x^2 - (m^2_B - m^2_F + p^2)x + p^2 + i\epsilon = 0,\nonumber \\&m^2_B y^2_i - (m^2_B - m^2_F + p^2_i)y_i + p^2_i + i\epsilon = 0. \end{aligned}$$

(A5)

For the case of $p^2_1 >0$ and $p^2_2 = 0$ we have

$$\begin{aligned}&B_{0}(0,m^2_B,m^2_F)=C_{UV} - \log (m^2_B) + 1\nonumber \\&\qquad + \frac{m^2_F}{m^2_B-m^2_F}\log \left( \frac{m^2_F}{m^2_B}\right) ,\nonumber \\&C_{0}(p^2_1,0,0,m^2_F,m^2_B,m^2_B)\nonumber \\&\quad = \frac{1}{p^2_1}\left[ \text {Li}_2\left( 1-\frac{m^2_F}{m^2_B}\right) -\sum _{\sigma =\pm }\text {Li}_2(y_{1\sigma }) \right] . \end{aligned}$$

(A6)

Results for the case of $p^2_1 = p^2_2 = 0$ have been provided in Ref. [17]. We finally note that the C functions in Eq. (A2) are independent of the auxiliary parameter $C_{UV}$, meaning that the final results are UV finite. The function $B_{0}^{(0)}$ is above given for the sake of completeness. The final results are independent of it.

Appendix B: Approximate results

Here we provide results for the case of small exotic-lepton masses, i.e. $m_{E_a}\ll m_Y$ and $m_{E_a}\ll m_{H^A}$. Furthermore, the numerical facts of $m_{\nu _a} \ll m_W$ and the approximation $m_1 = m_2 = 0$ is used as justified in Sect. 4.1. We therefore neglect all $D_L$ here. For the neutrino case, we have

$$\begin{aligned} D_R^{\nu W}&=-\frac{ieg^2}{32\pi ^2 m_W^2}\sum _{a=1}^3 U_{i_1 a}^{L \star }U_{i_2 a}^{L}\left( \frac{m^2_{\nu _a}}{4m^2_W}\right) ,\nonumber \\ D_R^{\nu H^+}&=-\frac{ieg^2}{32\pi ^2 m_W^2}\left( t^2_{v'v} + 6\right) \sum _{a=1}^3 U_{i_1 a}^{L \star }U_{i_2 a}^{L}\left( \frac{m^2_{\nu _a}}{12m^2_{H^+}}\right) . \end{aligned}$$

(B1)

For the exotic-lepton case

$$\begin{aligned} D_R^{E Y} =&-\frac{ieg^2}{32\pi ^2 m_Y^2}(3\sqrt{3}\beta -1)\sum _{a=1}^3 V_{i_1 a}^{L \star }V_{i_2 a}^{L}\left( \frac{m^2_{E_a}}{8m^2_Y}\right) ,\nonumber \\ D_R^{E H^A} =&-\frac{ieg^2}{32\pi ^2 m_Y^2}\sum _{a=1}^3 V_{i_1 a}^{L \star }V_{i_2 a}^{L}\left( \frac{m^2_{E_a}}{12m^2_{H^A}}\right) \left[ \frac{\beta \sqrt{3}+1}{2}\left( t^2_{v'u} + 6\right) \right. \nonumber \\&+\left. \frac{\beta \sqrt{3}-1}{2}\left( 2t^2_{v'u} - 18 - 12\log {\frac{m^2_{E_a}}{m^2_{H^A}}} \right) \right] . \end{aligned}$$

(B2)