Baryon production from cluster hadronisation

Abstract

We present an extension to the colour reconnection model in the Monte Carlo event generator Herwig to account for the production of baryons and compare it to a series of observables for soft physics. The new model is able to improve the description of charged-particle multiplicities and hadron flavour observables in pp collisions.

1 Introduction

With increasing precision from the LHC it becomes apparent that many non-perturbative aspects of elementary particle production are far from understood. Especially the description of the transition from the deconfined state to final state particles that are observed in the detectors has many unknown variables and raises a lot of questions. With the help of Monte Carlo event generators  [1,2,3,4,5] different models can be evaluated. Among the problems that are being observed are the correct description of high-multiplicity events and the flavour composition of final states. One striking observation, made recently by the ALICE collaboration, was that in high-multiplicity pp events properties similar to that of AA and pA collisions are observed [6].

Possible explanations of these effects are rooted in the possibility that partonic matter shows some collective behaviour as in a hydrodynamical description; see e.g. [7]. The other route to introduce strong and possibly quite long-range correlations among different hard partons in a single interaction goes via colour reconnections. Here, states of high partonic density may lead to some kind of absorption or neutralisation of colour charge. These ideas have been advocated in some way e.g. in the Dipsy rope model [8] where many overlapping strings are combined into a colour field of a higher representation. Thermodynamical string fragmentation in Pythia also addresses this issue where shifts of the transverse momentum of heavier particles to higher values are the main result [9]. The possibility to form string junctions within the Lund string fragmentation model has been introduced in [10].

In Herwig an accurate description of Minimum Bias (MB) and Underlying Event (UE) observables has been achieved with the recent development of a new model for soft and diffractive interactions [11], building on the earlier developments in [12,13,14,15]. Here, the importance of colour reconnections has already been observed. However, in this work only charged particles have been addressed as such and we have already pointed out shortcomings in the description of high-multiplicity tails. This observation lead to the consideration that the mere production of baryons by itself would lead to a reduction of charged multiplicity in favour of a rise of the multiplicity of heavier particles. We do not address effects that arise at high multiplicity in particular but rather aim at an improved global description of particle production in MB events.

In this study we therefore introduce a possible extension to the model for colour reconnection to account for the production of baryons. At the same time we reconsider the production of strange particles and find that with a slight modification of our parameters we can improve the production rates of strange mesons as well as baryons quite significantly. We compare these effects to recent observations made by CMS and ALICE. Especially charged-particle multiplicities and ratios of identified hadrons are of main interest.

2 Colour reconnection

In order to describe the full structure of a particle scattering process additional soft effects that are not accessible by perturbation theory have to be considered. Such effects include hadronisation, Multiple Parton Interactions (MPIs) and fragmentation processes. In general these non-perturbative effects are based on phenomenological considerations. The basis for the hadronisation model in Herwig is the cluster model [16], which forms colourless singlets from colour connected partons. The fragmentation of these clusters into hadrons depends on the invariant cluster mass and the flavour of the quarks inside the cluster. The colour connections between the partons in an event are determined by the $N_C\rightarrow \infty$ approximation which leads to a planar representation of colour lines [17]. Every quark is connected to an antiquark and gluons, carrying both colour and anti-colour, connected to two other partons. The goal of colour reconnection is to study whether different connection topologies, other than the predefined colour connection, are possible between the partons.

In hadronic collisions the colour reconnection mostly aims at a resurrection of the colour correlation between different hard partonic interactions. In the Monte Carlo modelling of MPIs, different hard partonic scatters are layered on top of each other without a clear understanding of how to introduce a pre-confined state when co-moving partons from different scattering centres should also lead to ‘closeness’ in colour space, i.e. to short colour lines between those partons. The importance of the effect has first been observed in [18]. The colour reconnection leads to a decrease of the charged multiplicity for a given partonic configuration and hence an increase of the average transverse momentum per charged particle. The effect gets stronger with denser states, e.g. as we increase the CM energy of the hadronic collider.

The effects of colour reconnection have also been studied in the context of $\mathrm{W}^+\mathrm{W}^-$ production at LEP-2 [19, 20]. Due to the large space-time overlap of the decaying bosons the two hadronic systems may be in contact with each other which leads to colour interchange and can cause one quark of the $\mathrm{W}^+$ boson to hadronize together with an antiquark of the $\mathrm{W}^-$ boson.

2.1 The colour reconnection model in Herwig

The algorithm for colour reconnection in Herwig is implemented directly before the cluster fission takes place [21]. The properties of a cluster are defined by the invariant cluster mass

$$\begin{aligned} M^2 = (p_1 + p_2)^2, \end{aligned}$$

(1)

where $p_1$ and $p_2$ are the four momenta of the cluster constituents. The fission and the decay of the cluster depend on the invariant cluster mass which directly influences the multiplicity of final state particles. Two algorithms for colour reconnection are currently implemented in Herwig, the plain colour reconnection and the statistical colour reconnection [21]. Both algorithms try to find configurations of clusters that would reduce the sum of invariant cluster masses,

$$\begin{aligned} \lambda = \sum _{i=1}^{N_{\mathrm {cl}}}M_{i}^2, \end{aligned}$$

(2)

where $N_{\mathrm {cl}}$ is the number of clusters in an event. The plain colour reconnection algorithm picks a cluster randomly from the list of clusters and compares it to all other clusters of that list. For every cluster the invariant masses of the original cluster configuration $M_{\mathrm{A}}+M_{\mathrm{B}}$ and the masses of the possible new clusters $M_{\mathrm{C}} + M_{\mathrm{D}}$ are calculated. The cluster configuration that results in the lowest sum of invariant cluster masses is then accepted for reconnection with a certain probability $p_{\mathrm{R}}$. If the reconnection is accepted the clusters $(\mathrm{A})$ and $(\mathrm{B})$ are replaced by the clusters $(\mathrm{C})$ and $(\mathrm{D})$. This algorithm works out clusters with lower invariant masses and therefore replaces heavier clusters by lighter ones. In Fig. 1 we show the distribution of invariant cluster masses for a centre-of-mass energy of $\sqrt{s}=7\,\mathrm {TeV}$ before and after the plain colour reconnection. Due to the colour reconnection procedure the distribution is enhanced in the low-mass peak region and suppressed in the high-mass tail.

Fig. 1

Distribution of invariant cluster masses before and after colour reconnection for a pp collision with centre-of-mass energy of $\sqrt{s}=7\,\mathrm {TeV}$

The statistical colour reconnection on the other hand uses a simulated annealing algorithm to find the configuration of clusters that results in the absolute lowest value of the colour length $\lambda$. While intensively computing, it was also found in [22] that the statistical colour reconnection prefers a quick cooling, which does not result in a global minimum of colour length $\lambda$ in order to describe the data best. In a recent paper the colour reconnection model was changed in a way, that it is forbidden to make a reconnection which would lead to a gluon produced in any stage of the parton-shower evolution becoming a colour-singlet after hadronisation [23].

2.2 Extension to the colour reconnection model

The only constraint upon forming a cluster is that the cluster has to be able to form a colourless singlet under $SU(3)_C$. In $SU(3)_C$ a coloured quark is represented as a triplet (3) and an anti-coloured anti-quark is represented as an anti-triplet $(\bar{3})$. Two triplets can be represented as an anti-triplet and two anti-triplets can be represented as a triplet,

$$\begin{aligned} 3 \otimes 3&= 6 \oplus \bar{3}, \end{aligned}$$

(3)

$$\begin{aligned} \bar{3} \otimes \bar{3}&= \bar{6} \oplus 3. \end{aligned}$$

(4)

The clusters are a combination of these coloured quarks were only combinations are allowed that result in a colourless singlet. Here we consider the following allowed cluster configurations based on the $SU(3)_C$ structure of QCD. We begin with the normal cluster configuration which will be referred to as a mesonic cluster

$$\begin{aligned} 3 \otimes \bar{3} = 8 \oplus 1. \end{aligned}$$

(5)

In strict $SU(3)_C$ the probability of two quarks having the correct colours to form a singlet would be 1/9. Next we consider possible extensions to the colour reconnection that allows us to form clusters made out of three quarks. A baryonic cluster consists of three quarks or three anti-quarks where the possible representations are

$$\begin{aligned} 3 \otimes 3 \otimes 3&= 10 \oplus 8 \oplus 8 \oplus 1, \end{aligned}$$

(6)

$$\begin{aligned} \bar{3} \otimes \bar{3} \otimes \bar{3}&= 10 \oplus 8 \oplus 8 \oplus 1. \end{aligned}$$

(7)

In full $SU(3)_C$ the probability to form a singlet made out of three quarks would be 1/27. In the following we will introduce the algorithm we used for the alternative colour reconnection model. In order to extend the current colour reconnection model, which only deals with mesonic clusters, we allow the reconnection algorithm to find configurations that would result in a baryonic cluster.

2.3 Algorithm

As explained before the colour reconnection algorithms in Herwig are implemented in such a way that they lower the sum of invariant cluster masses. For baryonic reconnection such a condition is no longer reasonable because of the larger invariant cluster mass a baryonic cluster carries. As an alternative we consider a simple geometric picture of nearest neighbours where we try to find quarks that approximately populate the same phase space region based on their rapidity y. The rapidity y is defined as

$$\begin{aligned} y = \frac{1}{2}\ln \left( \frac{E+p_z}{E-p_z}\right) \end{aligned}$$

(8)

and is usually calculated with respect to the z-axis. Here we consider baryonic reconnection if the quarks and the anti-quarks are flying in the same direction. This reconnection forms two baryonic clusters out of three mesonic ones. The starting point for the new rapidity-based algorithm is the predefined colour configuration that emerges once all the perturbative evolution by the parton shower has finished and the remaining gluons are split non-perturbatively into quark–anti-quark pairs. Then a list of clusters is created from all colour connected quarks and anti-quarks. The final algorithm consists of the following steps:

• 1. Shuffle the list of clusters in order to prevent the bias that comes from the order in which we consider the clusters for reconnection.

• 2. Pick a cluster $(\mathrm{A})$ from that list and boost into the rest frame of that cluster. The two constituents of the cluster $(q_{\mathrm{A}}, \bar{q}_{\mathrm{A}})$ are now flying back to back and we define the direction of the anti-quark as the positive z-direction of the quark axis.

• 3. Perform a loop over all remaining clusters and calculate the rapidity of the cluster constituents with respect to the quark axis in the rest frame of the original cluster for each other cluster in that list $(\mathrm{B})$.

• 4. Depending on the rapidities the constituents of the cluster $(q_{\mathrm{B}}, \bar{q}_{\mathrm{B}})$ fall into one of three categories:

  • Mesonic: $y(q_{\mathrm{B}})> 0 > y(\bar{q}_{\mathrm{B}})$.

  • Baryonic: $y(\bar{q}_{\mathrm{B}})> 0 > y(q_{\mathrm{B}})$.

  • Neither.

  If the cluster neither falls into the mesonic nor in the baryonic category listed above, the cluster is not considered for reconnection.

• 5. The category and the absolute value $|y(q_{\mathrm{B}})| +|y(\bar{q}_{\mathrm{B}})|$ for the clusters with the two largest sums is saved (these are clusters B and C in the following).

• 6. Consider the clusters for reconnection depending on their category. If the two clusters with the largest sum (B and C) are in the category baryonic consider them for baryonic reconnection (to cluster A) with probability $p_{\mathrm{B}}$. If the category of the cluster with the largest sum is mesonic then consider it for normal reconnection with probability $p_{\mathrm{R}}$. If a baryonic reconnection occurs, remove these clusters (A, B, C) from the list and do not consider them for further reconnection. A picture of the rapidity-based reconnection for a mesonic configuration is shown in Fig. 2 and a simplified sketch for baryonic reconnection is shown in Fig. 3.

• 7. Repeat these steps with the next cluster in the list.

Fig. 2

Representation of rapidity-based colour reconnection where the quark axis of one cluster is defined as the z-axis in respect to which the rapidities of the constituents from the possible reconnection candidate are calculated. $(\mathrm{A})$ and $(\mathrm{B})$ are the original clusters. $(\mathrm{C})$ and $(\mathrm{D})$ would be the new clusters after the reconnection

Fig. 3

Configuration of clusters that might lead to baryonic reconnection. The small black arrows indicate the direction of the quarks. A reconnection is considered if all quarks move in the same direction and all anti-quarks move in the same direction

We note that with this description we potentially exclude clusters from reconnection where both constituents have a configuration like $y(q_{\mathrm{B}})> y(\bar{q}_{\mathrm{B}}) > 0$ w.r.t. the quark axis but assume that these clusters already contain constituents who are close in rapidity and fly in the same direction. The exclusion of baryonically reconnected clusters from further re-reconnection biases the algorithm towards the creation of baryonic clusters whose constituents are not the overall nearest neighbours in rapidity. The extension to the colour reconnection model gives Herwig an additional possibility to produce baryons on a different, more elementary level than on the level of cluster fission and cluster decay [1]. In pp collisions with enhanced activity from MPI a high density of clusters leads to an increased probability of finding clusters that are suitable for baryonic reconnection. We expect this model therefore to have a significant effect on charged-hadron multiplicities, especially on the high-multiplicity region. We also expect the new model to have a significant impact on baryon and meson production since baryonic colour reconnection effectively makes baryons out of mesons. In Figs. 4 and 5 we see the influence of the new model for different values of $p_{\mathrm {B}}$ on the charged-particle multiplicities and the $p_{\perp }$ spectra of $\pi ^++\pi ^-$ and $\mathrm{p}+\bar{\hbox {p}}$ yields in inelastic pp collisions at $\sqrt{s} = 7 \,\mathrm {TeV}$ in the central rapidity region. As expected the model influences the hadronic multiplicities for large $N_{\mathrm{ch}}$ significantly. A larger baryonic reconnection probability reduces the number of high-multiplicity events and shifts them towards lower multiplicities. The $p_{\perp }$ distribution of the $\pi ^++\pi ^-$ shows an overall reduction while the $p_{\perp }$ spectra of the $\mathrm{p}+\bar{\hbox {p}}$ shows an overall enhancement due to baryonic colour reconnection. While the description of the low $p_{\perp }$ region improves, there are too many $\mathrm{p}+\bar{\hbox {p}}$ with a $p_{\perp } > 2.5\,\mathrm{GeV}$. In the next section we describe the tuning of the model to a wide range of data from hadron colliders.

Fig. 4

Measurement of the charged-particle multiplicity at $\sqrt{s}=7\,\mathrm {TeV}$ with ALICE at LHC [24]. Shown is a comparison of the new colour reconnection model for different reconnection probabilities with the default model of Herwig

Fig. 5

The transverse momentum spectra for $\mathrm {\pi ^++\pi ^-}$ and $\mathrm {K^++K^-}$ as measured by ALICE at $\sqrt{s}=7\,\mathrm {TeV}$ [25] in the very central rapidity region $|y|<0.5$

3 Tuning

The tuning is achieved by using the Rivet and Professor framework for Monte Carlo event generators [26, 27]. In a first tuning attempt we keep the hadronisation parameters that were tuned to LEP data at their default values and follow a similar tuning procedure as in [11]. We retune the main parameters of the MPI model in Herwig, the $p_{\perp ,0}^{\mathrm{min}}$ parameter and the inverse proton radius squared $\mu ^2$. Since we altered the colour reconnection model, we also retune the probability for normal colour reconnection $p_{\mathrm {R}}$. The only additional parameter we have to consider is the probability for baryonic reconnection $p_{\mathrm {B}}$. In order to capture general features of MB observables we tune the model to a large variety of MB data from the ATLAS and ALICE collaborations at $\sqrt{s}=7\,\mathrm{TeV}$ [25, 28]. The following observables were used with equal weights:

• The pseudorapidity distributions for $N_{\mathrm{ch}}\ge 1$, $N_{\mathrm{ch}}\ge 2$, $N_{\mathrm{ch}}\ge 6$, $N_{\mathrm{ch}}\ge 20$.

• The transverse momentum of charged particles for $N_{\mathrm{ch}}\ge 1$.

• The charged-particle multiplicity for $N_{\mathrm{ch}}\ge 2$.

• The mean charged transverse momentum vs. the multiplicity of charged particles for $p_{\perp }>500\,\mathrm{MeV}$ and $p_{\perp }>100\,\mathrm{MeV}$.

• The pion and the proton yield in the central rapidity region $|y|<0.5$.

The outcome of this tune is listed in Table 1 where we show the parameter values that resulted in the lowest value of $\chi ^2/N_\mathrm{dof}$ and the values from the default tune of Herwig 7.1 without the baryonic colour reconnection model. The change in the colour reconnection algorithm and the possibility to produce baryonic clusters results in an overall better description of the considered observables. While still being able to accurately describe MB data we see the expected improvement in the charged multiplicity distributions for the high-multiplicity region which is due to the baryonic colour reconnection. The results of the tuning procedure will be presented and discussed in the next section.

Table 1 Results of the parameter values from the tuning procedure that resulted in the smallest $\chi ^2 / N_{\mathrm {dof}}$ value for $\sqrt{s}=7\, \mathrm {TeV}$ centre-of-mass energy compared with the default tune from Herwig 7.1

Fig. 6

Multiplicity distributions as measured by ALICE for the central rapidity region $|\eta | < 1$ up to $N_{\mathrm {ch} = 70}$ [24] and ATLAS for $|\eta |<2.4$ up to $N_{\mathrm {ch}} = 200$ for all particles with $p_{\perp } > 100 \,\mathrm {MeV}$ [28]. We compare the old default colour reconnection model with the new baryonic colour reconnection model

Table 2 Results of the parameter values from the tuning procedure that resulted in the smallest $\chi ^2 / N_{\mathrm {dof}}$ value for $\sqrt{s}=7\, \mathrm {TeV}$ centre-of-mass energy compared with the default tune from Herwig 7.1

4 Results

Changes in the colour reconnection model are always deeply tied with the peculiarities of the hadronisation model. In principle one would have to retune all parameters that govern hadronisation in Herwig. This is usually done in a very dedicated and long study with LEP data. We propose a simplified procedure since little to no changes are expected with the extension to the colour reconnection model in the $\mathrm{e}^++\mathrm{e}^-$ environment. At LEP the colour structure of an event is not changed significantly through colour reconnection since it is already well defined by the parton shower. This was confirmed by comparing the new model to a wide range of experimental data from LEP. We therefore keep the hadronisation parameters that were tuned to LEP data (see Refs. [1, 3]) at their default values. We also note that this does not replace a dedicated study concerned with the tuning and validation of hadronisation parameters. Especially at pp collisions a different model for colour reconnection leads to changes in the interplay between the clusters and the hadronisation in an unforeseeable way. A possible way out of this dilemma would be to make a distinguished LHC tune and compare the results with LEP. Nonetheless we restrain ourselves to the explained simplified method in order to make qualitative statements about the new model for colour reconnection. The new model with the tuned parameters improves the description of all observables considered in the tuning procedure. The effect of the baryonic colour reconnection was already demonstrated in Fig. 4. In Fig. 6 we show the same distribution of the charged-particle multiplicity for the central region $|y| < 1$ with the tuned parameter values. Again we see the expected fall off for high multiplicities. The new model is able to describe the whole region fairly well compared to the old model. Only the low multiplicity region $n<10$ is overestimated by a factor of $\approx 10\%$ and for $n<5$ underestimated. In Fig. 6 we also show a similar observable for a wider rapidity region $|y|<2.4$ and up to $n=200$ as measured by CMS [28]. Again the central multiplicity region shows a significant improvement. For multiplicities $n>80$ we note a slight overestimation of the data but are still within error bars.

This can be understood quite simply: the more activity in an event, the more likely it becomes that a cluster configuration that leads to baryonic reconnection is found. The high-multiplicity events therefore exhibit a disproportionately large fraction of baryonic reconnections. Due to the highly restricted phase space for the production of baryons from baryonic clusters less particles are produced than with mesonic clusters of the same invariant mass, which lowers the charged multiplicity.

We also observe the proposed change in mesonic and baryonic activity in the $p_{\perp }$ spectra of pions and protons. Especially the $\mathrm{p}/\pi$ ratio and the $p_{\perp }$ distributions improve significantly which should be considered first in a model that tries to explain flavour multiplicities. When looking at the $p_{\perp }$ distributions of $\mathrm{K}$ and $\Lambda$ we see that none of the performed tunes is able to capture the essence of these distributions correctly which is no surprise since we have not touched or altered the production mechanism of strange particles. We merely observe a small increase in the $p_{\perp }$ distribution of $\Lambda$ baryons due to the baryonic reconnection. Changes that affect the hadronisation model usually have severe consequences for the hadronisation parameters. We restrict ourselves to the parameters that are responsible for strangeness production and allow one additional source of strangeness in the event generator work flow. We exploit the freedom one is given by LEP observables for the probability to select a strange quark during cluster fission PwtSquark and additionally allow non-perturbative gluon splitting into strange quarks with a given probability SplitPwtSquark. In a second tuning procedure we consider these two additional parameters and also tune to the $p_{\perp }$ distribution of the $\pi ^+\pi ^-$, $\mathrm{K}^++\mathrm{K}^-$, $\mathrm{p}+\bar{\hbox {p}}$ yields in inelastic pp collisions at $7\,\mathrm {TeV}$ [25] and the $p_{\perp }$ distribution of $\Lambda$ [29]. The parameter values that were obtained in the tuning are listed in Table 2.

Fig. 7

The transverse momentum spectra for $\pi ^++\pi ^-$ and $\mathrm {p}+\bar{\mathrm{p}}$ as measured by ALICE at $\sqrt{s}=7\,\mathrm {TeV}$ [25] in the very central rapidity region $|y|<0.5$

In addition to the tuned observables, many hadron flavour observables which were not considered in the tuning procedure show a significant improvement as well.

In order to compare the different effects from the new colour reconnection model and the possibility to produce strange quarks during gluon splitting we made runs with the default model (Herwig 7.1 default), the pure baryonic colour reconnection model (baryonic reconnection), one run where we allow the gluons to split into strange quarks ($g\rightarrow s\bar{s}$ splittings) and use the old colour reconnection model and a run where we use both extensions and the parameters that we obtained from the tuning (new model).

In Fig. 7 we show the $p_{\perp }$ distributions of $\pi$ and $\mathrm{K}$ in the central rapidity region as measured by ALICE [25] and in Fig. 8 the corresponding $\mathrm{p}+\bar{\mathrm{p}}$ distribution. While all options improve the description of pions we see that the $\mathrm{K}$ distribution can only be described if we take the additional source of strangeness into account. The proton $p_{\perp }$ distribution is mainly driven by baryonic reconnection. The rate increases for all $p_{\perp }$ regions but we overshoot the data by a large factor for $p_{\perp }>3\,\mathrm {GeV}$ and for the very low $p_{\perp }$ region. Since all options show the same trend this might indicate some problems with the hard part of the MPI model which dominates $p_{\perp }>3\,\mathrm {GeV}$. In Fig. 9 we consider the hadron ratios $\mathrm {K}/\pi$ and $\mathrm {p}/\pi$. The new model does a significant better job in describing the data and only the combined effect of the enhanced baryon production through the change in the colour reconnection model and gluon splitting into strange quarks is able to give a satisfying description of both observables.

Fig. 8

The transverse momentum spectrum for $\mathrm {p}+\bar{\mathrm{p}}$ as measured by ALICE at $\sqrt{s}=7\,\mathrm {TeV}$ [25] in the very central rapidity region $|y|<0.5$

Fig. 9

Transverse momentum spectra for the ratios $\mathrm {p}/\pi$ and $\mathrm {K}/\pi$ as measured by ALICE at $\sqrt{s}=7\,\mathrm {TeV}$ [25] in the very central rapidity region $|y|<0.5$

In Figs.  10, 11, 12, 13 we compare the model to $\sqrt{s} = 7\, \mathrm {TeV}$ data from CMS [29] for the strange flavour observables of $\mathrm {K}_{\mathrm{S}}^0$, $\Lambda$ and $\Xi ^-$. The new model improves the description for all observables published in this analysis. Again we show the effects of the different contributions and note that the best description can only be achieved by a combination of baryonic colour reconnection and gluon splitting into strange quarks (new-tune). The $\Lambda /\mathrm {K}_{\mathrm{S}}^0$ distribution shows a good description in the turn on region but the high $p_{\perp }$ tail is not well described. A similar observation was made with Pythia in [10]. Surprisingly the $\Xi ^-/\Lambda$ distribution is able to capture the general trend but due to large errors in the high $p_{\perp }$ region it is difficult to draw conclusions. We see significant improvement in the description of hadron flavour observables. Especially the rapidity distributions and the particle ratios $\Lambda /\mathrm {K}_{\mathrm{S}}^0$ and $\Xi ^-/\Lambda$ show a large enhancement compared to the default model. Again we point out the interplay between baryonic colour reconnection and the strangeness production mechanism which is responsible for the improvement in the description of the heavy baryons $\Lambda$ and $\Xi ^-$.

Fig. 10

The $\mathrm {K}_{\mathrm{S}}^0$ rapidity and $p_{\perp }$ distribution as measured by CMS at $\sqrt{s}=7\,\mathrm {TeV}$ [29]

Fig. 11

The $\Lambda$ rapidity and $p_{\perp }$ distribution as measured by CMS at $\sqrt{s}=7\,\mathrm {TeV}$ [29]

Fig. 12

The $\Xi ^-$ $p_{\perp }$ distribution as measured by CMS at $\sqrt{s}=7\,\mathrm {TeV}$ [29]

In a recent analysis by ALICE a significant enhancement of strange to non- strange hadron production with increasing particle multiplicity in pp collisions was observed [6]. Since we are developing a model that incorporates strangeness production and the enhanced production of baryons it is instructive to compare our model to the data published by the ALICE collaboration.

In Fig. 14 we show we show the $(\Lambda +\bar{\Lambda })/(\pi ^++\pi ^-)$ and the $\mathrm {K}_{\mathrm{s}}^0/(\pi ^{+}+\pi ^{-})$ ratio for the old model and the new model for colour reconnection. While the $\mathrm {K}_{\mathrm{s}}^0/(\pi ^{+}+\pi ^{-})$ ratio is reasonably well described, the $\Lambda /\pi$ ratio is underestimated by both, the old and the new model. The new model, on the other side, is able to capture the general trend of the observable and describe the rise of the fraction of $\Lambda$ baryons with respect to increasing particle multiplicity correctly. Also the increase in the fraction of multi-strange baryons $(\Xi ^{-}+\bar{\Xi }^+)$ and $(\Omega ^{-}+\bar{\Omega }^+)$ can qualitatively be described by the new model as is also shown in Fig. 14. Note that the Herwig 7.1 default model did not produce clusters heavy enough in order to account for the production of any $\Omega$-baryons.

In Fig. 15 we show the ratio of the single strange particles $(\Lambda +\bar{\Lambda })/2\mathrm {K}_{\mathrm{s}}^0$ and the ratio of $\mathrm {p}+\bar{\mathrm {p}}/(\pi ^{+}+\pi ^{-})$ which do not contain any strange quarks. In both cases Herwig is not able to describe the data correctly. We see a disproportionally large increase of the $(\Lambda +\bar{\Lambda })/2\mathrm {K}_{\mathrm{s}}^0$ ratio with increasing multiplicity which is due to the nature of our colour reconnection model, which enhances the production of baryons with increasing event multiplicity. This increase is not as pronounced in the $\mathrm {p}+\bar{\mathrm {p}}/(\pi ^{+}+\pi ^{-})$ ratio but still is present.

Fig. 13

The $\Lambda /\mathrm {K}_{\mathrm{S}}^0$ and the $\Xi ^-/\Lambda$ $p_{\perp }$ distribution as measured by CMS at $\sqrt{s}=7\,\mathrm {TeV}$ [29]

The comparison with ALICE data gives us interesting insights into our new model for colour reconnection. Although we manage to capture the general trend in the increasing fraction of (multi)-strange baryons to non-strange mesons, we are not able to reproduce all aspects of the observations made by ALICE. Especially the $\Lambda /\mathrm{K}$ ratio and the $\mathrm{p}/\pi$ ratios are not well described, since we have a mechanism that increases the production of baryons in total and does not lead to an increase in the strange baryons only.

Fig. 14

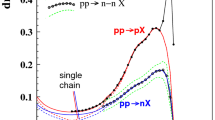
Integrated (multi)-strange particle yield ratios to $\pi ^{+}+\pi ^{-}$ as a function of $\langle \mathrm {d}N_{ch}/\mathrm {d}\eta \rangle$ for $|\eta |<0.5$. The values from the ALICE analysis [6] are compared to calculations from Herwig 7.1 with the old model and the new model for colour reconnection

Fig. 15

Integrated particle yield ratio of $\Lambda +\bar{\Lambda }/2\mathrm {K}_{\mathrm{s}}^0$ and $\mathrm {p}+\bar{\mathrm {p}}/\pi ^{+}+\pi ^-$ as a function of $\langle \mathrm {d}N_{ch}/\mathrm {d}\eta \rangle$ for $|\eta |<0.5$. The values from the ALICE analysis [6] are compared to calculations from Herwig 7.1 with the old model and the new model for colour reconnection

4.1 Spectra of cluster masses

In this section we discuss the effects of the new model for colour reconnection on the clusters and the distribution of cluster masses. This is only done for non-diffractive events, since colour reconnection has no effect on the simulation of diffraction. In Fig. 16 we show the effects of the new colour reconnection model on the distribution of cluster masses. It can still be seen that after colour reconnection the cluster masses get shifted towards smaller values as it was the case in the old model but the effect is not as severe as in the old model (see Fig. 17). In a direct comparison between the default model and the new model we see that the new model favours the production of more heavier clusters. In Fig. 18 we show the distribution of cluster masses after colour reconnection separately for baryonic and mesonic clusters. The contribution in the high-mass region mainly comes from mesonic clusters. Baryonic clusters dominate the mid-mass region between 1 and 13 GeV, while large baryonic clusters are highly suppressed.

Fig. 16

Comparison between the distributions of invariant cluster masses before and after the colour reconnection

With this in mind a picture of the cluster configuration emerges which, in order to be able to describe the data, favours the production of baryonic clusters with an intermediate cluster mass and small fluctuations towards clusters of very high masses. In general one can say that smaller clusters lead to less heavier particles due to the highly restricted phase space in the cluster decay stage. This makes the old default model for colour reconnection, which is based on the reduction of cluster masses not able to reproduce the observables concerned with heavier particles as discussed in Sect. 4 due to a lack of heavy clusters.

Fig. 17

Comparison between the distribution of invariant cluster masses after colour reconnection for the old model and the new model

Fig. 18

The invariant mass distribution of mesonic and baryonic clusters after colour reconnection

5 Conclusion and outlook

We have implemented a new model for colour reconnection which is entirely based on a geometrical picture instead of an algorithm that tries to directly minimize the invariant cluster mass. In addition, we allow reconnections between multiple mesonic clusters to form baryonic clusters which was not possible in the old model. With this mechanism we get an important lever on the baryon to meson ratio which is a necessary starting point in order to describe flavour observables. The amount of reconnection also depends on the multiplicity of the events which can be seen by comparing the model to the charged-particle multiplicities which get significantly better. In addition we allow for non-perturbative gluon splitting into strange quark–anti-quark pairs. Only with this additional source of strangeness it is possible to get a good description of the $p_{\perp }$ spectra of the kaons. The description of the heavy baryons $\Lambda$ and $\Xi ^{-}$ improves once we combine the new model for colour reconnection and the additional source of strangeness. The model was tuned to 7 TeV MB data and various hadron flavour observables. With the new model the full range of MB data can be described with a similar good quality as the old model and in addition we improve the description of hadron flavour observables significantly.

A comparison with ALICE data concerning the enhancement of (multi-)strange baryons led us to the conclusion that our simple model is able to reproduce the general trend of some of the observables, but fails to describe the data in its entirety. Nonetheless we see indications that the increase in the strange baryon fraction can also be explained by an approach with colour reconnection in combination with the cluster model. In order to arrive at a satisfying description of high-multiplicity events we suggest a model were these events are originating from less and heavier clusters instead of many lighter ones. This is necessary to raise the probability for producing heavy and strangeness containing hadrons. This could also in principle be solved in the framework of a colour reconnection model were many overlapping clusters (or a region of high cluster density) fuse together to form a heavy cluster which opens up the phase space for the production of strangeness and baryons in the cluster decay stage.

This issue could possibly be addressed by a space-time picture of cluster evolution which will be left for future work.

A shortcoming of the model lies in the algorithm which is biased by the order of clusters which are considered for reconnection and the fact that baryonic clusters cannot be re-reconnected. This will ultimately yield clusters which do not consist of the nearest neighbours in phase space but a small overlap between the clusters will still be present. Due to the sheer amount of possibilities on how to assign baryonic clusters we are forced to introduce some sort of arbitrariness when it comes to the cluster assignment. When comparing the new model with the old model, we see that the new colour reconnection model does not have the same effect on the invariant mass distribution in terms of reduction of cluster masses but fuses mesonic clusters together in order to form baryonic clusters and therefore adds an additional possibility to produce heavy baryons. According to the data a significant reduction in cluster mass is not favoured. The data prefers more fluctuations in cluster size and explicitly shows the possibility to produce baryonic clusters. Otherwise the production of heavy strange baryons is not possible and highly suppressed.

Understanding soft physics remains difficult but new approaches and models are necessary in order to improve the quality of Monte Carlo event generators. Overall, we have shown that small changes in the model for colour reconnection and the gluon-splitting mechanism can have significant effects on some observables.