Search for heavy neutrino in $K^{+} \rightarrow \mu ^{+} \nu _{H}$ decay

Abstract

A high statistics data sample of the $K^{+}\rightarrow \mu ^{+}\nu _{\mu }$ decay was accumulated by the OKA experiment in 2012. The missing mass analysis was performed to search for the decay channel $K^{+}\rightarrow \mu ^{+}\nu _{H}$ with a hypothetic stable heavy neutrino in the final state. The obtained missing mass spectrum does not show peaks that could be attributed to existence of stable heavy neutrinos in the mass range $(270< m_{\nu _{H}} < 375)$ MeV$/c^{2}$. As a result, upper limits on the branching ratio and on the value of the mixing element $|U_{\mu H}|^{2}$ are obtained.

1 Introduction

After the discovery of the Higgs boson there are no further guideline predictions from the Standard Model (SM) remained, hence, searches for a physics beyond the SM in a broad range of topics become an actual question. One of the promising research directions is inspired by observed neutrino oscillations [1,2,3,4] which require non zero neutrino masses which, in turn, open possibility for existence of a set of heavy sterile neutrinos in one of the SM extensions – the Neutrino Minimal Standard Model ($\nu$MSM) [5,6,7]. Depending on the lifetime of those heavy neutrinos ($\nu _{H}$) experimental approaches can be divided into searches for possible decay products of $\nu _{H}$, as, for example, reported in [8] or more recently in [9] and into searches for $\nu _{H}$ with a long lifetime with the missing mass approach [10] and, recently, in two high statistics experiments [11,12,13], which reported upper limits on branching for $\nu _{H}$ in a hundred MeV/c$^2$ range. To contribute to the latter approach we analyzed a large data sample of $K^{+} \rightarrow \mu ^{+} \nu$ recorded in 2012 by the OKA collaboration at IHEP-Protvino to search for a possible process $K^{+} \rightarrow \mu ^{+} \nu _{H}$, see Fig. 1, where $\nu _{H}$ stands for one of the expected sterile $\nu _{H}$ within $\nu$MSM and $U_{\mu H}$ represents mixing element between SM muon neutrino and $\nu _{H}$.

2 Separated kaon beam and OKA experiment

The OKA¹ experiment makes use of a secondary hadron beam of the U-70 Proton Synchrotron of NRC “Kurchatov Institute”-IHEP, Protvino, with enhanced fraction of kaons obtained by RF-separation with Panofsky scheme [14]. Corresponding deflectors are two superconducting Karlsruhe-CERN cavities used at SPS [15] and which were donated by CERN to IHEP in 1998. The cavities are cooled by superfluid He provided by the dedicated IHEP-build cryogenic system [16]. The design is optimized for the momentum of 12.5 and 17.7 GeV/c, the achieved fraction of kaons is up to 20% depending on the beam momentum, with the intensity of about $5\times 10^{5}$ kaons per U-70 spill of 3 seconds duration. The r.m.s. width of the momentum distribution is estimated to be 1.5%.

Fig. 1

Production of a heavy sterile neutrino in the $K^{+}$ decay

Fig. 2

Schematic elevation view of the OKA setup, see text for details

Fig. 3

The distribution of $p_{\mu }$ vs. $m^2_{miss}$ obtained from the analysis of the experimental data (plot a) in comparison with Monte-Carlo simulation for the background channels (plots $b,\ldots ,g$) and for the set of signals (plot h) for $m_{\nu _{H}} = \{200, 240, 280, 320, 360\}$ MeV/c$^2$. Note logarithmic scale for the third dimension. Only events which passed the selection cuts are shown. In case of MC, the initial statistics is indicated as well

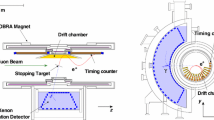
The OKA setup, Fig. 2, is a magnetic spectrometer complemented by electromagnetic and hadron calorimeters and a Decay Volume. The first magnet M$_{1}$ with surrounding 1 mm pitch PC’s (BPC$_{(1Y)}$, BPC$_{(2Y,2X)}$, BPC$_{(3X,3Y)}$, BPC$_{(4X,4Y)}$ of $\sim$1500 channels in total [17, 18]) serves as a beam spectrometer. It is supplemented by two threshold Cherenkov counters Č$_{1}$, Č$_{2}$ for kaon identification and by beam trigger scintillation counters S$_{(1)}$, S$_{(2)}$, S$_{(4)}$, each of $200\times 200\times 1$ mm$^{3}$, and a thicker one, $60\times 85\times 6$ mm$^{3}$, delivering the reference time, S$_{(3)}$. The 11 m long Decay Volume (DV) filled with helium contains 11 rings of guard system (GS), which consists of 670 Lead-Scintillator sandwiches (20 layers of 1.5 mm: 5 mm each) with WLS readout grouped in 300 ADC channels. To supplement GS, a gamma detector (BGD, made of $\sim$ 1050 $5\times 5\times 42$ cm$^3$ lead glass blocks [19]), located behind the DV is used as a veto at large angles, while low angle particles pass through a central opening. The wide aperture $200\times 140$ cm$^2$ magnet SM$_{(SP40A)}$, with a field integral of $\sim$ 1 Tm deflects charged particles in horizontal plane and serves as a spectrometer together with corresponding tracking chambers: 5k channels of 2 mm pitch PC’s (PC$_{1,\ldots ,8}$), 1k channels of 9 mm diameter straw tubes ST$_{(1,2,3)}$ and 300 channels of 40 mm diameter drift tubes DT$_{1,2}$. The matrix hodoscope HODO$_{(matrix)}$ is composed of 252 $12\times 12\times 1.5$ cm$^3$ scintillator tiles with WLS+SiPM readout. It is used to improve time resolution and track matching. Two scintillator counters S$_{bk1}$, S$_{bk2}$ (80 and 90 mm in diameter with a thickness of 3.9 and 5 mm) serve to suppress undecayed beam particles at the trigger level. At the end of the OKA setup there are two calorimeters: electromagnetic (GAMS-2000 of $\sim$ 2300 $3.8\times 3.8\times 45$ cm$^3$ lead glass blocks [20]) and a hadron one (HCAL of 120 $20\times 20\times 108$ cm$^3$ iron-scintillator sandwiches with WLS plates readout [21]) and, finally, four partially overlapping muon counters $\mu$C $(1\times 1$ m$^2$ scintillators with WLS fibres readout) behind the HCAL. The data acquisition system of the OKA setup [22] works at $\sim$ 25 kHz event rate with the mean event size of $\sim$ 4 kByte.

3 Search for heavy neutrinos

A search for $K^{+}\rightarrow \mu ^{+}\nu _{H}$ decay is done with the data set accumulated in November 2012 run with a 17.7 GeV/c beam momentum. Two prescaled triggers are used. The first one, with prescale factor of 1/10, selects beam kaons which decay inside the OKA setup: $\mathtt{Tr}_{\mathtt{Kdecay}}=\mathtt{S}_{\mathtt{1}}{\cdot }\mathtt{S}_{\mathtt{2}}{\cdot } \mathtt{S}_{\mathtt{3}}{\cdot }{} \mathtt{S}_{\mathtt{4}}{\cdot }\check{\mathtt{C}}_{\mathtt{1}}{\cdot } \overline{\check{\mathtt{C}}}_{\mathtt{2}}{\cdot }\overline{\mathtt{S}}_{\mathtt{bk}}$. The second one, $\mathtt{Tr_{K\rightarrow \mu X}=Tr_{Kdecay}{\cdot }{\mu }C}$, includes additionally muon counters $\mu$C and is prescaled by 1/4. The beam intensity ($\mathtt{S}_{\mathtt{1}}\cdot \mathtt{S}_{\mathtt{2}}\cdot \mathtt{S}_{\mathtt{3}}\cdot \mathtt{S}_{\mathtt{4}}$) is $\sim 2\cdot 10^{6}$ per spill, the fraction of kaons in the beam is $\sim$ 12.5%, i.e. the kaon intensity is $\sim$ 250k/spill. The total number of kaons entering the DV corresponds to $\sim 1.6\times 10^{10}$.

3.1 Event selection

The following criteria are applied to select $K^{+}\rightarrow \mu ^{+}\nu$ decay:

• events with single beam track and single secondary track are selected;

• a single secondary track segment after the SM magnet is present in the event and it is well matched to the muon like signals in both GAMS-2000 and HCAL calorimeters (i.e. one or two adjacent cells with the MIP energy deposition);

• sufficient number of points on all the track segments is present to optimize the missing mass resolution;

• the momentum of kaon is consistent with that delivered by beam settings of $\approx 17.7$ GeV/c, while the required momentum of the secondary muon is below 16.4 GeV/c;

• to ensure good decay vertex reconstruction and also to suppress events in which kaon decays after passing the DV, there is a requirement of 3 mrad minimal angle between the beam and the secondary track, and a requirement for the minimal distance between the beam and the secondary track to be $< 1$ cm;

• the decay vertex is inside DV, and is further restricted to be 3$\sigma$ (of z-vertex resolution) from the DV entrance and the position of Cu-target,² which reduces the effective length of DV to 7.5 m;

• other decay channels are suppressed by requiring the total energy deposition in GS and BGD to be below 50 MeV/c$^2$ and 100 MeV/c$^2$, respectively;

• the total energy deposition in GAMS-2000 and HCAL should be consistent with that of a single muon.

After applying these cuts, $26\times 10^{6}\ K^{+}\rightarrow \mu ^{+}\nu$ decays were selected for subsequent analysis.

3.2 Signal and background studies

A signal from heavy neutrino in $K^{+} \rightarrow \mu ^{+} \nu _{H}$ may show up itself as a peak in the missing mass distribution, $m^2_{\nu } = m^2_{miss} = (p_{K} - p_{\mu })_{i} \cdot (p_{K} - p_{\mu })^{i}$, $i = 1, 2, 3, 4$. We assume that heavy sterile neutrinos are stable.³ The investigation of possible signal and background contributions from kaon decays and from kaon scattering and interactions inside the OKA setup is done with a detailed GEANT-3 simulation with the subsequent off-line reconstruction and analysis. Different decay channels, simulated using Monte-Carlo (MC) are weighted according to corresponding matrix elements and branching ratios [23]. The experimental data and main backgrounds, which survived the selections cuts are shown in the $(m^2_{miss};p_{\mu })$ plots of Fig. 3.

In the region of low $m^{2}_{miss}$, both $K^{+} \rightarrow \mu ^{+} \nu _{\mu }$ and $K^{+} \rightarrow \mu ^{+} \nu _{\mu } \gamma$ dominate. In the region of $m^{2}_{miss} > 0.05~\hbox {GeV}2$/c$^4$, the dominant contribution is given by $K^{+}\rightarrow \pi ^{0}\mu ^{+}\nu _{\mu }$ decay channel, which can not be excluded by kinematic cuts without significant loss in acceptance due to its rather flat distribution in the region of interest (see Fig. 3d).

The $K^{+}\rightarrow \pi ^{+}\pi ^{0}$ decay channel is suppressed by four orders of magnitude, but it is responsible for a small peak at $m^{2}_{miss}$ around 0.1 GeV$^2$/c$^4$, which should be taken into account. Therefore we limit our acceptance (see Fig. 3e) from the low muon momentum side by a smooth curve excluding the high event density spot from $K^{+}\rightarrow \pi ^{+}\pi ^{0}$ at low $p_{\mu }\approx 2$ GeV/c (see Fig. 3e), while at high values of the muon momentum ($p_{\mu }$) we additionally introduce a smooth upper limit on $p_{\mu }$ to suppress a tail from badly reconstructed $K^{+} \rightarrow \mu ^{+} \nu _{\mu }$ events. The contributions due to a misidentified electron from the $K^{+} \rightarrow e^{+} \nu _{e} \pi ^{0}$ decay channel (Fig. 3f) and from processes when kaon either scatters or interacts while passing the setup (Fig. 3g) play a minor role.

Missing mass distribution $m^2_{miss}$ for the data and MC events inside kinematic region, indicated in Fig. 3e, is shown in Fig. 4. The distribution for the experimental data is shown in gray, dominant decay channels, obtained from simulation, are marked by different colors with the explanation in the top-right corner, while their sum is depicted in red. The normalization is done to the experimental data at $m^2_{miss}=0$. The relative normalization of different channels is done in accordance with their branching ratios. As seen from Fig. 4, there is a reasonable agreement between the experimental and MC data with some discrepancy in the $m^2_{miss}>0.05~\hbox {GeV}^2$/c$^4$ region. Since contributions from different background sources are strongly suppressed (by orders of magnitude) by our selection criteria, one may expect that efficiencies obtained from MC simulations are reproduced not at the same level of accuracy as it is the case for the main decay channel, $K^{+}\rightarrow \mu \nu _{\mu }$. A fit introducing an additional multiplication constant for each of the suppressed background sources, is done within a region of $m^2_{miss}>0.05~\hbox {GeV}^2$/c$^4$, see Fig. 5. The fit provides much better description of the background.

Fig. 4

Missing mass distribution $m^{2}_{miss}$ for the data and MC events inside kinematic region, indicated in Fig. 3e. Distribution for the experimental data is shown in gray, dominant decay channels, obtained from MC, are marked by different colors, while their sum is depicted in red. The normalization is relative to the experimental data

Fig. 5

Same as Fig. 4, but magnitudes of individual MC-simulation terms are tuned by the fit procedure for the best agreement with the data in the region of $m^2_{miss}>0.05~\hbox {GeV}^2$/c$^4$. Multiplicative efficiency correction is indicated for each background term

Fig. 6

Residual signal distribution after subtraction of the fitted background (see Fig. 5) from the experimental data in the range of $m^2_{miss}>0.05~\hbox {GeV}^2$/c$^4$. An example of the fit for the signal with the certain $m_{\nu _{H}}$ and appropriate width is shown by the smooth curve

3.3 Signal search with a subtraction of the MC simulated background

As a next step, the obtained background curve is subtracted (see Fig. 6) for the subsequent search for heavy neutrinos. For the signal search, a parametrization of the signal shape is essential. For that, a set of reconstructed heavy neutrino signals was produced by the MC simulation with a neutrino mass step of 20 MeV/c$^2$. The signal, as a function of $m^{2}_{miss}$, can be approximated by the Gaussian shape, with an integral error of $\sim$ 2%. Interpolations for the signal shape parameters (width and efficiency) between the generated set of masses is done with polynomial curves. The signal width follows the linear dependence $\sigma _{\nu _{H}}[\hbox {MeV}/c^{2}] = 22.1 - 0.053 \cdot m_{\nu _{H}}$ within a range 260–380 MeV/$c^{2}$, while the relative efficiency dependence is shown in Fig. 7.

Fig. 7

The ratio $\varepsilon _{\nu _{H}}$/$\varepsilon _{\nu _{\mu }}$ of total efficiencies obtained for the set of values of heavy neutrino masses as a function of $m_{\nu _{H}}$ together with the interpolation curve. The systematic uncertainty is also shown as gray shaded area, see Sect. 3.5

After that, series of fits of the residual distribution from Fig. 6 are done to extract a Gaussian shape signal at any given mass with width known from MC. The only parameter of the fit is the signal integral which is not restricted by positive values. The obtained number of events $N_{\nu _{H}}$ is shown with corresponding errors for each fit in Fig. 8.

Fig. 8

Number of heavy neutrino events $N_{\nu _{H}}$ obtained from the fit of the residual distribution for different values of $m^{2}_{\nu _{H}}$ (black points), vertical error bar stands for one standard deviation, $\sigma$. Solid curve corresponds to the upper limit for the number of signal events at 90% CL

No indication of signal from $\nu _{H}$ is found in the mass region of interest. The signal significance does not exceed two standard deviations in the studied mass interval. Since the number of events in each bin in the considered $m^2_{miss}$-region is sufficiently high $\sim 10^2$ one can apply here the Wald approximation for the likelihood ratio method of upper limits calculation for single parameter of interest [24, 25] which leads to the following single-sided upper limit for the signal at 90% CL:

$$\begin{aligned} N^{(Upp.Lim.)}_{\nu _{H}}= & {} 1.28\cdot \sigma + N^{(fit)}_{\nu _{H}},\quad \hbox {for } N^{(fit)}_{\nu _{H}}\ge 0,\\ N^{(Upp.Lim.)}_{\nu _{H}}= & {} 1.28\cdot \sigma ,\quad \hbox {for } N^{(fit)}_{\nu _{H}}<0, \end{aligned}$$

where $\sigma$ is the standard deviation for the $N_{\nu _{H}}$, estimated from the fit, while multiplier of 1.28 corresponds to one-sided estimate with 90% CL for the Gaussian case. The results are shown in Fig. 8.

Fig. 9

Upper limit for $Br(K^{+}\rightarrow \mu \nu _{H})$ at 90% CL as a function of a heavy neutrino mass for three procedures of fit: curve (a) represents procedure described in Sect. 3.3, while curves (b) and (c) are obtained in Sect. 3.4 within simultaneous signal and background fit procedures. Possible systematical effects due to cut variation for the procedure (b) are indicated by the pink vertically shaded area ended by the dash-dotted curve (s). Finally, the solid gray curve (f), with the gray oblique shaded area below it, include remaining systematic uncertainties, see Sect. 3.5

Fig. 10

The OKA upper limit on the mixing matrix element $|U_{\mu H}|^{2}$ at 90% CL is shown in solid dark-gray curve in comparison with preceding experiments: the long-dashed black curve represents the result from KEK-E-089 [10], the fine-dashed red curve corresponds to the result from BNL E949 [11] obtained with stopped kaons, while the dash-dotted green curve indicates the recent result from CERN NA62 [12, 13]

From that, an upper limit on branching, see bold curve (a) at Fig. 9, is obtained by normalization to the $K^{+}\rightarrow \mu \nu _{\mu }$ decay:

$$\begin{aligned} Br(K^{+} \rightarrow \mu \nu _{H}) = Br(K^{+} \rightarrow \mu \nu _{\mu }) \cdot \frac{N_{\nu _{H}}}{\varepsilon _{\nu _{H}}} \cdot \frac{\varepsilon _{\nu _{\mu }}}{N_{\nu _{\mu }}}, \end{aligned}$$

here $\varepsilon _{\nu _{H}}/\varepsilon _{\nu _{\mu }}$ is the relative total efficiency which is shown in Fig. 7 as a function of $m_{H}$; $N_{\nu _{\mu }}=25.8\times 10^{6}$ is a number of reconstructed $K^{+} \rightarrow \mu \nu _{\mu }$ events.

3.4 Upper limits with a common fit of signal and background

As an alternative, we do a series of fits of the initial $m^{2}_{miss}$ distribution of Fig. 5 for $m^{2}_{miss}>0.05~\hbox {GeV}^2/c^4$ with a sum of Gaussian signal for a given mass and all the MC background sources, again, with additional multiplication coefficients which now may be tuned at each mass point. Such a procedure is more signal favorable as compared to that of Sect. 3.3. The remaining part for the calculation of upper limits is done in the same way and the result is indicated in Fig. 9 by a thin smooth curve (b).

To confirm the obtained results we end up with a simplified approach, less dependent on MC, where the background contribution is taken from a 5-th order polynomial approximation of the $m^{2}_{miss}$ distribution of the experimental data within the range of $m^{2}_{miss}>0.05~\hbox {GeV}^2/c^4$. Again we do a common fit for signal plus background, where we allow the tuning of the background parameters for each investigated position. In this case the obtained upper limit at 90% CL is shown with the dashed curve (c) in Fig. 9. This approach, however, is more sensitive to impurity of the signal, so as the final result curve (b) shall be used, as it uses realistic information about background shape and does not artificially suppresses signal (in contrast to approach a). A difference between these three approaches can be can be treated as a systematic error of the method.

3.5 Systematic uncertainties

To study the systematics, we select the method from Sect. 3.4 with MC background as a basis.

(I) The effects arising from selection cuts variation are estimated by performing over hundred standard analyses with the cuts randomly and uniformly changing in the region of $\pm ~\sigma _{i}$ around nominal values, $\sigma _{i}$ being the experimental in the i-th variable, the main variables are: z-vertex left and right cuts, muon selection in GAMS-2000 and HCAL, while the thresholds in GS, BGD were varied within 20% of the nominal values. Also, the minimal number of points on the secondary track is changed by $\pm ~1$ and, independently, its $\chi ^2$ is relaxed by 25% during the set of tests. The result on relative efficiency variation is shown by the gray area in Fig. 7, while 10% truncated (from both sides of variation) area is shown for UL at Fig. 9 by pink vertically shaded area. The upper edge of this area corresponds to UL with effects of the cut variations taken into account.

(II) If the effect of discrepancy between the data and MC of Fig. 4 is interpreted as an extra data inefficiency in the region of interest, we get an additional correction factor which depends on $m_{miss}$ and reaches $\sim$ 15%. It is shown by the gray oblique shaded area in Fig. 9.

(III) A variation of the shape of the MC background was studied by exclusion of contributions from $K^{+} \rightarrow e^{+} \nu _{\mu } \pi ^{0}$ (Fig. 3f) and from undecayed kaon (Fig. 3g). The effect is negligible.

(IV) A possible muon trigger inefficiency which is not described in MC is searched for by a separate analysis of two triggers, the effect can be neglected.

Hence, the upper edge of gray area (curve f of Fig. 9) corresponds to UL with systematics taken into account.

3.6 Evaluation of the $|U_{\mu H}|^2$ mixing parameter upper limit

Finally, we obtain an upper limit on the mixing parameter $|U_{\mu H}|^2$ between the muon neutrino and the heavy sterile neutrino $\nu _{H}$, see Fig. 10.

The coupling strength (see Fig. 1) between muon neutrino and $\nu _{H}$ is obtained from the relation:

$$\begin{aligned} \frac{\varGamma (K \rightarrow \mu \nu _{H})}{\varGamma (K \rightarrow \mu \nu _{\mu })} = |U_{\mu H}|^{2} \cdot \lambda \cdot f_{\mathfrak {M}}, \end{aligned}$$

where $\lambda$ is a kinematic factor, $f_{\mathfrak {M}}$ is a helicity factor in the matrix element, both arising for the case of massive neutrino in the final state [26].

Since the obtained upper limit on $|U_{\mu H}|^{2}$ in the considered mass range does not exceed $10^{-5}$, the $\nu _{H}$ mean life time is estimated to be greater than $10^{-6}$ sec, assuming it decays to SM particles [12, 13]. The corresponding $\nu _{H}$ mean flight distance, estimated with a MC simulation for the $\nu _{H}$ masses considered, ranges between 5–25 km. Hence the heavy neutrino in our case, indeed, can be regarded as stable particle.

4 Conclusions

The OKA 2012 data set was analyzed to search for heavy sterile neutrinos. A peak search method in the missing mass spectrum was used in the analysis. No signal is observed and the upper limit on the mixing between muon neutrino and a heavy sterile neutrino is set in the mass range 270–375 MeV/c$^{2}$.