Abstract
Building on the open-loop algorithm we introduce a new method for the automated construction of one-loop amplitudes and their reduction to scalar integrals. The key idea is that the factorisation of one-loop integrands in a product of loop segments makes it possible to perform various operations on-the-fly while constructing the integrand. Reducing the integrand on-the-fly, after each segment multiplication, the construction of loop diagrams and their reduction are unified in a single numerical recursion. In this way we entirely avoid objects with high tensor rank, thereby reducing the complexity of the calculations in a drastic way. Thanks to the on-the-fly approach, which is applied also to helicity summation and for the merging of different diagrams, the speed of the original open-loop algorithm can be further augmented in a very significant way. Moreover, addressing spurious singularities of the employed reduction identities by means of simple expansions in rank-two Gram determinants, we achieve a remarkably high level of numerical stability. These features of the new algorithm, which will be made publicly available in a forthcoming release of the OpenLoops program, are particularly attractive for NLO multi-leg and NNLO real–virtual calculations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The continuous improvement of statistics and experimental systematics at the Large Hadron Collider (LHC) permits to challenge the Standard Model of particle physics at steadily increasing levels of energy and precision. In this context, the uncertainty of theoretical predictions starts playing a critical role in many areas of the physics program of the LHC, providing strong motivation for developing new techniques that make it possible to push theoretical calculations towards more complex processes and higher perturbative orders.
In the last decade, the advent of new powerful methods for the calculation of one-loop scattering amplitudes [1,2,3,4,5,6,7,8,9] has opened the door to the automation of next-to-leading order (NLO) calculations. Nowadays, one-loop calculations are supported by a number of highly automated tools [10,11,12,13,14,15,16,17,18,19,20] that provide the key to achieve NLO precision in the context of multi-purpose Monte Carlo generators [21,22,23,24,25,26,27]. This recent progress has enabled NLO calculations for a huge number of processes and has extended their reach up to multi-particle final states of unprecedented complexity [28,29,30,31,32]. Nevertheless, in various cases the technical limitations of one-loop generators still represent a serious bottleneck or even a show stopper. These issues can be encountered in processes with many final-state particles and for kinematic configurations with two or more widely separated scales. An important example is given by the real–virtual contributions to next-to-next-to leading order (NNLO) calculations, which require very fast and highly stable one-loop amplitudes in deeply infrared regions of phase space.
Motivated by these considerations, in this paper we introduce a new method that leads to very significant efficiency and stability improvements in the construction of one-loop amplitudes. This new method builds on OpenLoops [9, 16], a fully automated framework for the automated generation of scattering amplitudes in the Standard Model. The original implementation of the open-loop approach [9, 16] supports NLO QCD [31, 33,34,35,36,37,38,39] as well as NLO EW [40,41,42,43,44] calculations and is interfaced to various multi-purpose Monte Carlo tools. The OpenLoops program is also part of Matrix [45] and has already been applied to several NNLO calculations [46,47,48,49,50,51,52,53,54,55]. The essence of the open-loop method [9] consists of a numerical recursion that generates cut-open loop diagrams, called open loops, by multiplying, one after the other, the various building blocks that are connected through loop propagators. More precisely, the construction of N-point loop integrands is organised through the factorisation of N loop segments, which consist each of a loop propagator and a corresponding external subtree. Segment multiplications are implemented through process-independent numerical routines that correspond to the Feynman rules of the model at hand. This type of recursion was first proposed in the context of off-shell recurrence relations for colour-ordered gluon-scattering amplitudes [8]. Thanks to a tensorial representation that retains the loop-momentum dependence of all building blocks, this approach can be used in combination with reduction techniques based on tensor integrals [4] or with the OPP reduction method [5], resulting in both cases in very fast computer code [9].
The new method presented in this paper exploits the factorised structure of the open-loop representation in a completely new way. The key idea is that certain operations, which are usually done when all building blocks of Feynman diagrams have been assembled, can be anticipated and performed on-the-fly during the construction of the diagrams. Exploiting the factorised structure of the integrands, this on-the-fly approach permits to perform various types of operations at a much lower level of complexity, thereby boosting their efficiency. As we will show, it can be exploited in order to factorise helicity summations as well as the sums over different Feynman diagrams that share the same one-loop topology. Moreover, based on the integrand reduction method by del Aguila and Pittau [2], we will introduce an on-the-fly technique for the reduction of open loops. In this way, we will promote OpenLoops to an algorithm that combines the construction and the reduction of loop amplitudes in a unified numerical recursion. A notable feature of this approach is that it permits to avoid high-rank objects at any stage of the calculations. More precisely, tensor integrals are always kept at rank two or lower, thereby reducing the computational complexity in a dramatic way.
The on-the-fly technique leads to very significant improvements of CPU efficiency. For what concerns numerical stability, in order to avoid severe instabilities that result from squared inverse Gram determinants in the reduction identities of [2], we present a method that isolates such instabilities in certain triangle topologies and circumvents them via analytic expansions in the limit of small Gram determinants. In this way we obtain the first integrand-reduction algorithm that is essentially free from Gram-determinant instabilities. The achieved level of stability in double precision is competitive with the most sophisticated tools on the market [19] and with public implementations of OPP reduction in quadruple precision.
The paper is organized as follows. In Sect. 2 we review the original open-loop method. The on-the-fly approach is introduced in Sect. 3 for the case of helicity sums and for the merging of topologically equivalent open loops. In Sect. 4 the on-the-fly approach is generalised to the reduction of open loops. Details on the employed integrand-reduction identities and our treatment of Gram-determinant instabilities are discussed in Sect. 5. The entire algorithm and its implementation are outlined in Sect. 6, where we also present technical studies on the CPU performance and numerical stability. Our conclusions are presented in Sects. 7, and Appendix A deals with low-rank integrals that remain to be solved at the end of the on-the-fly recursion.
2 The open-loop method
In this section we review the original open-loop method [9], which is implemented in the publicly available OpenLoops 1 program [16]. At variance with the original publication [9], here we refine various aspects of the notation and we adopt a particular perspective that sets the stage for the new methods introduced in Sects. 3–5. These new techniques are going to become publicly available in the OpenLoops 2 release.
2.1 Helicity and colour bookkeeping
The task carried out by the open-loop algorithm is the calculation of the tree-level and one-loop contributions to the scattering probability density,
or the squared one-loop contribution
for loop-induced processes. The polarised matrix elements \(\mathcal {M}_0(h)\) and \(\mathcal {M}_1(h)\) should be understood as generic tree and one-loop amplitudes, in the sense that the techniques presented in this paper are applicable to any renormalisable theory, including the QCD and electroweak sectors of the Standard Model, as well as BSM theories. The sums in (1)–(2) run over all helicity and colour degrees of freedom of the scattering particles. While colour indices are kept implicit, the helicity dependence is characterised by a single index \(h\), which corresponds to the global helicity configuration of the event, as described below.
Scattering amplitudes are computed as sums of Feynman diagrams,
where \(\varOmega _{\mathrm {tree}}\) and \(\varOmega _{\mathrm {1-loop}}\) stand for the sets of tree and one-loop diagrams. Each tree and one-loop diagram can be factored into a colour factor \(\mathcal {C}(\mathcal {I})\) and a colour-stripped diagram amplitude,Footnote 1
for \(L=0,1\). The colour-stripped amplitudes \(\mathcal {A}_L(\mathcal {I},h)\) are the main source of complexity. In the open-loop approach, their calculation is addressed with numerical recursions as described in Sects. 2.2–2.4. For what concerns colour factors, exploiting the factorisation properties (4), all relevant operations can be reduced to the calculation of colour-summed interference terms of the form
which appear in the calculation of the scattering probabilities (1)–(2). This task must be addressed only once per process. It is handled by algebraically reducing all \(\mathcal {C}(\mathcal {I})\) to a standard basis \(\{\mathcal {C}_i\}\) and relating the terms (5) to the interference matrix [9, 56]
In OpenLoops we use a basis where all colour factors are expressed through products and traces of the SU(3) generators \(T^a_{ij}\) in the fundamental representation.
For the bookkeeping of external momenta and helicities in a process with \(N_{\mathrm {p}}\) scattering particles we introduce the set of particle indices
To characterise the helicity configurations s of individual particles we use labels
\(\forall \; i\in \mathcal {E}\). The configuration \(\lambda _i=0\) will also be used to characterise unpolarised particles, i.e. fermions or gauge bosons whose helicity is still unassigned or has already been summed over. Since a particle can have up to four different helicity states, it is convenient to adopt a helicity numbering scheme based on the labels
which correspond to a quaternary number with \(\lambda _i\in \{0,1,2,3\}\) as \(i{\mathrm {th}}\)-last digit and all other digits equal to zero. In this way, the helicity configurations \((\lambda _1,\ldots ,\lambda _{N_{\mathrm {p}}})\) of the full event can be uniquely identified with the label
which corresponds to a quaternary number of \(N_{\mathrm {p}}\) digits, each of which describes the helicity of a particular external particle. Let us also introduce the single-particle helicity spaces, \(\mathcal {\bar{H}}_{i}\ni \bar{h}_{i}\), defined as
where we do not include unpolarised states. Finally, the global helicity space for the full set of scattering particles, \(\mathcal {H}\ni h\), is defined as
where the product is understood as \(\mathcal {A}\otimes \mathcal {B}=\{a+b|a\in \mathcal {A},b\in \mathcal {B}\}\).
2.2 Tree amplitudes
At tree level, each colour-stripped Feynman diagram is constructed by contracting two so-called subtrees, which arise by cutting the diagram in two pieces in correspondence of an internal propagator,

A generic subtree \(w_a\) corresponds to the part of a certain Feynman diagram that connects an internal off-shell line with outgoing momentum \(k_{a}\) to a subset of external particles,
In the numbering scheme (9)–(10), the helicity configurations of a subtree are labeled
and the corresponding helicity space, \(\mathcal {H}_a\ni h_a\), is defined as
Subtrees are represented as complex n-tuples, \(w^{\sigma _a}_a(k_{a},h_a)\), where \(\sigma _a\) is the spinor or Lorentz index of the cut line. With this notation, the contraction (13) takes the form
where \(k_b=-k_a\), \(h=h_a+h_b\), and summation over repeated indices is implicitly understood. The propagator associated with the cut line is included only in the subtree \(w_a\) and not in \(\widetilde{w}_b\).
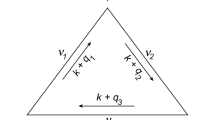
Subtrees are constructed by means of a numerical recursion that starts from the external wave functions and recursively merges subtrees by attaching their off-shell lines to the vertices that occur in the various tree diagrams. A recursion step for the case of a generic three-particle vertex is depictedFootnote 2 in Fig. 1. Its algebraic form reads
where the tensor \(X_{\sigma _b\sigma _c}^{\sigma _a}\) describes the vertex that connects \(w_b\) and \(w_c\) to \(w_a\), as well as the numerator of the propagator that connects to \(w_a\). The related denominator, \((k_a^2-m_a^2)\), appears explicitly in (18).
Diagrammatic representation of a subtree and its numerical construction through the recurrence relation (18). The outgoing momentum \(k_a\) and the spin or Lorentz index \(\sigma _a\) are associated with the off-shell internal line, which is shown explicitly, while the on-shell external particles with helicity \(h_a\) are implicitly understood
The momentum of the resulting subtree is \(k_{a}=k_{b}+k_{c}\) and its helicity is \(h_{a}=h_{b}+h_{c}\). Each recursion step must be repeated for all independent helicity configuration \(h_a\in \mathcal {H}_a=\mathcal {H}_b\otimes \mathcal {H}_c\). The corresponding recursion step for quartic vertices reads
The recursion ends when all off-shell propagators that have been cut in the beginning can be reconnected, such as to obtain the colour-stripped amplitudes (17) for the full set of tree diagrams.
Note that (18)–(19) are analogous to Berends–Giele recurrence relations for off-shell currents [58]. However, while each subtree corresponds to a single topology, off-shell currents incorporate all possible subtrees associated with a certain internal line. The inefficiency due to the usage of individual subtrees is compensated, especially at one-loop level, by the optimisation opportunities that result from the colour-factorisation identities (4) and from the fact that each subtree can occur in multiple Feynman diagrams at tree and loop level.
2.3 One-loop amplitudes
The amplitude of a colour-stripped N-point one-loop diagram, \(\mathcal {I}_N\), has the general form

Symbols carrying a bar denote quantities in \(D=4-2\varepsilon \) dimensions, and for the loop momentum \(\bar{q}\) we adopt the decomposition
where q and \(\tilde{q}\) denote its four-dimensional and \((D-4)\)-dimensional parts, respectively. The denominators read
where \(k_{j}\) is the external momentum flowing into the loop at the \(j^{\mathrm {th}}\) loop vertex. Internal momenta are chosen such that \(p_{0}=p_{N}=0\), i.e. the momentum flowing through the \(\bar{D}_{0}=\bar{D}_{N}\) propagator is \(\bar{q}\). The one-loop diagram \(\mathcal {I}_N\) in (20) can be regarded as a sequence of loop segments,
where the segment \(\mathcal {S}_i\) consists of a subtree \(w_i\) that involves a certain set \(\mathcal {E}_i\) of external particles and is connected to the \(i^{\mathrm {th}}\) loop vertex, \(v_i\), and to the adjacent loop propagator associated with \(\bar{D}_{i}\). Segments associated to a quartic vertex involve two subtrees, \(w_{i_1}\) and \(w_{i_2}\). The helicity configurations of the whole diagram are related to the ones of individual segments, \(h_i\in \mathcal {H}_i\), via
The trace in (20) stands for the full contraction of the spinor and Lorentz indices of propagators and vertices along the loop. In general, the numerator \(\bar{\mathcal {N}}(\bar{q})\) consists of a 4-dimensional part \(\mathcal {N}(q)\) and an \({\varepsilon }\)-dependent remnant \(\widetilde{{\mathcal {N}}}(\bar{q})\),
The terms that result from \(\widetilde{\mathcal {N}}(\bar{q})\) are known as rational terms of type \(R_2\) and can be reconstructed separately as counterterms using appropriate Feynman rules [59,60,61,62]. Thus, the full amplitude can be decomposed as
and in the following we focus on the nontrivial part
which stems from the four-dimensional part of the numerator but involves the D-dimensional denominators (22).
In the open-loop approach, loop diagrams are cut-open in correspondence of the \(\bar{D}_{0}\) propagator, in the sense that the loop numerator is constructed as a tensor,

where \(\beta _0\) and \(\beta _N\) are the spinor or Lorentz indices associated with the cut propagator. We use the Feynman gauge, which means that the numerator of the gluon propagator is simply \(-\mathrm {i}g^{\beta }_{\alpha }\). Once \(\big [\mathcal {N}(\mathcal {I}_{N},q,h)\big ]_{\beta _0}^{\beta _N}\) is determined, we take its trace,
where summation over repeated indices is implicitly understood.
A key feature of the open-loop approach is that, similarly to the product of loop denominators \(\bar{D}_{0}\cdots \bar{D}_{N-1}\) in (27), the loop numerator (28) is factored into a product of segments,
Here and in the following, the matrix structure is implicitly understood, i.e. (30) should be interpreted as
Segments involving a triple vertex have the generic form
where \(w_{i}^{\sigma _i}(k_{i},h_i)\) is the corresponding external subtree. The tensor \(X^{\beta _{i}}_{\beta _{i-1}\sigma _{i}}(q+p_{i-1},k_{i})\) corresponds to the interaction term in (18) and embodies the q-dependent contributions of the loop vertex \(v_i\) and of the numerator of the adjacent \(D_i\) propagator. In renormalisable theories, each segment \(S_i(q,h_i)\) is a q-polynomial of rank \(R\le 1\). In the SM, the structure of three-point vertices is

while four-point vertices have rank zero,

with \(h_i=h_{i_1}+h_{i_2}\) and \(k_i=k_{i_1}+k_{i_2}\).
The numerator (30) is built as a sequence of N segment multiplications, and we refer to such a multiplication as the dressing of a segment. In the following, we will represent the state of the numerator after k dressing steps as,
where \(S_{k+1},\ldots ,S_N\) are the still undressed segments, and
is a q-polynomial of rank \(R\le k\) that incorporates the k dressed segments. The symbol \(\hat{h}_k\) and its counterpart \(\check{h}_k=h-\hat{h}_k\) denote, respectively, the helicity configurations of the dressed and undressed parts of a diagram with k dressed segments and \(N-k\) undressed ones. They are defined through
where h is the global helicity state.
The corresponding helicity spaces, \(\mathcal {\hat{H}}_k\) and \(\mathcal {\check{H}}_k\), are defined by
The q-dependent polynomials (36) are denoted open loops, and this notion implicitly includes also the corresponding undressed segments \(S_{k+1},\ldots ,S_N\) and loop denominators \(\bar{D}_{0},\ldots ,\bar{D}_{N}\). A graphical representation of a generic open loop with k dressed segments is depicted in Fig. 2.
The dressing of open loops is implemented through a numerical recursion
where \(\hat{h}_{k}=\hat{h}_{k-1}+h_{k}\). This operation needs to be performed separately for all relevant helicity configurations \(\hat{h}_{k}\in \mathcal {\hat{H}}_k=\mathcal {\hat{H}}_{k-1}\otimes \mathcal {H}_k\) and iterated for \(k=1,\ldots ,N\). The initial condition is
where \(\hat{h}_{0}\in \mathcal {\hat{H}}_{0}=\{0\}\), and the identity operator is understood as \(\left[ 1\!\!1\right] _\beta ^{\beta '} = \delta _\beta ^{\beta '}\).
In order to capture the full q-dependence of open-loop polynomials we use the tensorial representation
and numerical operations are always performed at the level of the tensor coefficients \(\mathcal {N}_{k;\,\mu _1\cdots \mu _r}(\mathcal {I}_{N},\hat{h}_{k})\). In particular, the explicit form of a step of the dressing recursion (39) is
for a three-point vertex as defined in (33). For an efficient implementation the \(\mu _1\cdots \mu _r\) indices shall be symmetrised throughout.
2.4 Parent–child relations and cutting rule
The original open-loop algorithm can be boosted by using parts of pre-computed \((N-1)\)-point diagrams as a starting point for the construction of more involved N-point diagrams. This approach is based on so-called parent–child relations, which connect open loops of type

and

that start with identical segments \(\mathcal {S}_1,\ldots ,\mathcal {S}_k\). Since open loops are colour-stripped, i.e. they do not depend on the different colour factors of the loop diagrams
it is clear that the dressed parts of (43) and (44) remain identical up to step k of the recursion, i.e.
This allows one to construct the more involved N-point parent diagram (43) using a building block of the simpler \((N-1)\)-point child diagram (44). In general, such relations can be applied for any k with \(2\le k\le N-2\), and the maximum gain in efficiency is obtained when \(k=N-2\), so that only the last two segments of the parent diagram remain to be dressed.
The availability of child diagrams of type (44) is an obvious prerequisite for the applicability of the parent–child approach, and in QCD most one-loop diagrams turn out to be the parent of a corresponding child. Moreover, the correspondence between the first k dressed segments in (43) and (44) requires an appropriate cutting rule, i.e. a prescription that determines the cut propagator and the dressing direction in a similar way as in (43)–(44).
To this end, for each segment \(\mathcal {S}_i\) with external particles \(\mathcal {E}_i=\{\alpha _{i1},\ldots ,\alpha _{in_i}\}\) we introduce a binary weight defined as the sum of the weights \(2^{\alpha -1}{}\) for each particle \(\alpha \), i.e.
For example, \(F(\mathcal {S}_i)=2^0+2^1+2^3=11\) for a segment connected to the external legs \(\mathcal {E}_i=\{1,2,4\}\). For the merging of subtrees \(\mathcal {S}_i\) and \(\mathcal {S}_j\) into a single segment \(\mathcal {S}_i\oplus \mathcal {S}_j\) with external legs \(\mathcal {E}_i\cup \mathcal {E}_j\), the weight function obeys the useful distributive property
This implies that merged segments always outweigh the original segments. Based on this feature, for N-point diagrams we adopt the cutting rule [9]
The fact that the first segment is identified as the one with lowest weight guarantees its stability with respect to the merging of \(\mathcal {S}_{k+1}\oplus \mathcal {S}_{k+2}\) in (43)–(44), while (50) guarantees the stability of the dressing direction for all configurations with \(k\ge 2\). In this way, the parent–child approach permits to recycle the longest possible open loops.
Note that relations of type (46) can be exploited also for diagrams that involve the same number N of loop propagators and identical dressed segments, but different undressed ones.
Schematic representation of the on-the-fly helicity sums in (62). Taking the interference with the Born amplitude makes it possible to sum over the helicities \(h_1,\ldots ,h_k\) of the first k dressed segments of an open loop, while the remaining segments are still undressed
2.5 Helicity treatment and reduction to scalar integrals
In the following we discuss the operations that are required in order to determine the contribution of a loop diagram \(\mathcal {I}_N\) to the scattering probability density (1), starting form the output of the open-loop recursion, i.e. from an open-loop numerator (35) with \(k=N\) dressed segments.
Instead of proceeding via a direct construction of the one-loop amplitude \(\mathcal {A}_1(\mathcal {I}_N,h)\) defined in (27), we start with the associated colour structure \(\mathcal {C}(\mathcal {I}_N)\) defined in (4), and we proceed by building the colour-summed interference with the Born amplitude,
combining it with the trace of the colour-stripped loop numerator,
and performing helicity sums,
Here we use \(h=0\) for the configuration where all particles are unpolarised, in the sense that their helicities have been summed over. The above operations are performed at the level of q-coefficients in the tensorial representation (41), i.e. in practice we compute
After the summation over colours and helicities it is possible to combine all diagrams with the same one-loop topology, i.e. diagrams of type
with all possible combinations of segments,
that have the same external legs \(\mathcal {E}_i\) and loop propagators \(\bar{D}_{i}\) but different external subtrees \(w_i^{\alpha _i}\) and/or loop vertices \(v_i^{\alpha _i}\). To filter out combinations of segments that are not allowed by the Feynman rules we introduce the tensor
In this way, the full set of topologically equivalent one-loop diagrams can be defined as
and their sum yields
The contribution of the diagrams (58) to the scattering probability (1) reads
In OpenLoops 1, the calculation of the coefficients (59) is entirely based on the open-loop approach, but the reduction of the loop integrals (60) to scalar integrals, as well as the numerical evaluation of the latter, are performed by means of external libraries.
By default, OpenLoops 1 adopts the tensor representation on the rhs of (60) and computes the relevant tensor integrals with the Collier library [19], which implements the reduction techniques of [4, 63] and the scalar integrals of [64]. One of the powerful features of Collier lies in sophisticated analytic expansions [4] that avoid dangerous numerical instabilities in phase space regions with small Gram determinants.
Alternatively, the reduction to scalar integrals is performed with Cuttools [10], and scalar integrals are computed with OneLoop [65]. The Cuttools program implements the OPP reduction method [5], which is based on double, triple and quadruple cuts of the integrand on the lhs of (1). This requires a large number of evaluations of \(\mathcal {V}(\varOmega _N,q,0)\), and the high efficiency of the open-loop representation, \( \mathcal {V}(\varOmega _N,q,0)= \sum _{r=0}^R \mathcal {V}_{\mu _1\cdots \mu _r}(\varOmega _N,0) \,q^{\mu _1}\cdots q^{\mu _r}, \) results in a dramatic boost of the OPP method.
Another key feature behind the high speed of the open-loop method is the fact that, irrespectively of the reduction method, the time-consuming reduction to scalar integrals is performed after summing over colour and helicity degrees of freedom.
3 Summing helicities and diagrams on-the-fly
In this section we introduce a new technique that makes it possible to sum helicities and to merge different one-loop diagrams on-the-fly, i.e. after each step of the open-loop dressing recursion. Besides boosting the open-loop algorithm in a significant way, this approach is also a key aspect of the on-the-fly reduction technique introduced in the Sect. 4.
3.1 On-the-fly helicity summation
In the original formulation of the open-loop method, helicity sums (53) are performed at the end of the dressing recursion. This implies that the \(k\mathrm {th}\) dressing step (39) needs to be performed for all helicity configurations of the dressed segments \(\mathcal {S}_1,\ldots ,\mathcal {S}_k\). This feature, combined with the fact that the number of relevant helicity states and the cost of a single dressing step scale exponentially with k, result in a very rapid growth of the CPU cost of dressing operations in the course of the open-loop recursion. To avoid this negative trend, in this section we introduce a method that exploits the factorisation properties of the open-loop representation (30) in a way that makes it possible to perform helicity sums on-the-fly, after the dressing of each new segment.
The idea, sketched in Fig. 3, is that, upon taking the interference of open loops with the Born amplitude, it is possible to sum over the helicities of all dressed segments, irrespectively of the presence of still undressed segments. To introduce the technical aspects of this approach, let us rewrite the interference (53) between the colour-summed Born term \(\mathcal {U}_0(\mathcal {I}_N,h)\) and the one-loop numerator as
To take advantage of the factorisation of loop segments on the rhs of (61), we then postpone the trace operation and generalise (61) by defining
where the interference with \(\mathcal {U}_0(\mathcal {I}_N,h)\) is restricted to the first k dressed segments of the open loop, and the corresponding helicities, \(\hat{h}_k=h_1+\cdots +h_k\), are summed over. As a result, the first k segments become effectively unpolarised, and (62) depends only on the helicities of the remaining \(N-k\) undressed segments, \(\check{h}_k=h_{k+1}+\cdots +h_N\). Due to this dependence, which is induced by the fact that the Born term (51) depends on the helicities \(h=\hat{h}_k+\check{h}_k\) of all external particles (37), the sums over \(h_1,\ldots ,h_k\) in (62) cannot be entirely factorised. However, they can be cast in the nested form
which highlights the fact that each segment becomes effectively unpolarised after its dressing.
Diagrammatic representation of helicity sums and diagram merging. Upon taking the interference with the Born amplitude, the helicities of the k dressed segments are summed, and the full set of topologically equivalent diagrams with the same undressed segments \(\{\mathcal {S}_{k+1}^{\alpha _{k+1}},\ldots , \mathcal {S}_N^{\alpha _N}\}\) is merged in a single open loop. See (70) and (72)
In practice, in analogy with the standard open-loop recursion (39), the helicity-summed open loops (62) are constructed with the recurrence relation
where the helicities \(h_k\in \mathcal {H}_k\) of the dressed segment are summed on-the-fly. To this end, the dressing operation needs to be performed for all \(\check{h}_{k-1}=\check{h}_{k}+h_{k}\in \mathcal {\check{H}}_{k-1}\). The initial condition reads
i.e. a fully undressed open loop is given by the interference of its colour structure with the Born amplitude, whose helicity states \(h\) live in the global helicity space \(\mathcal {H}\). At each dressing step, helicity degrees of freedom are reduced by a factor equal to the number of helicity states of the dressed segment, i.e. by factor two for each external fermion or massless vector boson and a factor three for each external massive vector boson in the segment.
At the end of the recursion, when all N segments are dressed, no helicity dependence is left over (\(\check{h}_{N}\equiv 0\)), and the unpolarised loop numerator (53) is obtained by taking the trace
The recursion (64) is understood as matrix multiplication,
in the tensor representation
which leads to the same tensorial recursion as in (42).
In summary, performing helicity sums on-the-fly leads to a decreasing number of helicity degrees of freedom when the number k of dressed segments increases. In this way, the effect of the growing CPU cost of dressing operations at large k can be strongly attenuated. The price to pay is that the parent–child approach (43)–(46) is not applicable anymore, due to the fact that (65) incorporates the colour structure \(\mathcal {C}(\mathcal {I}_N)\) of the whole one-loop diagram. However, as we will see in Sect. 3.2, the parent–child relations can be replaced by a similarly efficient method based on the merging of topologically equivalent one-loop diagrams. Finally, let us note that the recursion (64)–(65) is not applicable to squared one-loop amplitudes. For this case we still rely on the original open-loop algorithm.
3.2 On-the-fly merging of topologically equivalent open loops
The key idea behind the recursion (64)–(65) is that, taking the interference between the Born amplitude and the one-loop colour structure \(\mathcal {C}(\mathcal {I}_N)\) as initial condition makes it possible to anticipate operations that are usually performed after completion of the construction of a one-loop diagram. In particular, such operations become applicable on-the-fly after the dressing of individual loop segments. This technique will be denoted as on-the-fly approach, and its applicability goes well beyond helicity sums.
As sketched in Fig. 4, the on-the-fly technique can be extended to the double sums over helicity states and topologically equivalent loop diagrams in (59). The idea is that, rather than being constructed one by one, the topologically equivalent diagrams
defined in (55)–(58), can be merged in a recursive way by summing over the various subtrees \(\mathcal {S}_i^{\alpha _i}\) as soon as they get dressed.
Example of a step of the diagram merging recursion (73). After dressing the second segment and summing over its helicity configurations \(h_2\), all diagrams with equivalent one-loop topology and identical undressed segments \(\mathcal {S}_3^{\alpha _3},\ldots , \mathcal {S}_N^{\alpha _N}\) are merged into a single open loop
To this end, let us define subsets of diagrams, \(\varOmega _N^k\subset \varOmega _N\), that share the same undressed segments, \(\{\mathcal {S}_{k+1}^{\alpha _{k+1}},\ldots , \mathcal {S}_N^{\alpha _N}\}\), after k dressing steps,
where the tensor \(\delta \), defined in (57), filters out one-loop diagrams that are not allowed by the Feynman rules. By construction, all diagrams in the set (70) must undergo identical future dressing steps, which can be performed only once after merging the first k segments. This operation can be organised in a very similar way as helicity summations in Sect. 3.1. Technically, taking as a starting point the nested helicity sums in (63), it is sufficient to generalise the loop segments and the Born term (65) by replacing
and to extend the summation over the helicities \(h_1,\ldots ,h_k\) of the dressed segments to the corresponding “diagrammatic” degrees of freedom \(\alpha _1,\ldots ,\alpha _k\). This leads to the identity
which defines an open-loop object with fixed undressed segments \(\{\mathcal {S}_{k+1}^{\alpha _{k+1}},\ldots \mathcal {S}_N^{\alpha _N}\}\) and helicities \(\check{h}_k=h_{k+1}+\cdots +h_N\) that incorporates all possible chains of dressed segments \(\{\mathcal {S}_{1}^{\alpha _1},\ldots , \mathcal {S}_k^{\alpha _k}\}\) forming a valid Feynman diagram, summed over the corresponding helicities \(h_1,\ldots ,h_k\).
Note that the dependence of (72) on the helicities \(h_{k+1},\ldots ,h_N\) and diagrammatic indices \(\alpha _{k+1},\ldots ,\alpha _N\) of the undressed segments is due to the fact that the Born term defined in (65) and (71) retains the full helicity dependence of the Born amplitude as well as the tensor (57) and the colour structure of the whole one-loop diagram.
In analogy with (39) and (64), the open-loop objects (72) can be constructed with the recurrence relation
where helicity sums and diagram merging are performed on-the-fly. An explicit example of an on-the-fly merging step is illustrated in Fig. 5. Similarly as for (64), the recursion (73) is implemented in the form of tensorial relations (42). The relevant initial conditions at \(k=0\) are
where each fully undressed contribution corresponds to an individual diagram,
with helicities \(h\) that live in the full helicity space \(\mathcal {H}\). Let us point out that, thanks to the absorption of the colour factors \(\mathcal {C}(\mathcal {I}_N^{\alpha _1\cdots \alpha _N})\) in the Born interference term (74), in (73) it is possible to merge parts of diagrams that carry different colour structures in a single object, while respecting the exact colour dependence.
After N recursion steps one obtains a single open-loop object \(\mathcal {V}_N(\varOmega ^N_N,q,\check{h}_N)\), which merges the full set of topologically equivalent diagrams (\(\varOmega ^N_N\equiv \varOmega _N\)) and is entirely unpolarised (\(\check{h}_N\equiv 0\)). At this stage, taking the trace that closes the loop one arrives at
which is equivalent to (59).
Evolution of the tensor rank R and the number \(N_{\mathrm {tcoeff}}\,(R)=\left( {\begin{array}{c}R+4\\ 4\end{array}}\right) \) of open-loop tensor coefficients (right vertical axis) as a function of the number k of dressed segments during the open-loop recursion. Each dressing step is assumed to increase the rank by one. The original open-loop algorithm, where tensor reduction is applied a posteriori (left), is compared to the on-the-fly reduction approach (right). The red diagonal lines illustrate the dressing steps and the blue vertical lines the reduction steps
As demonstrated in Sect. 6.2, performing helicity sums and merging diagrams on-the-fly yields a very significant efficiency improvement with respect to the original open-loop algorithm. More precisely, if helicity sums are performed at the end of the recursion as in (53), the merging approach and the parent–child relations (46) permit to achieve a similar speed-up factor of the order of two. However, contrary to the parent–child technique, the on-the-the-fly approach is applicable both to diagram merging and helicity sums. This leads to a further speed-up factor that can vary from two to three, depending on the process.
As we will see in Sect. 4, the on-the-fly approach will be a crucial ingredient in order to arrive at a new efficient algorithm that combines the operations of open-loop dressing and tensor reduction at the level of each individual step of the open-loop recursion.
4 On-the-fly reduction of open loops
In the original version of the OpenLoops program, the construction of integrand numerators and the reduction to scalar integrals are performed independently of one another using different tools. Open-loop numerators of N-point diagrams are constructed by recursively dressing N segments as described in Sect. 2.3. Each step of the recursion can increase the tensor rank by one, and, upon symmetrisation of all \(q^{\mu _1}\cdots q^{\mu _r}\) monomials with \(r\le R\), open-loop polynomials of rank R involve \(\left( {\begin{array}{c}R+4\\ 4\end{array}}\right) \) independent tensor coefficients. Thus their complexity grows exponentially with the number of recursion steps. For instance, open loops with \(R=6\) and \(R=7\) involve, respectively, 210 and 330 components, while only 5 components are present for \(R=1\). As illustrated in the left plot of Fig. 6, in the original open-loop algorithm tensorial complexity keeps growing until the maximum rank \(R\le N\) is reached at the end of the dressing recursion. At this stage, upon summation of helicity configurations and loop diagrams with equivalent one-loop topology, tensor integrals are reduced to scalar integrals using external libraries, such as Collier [66] or Cuttools [10], as described in Sect. 2.5.
Dealing with intermediate results with a large number of tensor components requires a considerable amount of computing power, both for the reduction of high-rank objects and at the level of the tensorial structure of the open-loop recursion (42), which needs to be performed for each relevant helicity configuration and each \([\ldots ]_{\beta _0}^{\beta _k}\) component. These operations can be significantly accelerated by means of the techniques introduced in Sect. 3. Nevertheless, they remain the most CPU intensive aspect of multi-particle one-loop calculations in OpenLoops.
Motivated by the above considerations, in this section we introduce a new approach that avoids the appearance of high-rank objects at any stage of the calculation. This is achieved by extending the on-the-fly approach introduced in Sect. 3 to the reduction of open loops. In this way, interleaving the operations of open-loop dressing and tensor reduction, we build a single recursive algorithm, where each increase of tensorial rank caused by a dressing step is compensated by an integrand-reduction step.
Diagrammatic representation of the on-the-fly reduction step (79) for an N-point open loop at step \(k=2\) of the dressing recursion. The symbols \(\mathcal {V}_k(\varOmega ^k_N)\) and \(\mathcal {V}_k(\varOmega ^k_N[j])\) correspond, respectively, to the rank-two polynomial on the lhs of (79) and its reduced rank-one counterparts on the rhs. The red crosses indicate the pinching of the \(\bar{D}_{j}\) propagators in the \(\mathcal {V}_k(\varOmega ^k_N[j])\) terms with \(j=0,\ldots ,3\). Since \(\bar{D}_{0}=\bar{D}_{N}\), in our graphical representation the \(\bar{D}_{0}\) denominator is located on the \(N^\mathrm {th}\) segment
As illustrated in the right plot of Fig. 6, the on-the-fly reduction approach avoids the appearance of any intermediate object with rank higher than two. Besides the CPU cost needed for the processing of high-rank objects, this alleviates also possible memory issues due to their storage.
4.1 On-the-fly integrand reduction
For the on-the-fly reduction of open-loop polynomials we are going to use the method of [2], which permits to reduce rank-two monomials of the loop momentum through identities of the form
The rank-one polynomial on the rhs is a linear combination of four loop denominators, \(D_0,\ldots ,D_3\), and the corresponding tensor coefficients, \(A_j^{\mu \nu }\) and \(B_{j,\lambda }^{\mu \nu }\), depend only on the three external momenta \(p_1,p_2,p_3\). The coefficients of loop denominators are labeled with indices \(j=0,\ldots ,3\), while \(j=-1\) is used for the constant parts. Their explicit expressions are presented in Sect. 5.2.
The identity (77) provides an exact reconstruction of \(q^\mu q^\nu \) in terms of four-dimensional loop denominators, but can be easily generalised to D-dimensional denominators by replacing
Note that \(\tilde{q}^2\) contributions resulting from the terms \(B^{\mu \nu }_{j,\lambda } D_j\) with \(j=0,1,2,3\) must cancel among each other in (77) since they generate rank-three terms of type \(q^\lambda \,\tilde{q}^2\) that are not consistent with the rank-two structure on the lhs. Thus the substitutions (78) generate only an extra term \(-\tilde{q}^2 A_0^{\mu \nu }\) on the rhs of (77).
The integrand reduction (77) holds at the integrand level, irrespectively of the presence of extra loop denominators \(D_4,\ldots ,D_{N-1}\) or additional q-dependent factors that may multiply the \(q^\mu q^\nu \) monomial. These properties, in combination with the factorisation of open loops into segments, make it possible to apply the reduction (77) at any intermediate stage of the recursion (73). This on-the-fly reduction approach is illustrated in Fig. 7, and the corresponding reduction identities for N-point integrands at step k of the dressing recursion have the form

where \(\varOmega ^k_N[j]\) for \(0\le j\le 3\) denote the \((N-1)\)-point subtopologies that arise from \(\varOmega ^k_N\) by pinching the \(\bar{D}_{j}\) propagator, while terms with \(j=-1\) on the rhs correspond to the original topology, \(\varOmega ^k_N[-1]=\varOmega ^k_N\). Note that the denominators \(\bar{D}_{j}\) can be pinched irrespectively of whether the related \(S_{j}(q)\) segments are already dressed or not. In (79) we adopt the approach of Sect. 3.2, where open-loop polynomials incorporate the colour-summed interference with the Born amplitude as well as helicity sums and merging of all dressed segments. However, for simplicity, the bookkeeping of helicities, merged diagrams, and \([\ldots ]_{\beta _0}^{\beta _k}\) indices is kept implicit.
The partially dressed open loops on the lhs and rhs of (79) have the general form
where four-dimensional loop-momentum components are accompanied by \(\tilde{q}^2\) terms that arise from (77) to (78). As discussed in Sect. 4.4, only a small fraction of the \(\tilde{q}^2\)-dependent terms can lead to non-vanishing contributions at the end of the recursion. Thus, in order to avoid the proliferation of tensor coefficients, all \(\tilde{q}^2\) terms that are expected to vanish are identified and discarded in advance at each dressing and reduction step.
In general, the relation (79) allows one to reduce any polynomial \(\mathcal {V}_{k}(\varOmega ^k_N,\bar{q})\) of rank \(R\ge 2\) to rank \(R-1\) polynomials \(\mathcal {V}_{k}(\varOmega ^k_N[j],\bar{q})\). But, in practice, the reduction (79) can be interleaved with the open-loop dressing recursion in a way that the tensor rank never exceeds two. For \(R=2\) the coefficients of the rank-one open-loop polynomials that arise from the reduction (79) read
The transformations (79)–(81) can be used to reduce any rank-two open loop with \(N\ge 4\) propagators to a rank-one N-point object and four \((N-1)\)-point pinched objects of rank one.
Rank-two open loops with only \(N=3\) loop propagators can be reduced to rank one in a very similar way [2]. The relevant identities (see Sect. 5.3) have the same structure as (77) but involve only three reconstructed propagators, \(\bar{D}_{0}\), \(\bar{D}_{1}\) and \(\bar{D}_{2}\). Moreover, they do not hold at the integrand level, but only upon integration over the loop momentum. The tensors \(A_j^{\mu \nu }\) and \(B_{j,\lambda }^{\mu \nu }\) for the case \(N=3\) depend only on \(p_1\) and \(p_2\). They are obtained from the ones for \(N=4\) by simply setting to zero the terms involving \(p_{3}\) (see Sect. 5.3).
The on-the-fly reduction formula for \(N=3\) has the form

where \(\mathcal {V}_{k}(\varOmega ^k_3,\bar{q})\) is an open loop of rank \(R=2\) that results from a certain number \(k\ge 2\) of dressing steps and \(k-2\) or less reduction steps. Possible undressed segments are denoted as \(S_{\mathrm {rem}}(q)\), and (82) is valid only for terms \(S_{\mathrm {rem}}(q)\) of rank zero or one. In general this allows for only \(N_{\mathrm {rem}}\le 1\) extra segments, i.e.
and these two cases are sufficient to cover all relevant \(N=3\) topologies and pinched subtopologies in renormalisable theories.Footnote 3 The relations between the rank-two polynomial \(\mathcal {V}_{k}(\varOmega ^k_3,\bar{q})\) and its reduced counterparts \(\mathcal {V}_{k}(\varOmega ^k_3[j],\bar{q})\) have the same form as in (81).
Although the above three-point reduction holds only at the integral level, the fact that the term \(S_{\mathrm {rem}}(q)\) can be factorised makes it possible to apply (82) as soon as the dressed open loop \(\mathcal {V}_{k}(\varOmega ^k_3,\bar{q})\) has reached rank two, independently of the remaining part of the numerator.
In summary, exploiting the fact that open loops are factorised into segments, the identities (77) and (82) can be applied on-the-fly during the dressing recursion, while an arbitrary number of segments is still undressed.Footnote 4 Thus, dressing and reduction steps can be interleaved in a way that the increase of tensorial rank resulting from dressing is promptly compensated through an on-the-fly reduction. More precisely, on-the-fly reduction steps are applied to diagrams and pinched sub-diagrams with \(N\ge 3\) at those stages of the recursion where the next dressing step would generate a rank-three object.Footnote 5 The reduced rank-one objects with N and \(N-1\) loop propagators are further dressed and possibly reduced until one arrives at fully dressed open loops of rank \(R\le 2\) for all two- and higher-point contributions. An this stage, the open-loop matrix structure can be eliminated by taking the trace (76), and all rank-two objects with \(N\ge 3\) can be reduced to rank one with a final reduction step of type (77) or (82).
After the above dressing and on-the-fly reduction steps, the following types of integrals remain to be reduced:
For their reduction to scalar integrals with \(N\le 4\) we use a combination of integral reduction and OPP reduction identities as described in Appendix A.
4.2 Merging pinched topologies
Since it allows one to keep the tensor rank low at any stage of the calculations, the on-the-fly reduction approach has the potential to accelerate one-loop calculations in a significant way. However, some aspects of the on-the-fly reduction approach could lead to a dramatic increase of the computational cost. First, the fact that the reduction is performed when the loop is still open, i.e. before taking the trace (76), implies that the entries of the \([\ldots ]_{\beta _0}^{\beta _k}\) matrix have to be processed as 16 independent objects. Second, the reduction has to be performed for all not yet summed helicity configurations of the undressed segments. Third, each reduction step (79) generates four pinched topologies that need to be processed as independent contributions in subsequent dressing and reduction steps.
Due to the proliferation of pinched subtopologies, the naive iteration of on-the-fly reduction steps would lead to a dramatic increase of the CPU cost. Fortunately, this can be avoided by means of the merging technique introduced in Sect. 3.2, which makes it possible to absorb pinched N-point open loops into unpinched \((N-1)\)-point open loops, in such a way that they do not need to be processed as separate objects. As explained in the following, the merging of pinched subtopologies requires a different implementation depending on whether the pinch belongs to the dressed part of the open loop or not, as well as for the special case of a \(\bar{D}_{0}\) pinch.
4.2.1 Pinching a dressed propagator
Let us consider the on-the-fly reduction of an N-point open loop with k dressed segments, focusing on contributions that result from the pinching of a \(\bar{D}_{j}\) denominator with \(j<k\),

Here, consistently with the notation of Sect. 3.2, we have restored the indices \(\alpha _i\) of the various undressed segments, while helicity indices are kept implicit. The pinched propagator in (85) is entirely dressed and merged, in the sense that both adjacent segments, \(S_{j}\) and \(S_{j+1}\), are dressed and merged. Thus, for what concerns all future dressing and reduction steps, apart from the disappearance of the \(\bar{D}_{j}\) denominator, the pinch has no effect. Consequently, the above contribution can be absorbed into unpinched \((N-1)\)-point open loops that involve the same loop denominators, \(\bar{D}_{0}\cdots \bar{D}_{j-1}\bar{D}_{j+1}\cdots \bar{D}_{N-1}\), and the same undressed segments, \(S_{k+1}^{\alpha _{k+1}},\ldots ,S_{N-1}^{\alpha _{N-1}}\). To this end, it is sufficient to bring the pinched open loop (85) in the standard form
Diagrammatic representation of formula (88) for the merging of pinched open loops. The first two unpinched diagrams on the rhs, where the generic subtrees \(w_j^{\alpha _j}\) and \(w_{j+1}^{\alpha _{j+1}}\) are directly connected to the loop propagators \(\widetilde{D}_{j-1}\) and \(\widetilde{D}_{j}\), correspond to the first term on the rhs of (88). The corresponding triple or quartic vertices of the Feynman rules play an analogous role as the crossed vertex in the pinched open loop (last diagram on the rhs). Besides merging all relevant unpinched combinations \(\alpha _j,\alpha _{j+1}\), also possible unpinched topologies where some of the external legs in \(w_j\) and \(w_{j+1}\) are interchanged (not shown) should be included

which corresponds to an unpinched \((N-1)\)-point open loop with \(k-1\) dressed segments. The crossed vertex on the lhs of (86) indicates that the two original segments that are connected by the pinched propagator should be regarded as a single effective segment. This symbolic contraction of segments does not change anything in the numerics of the open-loop numerator, and the transformation (86) is nothing but a trivial relabeling of the denominators and of the undressed segments that lie on the right side of the pinch,
The pinched open loop (86) can be merged with corresponding unpinched open loops to form a single \((N-1)\)-point object with \(k-1\) dressed segments. The corresponding formula reads

A diagrammatic representation of this identity is given in Fig. 8. The resulting object, for which we introduce the symbol \(\widetilde{\mathcal {V}}^{\alpha _k\cdots \alpha _{N-1}}_{k-1}\), is a combination of unpinched and pinched open loops, which enter, respectively, through the first and second term on the rhs of (88). By construction, the corresponding set of diagrams (\(\widetilde{\varOmega }_{N-1}^{k-1}\)) includes all unpinched (\(\varOmega _{N-1}^{k-1}\)) and pinched (\(\varOmega ^k_N[j]\)) diagrams with loop propagators \(\widetilde{D}_{0}\cdots \widetilde{D}_{N-2}\) and undressed segments \(S_{k+1}^{\alpha _{k+1}},\ldots ,S_{N-1}^{\alpha _{N-1}}\). The set of pinched diagrams \(\varOmega ^k_N[j]\) corresponds to an N-point topology that results from \(\varOmega _{k-1}^{N-1}\) by undoing a \(\bar{D}_{j}\) pinch, and (88) involves all possible \(\varOmega ^k_N[j]\) contributions with \(1\le j \le k\).
As a necessary condition for the merging operation (88) to be applicable, the different open loops on the rhs of (88) have to feature the same undressed segments. This implies that they must be at the same stage of the dressing recursion, and, most importantly, that the starting position and the directions of the respective dressing recursions should be equivalent to each other. With other words, \(\widetilde{D}_{0}\cdots \widetilde{D}_{N-2}\) and  should be two identical ordered sets of propagators. In particular they should start from the same cut propagator, \(\widetilde{D}_{0}=\bar{D}_{0}\). As discussed in Sect. 4.3 this can be guaranteed, to some extent, by means of an appropriate cutting rule.
should be two identical ordered sets of propagators. In particular they should start from the same cut propagator, \(\widetilde{D}_{0}=\bar{D}_{0}\). As discussed in Sect. 4.3 this can be guaranteed, to some extent, by means of an appropriate cutting rule.
Another obvious prerequisite for the absorption of pinched N-point open loops is the existence of corresponding unpinched \((N-1)\)-point Feynman diagrams. With other words, the crossed vertex in (86) should have a physical counterpart consisting of a triple or quartic vertex, which can directly connect the \(\bar{D}_{j-1}\) and \(\bar{D}_{j+1}\) propagators to subtrees involving the external legs attached to \(\hat{w}_j\) and \(\hat{w}_{j+1}\) (see Fig. 8). In QCD, this turns out to be the case for most pinched configurations.
Moreover, pinched N-point configurations of the form (86) can also be merged with other pinched higher-point diagrams that get the relevant pinches in past or future reduction steps. Thus, pinched objects of type (86) will always be denoted as absorbable, irrespective of whether corresponding unpinched \((N-1)\)-point Feynman diagrams exist or not.
The merging procedure (88) needs to be applied after any on-the-fly reduction step that creates new pinched objects. Thus merging operations have to be interleaved with iterated dressing and reduction steps. Since pinched N-point objects are absorbed into lower-point objects, the algorithm should start with the dressing and on-the-fly reduction of open loops with \(N=N_{\max }\), and continue towards lower N. The merging operation (88) starts at stage \(N-1 = N_{\max }-1\) and is applied after every dressing step, together with the merging of unpinched open loops (see Sect. 3.2). Note that, due to the iterative nature of the algorithm, the term \(\widetilde{\mathcal {V}}^{\alpha _k\ldots \alpha _{N-1}}_{k}\) on the rhs of (88) can be the result of multiple pinching and merging steps.
4.2.2 Pinching an undressed propagator
The possibility to absorb pinched open loops as in Fig. 8 is based on the fact that all future dressing and reduction operations can be performed only once at the level of a merged object. Thus, the undressed segments of pinched and unpinched open loops should be identical.
However, the segments connected to the \(\widetilde{D}_{j-1}\) and \(\widetilde{D}_{j}\) propagators are different for pinched and unpinched terms. In the pinched case there are two separate segments, which involve \(w_{j}\) and \(w_{j+1}\) and require two subsequent dressing steps. In contrast, unpinched open loops require a single dressing step, since \(w_{j}\) and \(w_{j+1}\) are combined in a single segment.
It is thus clear that pinched open loops can be absorbed only after the dressing of the segments that lie on the two sides of the pinch. If this is not the case, i.e. when a \(\bar{D}_{j}\) pinch is applied to an open loop with \(k\le j\) dressed segments, its absorption becomes possible only after \((k-j+1)\) additional dressing steps, which result in
where \(S_{k+1}\cdots S_{j+1}\) are dressed. Note that in (89) we also sum over all possible \(\alpha '_{i}\), and use indices \(\alpha _{j+1},\ldots ,\alpha _{N-1}\) with shifted labels for the undressed segments \(S_{j+2},\ldots ,S_{N}\) on the right side of the pinch.
As illustrated in Fig. 9, the dressing operation (89) combined with the relabeling (87) brings the pinched open loops in a configuration that can be absorbed with the merging formula (88). However, the absorption of undressed pinched propagators is more involved than the simplified picture of Fig. 9. Pinched open loops can require more than one dressing step to become absorbable, in which case, in general, also new reduction steps are needed in order to keep the tensor rank below three. Such new reductions generate additional pinches, and their iteration can lead to a proliferation of multi-pinched configurations.
Thus, to avoid dramatic inefficiencies, it is crucial to minimise the number of required dressing steps by keeping pinchable propagators as close as possible to the dressed part of the numerator. This is why we choose to perform the on-the-fly reduction using the denominators \(\bar{D}_{0},\ldots ,\bar{D}_{3}\).Footnote 6 In this way, when the first two segments are dressed and the first reduction step is applied (see Fig. 7), the various pinched propagators are located at most one left-dressing step (\(\bar{D}_{0}\)) and two right-dressing steps (\(\bar{D}_{3}\)) away from the dressed part.
In order to identify pinches that cannot be directly absorbed and to anticipate how they propagate through the recursion, let us consider generic open-loop configurations before the creation of a new pinch through a reduction step. At this stage the rank R must be equal to two. We first consider the very first reduction step, which can occur after \(k\ge R=2\) dressing steps, and we focus on a \(\bar{D}_{2}\) pinch in the case where only \(k=2\) segments are dressed. In this case, an on-the-fly reduction step and a subsequent dressing step yield

i.e. the \(\bar{D}_{2}\) pinch can be brought in the standard form (86) and can thus be absorbed into unpinched contributions. The same considerations apply also to \(\bar{D}_{1}\) and \(\bar{D}_{0}\) pinches (see Sect. 4.2.3) and can be generalised to any step of the recursion, since the structure of the dressed parts on the lhs and rhs of (90) is the same.
Also \(\bar{D}_{3}\) pinches can be absorbed in a similar way in case there are at least three dressed segments before the reduction step. Otherwise, when only two segments are dressed, the combination of an on-the-fly reduction step with a subsequent dressing step leads to

where the pinch is applied on the last dressed segment. Unless another dressing step can be applied before reaching rank three, this kind of pinch cannot be absorbed without a further reduction and dressing step. Dressing one more segment allows one to absorb the original \(D_3\) pinch as well as new \(\bar{D}_{0}\), \(\bar{D}_{1}\), and \(\bar{D}_{2}\) pinches that arise from the new reduction step. However, the new reduction leads again to a configuration with a \(\widetilde{D}_{3}\) pinch on the last dressed segment,

Again, the dressed parts on the lhs and rhs of (92) have the same structure, which implies that such \(\bar{D}_{3}\)-pinched configurations are stable with respect to further reduction steps. Thus, open loops with multiple non-absorbable pinches do not occur, and the only type of configuration with a single non-absorbable pinch is the one in (92).
4.2.3 Pinching the \(\bar{D}_{0}\) propagator
Finally, we consider open loops with k dressed segments and a pinched \(\bar{D}_{0}\) denominator,

For convenience, here and in the following we put \(\bar{D}_{0}\) at the end of the chain of denominators. Similarly as for the cases discussed in Sect. 4.2.2, the above pinched configuration becomes absorbable only when the segments connected to the \(\bar{D}_{0}\) propagator, i.e. \(S_N(q)\) and \(S_1(q)\), are dressed. However, this happens only at the end of the standard dressing recursion.
In order to anticipate the absorption of the most advanced pinch one could replace the denominators \(\bar{D}_{0},\ldots , \bar{D}_{3}\) used for the on-the-fly reduction by \(\bar{D}_{1},\ldots , \bar{D}_{4}\), which lie all directly on the right side of the cut. However, the absorption of each \(\bar{D}_{4}\) pinch would require up to three extra dressing steps and two related reduction steps, resulting in the creation of multiple new pinches. This problem can be circumvented by observing that the \(\bar{D}_{0}\) propagator lies only one step away from the dressed part of the open loop, if one reverts the dressing direction. Therefore, as illustrated in Fig. 10, the pinched \(\bar{D}_{0}\) propagator can be entirely dressed by means of a single left-dressing step. This operation results in
where the left multiplication of the \(N^{\mathrm {th}}\) segment should be understood as
Technically, as indicated on the rhs, this operation can be easily implemented through a standard right-dressing step upon transposition of the input matrices and back-transposition of the result.Footnote 7
As usual, before merging with unpinched open loops, the propagators and undressed segments that lie on the right side of the pinch need to be brought back in standard form. In case of a \(\bar{D}_{0}\) pinch, all remaining \(N-1\) denominators and segments preserve their relative position along the open loop. Thus, only \(\bar{D}_{N-1}\) needs to be relabeled, since it assumes the role of the new \(\widetilde{D}_{0}\). Moreover, the standard form \(\widetilde{D}_{0}=q^2-\widetilde{m}^2_0\) requires a loop momentum shift \(q\rightarrow q-p_{N-1}\) for the entire open loop. The corresponding reparametrisations for the various denominators and segments read
In terms of masses and momenta this corresponds to \(\widetilde{m}_0=m_{N-1}\), \(\widetilde{m}_i=m_i\) and \(\widetilde{p}_i =p_{i}+p_{N-1}\) for \(1\le i\le N-2\). With these transformations the left-dressed \(\bar{D}_{0}\)-pinched open loop (94) can be merged with related unpinched objects according to

Apart from the loop momentum shift, \(q\rightarrow q-p_{N-1}\), this formula is entirely analogous to (88). Let us note that, since the shift is applied to a single term, the identity (97) holds only upon loop momentum integration. Nevertheless, as far as the correctness of final results at integral level is concerned, it can be safely applied at the integrand level.
As demonstrated in Sect. 6.2, using the on-the fly reduction with pinch absorption in combination with the on-the-fly techniques of Sect. 3 results in a very fast and numerically stable one-loop algorithm. In particular, as compared to the original version of OpenLoops, we find very significant improvements, both in terms of speed and numerical stability. Actually, using only the new techniques of Sect. 3 without on-the-fly reduction yields even higher CPU efficiency. However, as we will see, the moderate extra CPU cost that results from the on-the-fly reduction approach is counterbalanced by a very significant gain in numerical stability, which implies a reduced usage of quadruple precision for exceptional phase space points.
4.3 Cutting rule
As pointed out in Sect. 4.2.1, the possibility to merge pinched N-point open loops and corresponding unpinched \((N-1)\)-point open loops depends on the way they are cut. In order to identify the relevant requirements, let us consider the cut-open topology defined by the following ordered set of loop segments,
Here we have applied our standard labeling scheme, where the cut is located between \(\mathcal {S}_N\) and \(\mathcal {S}_1\), i.e. on the \(\bar{D}_{0}\) propagator, while the dressing recursion starts with \(\mathcal {S}_1\) and is directed towards \(\mathcal {S}_2\). This configuration will be referred to as a \(\mathcal {S}_N\)/\(\mathcal {S}_1\) ordered cut. Since the labeling scheme is a consequence of the position of the cut, and not vice versa, we have to define a cutting rule that selects \(\mathcal {S}_N\)/\(\mathcal {S}_1\) out of all possible \(\mathcal {S}_i\)/\(\mathcal {S}_j\) cuts.
The cutting rule should enable the merging of pinched subtopologies that arise from (98) by pinching certain propagators \(\bar{D}_{j}\), i.e. by combining \(\mathcal {S}_j\) and \(\mathcal {S}_{j+1}\) in a single segment \(\mathcal {S}_j\oplus \mathcal {S}_{j+1}\). To this end, unless the cut propagator \(\bar{D}_{0}\) is pinched, the cutting rule should guarantee that the position of the cut and its direction remain unchanged after a pinch. More explicitly, the desired cut configurations after a \(\bar{D}_{j}\) pinch with \(j>0\) are
In this way, as required for the merging operations described in Sects. 4.2.1–4.2.2, the dressing of pinched and unpinched objects always starts and ends with segments that contain the external legs attached to \(\mathcal {S}_1\) and \(\mathcal {S}_N\), respectively. In the case of a \(\bar{D}_{0}\) pinch, where the original cut propagator disappears, in order to enable the merging of left-dressed pinched subtopologies described in Sect. 4.2.3, the cut should be moved to the left of \(\mathcal {S}_N\oplus \mathcal {S}_1\), so that
In order to ensure, at least in part, that pinched topologies are cut as in (99)–(102), we replace the original cutting rule (49)–(50) by the new prescriptions
where the weights \(F(\mathcal {S}_a)\) are defined in (47). The key property of the above cutting rule is the pinch-invariance of the selection rule, which determines the first segment \(\mathcal {S}_1\). In fact, if this condition is realised for (98), then it is guaranteed to hold also for all pinched configurations (99)–(102). For \(j=0,1\) this is an obvious consequence of the fact that \(F(\mathcal {S}_1\oplus \mathcal {S}_a)>F(\mathcal {S}_1)\) for any \(a\ne 1\). In the other cases, the fact that \(\mathcal {S}_1\) remains the first subtree in spite of the appearance of a new pinched subtree \(\mathcal {S}_j\oplus \mathcal {S}_{j+1}\) with weight \(F(\mathcal {S}_j)+F(\mathcal {S}_{j+1})\), is guaranteed by
This inequality is an automatic consequence of (103) and of the binary nature of the weights (47). This is easily understood by observing that, due to \(2^{N_{\mathrm {p}}-1}= 1+\sum _{\alpha =1}^{N_{\mathrm {p}}-1}\;2^{\alpha -1}\), the last external particle (\(\alpha =N_{\mathrm {p}}\)) outweighs the ensemble of all other particles. Therefore the last external particle must belong to the leading-weight subtree \(\mathcal {S}_1\), which implies that \(F(\mathcal {S}_1)\ge 2^{N_{\mathrm {p}}-1}\) and leads to (105).
Unfortunately, the direction rule (104) is not sufficient in order to preserve the direction of the cut. For instance, in case of a \(\bar{D}_{1}\) pinch, the desired cut (99) requires \(F(\mathcal {S}_N)>F(\mathcal {S}_3)\), which does not automatically follow from \(F(\mathcal {S}_N)>F(\mathcal {S}_2)\). More generally, apart from the case of a \(D_3\) pinch, where the second and last subtree do not change, there is no guarantee that the condition (104) preserves the direction of the cut.
Thus the above cutting rule does not allow one to absorb all pinched open loops. Nevertheless, as demonstrated in Sect. , it is sufficient to obtain a very fast on-the-fly reduction algorithm. Moreover, it should be possible to further increase CPU efficiency, either by means of an improved cutting rule or by inverting the dressing direction after certain pinches.
4.4 Rational terms of type \(R_1\)
As discussed in Sect. 4.1, each reduction step of type (79) and (82) generates terms \(\bar{D}_{i}-D_i=\tilde{q}^2\) that account for the mismatch between the D-dimensional and four-dimensional parts of loop denominators. The resulting tensor integrals with \((D-4)\)-dimensional \(\tilde{q}^{2}\) terms in the numerator can give rise to finite terms. As is well known [2, 59], these so-called rational terms of type \(R_1\) can arise only in the presence of \(1/(D-4)\) poles of ultraviolet type. Thus, vanishing integrals of type \(R_1\) can be easily identified by means of the simple power counting criterion
In a renormalisable theory, where each loop segment increases the rank at most by one, \(r+2s\le N\) and all integrals with \(N\ge 5\) and \(s\ge 1\) vanish. Thus, the only non-vanishing integrals of type \(R_1\) that remain at the end of the on-the-fly reductions of Sect. 4.1 are [2]
The power counting criterion (106) can be exploited in a way that makes it possible to discard irrelevant terms of type \(R_1\) at any intermediate step of the open-loop recursion. To this end, for each number k of dressing steps we anticipate the maximum rank \(R^{\max }_k\) of the segments \(S_{k+1}(q),\ldots ,S_{N}(q)\) that remain to be dressed. Given this information, it is clear that monomials of type \(q^{\mu _1}q^{\mu _2}\ldots q^{\mu _r}\,\tilde{q}^{2s}\) in the dressed open loop cannot give rise to terms of D-dimensional rank higher than \(r+2s+R^{\max }_k\) at the end of the recursion. Thus, we can anticipate that,
The systematic application of this condition allows one to filter out a very large number of \(\tilde{q}^2\) terms, thereby improving the efficiency of the algorithm.
Note also that the unpinched contributions \(\mathcal {V}_k(\varOmega _N^k[-1])\) in the reduction identities (81) involve terms that reduce \(r+2s-2N\), and thus the degree of ultraviolet divergence, by one and two. Depending on the values of N and \(R^{\max }_k\), this can result in vanishing \(R_1\) contributions that can also be immediately discarded. For instance, in the reduction of \(\int \mathrm {d}^Dq\, \frac{q^{\mu _1}q^{\mu _2}\tilde{q}^{2}}{\bar{D}_{0} \bar{D}_{1} \bar{D}_{2} \bar{D}_{3}}\) all unpinched contributions apart from those of type (110) can be neglected.
5 Reduction identities and numerical stability
This section deals with the reduction method of [2], which provides the basis of the on-the-fly reduction approach of Sect. 4.1. In Sects. 5.1–5.3 we outline the derivation of the tensor coefficients \(A_j^{\mu \nu }\) and \(B^{\mu \nu }_{j,\lambda }\) in the reduction identities (77) and (82). In doing so we set the stage for Sect. 5.4, where we discuss numerical instability problems and present a systematic approach for their solution.
5.1 The reduction basis
The reduction identities of [2] are based on a decomposition of the four-dimensional loop momentum,
in a basis \(l_1,\ldots ,l_4\), formed by massless momenta in two orthogonal planes,
This reduction basis is defined in terms of the external momenta \(p_1,p_2\), which enter the propagators \(D_1\),\(D_2\). The basis momenta \(l_{1,2}\) are chosen in the plane spanned by \(p_1\) and \(p_2\),
while \(l_{3,4}\) lie in the plane orthogonal to \(p_1\),\(p_2\) and are defined as
where u and \(\bar{v}\) are massless spinors. This definition of \(l_{3,4}\) implies \(l_3^{*}=e^{\mathrm {i}\chi }l_4\), where \(\chi \) is twice the phase difference between the u and v spinors. The normalization of the basis is chosen such that
and the \(\alpha _{1,2}\) coefficients in (114) readFootnote 8
where \(\varDelta \) is related to the rank-two Gram determinant \(\varDelta _{12}=\det (p_i\cdot p_j)\) via
The Gram determinant is related to the normalisation factor \(\gamma \) via
and these two parameters play a critical role for the stability of the reduction. In fact, in the limit of vanishing Gram determinant, (116) and (119) imply that \((l_1\cdot l_2)\propto (l_3\cdot l_4)\propto \gamma \propto \varDelta \). Thus
which implies that all light-like basis momenta \(l_i\) become parallel to each otherFootnote 9 leading to severe numerical instabilities in the decomposition (112).
Note that in [2] the basis momenta \(l_i\) contain an additional normalisation factorFootnote 10
which diverges like \(1/\sqrt{\varDelta }\) when \(\varDelta \rightarrow 0\). As a consequence, in [2] numerical instabilities are in part visible as factors \(\beta \) in the reduction formulas and in part hidden in the definition of the basis vectors. Instead, the basis momenta defined in (114)–(115) are stable in the \(\varDelta \rightarrow 0\) limit. Thus, in the reduction formulas presented in Sects. 5.2 and 5.3, instabilities related to the Gram determinant (118) are fully manifest in the form of inverse powers of the parameter \(\gamma \propto \varDelta \). More precisely, for \(p_1^2=0\) and \(p_2^2\ne 0\), Gram-determinant instabilities arise also from \(\alpha _2=\pm p_2^2/(2\sqrt{\varDelta })\). However, the parametrisation adopted in Sect. 5.3 ensures that \(\alpha _2\) is always regular.
5.2 On-the-fly box reduction
In the following we discuss the reduction identity (77), which can be rewritten in a slightly more compact form as
with \(D_{-1}=1\). Since \(q^\mu q^\nu \) is reconstructed in terms of \(D_0,D_1,D_2,D_3\), we denote (122) as box reduction identity, although it is applicable to any integrand with \(N\ge 4\) loop propagators. The starting point for its derivation is given by the decomposition (112). Since the basis momenta \(l_{1,2}\) and \(l_{3,4}\) lie in mutually orthogonal planes, it is natural to split the loop momentum into corresponding components,
with \(q_{\parallel }^\mu =c_1 l_1^\mu +c_2 l_2^\mu \) and \(q_\perp ^\mu =c_3 l_3^\mu +c_4 l_4^\mu \). The respective \(c_i\) coefficients can be easily related to scalar products \((q\cdot l_i)\) using (113) and (116). This leads to,Footnote 11
The \(q_{\parallel }^\mu \) component can be directly reduced to rank zero by reconstructing the scalar products \((q\cdot l_{1,2})\) in terms of \(D_0,D_1,D_2\) using
This yields
with
In order to obtain an identity that reduces also \(q_\perp \) to a linear combination of \(D_0,\ldots , D_3\) one has to move to rank two by squaring (123) in a way that does not generate \(q_{\parallel }^\mu q_{\parallel }^\nu \) terms. To this end one can write
Applying (126) to the rhs of (128) reduces \(q_{\parallel }^\mu q^\nu \) and \(q_{\parallel }^\mu q_\perp ^\nu \) to rank one, such that only
with \(\hat{l}_{3,4}=l_{4,3}\), remains to be reduced. This is achieved by means of the relations [2]
where the quadratic terms \((q\cdot l_i)(q\cdot l_j)\) with \(i,j=3,4\) are reconstructed in terms of \(D_0\) and \(D_3\) using also the external momentum \(p_{3}\).
Combining (126)–(131) leads to the reduction identity (122) with
where we have introduced
The relations between the \(A^{\mu \nu }_{j}\) and \(B^{\mu \nu }_{j,\lambda }\) tensors in the first two lines of (132) follow from the requirement that terms of rank different from two vanish on the rhs of (122). Note also that the tensor \(L^{\mu \nu }_{34}\) can be rewritten in terms of \(l_{1}, l_{2}\) and \(g^{\mu \nu }\) as
5.3 On-the-fly triangle reduction
The identity (82), which reconstructs \(q^\mu q^\nu \) in terms of \(D_0,D_1,D_2\) at the integral level, will be denoted as triangle reduction. Its derivation is based on the observation that the only terms that involve \(D_3\) and \(p_3\) in Sect. 5.2, i.e. the squared scalar products \((q\cdot l_{3})^2\) and \((q\cdot l_{4})^2\) in (131), do not contribute in three-point integrals of rank \(R\le 3\). More precisely [2], for \(i=3,4\),
As a consequence, the derivations of Sect. 5.2 are also applicable to three-point functions at the integral level upon replacing (129) by
In this way one arrives at the reduction identities

where \(S(q)=S+S_\rho q^\rho \) is an arbitrary rank-one polynomial, and the tensors \(A_j^{\mu \nu }\) and \(B_{j,\lambda }^{\mu \nu }\) are obtained from (132) through the trivial replacements
5.4 Treatment of Gram-determinant instabilities
As pointed out in Sect. 5.1, when the rank-two Gram determinant \(\varDelta _{12}\) tends to zero the reduction basis (114)–(115) becomes degenerate. This leads to spurious singularities that manifest themselves as factors \(\gamma ^{-k}\propto \varDelta _{12}^{-k}\) in the reduction identities. In practice, the residues of \(\varDelta _{12}^{-k}\) poles are suppressed at \(\mathcal {O}(\varDelta _{12}^{k})\) as a result of subtle numerical cancellations between various contributions. Thus, for \(\varDelta _{12}\rightarrow 0\) the results of the reduction are finite but suffer from severe numerical instabilities. As can be seen from (132), spurious singularities reach the maximum power \(k=2\), i.e. each reduction step results in a numerical instability that scales quadratically in the inverse Gram determinant \(\varDelta _{12}\).
The reduction (132) involves also spurious singularities related to the rank-three Gram determinant, \(\varDelta _{123}\), which enter through the terms \((l_3\cdot p_3)^{-1}\propto |\varDelta _{123}|^{-1/2}\) [2]. However, as compared to the \(\varDelta _{123}\rightarrow 0\) case, \(\varDelta _{12}\rightarrow 0\) instabilities are statistically more likely and are also more enhanced due to their \(\varDelta _{12}^{-2}\) scaling behaviour. In fact, studying high statistics samples for various representative processes, we have found that the numerical instabilities of the on-the-fly reductions of Sects. 5.2–5.3 are very strongly correlated to the parameter \(\gamma \propto \varDelta _{12}\). Therefore, as we will see in the following, avoiding \(\varDelta _{12}\rightarrow 0\) spurious singularities in a systematic way makes it possible to reach excellent numerical stability.
5.4.1 Box reduction
In the case of the on-the-fly box reduction (122), poles in \(\varDelta _{12}\) arise only through the factors \(1/\gamma ^2\) and \(1/\gamma \) in (132), which are a direct consequence of the choice of the momenta \(p_1,p_2\) for the construction of the reduction basis (114)–(115). Since rank-two Gram-determinant instabilities depend on only two of the three available momenta, they can be easily avoided by constructing the basis with \(p_1, p_3\) or \(p_2, p_3\) instead of \(p_1, p_2\), depending on the values of the respective Gram determinants \(\varDelta _{13},\varDelta _{23},\varDelta _{12}\).
In practice, in order to avoid small rank-two Gram determinants we perform the box reduction upon a permutation,
which orders loop denominators with related momenta and masses in such a way that
The scales \(Q^2_{ij}\), which render the above ratios dimensionless, are defined as the largest element of the respective Gram matrices, i.e.
Note that the permutation (139) can be applied without changing the order of the corresponding segments \(S_i(q)\), i.e. without any modification of the open-loop dressing recursion. Moreover, the choice of the optimal permutation (139)–(140) can be done in a fully flexible way at runtime and locally in individual reduction steps, depending on the kinematics of the actual phase space point. In practice (139) is applied only to compute the reduction basis and the coefficients (132), which are then converted back to the original ordering.
Avoiding a spurious \(\varDelta _{12}\rightarrow 0\) singularity with (139)–(140) does not guarantee its disappearance in future reduction steps. In fact, all reduced contributions where \(D_1\) and \(D_2\) remain unpinched will still involve the same small Gram determinant. However, the permutation trick (139) can be iterated as long as \(N\ge 4\) loop denominators are available. In this way, rank-two Gram-determinant instabilities can be isolated in triangle contributions, which arise only at later steps of the open-loop recursion for loop diagrams with \(N> 3\).
5.4.2 Triangle reduction
For the case of triangle topologies one can show that, excluding regions where the external particles become soft or collinear, vanishing \(\varDelta _{12}\) Gram determinants can arise only from the t-channel topology depicted in Fig. 11, where the triangle exhibits two space-like external momenta, \(p_1\) and \(p_2\), and a time-like external momentum, \(p_2-p_1\). Since the Gram determinant vanishes when \(p_1^2\rightarrow p_2^2\), we adopt the parametrisation
where \(p_1\) and \(p_2\) can be ordered such that \(\delta >0\). The parameters \(\varDelta \) and \(\gamma \) are related to \(\delta \) via
i.e. the \(\varDelta \rightarrow 0\) limit corresponds to \(\delta \rightarrow 0\).
In kinematic regions with small \(\delta \), the numerical reduction of rank-r triangles via iterated on-the-fly reductions (132) and subsequent rank-one reductions (A.12)–(A.14) can lead to spurious singularities up to order \(1/\delta ^{4r-2}\). In order to avoid numerical instabilities, we first perform a full algebraic reduction of 3-point tensor integrals,
to scalar integrals. This leads to a cancellation of the leading spurious singularites, and the resulting analytic expressions for rank-r triangles involve only poles up to order \(1/\delta ^{r+1}\). For instance, for the case of triangles with massless internal lines, \(m_0=m_1=m_2=0\), reducing tensor integrals of rank \(r=1,2,3\) to scalar integrals we obtain
with the tensors
where \(i,j,k=1,2\), and the sums are restricted to inequivalent permutations, e.g. \(p_{11}^{\mu \nu }=p_{1}^\mu p_{1}^\nu \), \(p_{112}^{\mu \nu }= p_{1}^\mu p_{1}^\nu p_{2}^\rho + p_{1}^\mu p_{2}^\nu p_{1}^\rho + p_{2}^\mu p_{1}^\nu p_{1}^\rho \), etc.
Analytic expression of type (145)–(147) guarantee a reduced sensitivity to Gram-determinant instabilities. Thus they are used as default for the reduction of triangles configurations of type (142) with \(\delta >\delta _{\mathrm {thr}}\). The freely adjustable threshold parameter \(\delta _{\mathrm {thr}}\) is set to \(\delta _{\mathrm {thr}}=10^{-3}\). To avoid numerical instabilities in regions with \(\delta < \delta _{\mathrm {thr}}\) we perform systematic expansions in \(\delta \). In particular, for a complete cancellation of the \(1/\delta \) poles also the \(\delta \)-dependent \(C_0\) and \(B_0\) scalar integrals have to be expanded in \(\delta \). To this end we use LiteRed [67], and expanding the residues of \(\delta ^{-k}\) poles up to order \(\delta ^{k+m}\) we obtain regular Taylor series including terms up to order \(\delta ^m\).
For the case \(m_1=m_2=m_3=0\), expanding up to order \(\delta ^2\) yields
where
Similar results have been obtained for the case of massive internal propagators. More precisely, we have implemented all needed mass configurations for NLO QCD calculations, i.e. \((m_{0}, m_{1}, m_{2})=(0,0,0)\), (m, m, m), (0, m, m) and (m, 0, 0), with \(m>0\), including terms up to order \(\delta ^2\) in the expansions. The extra cases needed for NLO EW calculations, i.e. \((0,m_1,m_2)\), \((m_1,m_2,m_2)\) and \((m_1,m_2,m_3)\), with \(m_i>0\), will be implemented soon.
Evolution of the total number N of loop segments and the number n of dressed segments during the open-loop recursion. Horizontal and diagonal arrows describe, respectively, dressing steps and the generation of pinched subtopologies in the on-the-fly reduction. Corresponding unpinched contributions, where the rank is reduced but (N, n) remains unchanged are not shown. The algorithm starts at \((N_{\mathrm {max}},0)\) and first proceeds towards the highest possible n before moving one step lower in N
Since the analytic expressions (145)–(147) and their expansions (149)–(151) reduce triangles of rank r to rank zero in a single step, in order to be able to apply them in a fully flexible way, the on-the-fly reduction of triangles (82) has to be postponed at the end of the open-loop recursion, where triangle contributions have reached the maximum rank. This means that, in addition to the contributions listed in (84), we also generate \(N=3\) terms with \(R=3\). After taking the trace (76), depending on the actual value of \(\delta \), the reduction of triangles is done either using the expansion formulas or the on-the-fly reduction (82) followed by Passarino–Veltman reduction steps (A.12)–(A.14).
6 Implementation and performance
This section summarises the key structure of the new algorithm, outlines some aspects of its implementation, and presents technical performance studies.
6.1 Structure and implementation of the new algorithm
Similarly as for the original open-loop method, given a certain scattering process the algorithm starts with the generation of all tree and one-loop diagrams. This is done in symbolic form, including only topological information and particle content. One-loop diagrams are colour stripped and cut-open, and the interference of their colour structure with the Born amplitude is taken as initial condition for the open-loop recursion.
The recursion is organised by grouping open loops according to the total number N of segments and the number n of dressed segments. Dressing steps increase n and reduction steps reduce N or keep it constant. Thus, as illustrated in Fig. 12, the (N, n) groups are dressed through a series of iterations with \(N=N_{\mathrm {max}},N_{\mathrm {max}}-1,N_{\mathrm {max}}-2,\ldots \), where N is kept fixed while all segments \(n=0,1,2,\ldots ,N\) are processed. A step of the open-loop recursion, to be applied to all objects in an (N, n)-group, consists of the following operations:
-
1.
Merge all open loops with the same one-loop topology, the same cut and the same undressed segments into a single object. Note that one can merge open loops of different rank.
-
2.
For each open loop with \(n<N\) and rank R determine the rank \(R_{\mathrm {next}}\) that would be reached by performing the subsequent dressing step.
-
2(a)
If \(R_{\mathrm {next}}=3\) or if \(n=N\) and \(R=2\) avoid the dressing step and perform an on-the-fly reduction, which generates unpinched and pinched terms with \(R=1\). The unpinched terms remain in the (N, n) group. As for the pinched terms, if the adjacent segments of a pinched propagator are dressed they can be reduced to a single effective segment, thereby turning \((N,n)\rightarrow (N-1,n-1)\). Otherwise, contributions with an undressed pinch stay in the (N, n) group.
-
2(b)
If \(n<N\) and \(R_{\mathrm {next}}\le 2\) perform a dressing step, which turns \((N,n)\rightarrow (N,n+1)\). If this step dresses a pinched propagator that was previously undressed, the corresponding segments can be reduced to a single effective segment turning \((N,n+1)\rightarrow (N-1,n)\).
-
3.
Sort all open loops into the proper group and repeat steps 1–3 for all open loops in the (N, n)-group until the group is empty or \(n=N\) and all open loops in the group have rank \(R\le R_{\mathrm {last}}\) (see below).
Topologies with \(N=2\) are dressed without reduction, and, in order to enable Gram-determinant expansions (see Sect. 5.4.2), also \(N=3\) contributions are dressed without on-the-fly reduction. Thus \(R_{\mathrm {last}}=N\) for \(N=2,3\), while open loops with \(N\ge 4\) are reduced on-the-fly down to \(R_{\mathrm {last}}=1\). The algorithm starts at \((N,n)=(N_{\mathrm {max}},0)\) and terminates with the dressing of two-point contributions at \((N,n)=(2,2)\). At this point all open loops are closed with the trace operation (76), and the last reduction steps described in Appendix A are applied.
The above on-the-fly algorithm has been implemented in the framework of the original OpenLoops program [16], which consists of a computer-algebraic code generator written in Mathematica and a numerical part written in Fortran 90. Given an arbitrary Standard Model process, the Mathematica generator simulates the full chain of recursion steps in symbolic form and translates it into Fortran 90 code for the calculation of the actual scattering amplitude. The only external tools that need to be interfaced to the new OpenLoops program are Feynarts [68], for the generation of tree and one-loop diagrams, and Collier [19], for the calculation of scalar integrals. All other aspects of the open-loop method are directly implemented as process-independent Mathematica and Fortran routines. This includes the management of colour algebra, the kernels of the dressing recursion at tree and one-loop level, the on-the-fly and integral reductions, the helicity bookkeeping system, \(R_2\) rational terms, UV counterterms, and several other aspects.
The entire program is fully automated, the new on-the-fly methods are implemented and widely tested at NLO QCD and they will soon be extended to NLO EW. These methods will be made publicly available with the upcoming release of OpenLoops 2. Similarly as for OpenLoops 1, numerical routines generated with the new on-the-fly techniques will be accessible through an automated download and installation system and the standard OpenLoops interfaces to a variety of public Monte Carlo programs. In addition to the on-the-fly approach, OpenLoops 2 will support also the original open-loop method, which requires additional third-party tools such as Collier or Cuttools [10] and OneLOop [65] for the reduction to scalar integrals.
Runtimes per phase space point for the calculation of the one-loop scattering probability (1) on a single \(\text {Intel}\) i7-4790K core with gfortran-4.8.5. Results for the processes in (153) are plotted versus the number of one-loop diagrams. Timings of OpenLoops 2 with on-the-fly reduction (\(t^{\text {OL2}}_{\text {on-the-fly}}\)) are shown in the upper frame. The lower frame presents a comparison to OpenLoops 2+Collier and OpenLoops 1+Collier (see Table 1)
6.2 Technical performance
In this section we study the technical performance of the new algorithm. Similarly as in [9], we present speed and stability benchmarks for the one-loop QCD corrections to four families of partonic processes,
with \(n=0,1,2,3\) additional gluons, i.e. including processes with up to 7 scattering particles. Top quarks and W bosons are not decayed, and sums over the colour and helicity degrees of freedom of the external particles are included throughout.
Benchmarks obtained with the new open-loop algorithm, denoted as OpenLoops 2, are based on Collier for the calculation of scalar integrals. In order to highlight the effect of the new on-the-fly methods of Sects. 3–4, we also consider variants of the OpenLoops program where these new methods are not used. Specifically, as detailed in Table 1, we restrict the on-the-fly approach to helicity sums and diagram merging, using Collier for tensor reduction. This approach is denoted as OpenLoops 2+Collier. Alternatively, we apply the original open-loop method in combination with tensor integrals (denoted as OpenLoops 1+Collier) or OPP reduction (denoted as OpenLoops 1+Cuttools). The OpenLoops 1+Cuttools mode relies on OneLOop for the scalar integrals and is used also to generate benchmarks in quadruple precision.
By default, OpenLoops calculations are monitored through a built-in stability system that estimates the level of instability of one-loop results and automatically triggers re-evaluations in double or quadruple precision for critical phase space points. In the following, in order to avoid any bias in the comparisons, the stability system is switched off. In this way, one-loop amplitudes are computed only once per phase space point in double precision. Unless stated otherwise, Gram-determinant expansions are always kept active, both in the on-the-fly reduction of OpenLoops2 and in Collier.
Probability of finding events with instability \(\mathcal {A}>\mathcal {A}_{\mathrm {min}}\) as a function of \(\mathcal {A}_{\mathrm {min}}\) in a sample of \(10^6\) \(\mathrm {g g} \rightarrow \mathrm {t}\bar{\hbox {t}}\mathrm {gg}\) events. The stability of quad-precision benchmarks (blue) is compared to different variants of the OpenLoops 2 algorithm in double precision. Unstable results without special treatment of Gram determinants (“on-the-fly”) are stabilised using the permutation trick (139) for boxes (“perm”), exact analytic formulas for triangles (“analytic”) and Gram-determinant expansions for \(\delta <\delta _{\mathrm {thr}}\) (“exp”). See Sect. 5.4.2
6.2.1 Speed benchmarks
To illustrate the speed of the new algorithm, in Fig. 13 we plot runtimes per phase space point for the calculation of the one-loop scattering probability (1). The processes listed in (153) involve a number of one-loop Feynman diagrams that ranges from the order of 1 to \(10^5\). The corresponding runtimes, measured on a single \(\text {Intel}\) i7-4790K core with gfortran-4.8.5, vary from the order of \(10^{-1}\) to \(10^4\) ms. In this range, we confirm that runtimes tend to grow linearly with the number of one-loop diagrams up to \(2\rightarrow 4\) processes [9], and we find that this scaling behaviour persists up to \(2\rightarrow 5\) processes. As compared to OpenLoops 1+Collier, the new algorithm with on-the-fly reduction is up to a factor 2–3 faster for multi-particle processes. Depending on the process, using OpenLoops 2+Collier, i.e. restricting the on-the-fly approach to helicity sums plus diagram merging and reducing tensor integrals with Collier, can result in a further significant speed-up. However, the moderate slowdown caused by the on-the-fly reduction can be counterbalanced by the improved numerical stability, which implies a reduced need of re-evaluations in quadruple precision (see Sect. 6.2.2).
6.2.2 Stability benchmarks
In this section we study the numerical stability of the new open-loop algorithm. To this end, one-loop scattering probability densities computed in double precision (\(\mathcal {W}^{\scriptscriptstyle {\text {DP}}}_{\mathrm {1-loop}}\)) are compared against benchmarks in quadruple precision (\(\mathcal {W}^{\scriptscriptstyle {\text {QP}}}_{\mathrm {1-loop}}\)). More precisely, defining the relative difference between two results as
we estimate the instability of double-precision results asFootnote 12
This quantity can be regarded, up to a minus sign, as the number of correct digits of the double-precision evaluation.
To estimate the intrinsic accuracy of quad-precision benchmarks, computed using OpenLoops 1+Cuttools and OneLoop, we use a so-called rescaling test [9, 69], where scattering amplitudes are computed with rescaled masses and momenta and scaled back according to their mass dimensionality. Thus for a given phase space point the accuracy of the quadruple precision benchmarks is assessed as
where \(\mathcal {W}^{\scriptscriptstyle {\text {QP}}}_{\mathrm {1-loop}}\) and \(\mathcal {W}^{\scriptscriptstyle {\text {QP,R}}}_{\mathrm {1-loop}}\) are the original and rescaled quad-precision evaluations. This quantity represents the finite resolution of the instability estimate (155). As we will see, quad-precision benchmarks can become more unstable than double-precision results obtained with OpenLoops 2. In this case, the instability estimate (155) yields \(\mathcal {A}_{\scriptscriptstyle {\text {DP}}}\sim \mathcal {A}_{\scriptscriptstyle {\text {QP}}}\) but should be interpreted as \(\mathcal {A}_{\scriptscriptstyle {\text {DP}}} < \mathcal {A}_{\scriptscriptstyle {\text {QP}}}\).
Correlation between the instability \(\mathcal {A}\) of OpenLoops 2 in double precision and the largest \((Q^4/\varDelta )^2\) in the event, where \(\varDelta \) is any rank-two Gram determinant and \(Q^2\) is the maximum scale in the corresponding Gram matrix. See (141). Probability densities correspond to \(10^6\) events. Unstable results without special treatment of Gram determinants (left) are stabilised using the permutation trick (139) for box reduction and analytic expressions for triangle reduction (middle) plus Gram-determinant expansions for \(\delta <\delta _{\mathrm {thr}}\) (right)
To assess the stability of OpenLoops 2, for each process in (153) we have studied a sample of \(10^6\) homogeneously distributed phase space points at \(\sqrt{s}=1\) TeV. To exclude soft and collinear regions we have required \(p_{i,\mathrm {T}} > 50\) GeV and \(\varDelta R_{ij} > 0.5\) for all massless final-state QCD partons.
Figure 14 illustrates the effect of Gram-determinant instabilities and the goodness of the solutions introduced in Sect. 5.4 in the case of \(\mathrm {g g} \rightarrow \mathrm {t}\bar{\hbox {t}}\mathrm {gg}\). For this challenging multi-particle process, using the OpenLoops 2 on-the-fly reductions without any special treatment of Gram determinants we observe an extremely high level of numerical instability in double precision. The probabilities to obtain one-loop results with less than four or zero correct digits are around \(10^{-1}\) and \(10^{-2}\), respectively, and the tail of the stability distribution extends up to a level of instability of ten orders of magnitude and more. Applying the permutation trick (139) (“perm”) and using analytic expressions for three-point integrals (“analytic”) result in a dramatic stability improvement for the box and triangle reductions, respectively. Combining these two improvements (“analytic+perm”) reduces the probability of finding points with only few correct digits by three orders of magnitude, and yields a maximum level of instability around \(10^2\). Finally, switching on the Gram-determinant expansions for \(\delta <\delta _{\mathrm {thr}}\) leads to a further very drastic reduction of the probability of finding results with less than 3–4 correct digits. In this range, we observe an overlap with the tail of the quad-precision distribution. As discussed above, this indicates that OpenLoops 2 in double precision is more stable than the quad-precision benchmarks, and its estimated instability represents only an upper bound. Most likely, the tail of the true OpenLoops 2 stability distribution ends at \(10^{-3}\).
To gain more insights into the origin of numerical instabilities in the on-the-fly reduction of OpenLoops 2, let us investigate the correlation between the instability (155) and rank-two Gram determinants \(\varDelta \) in the \(\mathrm {g g} \rightarrow \mathrm {t}\bar{\hbox {t}}\mathrm {gg}\) sample of Fig. 14. More precisely, in Fig. 15 we consider the minimal value of the dimensionless parameter \(\varDelta _{ij}/Q_{ij}^4\) in the event, where \(Q_{ij}^2\) is the largest \(|p_i\cdot p_j|\) in the corresponding Gram matrix (see Sect. 5.4.1). As demonstrated by the left plot in Fig. 15, the instability of the entire scattering amplitude features a remarkably strong correlation with rank-two Gram determinants over twenty orders of magnitude. Moreover we observe a quadratic or faster scaling in \(Q^4/\varDelta \), consistent with the form of the \(\gamma ^{-2}\sim \varDelta ^{-2}\) poles in (132). The middle plot shows the combined effect of the permutation trick (139), which avoids the smallest Gram determinant of the event in all reductions with \(N\ge 4\) loop denominators, and the attenuation of spurious singularites through analytic expressions for three-point configurations of type (142). In this way the probability of having less than four correct digits is reduced to 0.1 permil. Finally, in the right plot we see that points with less than 3–4 correct digits disappear completely when Gram-determinant expansions are switched on.Footnote 13 As one can clearly recognise in the right plot, the threshold for the activation of Gram-determinant expansions corresponds to \((Q^4/\varDelta )^2\sim \delta _{\mathrm {thr}}^{-4}=10^{12}\).
Finally, in Figs. 16 and 17 we compare the stability of OpenLoops 2 against OpenLoops 1+Collier and OpenLoops 1+Cuttools for the \(2\rightarrow 3\) and \(2\rightarrow 4\) processes in (153). In OpenLoops 2 the stability improvements of Sect. 5.4 are applied throughout. The results of OpenLoops 1+Cuttools feature the highest instability tails for all considered processes. The probability of finding less than four correct digits can exceed \(10^{-3}\) in \(2\rightarrow 3\) and \(10^{-2}\) in \(2\rightarrow 4\) processes, while the fraction of fully unstable points with \(\mathcal {A}\ge 0\) can reach \(10^{-3}\) in \(2\rightarrow 4\) processes. Switching to OpenLoops 1+Collier we find that, depending on the process, the probability of finding only a few correct digits goes down by one to three orders of magnitude, while in eight samples of \(10^6\) points we do not find a single result with \(\mathcal {A}>0\).Footnote 14
Stability distributions for \(2 \rightarrow 3\) processes defined as in Fig. 14. The stability of OpenLoops 2 with on-the-fly reduction is compared to OpenLoops 1 with Collier or Cuttools. The instability of the employed quad precision benchmarks is also shown
Stability distributions for \(2 \rightarrow 4\) processes defined as in Fig. 16
Using OpenLoops 2 can lead to a further significant stability improvement. This is especially evident for \(2\rightarrow 3\) processes, where the stability of the on-the-fly reduction in OpenLoops 2 is remarkably close to the quad-precision benchmarks and even superior than quad precision for the case of \(\mathrm {t}\bar{\hbox {t}}\mathrm {g}\) production. When quad precision is sufficiently accurate to resolve the instabilities of OpenLoops 2 we observe improvements of one–two orders of magnitude with respect to OpenLoops 1+Collier. In the case of \(2\rightarrow 4\) processes, depending on the process and the considered number of digits, OpenLoops 2 can perform somewhat better or slightly worse than OpenLoops 1+Collier, like in the case of \(\mathrm {u} \bar{\hbox {d}} \rightarrow \mathrm {W}^{+}\mathrm {gg g}\) or \(\mathrm {u} \bar{\hbox {u}} \rightarrow \mathrm {W}^{+}\mathrm {W}^\mathrm {-g} \mathrm {g}\), respectively. However, both approaches guarantee excellent numerical stability.
7 Conclusions and outlook
We have presented a new approach for the automated calculation of scattering amplitudes at one loop. This new technique is based on the open-loop approach, where cut-open loop integrands are factored into a product of loop-momentum dependent segments that are combined through recursive tensorial multiplications.
The key idea behind the new method is that various operations, which are typically done at the level of full Feynman diagrams or amplitudes, can be performed on-the-fly during the open-loop recursion, i.e. after the multiplication of each loop segment. Since it exploits the factorised structure of open loops in a systematic way, this on-the-fly approach can reduce the complexity of certain operations in a very significant way.
We have first applied the on-the-fly method to helicity summations and to the merging of topologically equivalent open loops, finding speed-up factors of up to two or three as compared to the original open-loop algorithm. Moreover, using the integrand reduction method by del Aguila and Pittau, we have introduced an on-the-fly technique for the reduction of open loops. With this approach, the construction of loop amplitudes and their reduction are interleaved step by step within a single numerical recursion. In this way, objects with tensor rank higher than two are avoided throughout, and the complexity of the calculations is reduced in a very drastic way. The proliferation of pinched subtopologies that emerge from the reduction is avoided by absorbing them on-the-fly into topologically equivalent open loops.
The employed integrand reduction method suffers from severe numerical instabilities that are dominated by kinematic regions with small rank-two Gram determinants \(\varDelta \) and scale like \(1/\varDelta ^{2}\). In the reduction of N-point objects with \(N\ge 4\), we have shown that \(\varDelta \)-instabilities can easily be avoided through appropriate permutations of the loop denominators. In this way we were able to isolate \(\varDelta \)-instabilities in triangle topologies with a particular kinematic configuration and to cure them by means of analytic expansions in \(\varDelta \). This approach is the first example of an integrand reduction algorithm that is essentially free from Gram-determinant instabilities. The level of stability that is achieved in double precision is competitive with public implementations of OPP reduction in quadruple precision.
The new algorithm is fully automated and validated at NLO QCD and can be extended to electroweak interactions. It will become publicly available in the upcoming release of OpenLoops 2. Its technical features can be especially beneficial in NLO calculations for challenging multi-particle processes. Moreover, in view of its excellent numerical stability, the new algorithm is very attractive for the calculation of real–virtual contributions at NNLO. Finally, the idea of simplifying the construction of loop amplitudes through the factorisation of loop integrands and their on-the-fly reduction may open new interesting perspectives for the automation of two-loop calculations.
Notes
Quartic gluon couplings involve three independent colour structures. Thus each diagram involving k quartic couplings needs to be split into \(3^k\) contributions of type (4) that are effectively handled as separate diagrams.
To draw Feynman diagrams we use Axodraw [57].
The fact that \(N_{\mathrm {rem}}\le 1\) follows from the inequality \( N_{\mathrm {rem}} + R - N_{\mathrm {unpinched}}\le 0, \) where \(R=2\) is the rank of \(\mathcal {V}_{k}(\varOmega ^k_3,\bar{q})\), and \(N_{\mathrm {unpinched}}=3\) is the number of unpinched propagators in (82). The above inequality is obviously fulfilled at the beginning of the open-loop recursion, where \(k=R=N_{\mathrm {rem}}-N_{\mathrm {unpinched}}=0\), and its validity is guaranteed by the fact that, in renormalisable theories, dressing and reduction steps cannot increase \(N_{\mathrm {rem}} + R- N_{\mathrm {unpinched}}\).
This means that, before performing an on-the-fly reduction, rank-two open loops are first dressed with all possible adjacent segments of rank zero. Delaying the reduction step in this way reduces the additional CPU cost that results from the appearance of new pinched objects.
The on-the-fly reduction (79) can be performed using any set of four propagators, \(\bar{D}_{i_0},\ldots ,\bar{D}_{i_3}\).
Note that in a three-gluon vertex this transposition leads to a flip of the colour indices of the two gluons in the loop and hence a minus sign in the colour factor. Since the colour factor has been fixed in the beginning this minus sign has to be taken into account in the colour-stripped open loop.
The sign of the square root is chosen such that \(\pm \sqrt{\varDelta }=\mathrm {sign}(p_{1}\cdot p_{2})\sqrt{\varDelta }\). This guarantees that the limits \(\lim \limits _{p_i^2\rightarrow 0}\alpha _{i}=0\) are approached in a smooth way.
As a consequence of \(l_{1,2}^\mu \in \mathbb {R}\) and \((l_1 \cdot l_2)=E_{1} E_{2} (1-\cos (\theta _{12}))\rightarrow 0\), the first two basis vectors become parallel to each other, i.e. \(l^\mu _{1,2}\rightarrow \xi _{1,2}\, \eta ^\mu \) with \(\xi _{1,2}\in \mathbb {R}\) and \(\eta ^\mu \in \mathbb {R}\). As for the \(\mathbb {C}\)-valued basis vectors \(l_{3,4}\), using \(l_{3}^*=e^{\mathrm {i}\chi }{l_{4}}\) one can define their real and imaginary parts as \(l_{3(4),+}=[l_{3(4)}+e^{\mathrm {i}\chi }{l_{4(3)}}]/2\), \(l_{3(4),-}=[l_{3(4)}-e^{\mathrm {i}\chi }{l_{4(3)}}]/(2\mathrm {i})\), and show that (120) leads to \((\tilde{l}_i\cdot \tilde{l}_j)\rightarrow 0\) for all real-valued vectors \(\tilde{l}_i,\tilde{l}_j\in \{l_1,l_2,l_{3,\pm },l_{4,\pm }\}\). Thus, similarly as for \(l_{1,2}\) we have \(\tilde{l}_i\rightarrow \tilde{\xi }_i \eta ^\mu \; \forall \; i\), and we arrive at \(l^\mu _{3,4}\rightarrow z_{3,4} \eta ^\mu \) with \(z_3=z_4^*\in \mathbb {C}\), i.e. also the basis vectors \(l_{3,4}\) become parallel to \(l_{1,2}\).
More explicitly, the basis momenta of [2] correspond to \(\tilde{l}_i=\beta l_i\) and the various \(l_i\)-dependent quantities are related in a similar way, e.g. \(\tilde{\gamma }=\beta ^2\gamma \), while \(l_i\)-independent quantities such as \(\varDelta \) and \(\alpha _i\) are identical.
This decomposition of q corresponds to \(q_{\parallel }^\mu =D^\mu /\gamma \) and \(q_\perp ^\mu =-Q^\mu /(2\gamma )\) in [2].
Note that, in order to avoid possible sources of bias, the quad-precision benchmark \(\mathcal {W}^{\scriptscriptstyle {\text {QP,R}}}_{\mathrm {1-loop}}\) is computed with rescaled kinematics as detailed below.
Points with unreliable quad-precision benchmarks (\(\mathcal {A}_{\scriptscriptstyle {\text {QP}}}\sim \mathcal {A}_{\scriptscriptstyle {\text {DP}}}\)) are not considered in Fig. 15.
As discussed above, due to the insufficient quality of quad-precision benchmarks, instability estimates in the tail of \(\mathrm {g g} \rightarrow \mathrm {t}\bar{\hbox {t}}\mathrm {gg}\) are not significant.
References
R. Britto, F. Cachazo, B. Feng, Generalized unitarity and one-loop amplitudes in \(N=4\) super-Yang-Mills. Nucl. Phys. B 725, 275–305 (2005). arXiv:hep-th/0412103
F. del Aguila, R. Pittau, Recursive numerical calculus of one-loop tensor integrals. JHEP 07, 017 (2004). arXiv:hep-ph/0404120
Z. Bern, L.J. Dixon, D.A. Kosower, Bootstrapping multi-parton loop amplitudes in QCD. Phys. Rev. D 73, 065013 (2006). arXiv:hep-ph/0507005
A. Denner, S. Dittmaier, Reduction schemes for one-loop tensor integrals. Nucl. Phys. B 734, 62–115 (2006). arXiv:hep-ph/0509141
G. Ossola, C.G. Papadopoulos, R. Pittau, Reducing full one-loop amplitudes to scalar integrals at the integrand level. Nucl. Phys. B 763, 147–169 (2007). arXiv:hep-ph/0609007
D. Forde, Direct extraction of one-loop integral coefficients. Phys. Rev. D 75, 125019 (2007). arXiv:0704.1835
W.T. Giele, Z. Kunszt, K. Melnikov, Full one-loop amplitudes from tree amplitudes. JHEP 04, 049 (2008). arXiv:0801.2237
A. van Hameren, Multi-gluon one-loop amplitudes using tensor integrals. JHEP 07, 088 (2009). arXiv:0905.1005
F. Cascioli, P. Maierhöfer, S. Pozzorini, Scattering amplitudes with open loops. Phys. Rev. Lett. 108, 111601 (2012). arXiv:1111.5206
G. Ossola, C.G. Papadopoulos, R. Pittau, CutTools: a program implementing the OPP reduction method to compute one-loop amplitudes. JHEP 03, 042 (2008). arXiv:0711.3596
C.F. Berger, Z. Bern, L.J. Dixon, F. Febres Cordero, D. Forde, H. Ita et al., An automated implementation of on-shell methods for one-loop amplitudes. Phys. Rev. D 78, 036003 (2008). arXiv:0803.4180
A. van Hameren, C.G. Papadopoulos, R. Pittau, Automated one-loop calculations: a proof of concept. JHEP 09, 106 (2009). arXiv:0903.4665
V. Hirschi, R. Frederix, S. Frixione, M.V. Garzelli, F. Maltoni, R. Pittau, Automation of one-loop QCD corrections. JHEP 05, 044 (2011). arXiv:1103.0621
P. Mastrolia, G. Ossola, T. Reiter, F. Tramontano, Scattering amplitudes from unitarity-based reduction algorithm at the integrand-level. JHEP 08, 080 (2010). arXiv:1006.0710
S. Badger, B. Biedermann, P. Uwer, V. Yundin, Numerical evaluation of virtual corrections to multi-jet production in massless QCD. Comput. Phys. Commun. 184, 1981–1998 (2013). arXiv:1209.0100
F. Cascioli, J.M. Lindert, P. Maierhöfer, S. Pozzorini, The OpenLoops one-loop generator. http://openloops.hepforge.org
G. Cullen, GOSAM-2.0: a tool for automated one-loop calculations within the Standard Model and beyond. Eur. Phys. J. C 74, 3001 (2014). arXiv:1404.7096
T. Peraro, Ninja: automated integrand reduction via laurent expansion for one-loop amplitudes. Comput. Phys. Commun. 185, 2771–2797 (2014). arXiv:1403.1229
A. Denner, S. Dittmaier, L. Hofer, Collier: a fortran-based complex one-loop library in extended regularizations. Comput. Phys. Commun. 212, 220–238 (2017). arXiv:1604.06792
S. Actis, A. Denner, L. Hofer, J.-N. Lang, A. Scharf, S. Uccirati, RECOLA: recursive computation of one-loop amplitudes. Comput. Phys. Commun. 214, 140–173 (2017). arXiv:1605.01090
T. Gleisberg, S. Hoeche, F. Krauss, M. Schonherr, S. Schumann, F. Siegert, Event generation with SHERPA 1.1. JHEP 02, 007 (2009). arXiv:0811.4622
S. Alioli, P. Nason, C. Oleari, E. Re, A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX. JHEP 06, 043 (2010). arXiv:1002.2581
G. Bevilacqua, M. Czakon, M.V. Garzelli, A. van Hameren, A. Kardos, C.G. Papadopoulos et al., HELAC-NLO. Comput. Phys. Commun. 184, 986–997 (2013). arXiv:1110.1499
J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer et al., The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP 07, 079 (2014). arXiv:1405.0301
T. Sjöstrand, S. Ask, J.R. Christiansen, R. Corke, N. Desai, P. Ilten et al., An introduction to PYTHIA 8.2. Comput. Phys. Commun. 191, 159–177 (2015). arXiv:1410.3012
C. Weiss, B. Chokoufe Nejad, W. Kilian, J. Reuter, Automated NLO QCD Corrections with WHIZARD, PoS EPS-HEP2015 (2015) 466, arXiv:1510.02666
J. Bellm, Herwig 7.0/Herwig++ 3.0 release note. Eur. Phys. J. C 76, 196 (2016). arXiv:1512.01178
Z. Bern, L.J. Dixon, F. Febres Cordero, S. Höche, H. Ita, D.A. Kosower et al., Next-to-leading order \(W + 5\)-jet production at the LHC. Phys. Rev. D 88, 014025 (2013). arXiv:1304.1253
S. Badger, B. Biedermann, P. Uwer, V. Yundin, Next-to-leading order QCD corrections to five jet production at the LHC. Phys. Rev. D 89, 034019 (2014). arXiv:1309.6585
G. Bevilacqua, H.B. Hartanto, M. Kraus, M. Worek, Top quark pair production in association with a jet with next-to-leading-order QCD off-shell effects at the large hadron collider. Phys. Rev. Lett. 116, 052003 (2016). arXiv:1509.09242
S. Höche, P. Maierhöfer, N. Moretti, S. Pozzorini, F. Siegert, Next-to-leading order QCD predictions for top-quark pair production with up to three jets. Eur. Phys. J. C 77, 145 (2017). arXiv:1607.06934
A. Denner, J.-N. Lang, M. Pellen, S. Uccirati, Higgs production in association with off-shell top-antitop pairs at NLO EW and QCD at the LHC. JHEP 02, 053 (2017). arXiv:1612.07138
F. Cascioli, S. Höche, F. Krauss, P. Maierhöfer, S. Pozzorini et al., Precise Higgs-background predictions: merging NLO QCD and squared quark-loop corrections to four-lepton + 0,1 jet production. JHEP 1401, 046 (2014). arXiv:1309.0500
F. Cascioli, P. Maierhöfer, N. Moretti, S. Pozzorini, F. Siegert, NLO matching for \(t\bar{t} b \bar{b}\) production with massive \(b\)-quarks. Phys. Lett. B 734, 210–214 (2014). arXiv:1309.5912
F. Cascioli, S. Kallweit, P. Maierhöfer, S. Pozzorini, A unified NLO description of top-pair and associated Wt production. Eur. Phys. J. C 74, 2783 (2014). arXiv:1312.0546
S. Höche, F. Krauss, P. Maierhöfer, S. Pozzorini, M. Schönherr et al., Next-to-leading order QCD predictions for top-quark pair production with up to two jets merged with a parton shower. arXiv:1402.6293
S. Höche, F. Krauss, S. Pozzorini, M. Schönherr, J. Thompson et al., Triple vector boson production through Higgs-Strahlung with NLO multijet merging. Phys. Rev. D 89, 093015 (2014). arXiv:1403.7516
T. Ježo, J.M. Lindert, P. Nason, C. Oleari, S. Pozzorini, An NLO+PS generator for \(t\bar{t}\) and \(Wt\) production and decay including non-resonant and interference effects. Eur. Phys. J. C 76, 691 (2016). arXiv:1607.04538
B. Chokoufé Nejad, W. Kilian, J.M. Lindert, S. Pozzorini, J. Reuter, C. Weiss, NLO QCD predictions for off-shell \( t\overline{t} \) and \( t\overline{t}H \) production and decay at a linear collider. JHEP 12, 075 (2016). arXiv:1609.03390
S. Kallweit, J.M. Lindert, P. Maierhöfer, S. Pozzorini, M. Schönherr, NLO electroweak automation and precise predictions for W+multijet production at the LHC. JHEP 04, 012 (2015). arXiv:1412.5157
S. Kallweit, J.M. Lindert, P. Maierhofer, S. Pozzorini, M. Schönherr, NLO QCD+EW predictions for V + jets including off-shell vector-boson decays and multijet merging. JHEP 04, 021 (2016). arXiv:1511.08692
S. Kallweit, J.M. Lindert, S. Pozzorini, M. Schonherr, NLO QCD+EW predictions for \(2\ell 2\nu \) diboson signatures at the LHC. arXiv:1705.00598
J.M. Lindert et al., Precise predictions for V+jets dark matter backgrounds. arXiv:1705.04664
F. Granata, J.M. Lindert, C. Oleari, S. Pozzorini, NLO QCD+EW predictions for HV and HV +jet production including parton-shower effects. JHEP 09, 012 (2017). arXiv:1706.03522
M. Wiesemann, M. Grazzini, S. Kallweit, D. Rathlev, Fully-differential NNLO predictions for vector-boson pair production with MATRIX. PoS LL2016, 072 (2016)
M. Grazzini, S. Kallweit, D. Rathlev, A. Torre, \(Z\gamma \) production at hadron colliders in NNLO QCD. Phys. Lett. B 731, 204–207 (2014). arXiv:1309.7000
F. Cascioli, T. Gehrmann, M. Grazzini, S. Kallweit, P. Maierhöfer et al., ZZ production at hadron colliders in NNLO QCD. Phys. Lett. B 735, 311–313 (2014). arXiv:1405.2219
T. Gehrmann, M. Grazzini, S. Kallweit, P. Maierhöfer, A. von Manteuffel et al., \(W^+W^-\) production at hadron colliders in next to next to leading order QCD. Phys. Rev. Lett. 113, 212001 (2014). arXiv:1408.5243
M. Grazzini, S. Kallweit, D. Rathlev, \(W\gamma \) and \(Z\gamma \) production at the LHC in NNLO QCD. JHEP 07, 085 (2015). arXiv:1504.01330
M. Grazzini, S. Kallweit, D. Rathlev, M. Wiesemann, Transverse-momentum resummation for vector-boson pair production at NNLL+NNLO. JHEP 08, 154 (2015). arXiv:1507.02565
M. Grazzini, S. Kallweit, D. Rathlev, ZZ production at the LHC: fiducial cross sections and distributions in NNLO QCD. Phys. Lett. B 750, 407–410 (2015). arXiv:1507.06257
M. Grazzini, S. Kallweit, D. Rathlev, M. Wiesemann, \(W^{\pm }Z\) production at hadron colliders in NNLO QCD. arXiv:1604.08576
M. Grazzini, S. Kallweit, S. Pozzorini, D. Rathlev, M. Wiesemann, \(W^+W^-\) production at the LHC: fiducial cross sections and distributions in NNLO QCD. arXiv:1605.02716
D. de Florian, M. Grazzini, C. Hanga, S. Kallweit, J.M. Lindert, P. Maierhöfer et al., Differential Higgs boson pair production at next-to-next-to-leading order in QCD. JHEP 09, 151 (2016). arXiv:1606.09519
M. Grazzini, S. Kallweit, D. Rathlev, M. Wiesemann, \(W^\pm Z\) production at the LHC: fiducial cross sections and distributions in NNLO QCD. arXiv:1703.09065
A. Bredenstein, A. Denner, S. Dittmaier, S. Pozzorini, NLO QCD corrections to top anti-top bottom anti-bottom production at the LHC: 2. full hadronic results. JHEP 03, 021 (2010). arXiv:1001.4006
J.A.M. Vermaseren, Axodraw. Comput. Phys. Commun. 83, 45–58 (1994)
F.A. Berends, W.T. Giele, Recursive calculations for processes with n gluons. Nucl. Phys. B 306, 759–808 (1988)
G. Ossola, C.G. Papadopoulos, R. Pittau, On the rational terms of the one-loop amplitudes. JHEP 05, 004 (2008). arXiv:0802.1876
P. Draggiotis, M.V. Garzelli, C.G. Papadopoulos, R. Pittau, Feynman rules for the rational part of the QCD 1-loop amplitudes. JHEP 04, 072 (2009). arXiv:0903.0356
M.V. Garzelli, I. Malamos, R. Pittau, Feynman rules for the rational part of the electroweak 1-loop amplitudes. JHEP 01, 040 (2010). arXiv:0910.3130
R. Pittau, Primary Feynman rules to calculate the epsilon-dimensional integrand of any 1-loop amplitude. JHEP 02, 029 (2012). arXiv:1111.4965
A. Denner, S. Dittmaier, Reduction of one-loop tensor 5-point integrals. Nucl. Phys. B 658, 175–202 (2003)
A. Denner, S. Dittmaier, Scalar one-loop 4-point integrals. Nucl. Phys. B 844, 199–242 (2011)
A. van Hameren, OneLOop: for the evaluation of one-loop scalar functions. Comput. Phys. Commun. 182, 2427–2438 (2011). arXiv:1007.4716
A. Denner, S. Dittmaier, L. Hofer, COLLIER—a fortran-library for one-loop integrals. arXiv:1407.0087
R.N. Lee, LiteRed 1.4: a powerful tool for reduction of multiloop integrals. J. Phys. Conf. Ser. 523, 012059 (2014). arXiv:1310.1145
T. Hahn, Generating Feynman diagrams and amplitudes with FeynArts 3. Comput. Phys. Commun. 140, 418–431 (2001). hep-ph/0012260
S. Badger, B. Biedermann, P. Uwer, NGluon: a package to calculate one-loop multi-gluon amplitudes. Comput. Phys. Commun. 182, 1674–1692 (2011). arXiv:1011.2900
G. Passarino, M.J.G. Veltman, One loop corrections for e+ e- annihilation into mu+ mu- in the Weinberg model. Nucl. Phys. B 160, 151–207 (1979)
A. Denner, Techniques for calculation of electroweak radiative corrections at the one loop level and results for W physics at LEP-200. Fortsch. Phys. 41, 307–420 (1993). arXiv:0709.1075
Acknowledgements
We are grateful to P. Maierhöfer and J. Lindert for discussions and extensive technical support. This research was supported in part by the Swiss National Science Foundation (SNF) under contracts PP00P2-128552 and BSCGI0-157722 as well as by the Research Executive Agency (REA) of the European Union under the Grant agreement PITN–GA–2012–316704 (HiggsTools).
Author information
Authors and Affiliations
Corresponding author
Appendix A: Reduction of the remaining tensor integrals
Appendix A: Reduction of the remaining tensor integrals
After the on-the-fly reduction described in Sect. 4.1 we are left with a few types of low-rank integrals (84) that need to be reduced to the standard basis of one-loop scalar integrals. The relevant reductions are performed upon taking the trace (76) as described in the following. In this appendix we restrict ourselves to tensor integrals with four-dimensional \(q^\mu \) terms in the numerator, while contributions with additional \(\tilde{q}^{2}\) terms in the numerator are described in Sect. 4.4.
1.1 A.1: Five- and higher-point integrals with \(R=0,1\)
Integrals with \(N\ge 5\) loop propagators and a numerator of rank \(R\le 1\),
can be reduced to a linear combination of scalar boxes,
To determine the box coefficients we use the OPP reduction formula [5]
where \(q_0^{\pm }\) are the solutions of the quadruple-cut conditions \(\bar{D}_{i_0}=\bar{D}_{i_1}=\bar{D}_{i_2}=\bar{D}_{i_3}=0\), and
are the corresponding residues.
For the special case \(d_{0123}\), where \(p_{i_0}=p_0=0\), the explicit solutions of the quadruple cut equations read
where \(l_i\) are the basis momenta defined in (114)–(115). The \(x_{1,2}\) coefficients are given by
with \(d_i = m_i^2 - p_i^2\). The terms \(\alpha _{1,2}\) and \(\gamma \) are defined in Sect. 5, and the remaining coefficients in (A.5) are given by
with \(a = (p_3\cdot l_3)/(p_3\cdot l_4)\) and
The other coefficients \(d_{i_0i_1i_2i_3}\) can be obtained from the above formulas through an obvious reparametrisation of masses and momenta (\(i_0i_1i_2i_3\rightarrow 0123\)) and a subsequent momentum shift, \(p_i^\mu \rightarrow p_i^\mu -p_0^\mu \) for \(i=0,1,2,3\), which has to be applied throughout in (A.4)–(A.8).
1.2 A.2: Four-point functions with \(R=1\)
The reduction of rank-one boxes,

results into a scalar box (\(j=-1\)) and four scalar triangles (\(j=0,1,2,3\)). For the corresponding coefficients we use the reduction formulas [2],
and
The relevant ingredients, \(\gamma , \alpha , l^\mu _i, r^\mu _i, f_{i0}\), are defined in Sect. 5.
1.3 A.3: Three-point integrals with \(R=1\)
For rank-one triangles we use the covariant decomposition
where \(C_{{\varepsilon }}={(2\pi \mu )^{2{\varepsilon }}}/{(\mathrm {i}\pi ^2)}\), and we compute the \(C_i\) coefficients via Passarino–Veltman reduction [70, 71].
1.4 A.4: Two-point integrals with \(R=1,2\)
Also for two-point integrals with rank \(R=1,2\) we perform a Passarino–Veltman reduction [70, 71] based on the covariant decomposition
Besides the standard reduction formulas for \(B_1\), \(B_{11}\), and \(B_{00}\), for \(p^2=0\) we have implemented the special cases
with the scalar master integrals
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Buccioni, F., Pozzorini, S. & Zoller, M. On-the-fly reduction of open loops. Eur. Phys. J. C 78, 70 (2018). https://doi.org/10.1140/epjc/s10052-018-5562-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-5562-1