Impact of $\mathcal {CP}$-violating interference effects on MSSM Higgs searches

Abstract

Interference and mixing effects between neutral Higgs bosons in the MSSM with complex parameters are shown to have a significant impact on the interpretation of LHC searches for additional Higgs bosons. Complex MSSM parameters introduce mixing between the $\mathcal {CP}$-even and $\mathcal {CP}$-odd Higgs states h, H, A into the mass eigenstates $h_1, h_2, h_3$ and generate $\mathcal {CP}$-violating interference terms. Both effects are enhanced in the case of almost degenerate states. Employing as an example an extension of a frequently used benchmark scenario by a non-zero phase $\phi _{A_t}$, the interference contributions are obtained for the production of neutral Higgs bosons in gluon-fusion and in association with b-quarks followed by the decay into a pair of $\tau$-leptons. While the resonant mixing increases the individual cross sections for the two heavy Higgs bosons $h_2$ and $h_3$, strongly destructive interference effects between the contributions involving $h_2$ and $h_3$ leave a considerable parameter region unexcluded that would appear to be ruled out if the interference effects were neglected.

1 Introduction

Despite a rich program of searches for additional Higgs bosons at the LHC, no new scalars beyond the state at about $125\,\text {GeV}$ have been found so far. Additional Higgs bosons may be hiding from the searches at the LHC where possible reasons can be reduced couplings, large masses or cancellations such as destructive interference effects.

Extended Higgs sectors are predicted by various models beyond the Standard Model (SM) such as the Two-Higgs-Doublet Model (2HDM), the Minimal Supersymmetric Standard Model (MSSM) and singlet extensions such as the Next-to-Minimal Supersymmetric Standard Model (NMSSM). In this paper we focus on interpretations within the MSSM. The most obvious possibility in this model is to identify the discovered state with a mass of $M_h^{\mathrm{exp}}=125.09\pm 0.24\,\text {GeV}$ [1] with the lightest MSSM Higgs boson, which implies the existence of two heavier neutral Higgs bosons in the spectrum. The possibility that the discovered state could be the next-to-lightest Higgs boson [2, 3] is highly constrained within the MSSM, but not ruled out (see Ref. [4] for a recent update).

Although the properties of the discovered scalar are so far compatible with the ones predicted for the SM Higgs boson within the present experimental uncertainties, significant deviations from the SM are possible in individual Higgs couplings, cross sections and branching ratios. Concerning the $\mathcal {CP}$ properties of the discovered state, a pure $\mathcal {CP}$-odd nature could be ruled out [5, 6], while only very weak bounds exist so far on an admixture of $\mathcal {CP}$-even and $\mathcal {CP}$-odd components. If a non-zero $\mathcal {CP}$-odd admixture of the state at 125 GeV could be experimentally established, this would be a direct manifestation of the presence of $\mathcal {CP}$ violation in the Higgs sector. In general $\mathcal {CP}$ violation gives rise to a mixing between all neutral Higgs bosons in the Higgs sector. $\mathcal {CP}$-violating mixing in the production and decay of the state at 125 GeV has been investigated in Refs. [7, 8]. On the one hand, in the decoupling region of the MSSM the lightest neutral Higgs boson is SM-like and almost purely $\mathcal {CP}$-even. On the other hand, the two heavy neutral Higgs bosons in this case can very significantly differ from $\mathcal {CP}$ eigenstates and have a large mixing with each other. The search for additional heavy Higgs bosons should therefore take into account the possibility that those heavy Higgs bosons are not necessarily $\mathcal {CP}$ eigenstates.

In the Higgs sector of the MSSM, $\mathcal {CP}$-violation is induced by potentially large loop corrections involving complex parameters. As a consequence, in the general case of complex MSSM parameters the $\mathcal {CP}$-even states h and H mix with the $\mathcal {CP}$-odd state A into the mass eigenstates $h_1, h_2, h_3$ (ordered by increasing mass) which are no longer eigenstates of $\mathcal {CP}$. LHC searches for neutral MSSM Higgs bosons, following on from earlier searches at LEP [9] and the Tevatron [10,11,12,13], are carried out in the inclusive gluon fusion production channel, $gg\rightarrow h_a~(a=1,2,3)$, and in the production process in association with a pair of bottom quarks. For higher-order calculations of the cross sections of these two production processes within the MSSM see e.g. Refs. [14,15,16,17,18,19,20] (assuming $\mathcal {CP}$ conservation in the Higgs sector) and [21,22,23,24] (including $\mathcal {CP}$ violation). The latter process, which dominates in the MSSM for high $\tan \beta$ values owing to an enhanced bottom Yukawa coupling, is usually written as $b{\bar{b}}\rightarrow h_a$ (according to the five-flavour scheme where the bottom quark is regarded as a parton in the proton) or $gg\rightarrow b{\bar{b}} h_a$ (according to the four-flavour scheme without a bottom parton density distribution in the proton). Searches for neutral MSSM Higgs bosons decaying to down-type fermions have been carried out at the LHC in the $\tau ^{+}\tau ^{-}$ [25,26,27,28,29], in the $\mu ^{+}\mu ^{-}$ [30,31,32,33] and in the $b{\bar{b}}$ [34, 35] decay channels, where the $\tau ^{+}\tau ^{-}$ channel provides by far the highest sensitivity. The decay modes of the heavy MSSM Higgs bosons to down-type fermions are enhanced at large $\tan \beta$, whereas the branching ratios of the heavy Higgs bosons into vector bosons vanish in the decoupling limit [36].

The results of the searches are on the one hand reported as nearly model-independent limits on the product of the on-shell production cross section (separately for the inclusive production in gluon fusion and the production in association with bottom quarks) and the considered branching ratio of a single scalar resonance, assuming a narrow width. On the other hand, the search results are also interpreted in model-specific contexts using appropriate benchmark scenarios, for instance the $M_h^{\mathrm{mod+}}$ scenario of the MSSM [37].

In the MSSM the signal is potentially comprised of contributions of all three neutral Higgs bosons. The parameter region in which the masses of the two heavier neutral Higgs bosons of the MSSM are significantly heavier than the mass of the lightest neutral Higgs, where the latter needs to be close to 125 GeV for a phenomenologically viable scenario, corresponds to the decoupling region of the MSSM. The two heavier Higgs states are nearly mass-degenerate over this whole region, with mass splittings that are often below the experimental resolution. In the non-decoupling region even the masses of all three neutral Higgs bosons can be close to each other. In all model-specific interpretations at the LHC it has been assumed so far that the signal contributions from different Higgs bosons can be added incoherently, i.e. no interference contributions have been taken into account. Under the assumption that $\mathcal {CP}$ is conserved in the Higgs sector, which is realised in the MSSM with real parameters, the mass eigenstates are states of definite $\mathcal {CP}$, comprising the light and heavy $\mathcal {CP}$-even states h and H, as well as the $\mathcal {CP}$-odd state A. In this case interference effects between the heavy Higgs states H and A are absent, while the $\mathcal {CP}$-even states h and H can interfere with each other. If the assumption of $\mathcal {CP}$ conservation in the Higgs sector is dropped, interference effects occur also between the two heavy Higgs states, which can be enhanced by a small mass difference between the two states.

The phenomenological consequences of $\mathcal {CP}$-violating effects in the Higgs sector of the MSSM have been investigated for the Higgs searches at LEP [9, 38]. In the analyses using the CPX benchmark scenario [39] the presence of a non-zero phase of the trilinear couplings $A_{t,b}$ and the mixing between the $\mathcal {CP}$-even and $\mathcal {CP}$-odd states were found to have a significant impact on the limits, giving rise to unexcluded parameters regions at much smaller values of the lightest Higgs mass than for the $\mathcal {CP}$-conserving case [9, 38, 40, 41].

In the context of Higgs searches at the LHC, interference effects between the light and the heavy neutral Higgs boson for the case of $\mathcal {CP}$-conservation in an extended Higgs sector have been analysed in Ref. [42] for Higgs production in the MSSM via the decay of a heavy neutralino, in Ref. [43] for $gg\rightarrow h/H \rightarrow VV,\,V=W,Z$ within the 2HDM including background contributions, and in Ref. [44] for the singlet extension of the SM. The interference of two light NMSSM Higgs bosons decaying to two photons has been investigated in Ref. [45] for the $\mathcal {CP}$-violating case. For discussions of interference effects of heavy neutral Higgs bosons with each other and with the background at low $\tan \beta$ in the $t{\bar{t}}$ final state see Refs. [46,47,48] and for interference with the background without $H-A$ interference see Refs. [49, 50]

In the present paper we investigate the impact of mixing and interference effects on the search for heavy Higgs bosons at the LHC in the channels $\left\{ b{{\bar{b}}}, gg \right\} \rightarrow h_1, h_2, h_3 \rightarrow \tau ^+\tau ^-$, where the production modes denote the inclusive production in gluon fusion and the production in association with bottom quarks as discussed above. In order to incorporate the interference effects we make use of a generalised narrow-width approximation (NWA) [42, 51], where in contrast to the standard NWA interference contributions are taken into account. Our analysis is carried out in a benchmark scenario that is extended such that it contains a non-zero phase of the trilinear coupling $A_t$. The exclusion bounds are evaluated with the help of the program HiggsBounds [52,53,54,55]. We find that the mixing effects between the two heavy Higgs bosons are resonantly enhanced in the parameter regions where the two Higgs bosons are nearly mass-degenerate. The corresponding contributions of the intermediate Higgs states would yield a significant increase of the cross section for the case of complex parameters as compared to the case of real parameters if the interference contributions were neglected. However, the interference effect between the two heavy Higgs bosons gives rise to a very large destructive interference contribution, so that the net effect turns out to be a large suppression of the total cross section times branching ratio in the resonance region (see also Refs. [56,57,58]). As a consequence, a parameter region remains unexcluded by LHC searches from Run 1 that would appear to be excluded if interference effects were neglected.

The paper is structured as follows. After fixing the notation for the MSSM with complex parameters at tree level in Sect. 2, we summarise higher-order propagator-mixing in the Higgs sector and discuss the mixing-enhancement of Higgs production cross sections in Sect. 3. In Sect. 4, we quantify and investigate the interference contributions in the processes $\left\{ b{{\bar{b}}}, gg \right\} \rightarrow h_1, h_2, h_3 \rightarrow \tau ^+\tau ^-$. Subsequently in Sect. 5, we compare the predicted cross sections with mixing and interference contributions to experimental limits and evaluate their impact on the exclusion bounds in a benchmark scenario with a non-zero phase of the trilinear coupling $A_t$. Our conclusions are given in Sect. 6.

2 The MSSM with complex parameters at tree level

Before discussing higher-order mixing of Higgs bosons in Sect. 3, in this section we will specify the notation for the MSSM with complex parameters at tree level, following Ref. [59].

Sfermion sector Sfermions $\tilde{f}_L, \tilde{f}_R$ mix into the mass eigenstates $\tilde{f}_1, \tilde{f}_2$ within one generation according to the mass matrix

$$\begin{aligned} M_{\tilde{f}}^{2}&=\left( \begin{matrix} M_{\tilde{f}_L}^{2}+m_f^{2}+M_Z^{2}\cos 2 \beta (I_f^{3}-Q_fs_{W}^{2}) &{}\quad m_f X_f^{*}\\ m_f X_f &{}\quad M_{\tilde{f}_R}^{2}+m_{f}^{2}+M_Z^{2}\cos 2\beta Q_fs_{W}^{2} \end{matrix} \right) , \end{aligned}$$

(1)

where $X_f := A_f - \mu ^{*}\cdot \left\{ \cot \beta , \tan \beta \right\}$ for f being an up- or down-type quark, respectively. Besides the trilinear couplings $A_f=|A_f|e^{i\phi _{A_f}}$ also the higgsino mass parameter $\mu =|\mu |e^{i\phi _{\mu }}$ can be complex. Starting from one-loop order, these phases may influence the Higgs sector via sfermion loops.

Gluino sector The mass of a gluino $\tilde{g}^{a},~a=1,2,3,$ is given by $m_{\tilde{g}}=|M_3|$, where $M_3=|M_3|\,e^{i\phi _{M_3}}$ is the possibly complex gluino mass parameter. The gluino does not directly couple to Higgs bosons. Hence, the phase $\phi _{M_3}$ enters the predictions for the Higgs-boson masses and the wave function normalisation factors for external Higgs bosons only from the two-loop level onwards whereas it has an impact for example on the bottom Yukawa coupling already at one-loop order.

Neutralino and chargino sector The charginos $\widetilde{\chi }_i^{\pm },~i=1,2$, are admixtures of the charged winos $\widetilde{W}^{\pm }$ and higgsinos $\widetilde{H}^{\pm }$ via the mass matrix

$$\begin{aligned} X = \begin{pmatrix}M_2 &{}\quad \sqrt{2}M_Ws_{\beta }\\ \sqrt{2}M_W c_{\beta }&{}\quad \mu \end{pmatrix}. \end{aligned}$$

(2)

Likewise the neutralinos $\widetilde{\chi }_i^{0},\,i=1,\ldots ,4$, are composed of the neutral electroweak gauginos $\widetilde{B},\,\widetilde{W}^{3}$ and the neutral Higgsinos $\tilde{h}_d^0,\, \tilde{h}_u^0$:

$$\begin{aligned} Y = \left( \begin{matrix} M_1 &{}\quad 0 &{}\quad -M_Z c_{\beta }s_W &{}\quad M_Z s_{\beta }s_W\\ 0 &{}\quad M_2 &{}\quad M_Z c_{\beta }c_W &{}\quad -M_Z s_{\beta }c_W \\ -M_Z c_{\beta }s_W &{}\quad M_Z c_{\beta }c_W &{}\quad 0 &{}\quad -\mu \\ M_Z s_{\beta }s_W &{}\quad -M_Z s_{\beta }c_W &{}\quad -\mu &{}\quad 0\\ \end{matrix} \right) . \nonumber \\ \end{aligned}$$

(3)

Thus, at tree-level, mixing in the chargino sector is governed by the higgsino and wino mass parameters $\mu$ and $M_2$, respectively, and in the neutralino sector in addition by the bino mass parameter $M_1$. Although all of these three parameters can be complex in principle, only two of the phases are independent, and the choice $\phi _{M_2}=0$ is a common convention.

Higgs sector The two complex scalar Higgs doublets of the MSSM are denoted as

$$\begin{aligned} \mathcal {H}_1&= \begin{pmatrix}h_d^{0}\\ h_d^{-}\end{pmatrix} =\begin{pmatrix}v_d+\frac{1}{\sqrt{2}}(\phi _1^{0}-i\chi _1^{0})\\ -\phi _1^{-}\end{pmatrix}, \end{aligned}$$

(4)

$$\begin{aligned} \mathcal {H}_2&= \begin{pmatrix}h_u^{+}\\ h_u^{0}\end{pmatrix} = \begin{pmatrix}\phi _2^{+}\\ v_u+\frac{1}{\sqrt{2}}(\phi _2^{0}+i\chi _2^{0})\end{pmatrix}. \end{aligned}$$

(5)

As a possible relative phase between both doublets vanishes at the minimum of the Higgs potential and the phase of the coefficient of the bilinear term in the Higgs potential can be rotated away, the Higgs sector is $\mathcal {CP}$ conserving at lowest order. The tree level mass eigenstates as eigenstates of $\mathcal {CP}$ result from the diagonalisation of the mass matrices of the neutral and the charged components, respectively,

$$\begin{aligned}&\begin{pmatrix}h\\ H\\ A\\ G \end{pmatrix}= \begin{pmatrix}-\,s_{\alpha }&{}\quad c_{\alpha }&{}\quad 0 &{}\quad 0\\ c_{\alpha }&{}\quad s_{\alpha }&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad -\,s_{\beta _n}&{}\quad c_{\beta _n}\\ 0&{}\quad 0 &{}\quad c_{\beta _n}&{}\quad s_{\beta _n}\end{pmatrix}\begin{pmatrix}\phi _1^{0}\\ \phi _2^{0}\\ \chi _1^{0}\\ \chi _2^{0}\end{pmatrix},\nonumber \\&\begin{pmatrix}H^{\pm }\\ G^{\pm }\end{pmatrix}= \begin{pmatrix}-s_{\beta _c}&{}\quad c_{\beta _c}\\ c_{\beta _c}&{}\quad s_{\beta _c}\end{pmatrix}\begin{pmatrix}\phi _1^{\pm }\\ \phi _2^{\pm }\end{pmatrix}, \end{aligned}$$

(6)

with the short-hand notation $s_x\equiv \sin x,~c_x\equiv \cos x$. The mixing angle $\alpha$ is associated with the $\mathcal {CP}$-even Higgs bosons h, H; $\beta _n$ with the neutral $\mathcal {CP}$-odd Higgs A and Goldstone boson G, and $\beta _c$ with the charged Higgs $H^{\pm }$ and the charged Goldstone boson $G^{\pm }$. The masses of the $\mathcal {CP}$-odd and the charged Higgs bosons are at tree level related by $m_{H^{\pm }}^{2} = m_A^{2} + M_W^{2}$. At lowest order, the Higgs sector is fully determined by the two SUSY input parameters (in addition to SM masses and gauge couplings) $\tan \beta \equiv v_u/v_d$ and $m_{H^{\pm }}$ (or, for conserved $\mathcal {CP}$, equivalently $m_A$). We use in this paper a lower-case and upper-case notation in order to indicate tree-level and loop-corrected masses, respectively.

In the decoupling limit of $M_A\gg M_Z$ the MSSM Higgs sector appears SM-like, and the heavy Higgs bosons are difficult to detect in production and decay channels involving gauge bosons. On the other hand, the couplings to fermions can be either suppressed or enhanced, depending on the angles $\alpha$ and $\beta$. In the processes considered in this work, in particular the couplings of the neutral Higgs bosons $i=h,H,A$ to down-type fermions $f_d$ such as $\tau$-leptons and b-quarks are involved [60],

$$\begin{aligned} g_{i,f_d\bar{f}_d}^{\mathrm{tree}} = -\frac{igm_{f_d}}{2M_W} \,\cdot \left\{ -\frac{s_{\alpha }}{c_{\beta }},~\frac{c_{\alpha }}{c_{\beta }},~ i\gamma _5\tan \beta \right\} ,\quad i=h,H,A.\nonumber \\ \end{aligned}$$

(7)

As $c_{\alpha }\rightarrow s_{\beta }$ in the decoupling limit, the couplings of H and A to down-type fermions are enhanced by large values of $\tan \beta$.

3 Higher-order $\mathcal {CP}$-violating Higgs mixing

Higher-order corrections have a sizeable impact on the MSSM Higgs sector. In loop diagrams, particles from all other sectors contribute to Higgs observables such that in particular the trilinear couplings $A_f$, the stop and sbottom masses, the gluino mass, and in the sub-leading terms the higgsino mass parameter $\mu$, play – besides $M_{H^{\pm }}$ (or $M_A$) and $\tan \beta$ as at lowest order – an important role in the Higgs phenomenology. While $\mathcal {CP}$ is conserved in the Higgs sector at lowest order, those parameters from other sectors that are a priori complex can introduce $\mathcal {CP}$ violation in the Higgs sector at higher orders. In the $\mathcal {CP}$-conserving case, there is only a $2\times 2$ mixing among the two $\mathcal {CP}$-even neutral Higgs bosons, h and H. On the contrary, the non-zero phases of complex parameters cause a $\mathcal {CP}$-violating mixing of the scalars h, H and the pseudoscalar A into the mass eigenstates $h_1, h_2, h_3$ (in addition, there is also mixing with the neutral Goldstone and vector bosons that we will neglect in this work, see Ref. [59] for a discussion). This $3\times 3$ mixing structure is reflected in the mass matrix of the h, H, A system and in the on-shell wave-function normalisation factors, $\hat{\mathbf{Z }}$, as we will outline in Sect. 3.1 following Refs. [41, 59, 61]. In Sect. 3.2 we will discuss the consequences of highly admixed mass eigenstates on the production cross sections of each resonance.

For the calculation of radiative corrections, we adopt the hybrid on-shell and $\overline{\mathrm{DR}}$-renormalisation scheme defined in Ref. [59] such that the masses are renormalised on-shell whereas $\overline{\mathrm{DR}}$ conditions are employed for the fields and $\tan \beta$. We evaluate the Higgs masses, widths, branching ratios and self-energies with FeynHiggs-2.10.2 [62,63,64,65,66],¹ including the full momentum-dependent one-loop corrections and leading two-loop contributions.

3.1 Propagator corrections and the $\hat{\mathbf{Z }}$-matrix

Propagator matrix In the general case, all renormalised self-energies $\hat{\Sigma }_{ij}(p^{2})$ of the Higgs bosons $i,j=h,H,A$ are non-zero. Hence, the mass-square matrix $\mathbf M$ of the neutral Higgs bosons does not only consist of the tree-level masses-squares $m_i^2$ in the diagonal entries, but also of the momentum-dependent renormalised self-energies $\hat{\Sigma }_{ij}(p^{2})$ on the diagonal and off-diagonal positions. Therefore the matrix of mass-squares becomes

$$\begin{aligned} \mathbf M (p^{2}) = \begin{pmatrix}m_h^{2}-\hat{\Sigma }_{hh}(p^{2}) &{}\quad -\hat{\Sigma }_{hH}(p^{2}) &{}\quad -\hat{\Sigma }_{hA}(p^{2})\\ -\hat{\Sigma }_{Hh}(p^{2}) &{}\quad m_H^{2}-\hat{\Sigma }_{HH}(p^{2}) &{}\quad -\hat{\Sigma }_{HA}(p^{2})\\ -\hat{\Sigma }_{Ah}(p^{2}) &{}\quad -\hat{\Sigma }_{AH}(p^{2}) &{}\quad m_A^{2}-\hat{\Sigma }_{AA}(p^{2}) \end{pmatrix}.\nonumber \\ \end{aligned}$$

(8)

The self-energies $\hat{\Sigma }_{ij}p^{2}$ also contribute to the renormalised irreducible two-point vertex functions,

$$\begin{aligned} \hat{\Gamma }_{ij}(p^{2})= i\left[ (p^{2}-m_i^{2})\delta _{ij}+\hat{\Sigma }_{ij}(p^{2})\right] , \end{aligned}$$

(9)

whose elements form the $3\times 3$ matrix $\hat{{\varvec{\Gamma }}}_{hHA}(p^{2})$ that is related to the mass-square matrix $\mathbf M (p^{2})$ and to the propagator matrix $\varvec{\Delta }(p^{2})$ via

$$\begin{aligned} \varvec{\Delta }_{hHA}(p^{2}) = - \left[ \hat{{\varvec{\Gamma }}}_{hHA}(p^{2}) \right] ^{-1} = - \left[ i\left( p^{2}\mathbf 1 -\mathbf M (p^{2}) \right) \right] ^{-1}. \nonumber \\ \end{aligned}$$

(10)

The elements of $\varvec{\Delta }(p^{2})$ are the propagators $\Delta _{ij}(p^{2})$ starting as Higgs boson i and ending on j with all possible mixings in between. The off-diagonal propagators ($i\ne j$) have the form

$$\begin{aligned}&\Delta _{ij}(p^{2})\nonumber \\&\quad = \frac{\hat{\Gamma }_{ij}\hat{\Gamma }_{kk}- \hat{\Gamma }_{jk}\hat{\Gamma }_{ki}}{\hat{\Gamma }_{ii}\hat{\Gamma }_{jj}\hat{\Gamma }_{kk} +2\hat{\Gamma }_{ij}\hat{\Gamma }_{jk}\hat{\Gamma }_{ki}-\hat{\Gamma }_{ii}\hat{\Gamma }_{jk}^{2} -\hat{\Gamma }_{jj}\hat{\Gamma }_{ki}^{2}-\hat{\Gamma }_{kk}\hat{\Gamma }_{ij}^{2}} ,\nonumber \\ \end{aligned}$$

(11)

where the explicit $p^{2}$-dependence of all $\hat{\Gamma }(p^{2})$ has been suppressed in order to simplify the notation. The diagonal propagator can be expressed as

$$\begin{aligned}&\Delta _{ii}(p^{2})\nonumber \\&\quad = \frac{\hat{\Gamma }_{jj}\hat{\Gamma }_{kk}-\hat{\Gamma }_{jk}^{2}}{-\hat{\Gamma }_{ii}\hat{\Gamma }_{jj}\hat{\Gamma }_{kk} + \hat{\Gamma }_{ii}\hat{\Gamma }_{jk}^{2} - 2\hat{\Gamma }_{ij}\hat{\Gamma }_{jk}\hat{\Gamma }_{ki} + \hat{\Gamma }_{jj}\hat{\Gamma }_{ki}^{2} +\hat{\Gamma }_{kk}\hat{\Gamma }_{ij}^{2}} \end{aligned}$$

(12)

$$\begin{aligned}&\quad = \frac{i}{p^{2}-m_i^{2} + \hat{\Sigma }^{{\mathrm{eff}}}_{ii}(p^{2})}, \end{aligned}$$

(13)

where in the last step the effective self-energy $\hat{\Sigma }^{{\mathrm{eff}}}_{ii}$ is defined as

$$\begin{aligned}&\hat{\Sigma }^{{\mathrm{eff}}}_{ii}(p^{2}) = \hat{\Sigma }_{ii}(p^{2}) \nonumber \\&\quad -\, i \frac{2\hat{\Gamma }_{ij}(p^{2})\hat{\Gamma }_{jk}(p^{2})\hat{\Gamma }_{ki}(p^{2})- \hat{\Gamma }_{ki}^{2}(p^{2})\hat{\Gamma }_{jj}(p^{2})-\hat{\Gamma }_{ij}^{2}(p^{2})\hat{\Gamma }_{kk}(p^{2})}{\hat{\Gamma }_{jj}(p^{2})\hat{\Gamma }_{kk}(p^{2})-\hat{\Gamma }_{jk}^{2}(p^{2})} , \end{aligned}$$

(14)

starting with the diagonal self-energy $\hat{\Sigma }_{ii}$ at one-loop order and containing the mixing 2-point functions whose products in $\hat{\Sigma }^{{\mathrm{eff}}}_{ii}$ arise from two-loop order onwards. The complex poles $\mathcal {M}^{2}_{a}$, where $a = 1, 2, 3$ label the mass eigenstates, are determined as solutions of the equations

$$\begin{aligned} p^{2}-m_i^{2} + \hat{\Sigma }^{{\mathrm{eff}}}_{ii}(p^{2})= 0 , \end{aligned}$$

(15)

with $i = h, H, A$.

Z-factors For the correct normalisation of the S-matrix elements appropriate on-shell properties of all external particles are required. Pure on-shell renormalisation schemes guarantee these properties, whereas the $\overline{\mathrm{DR}}$ field renormalisation conditions make the finite on-shell wave-function normalisation factors necessary which ensure that external particles have unit residue and that all mixing contributions vanish on-shell. According to the LSZ formalism [68], they are obtained from the residue of the propagator of the external field, here a neutral Higgs boson $i=h,H,A$, evaluated at one of the complex poles $\mathcal {M}^{2}_a,~a=1,2,3$ [40, 41, 61, 69, 70],

$$\begin{aligned} \hat{Z}_i^{a}&=\frac{1}{1+\hat{\Sigma }^{{\mathrm{eff'}}}_{ii}(\mathcal {M}^{2}_a)} . \end{aligned}$$

(16)

The normalisation of each external particle i at the mass shell $p^{2}=\mathcal {M}^{2}_a$ is accounted for by a factor of $\sqrt{\hat{Z}_i^{a}}$. Furthermore, if mixing between i and j occurs on an external line at $\mathcal {M}^{2}_a$, the transition factor

$$\begin{aligned} \hat{Z}_{ij}^{a} = \frac{\Delta _{ij}(p^{2})}{\Delta _{ii}(p^{2})}\bigg |_{p^{2}=\mathcal {M}^{2}_a} \end{aligned}$$

(17)

restores the correct normalisation. The products of the overall normalisation factors $\sqrt{\hat{Z}_a}$ and transition ratios $\hat{Z}_{aj}$ (note the difference between $\hat{Z}_{aj}$ and $\hat{\mathbf{Z }}_{aj}$),

$$\begin{aligned} \hat{\mathbf{Z }}_{aj}&= \sqrt{\hat{Z}_a}\hat{Z}_{aj}, \end{aligned}$$

(18)

form the non-unitary matrix $\hat{\mathbf{Z }}$. The imaginary parts of the self-energies of unstable particles, evaluated at non-vanishing incoming momentum, cause $\hat{\mathbf{Z }}$ to be non-unitary. Accordingly, it does not provide a unitary transformation between the lowest order states h, H, A and the loop-corrected mass eigenstates $h_1, h_2, h_3$.

Fig. 1

Ratios of cross sections $\sigma (P\rightarrow h_a)_{3\times 3}/\sigma (P\rightarrow h_a)_{2\times 2}$ with $3\times 3$ mixing ($\mathbb {C}M_h^{\mathrm{mod+}}$ scenario with $\phi _{A_t}=\pi /4$) in the $\hat{\mathbf{Z }}$ factors vs. $2\times 2$ mixing ($\phi _{A_t}=0$) for the production modes $P=b{{\bar{b}}}$ (a, b) and $P=gg$ (c, d) with $h_a=h_2$ (a, c) and $h_3$ (b, d)

The $\hat{\mathbf{Z }}$-matrix allows one to express the one-particle irreducible (1PI) vertex functions $\hat{\Gamma }_{h_a}$ involving an external loop-corrected mass eigenstate $h_1,h_2,h_3$ as a linear combination of the 1PI vertex functions of the lowest-order states, $\hat{\Gamma }_i$:

$$\begin{aligned} \hat{\Gamma }_{h_a}&=\hat{\mathbf{Z }}_{ah}\hat{\Gamma }_h+\hat{\mathbf{Z }}_{aH}\hat{\Gamma }_H+\hat{\mathbf{Z }}_{aA}\hat{\Gamma }_A + \cdots \nonumber \\&\equiv \sqrt{\hat{Z}_a}\,\left( \hat{Z}_{ah}\hat{\Gamma }_h+\hat{Z}_{aH}\hat{\Gamma }_H+\hat{Z}_{aA}\hat{\Gamma }_A\right) + \cdots , \end{aligned}$$

(19)

where the ellipsis denotes additional contributions from the mixing of Higgs bosons with Goldstone and vector bosons, which are not contained in the $\hat{\mathbf{Z }}$-matrix and need to be calculated explicitly if needed. As in the full propagator matrix $\varvec{\Delta }_{hHA}(p^{2})$, if $\mathcal {CP}$ is conserved in the Higgs sector, the $\hat{\mathbf{Z }}$-matrix is reduced to the $2\times 2$ mixing among the $\mathcal {CP}$ even states h and H, with $\hat{\mathbf{Z }}_{3A}=1$, $\hat{\mathbf{Z }}_{a3}=\hat{\mathbf{Z }}_{3i}=0$ for $a=1,2$ and $i=h,H$. If, on the contrary, complex parameters are present, all elements of $\hat{\mathbf{Z }}$ can have non-vanishing values and represent the $3\times 3$ mixing.

Mixing propagators in terms of the mass eigenstates While the propagators $\Delta _{ij}(p^{2})$ contain the full momentum dependence of the lowest-order propagators and the self-energies, the mixing properties and the leading momentum dependence around the complex pole is adequately approximated by the sum of Breit–Wigner propagators of each mass eigenstate in combination with the on-shell wave-function normalisation factors, $\hat{\mathbf{Z }}$. The expansion of the full propagator $\Delta _{ij}(p^{2})$ around all of its complex poles $\mathcal {M}^{2}_a=M_{h_a}^{2}-iM_{h_a}\Gamma _{h_a}$ results in [61]

$$\begin{aligned} \Delta _{ij}(p^{2})&\simeq \sum _{a=1}^{3}\hat{\mathbf{Z }}_{ai}\,\Delta ^{{\text {BW}}}_a(p^{2})\,\hat{\mathbf{Z }}_{aj} , \end{aligned}$$

(20)

where the resonant contribution of a mass eigenstate $h_a,~a=1,2,3$, with the loop-corrected mass $M_{h_a}$ and the total width $\Gamma _{h_a}$ is described by a Breit–Wigner propagator with a constant width,

$$\begin{aligned} \Delta ^{{\text {BW}}}_a(p^{2}):=\frac{i}{p^{2}- \mathcal {M}^{2}_{a}} = \frac{i}{p^{2}- M_{h_a}^2 + i M_{h_a}\Gamma _{h_a}} . \end{aligned}$$

(21)

Hence, although the $\hat{\mathbf{Z }}$ matrix has been introduced for the correct normalisation of external Higgs bosons, it is also applicable to internal Higgs bosons to account for the higher-order mixing properties to a high accuracy. Equation (20) implies that the amplitude $\mathcal {A}$ of a process with Higgs exchange between the initial X and final state Y can be written as

$$\begin{aligned} \mathcal {A}&= \sum _{i,j=h,H,A} \hat{\Gamma }_i^{X} \,\Delta _{ij}(p^{2})\, \hat{\Gamma }_j^{Y} \simeq \sum _{a=1}^{3} \hat{\Gamma }_{h_a}^{X}\,\Delta ^{{\text {BW}}}_a(p^{2})\,\hat{\Gamma }_{h_a}^{Y} , \end{aligned}$$

(22)

with $\hat{\Gamma }_{h_a}^{X}=\sum _{i=h,H,A}\hat{\mathbf{Z }}_{ai}\hat{\Gamma }_i^{X}$ as in Eq. (19). The formulation on the RHS of Eq. (22) allows one to divide the full amplitude into the separate contributions of each resonance $h_a$:

$$\begin{aligned}&\mathcal {A}_{h_a} \equiv \hat{\Gamma }_{h_a}^{X}\, \Delta ^{{\text {BW}}}_a(p^{2})\, \hat{\Gamma }_{h_a}^{Y}\nonumber \\&\quad \quad = \sum _{i,j=h,H,A} \hat{\Gamma }_i^{X}\, \hat{\mathbf{Z }}_{ai}\, \Delta ^{{\text {BW}}}_a(p^{2})\, \hat{\mathbf{Z }}_{aj}\, \hat{\Gamma }_j^{Y} , \end{aligned}$$

(23)

which will be useful in Sect. 4 to compare the coherent and incoherent sums of amplitudes of several mass eigenstates.

3.2 Resonant mixing-enhancement of cross sections

Since the $\hat{\mathbf{Z }}$-matrix is non-unitary, cross sections including mixing contributions [with $\hat{\mathbf{Z }}$ from Eqs. (16–18)] can be enhanced compared to the case without mixing, which would correspond to a diagonal $\hat{\mathbf{Z }}$-matrix (with $\hat{\mathbf{Z }}=\mathbb {1}$ for the case where the external states are properly normalised). In particular, in the case of quasi-degenerate states a resonance enhancement is possible as a consequence of significant off-diagonal and imaginary parts of the self-energies and the $\hat{\mathbf{Z }}$-factors.

The $3 \times 3$ mixing occurring in the general case of complex parameters can change the phenomenology very significantly as compared to the $\mathcal {CP}$-conserving case of real parameters. This is in particular due to the $\mathcal {CP}$-violating mixing of H, A into $h_2, h_3$ since the heavy Higgs bosons $h_2, h_3$ are almost mass-degenerate in the wide range of parameter space characterised by the decoupling limit. This degeneracy and the properties of $h_2$ and $h_3$ lead to a significant H, A-mixing and an enhancement of the squared amplitudes.

For a large mass difference between the two heavy states H and A and the light state h, the mixing of h with H and A can be neglected in good approximation. In this limit, the squared amplitudes of the production processes of $h_2$ and $h_3$, $\left| \mathcal {P}_{h_a}\right| ^2$ for $a=2,3$, scale with $|\hat{\mathbf{Z }}_{aH}|^2 \,|\hat{\Gamma }_H|^2 +|\hat{\mathbf{Z }}_{aA}|^2 \,|\hat{\Gamma }_A|^2$, which can become significantly larger than $|\hat{\Gamma }_i|^2$, $i=H,A$. In the case of $|\hat{\Gamma }_H| \simeq |\hat{\Gamma }_A|$, this scaling factor further simplifies to $|\hat{\mathbf{Z }}_{aH}|^2+|\hat{\mathbf{Z }}_{aA}|^2$, which can exceed 1. Hence, the cross sections of $\sigma (pp\rightarrow h_2)$ and $\sigma (pp\rightarrow h_3)$ receive an enhancement from the mixing contributions. We are particularly interested here in the production modes in association with a pair of bottom quarks ($b{{\bar{b}}}$) and via gluon fusion (gg).

Fig. 2

Difference between the complex and the real scenario: $\Delta X \equiv X(\phi _{A_t}=\pi /4)-X(\phi _{A_t}=0)$ for a the mass $X=M_{h_2}$ and b total width $X=\Gamma _{h_2}$ (similar results for $h_3$) evaluated with FeynHiggs

As an example case featuring such an enhancement effect, we illustrate the $\mathcal {CP}$-violating mixing in a modified version of the $M_h^{\mathrm{mod+}}$ scenario, originally defined in Ref. [71], where we introduce as in Refs. [57, 58, 61] the complex phase $\phi _{A_t}=\frac{\pi }{4}$, set $\phi _{A_b}=\phi _{A_{\tau } }=\phi _{A_t}$, and increase the value of the higgsino mass parameter to $\mu =1000\,\text {GeV}$ (as also proposed in Ref. [71]), which amplifies the $\mathcal {CP}$-violating terms. The input parameters being varied are ${M_{H^{\pm }}}$ and $\tan \beta$. We refer to this scenario as $\mathbb {C}M_h^{\mathrm{mod+}}$.

Figure 1 shows the single-particle production cross sections $\sigma (P\rightarrow h_a)$ for $h_2$ and $h_3$ in association with a pair of bottom quarks and via gluon fusion. The cross sections for the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario with $\phi _{A_t}=\pi /4$, denoted by $3\times 3$, have been normalised in Fig. 1 to the ones for the corresponding $\mathcal {CP}$-conserving scenario with $\phi _{A_t}=0$, denoted by $2\times 2$. The predictions for the cross sections have been obtained with FeynHiggs. The displayed results for the ratios $R_{\sigma }(P,h_a):= \sigma (P\rightarrow h_a)_{3\times 3}/\sigma (P\rightarrow h_a)_{2\times 2}$ show enhancements by factors of more than 5 in certain areas of parameter space where $h_2$ and $h_3$ are highly admixed states, especially around ${M_{H^{\pm }}}\simeq 480\,\text {GeV}$ and $\tan \beta \simeq 29$. Accordingly, the enhancement can indeed be related to a resonance-type mixing between the $\mathcal {CP}$ eigenstates H and A. The observed patterns are similar for $h_2$ (Fig. 1a, c) and $h_3$ (Fig. 1b, d) and, to a lesser extent, also for production via $b{{\bar{b}}}$ (Fig. 1a, b) and gg (Fig. 1c, d). The observed similarities are related to the involved pattern of $\hat{\mathbf{Z }}$-factors, as discussed above. The differences between the production via $b{{\bar{b}}}$ and gg arise from the structure of the amplitudes. While the production in association with a pair of bottom quarks is dominated by the respective Higgs coupling to bottom quarks (where the phase $\phi _{A_t}$ enters via the correction to the relation between the bottom-quark mass and the bottom Yukawa coupling, $\Delta _b$, see e.g. Ref. [24]), the loop-induced production via gluon fusion at leading order comprises contributions from the bottom- and top-quark loops as well as from their scalar superpartners (the latter induce an explicit dependence on $\phi _{A_t}$).² Those contributions from up-type (s)fermions to gluon fusion have a sizeable impact at lower values of $\tan \beta$. The edge along $\tan \beta \simeq 30$ for ${M_{H^{\pm }}}\gtrsim 600\,\text {GeV}$ in the plots for gg-induced production is caused by the swap of the composition of $h_2$ and $h_3$ being mostly H- or A-like, respectively.

In addition to the cross sections, also the masses are affected by the phase. Figure 2 shows the shift of the mass as $\Delta M_{h_2} \equiv M_{h_2}(\phi _{A_t}=\pi /4)-M_{h_2}(\phi _{A_t}=0)$ as well as the shift of the width $\Delta \Gamma _{h_2} \equiv \Gamma _{h_2}(\phi _{A_t}=\pi /4)-\Gamma _{h_2}(\phi _{A_t}=0)$ in the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario in the (${M_{H^{\pm }}}$, $\tan \beta$) plane, evaluated with FeynHiggs. Comparable results are obtained for the mass and width of $h_3$. The small shifts of less than $\pm \, 2(1)\,\text {GeV}$ of the mass of $h_2$ ($h_3$) for ${M_{H^{\pm }}}\gtrsim 200\,\text {GeV}$ and $\tan \beta \gtrsim 3$ show on the one hand the impact of a non-zero phase on the properties of the heavy Higgs bosons, on the other hand the shifts are too small (below the experimental resolution of roughly 20–40% of the reconstructed mass [28, 72]) to cause relevant phase space effects. The total widths $\Gamma _{h_2}, \Gamma _{h_3}$ are increased by several GeV in the parameter region of strongest mixing due to the $\hat{\mathbf{Z }}$-factors, such as observed for the production cross sections in Fig. 1.

Fig. 3

Higgs boson production at LO via $b{{\bar{b}}}$ (left) and gg (right) with decay into $\tau ^+\tau ^-$. The couplings of the mass eigenstates $h_a=h_1, h_2, h_3$ (blue, dashed) to the initial and final state contain a combination of $\hat{\mathbf{Z }}$-factors (denoted by blue circles)

While so far we have restricted our discussion to the individual cross sections of $h_2$ and $h_3$ and their masses, in the next section we will analyse the $\mathcal {CP}$-violating interference contributions to the full process involving production and decay.

4 Interference contributions to the processes$\left\{ b{{\bar{b}}}, gg \right\} \rightarrow h_1, h_2, h_3 \rightarrow \tau ^+\tau ^-$

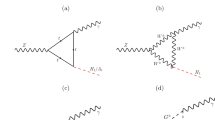
For the investigation of a full process of Higgs production and decay where the Higgs bosons appear as internal propagators, we calculate the interference of amplitudes with s-channel $h_1, h_2, h_3$ exchange. We consider the production processes via gg and the subsequent decay into a pair of $\tau$-leptons, as illustrated in Fig. 3,

$$\begin{aligned} b{\bar{b}} ~\rightarrow & {} h_a~\rightarrow ~\tau ^{+}\tau ^{-}, \end{aligned}$$

(24)

$$\begin{aligned} gg ~\rightarrow & {} h_a~\rightarrow ~\tau ^{+}\tau ^{-}. \end{aligned}$$

(25)

In order to be able to make use of precise predictions for the separate production [24] and decay [63] processes we focus here on the relative interference contribution. For the phenomenological prediction of the complete processes including interference, higher-order corrections and quark- and gluon-luminosities at the LHC, we will combine those relative interference contributions with the computations of hadronic cross sections and branching ratios from the existing literature including available higher-order corrections. Regarding the determination of the relative interference contributions, we restrict ourselves to the computation of the relevant $2\rightarrow 2$ partonic processes at leading order (LO). This means that process (24), which involves $b\bar{b}h_a$-associated production, is treated at tree-level, while the leading contributions to gluon fusion entering process (25) consist of one-loop diagrams with quarks q and squarks ${\tilde{q}}$, in particular those of the third generation. Besides, we take propagator-type corrections into account by using Higgs masses, total widths and $\hat{\mathbf{Z }}$-factors from FeynHiggs including the full one-loop and dominant two-loop corrections. The procedure to evaluate the relative interference contributions on the basis of leading-order diagrams is motivated by the fact that the vertex corrections to the production and decay factorise (apart from non-factorisable initial-to-final state radiation). It furthermore avoids double-counting of higher-order contributions that are incorporated in the separate production and decay processes. We calculate the LO contributions to the amplitude and the cross section of the full process of production and decay using FeynArts [73,74,75,76,77] with a model file containing $\hat{\mathbf{Z }}$-factors for the Higgs vertices (in this way the Higgs propagators are expressed in terms of $\hat{\mathbf{Z }}$-factors and lowest-order Breit–Wigner propagators as given in (20)), FormCalc [78,79,80,81,82] and, as mentioned above, FeynHiggs for quantities from the Higgs sector.

Fig. 4

Relative interference contribution $\eta [\%]$ of the Higgs bosons $h_1,h_2,h_3$ decaying to $\tau ^{+}\tau ^{-}$ in the complex $M_h^{\mathrm{mod+}}$ scenario with $\mu =1000\,\text {GeV}$ and $\phi _{A_t}=\frac{\pi }{4}$. a $b\bar{b}$ initial state, b gg initial state (note the different scale of the colour code)

Quantifying the interference In order to determine the interference term in each of the two processes (24, 25), we distinguish between the coherent sum of the $2\rightarrow 2$ amplitudes with $h_1,h_2,h_3$-exchange including the interference and their incoherent sum without the interference,

$$\begin{aligned} |\mathcal {A}|^{2}_{\text {coh}} = \bigg |\sum _{a=1}^{3} \mathcal {A}_{h_a} \bigg |^{2} , ~~~~~~~~~~~ |\mathcal {A}|^{2}_{\text {incoh}} = \sum _{a=1}^{3} \bigg |\mathcal {A}_{h_a} \bigg |^{2} . \end{aligned}$$

(26)

The interference term is then obtained from the difference,

$$\begin{aligned} |\mathcal {A}|^{2}_{\text {int}} = |\mathcal {A}|^{2}_{\text {coh}} -|\mathcal {A}|^{2}_{\text {incoh}} = \sum _{a<b}2\,\text {Re}\left[ \mathcal {A}_{h_a} \mathcal {A}_{h_b}^{*}\right] . \end{aligned}$$

(27)

Accordingly, the coherent cross section refers to the cross section based on the coherent sum of amplitudes, $\sigma _{\text {coh}}\equiv \sigma \left( |\mathcal {A}|^{2}_{\text {coh}}\right)$, and likewise for the incoherent cross section $\sigma _{\text {incoh}}$ (omitting the interference term) and the interference part of the cross section $\sigma _{\text {int}}$. Furthermore, we define the relative interference term for each production mode $P=b{{\bar{b}}}, gg$ as

$$\begin{aligned} \eta ^P :=\frac{\sigma ^P_{\mathrm{int}}}{\sigma ^P_{\mathrm{incoh}}}. \end{aligned}$$

(28)

Beyond this overall interference term, it is also useful to differentiate between the three “squared” terms of each Higgs boson $h_a$ in $\sigma _{h_a}$ and the three interference terms $\sigma _{\mathrm{int}_{ab}}$ involving two Higgs bosons $h_a, h_b$ out of the three, respectively, again separately for both production modes P,

$$\begin{aligned} \sigma ^{P}&=\sigma ^{P}_{h_1}+\sigma ^{P}_{h_2}+\sigma ^{P}_{h_3} +\sigma ^{P}_{\mathrm{int}_{12}} +\sigma ^{P}_{\mathrm{int}_{13}} +\sigma ^{P}_{\mathrm{int}_{23}}. \end{aligned}$$

(29)

In order to express the cross section into separate Higgs contributions (as in the incoherent case), we introduce relative interference factors $\eta _a^P$ that rescale the individual Higgs rates:

$$\begin{aligned} \sigma ^{P}&=\sigma ^{P}_{h_1}\,(1+\eta _1^P) + \sigma ^{P}_{h_2}\,(1+\eta _2^P) + \sigma ^{P}_{h_3}\,(1+\eta _3^P), \end{aligned}$$

(30)

where we define $\eta _a^P$ by weighting $\sigma _{\mathrm{int}_{ab} }^{P}$ according to the $\sigma _{h_a},~\sigma _{h_b}$ contributions with the weight (for $a,b,c=1,2,3$)

$$\begin{aligned} w_{ab}^{P,a} = \frac{\sigma _{h_a }^{P}}{\sigma ^{P}_{h_a}+\sigma ^{P}_{h_b}} \equiv 1 - w_{ab}^{P,b}, \end{aligned}$$

(31)

resulting in

$$\begin{aligned} \eta ^{P}_a&= \frac{w_{ab}^{P,a}\,\sigma ^{P}_{\mathrm{int}_{ab}} + w_{ac}^{P,a}\,\sigma ^{P}_{\mathrm{int}_{ac}}}{\sigma _{h_a}^{P}} = \frac{\sigma ^{P}_{\mathrm{int}_{ab}}}{\sigma _{h_a}^{P}+\sigma _{h_b}^{P}} +\frac{\sigma ^{P}_{\mathrm{int}_{ac}}}{\sigma _{h_a}^{P}+\sigma _{h_c}^{P}}. \end{aligned}$$

(32)

This definition of $\eta _a^P$ is stable also in the case that one of the individual contributions $\sigma _{h_a}^P$ is suppressed.

The relative interference contributions $\eta _a^P$ can then be applied to obtain a result consisting of the separate predictions for the production and decay processes and the respective interference contributions

$$\begin{aligned}&\sigma (pp\rightarrow P\rightarrow h_{1,2,3}\rightarrow \tau ^+\tau ^-)\nonumber \\&\quad \simeq \sum _{a=1}^3 \sigma (pp\rightarrow P\rightarrow h_a)\cdot (1+\eta _a^P)\cdot \text {BR}(h_a\rightarrow \tau ^+\tau ^-). \nonumber \\ \end{aligned}$$

(33)

In order to confront the theoretical predictions in the considered scenario with the existing experimental bounds we use the program HiggsBounds-4.2.0 [52,53,54,55]. For the incorporation of the interference contributions it is convenient to rescale the ratio of the production cross sections $P\rightarrow h_a$ in the MSSM with respect to the SM, which is supplied as an input to HiggsBounds, in the following way,

$$\begin{aligned} \frac{\sigma ^{\mathrm{MSSM}}(P\rightarrow h_a)}{\sigma ^{\mathrm{SM}}(P\rightarrow h_a)} ~~ \longrightarrow ~~ \frac{\sigma ^{\mathrm{MSSM}}(P\rightarrow h_a)}{\sigma ^{\mathrm{SM}}(P\rightarrow h_a)}\,\cdot (1+\eta _a^P). \nonumber \\ \end{aligned}$$

(34)

The choice of associating the interference contributions with the production processes in HiggsBounds while leaving the branching ratios $\text {BR}(h_a\rightarrow \tau ^{+}\tau ^{-})$ unchanged is of course of purely technical nature. One always needs to ensure that interference contributions are properly taken into account for the full process including production and decay, see Ref. [67].

For the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario the results $\eta ^{b{{\bar{b}}}}$ and $\eta ^{gg}$ as defined in (28), given in $\%$, are shown in Fig. 4 within the (${M_{H^{\pm }}}$, $\tan \beta$) parameter planes. The interference effect in both processes exhibits a similar pattern. First of all, it is destructive, i.e. $\eta ^P<0$, throughout the parameter plane (apart from the small dark red regions). Due to the approximate mass degeneracy of $h_2$ and $h_3$ and the sizeable $H-A$ mixing, the interference contribution becomes in both processes very large in significant parts of the parameter space. At ${M_{H^{\pm }}}\simeq 480\,\text {GeV}$ and $\tan \beta \simeq 29$, the relative interference contribution reaches a minimum of $\eta ^P\simeq -\,97\%$ in both processes so that the cross section is almost completely cancelled by the drastic, negative interference term. This strongest interference region is surrounded by a “valley” of also substantial destructive interference.

Fig. 5

a Ratio $R_{32}$ of mass difference $M_{h_3}-M_{h_2}$ and sum of total widths $\Gamma _{h_2}+\Gamma _{h_3}$. b Ratio $c_{23}$ of couplings in the interference term of the $b{{\bar{b}}}$-initiated process compared to those in the incoherent sum, including $\hat{\mathbf{Z }}$-factors

Conditions for a sizeable interference term Having observed the occurrence of a large destructive interference contribution at the example of the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario in Fig. 4, we now investigate in more detail under which conditions such an interference can arise. An important criterion is the overlap of two resonances which is determined by the mass splitting and the total widths. In the decoupling limit, $h_2$ and $h_3$, which are involved in the relevant interference, are quasi degenerate while $h_1$ is much lighter. Because of the significant total widths $\Gamma _{h_2}, \Gamma _{h_3}$, the $h_2-h_3$ overlap

$$\begin{aligned} R_{32}:=\frac{M_{h_3}-M_{h_2}}{\Gamma _{h_2}+\Gamma _{h_3}}< 1 \end{aligned}$$

(35)

is also fulfilled for not exactly degenerate states as displayed in Fig. 5a.

In order to understand the location of the strongest interference, we examine the couplings that play a role in the interference term compared to those in the incoherent sum of the $b{{\bar{b}}}$-initiated process:

$$\begin{aligned} c_{23} = \frac{2\text {Re}[g_{h_2\tau \tau }\,g_{h_2 bb}\, g^{*}_{h_3\tau \tau }\,g^{*}_{h_3 bb}]}{|g_{h_2\tau \tau }\,g_{h_2 bb}|^{2} + |g_{h_3\tau \tau }\,g_{h_3 bb}|^{2}} , \end{aligned}$$

(36)

where $g_{h_af{\bar{f}}}$ with $a=1,2,3,~f=\tau ,b$ are the tree-level couplings $g_{if{\bar{f}}}$ from Eq. (7) for $i=h,H,A$, combined with two-loop $\hat{\mathbf{Z }}$-factors from FeynHiggs according to Eq. (19):

$$\begin{aligned} g_{h_a f{\bar{f}}} = \sum _{i=h,H,A} \hat{\mathbf{Z }}_{ai} g_{i f{\bar{f}}}. \end{aligned}$$

(37)

Since the masses $m_{\tau }, m_b$ and other constants cancel out in Eq. (36), the ratio $c_{23}$ is determined by the on-shell $\hat{\mathbf{Z }}$-factors and the angles $\cos \alpha$ and $\sin \beta$. Figure 5b shows that the behaviour of $c_{23}$ largely determines the pattern of the relative interference contribution observed in Fig. 4, whereas effective couplings based on a $p^{2}=0$ approximation of the self-energies or the pure tree-level couplings would yield a completely different pattern, see Ref. [57]. The interference contribution on the squared matrix element level is proportional to [56]

$$\begin{aligned}&|\mathcal {A}|^{2}_{\mathrm{int}} \propto c_{\beta }^{-4}\, 2\text {Re}\left[ (c_{\alpha }^{2}\hat{\mathbf{Z }}_{2H}\hat{\mathbf{Z }}_{3H}^{*}\right. \nonumber \\&\quad \left. \,+\,s_{\beta }^{2}\hat{\mathbf{Z }}_{2A}\hat{\mathbf{Z }}_{3A}^{*} )^{2} \Delta ^{{\text {BW}}}_2(s) \Delta ^{{\text {BW*}}}_3(s) \right] . \end{aligned}$$

(38)

In the decoupling region of $M_H^\pm \gg M_Z$, the heavy Higgs bosons $h_2$ and $h_3$ have very similar masses $M_{h_2}\simeq M_{h_3}$ and widths $\Gamma _{h_2}\simeq \Gamma _{h_3}$ so that the product $\Delta ^{{\text {BW}}}_2(s) \Delta ^{{\text {BW*}}}_3(s) \simeq |\Delta ^{{\text {BW}}}_2|^{2}$ becomes approximately real. In this limit, the relations $\hat{\mathbf{Z }}_{2H}\simeq \hat{\mathbf{Z }}_{3A}$, $\hat{\mathbf{Z }}_{2A}\simeq -\hat{\mathbf{Z }}_{3H}$ and $\cos \alpha \simeq \sin \beta$ simplify Eq. (38) to:

$$\begin{aligned}&|\mathcal {A}|^{2}_{\text {int}} \propto -8\tan \beta ^{4}\, (\text {Im}\hat{\mathbf{Z }}_{2H}\,\text {Re}\hat{\mathbf{Z }}_{2A}\nonumber \\&\quad - \text {Re}\hat{\mathbf{Z }}_{2H}\,\text {Im}\hat{\mathbf{Z }}_{2A})^{2}\,|\Delta ^{{\text {BW}}}_2(s)|^{2} . \end{aligned}$$

(39)

As expected, the interference term of $h_2$ and $h_3$ vanishes for the case of $\mathcal {CP}$ conservation in the Higgs sector, in which case $\hat{\mathbf{Z }}_{2A}=\hat{\mathbf{Z }}_{3H}=0$ holds. In addition to the $\mathcal {CP}$-violating mixing, a non-zero interference term requires non-vanishing imaginary parts of the $\hat{\mathbf{Z }}$-factors, which originate from the imaginary parts of the Higgs self-energies. Consequently, replacing the on-shell $\hat{\mathbf{Z }}$-factors by real mixing factors $\mathbf{U }$ (see e.g. Refs. [59, 61]) in an effective coupling approach with $p^{2}=0$ renders the interference term zero in the decoupling limit even though the $\mathbf{U }$-matrix may contain equally large diagonal and off-diagonal elements. Even if the conditions of $\mathcal {CP}$-violating mixing and the presence of non-vanishing imaginary parts are fulfilled, there might still be a cancellation between the two terms within the bracket in Eq. (39).

Outside the decoupling limit, with unequal masses, widths and mixing properties of $h_2$ and $h_3$, the full product of angles from the couplings, $\hat{\mathbf{Z }}$-factors and complex Breit–Wigner functions has to be taken into account. However, in the relevant part of the considered parameter plane, the decoupling limit is reached. Given the quasi-degeneracy of $M_{h_2}$ and $M_{h_3}$ shown in Fig. 5a, the structure of the $\hat{\mathbf{Z }}$-matrix provides in fact a well-suited indication of the relevance of the interference term. In particular, the square of the bracket and the absolute square of the Breit–Wigner function in combination with the overall minus sign in Eq. (39) explain the observed destructive interference effect.

5 Impact of interference and mixing on exclusion bounds

As two consequences of the $\mathcal {CP}$-violating mixing, in the previous sections we have investigated the enhancement of production cross sections for the mass eigenstates and the reduction of the complete processes of production and decay due to destructive interference. In this section we will compare these theory predictions with experimental limits from searches for heavy additional Higgs bosons in the $\tau ^+\tau ^-$ final state at Run 1 of the LHC [28, 72]. In the LHC searches for additional Higgs bosons in supersymmetric models so far it has been assumed that $\mathcal {CP}$ is conserved, so that no mixing occurs between $\mathcal {CP}$-even and $\mathcal {CP}$-odd states. Under this assumption, the contributions from $\mathcal {CP}$-even and $\mathcal {CP}$-odd states can be added as an incoherent sum. The question arises in this context in how far the exclusion bounds that have been obtained under the assumption of $\mathcal {CP}$ conservation will be modified in the general case where the possibility of $\mathcal {CP}$-violating mixing and interference effects is taken into account. In the following we will first as an illustration compare single cross section limits with the theory predictions, before performing a more detailed analysis of the exclusion limits in the $({M_{H^{\pm }}},\tan \beta )$ parameter plane of the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario using the tool HiggsBounds.

Fig. 6

Comparison of predicted Higgs cross sections times branching ratio into $\tau ^+\tau ^-$ with and without the interference and with $2\, \times \,2$ and $3 \,\times \, 3$ mixing, for a fixed value of $\tan \beta$, to experimental exclusion bounds. Left column (a, c): production via $b{{\bar{b}}}$. Right column (b, d): production via gg. Upper row (a, b): strongest interference effect at $\tan \beta =29$. Lower row: c $\tan \beta =25$, d $\tan \beta =19$. Each plot shows the CMS observed (black, solid) and expected (black, dotted) exclusion bounds at 95% CL at $8\,\mathrm {TeV}$ with $\int \mathcal {L}=24.6\,\mathrm {fb} ^{-1}$ from Refs.  [27, 72, 83], as well as the theory prediction in the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario for the combined cross section of $h_2$ and $h_3$ as the incoherent sum restricted to $\mathcal {CP}$-conserving mixing for $\phi _{A_t}=0$ (turquoise, dotted, labelled as “$2\times 2$”), the incoherent sum with $\mathcal {CP}$-violating mixing for $\phi _{A_t}=\pi /4$ (turquoise, dashed, labelled as “$3\times 3$ incoherent”) and the coherent sum (i.e. including the interference term) with $\mathcal {CP}$-violating mixing for $\phi _{A_t}=\pi /4$ (turquoise, solid, labelled as “$3\times 3$ coherent”)

5.1 Coherent and incoherent cross sections

In Fig. 6 we show the theory predictions (turquoise) for $\sigma (pp\rightarrow P \rightarrow h_2, h_3 \rightarrow \tau ^+\tau ^-)$ depending on the mass ${M_{\phi }}$ of a neutral scalar resonance $\phi$ for each of the production modes $P=b{{\bar{b}}},gg$ in comparison with the respective experimental limits on the production of a single resonance (black). The displayed experimental results represent the expected (dotted) and observed (solid) CMS exclusion bound at the $95\%$ CL from Run 1 of the LHC with $\int \mathcal {L}=24.6\,\mathrm {fb} ^{-1}$ reported in Ref. [83] (which is also used in HiggsBounds).

The theory prediction has been calculated using ${M_{H^{\pm }}}$ and $\tan \beta$ as input parameters and is shown as a function of ${M_{\phi }}:=M_{h_3}$ ($\simeq M_{h_2}$ in the relevant region) for representative values of $\tan \beta$. The differences between the incoherent sum restricted to $\mathcal {CP}$-conserving $2\times 2$ mixing for $\phi _{A_t}=0$ (dotted), the incoherent sum with $\mathcal {CP}$-violating $3\times 3$ mixing for $\phi _{A_t}=\pi /4$ (dashed) and the coherent sum including $3\times 3$ mixing and the interference term for $\phi _{A_t}=\pi /4$ (solid) are visible. Figure 6a, c show the bb-initiated process, whereas Fig. 6b, d show the gg-initiated one. The two upper plots correspond to $\tan \beta =29$, where the strongest interference is observed, while the lower two plots represent $\tan \beta =25$ and $\tan \beta =19$, respectively, with still a large interference albeit less drastic effect in the gg-process. The comparison of the predicted cross sections times branching ratios with and without the interference term to the experimental bound reveals that the presence of a non-vanishing value of the phase of the parameter $A_t$ in this scenario has a large impact on the exclusion bounds. In comparison with the case where $\mathcal {CP}$ conservation is assumed ($\phi _{A_t}=0$), the cross section in the case of $3\times 3$ mixing would be significantly enhanced in the resonance region if only the incoherent sum of the contributions were taken into account. In contrast, the incorporation of the interference contribution in fact has the overall effect of a reduction of the cross section in the resonance region.

In the comparison of the theory predictions with a single cross section limit considered here, for a given value of $\tan \beta$ one obtains an exclusion at the $95\%$ CL for ${M_{\phi }}$ values where the prediction of $\sigma \times \text {BR}$ is larger than the observed limit. Accordingly, the exclusion based on the mixing-enhanced $3\times 3$ incoherent cross section would be stronger than for the case where $\mathcal {CP}$ conservation is assumed ($2\times 2$ with $\phi _{A_t}=0$), while the inclusion of the interference contribution in the full result leads to weaker bounds than for the case where $\mathcal {CP}$ conservation is assumed. Therefore in general the lower bound on ${M_{\phi }}$ for a given value of $\tan \beta$ that can be set by this comparison is reduced as compared to the case where $\mathcal {CP}$ conservation is assumed.

While this shift of the lower bound on ${M_{\phi }}$ is only moderate if the intersection between the prediction and the observed limit occurs outside of the resonance region, as it is the case in Fig. 6b, d for the gg production mode (which is less constraining than the $b{{\bar{b}}}$ process in the parameter regions considered here), the situation is different if the large destructive interference contribution in the resonance region reduces the cross section such that it falls below the observed limit. This can be seen in Fig. 6a for the $b{{\bar{b}}}$ production mode. In addition to the shift in the lower bound on ${M_{\phi }}$ from about 695 GeV for the case $\phi _{A_t}=0$ to about 675 GeV for the case $\phi _{A_t}=\pi /4$, in this case a range of unexcluded values of ${M_{\phi }}$ opens up between 465 GeV and 485 GeV which would appear to be excluded under the assumption of $\mathcal {CP}$ conservation. A similar effect can be seen in Fig. 6c for the $b{{\bar{b}}}$ production mode for the smaller value of $\tan \beta$ which is somewhat off the resonance. As a consequence, the resulting interference effect and also the enhancement of the incoherent cross section are less sharp. In this case the lower bound on ${M_{\phi }}$ is shifted from about 650 GeV for the case $\phi _{A_t}=0$ to about 520 GeV for the case $\phi _{A_t}=\pi /4$. If instead the interference contribution were neglected for the $3 \times 3$ case, the incoherent cross section would indicate an exclusion on ${M_{\phi }}$ up to about 690 GeV in this case.

Fig. 7

Comparison of the coherent $h_2$ and $h_3$ Higgs cross sections times branching ratio into $\tau ^+\tau ^-$ (including the interference contribution) in the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario with $\phi _{A_t}=\pi /4$ for different values of $\tan \beta$ with $95\%$ CL exclusion bounds obtained by CMS at $8\,\mathrm {TeV}$. See the respective colour coding for $\tan \beta =25,28,29,30,33$. The displayed exclusion bounds are the same as in Fig. 6. In a the production via $b{{\bar{b}}}$ is shown, in the b production via gg

In order to display the behaviour in the resonance region in more detail, Fig. 7 shows the results for the coherent cross sections with $\phi _{A_t}=\pi /4$ (including the interference contribution) for different values of $\tan \beta$ across the resonance region. Both for the $b{{\bar{b}}}$ and gg production modes, the most pronounced interference effect occurs at about $\tan \beta =29$. The interference effect is similarly large for $\Delta \tan \beta = \pm \, 1$, while it can be seen to be largely washed out and significantly shifted towards smaller (larger) values of ${M_{\phi }}$ for $\Delta \tan \beta = + \,4$ ($\Delta \tan \beta = - \,4$) in this example. As before, the sensitivity of the gg production mode is much smaller in this parameter region, which gives rise to the fact that the main modification of the cross section caused by the interference contribution occurs in the region much below the excluded cross section. For the $b{{\bar{b}}}$ production mode, on the other hand, the interference contribution can reduce the cross section to a level below the exclusion limit within the resonance region.

In should be noted in this context that the comparison between the predicted cross section and the observed exclusion limit is of course affected by theoretical (see the discussion in Ref. [17]) and experimental [83] uncertainties. Since the main purpose of our discussion has been the illustration of the qualitative features of the $3\times 3$ mixing and the interference contribution, we do not address the issue of uncertainties in detail here. Assuming comparable experimental uncertainties in the scenario considered in this work and in the standard $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario analysed in Refs. [27, 83], the impact of the mixing and interference effects extends beyond the experimental uncertainty band. Concerning the theoretical uncertainty of the interference contribution, it should be noted that our approach outlined in Sect. 3 involves a systematic treatment of the finite widths of the resonantly produced Higgs bosons, which is crucial for a proper treatment of the interference effects. For a more detailed discussion of the uncertainties related to the incorporation of the interference contribution we refer to Ref. [67].

Beyond the uncertainty band of Ref. [83], also the experimental mass resolution should be considered. If the mass difference of two nearby resonances is smaller than the resolution, they cannot be separated. In the analysed scenario, the mass differences of $M_{h_3}-M_{h_2}\lesssim 1\,\text {GeV}$ for ${M_{H^{\pm }}}\gtrsim 200\,\text {GeV}$ and $\tan \beta \gtrsim 5$ are clearly smaller than the experimental mass resolution of 20–40% [28, 72] and therefore the two resonances cannot be distinguished.

However, in case the resolution improves significantly or the masses are more separated, two resonances could be resolved, which would change the analysis and the application of the relative interference factors. This configuration would affect resonance searches both in the $\mathcal {CP}$-conserving and the $\mathcal {CP}$-violating case because the cross sections of two distinguishable resonances cannot simply be added. In distributions, the peaks will show up in different bins. It should be kept in mind, though, that in case of a large mass splitting, the phenomenological effect of the interference term will be reduced.

Fig. 8

Exclusion bounds in the $({M_{H^{\pm }}},\tan \beta )$ plane of the MSSM obtained with HiggsBounds. a $M_h^{\mathrm{mod+}}$ scenario with real parameters for $\mu =200\,\text {GeV}$ (green) and $\mu =1\,\mathrm {TeV}$ (orange); exclusion bound that would be obtained in the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario with $\phi _{A_t}=\pi /4$ for the incoherent sum of cross sections with $3\times 3$ mixing but without the interference contribution (blue). b $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario with $3\times 3$ mixing but without the interference contribution (blue, same as in a), including the interference contribution in both the $b{{\bar{b}}}$ and the gg processes (red), including the interference contribution only in $b{{\bar{b}}}$ (black line) or only in gg (grey line)

In addition to the mass difference of two nearby resonances, also their total widths play a decisive role in the question whether they can be resolved. First of all, in order to verify that the experimental search for a narrow resonance is applicable to our scenario, we evaluated the ratio of $\Gamma _{h_a}/M_{h_a}$ for $a=2,3$. Due to the $\hat{\mathbf{Z }}$-factor enhancement of the total widths in the region of strongest mixing (see Fig. 2), this ratio reaches up to 5% around ${M_{H^{\pm }}}\simeq 490\,\text {GeV},~\tan \beta \simeq 29$, which is higher than in the $\mathcal {CP}$-conserving scenario of $\phi _{A_t}=0$, but still much smaller than the experimental resolution. Hence, $h_2$ and $h_3$ can be considered narrow in the experimental sense. Second, the mutual overlap of two resonances is determined by their mass splitting compared to the sum of their total widths, whose ratio $R_{32}=(M_{h_3}-M_{h_2})/(\Gamma _{h_2}+\Gamma _{h_3})$ is significantly smaller than one, see Eq. (35) and Fig. 5a. Consequently, $h_2$ and $h_3$ overlap strongly. This implies that even a drastically improved experimental resolution will not reveal two distinct peaks. Intermediate configurations should be kept in mind where the mass splitting is on the one hand larger than the (future) resolution, but on the other hand the peaks are smeared by sizeable widths that are narrow in comparison to the masses and broad in comparison to the mass splitting. Also in such a case, the two resonances would not be completely separate. However, depending on the splitting-to-widths ratio, two peaks might be distinguishable over the overlapping tails. This would require a dedicated study.

5.2 Exclusion bounds with mixing and interference

We now turn to an analysis of the exclusion limits in the $({M_{H^{\pm }}},\tan \beta )$ parameter plane of the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario using the program HiggsBounds-4.2.0 [52,53,54,55], in which comprehensive information about limits from a variety of searches at LEP, the Tevatron and Run 1 of the LHC in different channels is implemented. Among the channels that are most important for constraining the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario are the ATLAS and CMS searches for neutral heavy Higgs bosons decaying to $\tau \tau$ [27, 28] and to $ZZ(\rightarrow 4l)$ [84, 85], as well as analyses of the neutral Higgs boson at a mass of $125\,\text {GeV}$ [86, 87] and searches for charged Higgs bosons [88, 89]. For each parameter point, HiggsBounds determines the search channel at LEP, Tevatron or the LHC with the highest expected sensitivity for an exclusion. For this channel the observed limit is confronted with the predicted cross section in order to determine whether the considered parameter point is excluded at the 95% CL. For the channels $\sigma _{b{{\bar{b}}}}(\phi )\,\text {BR}(\phi \rightarrow \tau ^+\tau ^-)$ and $\sigma _{gg}(\phi )\,\text {BR}(\phi \rightarrow \tau ^+\tau ^-)$ the 2-dimensional likelihood information provided by CMS [27, 72] has been implemented.³ For the incorporation of interference effects we have rescaled the ratio of production cross sections used as input for HiggsBounds as described in (33) and (34).

In order to disentangle the interference effects from other effects due to the modified scenario, the result for the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario with $\phi _{A_t}=\pi /4$ and $\mu =1000\,\text {GeV}$ is shown in Fig. 8 together with the familiar exclusion region in the well-known $M_h^{\mathrm{mod+}}$ scenario [71] with real parameters (in particular $\phi _{A_t}= 0$) and the default value of $\mu =200\,\text {GeV}$. The latter exclusion region is indicated in green in Fig. 8a, where the unexcluded parameter region in this type of plot is often denoted as the “LHC wedge” region. The corresponding exclusion region for $\mu =1000\,\text {GeV}$ is shown in orange. The larger value of $\mu$ yields stronger exclusion limits since in this case the decay channel of a heavy Higgs boson into higgsino-like neutralinos and charginos is kinematically closed, resulting in an enhancement of the branching ratio into $\tau ^{+}\tau ^{-}$. The excluded region that one would obtain for the incoherent sum of cross sections of the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario with $\phi _{A_t}=\pi /4$ and $\mu =1000\,\text {GeV}$ ($3\times 3$ mixing, no interference contribution taken into account) is displayed in blue in the same plot. We find that the incoherent cross section of the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario with $\phi _{A_t}= \pi /4$ would result in a stronger exclusion than the corresponding scenario with real parameters and the same value of $\mu$ because of the mixing-enhanced production cross sections as discussed in Sects. 3.2 and 5.1.

In Fig. 8b the impact of the interference contributions on the excluded regions in the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario is investigated. The blue area (the same as in Fig. 8a) corresponds to the incoherent sum of cross sections without the interference contribution. In contrast, taking the interference contribution into account in both the $b{{\bar{b}}}$- and the gg-initiated processes leads to the weaker exclusion limit given by the red area, as a consequence of the destructive interference effect as discussed in Sect. 5.1. The black line indicates the boundary of the excluded region that one would obtain if the interference contribution were taken into account only for the $b{{\bar{b}}}$-initiated process, while the grey line indicates the boundary of the excluded region that one would obtain if the interference contribution were taken into account only for the gg-initiated process.

The features visible in Fig. 8b can be related to the results of Sect. 5.1, since each horizontal line of constant $\tan \beta$ in Fig. 8b approximately corresponds to one plot as in Fig. 6 for the same $\tan \beta$, separately for each process. It should be noted in this context, however, that in Fig. 8b also contributions from the lightest neutral Higgs boson of the MSSM are taken into account, and the experimental information implemented in HiggsBounds is employed, consisting in particular of a 2-dimensional likelihood distribution [91] for the production via $b{{\bar{b}}}$ and gg, instead of a single cross-section limit. Furthermore, the quantity on the x-axis of Fig. 8b is ${M_{H^{\pm }}}$, while the results in Figs. 6 and 7 are expressed in terms of the mass of a (single) neutral resonance, ${M_{\phi }}$. While the interference contributions have little impact on the exclusion region for $\tan \beta$ values below about 15, their effect is clearly visible for $\tan \beta \gtrsim 15$ up to the highest values of $\tan \beta$ shown in the plot. The unexcluded “fjord” between about (${M_{H^{\pm }}} = 480\,\text {GeV}, \tan \beta = 29$) and (${M_{H^{\pm }}} = 600\,\text {GeV}, \tan \beta = 20$) is a consequence of the destructive interference contributions in the resonance region discussed in Sect. 5.1. It is interesting to note that the full “fjord” only occurs as a consequence of incorporating the interference contributions in both the $b{{\bar{b}}}$- and gg-initiated processes. If the interference contribution were incorporated only for the $b{{\bar{b}}}$-initiated process but neglected for the gg-initiated process the resulting exclusion region would have the “bay” shape indicated by the black line in Fig. 8b. The “fjord” between $25 \lesssim \tan \beta \lesssim 29$ would appear to be excluded in this case. The reason for this relatively large impact of the gg-initiated process in a parameter region where it is sub-dominant (see Figs. 6, 7) is mainly due to the enhancement of the gg-initiated process in the resonance region that would occur for a non-zero phase if the interference contribution were neglected, see Fig. 6b. While this parameter region is allowed by the coherent $b{{\bar{b}}}$ cross section (see Fig. 6a), it would appear to be excluded by the incoherent enhanced gg cross section in this case (see Fig. 6b). On the other hand, incorporating the interference contribution only for the gg-initiated processes but not for the $b{{\bar{b}}}$-initiated one would only have a minor impact, as can be seen by comparing the grey line in Fig. 8b with the boundary of the blue area.

6 Conclusions

In the present paper we have investigated how the limits from the LHC searches for additional heavy SUSY Higgs bosons get modified if instead of the assumption of $\mathcal {CP}$ conservation in the Higgs sector the general case of complex parameters giving rise to $\mathcal {CP}$-violating effects is taken into account. We have considered neutral Higgs boson production in gluon fusion and in association with $b{{\bar{b}}}$, and the decay into a pair of $\tau$-leptons in an extension of the well-known $M_h^{\mathrm{mod+}}$ benchmark scenario of the MSSM where $\mathcal {CP}$-violating effects are induced by a non-zero phase of the trilinear coupling $A_t$, $\phi _{A_t}=\pi /4$.

While in the LHC searches for additional Higgs bosons in supersymmetric models so far it has been assumed that the contributions from $\mathcal {CP}$-even and $\mathcal {CP}$-odd states to the signal cross section can be added as an incoherent sum, such an assumption is not valid in the general case where $\mathcal {CP}$-violating effects in the Higgs sector are taken into account. In the Higgs sector of the MSSM, complex parameters enter via loop corrections, causing $\mathcal {CP}$-violating effects beyond the tree level. As a consequence, the $\mathcal {CP}$ eigenstates h, H, A mix into the mass eigenstates $h_1, h_2, h_3$. The Higgs sectors of the NMSSM and of a non-supersymmetric 2HDM are in general $\mathcal {CP}$-violating already at lowest order. The most obvious realisation of an extended Higgs sector that is compatible with the present experimental constraints is a scenario where one neutral scalar is SM-like and has a mass of about 125 GeV, while the other neutral Higgs bosons are significantly heavier. In such a decoupling-type scenario the heavy neutral Higgs bosons of the extended Higgs sector are typically nearly mass-degenerate. If $\mathcal {CP}$-violating effects are present, potentially large mixing and interference effects between the heavy neutral Higgs bosons occur as a generic feature of such extended Higgs sectors. These kind of effects should therefore be taken into account in the interpretation of the limits from the searches for additional neutral Higgs bosons.

Using an approximation of the $(3\times 3)$ Higgs propagator matrix in terms of wave function normalisation factors evaluated at the complex poles and Breit–Wigner propagator factors, we have determined the relative interference contributions to the full process of production and decay. We have demonstrated how these interference contributions can be combined with the results for the on-shell production and decay of individual Higgs bosons in order to arrive at a prediction for the full process incorporating interference effects. We have compared this result based on a coherent sum of the relevant contributions with the corresponding incoherent sum that would be obtained if interference contributions were omitted.

Furthermore, we have analytically investigated the relative interference contribution with respect to its dependence on the couplings, wave function normalisation factors, masses and widths. We have pointed out that besides the well-know criterion in terms of the mass difference and sum of the total Higgs widths, the occurrence of a sizeable $\mathcal {CP}$-violating interference effect is also directly related to the presence of imaginary contributions in the propagator matrix. Since the latter can be well approximated by the wave function normalisation factors, we could derive a simple criterion indicating whether interference effects are expected to be relevant. While the current experimental resolution is much larger than the mass splitting of the two nearby resonances, a significant improvement of the resolution in combination with a larger mass difference than in our scenario could in principle lead to two resolvable peaks. We discussed that even in the case of an improved resolution, the two resonances may be smeared too much by sizeable widths to be separable from each other.

In the considered scenario we have found that both the mixing effects and the interference contributions are large in the resonance region where the above criteria are fulfilled. In fact, if interference effects were omitted, the mixing effect between the nearly mass-degenerate heavy neutral Higgs bosons $h_2$ and $h_3$ would give rise to a significant enhancement of the total cross section in this region. However, the large destructive interference contribution, which in the considered scenario reaches a minimum of $-\,97\%$ at ${M_{H^{\pm }}}\simeq 480\,\text {GeV}$ and $\tan \beta \simeq 29$ in both production processes, overcompensates this effect. The net effect is therefore a large suppression of the total cross section times branching ratio in the resonance region as compared to the case of real parameters.

We have studied the impact of those modifications from mixing and interference effects in the presence of complex parameters on the limits obtained from the LHC searches in comparison with the limits for the $\mathcal {CP}$-conserving case of real parameters. For illustration we have first investigated single cross section limits, followed by a more comprehensive analysis in the $({M_{H^{\pm }}},\tan \beta )$ parameter plane of the $\mathbb {C}M_h^{\mathrm{mod+}}$ scenario using the tool HiggsBounds. As expected by our analytical investigation, we have found that both the mixing enhancement and the relative effect of the destructive interference are similar for the two production modes of gluon fusion and associated production with $b{{\bar{b}}}$. For moderate and large values of $\tan \beta$, the $b{{\bar{b}}}$ cross section is larger than the gluon fusion one, but both processes are relevant for the analysed parameters. We have demonstrated that the $\mathcal {CP}$-violating mixing and interference effects cause a substantial shift of the exclusion bounds in the parameter space along the “LHC wedge” region in comparison to the limits that would be obtained in the corresponding scenario with real parameters. We have shown that in order to obtain those results it is important to incorporate the interference contribution both for the $b{{\bar{b}}}$ associated production and the gluon fusion process. Our analysis has indicated that a considerable parameter region remains unexcluded by LHC searches from Run 1 that would appear to be ruled out if interference effects were neglected.

The illustrative study carried out in this paper motivates the analysis of current and future LHC results in scenarios with complex parameters, taking interference effects into account. While in our qualitative investigation we have restricted ourselves to the analysis of the experimental results that were obtained at Run 1 of the LHC and we have used an approximate treatment of the cross sections for the production processes, our results lay the foundation for a more detailed phenomenological analysis incorporating the latest experimental results and the most accurate theoretical predictions. We defer such a more detailed investigation taking into account the latest experimental results from Run 2 of the LHC, employing the recently released tool SusHiMi [24] for the accurate prediction of the Higgs production processes in gluon fusion and $b{{\bar{b}}}$ associated production, and studying the variation of the phases of several relevant MSSM parameters, in particular the phase of the gluino mass parameter, to future work [67].