1 Introduction

Dark energy is one of the fascinated issue of modern cosmology that has encouraged the modification of Einstein Hilbert action. The modified gravitational part of Einstein Hilbert action leads to the notion of modified theories of gravity which modify the dynamic of the universe at large distances. In another scenario, modified matter part of Einstein Hilbert action results dynamical models such as cosmological constants, quintessence, k-essence, Chaplygin gas and holographic dark energy (HDE) models [1,2,3,4,5,6,7,8,9]. Moreover, several modified theories of gravity are f(R), f(T) [10,11,12,13,14,15], \(f(R,{\mathcal {T}})\) [16, 17], f(G) [18,19,20,21,22,23], \(f(T,T_G)\) [24,25,26], \(f(T,T )\) [27, 28] (where R is the curvature scalar, T denotes the torsion scalar, \({\mathcal {T}}\) is the trace of the energy momentum tensor and G is the invariant of Gauss–Bonnet defined as \(G=R^2-4R_{\mu \nu }R^{\mu \nu }+ R_{\mu \nu \lambda \sigma }R^{\mu \nu \lambda \sigma }\)). For clear review of DE models and modified theories of gravity, see the reference [9]. Some authors [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46] have also discussed various DE models in different frameworks and found interesting results.

The scalar tensor models of modified gravity have taken remarkable attention. The reason is that scalar fields for consistent condition appear in different branches of theoretical physics such as, the low energy limit of the string theory leads to a scalar degree of freedom. The Brans–Dicke (BD) theory [47, 48] is a prototype of scalar tensor gravity which is based upon Dirac hypothesis. It relates scalar field \((\phi )\) with dynamical gravitational constant (\(G=\frac{G_{0}}{\phi }\)) and involves a tuneable constant coupling parameter \(\omega \). The scalar field is a fundamental feature of this gravity which is considered as a dark energy candidate. The parameter \(\omega \) can adjust results according to the requirement and in the limit \(\omega \rightarrow \infty \), it reduces BD theory into general relativity (GR).

The standard BD theory remains unable to probe cosmic evolution accurately. In this context, many researchers have generalized BD theory in different scenario like, self-interacting potential model, model having time- dependent coupling parameter \((\omega )\) [49,50,51]. Brans–Dicke cosmological models with constant deceleration parameter in the form of particle creation [52]. The Friedman models (with zero curvature) under the effects of time dependent bulk viscosity [53]. Similarly, the modification of BD theory also involve interaction with dark matter, such as the concept of dissipative cold dark matter in BD gravity [54, 55], model representing transfer of energy between BD gravity and dark matter [56, 57]. Recently, Kofinas et al. [58] introduced the most generalized or corrected form of BD gravity by relaxing the standard conservation law of matter contribution (energy momentum of matter). He used a new dimensionless parameter \(\nu \) in the theory. This new version of BD gravity has explored cosmic evolution in accords to observational data by involving matter-scalar field interaction.

In literature, the relation between gravitation and thermodynamics has been discussed extensively. Moreover, by inspiring the black hole theory, there is a deep connection between gravitation and thermodynamics. In GR, Hawking radiation [59] can be studied by using the proportionality relation between the surface gravity and temperature, and also developed the connection between the horizon entropy and area of thermodynamics. On the other hand, Jacobian in [60] was studied the Einstein field equations from the Clausis relation. By using this approach, the authors [61, 62] have checked validity of generalized second law of thermodynamics (GSLT). In literature many researchers have been studied the validity of GSLT in GR as well as modified theory. However, it should be noted that the definition of entropy would rather be modified in order to include quantum effects motivated from the loop quantum gravity [63, 64]. In this work we are focused on GSLT with modified BD theory involving dark matter and the dark energy with a scalar field.

The present paper is organized as follows. In Sect. 2 we give a brief description of the BD theory and then derive the late-time cosmic field equation with a perfect fluid. In Sect. 3, we formulate the Friedman equation of the late-time cosmological equation in the absence of \(\nu =0\). In Sect. 4 we analyze the GSLT with entropy corrections. In this section we check validity of GSLT by using the logarithmic, power-law corrections at apparent as well as event horizon and obtain the graphical results. At the end, a discussion of this work is presented.

2 Modified Brans–Dicke field equations

The action for standard BD theory in terms of Jorden frame is given by [47, 48]

$$\begin{aligned} S_{_{BD }}= & {} \frac{1}{16\pi }\int \bigg (\phi R-\frac{\omega }{\phi }g^{\mu \nu }\phi _{, \mu }\phi _{, \nu }\bigg )\sqrt{-g} d^{4}x\nonumber \\&+\int \sqrt{-g}L_{m}d^{4}x, \end{aligned}$$
(1)

where \(L_{m}\) represents the matter Lagrangian depending on scalar field \(\psi ,~\sqrt{-g}d^{4}x\) denotes four dimensional volume, \(\omega \) is the coupling constant which depends on dimensionless parameter \(\lambda (\ne 0)\) as \(\omega =\frac{2-3\lambda }{2\lambda },~\phi \) shows the scalar field and R is the Ricci scalar. The corresponding field equations are

$$\begin{aligned} {G^{\mu }}_{\nu }= & {} \frac{8\pi }{\phi }\bigg ({T^{\mu }}_{\nu }+{\tau ^{\mu }}_{\nu }\bigg ), \end{aligned}$$
(2)
$$\begin{aligned} {T^{\mu }}_{\nu }= & {} \frac{2-3\lambda }{16\pi \lambda \phi }\bigg (\phi ^{; \mu }\phi _{; \nu }-\frac{1}{2}\delta ^{\mu }_{\nu }\phi ^{; \rho }\phi _{; \rho }\bigg )\nonumber \\&+\frac{1}{8\pi }\bigg ({\phi ^{; \mu }}_{;\nu }-{\delta ^{\mu }}_{\nu }\Box \phi \bigg ),\end{aligned}$$
(3)
$$\begin{aligned} \Box \phi= & {} 4\pi \lambda \tau ,\end{aligned}$$
(4)
$$\begin{aligned} {\tau ^{\mu }}_{\nu ;\mu }= & {} 0. \end{aligned}$$
(5)

Here \({\tau ^{\mu }}_{\nu }\) is the energy–momentum tensor for matter and \(\tau ^{\mu }_{\mu }\) is its trace. The BD theory has proposed in a generalized simple form by relaxing conservation equations (5) [58]. In this modified form, the energy momentum tensor of scalar field is constructed through terms that contain \(\phi \) itself or two derivatives of one or two scalar fields. Thus, the generalized field equations contain modified form of Eqs. (3) and (5) given as

$$\begin{aligned} {T^{\mu }}_{\nu }= & {} \frac{\phi }{2\lambda (\nu +8\pi \phi ^{2})^{2}} \{2((1+\lambda )\nu + 4\pi (2-3\lambda )\phi ^{2})\phi ^{; \mu }\phi _{; \nu }\nonumber \\&-((1+2\lambda )\nu +4\pi (2-3\lambda )\phi ^{2}){\delta ^{\mu }}_{\nu }\phi ^{; \rho }\phi _{;\rho }\}\nonumber \\&+\,\frac{\phi ^{2}}{\nu +8\pi \phi ^{2}}\left( {\phi ^{; \mu }}_{;\nu }-{\delta ^{\mu }}_{\nu }\Box \phi \right) , \end{aligned}$$
(6)
$$\begin{aligned} {\tau ^{\mu }}_{\nu ;\mu }= & {} \frac{\nu }{\phi (\nu +8\pi \phi ^{2})} {\tau ^{\mu }}_{\nu }\phi _{;\mu }, \end{aligned}$$
(7)

while the remaining equations remain same. Here, \(\nu \) is an arbitrary function of integration which numerical values as well as sign can be determined experimentally. For \(\nu =0\) the above system of equations reduces to the standard BD model ((2)–(5)).

The FRW metric is

$$\begin{aligned} ds^{2}=-\,dt^{2}+a(t)^{2}\left[ \frac{dr^{2}}{1-kr^{2}}+r^{2}(d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2})\right] ,\nonumber \\ \end{aligned}$$
(8)

where a is the scale factor and \(k=-1, 0, 1\) represent spatial curvatures. According to the symmetry of scale factor, the scalar field behaves as a function of time, i.e., \(\phi =\phi (t)\). For matter distribution, we take energy momentum tensor of perfect fluid as \(\tau ^{\mu }_{\nu }=diag(-\rho , p, p, p)\) with \(\rho (t)\) be its energy density and p(t) its pressure. Equations (2), (4), (6) and (7) along with above metric lead to

$$\begin{aligned}&H^{2}+\frac{k}{a^{2}}=\frac{8\pi }{3\phi }\rho -\frac{8\pi \phi }{\nu +8\pi \phi ^{2}}H{\dot{\phi }}\nonumber \\&\qquad +\frac{4\pi }{3\lambda }\frac{\nu + 4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}{\dot{\phi }}^{2}, \end{aligned}$$
(9)
$$\begin{aligned}&2{\dot{H}}+3H^{2}+\frac{k}{a^{2}}\nonumber \\&\quad =-\frac{8\pi }{\phi }\bigg [p+\frac{\phi }{2\lambda }\frac{(1+2\lambda )\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}{\dot{\phi }}^{2}\nonumber \\&\qquad +\frac{\phi ^{2}}{\nu +8\pi \phi ^{2}} (2H{\dot{\phi }}+\ddot{\phi })\bigg ],\end{aligned}$$
(10)
$$\begin{aligned}&\ddot{\phi }+3H{\dot{\phi }}+4\pi \lambda (3p-\rho )=0, \end{aligned}$$
(11)
$$\begin{aligned}&{\dot{\rho }}+3H(p+\rho )=\frac{\nu }{\phi (\nu +8\pi \phi ^{2})}\rho {\dot{\phi }}. \end{aligned}$$
(12)

For \(\nu =0\), the above define equations reduce to standard BD model. Integrating Eq. (11), using \(p=\omega \rho \), we get

$$\begin{aligned} \rho= & {} \frac{\rho _{*}}{a^{3(1+\omega )}}\frac{\mid \phi \mid }{\sqrt{\mid \nu +8\pi \phi ^{2}}\mid }, \end{aligned}$$
(13)

where \(\rho _{*}\) is an integration constant. This obtain relation of energy density represents a direct coupling of scalar field and matter density.

In effective scenario, the field Eqs. (9) and (10) can be rewritten as

$$\begin{aligned} H^{2}+\frac{k}{a^{2}}= & {} \frac{8\pi }{3}\rho _{eff }, \end{aligned}$$
(14)
$$\begin{aligned} 2{\dot{H}}+3H^{2}+\frac{k}{a^{2}}= & {} -8\pi p_{eff }. \end{aligned}$$
(15)

Here the effective energy density and pressure are defined by

$$\begin{aligned} \rho _{eff }= & {} \frac{1}{\phi }(\rho +\rho _{de}),\quad p_{eff }=\frac{1}{\phi }(p+p_{de}), \end{aligned}$$
(16)
$$\begin{aligned} \rho _{de}= & {} -\frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}} +\frac{\phi {\dot{\phi }}^{2}}{2\lambda }\left( \frac{\nu +4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\right) , \end{aligned}$$
(17)
$$\begin{aligned} p_{de}= & {} \frac{\phi {\dot{\phi }}^{2}}{2\lambda }\left( \frac{(1+2\lambda )\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\right) \nonumber \\&+\frac{\phi ^{2}(2H{\dot{\phi }} +\ddot{\phi })}{\nu +8\pi \phi ^{2}}. \end{aligned}$$
(18)

3 Generalized second law of thermodynamics

In this section, we will study the validity of GSLT in the framework of modified BD theory on the apparent and event horizons. According to GSLT, the combination of entropy of horizon and entropy of all matter sources inside horizon does not decrease with time. Mathematically, it can be expressed as

$$\begin{aligned} {\dot{S}}_{tot}={\dot{S}}_{h}+{\dot{S}}_{in}\ge 0, \end{aligned}$$
(19)

where \({\dot{S}}_{h}\) represents the entropy related to the horizon and \({\dot{S}}_{in}\) is the sum of all entropies inside the horizon. Let us start from Gibb’s equations which evolutes the entropy of matter and energy source to the pressure inside the horizon, given as

$$\begin{aligned} T_{in}dS_{in}=dE_{in}+p_{in}dV, \end{aligned}$$
(20)

which leads to

$$\begin{aligned} T_{in}{\dot{S}}_{in}=(p_{in}+\rho _{in})4\pi R^{2}_{h}({\dot{R}}_{h}-HR_{h}). \end{aligned}$$
(21)

Thus the total entropy inside the horizon can be written as

$$\begin{aligned} T_{in}{\dot{S}}_{in}=(p_{eff }+\rho _{eff }) 4 \pi R^{2}_{h}({\dot{R}}_{h}-HR_{h}). \end{aligned}$$
(22)

Also, the Hawking entropy relation is defined by

$$\begin{aligned} S_{h}=\frac{A}{4G}, \end{aligned}$$
(23)

where \(A=4\pi R^{2}_{h}\) is the area of horizon.

3.1 Apparent horizon

Let us assume FRW universe which comprises of apparent horizon and is defined as a null space with vanishing expansion. For spatially flat FRW metric, the radius and temperature are defined as

$$\begin{aligned} R_{h}=r_{A}=\left( H^{2}+\frac{k}{a^{2}}\right) ^{-\frac{1}{2}}, \quad T_{A}=\frac{1}{2\pi r_{A}}\left( 1-\frac{{\dot{r}}_{A}}{2H r_{A}}\right) .\nonumber \\ \end{aligned}$$
(24)

Substituting the value of area at apparent horizon in Eq. (23) and taking the derivative, we get

$$\begin{aligned} {\dot{S}}_{A}=2\pi \phi {\dot{\phi }}r^{2}_{A}+2 \pi \phi ^{2}r_{A}{\dot{r}}_{A}, \end{aligned}$$
(25)

which leads to

$$\begin{aligned} T_{A}{\dot{S}}_{in}=\frac{4\pi }{3}R^{2}_{h}[3(\rho _{eff }+ p_{eff }){\dot{R}}_{h}+R_{h}{\dot{\rho }}]. \end{aligned}$$
(26)

By re-arranging above equation, we get

$$\begin{aligned} {\dot{S}}_{in}=\frac{16\pi ^{2}H R^{4}_{h}}{2HR_{H}-{\dot{r}}_{A}}((\rho _{eff } +p_{eff })({\dot{R}}_{h}-H R_{{h}})). \end{aligned}$$
(27)

The radius at apparent horizon in the form of \(\rho _{eff }\) can be defined as

$$\begin{aligned} r_{A}=\left( \frac{8\pi }{3}\rho _{eff }\right) ^{-\frac{1}{2}}. \end{aligned}$$
(28)

Using the derivative of Eq. (28) into Eq. (27), the entropy of fluid turns out to be

$$\begin{aligned} {\dot{S}}_{in}= & {} -\frac{16\pi ^{2}H R^{2}_{h}}{2H(\frac{8\pi }{3}\rho _{eff })^{-\frac{1}{2}}+ \frac{1}{2}(\frac{8\pi }{3})^{-\frac{1}{2}} (\rho _{eff })^{-\frac{3}{2}}{\dot{\rho }}_{eff }} \times \left[ (\rho _{eff }+p_{eff })\phantom {\frac{8\pi }{3}}\right. \\&\left. \times \left\{ \frac{1}{2} \left( \frac{8\pi }{3}\right) (\rho _{eff })^{-\frac{1}{2}} (\rho _{eff })^{-\frac{3}{2}}{\dot{\rho }}_{eff }+ H\left( \frac{8\pi }{3}H\rho _{eff }\right) ^{-\frac{1}{2}}\right\} \right] . \end{aligned}$$

After simplification, we get

$$\begin{aligned} {\dot{S}}_{in}= & {} -\frac{16\pi ^{2}H(\frac{8\pi }{3}\rho _{eff })^{-2}}{2H+\frac{1}{2}(\rho _{eff })^{-1}{\dot{\rho }}_{eff }}\nonumber \\&\times \left[ (\rho _{eff }+p_{eff } )\left( \frac{1}{2}(\rho _{eff })^{-1}{\dot{\rho }}_{eff }+H\right) \right] . \end{aligned}$$
(29)

Now we would like to check the validity of the GSLT of the system which is enclosed by apparent horizon. Hence, the total entropy turns out to be

$$\begin{aligned} {\dot{S}}_{Atot}= & {} 2\pi {\dot{\phi }}r^{2}_{A}+2\pi \phi ^{2}{\dot{r}}_{A}r_{A}-\frac{16\pi ^{2}H(\frac{8\pi }{3}\rho _{eff })^{-2}}{2H+\frac{1}{2}(\rho _{eff })^{-1}\dot{\rho }_{eff }}\\&\times \left[ (\rho _{eff }+p_{eff }) \left( \frac{1}{2}(\rho _{eff })^{-1}{\dot{\rho }}_{eff }+H\right) \right] . \end{aligned}$$

By invoking the values of \(\rho _{eff }\) and \({\dot{\rho }}_{eff }\) in above equation, we get

$$\begin{aligned} {\dot{S}}_{Atot}= & {} 2\phi {\dot{\phi }}\left( \frac{8\pi }{3}\rho _{eff }\right) ^{-1}\\&+2\pi \phi ^{2}\left[ \left( \frac{8\pi }{3}\rho _{eff }\right) ^{-\frac{1}{2}} \left( -\frac{1}{2}\left( \frac{8\pi }{3}\rho _{eff } \right) ^{-\frac{1}{2}}(\rho _{eff })^{-1}{\dot{\rho }}_{eff } \right) \right] \\&-\frac{16\pi ^{2}H\left( \frac{8\pi }{3}\frac{1}{\phi }(\rho +\rho _{{de}}) \right) ^{-2}}{2H+\frac{1}{2}\left( \frac{1}{\phi } (\rho +\rho _{de})\right) ^{-1}\left( -\frac{{\dot{\phi }}}{\phi }^{2} (\rho +\rho _{de})+\frac{1}{\phi } ({\dot{\rho }}+\dot{\rho _{de}})\right) }\\&\times \left[ \left\{ \frac{1}{\phi }(\rho +\rho _{de}+p+p_{de})\right\} \left( \frac{1}{2}\left( \frac{1}{\phi }(\rho +\rho _{de})\right) \right) ^{-1}\right. \\&\left. \times \left\{ \left( -\frac{{\dot{\phi }}}{\phi ^{2}}( \rho +\rho _{de})+\frac{1}{\phi }({\dot{\rho }} +{\dot{\rho }}_{de}+H)\right) \right\} \right] . \end{aligned}$$

The derivatives of Eqs. (16)–(18) become

$$\begin{aligned} {\dot{\rho }}= & {} \frac{-3(1+\omega )a^{-1-3(1+\omega )}\rho _{*}\phi {\dot{a}}}{\sqrt{\nu +8\pi \phi ^{2}}}-\frac{8\pi a^{-3(1+\omega )}\rho _{*}\phi ^{2}{\dot{\phi }}}{(\nu +8\pi \phi ^{2})^{\frac{3}{2}}}\nonumber \\&+\frac{a^{-3(1+\omega )}\rho _{*}{\dot{\phi }}}{\sqrt{\nu +8\pi \phi ^{2}}},\end{aligned}$$
(30)
$$\begin{aligned} {\dot{\rho }}_{de}= & {} \frac{48\phi ^{3}{\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})^{2}}+ \frac{(\nu +4(2-3\lambda )\pi )\phi ^{3}{\dot{\phi }}^{2}}{2\lambda (\nu +8\pi \phi ^{2})} -\frac{6H\phi {\dot{\phi }}^{2}}{\nu +8\pi \phi ^{2}}\nonumber \\&-\frac{3H\phi ^{2}\ddot{\phi }}{\nu +8\pi \phi ^{2}}, \end{aligned}$$
(31)
$$\begin{aligned} {\dot{p}}_{de}= & {} \frac{\phi }{2\lambda }\frac{(1+2\lambda )\nu +4\pi (2-3\lambda )\phi ^{2}{\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})^{2}}\nonumber \\&+\frac{\phi ^{2}}{\nu +8\pi \phi ^{2}}(2H\dot{\phi +\ddot{\phi }}). \end{aligned}$$
(32)

Using Eqs. (30)–(32), GSLT takes the form

$$\begin{aligned} {\dot{S}}_{Atot}= & {} 2\pi \phi {\dot{\phi }} \left[ \frac{8\pi }{3\phi }\left\{ \frac{\rho _{*}}{a^{3(1+\omega )}} \frac{\phi }{\sqrt{\nu +8\pi \phi ^{2}}}- \frac{3\phi ^{2}}{\nu +8\pi \phi ^{2}}H{\dot{\phi }}+\frac{\phi {\dot{\phi }}^{2}}{2\lambda }\times \left( \frac{\nu +4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\right) \right\} \right] ^{-1}\\&-\pi \phi ^{2}\left( \frac{8\pi }{3}\right) ^{-1} \left[ \frac{{\dot{\phi }}^{2}}{\phi }\left\{ \frac{\rho _{*}}{a^{3(1+\omega )}}\frac{\phi }{\sqrt{\nu +8\pi \phi ^{2}}}-\frac{3\phi ^{2}}{\nu +8\pi \phi ^{2}}H{\dot{\phi }}+ \frac{\phi }{2\lambda }\left( \frac{\nu +4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\right) \right\} \right] ^{-2}\\&\times \left[ -\frac{{\dot{\phi }}}{\phi }^{2}\left\{ \frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}+\frac{\rho }{a^{3(1+\omega )}\frac{\phi }{\sqrt{\nu +8\pi ^{2}}}} +\frac{\phi {\dot{\phi }}^{2}}{2\lambda }\frac{\nu +4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\right\} +\frac{1}{\phi } \left\{ \frac{8\pi a^{-3(1+\omega )}\rho _{*}\phi ^{2}{\dot{\phi }}}{(\nu +8\pi \phi ^{2})^{\frac{3}{2}}}\right. \right. \\&-\frac{3(1+\omega )a^{-1-3(1+\omega )\rho _{*}}\phi {\dot{a}}}{\sqrt{\nu +8\pi \phi ^{2}}}+\frac{(\nu +4\pi (2-3\lambda )\phi ^{3})}{2\lambda ( \nu +8\pi \phi ^{2})}{\dot{\phi }}^{2} +\frac{a^{-3(1+\omega )} \rho _{*}{\dot{\phi }}}{\sqrt{\nu +8\pi \phi ^{2}}} \left. \left. -\frac{6H\phi {\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2}) -\frac{3H\phi ^{2}\ddot{\phi }}{\nu +8\pi \phi ^{2}}}+ \frac{48\pi \phi ^{3}{\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})^{2}}\right\} \right] \\&+\frac{1}{\phi } \left( -\frac{8\pi a^{-3(1+\omega )}\rho _{*}\phi ^{2}{\dot{\phi }}}{(\nu +8\pi \phi ^{2})^{\frac{3}{2}}}\right. -\frac{3(1+\omega )a^{-1-3(1+\omega )\rho _{*}}\phi {\dot{a}}}{\sqrt{\nu +8\pi \phi ^{2}}}+ \frac{(\nu +4\pi (2-3\lambda )\phi ^{3})}{2\lambda ( \nu +8\pi \phi ^{2})}{\dot{\phi }}^{2} +\frac{a^{-3(1+\omega )} \rho _{*}{\dot{\phi }}}{\sqrt{\nu +8\pi \phi ^{2}}}+ \frac{48\pi \phi ^{3}{\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})^{2}}\\&\left. \left. -\frac{6H\phi {\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})- \frac{3H\phi ^{2}\ddot{\phi }}{\nu +8\pi \phi ^{2}}}\right) \right) \left[ \frac{1}{\phi }\left( \frac{\rho _{*}}{a^{3(1+\omega )}} \frac{\phi }{\sqrt{\nu +8\pi \phi ^{2}}}\right. \right. -\frac{3\phi ^{2}}{\nu +8\pi \phi ^{2}}H{\dot{\phi }}\\&\left. +\frac{\phi }{2\lambda }\left( \frac{\nu +4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\right) {\dot{\phi }}^{2}+\frac{\phi ^{2}(2H{\dot{\phi }}+\ddot{\phi })}{\nu +8\pi \phi ^{2}}\right) \frac{1}{2}\left[ \frac{1}{\phi }\left( \frac{\rho _{*}\phi }{a^{3(1+\omega )} \sqrt{\nu +8\pi \phi ^{2}}}+\frac{\phi {\dot{\phi }}^{2}}{2\lambda } \left( \frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\right) \right) \right. \\&\left. -\frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}\right] ^{-1}\times \left[ -\frac{{\dot{\phi }}}{\phi }^{2}\left\{ \frac{\rho }{a^{3(1+\omega )}\frac{\phi }{ \sqrt{\nu +8\pi ^{2}}}}-\frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}\right. \right. \left. +\frac{\phi {\dot{\phi }}^{2}}{2\lambda }\frac{\nu +4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\right\} +\frac{1}{\phi }\\&\times \left\{ H+\left( \frac{-3(1+\omega )a^{-1-3(1+\omega ) \rho _{*}}\phi {\dot{a}}}{\sqrt{\nu +8\pi \phi ^{2}}}-\frac{8\pi a^{-3(1+\omega )}\rho _{*}\phi ^{2}{\dot{\phi }}}{(\nu +8\pi \phi ^{2})^{\frac{3}{2}}}\right. \right. +\frac{48\pi \phi ^{3}{\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})^{2}}+\frac{a^{-3(1+\omega )} \rho _{*}{\dot{\phi }}}{\sqrt{\nu +8\pi \phi ^{2}}}+ \frac{{\dot{\phi }}^{2}(\nu +4\pi (2-3\lambda )\phi ^{3})}{2\lambda ( \nu +8\pi \phi ^{2})}\\&\left. \left. \left. -\frac{6H\phi {\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2}) -\frac{3H\phi ^{2}\ddot{\phi }}{\nu +8\pi \phi ^{2}}}\right) \right\} \right] -\left[ {}-\frac{{\dot{\phi }}}{\phi }^{2}\left\{ \frac{\rho }{a^{3(1+\omega )}\frac{\phi }{ \sqrt{\nu +8\pi ^{2}}}}-\frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}\right. \right. \left. +\frac{\phi {\dot{\phi }}^{2}}{2\lambda }\frac{\nu +4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\right\} \\&\left. \times \frac{16\pi ^{2}H\left\{ \frac{8\pi }{3\phi } \left( \frac{\rho _{*}}{a^{3(1+\omega )}}\frac{\phi }{\sqrt{\nu +8\pi \phi ^{2}}}- \frac{3\phi ^{2}}{\nu +8\pi \phi ^{2}}H{\dot{\phi }}+\frac{\phi }{2\lambda } \left( \frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\right) {\dot{\phi }}^{2}\right) \right\} ^{-2}}{2H+\frac{1}{2}\left\{ \frac{1}{\phi }(\frac{\rho _{*}}{a^{3(1+\omega )}} \frac{\phi }{\sqrt{\nu +8\pi \phi ^{2}}}- \frac{3\phi ^{2}}{\nu +8\pi \phi ^{2}}H{\dot{\phi }}+ \frac{\phi }{2\lambda }\left( \frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{ (\nu +8\pi \phi ^{2})^{2}}\right) {\dot{\phi }}^{2})\right\} ^{-1}}\right] . \end{aligned}$$

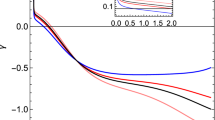
It would be interesting to study power-law solutions in this modified gravity that are indicated by various eras of cosmic evolution. These solutions are very helpful to clarify cosmic evolution, with the help of different epochs like dark energy, matter and radiation dominated eras. For this model, scale factor is \(\phi =\phi _{0}t^{m}\), \(a=a_{0}t^{n}\), where m, n are constants with \(n>1\). In the present scenario, analysis of GSLT depend on the different cosmological parameters. So, we take different values of cosmological parameters to discuss GSLT as \(\lambda =1.5,~a_0=1,~n=4,~\omega =0.3,~\phi _0=1,~\nu =100\) in Fig. 1. It is observed from this figure that GSLT holds for \(m =1\) because \({\dot{S}}_{Atot}\ge 0\), while does not remain valid for \(m=2\) and \(m=3\) because \({\dot{S}}_{Atot}>0\).

Fig. 1
figure 1

Plots of \({\dot{S}}_{Atot}\) versus t for the values \(\lambda =1.5,~a_0=1,~n=4,~\omega =0.3,~\phi _0=1,~\nu =100\). The red, green and blue lines correspond to parameter \(m=1,~2,~3\), respectively

Full size image

3.2 Event horizon

In this subsection, we study GSLT at event horizon which can be written as

$$\begin{aligned} {\dot{S}}_{tot}={\dot{S}}_{E}+{\dot{S}}_{in}. \end{aligned}$$
(33)

The radius of event horizon is defined as

$$\begin{aligned} R_{E}=a(t)\int _{t}^{\infty }\frac{d{\hat{t}}}{a{{\hat{t}}}}=a(t)\int _{a}^{t}\frac{d\acute{a}}{H\acute{a}^{2}}, \quad {\dot{R}}_{E}=HR_{E}-1.\nonumber \\ \end{aligned}$$
(34)

In this case, we utilized the following temperature

$$\begin{aligned} T_{in}=\frac{bH}{2\pi }=T_{h}, \end{aligned}$$
(35)

where b is a constant parameter. The time derivative of entropy at event horizon can be evaluated as

$$\begin{aligned} {\dot{S}}_{E}=\pi {\dot{\phi }} R^{2}_{E}+2\pi \phi {\dot{R}}_{E}R_{E}. \end{aligned}$$
(36)

Using relations (34) into Eq. (36), we get

$$\begin{aligned} {\dot{S}}_{E}=\pi ({\dot{\phi }}+2H \phi )\left( \frac{t}{n-1}\right) ^{2}-2\pi \phi \left( \frac{t}{n-1}\right) . \end{aligned}$$
(37)

Similarly, the entropy at inside the horizon in case of event is

$$\begin{aligned} {\dot{S}}_{in}=-\frac{6 \pi }{bH}(\rho _{eff }+p_{eff }). \end{aligned}$$
(38)

Thus \({\dot{S}}_{tot}\) can be obtained (for event horizon) from Eqs. (38), (37) and (33) as follows

$$\begin{aligned} {\dot{S}}_{tot}= & {} \pi ({\dot{\phi }}+2 H \phi )\bigg (\frac{t}{n-1}\bigg )^{2}-2\pi \phi \bigg (\frac{t}{n-1}\bigg )\\&-\frac{6\pi }{bH}\frac{1}{\phi }\bigg [\frac{\rho _{*}}{a^{3(1+\omega )}} \times \frac{\phi }{\sqrt{\nu +8\pi \phi ^{2}}}\\&-\frac{3\phi ^{2}}{(\nu +8\pi \phi ^{2})}H{\dot{\phi }}+\frac{\phi }{2\lambda } \frac{\nu +4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}{\dot{\phi }}^{2}\\&+\frac{\phi }{2\lambda }\frac{(1+2\lambda )+4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}{\dot{\phi }}^{2}\\&+\frac{\phi ^{2}}{\nu +8 \pi \phi ^{2}}\bigg (2H{\dot{\phi }}+\ddot{\phi }\bigg )\bigg ]. \end{aligned}$$
Fig. 2
figure 2

Plots of \({\dot{S}}_{Etot}\) versus t for the values \(\lambda =1.5,~a_0=1,~n=4,~\omega =0.3,~\phi _0=1,~\nu =100\). The red, green and blue lines correspond to parameter \(m=1,~2,~3\), respectively

Full size image

The plot of \({\dot{S}}_{tot}\) versus t at event horizon is shown in Fig. 2. The values of constant parameters are same as utilized in figure. It can be seen from Fig. 2 that all trajectories of \({\dot{S}}_{tot}\) are increasing function of time and remain positive. Hence, GSLT satisfied for the present system enclosed by event horizon.

4 Entropy corrections with event horizon

In GR, entropy area relation with motivation of quantum loop gravity leads to the curvature corrections in the Hilbert–Einstein action [65, 66]. In this section, we will discuss two types of corrections.

4.1 Logarithmic correction

Recently, logarithmic correction has studied for black hole in quantum gravity due to the fluctuation of thermal equilibrium [67,68,69]. Then, Sadjadi and Jamil [70] explored the GSLT for flat FRW metric with logarithmic correction. The logarithmic corrected entropy is expressed by the given relation

$$\begin{aligned} S_{LE}=\frac{A}{4G}+\alpha \frac{\ln A}{4G}+\beta \frac{4G}{A}+\gamma , \end{aligned}$$
(39)

where \(\alpha \), \(\beta \) and \(\gamma \) are dimensionless constants. Taking the derivative of above equation, we get

$$\begin{aligned} {\dot{S}}_{LE}=\frac{2\pi R_{E}{\dot{R}}_{E}}{G}\left( 1+\frac{\alpha G}{\pi R^{2}_{E}}-\frac{\beta G^{2}}{\pi ^{2} R^{4}}_{E}\right) . \end{aligned}$$
(40)

By following the same procedure, inserting Eqs. (40), (38) into (33), we get

$$\begin{aligned} {\dot{S}}_{tot}= & {} \frac{2\pi }{G}\left( \frac{t}{n-1}\right) \{HR_{E}-1\}\left[ \left( 1+\frac{\alpha G}{\pi R^{2}_{E}}-\frac{\beta G^{2}}{\pi ^{2}R^{4}}_{E}\right) \right] \nonumber \\&-\frac{6\pi }{bH}\left\{ \frac{1}{\phi }(\rho +\rho _{de}+p_{de})\right\} . \end{aligned}$$
(41)

Its illustrated form leads to

$$\begin{aligned} {\dot{S}}_{tot}= & {} \frac{2 \pi }{G}\left( -\frac{t}{n-1}\right) \left\{ \left( \frac{t}{n}\right) \left( \frac{t}{n-1}\right) -1\right\} \\&\times \left[ \left( 1+\frac{\alpha G}{\pi \left( \frac{t}{n-1}\right) ^{2}}- \frac{\beta G^{2}}{ \pi ^{2}\left( \frac{t}{n-1}\right) ^{4}}\right) \right] \\&-\frac{6\pi }{bH}\left[ \frac{1}{\phi }\left( \frac{\rho _{*}\phi }{a^{3(1+\omega )}\sqrt{\nu +8\pi \phi ^{2}}}\right. \right. \\&+\frac{\phi {\dot{\phi }}^{2}}{2\lambda } \frac{\nu +4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}-\frac{3\phi ^{2}H{\dot{\phi }}}{(\nu +8\pi \phi ^{2})}\\&\left. +\frac{\phi }{2\lambda }\frac{(1+2\lambda )+4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}{\dot{\phi }}^{2}\right. \\&\left. +\frac{\phi ^{2}}{\nu +8 \pi \phi ^{2}}(2H{\dot{\phi }}+\ddot{\phi })\right] . \end{aligned}$$
Fig. 3
figure 3

Plots of \({\dot{S}}_{LEtot}\) versus t for the values \(\lambda =1.5,~a_0=1,~n=4,~\omega =0.3,~\phi _0=1,~\nu =100\), \(\alpha =3.8,~\beta =3\). The red, green and blue lines correspond to parameter \(m=1,~2,~3\), respectively

Full size image

In order to observe the validity of GSLT for logarithmic correction at event horizon, we plot it in Fig. 3. We plot \({\dot{S}}_{tot}\) versus t by taking different values of \(\alpha \), \(\beta \) as \(\alpha =3.8,~\beta =3\) and using values of other parameters same. This figure shows that the trajectories of \({\dot{S}}_{tot}\) remains positive and exhibits the increasing behavior at the present as well as initial epoch while turn negative after some interval of time. Hence, GSLT holds at initial epoch for all cases of m while does not satisfy at later epoch.

4.2 Power law correction

Power law correction for event horizon can be defined as [71, 72]

$$\begin{aligned} S=\frac{A}{4G}\bigg [1-K_{\alpha }A^{1-\frac{\alpha }{2}}\bigg ], \end{aligned}$$
(42)

where

$$\begin{aligned} K_{\alpha }=\frac{\alpha (4\pi )^{\frac{\alpha }{2}-1}}{(4-\alpha )r_{c}^{2-\alpha }}, \end{aligned}$$
(43)

and \(r_{c}\) is the crossover scale and \(\alpha \) is dimensionless constant. The second term in (42), as a power-law correction to the entropy, has been appeared from the scalar field of the wave-functions between two excitation states. The higher the excitation state is the more significant than the correction term. The time rate of change of entropy for power-law correction is given as

$$\begin{aligned} {\dot{S}}_{PE}= & {} \frac{2\pi R_{E}{\dot{R}}_{E}}{G}\bigg [1-k_{\alpha }(4\pi )^{1-\frac{\alpha }{2}}\bigg (2-\frac{\alpha }{2}\bigg )R^{2-\alpha }_{E}\bigg ]. \end{aligned}$$
(44)

Using Eqs. (44), (38) into (33), we obtain

$$\begin{aligned} {\dot{S}}_{PEtot}= & {} \frac{2\pi }{G}\left( \frac{t}{n-1}\right) \left\{ \left( \frac{t}{n}\right) \left( \frac{t}{n-1}\right) -1\right\} \\&\times \left[ 1-k _{\alpha }(4\pi )^1-\frac{\alpha }{2}\left( 2-\frac{\alpha }{2}\right) R^{2-\alpha }_{E}\right] \\&-\frac{6\pi }{bH}\left[ \frac{1}{\phi }\left( \frac{\rho _{*}}{a^{3(1+\omega )}} \frac{\phi }{\sqrt{\nu +8\pi \phi ^{2}}}\right. \right. \\&+\frac{\phi {\dot{\phi }}^{2}}{2\lambda }\frac{(1+2\lambda )+4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\\&-\frac{3\phi ^{2}}{(\nu +8\pi \phi ^{2})}H{\dot{\phi }}+\frac{\phi }{2\lambda } \frac{\nu +4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}{\dot{\phi }}^{2}\\&\left. +\frac{\phi ^{2}(2H{\dot{\phi }}+\ddot{\phi })}{\nu +8 \pi \phi ^{2}}\right] . \end{aligned}$$
Fig. 4
figure 4

Plots of \({\dot{S}}_{PEtot}\) versus t for the values \(\lambda =1.5,~ a=1,~ n=4,~ \Omega =0.3,~ \phi =1,~ \nu =100\)

Full size image

The total rate of change of entropy for power law correction at event horizon verses t is shown in Fig. 4. It can be observed that \({\dot{S}}_{tot} \) shows increasing behavior for all values of m at early, present as well as later epoch. However, GSLT holds for all cases for \(t>3.2\).

5 Entropy corrections with apparent horizon

In this section, we investigate the validity of GSLT of the system by assuming entropy corrections on the apparent horizon.

5.1 Logarithmic correction

In case of apparent horizon, Eq. (39) implies

$$\begin{aligned} {\dot{S}}_{A}=\frac{2\pi R_{A}{\dot{R}}_{A}}{G}\left( 1+\frac{\alpha G}{\pi R^{2}_{A}}-\frac{\beta G^{2}}{\pi ^{2} R^{4}}_{A}\right) . \end{aligned}$$
(45)

By replacing the values of \(R_{A}\) and \({\dot{R}}_{A}\) in Eq. (45), we obtain

$$\begin{aligned} {\dot{S}}_{A}= & {} -\frac{(\frac{8\pi }{3}\rho _{eff })^{-1} (\rho _{eff })^{-1}(\rho _{eff })}{G}\nonumber \\&\times \left[ 1+\frac{\alpha G}{\pi (\frac{8 \pi }{3}\rho _{eff })^{2}}-\frac{\beta G^{2}}{\pi ^{2}(\frac{8 \pi }{3}\rho {eff })^{4}}\right] , \end{aligned}$$
(46)

which leads to

$$\begin{aligned}&{\dot{S}}_{tot}\\&\quad =-\frac{1}{G}\bigg [ -\pi \bigg (\frac{8\pi }{3}\bigg )^{-1} \bigg \{\frac{1}{\phi }\bigg (\frac{\rho _{*}}{a^{3(1+\omega )}}\frac{\phi }{\sqrt{\nu +8\pi \phi ^{2}}}\\&\qquad - \frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}+\frac{\phi {\dot{\phi }}^{2}}{2\lambda } \frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\bigg )\bigg \}\bigg ]^{-1}\\&\qquad -\bigg [-\frac{{\dot{\phi }}}{\phi }^{2}\bigg (\frac{\rho }{a^{3(1+\omega )}\frac{\phi }{ \sqrt{\nu +8\pi ^{2}}}}-\frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}\\&\qquad +\frac{\phi {\dot{\phi }}^{2}}{2\lambda }\frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\bigg )\bigg ]\times \pi \phi ^{2}\left( \frac{8\pi }{3}\right) ^{-1}\\&\qquad +\frac{1}{\phi } \times \bigg (\frac{-3(1+\omega )a^{-1-3(1+\omega )\rho _{*}}\phi {\dot{a}}}{\sqrt{\nu +8\pi \phi ^{2}}} +\frac{1}{\phi } \frac{-3(1+\omega )a^{-1-3(1-\omega )\rho _{*}}\phi {\dot{a}}}{\sqrt{\nu +8\pi \phi ^{2}}}\\&\qquad -\frac{8\pi a^{-3(1+\omega )}\rho _{*}\phi ^{2}}{(\nu +8\pi \phi ^{2})}^{\frac{2}{3}}+\frac{a^{-3(1+\omega )}\rho _{*}{\dot{\phi }}}{\sqrt{\nu +8\pi \phi ^{2}}}\bigg )\times \bigg [1+\alpha G\\&\qquad \times \left[ \frac{8\pi }{3\phi }\bigg (- \frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}+\frac{\rho _{*}\phi }{a^{3(1+\omega )}\sqrt{\nu +8\pi \phi ^{2}}}+\frac{\phi {\dot{\phi }}^{2}}{2\lambda }\frac{\nu +4 \pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\bigg )^{-2}\right. \\&\qquad \left. +\frac{\beta G^{2}}{\bigg (\frac{1}{\phi }(\frac{\rho _{*}}{a^{3(1+\omega )}}\frac{\phi }{\sqrt{\nu +8\pi \phi ^{2}}}- \frac{3\phi ^{2}}{\nu +8\pi \phi ^{2}}H{\dot{\phi }}+\frac{\phi }{2\lambda } (\frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}){\dot{\phi }}^{2})\bigg )^{4}}\right] \\&\qquad -\frac{16\pi ^{2}H\bigg (\frac{8\pi }{3\phi } (\frac{\rho _{*}}{a^{3(1+\omega )}}\frac{\phi }{\sqrt{\nu +8\pi \phi ^{2}}}- \frac{3\phi ^{2}}{\nu +8\pi \phi ^{2}}H{\dot{\phi }}+\frac{\phi }{2\lambda } (\frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}){\dot{\phi }}^{2})\bigg )^{-2}}{2H+\frac{1}{2}\bigg (\frac{1}{\phi }(\frac{\rho _{*}}{a^{3(1+\omega )}}\frac{\phi }{\sqrt{\nu +8\pi \phi ^{2}}}- \frac{3\phi ^{2}}{\nu +8\pi \phi ^{2}}H{\dot{\phi }}+ \frac{\phi }{2\lambda }(\frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}) {\dot{\phi }}^{2})\bigg )^{-1}}\\&\qquad \times \left( -\frac{{\dot{\phi }}}{\phi }^{2}\left( \frac{\rho }{a^{3(1+\omega )}\frac{\phi }{ \sqrt{\nu +8\pi ^{2}}}}-\frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}+ \frac{\phi {\dot{\phi }}^{2}}{2\lambda }\frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\right. \right) \\&\qquad +\frac{1}{\phi }\bigg (\frac{-3(1+\omega )a^{-1-3(1+\omega ) \rho _{*}}\phi {\dot{a}}}{\sqrt{\nu +8\pi \phi ^{2}}}-\frac{8\pi a^{-3(1+\omega )}\rho _{*}\phi ^{2}{\dot{\phi }}}{(\nu +8\pi \phi ^{2})^{\frac{3}{2}}}+\frac{a^{-3(1+\omega )} \rho _{*}{\dot{\phi }}}{\sqrt{\nu +8\pi \phi ^{2}}}\\&\qquad +\frac{48\pi \phi ^{3}{\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})^{2}}+ \frac{(\nu +4\pi (2-3\lambda )\phi ^{3})}{2\lambda ( \nu +8\pi \phi ^{2})}{\dot{\phi }}^{2}-\frac{6H \phi {\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})- \frac{3H\phi ^{2}\ddot{\phi }}{\nu +8\pi \phi ^{2}}})\bigg )\\&\qquad \times \bigg [\frac{1}{\phi }\bigg (\frac{\rho _{*}}{a^{3 (1+\omega )}}\frac{\phi }{\sqrt{\nu +8\pi \phi ^{2}}}- \frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}+ \frac{\phi {\dot{\phi }}^{2}}{2\lambda }\frac{\nu +4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\\&\qquad +\frac{\phi ^{2}(2H{\dot{\phi }}+\ddot{\phi })}{\nu +8\pi \phi ^{2}}\bigg ) \times \frac{1}{2}\bigg (\frac{1}{\phi }(\frac{\rho _{*}\phi }{a^{3(1+\omega )} \sqrt{\nu +8\pi \phi ^{2}}}+\frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\\&\qquad \times \frac{\phi {\dot{\phi }}^{2}}{2\lambda }- \frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}} \bigg )^{-1}\bigg [-\frac{{\dot{\phi }}}{\phi }^{2} \bigg \{\frac{\phi }{2\lambda }\frac{\nu +4\pi (2-3 \lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}{\dot{\phi }}^{2}- \frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}\\&\qquad +\frac{\rho }{a^{3(1+\omega )}\frac{\phi }{ \sqrt{\nu +8\pi ^{2}}}}\bigg \}+\frac{1}{\phi } \bigg (\frac{-3(1+\omega )a^{-1-3(1+\omega )\rho _{*}} \phi {\dot{a}}}{\sqrt{\nu +8\pi \phi ^{2}}}-\frac{8\pi a^{-3(1+\omega )}\rho _{*}\phi ^{2}{\dot{\phi }}}{(\nu +8\pi \phi ^{2})^{\frac{3}{2}}}\\&\qquad +\frac{a^{-3(1+\omega )}\rho _{*}{\dot{\phi }}}{\sqrt{\nu +8\pi \phi ^{2}}}+ \frac{48\pi \phi ^{3}{\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})^{2}}- \frac{6H\phi {\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})- \frac{3H\phi ^{2}\ddot{\phi }}{\nu +8\pi \phi ^{2}}})\bigg )+H\bigg )\bigg ]. \end{aligned}$$
Fig. 5
figure 5

Plots of \({\dot{S}}_{LAtot}\) versus t for the values \(\lambda =1.5,~a_0=1,~n=4,~\omega =0.3,~\phi _0=1,~\nu =100\), \(\alpha =3.8,~\beta =3\). The red, green and blue lines correspond to parameter \(m=1,~2,~3\), respectively

Full size image

The display of total rate of change of entropy for logarithmic correction on apparent horizon versus cosmic time is shown in Fig. 5. All constant parameters are same as utilized in previous plots. It can be observed that \({\dot{S}}_{tot}\) shows increasing behavior and remains positive for all cases of m. This exhibits its validity for the present scenario.

5.2 Power law correction

The rate of change of power law correction at apparent horizon is given by

$$\begin{aligned}&{\dot{S}}_{PEtot}\nonumber \\&\quad =-\frac{1}{G}\bigg [ -\pi \bigg (\frac{8\pi }{3}\bigg )^{-1}\bigg \{\frac{1}{\phi }\bigg (\frac{\rho _{*}}{a^{3(1+\omega )}}\frac{\phi }{\sqrt{\nu +8\pi \phi ^{2}}}- \frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}\nonumber \\&\qquad +\frac{\phi {\dot{\phi }}^{2}}{2\lambda }\frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\bigg )\bigg \}\bigg ]^{-1}- \bigg [-\frac{{\dot{\phi }}}{\phi }^{2}\bigg (\frac{\rho }{a^{3(1+\omega )}\frac{\phi }{ \sqrt{\nu +8\pi ^{2}}}}\nonumber \\&\qquad -\frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}+ \frac{\phi {\dot{\phi }}^{2}}{2\lambda }\frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\bigg )\bigg ]\times \pi \phi ^{2}\left( \frac{8\pi }{3}\right) ^{-1}+\frac{1}{\phi } \nonumber \\&\qquad \times \bigg (\frac{-3(1+\omega )a^{-1-3(1+\omega )\rho _{*}}\phi {\dot{a}}}{\sqrt{\nu +8\pi \phi ^{2}}}+\frac{1}{\phi } \frac{-3(1+\omega )a^{-1-3(1-\omega )\rho _{*}}\phi {\dot{a}}}{\sqrt{\nu +8\pi \phi ^{2}}}\nonumber \\&\qquad \left. -\frac{8\pi a^{-3(1+\omega )}\rho _{*}\phi ^{2}}{(\nu +8\pi \phi ^{2}}\right) ^{\frac{2}{3}}+\frac{a^{-3(1+\omega )}\rho _{*}{\dot{\phi }}}{\sqrt{\nu +8\pi \phi ^{2}}}\bigg )\nonumber \\&\qquad \times \bigg [1-K_{\alpha }(4\pi )^{1-\frac{\alpha }{2}}\left( 2-\frac{\alpha }{2}\right) \nonumber \\&\qquad \times \bigg \{\frac{8\pi }{3}\bigg (\frac{\rho }{a^{3(1+\omega )} \frac{\phi }{\sqrt{\nu +8\pi ^{2}}}}-\frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}\nonumber \\&\qquad +\frac{\phi {\dot{\phi }}^{2}}{2\lambda }\frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\bigg )\bigg \}^{2-\alpha }\bigg ]\nonumber \\&\qquad -\frac{16\pi ^{2}H\bigg [\frac{8\pi }{3\phi } (\frac{\rho _{*}}{a^{3(1+\omega )}}\frac{\phi }{\sqrt{\nu +8\pi \phi ^{2}}}- \frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}+ \frac{\phi {\dot{\phi }}^{2}}{2\lambda }(\frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}))\bigg ]^{-2}}{2H+\frac{1}{2} \bigg \{\frac{1}{\phi }\bigg (\frac{\rho _{*}\phi }{a^{3(1+\omega )} \sqrt{\nu +8\pi \phi ^{2}}}-\frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}+\frac{\phi {\dot{\phi }}^{2}}{2\lambda } \frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\bigg ) \bigg \}^{-1}}\nonumber \\&\qquad \times \bigg [-\frac{{\dot{\phi }}}{\phi }^{2} \bigg (\frac{\rho }{a^{3(1+\omega )}\frac{\phi }{ \sqrt{\nu +8\pi ^{2}}}}-\frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}\nonumber \\&\qquad +\frac{\phi {\dot{\phi }}^{2}}{2\lambda }\frac{\nu +4 \pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\bigg ) \bigg ]\nonumber \\&\qquad +\frac{1}{\phi }\bigg \{\frac{-3(1+\omega )a^{-1-3(1+\omega ) \rho _{*}}\phi {\dot{a}}}{\sqrt{\nu +8\pi \phi ^{2}}}-\frac{8\pi a^{-3(1+\omega )}\rho _{*}\phi ^{2}{\dot{\phi }}}{(\nu +8\pi \phi ^{2})^{\frac{3}{2}}}\nonumber \\&\qquad +\frac{a^{-3(1+\omega )}\rho _{*}{\dot{\phi }}}{\sqrt{\nu +8 \pi \phi ^{2}}}+\frac{48\pi \phi ^{3}{\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})^{2}}+ \frac{(\nu +4\pi (2-3\lambda )\phi ^{3})}{2\lambda ( \nu +8\pi \phi ^{2})}{\dot{\phi }}^{2}\nonumber \\&\qquad \left. \left. -\frac{6H\phi {\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})-\frac{3H\phi ^{2}\ddot{\phi }}{\nu +8\pi \phi ^{2}}}\right) \right\} \bigg [\frac{1}{\phi }\bigg (\frac{\rho _{*}\phi }{a^{3(1+\omega )} \sqrt{\nu +8\pi \phi ^{2}}}\nonumber \\&\qquad -\frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}+ \frac{\phi {\dot{\phi }}^{2}}{2\lambda }\left( \frac{\nu +4\pi (2-3\lambda ) \phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}\right) \nonumber \\&\qquad +\frac{\phi ^{2}(2H{\dot{\phi }}+\ddot{\phi })}{\nu +8\pi \phi ^{2}}\bigg ) \times \frac{1}{2}\left\{ \frac{1}{\phi }\left( \frac{\rho _{*}\phi }{a^{3(1+\omega )}\sqrt{\nu +8\pi \phi ^{2}}}\right. \right. \nonumber \\&\qquad -\frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}+ \frac{\phi {\dot{\phi }}^{2}}{2\lambda }\frac{\nu +4\pi (2-3\lambda )\phi ^{2}}{(\nu +8\pi \phi ^{2})^{2}}) \bigg \}^{-1}\nonumber \\&\qquad \times \bigg \{-\frac{{\dot{\phi }}}{\phi }^{2}\left( \frac{\rho \phi }{a^{3(1+\omega ) \sqrt{\nu +8\pi ^{2}}}}\right. -\frac{3\phi ^{2}H{\dot{\phi }}}{\nu +8\pi \phi ^{2}}+ \frac{\phi }{2\lambda }\nonumber \\&\qquad \times \frac{\nu +4\pi (2-3\lambda )\phi ^{2}{\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})^{2}}\bigg \}\nonumber \\&\qquad +\frac{1}{\phi }\bigg (\frac{-3(1+\omega )a^{-1-3(1+\omega ) \rho _{*}}\phi {\dot{a}}}{\sqrt{\nu +8\pi \phi ^{2}}}+\frac{48 \pi \phi ^{3}{\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})^{2}}\nonumber \\&\qquad -\frac{8\pi a^{-3(1+\omega )}\rho _{*}\phi ^{2}{\dot{\phi }}}{(\nu +8\pi \phi ^{2})^{\frac{3}{2}}}+\frac{a^{-3(1+\omega )} \rho _{*}{\dot{\phi }}}{\sqrt{\nu +8\pi \phi ^{2}}}-\frac{6H\phi {\dot{\phi }}^{2}}{(\nu +8\pi \phi ^{2})- \frac{3H\phi ^{2}\ddot{\phi }}{\nu +8\pi \phi ^{2}}}\nonumber \\&\qquad +\frac{(\nu +4\pi (2-3\lambda )\phi ^{3})}{2\lambda ( \nu +8\pi \phi ^{2})}{\dot{\phi }}^{2}\bigg )\bigg )+H\bigg \}\bigg ]. \end{aligned}$$
(47)
Fig. 6
figure 6

Plots of \({\dot{S}}_{PAtot}\) versus t for the values \(\lambda =1.5,~ a=1,~ n=4, ~\Omega =0.3,~ \phi =1,~ \nu =100\)

Full size image

The plot of GSLT for the power law correction on the apparent horizon is shown in Fig. 6. It is observed that the trajectories of \({\dot{S}}_{tot}\) is increasing for all values of m and remain positive. Thus GSLT is satisfied for the present scenario on the apparent horizon.

6 Conclusion

We have investigated the thermodynamics in the frame-work of recently proposed theory called modified Brans–Dicke gravity [58]. For this purpose, we have developed the GSLT by assuming usual entropy as well as its corrected forms (logarithmic and power law corrected) on the apparent and event horizons. In order to analyzed the clear view of thermodynamic law, we have assumed the power law forms of scalar field and scale factor is being assumed. We have evaluated the results graphically and summarized them in the following.

  • In phase one, we have analyzed GSLT on the apparent as well as event horizon by assuming usual entropy. In this case, we have observed that GSLT holds for \(m =1\) because \({\dot{S}}_{Atot}\ge 0\), while does not remain valid for \(m=2\) and \(m=3\) because \({\dot{S}}_{Atot}>0\) (Fig. 1). The plot of \({\dot{S}}_{tot}\) versus t at event horizon has shown in Fig. 2. It has been seen from Fig. 2 that all trajectories of \({\dot{S}}_{tot}\) are increasing function of time and remain positive. Hence, GSLT satisfied for the present system enclosed by event horizon.

  • In second phase, the validity of GSLT on the apparent as well as event horizon has been analyzed by assuming logarithmic entropy correction. It has been observed from Fig. 3 that the trajectories of \({\dot{S}}_{tot}\) (on the event horizon) remains positive and exhibits the increasing behavior at the present as well as initial epoch while turn negative after some interval of time. Hence, GSLT holds at initial epoch for all cases of m while does not satisfy at later epoch. The display of total rate of change of entropy for logarithmic correction on the apparent horizon versus cosmic time is shown in Fig. 5. It can be observed that \({\dot{S}}_{tot}\) shows increasing behavior and remains positive for all cases of m. This exhibits its validity for the present scenario.

  • In third phase, the validity of GSLT on the event as well as apparent horizon has been analyzed by assuming power law entropy correction. The total rate of change of entropy for power law correction at event horizon verses t is shown in Fig. 4. It has observed that \({\dot{S}}_{tot}\) shows increasing behavior for all values of m at early, present as well as later epoch. However, GSLT holds for all cases for \(t>3.2\). The plot of GSLT for the power law correction on the apparent horizon is shown in Fig. 6. It has observed that the trajectories of \({\dot{S}}_{tot}\) is increasing for all values of m and remain positive. Thus GSLT is satisfied for this scenario on the apparent horizon.