1 Introduction

According to cosmological observations, the universe has entered a stage of an accelerated expansion with a redshift smaller than 1 [1, 2]. Since all usual types of matter with positive pressure decelerate the expansion of the universe, a sector with negative pressure named dark energy was suggested to account for the invisible fuel that accelerates the expansion rate of the current universe [3, 4].

The simplest cosmological model of dark energy is the so-called Lambda cold dark matter (\(\Lambda \)CDM) model, in which vacuum energy plays the role of dark energy. Although \(\Lambda \)CDM model provides an excellent fit to a wide range of astronomical data so far, such a model in fact is theoretically problematic because of two cosmological constant problems, the fine tuning problem, concerning why is the observational vacuum density is so small compared to the theoretical one, and the coincidence problem which asks why the observational vacuum density is coincidentally comparable with the critical density at the present epoch in the long history of the universe. In order to alleviate the latter, various ideas as regards evolving and spatially homogeneous scalar fields, including quintessence [5], phantom [6], dilatonic [7], tachyon [8] and quintom [9] models, etc. were suggested to take the vacuum energy’s place. In these models, the resolution of the coincidence problem typically leads to a fine tuning of the model parameters.

Since experimental evidence of cosmology-specific scalar particles has not been discovered yet, there is no reason to exclude the possibility of some other high form field to be dark energy. Indeed, the three-form cosmology proposed in [10, 11] could be a good alternative to scalar cosmology, because such a high form field not only respects the Friedmann–Robertson–Walker (FRW) symmetry naturally but also can accelerate the expansion rate of the current universe without a slow-roll condition. Moreover, some interesting results, e.g. three-forms with simple potentials, lead to models of inflation with potentially large non-Gaussian signatures [12], etc., in three-form cosmology.

The coincidence problem mentioned above is just that the amount of dark matter is comparable to that of dark energy in the present universe, so it is natural to consider an interaction between these two components. As was pointed out in Ref. [13], in comparison to coupled scalar dark energy model [14], some new features appear in coupled three-form dark energy model, including one that the stress tensor is modified by the interaction between two dark sectors, hence it is problematic to consider a coupled three-form dark energy model in a phenomenological way [15], and one needs to construct it in a Lagrangian formalism. Different from modeling dark matter as point particles [13], we follow the thread of describing the interaction between dark energy and dark matter from a fundamental field theory point of view [16] and consider dark matter to be a Dirac spinor field.

The contents of this paper are as follows. In Sect. 2, we present a type of Lagrangians describing the interaction between a three-form field and a Dirac spinor field in curved space-time and then derive the field equations from such Lagrangians. In Sect. 3, we consider these field equations in a FRW space-time by assuming the effective mass of dark matter as a power-law function of the three-form field and setting the potential of dark energy to be zero. In Sect. 4, we carry out a simple likelihood analysis of the model with the use of 580 SN Ia data points from recently released Union2.1 compilation [17] and BAO data from the WiggleZ Survey [18], SDSS DR7 Galaxy sample [19] and 6dF Galaxy Survey datasets [20], together with CMB data from WMAP7 observations [21]. In the last section, we present a brief conclusion with this paper.

2 A type of field theories of three-form and Dirac spinor in curved space-time

This section involves some concepts that are used to include fermionic sources in the Einstein theory of gravitation; for a more detailed analysis the reader is referred to [22,23,24,25].

A type of Lagrangians which describe the interaction between a canonical three-form field \(A_{\alpha \beta \gamma }\) with a potential \(V(A^{2})\) and a Dirac spinor field \(\psi \) in a curved space-time can be constructed as

$$\begin{aligned} \mathcal {L}_{m}= & {} -\frac{1}{48}F^{2}-V(A^{2})+\frac{i}{2} [\bar{\psi }\Gamma ^{\mu }D_{\mu }\psi -D_{\mu }\bar{\psi }\Gamma ^{\mu }\psi ]\nonumber \\&-\,M(A^{2})\bar{\psi }\psi \end{aligned}$$
(1)

where \(F=\mathrm{d}A\) represents the field strength tensor and \(D_{\mu }\) is the covariant derivative of the spinor, which satisfies

$$\begin{aligned} D_{\mu }\psi= & {} \partial _{\mu }\psi +\Omega _{\mu }\psi ,\end{aligned}$$
(2)
$$\begin{aligned} D_{\mu }\bar{\psi }= & {} \partial _{\mu }\bar{\psi }-\bar{\psi }\Omega _{\mu }. \end{aligned}$$
(3)

The \(\Omega _{\mu }=\frac{1}{2}\omega _{\mu a b}\Sigma ^{a b}\) appearing in (2), (3) denotes the spin connection which is constituted by the Ricci spin coefficients \(\omega _{\mu a b}=e_{a}^{\nu }\nabla _{\mu }e_{\nu b}\) and the generators of the spinor representation of the Lorentz group \(\Sigma ^{a b}=\frac{1}{4}[\gamma ^{a},\gamma ^{b}]\). \(\gamma ^{a}\) and \(\Gamma ^{\mu }=e_{a}^{\mu }\gamma ^{a}\) are the Dirac–Pauli matrices and their curved space-time counterparts, respectively. Following the general covariance principle, the tetrad \(e_{a}^{\nu }\) is related to the metric by \(g^{\mu \nu }=e_{a}^{\mu }e_{b}^{\nu }\eta ^{a b}\) with \(\eta ^{a b}=\mathrm{diag}(1,-1,-1,-1)\). In such Lagrangians, the coupling between two fields is demonstrated by the function \(M(A^{2})\), which is the effective mass of dark matter.

One now can obtain the field equations from the total action,

$$\begin{aligned} S[A,g,\psi ,\bar{\psi }]=\int \mathcal {L}\sqrt{-g}\mathrm{d}^{4}x \end{aligned}$$
(4)

where \(\mathcal {L}=\mathcal {L}_{g}+\mathcal {L}_{m}=\frac{R}{2\kappa ^{2}}+\mathcal {L}_{m}\) is the Lagrangian including gravity, R denotes the Ricci scalar and \(\kappa =\sqrt{8\pi G}\) is the inverse of the reduced Planck mass.

By varying the total action with respect to the three-form field and the Dirac field, we have the following equations of motion, which are quite similar to those of electrodynamics:

$$\begin{aligned}&\nabla _{\alpha }F^{\alpha \mu \nu \rho } = 12 \left( \frac{\mathrm{d}V}{\mathrm{d}A^{2}}+\frac{\mathrm{d}M}{\mathrm{d}A^{2}}{\bar{\psi }\psi }\right) A^{\mu \nu \rho } ,\end{aligned}$$
(5)
$$\begin{aligned}&iD_{\alpha }\bar{\psi }\Gamma ^{\alpha }+M\bar{\psi } = 0 ,\end{aligned}$$
(6)
$$\begin{aligned}&-\,i\Gamma ^{\alpha }D_{\alpha }\psi +M\psi = 0. \end{aligned}$$
(7)

The variation of the action with respect to the tetrad leads to the Einstein field equation,

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R=-\kappa ^{2}T_{\mu \nu } \end{aligned}$$
(8)

where the total energy-momentum tensor for two fields is given by

$$\begin{aligned} T_{\mu \nu }= & {} -\frac{1}{6}F_{\mu \alpha \beta \gamma }F_{\nu }^{\alpha \beta \gamma } -6\left( \frac{\mathrm{d}V}{\mathrm{d}A^{2}}+\frac{\mathrm{d}M}{\mathrm{d}A^{2}}\bar{\psi }\psi \right) A_{\mu }^{\alpha \beta }A_{\nu \alpha \beta }\nonumber \\&+\,\frac{1}{2}Re[\bar{\psi }i(\Gamma _{\mu }D_{\nu }+\Gamma _{\nu }D_{\mu })\psi ]-g_{\mu \nu }\mathcal {L}_{m}. \end{aligned}$$
(9)

In the end of this section, we show the dual description of the above three-form field theory to place this field theory in a context more familiar to most of the community, such dual description has the following action:

$$\begin{aligned} \widetilde{S}[\widetilde{A},g,\psi ,\bar{\psi }]=\int \mathcal {\widetilde{L}}\sqrt{-g}\mathrm{d}^{4}x \end{aligned}$$
(10)

where \(\mathcal {\widetilde{L}}=\mathcal {L}_{g}+\mathcal {\widetilde{L}}_{m}\) and

$$\begin{aligned} \mathcal {\widetilde{L}}_{m}= & {} ({\nabla _{\alpha }\widetilde{A}^{\alpha }})^2-\widetilde{V}(\widetilde{A}^{2})+\frac{i}{2}[\bar{\psi }\Gamma ^{\mu }D_{\mu }\psi -D_{\mu }\bar{\psi } \Gamma ^{\mu }\psi ]\nonumber \\&-\,\widetilde{M}(\widetilde{A}^{2})\bar{\psi }\psi ; \end{aligned}$$
(11)

\(\widetilde{A}\) represents the dual of the three-form. \(\widetilde{V}(\widetilde{A}^{2})\) and \(\widetilde{M}(\widetilde{A}^{2})\) represent the self-coupling of \(\widetilde{A}\) and the coupling between two fields, respectively. By varying the action with respect to \(\widetilde{A}\), \(\psi \) and \(\bar{\psi }\), we have the following equations of motion:

$$\begin{aligned}&\partial _{\mu }\nabla _{\alpha }\widetilde{A}^{\alpha }+ \left( \frac{\mathrm{d}\widetilde{V}}{\mathrm{d}\widetilde{A}^{2}}+ \frac{\mathrm{d}\widetilde{M}}{\mathrm{d}\widetilde{A}^{2}}{\bar{\psi }\psi }\right) \widetilde{A}_{\mu }= 0 ,\end{aligned}$$
(12)
$$\begin{aligned}&iD_{\alpha }\bar{\psi }\Gamma ^{\alpha }+\widetilde{M}\bar{\psi } = 0 , \end{aligned}$$
(13)
$$\begin{aligned}&-\,i\Gamma ^{\alpha }D_{\alpha }\psi +\widetilde{M}\psi = 0, \end{aligned}$$
(14)

which are different from that of the three-form model.

3 Cosmological evolution of the power-law coupled three-form dark energy model

We now consider the field equations in a homogeneous, isotropic, and spatially flat space-time described by the metric

$$\begin{aligned} \mathrm{d}s^{2}=\mathrm{d}t^{2}-a(t)^{2}\mathrm{d}\vec {x}^{2} \end{aligned}$$
(15)

where a(t) refers to the scale factor.

To be compatible with FRW symmetries, the three-form field is assumed as the time-like component of the dual vector field, i.e.

$$\begin{aligned} A_{i j k}=X(t)a(t)^{3}\varepsilon _{ijk}. \end{aligned}$$
(16)

Since a three-form field without a potential can accelerate the expansion rate of the current universe,Footnote 1 for simplicity, we set the potential zero in the following discussions, together with choosing the coupling function as the following power-law form:

$$\begin{aligned} M=m\left[ \left( -\frac{\kappa ^{2}}{6}A^{2}\right) \right] ^{\frac{\lambda }{2}} =m(\kappa X)^{\lambda }. \end{aligned}$$
(17)

We have the following Friedmann equationsFootnote 2:

$$\begin{aligned} H^{2}= & {} \frac{\kappa ^{2}}{3}\rho , \end{aligned}$$
(18)
$$\begin{aligned} \dot{H}= & {} -\frac{\kappa ^{2}}{2}(\rho +p), \end{aligned}$$
(19)

with

$$\begin{aligned} \rho= & {} T_{0}^{0}=g^{00}T_{00}=\frac{1}{2}(3HX+\dot{X})^{2}+m(\kappa X)^{\lambda }\bar{\psi }\psi \end{aligned}$$
(20)
$$\begin{aligned} p= & {} -T_{i}^{i}\nonumber \\= & {} -g^{ii}T_{ii}=-\frac{1}{2}(3HX+\dot{X})^{2}+\lambda m(\kappa X)^{\lambda }\bar{\psi }\psi ; \end{aligned}$$
(21)

\(\lambda \) is a dimensionless constant representing the strength of the coupling, and this means that if \(\lambda =0\), such a field theory becomes a free field theory, so the constant m with mass dimension is, in fact, the mass of dark matter in a free field theory. Since typically it is very difficult for dark energy to couple dark matter with mass larger than milli-eV [26], we choose m to be smaller than milli-eV. Although the phenomenological bounds on the dark matter mass coming from large scale structure require that most of the dark matter is considerably heavier than milli-eV [27], some dark matter’s mass can be smaller than milli-eV. Indeed, Rajagopal, Turner and Wilczek considered the axino in the keV range and they obtained the axino mass bound \(m_{a}<2\) keV for an axino that constitutes warm dark matter [28].

In the FRW space-time, there is only one independent equation of motion of the three-form field,

$$\begin{aligned} \ddot{X}+3(\dot{H}X+H\dot{X})+\lambda \kappa m(\kappa X)^{\lambda -1}\bar{\psi }\psi =0 \end{aligned}$$
(22)

from the equations of motion of the spinor field and its Dirac adjoint, and one can obtains the following equation:

$$\begin{aligned} \frac{\mathrm{d}(\bar{\psi }\psi )}{\mathrm{d}t}+3H(\bar{\psi }\psi )=0, \end{aligned}$$
(23)

with its simple solution

$$\begin{aligned} \bar{\psi }\psi =(\bar{\psi }\psi )_{0}a^{-3}, \end{aligned}$$
(24)

which shows that our model indeed returns to the \(\Lambda \)CDM model when the coupling constant \(\lambda \) becomes 0.

Keeping in mind the equations of motion, we have the continuity equations for both components,

$$\begin{aligned} \dot{\rho }_{X}+3H(\rho _{X}+p_{X})= & {} -\,\delta H\rho _{m} ,\end{aligned}$$
(25)
$$\begin{aligned} \dot{\rho }_{m}+3H(\rho _{m}+p_{m})= & {} \delta H\rho _{m}, \end{aligned}$$
(26)

with

$$\begin{aligned} \rho _{X}= & {} \frac{1}{2}(3HX+\dot{X})^{2}, \quad p_{X}=p ,\end{aligned}$$
(27)
$$\begin{aligned} \rho _{m}= & {} m(\kappa X)^{\lambda }\bar{\psi }\psi , \quad p_{m}=0 ,\end{aligned}$$
(28)
$$\begin{aligned} \delta= & {} \lambda \frac{X^{\prime }}{X}; \end{aligned}$$
(29)

the prime stands for a derivative with respect to the e-folding time \(N=\ln a\) here and in the following.

In order to study cosmological dynamics in such a coupled dark energy model, it is convenient to introduce the following dimensionless variable [29]:

$$\begin{aligned} x=\kappa X, \quad y=\frac{\kappa }{\sqrt{6}}(X^{\prime }+3X), \quad \omega ^{2}=\frac{\kappa ^{2}\rho _{m}}{3H^{2}}. \end{aligned}$$
(30)

By applying the Friedmann equations and equations of motion, one can obtains the autonomous system of evolution equations

$$\begin{aligned} x^{\prime }= & {} \sqrt{6}y-3x ,\end{aligned}$$
(31)
$$\begin{aligned} y^{\prime }= & {} \frac{1}{2}\left( \frac{\lambda }{x}\left( \sqrt{6}-3xy\right) -3y\right) \left( y^{2}-1\right) . \end{aligned}$$
(32)

We note that \(\omega ^{2}\) has been eliminated by the Friedmann constraint written in terms of these variables: \(y^{2}+\omega ^{2}=1\).

There are two fixed points for such an autonomous system. One of them is \(\left( \sqrt{\frac{2}{3}},1\right) \), which is an attractor since its eigenvalues \((-\,3,-\,3)\) are both negative. By rewriting the density and pressure in terms of the dimensionless variables, we have the total EOS

$$\begin{aligned} \omega _{tot}=\frac{p}{\rho }=-1+(1+\lambda )\left( 1-y^{2}\right) =-1 , \end{aligned}$$
(33)

indicating that such fixed point represents a three-form saturated de Sitter universe. The other one \(\left( \sqrt{\frac{2\lambda }{3(1+\lambda )}},\sqrt{\frac{\lambda }{(1+\lambda )}}\right) \) with eigenvalues \(\frac{3}{4}\left( \left( -1+\sqrt{17}\right) ,\left( -1-\sqrt{17}\right) \right) \) is a saddle point; strictly this fixed point exists only when \(\lambda >0\). It can be inferred from \(\omega _{X}=\frac{p_{X}}{\rho _{X}}=-1+\frac{\lambda \left( 1-y^{2}\right) }{y^{2}}=0\), \(\delta =0\), that such a fixed point is a tracking solution which can be used to alleviate the coincidence problem with fine-turning of the model parameters.

The trajectories with respect to x(N) and y(N) with a wide range of initial conditions and the assumption that \(\lambda =0.01\) (we will see that this is a good choice in the next section) can be visualized by Fig. 1.

Fig. 1
figure 1

The larger black point represents the stable point, and the smaller one represents the saddle point

Full size image

As is showed in Fig. 1, the trajectories run toward the de Sitter attractor, coasting along the saddle point. Also, one should note that the present value of x must be equal to or larger than a certain value \(x_{*}\), which depends on both \(\lambda \) and y(0), to make sure in high redshift that the autonomous system does not encounter a singularity. After specifying \(\lambda \) and y(0), if \(\widetilde{x}\) is the present value of x leading to the condition that x(N) is positive-definite for arbitrary non-infinite N, i.e. \(x(N)>0(-\infty<N< +\infty )\), then \(x_{*}\) is the lower limit of \(\widetilde{x}\).

Now let us solve the autonomous system of evolution equations by assuming a large \(x_{0}\). With the constraint \(y^{2}<1\), it can be well approximated by two independent equations,

$$\begin{aligned} x^{\prime }= & {} -3x , \end{aligned}$$
(34)
$$\begin{aligned} y^{\prime }= & {} \frac{3}{2}(1+\lambda )y(1-y^{2}) , \end{aligned}$$
(35)

which have the following solutions:

$$\begin{aligned} x\approx & {} x_{0}(1+z)^{3} , \end{aligned}$$
(36)
$$\begin{aligned} y^{2}\approx & {} \frac{1}{1+\frac{\Omega _{m0}}{1-\Omega _{m0}}(1+z)^{3(1+\lambda )}}; \end{aligned}$$
(37)

we have replaced e-folding time by the redshift here.

Substituting the solutions into (27)–(29), we have

$$\begin{aligned} \rho _{X}\approx & {} \frac{3H_{0}^{2}(1-\Omega _{m0})}{\kappa ^{2}} , \end{aligned}$$
(38)
$$\begin{aligned} p_{X}\approx & {} -\frac{3H_{0}^{2}(1-\Omega _{m0})}{\kappa ^{2}}+\lambda \frac{3H_{0}^{2}\Omega _{m0}}{\kappa ^{2}}(1+z)^{3(1+\lambda )}, \end{aligned}$$
(39)
$$\begin{aligned} \delta\approx & {} -3\lambda ; \end{aligned}$$
(40)

noting that although \(\delta \) is a constant, such solutions are different from the models proposed in [30,31,32] since

$$\begin{aligned} \omega _{X}\approx -1+\lambda \frac{\Omega _{m0}}{1-\Omega _{m0}}(1+z)^{3(1+\lambda )} \end{aligned}$$
(41)

is not a constant.

It can be inferred from (40) and (41) that the energy transfer between two dark sectors keeps the density of dark energy constant even when its EOS deviates from \(-1\).

To compare the solutions with uncoupled dark energy model, let us rewrite the Hubble parameter as

$$\begin{aligned} \frac{H^{2}(z)}{H_{0}^{2}}= & {} \frac{\Omega _{m0}\left( \frac{x}{x_{0}}\right) ^{\lambda }(1+z)^{3}}{1-y^{2}} \nonumber \\= & {} \Omega _{m0}(1+z)^{3}+(1-\Omega _{m0})\frac{\rho _{X\mathrm{eff}}}{\rho _{X\mathrm{eff}0}}, \end{aligned}$$
(42)

where

$$\begin{aligned} \frac{\rho _{X\mathrm{eff}}}{\rho _{X\mathrm{eff}0}}= & {} \frac{\Omega _{m0}}{1-\Omega _{m0}}\left( \frac{\left( \frac{x}{x_{0}}\right) ^{\lambda }(1+z)^{3}}{1-y^{2}}-(1+z)^{3}\right) \nonumber \\= & {} \exp \left[ \int _{0}^{z}\frac{3(1+\omega _{X\mathrm{eff}}(\tilde{z}))}{1+\tilde{z}}\mathrm{d}\tilde{z}\right] \end{aligned}$$
(43)

is the normalized effective dark energy density and

$$\begin{aligned} \omega _{X\mathrm{eff}}(z)=-1+\frac{1}{3}\frac{x^{\lambda }\left( 3+\frac{\lambda (1+z)}{x}\frac{\mathrm{d}x}{\mathrm{d}z}\right) (1-y^{2})+(1+z)\frac{\mathrm{d}y^{2}}{\mathrm{d}z}x^{\lambda }-3(1-y^{2})^{2}x_{0}^{\lambda }}{\left( x^{\lambda }-(1-y^{2})x_{0}^{\lambda }\right) (1-y^{2})} \end{aligned}$$
(44)

is the effective EOS of dark energy.

By substituting the approximate solutions into (43) and (44), we have

$$\begin{aligned} \frac{\rho _{X\mathrm{eff}}}{\rho _{X\mathrm{eff}0}}\approx & {} 1+\frac{\Omega _{m0}}{1-\Omega _{m0}}\left( (1+z)^{3(1+\lambda )}-(1+z)^{3}\right) , \end{aligned}$$
(45)
$$\begin{aligned} \omega _{X\mathrm{eff}}\approx & {} \frac{-1+\lambda \frac{\Omega _{m0}}{1-\Omega _{m0}}(1+z)^{3(1+\lambda )}}{1+\frac{\Omega _{m0}}{1-\Omega _{m0}}\left( (1+z)^{3(1+\lambda )}-(1+z)^{3}\right) }; \end{aligned}$$
(46)

as one can see, depending on the sign of \(\lambda \), there are two different high redshift approximate expressions for the effective energy density or the effective EOS. More specifically, the effective energy density is approximately \(\frac{\Omega _{m0}}{1-\Omega _{m0}}(1+z)^{3(1+\lambda )}(\lambda >0)\) and \(-\frac{\Omega _{m0}}{1-\Omega _{m0}}(1+z)^{3}(\lambda <0)\) at high redshift, and the effective EOS of dark energy is approximately \(\lambda (\lambda >0)\) and \(\lambda (1+z)^{3\lambda }(\lambda <0)\) at high redshift.

At the end of this section, we place another restriction on the likelihood function of \((x_{0},\lambda ,\Omega _{m0})\) with the aid of the approximate solution of the autonomous system of evolution equations; in fact we can see from (45) and (46) immediately that the Hubble parameter is independent of \(x_{0}\) assuming \(x_{0}\) to take a large value, which means that the likelihood function becomes a non-zero constant (in fact a large \(x_{0}\) with proper values of \(\lambda \) and \(\Omega _{m0}\) is quite favored by observations) with respect to \(x_{0}\) if \(x_{0}\) is large enough. Given this behavior of the likelihood function L, we have such a formula

$$\begin{aligned} \int _{0}^{+\infty }L(x_{0},\lambda ,\Omega _{m0})\mathrm{d}x_{0} \propto \lim _{x_{0}\rightarrow +\infty }L(x_{0},\lambda ,\Omega _{m0}), \end{aligned}$$
(47)

which can be used to marginalize over \(x_{0}\) without a prior.

4 Confront the power-law coupled three-form dark energy model with observations

In this section, we perform a simple likelihood analysis on the free parameters of the model with the combination of data from Type Ia Supernova (SN Ia), Baryon Acoustic Oscillations (BAOs) and Cosmic Microwave Background (CMB) radiation observations.

Firstly, we construct the following \( \chi ^{2}\) function for SN Ia, by using the recently released Union2.1 compilation with 580 data points:

$$\begin{aligned} \chi _{\mathrm{SN}\, \mathrm{Ia}}^{2}= P- \frac{Q^{2}}{R} \end{aligned}$$
(48)

where P, Q and R are defined as

$$\begin{aligned} P= & {} \sum _{i=0}^{580}\frac{\left( \mu _{\mathrm{th}}(z_{i})-\mu _{\mathrm{obs}}(z_{i})\right) ^{2}}{\sigma _{\mu }^{2}(z_{i})}, \end{aligned}$$
(49)
$$\begin{aligned} Q= & {} \sum _{i=0}^{580}\frac{\left( \mu _{\mathrm{th}}(z_{i})-\mu _{\mathrm{obs}}(z_{i})\right) }{\sigma _{\mu }^{2}(z_{i})}, \end{aligned}$$
(50)
$$\begin{aligned} R= & {} \sum _{i=0}^{580}\frac{1}{\sigma _{\mu }^{2}(z_{i})}, \end{aligned}$$
(51)

where \(\mu _{\mathrm{th}}=5\log _{10}\left[ (1+z)\int _{0}^{z}\frac{H_{0}}{H(z^{\prime })}\mathrm{d}z^{\prime }\right] +25\) denotes the distance modulus predicted by theory and \(\mu _{\mathrm{obs}}\) represents the observed one with a statistical uncertainty \(\sigma _{\mu }\).

Fig. 2
figure 2

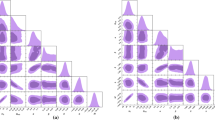
The figure on the left shows observational constraints on parameters \((\lambda ,\Omega _{m0})\) with the combination of SN Ia and BAO/CMB datasets, in which the light blue and blue region correspond to the \(2\sigma \) and \(1\sigma \) region, respectively, while the black point (0.013,0.269) with \(\chi ^{2}=564.811\) represents the best-fit value of the pair \((\lambda ,\Omega _{m0})\). The figure on the right is the likelihood function of \(\lambda \), which is marginalized with a flat prior that becomes zero if \(\Omega _{m0}\) is bigger than 0.38 or smaller than 0.16, suggesting \(-\,0.017<\lambda <0.047\) (\(2\sigma \) confidence level)

Full size image

In the second step, we consider BAO data from the WiggleZ Survey, SDSS DR7 Galaxy sample and 6dF Galaxy Survey together with CMB data from WMAP 7 years observations to obtain the BAO/CMB constraints on the model parameters by defining \(\chi _{\mathrm{BAO/CMB}}^{2}\) as [33,34,35]

$$\begin{aligned} \chi _{\mathrm{BAO/CMB}}^{2}=X^{T}C^{-1}X \end{aligned}$$
(52)

where

$$\begin{aligned} X=\left( \begin{array}{c} \frac{d_{A}(z_{*})}{D_{v}(0.106)}-30.95,\\ \frac{d_{A}(z_{*})}{D_{v}(0.2)}-17.55,\\ \frac{d_{A}(z_{*})}{D_{v}(0.35)}-10.11,\\ \frac{d_{A}(z_{*})}{D_{v}(0.44)}-8.44,\\ \frac{d_{A}(z_{*})}{D_{v}(0.6)}-6.69,\\ \frac{d_{A}(z_{*})}{D_{v}(0.73)}-5.45, \end{array} \right) \end{aligned}$$
(53)

in which \(d_{A}(z)=\int _{0}^{z}\frac{1}{H(z^{\prime })}\mathrm{d}z^{\prime }\) and \(D_{V}(z)=\left[ d_{A}(z)^{2}\frac{z}{H(z)}\right] ^{\frac{1}{3}}\) represent the co-moving angular-diameter distance and the dilation scale, respectively, while \(z_{*}\approx 1091\) is the decoupling time. We have

$$\begin{aligned} C^{-1}=\left( \begin{matrix} 0.48435 &{}\quad -\,0.101383 &{}\quad -\,0.164945 &{}\quad -\,0.0305703 &{}\quad -\,0.097874 &{}\quad -\,0.106738 \\ -\,0.101383 &{}\quad 3.2882 &{}\quad -\,2.45497 &{}\quad -\,0.0787898 &{}\quad -\,0.252254 &{}\quad -\,0.2751 \\ -\,0.164945 &{}\quad -\,2.45497 &{}\quad 9.55916 &{}\quad -\,0.128187 &{}\quad -\,0.410404 &{}\quad -\,0.447574 \\ -\,0.0305703 &{}\quad -\,0.0787898 &{}\quad -\,0.128187 &{}\quad 2.78728 &{}\quad -\,2.75632 &{}\quad 1.16437 \\ -\,0.097874 &{}\quad -\,0.252254 &{}\quad -\,0.410404 &{}\quad -\,2.75632 &{}\quad 14.9245 &{}\quad -\,7.32441 \\ -\,0.106738 &{}\quad -\,0.2751 &{}\quad -\,0.447574 &{}\quad 1.16437 &{}\quad -\,7.32441 &{}\quad 14.5022 \end{matrix} \right) \end{aligned}$$

is the inverse of the correlation matrix.

Finally, the total \(\chi ^{2}\) function for the combined observational datasets is given by \(\chi ^{2}=\chi _{\mathrm{SN}\, \mathrm{Ia}}^{2}+\chi _{\mathrm{BAO/CMA}}^{2}\), from which we can construct the likelihood function as \(L=L_{0} e^{-\frac{1}{2}\chi ^{2}}\); here \(L_{0}\) is a normalized constant which is independent of the free parameters.

Providing with the likelihood function, one can then obtain the best-fit values of the free parameters by maximizing it. However, as was mentioned in the previous section, the parameter \(x_{0}\) cannot be strictly restricted, so we leave it out of the discussions and consider the likelihood function that has been marginalized over \(x_{0}\) without a prior. With the aid of (47), such a function is proportional to

$$\begin{aligned} \lim _{x_{0}\rightarrow +\infty }L(x_{0},\lambda ,\Omega _{m0})\approx L(\tilde{x_{0}},\lambda ,\Omega _{m0}) \end{aligned}$$
(54)

where \(\tilde{x_{0}}\) is a large number, and one can choose it as 10000, for example. We now present the fitting result in Fig. 2 by analyzing such a likelihood.

One may note that the marginalized likelihood in the right panel of Fig. 2 appears to be a little non-Gaussian; this is mainly because of the non-Gaussian structure of the likelihood that has not been marginalized. One also can see from Fig. 2 that the observations favor a small positive coupling constant which, as we mentioned above, allows for the existence of a tracking solution that can be used to alleviate the coincidence problem with fine-tuning of the model parameters.

Moreover, one thing here needs to be noticed: since \(x_{0}\) cannot be strictly restricted, the interaction behavior between two dark sectors still remains uncertain, which can be inferred from Fig. 3. However, one may decrease such an uncertainty by taking into account observational constraints from future measurements.

Fig. 3
figure 3

\(\delta =\lambda \frac{x^{\prime }}{x}\) here represents the strength of the interactions, the blue, orange and green curve correspond to the case with \((\lambda ,x_{0},\Omega _{m0})=(0.01,0.6,0.27),(0.01,10,0.27),(0.01,100,0.27)\), respectively

Full size image

From Fig. 3, it can be inferred that the direction of energy transfer can be changed if \(x_{0}\) is sufficiently close to \(x_{*}\), which is around 0.6 in such a case, and the behavior of \(\delta \) is almost the same for the choices of \(x_{0}=10\) and \(x_{0}=100\) if the redshift \(z>0\), which is consistent with the conclusion that the likelihood function becomes a constant with respect to \(x_{0}\) if \(x_{0}\) is adequately large, as we have described in Sect. 3. In fact we can prove this conclusion in a inductive way by plotting \(\chi ^{2}\) (see Fig. 4).

Fig. 4
figure 4

The blue, orange and green line correspond to the case with \((\lambda ,\Omega _{m0})=(0.01,0.3),(0.02,0.3),(0.01,0.2)\), respectively. Here \(x_{0}\) ranges from 10 to 10000

Full size image

5 Conclusions

In this paper we have studied a power-law coupled dark energy model which considers dark energy as a three-form field and dark matter as a spinor field. By performing a dynamical analysis on the field equations with the introduction of three dimensionless variables, we obtained two fixed points of the autonomous system of evolution equations, among which one is a de Sitter attractor, and the other is a tracking solution, assuming \(\lambda >0\), which provides a possible solution of the coincidence problem.

By marginalizing over \(x_{0}\), we have also carried out a likelihood analysis on the free parameters \(\lambda \) and \(\Omega _{m0}\) with the combination of SN Ia+BAO/CMB datasets, through which we have a best-fit value of the pair \((\lambda ,\Omega _{m0})\) as (0.013, 0.269). In addition, the likelihood function marginalized over \(x_{0}\) and \(\Omega _{m0}\) showed that \(\lambda \) is restricted by \(-\,0.017<\lambda <0.047\) (\(2\sigma \) confidence level, with a best-fit value 0.01), indicating that the measurements considered here are quite consistent as regards the \(\Lambda CDM\) and our three-form model. However, future measurements might allow us to tell them apart.

This notwithstanding, it can be told from the fitting result that \(\lambda \) and \(\Omega _{m0}\) are strictly restricted, \(x_{0}\) can be any value beyond \(x_{*}\). However, as mentioned above, future measurements might decrease the uncertainty on \(x_{0}\).