1 Introduction

The quest to construct a covariant renormalizable quantum gravity attracted more attention in recent years. The various motivations to quantize gravity are classified by Kiefer [1] into three categories. First, the unification. After having got a worthy quantum field theory for non-gravitational interactions, unifying quantum theory and general relativity would be a logical wish. The next motivation comes from singularities of general theory of relativity. It seems that these singularities break down the theory and it is expected to be solved with an appropriate quantum theory of gravity. Finally, the last motivation arises from the fact that there are different concepts of time in quantum theory and general relativity. Time in the latter theory is a dynamical object, in contrast to quantum theory, in which it is introduced as an external parameter. Quantum gravity may modify the concept of time in one or both of these theories.

There are various approaches for building a quantum theory of gravity. In [2], these approaches are categorized in three sets. The first category is the covariant line, which is simply the quantum field theory of fluctuations over some background metric. This idea leads to higher derivative theories and string theory. The canonical line is the second approach, in which there is no need to introduce the background metric. The Hilbert space can be considered as a representation of operators corresponding to the metric or functions of it. Loop quantum gravity seems to be the latest one in this category. Finally, the name sum over histories is assigned to the third set, which contains versions of Feynman’s functional integral quantization for the suggested quantum gravity theory. Discrete approaches and the spin-foam formalism belong to this set.

In any perturbative approach, which is attractive to particle physicists, offering a finite quantity is an important point in a theory. One of the difficulties in perturbative quantization of gravity is the negative (mass) dimension of gravity coupling, i.e. the Newton constant, which leads to divergences at short distances or high energies. Although renormalization of divergences necessarily does not result in a covariant formalism, it would be a vital issue in the suggested quantum gravity theory. In this context, Weinberg’s asymptotic safety suggestion in 1979 [3, 4], based on the existence of a finite number of non-Gaussian fixed points, for which the renormalization group (RG) flow is attracted by them at infinity, is notable. Much successful research work has been done on the existence of these fixed points (see the references in [5]). The attraction of the RG-flow to these non-Gaussian UV fixed points at short distances protects the theory from divergences in that limit.

In 1998, Reuter suggested the truncated exact renormalization group (ERG) method [6, 7] for probing non-Gaussian fixed points, where the trajectories of running essential gauge couplings lie on the finite dimensional subspace of the theory space [8]. It is known that the \(\beta \)-functions give us running couplings of the theory which are screened or anti-screened by loop corrections at short distances. Treating couplings as fields can be found in other theories such as scalar–tensor theories (see the references in [9]), but here couplings run because of quantization in a systematic manner, i.e. RG equation. This evolved constant parameter, i.e. the running coupling constant, can change the behavior of gravitational phenomena like black holes [10, 11], galaxy rotation [12], CMB, etc.

In this paper, we investigate the effects of the improvement of gravitational and cosmological constants on the Mukhanov–Sassaki equation (MSE). This equation describes the growth of gauge invariant quantities constructed from quantum perturbations of metric and the inflation scalar field. These perturbations are usually considered as the primary seeds for inhomogeneities of CMB and the structure formation. Therefore investigation of the effects of RG improved couplings on the MSE would be remarkable.

The next section is dedicated to a brief introduction of ERG and various improvement methods. Then the improved MSE (IMSE) would be derived in Sect. 3. In Sect. 4, we obtain the solution of IMSE for two models, one with a scalar field responsible for the inflation, and one with a cosmological constant. Finally, in Sect. 5, the effects of this improvement on the power spectrum are studied.

It should be noted that although we are investigating the improvement of the cosmological power spectrum via the running coupling constants obtained from the asymptotic safe theory, there are other points of view to see the potential impact of renormalization in the power spectrum. For example see [13, 14].

2 Truncated ERG in asymptotically safe gravity

Truncated ERG is one of the several methods for probing non-Gaussian fixed points of gravity theory [5]. In this approach, by truncating the scale-dependent effective action \( \Gamma _k[g_{\alpha \beta }] \) up to appropriate interaction terms, other non-effective interaction terms would be ignored. The evolution of these remaining gauge couplings, which cannot be eliminated by a redefinition of the fields, is obtained from the exact renormalization group equation (ERGE). The trajectory of RG flow is

$$\begin{aligned} k\partial _{k}\Gamma _{k}=\frac{1}{2}Tr[(\Gamma ^{(2)}_{k}+\mathcal {R}_{k})^{-1}k\partial _{k}\mathcal {R}_{k}], \end{aligned}$$
(1)

where \( \Gamma _k\) integrates out all the fluctuations at scale k and connects the admissible fundamental action at \( \Gamma _{k \rightarrow \infty } = S \) to the conventional effective action at \( \Gamma _{k \rightarrow 0} = \Gamma \). This average-like effective action at tree level describes all gravitational phenomena for each momentum of order k [15]. Indeed, the IR-cutoff \( \mathcal {R}_k(p^2) \), which appears in the definition of \( \Gamma _{k}\), eliminates the effects of fluctuations of \( p^{2} < k^{2} \) on RG flow and is defined by an arbitrary smooth function \( \mathcal {R}_k(p^2) \propto k^2 \mathcal {R}^{(0)}(\frac{p^2}{k^2}) \) where \( \mathcal {R}^{(0)}(\psi ) \) satisfies the conditions \( \mathcal {R}^{(0)}(0) =1 \) and \( \mathcal {R}^{(0)}(\psi \rightarrow \infty ) \rightarrow 0 \). The exponential form \( \mathcal {R}^{(0)}(\psi ) = \frac{\psi }{\exp (\psi ) -1} \) is a common chosen form in the literature [16]. Since the multiplicity of couplings in the effective action makes the \(\beta \)-function intricate, truncation would project the RG flow into the finite dimensional subspace spanned by the essential couplings. This method gives a finite number of ordinary differential equations.

The Einstein–Hilbert truncation,

$$\begin{aligned} \Gamma _k[g_{\alpha \beta }] = \frac{1}{16\pi G_{k}}\int {\mathrm{d}^{4}x\sqrt{g}(-R(g)+2\Lambda _{k})}, \end{aligned}$$
(2)

is a common truncation for cosmological models.

It is shown numerically in [17] that, for small values of the cutoff \( k \rightarrow 0 \), at perturbative regime, the solutions of \(\beta \)-functions for this model lead to the following power-series for dimensionful couplings

$$\begin{aligned}&G(k) = G_0 \left[ 1 - \omega G_0 k^2 + \mathcal {O}(G_0^2 k^4)\right] ,\end{aligned}$$
(3)
$$\begin{aligned}&\Lambda (k) = \Lambda _0 + \nu G_0 k^4 \left[ 1 + \mathcal {O}(G_0 k^2) \right] , \end{aligned}$$
(4)

where \(\omega = \frac{1}{6 \pi } [ 24 \Phi ^2_2(0) - \Phi ^1_1(0) ]\), \(\nu = \frac{1}{4 \pi } \Phi ^1_2(0)\) and \( \Phi ^p_n(w) \) is the threshold function, which depends on the IR-cutoff:

$$\begin{aligned} \Phi ^p_n(w)=\frac{1}{\Gamma (n)} \int \psi ^{n-1} \frac{\mathcal {R}^{(0)}(\psi )-\psi \mathcal {R}^{(0)'}(\psi )}{[\psi +\mathcal {R}^{(0)}(\psi )+w]^p} \mathrm{{d}}\psi ; \end{aligned}$$

\(G_{0}\) and \(\Lambda _{0}\) are the non-improved coupling constants.

Indeed, at the fixed point regime, i.e. \( k \gg m_\mathrm{Pl}\) (where \( m_\mathrm{Pl} = G_0^{-\frac{1}{2}} \) is the Planck mass), the numerical analysis suggests

$$\begin{aligned} G(k) = \frac{g_{*}^{UV}}{k^2} \quad , \quad \Lambda (k) = \lambda _{*}^{UV} k^2 \end{aligned}$$

where \( g_{*}^{UV} = 0.27\) and \(\lambda _{*}^{UV} = 0.36\) are the non-Gaussian fix point values of the dimensionless couplings \( g(k) \equiv k^{2} G(k) \) and \( \lambda (k) \equiv \frac{\Lambda (k)}{k^{2}} \), respectively.

In the following, we are dealing with the end of the inflation epoch with \( k \lesssim m_\mathrm{Pl}\), and thus it is logical to use the perturbative regime. Hence we use Eqs. (3) and (4) as the running couplings for this period.

As is the case for any quantum field theory, running couplings are scaled with momentum k. On the other hand, in effective field theory, \(\Gamma _k\) uses this scaling to specify the cutoff point where the fluctuations with momenta smaller than k are ignored. In the space-time picture this cutoff momentum should be related to the inverse of some physical length. Generally speaking, using isotropy and homogeneity of FRW metric, a suitable function \(k(t,a(t),\dot{a}(t),...)\) seems to be the best choice for scaling parameter. Noting that in the standard cosmology, when the universe is aged t, fluctuations of frequency smaller than 1 / t are ignorable, and taking into account the dimensional consideration,s one observes that the cutoff identification

$$\begin{aligned} k = \frac{\xi }{t} \end{aligned}$$
(5)

is a suitable approximation. Here \(\xi \) is a positive constant of order unity. (This may also be justified for the fixed point regime, where \(\Lambda (k) \propto k^2 \), and since we know that \(\Lambda \propto H^{2}(t) \). See [18, 19]). One may also use the conformal time \(\int \mathrm{{d}}t/a(t)\) instead of t, but the difference is ignorable because of the ignorance of frequencies less than 1 / t. As a result, the above cutoff identification is usually used for improvement of the cosmological models in the literature. For more details as regards the cutoff identification, the reader is referred to [15, 20].

With this identification, we shall have the time dependent parameters G(k) and \( \Lambda (k)\)

$$\begin{aligned}&G(t) = G_0 \left[ 1- \tilde{\omega }\bigg (\frac{t_\mathrm{Pl}}{t}\bigg )^2 + \mathcal {O}\bigg (\frac{t_\mathrm{Pl}}{t}\bigg )^4 \right] , \end{aligned}$$
(6)
$$\begin{aligned}&\Lambda (t) = \Lambda _0 + \tilde{\nu } m^2_\mathrm{Pl} \bigg (\frac{t_\mathrm{Pl}}{t}\bigg )^4 \left[ 1 + \mathcal {O}\bigg (\frac{t_\mathrm{Pl}}{t}\bigg )^2 \right] , \end{aligned}$$
(7)

where \( \tilde{\omega } \equiv \omega \xi ^2 \) and \(\tilde{\nu } \equiv \nu \xi ^4 \).

The conversion of fundamental units such as c, \( \hbar \) and G to variable ones is a debatable issue [21]. In this regard, considering G as a coupling constant, the decision of where and how we should apply the improvement of \(G_0\) to G(x) is an important question.

The first and simplest way to do this can be called the solution improvement, in which the parameter \(G_0\) is replaced by G(x) in any solution of the non-improved theory. The second approach is the equation improvement. This is done at the level of the equations of motion, not the solutions. The difference between these two methods becomes bold for non-vacuum solutions and the latter seems to be more acceptable if the quantum corrections are negligible in the action. Generally speaking the improvement of the equations of motion may lead to solutions different from the former method.

By the third approach which we call the action parameters improvement [22], one means a substitution of \(G_0\) with G(x) in the action, without adding any kinetic term for it. The improved field equations are obtained from this new action and the externally prescribed field G(x) equation comes from the RGE. If one adds some kinetic term for it, there would be no guaranty that the obtained G(x) coincides with the result of RGE. Finding a suitable kinetic term is very intricate.

Here we shall improve the equations of motion, which seems more suitable.

3 Improved perturbations and MSE

Metric perturbation during the inflation era and its relation to the matter inhomogeneity is an apt quantum mechanical mechanism generating initial seeds of structure formation (for a complete review see Ref. [23]). The perturbed metric has 10 df, but only six of them are physical. The others are unphysical because of gauge (coordinate) transformations. Therefore, introducing gauge invariant quantities helps us to have results that are independent of the chosen coordinate system. Among different gauge invariant quantities, the comoving curvature perturbation R would be an appropriate quantity to analyze the power spectrum of the CMB. The symmetries of perturbation equations under translations make it easier to work with Fourier modes, \(R_q\).

The evolution of \( R_q\) in the non-improved theory follows the MSE [23]:

$$\begin{aligned} \frac{\mathrm{d}^2 R_q}{\mathrm{d}\tau ^2} + \frac{2}{z}\frac{\mathrm{d}z}{\mathrm{d}\tau }\frac{\mathrm{d}R_q}{\mathrm{d}\tau }+q^2R_q=0, \end{aligned}$$
(8)

where \( \tau = \int ^t_{t_0} \frac{\mathrm{d}t'}{a(t')} \) is the conformal time and z, which is related to the time derivative of the scalar field by \(z=a\dot{\varphi }/H\), can be considered as the redshift. Since the Fourier transformation of the 2-point function of the inflation field, i.e. the power spectrum, needs the solution of this differential equation, introducing the initial conditions is unavoidable.

The wave number q is proportional to the inverse of the comoving wavelength of the perturbations, and the conformal time is the comoving horizon, hence the quantity \( -q\tau \) will be the ratio of causal horizon length to the comoving wavelength of the perturbations. For \( -q\tau \ll 1 \), the wavelength of the perturbations is larger than the length of the causal horizon and the perturbations exit the horizon before the end of inflation. At the end of inflation, with growing comoving Hubble radius, \( \frac{1}{aH} \), the wavelength of the perturbations becomes smaller than the comoving Hubble radius and thus the inhomogeneities and their effect on CMB gradually become observable.

Here we are interested in investigating the effects of quantum improvements of \(G_{0}\) and \(\Lambda _{0}\) on these observables. Therefore, at the first step, we have to study briefly the effect of an improvement on the perturbation equations. Then IMSE in the \( \Lambda \)CDM universe will be obtained.

3.1 Perturbation equations with G(t) & \(\Lambda (t)\)

The perturbed metric can be written as the sum of the background metric \(\bar{g}_{\alpha \beta }\) and the perturbation \(h_{\alpha \beta }\), \(g_{\alpha \beta }=\bar{g}_{\alpha \beta }+h_{\alpha \beta }\). We choose the background to be a flat homogeneous and isotropic FLRW metric:

$$\begin{aligned} \bar{g}_{00} = -1 \quad , \quad \bar{g}_{0i} = \bar{g}_{i0} = 0 \quad , \quad \bar{g}_{ij} = a^2(t) \delta _{ij}, \end{aligned}$$
(9)

with scale factor a(t), and the perturbation decomposed into (spatial) scalar, vector, and tensor modes. Hence, the line element becomes

$$\begin{aligned}&\mathrm{{d}}s^{2} = -(1+E)\mathrm{{d}}t^{2} + a(t) \left[ \partial _{i} F + G_{i} \right] \mathrm{{d}}t \mathrm{{d}}x^{i}\nonumber \\&+\,\, a^{2}(t) \left[ \delta _{ij} + A \delta _{ij} + 2 B_{,ij} + 2 C_{(i,j)} + D_{ij} \right] \mathrm{{d}}x^{i}\mathrm{{d}}x^{j},\nonumber \\ \end{aligned}$$
(10)

where A, B, E and F are scalars, \( C_{i} \) and \( G_{i} \) are divergenceless vectors and \( D_{ij} \) is a symmetric divergenceless–traceless tensor.

Analogous to the metric decomposition, the perfect fluid energy-momentum tensor, \( \bar{T}_{\alpha \beta } = \bar{p}\bar{g}_{\alpha \beta }+(\bar{p}+\bar{\rho }) \bar{u}_{\alpha } \bar{u}_{\beta }\) is perturbed as

$$\begin{aligned}&\delta T_{00} = - \bar{\rho } h_{00} +\delta \rho , \end{aligned}$$
(11)
$$\begin{aligned}&\delta T_{i0} = \bar{p} h_{i0} - \bigg ( \bar{\rho } + \bar{P} \bigg ) \bigg ( \partial _{i} \delta u + \delta u_{i}^{V} \bigg ), \end{aligned}$$
(12)
$$\begin{aligned}&\delta T_{ij} = \bar{p} h_{ij} + a(t)^{2} \left[ \delta _{ij} \delta p + \partial _{i} \partial _{j} \pi ^{S}+ 2 \partial _{(i,}\pi _{j)}^{V} + \pi _{ij}^{T} \right] , \end{aligned}$$
(13)

where a bar over any quantity represents its non-perturbed value. \( \delta p \) and \( \delta \rho \) are pressure and density perturbations. The velocity perturbation is decomposed as \( \delta u_i = \partial _{i} \delta u + \delta u_{i}^{V} \) to a scalar velocity potential \(\delta u \) and a divergenceless vector \(\delta u_i \). The other parameters in \(\delta T_{ij}\), i.e. the scalar \( \pi _{i}^{S} \), the divergenceless vector \( \pi _{i}^{V} \) and the symmetric divergenceless–traceless tensor \( \pi _{ij}^{T} \), characterize the departure from the energy-momentum tensor of a perfect fluid.

Since the CMB inhomogeneity comes from scalar perturbation, in the following we omit the vector and tensor perturbations and just consider the scalar mode. Separating these terms on both sides of the Einstein perturbed equation, \( \delta R_{\alpha \beta } = -\,8\pi G(t) ( \delta T_{\alpha \beta } - \frac{1}{2} \bar{g}_{\alpha \beta } \delta T^{\lambda }_{\lambda } - \frac{1}{2} h_{\alpha \beta } \bar{T}^\lambda _\lambda ) \), yields

$$\begin{aligned}&-4\pi G(t) a^{2} \left[ \delta \rho -\delta p - \nabla ^{2}\pi ^{S} \right] \nonumber \\&\quad = \frac{1}{2} a \dot{a} \dot{E} + \bigg (2 \dot{a}^{2} + a\ddot{a} \bigg ) E + \frac{1}{2} \nabla ^{2} A \nonumber \\&-\frac{1}{2} a^{2} \ddot{A} - 3 a \dot{a} \dot{A} -\frac{1}{2} a \dot{a} \nabla ^{2} \dot{B} + \dot{a}\nabla ^{2} F, \end{aligned}$$
(14)
$$\begin{aligned}&\partial _{j}\partial _{k} \Big [16 \pi G(t) a^{2} \pi ^{S} + E + A - a^{2}\ddot{B}-3a\dot{a}\dot{B}\nonumber \\&+ 2a\dot{F} + 4\dot{a}F \Big ] = 0, \end{aligned}$$
(15)
$$\begin{aligned}&8 \pi G(t) a \bigg ( \bar{\rho }+\bar{p} \bigg ) \partial _{j} \delta u = -\, \dot{a} \partial _{j} E + a \partial _{j}\dot{A} , \end{aligned}$$
(16)
$$\begin{aligned}&-4 \pi G(t) \left[ \delta \rho + 3 \delta p + \nabla ^{2} \pi ^{S} \right] =\nonumber \\&-\frac{1}{2 a^{2}} \nabla ^{2} E - \frac{3 \dot{a}}{2 a} \dot{E} - \frac{1}{a} \nabla ^{2}\dot{F} - \frac{\dot{a}}{a^2} \nabla ^2 F \nonumber \\&+ \frac{3}{2} \ddot{A} + \frac{3 \dot{a}}{a} \dot{A} - \frac{3 \ddot{a}}{a} E + \frac{1}{2} \nabla ^{2} \ddot{B} + \frac{\dot{a}}{a} \nabla ^{2}\dot{B}, \end{aligned}$$
(17)

and the perturbed energy-momentum conservation equation gives

$$\begin{aligned}&\partial _j \left[ \delta p + \nabla ^{2} \pi ^{S} + \partial _{0} \left[ \bigg ( \bar{\rho } + \bar{p} \bigg ) \delta u \right] + \frac{3 \dot{a}}{a} ( \bar{\rho } + \bar{p} ) \delta u \right. \nonumber \\&\quad \left. + \frac{1}{2} \bigg ( \bar{\rho } + \bar{p} \bigg ) E \right] = 0 \end{aligned}$$
(18)
$$\begin{aligned}&\delta \dot{\rho } + \frac{3 \dot{a}}{a} \bigg ( \delta \rho + \delta p \bigg ) + \nabla ^{2}\left[ - \,a^{-1} \bigg ( \bar{\rho } + \bar{p} \bigg ) F \right. \nonumber \\&\quad \left. +\, a^{-2} \bigg ( \bar{\rho } + \bar{p} \bigg ) \delta u + \frac{\dot{a}}{a} \pi ^S \right] \nonumber \\&+ \frac{1}{2} \bigg ( \bar{\rho } + \bar{p} \bigg ) \partial _{0} \left[ 3 A + \nabla ^{2} B \right] = 0 . \end{aligned}$$
(19)

These are constraints on the perturbation evolutions, by which we shall obtain the IMSE in the next subsection. Note that the perturbation equations differ from the non-improved ones only in changing \(G_{0}\) to G(t), as is expected in the equation of motion improvement method.

3.2 IMSE

Assuming the inhomogeneity of CMB to be produced by the perturbation of the background inflation field \(\bar{\varphi }\), the action functional would be

$$\begin{aligned} S= & {} S_{\text {Gravity}}+\int \mathrm{{d}}^{4}x \sqrt{-g} \nonumber \\&\times \left[ -\frac{1}{2} g^{\alpha \beta } \partial _\alpha \bar{\varphi } \partial _\beta \bar{\varphi } - V(\bar{\varphi }) - 2 M_\mathrm{Pl}^{2} \Lambda \right] , \end{aligned}$$
(20)

where \( M_\mathrm{Pl}^{2} = (8 \pi G_{0} )^{-\frac{1}{2}}\) is the reduced Planck mass.

The dynamics of the model is given by the Friedmann equation for the classical background field \(\bar{\varphi }\):

$$\begin{aligned} H^{2} = \frac{8 \pi G_{0}}{3} \bigg ( \bar{\rho }_\varphi + \bar{\rho }_\Lambda \bigg ), \end{aligned}$$
(21)

where \( \bar{\rho }_\varphi = \frac{1}{2} \dot{\bar{\varphi }}^{2} + V(\bar{\varphi }) \) and \( \bar{\rho }_\Lambda = \frac{\Lambda (t)}{8 \pi G(t) } \), with the improved conservation equation (because of the improved Einstein equation \(G_{\mu \nu }=-\,8\pi G(t) T_{\mu \nu }\)):

$$\begin{aligned} \dot{\bar{\rho }} = -3 H ( \bar{\rho } + \bar{p} ) - \frac{\dot{G(t)}}{G(t)} \bar{\rho }, \end{aligned}$$
(22)

where \( \bar{\rho } = \bar{\rho }_\varphi + \bar{\rho }_\Lambda \) and \(\bar{p} = \bar{p}_\varphi + \bar{p}_\Lambda \) are the total density and power, respectively. Note that the dynamics of the background field is assumed to be not affected by the improvement and the effect of RG improvement on the perturbations would be investigated.

Eliminating the potential of the scalar field using (21) and (22), the time evolution of the scalar non-perturbed field would be given by

$$\begin{aligned} \dot{\bar{\varphi }}^{2} = \frac{1}{4 \pi G(t)} \bigg ( H \frac{\dot{G}(t)}{2 G(t)} - \dot{H} \bigg ) . \end{aligned}$$
(23)

In order to get the evolution equation of the gauge invariant quantity, we have to fix the gauge. We take the same gauge as in [23] and consider \( \delta \varphi _{q} = 0 \) and \( B_{q} = 0 \) to find \(R_q\). Hence \(\delta u \) vanishes. Indeed, perturbations of pressure and density in this gauge are \( \delta \rho _{\varphi } = \delta p_{\varphi } = -\frac{1}{2} E \dot{\bar{\varphi }}^{2} \). Therefore the energy-momentum conservation (19) leads to

$$\begin{aligned}&- \frac{2}{a} H \nabla ^{2} F - \ddot{A} + \frac{\dot{A}}{\frac{\dot{G}(t)}{2 G(t)}} \bigg ( - \frac{G(t)}{2} \frac{\mathrm{d}}{\mathrm{d} t} \bigg (\frac{\dot{G}(t)}{G(t)^{2}} \bigg )\nonumber \\&+\, G(t) \frac{\mathrm{d}}{\mathrm{d} t} \bigg ( \frac{\dot{H}}{H G(t)} \bigg ) + 3 \dot{H} -\frac{3}{2} H \frac{\dot{G}(t)}{G(t)} \bigg ) = 0. \end{aligned}$$
(24)

It is worth noting that the improvement given by the solutions of RGE does not change Eqs. (14) and (16), but the conservation equation of the background field changes, as given by (24), since the scalar field exchanges energy with the quantum improved part. This energy exchange can be seen more explicitly in Eq. (22) where the dynamics of the scalar field is under the influence of the improvement term, \(\frac{1}{\bar{\dot{\varphi }}} \bigg ( \frac{\dot{\Lambda }(t)}{8 \pi G(t)} - \frac{\Lambda (t) \dot{G(t)}}{8 \pi G(t)^{2}} \bigg ) \).

Substituting \( E = \frac{\dot{A}}{H} \) from (16) and using (14), the evolution equation of A can be written in the form

$$\begin{aligned}&\ddot{A} + \dot{A} \bigg ( 3 H - \frac{2 \dot{H}}{H} + \frac{\ddot{H}}{\dot{H}} + \frac{\dot{G}(t)}{2 G(t)} \frac{H}{\dot{H}} \frac{\mathrm{d}}{\mathrm{d} t} \ln \bigg (\frac{G(t)^{2} \dot{H}}{\dot{G}(t) H^{3}}\bigg ) \bigg ) \nonumber \\&\quad -\, a^{-2} \nabla ^{2} A = 0. \end{aligned}$$
(25)

As mentioned previously, working with Fourier modes is easier, and thus in what follows we use Fourier transformed equations.

It is clear that the scalar perturbations of metric would not be invariant under a transformation of \( x^{\alpha } \rightarrow x^{\alpha } + \xi ^{\alpha } \). The mentioned transformation changes the perturbation \(A_{q}\) to \( \tilde{A}_q = A_{q} + H(t)\xi ^{0} \). To have a covariant description, usually in the non-improved theory the gauge invariant quantity \( R_{q} \equiv -\frac{A_{q}}{2} + H\delta u_{q} \) is defined. Since in this special gauge the coefficients of G(t) in Eqs. (14) and (16) vanish, the corrections due to running couplings do not affect the scalar perturbations. The corrections manifest themselves in the conservation equation of the background flow. The Hubble parameter, H(t), has a correction term in \(R_{q}\) which leads to a second order perturbation in gauge invariant quantity and can be ignored. Therefore, the non-improved form of the gauge invariant quantity saves its invariance after improvement of the couplings. On the other hand the assumption \( -q\tau \ll 1 \) at the late time of inflation causes the ignorance of the term \( H\delta u_{q} \) with respect to the scalar metric perturbation, \( \frac{A_{q}}{2} \), in \(R_{q}\).

Finally, considering the conformal time as an independent variable, \( R_{q} \) evolves as

$$\begin{aligned} R_{q}'' \,+\, \bigg ( \frac{\mathrm{d}}{\mathrm{d}\tau } \ln \bigg ( \frac{a H'}{H^{2}}\bigg ) \,+ \,\frac{G'}{2 G} \frac{H}{H'} {\frac{\mathrm{d}}{\mathrm{d}}\tau } \ln \bigg (\frac{G^{2} H'}{G' H^{3}}\bigg )\bigg ) R_{q}' \,+\, q^{2} R_{q} \!=\! 0. \end{aligned}$$
(26)

Here the prime denotes the derivative with respect to the conformal time. This is the improved Mukhanov–Sassaki equation (IMSE).

Denoting the coefficient of \( R_{q}^{'} \) by \( S(\tau ) \):

$$\begin{aligned} S(\tau )= \frac{\mathrm{d}}{\mathrm{d}\tau } \ln \bigg (\frac{a H'}{H^{2}}\bigg ) + \frac{G'}{2 G} \frac{H}{H'} \frac{\mathrm{d}}{\mathrm{d}\tau } \ln \bigg (\frac{G^{2} H'}{G' H^{3}}\bigg ), \end{aligned}$$
(27)

we see that it can be decomposed as

$$\begin{aligned} S(\tau ) = S_0(\tau ) + S_{I}(\tau ), \end{aligned}$$
(28)

in which \( S_0(\tau ) = \frac{\mathrm{d}}{\mathrm{d}\tau } \ln \bigg ( \frac{a H'}{H^{2}} \bigg ) \), and \( S_{I}(\tau ) = \frac{G'}{2 G} \frac{H}{H'} \frac{\mathrm{d}}{\mathrm{d}\tau } \ln \bigg (\frac{G^{2} H'}{G' H^{3}}\bigg ) \) is the improved part. It can be seen that in the non-improved limit, where G and \( \Lambda \) are constants, Eq. (8), the MSE, is recovered.

4 Solutions of IMSE

In this section the solution of the IMSE for two cases will be obtained. First, for a model in which \( \Lambda _{0} = 0 \) and remaining zero as time passing. Second, for the \( \Lambda \)-inflation model. We shall see that IMSE can be solved iteratively for both cases.

4.1 Case I: \(\Lambda _0=0\)

The Friedmann equation and conservation equation in this case are

$$\begin{aligned}&H^{2} = \frac{8 \pi G(t)}{3} \bigg ( \frac{1}{2} \dot{\varphi }^{2} + V(\varphi ) \bigg ) \end{aligned}$$
(29)
$$\begin{aligned}&\dot{H} = -\,4 \pi G(t) \dot{\varphi }^{2} + \frac{H \dot{G}(t)}{2 G(t)}. \end{aligned}$$
(30)

Considering the well-known exponential potential \( V(\varphi ) = g e^{-\lambda \varphi }\), where g and \( \lambda \) are arbitrary real constants, the perturbed \( H = H_{0} +\tilde{\omega }H_{1} \) and \( \varphi = \varphi _{0} +\tilde{\omega }\varphi _{1} \) seem to be appropriate solutions for (29) and (30) up to first order. Substituting G(t) from (6) gives \( H_{1} \) and its time evolution, \( \dot{H_{1}} \), up to \( \mathcal {O}(1)\):

$$\begin{aligned} \tilde{\omega }H_{1}&= \frac{8 \pi G_{0}}{3} \frac{\epsilon }{\lambda }\tilde{\omega }\dot{\varphi }_{1} - \frac{\lambda }{6} \frac{3-\epsilon }{\epsilon } \frac{\tilde{\omega }\varphi _{1}}{t}\nonumber \\&\quad -\, \frac{8 \pi G_{0}}{3} \frac{\epsilon }{\lambda ^{2}} \frac{\tilde{\omega }t_\mathrm{Pl}^{2}}{t^{3}} - \frac{3 - \epsilon }{6 \epsilon } \frac{\tilde{\omega }t_\mathrm{Pl}^{2}}{t^{3}} , \end{aligned}$$
(31)
$$\begin{aligned} \tilde{\omega }\dot{H_{1}}&= \frac{16 \pi G_{0}}{\lambda ^{2}} \frac{\tilde{\omega }t^{2}_\mathrm{Pl}}{t^{4}} -\frac{16 \pi G_{0}}{\lambda } \frac{\tilde{\omega }\dot{\varphi }_{1}}{t} + \frac{1}{\epsilon } \frac{\tilde{\omega }t^{2}_\mathrm{Pl}}{t^{4}}, \end{aligned}$$
(32)

where \( \epsilon \equiv -\frac{\dot{H}_{0}}{H_{0}^{2}} \) is a positive dimensionless quantity. Suggesting power-law solutions of the form \( H_{1} = \frac{b}{t^{3}} \) and \( \varphi _{1} = \frac{c}{t^{2}} \) and determining the coefficients b and c by substitution in (29) and (30), one obtains the Hubble parameter and the scalar fields in the RG improvement approach up to first order:

$$\begin{aligned}&\varphi = \frac{1}{\lambda } \ln \bigg ( \frac{8 \pi G_{0} g \epsilon ^{2} t^{2} }{3-\epsilon }\bigg ) + \frac{\tilde{\omega }t^{2}_\mathrm{Pl}}{\bigg (16 \pi G_{0} \epsilon \bigg )^{\frac{1}{2}} \bigg ( \epsilon -1 \bigg ) }\frac{1}{t^{2}} , \end{aligned}$$
(33)
$$\begin{aligned}&H = \frac{1}{\epsilon t} - \frac{2\tilde{\omega }t^{2}_\mathrm{Pl}}{3\bigg (\epsilon -1\bigg )} \frac{1}{t^{3}} . \end{aligned}$$
(34)

The independent variable in the IMSE is the conformal time, \( \tau \). To determine \( t(\tau ) \), the scale factor a(t) is necessary. Since \( H = \frac{\dot{a}(t)}{a(t)} \), the scale factor becomes

$$\begin{aligned} a(t) = \tilde{a}_* t^{\frac{1}{\epsilon }} e^{-\frac{\gamma }{t^2}}, \end{aligned}$$
(35)

where \(\gamma =\frac{\tilde{\omega }t_\mathrm{Pl}^{2}}{3(1-\epsilon )} \), and \(\tilde{a}_*\) is a constant. Then the conformal time becomes

$$\begin{aligned} \tau = \int ^{t}_{t_{*}\rightarrow \infty } \frac{\mathrm{d}t'}{a(t')} = \frac{1}{\tilde{a}_*} \bigg ( \frac{\epsilon }{\epsilon -1} t^{\frac{\epsilon -1}{\epsilon }} - \frac{\epsilon \gamma }{\epsilon +1} t^{-\frac{\epsilon +1}{\epsilon }} \bigg ) . \end{aligned}$$
(36)

Inverting this, it can be shown that

$$\begin{aligned} t = \bigg ( \frac{\tau }{C} \bigg )^{\frac{1}{1-\frac{1}{\epsilon }}} + \frac{D}{\frac{1}{\epsilon }-1} \bigg ( \frac{\tau }{C} \bigg )^{\frac{-1}{1-\frac{1}{\epsilon }}} \end{aligned}$$
(37)

where \( C = \frac{\epsilon }{\epsilon -1} \frac{1}{\tilde{a_{*}}} \) and \( D = \frac{\tilde{\omega }t^{2}_\mathrm{Pl}}{3(1+\epsilon )} \).

Finally, to obtain the IMSE, we can use the above results to get

$$\begin{aligned} S_0(\tau )=-\frac{2}{1-\epsilon }\frac{1}{\tau } \end{aligned}$$
(38)

and

$$\begin{aligned} S_I(\tau )=-K \tau ^{\frac{1-3\epsilon }{\epsilon -1}} \end{aligned}$$
(39)

where \( K = \bigg (\frac{\epsilon }{(\epsilon -1)\tilde{a_{*}}}\bigg )^{\frac{2 \epsilon }{\epsilon -1}} \bigg (\frac{4\tilde{\omega }\epsilon (2 \epsilon ^{2}-3)}{3 (1-\epsilon )(1-\epsilon ^{2})}\bigg ) \).

Therefore the IMSE is given by

$$\begin{aligned} R''_{q} - \frac{2}{1-\epsilon } \frac{1}{\tau } R'_{q} + q^{2} R_{q} = K \tau ^{\frac{1-3\epsilon }{\epsilon -1}} R'_{q}. \end{aligned}$$
(40)

Since the right hand side of IMSE is just a small correction, we can solve it iteratively. At zeroth order of iteration, ignoring this term, the solution is Hankel functions \(H_{\alpha }^{(1)}(-q\tau )\) and \(H_{\alpha }^{(2)}(-q\tau )\). We choose the sub-horizon initial condition as \( \exp (-iq\tau )\) at large \(-q\tau \). This initial condition is the result of applying WKB methods suggesting a plane wave solution for the initial conditions at early times, \(\frac{q}{a} \gg H \), as in [23]. With the conditions

$$\begin{aligned} \frac{2\dot{\Lambda }(t)}{\dot{G}(t)}-\frac{2\Lambda (t)}{G(t)} \ll \frac{q^2}{a^2} \quad , \quad \frac{H\dot{G}(t)}{2 G(t)} \ll \frac{q^2}{a^2}, \end{aligned}$$

for the \(\Lambda \)CDM model of the universe, we have the same initial condition as for the non-improved model:

$$\begin{aligned}&\delta \varphi _q(t) \rightarrow \frac{1}{(2\pi )^{\frac{3}{2}} a(t) \sqrt{2 q}} \exp (-iq \tau ), \end{aligned}$$

which in the limit \( a(t)\rightarrow 0 \) causes \(R_q\) to approach \(- H\frac{\delta \varphi _q}{\dot{\bar{\varphi }}}\).

Since at large \(-q\tau \), \( H^{(1)}_{\alpha } (-q\tau ) \) tends to \( \sqrt{\frac{2}{\pi (-q\tau )}} \exp ( i(-q\tau ) - i\alpha \frac{\pi }{2} - i\frac{\pi }{4} ) \), the first Hankel function would be an appropriate choice. After renormalizing the zeroth order solution becomes

$$\begin{aligned} R_{q_{(0)}}(\tau ) = K'(-\tau )^\alpha H^{(1)}_\alpha (-q\tau ), \end{aligned}$$
(41)

where \( K' = \frac{-\lambda \sqrt{\pi }}{4 (2\pi )^{\frac{3}{2}} \epsilon }\left( \frac{\epsilon }{1-\epsilon }\right) ^{\frac{-1}{1-\epsilon }} \exp (\frac{i \pi \alpha }{2}+\frac{i \pi }{4}) \) and \( \alpha = \frac{\epsilon -3}{2(\epsilon -1)} \).

To obtain the solution of IMSE up to the next order of iteration we have to substitute the zeroth order solution in the right hand side of (40) and solve the equation. Defining

$$\begin{aligned}&\mathcal {F}_{\alpha } = (-q)^{3-2\alpha }\int _0^{-q\tau } \mathrm{{d}}(-q\tau )(-q\tau )^{2\alpha -4} J_\alpha (-q\tau ) \nonumber \\&\qquad \times \Big [\left. -q\tau H^{(1)}_{\alpha -1}(-q\tau ) + 2\alpha H^{(1)}_{\alpha }(-q\tau )+q\tau H^{(1)}_{\alpha +1}(-q\tau )\right] \nonumber \\&\qquad + \mathcal {D}_{1(\alpha )}(q), \end{aligned}$$
(42)
$$\begin{aligned}&\mathcal {G}_{\alpha } =(-q)^{3-2\alpha }\int _0^{-q\tau } d(-q\tau )(-q\tau )^{2\alpha -4} Y_\alpha (-q\tau ) \nonumber \\&\qquad \times \Big [ \left. -q\tau H^{(1)}_{\alpha -1}(-q\tau ) + 2\alpha H^{(1)}_{\alpha }(-q\tau )+q\tau H^{(1)}_{\alpha +1}(-q\tau )\right] \nonumber \\&\qquad + \mathcal {D}_{2(\alpha )}(q) , \end{aligned}$$
(43)

in which \( \mathcal {D}_{1(\alpha )}(q)\) and \(\mathcal {D}_{2(\alpha )}(q) \) are integration constants, the solution up to first order becomes

$$\begin{aligned}&R_{q(1)}(\tau ) = K' (-\tau )^{\alpha } \bigg ( H^{(1)}_\alpha (-q\tau ) -\frac{K \pi }{4} \nonumber \\&\quad \left[ \mathcal {F}_{\alpha } Y_\alpha (-q \tau )+\mathcal {G}_{\alpha } J_\alpha (-q\tau )\right] \bigg ). \end{aligned}$$
(44)

The perturbations outside the horizon are defined by the limit \( -q \tau \ll 1 \). At this limit, for \( \alpha > 0 \), the term \(J_\alpha (-q\tau )\rightarrow (\frac{-q\tau }{2})^{\alpha }\frac{1}{\Gamma (\alpha +1)} \) can be ignored with respect to \(Y_\alpha (-q \tau ) \rightarrow \frac{-\Gamma (\alpha )}{\pi } (\frac{-q\tau }{2})^{-\alpha }\). On the other hand, \(\mathcal {F}_\alpha \) at \( -q \tau \ll 1 \) becomes

$$\begin{aligned} \mathcal {F}_\alpha= & {} (-q)^{3-2\alpha } ( \mathcal {A}_{\alpha }(-q\tau )^{4\alpha -3} \nonumber \\&+ \mathcal {B}_{\alpha }(-q\tau )^{4\alpha -1} + \mathcal {C}_{\alpha }(-q\tau )^{2\alpha -1} )+ \mathcal {D}_{1(\alpha )}(q), \end{aligned}$$
(45)

with

$$\begin{aligned} \mathcal {A}_{\alpha }&= \frac{1}{4\alpha -3}\bigg (\frac{2^{1-2\alpha }\alpha }{\Gamma (1+\alpha )^2}\\&- \frac{i2^{1-2\alpha }(\cos ((-1+\alpha )\pi )\Gamma (1-\alpha )+\alpha \cos (\alpha \pi )\Gamma (-\alpha ))}{\pi \Gamma (1+\alpha )}\\&+\frac{2^{1-2\alpha }}{\Gamma (\alpha )\Gamma (1+\alpha )}\bigg ) , \\ \mathcal {B}_{\alpha }&= \frac{1}{4\alpha -1}\Bigg ( \frac{2^{-2\alpha }\alpha }{(1+\alpha )\Gamma (1+\alpha )^2} \\&+ \frac{i 2^{-1-2\alpha }\cos ((1+\alpha )\pi )\Gamma (-1-\alpha )}{\pi \Gamma (1+\alpha )}\\&+\frac{2^{-1-2\alpha }(1+2\alpha )}{\alpha (1+\alpha )\Gamma (\alpha )\Gamma (1+\alpha )}\\&+ \frac{i 2^{-1-2\alpha }(1+2\alpha )\cos ((-1+\alpha )\pi )\Gamma (1-\alpha )}{\pi \alpha (1+\alpha )\Gamma (1+\alpha )}\\&+ \frac{i2^{-2\alpha }\alpha \cos (\alpha \pi )\Gamma (-\alpha )}{\pi (1+\alpha )\Gamma (1+\alpha )}\\&- \frac{2^{-1-2\alpha }}{\Gamma (1+\alpha )\Gamma (2+\alpha )} \Bigg ) \end{aligned}$$
$$\begin{aligned} \mathcal {C}_{\alpha }&=\frac{1}{2\alpha -1}\\&\times \bigg ( -i\frac{-\alpha \Gamma (-1+\alpha )+\alpha ^2\Gamma (-1+\alpha )+\alpha ^2\Gamma (\alpha )+\Gamma (1+\alpha )-\alpha \Gamma (1+\alpha )}{2\pi (-1+\alpha )\alpha \Gamma (1+\alpha )} \bigg ). \end{aligned}$$

All this leads to the following relation for the perturbations outside the horizon:

$$\begin{aligned} R_{q}(\tau ) \longrightarrow R^{o}_{q}(\tau ) = \frac{-i K'}{8\pi } \Gamma (\alpha ) q^{-\alpha } \left[ 1-\frac{K\pi }{4} \mathcal {F}_{\alpha } \right] . \end{aligned}$$
(46)

The parameter \(\alpha \) will approach 3 / 2 on applying the slow roll condition, \( \epsilon \ll 1 \). Since \( -q \tau \ll 1 \), in the slow roll inflation, the terms \((-q\tau )^{4\alpha -3}=(-q\tau )^3 \) and \( (-q\tau )^{4\alpha -1}=(-q\tau )^5\) do not have any significant contribution in \(\mathcal {F}_{\alpha }\). Beside, if we consider the case in which the non-improved solution at \(\tau _0\) satisfies the initial condition \( R_{q_{(0)}}(\tau _0) = 0\), we obtain \( \mathcal {D}_{1(\alpha )}(q) = -\mathcal {C}_{\alpha }(-q\tau _{0})^{2\alpha -1}\). The gauge invariant quantity with this initial condition becomes

$$\begin{aligned} R^{o}_{q}(\tau ) = \eta q^{-3/2} \bigg ( 1 - \frac{K}{4\pi }\mathcal {C}_{\frac{3}{2}}\left[ (-q\tau )^2-(-q\tau _0)^2\right] \bigg ) \end{aligned}$$
(47)

where \(\eta = -i\frac{K'}{8\pi }\Gamma (\frac{3}{2})\) is a constant with the dimension of \([L]^{-1}\) and \(\mathcal {C}_{\frac{3}{2}} = -\frac{4i}{6\pi }\). Clearly the second term in the parentheses is a consequence of the improvement.

Before continuing, we have to note that here (26), the IMSE, for inflation with exponential potential \(V(\varphi ) = g \mathrm{{e}}^{-\lambda \varphi }\), was solved. One may wonder how the results depend on the specific inflationary model we used. Therefore, it seems appropriate to take a look at the other models such as the model due to Starobinsky [25] or chaotic inflation [26]. The former, which seems to have a compatible description of the CMB, is the result of a specific f(R) gravity (with \(f(R) = R + R^2/6M^2\)). The Starobinsky model in the Einstein frame (obtained by the conformal transformation \( g_{\mu \nu } \rightarrow \tilde{g}_{\mu \nu } = \mathrm{{e}}^{\sqrt{\frac{16\pi G}{3}}\varphi } g_{\mu \nu } \)) is described by the action

$$\begin{aligned} S = \int {\mathrm{d}^{4}x\sqrt{-\tilde{g}}\left( \frac{1}{16\pi G}\tilde{R}-\dfrac{1}{2}\tilde{g}^{\mu \nu }\partial _{\mu }\varphi \partial _{\nu }\varphi -V(\varphi )\right) }, \end{aligned}$$
(48)

where \(V(\varphi )=3M^2\left( 1-\mathrm{{e}}^{-\sqrt{\frac{16\pi G}{3}}\varphi }\right) ^2 / 32\pi G\). For the FRW background this leads to an inflationary scale factor \(a(t) \sim \mathrm{{e}}^{t^2/12 t_\mathrm{Pl}^2}\). Since we are interested in the effects of the improvement at the horizon exit time, and expanding \(t\simeq t_0+\delta t \) (with \(t_0\) much larger than \(t_\mathrm{Pl}\)), the behavior of the scale factor at times that we are interested in is given by

$$\begin{aligned} a(t) \sim \exp \bigg (\frac{t_{0}\delta t}{6t_\mathrm{Pl}^{2}}\bigg ) . \end{aligned}$$
(49)

This is a similar behavior to the one obtained by the exponential potential

$$\begin{aligned} a(t) \sim (t/t_\mathrm{Pl})^{1/\epsilon } \sim \exp \bigg (\frac{\bar{t}_{0}\delta t}{\epsilon t_\mathrm{Pl}^{2}}\bigg ) . \end{aligned}$$
(50)

A similar treatment is in order for the chaotic inflation models with potential \(V(\varphi ) = g \varphi ^n\). For example the scale factor for typical \(n=2\) is given as \(a(t) \sim \mathrm{{e}}^{-\alpha (\beta + t/t_\mathrm{Pl})^2}\), leading to the same behavior for the times that we are interested in.

This is what is expected, since all the inflationary models are built to purge the effects of the initial conditions, although they have different scale factors at the start of the inflation era.

As a result of the above discussion, one can conclude that although the details of the improved gauge invariant quantity (47) depend on the inflationary model used, the general behavior is the same. Because of this, we confine ourselves to Eq. (47) in the next sections.

4.2 Case II: \(\Lambda \)-inflation

For a \(\Lambda \)-inflation model we consider the running gauge coupling, \(\Lambda (t)\) and not the \(\varphi \)-field, as the agent that produces exponential expansion in the inflation era. Although this not a good model (because of giving a non-improved spectral index \(n_s=-2\)), we investigate it to see how the improvement affects such a model.

For simplicity, here we use the IMSE in terms of time t, instead of the cosmological time:

$$\begin{aligned} \frac{\mathrm{d}^2R_{q}}{\mathrm{d}t^{2}} + S(t) \frac{\mathrm{d}R_{q}}{\mathrm{d}t} +\frac{q^{2}}{a^{2}} R_{q} =0, \end{aligned}$$
(51)

in which

$$\begin{aligned} S(t) = 3 H - \frac{2 \dot{H}}{H} + \frac{\ddot{H}}{\dot{H}} + \frac{\dot{G}(t)}{2 G(t)} \frac{H}{\dot{H}} \frac{\mathrm{d}}{\mathrm{d} t} \ln \bigg (\frac{G(t)^{2} \dot{H}}{\dot{G}(t) H^{3}}\bigg ) . \end{aligned}$$
(52)

If we assume that the inflation field only produces the scalar perturbations and does not affect the expansion rate of universe, we can neglect \( \rho _\varphi \) with respect to \(\rho _\Lambda \). Substituting \( H = \sqrt{\frac{\Lambda (t)}{3}}\) and G(t) and \( \Lambda (t) \) from (6) and (7) in (52), we get

$$\begin{aligned} S(t) \simeq&+\frac{a_{0} \mathrm{{e}}^{\sqrt{\frac{\Lambda (t)}{3}} t}}{t} \left[ \alpha _1\beta _2 \bigg (\frac{t_\mathrm{Pl}}{t}\bigg )^{-2}\right. \nonumber \\&\left. + \bigg ( \alpha _{1} \gamma _{2}\!+\!\beta _{1}\beta _{2} \bigg ) \!+\! \bigg ( \alpha _{1} \delta _{2}\!+\!\beta _{1} \gamma _{2} + \gamma _{1}\beta _{2} \bigg )\bigg (\frac{t_\mathrm{Pl}}{t}\bigg )^{2} {} \nonumber \right. \nonumber \\&\left. +\bigg (\alpha _{1} \Sigma _{2} + \beta _{1} \delta _{2} + \gamma _{1} \gamma _{2} + \delta _{1} \beta _{2} \bigg )\bigg (\frac{t_\mathrm{Pl}}{t}\bigg )^{4} \right] \nonumber \\&+ \sqrt{3\Lambda _{0}} - \frac{5}{t} + \mathcal {O}\bigg (\bigg (\frac{t}{t_\mathrm{Pl}}\bigg )^{-5}\bigg ), \end{aligned}$$
(53)

where

$$\begin{aligned}&\alpha _{1} = -\frac{\Lambda _{0} \tilde{\omega }}{2 \tilde{\nu } m_\mathrm{Pl}^{2}}, \\&\beta _{1} = -\frac{\Lambda _{0}}{2 \tilde{\nu } m_\mathrm{Pl}^{2}} \left( -2 \Omega + \tilde{\omega ^{2}} \right) ,\\&\beta _{2} = -2 ,\\&\gamma _{1} = -\frac{\Lambda _{0}}{2 \tilde{\nu } m_\mathrm{Pl}^{2}} \left( -3 \Omega \tilde{\omega } + \frac{\tilde{\nu }\tilde{\omega }m_\mathrm{Pl}^{2}}{\Lambda _0} \right) ,\\&\gamma _{2} = -4 \left( \frac{\Omega }{\tilde{\omega }} - \tilde{\omega } \right) ,\\&\Sigma _{2} = -80 \Omega \left( \frac{\Omega }{\tilde{\omega }}-\omega \right) ,\\&\delta _{1} = -\frac{\Lambda _{0}}{2 \tilde{\nu } m_\mathrm{Pl}^{2}} \left( 2 \Omega ^{2} - 2 \Omega \frac{\tilde{\nu }m_\mathrm{Pl}^{2}}{\Lambda _{0}} +\frac{\tilde{\omega }^{2} \tilde{\nu }m_\mathrm{Pl}^{2}}{\Lambda _0} \right) ,\\&\delta _{2} = 16\left( \Omega +\left( \frac{\Omega }{\tilde{\omega }}-\tilde{\omega }\right) ^{2}\right) . \end{aligned}$$

In terms of the dimensionless time \( T =\frac{t}{t_\mathrm{Pl}}\) this reads

$$\begin{aligned} S(T)\simeq & {} +\frac{a_{0}}{T} \Bigl [ z_{1} T^{2} +z_{2} + z_{3}T^{-2} +z_{4}T^{-4} \Bigr ]\nonumber \\&+ \sqrt{3\Lambda _{0}}t_\mathrm{Pl} - \frac{5}{T} + \mathcal {O}\bigg (\bigg (\frac{t}{t_\mathrm{Pl}}\bigg )^{-5}\bigg ), \end{aligned}$$
(54)

where \(z_{1} = \alpha _1\beta _2\), \(z_{2} = \alpha _{1} \gamma _{2}+\beta _{1}\beta _{2}\), \(z_{3} = \alpha _{1} \delta _{2}+\beta _{1} \gamma _{2} + \gamma _{1}\beta _{2}\) and \(z_{4} = \alpha _{1} \Sigma _{2} + \beta _{1} \delta _{2} + \gamma _{1} \gamma _{2} + \delta _{1} \beta _{2}\). Since at the end of inflation

$$\begin{aligned}&z_{1}T_{EI}^2\simeq 1.32\times 10^{-12},\\&z_{2}\simeq -1.57\times 10^{-36},\\&z_{3}T_{EI}^{-2}\simeq 1.19\times 10^{-24},\\&z_{4}T_{EI}^{-4} \simeq -1.42\times 10^{-48}, \end{aligned}$$

we can ignore \(z_{2}\), \(z_{3} T^{-2}\), \(z_{4} T^{-4}\) and the constant \( \sqrt{3\Lambda _{0}}t_\mathrm{Pl} \). As a result the IMSE in this case is given by

$$\begin{aligned} \frac{\mathrm{d}^{2}R_{q}}{\mathrm{d}T^{2}} -\frac{5}{T} \frac{\mathrm{d}R_{q}}{\mathrm{d}T} +\mathcal {Q}^{2}_{q} R_{q} = a_{0} z_{1} T \frac{\mathrm{d}R_{q}}{\mathrm{d}T}, \end{aligned}$$
(55)

where

$$\begin{aligned} \mathcal {Q}_{q}=\frac{qt_\mathrm{Pl}}{a}\simeq \frac{qt_\mathrm{Pl}}{a_{0}}. \end{aligned}$$
(56)

It has to be noted that the term \(\frac{5}{T}\) comes from \(a\frac{\mathrm{d}}{\mathrm{d}t} \ln (a^2\sqrt{\frac{3}{\Lambda }}\frac{\dot{\Lambda }}{2\Lambda })\) and has the highest contribution in this model. In contrast, \(-a_{0} z_{1} T\) is a consequence of the running gravitational coupling.

Fig. 1
figure 1

The normalized non-improved (solid line) and improved (dotted line) correlation function versus the normalized wave number (q), with \(\epsilon =0.3\)

Full size image

In a very similar way like the previous subsection the solution to (55) can be obtained:

$$\begin{aligned} R_{q_{(0)}}(T) = K'' T^{3} H^{(1)}_{3} (\mathcal {Q}_{q} T) \end{aligned}$$
(57)

where \( K'' \) is a constant. It is notable that the parameter \(\alpha \) in the Hankel function \(H^{(1)}_{\alpha }(\mathcal {Q}_{q} T)\) is fixed now.

As for the previous model the solution in the next order of iteration can be obtained leading to the following perturbations outside the horizon:

$$\begin{aligned} R_{q}(T) \longrightarrow R^{o}_{q}(T) = \frac{-i K''}{8\pi } \Gamma (3) \mathcal {Q}_{q}^{-3} \left[ 1+\frac{a_{0} z_{1}\pi }{4} \mathcal {F}'_{3} \right] \end{aligned}$$
(58)

where

$$\begin{aligned} \mathcal {F}'_{3} = -\frac{i}{24\pi }\mathcal {Q}_{q}^{-2}[(\mathcal {Q}_{q}T)^{4}-(\mathcal {Q}_{q}T_{0})^{4})]. \end{aligned}$$
(59)

Putting everything in place, the gauge invariant quantity would be

$$\begin{aligned} R^{o}_{q}(T) \!= \!\frac{-i K''}{4\pi } \mathcal {Q}_{q}^{-3} \left[ 1\!-\!i\frac{a_{0} z_{1}}{96} \mathcal {Q}_{q}^{-2}[(\mathcal {Q}_{q}T)^{4}\!-\!(\mathcal {Q}_{q}T_{0})^{4})] \right] \!. \end{aligned}$$
(60)

In the next section, we shall investigate the effect of these improvements on the gauge invariant quantity on the power spectrum of perturbations for Case I, which is a realistic model.

5 Improved power spectrum

The freezing of a gauge invariant quantity after exiting from the horizon leads one to propose cosmological observable quantities such as the correlation function, \(\Phi (q)\), which is the Fourier transform of the 2-point function and gives us some information as regards the inhomogeneities. It is given by the relation

$$\begin{aligned} \langle R_q R^{*}_{q'}\rangle = (2\pi )^{3} \delta (q+q') \Phi (q). \end{aligned}$$
(61)

Using the results of the previous section we can easily obtain the correlation function for the first case (\(\Lambda _0=0\)) as

$$\begin{aligned} \Phi (q)\propto q^{-3}\left| \bigg ( 1+\frac{iK}{6\pi ^2} \bigg (\frac{q}{q_0}\bigg )^{2} \bigg ( 1-(\frac{\tau _0}{\tau })^2 \bigg )\bigg ) \right| ^{2}, \end{aligned}$$
(62)

in which q is normalized to \(q_{0}=1/\tau \). The normalized correlation function both in the non-improved and improved cases are plotted in Fig. 1.

One can see in this plot that the effect of improvement coming from the running couplings is to have a little larger correlation for large wave numbers.

The relative correction of the correlation function is shown in Fig. 2 for three different values of the slow roll parameter. It shows that the correction becomes smaller as the slow roll parameter decreases. This correction is about (for \(q=q_{0}\)) 5 % for \(\epsilon =0.300\), \(5\times 10^{{-2}}\) % for \(\epsilon =0.030\) and \(5\times 10^{-4}\) % for \(\epsilon =0.003\).

Fig. 2
figure 2

Relative deviation of improved correlation function from the non-improved one versus the normalized wave number. \(\epsilon =0.300\) for the solid curve, \(\epsilon =0.030\) for the dotted curve, and \(\epsilon =0.003\) for the dashed curve

Full size image

In order to obtain the power spectrum, note that the improved form of G(t) (6) quickly approaches \(G_0\) for larger times and thus can be considered constant after inflation and in the radiation and matter dominated era. This means that the non-improved growth of perturbations works also in this case and the transfer function does not have any improvement and is given by the standard one [23]. Therefore the power spectrum is given by

$$\begin{aligned} \mathcal {P}(\kappa )\propto \kappa \mathcal {T}^{2}(\kappa ) \Phi (\kappa ), \end{aligned}$$
(63)

where \(\mathcal {T}\) is the transfer function [23], \(\kappa =\sqrt{2} q/q_{EQ}\), \(q_{EQ}\simeq \Omega _{M}h^{2}/13.6\, \text {Mpc}\) (with \(\Omega _{M}\) the matter density parameter, and \(H=h\times 100 \, \text {km/s Mpc}\)) is the exit wave number at radiation–matter equality time, and

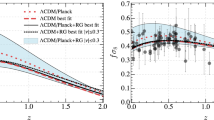
$$\begin{aligned} \Phi (\kappa ) \propto 1+\frac{\mathbf{Im }(K)}{6\pi ^2}\kappa ^2+\frac{\mathbf{Re }(K)^2+\mathbf{Im }(K)^2}{144\pi ^4}\kappa ^4. \end{aligned}$$
(64)

The result is plotted in Fig. 3 and the improved power spectrum is compared with the non-improved one.

Fig. 3
figure 3

Comparison of improved power spectrum with the non-improved one. The solid curve is the standard non-improved result, the dotted curve is improved with \(\epsilon =0.010\), the dashed curve with \(\epsilon =0.025\), and the dot–dashed curve with \(\epsilon =0.050\)

Full size image

As can be seen from this plot, the RG improvement changes slightly the power spectrum for large wave numbers. In order to see how much such an improvement is, the observational data and the obtained results are compared in Fig. 4.

The observational data are from [24], the solid curve is the non-improved power spectrum with the spectral index \(n_s=0.967\) (\(\kappa ^{n_s}\mathcal {T}(\kappa )\)). The dashed curve is the prediction of the improved model considered in this paper with the slow roll parameter \(\epsilon =0.008\). In both curves we choose \(\Omega _Mh=0.16\).

As is seen from the results, the effect of the improvement is to bring the tail of the graph up and leads to more accurate fit with the observed results.

Fig. 4
figure 4

Comparison of improved power spectrum with observational data. The solid curve is the standard non-improved result with \(n_s=0.967\) and \(\Omega _Mh=0.16\), the dashed curve is the improved result with \(\epsilon =0.008\) and \(\Omega _Mh=0.16\). The main effect of increasing the parameter \(\epsilon \) is to raise the tail of the improved power spectrum, as shown in the closeup

Full size image

6 Conclusions

As the asymptotically safe gravity leads to running gravitational and cosmological couplings, it is a natural question to look for its effect on the cosmological models. The effect of RG improvement of the couplings as a result of asymptotic safety becomes more important at early universe.

Here we have investigated the effect of running couplings on the curvature invariant as the seed for initial perturbations, by deriving the improved Mukhanov–Sassaki equation. We saw that this can be solved iteratively.

The gravitational coupling is almost constant in the radiation and matter dominated eras and thus the transfer function of perturbations to the power spectrum is not improved. We obtained the improved power spectrum and observed that it is slightly improved for large wave numbers. This means that the tail of the predicted power spectrum comes more closer to the observed data.