Abstract
Giving up the solutions to the fine-tuning problems, we propose the non-supersymmetric flipped \(SU(5)\times U(1)_X\) model based on the minimal particle content principle, which can be constructed from the four-dimensional SO(10) models, five-dimensional orbifold SO(10) models, and local F-theory SO(10) models. To achieve gauge coupling unification, we introduce one pair of vector-like fermions, which form a complete \(SU(5)\times U(1)_X\) representation. The proton lifetime is around \(5\times 10^{35}\) years, neutrino masses and mixing can be explained via the seesaw mechanism, baryon asymmetry can be generated via leptogenesis, and the vacuum stability problem can be solved as well. In particular, we propose that inflaton and dark matter particles can be unified to a real scalar field with \(Z_2\) symmetry, which is not an axion and does not have the non-minimal coupling to gravity. Such a kind of scenarios can be applied to the generic scalar dark matter models. Also, we find that the vector-like particle corrections to the \(B_s^0\) masses might be about 6.6%, while their corrections to the \(K^0\) and \(B_d^0\) masses are negligible.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is well known that a Standard Model (SM) like Higgs boson (h) with mass \(m_h=125.09 \,{\pm }\, 0.24\) GeV was discovered at the LHC [1,2,3], and thus the SM particle content has been confirmed. Moreover, there are many possible directions for new physics beyond the SM: supersymmetry, extra dimensions, strong dynamics or say composite Higgs field, extra gauge symmetries, and Grand Unified Theory (GUT), etc. However, we do not have any new physics signal at the 13 TeV Large Hadron Collider (LHC) yet. Therefore, we may need to reconsider the principle for new physics beyond the SM, and then propose promising models.
First, let us briefly review the convincing evidence for new physics beyond the SM
\(\bullet \) Dark Matter (DM) is a necessary ingredient of cosmology, considering the cosmic microwave background (CMB) or the rotation curves of spiral galaxies, etc [4, 5].
\(\bullet \) Dark energy (DE) is required due to the concordance of data from cosmic microwave anisotropy [4], galaxy clusters (see, e.g., [6]), and high-redshift Type-IA supernovae [7, 8].
\(\bullet \) The non-zero masses and mixing of neutrinos have been found from the atmospheric [9] and solar neutrino experiments [10], as well as the reactor anti-neutrino experiments [11], etc.
\(\bullet \) A larger fraction of baryonic matter is found compared to anti-matter in the Universe, i.e., the cosmic baryon asymmetry \(\eta = n_B/n_{\gamma } = 6.05 \pm 0.07 \times 10^{-10}\) [5].
\(\bullet \) The nearly scale-invariant, adiabatic, statistically isotropic, and Gaussian density fluctuations (see, e.g., [12]) point to cosmic inflation, which can solve the horizon and flatness problems of the Universe as well.
Second, there are two kinds of theoretical problems in the SM: fine-tuning problems and aesthetic problems. The fine-tuning problems are: (i) The cosmological constant problem: why is the cosmological constant so tiny? (ii) The gauge hierarchy problem: the SM Higgs boson mass square is not stable against quantum corrections and has quadratic divergences, while the electroweak scale is about 16 order smaller than the reduced Planck scale \(M_{\mathrm{Pl}}\simeq 2.43\times 10^{18}~\mathrm{GeV}\). (iii) The strong CP problem: the \(\theta \) parameter of Quantum Chromodynamics (QCD) is smaller than \(10^{-10}\) from the measurements of the neutron electric dipole moment [13, 14]. (iv) The SM fermion mass hierarchy problem: the electron mass is about 5 orders smaller than top quark mass. Also, the aesthetic problems are: (i) there is no explanation for the structure of gauge interactions; (ii) there is no explanation of fermion mass structures; (iii) there is no explanation for charge quantization; (iv) there is no realization of gauge coupling unification. The aesthetic problems can be solved in Grand Unified Theories (GUTs) if we can realize gauge coupling unification. In addition, the SM Higgs quartic coupling becomes negative around \(10^{9}\) GeV for central measured values of the SM parameters. Thus, the SM Higgs vacuum is not stable, which is called the stability problem [15,16,17]. Interestingly, the measured Higgs mass roughly corresponds to the minimal values of the Higgs quartic and top Yukawa coupling as well as the maximal values of the SM gauge couplings allowed by vacuum meta-stability [17]. In short, the SM vacuum might be meta-stable while not absolutely stable.
Neglecting the fine-tuning and aesthetic problems, Davoudiasl et al. proposed the New Minimal Standard Model (NMSM) to address the above new physics evidence based on the principle of the minimal particle content and most general renormalizable Lagrangian [18]. Dark energy is explained by a tiny cosmological constant, the dark matter particle is a real scalar with \(Z_2\) symmetry, the inflaton is another real scalar, neutrino masses and mixing can be addressed via the seesaw mechanism [19,20,21,22,23], and baryon asymmetry is generated via leptogenesis [24]. Interestingly, inflation is still consistent with current observations if we consider polynomial inflation [25], and the NMSM is still fine via meta-stability due to the minimality principle. Later, Asaka, Blanchet and Shaposhnikov proposed the \(\nu \)MSM to explain baryon asymmetry, neutrino oscillations, and dark matter via sterile right-handed neutrinos with masses around a few KeV [26, 27]. In 2015, Salvio proposed a simple SM completion [28]. Compared to the NMSM, the main differences are: (i) the dark matter candidate is the axion, and the strong CP problem is solved via the invisible axion model proposed by Kim, Shifman, Vainshtein, and Zakharov (KSVZ) [29, 30]; (ii) Higgs field as the inflaton. On the other hand, the string landscape can explain the cosmological constant problem and gauge hierarchy problem [31,32,33,34,35,36], but it cannot explain the strong CP problem [37]. However, for the non-supersymmetric KSVZ model, at least it is not clear whether the string landscape can stabilize the axion. This is the reason why Barger et al. proposed the intermediate-scale supersymmetric KSVZ axion model [38]. Also, there exists a serious difficulty for Higgs inflation since the scale of the Higgs field during inflation is larger than that of the perturbative unitarity violation [39, 40]. Recently, Ballesteros, Redondo, Ringwald and Tamarit proposed the SM Axion Seesaw Higgs portal inflation (SMASH) model [41, 42] to explain the above new physics evidence and the strong CP problem, where the axion is a dark matter candidate, as in Ref. [28].
In this paper, we still neglect the fine-tuning problems, and we study the Minimal GUT which can solve all the aesthetic problems in the SM. We consider the non-supersymmetric flipped \(SU(5)\times U(1)_X\) models [43,44,45]. To achieve gauge coupling unification, we introduce one pair of vector-like fermions, which form a complete \(SU(5)\times U(1)_X\) representation. This kind of models can be constructed in the four-dimensional SO(10) models [46], five-dimensional orbifold SO(10) models [47], and local F-theory SO(10) models [48, 49]. The doublet–triplet splitting problem can be solved at tree level, the proton lifetime is about \(5\times 10^{35}\) years, neutrino masses and mixing can be explained via the seesaw mechanism, baryon asymmetry can be generated via leptogenesis, and the stability problem can be solved as well. Especially, we for the first time show that inflaton and dark matter particle can be unified to a real scalar field with \(Z_2\) symmetry, unlike all the previous models where such a scalar is either an axion or has non-minimal coupling to gravity (Ricci scalar R) [28, 41, 42, 50,51,52]. In other words, this is a brand new unification of the inflaton and dark matter particle. After inflation, the interaction between inflaton and Higgs field is reduced to that in the NMSM. Thus, such a kind of scenarios can be applied to the general scalar dark matter models. Furthermore, we find that the corrections to the \(B_s^0\) masses from vector-like particles might be about 6.6%, while their corrections to the \(K^0\) and \(B_d^0\) masses are negligible.
2 Model building
We introduce three families of the SM fermions, two Higgs fields H and h, and one pair of vector-like particles (\(F_x\), \({\overline{F}}_x\)), whose quantum numbers under the \(SU(5)\times U(1)_{X}\) gauge group and SM particle contents are
where \(i=1, 2, 3\), and \(Q_i\), \(L_i\), \(U_i^c\), \(D_i^c\), \(L_i\), \(E_i^c\), \(N_i^c\), and H are the left-handed quark and lepton doublets, right-handed up-type quarks, down-type quarks, charged leptons, neutrinos, and Higgs field, respectively.
To break the \(SU(5)\times U(1)_{X}\) gauge symmetry down to the SM gauge symmetry, we introduce the following Higgs potential at the GUT scale:
where i, j, k, l, and m are SU(5) Lie algebra indices. After minimizing the potential, the \(\Phi \) field acquires a Vacuum Expectation Value (VEV) at \(<N^c_\Phi >=v_{\mathrm{GUT}}\) component, and then the \(SU(5)\times U(1)_X\) gauge symmetry is broken down to the SM gauge symmetry. As a result, \(Q_{\Phi }\) and the imaginary component of \(N^c_{\Phi }\) are eaten by superheavy gauge bosons, while \(D_\Phi ^c\) and the real component of \(N^c_{\Phi }\) acquire GUT-scale masses. The last term in Eq. (2) will generate the GUT-scale mass to \(D_\phi \) but not the SM Higgs doublet H. Thus, we naturally obtain the doublet–triplet splitting at tree level, but we do need fine-tuning to keep the doublet light due to quantum corrections.
The Yukawa coupling and vector-like mass terms are
where \(M_{\mathrm{Pl}}\) is the reduced Planck scale. Once \(\Phi \) field develops a VEV, the \(N^c_i\), \(N^c_x\), and \(N_x\) can obtain masses around \(10^{14}\) GeV times their corresponding Yukawa couplings. Assuming \(M_V \approx 1\) TeV and \( \mu _i \approx 0\) TeV, we have the vector-like particles \((Q_x,~Q_x^c)\) and \((D_x,~ D_x^c)\) at low energy without involving any more fine tuning. As shown previously, this particle content leads to gauge coupling unification [53,54,55,56,57,58]. The main difference is that these vector-like particles in our models form the complete GUT multiplets, which is an interesting point as well.
3 Gauge coupling unification
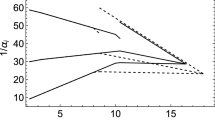
We study the gauge coupling unification by taking \(M_V =1~\mathrm{TeV}\) and \( \mu _i =0\) in Eq. (3) and using two-loop Renormalization Group Equations (RGEs). The result is given in Fig. 1. Defining the gauge coupling unification condition as \(\alpha ^{-1}_{\mathrm{GUT}} \equiv \alpha ^{-1}_{1}=( \alpha ^{-1}_{2}+ \alpha ^{-1}_{3})/2\), we obtain \(\alpha ^{-1}_{\mathrm{GUT}}=35.7\) and the GUT scale \(M_{\mathrm{GUT}}=2.2 \times 10^{16}\) GeV. The difference between \(\alpha ^{-1}_{\mathrm{GUT}}\) and \(\alpha ^{-1}_{2}/\alpha ^{-1}_{3}\) is about \(1.0\%\) or so. With the approximation formulas in Ref. [59], we obtain the proton lifetime for the decay channel \(p\rightarrow e^+ \pi ^0\) via heavy gauge boson exchanges to be around \(5\times 10^{35}\) years.
4 Dark energy
Similar to the NMSM, we simply postulate a cosmological constant of the observed size,
5 Neutrino masses and mixing and baryon asymmetry
The neutrino masses and mixing can be explained via the seesaw mechanism [19,20,21,22,23] since the right-handed neutrinos (and \(N_x^c/N_x\)) are very heavy from Eq. (3). Also, the baryon asymmetry can be explained via thermal leptogenesis [24]. The right-handed neutrinos are in the thermal equilibrium in the early Universe, and the lepton asymmetry is generated from the CP violating decays of the lightest right-handed neutrino when it is out of thermal equilibrium. The nonperturbative sphaleron interactions violate \(B+L\) but preserve \(B-L\), and then the baryon asymmetry is generated from the lepton asymmetry.
6 Dark matter and inflation
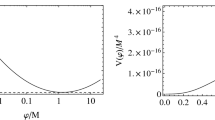
To unify the dark matter particle and the inflaton, we introduce a real scalar S with a \(Z_2\) symmetry so that it is stable. The potential for S and \(\phi \) is
where \(m_S\) is around the electroweak scale, and f is a mass parameter in the unit of the reduced Planck scale \(M_{\mathrm{Pl}}\). Thus, the inflaton potential is given by \(V_I(S)\), which is the \(\alpha \)-attractor model [60]. In terms of the well-known slow-roll parameters
where \(X' \equiv \mathrm{{d}}X/\mathrm{{d}}S\), the scalar spectral index, the tensor-to-scalar ratio, the running of the scalar spectral index, and the power spectrum are, respectively,
From the Planck, Baryon Acoustic Oscillations (BAO), and BICEP2/Keck Array data [61, 62], we have
\(n_s\) versus r plots compared with Planck 2015 results [61] for TT, TE, EE \(+\) lowP, at the 95% CL and 68% CL
In Fig. 2, we present the numerical results for r versus \(n_s\), where the inner and outer circles are \(1\sigma \) and \(2\sigma \) boundaries, respectively, from the Planck 2015 results [61] for TT, TE, and EE \(+\) lowP. Therefore, our model might be highly consistent with the experimental data. Because f is the only parameter which determines the inflationary observable \(n_s\), r, and \(\alpha _s\), we present the slow-roll parameters \(\epsilon \), \(\eta \), and \(\xi \) versus f in Fig. 3. Inflation ends when any slow-roll parameter violates the slow-roll condition. When \(f\le 1.0~M_{\mathrm{Pl}}\) and \(f\ge 3.3~M_{\mathrm{Pl}}\), \(\eta \) violates the slow-roll condition \(|\eta |<1\). When \(1.0~M_{\mathrm{Pl}}<f\le 3.0~M_{\mathrm{Pl}}\), \(\zeta \) violates the slow-roll condition \(|\zeta |<1\). When, finally, \(3.0~M_{\mathrm{Pl}}<f\le 3.2~M_{\mathrm{Pl}}\), \(\epsilon \) violates the slow-roll condition \(\epsilon <1\).
To have \((n_{s}, r)\) within the 1\(\sigma \) and 2\(\sigma \) regions of the Planck 2015 results for TT, TE, and EE\(+\) lowP in Fig. 2, we find that f should lie in the ranges \(0< f\le 13.4~M_{\mathrm{Pl}}\) for \(N=60\) and \(0< f\le 7.3~M_{\mathrm{Pl}}\) for \(N=50\), and in the ranges \(0< f\le 18.8~M_{\mathrm{Pl}}\) for \(N=60\) and \(0< f\le 11.2~M_{\mathrm{Pl}}\) for \(N=50\), respectively. The numerical values of \(\alpha _{s}\) are always very small, at the order of \(10^{-4}\). Also, the minimum of the inflaton potential \(V_I(S)\) is at \(\phi =0\), and interestingly, the inflaton potential will not give any mass to S due to \((d^2V_I(S)/dS^2)^{1/2}|_{S=0}=0\). Thus, after inflation, S becomes a dark matter particle, and its Lagrangian is reduced to that of the NMSM since \(V_I(S)\) is negligible at low energy. Therefore, S can be a viable dark matter candidate. The current viable parameter space is that the dark matter mass is close to 62.5 GeV via Higgs resonance for small k (\(k \sim 0.06\) or smaller), or the dark matter mass is larger than about 450 GeV for relatively large \(k \sim 0.2\) [63, 64]. Let us give a benchmark point with \(f=10.0~M_{\mathrm{Pl}}\). We obtain \(n_s=0.964592\), \(r=0.0442495\), \(\alpha _{s}=-0.0006154\) and \(N=60\) for the initial value \(S_i=15.3542 ~ M_{\mathrm{Pl}}\) and final value \(S_e=3.13524 ~ M_{\mathrm{Pl}}\) from the violation of the slow-roll condition, which fit the experimental data very well. Also, \(A=2.08924\times 10^{-9}~ M^4_{\mathrm{Pl}}\) can be determined from \(P_s=2.20\times 10^{-9}\). We expand \(V_I(S)\) at \(S=0\), and get
Therefore, \(V_I(S)\) can indeed be neglected at low energy.
7 Stability problem
We study the two-loop RGE running of the Higgs quartic coupling. Because it is very sensitive to the top quark mass, we consider the central value \(m_t=173.34~\mathrm{GeV}\) and \(1\sigma \) deviations of top quark mass [65]. The numerical results are given in Fig. 4. For comparison, we also present that in the SM by taking the central value of the top quark mass. In addition, we include the dark matter contribution from the k term in Eq. (5) by considering both the small \(k \sim 0.06\), and the relatively large \(k \sim 0.2\) for the viable dark matter parameter space [63]. We show numerically that the k term can indeed be neglected. Similarly, the Yukawa coupling \(\lambda \) in Eq. (2) between the SM Higgs field and GUT Higgs field can also be neglected if such a coupling is not large, for example, 0.5, because of its short RGE running. Therefore, to evade the stability problem, we predict the top quark mass to be smaller than its one sigma upper bound, \(m_t=174.1\) GeV. The key point is that the SM gauge couplings become stronger at high scale due to the extra vector-like particles.
8 Neutral meson mixing
We would like to demonstrate that the corrections to the neutral meson (\(B^0, K^0\)) mixing in our model satisfy the strict experimental constraints on the flavor changing neutral current processes. Here, we assume the mass of vector-like fermions is 1 TeV. The neutral meson mixing, like \(B_{d}^{0}\)–\({\overline{B}}_{d}^{0}\) and \(B_{s}^{0}\)–\({\overline{B}}_{s}^{0}\), is dominated by the box diagram in which top quark and vector-like up-type quark are running in the loop. In our model, the correct values of the SM quark masses and CKM mixing can be generated through the mixings of vector-like quarks with SM quarks [69]. We assume that all the elements in up-type and down-type quark mass matrices are zero except the top quark mass. We can use bi-unitary transformation to diagonalize the mass matrices in up-type and down-type sectors, and define a general \(5\times 5\) non-unitary CKM matrix, following the approach in Ref. [66]. Here, we present one of the realistic moduli examples of \(5\times 5\) non-unitary CKM matrix (\(V_{ab}\)) obtained in our model (see Eq. (3)),
We define \(\lambda _{qq^{'}}^{a} \equiv V_{aq'}^{*}V_{aq}\) for mesons with down quarks. The correction to the mixing \(\left( M_{12}\right) _{qq^{'}}\), which is the 12 element of \(2\times 2\) mass matrix in the neutral meson oscillation system, is
where \(qq^{'}\) stands for quarks participating in the box diagram leading to the neutral meson mixing [66]. \(S\left( x_{t}\right) \) and \(S\left( x_{U},\,x_{t}\right) \) are the IL functions defined as in Ref. [67], \(x_{t}=\left( m_{t}/M_{W}\right) ^{2}\) and \(x_{U}=\left( m_{U}/M_{W}\right) ^{2}\). Following their convention, the corrections with respect to the SM predictions are defined as \( \Delta \left( P_{0}\right) \equiv \left| \left( {M_{12}}/{M_{12}^{SM}}\right) _{P_{0}}\right| -1,~ \) where \(P_{0}\) could be \(K^{0}\), \(B_{d}^{0}\) and \(B_{s}^{0}\). Using the \(5\times 5\) CKM matrix shown above, we can obtain the corrections with respect to the SM predictions in our model \(\left( \Delta \left( K^{0}\right) ,~ \Delta \left( B_{d}^{0}\right) ,~ \Delta \left( B_{s}^{0}\right) \right) = \left( 5.5\cdot 10^{-5},~ 6.3\cdot 10^{-4},~ 0.066\right) \). Thus, the corrections to \(\Delta M_{K^{0}}\) and \(\Delta M_{B_{d}^{0}}\) are very small compared with the SM predictions. However, the correction to \(\Delta M_{B_{s}^{0}}\) in our model is 6.6%, which cannot be neglected.
9 Comments on reheating
The challenging question for our inflaton and dark matter unification scenario is reheating. There are two kinds of solutions: (i) Inflaton decay only occurs during the initial stage of field oscillations after inflation and then is kinematically forbidden at late time [68]. In this approach, we need to introduce two SM singlet fermions, and then it is not minimal. (ii) \(Z_2\) symmetry is broken at high scale at a meta-stable vacuum and thus the inflaton can decay for reheating. After the meta-stable vacuum decays into the real vacuum, the \(Z_2\) symmetry is restored, and then the inflaton is a dark matter candidate. Because the first solution has already been studied previously [68], we will not repeat it here. Thus, we shall briefly explain the idea for the second solution [69]. In this solution, we consider the following inflaton potential \(V_I(S)\):
where \(0< S_a< v_S< S_b < S_e\). To have the continuous inflaton potential, we require
at \(|S|= S_a\) and \(|S| = S_b\). Thus, \(\langle S \rangle =v_S\) is a meta-stable vacuum, and the \(Z_2\) symmetry is broken at this vacuum. With \(\lambda _S > k\), we have \(m_S > 2 m_\phi \) at the meta-stable vacuum, and S might decay into two Higgs particles. Thus, we can indeed realize the reheating. Moreover, we choose the proper parameters \(\Lambda _S\), \(\lambda _S\), and \(v_S\) so that the meta-stable vacuum can decay into the real vacuum with \(\langle S \rangle =0\) just after reheating. Thus, the \(Z_2\) symmetry will be restored, and S is a dark matter candidate as well. The detailed study will be given elsewhere [69].
10 Discussions and conclusion
We have proposed the non-supersymmetric minimal GUT with flipped \(SU(5)\times U(1)_X\) gauge symmetry and one pair of vector-like particles, which can incorporate all the convincing new physics beyond the SM based on the principle of the minimal particle content. The gauge coupling unification can be realized, the proton lifetime is about \(5\times 10^{35}\) years, and the doublet–triplet splitting problem at tree level as well as the stability problem can be solved. The possible signals from neutral meson mixing have been studied as well. Remarkably, we proposed a brand new scenario for the unification of inflaton and dark matter particle, which might be applied to the generic scalar dark matter models.
References
G. Aad et al., (ATLAS Collaboration), Phys. Lett. B 716, 1 (2012). arXiv:1207.7214 [hep-ex]
S. Chatrchyan et al., (CMS Collaboration), Phys. Lett. B 716, 30 (2012). arXiv:1207.7235 [hep-ex]
https://twiki.cern.ch/twiki/bin/view/AtlasPublic/HiggsPublicResults, Accessed 18 Nov 2017; https://twiki.cern.ch/twiki/bin/view/CMSPublic/PhysicsResultsHIG, Accessed 19 Oct 2017
D.N. Spergel et al., Astrophys. J. Suppl. 148, 175 (2003)
P.A.R. Ade et al., (Planck Collaboration), Astron. Astrophys. 594, A13 (2016). arXiv:1502.01589 [astro-ph.CO]
L. Verde et al., Mon. Not. R. Astron. Soc. 335, 432 (2002)
S. Perlmutter et al., Astrophys. J. 517, 565 (1999)
A.G. Riess et al., Astron. J. 116, 1009 (1998)
Y. Fukuda et al., Phys. Rev. Lett. 81, 1562 (1998)
S.N. Ahmed et al., Phys. Rev. Lett. 92, 181301 (2004). arXiv:nucl-ex/0309004
K. Eguchi et al., Phys. Rev. Lett. 92, 071301 (2004)
E. Komatsu et al., Astrophys. J. Suppl. 148, 119 (2003)
J.M. Pendlebury et al., Phys. Rev. D 92(9), 092003 (2015). https://doi.org/10.1103/PhysRevD.92.092003. arXiv:1509.04411 [hep-ex]
P. Schmidt-Wellenburg (2016). arXiv:1607.06609 [hep-ex]
G. Degrassi, S. Di Vita, J. Elias-Miro, J.R. Espinosa, G.F. Giudice, G. Isidori, A. Strumia, JHEP 1208, 098 (2012). arXiv:1205.6497 [hep-ph]
Y. Tang, Mod. Phys. Lett. A 28, 1330002 (2013). arXiv:1301.5812 [hep-ph]
D. Buttazzo, G. Degrassi, P.P. Giardino, G.F. Giudice, F. Sala, A. Salvio, A. Strumia, JHEP 1312, 089 (2013). arXiv:1307.3536 [hep-ph]
H. Davoudiasl, R. Kitano, T. Li, H. Murayama, Phys. Lett. B 609, 117 (2005). arXiv:hep-ph/0405097
P. Minkowski, Phys. Lett. 67B, 421 (1977)
M. Gell-Mann, P. Ramond, R. Slansky, in Supergravity, ed. by F. van Nieuwenhuizen, D. Freedman (North Holland, Amsterdam, 1979) p. 315
T. Yanagida, Proc. of the Workshop on Unified Theory and the Baryon Number of the Universe (KEK, Japan, 1979)
S. Weinberg, Phys. Rev. Lett. 43, 1566 (1979)
R.N. Mohapatra, G. Senjanovic, Phys. Rev. Lett. 44, 912 (1980)
M. Fukugita, T. Yanagida, Phys. Lett. B 174, 45 (1986)
T. Li, Z. Sun, C. Tian, L. Wu, Eur. Phys. J. C 75(7), 301 (2015). arXiv:1407.8063 [hep-ph]
T. Asaka, S. Blanchet, M. Shaposhnikov, Phys. Lett. B 631, 151 (2005). arXiv:hep-ph/0503065
T. Asaka, M. Shaposhnikov, Phys. Lett. B 620, 17 (2005). arXiv:hep-ph/0505013
A. Salvio, Phys. Lett. B 743, 428 (2015). arXiv:1501.03781 [hep-ph]
J.E. Kim, Phys. Rev. Lett. 43, 103 (1979)
M. Shifman, A. Vainshtein, V. Zakharov, Nucl. Phys. B 166, 493 (1980)
R. Bousso, J. Polchinski, JHEP 0006, 006 (2000). arXiv:hep-th/0004134
S. Kachru, R. Kallosh, A. Linde, S.P. Trivedi, Phys. Rev. D 68, 046005 (2003). arXiv:hep-th/0301240
L. Susskind, in ed. by C. Bernard. Universe or multiverse, pp. 247–266. arXiv:hep-th/0302219
M.R. Douglas, JHEP 0305, 046 (2003). arXiv:hep-th/0303194
F. Denef, M.R. Douglas, JHEP 0405, 072 (2004). arXiv:hep-th/0404116
S. Weinberg, Phys. Rev. Lett. 59, 2607 (1987)
J.F. Donoghue, Phys. Rev. D 69, 106012 (2004) [Erratum-ibid. D 69, 129901 (2004)] arXiv:hep-th/0310203
V. Barger, C.W. Chiang, J. Jiang, T. Li, Nucl. Phys. B 705, 71 (2005). arXiv:hep-ph/0410252
C.P. Burgess, H.M. Lee, M. Trott, JHEP 0909, 103 (2009). arXiv:0902.4465 [hep-ph]
J.L.F. Barbon, J.R. Espinosa, Phys. Rev. D 79, 081302 (2009). arXiv:0903.0355 [hep-ph]
G. Ballesteros, J. Redondo, A. Ringwald, C. Tamarit, Phys. Rev. Lett. 118(7), 071802 (2017). arXiv:1608.05414 [hep-ph]
G. Ballesteros, J. Redondo, A. Ringwald, C. Tamarit, JCAP 1708(08), 001 (2017). arXiv:1610.01639 [hep-ph]
S.M. Barr, Phys. Lett. B 112, 219 (1982)
J.P. Derendinger, J.E. Kim, D.V. Nanopoulos, Phys. Lett. B 139, 170 (1984)
I. Antoniadis, J.R. Ellis, J.S. Hagelin, D.V. Nanopoulos, Phys. Lett. B 194, 231 (1987)
C.S. Huang, T. Li, C. Liu, J.P. Shock, F. Wu, Y.L. Wu, JHEP 0610, 035 (2006). arXiv:hep-ph/0606087
S.M. Barr, I. Dorsner, Phys. Rev. D 66, 065013 (2002). arXiv:hep-ph/0205088
J. Jiang, T. Li, D.V. Nanopoulos, D. Xie, Phys. Lett. B 677, 322 (2009). arXiv:0811.2807 [hep-th]
J. Jiang, T. Li, D.V. Nanopoulos, D. Xie, Nucl. Phys. B 830, 195 (2010). arXiv:0905.3394 [hep-th]
A.G. Dias, A.C.B. Machado, C.C. Nishi, A. Ringwald, P. Vaudrevange, JHEP 1406, 037 (2014). arXiv:1403.5760 [hep-ph]
T. Tenkanen, JHEP 1609, 049 (2016). arXiv:1607.01379 [hep-ph]
R. Daido, F. Takahashi, W. Yin, JCAP 1705(05), 044 (2017). arXiv:1702.03284 [hep-ph]
U. Amaldi, W. de Boer, P.H. Frampton, H. Furstenau, J.T. Liu, Phys. Lett. B 281, 374 (1992)
J.L. Chkareuli, I.G. Gogoladze, A.B. Kobakhidze, Phys. Lett. B 340, 63 (1994)
J.L. Chkareuli, I.G. Gogoladze, A.B. Kobakhidze, Phys. Lett. B 376, 111 (1996)
D. Choudhury, T.M.P. Tait, C.E.M. Wagner, Phys. Rev. D 65, 053002 (2002)
D.E. Morrissey, C.E.M. Wagner, Phys. Rev. D 69, 053001 (2004)
I. Gogoladze, B. He, Q. Shafi, Phys. Lett. B 690, 495 (2010). arXiv:1004.4217 [hep-ph]
B. Dutta, Y. Gao, T. Ghosh, I. Gogoladze, T. Li, Q. Shafi, J.W. Walker, (2016). arXiv:1601.00866 [hep-ph]
R. Kallosh, A. Linde, D. Roest, JHEP 1311, 198 (2013). arXiv:1311.0472 [hep-th]
P.A.R. Ade et al., [Planck Collaboration], Astron. Astrophys. 594, A20 (2016). arXiv:1502.02114 [astro-ph.CO]
P.A.R. Ade et al., (BICEP2 and Keck Array Collaborations), Phys. Rev. Lett. 116, 031302 (2016). arXiv:1510.09217 [astro-ph.CO]
X.G. He, J. Tandean, JHEP 1612, 074 (2016). arXiv:1609.03551 [hep-ph]
M. Escudero, A. Berlin, D. Hooper, M.X. Lin, JCAP 1612, 029 (2016). arXiv:1609.09079 [hep-ph]
(ATLAS and CDF and CMS and D0 Collaborations), (2014). arXiv:1403.4427 [hep-ex]
F.J. Botella, G.C. Branco, M. Nebot, M.N. Rebelo, J.I. Silva-Marcos, arXiv:1610.03018 [hep-ph]
G.C. Branco, L. Lavoura, J.P. Silva, in “CP Violation,” Int. Ser. Monogr. Phys. vol. 103. (Oxford University Press, 1999)
M. Bastero-Gil, R. Cerezo, J.G. Rosa, Phys. Rev. D 93(10), 103531 (2016) arXiv:1501.05539 [hep-ph]
H.-Y. Chen, I. Gogoladze, S. Hu, T. Li, L. Wu, X. Zhang, in preparation
Acknowledgements
This research was supported in part by the Projects 11605049, 11475238 and 11647601 supported by National Science Foundation of China, and by Key Research Program of Frontier Sciences, CAS. The work of IG is supported in part by Bartol Research Institute.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3.
About this article
Cite this article
Chen, HY., Gogoladze, I., Hu, S. et al. The minimal GUT with inflaton and dark matter unification. Eur. Phys. J. C 78, 26 (2018). https://doi.org/10.1140/epjc/s10052-017-5496-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-017-5496-z