Generating a resonance-like structure in the reaction $B_c\rightarrow B_s \pi \pi$

Abstract

We investigate the process $B_c^+\rightarrow B_s^0\pi ^+\pi ^0$ via $B\bar{K}^*$ rescattering. The kinematic conditions for triangle singularities are perfectly satisfied in the rescattering diagrams. A resonance-like structure around the $B\bar{K}$ threshold, which we denote X(5777), is predicted to be present in the invariant mass distribution of $B_s^0 \pi ^+$. Because the relative weak $B\bar{K}$ $(I=1)$ interaction does not support the existence of a dynamically generated hadronic molecule, X(5777) can be identified as a pure kinematical effect due to the triangle singularity. Its observation may help to establish a non-resonance interpretation for some XYZ particles.

1 Introduction

Hadron spectroscopy, in particular due to the appearance of the so-called exotic states, is experiencing a renaissance in recent years. Since 2003, dozens of resonance-like structures have been observed by many experimental collaborations in various reactions. These structures are usually called XYZ particles, because most of them do not fit into the conventional quark model (QM), which has been very successful in describing the low-lying hadrons. These experimental observations have also inspired a flurry of theoretical investigations trying to understand their intrinsic structures. We refer to Refs. [1,2,3,4,5,6] for some recent reviews of the study of exotic hadrons. Among the popular theoretical interpretations of exotic hadrons, the multi-quark (tetraquark, pentaquark, etc.) interpretation usually tends to imply the existence of a large number of degenerate states. In contrast, the observed spectrum in experiments appears to be very sparse, which is a challenge for this interpretation. An intriguing characteristic of XYZ states is that many of them are located around two-hadron thresholds. This phenomenon can be considered evidence for regarding some XYZ states as hadronic molecules – bound systems of two hadrons analogous to conventional nuclei. The deuteron, which is composed of a proton and a neutron, is a typical example of a hadronic molecule. With proper interactions, the existence of molecular states composed of other hadrons is also expected. A prime example is $\Lambda (1405)$, which was predicted as a $\bar{K}N$ molecule long before the QM. In many cases, however, the detailed multi-hadron dynamics is not so well understood. For a recent review of hadronic molecules, see Ref. [7].

Concerning the underlying structures of those XYZ states, besides genuine resonances interpretations mentioned above, some non-resonance interpretations which connect the kinematic singularities of rescattering amplitudes with the resonance-like peaks were also proposed in the literature, such as the cusp model [8,9,10], or the triangle singularity (TS) mechanism. The TS mechanism was first noticed in 1960s [11,12,13,14]. Unfortunately, most of the proposed reactions at that time were lacking experimental data. It was rediscovered in recent years and used to interpret some exotic phenomena, such as the large isospin violation in $\eta (1405)\rightarrow 3\pi$, the production of the axial-vector state $a_1(1420)$, the production of the $Z_c^\pm (3900)$ and so on [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. It was shown that sometimes it is not necessary to introduce a genuine resonance to describe a resonance-like peak, because the TSs of rescattering amplitudes could generate bumps in the corresponding invariant mass distributions. Before claiming that a resonance-like peak corresponds to a genuine particle, it is also necessary to exclude or confirm the possibility of this non-resonance interpretation.

The TS peak usually appears in the vicinity of a threshold of scattering particles. From this point of view, the TS mechanism is similar to the hadronic molecule interpretation, and it also implies that the genuine dynamic pole may mix with the TS peak. This brings about some ambiguities in our understanding of the nature of some resonance-like peaks observed in experiments. If we can find some “clean” processes where the TS peaks can be distinguished from the genuine resonances, it may help us to establish the TS mechanism. Since the pole position of a genuine state should not depend on a specific process, while the TS peak is rather sensitive to the kinematic conditions, one would expect that a genuine state should still appear in the processes where kinematic conditions for the TS are not fulfilled, but the TS peak should disappear. Vice versa, if one observes a resonance-like peak in a process where the genuine state does not contribute but the TS kinematic conditions can be fulfilled, it will also help to verify the availability of TS mechanism. In this paper, we focus on a process through which the TS mechanism could be confirmed in experiments.

Fig. 1

$B_c^+\rightarrow B_s^0 \pi ^+\pi ^0$ via the triangle rescattering diagrams

2 TS mechanism

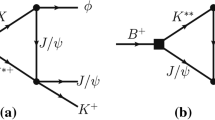
For the triangle diagram describing the rescattering process, such as the one in Fig. 1, there are two kinds of intriguing singularities which may appear in the amplitude. When only two of the three intermediate states are on-shell, the singularity at threshold is a finite square-root branch point, which corresponds to a cusp effect. In some special kinematical configurations, all of the three intermediate states can be on-shell simultaneously, and the momenta of $\bar{K}$ and B are parallel in the rest frame of $B_c^+$. In this case, the amplitude has a leading Landau singularity, which is usually called the TS. The TS may result in a narrow peak in the corresponding spectrum.

For the decay process $B_c^+\rightarrow B_s^0 \pi ^+\pi ^0$ via the $\bar{K}^*B \bar{K}$-loop in Fig. 1, we define the invariants $s_1\equiv p_{B_c^+}^2=m_{B_c^+}^2$, and $s_2\equiv (p_{B_s^0}+p_{\pi ^+})^2=M_{B_s^0\pi ^+}^2$. The position of the TS in the $s_1$ or $s_2$ complex plane of the scattering amplitude $\mathcal {A}(s_1,s_2)$ can be determined by solving the so-called Landau equation [12, 23, 35,36,37]. For Fig. 1a, by means of Eqs. (3) and (4) of Ref. [23], assuming we do not know the physical mass $m_{B_c^+}$, when $\sqrt{s_1}$ increases from 6.175 GeV, i.e. the $B\bar{K}^*$ threshold, to 6.294 GeV, the TS in $\sqrt{s_2}$ moves from 5.848 GeV to the $B\bar{K}$ threshold at 5.777 GeV. Vice versa, when $\sqrt{s_2}$ increases from 5.777 to 5.848 GeV, the TS in $\sqrt{s_1}$ moves from 6.294 to 6.175 GeV. These are the kinematical regions where the TS can be present in the physical rescattering amplitude. It is interesting to note that the mass of $B_c^+\sim 6.275$ GeV just falls into the TS kinematical region.

Taking Fig. 1a as an example, the physical picture concerning the TS mechanism can be understood like this: The initial particle $B_c^+$ first decays into $B^+$ and $\bar{K}^{*0}$, then the particle $\bar{K}^0$ emitted from $\bar{K}^{*0}$ catches up with $B^+$, and finally $B^+\bar{K}^0$ scatters into $B_s^0 \pi ^+$. This implies that the rescattering diagram can be interpreted as a classical process in space-time in the presence of TS, and the TS will be located on the physical boundary of the rescattering amplitude [12].

In Ref. [14], it was argued that, for the single channel rescattering process, when the corresponding resonance-production tree diagram is added coherently to the triangle rescattering diagram, the effect of the triangle diagram is nothing more than a multiplication of the singularity from the tree diagram by a phase factor. Therefore the TSs cannot produce obvious peaks in the Dalitz plot projections. This is the so-called Schmid theorem. But for the coupled-channel cases, the situation is different from the single channel case discussed in Ref. [14]. For the rescattering diagrams studied in this paper, the intermediate and final states are different, therefore the TS peak induced by the rescattering processes are still expected to be visible in the Dalitz plot projections. The reader is referred to Refs. [11, 38] for some comments about the Schmid theorem, and Refs. [39, 40] for more discussion of the coupled-channel case.

3 Rescattering amplitude

The $B_c^+$ meson, lying below the BD threshold, can only decay via weak interactions, and about $70\%$ of its width is due to c quark decay with the b quark as spectator [41]. The decay $B_c^+\rightarrow B^+ \bar{K}^{*0}$, as a Cabibbo-favored process, is expected to be one important nonleptonic decay mode of $B_c^+$ [42,43,44,45,46,47,48,49,50,51]. There is no direct measurement on this channel at present. Its branching ratio is usually predicted to be larger than $10^{-3}$, which implies the rescattering processes in Fig. 1 may play a role in $B_c^+\rightarrow B_s^0\pi ^+\pi ^0$. Following Refs. [42, 43], by means of the factorization approach, the decay amplitude can be expressed as

$$\begin{aligned} \mathcal {A}(B_c^+\rightarrow B^+ \bar{K}^{*0})= & {} \sqrt{2} G_F F_1^{B_c \rightarrow B_u} f_{{K}^*} m_{\bar{K}^*} \nonumber \\&\times (p_{B_c^+}\cdot \epsilon ^*_{\bar{K}^*}) V_{ud}^{} V_{cs}^* a_2, \end{aligned}$$

(1)

where $G_F$ is the Fermi coupling constant, $F_1^{B_c \rightarrow B_u}$ is the $B_c^+\rightarrow B^+$ transition form factor, $f_{{K}^*}$ is the decay constant of $K^*$, $V_{ud}^{}$, $V_{cs}^*$ are the CKM matrix elements, and $a_2$ is a combination of Wilson coefficients. For $B_c^+\rightarrow B^+ \bar{K}^{*0}$, the velocity of the recoiling $B^+$ is very low in the rest frame of $B_c^+$, and the wave functions of $B_c^+$ and $B^+$ overlap strongly. The form factor $F_1^{B_c \rightarrow B_u}$ is then expected to be close to unity [42, 43, 52]. In our numerical calculation, we take $F_1^{B_c \rightarrow B_u}=1$ as an approximation. The decay constant $f_{K^*}$ and coefficient $a_2$ are fixed to be $220\ \text{ MeV }$ and $-0.4$, respectively [43]. Concerning the other parameters in Eq. (1), we input the standard Particle Data Group values [53]. The branching ratio $Br(B_c^+\rightarrow B^+ \bar{K}^{*0})$ is then estimated to be around $3.8\times 10^{-3}$.

For $\bar{K}^*\rightarrow \bar{K}\pi$, the amplitudes read $\mathcal {A}(\bar{K}^{*0}\rightarrow \bar{K}^0\pi ^0)= 2G_V p_{\pi ^0} \cdot \epsilon _{\bar{K}^*}$, and $\mathcal {A}(\bar{K}^{*0}\rightarrow K^-\pi ^+)= -2\sqrt{2} G_V p_{\pi ^+} \cdot \epsilon _{\bar{K}^*}$, where the coupling constant $G_V$ can be determined by the decay width of the $\bar{K}^*$.

There have been many theoretical studies about the pesudo-Nambu–Goldstone bosons ($\pi$, K, etc.) scattering off the heavy–light mesons ($D^{(*)}$, $B^{(*)}$, etc.). By means of lattice QCD (LQCD) simulations and chiral extrapolation, in Ref. [54] the S-wave scattering length of the isoscalar DK channel $a_{DK}^{I=0}$ is predicted to be $-0.86\pm 0.03\,$fm at the physical pion mass. Employing both $\bar{s}c$ and DK interpolating fields, in Ref. [55] the authors performed a direct lattice simulation and obtain the DK scattering length $a_{DK}^{I=0}= -1.33(20)\,$fm at the pion mass $m_\pi =156\ \text{ MeV }$. It should be mentioned that in Ref. [56], the authors argued that the lattice ensemble for the $m_\pi =156\ \text{ MeV }$ datum has a rather small volume with $m_\pi L \simeq 2.3$, which is a bit too small for Luescher’s finite volume formalism to be strictly applicable, and thus this datum might bear a large systematic uncertainty. Anyway, the scattering length $a_{DK}^{I=0}$ is generally predicted to be large. The large negative scattering length $a_{DK}^{I=0}$ means the DK ($I=0$) interaction is strong, and further indicates the presence of an isoscalar state below threshold. It is generally supposed that the $D_{s0}^{*}(2317)$/$D_{s1}(2460)$ is the hadronic molecule dynamically generated by the strong DK/$D^*K$ ($I=0$) interaction in the coupled-channels dynamics [1, 54,55,56,57,58,59,60,61,62]. On the other hand, the scattering length of the isospin-1 DK channel $a_{DK}^{I=1}$ is predicted to be $0.07\pm 0.03 + i(0.17^{+0.02}_{-0.01})\,$fm in Ref. [54], which is much smaller than $a_{DK}^{I=0}$ and implies the DK ($I=1$) interaction is weak. According to the heavy quark spin and flavor symmetry, the above results can easily be extended to the ${B}^{(*)} \bar{K}$ cases. The bottom-quark counterpart of $D_{s0}^{*}(2317)$/$D_{s1}(2460)$ is ${B}_{s0}^*$/${B}_{s1}$, which is supposed to be the isoscalar ${B}\bar{K}$/${B}^*\bar{K}$ hadronic molecule. But ${B}_{s0}^*$ and ${B}_{s1}$ have not been observed in experiments yet. Being similar to the DK ($I=1$) interaction, the $B\bar{K}$ ($I=1$) interaction is also generally supposed to be weak. Within the framework of an unitary chiral effective field theory, the S-wave scattering length of isovector $B\bar{K}$ channel $a_{B\bar{K}}^{I=1}$ is predicted to be $0.02-0.23i\,$fm [61, 63]. The relative weak interactions in the $B\bar{K}$-$B_s\pi$ coupled-channels do not support the presence of an isovector hadronic molecule around $B\bar{K}$ threshold.

In 2016, the D0 collaboration reported the observation of a narrow structure X(5568) in the $B_s^0\pi ^\pm$ invariant mass spectrum [64]. Considering its mass and quark contents, some theorists suppose it could be an isovector hadronic molecule composed of $B\bar{K}$ [65]. Using a chiral unitary approach, the authors reproduce the reported spectrum of D0 collaboration. However, the authors of Ref. [65] also point out to reproduce the spectrum an “unnatural” cutoff $\Lambda \simeq 2.8\ \text{ GeV }$ is adopted in the T-matrix regularization, which is much larger than the “natural” value $\Lambda \simeq 1\ \text{ GeV }$. Furthermore, in Ref. [65], only the leading order (LO) potential was adopted, but in Ref. [61] it was shown that the LO potential cannot describe the LQCD scattering lengths of Ref. [54]. Employing the covariant formulation of the unitary chiral perturbation theory (UChPT), the authors found no bound state or resonant state via a direct searching on different Riemann sheets in Refs. [61, 63], where the driving potentials up to next-to-leading order (NLO) are constructed. In a recent experimental result reported by the LHCb collaboration [66], the existence of X(5568) is not confirmed based on their pp collision data, which makes the production mechanism and underlying structure of X(5568) more puzzling. In fact, right after the observation by D0, the possible existence of this state was challenged on theoretical grounds; see Refs. [67,68,69]. The reason of its appearance in the D0 and absence in LHCb and CMS experiments is discussed in Ref. [70].

What we are interested in this paper is not X(5568) but a predicted resonance-like peak denoted $X^\pm (5777)$ located around the $B\bar{K}$ threshold in the $B_s\pi ^\pm$ distributions. Because the existence of an isovector $B\bar{K}$ hadronic molecule is rather questionable, for the decay process $B_c^+\rightarrow B_s^0 \pi ^+\pi ^0$, if one finds a peak in the $B_s^0\pi ^+$ invariant mass spectrum around $B\bar{K}$ threshold, it is quite reasonable to suppose that the peak is induced by the TS mechanism as illustrated in Fig. 1.

For the vertex $B\bar{K}\rightarrow B_s\pi$ in Fig. 1, we employ the amplitude which is unitarized according to the method of UChPT  [71,72,73]. We consider the S-wave $B\bar{K}$ and $B_s\pi$ coupled-channel scattering. The unitary T-matrix is given by $T=(1-VG)^{-1}V$, where V stands for the S-wave projection of the driving potential, and G is a diagonal matrix composed of two-meson-scalar-loop functions [71,72,73]. We only focus on the S-wave scattering in this paper, because the higher partial wave contributions will be highly suppressed for the near-threshold scattering. In our numerical calculations, the NLO potential is used. For the pertinent low-energy-constants and subtraction constant, we adopt the values of Ref. [61], which are determined by fitting the recent LQCD result of Ref. [54]. See Refs. [54, 58, 61, 62, 71] for more details as regards the formulation of NLO potentials.

The rescattering amplitude of $B_c^+\rightarrow B_s^0\pi ^+\pi ^0$ via the $\bar{K}^{*0}(q_1) B^+(q_2) \bar{K}^0 (q_3)$ loop in Fig. 1a is given by

$$\begin{aligned}&\mathcal {A}_{B_c^+\rightarrow B_s^0\pi ^+\pi ^0}^{[ \bar{K}^{*0} B^+ \bar{K}^0 ]} = \frac{1}{i} \int \frac{\mathrm{d}^4q_3}{(2\pi )^4} \frac{\mathcal {A}(B_c^+\rightarrow B^+ \bar{K}^{*0}) }{ (q_1^2-m_{\bar{K}^*}^2 +i m_{\bar{K}^*}\Gamma _{\bar{K}^*}) } \nonumber \\&\quad \times \frac{ \mathcal {A}(\bar{K}^{*0}\rightarrow \bar{K}^0\pi ^0) \mathcal {A}(B^+\bar{K}^0\rightarrow B_s^0\pi ^+) }{ (q_2^2-m_{B^+}^2) (q_3^2-m_{\bar{K}^0}^2) } \mathbb {F}(q_3^2), \end{aligned}$$

(2)

where the sum over polarizations of intermediate state is implicit. The amplitude of Fig. 1b is similar to that of Fig. 1a. As long as the TS kinematical conditions are satisfied, it implies that one of the intermediate state ($\bar{K}^*$ here) must be unstable. It is necessary to take into account the width effect of the intermediate state. We therefore employ a Breit–Wigner (BW) type propagator in Eq. (2). The complex mass in the propagator will remove the TS from physical boundary by a small distance, and makes the physical scattering amplitude finite. Since the location of TS is not far from the physical boundary, the physical amplitude can still feel its influence. In Eq. (2), we also introduce a monopole form factor $\mathbb {F}(q_3^2)=(m_{\bar{K}}^2-\Lambda ^2 )/(q_3^2-\Lambda ^2)$ to account for the off-shell effect and kill the ultraviolet divergence that appears in the loop integral. In the future, this has to be replaced by a better regularization procedure.

Fig. 2

Simulated Dalitz plot of $B_c^+\rightarrow B_s^0 \pi ^+\pi ^0$ by only taking into account the rescattering processes in Fig. 1a, b. The parameter values $a_2=-0.4$ and $\Lambda =1\ \text{ GeV }$ are adopted

Fig. 3

Invariant mass distributions of $B_s^0\pi ^+$ via the rescatterings in Fig. 1. The vertical dashed line indicates the $B^+\bar{K}^0$ threshold

By only taking into account the rescattering processes in Fig. 1a, b, the simulated Dalitz plot of $B_c^+\rightarrow B_s^0\pi ^+\pi ^0$ is displayed in Fig. 2. The vertical and horizontal band in this Dalitz plot are associated with the TS of Fig. 1a in $M_{B_s^0\pi ^+}$ and the TS of Fig. 1b in $M_{B_s^0\pi ^0}$, respectively. The Dalitz plot projection in the invariant mass of $B_s^0\pi ^+$ is displayed in Fig. 3, where a narrow peak around 5.777 GeV can be seen. This resonance-like peak is what we call the X(5777). As analyzed above, X(5777), as discussed here, is not a dynamically generated pole in the coupled-channel dynamics. Its presence is due to the TS kinematical conditions being fulfilled in the rescattering diagram Fig. 1a. The relatively broader bump around 5.9 GeV or the dip around 5.82 GeV in Fig. 3 is due to the reflection of the horizontal band in the Dalitz plot of Fig. 2. It should be mentioned that in this paper we are only interested in the narrower resonance-like structure in the $B_s^0\pi ^+$ spectrum. Because for a state which decays into $B_s^0\pi ^+$ via strong interactions, it must contain at least four different valence quarks, or, in other words, its flavor quantum number must be exotic. However, for a state which decays into $B_s^0\pi ^0$, its flavor quantum number does not have to be exotic. The normal $\bar{b}s$ state can also decays into $B_s^0\pi ^0$ via the isospin-violation process.

For the two $B_s^0\pi ^+$ distribution curves in Fig. 3, the cutoff energy $\Lambda$ is taken to be 1 GeV and 3 GeV respectively. It can be seen that the lineshape is not sensitive to the value of $\Lambda$. The two curves nearly coincide with each other, even though the cutoff energies are rather different. One of the reasons is because the dominant contribution to the loop integral in Eq. (2) comes from the region where intermediate particles are (nearly) on-shell, i.e. when $q_3^2=m_{\bar{K}}^2$, $\mathbb {F}(q_3^2)$ gives 1. Furthermore, if we use extremely large values of $\Lambda$, the form factor $\mathbb {F}(q_3^2)$ will always be nearly 1 within a large integration interval.

It should be mentioned that in Eq. (2), one can use either $\mathbb {F}(q_1^2)$, $\mathbb {F}(q_2^2)$ or $\mathbb {F}(q_3^2)$ to kill the ultraviolet divergence. In this paper, $\mathbb {F}(q_3^2)$ is taken to be a monopole form factor, which is enough to kill the divergence. Introducing another similar form factor, such as $\mathbb {F}(q_2^2)$, is to some extent superfluous in the sense of killing divergence. In addition, we have shown that the numerical results are not sensitive to the cutoff energy $\Lambda$. Even if we introduce another form factor, $\mathbb {F}(q_2^2)$, to account for the off-shell effects of $\bar{K}^*$, it would not be sensitive to the corresponding cutoff either.

If the width of $\bar{K}^*$ is ignored, the TS in $M_{B_s^0\pi ^+}$ lies at 5.777 GeV, which nearly coincides with the $B\bar{K}$ threshold. Therefore, both the threshold cusp effect and the TS can contribute to the peak structure in Fig. 3. However, it should be mentioned that in Ref. [19] it was shown that the pure kinematic threshold cusp cannot produce a narrow peak in the invariant mass distribution in contrast with a genuine S-matrix pole. The two-body threshold singularity is a square-root branch point of the amplitude, whose contribution is finite and leads to the discontinuous first derivative on the peak of Fig. 3. But the sharp peak structure is dominantly generated by the TS, which is a logarithmic singularity. We refer to Refs. [19, 29] for more discussion of the threshold singularity and TS.

The program LoopTools [74] is employed to calculate the pertinent loop integrals in this paper.

4 Background analysis

The rescattering processes in Fig. 1 is just one of the contributions to three-body decay $B_c^+\rightarrow B_s^0\pi ^+\pi ^0$. Since the TS peak can appear in these diagrams, we define them as the “signal” processes. But the dominant contribution to $B_c^+\rightarrow B_s^0\pi ^+\pi ^0$ is expected to be via the process $B_c^+\rightarrow B_s^0 \rho ^+ \rightarrow B_s^0\pi ^+\pi ^0$. This is because compared to $B_c^+\rightarrow B_s^0 \rho ^+$, $B_c^+\rightarrow B^+ \bar{K}^{*0}$ is a color-suppressed process in the naive factorization approach. The branching ratio of $B_c^+\rightarrow B_s^0 \rho ^+$ is generally predicted to be larger than $1\%$ [43], which is about one order of magnitude larger than that of $B_c^+\rightarrow B^+ \bar{K}^{*0}$. To study the “signal” in the $B_s^0\pi ^+$ distribution, it is also necessary to know the influence of possible backgrounds, especially $B_c^+\rightarrow B_s^0 \rho ^+$.

Using the factorization approach, the amplitude of $B_c^+\rightarrow B_s^0 \rho ^+$ can be written as

$$\begin{aligned} \mathcal {A}(B_c^+\rightarrow B_s^0 \rho ^+)= & {} \sqrt{2} G_F F_1^{B_c \rightarrow B_s} f_\rho m_\rho \nonumber \\&\times (p_{B_c^+}\cdot \epsilon ^*_{\rho }) V_{ud}^{} V_{cs}^* a_1, \end{aligned}$$

(3)

where we use $F_1^{B_c \rightarrow B_s}=1$, $f_\rho =216\ \text{ MeV }$ in the numerical calculations [43]. For $B_c^+\rightarrow B_s^0 \pi ^+$, its amplitude is also proportional to $a_1$ in the factorization approach [43], and its branching fraction is measured to be about $10\%$ [75]. Using this branching fraction as an input, the coefficient $a_1$ is determined to be about 1.14, and the obtained branching ratio $Br(B_c^+\rightarrow B_s^0 \rho ^+ )$ is about $3.9\%$. The amplitude of $\rho ^+\rightarrow \pi ^+\pi ^0$ reads $\mathcal {A}(\rho ^+\rightarrow \pi ^+\pi ^0) = 4G_V p_{\pi ^0} \cdot \epsilon _{\rho }$. The complete amplitude of $B_c^+\rightarrow B_s^0\pi ^+\pi ^0$ is then given by

$$\begin{aligned} \mathcal {A}(B_c^+\rightarrow B_s^0\pi ^+\pi ^0) = e^{i\theta }\mathcal {A}_\rho ^{\text{ tree }} +\mathcal {A}^{\text{ loop }}\mathcal {F}(s_{\pi \pi }), \end{aligned}$$

(4)

with

$$\begin{aligned} \mathcal {A}_\rho ^{\text{ tree }}= & {} \sum _\mathrm{pol.} \mathcal {A}(B_c^+\rightarrow B_s^0 \rho ^+) \mathcal {A}(\rho ^+\rightarrow \pi ^+\pi ^0) \nonumber \\&\times \frac{i}{s_{\pi \pi }-{m}_\rho ^2+i m_\rho \Gamma _\rho } \end{aligned}$$

(5)

and

$$\begin{aligned} \mathcal {A}^{\text{ loop }}=\mathcal {A}_{B_c^+\rightarrow B_s^0\pi ^+\pi ^0}^{[ \bar{K}^{*0} B^+ \bar{K}^0 ]} + \mathcal {A}_{B_c^+\rightarrow B_s^0\pi ^+\pi ^0}^{[ \bar{K}^{*0} B^+ K^- ]}, \end{aligned}$$

(6)

where the normal BW type propagator is adopted in $\mathcal {A}_\rho ^{\text{ tree }}$. The factor $e^{i\theta }$ stands for the relative phase between $\mathcal {A}(B_c^+\rightarrow B_s^0 \rho ^+)$ and $\mathcal {A}(B_c^+\rightarrow B^+ \bar{K}^{*0})$, which is actually not fixed in the factorization approach. In Eq. (4), we also introduce a function $\mathcal {F}(s_{\pi \pi }=M_{\pi ^+\pi ^0}^2)$ to account for the strong $\pi \pi$ final-state interaction [16, 76, 77]. Due to the generalized Bose statistics, $\pi ^+\pi ^0$ can only stay in relative odd partial waves. For the lowest P-wave $\pi \pi$ scattering, the phase shift in the isospin-1 channel can be well reproduced by the intermediate $\rho$-meson exchange. The function $\mathcal {F}(s_{\pi \pi })$ can be further parametrized as $\mathcal {F}(s_{\pi \pi })=\alpha (s_{\pi \pi })/(s_{\pi \pi }-{m}_\rho ^2+i m_\rho \Gamma _\rho )$. $\alpha (s_{\pi \pi })$ is a polynomial function of $s_{\pi \pi }$, which should be fixed according to the experimental data. But since we are going to make a prediction here, we approximately take $\alpha (s_{\pi \pi })=s_{\pi \pi }-\overset{\circ }{m}_\rho ^2$, where $\overset{\circ }{m}_\rho$ is the bare mass of $\rho$ meson without the effect of $\pi \pi$ meson loop. By reproducing the P-wave $\pi \pi$ scattering phase shift data, $\overset{\circ }{m}_\rho$ is fixed to be 0.81 GeV according to a vector-meson-dominance model employed in Ref. [78]. This rather model-dependent scheme should eventually be replaced by taking a more improved spectral function; see e.g. Refs. [79,80,81,82] (and the references therein).

The significance of the TS signal mainly depends on the ratio $|\mathcal {A}^{\text{ loop }}/\mathcal {A}_\rho ^{\text{ tree }}|$, which is proportional to $|a_2/a_1|$. In most of the theoretical calculations [42,43,44,45,46,47,48,49,50,51], the ratio $R_{K^*/\rho }\equiv Br(B_c^+\rightarrow B^+ \bar{K}^{*0})/Br(B_c^+\rightarrow B_s^0 \rho ^+ )$ lies between 0.06 and 0.16. In order to account for this uncertainty, we fix $a_1=1.14$, and vary $a_2$ from $-\,0.31$ to $-\,0.51$ correspondingly.

One simulated Dalitz plot in terms of Eq. (4) is displayed in Fig. 4, where the parameters are fixed at some specific values. It can be seen that there is a narrow vertical band around $B\bar{K}$ threshold, which is associated with the TS of Fig. 1a in $M_{B_s^0\pi ^+}$. But compared with the $\rho$ resonance background, this vertical band is relatively weak. The reflection of the TS of Fig. 1b in $M_{B_s^0\pi ^0}$ is distributed over a relatively larger kinematic region in the $B_s^0\pi ^+$ invariant mass spectrum, of which the influence is even weaker. When we study the Dalitz plot projection in $M_{B_s^0\pi ^+}^2$, the structure induced by the reflection effect corresponding to Fig. 1b is very vague, which is different from the distribution curves of Fig. 3 without background.

Fig. 4

Simulated Dalitz plot of $B_c^+\rightarrow B_s^0 \pi ^+\pi ^0$ according to Eq. (4). The parameters $a_1=1.14$, $a_2=-0.4$, $\theta =\pi /2$ and $\Lambda =1\ \text{ GeV }$ are used in the numerical calculation

Fig. 5

Simulated $B_s^0\pi ^+$ distributions. The solid line indicates the background without contributions of Fig. 1. For $\theta =0$ and $\pi /2$ ($\pi$ and $3\pi /2$), the lower (upper) and upper (lower) boundary curves around 5.777 GeV correspond to $a_2=-0.31$ and $a_2=-0.51$, respectively

Fortunately, although the TS signal is relatively weak, it can still be well separated from the $\rho$ resonance in the Dalitz plot, which can be seen in Fig. 4. We can concentrate the discussion on the kinematic region around the $B\bar{K}$ threshold. Several simulated $B_s^0\pi ^+$ distribution curves are displayed in Fig. 5, where the relative phase $\theta$ is taken to be 0, $\pi /2$, $\pi$ and $3\pi /2$, respectively. The cutoff energy $\Lambda$ is fixed to be $1\,$GeV in the calculations. The $B_s^0\pi ^+$ distribution is dominated by the reflection of the $\rho$ resonance as illustrated in the Dalitz plot, but all of the four curves in Fig. 5 deviate significantly from the reflection around 5.777 GeV. When $\theta =0\ (\pi )$, there is a sudden fall (rise) in the distributions. When $\theta =\pi /2\ (3\pi /2)$, there is a narrow peak (dip) in the distributions. The TS of the rescattering process generates different structures due to different interferences. When $\theta =\pi /2$, by integrating over part of the phase space $5.72\ \text{ GeV }<M_{B_s^0 \pi ^+}<5.82\ \text{ GeV }$, it is estimated that the rescattering processes could contribute $4.4{-}7.5\%$ of the $B_c^+\rightarrow B_s^0\pi ^+\pi ^0$ yield, corresponding to $a_2$ varying from $-0.31$ to $-0.51$.

Another background may come from the isospin-violation process $B_c^+\rightarrow B_{s0}^{*}\pi ^+\rightarrow B_s^0\pi ^0\pi ^+$. But since the $B_{s0}^{*}$ peak in the $B_s^0\pi ^0$ distribution may not have a very large influence in the $B_s^0\pi ^+$ distribution, this contribution is neglected in the current work.

Finally, we give some estimations on the errors of the numerical results displayed above. The dominant uncertainty is from the ratio $|a_2/a_1|$, which is about $24\%$. Another uncertainty is from the coupling of $B\bar{K}\rightarrow B_s\pi$. In the framework of heavy meson chiral perturbation theory, the pertinent LO Lagrangian is only in relevant with the pion decay constant [54, 56,57,58,59,60,61,62], which is model independent. The contribution associated with the NLO Lagrangian is estimated to be around $4.1\%$ in our calculation, which depends on some parameters obtained by fitting the lattice data. We therefore estimate that the uncertainty from the coupling $B\bar{K}\rightarrow B_s\pi$ is about $4.1\%$. According to the results displayed in Fig. 3, it is roughly estimated that the uncertainty from the form factors is around $10\%$. Summing all the above uncertainties in quadrature we see that the total uncertainty is about $26\%$.

5 Summary

We have investigated the possibility of generating a resonance-like structure X(5777) in the $B_s^0\pi ^+$ distribution in reaction $B_c^+\rightarrow B_s^0\pi ^+\pi ^0$. There are several advantages that the proposed rescattering processes may help us to establish a non-resonance interpretation of some XYZ particles, i.e., the TS mechanism. First, the TS kinematical conditions are perfectly fulfilled in those triangle rescattering diagrams. Second, the weak $B\bar{K}$ $(I=1)$ interaction does not support the existence of a narrow dynamically generated resonant or bound state. Third, the relevant backgrounds in this channel are also expected to be simple. Therefore, if one observes the X(5777) structure in the invariant mass spectrum of $B_s^0\pi ^+$, it is very likely to conclude that this structure originates from the TS and is not a genuine particle. A similar analysis of this paper can be naively extended to the charge conjugate channel $B_c^-\rightarrow \bar{B}_s^0\pi ^-\pi ^0$.

We finally give a very preliminary estimation on the experimental feasibility of observing the TS phenomena discussed in this paper. Fixing the parameters $a_1=1.14$, $a_2=-0.4$ and $\theta =\pi /2$, in the kinematic region $5.72\ \text{ GeV }<M_{B_s^0 \pi ^+}<5.82\ \text{ GeV }$, we have $N_\mathrm{s}/N_\mathrm{b}\simeq 5.5\%$, where $N_\mathrm{s}$ and $N_\mathrm{b}$ represent the signal and background events associated with the rescattering processes and the $\rho$ resonance, respectively. If one requires the signal significance to be $N_\mathrm{s}/\sqrt{N_\mathrm{b}}=5$, we obtain $N_\mathrm{s}\simeq 455$ and $N_\mathrm{b}\simeq 8264$. This requirement further leads to the statement that around $9.6\times 10^5$ $B_c^+$ or $B_c^-$ evens are needed to observe the TS phenomena. The corresponding experiments may be done at LHCb. Note, however, a disadvantage for the proposed rescattering processes: there is a neutral pion in the final states. For the LHCb experiments, it is not easy to identify a neutral pion, and thus this poses a severe challenge.