Bouncing solutions from generalized EoS

Abstract

We present an exact analytical bouncing solution for a closed universe filled with only one exotic fluid with negative pressure, obeying a generalized equation of state (GEoS) of the form $p(\rho )=A\rho +B\rho ^{\lambda }$, where A, B and $\lambda$ are constants. In our solution $A=-1/3$, $\lambda =1/2$, and $B<0$ is kept as a free parameter. For particular values of the initial conditions, we find that our solution obeys the null energy condition (NEC), which allows us to reinterpret the matter source as that of a real scalar field, $\phi$, with a positive kinetic energy and a potential $V(\phi )$. We numerically compute the scalar field as a function of time as well as its potential $V(\phi )$, and we find an analytical function for the potential that fits very accurately with the numerical data obtained. The shape of this potential can be well described by a Gaussian-type of function, and hence there is no spontaneous symmetry minimum of $V(\phi )$. We show numerically that the bouncing scenario is structurally stable in a small vicinity of the value $A=-1/3$. We also include the study of the evolution of the linear fluctuations due to linear perturbations in the metric. These perturbations show an oscillatory behavior near the bouncing and approach a constant at large scales.

1 Introduction

Non-singular cosmologies such as described by an emergent or bouncing universe have been studied during the last decades as alternative scenarios to the inflationary paradigm, which is the one most widely accepted to describe the early universe [1, 2]. Nevertheless, in inflation the problem of the initial singularity still remains [3]. On the other hand, the scale-invariant spectrum of cosmological perturbations can be obtained in most inflationary models and one natural question is if in these non-singular scenarios a scale-invariant spectrum can also be obtained.

In the case of bouncing models the universe has emerged from a cosmological bounce, where the scale factor takes a non-zero minimum value so there is no initial singularity. Bouncing universes have been investigated in a wide variety of frameworks, which include higher order theories of gravity, scalar–tensor theories and braneworlds. See [4] for a detailed discussions of different approaches to obtaining bouncing solutions. A more recent review of bouncing models driven by quantum gravity, canonical quantum cosmology, ekpyrotic scenarios, string theory, galileons, massive gravity, Horǎva–Lifshitz, among others, is presented in [5].

In this paper our aim was to find bouncing solutions for a universe only filled with one exotic fluid with negative pressure, obeying a GEoS, in the framework of general relativity. It is worthwhile mentioning that in the case of Ref. [4], examples with GEoS in the framework of general relativity are scarcely mentioned, except in the discussion of a viscous fluid as a source, where the non-singular cosmological solutions found are unstable and display non-causal propagations, in the context of the Eckart approach for non-equilibrium thermodynamics. An inhomogeneous time-dependent EoS for the dark energy has also been discussed as the corresponding fluid-like description of modified theories of gravity (see [6]). In particular, inhomogeneous viscous fluids [7,8,9] were investigated in order to obtain bouncing solutions [10,11,12], leading to a bouncing cosmology. A common method of these articles consists in proposing different Ansatzes for the scale factor a(t)-displaying a bouncing behavior—which leads as a consequence to particular equations of state.

A wide variety of cosmological models have been investigated considering a GEoS of the form

$$\begin{aligned} p(\rho )=A\rho +B\rho ^{\lambda }, \end{aligned}$$

(1)

where $\rho$ is the energy density and p is the pressure of the fluid. The above factors A, B and $\lambda$ are constants. In the framework of general relativity the inclusion of Eq. (1) has been used to describe the behavior of the cosmic fluid components at early and late times, as well as the possible present phantom epoch. For example, at early times and aiming to extend the range of known inflationary behaviors, Barrow [13] assumed a GEoS with $A=-1$ and $B>0$, which corresponds to the standard EoS of a perfect fluid $p=(B -1)\rho$ when $\lambda =1$. A non-singular flat universe was found for the case $\lambda =1/2$ and $B <0$, representing an emergent cosmological solution. It is interesting to mention that the doubled exponential behavior of this solution was previously found for a bulk viscous source in the presence of an effective cosmological constant [14]. This is a consequence of the inclusion of bulk viscosity in Eckart’s theory, which leads to a viscous pressure $\Pi$ of the form $-3\xi H$, where $\xi$ is usually assumed to be of the form $\xi =\xi _{0} \rho ^{\lambda }$. Other emergent flat solutions were found by Mukherjee et al. [15] for $A >-1$ and $B >0$.

The GEoS represented in Eq. (1) can also be seen as the sum of the standard linear EoS $p=A\rho$ and a polytropic EoS with the polytropic exponent $\lambda = n/(n+1)$, where n is the polytropic index. Non-singular inflationary scenarios were investigated in [16] taking particular values for A, B, and $n>0$.

In the study of late time evolution of the universe, there has also been assumed a GEoS of the type given by Eq. (1), motivated by the fact that the constraints from the observational data imply $\omega \approx -1$ for the EoS of the dark energy component, if it is described by a barotropic EoS. Nevertheless, the values $\omega < -1$, corresponding to a phantom fluid, or $\omega > -1$, corresponding to quintessence, cannot be discarded. Within a phenomenological approach to phantom fluids, a GEoS of the form $p=-\rho -f(\rho )$, with $f(\rho )>0$, was proposed in [8, 17]. To overcome the hydrodynamic instability of a fluid with an EoS $p=w\rho$, with $w=const<0$, a general linear EoS of the form $p=A(\rho -\rho _{0})$ was postulated in [19], A and $\rho _{0}$ being constant and free parameters. This EoS corresponds to the particular choice $\lambda =0$ and $B=A\rho _{0}$ and was investigated as a dark fluid filling the universe. A bouncing solution was obtained when $1+A <0$ and $A\rho _{0}<0$. For a Bianchi-I cosmology, the inclusion of a perfect fluid obeying a GEoS with $\lambda =2$ leads to a great suppression on the anisotropies in the contracting phase of a bouncing cosmology [20, 21].

The case with $A=-1$ and $\lambda =1/2$ was considered in [8, 17, 18]. In both references the cosmological solutions of dark energy models with this fluid was analyzed, focusing in the future expansion of the universe. A late time behavior of a universe filled with a dark energy component with an EoS given by Eq. (1) has been investigated in [22, 23], where the allowed values of the parameters A and $\gamma$ were constrained using $\mathrm{H}(\mathrm{z})-\mathrm{z}$ data, a model-independent BAO peak parameter and a cosmic parameter (WMAP7 data).

Also theoretical studies like the so-called running vacuum energy in QFT (see [24,25,26]) give rise to a cosmological constant with a dynamical evolution during the cosmic time, which allows one to conclude that GEoS of the type of Eq. (1) could also effectively represent these scenarios under some specific assumptions.

In this paper we use a rather conservative setup, introducing a positive curvature and the particular values $A=-1/3$ and $\lambda =1/2$, letting $B<0$ be a free parameter of the model. With this choice the strong energy condition is violated, which is a condition to have bouncing solutions, but the NEC holds, and thus our particular GEoS has a parameter $\omega$ that evolves with cosmic time, but it lies in the range of quintessence fluids, for some choice of the initial conditions, except for $t\rightarrow \pm \infty$, where the fluid behaves like a cosmological constant. These particular values of A and $\lambda$ allow one to find an exact analytical bouncing solution for the scale factor, which for some initial conditions coincides with the usual de Sitter solution for a closed universe. This exact solution has the positive feature that it allows one to interpret the fluid involved by the GEoS of Eq. (1) in terms of known fluids. The importance of this result lies, contrarily to many investigations in which the scale factor a(t) is proposed as an Ansatz, from which different equations of state are derived, in the fact that we are proposing a physically well-motivated GEoS, which leads to a bouncing solution, which in addition happens to be analytic.

It has to be pointed out that the presence of a positive curvature leads to bouncing solutions with a matter content which has a strictly positive energy density. For bouncing models with a vanishing spatial curvature, the inclusion of negative energy fields is required. In the framework of general relativity it has been shown that, for a bouncing model dominated by a single exotic hydrodynamical perfect fluid, the adiabatic perturbations grow without bounds either at the bouncing point or at an exact time, when the NEC is violated or restored. Nevertheless, since NEC is not violated in our case, the solution is free of instabilities that may result, for example, from the introduction of ghost fields [27].

Reinterpreting the matter source in terms of a real scalar field, we can compute numerically the scalar field and its potential. We also found an analytical expression for this potential that fits very accurately the numerical solutions, with a coefficient of determination ($r^{2}$) equal to $r^{2}=0.99999$.

We also study the robustness of the bouncing solution when the GEoS is modified by including a perturbative term in the standard linear coefficient A. We find that under reasonable constraints on the perturbative parameter, the solution is analytic in $\epsilon$ and the first order correction allows one to extend the behavior of the bouncing solution beyond the value $-1/3$, for which an explicit analytic solution was found. The perturbative expansion leads us as well to conclude that the properties of the scalar potential (shape and minimum) proposed as the source for the effective equation of state are stable, provided $\epsilon$ remains small enough.

This paper is organized as follows. In Sect. 2 we present the particular considered GEoS and show the analytical bouncing solution found and the main properties. In particular, we present the evolution of the parameter $\omega$ with cosmic time, discussing its quintessential behavior and how this allows one to describe the matter content by the usual real scalar field with a potential. At the end of this section we study the evolution of linear scalar perturbations to the metric. In Sect. 3 we evaluate numerically the scalar field and its potential associated to our exact solution. We also find an analytical expression for this potential that fits the numerical results found. In Sect. 4 we investigate the stability of the bouncing solution when the GEoS is modified on disturbing the parameter A by a small quantity. So in this case, we perform a study of the structural stability under small variations of the parameter A. Finally, in Sect. 5 we discuss some features and their further possible applications to suitable bouncing models.

2 Exact bouncing solution from GEoS

In what follows we will discuss an analytical solution for a closed universe as found in [28], for the case in which the parameter A takes the value $-\,1/3$ and $\lambda =1/2$ in Eq. (1). As we discuss below, the $\omega = p/\rho$ parameter can represent phantom and quintessence fluid, depending on the initial conditions. This exact solution describes a bouncing universe, assuming that one fluid with a GEoS is present in the early universe.

We consider the Friedmann–Robertson–Walker metric,

$$\begin{aligned} \mathrm{d}s^{2}=-\mathrm{d}t^{2}+a(t)^{2}\left( \frac{\mathrm{d}r^{2}}{1-Kr}+r^{2}\mathrm{d}\theta ^{2}+r^{2}\sin ^{2}, \theta \mathrm{d}\phi ^{2}\right) , \end{aligned}$$

(2)

and the energy-momentum tensor for a perfect fluid, with energy density $\rho$ and pressure p,

$$\begin{aligned} T_{\mu \nu } = (\rho + p)u_{\mu }u_{\nu } -pg_{\mu \nu }, \end{aligned}$$

(3)

where we have chosen $8\pi G = 1 = c$.

For a universe with positive curvature ($K=1$), the equation of constraint of the Friedmann equations is given by ($\Lambda = 0$)

$$\begin{aligned} \rho =3\left( \frac{\dot{a}}{a}\right) ^{2}+\frac{3}{a^{2}}, \end{aligned}$$

(4)

and the equation of continuity by

$$\begin{aligned} \dot{\rho }+3H( \rho +p) =0. \end{aligned}$$

(5)

Using the change of variable $s=-\frac{2}{B\sqrt{3}}$ the GEoS of Eq. (1) can be rewritten as

$$\begin{aligned} p(\rho )=-\frac{1}{3}\rho -\frac{2}{s\sqrt{3}}\rho ^{1/2}. \end{aligned}$$

(6)

Solving the above equations one finds the following solution:

$$\begin{aligned} a(t)=s\left[ \cosh \left( \frac{t-t_{0}}{s}\right) -c\right] , \end{aligned}$$

(7)

where $t_{0}$ and c are integration constants. The bouncing solution is obtained when $s>0$. This solution represents a universe expanding exponentially for $t \in (-\infty ,\infty )$. The scale factor takes a minimum value $a(t=t_{0})= s(1-c)$. The positivity of the scale factor constrains c to be in the range $(-\infty ,1)$. Before we express c in terms of the initial energy density we evaluate H, $\dot{H}$ and $\ddot{H}$ using Eq. (7). Their expressions are the following:

$$\begin{aligned} H(u)= & {} \frac{\sinh (u)}{s(\cosh (u)-c)}, \end{aligned}$$

(8)

$$\begin{aligned} \dot{H}(u)= & {} \frac{1-c \cosh { \left( u\right) }}{ \left[ s(\cosh { \left( u\right) }-c) \right] ^{2}}, \end{aligned}$$

(9)

$$\begin{aligned} \ddot{H}(u)= & {} \sinh (u)\frac{c^{2}+c\cosh (u)-2}{s^{3}(\cosh (u)-c)^{3}}, \end{aligned}$$

(10)

where

$$\begin{aligned} u={t-t_{0}\over s}. \end{aligned}$$

(11)

For $c <0$ the Hubble parameter is a strictly increasing function, so there are no critical points and we have $H(t\rightarrow -\,\infty )= -\frac{1}{s}$ and $H(t\rightarrow \infty )= \frac{1}{s}$, then for late times this solution behaves like a de Sitter universe.

It is straightforward to evaluate the energy density as a function of the cosmic time using Eq. (4) and the expression for a(t) and H(t) given by Eq. (7) and Eq. (8), respectively. The expression for the energy density is then given by

$$\begin{aligned} \rho =\frac{3\cosh ^{2}(u)}{\left[ s(\cosh (u) -c)\right] ^{2}}. \end{aligned}$$

(12)

Using the initial conditions $a(t_{0})=a_{0}$ in (7) and $\rho (t_{0})=\rho _{0}$ in (12) we find that

$$\begin{aligned} \begin{array}{c} a_{0}=s(1-c), \quad 3=a_{0}^{2}\rho _{0}. \end{array} \end{aligned}$$

(13)

A dimensional restoration as regards Eq. (13) takes the following form:

$$\begin{aligned} \begin{array}{c} a_{0}=s(1-c)\frac{v^{2}}{R_{0}\sqrt{8\pi G}}, \quad \frac{v^{2}}{R_{0}^{2}}=\frac{8\pi G}{3}\rho _{0}a_{0}^{2}, \end{array} \end{aligned}$$

(14)

where v is the speed of light, $R_{0}$ is the radius of curvature, G is the gravitational constant and $\rho$ is the energy density. Because the model considers the universe with positive curvature, the radius of the curvature $R_{0}$ also is a free parameter.

A very special situation occurs for $c =0$ or equivalently $\rho _{0}=3/s^{2}$ and $a_{0}=s$, because the energy density preserves this constant value during all the cosmic evolution. It means that, for a closed universe with the EoS that we are considering, the universe expands with acceleration but the energy density remains constant, like in a de Sitter solution for a closed universe. Note that the Hubble parameter for the de Sitter solution is given by

$$\begin{aligned} H(t)=\sqrt{\frac{\lambda }{3}}\tanh \left( \sqrt{\frac{\lambda }{3}}(t-t_{0})\right) , \end{aligned}$$

(15)

and in our case Eq. (8) with $c =0$ takes a similar form:

$$\begin{aligned} H(t)=\frac{1}{s}\tanh \left( \frac{t-t_{0}}{s}\right) . \end{aligned}$$

(16)

In the next subsection we give an interpretation of the used GEoS in terms of well-known fluids.

2.1 Fluid sources of the bouncing solution

We can obtain the energy density as a function of the scale factor if we substitute Eq. (7) in Eq. (12),

$$\begin{aligned} \rho (a)=3\left( \frac{1}{s}+\frac{c}{a}\right) ^{2}. \end{aligned}$$

(17)

Introducing Eq. (17) in Eq. (6) we obtain the fluid pressure as a function of the scale factor,

$$\begin{aligned} p(a)=-\left( \frac{1}{s}+\frac{c}{a}\right) ^{2}-\frac{2}{s}\left( \frac{1}{s}+\frac{c}{a}\right) . \end{aligned}$$

(18)

Expanding the terms of the above expressions yields

$$\begin{aligned} \rho (a)= & {} \frac{3}{s^2}+\frac{6c}{sa}+\frac{3c^{2}}{a^{2}}=\rho _1+\rho _2+\rho _3, \end{aligned}$$

(19)

$$\begin{aligned} p(a)= & {} -\frac{3}{s^2}-\frac{4c}{sa}-\frac{c^{2}}{a^{2}}=p_1+p_2+p_3. \end{aligned}$$

(20)

Comparing each term of the expansions our fluid can be seen as the sum of three fluids with the EoS given by $\omega _{1}= p_{1}/\rho _{1}=-\,1$, $\omega _{2}= p_{2}/\rho _{2}=-\,2/3$ and $\omega _{3}= p_{3}/\rho _{3}=-\,1/3$, respectively. So the first fluid corresponds to a cosmological constant, the second one is a quintessence term and the last corresponds to a fluid which drives an expanding universe with zero acceleration. Notice that in the above decomposition the EoS of each fluid is constant. Therefore, each $\omega _{i}$ is independent of the parameters s, $t_{0}$ and c.

Lets us evaluate the EoS, $\omega = p/\rho$, for this fluid, which in terms of the cosmic time obeys the expression

$$\begin{aligned} \omega =-1+\frac{2c}{3\cosh \left( {t-t_{0}\over s}\right) }. \end{aligned}$$

(21)

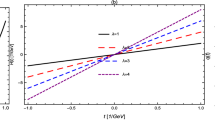
The lower plot in Fig. 1 depicts the behavior of this parameter $\omega$.

Fig. 1

Plot of the parameter $\omega$ given by Eq. (21), for the parameter values $c=\pm 0.5$, $s=1$ and $t_{0} =0$

Note that the GEoS becomes like a cosmological constant $\omega \rightarrow -1$ for $t\rightarrow \pm \infty$. For the case with $c =0.5$ the fluid described by the GEoS given in Eq. (21) behaves like quintessence for the lapse associated with the time of bouncing. For the case $c=-0.5$ the GEoS behaves like a phantom fluid within the period associated to the bouncing. We will focus on the particular interval $1>c>0$, because in this case the GEoS leads to a quintessence-type of behavior. With c within this range, the matter content of the universe can be described by a canonical scalar field with a lagrangian minimally coupled to gravity given by

$$\begin{aligned} \mathcal {L}= -\frac{1}{2} \phi _{,\mu }\phi ^{,\mu } -V(\phi ), \end{aligned}$$

(22)

where we have used the (−, $+$, $+$, $+$) signature. In order to reinterpret the matter source as that of a scalar field, we will evaluate the scalar field $\phi$ and the potential $V(\phi )$ in the next section.

2.2 Linear perturbations

In this section we consider the evolution of the scalar linear perturbations of the bouncing model. In what follows we use the metric notation inspired by [29, 30],

$$\begin{aligned} \begin{array}{ll} \mathrm{d}s^{2}&{}= -a^{2}(1+2\alpha )\mathrm{d}\eta ^{2}-2a^{2}(\beta ,_{i} + B^{(v)}_{i})\mathrm{d}\eta \mathrm{d}x^{i} \\ \\ &{}\quad +\;a^{2}\left[ g_{i j }^{(3)}(1+2\varphi ) +2\gamma ,_{i |j} \right. \\ \\ &{}\quad \left. +\;2C^{(v)}_{(i | j)}+2C^{(t)}_{i j }\right] \mathrm{d}x^{i }\mathrm{d}x^{j}, \end{array} \end{aligned}$$

(23)

where the perturbed order variables $\alpha$, $\beta$, $\varphi$ and $\gamma$ are scalar-type perturbations; the transverse $B^{(v)}_{\alpha }$ and $C^{(v)}_{\alpha }$ are vector-type perturbations (rotation); and a transverse traceless $C^{(t)}_{\alpha \beta }$ is tensor-type perturbation (gravitational wave). The energy-momentum tensor is

$$\begin{aligned} \begin{aligned} T^{0}_{0}&\equiv -(\bar{\rho }+\delta \rho ), \\ T^{0}_{i }&\equiv (\rho + p)\left[ -(1/k)v ,_{i} + v^{(v)}_{i}\right] , \\ T^{i }_{j}&\equiv (\bar{p}+\delta p)\delta ^{i }_{j } + \pi ^{i }_{j}, \end{aligned} \end{aligned}$$

(24)

where the traceless entity $\pi ^{i }_{j }$ is the anisotropic stress tensor.

Defining the variable $\Phi$ as [31,32,33,34,35]

$$\begin{aligned} \Phi \equiv \varphi - \frac{2K/a^{2}}{\rho + p}\varphi _{\chi }, \end{aligned}$$

(25)

the scalar-type perturbation of a fluid with vanishing anisotropic stress in the Einstein gravity is described by [35]

$$\begin{aligned}&\Phi = \frac{2H^{2}}{(\rho + p)a}\frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{a}{H}\varphi _{\chi }\right) , \end{aligned}$$

(26)

$$\begin{aligned}&\dot{\Phi } =-\frac{2Hc_{s}^{2}}{\rho + p}\frac{k^{2}}{a^{2}}\varphi _{\chi }-\frac{H}{\rho + p}e, \end{aligned}$$

(27)

$$\begin{aligned}&\frac{k^{2}-3}{a^{2}}\varphi _{\chi } = \frac{1}{2}\delta _{v}\rho , \end{aligned}$$

(28)

where $c_{s}^{2}=\dot{p}/\dot{\rho }$, $\varphi _{v}\equiv \varphi - (aH/k)v$, $\varphi _{\chi }\equiv \varphi -aH(\beta +a\dot{\gamma })$, $\delta _{v} \equiv \delta \,+\, 3(aH/k)(1+\omega )v$ and $\delta = (\rho - \bar{\rho })/\bar{\rho }$. The functions $\varphi _{v}$, $\varphi _{\chi }$ and $\delta _{v}$ are gauge-invariant combinations [29, 30]; $\varphi _{v}$ is the same as $\varphi$ in the comoving gauge ($v\equiv 0$), and $\varphi _{\chi }$ is the same as $\varphi$ in the zero-shear gauge ($a(\beta +a\dot{\gamma })\equiv 0$), etc. In a positive curvature model the wave number varies as $k=\sqrt{(n^2-1)K}$ where n is a natural not equal to 1 or 2 [37].

In the case of a minimally coupled scalar field, we have an additional nonvanishing entropic perturbation (the isotropic stress), $e=(1-c_{s}^{2})\delta _{v}\rho$).

In the notation of Bardeen [36] we have

$$\begin{aligned} \delta _{v}=\epsilon _{m}, \quad \varphi _{\chi } = \Phi _{H}, \quad \varphi _{v}= \phi _{m}. \end{aligned}$$

(29)

We have $\varphi _{v}= \mathcal {R}$ in [38]; $\varphi _{v}$ was also originally introduced by Lukash as $-\frac{1}{3}q$ in [39, 40].

From Eqs. (26) and (27) we can derive the following differential equation:

$$\begin{aligned} \ddot{\varphi } _{\chi } +2\frac{\dot{z}}{z}\dot{\varphi }_{\chi } + \left( \frac{\ddot{z}}{z}+\frac{c_{s}^{2}k^{2}}{a^{2}}-\frac{\ddot{y}}{y}\right) \varphi _{\chi }=0, \end{aligned}$$

(30)

where $z=\sqrt{a/(\rho + p)}$ and $y=H/\sqrt{(\rho + p)a}$. Given the explicit solutions given by Eq. (7), we solve the numerical equations (30), (28) and (26) for $\varphi _{\chi }$, $\delta _{v}$ and $\Phi$, respectively, by using Wolfram Mathematica. The solutions are displayed in Figs. 2 and 3 and correspond to the even and odd solutions of Eqs. (26) and (30), respectively. As no exponential grow/decay is displayed by the solutions $\Phi$ and $\varphi _{\chi }$, the perturbations in this model show stability represented by an oscillatory type of behavior, close to the bouncing region. In the large scale (expanding region) $\Phi$ and $\varphi _{\chi }$ and $\delta _{v}$ asymptotically approach a constant.

Fig. 2

Time evolutions of $\varphi _{\chi }$ (blue, line), $\Phi$ (red, dash dotted) and $\delta _{v}$ (green, dotted). The upper panels show the behavior of $\varphi _{\chi }$ and $\Phi$ at a large scale (left) and in a region close to the bouncing (right). The lower panels show the behavior of $\delta _{v}$ at a large scale (left) and in a region close to the bouncing (right). We choose $c=0.5$, $s=1$, $t_{0}=0$, $n=10$, and $K=1$. The initial conditions are set to $\varphi _{\chi } (0)=1$ and $\dot{\varphi _{\chi }} (0)=0$

Fig. 3

Time evolutions of $\varphi _{\chi }$ (blue, line), $\Phi$ (red, dash dotted) and $\delta _{v}$ (green, dotted). The upper panels show the behavior of $\varphi _{\chi }$ and $\Phi$ at a large scale (left) and in a region close to the bouncing (right). The lower panels show the behavior of $\delta _{v}$ at a large scale (left) and in a region close to the bouncing (right). We choose $c=0.5$, $s=1$, $t_{0}=0$, $n=10$, and $K=1$. The initial conditions are set to $\varphi _{\chi } (0)=0$ and $\dot{\varphi _{\chi }} (0)=1$

3 Computation of the scalar field and its potential

If we consider the matter content of the universe modeled by a perfect fluid, then the density and pressure in terms of the scalar field are given by

$$\begin{aligned} \begin{array}{c} \rho = \frac{1}{2}\dot{\phi } ^{2}+V(\phi ), \quad p=\frac{1}{2}\dot{\phi } ^{2}-V(\phi ). \\ \end{array} \end{aligned}$$

(31)

Using Eqs. (6) and (12) in Eq. (31) we obtain

$$\begin{aligned} \frac{\mathrm{d}\phi }{\mathrm{d}u}= & {} \pm \frac{\sqrt{2c\cosh (u)}}{\cosh (u)-c}, \end{aligned}$$

(32)

$$\begin{aligned} V(u)= & {} \frac{\cosh (u)(2\cosh (u)-c)}{\left[ s(\cosh (u)-c)\right] ^{2}}, \end{aligned}$$

(33)

where u is given by Eq. (11). Integrating Eq. (32), the function $\phi$ is obtained:

$$\begin{aligned} \phi (\text {u})=-i\sqrt{8c}\left[ F\left( \frac{i\text {u}}{2},\sqrt{2}\right) +\frac{c}{1-c}\Pi \left( \frac{i\text {u}}{2}, \frac{2}{1-c}, \sqrt{2} \right) \right] , \end{aligned}$$

(34)

where i is the imaginary unit, F is the elliptic integral of the first kind and $\Pi$ is the elliptic integral of the third kind. Both are defined in [46].

The function $\mathrm{d}\phi \over \mathrm{d}u$ in Eq. (32) is a continuous function. Therefore, this function has a real primitive function, but this cannot be represented by elementary functions. Thus the imaginary value in $\phi (u)$ in Eq. (34) is only a artifice of the representation of the function.

In order to numerically obtain $\phi (u)$ from the above equations, we have used standard integration subroutines from Matlab, imposing for consistence the initial condition $\phi (0)=0$. The result is displayed in Fig. 4, where for comparison we have also plotted its Maclaurin expansion up to order 14, whose coefficients are obtained in Appendix A. In addition, in this appendix the convergence radius of this series is shown to be $\arccos (c)$. A remarkable agreement between the two results is found, within the common range of u, which represents a severe test of the accuracy to the numerical solution.

Fig. 4

Plot of $\phi (u)$ using the Maclaurin series obtained from Eq. (A14) and its numerical solution for the parameter values $c=0.5$ and $s =1$

Moreover, we have compared the results for $\phi (u)$ obtained by the Maclaurin series with the one obtained by the numerical integration by computing the Pearson coefficient $r=0.999985$, which allows one to use the numerical solution beyond the convergence radius of the series expansion.

We have also computed numerically $V(\phi )$ from Eq. (33) as well as its Maclaurin expansion using the expression deduced in Appendix A (see Eq. (A21)). Similarly to the analysis presented above, we have measured the degree of agreement among both methods by computing the Pearson coefficient, which in this case is 1 ($r=1$). Both results are displayed in Fig. 5.

Fig. 5

Plot of $V(\phi )$ using the Maclaurin series obtained in Appendix A, Eq. (A21), as well as by the numerical integration from Eq. (33), for the particular parameter values $c=0.5$ and $s =1$

In the next subsection we will find analytical expressions for the field $\phi$ and its potential V by performing high accuracy fits.

3.1 Analytical representation of $\phi (u)$ and $V(\phi )$

In order to characterize analytically the shape of the scalar potential and eventually to compare it with other quintessence potentials, we perform a fit of the numerical data for $\phi (u)$ using the function $\tanh (x)$,

$$\begin{aligned} \phi (u)= \theta _{1}\cdot \tanh (\theta _{2}\cdot u), \end{aligned}$$

(35)

where $\theta _{1}$ and $\theta _{2}$ are positive parameters of the fit. The fit of field $\phi$ can be observed in Fig. 6.

The fit represented by Eq. (35) is of high quality, as the corresponding coefficient of determination is $r^{2}=0.99981$, for the fit parameters $\theta _{1}\approx 3.5892$ and $\theta _{2}\approx 0.42631$.

We have also fitted the numerical data for the field $\phi (u)$ to the function $\theta _{1} \arctan (\theta _{2} u )$, where $\theta _{1}$ and $\theta _{2}$ are the fit parameters, but the quality of the fit was not quite comparable to the one obtained by using the analytic form given by Eq. (35).

Because of the shape of the scalar potential $V(\phi )$, we have used a Gaussian as a trial function:

$$\begin{aligned} V(\phi )=\sigma _{1}\cdot \exp \left( -\sigma _{2}\cdot \phi ^{2} \right) +\sigma _{3}, \end{aligned}$$

(36)

where $\sigma _{1}$, $\sigma _{2}$ and $\sigma _{3}$ are fit parameters. The result of this fit is displayed in Fig. 7.

Fig. 6

Plot of $\phi (u)$ obtained from its numerical solution as well as from the fit given by Eq. (35) for the values $c=0.5$ and $s =1$

Fig. 7

Plot of the numerical data for $V(\phi )$ and the Gaussian fit defined by Eq. (36), for the values $c=0.5$ and $s =1$

As shown in Fig. 7, the Gaussian function fits very accurately the numerical data; moreover, the coefficient of determination $r^{2}=0.99965$ for the fit parameters $\sigma _{1}\approx 7.2164$, $\sigma _{2}\approx 0.32953$ and $\sigma _{3}\approx 2.896$.

Due to the bounded domain of the potential $V (\phi )$, one has to modify the Gaussian such that it falls off to zero as the field $\phi$ approaches the limits $\pm \phi _{ \mathrm{max}}$. We have fulfilled this constraint by introducing the modified trial function:

$$\begin{aligned} V(\phi )=(V_{\mathrm{max}}-V_{\mathrm{min}}) \exp \left[ \displaystyle -\sigma _{1} \phi ^{2}-\frac{\sigma _{2} \phi ^{2}}{\phi _{\mathrm{max}}^{2}-\phi ^{2}}\right] +V_{\mathrm{min}} \end{aligned}$$

(37)

where $\sigma _{1}$ and $\sigma _{2}$ are the fit parameters. $\phi _{\mathrm{max}}$ turns out to be $\phi _{\mathrm{max}}\approx 3.6009$ for $c=0.5$. $V_{\mathrm{max}}$ and $V_{\mathrm{min}}$ are the maximum and minimum values of the potential $V(\phi )$. They can explicitly be seen as follows: inserting Eqs. (17) and (18) into Eq. (31) one obtains

$$\begin{aligned} \begin{array}{l} \dot{\phi }(a)=\frac{2c}{sa}+\frac{2c^{2}}{a^{2}},\quad V(a)=\frac{3}{s^{2}}+\frac{5c}{sa}+\frac{2c^{2}}{a^{2}}. \end{array} \end{aligned}$$

(38)

Since the constants c and s are positive, the maximum (minimum) of V is obtained when a is a minimum (maximum). But from Eq. (7) the maximum and minimum values of a(t) are $\infty$ and $s(1-c)$, respectively. Inserting these values into Eq. (38) we obtain

$$\begin{aligned} \begin{array}{l} V_{\mathrm{max}}=\frac{3-c}{s^{2}(1-c)^2}, \quad V_{\mathrm{min}}=\frac{3}{s^{2}}. \end{array} \end{aligned}$$

(39)

The result of the fit of $V(\phi )$ using the function defined in Eq. (37) is shown in Fig. 8.

Fig. 8

Plot of $V (\phi )$ obtained from the numerical solution and by the fit defined by Eq. (37), for the values $c=0.5$ and $s =1$

The modified Gaussian function fits remarkably well the numerical data for $V(\phi )$ as the coefficient of determination is $r^{2}=0.99999$ for the values $\sigma _{1}=0.29243$ and $\sigma _{2}=0.32674$. Considering the constraint on the domain of $\phi$ and the higher accuracy of this modified Gaussian function, we conclude that the expression given by Eq. (37) is the most faithful representation of $V(\phi )$.

3.2 Analysis of the modified Gaussian potential

As a consistency check it is possible to start with the expression of Eq. (37) for the potential $V(\phi )$ and solve numerically the set of equations (38). By using standard integration subroutines this numerical strategy allows one to obtain the functions $\phi (t)$ and a(t), whose results are displayed in Figs. 9 and 10. For comparison, we have included the exact solutions given by Eqs. (34) and (7), respectively.

The two figures show a remarkable agreement between the numerical solutions and the exact expressions, which is quantified by the coefficients of determination $r^{2}=0.99999$ for the scalar field $\phi (t)$, and $r^{2}=0.99962$ for the scale factor a(t).

Fig. 9

Plot of $\phi$ as a function of time obtained numerically from Eq. (38) using the fitted expression for V given by Eq. (37), as well as from the exact solution of Eq. (7), for the parameter values $c=0.5$ and $s=1$

Fig. 10

Plot of a(t) obtained of Eq. (38) used V given by Eq. (37), as well as from the exact solution of Eq. (7), for the parameter values $c=0.5$ and $s=1$

4 Structural stability of the GEoS and prevalence of the bouncing solution

Since an exact bouncing solution is obtained for the very particular value $A=-1/3$, it is an open question whether variations of the parameter A lead to structural stability of the field equations, or in other words whether the system still have bouncing solutions when the GEoS is modified by disturbing the parameter A by $A\rightarrow A+\epsilon$ in Eq. (1). We will explore this issue taking into account a GEoS of the form

$$\begin{aligned} p=\left( -{1\over 3}+\epsilon \right) \rho - \frac{2}{s\sqrt{3}}\rho ^{1/2}, \end{aligned}$$

(40)

where $\epsilon \ll |1/3|$. We study first perturbations of the exact solution found, driven by the initial GEoS of Eq. (6). We shall consider the following perturbations on the parameters a, $\rho$ and P:

$$\begin{aligned} \begin{array}{l} a(u)=a_{(0)}(u)+\epsilon a_{(1)}(u)+O(\epsilon ^{2}), \\ \rho (u)=\rho _{(0)}(u)+\epsilon \rho _{(1)}(u)+O(\epsilon ^{2}), \\ p(u)=p_{(0)}(u)+\epsilon p_{(1)}(u)+O(\epsilon ^{2}), \end{array} \end{aligned}$$

(41)

where for the case $\epsilon =0$ the solutions are given by the Eq. (7) in the following form:

$$\begin{aligned} \begin{array}{l} a_{(0)}(u)=s\left( \cosh (u)-c\right) , \\ \rho _{(0)}(u)=\frac{3(\cosh (u))^{2}}{s^{2}(\cosh (u)-c)^{2}}, \\ p_{(0)}(u)=-\frac{1}{3}\rho _{(0)}-\frac{2}{s\sqrt{3}}\rho _{(0)}^{1/2}. \end{array} \end{aligned}$$

(42)

Then using Eq. (4) and the continuity equation

$$\begin{aligned} \dot{\rho }=-3\frac{\dot{a}}{a}(\rho + P), \end{aligned}$$

(43)

we can obtain a system to first order in $\epsilon$, which allows one to find $a_{(1)}$ and $\rho _{(1)}$. The system is

$$\begin{aligned} a'_{1}(u)= & {} A(u)a_{1}(u)+B(u)\rho _{1}(u), \nonumber \\ \rho ' _{1}(u)= & {} C(u)a'_{1}(u)+D(u)a_{1}(u)+E(u)\rho _{1}(u)+F(u), \nonumber \\ \end{aligned}$$

(44)

where the prime $({_{\prime } })$ denotes the derivative with respect to u, and the coefficients A(u), B(u), C(u), D(u), E(u) , F(u) are obtained in Appendix B (see Eqs. (B4) and (B7)).

Solving the system using the given initial condition,

$$\begin{aligned} \begin{array}{l} a(u=0)=a_{(0)}(0),\quad \dot{a}(u=0)=\dot{a}_{(0)}(0), \end{array} \end{aligned}$$

(45)

we find that the first order contribution for the scale factor, the energy density and the pressure are given by

$$\begin{aligned} a_{(1)}= & {} \frac{3s}{2} \left\{ \phantom {\frac{2c\arctan \left( N\right) }{\sqrt{1-c^{2}}}} -1+ \cosh (u) +c\ln \left[ M\right] \right. \nonumber \\&\left. -\;\sinh (u) \left[ u+\frac{2c\arctan \left( N\right) }{\sqrt{1-c^{2}}} \right] \right\} , \nonumber \\ \rho _{(1)}= & {} \frac{9\cosh (u)}{s^{2}(\cosh (u)-c)^{3}}\left\{ \phantom {\frac{2c\arctan \left( N\right) }{\sqrt{1-c^{2}}}} \cosh (u)-\cosh ^{2}(u)+cu\sinh (u)\right. \nonumber \\&\left. +\;\frac{2c^{2}\sinh (u)\arctan \left( N \right) }{\sqrt{1-c^{2}}}-c\cosh (u)\ln \left[ M \right] \right\} , \nonumber \\ p_{(1)}= & {} \rho _{(0)}-\frac{\rho _{(1)}}{3}-\frac{\rho _{(1)}}{s\sqrt{3}\rho _{(0)}^{1/2}},\quad \text {where } M=\frac{\cosh (u)-c}{1-c} \nonumber \\ \text {and } \ N= & {} \frac{(1+c)\tanh (u/2)}{\sqrt{1-c^{2}}}. \end{aligned}$$

(46)

Now, we analyze the functions $a_{1}$ and $\rho _{1}$ of the above equation. Let us consider the first two non-zero terms of the Maclaurin expansion of Eq. (42), which represent $a_{0}$, and the first non-zero of the Maclaurin expansion of the expression for $a_{1}$, which is given by Eq. (46). We find that

$$\begin{aligned} a_{0}(u)=s(1-c)+\frac{su^{2}}{2}, \quad a_{1}(u)=-\frac{3su^{2}}{4(1-c)}. \end{aligned}$$

(47)

Note that $a_{1}(0)=0$ and that the sign of $a_{1}$ is always negative, contrary to $a_{0}$, which is positive. For this reason, for $\epsilon >0$ the scale factor of the bouncing universe in a neighborhood of $u=0$ grows smaller than the original solution and for $\epsilon <0$ the scale factor grows faster than the original one. This behavior can be seen from Eq. (40), since for $\epsilon >0$ the GEoS is the same that the original GEoS plus the term $\epsilon \rho$. Therefore, the expected behavior of the new scale factor should be less pronounced than the scale factor of the original solution, because the new quintessence fluid have one state parameter $\omega$ greater than original. Finally, if we compare magnitudes of the order $u^{2}$ for $a_{0}$ and $a_{1}$, and if in addition we include the term $\epsilon$ in $a_{1}$, we obtain

$$\begin{aligned} \left| \frac{s}{2}\right| >|\epsilon |\left| -\frac{3s}{4(1-c)}\right| \Leftrightarrow c<1-\frac{3|\epsilon |}{2}. \end{aligned}$$

(48)

Therefore, we will have a bouncing behavior for $u\approx 0$ for any couple of constants c and $\epsilon$ that satisfy Eq. (48). Note that for any c in (0, 1) there always exist $\epsilon >0$ and $|\epsilon | \ll {1\over 3}$ which satisfy the above equation.

Now, let us analyze $\rho _{1}$ of Eq. (46). Evaluating the first non-zero terms of the Maclaurin series of $\rho _{0}$ and $\rho _{1}$, we obtain

$$\begin{aligned} \rho _{0}= \frac{3}{s^{2}(1-c)^2}-\frac{3 c u^2}{s^{2}(1-c)^3 }, \quad \rho _{1}=-\frac{9 (1-2 c) u^2}{2 s^{2}(1-c)^4 }. \end{aligned}$$

(49)

Note that $a_{1}(0)=\rho _{1}(0)=0$ and also that the sign of $\rho _{1}$ is negative for $c<0.5$ and positive for $c>0.5$. In the case $c=0.5$ the first term, $\rho _{1}=0$. Thus, for any $|\epsilon |\ll {1\over 3}$, $\rho _{0}$ will dominate over $\rho _{1}$ for $u\approx 0$. Now, if we compare magnitudes of the order $u^{2}$ for $\rho _{0}$ and $\rho _{1}$, and if in addition we include the term $\epsilon$ in $\rho _{1}$, we find that for $c\ne 0.5$

$$\begin{aligned} \left| \frac{3 c }{s^{2}(1-c)^3 }\right|>|\epsilon |\left| \frac{9 (1-2 c) }{2 s^{2}(1-c)^4 }\right| \Leftrightarrow \frac{2c(1-c)}{3|1-2c|}>|\epsilon |. \end{aligned}$$

(50)

This equation tell us what values of c and $\epsilon$ lead $\rho _{0}$ to dominate over $\rho _{1}$ for $u\approx 0$.

The behavior of the original scale factor and the perturbed ones are shown in Fig. 11. The $\epsilon$ that we consider in the graphics corresponds to a $45 \%$ of 1 / 3 and $c=0.5$. With these c and $\epsilon$ we find that Eq. (48) is satisfied and, therefore, there is a bouncing behavior.

The coefficient of determination is $r^{2}=0.94759$, for $a_{0}$ and $a_{0}+\epsilon a_{1}$, and $r^{2}=0.99875$, for $a_{0}$ and $a_{0}-\epsilon a_{1}$. The energy density $\rho _{1}$ given by Eq. (46) is shown in Fig. 12.

Fig. 11

Plot of the scale factor and its first order correction, obtained from Eq. (46), for the values $\epsilon =0$.15, $c=0$.5 and $s=1$

Fig. 12

Plot of energy density $\rho$ and its first order correction obtained from Eq. (46), for the parameter values $\epsilon =0.15$, $c=0.5$ and $s=1$

The coefficient of determination is $r^{2}=0.99980$, for $\rho _{0}$ and $\rho _{0}+\epsilon \rho _{1}$ and $r^{2}=0.98566$, for $\rho _{0}$ and $\rho _{0}-\epsilon \rho _{1}$. We may note that despite the high value of $\epsilon$, the behavior of the scale factor and of the energy density perturbed to first order are quite similar to the one obtained with the exact solution. Moreover, if we change the parameters c and s in their respective domain we will get universes keeping the same shape of the bouncing but with different growths.

We evaluate numerically the first order perturbation of the field $\phi$, which we denoted by $\phi _{1}(u)$. Its behavior is showed in Fig. 13.

Fig. 13

Plot of the scalar field $\phi$ and its first order correction, for the parameter values $\epsilon =0.15$, $c=0.5$ and $s=1$

Like the scale factor and the energy density, we find that the first order perturbed field $\phi _{1}$ preserves the shape of the unperturbed solution $\phi _{0}$. The coefficient of determination is $r^{2}=0.99999$, for $\phi _{0}$ and $\phi _{0}+\epsilon \phi _{1}$, and $r^{2}=0.99998$ for $\phi _{0}$ and $\phi _{0}-\epsilon \phi _{1}$.

To obtain the potential $V_{1}$ we expand the function $V(\phi )$ in $\epsilon$. From this expansion we obtain the following expression:

$$\begin{aligned} V(\phi ) = V_{(0)}(\phi _{0})+\epsilon \left[ V'_{(0)}(u)\cdot \frac{\phi _{(1)}}{\phi '_{(0)}} +V_{(1)}(\phi _{(0)}) \right] +O(\epsilon ^{2}). \end{aligned}$$

(51)

The potential $V(\phi )$ is plotted in Fig. 14.

Fig. 14

Plot of the potential $V(\phi )$ and its first order correction, for the parameter values $\epsilon =0$.01, $c=0$.5 and $s=1$

We obtain a $r^{2}=0.99975$ for $V_{0}$ and $V_{0}+\epsilon V_{1}$ and a $r^{2}=0.99975$, for $V_{0}$ and $V_{0}-\epsilon V_{1}$.

The perturbation of the GEoS in the parameter A around the value $-1/3$ leads also to bouncing solutions whose behavior in the scale factor and in the energy density are quite similar to the exact analytical solution found in this work. This also applied for the scenario in which a scalar field describes the matter content of the universe.

5 Conclusions

The study of GEoS has been very important in the exploration of new scenarios in the very early phases of the universe like inflation, or bouncing universe theories in which there are no initial singularities.

In this work we have found an exact analytical bouncing solution for a closed universe filled with one fluid which obeys a GEoS of the form $p= -1/3 \rho +B\rho ^{1/2}$, where $B<0$ is a free parameter. We have chosen the initial conditions that allow no violation of NEC, which leads the parameter $\omega$ to evolve with the cosmic time in the domain of quintessence. For $t\rightarrow \pm \infty$, $\omega \rightarrow -1$, and the fluid behaves like a cosmological constant. We have also shown that the well-known de Sitter solution with positive curvature is obtained as a particular case of our exact analytical bouncing solution.

Another interesting feature, derived from the fact that we have an exact solution, is the possibility to interpret the fluid described by the GEoS of Eq. (1) in terms of known fluids. In fact, expanding the expressions for the pressure, p, and the energy density, $\rho$, in terms of the scale factor and inserting them into the GEoS, we found that the matter content can be seen as the sum of the contributions coming from three fluids: a cosmological constant, quintessence ($\omega = -\,2/3$) and the corresponding fluid which arises from the particular value $\omega = -\,1/3$.

Since the investigated fluid behaves effectively like quintessence, it is possible to reinterpret the matter source in terms of an ordinary scalar field $\phi$, minimally coupled to gravity with a positive kinetic term and a potential $V(\phi )$. Moreover, since NEC is not violated, the solution is free of instabilities at the perturbative level.

We have solved for $\phi$ and $V(\phi )$ the set of coupled equations (31) by using Maclaurin expansions up to 14th order and, in parallel, as an accuracy test, we have computed them numerically from the implicit equations (32) and (33). Remarkable agreement was found by comparing the scalar field $\phi$ and the potential $V(\phi )$ obtained by the two methods, whose precision is characterized by coefficients of determination $r^{2}= 0.99997$ and $r^{2}= 1$, respectively (see Figs. 4 and 5), holding in the common range.

Performing a high accuracy fit we have found an analytical expression for the field and its scalar potential with coefficients of determination typically of the order of 1 up to $10^{-4}$ and $10^{-5}$, respectively (see Eqs. (35) and (37). The shape of this potential can be very precisely described by a Gaussian-type of function that has a bounded domain given by the condition $\phi _{\mathrm{min}}< \phi < \phi _{\mathrm{max}}$. With this exact analytical expression for the scalar potential we evaluated numerically the scale factor, finding a curve very close to the exact analytical bouncing solution already found. This represents a very stringent test on the accuracy of the numerical method used to compute the scalar potential $V(\phi )$.

We have also studied the structural stability of the analytical bouncing solution when the GEoS is modified by including a perturbative term in the standard linear coefficient A (see Eq. 40). For sufficiently small $\epsilon$, the scenario predicted by the analytic solution is still preserved as the scale factor a and the density $\rho$ behave quite similar to the unperturbed solutions (see Figs. 11 and 12). The shape of the scalar potential – introduced as a possible source to generate the effective GeoS – also confirms the unperturbed scenario: the absence of a spontaneous symmetry breaking minimum, for $\epsilon$ small enough within the validity range of the first order approximation.

In summary, the exact analytical bouncing solution can be extended to a vicinity of $A=-1/3$, confirming a bouncing scenario beyond the particular value required for the exact solution. Moreover, an analytical quintessence potential has been found by using a high accuracy fit to the numerical data. A scalar field theory minimally coupled to gravity and ruled by this potential leads to bouncing solutions for closed universes, which does not present spontaneous symmetry breaking.

We have studied the time evolution of the scalar-type perturbations in terms of the variables $\Phi$, $\varphi _{\chi }$ and $\delta _{v}$. We have found that an oscillatory behavior characterizes both $\Phi$ and $\varphi _{\chi }$ in a region close to the bouncing, while a constant behavior is displayed for large scales. In the case of $\delta _{v}$, it keeps essentially constant on the whole scale. As a consequence, the scalar perturbations in this model do not lead to instability.

An analytic scalar potential was found in this article, and it can further be used to study perturbations in the background metric in the trivial minimum and in the absence of spontaneous symmetry breaking.

Appendices

Appendix A: Maclaurin coefficients of $\phi$ and $V(\phi )$

We will find the coefficients of Maclaurin series of the functions $\phi (u)$ and $V(\phi )$ and we will compute their convergence radius. These formal expansions up to order 14 are required in Figs. 4 and 5. We will firstly find the Maclaurin series of $\phi (u)$, and then we will invert this series to obtain the expansion for $u(\phi )$. These expressions will allow us to obtain the Maclaurin series of $V(\phi )$. In fact, starting with the definitions of the coefficients $\alpha _{n}$, $\beta _{n}$, and $c_{n}$ through the formal expansions

$$\begin{aligned} \begin{array}{l} \phi (u)=\sum _{n=0}^{\infty } \alpha _{n} u^{n}, \quad V (u)=\sum _{n=0}^{\infty } c_{n} u^{n}, \\ V (\phi )=\sum _{n=0}^{\infty } \beta _{n} \phi ^{n}, \\ \end{array} \end{aligned}$$

(A1)

we will proceed finding the $\beta _{n}$ coefficients in three steps:

• First, we find the coefficients $\alpha _{n}$ of the Maclaurin series of $\phi (u)$, using its exact analytical expression.

• Second, we find the coefficients $c _{n}$ of the Maclaurin series of V(u) by using Eq. (33).

• third, we find the coefficients $\beta _{n}$ of the Maclaurin series of $V(\phi )$ solving the implicit expression:

  $$\begin{aligned} V(\phi )=\sum _{n=0}^{\infty } c _{n}u^{n}(\phi ). \end{aligned}$$

  (A2)

Here $u(\phi )$ should be computed by inverting the expansion for $\phi (u)$ (see Eq. A1). We begin by finding $\alpha _{n}$. To find the Maclaurin series of $\phi (u)$ we integrate Eq. (32), which gives

$$\begin{aligned} \phi (u)=\pm \sqrt{2c}\int {\sqrt{\cosh (u)}\over \cosh (u)-c}\mathrm{d}u +s_{1}, \end{aligned}$$

(A3)

with $s_{1}$ being an integration constant. Now we need the Maclaurin series of the integrand ${\sqrt{\cosh (u)}\over \cosh (u)-c}$, which can be derived by using the identity

$$\begin{aligned} f^{(n)}(u) = \sum _{k=1}^{n}{U_{k}(u)\over k!}F^{(k)}(y), \quad n\ge 1, \end{aligned}$$

(A4)

where

$$\begin{aligned} U_{k}(u)= & {} \sum _{i=1}^{k}\frac{(-1)^{i+1}}{(i-1)!}y^{i-1}(u)\left[ \left( y^{k+1-i}(u)\right) ^{(n)}(u)\right] \\&\times \;\left[ \mathop {\Pi }\limits _{j=1}^{i-1}(k+1-j)\right] , \quad \hbox { and } \quad f(u)=(F\circ y)(u). \end{aligned}$$

Note that each $U_{k}$ also depends on n. If we consider $F(y)={\sqrt{y}\over y-c}$ and $y (u)=\cosh (u)$, we find f(u), which is precisely the integrand of Eq. (A3).

Now, replacing $y=\cosh (u)$ in Eq. (A4) and evaluating u at $u=0$, we obtain

$$\begin{aligned} f^{(n)}(0)=\sum _{k=1}^{n}{U_{k}(0)\over k!}F^{(k)}(\cosh (0)), \end{aligned}$$

(A5)

where

$$\begin{aligned} U_{k}(0)= & {} \sum _{i=1}^{k}{(-1)^{i+1}\over (i-1)!} \left[ \left( \cosh ^{k+1-i}(u)\right) ^{(n)}(0)\right] \\&\times \;\left[ \prod _{j=1}^{i-1}(k-j+1)\right] . \end{aligned}$$

Using Leibniz’s rule for the derivative of a product

$$\begin{aligned} (AB)^{(k)}(y)=\sum _{i=0}^{k}{k \atopwithdelims ()i}A^{(k-i)}(y)B^{(i)}(y), \end{aligned}$$

(A6)

with $A(y)=\sqrt{y}$ and $B(y)=(y-c)^{-1}$, and the expressions

$$\begin{aligned} \begin{array}{l} A^{(n)}(y)={(-1)^{n+1}(2n-3)!!\over 2^{n}}y^{{1\over 2}-n}, \\ B^{(n)}(y)=n!(-1)^{n}(y-c)^{-n-1}, \end{array} \end{aligned}$$

(A7)

we obtain

$$\begin{aligned} F^{(k)}(\cosh (0))=\sum _{i=0}^{k}{k!\over (k-i)!}\cdot {(2k-2i-3)!!\over 2^{k-i}}{(-1)^{k+1}\over (1-c)^{i+1}}. \end{aligned}$$

(A8)

In order to obtain the functions $U_{k}(0)$ we use the identities

$$\begin{aligned} \cosh ^{2k}(u)= & {} 2^{-2k}\left[ \sum _{i=0}^{k-1}2{2k \atopwithdelims ()i}\cosh (2(k-i)u) + {2k \atopwithdelims ()k} \right] , \nonumber \\ \cosh ^{2k-1}(u)= & {} 2^{2-2k}\sum _{i=0}^{k-1}{2k-1 \atopwithdelims ()i}\cosh ((2k-2i-1)u). \end{aligned}$$

(A9)

From these we obtain for $l\ge 1$ and $n\ge 1$

$$\begin{aligned} \left( \cosh ^{l}(u)\right) ^{(2n-1)} (0)= & {} 0, \nonumber \\ \left( \cosh ^{2l}(u)\right) ^{(2n)}(0)= & {} 2^{-2l}\sum _{i=0}^{l-1}2{2l \atopwithdelims ()i}(2(l-i))^{2n}, \nonumber \\ \left( \cosh ^{2l-1}(u)\right) ^{(2n)} (0)= & {} 2^{2-2l}\sum _{i=0}^{l-1}{2l-1\atopwithdelims ()i}(2l-2i-1)^{2n}. \nonumber \\ \end{aligned}$$

(A10)

Moreover, using Eqs. (A5), (A8) and (A10), we find

$$\begin{aligned} \begin{array}{ll} f^{(m)}(0)&{}= f^{(2n)}(0)=\displaystyle \sum \limits _{k=1}^{2n}(-1)^{k+1}U_{k}(0)\delta _{k} \\ &{}=\displaystyle \sum \limits _{k=1}^{n}U_{2k-1}(0)\delta _{2k-1}-\displaystyle \sum \limits _{k=1}^{n}U_{2k}(0)\delta _{2k},\\ \\ \end{array} \end{aligned}$$

(A11)

where $\delta _{k}=\sum _{i=0}^{k}{(2k-2i-3)!!\over (k-i)!2^{k-i}}(1-c)^{-i-1}$, which leads to the expression

$$\begin{aligned} f^{(2n)}(0)=\sum _{k=1}^{n}(U_{2k-1}(0)\delta _{2k-1}-U_{2k}(0)\delta _{2k}), \end{aligned}$$

(A12)

where $\ n\ge 1$, and

$$\begin{aligned} U_{2k}(0)= & {} \sum _{i=1}^{k}\left\{ {\eta _{i,k}\over (2i-2)!}\left[ \prod _{j=1}^{2i-2}(2k-j+1)\right] \right. \, \\&\left. -{\gamma _{i,k}\over (2i-1)!}\left[ \prod _{j=1}^{2i-1}(2k-j+1)\right] \right\} , \, \\ U_{2k-1}(0)= & {} (2k-1)+\sum _{i=1}^{k-1}\left\{ {\gamma _{i,k}\over (2i-2)!}\left[ \prod _{j=1}^{2i-2}(2k-j)\right] \right. \, \\&\left. -{\eta _{i+1,k}\over (2i-1)!}\left[ \prod _{j=1}^{2i-1}(2k-j)\right] \right\} ,\, \\ \eta _{i,k}= & {} 2^{2i-2k-1}\sum _{j=0}^{k-i}{2(k+1-i)\atopwithdelims ()j}(2(k+1-i-j))^{2n}, \, \\ \gamma _{i,k}= & {} 2^{2i-2k}\sum _{j=0}^{k-i}{2k+1-2i\atopwithdelims ()j}(2k+1-2i-2j)^{2n}. \end{aligned}$$

Finally, using the above results for f(u) we obtain

$$\begin{aligned} f(u)={\sqrt{\cosh (u)}\over \cosh (u)-c}={1\over 1-c}+\sum _{n=1}^{\infty }{f^{(2n)}(0)\over (2n)!}u^{2n}. \end{aligned}$$

(A13)

Now, inserting Eq. (A13) into Eq. (A3) it follows that

$$\begin{aligned} \begin{array}{l} \phi (u)=\pm \sqrt{2c}\left[ {u\over 1-c}+\sum \limits _{n=1}^{\infty }{f^{(2n)}(0)\over (2n)!} {u^{2n+1}\over 2n+1}\right] +s_{1}.\\ \end{array} \end{aligned}$$

(A14)

From the above expression, one can compute the first coefficients of the Maclaurin series of $\phi (u)$,

$$\begin{aligned} \begin{array}{l} \alpha _{0}= s_{1}, \quad \alpha _{1}=\pm \frac{\sqrt{2c}}{1-c}, \quad \alpha _{2}=0, \\ \alpha _{3}=\mp \frac{\sqrt{2c}}{12}\frac{1+c}{(1-c)^{2}},\quad \alpha _{4}=0. \end{array} \end{aligned}$$

(A15)

Using the fact that the convergence radius of a power series of an analytic function is the distance from the center of the power series to the closest singularity and that $0<c<1$, we conclude that the convergence radius of Maclaurin series of $\phi (u)$ of Eq. (A14) is equal to $\arccos (c)$.

Now, we will compute the coefficients $\beta _{n}$ of the Maclaurin series of $V(\phi )$. To this aim, we use the coefficients $c_{n}$, which can be obtained in a similar way to how the coefficients $\alpha _{n}$ were computed, since we can rewrite Eq. (33) as

$$\begin{aligned} V(u)= & {} {9B^{2}\over 4}\left\{ 1 +{5c\over 3}\left[ \left( 1+{2c\over 5}\left( {1\over \cosh (u)-c}\right) \right) \right. \right. \nonumber \\&\left. \left. \times \;\left( {1\over \cosh (u)-c}\right) \right] \right\} . \end{aligned}$$

(A16)

A straightforward computation yields

$$\begin{aligned} V(u)={9B^{2}\over 4}\left[ {-c+3\over 3(1-c)^{2}}+{5\over 3}c\sum _{n=1}^{\infty }{Y^{(2n)}\over (2n)!}u^{2n}\right] , \end{aligned}$$

(A17)

where $Y^{(2n)}= {2c\over 5}\sum _{k=1}^{n-1}{2n\atopwithdelims ()2k}g_{2(n-k)}g_{2k} + \left( 1+{4c\over 5(1-c)}\right) g_{2n}$, with $Y^{(2n-1)}=0$ for $n\ge 1$, and the constants $g_{2n}$ given by

$$\begin{aligned} g_{2n}=\sum _{k=1}^{n}(U_{2k}\delta _{2k}-U_{2k-1}\delta _{2k-1}), \quad n\ge 1, \end{aligned}$$

(A18)

with

$$\begin{aligned} U_{2k}= & {} \sum _{i=1}^{k}\left\{ {\eta _{i,k}\over (2i-2)!}\left[ \prod _{j=1}^{2i-2}(2k-j+1)\right] \right. \\&\left. -\;{\gamma _{i,k}\over (2i-1)!}\left[ \prod _{j=1}^{2i-1}(2k-j+1)\right] \right\} , \\ U_{2k-1}= & {} (2k-1)+\sum _{i=1}^{k-1}\left\{ {\gamma _{i,k}\over (2i-2)!}\left[ \prod _{j=1}^{2i-2}(2k-j)\right] \right. , \\&\left. -\;{\eta _{i+1,k}\over (2i-1)!}\left[ \prod _{j=1}^{2i-1}(2k-j)\right] \right\} , \\ \eta _{i,k}= & {} 2^{2i-2k-1}\sum _{j=0}^{k-i}{2(k+1-i)\atopwithdelims ()j}(2(k+1-i-j))^{2n}, \\ \gamma _{i,k}= & {} 2^{2i-2k}\sum _{j=0}^{k-i}{2k+1-2i\atopwithdelims ()j}(2k+1-2i-2j)^{2n}, \\ \delta _{k}= & {} (1-c)^{-1-k}. \end{aligned}$$

The expansion of Eq. (A17) has a convergence radius $r_{c}=\arccos (c)$. Now we are equipped with the required relations to finally obtain the coefficients $\beta _{n}$ of the expansion of $V(\phi )$. We use Eq. (A2) together with the following identity:

$$\begin{aligned} \left( \sum _{k=0}^{\infty }a_{k}u^{k}\right) ^{n}=\sum _{k=0}^{\infty }c_{(k,n)}u^{k}, \quad n\ge 0, \end{aligned}$$

(A19)

where $c_{(0,n)}=a_{0}^{n}$, and $c_{(m,n)}={1\over ma_{0}}\sum _{k=1}^{m}(kn-m+k)a_{k}c_{(m-k,n)}$ for $m\ge 1$. For the particular case $s_{1}=0$, which leads to a well-defined and unique solution for the parameters $\beta _{n}$, we obtain

$$\begin{aligned} \begin{array}{c} c_{0}=\beta _{0}, \quad c_{n}=\sum \limits _{k=1}^{n}\beta _{k}c_{(n-k,k)} \quad \text {for } \; n\ge 1. \end{array} \end{aligned}$$

(A20)

To obtain the coefficient $\beta _{k}$, we used the fact that $\phi (u)$ is an odd function, while V(u) is an even function of the argument. Thus solving Eq. (A20) for $\beta _{k}$ we obtain

$$\begin{aligned} V(\phi )= & {} \sum _{k=0}^{\infty }\beta _{k}\phi ^{k},\quad \beta _{0} =c_{0}, \quad \beta _{2n-1}=0, \nonumber \\ \beta _{2n}= & {} {c_{2n}\over c_{(0,2n)}}-{\sum _{i=1}^{n-1}\beta _{2i}c_{(2n-2i,2i)}\over c_{(0,2n)}}, \quad n\ge 1. \end{aligned}$$

(A21)

The convergence radius of $V (\phi )$ is $r_{c}=\phi (\arccos (c))$. Finally, we evaluate explicitly the first $\beta _{n}$ coefficients from the relations of Eq. (A21),

$$\begin{aligned} \begin{array}{l} \beta _{0}= \frac{3B^{2}(3-c)}{4(1-c)^{2}}, \quad \beta _{1}=0, \quad \beta _{2} =- \frac{3B^{2}(5-c)}{16(1-c)}, \\ \beta _{3}=0, \quad \beta _{4}=\frac{B^{2}(15+4c+c^{2})}{128c}. \end{array} \end{aligned}$$

(A22)

Appendix B: Differential equations for a and $\rho$ up to first order

We will compute the coefficients A, B, C, D, E and F that appear in Eq. (44). We first compute the function $p_{(1)}$ appearing in Eqs. (40) and (41):

$$\begin{aligned} p_{(1)}=\rho _{(0)}-\frac{\rho _{(1)}}{3}-\frac{\rho _{(1)}}{s\sqrt{3}\rho _{(0)}^{1/2}}, \end{aligned}$$

(B1)

which corresponds to Eq. (46). Now, in order to obtain the coefficients A, B, C, D, E and F, we insert Eqs. (41) and (42) into Eq. (4), which leads to the following expression:

$$\begin{aligned} a_{(1)}'=s a_{(1)}\left( \frac{a_{(0)}'}{sa_{(0)}}+\frac{s}{a_{(0)}'a_{(0)}}\right) + \frac{s^{2}\rho _{(1)}a_{(0)}^{2}}{6a_{(0)}'}, \end{aligned}$$

(B2)

where the prime $({_{\prime } })$ denotes the derivative with respect to u. Now, inserting $a_{0}(u)$, $\rho _{0}(u)$ and $a'_{0}(u)$ in the above equation we obtain

$$\begin{aligned} a'_{1}(u)=A(u)a_{1}(u)+B(u)\rho _{1}(u), \end{aligned}$$

(B3)

where

$$\begin{aligned} \begin{array}{l} A(u) = \frac{\cosh ^{2}(u)}{\sinh (u)(\cosh (u)-c)}, B(u)=\frac{s^{3}(\cosh (u)-c)^{2}}{6\sinh (u)}. \end{array} \end{aligned}$$

(B4)

Moreover, if we use Eqs. (41) and (43), we obtain

$$\begin{aligned} \begin{array}{ll} \rho _{(1)}'&{}=\rho _{(1)} \frac{3a_{(0)}'}{a_{(0)}}\left( \frac{1}{s\sqrt{3}\rho _{(0)}^{1/2}}-\frac{2}{3}\right) -\frac{3a_{(1)}'}{a_{(0)}}\left( \rho _{(0)}+p_{(0)}\right) \\ &{}\quad +\;\frac{3a_{(1)}a_{(0)}'}{a_{(0)}^{2}}\left( \rho _{(0)}+p_{(0)}\right) -\frac{3a_{(0)}'}{a_{(0)}}\rho _{(0)}. \end{array} \end{aligned}$$

(B5)

When the functions $a_{0}(u)$, $\rho _{0}(u)$, $p_{0}(u)$ and $a'_{0}(u)$ are inserted into Eq. (B5), $\rho '_{1}(u)$ can explicitly be expressed as

$$\begin{aligned} \rho ' _{1}(u)=C(u)a'_{1}(u)+D(u)a_{1}(u)+E(u)\rho _{1}(u)+F(u) \end{aligned}$$

(B6)

where

$$\begin{aligned} C(u)= & {} \frac{-6c\cosh (u)}{s^{3}(\cosh (u)-c)^{3}}, \nonumber \\ D(u)= & {} \frac{6c\cosh (u)\sinh (u)}{s^{3}(\cosh (u)-c)^{4}}, \nonumber \\ E(u)= & {} -\frac{\sinh (u)(\cosh (u)+c)}{\cosh (u)(\cosh (u)-c)}, \nonumber \\ F(u)= & {} -\frac{9\cosh ^{2}(u)\sinh (u)}{s^{2}(\cosh (u)-c)^{3}}. \end{aligned}$$

(B7)