Bianchi type I expanding universe in Weyl-invariant gravity with a quartic interaction term

Abstract

We will focus on the effect of a Weyl-invariant model with a quadratic interaction term and a free scalar field $\psi$. A set of analytic solutions will be obtained for this model. This model provides a dynamical alternative to the standard $\Lambda$CDM model. In particular, we will show that the quartic Weyl-invariant model prediction is consistent with the Hubble diagram observations.

1 Introduction

The Lambda cold dark matter ($\Lambda$CDM) model [1] is known to be a successful model for the prediction of Hubble diagram. The energy-momentum tensor of the minimal $\Lambda$CDM model is composed of the cosmological constant ($\Lambda$), the cold dark matter (CDM) and the radiation dominated (RD) matter terms [2,3,4]. In this paper, we would like to introduce a physical model that is capable of providing a dynamical resolution to the cosmological constant ($\Lambda$), the cold dark matter (CDM) and the radiation dominated (RD) matter interactions. Indeed, we will show that the current equation of state (EOS) of a physical model is effectively a combination of cosmological constant, matter dominant (MD) and radiation dominant (RD) components with appropriate ratio. In particular, cosmological constant can be introduced by the Weyl-invariant (WI) model [5,6,7,8,9,10,11,12,13] or the massive gravity model [14,15,16,17,18,19]. In fact, there are quite a number ways to induce a cosmological constant. The WI model happens to be a perfect way to induce a cosmological constant by choosing an unitary gauge.

Indeed, WI (or local scale-invariant) gravity is a useful model as an effective theory [20,21,22,23,24,25,26,27,28,29]. A scale transformation contains enriched symmetry that plays a certain and important role in many areas of physics [30,31,32,33]. In addition, the Weyl gauge field has also been proposed as a possible candidate of dark matter [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83]. The WI massive gravity theory can also be generalized, with the introduction of a Weyl vector meson $S_a$, to the Weyl invariant dRGT model [84]. It is also shown that the Weyl symmetry does not affect the ghost-free nature of the massive gravity model. In fact, the resulting theory is equivalent to a dRGT model coupled to a massive $U_1$ gauge field in the unitary gauge.

In this paper, we will show that the inclusion of a scalar field $\psi$ to the $\Lambda$CDM model will change the RD phase significantly. The effect of the free scalar field will induce an additional $w=1$ phase during the early epoch due to the nature of the free scalar field. Note that w denotes the matter equation of state. In particular, we will start with a minimal WI model in Sect. 3. It will be shown that the minimal WI model could not produce a compatible resolution for a current universe with a small anisotropy. We will later show that the inclusion of a quartic interaction terms of the Weyl vector meson and scalar field $\psi$ will provide a resolution compatible with the small anisotropy problem. In particular, the quartic Weyl-invariant (QWI) model can also provide a successful fitting of the Hubble diagram and a reasonable prediction of current equation of state predicted by the $\Lambda$CDM model.

WI model

The Weyl transformation is a local scale transformation that relates all physical fields in different length scales. The scale transformation of field is determined by its conformal dimension. For example, the conformal dimensions of the scalar field, metric field $g_{ab}$ are 1 and $-2$, respectively. Hence they should transform as [32, 33, 52]

$$\begin{aligned} \phi \rightarrow \phi ^{\Omega }= & {} \Omega ^{-1}\phi \,, \end{aligned}$$

(1)

$$\begin{aligned} g_{a b} \rightarrow g^{\Omega }_{a b}= & {} \Omega ^2 g_{a b}, \end{aligned}$$

(2)

respectively. The Weyl symmetry can be preserved by the introduction of the Weyl-covariant derivative $\nabla _a$ (or ${\tilde{\partial }}_{c }$) in place of the ordinary derivative $\partial _a$. As a result, the transformation property of $\nabla _a {\phi }$ is made identical to the transformation property of the scalar field ${\phi }$. Indeed, the Weyl-covariant derivative of a scalar field $\phi$ and $g_{a b}$ can be defined as

$$\begin{aligned} \nabla _{a}\phi= & {} \left( \partial _{a} - S_{a} \right) \phi \,, \end{aligned}$$

(3)

$$\begin{aligned} {\tilde{\partial }}_{c } g_{a b}= & {} \left( \partial _{a} + 2 S_{c } \right) g_{a b} \; \end{aligned}$$

(4)

with $S_a$ the Weyl gauge field (or Weyl vector meson). Hence the scalar field and metric field will transform as

$$\begin{aligned} \nabla _{a} \phi \rightarrow (\nabla _{a} \phi )^\Omega= & {} \Omega ^{-1} \nabla _{a} \phi ~, \end{aligned}$$

(5)

$$\begin{aligned} ( {\tilde{\partial }}_{c } g_{a b})^\Omega= & {} \Omega ^{2} {\tilde{\partial }}_{c } g_{a b}, \end{aligned}$$

(6)

if the Weyl gauge field also transforms as

$$\begin{aligned} S_a \rightarrow S^\Omega _a=S_a- \partial _a \ln \Omega . \end{aligned}$$

(7)

In addition, we can show that

$$\begin{aligned} \left( {\tilde{\Gamma }}^{c }_{~\, a b}~\right) ^\Omega = {\tilde{\Gamma }}^{c }_{~\, a b}~ \end{aligned}$$

(8)

with the WI generalization of the spin connection

$$\begin{aligned} {\tilde{\Gamma }}^{c }_{~\, a b}= {1 \over 2} g^{c d}\left( {\tilde{\partial }}_{a} g_{b d}+{\tilde{\partial }}_{b} g_{a d}-{\tilde{\partial }}_{d} g_{a b} \right) . \end{aligned}$$

(9)

As a result, the action [52, 85,86,87,88,89]

$$\begin{aligned} S = \int {\mathrm{d}^4 } x \sqrt{ g} \left( \frac{\epsilon }{2}\phi ^2 {\tilde{R}} - {1 \over 2}{\nabla _{a} \phi } {\nabla ^{a}\phi } - \frac{1}{4 } H^2-\frac{\lambda }{4 }\phi ^4\right) ,\nonumber \\ \end{aligned}$$

(10)

can be shown to be a WI extension of the conventional Einstein–Hilbert action. Here $\epsilon \phi ^2$ and $\lambda \phi ^4/4$ act as dynamical coupling constants $M_p^2$ and $\Lambda$ respectively in the unitary gauge by setting $\phi =1$. In addition, the WI $S_a$ field tensor is defined as

$$\begin{aligned} H_{ab}=\partial _a S_b-\partial _b S_a. \end{aligned}$$

(11)

Moreover, we can show that the Weyl-covariant Ricci curvature tensor ${\tilde{R}}_{a b}$ can be shown to be

$$\begin{aligned} {\tilde{R}}_{a b}= & {} {R}_{a b}-\left( D_a S_b+D_b S_a\right) -D_d S^d g_{a b}\nonumber \\&+\, 2\left( S_a S_b - S_d S^d g_{a b}\right) ~, \end{aligned}$$

(12)

with ${\tilde{R}}_{a b}$ defined as

$$\begin{aligned} {\tilde{R}}_{a b}=R_{a b}\left( ~ \partial _{c } g_{d e} \rightarrow {\tilde{\partial }}_{c } g_{d e} ~\right) . \end{aligned}$$

(13)

As a result, the WI scalar curvature reduces to

$$\begin{aligned} {\tilde{R}}={\tilde{R}}^a _{~\; a}=R- 6 D_aS^a -6S_aS^a. \end{aligned}$$

(14)

This paper will be organized as follows: (i) A brief review and motivation has been presented in Sect. 1. (ii) The $\Lambda$CDM model will be introduced in Sect. 2. (iii) We will focus on the minimal WI model in Sect. 3. (iv) A quartic Weyl invariant model will be introduced in Sect. 4. We will show that the QWI model provides a consistent fit to the Hubble diagram in this section. For comparison, we will also show that the QWI model prediction of current EOS also agrees reasonably well with the $\Lambda$CDM model. (v) The stability problem of the solutions obtained in the paper will be discussed in Sect. 5. (vi) Finally, concluding remarks will be made in Sect. 6.

2 $\Lambda$CDM model

We will focus on the flat $\Lambda$CDM model [1] for simplicity in this section [90, 91]. The metric of the flat $\Lambda$CDM model is the flat FRW metric given by

$$\begin{aligned} \mathrm{d}s^2=-\mathrm{d}t^2+e^{2\alpha }\left( \mathrm{d}x^2+\mathrm{d}y^2+\mathrm{d}z^2\right) . \end{aligned}$$

(15)

As a result, the Einstein tensor can be shown to be

$$\begin{aligned} G^a_{\;\;b}= \begin{pmatrix} -3{\dot{\alpha }}^2 &{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad -2{\ddot{\alpha }}-3{\dot{\alpha }}^2 &{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad -2{\ddot{\alpha }}-3{\dot{\alpha }}^2&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad -2{\ddot{\alpha }}-3{\dot{\alpha }}^2 \end{pmatrix}.\nonumber \\ \end{aligned}$$

(16)

The energy-momentum tensor for the $\Lambda$CDM model can also be shown to be

$$\begin{aligned} T^a_{\;\;b}=-\Lambda g^a_{\;\;b}+\rho _{_M} \begin{pmatrix} -1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix} +\rho _{_{R}} \begin{pmatrix} -1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad \frac{1}{3} &{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \frac{1}{3}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad \frac{1}{3} \end{pmatrix}.\nonumber \\ \end{aligned}$$

(17)

The conservation law $D_aT^a_{\;\;b}$ implies that $\Lambda =$ constant, $\rho _{_M} \propto e^{-3\alpha }$ and $\rho _{_{R}} \propto e^{-4 \alpha }$. Here $\rho _{_M}$ and $\rho _{_{R}}$ denote the energy density of cold dark matter and RD ultra-relativistic matter, respectively.

In addition, the ratios of energy densities can be defined as

$$\begin{aligned} \Omega _\Lambda\equiv & {} \frac{\Lambda }{\rho } \;, \end{aligned}$$

(18)

$$\begin{aligned} \Omega _M\equiv & {} \frac{ \rho _M }{\rho } \;, \end{aligned}$$

(19)

$$\begin{aligned} \Omega _{R}\equiv & {} \frac{\rho _R }{\rho }, \end{aligned}$$

(20)

with $\rho =-T^0_{\;\;0}$.

Fig. 1

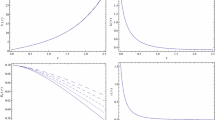
The evolution of w for the $\Lambda$CDM model with an additional free scalar field. The parameters are set $\Omega _\Lambda :\Omega _M:\Omega _{RD}=0.7:0.2999:0.0001$ as of today. The effect of the scalar field is also included by setting the current value of $\Omega _\psi$ as $0, 10^{-19}, 10^{-16}$ and $10^{-13}$. They are plotted as a black-long-dashed curve, a red-solid curve, a green-short-dashed curve and a blue dotted curve, respectively

Note that the current ratios of energy densities are $\Omega _\Lambda (t_0) \simeq 0.7$ and $\Omega _M(t_0) \simeq 0.3$ at $t=t_0$ today according to the $\Lambda$CDM model [90, 91]. In addition, $\Omega _{RD}(t_0) \simeq \Omega _M(t_0)/(1+z_{\mathrm{eq}}) \simeq 0.0001$ for $z_{\mathrm{eq}}\sim 3400$ [90, 91]. Note that the redshift z is defined by the relation

$$\begin{aligned} z+1 \equiv e^{-\alpha } \end{aligned}$$

(21)

with $z_{\mathrm{eq}}$ the redshift when $\Omega _M=\Omega _{RD}$.

Equation of state for the model with an additional free scalar field $\psi$

The energy-momentum tensor for the $\Lambda$CDM model with an additional free scalar field $\psi$ can be shown to be

$$\begin{aligned} T^a_{\;\;b}= & {} -\Lambda g^a_{\;\;b}+\rho _{_M} \begin{pmatrix} -1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix} +\rho _{_{RD}} \begin{pmatrix} -1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad \frac{1}{3} &{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \frac{1}{3}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad \frac{1}{3} \end{pmatrix} \nonumber \\&+\rho _\psi \begin{pmatrix} -1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 1 &{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix}\; \end{aligned}$$

(22)

with the scalar Lagrangian given by $-\partial _a \psi \partial ^a \psi /2$. As a result, scalar field equation can be solved to give $\rho _\psi = {\dot{\psi }}^2 /2 \propto e^{-6 \alpha }$. Note also that the equation of state can be defined as

$$\begin{aligned} w \equiv \frac{P}{\rho }, \end{aligned}$$

(23)

for the total energy density and the total pressure given by $\rho \equiv -T^0_{\;\;0}$ and $P\equiv T^i_{\;\;i}$, respectively.

With the conditions $\alpha _0 \equiv \alpha (t_0)=0$ at $z=0$ today, we can plot the evolution of w (Fig. 1).

It is apparent that the inclusion of the free scalar field affects the large z region quite appreciably. In particular, the $w=1/3$ RD phase is also affected quite appreciably. Indeed, the scalar field induces a $w=1$ phase in the large z region even with a tiny scalar field contribution. On the other hand, the $w=0$ matter-dominated (MD) and $w=-1$ VD phases in the small and negative z region are not affected appreciably with the inclusion of the scalar field.

Note that the $w =1$ phase at the early stage is a reflection of the free scalar $\psi$. Indeed, the presence of a scalar field will introduce an equation of state,

$$\begin{aligned} w_\psi = { {{\dot{\psi }}} ^2/2 -V(\psi ) \over {{\dot{\psi }}} ^2/2 +V(\psi )}, \end{aligned}$$

(24)

if a potential V is present. The equation of state could also induce a state with $w_\psi >1$ if $V <0$. In the absence of the potential V, the equation of state $w_\psi =1$ will hold during the very early stage. Indeed, it can be shown that the density of the scalar field $\psi$ evolves as $1/a^6$. As a result, the $1/a^6$ term will dominate the energy density when $a \ll 1$. This is the main reason that the presence of a free scalar does introduce an $w=1$ phase at the early epoch.

3 Weyl-invariant BI expanding universe

In this section, we will focus on the effect of the WI model given by

$$\begin{aligned} S= & {} \int \mathrm{d}^N x \sqrt{g} \left[ \frac{1}{2}\epsilon \phi ^{N-2} {\tilde{R}}- \lambda \phi ^N - \frac{1}{2}\phi ^{N-4}\nabla _a \phi \nabla ^a \phi \right. \nonumber \\&\left. -\frac{1}{4} \phi ^{N-4} H_{ab}H^{ab} \right] . \end{aligned}$$

(25)

Note that we can set the gauge choice $\Omega = \phi$ and turn off the direct contribution of the scalar field $\phi$. The gauge choice, equivalent to setting $\phi =1$, is also known as the unitary gauge. As a result, the WI action (25) is equivalent to the effective action

$$\begin{aligned} S=\int \mathrm{d}^N x \sqrt{g} \left[ \frac{\epsilon }{2}R - \epsilon \Lambda - \frac{\kappa ^2 }{2}S_a S^a -\frac{1}{4}H_{ab}H^{ab} \right] \end{aligned}$$

(26)

in unitary gauge. Here we have set $\epsilon \Lambda = \lambda$ and $\kappa ^2 =1+6 \epsilon$ for convenience.

In this section, we will focus on the evolution of this model in an anisotropically expanding Bianchi type I (BI) space with the invariant length given by

$$\begin{aligned} \mathrm{d}s^2=-\mathrm{d}t^2+a_1^2(t)\mathrm{d}x^2+a_2^2(t) \mathrm{d}y^2+a_3^2(t)\mathrm{d}z^2. \end{aligned}$$

(27)

Here the scale factors are defined as

$$\begin{aligned} a_1 \equiv e^{\alpha -2\sigma _+ } \;,\quad a_2 \equiv e^{\alpha +\sigma _+ +\sqrt{3} \sigma _- }\;,\quad a_3 \equiv e^{\alpha +\sigma _+ -\sqrt{3} \sigma _- } \;\nonumber \\ \end{aligned}$$

(28)

with $\alpha$, $\sigma _+$ and $\sigma _-$ the isotropy and anisotropies parameters, respectively. As a result, the linear combinations of the Einstein tensor $G^a_{\;\;b}$ can be shown to be

$$\begin{aligned} -G^0_{\;\;0}= & {} 3{\dot{\alpha }}^2-3{\dot{\sigma }}_+^2-3{\dot{\sigma }}_-^2 \;, \end{aligned}$$

(29)

$$\begin{aligned} G^2_{\;\; 2}- G^3_{\;\; 3}= & {} 2\sqrt{3}({\ddot{\sigma }}_- +3{\dot{\alpha }}{\dot{\sigma }}_-) \;, \end{aligned}$$

(30)

$$\begin{aligned} G^2_{\;\; 2}+ G^3_{\;\; 3}-2 G^1_{\;\; 1}= & {} 6 ({\ddot{\sigma }}_+ +3{\dot{\alpha }}{\dot{\sigma }}_+)\;. \end{aligned}$$

(31)

3.1 Energy-momentum tensor and field equations

The energy-momentum tensor of this model can be shown to be

$$\begin{aligned} T^a_{\;\;b}= & {} -\Lambda g^a_{\;\; b}+\frac{1}{ \epsilon } \left[ \kappa ^2 S^a S_b-\frac{\kappa ^2}{2}S^c S_c g^a_{\;\;b}+H^{ac} H_{bc}\right. \nonumber \\&\left. -\frac{1}{4}H^{cd} H_{cd} g^a_{\;\;b} \right] \; \end{aligned}$$

(32)

by choosing the unitary gauge $\phi =1$ and setting $\lambda =\epsilon \Lambda$ in the field equation $G^a_{\;\;b}=T^a_{\;\;b}$.

Moreover, the BI-compatible Weyl vector $S_a$ [84] can be shown to be

$$\begin{aligned} S_a=\left( 0, S_1(t), 0 ,0 \right) . \end{aligned}$$

(33)

As a result, the energy-momentum tensor reduces to

$$\begin{aligned} T^a_{\;\;b}= & {} -\Lambda g^a_{\;\; b}+ \frac{\kappa ^2S_1^2}{2 \epsilon }{ g^{11}} \begin{pmatrix} -1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad -1&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad -1 \end{pmatrix}\nonumber \\&+\frac{\dot{S}_1^2}{2 \epsilon }{ g^{11}} \begin{pmatrix} -1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad -1&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix}. \end{aligned}$$

(34)

Consequently, the Friedmann equation ($G^0_{\;\; 0}= T^0_{\;\; 0})$ reads

$$\begin{aligned} 3{\dot{\alpha }}^2-3{\dot{\sigma }}_+^2-3{\dot{\sigma }}_-^2 =\Lambda +\frac{1}{2\epsilon } e^{-2\alpha +4\sigma _+}\left[ \kappa ^2 S_1^2 +\dot{S}_1^2 \right] . \end{aligned}$$

(35)

In addition, the $G^2_{\;\; 2}- G^3_{\;\; 3}=T^2_{\;\; 2}- T^3_{\;\; 3}$ equation reads

$$\begin{aligned} {\ddot{\sigma }}_- +3{\dot{\alpha }}{\dot{\sigma }}_- =0. \end{aligned}$$

(36)

Finally, the $G^2_{\;\; 2}+ G^3_{\;\; 3}-2 G^1_{\;\; 1} = T^2_{\;\; 2}+ T^3_{\;\; 3}-2 T^1_{\;\; 1}$ equation becomes

$$\begin{aligned} 6 ({\ddot{\sigma }}_+ +3{\dot{\alpha }}{\dot{\sigma }}_+)=\frac{2}{\epsilon } e^{-2\alpha +4\sigma _+} \left[ -\kappa ^2 S_1^2 +\dot{S}_1^2 \right] . \end{aligned}$$

(37)

Furthermore, the Weyl gauge field equations for $S_1$ can be shown to be

$$\begin{aligned}&\ddot{S}_1+({\dot{\alpha }}+4{\dot{\sigma }}_+ )\dot{S}_1 + \kappa ^2 S_1 =0 \;. \end{aligned}$$

(38)

Therefore, we need to solve a set of four equations (35)–(38) with the four field variables $\alpha$, $\sigma _-$, $\sigma _+$, $S_1$.

First of all, the field equation (36) can be integrated directly to give

$$\begin{aligned} {\dot{\sigma }}_- = A \kappa e^{-3\alpha } \end{aligned}$$

(39)

with A a dimensionless constant. Moreover, Eq. (37) can also be integrated to give

$$\begin{aligned} {\dot{\sigma }}_+ = B_0 \; \kappa e^{-3\alpha } + \frac{1}{3\epsilon }e^{-2\alpha +4\sigma _+} S_1 \dot{S}_1 \end{aligned}$$

(40)

with the help of (38). Here $B_0$ denotes an integration constant. $\sigma _-$ and $\sigma _+$ in Eqs. (35) and (38) can be eliminated according to Eqs. (39) and (40). As a result, we are left with two equations, Eqs. (35) and (38), and two independent field variables, $\alpha$ and $S_1$.

3.2 WI BI solution in the background of an isotropic field energy-momentum tensor

For simplicity, we will assume that the associated energy-momentum of the system is isotropic in large scale. As a result, we are lead to the following equations:

$$\begin{aligned} \dot{S}_1^2 -\kappa ^2 S_1^2= & {} 0, \end{aligned}$$

(41)

$$\begin{aligned} {\ddot{\sigma }}_+ +3{\dot{\alpha }}{\dot{\sigma }}_+= & {} 0, \end{aligned}$$

(42)

by comparing Eqs. (36) and (37). Note that Eq. (41) can be solved directly to give

$$\begin{aligned} S_1=\sqrt{\epsilon } Q e^{-\kappa t}. \end{aligned}$$

(43)

In addition, Eq. (42) can be integrated to give

$$\begin{aligned} {\dot{\sigma }}_+ =B_1\; \kappa e^{-3\alpha } \end{aligned}$$

(44)

with $B_1$ the dimensionless integration constant. Finally, Eq. (38) can be written as

$$\begin{aligned} {\dot{\alpha }} =2\kappa -4B \kappa e^{-3\alpha } \; \end{aligned}$$

(45)

with the help of Eqs. (43) and (44). As a result, Eq. (45) can be integrated to obtain the solution of $\alpha$:

$$\begin{aligned} e^{3\alpha }= & {} C e^{6\kappa t}+2B \; \end{aligned}$$

(46)

with C a dimensionless integration constant. We will write $D \equiv B/C$ for convenience and express the field parameters by

$$\begin{aligned} {\dot{\alpha }}= & {} \frac{2\kappa e^{6\kappa t} }{e^{6\kappa t}+2D } \;, \end{aligned}$$

(47)

$$\begin{aligned} {\dot{\sigma }}_+= & {} \frac{D\kappa }{ e^{6\kappa t}+2D }. \end{aligned}$$

(48)

We will also set the time now as $t_0=0$ for convenience. Or equivalently, t will represent $t-t_0$ throughout this paper from now on. In addition, $\alpha _0 \equiv \alpha (t=0)$, $\sigma _0\equiv \sigma _+(t=0)$. Consequently, we can also integrate Eqs. (47) and (48) to obtain the solutions for $\alpha$ and $\sigma _+$:

$$\begin{aligned} \alpha= & {} \frac{1}{3} \ln \left( \frac{e^{6\kappa t }+2D}{1+2D} \right) +\alpha _0, \end{aligned}$$

(49)

$$\begin{aligned} \sigma _+= & {} \frac{-1}{12} \ln \left( \frac{1+2D e^{-6\kappa t }}{1+2D} \right) +\sigma _0. \end{aligned}$$

(50)

As a result, the Friedmann equation (35) can be shown to give the following constraint:

$$\begin{aligned} \frac{3\kappa ^2(4e^{12\kappa t} -D^2 -E^2) }{(e^{6\kappa t}+2D)^2} =\Lambda +\frac{\kappa ^2 Q^2 (1+2D) }{e^{6\kappa t}+2D} e^{-2\alpha _0+4 \sigma _0}\; \end{aligned}$$

(51)

with the help of the expressions for $\alpha$ and $\sigma _+$ given above. Here we have written $E \equiv A/C$ for convenience. Consequently, the solution to the Friedmann equation exists only when

$$\begin{aligned} E^2= & {} 15D^2 \;, \end{aligned}$$

(52)

$$\begin{aligned} \Lambda= & {} 12 \kappa ^2 \;, \end{aligned}$$

(53)

$$\begin{aligned} \frac{D}{1+2D}= & {} -\frac{Q^2}{48} e^{-2\alpha _0+4 \sigma _0}. \end{aligned}$$

(54)

Note that Q, $\kappa$, $\alpha _0$ and $\sigma _0$ are integration constants to be set by appropriate boundary conditions.

Note also that the energy-momentum tensor can be shown to be

$$\begin{aligned} T^a_{\;\;b}= & {} -\Lambda g^a_{\;\; b} +\kappa ^2 g^{11} S_1^2\begin{pmatrix} -1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix} \end{aligned}$$

(55)

with $T^0_{\;\;0} = -\rho$. Hence the energy-momentum tensor given above is similar to the energy-momentum tensor of the $\mathrm \Lambda CDM$ model in the absence of the RD field. Indeed, by writing the CDM energy density as

$$\begin{aligned} \rho _m(t) \equiv \kappa ^2 g^{11} S_1^2 =\frac{-48 D \kappa ^2 }{e^{6\kappa t}+2D} \;, \end{aligned}$$

(56)

we can show that $\Lambda =12 \kappa ^2$ leads to the current $\Lambda /\rho$ ratio

$$\begin{aligned} \Lambda : \rho _{m}(0) = 1:\frac{-4 D }{1+2D}. \end{aligned}$$

(57)

Note that the standard $\Lambda$CDM model is a model with a cold dark matter (CDM) energy density $\rho _M \propto \Omega _M (1+z)^3$. Here $\Omega _M$ denotes the density parameter of the CDM. In our approach, the Weyl gauge field behaves similarly to the CDM field when $t \gg 1$ even it is not a CDM field. The comparison done here also shows that the gauge field $S_1$ does behave as a CDM at large t era.

By setting the current ratio of dark energy density and dark matter density [90, 91]

$$\begin{aligned} \Lambda : \rho _{m}(0) = 7:3 \;, \end{aligned}$$

(58)

the consistent solution for D requires that $D= -3/34$. Consequently, the current anisotropies become

$$\begin{aligned} \frac{ {\dot{\sigma }}_+ (0) }{ {\dot{\alpha }}(0) }= & {} \frac{D}{2}, \end{aligned}$$

(59)

$$\begin{aligned} \frac{ {\dot{\sigma }}_- (0) }{ {\dot{\alpha }}(0) }= & {} \frac{\pm \sqrt{15}D}{2}. \end{aligned}$$

(60)

Therefore the current anisotropies of this model are of the order $O(10^{-1})$. It is not small enough to accommodate the latest observations. Hence the isotropic model shown in this section, without the inclusion of radiation hot matter, cannot produce a universe with small enough anisotropies. In order to minimize the anisotropies, we will try to introduce an additional scalar field $\psi$ that will evolve with a rate given by ${\dot{\psi }}\propto \dot{\sigma _\pm }\propto e^{-3\alpha }$. In Sect. 4, a quartic term will also be included.

4 Quartic interactions

We will show in this section that the inclusion of another free scalar field $\psi$ and the quartic interaction terms is capable of resolving the small anisotropy problem plagued with the model shown in Sect. 3. The WI model we are interested in is given by

$$\begin{aligned} S= & {} \int \mathrm{d}^4 x \sqrt{g} \left[ \frac{1}{2}\epsilon R-\epsilon \Lambda - \frac{\kappa ^2 }{2}S_a S^a - \frac{B}{2}S_a S^aS_b S^b\right. \nonumber \\&\left. -\frac{1}{4}H_{ab}H^{ab} -\frac{1}{2} (\partial _a \psi )(\partial ^a \psi ) \right] \; \end{aligned}$$

(61)

with a coupling constant B. Note that the unitary gauge $\phi =\phi _0=1$ has also been adopted in writing the action (61). The quartic term and the $\psi$-Lagrangian can be derived from the WI interaction terms $\int \mathrm{d}^4x \sqrt{g} (\nabla _a \phi )(\nabla ^a \phi )(\nabla _b \phi )(\nabla ^b \phi )$. Note that $\nabla _a \psi =\partial _a \psi$ for a dimensionless scalar field $\psi$.

In fact, there are more quartic terms that can be included for a more complete higher derivative theory. Many of them can be shown to be related to each other via proper integration by parts. Note, however, that the gauge field $S_a$ always shows up in the covariant derivative $\nabla _a$ along with the ordinary derivative, e.g. $\nabla _a \phi = (\partial _a -S_a) \phi$. Hence $S_a$ should be considered effectively as the order of one-derivative term. Hence the quartic $S^4$ term can be considered as being of the same order as the $H^2$ term. In addition, the BI-compatible $S_a$ solution ensures that $D_aS^a=0$ in unitary gauge. Hence the $D_aS^a$ related terms will not contribute to the effective action. As a result, the only compatible quartic term not included in the model is the term proportional to $D_aS_b D^aS^b$. Therefore, the quartic term considered in this paper is quite unique in this sense. Note that the model (61) will be referred to as quartic Weyl-invariant gravity (QWI) model throughout this paper.

Note that the main purpose of this paper is to show that the effect of the quartic term does have some significant contribution to the evolution of our universe. Hence, we will focus on the effect of the quartic term introduced in action (61). We will also try to show that it will resolve the anisotropy problem mentioned in Sect. 3. In addition, we will also show that this model also provides a better fit to the Hubble diagram. Moreover, the current $\Omega$ prediction will also agree reasonably well with the prediction of the $\Lambda$CDM model.

Note that the energy-momentum tensor associated with the action (61) can be shown to be

$$\begin{aligned} T^a_{\;\;b}= & {} -\Lambda g^a_{\;\; b}+\frac{1}{ \epsilon } \left[ \kappa ^2 S^a S_b-\frac{\kappa ^2}{2}S^c S_c g^a_{\;\;b}+ 2B S^a S_b S^cS_c \right. \nonumber \\&\left. -\frac{B}{2}S^c S_c S^dS_d g^a_{\;\;b} +H^{ac} H_{bc}-\frac{1}{4}H^{cd} H_{cd} g^a_{\;\;b}\right. \nonumber \\&\left. +(\partial ^a \psi )(\partial _b \psi )-\frac{1}{2}(\partial ^c \psi )(\partial _c \psi )g^a_{\;\;b}\right] . \end{aligned}$$

(62)

Similar to Sect. 3, the field equations can be written as

$$\begin{aligned}&3{\dot{\alpha }}^2-3{\dot{\sigma }}_+^2-3{\dot{\sigma }}_-^2 = \Lambda +\frac{1}{2\epsilon } e^{-2\alpha +4\sigma _+}\left[ \kappa ^2 S_1^2 +\dot{S}_1^2 \right] \nonumber \\&\quad +\frac{B}{2\epsilon }e^{-4 \alpha +8\sigma _+}S_1^4 +\frac{{\dot{\psi }}^2}{2\epsilon } ,\end{aligned}$$

(63)

$$\begin{aligned}&2 \sqrt{3}({\ddot{\sigma }}_- +3{\dot{\alpha }}{\dot{\sigma }}_-) =0,\end{aligned}$$

(64)

$$\begin{aligned}&6 ({\ddot{\sigma }}_+ +3{\dot{\alpha }}{\dot{\sigma }}_+)=\frac{2}{\epsilon } e^{-2\alpha +4\sigma _+} \left[ -\kappa ^2 S_1^2 +\dot{S}_1^2 \right] \nonumber \\&\quad -\frac{4B}{ \epsilon }e^{-4 \alpha +8\sigma _+}S_1^4 ,\end{aligned}$$

(65)

$$\begin{aligned}&\ddot{S}_1+({\dot{\alpha }}+4{\dot{\sigma }}_+ )\dot{S}_1 + \kappa ^2 S_1 +2Be^{-2\alpha +4\sigma _+}S_1^3 = 0,\end{aligned}$$

(66)

$$\begin{aligned}&{\ddot{\psi }}+3{\dot{\alpha }}{\dot{\psi }} = 0, \end{aligned}$$

(67)

in a BI metric space. Note that these equations correspond to $G^0_{\;\; 0}$, $G^2_{\;\; 2}- G^3_{\;\; 3}$, $G^2_{\;\; 2}+ G^3_{\;\; 3}-2 G^1_{\;\; 1}$, $S_1$, and $\psi$ equations respectively. Here we have also assumed that $\psi =\psi (t)$ as a consistent solution that is compatible with the BI metric space. We will also assume that the energy-momentum tensor is isotropic for convenience. Hence, the left-hand side (LHS) of Eq. (65) becomes

$$\begin{aligned} {\ddot{\sigma }}_+ +3{\dot{\alpha }}{\dot{\sigma }}_+ =0. \end{aligned}$$

(68)

For convenience, we will define a new variable p

$$\begin{aligned} p \equiv \frac{\dot{S}_1 }{S_1}. \end{aligned}$$

(69)

As a result, the right-hand side (RHS) of Eqs. (65) and (66) imply that

$$\begin{aligned}&e^{-2\alpha +4\sigma _+} S_1^2 = \frac{p^2-\kappa ^2 }{2B} , \end{aligned}$$

(70)

$$\begin{aligned}&\dot{p}+p^2+({\dot{\alpha }}+4{\dot{\sigma }}_+ )p + \kappa ^2 +2Be^{-4 \alpha +8\sigma _+}S_1^2 =0. \end{aligned}$$

(71)

Moreover, Eq. (71) can be written as

$$\begin{aligned} \dot{p}+2p^2+({\dot{\alpha }}+4{\dot{\sigma }}_+ )p =0, \end{aligned}$$

(72)

with the help of Eq. (70). Hence we have

$$\begin{aligned} \alpha +4 \sigma _+= & {} -\ln (-S_1 \dot{S}_1 ) +2\ln A \end{aligned}$$

(73)

with A an integration constant. Hence Eq. (70) can be solved to give

$$\begin{aligned} e^{-3\alpha } = \frac{-1}{2B A^2 }(p^2-\kappa ^2)p \; \end{aligned}$$

(74)

with the help of Eq. (73) and the proper rearrangement of the field variables according to $e^{-2\alpha +4 \sigma _+ }={ e^{\alpha +4 \sigma _+}} e^{-3\alpha }$. For convenience, we will also define a new variable f(t) according to the definition

$$\begin{aligned} p \equiv \frac{ -\kappa }{\sqrt{1+f} }. \end{aligned}$$

(75)

As a result, $S_1$ and $\alpha$ can be written as

$$\begin{aligned} e^{-2\alpha +4\sigma _+} S_1^2= & {} \frac{\kappa ^2 }{2B}\frac{-f}{1+f} \;, \end{aligned}$$

(76)

$$\begin{aligned} e^{-3\alpha }= & {} \frac{ \kappa ^3 }{2B A^2 }\frac{ -f}{ (1+f)^{3/2} } \;, \end{aligned}$$

(77)

$$\begin{aligned} {\dot{\alpha }}= & {} \frac{-\dot{f} }{3f}+\frac{ \dot{f} }{ 2(1+f) }, \end{aligned}$$

(78)

with the help of Eqs. (70) and (74). Note that $f/B < 0$ is required to accommodate real solutions. The results show that the presence of the quartic term (B) affects every component of the field variables. Note also that Eqs. (64), (67), and (68) imply ${\dot{\sigma }}_\pm$ and ${\dot{\psi }}$ are both proportional to $e^{-3\alpha }$. Therefore we can write the solutions as

$$\begin{aligned} {\dot{\sigma }}_+= & {} K_+ \frac{ f}{ (1+f)^{3/2} } \;, \end{aligned}$$

(79)

$$\begin{aligned} {\dot{\sigma }}_-= & {} K_- \frac{ f}{ (1+f)^{3/2} }\;, \end{aligned}$$

(80)

$$\begin{aligned} {\dot{\psi }}= & {} \psi _0 \frac{ f}{ (1+f)^{3/2} } \;, \end{aligned}$$

(81)

with $K_\pm$ and $\psi _0$ appropriate constants of integration. Therefore, Eq. (72) reduces to

$$\begin{aligned} \dot{f} =\frac{-6\kappa f}{\sqrt{1+f} }+\frac{12K_+ f^2}{(1+f)^{3/2} }. \end{aligned}$$

(82)

In addition, Eq. (78) can be written as

$$\begin{aligned} {\dot{\alpha }}= \frac{2\kappa }{\sqrt{1+f} } -\frac{(3\kappa +4K_+ )f}{(1+f )^{3/2}}+\frac{6K_+ f^2}{(1+f )^{5/2}} \; \end{aligned}$$

(83)

with the help of Eq. (82). Finally, the Friedmann equation (63) can be treated as a polynomial equation of f. The result generates a few constraints relating all field parameters. First of all, by checking the term proportional to $f^2/(1+f )^{5/2}$, it is easy to show that a consistent solution implies that $K_+ = 0$ if f is not a constant. Hence we are lead to the constraint equation:

$$\begin{aligned} {\dot{\sigma }}_+ =0. \end{aligned}$$

(84)

As a result, Eqs. (82) and (83) also reduce to

$$\begin{aligned} \dot{f}= & {} \frac{-6\kappa f}{\sqrt{1+f} } \;, \end{aligned}$$

(85)

$$\begin{aligned} {\dot{\alpha }}= & {} \frac{2\kappa }{\sqrt{1+f} } -\frac{3\kappa f}{(1+f )^{3/2}}. \end{aligned}$$

(86)

In addition, the Friedmann equation (63) reads

$$\begin{aligned}&\frac{12\kappa ^2 }{1+f}-\frac{36\kappa ^2 f}{(1+f)^2}+\frac{ (27 \kappa ^2 -3K_-^2)f^2 }{(1+f)^3} \nonumber \\&\quad =\Lambda +\frac{1}{8\epsilon B}\frac{ -\kappa ^4 f}{(1+f)}\left[ \frac{3 }{(1+f) }+1 \right] +\frac{1}{2\epsilon }\psi _0^2\frac{ f^2}{ (1+f)^{3} }.\nonumber \\ \end{aligned}$$

(87)

Hence this polynomial equation implies that the following constraints must be obeyed:

$$\begin{aligned} \Lambda= & {} 12 \kappa ^2, \end{aligned}$$

(88)

$$\begin{aligned} K_-^2 +\frac{\psi _0^2 }{6\epsilon }= & {} 9\kappa ^2, \end{aligned}$$

(89)

$$\begin{aligned} B= & {} \frac{ \kappa ^2 }{ 96\epsilon }. \end{aligned}$$

(90)

Hence Eq. (89) implies that the scalar field $\psi$ does help in decreasing the anisotropy (related to $K_-$) given by ${\dot{\sigma }}_-/{{\dot{\alpha }}}$. Moreover, the limit $\psi _0^2 = 54\epsilon \kappa ^2$ will lead us back to the isotropic background shown in Sect. 3. Indeed, we can show that the anisotropy becomes

$$\begin{aligned} {{{\dot{\sigma }}}_- \over {{\dot{\alpha }}}}={K_- f \over \kappa (2-f)}. \end{aligned}$$

(91)

It is apparent that the current anisotropy (i.e. the anisotropy measured now) can be accommodated with a proper choice of the field parameters.

4.1 Energy-momentum tensor

With the constraints given above, the isotropic energy-momentum tensor can be arranged as

$$\begin{aligned} T^a_{\;\;b}= & {} -12 \kappa ^2 g^a_{\;\;b}+48(p^2-\kappa ^2) \begin{pmatrix} -1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix}\nonumber \\&+\frac{12}{\kappa ^2}(p^2-\kappa ^2)^2 \begin{pmatrix} -3&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix} \nonumber \\&+\frac{\psi _0^2}{2\epsilon }\frac{p^2(p^2-\kappa ^2)^{ 2}}{ \kappa ^6 } \begin{pmatrix} -1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix}. \end{aligned}$$

(92)

The result can be determined by appropriate choice of p and other constants. On the RHS of Eq. (92), the first term represents the effective cosmological constant with $\Lambda =12\kappa ^2$. The second term and the third term are the WI matter that act effectively as CDM and radiation hot matter (RHM). The fourth term is the contribution of the scalar field $\psi$ that dominates in the early epoch. Hence the QWI model does approach $\Lambda$CDM at current epoch as shown in Eq. (92) with appropriate terms corresponding to the cosmological constant, MD term and traceless RD term.

Note, however, that these effective coupling constants are constrained by the field equations. They also act effectively in a nontrivial way shown above even though they are not belonging to a genuine CDM model. In particular, the traceless RD term comes from the $p^4$ order term of the QWI action. It is well known that an isotropic gauge field cannot accommodate a traceless energy-momentum tensor in BI space. This model does provide a nice resolution in a dynamical way. In short, the existence of a set of analytic solutions shown earlier drives the QWI model to act effectively in a way quite similar to the $\Lambda$CDM model.

Note also that the total energy densities is $\rho =-T^0_{\;\;0}$. Hence the ratios of energy densities can be defined as

$$\begin{aligned} \Omega _\Lambda= & {} \frac{12\kappa ^2 }{\rho }\;, \end{aligned}$$

(93)

$$\begin{aligned} \Omega _M= & {} \frac{48(p^2-\kappa ^2 )}{\rho }\;,\end{aligned}$$

(94)

$$\begin{aligned} \Omega _{RD}= & {} \frac{36(p^2-\kappa ^2 )^2}{\rho \kappa ^2 }\;,\end{aligned}$$

(95)

$$\begin{aligned} \Omega _\psi= & {} \frac{\psi _0^2}{2\epsilon }\frac{p^2(p^2-\kappa ^2)^{ 2}}{\rho \kappa ^6 }. \end{aligned}$$

(96)

Here $\Omega _\Lambda$, $\Omega _M$, $\Omega _{RD}$ and $\Omega _\psi$ represent the ratio of energy density for the dark energy density $\Lambda$, CDM, RD matter and the scalar field $\psi$ associated with the WI matter, respectively.

In addition, Eq. (85) can be integrated to give

$$\begin{aligned} 3 \kappa (t-t_{i})= & {} y- \tanh \, y \; \end{aligned}$$

(97)

with a change of variable $f\equiv -1/\cosh ^2 \, y$. Here $t_{i}$ denotes the initial time along with the initial conditions set as $y_i \equiv y(t_{i})=0$, $f_i \equiv f(t_{i})=-1$, $e^{\alpha _i } \equiv e^{\alpha (t_{i}) }=0$.

4.2 The Hubble diagram

We can show that the complicated expression of Eq. (97) can be reduced to a very simple expression in terms of the conformal time $\eta$ through the definition

$$\begin{aligned} \eta \equiv \int e^{-\alpha } \mathrm{d}t. \end{aligned}$$

(98)

First of all, we will start by defining the current conditions as

$$\begin{aligned} f(t_0)\equiv & {} f_0,\end{aligned}$$

(99)

$$\begin{aligned} \alpha (t_0)\equiv & {} \alpha _0,\end{aligned}$$

(100)

$$\begin{aligned} \eta (t_0)\equiv & {} \eta _0, \end{aligned}$$

(101)

with $t=t_0$ denotes the current time today. As a result, Eq. (77) can be written as

$$\begin{aligned} e^{-3\alpha } = \frac{f (1+f_0)^{3/2} }{f_0(1+f)^{3/2}}e^{-3\alpha _0}. \end{aligned}$$

(102)

With the help of Eq. (85), Eq. (102) can therefore be written as

$$\begin{aligned} e^{-3\alpha } = \frac{f (1+f_0)^{3/2} }{f_0(1+f)^{3/2}} \left( \frac{\dot{f}\sqrt{1+f} }{-6\kappa f } \right) ^3 e^{-3\alpha _0}. \end{aligned}$$

(103)

Consequently, the conformal time can be integrated directly to give

$$\begin{aligned} \eta -\eta _0 = \frac{\sqrt{1+f_0} }{-2\kappa } \left[ \left( \frac{f}{f_0}\right) ^{1/3} -1\right] e^{-\alpha _0} \; . \end{aligned}$$

(104)

Therefore, the function f can be expressed as

$$\begin{aligned} f= f_0\left[ 1- \frac{2\kappa (\eta -\eta _0)e^{\alpha _0}}{\sqrt{1+f_0} } \right] ^{3} \end{aligned}$$

(105)

in terms of the conformal time $\eta$ as promised earlier.

Note that the luminous distance $d_L$ [1] is defined as

$$\begin{aligned} d_L \equiv (1+z) \int ^z_0 \frac{d x }{H(x)} = (1+z) |\eta -\eta _0| \; \end{aligned}$$

(106)

with the redshift defined as $1+z \equiv e^{-\alpha }$. As a result, the luminous distance $d_L$ can be shown to be

$$\begin{aligned} d_L=\frac{1+f_0 }{2\kappa \sqrt{1+f} } \left[ \left( \frac{f}{f_0}\right) ^{1/3} -1\right] \left( \frac{f}{f_0}\right) ^{1/3} \end{aligned}$$

(107)

from Eqs. (102) and (104). In addition, the parameter $\kappa$ and the current Hubble parameter $H_0 = \dot{\alpha _0}$ are related by the following equation:

$$\begin{aligned} \kappa= & {} H_0 \frac{(1+f_0)^{3/2} }{2-f_0}\; \end{aligned}$$

(108)

according to Eq. (86). As a result, we have

$$\begin{aligned} d_L=\frac{2-f_0}{2H_0 (1+f_0)^{1/2} (1+f)^{1/2} } \left[ \left( \frac{f}{f_0}\right) ^{1/3} -1\right] \left( \frac{f}{f_0}\right) ^{1/3}.\nonumber \\ \end{aligned}$$

(109)

Note that the current value of $H_0$ is known to be around

$$\begin{aligned} H_0 \simeq 70 \;\; \mathrm{km/s/Mpc}. \end{aligned}$$

(110)

Note also that $H_0 \simeq 70 /300000$ (c/Mpc).

The Hubble diagram (distance modulus vs. redshift) is the plot of distance modulus $\mu$ against the redshift z. In addition, the distance modulus $\mu$ is defined as

$$\begin{aligned} \mu = 5\log (d_L)+25, \end{aligned}$$

(111)

with $d_L$ measured in units of Mpc.

Fig. 2

The red-dotted curve represents the Hubble diagram for the $\Lambda$CDM model with $H_0=0.68 (100\,\mathrm{km/s/Mpc})$, $\Omega _\Lambda =0.69$ and $\Omega _M=0.31$ [90, 91]. The blue-solid curve is the distance modulus of the QWI model with $f_0=-0.06$ and $H_0=0.70 (100\,\mathrm{km/s/Mpc})$. The green-dashed curve represents the best-fit result for the Chevalier–Polarski–Linder (CPL) parametrization [92] by choosing $\Omega _M=0.24$, $\Omega _\Lambda =0.76$, $w_0=-0.29$, $w_1=-0.12$ and $H_0=0.74 (100\,\mathrm{km/s/Mpc})$. The observation data (shown in gray points) is taken from the gamma-ray bursts (GRBs). [92]

In Fig. 2, we choose $f_0=-0.06$ and $H_0=0.70 (100\,\mathrm{km/}\mathrm{{s/Mpc}})$ for the QWI model. The result shows that the QWI-prediction agrees very well with the result of $\Lambda$CDM model in the small z region. In addition, the QWI result also agrees within small deviation from the GRBs Hubble diagram [92] in the large z region. Note also that the observation data fluctuates along the fitting curves indicating that enriched physics is involved. Nonetheless, the QWI model appears to provide a reasonable resolution as shown above. Note also that the best-fit Hubble constant also varies from $H_0=0.73 (100\,\mathrm{km/s/Mpc})$ [93] to $H_0=0.68 (100\,\mathrm{km/s/Mpc})$ from the Planck base $\Lambda$CDM model [90, 91] indicating that the hidden physics unknown to us is probably far more interesting than we can imagine. In summary, our result agrees better with the $\Lambda$CDM model in the small z region, and it agrees better with the CPL model in the large z region.

Note that the Chevalier–Polarski–Linder (CPL) parametrization [92] of the equation of state is defined as

$$\begin{aligned} w(z)=w_0+w_1 { z \over 1+z} \, \end{aligned}$$

(112)

with $w_0, w_1$ the constant fitting parameters. As a result, the Hubble parameter can be shown to be

$$\begin{aligned} H(z)=H_0 \left[ \; \Omega _M(z+1)^3 + \Omega _\Lambda g(z) \; \right] ^{1/2} \; \end{aligned}$$

(113)

with

$$\begin{aligned} g(z)= & {} \exp \left[ \; 3 \int ^z_0 { w+1 \over x+1} \mathrm{d}x \; \right] \nonumber \\= & {} \exp \left[ \; - \frac{3w_1 z}{z+1} \; \right] (1+z)^{3(w_0+w_1+1)}. \end{aligned}$$

(114)

In addition, we have chosen $\Omega _M=0.24$, $\Omega _\Lambda =0.76$, $w_0=-0.29$, $w_1=-0.12$ and $H_0=0.74 (100$ km/s/Mpc) in plotting the green-dashed curve of the Fig. 2. Note also that the Hubble parameter is

$$\begin{aligned} H(z)=H_0\left[ \; \Omega _M(z+1)^3 + \Omega _\Lambda \; \right] ^{1/2} \end{aligned}$$

(115)

for the $\Lambda$CDM model shown in Fig. 2.

In addition, Eqs. (93)–(96) with $\psi _0^2/(2\epsilon )=27\kappa ^2$ and $f_0=-0.06$ imply that the current ratios of energy densities can be shown to be

$$\begin{aligned} \Omega _\Lambda : \Omega _M :\Omega _{RD} : \Omega _\psi \simeq 0.78:0.20:0.01:0.01 . \end{aligned}$$

(116)

Note that the error bar of $\Omega _\Lambda$ is $\pm 0.02$ [90, 91]. Therefore, the result with $\Omega _{RD}$ and $\Omega _\psi$ close to 0.01 is within a reasonable range. The ratio $\Omega _M=0.2$ is a little bit off the prediction of $\Lambda$CDM model. As we mentioned earlier, QWI model provides a dynamical approach to the matter contributions that behave similar to the CDM at out current stage. The most important thing is, however, the agreement in the predictions of Hubble diagram. Nonetheless, the QWI model does lead to a similar effect close to the physical evolution of the CDM model.

In summary, we have introduced a quartic interaction proportional to ${S_a}^4$ and an additional free scalar $\psi$ in the BI metric space. The presence of the free scalar field is capable of minimizing the current anisotropy ${{\dot{\sigma }}}_- / {{\dot{\alpha }}}$ as expected. Indeed, we have shown that

$$\begin{aligned} K_-^2 +\frac{\psi _0^2 }{6\epsilon }= & {} 9\kappa ^2 \;, \nonumber \\ \left. {{{\dot{\sigma }}}_- \over {{\dot{\alpha }}}}\right| _0= & {} {K_- f_0 \over \kappa (2-f_0)}, \nonumber \\ \kappa= & {} H_0 \frac{(1+f_0)^{3/2} }{2-f_0}\; \end{aligned}$$

(117)

in Eqs. (89), (91) and (108). As a result, by choosing $f_0=-0.06$, $H_0=0.70 (100\,\mathrm{km/s/Mpc})$ and ${\psi _0^2 }/{\epsilon } \sim 54 \kappa ^2$ for the QWI model when we plot Fig. 2, we can successfully minimize the current anisotropy consistent with the CMB observations. It is also apparent that $K_-$ cannot be minimized in the absence of the free scalar field $\psi$.

The existence of a consistent analytic solution shown in this paper requires that the cosmological constant is related to $\kappa$ (affecting the mass term of $S_a$) through the relation $\Lambda =12 \kappa ^2$. In addition, the QWI model behaves similarly to the prediction of the $\Lambda$CDM model at the current stage as shown in Eq. (92). Moreover, the QWI model prediction of the Hubble diagram also agrees reasonably well with current observations. These results show that quartic term and the free scalar field $\psi$ do play an important role in the evolution of our universe.

5 Perturbations and stability analysis

In Sect. 4 we have obtained a set of analytic solutions for the QWI model in BI space. We wish to show that this set of analytic solutions are stable solutions when small perturbations are introduced in this section. The stability analysis will show that the QWI model does provide a useful approach for the physical universe with a consistent and stable state for the evolution.

Recalling that Eqs. (85), (76), and (77) are the solutions of the field parameters $f, \alpha$, and $S_1$:

$$\begin{aligned} \dot{f}= & {} \frac{-6\kappa f}{\sqrt{1+f} }\;,\end{aligned}$$

(118)

$$\begin{aligned} e^{-3\alpha }= & {} \frac{ \kappa ^3 }{2B A^2 }\frac{ -f}{ (1+f)^{3/2} }\;,\end{aligned}$$

(119)

$$\begin{aligned} e^{-2\alpha +4\sigma _+} S_1^2= & {} \frac{\kappa ^2 }{2B}\frac{-f}{1+f}. \end{aligned}$$

(120)

We would like to find the stability behavior of these solutions by performing perturbations on the field parameters according to $\alpha \rightarrow \alpha + \delta \alpha$, $\sigma _\pm \rightarrow \sigma _\pm + \delta \sigma _\pm$, $\psi \rightarrow \psi + \delta \psi$ and $S_1 \rightarrow S_1 (1+ \delta q )$. As a result,

$$\begin{aligned} \delta p =\delta \dot{q}, \end{aligned}$$

(121)

following from the definition of $p \equiv \partial _t \ln S_1$. Consequently, we can show that perturbing the field equations (63), (64), (65), (66)/$S_1$, and (67) will lead to the following set of perturbation equations:

$$\begin{aligned}&6 {\dot{\alpha }} \delta {\dot{\alpha }} -6{\dot{\sigma }}_-\delta {\dot{\sigma }}_-\nonumber \\&\quad = \frac{1}{\epsilon }e^{-2\alpha +4\sigma _+ }S_1^2 \left[ \left( \delta q-\delta \alpha +2\delta \sigma _+ \right) (\kappa ^2+p^2)+p \delta \dot{q} \right] \nonumber \\&\qquad + \frac{2B}{\epsilon }e^{-4 \alpha +8\sigma _+ }S_1^4\left( \delta q-\delta \alpha +2\delta \sigma _+ \right) +\frac{{\dot{\psi }}\delta {\dot{\psi }} }{\epsilon }, \end{aligned}$$

(122)

$$\begin{aligned}&\delta {\ddot{\sigma }}_- + 3{\dot{\alpha }} \delta {\dot{\sigma }}_- + 3(\delta {\dot{\alpha }}){\dot{\sigma }}_- =0 \;, \end{aligned}$$

(123)

$$\begin{aligned}&\delta {\ddot{\sigma }}_+ + 3{\dot{\alpha }} \delta {\dot{\sigma }}_+ \nonumber \\&\quad = \frac{2 }{3\epsilon }e^{-2\alpha +4\sigma _+ }S_1^2 \left[ p \delta \dot{q} - 2Be^{-2\alpha +4\sigma _+ }\right. \nonumber \\&\left. \quad S_1^2 \left( \delta q-\delta \alpha +2\delta \sigma _+ \right) \right] , \end{aligned}$$

(124)

$$\begin{aligned}&\delta \ddot{q} +{\dot{\alpha }} \delta \dot{q} + (2\delta \dot{q}+\delta {\dot{\alpha }}\nonumber \\&\qquad +4\delta {\dot{\sigma }}_+) p +4B e^{-2\alpha +4\sigma _+ }S_1^2 \left( \delta q-\delta \alpha +2\delta \sigma _+ \right) =0 \;, \nonumber \\ \end{aligned}$$

(125)

$$\begin{aligned}&\delta {\ddot{\psi }} + 3{\dot{\alpha }} \delta {\dot{\psi }} + 3(\delta {\dot{\alpha }}){\dot{\psi }} =0. \end{aligned}$$

(126)

First of all, $\delta {\dot{\psi }}$ and $\delta {\dot{\sigma }}_-$ can be integrated directly as functions of $\delta \alpha$:

$$\begin{aligned} \delta {\dot{\psi }}= & {} \frac{3\psi _0 f}{(1+f)^{3/2}} \delta \alpha \;, \end{aligned}$$

(127)

$$\begin{aligned} \delta {\dot{\sigma }}_-= & {} \frac{3K_- f}{(1+f)^{3/2}}\delta \alpha \;, \end{aligned}$$

(128)

with the help of Eqs. (80), (81), and (119).

Consequently, there are three remaining equations (125), (124) and (122) left to be analyzed. Note that we also have the identity

$$\begin{aligned} {\dot{\sigma }}_-\delta {\dot{\sigma }}_- +\frac{{\dot{\psi }}\delta {\dot{\psi }} }{6\epsilon } = - \frac{27 \kappa ^2 f^2}{(1+f)^3} \delta \alpha , \end{aligned}$$

(129)

following from Eq. (89), relating the parameters $K_-, \psi _0$ and $\kappa$.

As a result, the perturbation equations can be written as

$$\begin{aligned}&\delta \ddot{q} +{\dot{\alpha }} \delta \dot{q} + p(4\delta \dot{q}+\delta {\dot{\alpha }}+4\delta {\dot{\sigma }}_+-\delta \dot{u}) =0 \;, \end{aligned}$$

(130)

$$\begin{aligned}&\delta {\ddot{\sigma }}_+ + 3{\dot{\alpha }} \delta {\dot{\sigma }}_+ = \frac{2 }{3\epsilon }e^{-2\alpha +4\sigma _+ }S_1^2 p \delta \dot{u} \;, \end{aligned}$$

(131)

$$\begin{aligned}&{\dot{\alpha }} \delta {\dot{\alpha }} +\frac{27\kappa ^2 f^2}{(1+f)^3} \delta \alpha \nonumber \\&\quad = \frac{1}{6\epsilon }e^{-2\alpha +4\sigma _+ }S_1^2 \left[ 2p^2\left( -\delta \alpha +2\delta \sigma _+ +\delta q \right) +p \delta \dot{q} \right] .\nonumber \\ \end{aligned}$$

(132)

Note that Eq. (130) is derived with the help of Eq. (129). Here the new variable $\delta u(t)$ is also defined as

$$\begin{aligned} p\delta \dot{u} \equiv p \delta \dot{q} - 2B e^{-2\alpha +4\sigma _+ }S_1^2 \left( \delta q-\delta \alpha +2\delta \sigma _+ \right) \; \end{aligned}$$

(133)

for convenience. Note that Eq. (130) can be integrated directly to give the following identity:

$$\begin{aligned} \delta \dot{q} =-p ( \delta \alpha +2\delta q -2\delta u+4\delta \sigma _+ )\; \end{aligned}$$

(134)

with the help of Eq. (72). Indeed, ${\dot{\alpha }}=-2p-\dot{p}/p$ when ${\dot{\sigma }}_+=0$.

With the background solutions (119) and (120) for $\alpha$ and $S_1$ along with the constraints $B=\frac{ \kappa ^2 }{ 96\epsilon }$ and $p=-\kappa /\sqrt{1+f}$, Eq. (131) can be integrated directly as

$$\begin{aligned} \delta {\dot{\sigma }}_+ = \frac{32 \kappa f}{ (1+f)^{3/2} } \delta u \; . \end{aligned}$$

(135)

Finally, with Eqs. (120), (135), and (134), Eq. (132) can be written as

$$\begin{aligned}&\left[ \frac{2\kappa }{\sqrt{1+f} } -\frac{3\kappa f}{(1+f )^{3/2}} \right] \delta {\dot{\alpha }} +\frac{27 \kappa ^2 f^2}{(1+f)^3} \delta \alpha \nonumber \\&\quad = \frac{8\kappa ^2 f}{(1+f)^2} \left[ 3\delta \alpha -2\delta u \right] . \end{aligned}$$

(136)

With the re-scaling of the variables

$$\begin{aligned} \delta q\equiv & {} \frac{1}{\sqrt{1+f} } X \;, \end{aligned}$$

(137)

$$\begin{aligned} \delta \alpha\equiv & {} \frac{(-2+f)}{(1+f)^{3/2}}Y, \end{aligned}$$

(138)

the perturbation equations (133), (134), and (136) can be further simplified as

$$\begin{aligned} \sqrt{1+f} \dot{X}-\delta \dot{u}= & {} \frac{\kappa f}{\sqrt{1+f}} \left[ -2\delta u +\int \frac{192 \kappa f \delta u}{ (1+f)^{3/2} } \mathrm{d}t \right] \;, \nonumber \\ \end{aligned}$$

(139)

$$\begin{aligned} \frac{1}{\sqrt{1+f} }\dot{X}= & {} \frac{\kappa }{\sqrt{1+f} } \left[ \frac{(-2+f)(Y-X)}{(1+f)^{3/2}} \right. \nonumber \\&\left. -2\delta u+\int \frac{128 \kappa f \delta u}{ (1+f)^{3/2} } \mathrm{d}t \right] \;, \end{aligned}$$

(140)

$$\begin{aligned} \frac{(2-f)^2 }{(1+f)}\dot{Y}= & {} 16\kappa f \delta u. \end{aligned}$$

(141)

Note that $\delta u$ has already been written as a function of $\dot{Y}$ according to Eq. (141). Hence we are left with the two independent equations (139) and (140) for the variables X and Y. As a result, Eq. (141) implies that

$$\begin{aligned} \delta \dot{u}=\frac{3(2-f)}{8(1+f)^{3/2}}\left[ \frac{2}{f}+\frac{3}{1+f} \right] \dot{Y}+\frac{(2-f)^2}{16\kappa f(1+f)}\ddot{Y}. \nonumber \\ \end{aligned}$$

(142)

Note that there is a particular solution $\delta u =0$ that leads to constant $\delta \sigma _+$, X, and Y solutions. Hence the perturbations $\delta q$ and $\delta \alpha$ will all be constants as $f \rightarrow 0$ representing a stable mode.

Finally, the perturbation equations in terms of X and Y can be shown to be

$$\begin{aligned} \sqrt{1+f} \dot{X}= & {} \frac{(2-f)^2}{16\kappa f(1+f)}\ddot{Y}\nonumber \\&+ \frac{(2-f)}{8(1+f)^{3/2}}\left[ \frac{6}{f}+\frac{9}{(1+f)} -2+ f \right] \dot{Y} \nonumber \\&+ \frac{12 \kappa f }{\sqrt{1+f} } \int \frac{(2-f)^2}{(1+f)^{5/2}}\dot{Y}\mathrm{d}t , \end{aligned}$$

(143)

$$\begin{aligned} \kappa X= & {} \frac{(2-f)}{16\kappa f}\ddot{Y}+\frac{1}{\sqrt{1+f} }\left[ \frac{1}{f}+\frac{9}{8(1+f)}-\frac{1}{8} \right] \dot{Y}\nonumber \\&+\kappa Y -4\kappa \sqrt{1+f} \int \frac{(2-f)^2}{(1+f)^{5/2}}\dot{Y}\mathrm{d}t . \end{aligned}$$

(144)

Hence differentiation of Eq. (144) leads to a non-linear differential equation of Y:

$$\begin{aligned}&\frac{(f-2)\sqrt{1+f} }{16\kappa ^2 f}\dddot{Y} -\left[ \frac{9}{8}+\frac{ 3(2-f)(7f+4)}{16f(1+f)} \right] \frac{\ddot{Y}}{\kappa } \nonumber \\&\quad +\left[ -27+\frac{9(2-f)(5f^2+7f-2)}{8f(1+f)} \right] \frac{ \dot{Y}}{(1+f)^{3/2}} =0. \nonumber \\ \end{aligned}$$

(145)

Note that we are interested in the large t behavior of these equations with $f \rightarrow -\exp [-6\kappa t]$ as $t \rightarrow \infty$. Hence Eq. (145) can be shown to approach

$$\begin{aligned} \frac{\dddot{Y} }{ \kappa ^2 } +\frac{12}{\kappa }\ddot{Y} +36\dot{Y} \simeq 0 \end{aligned}$$

(146)

with the solution

$$\begin{aligned} \dot{Y} \simeq y_1 e^{ -6\kappa t } \end{aligned}$$

(147)

at $t \rightarrow \infty$. Here $y_1$ is an integration constant. As a result, Eq. (144) can be solved to give

$$\begin{aligned} \kappa X \simeq \frac{-1 }{4}y_1, \end{aligned}$$

(148)

implying that X and Y are both constants. Therefore, we have shown that the set of solutions parametrized by Eqs. (118)–(120) is indeed a set of stable solutions.

6 Conclusion

In this paper, we have shown that the inclusion of a free scalar field $\psi$ to the $\Lambda$CDM model changes the RD phase significantly. We have shown that the WI model without a quartic interaction and scalar field could not produce a compatible resolution for a current universe with a small anisotropy. The inclusion of a quartic interaction terms of the Weyl vector meson and scalar field $\psi$ is thus introduced in Sect. 4. As a result, the QWI model is shown to provide a compatible resolution to the small anisotropy problem. In addition, the quartic WI model also provides a successful alternative to the fitting of the Hubble diagram. Its current EOS prediction also agrees reasonably well with the $\Lambda$CDM model.

To be more specific, we have introduced a quartic interaction proportional to ${S_a}^4$ and an additional free scalar $\psi$ in the BI metric space. The presence of the free scalar field is capable of minimizing the current anisotropy ${{\dot{\sigma }}}_- / {{\dot{\alpha }}}$, as expected. As a result, we have shown that Eqs. (89), (91) and (108) constrain the field parameters $K_-, \kappa , \psi _0, H_0$ and $f_0$ in a harmonic way such that consistent anisotropy can be induced. In addition, by choosing $f_0=-0.06$, $H_0=0.70 (100\,\mathrm{km/s/Mpc})$ and ${\psi _0^2 }/{\epsilon } \sim 54 \kappa ^2$ for the QWI model in plotting the Hubble diagram (Fig. 2), we can successfully minimize the current anisotropy consistent with the CMB observations.

It was shown apparently that $K_-$ cannot be minimized in the absence of the free scalar field $\psi$. The existence of a consistent analytic solution shown in this paper requires that the cosmological constant is related to $\kappa$ (affecting the mass term of $S_a$) through the relation $\Lambda =12 \kappa ^2$. In addition, the QWI model can also resemble the $\Lambda$CDM model at current stage as shown in Eq. (92). In addition, the QWI model prediction of the Hubble diagram also agrees reasonably well with current observations. These results show that quartic term and free scalar field $\psi$ do play important roles in the evolution of our universe.

The result shown in this paper indicates that the WI model provides a successful resolution to the evolution of our physical universe. Hopefully, a more detailed study of related models will shed light to the underlying importance of the scale symmetry and its generalized alternative.