1 Introduction

The anisotropies observed in the cosmic microwave background (CMB) are compatible with an adiabatic primordial scalar perturbation which is nearly Gaussian with a nearly scale-invariant power spectrum [1]. Cosmic inflation is the most successful theoretical framework in describing the very early stages of universe and also solves some shortcomings of the hot big-bang model, such as the horizon, flatness and monopole [2, 3] problems. However, the key feature of inflation is that it may be able to generate a causal mechanism to explain the large scale structure (LSS) of the universe [4] and the origin of the anisotropies observed in the CMB, since primordial density perturbations may be sourced from quantum fluctuations of the inflaton scalar field during the inflationary expansion. The standard cold inflation scenario [5,6,7,8] is divided into two regimes: the slow-roll and reheating phases. In the slow-roll period the universe undergoes an accelerated expansion as the potential energy of the inflaton field dominates over its kinetic energy and all interactions of the inflaton scalar field with other field degrees of freedom are typically neglected. Subsequently, a reheating period is invoked to end the brief acceleration. During reheating, the kinetic energy of the inflaton field becomes comparable to its potential energy, and by transferring its energy to massless particles it oscillates around the minimum of the potential. After reheating, the universe is filled with relativistic particles and then the universe enters in the radiation big-bang epoch.

Alternatively, there is another dynamical mechanism for obtaining a successful slow-roll inflation, i.e., the warm inflation scenario [9,10,11,12,13]. As opposed to standard cold inflation, warm inflation has the essential feature that a reheating phase is avoided at the end of the accelerated expansion due to the decay of the inflaton into radiation and particles during the slow-roll phase. However, the key difference is the origin of the density fluctuations. In the warm inflation scenario, a thermalized radiation component is present at temperature T, \(T>H\), where H is the Hubble rate. In this way, the inflaton fluctuations \(\delta \phi \) are predominantly thermal instead of quantum [9,10,11,12,13].

Regarding standard cold inflation, Linde [14] introduced the concept of chaotic inflation in order to interpret the initial conditions for scalar field driving inflation which may help in solving the persisting problems of the old inflation models. In this model, the inflaton potential was chosen to be quadratic or quartic form, i.e. \(\frac{m^2}{2}\phi ^2\) or \(\frac{\lambda }{4}\phi ^4\), terms that are always present in the scalar potential of the Higgs sector in all renormalizable gauge field theories [15] in which the gauge symmetry is spontaneously broken via the Englert–Brout–Higgs mechanism [16, 17]. Such a model is interesting for its simplicity, and it has become one of the most favored, because it predicts a significant amount of tensor perturbations due to the inflaton field getting across the trans-Planckian distance during inflation [18].

After introducing chaotic inflation, several works have been published in this direction. Herrera [19] discussed the warm inflation by assuming the chaotic potential in loop quantum cosmology and found consistency of the results with observational data. The warm inflation was also investigated by del Campo and Herrera [20] driving by a scalar field with canonical kinetic term and a power-law dependence in the inflaton field for the dissipative coefficient, i.e., \(\Gamma \propto \phi ^{n}\), in the generalized Chaplygin gas (GCG) scenario. Further, Setare and Kamali investigated warm inflation driven by a tachyonic field and assumed the scale factor evolves according to intermediate [21] and logamediate [22] models. On the other hand, Bastero-Gill et al. [23] obtained analytic expressions for the dissipative coefficient in supersymmetric (SUSY) models and found that their results provide a realization of warm inflation in SUSY field theories. After that, Bastero-Gill et al. [24] have also explored chaotic inflation by assuming the quartic potential. On the other hand, Herrera et al. studied intermediate inflation in the context of GCG using standard and tachyon scalar field models [25]. More recently, in Ref. [26], the dynamics of warm inflation in a modified Chaplygin gas (MCG) was studied.

Panotopoulos and Videla [27] discussed warm inflation by assuming the quartic potential and an inflaton decay rate proportional to the temperature and found that their results are in agreement with the latest Planck data, obtaining a lower value for the tensor-to-scalar ratio compared to the cold inflation scenario. Going further, several authors have investigated the warm inflation scenario in various alternative/modified theories of gravity [28,29,30,31,32,33,34,35,36,37,38,39,40,41]. Moreover, a new family of inflation models is being developed named as shaft inflation [42]. In Refs. [43, 44], the authors have developed inflationary parameters by considering a shaft potential and a tachyon scalar field and found that their results are consistent with current observational data. Recently, Kobayashi and Seto [45] investigated the polynomial warm inflation and reported that their results are in consistence with BICEP2 and Planck data.

The main goal of the present paper is to study the consequences of considering a polynomial inflationary potential in the context of the generalized, modified, and generalized cosmic Chaplygin gas models. In addition, we consider dissipative effects by coupling the inflation field to radiation, i.e., the inflationary dynamics will be studied in the warm inflation scenario. We take into account a general parametrization of the dissipative coefficient \(\Gamma \) for describing the decay of the inflaton field into radiation. The outline of the paper is as follows: In the next section, we provide the basic set of equations describing the warm inflationary scenario. In Sects. 3, 4 and 5, we obtain the various inflationary observables in view of GCG, the modified Chaplygin gas (MCG), and the generalized cosmic Chaplygin gas (GCCG) models for positive/negative quadratic and quartic potentials. In Sect. 6, we summarize our findings and present our conclusions.

2 Basics of warm inflation scenario

2.1 Background evolution

The Friedmann equation for a flat FRW universe in the presence of the standard scalar field and a radiation fluid takes the following form:

$$\begin{aligned} H^2=\frac{1}{3M_\mathrm{p}^2}\left( \rho _{\phi }+\rho _{\gamma }\right) , \end{aligned}$$
(1)

where \(M_\mathrm{p}=\frac{1}{\sqrt{8\pi \text {G}}}\) is the reduced Planck mass. The energy density of standard scalar field can be defined as \(\rho _{\phi }=\dot{\phi }^2/2 +V(\phi )\) where dots represent the derivative with respect to cosmic time. On the other hand, \(\rho _{\gamma }\) corresponds to the energy density of radiation fluid. The corresponding conservation equations for both standard scalar field and radiation turn out to be

$$\begin{aligned} \dot{\rho }_{\phi }+3H(\rho _{\phi }+p_{\phi })=-\Gamma \dot{\phi }^2,\quad \dot{\rho }_{\gamma }+4H(\rho _{\gamma })=\Gamma \dot{\phi }^2, \end{aligned}$$
(2)

where \(p _{\phi }\) denotes the pressure of standard scalar field, given by \(p_{\phi }= \dot{\phi }^2/2 -V(\phi )\). By replacing the expressions for the energy densities for the scalar field as well as radiation in the first conservation equation, we get

$$\begin{aligned} \ddot{\phi }+(3H+\Gamma )\dot{\phi }+V'=0, \end{aligned}$$
(3)

where the primes denote derivatives with respect to \(\phi \). On the other hand, \(\Gamma \dot{\phi }\) denotes the interaction term between the scalar field and radiation, whereas \(\Gamma \) is responsible for the decay of the scalar field into radiation. This inflaton decay rate may depend on the scalar field and the temperature of the thermal bath, or both quantities, or even it can be a constant. During warm inflation, the production of radiation is quasi-stable, i.e., \(\dot{\rho }_{\gamma }\ll 4H\rho _{\gamma }\) and \(\dot{\rho }_{\gamma }\ll \Gamma \dot{\phi }^2\) [4, 21, 23, 46, 47]. This implies that energy density related to the scalar field dominates over the energy density of radiation field and hence the equations of motion in the slow-roll approximation turn out to be

$$\begin{aligned} 3H(1+R)\dot{\phi }\simeq -V',\quad 4H\rho _{\gamma }\simeq \Gamma \dot{\phi }^2, \end{aligned}$$
(4)

where \(R=\frac{\Gamma }{3H}\) characterizes two dissipative regimes such as weak (\(R\ll 1\)) and strong (\(R\gg 1\)). A general parametrization of the inflaton decay rate is given by

$$\begin{aligned} \Gamma =c\frac{T^n}{\phi ^{n-1}}, \end{aligned}$$
(5)

where c is a constant parameter and n is an integer [48, 49]. Several expressions for the dissipative coefficient, corresponding to different values of n, have been studied in the literature [50, 51]. On the other hand, the energy density of the radiation field can be written as \(\rho _{\gamma }=C_{*}T^4\), with \(C_{*}=\pi ^2 g_{*}/30\) and \(g_{*}\) represents the number of relativistic degrees of freedom. In the minimal SUSY standard model, \(g_{*}=228.75\) and \(C_{*}\simeq 70\) . By using Eq. (4) and \(\rho _{\gamma }\propto T^4\), we may find an expression for the temperature of thermal bath, which is given by

$$\begin{aligned} T=\left( \frac{\Gamma V'^2 }{6^2C_{*}H^3(1+R)^2}\right) ^\frac{1}{4}. \end{aligned}$$
(6)

The set of slow-roll parameters for warm inflation is given by [46]

$$\begin{aligned} \epsilon =\frac{-\dot{H}}{H^2},\quad \eta =\frac{-\ddot{H}}{H\dot{H}},\quad \beta =\frac{-1}{H}\frac{\mathrm{d}}{\mathrm{d}t}(\ln \Gamma ). \end{aligned}$$
(7)

The number of e-folds is defined as

$$\begin{aligned} N=\int _{t_{*}}^{t_{\mathrm{end}}} Hdt, \end{aligned}$$
(8)

where \(t_{*}\) and \(t_{\mathrm{end}}\) denote the moment when the cosmological scale crosses the Hubble radius and the end of inflation, respectively.

2.2 Cosmological perturbations

In the warm inflation scenario, a thermalized radiation component is present with \(T>H\), then the inflaton fluctuations \(\delta \phi \) are predominantly thermal instead of quantum. In this way, following Ref. [13], the amplitude of the power spectrum of the curvature perturbation is given by

$$\begin{aligned} \mathcal {P}_{\mathcal {R}}\simeq \left( \frac{H}{2\pi }\right) \left( \frac{3H^2}{V^{\prime }}\right) (1+R)^{5/4}\left( \frac{T}{H}\right) ^{1/2}, \end{aligned}$$
(9)

where the normalization has been chosen in order to recover the standard cold inflation result when \(R\,\rightarrow \,0\) and \(T\simeq H\).

On the other hand, the scalar spectral index \(n_\mathrm{s}\), to leading order in the slow-roll approximation, becomes

$$\begin{aligned} n_{\mathrm{s}}=1+\frac{\mathrm{d}P_{R}}{\mathrm{d}lnk}\simeq 1-\frac{9\epsilon }{4}+\frac{3\eta }{2}-\frac{9\beta }{4}, \end{aligned}$$
(10)

while for the tensor-to-scalar ratio we have [13]

$$\begin{aligned} r\simeq \left( \frac{H}{T}\right) \frac{16 \epsilon }{(1+R)^{5/2}}. \end{aligned}$$
(11)

When a specific form of the scalar potential and the dissipative coefficient G are considered, it is possible to study the background evolution under the slow-roll regime and the primordial perturbations in order to test the viability of warm inflation. In the following we will study a polynomial potential, which has quadratic and quartic powers of the inflaton scalar field. A generalized expressions for the polynomial potential is proposed in [45], given by

$$\begin{aligned} V=t_{1}+t_{2}\phi ^{2} +t_{4}\phi ^{4}. \end{aligned}$$
(12)

Since it is not easy to deal with several parameters, for convenience we consider terms up to \(\phi ^{4}\), which might be motivated by the renormalizability for this potential in quantum field theory. Thus, we consider two kinds of polynomial potentials:

  • negative quadratic and quartic potential

    $$\begin{aligned} V=s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*}}{4}\phi ^4, \quad V'=-\sigma ^2\phi +\lambda _{*}\phi ^3, \end{aligned}$$
    (13)

  • positive quadratic and quartic potential

    $$\begin{aligned} V=\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*}}{4}\phi ^4, \quad V'=\sigma ^2\phi +\lambda _{*}\phi ^3, \end{aligned}$$
    (14)

where \(s,~\lambda _{*}\) and \(\sigma \) are arbitrary constants. In the following sections, we illustrate the inflationary parameters for the above-mentioned scenario in the presence of three Chaplygin gas models (GCG, MCG and GCCG) by assuming weak and strong dissipative regimes with the inflaton decay rate given by the generalized expression (5).

3 Generalized Chaplygin gas model

It is believed that the universe undergoes an accelerated expansion of the universe and an exotic component having a negative pressure, usually known as dark energy (DE), is responsible for this expansion. Several models have been already proposed to be DE candidates, such as the cosmological constant [52], quintessence [53,54,55], k-essence [56,57,58], tachyon [59,60,61], phantom [62,63,64], the Chaplygin gas [65], holographic DE [68], in order to modify the matter sector of the gravitational action. Despite there being plenty models, the nature of the dark sector of the universe, i.e. DE and dark matter, is still unknown. There exists another way of understanding the observed universe in which dark matter and DE are described by a single unified component. Particularly, CG contains the unification of DE and dark matter and behaves as a pressureless matter at early times and like a cosmological constant at late times [65]. It is noted that CG describes the universe in agreement with current observations of cosmic acceleration. The GCG is the extended form of CG and its equation of state (EoS) is [65]

$$\begin{aligned} p_{gcg}=-\frac{C_{1}}{\rho _{gcg}^\alpha } \end{aligned}$$
(15)

where \(p_{gcg}\) and \(\rho _{gcg}\) represent the pressure and energy density of GCG model, respectively, with \(0<\alpha \le 1\), and \(C_{1}\) is a positive constant [65]. Also, \(\rho _{gcg}\) can be obtained through the conservation equation as follows:

$$\begin{aligned} \rho _{gcg}=\bigg (C_{1}+\frac{C_{2}}{a^{3(1+\alpha )}}\bigg )^\frac{1}{1+\alpha }, \end{aligned}$$
(16)

here \(C_{2}\) is a positive constant after integration. In this way, the term proportional to \(a^{-3}\) is identified as the energy density of matter \(\rho _\mathrm{m}\).

In order to obtain inflation in the Chaplygin-like gas scenarios studied in the present work, we follow Ref. [66]. The energy density of matter \(\rho _\mathrm{m}\) is identified with the contribution of the energy density associated to the standard scalar field \(\rho _{\phi }\) through an extrapolation of Eq. (16), yielding

$$\begin{aligned} \rho _{gcg}=(C_{1}+\rho ^{1+\alpha }_{\mathrm{m}})^\frac{1}{1+\alpha }\quad \longrightarrow (C_{1}+\rho ^{1+\alpha }_{\phi })^\frac{1}{1+\alpha }. \end{aligned}$$
(17)

In this sense, we will not consider Eq. (17) as a consequence of Eq. (16), but a non-covariant modification of gravity instead, resulting in a modified Friedmann equation, as pointed out in Ref. [67].

In this scenario, we consider a spatially flat universe which contains a self-interacting inflation field \(\phi \) and a radiation field, then the Friedmann equation (1) turns out to be

$$\begin{aligned} H^2=\frac{1}{3M^2_\mathrm{p}}\bigg [(C_{1}+\rho _\phi ^{1+\alpha })^\frac{1}{1+\alpha } +\rho _{\gamma }\bigg ]. \end{aligned}$$
(18)

We stress that the Friedmann equation (18) comes from a non-covariant modification of gravity. However, as pointed out in Ref. [66], it may be assumed that the effect giving rise to Eq. (18) preserves diffeomorphism invariance in (\(3+1\)) dimensions, whence total stress-energy conservation follows.

During inflation, the energy density of the scalar field dominates the energy density of the radiation field, i.e., \(\rho _{\phi \gg }\rho _{\gamma }\), which leads to \(\rho _{\phi }\sim V\). Here we take \(\alpha =1\) for the sake of simplicity. Then the Friedmann equation (18) becomes

$$\begin{aligned} H^2=\frac{1}{3M^2_\mathrm{p}}\sqrt{C_{1}+\rho ^2_{\phi }}\sim \frac{1}{3M^2_\mathrm{p}}\sqrt{C_{1}+V^2}. \end{aligned}$$
(19)

Further, we will construct the inflationary parameters in two cases of dissipative coefficients: in the weak dissipative regime (\(R\le 1\)) and the strong dissipative regime (\(R\ge 1\)) for the present case of GCG.

3.1 Weak dissipative regime

For the first case, the temperature turns out to be \(T=(\frac{cV'^2}{6^2C_{*}H^3\phi ^{n-1}})^\frac{1}{4-n}\) in the presence of the generalized dissipative coefficient \(\Gamma =c\frac{T^n}{\phi ^{n-1}}\). With this temperature and under the weak dissipative regime condition, the slow-roll parameters (7) in terms of the potential (V) can be written as

$$\begin{aligned} \epsilon= & {} \frac{M^2_\mathrm{p}VV'^2}{2(C_{1}+V^2)^\frac{3}{2}},\quad \eta =\frac{M^2_\mathrm{p}}{(C_{1}+V^2)^\frac{1}{2}}\\&\times \left( V''+\frac{V'^2}{V} -\frac{3VV'^2}{2(C_{1}+V^2)}\right) ,\\ \beta= & {} M_\mathrm{p}^2\bigg (2(C_{1}+V^2)(2nV'' -n V'(n-1)\phi ^{-1}\\&-V'(4-n)(n-1)\times \phi ^{-1})-3n V'^2V\bigg )\\&\times \bigg ({2(C_{1}+V^2)^{\frac{3}{2}}(4-n)}\bigg )^{-1}. \end{aligned}$$

With the help of Eq. (8), the number of e-folds becomes

$$\begin{aligned} N=\frac{1}{M^2_\mathrm{p}}\int _{\phi _{\mathrm{end}}}^{\phi _{e}}\frac{\sqrt{C_{1}+V^2}}{V'}\mathrm{d}\phi . \end{aligned}$$

Equations (9)–(11) provide the power spectrum, the scalar spectral index and tensor-to-scalar ratio in terms of potential (V) as follows:

$$\begin{aligned}&\mathcal {P}_{\mathcal {R}}=\left( \frac{\pi }{4}\right) ^{\frac{1}{2}}\frac{9\left( C_1+V^2\right) ^{\frac{3(5-2n)}{4(4-n)}} c^{\frac{3}{4-n}}}{3^{\frac{3(5-2n)}{2(4-n)}} M_\mathrm{p}^{\frac{3(5-2n)}{4-n}}V'^{\frac{6-3n}{4-n}}\phi ^{\frac{(n-1)(4-n)+(n-1)(n+2)}{2(4-n)}}6^{\frac{n+2}{4-n}}C_{*}^{\frac{n+2}{2(4-n)}}},\nonumber \\&n_\mathrm{s}-1=\frac{3M_\mathrm{p}^2}{2(C_{1}+V^2)^{\frac{1}{2}}}\bigg (\frac{-9V V'^2}{4(C_{1}+V^2)}-\frac{3}{2}\bigg (2(C_{1}+V^2)\bigg (2n V''\nonumber \\&\quad -n V'(n-1)\phi ^{-1}-V'(4-n)(n-1)\phi ^{-1}\bigg )-3n V'^2V\bigg )\nonumber \\&\quad \times \bigg ({2(C_{1}+V^2)(4-n)}\bigg )^{-1}+V''+\frac{V'^2}{V}\bigg ),\nonumber \\&r=\frac{32{G V}^{ \prime ^{\frac{6-3n}{4-n}}}\phi ^{\frac{(n-1)(4-n)+(n-1)(n+2)}{2(4-n)}}6^{\frac{n+2}{4-n}}C_{*}^{\frac{n+2}{2(4-n)}} 3^{\frac{7-4n}{2(4-n)}}M_\mathrm{p}^{\frac{7-4n}{4-n}}}{9c^{\frac{3}{4-n}}\pi ^{\frac{3}{2}}\left( C_{1}+V^2\right) ^{\frac{7-4n}{4(4-n)}}}.\nonumber \\ \end{aligned}$$
(20)

For positive quadratic and quartic potential: The above expressions of r and \(n_{\mathrm{s}}\) in terms of the scalar field lead to

$$\begin{aligned}&r=32G\bigg (\sigma ^2\phi +\lambda _{*} \phi ^3\bigg )^{^{\frac{6-3n}{4-n}}}\phi ^{\frac{(n-1)(4-n)+(n-1)(n+2)}{2(4-n)}}6^{\frac{n+2}{4-n}}C_{*}^{\frac{n+2}{2(4-n)}} 3^{\frac{7-4n}{2(4-n)}}\\&\quad \times M_\mathrm{p}^{\frac{7-4n}{4-n}}\bigg (9c^{\frac{3}{4-n}}\pi ^{\frac{3}{2}}\left( C_{1}+\left( \frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) ^2\right) ^{\frac{7-4n}{4(4-n)}}\bigg )^{-1},\\&n_\mathrm{s}-1=\frac{3M_\mathrm{p}^2}{2(C_{1}+(\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4})^2)^{\frac{1}{2}}}\bigg (-9\left( \frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) \\&\quad \times (\sigma ^2\phi +\lambda _{*} \phi ^3)^2\bigg ({4\left( C_{1}+\left( \frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) ^2\right) }\bigg )^{-1}\nonumber \\&\quad -\frac{3}{2}\bigg ( 2(C_{1}+(\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4})^2)\bigg (2n (\sigma ^2+3\lambda _{*} \phi ^2)\\&\quad -n(\sigma ^2\phi +\lambda _{*} \phi ^3)(n-1)\phi ^{-1}-(\sigma ^2\phi +\lambda _{*} \phi ^3)(4-n)\\&\quad \times (n-1)\phi ^{-1}\bigg )-3n(\sigma ^2\phi +\lambda _{*} \phi ^3)^2\times \left( \frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) \\&\quad \times \left( 2\left( 2\left( C_{1}+\left( \frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) ^2\right) \right) (4-n)\right) ^{-1}\bigg )\\&\quad +(\sigma ^2+3\lambda _{*} \phi ^2)+\frac{(\sigma ^2\phi +\lambda _{*} \phi ^3)^2}{\left( \frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) }\bigg ). \end{aligned}$$

For negative quadratic and quartic potential: The expressions of r and \(n_{\mathrm{s}}\) for negative potential turn out to be

$$\begin{aligned}&r=\frac{32G\left( -\sigma ^2\phi +\lambda _{*} \phi ^3\right) ^{^{\frac{6-3n}{4-n}}}\phi ^{\frac{(n-1)(4-n)+(n-1)(n+2)}{2(4-n)}}6^{\frac{n+2}{4-n}}C_{*}^{\frac{n+2}{2(4-n)}} 3^{\frac{7-4n}{2(4-n)}}M_\mathrm{p}{}^{\frac{7-4n}{4-n}}}{9c^{\frac{3}{4-n}}\pi ^{\frac{3}{2}}\left( C_{1}+\left( s-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) ^2\right) ^{\frac{7-4n}{4(4-n)}}},\\&n_\mathrm{s}=1+\frac{3M_\mathrm{p}^2}{2\left( C_{1}+\left( s-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) ^2\right) ^{\frac{1}{2}}}\\&\quad \times \left( -9\left( s-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) \times (-\sigma ^2\phi +\lambda _{*} \phi ^3)^2\right. \\&\quad \times \left. \left( {4\left( C_{1}+\left( s-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) ^2\right) }\right) ^{-1}-\frac{3}{2}\right. \\&\quad \times \left. \left( 2\left( C_{1}+\left( s-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) ^2\right) \right. \right. \\&\quad \times \left. \left. (2n(-\sigma ^2+3\lambda _{*} \phi ^2)-n\right. \right. \\&\quad \times \left. \left. (-\sigma ^2\phi +\lambda _{*} \phi ^3)(n-1)\phi ^{-1}\right. \right. \\&\quad \left. \left. -(-\sigma ^2\phi +\lambda _{*} \phi ^3)(4-n)\right. \right. \\&\quad \left. \left. \times (n-1)\phi ^{-1})-3n(-\sigma ^2\phi +\lambda _{*} \phi ^3)^2\right. \right. \\&\quad \times \left. \left. \left( s-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) \right. \right. \\&\quad \times \left. \left. \left( 2\left( 2\left( C_{1}+\left( s-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) ^2\right) \right) \right. \right. \right. \\&\qquad \left. \left. \left. (4-n)\right) ^{-1}\right) +(-\sigma ^2\right. \\&\quad \left. +3\lambda _{*} \phi ^2)+\frac{(-\sigma ^2\phi +\lambda _{*} \phi ^3)^2}{(s-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4})}\right) . \end{aligned}$$

3.2 Strong dissipative regime

In this case, the temperature becomes \(T=(\frac{V'^2\phi ^{n-1}}{4cc_{*}H})^\frac{1}{n+4}\). The slow-roll parameters lead to

$$\begin{aligned} \epsilon= & {} \frac{M^2_\mathrm{p}VV'^2}{2R(C_{1}+V^2)^\frac{3}{2}},\quad \eta =\frac{M^2_\mathrm{p}}{R(C_{1}+V^2)^\frac{1}{2}}\\&\times \bigg (V''+\frac{V'^2}{V}-\frac{3VV'^2}{2(C_{1}+V^2)}\bigg ),\quad \\ \beta= & {} \frac{nM^2_\mathrm{P}}{(n+4)R}\left( \frac{4V''(C_{1}+V^2)-VV'^2}{2(C_{1}+V^2)^\frac{3}{2}}\right) . \end{aligned}$$

The power spectrum, scalar spectral index and tenor-to-scalar ratio turn out to be

$$\begin{aligned}&\mathcal {P}_{\mathcal {R}}=\left( \frac{\pi }{4}\right) ^{\frac{1}{2}}\frac{c^{\frac{23-5n}{10}}\left( C_{1}+V^2\right) ^{\frac{23-5n}{40}}}{V'^{\frac{8-5n}{5}}(4c_{*})^{\frac{5n+2}{10}} M_\mathrm{p}{}^{\frac{23-5n}{10}}3^{\frac{23-5n}{20}}},\nonumber \\&n_\mathrm{s}-1= \bigg (\frac{3(4c_{*})^{\frac{1}{5}}}{c^{\frac{4}{5}}V'^{\frac{2}{5}}}\bigg )\frac{(3M_\mathrm{p}^2) ^{\frac{2}{5}}}{2(C_{1}+V^2)^{\frac{1}{5}}}\bigg (V''+\frac{V^{\prime ^2}}{V} \nonumber \\&\quad -\frac{9V V'^2}{4(C_{1}{+}V^2)}-\frac{3(n)}{2(n+4)}\bigg (\frac{4V''(C_{1}+V^2)-V V^{\prime ^2}}{2(C_{1}+V^2)}\bigg )\bigg ) , \nonumber \\&r=\frac{32G V^{\prime ^{\frac{8-5n}{5}}}\phi ^{\frac{5(n-1)}{2}}(4c_{*})^{\frac{5n+2}{10}}\left( C_{1}+V^2\right) ^{\frac{5n-3}{40}}}{\pi ^{\frac{3}{2}}c^{\frac{23-5n}{10}}3^{\frac{5n-3}{20}}M_\mathrm{p}^{\frac{5n-3}{10}}}. \end{aligned}$$
(21)

For positive quadratic and quartic potential: The scalar spectral index and tensor-to-scalar ratio in the case of the strong dissipative regime turns out to be

$$\begin{aligned}&r=\frac{32G \left( \sigma ^2\phi +\lambda _{*} \phi ^3\right) ^{^{\frac{8-5n}{5}}}\phi ^{\frac{5(n-1)}{2}}(4c_{*})^{\frac{5n+2}{10}}\left( C_{1}+\left( \frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) ^2\right) ^{\frac{5n-3}{40}}}{\pi ^{\frac{3}{2}}b^{\frac{23-5n}{10}}3^{\frac{5n-3}{20}}M_\mathrm{p}^{\frac{5n-3}{10}}},\nonumber \\&n_\mathrm{s}-1= \bigg (\frac{3(4c_{*})^{\frac{1}{5}}}{c^{\frac{4}{5}}(\sigma ^2\phi +\lambda _{*} \phi ^3)^{\frac{2}{5}}}\bigg )\frac{(3M_\mathrm{p}^2)^{\frac{2}{5}}}{2(C_{1}+(\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4})^2)^{\frac{1}{5}}}\nonumber \\&\quad \times \bigg ((\sigma ^2+3\lambda _{*} \phi ^2)+\frac{(\sigma ^2\phi +\lambda _{*} \phi ^3)^{^2}}{(\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4})}\nonumber \\&\quad -\frac{9(\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4})(\sigma ^2\phi +\lambda _{*} \phi ^3)^2}{4(C_{1}+(\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4})^2)}-\frac{3(n)}{2(n+4)}\nonumber \\&\quad \times \bigg (4(\sigma ^2+3\lambda _{*} \phi ^2)\left( C_{1}+\left( \frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) ^2\right) \nonumber \\&\quad -\left( \frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\right) (\sigma ^2\phi +\lambda _{*} \phi ^3)^{^2}\nonumber \\&\quad \times \bigg (2\bigg (C_{1}+\bigg (\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\bigg )^2\bigg )\bigg )^{-1}\bigg )\bigg ). \end{aligned}$$
(22)
Fig. 1
figure 1

Plot of r versus \(n_{\mathrm{s}}\) for GCG model in weak (left panel) and strong (right panel) dissipative regimes for positive potential with \(n=1\)

Full size image
Fig. 2
figure 2

Plot of r versus \(n_{\mathrm{s}}\) for GCG model in weak (left panel) and strong (right panel) dissipative regimes for positive potential with \(n=-1\)

Full size image
Fig. 3
figure 3

Plot of r versus \(n_{\mathrm{s}}\) for GCG model in weak (left panel) and strong (right panel) dissipative regimes for positive potential with \(n=-2\)

Full size image

By utilizing the value of the negative quadratic and quartic potential and its derivative in Eqs. (21) of the scalar spectral index and tensor-to-scalar ratio, we obtain

$$\begin{aligned}&r=\frac{32G \left( -\sigma ^2\phi +\lambda _{*} \phi ^3\right) ^{^{\frac{8-5n}{5}}}\phi ^{\frac{5(n-1)}{2}}(4c_{*})^{\frac{5n+2}{10}}(C_{1}+({s}-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4})^2)^{\frac{5n-3}{40}}}{\pi ^{\frac{3}{2}}c^{\frac{23-5n}{10}}3^{\frac{5n-3}{20}}M_\mathrm{p}^{\frac{5n-3}{10}}},\nonumber \\&n_\mathrm{s}=1+ \bigg (\frac{3(4c_{*})^{\frac{1}{5}}}{c^{\frac{4}{5}}(-\sigma ^2\phi +\lambda _{*} \phi ^3)^{\frac{2}{5}}}\bigg )\frac{(3M_\mathrm{p}^2)^{\frac{2}{5}}}{2(C_{1}+({s}-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4})^2)^{\frac{1}{5}}}\nonumber \\&\quad \times \bigg ((-\sigma ^2+3\lambda _{*} \phi ^2)+\frac{(-\sigma ^2\phi +\lambda _{*} \phi ^3)^{^2}}{\bigg ({s}-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\bigg )}-9\bigg ({s}-\frac{\sigma ^2\phi ^2}{2}\nonumber \\&\quad +\frac{\lambda _{*} \phi ^4}{4})(-\sigma ^2\phi +\lambda _{*} \phi ^3)^2\bigg ({4\bigg (C_{1}+\bigg ({s}-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\bigg )^2\bigg )}\bigg )^{-1}\nonumber \\&\quad -\frac{3(n)}{2(n+4)}\bigg (4(-\sigma ^2+3\lambda _{*} \phi ^2)\bigg (C_{1}+\bigg ({s}-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\bigg )^2\bigg )\nonumber \\&\quad -\bigg ({s}-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\bigg )\bigg (-\sigma ^2\phi +\lambda _{*} \phi ^3\bigg )^{^2}\nonumber \\&\quad \times \bigg (2\bigg (C_{1}+\bigg ({s}-\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4}\bigg )^2\bigg )\bigg )^{-1}\bigg )\bigg ). \end{aligned}$$
(23)
Table 1 WMAP9 [69] and Planck 2015 [70] data for r and \(n_\mathrm{s}\)
Full size table
Table 2 GCG Weak and strong dissipative regimes with positive quadratic and quartic potential
Full size table
Fig. 4
figure 4

Plot of r versus \(n_{\mathrm{s}}\) for GCG model in weak (left panel) and strong (right panel) dissipative regimes for negative potential with \(n=1\)

Full size image
Fig. 5
figure 5

Plot of r versus \(n_{\mathrm{s}}\) for GCG model in weak (left panel) and strong (right panel) dissipative regimes for negative potential with \(n=-1\)

Full size image

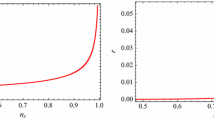
We plot the graphs of r and \(n_{\mathrm{s}}\) for both weak and strong dissipative regimes by assuming the positive quadratic and quartic potential for three different values of \(n=1,-1,-2\), respectively, as shown in Figs. 1, 2 and 3. The other constant parameters appearing in the model are assumed to be as follows: \(M_\mathrm{p}=1, \alpha =10^{-13}, C_{1}=10^{-45},\, \lambda _{*}=10^{-3}, \,c=0.3,\, C_{*}=70\). The constraints of the inflationary parameters such as the tensor-to-scalar ratio and the spectral index are displayed in Table 2. It is found that the results are compatible with WMAP9 [69] and Planck 2015 [70], which are given in Table 1.

Fig. 6
figure 6

Plot of r versus \(n_{\mathrm{s}}\) for GCG model in weak (left panel) and strong (right panel) dissipative regimes for negative potential with \(n=-2\)

Full size image

Figures 4, 5 and 6 show the behavior of r and \(n_{\mathrm{s}}\) for negative quadratic and quartic potential in the weak and strong dissipative regimes. The parameters appearing in the model attained the values \(M_\mathrm{p}=1, s=2\), \(\alpha =10^{-5}\), \(C_{1}=10^{-45}, c=0.3, C_{*}=70, \lambda _{*}=10^{-13}, c=10^{-7}, G=0.0398\). The results for negative quadratic and quartic potential are shown in Table 3. The values of tensor-to-scalar ratio and spectral index are in consistence with observational WMAP9 [69] and Planck 2015 [70] data.

Table 3 GCG Weak and strong dissipative regime with negative quadratic and quartic potential
Full size table

4 Modified Chaplygin gas

The EoS of MCG is given as [71]

$$\begin{aligned} p_{mcg}=\zeta \rho _{mcg}-\frac{\xi }{\rho _{mcg}^\alpha }, \end{aligned}$$
(24)

where \(p_{mcg}\) and \(\rho _{mcg}\) represent the pressure and energy density of MCG, respectively, and \(0\le \alpha \le 1\), while \(\zeta \) and \(\xi \) are positive constants. The energy density \(\rho _{mcg}\) can be calculated by using energy conservation equation as follows:

$$\begin{aligned} \rho _{mcg}=\bigg (C_{3}+\frac{C_{4}}{a^{3(1+\alpha )(1+\zeta )}}\bigg )^\frac{1}{1+\alpha }, \end{aligned}$$
(25)

here \(C_{4}\) is an integration constant and \(C_{3}=\frac{\xi }{1+\zeta }\). In view of MCG, the Friedmann equation takes the following form:

$$\begin{aligned} H^2=\frac{1}{3M^2_\mathrm{p}}\bigg [(C_{3}+\rho _\phi ^{(1+\alpha ) (1+\zeta )})^\frac{1}{1+\alpha }+\rho _{\gamma }\bigg ]. \end{aligned}$$
(26)

Under certain conditions as mentioned in the GCG case, the above Friedmann equation reduces to

$$\begin{aligned} H^2= & {} \frac{1}{3M^2_\mathrm{p}}(C_{3}+\rho ^{(1+\alpha )(1+\zeta )}_{\phi })^\frac{1}{1+\alpha }\nonumber \\\sim & {} \frac{1}{3M^2_\mathrm{p}}(C_{3}+V^{(1+\alpha )(1+\zeta )})^\frac{1}{1+\alpha }. \end{aligned}$$
(27)

Next, we extract the inflationary parameters for both cases of dissipative coefficients.

4.1 Weak dissipative regime

Here, the temperature remains the same as in the case of GCG, while the slow-roll parameters turn out to be

$$\begin{aligned} \epsilon= & {} \frac{M^2_\mathrm{P}(1+\zeta )V^{(1+\alpha )(1+\zeta )-1}V'^2}{2(C_{3}+V^{(1+\alpha )(1+\zeta )})^\frac{2+\alpha }{1+\alpha }},\quad \\ \eta= & {} \frac{M^2_\mathrm{p}}{(C_{3}+V^{(1+\alpha )(1+\zeta )})^\frac{1}{1+\alpha }}\\&\times \bigg (2V''+\frac{V'^2((1+\alpha ) (1+\zeta )-1)}{V}\\&-\frac{V^{(1+\alpha )(1+\zeta )-1}V'^2(1+\alpha )(1+\zeta )}{(C_{3}+V^{(1+\alpha )(1+\zeta )})}\bigg ),\\ \beta= & {} M_\mathrm{p}^2\bigg ((C_{3}+V^{(1+\alpha )(1+\zeta )})2(2n V''-{n} V'(n-1)\phi ^{-1}\\&-V'\times (4-n)(n-1)\phi ^{-1})((2(4-n)\\&\times (C_{3}+V^{(1+\lambda )(1+\zeta )})^{\frac{2+\alpha }{1+\alpha }})^{-1}\\&-\frac{3n(1+\zeta )V'^2V^{(1+\alpha )(1+\zeta )-1}}{2(4-n)(C_{3}+V^{(1+\alpha )(1+\zeta )})^{\frac{2+\alpha }{1+\alpha }}}\bigg ). \end{aligned}$$

Similarly, by using Eq. (8), the number of e-folds becomes

$$\begin{aligned} N=\frac{1}{M^2_\mathrm{P}}\int _{\phi _{\mathrm{end}}}^{\phi _{*}} \frac{(C_{3}+V^{(1+\alpha )(1+\zeta )})^\frac{1}{1+\alpha }}{V'}\mathrm{d}\phi . \end{aligned}$$
(28)

With the help of Eqs. (9)–(11), power spectrum, scalar spectral index and tensor-to-scalar ratio in terms of the potential are given by

$$\begin{aligned}&\mathcal {P}_{\mathcal {R}}=\left( \frac{81\pi }{4}\right) ^{\frac{1}{2}}\left( \frac{M_\mathrm{p}^{\frac{6n-15}{4-n}}\left( C_{3}+V^{(1+\alpha )(1+\zeta )}\right) ^{\frac{15-6n}{2(4-n)(1+\alpha )}}c^{\frac{3}{4-n}}}{3^{\frac{15-6n}{2(4-n)}}C_{*}^{\frac{n+2}{2(n+4)}}V'^{\frac{6-3n}{4-n}}6^{\frac{n+2}{4-n}}\phi ^{\frac{(n-1)(4-n)+(n-1)(n+2)}{2(4-n)}}}\right) , \nonumber \\&n_\mathrm{s}-1=\frac{3M_\mathrm{p}^2}{2(C_{3}+V^{(1+\alpha )(1+\zeta )})^{\frac{1}{1+\alpha }}}\bigg (\frac{V'^2((1+\alpha )(1+\zeta )-1)}{V}\nonumber \\&\quad -\frac{V^{(1+\alpha )(1+\zeta )-1}V'^2}{(C_{3}+V^{(1+\alpha )(1+\zeta )})} \bigg (\frac{3}{4}(1+\zeta )+(1+\alpha )(1+\zeta )\bigg )\nonumber \\&\quad +2V''-\frac{3}{2}\bigg ((C_{3}+V^{(1+\alpha )(1+\zeta )})2(2\text {n} V''-\text {n} V'(n-1)\phi ^{-1}\nonumber \\&\quad -V'(4-n)(n-1)\phi ^{-1}-3n(1+\zeta )\nonumber \\&\quad \times V^{(1+\alpha )(1+\zeta )-1}V'^2))(2(4-n)(C_{3}+V^{(1+\alpha )(1+\zeta ))}))^{-1}\bigg )\bigg ), \end{aligned}$$
(29)
$$\begin{aligned}&r=\frac{32\text {G} V'^{\frac{6-3n}{4-n}}\phi ^{\frac{(n-1)(4-n)+(n-1)(n+2)}{2(4-n)}}6^{\frac{n+2}{4-n}}C_{*}^{\frac{n+2}{2(4-n)}} 3^{\frac{7-4n}{2(4-n)}}M_\mathrm{p}^{\frac{7-4n}{4-n}}}{9c^{\frac{3}{4-n}}\pi ^{\frac{3}{2}}\left( C_{3}+V^{(1+\alpha )(1+\zeta )}\right) ^{\frac{7-4n}{(4-n)(2+2\alpha )}}}. \end{aligned}$$
(30)

For positive quadratic and quartic potential, we get the following expressions of r and \(n_{\mathrm{s}}\):

$$\begin{aligned}&r=\frac{32G\bigg (\sigma ^2\phi +\lambda _{*} \phi ^3\bigg )^{\frac{6-3n}{4-n}}\phi ^{\frac{(n-1)(4-n)+(n-1)(n+2)}{2(4-n)}}6^{\frac{n+2}{4-n}}C_{*}^{\frac{n+2}{2(4-n)}} 3^{\frac{7-4n}{2(4-n)}}}{9c^{\frac{3}{4-n}}\pi ^{\frac{3}{2}}M_\mathrm{p}^{\frac{4n-7}{4-n}}\bigg (C_{3}+\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\zeta )}\bigg )^{\frac{7-4n}{(4-n)(2+2\alpha )}}},\nonumber \\&n_\mathrm{s}-1=\frac{3M_\mathrm{p}^2}{2\{C_{3}+(\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\zeta )}\}^{\frac{1}{1+\alpha }}}\nonumber \\&\quad \times \bigg [(\sigma ^2\phi +\lambda _{*} \phi ^3)^2\{(1+\alpha )\times (1+\zeta )-1\}\nonumber \\&\quad \times \bigg ({\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4}\bigg )^{-1}-\bigg (\frac{1}{2}\sigma ^2\phi ^2\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\zeta )-1}\nonumber \\&\quad \times (\sigma ^2\phi +\lambda _{*} \phi ^3)^2\bigg \{{C_{3}+\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\zeta )}}\bigg \}^{-1}\nonumber \\&\quad \times \bigg (\frac{3}{4}(1+\zeta )+(1+\alpha )(1+\zeta )\bigg )+2(\sigma ^2+3\lambda _{*} \phi ^2)-\frac{3}{2}\nonumber \\&\quad \times \bigg \{2\bigg (C_{3}+\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\zeta )}\bigg )\bigg (2n(\sigma ^2+3\lambda _{*} \phi ^2)\nonumber \\&\quad -n(\sigma ^2\phi +\lambda _{*} \phi ^3)(n-1)\phi ^{-1}-(\sigma ^2\phi +\lambda _{*} \phi ^3)(4-n)(n-1)\phi ^{-1}\nonumber \\&\quad -3n(1+\zeta )\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\zeta )-1}(\sigma ^2\phi +\lambda _{*} \phi ^3)^2\nonumber \\&\quad \times \bigg (2(4-n)\bigg (C_{3}+\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\zeta )}\bigg )\bigg )^{-1}\bigg )\bigg \}\bigg ].\nonumber \\ \end{aligned}$$
(31)

For negative quadratic and quartic potential, the relations of r and \(n_{\mathrm{s}}\) become

$$\begin{aligned}&r=\frac{32G\left( -\sigma ^2\phi +\lambda _{*} \phi ^3\right) ^{\frac{6-3n}{4-n}}\phi ^{\frac{(n-1)(4-n)+(n-1)(n+2)}{2(4-n)}}6^{\frac{n+2}{4-n}}C_{*}^{\frac{n+2}{2(4-n)}} 3^{\frac{7-4n}{2(4-n)}}}{9c^{\frac{3}{4-n}}\pi ^{\frac{3}{2}}M_\mathrm{p}^{\frac{4n-7}{4-n}}(C_{3}+(s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\zeta )})^{\frac{7-4n}{(4-n)(2+2\alpha )}}},\nonumber \\&n_\mathrm{s}-1=\frac{3M_\mathrm{p}^2}{2\bigg \{C_{3}+\bigg (s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\zeta )}\bigg \}^{\frac{1}{1+\alpha }}}\nonumber \\&\quad \times \bigg [\bigg (-\sigma ^2\phi {+}\lambda _{*} \phi ^3\bigg )^2\{(1{+}\alpha )(1{+}\zeta )-1\}\bigg ({s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4}\bigg )^{-1}\nonumber \\&\quad -\frac{(s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\zeta )-1}(-\sigma ^2\phi +\lambda _{*} \phi ^3)^2}{C_{3}+(s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\zeta )}}\nonumber \\&\quad \times \bigg (\frac{3}{4}(1+\zeta )+(1+\alpha )(1+\zeta )\bigg )+2(-\sigma ^2+3\lambda _{*} \phi ^2)\nonumber \\&\quad -\frac{3}{2}\bigg \{\bigg (C_{3}+(s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\zeta )}\bigg )2\bigg (2n(-\sigma ^2\nonumber \\&\quad +3\lambda _{*} \phi ^2)-n(-\sigma ^2\phi +\lambda _{*} \phi ^3)(n-1)\phi ^{-1}-(-\sigma ^2\phi +\lambda _{*} \phi ^3)\nonumber \\&\quad \times (4-n)(n-1)\phi ^{-1}\bigg )-3n(1+\zeta )\nonumber \\&\quad \times \bigg (s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\zeta )-1}\nonumber \\&\quad \times \bigg (2(4-n)\bigg (C_{3}+\bigg (s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\zeta )}\bigg )\bigg )^{-1}\nonumber \\&\quad \times (-\sigma ^2\phi +\lambda _{*} \phi ^3)^2\bigg \}\bigg ]. \end{aligned}$$
(32)

4.2 Strong dissipative regime

In this case, the slow-roll parameters become

$$\begin{aligned}&\epsilon =\frac{M^2_\mathrm{P}(1+\zeta )V^{(1+\alpha )(1+\zeta )-1}V'^2}{2R(C_{3}+V^{(1+\alpha )(1+\zeta )})^\frac{2+\alpha }{1+\alpha }},\quad \\&\eta =\frac{M^2_\mathrm{p}}{R(C_{3}+V^{(1+\alpha )(1+\zeta )})^\frac{1}{1+\alpha }}(2V''\\&\quad +\frac{V'^2((1+\alpha )(1+\zeta )-1)}{V}\\&\quad -\frac{V^{(1+\alpha )(1+\zeta )-1}V'^2(1+\alpha )(1+\zeta )}{(C_{3}+V^{(1+\alpha )(1+\zeta )})},\\&\beta =\frac{n}{R}M_\mathrm{p}^2\left( \frac{4V''\left( C_{3}+V^{(1+\alpha )(1+\zeta )}\right) -(1+\zeta )V'^2V^{(1+\alpha )(1+\zeta )-1}}{2(n+4)\left( C_{3}+V^{(1+\alpha )(1+\zeta )}\right) ^{\frac{2+\alpha }{1+\alpha }}}\right) . \end{aligned}$$

The number of e-folds turns out to be

$$\begin{aligned} N=\frac{1}{M^2_\mathrm{P}}\int _{\phi _{\text {end}}}^{\phi _{*}}\frac{(C_{3} +V^{(1+\alpha )(1+\zeta )})^{\frac{1}{1+\alpha }}}{V'}R\mathrm{d}\phi . \end{aligned}$$

The relations for perturbation, tensor-to-scalar ratio, and spectral index can be obtained by utilizing Eqs. (9)–(11) as follows:

$$\begin{aligned}&\mathcal {P}_{\mathcal {R}}=\left( \frac{\pi }{4}\right) ^{\frac{1}{2}} \frac{c^{\frac{9}{n+4}} \left( C_{3}+V^{(1+\alpha )(1+\zeta )}\right) ^{\frac{9}{2(1+\alpha )(n+4)}}}{(4C_{*})^{\frac{5n+2}{2(n+4)}}\phi ^{\frac{5(n-1)(n+4)-(n-1)(5n+2)}{2(n+4)}}V'^{\frac{6-3n}{n+4}} M_\mathrm{p}^{\frac{9}{n+4}}3^{\frac{9}{2(n+4)}}},\\&n_\mathrm{s}-1=\frac{3(4c_{*})^{\frac{n}{n+4}}\phi ^{\frac{(n+4)(n-1)-n(n-1)}{n+4}}3^{\frac{2}{n+4}}M_\mathrm{p}^{\frac{4}{n+4}}}{2c^{\frac{4}{n+4}}V'^{\frac{2n}{n+4}}(C_{3}+V^{(1+\alpha )(1+\zeta )})^{\frac{2}{(1+\alpha )(n+4)}}}\\&\quad \times \bigg [\frac{V'^2}{{V}^{1}}\bigg ((1+\alpha )(1+\zeta )\\&\quad \times -1\bigg )-\frac{V^{(1+\alpha )(1+\zeta )-1}V'^{2 }}{(C_{3}+V^{(1+\alpha )(1+\zeta )})}\\&\quad \times \bigg (\frac{3}{4}(1+\zeta )+(1+\alpha )(1+\zeta )\bigg )\\&\quad +2V''-\bigg (\frac{3n}{2}\bigg (4V''(C_{3}+V^{(1+\alpha )(1+\zeta )})\\&\quad -(1+\zeta )V'^2V^{(1+\alpha )(1+\zeta )-1}\bigg )\\&\quad \times \bigg ({2(n+4)(C_{3}+V^{(1+\alpha )(1+\zeta )})}\bigg )^{-1}\bigg )\bigg ],\\&{r}=\frac{32G(4C_{*})^{\frac{5n+2}{10}}\phi ^{\frac{5(n-1)}{2}}V'^{\frac{8-5n}{5}}\left( C_{3}+V^{(1+\alpha )(1+\zeta )}\right) ^{\frac{5n-3}{20(1+\alpha )}}}{c^{\frac{23-5n}{10}}\pi ^{\frac{3}{2}}3^{\frac{5n-3}{20}}M_\mathrm{p}^{\frac{5n-3}{10}}}. \end{aligned}$$

For positive quadratic and quartic potential, the tensor-to-scalar ratio and scalar spectral index in terms of \(\phi \) are given by

Fig. 7
figure 7

Plot of r versus \(n_{\mathrm{s}}\) for MCG model in weak (left panel) and strong (right panel) dissipative regimes for positive potential with \(n=1\)

Full size image
Fig. 8
figure 8

Plot of r versus \(n_{\mathrm{s}}\) for MCG model in weak (left panel) and strong (right panel) dissipative regimes for positive potential with \(n=-1\)

Full size image
$$\begin{aligned}&r=\frac{32G(4C_{*})^{\frac{5n+2}{10}}\phi ^{\frac{5(n-1)}{2}}\bigg (C_{3}+(\frac{\sigma ^2\phi ^2}{2}+\frac{\lambda _{*} \phi ^4}{4})^{(1+\alpha )(1+\zeta )}\bigg )^{\frac{5n-3}{20(1+\alpha )}}}{c^{\frac{23-5n}{10}}\pi ^{\frac{3}{2}}3^{\frac{5n-3}{20}}M_\mathrm{p}^{\frac{5n-3}{10}}\left( \sigma ^2\phi +\lambda _{*} \phi ^3\right) ^{\frac{5n-8}{5}}},\nonumber \\&n_\mathrm{s}-1=\frac{3c^{\frac{-4}{n+4}}(4c_{*})^{\frac{n}{n+4}}\phi ^{\frac{(n+4)(n-1)-n(n-1)}{n+4}}3^{\frac{2}{n+4}}M_\mathrm{p}^{\frac{4}{n+4}}}{2(\sigma ^2\phi +\lambda _{*} \phi ^3)^{\frac{2n}{n+4}}(C_{3}+(\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} \phi ^4}{4})^{(1+\alpha )(1+\zeta )})^{\frac{2}{(1+\alpha )(n+4)}}}\nonumber \\&\quad \times \bigg [\frac{(\sigma ^2\phi +\lambda _{*} \phi ^3)^2((1+\alpha )(1+\zeta )-1)}{\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} \phi ^4}{4}}-(\sigma ^2\phi +\lambda _{*} \phi ^3)^{2 }\nonumber \\&\quad \times \bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} \phi ^4}{4}\bigg )^{(1+\alpha )(1+\zeta )-1}\nonumber \\&\quad \times \bigg (\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} \phi ^4}{4}\bigg )^{(1+\alpha )(1+\zeta )}+C_{3}\bigg )^{-1}\nonumber \\&\quad \times \bigg (\frac{3}{4}(1+\zeta )+(1+\alpha )(1+\zeta )\bigg )+2(\sigma ^2+3\lambda _{*} \phi ^2)\nonumber \\&\quad -\frac{3n}{2}\bigg (4(\sigma ^2+3\lambda _{*} \phi ^2)\bigg (C_{3}+\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} \phi ^4}{4}\bigg )^{(1+\alpha )(1+\zeta )}\bigg )\nonumber \\&\quad -(1+\zeta )(\sigma ^2\phi +\lambda _{*} \phi ^3)^2\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} \phi ^4}{4}\bigg )^{(1+\alpha )(1+\zeta )-1}\nonumber \\&\quad \times (2(n+4)\bigg (C_{3}+\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} \phi ^4}{4}\bigg )^{(1+\alpha )(1+\zeta )}\bigg )\bigg )^{-1}\bigg )\bigg ]. \end{aligned}$$
(33)

For negative quadratic and quartic potential, the tensor-to-scalar ratio and scalar spectral index in terms of \(\phi \) become

Fig. 9
figure 9

Plot of r versus \(n_{\mathrm{s}}\) for MCG model in weak (left panel) and strong (right panel) dissipative regimes for positive potential with \(n=-2\)

Full size image
Fig. 10
figure 10

Plot of r versus \(n_{\mathrm{s}}\) for MCG model in weak (left panel) and strong (right panel) dissipative regimes for negative potential with \(n=1\)

Full size image
Fig. 11
figure 11

Plot of r versus \(n_{\mathrm{s}}\) for MCG model in weak (left panel) and strong (right panel) dissipative regimes for negative potential with \(n=-1\)

Full size image
Fig. 12
figure 12

Plot of r versus \(n_{\mathrm{s}}\) for MCG model in weak (left panel) and strong (right panel) dissipative regimes for negative potential with \(n=-2\)

Full size image
$$\begin{aligned}&r=32G(4C_{*})^{\frac{5n+2}{10}}\phi ^{\frac{5(n-1)}{2}}(-\sigma ^2\phi +\lambda _{*} \phi ^3)^{\frac{8-5n}{5}}\bigg (C_{3}+\bigg (\frac{\sigma ^2\phi ^2}{2}\nonumber \\&\quad +\frac{\lambda _{*} \phi ^4}{4}\bigg )^{(1+\alpha )(1+\zeta )}\bigg )^{\frac{5n-3}{20(1+\alpha )}}\bigg (c^{\frac{23-5n}{10}}\pi ^{\frac{3}{2}}3^{\frac{5n-3}{20}}M_\mathrm{p}^{\frac{5n-3}{10}}\bigg )^{-1}.\nonumber \\&n_\mathrm{s}-1{=}3(4c_{*})^{\frac{n}{n{+}4}}\phi ^{\frac{(n{+}4)(n-1)-n(n-1)}{n{+}4}}3^{\frac{2}{n+4}}M_\mathrm{p}^{\frac{4}{n+4}}\bigg (2c^{\frac{4}{n+4}}(-\sigma ^2\phi \nonumber \\&\quad +\lambda _{*} \phi ^3)^{\frac{2n}{n+4}}\bigg (C_{3}+\bigg (s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} \phi ^4}{4}\bigg )^{(1+\alpha )(1+\zeta )}\bigg )^{\frac{2}{(1+\alpha )(n+4)}}\bigg )^{-1}\nonumber \\&\quad \times \bigg (\frac{(-\sigma ^2\phi +\lambda _{*} \phi ^3)^2((1+\alpha )(1+\zeta )-1)}{s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} \phi ^4}{4}}-\bigg (s-\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad +\frac{\lambda _{*} \phi ^4}{4}\bigg )^{(1+\alpha )(1+\zeta )-1}(-\sigma ^2\phi +\lambda _{*} \phi ^3)^{2 }((C_{3}+(s-\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad +\frac{\lambda _{*} \phi ^4}{4})^{(1+\alpha )(1+\zeta )}))^{-1}\bigg (\frac{3}{4}(1+\zeta )+(1+\alpha )(1+\zeta )\bigg )+2\nonumber \\&\quad \times (-\sigma ^2+3\lambda _{*} \phi ^2)-\frac{3n}{2}\bigg (4(-\sigma ^2+3\lambda _{*} \phi ^2)(C_{3}+(s\nonumber \\&\quad -\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} \phi ^4}{4})^{(1+\alpha )(1+\zeta )})-(1+\zeta )(-\sigma ^2\phi +\lambda _{*} \phi ^3)^2\nonumber \\&\quad \times \bigg (s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} \phi ^4}{4}\bigg )^{(1+\alpha )(1+\zeta )-1}\bigg )\nonumber \\&\quad \times \bigg (2(n+4)\bigg (C_{3}+\bigg (s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} \phi ^4}{4}\bigg )^{(1+\alpha )(1+\zeta )}\bigg )\bigg )^{-1}\bigg )\bigg ).\nonumber \\ \end{aligned}$$
(34)

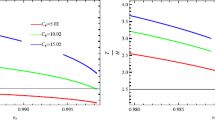
For the MCG model, the plots of r and \(n_{\mathrm{s}}\) for both weak/strong dissipative regimes for both positive/negative quadratic and quartic potential for three different values of \(n=1,-1,-2\), respectively, are shown in Figs. 7, 8, 9, 10, 11 and 12. The observed constraints of scalar ratio and spectral index are displayed in Tables 4 and 5. It is found that the results are compatible with WMAP9 [69] and Planck 2015 [70].

5 Generalized cosmic Chaplygin gas

This model is introduced by Gonzalez-Diaz [72] and its EoS is

$$\begin{aligned} \rho _{gccg}=-\rho ^{-\alpha }\left( C_{5}+(\rho ^{1+\alpha }_{gccg}-C_{5})^{-\delta }\right) . \end{aligned}$$
(35)

Here, \(C_{5}=\frac{D}{1+\delta }-1\), D takes positive or negative value, \(\alpha \) is a positive constant and \(-l<\delta <0,~l>1\). In the limiting case \(\delta \longrightarrow 0\), GCCG reduces to GCG. For the GCCG model, the energy density has the following form:

$$\begin{aligned} \rho _{gccg}=\left( C_{5}+(1+\frac{C_{6}}{a^{3(1+\alpha )(1+\delta )}})^\frac{1}{1+\delta }\right) ^\frac{1}{1+\alpha }. \end{aligned}$$
(36)

The corresponding Friedmann equation becomes

Table 4 MCG weak and strong dissipative regimes with positive quadratic and quartic potential
Full size table
Table 5 MCG weak and strong dissipative regime with negative quadratic and quartic potential
Full size table
$$\begin{aligned} H^2=\frac{1}{3M_\mathrm{p}^2}\left( \left( C_{5}+(1+\rho ^{(1+\alpha )(1+\delta )}_\phi )^\frac{1}{1+\delta })\right) ^\frac{1}{1+\alpha }+\rho _{\gamma }\right) . \end{aligned}$$
(37)

Under certain assumptions, the above Friedmann equation takes the following form:

$$\begin{aligned} H^2\sim & {} \frac{1}{3M_\mathrm{p}^2}\left( C_{5}+\left( 1+V^{(1+\alpha )(1+\delta )}\right) ^\frac{1}{1+\delta }\right) ^\frac{1}{1+\alpha }. \end{aligned}$$
(38)

5.1 Weak dissipative regime

The temperature remains the same as in the two above cases but the slow-roll parameters in this case take the form

$$\begin{aligned}&\epsilon =\frac{M_\mathrm{p}^2V^{(1+\alpha )(1+\delta )-1}(1+V^{(1+\alpha )(1+\delta )})^\frac{-\delta }{1+\delta }V'^2}{2(C_{5}+(1+V^{(1+\alpha )(1+\delta )})^\frac{1}{1+\delta })^\frac{2+\alpha }{1+\alpha }},\nonumber \\&\eta =\frac{M^2_\mathrm{P}}{(C_{5}+(1+V^{(1+\alpha )(1+\delta )})^\frac{1}{1+\delta })^\frac{1}{1+\alpha }} (2V''\nonumber \\&\quad +\frac{V'^2((1+\alpha )(1+\delta )-1)}{V}-\frac{\delta (1+\alpha )V^{(1+\alpha )(1+\delta )-1}V'^2}{(1+V^{(1+\alpha )(1+\delta )})}\nonumber \\&\quad -\frac{(1+V^{(1+\alpha )(1+\delta )})^\frac{-\delta }{1+\delta }V'^2}{(C_{5}+(1+V^{(1+\alpha )(1+\delta )})^\frac{1}{1+\delta })}(1+\alpha )V^{(1+\alpha )(1+\delta )-1}),\nonumber \\&\beta = M_\mathrm{p}^2\bigg (2(C_{5}+(1+V^{(1+\alpha )(1+\delta )})^{\frac{1}{1+\delta }})\nonumber \\&\quad \times (2{n V}''-{n V}'(n-1)\phi ^{-1}\nonumber \\&\quad -V'(4-n)(n-1)\phi ^{-1}\bigg )-3{n V}'^2V^{(1+\alpha )(1+\delta )-1}\nonumber \\&\quad \times (1+V^{(1+\alpha )(1+\delta )})^{\frac{-\delta }{1+\delta }}\nonumber \\&\quad \times \bigg (2(4-n)(C_{5}+(1+V^{(1+\alpha )(1+\delta )})^{\frac{1}{1+\delta }})^{\frac{2+\alpha }{1+\alpha }}\bigg )^{-1}\bigg ).\nonumber \\ \end{aligned}$$
(39)

Taking into account Eq. (8), the relation for the number of e-folds becomes

$$\begin{aligned} N=\frac{1}{M^2_\mathrm{P}}\int _{\phi _{\mathrm{end}}}^{\phi _{*}}\frac{\left( C_{5}+(1+V^{(1+\alpha )(1 +\delta )})^{\frac{1}{1+\delta }}\right) ^\frac{1}{1+\alpha }}{V'}\mathrm{d}\phi . \end{aligned}$$

For this model, the power spectrum, scalar spectral index and tensor-to-scalar ratio in terms of the potential can be found by using Eqs. (9)–(11) as follows:

$$\begin{aligned}&\mathcal {P}_{\mathcal {R}}=\left( \frac{81\pi }{4}\right) ^{\frac{1}{2}}\frac{\left( C_{5}+\left( 1+V^{(1+\alpha )(1+\delta )}\right) ^{\frac{1}{1+\delta }}\right) ^{\frac{(15-6n)}{2(1+\alpha )(4-n)}}c^{\frac{3}{4-n}}}{3^{\frac{15-6n}{2(4-n)}}M_\mathrm{p}^{\frac{15-6n}{4-n}} V'^{\frac{6-3n}{4-n}}6^{\frac{n+2}{4-n}}C_{*}^{\frac{n+2}{2(4-n)}}\phi ^{\frac{(n-1)(4-n)-(n-1)(n+2)}{2(4-n)}}}, \end{aligned}$$
(40)
$$\begin{aligned}&n_\mathrm{s}-1=\frac{3M_\mathrm{p}^2}{2(C_{5}+(1+V^{(1+\alpha )(1+\delta )})^{\frac{1}{1+\delta }})^{1+\alpha }}\bigg (\frac{V'^{2}{((1+\alpha )(1+\delta )-1)}}{V}\nonumber \\&\quad -\Bigg (3(2(C_{5}+(1+V^{(1+\alpha )(1+\delta )})^{\frac{1}{1+\delta }})(2\text {n V}''-\text {n V}'(n-1)\phi ^{-1}\nonumber \\&\quad -V'(4-n)(n-1)\phi ^{-1})-3\text {n V}'^2V^{(1+\alpha )(1+\delta )-1}\nonumber \\&\quad \times (1+V^{(1+\alpha )(1+\delta )})^{\frac{-\delta }{1+\delta }}\Bigg )\nonumber \\&\quad \times \bigg ({2(2)(4-n)(C_{5}+(1+V^{(1+\alpha )(1+\delta )})^{\frac{1}{1+\delta }})}\bigg )^{-1}+2V''-\delta (1+\alpha )\nonumber \\&\quad \times V^{(1+\alpha )(1+\delta )-1}V'^2\bigg ((1+V^{(1+\alpha )(1+\delta )})\bigg )^{-1}-\bigg (1+V^{(1+\alpha )(1+\delta )}\bigg )^{\frac{-\delta }{1+\delta }}\nonumber \\&\quad \times V'^2(1+\alpha )V^{(1+\alpha )(1+\delta )-1}\bigg (C_{5}+(1+V^{(1+\alpha )(1+\delta )})^{\frac{1}{1+\delta }})\bigg )^{-1}\nonumber \\&\quad \times (\frac{3}{4}+(1+\alpha ))\bigg ), \end{aligned}$$
(41)
$$\begin{aligned}&r=\frac{32\text {G V}'^{\frac{6-3n}{4-n}}\phi ^{\frac{(n-1)(4-n)+(n-1)(n+2)}{2(4-n)}}6^{\frac{n+2}{4-n}}c_{*}^{\frac{n+2}{2(4-n)}} 3^{\frac{7-4n}{2(4-n)}}M_\mathrm{p}^{\frac{7-4n}{4-n}}}{9c^{\frac{3}{4-n}}\pi ^{\frac{3}{2}}\left( C_{5}+\left( 1+V^{(1+\alpha )(1+\delta )}\right) ^{\frac{1}{1+\delta }}\right) ^{\frac{7-4n}{2(4-n)(1+\alpha )}}}. \end{aligned}$$
(42)

For positive quadratic and quartic potential, the relations of r and \(n_{\mathrm{s}}\) in terms of the scalar field can be expressed as

$$\begin{aligned}&r=\frac{32G\left( \sigma ^2\phi +\lambda _{*} \phi ^3\right) ^{\frac{6-3n}{4-n}}\phi ^{\frac{(n-1)(4-n)+(n-1)(n+2)}{2(4-n)}}6^{\frac{n+2}{4-n}}c_{*}^{\frac{n+2}{2(4-n)}}3^{\frac{7-4n}{2(4-n)}}M_\mathrm{p}^{\frac{7-4n}{4-n}}}{9c^{\frac{3}{4-n}}\pi ^{\frac{3}{2}}\left( C_{5}+\left( 1+\left( \frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\right) ^{(1+\alpha )(1+\delta )}\right) ^{\frac{1}{1+\delta }}\right) ^{\frac{7-4n}{2(4-n)(1+\alpha )}}}, \end{aligned}$$
(43)
$$\begin{aligned}&n_\mathrm{s}-1=\frac{3M_\mathrm{p}^2}{2(C_{5}+(1+(\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )})^{\frac{1}{1+\delta }})^{1+\alpha }}\nonumber \\&\quad \times \bigg ((\sigma ^2\phi +\lambda _{*} \phi ^3)^2((1+\alpha )(1+\delta )-1)^{\text { }}((\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad +\frac{\lambda _{*} }{4}\phi ^4))^{-1}-\bigg (3\bigg (2\bigg (C_{5}+\bigg (1+(\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad +\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )}\bigg )^{\frac{1}{1+\delta }}\bigg )\bigg (2n \bigg (\sigma ^2+3\lambda _{*} \phi ^2\bigg )-n(\sigma ^2\phi \nonumber \\&\quad +\lambda _{*} \phi ^3)(n-1)\phi ^{-1}-(\sigma ^2\phi +\lambda _{*} \phi ^3)(4-n)(n\nonumber \\&\quad -1)\phi ^{-1}\bigg )-3n(\sigma ^2\phi +\lambda _{*} \phi ^3)^2\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )-1}\nonumber \\&\quad \times \bigg (1+\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )}\bigg )^{\frac{-\delta }{1+\delta }}\bigg )\bigg )/\bigg (2(2)(4-n)\nonumber \\&\quad \times \bigg (C_{5}+\bigg (1+\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )}\bigg )^{\frac{1}{1+\delta }}\bigg )\bigg )\nonumber \\&\quad +2(\sigma ^2+3\lambda _{*} \phi ^2)-\delta (1+\alpha )\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )-1}\nonumber \\&\quad \times (\sigma ^2\phi +\lambda _{*} \phi ^3)^2\bigg (\bigg (\bigg (1+\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )}\bigg )\bigg )^{-1}\nonumber \\&\quad -\bigg (1+\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )}\bigg )^{\frac{-\delta }{1+\delta }}(\sigma ^2\phi +\lambda _{*} \phi ^3)^2\nonumber \\&\quad \times (1+\alpha )\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )-1}\bigg (C_{5}+(1\nonumber \\&\quad +\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )})^{\frac{1}{1+\delta }}\bigg )\bigg )^{-1}\bigg (\frac{3}{4}+(1+\alpha )\bigg )\bigg ). \end{aligned}$$
(44)

For negative quadratic and quartic potential, the relations of r and \(n_{\mathrm{s}}\) in terms of the scalar field are given by

$$\begin{aligned}&r=\frac{32G\left( -\sigma ^2\phi +\lambda _{*} \phi ^3\right) ^{\frac{6-3n}{4-n}}\phi ^{\frac{(n-1)(4-n)+(n-1)(n+2)}{2(4-n)}}6^{\frac{n+2}{4-n}}c_{*}^{\frac{n+2}{2(4-n)}} 3^{\frac{7-4n}{2(4-n)}}M_\mathrm{p}^{\frac{7-4n}{4-n}}}{9c^{\frac{3}{4-n}}\pi ^{\frac{3}{2}}\left( C_{5}+\left( 1+\left( s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\right) ^{(1+\alpha )(1+\delta )}\right) ^{\frac{1}{1+\delta }}\right) ^{\frac{7-4n}{2(4-n)(1+\alpha )}}}, \end{aligned}$$
(45)
$$\begin{aligned}&n_\mathrm{s}-1=\frac{3M_\mathrm{p}^2}{2\bigg (C_{5}+\bigg (1+(s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )}\bigg )^{\frac{1}{1+\delta }}\bigg )^{1+\alpha }}\nonumber \\&\quad \times \bigg (\frac{(-\sigma ^2\phi +\lambda _{*} \phi ^3)^2((1+\alpha )(1+\delta )-1)^{\text { }}}{(s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)}-\bigg (3\bigg (2\bigg (C_{5}\nonumber \\&\quad +\bigg (1+(s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )}\bigg )^{\frac{1}{1+\delta }}\bigg )\bigg (2n(\nonumber \\&\quad -\sigma ^2+3\lambda _{*} \phi ^2)-n(-\sigma ^2\phi +\lambda _{*} \phi ^3)(n-1)\phi ^{-1}-(\nonumber \\&\quad -\sigma ^2\phi +\lambda _{*} \phi ^3)(4-n)(n-1)\phi ^{-1}\bigg )-3n(-\sigma ^2\phi \nonumber \\&\quad +\lambda _{*} \phi ^3)^2(s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )-1}\bigg (1+(s-\frac{1}{2}\nonumber \\&\quad \times \sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )}\bigg )^{\frac{-\delta }{1+\delta }}\bigg )\bigg )/\bigg (2(2)(4-n)\bigg (C_{5}\nonumber \\&\quad +\bigg (1+(s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )}\bigg )^{\frac{1}{1+\delta }}\bigg )\bigg )\nonumber \\&\quad +2(-\sigma ^2+3\lambda _{*} \phi ^2)\nonumber \\&\quad -\frac{\delta (1+\delta )(s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )-1}(-\sigma ^2\phi +\lambda _{*} \phi ^3)^2}{\bigg (1+(s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )}\bigg )}\nonumber \\&\quad -\bigg (1+(s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )}\bigg )^{\frac{-\delta }{1+\delta }}\nonumber \\&\quad (-\sigma ^2\phi +\lambda _{*} \phi ^3)^2(1+\alpha )\nonumber \\&\quad \times (s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )-1}(\bigg (C_{5}+\bigg (1+(s-\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad +\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )}\bigg )^{\frac{1}{1+\delta }}\bigg ))^{-1}\bigg (\frac{3}{4}+(1+\alpha )\bigg )\bigg ). \end{aligned}$$
(46)

5.2 Strong dissipative regime

In the second case, the slow-roll parameters become

$$\begin{aligned} \epsilon= & {} \frac{M_\mathrm{p}^2V^{(1+\alpha )(1+\delta )-1}(1+V^{(1+\alpha )(1 +\delta )})^\frac{-\delta }{1+\delta }V'^2}{2R(C_{5}+(1+V^{(1+\alpha )(1 +\delta )})^\frac{1}{1+\delta })^\frac{2+\alpha }{1+\alpha }},\quad \nonumber \\ \eta= & {} \frac{M^2_\mathrm{P}}{R(C_{5}+(1+V^{(1+\alpha )(1+\delta )})^\frac{1}{1 +\delta })^\frac{1}{1+\delta }}\nonumber \\&\times (2V''+\frac{V'^2((1+\alpha )(1+\delta ) -1)}{V}\nonumber \\&-\frac{\delta (1+\alpha )V^{(1+\alpha )(1+\delta ) -1}V'^2}{(1+V^{(1+\alpha )(1+\delta )})}\nonumber \\&-\frac{(1+V^{(1+\alpha )(1 +\delta )})^\frac{-\delta }{1+\delta }V'^2}{(C_{5}+(1+V^{(1+\alpha ) (1+\delta )})^\frac{1}{1+\delta })}\nonumber \\&\times (1+\alpha )V^{(1+\alpha )(1+\delta )-1}),\quad \nonumber \\ \beta= & {} {n M}_\mathrm{p}^2\bigg (4V''(C_{5}+(1+V^{(1+\alpha )(1+\delta )})^{\frac{1}{1+ }})\nonumber \\&-\bigg (\bigg (1+V^{(1+\alpha )(1+\delta )}\bigg )^{\frac{-\delta }{1+\delta }}V'^2V^{(1+\alpha )(1+\delta )-1}\bigg )\bigg )\nonumber \\&\times (2R(n+4)\times (C_{5}+\bigg (1+V^{(1+\alpha )(1+\delta )})^{\frac{1}{1+\delta }})^{\frac{2+\alpha }{1+\alpha }})^{-1}.\nonumber \\ \end{aligned}$$
(47)

The expression of the number of e-folds is given by

$$\begin{aligned} N=\frac{1}{M^2_\mathrm{P}}\int _{\phi _{\mathrm{end}}}^{\phi _{*}}\frac{\left( C_{5}+(1+V^{(1 +\alpha )(1+\delta )})^\frac{1}{1+\delta }\right) ^\frac{1}{1+\alpha }}{V'}R\mathrm{d}\phi . \end{aligned}$$

The perturbation quantities turn out to be

$$\begin{aligned}&\mathcal {P}_{\mathcal {R}}= \left( \frac{\pi }{4}\right) ^{\frac{1}{2}}\frac{\left( C_{5}+\left( 1+V^{(1+\alpha )(1+\delta )}\right) ^{\underset{1+\delta }{1}}\right) ^{\frac{9}{2(1+\alpha )(n+4)}}c^{\frac{9}{n+4}}}{3^{\frac{9}{2(n+4)}}M_\mathrm{p}^{\frac{9}{n+4}}(4C_{*})^{\frac{5n+2}{2(n+4)}}\phi ^{\left. \frac{5(n-1)(n+4)-(n-1)(5n+2}{2(n+4)}\right) V'^{\frac{6-3n}{n+4}}}}, \nonumber \\&r=\frac{32\text {G V}'^{\frac{8-5n}{5}}\phi ^{\frac{5(n-1)}{2}}(4C_{*})^{\frac{5n+2}{10}}\left( C_{5}+\left( 1+V^{(1+\alpha )(1+\delta )}\right) \right) ^{\frac{5n-3}{20(1+\alpha )}}}{c^{\frac{23-5n}{10}}\pi ^{\frac{3}{2}}3^{\frac{5n-3}{20}}M_\mathrm{p}^{\frac{5n-3}{10}}}, \nonumber \\&n_\mathrm{s}-1=\frac{3M_\mathrm{p}^{\frac{4}{n+4}}3^{\frac{2}{n+4}}(4C_{*})^{\frac{n}{n+4}}\phi ^{\frac{(n+4)(n-1)-n(n-1)}{n+4}} }{2c^{\frac{4}{n+4}}V'^{\frac{2n}{n+4}}(C_{5}+(1+V^{(1+\alpha )(1+\delta )})^{\frac{1}{1+\delta }})^{\frac{2}{(n+4)(1+\alpha )}}}\nonumber \\&\quad \times \bigg (\frac{V'^{2((1+\alpha )(1+\delta )-1)}}{V}-3n\bigg (4V''(C_{5}+(1+V^{(1+\alpha )(1+\delta )})^{\frac{1}{1+\delta }})\nonumber \\&\quad -(1+V^{(1+\alpha )(1+\delta )})^{\frac{-\delta }{1+\delta }}V'^2V^{(1+\alpha )(1+\delta )-1}\bigg )(4(n+4)(C_{5}+(1\nonumber \\&\quad +V^{(1+\alpha )(1+\delta )})^{\frac{1}{1+\delta }}))^{-1}+2V''-\frac{\delta (1+\alpha )V^{(1+\alpha )(1+\delta )-1}V'^2}{(1+V^{(1+\alpha )(1+\delta )})}\nonumber \\&\quad -\frac{(1+V^{(1+\alpha )(1+\delta )})^{\frac{-\delta }{1+\delta }}V'^2(1+\alpha )V^{(1+\alpha )(1+\delta )-1}}{(C_{5}+(1+V^{(1+\alpha )(1+\delta )})^{\frac{1}{1+\delta }})}\nonumber \\&\quad \times \bigg (\frac{3}{4}+(1+\alpha )\bigg )\bigg ). \end{aligned}$$
(48)

For positive quadratic and quartic potential, the tensor-to-scalar ratio and scalar spectral index in terms of \(\phi \) can be expressed as follows:

$$\begin{aligned}&r=32G(\sigma ^2\phi +\lambda _{*} \phi ^3)^{\frac{8-5n}{5}}\phi ^{\frac{5(n-1)}{2}}(4C_{*})^{\frac{5n+2}{10}}\nonumber \\&\quad \times \bigg (C_{5}+\bigg (1+\bigg (\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad +\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )}\bigg )\bigg )^{\frac{5n-3}{20(1+\alpha )}}\nonumber \\&\quad \times \bigg (c^{\frac{23-5n}{10}}\pi ^{\frac{3}{2}}3^{\frac{5n-3}{20}}M_\mathrm{p}^{\frac{5n-3}{10}}\bigg )^{-1}, \nonumber \\&n_\mathrm{s}-1=3M_\mathrm{p}^{\frac{4}{n+4}}3^{\frac{2}{n+4}}(4C_{*})^{\frac{n}{n+4}}\phi ^{\frac{(n+4)(n-1)-n(n-1)}{n+4}}\nonumber \\&\quad \times \bigg (2c^{\frac{4}{n+4}}(\sigma ^2\phi +\lambda _{*} \phi ^3)^{\frac{2n}{n+4}}(C_{5}\nonumber \\&\quad +\bigg (1+\bigg (\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad +\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )}\bigg )^{\frac{1}{1+\delta }})^{\frac{2}{(n+4)(1+\alpha )}}\bigg )^{-1}\nonumber \\&\quad \times \bigg (\frac{(\sigma ^2\phi +\lambda _{*} \phi ^3)^2((1+\alpha )(1+\delta )-1)}{(\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)}\nonumber \\&\quad -3n\bigg (4(\sigma ^2+3\lambda _{*} \phi ^2)\nonumber \\&\quad \times \bigg (C_{5}+\bigg (1+\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )}\bigg )^{\frac{1}{1+\delta }}\bigg )\nonumber \\&\quad -\bigg (1+\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )}\bigg )^{\frac{-\delta }{1+\delta }}\nonumber \\&\quad \times (\sigma ^2\phi +\lambda _{*} \phi ^3)^2\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )-1}\bigg )\nonumber \\&\quad \times \bigg (4(n+4)\bigg (C_{5}+\bigg (1+\bigg (\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad \times +\frac{\lambda _{*}}{4}\phi ^{4}\bigg )^{(1+\alpha )(1+\delta )}\bigg )^{\frac{1}{1+\delta }}\bigg )\bigg )^{-1}+2\times (\sigma ^2+3\lambda _{*} \phi ^2)\nonumber \\&\quad -\frac{\delta (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )-1}(\sigma ^2\phi +\lambda _{*} \phi ^3)^2}{(1+\alpha )^{-1}(1+(\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )})}\nonumber \\&\quad -\bigg (1+\bigg (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )}\bigg )^{\frac{-\delta }{1+\delta }}\nonumber \\&\quad \times (\sigma ^2\phi +\lambda _{*} \phi ^3)^2(1+\alpha )\nonumber \\&\quad \times (\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )-1}\nonumber \\&\quad \times \bigg (\bigg (C_{5}+(1+(\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad +\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )})^{\frac{1}{1+\delta }}\bigg )\bigg )^{-1}\bigg (\frac{3}{4}+(1+\alpha )\bigg )\bigg ). \end{aligned}$$
(49)
Fig. 13
figure 13

Plot of r versus \(n_{\mathrm{s}}\) for GCCG model in weak (left panel) and strong (right panel) dissipative regimes for positive potential with \(n=1\)

Full size image

For negative quadratic and quartic potential, the tensor-to-scalar ratio and scalar spectral index in terms of \(\phi \) can be obtained:

$$\begin{aligned}&r=32G(-\sigma ^2\phi +\lambda _{*} \phi ^3)^{\frac{8-5n}{5}}\phi ^{\frac{5(n-1)}{2}}(4C_{*})^{\frac{5n+2}{10}}\nonumber \\&\quad \times \bigg (C_{5}+\bigg (1+\bigg (s-\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad +\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )}\bigg )\bigg )^{\frac{5n-3}{20(1+\alpha )}}\bigg (c^{\frac{23-5n}{10}}\pi ^{\frac{3}{2}}3^{\frac{5n-3}{20}}M_\mathrm{p}^{\frac{5n-3}{10}}\bigg )^{-1}, \nonumber \\&n_\mathrm{s}-1=3M_\mathrm{p}^{\frac{4}{n+4}}3^{\frac{2}{n+4}}(4C_{*})^{\frac{n}{n+4}}\phi ^{\frac{(n+4)(n-1)-n(n-1)}{n+4}}\nonumber \\&\quad \times (2c^{\frac{4}{n+4}}(-\sigma ^2\phi +\lambda _{*} \phi ^3\times )^{\frac{2n}{n+4}}\nonumber \\&\quad \times \bigg (C_{5}+\bigg (1+\bigg (s-\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad \times +\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )}\bigg )^{\frac{1}{1+\delta }})^{\frac{2}{(n+4)(1+\alpha )}})^{-1}\nonumber \\&\quad \times \bigg (\frac{(-\sigma ^2\phi +\lambda _{*} \phi ^3)^2((1+\alpha )(1+\delta )-1)}{\bigg (s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )}\nonumber \\&\quad \times -3n\bigg (4(-\sigma ^2+3\lambda _{*} \phi ^2)\nonumber \\&\quad \times \bigg (C_{5}+\bigg (1+\bigg (s-\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad +\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )}\bigg )^{\frac{1}{1+\delta }}\bigg )-\bigg (1+\bigg (s-\frac{1}{2}\nonumber \\&\quad \times \sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )}\bigg )^{\frac{-\delta }{1+\delta }}(-\sigma ^2\phi +\lambda _{*} \phi ^3)^2\nonumber \\&\quad \times \bigg (s-\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\times )^{(1+\alpha )(1+\delta )-1})\nonumber \\&\quad \times (4(n+4)(C_{5}+\bigg (1+\bigg (s-\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad +\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )}\bigg )^{\frac{1}{1+\delta }}\bigg )\bigg )^{-1}+2(-\sigma ^2+3\lambda _{*} \phi ^2)\nonumber \\&\quad -\delta (1+\alpha )\bigg (s-\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad +\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )-1}(-\sigma ^2\phi +\lambda _{*} \phi ^3)^2\nonumber \\&\quad \times \bigg (\bigg (1+\bigg (s-\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad +\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )}\bigg )\bigg )^{-1}-\bigg (1+\bigg (s-\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad +\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )})^{\frac{-\delta }{1+\delta }}(-\sigma ^2\nonumber \\&\quad \times \phi +\lambda _{*} \phi ^3)^2(1+\alpha )\bigg (s-\frac{1}{2}\sigma ^2\phi ^2\nonumber \\&\quad \times +\frac{\lambda _{*} }{4}\phi ^4)^{(1+\alpha )(1+\delta )-1}((C_{5}+(1+(s\nonumber \\&\quad -\frac{1}{2}\sigma ^2\phi ^2+\frac{\lambda _{*} }{4}\phi ^4\bigg )^{(1+\alpha )(1+\delta )}\bigg )^{\frac{1}{1+\delta }}\bigg )\bigg )^{-1}\nonumber \\&\quad \times \bigg (\frac{3}{4}+(1+\alpha )\bigg )\bigg ). \end{aligned}$$
(50)
Fig. 14
figure 14

Plot of r versus \(n_{\mathrm{s}}\) for GCCG model in weak (left panel) and strong (right panel) dissipative regimes for positive potential with \(n=-1\)

Full size image
Fig. 15
figure 15

Plot of r versus \(n_{\mathrm{s}}\) for GCCG model in weak (left panel) and strong (right panel) dissipative regimes for positive potential with \(n=-2\)

Full size image
Fig. 16
figure 16

Plot of r versus \(n_{\mathrm{s}}\) for GCCG model in weak (left panel) and strong (right panel) dissipative regimes for negative potential with \(n=1\)

Full size image
Fig. 17
figure 17

Plot of r versus \(n_{\mathrm{s}}\) for GCCG model in weak (left panel) and strong (right panel) dissipative regimes for negative potential with \(n=-1\)

Full size image
Fig. 18
figure 18

Plot of r versus \(n_{\mathrm{s}}\) for GCCG model in weak (left panel) and strong (right panel) dissipative regimes for negative potential with \(n=-2\)

Full size image

For GCCG model, the plots of r and \(n_{\mathrm{s}}\) for weak/strong dissipative regimes for both positive/negative quadratic and quartic potential for three different values of \(n=1,-1,-2\), respectively, are shown in Figs. 13, 14, 15, 16, 17 and 18. The observed constraints of scalar ratio and spectral index are displayed in Tables 6 and 7. It is found that the results are compatible with WMAP9 [69] and Planck 2015 [70].

6 Concluding remarks

We have studied warm polynomial inflation (with positive/negative quadratic and quartic potentials) by assuming the generalized form of the dissipative coefficient (\(\Gamma =c\frac{T^{n}}{\phi ^{n-1}}\)). In order to get the consistency of the results, we have considered various CG models, like GCG, MCG, and GCCG. We have calculated the inflationary parameters for both weak and strong dissipative regimes, such as the number of e-folds, scalar spectrum, scalar spectral index and tensor-to-scalar ratio. For clear analysis of the results, we have displayed the trajectories between tensor-to-scalar ratio (r) and spectral index (\(n_{\mathrm{s}}\)) in the weak and strong dissipative regimes for all CG models. The obtained results for all CG models in the form of upper bounds of r and \(n_{\mathrm{s}}\) are summarized below: GCG model:

  • For positive quadratic and quartic potential, \(r\le 0.0104168,~1.2\times 10^{-6},~1.4\times 10^{-14}\) with respect to \(n_{\mathrm{s}}=0.98_{-0.01}^{+0.01}\), \(0.96_{-0.02}^{+0.02}\), \(1.00001_{-0.00001}^{+0.00001}\), respectively, for \(n=1, -1, -2\) in the weak dissipative regime. However, for strong dissipative regime, \(r\le 0.06\), \(3.0\times 10^{-15}\), \(3.7\times 10^{-43}\) for \(n_{\mathrm{s}}=0.90_{-0.06}^{+0.06}\), \(0.94_{-0.02}^{+0.02}\), \(1.00011_{-0.00001}^{+0.00001}\), respectively.

  • For negative quadratic and quartic potential, the results of tensor-to-scalar ratio and scalar spectral index in the weak dissipative regime are \(r\le 0.38\), 0.000041, \(4.5\times 10^{-6}\) according to \(n_{\mathrm{s}} =1.0000_{-0.0001}^{+0.0001}\), \(1.0031_{-0.0001}^{+0.0001}\), \(1.0040_{-0.0001}^{+0.0001}\), respectively, and for the strong dissipative regime \(r\le 0.0055\), \(4.0\times 10^{-28}\), \(5.2\times 10^{-44}\) for \(n_{\mathrm{s}}=1.0004_{-0.0001}^{+0.0001}\), \(1.000057_{-0.000001}^{+0.000001}\), \(1.00002_{-0.00001}^{+0.00001}\), respectively.

Table 6 GCCG weak and strong dissipative regime with positive quadratic and quartic potential
Full size table
Table 7 GCCG weak and strong dissipative regime with negative quadratic and quartic potential
Full size table

MCG model:

  • For positive quadratic and quartic potential, \(r\le 0.005\), 0.05, 0.000025 according to \(n_{\mathrm{s}}=1.00001_{-0.00001}^{+0.00001}\), \(1.17_{-0.001}^{+0.001}\), \(0.98_{-0.011}^{+0.01}\), respectively. Similarly, for the strong dissipative regime, the results are \(r\le 0.00025\), 0.00028, \(2.5\times 10^{-14}\) for \(n_{\mathrm{s}}=1.0000_{-0.0001}^{+0.0001}\), \(1.034_{-0.001}^{+0.001}\), \(0.9_{-0.1}^{+0.1}\).

  • The results with negative quadratic and quartic potential are \(r\le 0.5\), 0.00007, \(7.2\times 10^{-6}\) for \(n_{\mathrm{s}}=1.0009_{-0.0001}^{+0.0001}\), \(1.019_{-0.001}^{+0.001}\), \(1.019_{-0.001}^{+0.001}\) and for strong dissipative regime \(r\le 0.0052\), 0.00028, \(2.5\times 10^{-8}\) with respect to \(n_{\mathrm{s}}=1.00000_{-0.00001}^{+0.00001}\), \(1.034_{-0.001}^{+0.001}\), \(0.9_{-0.1}^{+0.1}\).

GCCG model:

  • For positive quadratic and quartic potential, \(r\le 0.0007\), 0.000062, \(8.2\times 10^{-6}\) with respect to \(n_{\mathrm{s}}=1.0029_{-0.0001}^{+0.0001}\), \(1.004_{-0.001}^{+0.001}\), \(1.011_{-0.001}^{+0.001}\). In a similar way, for the strong dissipative regime, the constraints are \(r\le 0.00032\), \(3.5\times 10^{-18}\), \(1.5\times 10^{-46}\) for \(n_{\mathrm{s}}=1.0000_{-0.0001}^{+0.0001}\), \(1.000_{-0.001}^{+0.001}\), \(0.9_{-0.1}^{+0.1}\).

  • For negative quadratic and quartic potential, the results for tensor-to-scalar ratio and scalar spectral index in the weak dissipative regime are \(r\le 0.8\), 0.000025, \(2.7\times 10^{-6}\) for \(n_{\mathrm{s}}=0.999_{-0.001}^{+0.001}\), \(1.034_{-0.001}^{+0.001}\), \(1.06_{-0.01}^{+0.01}\), and for the strong dissipative regime, the results are \(r\le 0.00033\), \(7.2\times 10^{-10}\), \(2.7\times 10^{-10}\) for \(n_{\mathrm{s}}=1.0000_{-0.0001}^{+0.0001}\), \(1.0000_{-0.0001}^{+0.0001}\), \(1.0000_{-0.0001}^{+0.0001}\), respectively.

It is interesting to mention here that the above results of r and \(n_\mathrm{s}\) lie within the constraints of WMAP9 [69] and Planck 2015 [70] (as mentioned in Table 1).