Weak decays of doubly heavy baryons: the $1/2\rightarrow 1/2$ case

Abstract

Very recently, the LHCb collaboration has observed in the final state $\Lambda _c^+ K^-\pi ^+\pi ^+$ a resonant structure that is identified as the doubly charmed baryon $\Xi _{cc}^{++}$. Inspired by this observation, we investigate the weak decays of doubly heavy baryons $\Xi _{cc}^{++}$, $\Xi _{cc}^{+}$, $\Omega _{cc}^{+}$, $\Xi _{bc}^{(\prime )+}$, $\Xi _{bc}^{(\prime )0}$, $\Omega _{bc}^{(\prime )0}$, $\Xi _{bb}^{0}$, $\Xi _{bb}^{-}$ and $\Omega _{bb}^{-}$ and focus on the decays into spin 1 / 2 baryons in this paper. At the quark level these decay processes are induced by the $c\rightarrow d/s$ or $b\rightarrow u/c$ transitions, and the two spectator quarks can be viewed as a scalar or axial vector diquark. We first derive the hadronic form factors for these transitions in the light-front approach and then apply them to predict the partial widths for the semileptonic and nonleptonic decays of doubly heavy baryons. We find that the number of decay channels is sizable and can be examined in future measurements at experimental facilities like LHC, Belle II and CEPC.

1 Introduction

The constituent quark model predicts the existence of multiplets of baryon and meson states [1]. Including the heavy charm and bottom quark, baryons made of three quarks are in a big family of hadron spectroscopy. When considering u, d, s and c, the baryon ground states, those with no orbital or radial excitations, consist of a 20-plet with $J^P=1/2^+$ and a 20-plet with $J^P=3/2^+$. For the five flavors, u, d, s, c, b, the ground states are then composed of a 40-plet with $J^P=1/2^+$ and 35-plet with $J^P=3/2^+$. All these ground states with zero or one heavy quark have been well established on the experimental side [2].

The search for doubly heavy baryons is a long-standing problem in the last decade. The only evidence in the past from the experimental side was found for $\Xi _{cc}^+$ by the SELEX collaboration [3, 4]. However, this evidence has not been confirmed by any other experiments [5,6,7,8]. Very recently, the LHCb collaboration has observed the doubly charmed baryon $\Xi _{cc}^{++}$ with mass given as [9]

$$\begin{aligned} m_{\Xi _{cc}^{++}} = (3621.40\pm 0.72\pm 0.27\pm 0.14)\;\mathrm{MeV}. \end{aligned}$$

(1)

It is anticipated that this observation will have a great impact on the hadron spectroscopy and with no doubt it will trigger much more interest in this research field. On the other hand, after the observation in the $\Xi _{cc}^{++}\rightarrow \Lambda _c^+ K^-\pi ^+\pi ^+$ decay mode, we also believe that experimental investigations should be conducted in a number of other decay channels. Thus from this viewpoint theoretical studies on weak decays of doubly heavy baryons, not only $\Xi _{cc}^{++}$, will be of great importance and are highly demanded. Some attempts have been made in Refs. [10,11,12,13,14,15,16,17,18,19,20,21], but a comprehensive study is not available in the recent literature, and the aim of this work and the forthcoming ones is to fill this gap. To do so, we will calculate the transition form factors and use these results to study the weak decays of bottom quark and charm quark.

The quantum numbers of the doubly heavy baryons are given in Table 1. Among various doubly charmed baryons, three of them can decay only through weak interactions, a $\Xi _{cc}$ isodoublet ccu, ccd, and an $\Omega _{cc}$ isosinglet ccs. There are three doubly bottom baryons similarly. For the bottom–charm baryons, the ones with two different heavy flavors, there are two sets of SU(3) triplets, $\Xi _{bc},\Omega _{bc}$ and $\Xi _{bc}',\Omega _{bc}'$. These two triplets have different total spin for the heavy quark system bc, but in reality they will probably mix with each other. Only the lighter ones can weak decay with sizable branching fractions. The mixing scheme between the two triplets is unknown yet, and we will consider both types in this work. All these baryons that can weak decay have spin 1 / 2. The ones with spin 3 / 2 can radiatively decay into the lowest-lying ones if the mass splitting is not large enough, or decay into the lowest-lying ones with the emission of a light pion when they are heavy enough.

Table 1 Quantum numbers and quark content for the ground state of doubly heavy baryons. The $S_{h}^{\pi }$ denotes the spin of the heavy quark system. The light quark q corresponds to u, d quark.

Fig. 1

Antitriplets (a) and sextets (b) of charmed baryons with one charm quark and two light quarks. It is similar for the baryons with a bottom quark. The total spin of these baryons is 1 / 2, while another sextets have spin 3 / 2

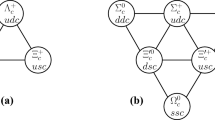
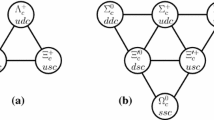
The decay final state of $\Xi _{cc}$ and $\Omega _{cc}$ contains baryons with one charm quark. These baryons form an antitriplets and sextets of charmed baryons, as shown in Fig. 1. This is similar for baryons with one bottom quark. The total spin of the baryons in Fig. 1 is 1 / 2, while another sextet has spin 3 / 2. In this work, we shall focus on the $1/2\rightarrow 1/2$ transition and leave the $1/2\rightarrow 3/2$ transition to a forthcoming publication.

To be more explicit, we will investigate the following decay modes of doubly heavy baryons.

• cc sector

  $$\begin{aligned} \Xi _{cc}^{++}(ccu)&\rightarrow \Lambda _{c}^{+}(dcu)/\Sigma _{c}^{+}(dcu)/\Xi _{c}^{+}(scu)/\Xi _{c}^{\prime +}(scu),\\ \Xi _{cc}^{+}(ccd)&\rightarrow \Sigma _{c}^{0}(dcd)/\Xi _{c}^{0}(scd)/\Xi _{c}^{\prime 0}(scd),\\ \Omega _{cc}^{+}(ccs)&\rightarrow \Xi _{c}^{0}(dcs)/\Xi _{c}^{\prime 0}(dcs)/\Omega _{c}^{0}(scs), \end{aligned}$$

• bb sector

  $$\begin{aligned} \Xi _{bb}^{0}(bbu)&\rightarrow \Sigma _{b}^{+}(ubu)/\Xi _{bc}^{+}(cbu)/\Xi _{bc}^{\prime +}(cbu),\\ \Xi _{bb}^{-}(bbd)&\rightarrow \Lambda _{b}^{0}(ubd)/\Sigma _{b}^{0}(ubd)/\Xi _{bc}^{0}(cbd)/\Xi _{bc}^{\prime 0}(cbd),\\ \Omega _{bb}^{-}(bbs)&\rightarrow \Xi _{b}^{0}(ubs)/\Xi _{b}^{\prime 0}(ubs)/\Omega _{bc}^{0}(cbs)/\Omega _{bc}^{\prime 0}(cbs), \end{aligned}$$

• bc sector with the c quark decay

  $$\begin{aligned} \Xi _{bc}^{+}(cbu)/\Xi _{bc}^{\prime +}(cbu)&\rightarrow \Lambda _{b}^{0}(dbu)/\Sigma _{b}^{0}(dbu)/\Xi _{b}^{0}(sbu)/\Xi _{b}^{\prime 0}(sbu),\\ \Xi _{bc}^{0}(cbd)/\Xi _{bc}^{\prime 0}(cbd)&\rightarrow \Sigma _{b}^{-}(dbd)/\Xi _{b}^{-}(sbd)/\Xi _{b}^{\prime -}(sbd),\\ \Omega _{bc}^{0}(cbs)/\Omega _{bc}^{\prime 0}(cbs)&\rightarrow \Xi _{b}^{-}(dbs)/\Xi _{b}^{\prime -}(dbs)/\Omega _{b}^{-}(sbs), \end{aligned}$$

• bc sector with the b quark decay

  $$\begin{aligned} \Xi _{bc}^{+}(bcu)/\Xi _{bc}^{\prime +}(bcu)&\rightarrow \Sigma _{c}^{++}(ucu)/\Xi _{cc}^{++}(ccu),\\ \Xi _{bc}^{0}(bcd)/\Xi _{bc}^{\prime 0}(bcd)&\rightarrow \Lambda _{c}^{+}(ucd)/\Sigma _{c}^{+}(ucd)/\Xi _{cc}^{+}(ccd),\\ \Omega _{bc}^{0}(bcs)/\Omega _{bc}^{\prime 0}(bcs)&\rightarrow \Xi _{c}^{+}(ucs)/\Xi _{c}^{\prime +}(ucs)/\Omega _{cc}^{+}(ccs). \end{aligned}$$

In the above, the quark components have been explicitly shown in the brackets, in which the first quarks denote the quarks participating in the weak decays.

Table 2 Masses (in units of GeV) and lifetimes (in units of fs) of doubly heavy baryons. We have used the experimental data for the mass of $\Xi _{cc}^{++}$ [9] and theoretical results from Refs. [21, 46, 58, 61, 62]

To deal with the strong interaction in the transition, we will adopt the light-front approach and calculate the decay form factors. This approach has been widely applied to various mesonic transitions [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39], and some analyses of baryonic transitions in this approach can be found in Refs. [40,41,42]. We will use diquark picture and only consider the ground states of baryons, thereby the two spectator quarks are considered to be a scalar diquark with $J^{P}=0^{+}$ or an axial vector diquark with $J^{P}=1^{+}$. Both types of diquarks will contribute and their contributions are calculated, respectively.

The rest of this paper is organized as follows. In Sect. 2, we will give a very brief overview of the spectroscopy and lifetimes of the doubly heavy baryons. Section 3 is devoted to the calculation of transition form factors in the covariant light-front quark model. In Sect. 4 and  5, we apply our results to calculate the partial widths for semileptonic $B\rightarrow B'\ell \bar{\nu }_\ell$ decays, and the nonleptonic decays, respectively. A brief summary and some discussions on the future improvements are given in the last section.

2 Spectroscopy and lifetimes

The doubly heavy baryon systems with the quark contents $Q_{1}Q_{2}q$ with $Q_{1,2}=b,c$ and $q=u,d,s$ have been studied extensively using various theoretical methods, such as quark models [43,44,45,46], the bag model [47], QCD sum rules [48], heavy quark effective theory [49, 50], Lattice QCD simulation [51,52,53,54,55,56,57], etc. For $\Xi _{cc}$, most predictions are in the range 3.5 to 3.7 GeV. For instance Refs. [46] and [58] give, respectively, $m_{\Xi _{cc}}= 3.627$ GeV and $m_{\Xi _{cc}}= 3.610$ GeV which are very close to the LHCb measurement in Eq. (1). Thus in this calculation we will use the results from Refs. [46] and [58] if available. These results are collected in Table 2.

In Table 2, we have neglected the isospin splittings, that is, we have used $m_{\Xi _{cc}^{++}}=m_{\Xi _{cc}^{+}}$, $m_{\Xi _{bc}^{+}}=m_{\Xi _{bc}^{0}}$ and $m_{\Xi _{bb}^{0}}=m_{\Xi _{bb}^{-}}$. The isospin splittings for doubly heavy baryons have been studied in Ref. [59] with the results:

$$\begin{aligned} m_{\Xi _{cc}^{++}}- m_{\Xi _{cc}^{+}}= & {} (1.5\pm 2.7)\;\mathrm{MeV}, \nonumber \\ m_{\Xi _{bb}^{-}}- m_{\Xi _{bb}^{0}}= & {} (6.3\pm 1.7)\;\mathrm{MeV},\nonumber \\ m_{\Xi _{bc}^{+}}- m_{\Xi _{bc}^{0}}= & {} (-1.5\pm 0.9)\;\mathrm{MeV}. \end{aligned}$$

(2)

As one can see from the above equation, the isospin splittings are at most a few MeV. We find that their impact on the form factors and decay widths of semileptonic and nonleptonic decays is small especially compared to hadronic uncertainties. This, however, will be improved when the experimental data for the masses are available.

For the baryons with a strange quark, one expects that they should be heavier than the corresponding states with a u or d quark. Theoretical results from Ref. [58] did respect this expectation for the ccq and bbq baryons, however, the predicted mass for $\Omega _{bc}$ is only 55 MeV higher than that for $\Xi _{bc}$. One should be warned that using these results might introduce some theoretical uncertainties to form factors and decay widths.

The lifetime of the baryons is determined by the inclusive decays. Thus one can in principle use the optical theorem to obtain the total width (lifetime) of the heavy hadron by calculating the absorptive part of the forward-scattering amplitude. The lifetimes of the baryons have been studied in Refs. [46, 60,61,62,63,64,65,66,67,68], where the results differ significantly. For the instance, the lifetime of the $\Xi _{cc}^{++}$ baryon is predicted in the range 200 fs to 700 fs. This large ambiguity will introduce dramatic uncertainties to the decay branching fractions, and we intend to improve the precision of the lifetime in the future. In this work, for the lifetime of $\Xi _{cc}$ we will use the results from Ref. [21], while other lifetimes are taken from Refs. [46, 61, 62].

In heavy quark limit, the interaction between the heavy quark and gluon is independent of the heavy quark spin. Thus the spin of heavy quarks is conserved and can be used for classification of hadrons. For the lowest-lying bbq and ccq ($q=u,d,s$) system with $L=0$, bb and cc must have spin 1 due to the symmetry between the two heavy quarks. For the bcq baryon, the bc system can have spin 0, corresponding to 1 / 2 baryons, or spin 1, corresponding to the 1 / 2 or 3 / 2 baryons as shown in Table 1. The physical hadrons, mass eigenstates, might be mixtures of the spin eigenstates of heavy quark subsystem:

$$\begin{aligned}&\left( \begin{array}{c} \Xi ^{(1)}_{bc}\\ \Xi ^{(2)}_{bc} \\ \end{array}\right) = \left( \begin{array}{cc} \cos \theta _{\Xi } &{}\quad \sin \theta _{\Xi }\\ -\sin \theta _{\Xi }&{}\quad \cos \theta _{\Xi } \\ \end{array}\right) \left( \begin{array}{c} \Xi _{bc}\\ \Xi ^{\prime }_{bc} \\ \end{array}\right) , \end{aligned}$$

(3)

$$\begin{aligned}&\left( \begin{array}{c} \Omega ^{(1)}_{bc}\\ \Omega ^{(2)}_{bc} \\ \end{array}\right) = \left( \begin{array}{cc} \cos \theta _{\Omega } &{}\quad \sin \theta _{\Omega }\\ -\sin \theta _{\Omega }&{}\quad \cos \theta _{\Omega } \\ \end{array}\right) \left( \begin{array}{c} \Omega _{bc}\\ \Omega ^{\prime }_{bc} \\ \end{array}\right) . \end{aligned}$$

(4)

We expect the mixing effects are at the order $\Lambda _{\mathrm{QCD}}/m_Q$, and in this case $m_Q$ is very probably the charm quark mass. But currently we are unable to determine the mixing angle in a reliable way, and thus in the following we will calculate the decays for both $\Xi _{bc}$ and $\Xi _{bc}'$. It is necessary to point out that once the mixing scheme is determined, only one of the two sets of baryons have sizable branching fractions for weak decays. The ones with higher mass will radiatively decay into the lower one.

3 Transition form factors in the light-front approach

3.1 Light-front approach for baryons

Doubly heavy baryons are made of two heavy quarks and a light quark. For a very solid analysis from QCD of their weak decays, one has to take into account all three quarks, which is very complicated and far beyond our capability now. Starting from the initial doubly heavy baryons, it might be better to treat the two heavy quarks in the initial state as a diquark system. However, if one adopts the heavy-QQ-diquark picture for the doubly heavy baryons, the diquark system must be smashed in the weak transition of doubly heavy system to singly heavy system. An observation is, in the decay transition, one of the two heavy quarks decays, while the other heavy quark and the light quark will act as spectators. Thus as an approximation it might be plausible to treat the two spectators as a system. Here it should be stressed that this system is not tightly bounded as a usual diquark system. Only for brevity, we use the symbol di to denote the heavy–light system.

In the light-front approach, it is convenient to use the light-front decomposition of the momentum $p=(p^{-},p^{+},p_{\perp })$, with $p^{\pm }=p^{0}\pm p^{3}$ and $p_{\perp }=(p^{1},p^{2})$ and thus $p\cdot p=p^{-}p^{+}-p_{\perp }^{2}$. A baryon with total momentum P, spin $S=\frac{1}{2}$ and a scalar/axial vector diquark can be expanded as

$$\begin{aligned}&|B(P,S,S_{z})\rangle =\int \{\mathrm{d}^{3}p_{1}\}\{\mathrm{d}^{3}p_{2}\}2(2\pi )^{3}\delta ^{3}(\tilde{P}-\tilde{p}_{1}-\tilde{p}_{2})\nonumber \\&\quad \times \sum _{\lambda _{1},\lambda _{2}}\Psi ^{SS_{z}}(\tilde{p}_{1},\tilde{p}_{2},\lambda _{1},\lambda _{2})|q_{1}(p_{1},\lambda _{1})[di](p_{2},\lambda _{2})\rangle , \end{aligned}$$

(5)

where $p_{1}$ and $p_{2}$ are the momenta of the quark $q_{1}$ and the diquark [di], respectively. The convention is chosen thus:

$$\begin{aligned}&\tilde{p}=(p^{+},p_{\perp }),\;\; \{\mathrm{d}^{3}p\} \equiv \frac{\mathrm{d}p^{+}\mathrm{d}^{2}p_{\perp }}{2(2\pi )^{3}},\nonumber \\&\delta ^{3}(\tilde{p})=\delta (p^{+})\delta ^{2}(p_{\perp }). \end{aligned}$$

(6)

The baryon mass is denoted as M, and the masses of the quark $q_{1}$ and the diquark [di] are denoted as $m_{1}$ and $m_{2}$, respectively. The minus component of the momenta can be determined by their corresponding on-shell condition,

$$\begin{aligned} p^{-}=\frac{p_{\perp }^{2}+m^{2}}{p^{+}}. \end{aligned}$$

(7)

One can introduce the momentum fraction $x_{1,2}$ of $q_{1}$ and [di] through

$$\begin{aligned} p_{1}^{+}&=x_{1}P^{+},\quad p_{2}^{+}=x_{2}P^{+},\quad x_{1}+x_{2}=1. \end{aligned}$$

(8)

It is often convenient to use $x\equiv x_{2}$ and hence $x_{1}=1-x$. Denote $\bar{P}\equiv p_{1}+p_{2}$ and $M_{0}^{2}\equiv \bar{P}^{2}$. In $\bar{P}$ rest frame, $e_{1,2}$ corresponds to the energy of $q_{1}$ and [di], respectively. The 3-momentum of [di] is $\mathbf {k}=(k_{\perp },k_{z})$. Then $M_{0}$ can be expressed as a function of the internal variables x and $k_{\perp }$:

$$\begin{aligned} M_{0}^{2}&=\frac{k_{\perp }^{2}+m_{1}^{2}}{x_{1}}+\frac{k_{\perp }^{2}+m_{2}^{2}}{x_{2}}. \end{aligned}$$

(9)

Using $e_{1}+e_{2}=M_{0}$ and the on-shell conditions of $q_{1}$ and [di], one obtains

$$\begin{aligned} e_{i}&=\frac{x_{i}M_{0}}{2}+\frac{m_{i}^{2}+k_{\perp }^{2}}{2x_{i}M_{0}}, \end{aligned}$$

(10)

$$\begin{aligned} k_{z}&=\frac{xM_{0}}{2}-\frac{m_{2}^{2}+k_{\perp }^{2}}{2xM_{0}}. \end{aligned}$$

(11)

Here $e_{i}$ and $k_{z}$ have also been expressed in terms of the internal variables x and $k_{\perp }$.

The momentum-space wave function $\Psi ^{SS_{z}}$ is expressed as [26]

$$\begin{aligned}&\Psi ^{SS_{z}}(\tilde{p}_{1},\tilde{p}_{2},\lambda _{1},\lambda _{2}) \nonumber \\&\quad =\sum _{s_{1},s_{2}}\langle \lambda _{1}|\mathcal{R}_{M}^{\dagger }(x_{1},-k_{\perp },m_{1})|s_{1}\rangle \langle \lambda _{2}|\mathcal{R}_{M}^{\dagger }(x_{2},k_{\perp },m_{2})|s_{2}\rangle \nonumber \\&\qquad \times \left\langle \frac{1}{2}s_{1};s_{[di]}s_{2}|\frac{1}{2}S_{z} \right\rangle \varphi (x,k_{\perp }), \end{aligned}$$

(12)

where $\varphi (x,k_{\perp })$ is the light-front wave function which describes the momentum distribution of the constituents in the bound state; $\langle \frac{1}{2}s_{1};s_{[di]}s_{2}|\frac{1}{2}S_{z}\rangle$ is the Clebsch–Gordan coefficient with $s_{[di]}=s_{2}=0$ for the scalar diquark and $s_{[di]}=1,\,s_{2}=0,\pm 1$ for the axial vector diquark. $\langle \lambda _{1}|\mathcal{R}_{M}^{\dagger }(x_{1},-k_{\perp },m_{1})|s_{1}\rangle$ is the Melosh transformation matrix element which transforms the conventional spin states in the instant form into the light-front helicity eigenstates. It can be shown that [26]:

$$\begin{aligned}&\sum _{s_{1},s_{2}}\langle \lambda _{1}|\mathcal{R}_{M}^{\dagger }(1-x,-k_{\perp },m_{1})|s_{1}\rangle \langle \lambda _{2}|\mathcal{R}_{M}^{\dagger }(x,k_{\perp },m_{2})|s_{2}\rangle \nonumber \\&\qquad \times \left\langle \frac{1}{2}s_{1};s_{[di]}s_{2}|\frac{1}{2}S_{z}\right\rangle \nonumber \\&\quad =\frac{1}{\sqrt{2(p_{1}\cdot \bar{P}+m_{1}M_{0})}}\bar{u}(p_{1},\lambda _{1})\Gamma u(\bar{P},S_{z}), \end{aligned}$$

(13)

with $\Gamma =1$ for the scalar diquark and for the axial vector diquark [42].

The light-front wave function is given as

$$\begin{aligned} \varphi (x,k_{\perp })=A\phi (x,k_{\perp }), \end{aligned}$$

(14)

where $A=1$ for the scalar diquark and $A=\sqrt{\frac{3(M_{0}m_{1}+p_{1}\cdot \bar{P})}{3M_{0}m_{1}+p_{1}\cdot \bar{P}+(2p_{1}\cdot p_{2}p_{2}\cdot \bar{P})/m_{2}^{2}}}$ for the axial vector diquark. The baryon state is normalized as

$$\begin{aligned} \langle B(P^{\prime },S^{\prime },S_{z}^{\prime })|B(P,S,S_{z})\rangle \,{=}\,2(2\pi )^{3}P^{+}\delta ^{3}(\tilde{P}^{\prime }-\tilde{P})\delta _{S^{\prime }S}\delta _{S_{z}^{\prime }S_{z}}, \end{aligned}$$

(15)

which implies that the light-front wave function $\phi (x,k_{\perp })$ should satisfy the following constraint:

$$\begin{aligned} \int \frac{\mathrm{d}x\mathrm{d}^{2}k_{\perp }}{2(2\pi )^{3}}|\phi (x,k_{\perp })|^{2}=1. \end{aligned}$$

(16)

In the practical calculations, a Gaussian form function is widely used,

$$\begin{aligned} \phi (x,k_{\perp })=N\sqrt{\frac{\partial k_{z}}{\partial x_{2}}}\exp \left( \frac{-\mathbf {k}^{2}}{2\beta ^{2}}\right) , \end{aligned}$$

(17)

with

$$\begin{aligned} N=4\left( \frac{\pi }{\beta ^{2}}\right) ^{3/4},\quad \frac{\partial k_{z}}{\partial x_{2}}=\frac{e_{1}e_{2}}{x_{1}x_{2}M_{0}}, \end{aligned}$$

(18)

where the parameter $\beta$ characterizes the momentum distributions between the constituents, and is usually obtained by fitting the data.

3.2 Transitions with scalar diquarks

The baryon–baryon weak transiting matrix elements are expressed in terms of form factors as

$$\begin{aligned}&\langle B^{\prime }(P^{\prime },S_{z}^{\prime })|(V-A)_{\mu }|B(P,S_{z})\rangle \nonumber \\&=\bar{u}(P^{\prime },S_{z}^{\prime })\left[ \gamma _{\mu }f_{1}(q^{2}) +i\sigma _{\mu \nu }\frac{q^{\nu }}{M}f_{2}(q^{2})+\frac{q_{\mu }}{M}f_{3}(q^{2})\right] u(P,S_{z}),\nonumber \\&\quad - \bar{u}(P^{\prime },S_{z}^{\prime })\left[ \gamma _{\mu }g_{1}(q^{2}) +i\sigma _{\mu \nu }\frac{q^{\nu }}{M}g_{2}(q^{2})+\frac{q_{\mu }}{M}g_{3}(q^{2}) \right] \gamma _{5}u(P,S_{z}), \end{aligned}$$

(19)

where $(V-A)_{\mu }$ is the weak current, $q=P-P^{\prime }$, and M denotes the mass of the parent baryon B. With the baryon state in the light-front approach in (5), the above matrix elements are

(20)

where

$$\begin{aligned} \bar{\Gamma }^{\prime }=\gamma _{0}\Gamma ^{\dagger }\gamma _{0}=\Gamma =1, \end{aligned}$$

(21)

for the transitions with scalar diqaruks, $m_{1}$, $m_{1}^{\prime }$ and $m_{2}$ are the masses of initial quark, final quark and diquark with momenta $p_{1}$, $p_{1}^{\prime }$ and $p_{2}$, respectively, P and $P^{\prime }$ are the momenta of initial and final baryons, respectively, $\bar{P}$ and $\bar{P}^{\prime }$ are defined as $\bar{P}=p_{1}+p_{2}$ and $\bar{P}^{\prime }=p_{1}^{\prime }+p_{2}$, respectively. The Feynman diagram of the baryon–baryon transitions in the diquark picture is shown in Fig. 2.

Fig. 2

Feynman diagrams for baryon–baryon transitions in the diquark picture. $P^{(\prime )}$ is the momentum of the incoming (outgoing) baryon, $p_{1}^{(\prime )}$ is the quark momentum, $p_{2}$ is the diquark momentum and the cross mark denotes the corresponding vertex of weak interaction

Since the momentum distribution wavefunction $\phi ^{\prime }$ is real, (20) becomes

(22)

With the relations of

$$\begin{aligned} \langle&B^{\prime }(P^{\prime },S_{z}^{\prime })|V^{+}|B(P,S_{z})\rangle \nonumber \\&\quad =2\sqrt{P^{+}P^{\prime +}}\left[ f_{1}(q^{2})\delta _{S_{z}{}^{\prime }S_{z}} +\frac{f_{2}(q^{2})}{M}(\mathbf {\sigma } \cdot \mathbf {q}_{\perp } \sigma ^{3})_{S_{z}^{\prime }S_{z}}\right] ,\nonumber \\&\langle B^{\prime }(P^{\prime },S_{z}^{\prime })|A^{+}|B(P,S_{z})\rangle \nonumber \\&\quad =2\sqrt{P^{+}P^{\prime +}}\left[ g_{1}(q^{2})(\sigma ^{3})_{S_{z}{}^{\prime }S_{z}} +\frac{g_{2}(q^{2})}{M}(\mathbf {\sigma }\cdot \mathbf {q}_{\perp })_{S_{z}^{\prime }S_{z}}\right] , \end{aligned}$$

(23)

one can obtain form factors as [40]

(24)

The final expressions for form factors are given:

$$\begin{aligned}&f_{1}(q^{2})= \int \frac{\mathrm{d}x\mathrm{d}^{2}k_{\perp }}{2(2\pi )^{3}}\nonumber \\&\quad \times \frac{\phi ^{\prime }(x^{\prime },k_{\perp }^{\prime }) \phi (x,k_{\perp })[k_{\perp }\cdot k_{\perp }^{\prime }+(x_{1}M_{0}+m_{1}) (x_{1}^{\prime }M_{0}^{\prime }+m_{1}^{\prime })]}{\sqrt{\left[ (m_{1}+x_{1}M_{0})^{2} +k_{\perp }^{2}\right] \left[ (m_{1}^{\prime }+x_{1}^{\prime }M_{0}^{\prime })^{2} +k_{\perp }^{\prime 2}\right] }},\nonumber \\&g_{1}(q^{2})= \int \frac{\mathrm{d}x\mathrm{d}^{2}k_{\perp }}{2(2\pi )^{3}}\nonumber \\&\quad \times \frac{\phi ^{\prime }(x^{\prime },k_{\perp }^{\prime }) \phi (x,k_{\perp })[-k_{\perp }\cdot k_{\perp }^{\prime }+(x_{1}M_{0}+m_{1}) (x_{1}^{\prime }M_{0}^{\prime }+m_{1}^{\prime })]}{\sqrt{\left[ (m_{1}+x_{1}M_{0})^{2} +k_{\perp }^{2}\right] \left[ (m_{1}^{\prime }+x_{1}^{\prime }M_{0}^{\prime })^{2} +k_{\perp }^{\prime 2}\right] }},\nonumber \\&\frac{f_{2}(q^{2})}{M}= \frac{1}{q_{\perp }^{2}}\int \frac{\mathrm{d}x\mathrm{d}^{2}k_{\perp }}{2(2\pi )^{3}}\nonumber \\&\quad \times \frac{\phi ^{\prime } (x^{\prime },k_{\perp }^{\prime })\phi (x,k_{\perp })[-(m_{1}+x_{1}M_{0}) k_{\perp }^{\prime }\cdot q_{\perp }+(m_{1}^{\prime }+x_{1}^{\prime }M_{0}^{\prime }) k_{\perp }\cdot q_{\perp }]}{\sqrt{\left[ (m_{1}+x_{1}M_{0})^{2} +k_{\perp }^{2}\right] \left[ (m_{1}^{\prime }+x_{1}^{\prime }M_{0}^{\prime })^{2} +k_{\perp }^{\prime 2}\right] }},\nonumber \\&\frac{g_{2}(q^{2})}{M}= \frac{1}{q_{\perp }^{2}}\int \frac{\mathrm{d}x\mathrm{d}^{2}k_{\perp }}{2(2\pi )^{3}}\nonumber \\&\quad \times \frac{\phi ^{\prime } (x^{\prime },k_{\perp }^{\prime })\phi (x,k_{\perp })[-(m_{1}+x_{1}M_{0}) k_{\perp }^{\prime }\cdot q_{\perp }-(m_{1}^{\prime }+x_{1}^{\prime }M_{0}^{\prime }) k_{\perp }\cdot q_{\perp }]}{\sqrt{\left[ (m_{1}+x_{1}M_{0})^{2} +k_{\perp }^{2}\right] \left[ (m_{1}^{\prime }+x_{1}^{\prime }M_{0}^{\prime })^{2} +k_{\perp }^{\prime 2}\right] }}, \end{aligned}$$

(25)

where $x^{\prime }=x$, $x_{1}^{\prime }=x_{1}=1-x$ and $k_{\perp }^{\prime }=k_{\perp }+x_{2}q_{\perp }$ since we choose the coordinate system which satisfies $q^{+}=0$.

3.3 Transitions with axial vector diquarks

With in (13) for the transitions with axial vector diquarks, the form factors can be obtained similarly [42], given as

(26)

3.4 Mixing of transition form factors

Table 3 Mixing coefficients of the transition matrix elements for the doubly charmed baryon decays. Taking the $\Xi _{cc}^{++}\rightarrow \Lambda _{c}^{+}$ as an example, the physical transition matrix elements can be evaluated as follows. $\langle \Lambda _{c}^{+}|(V-A)_{\mu }|\Xi _{cc}^{++}\rangle = c_{S} \langle d[cu]_{S}|(V-A)_{\mu }|c[cu]_{S}\rangle + c_{A} \langle d[cu]_{A}|(V-A)_{\mu }|c[cu]_{A}\rangle$ with $c_{S}=\sqrt{6}/4$ and $c_{A}=\sqrt{6}/4$

Table 4 Same as Table 3 but for the doubly bottom baryon decays

Table 5 Same as Table 3 but for the bottom–charm baryons with charm decays

Table 6 Same as Table 3 but for the bottom–charm baryons with b decays

Table 7 The shape parameters $\beta$ in the Gaussian-type wave functions Eq. (17) and the final baryon masses (in units of GeV)

Table 8 Transition form factors of doubly charmed baryon decays with scalar ($0^{+}$) diquarks. The formula of (35) is adopted

Table 9 Transition form factors of doubly charmed baryon decays with the axial vector $(1^{+})$ diquarks. The formula of (36) is adopted for the ones with asterisk, and that of (35) for all the others

Table 10 Same as Table 8 but for the doubly bottom baryon decays with scalar ($0^{+}$) diquarks

Table 11 Same as Table 9 but for the doubly bottom baryons with axial vector $(1^{+})$ diquarks

Table 12 Same as Table 8 but for the charm decays of bottom–charm baryons with scalar $(0^{+})$ diquarks

Table 13 Same as Table 9 but for the charm decays of bottom–charm baryons with axial vector $(1^{+})$ diquarks

Table 14 Same as Table 8 but for the b decays of bottom–charm baryons with scalar $(0^{+})$ diquarks

Table 15 Same as Table 9 but for the b decays of bottom–charm baryons with axial vector $(1^{+})$ diquarks

It should be noted that, in the above calculation, what we have obtained is simply the transition matrix elements $\langle q_{1}[Q_{2}q]_{S}|(V-A)_{\mu }|Q_{1}[Q_{2}q]_{S}\rangle$ or $\langle q_{1}[Q_{2}q]_{A}|(V-A)_{\mu }|Q_{1}[Q_{2}q]_{A}\rangle$ with S and A denoting a scalar or axial vector diquark spectator, respectively. The physical hadronic transition matrix elements are actually linear combinations of the ones with the scalar diquarks and the ones with the axial vector diquarks.

$$\begin{aligned}&\langle B^{\prime }|(V-A)_{\mu }|B\rangle =c_{S}\langle q_{1}[Q_{2}q]_{S}|(V-A)_{\mu }|Q_{1}[Q_{2}q]_{S}\rangle \nonumber \\&\quad +\,c_{A}\langle q_{1}[Q_{2}q]_{A}|(V-A)_{\mu }|Q_{1}[Q_{2}q]_{A}\rangle , \end{aligned}$$

(27)

where the coefficients $c_{S,A}$ are determined by the wave functions of the initial and final states.

For the doubly charmed baryons, the wave functions are

$$\begin{aligned} \mathcal {B}_{cc}=\frac{1}{\sqrt{2}}\left[ \left( -\frac{\sqrt{3}}{2}c^{1}(c^{2}q)_{S}+\frac{1}{2}c^{1}(c^{2}q)_{A}\right) +(c^{1}\leftrightarrow c^{2})\right] , \end{aligned}$$

(28)

with $q=u$, d or s for $\Xi _{cc}^{++}$, $\Xi _{cc}^{+}$ or $\Omega _{cc}^{+}$, respectively. The superscripts describe the symmetry between the two charm quarks. The ones of the doubly bottom baryons are replaced by $c\rightarrow b$. For the bottom–charm baryons, there are two sets of states, with bc as a scalar or an axial vector diquarks. The wave functions of bottom–charm baryons with axial vector bc diquark are

$$\begin{aligned} \mathcal {B}_{bc}&= -\frac{\sqrt{3}}{2}b(cq)_{S}+\frac{1}{2}b(cq)_{A} = -\frac{\sqrt{3}}{2}c(bq)_{S}+\frac{1}{2}c(bq)_{A}, \end{aligned}$$

(29)

while those with a scalar bc diquark are given as

$$\begin{aligned} \mathcal {B}_{bc}^{\prime }&= -\frac{1}{2}b(cq)_{S}-\frac{\sqrt{3}}{2}b(cq)_{A} = \frac{1}{2}c(bq)_{S}+\frac{\sqrt{3}}{2}c(bq)_{A} , \end{aligned}$$

(30)

with $q=u$, d or s for $\Xi _{bc}^{(\prime )+}$, $\Xi _{bc}^{(\prime )0}$ or $\Omega _{bc}^{(\prime )0}$, respectively.

The wave functions of the antitriplet singly charmed baryons are

$$\begin{aligned} \Lambda _{c}^{+}&= -\frac{1}{2}d(cu)_{S}+\frac{\sqrt{3}}{2}d(cu)_{A} = \frac{1}{2}u(cd)_{S}-\frac{\sqrt{3}}{2}u(cd)_{A},\nonumber \\ \Xi _{c}^{+}&= -\frac{1}{2}s(cu)_{S}+\frac{\sqrt{3}}{2}s(cu)_{A} = \frac{1}{2}u(cs)_{S}-\frac{\sqrt{3}}{2}u(cs)_{A} ,\\ \Xi _{c}^{0}&= -\frac{1}{2}s(cd)_{S}+\frac{\sqrt{3}}{2}s(cd)_{A} = \frac{1}{2}d(cs)_{S}-\frac{\sqrt{3}}{2}d(cs)_{A}.\nonumber \end{aligned}$$

(31)

For the sextet of singly charmed baryons, the wave functions are

$$\begin{aligned} \Sigma _{c}^{++}&=\frac{1}{\sqrt{2}}\left[ \frac{\sqrt{3}}{2}u^{1}(cu^{2})_{S}+\frac{1}{2}u^{1}(cu^{2})_{A}+(u^{1}\leftrightarrow u^{2})\right] ,\nonumber \\ \Sigma _{c}^{+}&= \frac{\sqrt{3}}{2}d(cu)_{S}+\frac{1}{2}d(cu)_{A} = \frac{\sqrt{3}}{2}u(cd)_{S}+\frac{1}{2}u(cd)_{A}, \\ \Sigma _{c}^{0}&=\frac{1}{\sqrt{2}}\left[ \frac{\sqrt{3}}{2}d^{1}(cd^{2})_{S}+\frac{1}{2}d^{1}(cd^{2})_{A}+(d^{1}\leftrightarrow d^{2})\right] ,\nonumber \\ \Xi _{c}^{\prime +}&= \frac{\sqrt{3}}{2}s(cu)_{S}+\frac{1}{2}s(cu)_{A} = \frac{\sqrt{3}}{2}u(cs)_{S}+\frac{1}{2}u(cs)_{A},\nonumber \\ \Xi _{c}^{\prime 0}&= \frac{\sqrt{3}}{2}s(cd)_{S}+\frac{1}{2}s(cd)_{A} = \frac{\sqrt{3}}{2}d(cs)_{S}+\frac{1}{2}d(cs)_{A},\nonumber \\ \Omega _{c}^{0}&=\frac{1}{\sqrt{2}}\left[ \frac{\sqrt{3}}{2}s^{2}(cs^{1})_{S}+\frac{1}{2}s^{2}(cs^{1})_{A}+(s^{1}\leftrightarrow s^{2})\right] .\nonumber \end{aligned}$$

(32)

The ones of the singly bottom baryons are similar on replacing of c by b.

With the wave functions given above, the mixing coefficients for the transition matrix elements in (27) are given in Tables 3, 4, 5 and 6.

3.5 Numerical results for transition form factors

The masses of quarks (in units of GeV) are used as [31,32,33,34,35,36,37,38,39]

$$\begin{aligned} m_u=m_d= 0.25, \;\; m_s=0.37, \;\; m_c=1.4, \;\; m_b=4.8. \end{aligned}$$

(33)

The diquark masses $m_{[ci]}$ and $m_{[bj]}$ are approximated, respectively, by the sum of $m_{c}+m_{i}$ and $m_{b}+m_{j}$ with $i,j=u,d,s$.

The $\beta$ parameters in the wave functions of the doubly and singly heavy flavor baryons are approximately the same as those of the corresponding mesons, since the heavy–light diquark behaves a color antitriplet just like an heavy antiquark. Taking $\Xi _{cc}^{++}$ as an example, $\beta _{c[cu]}\approx \beta _{c\bar{c}}$, which is the $\beta$ parameter of $\eta _{c}$. The $\beta$ parameters are then obtained by following Eq. (2.17) of [26], with the decay constants as [69,70,71]

$$\begin{aligned} f_{D}= & {} 207.4\;\mathrm{MeV},\quad f_{D_{s}}=247.2\;\mathrm{GeV},\nonumber \\ f_{\eta _{c}}= & {} 387\;\mathrm{MeV},\quad f_{\Upsilon }=715\;\mathrm{MeV}. \end{aligned}$$

(34)

The values of the $\beta$ parameters are then listed in Table 7. The other $\beta$ are taken directly from [39]. The masses of singly heavy flavor baryons are also collected in Table  7 [2, 72].

With the above inputs, the form factors in Eqs. (25) and (26) respectively with the scalar and axial vector diquarks involved can be obtained. To access the $q^2$ distribution of the form factors, we adopt the following parametrized form:

$$\begin{aligned} F(q^{2})=\frac{F(0)}{1-\frac{q^{2}}{m_{\mathrm{fit}}^{2}}+\delta \left( \frac{q^{2}}{m_{\mathrm{fit}}^{2}}\right) ^{2}}, \end{aligned}$$

(35)

where F(0) is the form factor at $q^2=0$. The $m_\mathrm{fit}$ and $\delta$ are two parameters to be fitted from numerical results. For the form factor $g_2$, the above formula may lead to an imaginary result for $m_\mathrm{fit}$ and in this case we adopt the following modified form:

$$\begin{aligned} F(q^{2})=\frac{F(0)}{1+\frac{q^{2}}{m_{\mathrm{fit}}^{2}}+\delta \left( \frac{q^{2}}{m_{\mathrm{fit}}^{2}}\right) ^{2}}. \end{aligned}$$

(36)

The results for form factors with scalar diquark spectators are given in Tables 8, 10, 12 and 14, while those with axial vector diquarks are shown in Tables 9, 11, 13 and 15. With the results of these form factors, the physical hadronic transition matrix elements can be obtained through Eq. (27).

4 Semileptonic decays

4.1 Semileptonic $B\rightarrow B'\ell \bar{\nu }$ decay widths

The effective electroweak Hamiltonian reads

$$\begin{aligned} \mathcal{H}_{\mathrm{eff}}= & {} \frac{G_{F}}{\sqrt{2}}\bigg (V_{cs}^{*}[\bar{s}\gamma _{\mu } (1-\gamma _{5})c][\bar{\nu }\gamma ^{\mu }(1-\gamma _{5})l]\nonumber \\&+V_{cd}^{*}[\bar{d}\gamma _{\mu }(1-\gamma _{5})c][\bar{\nu }\gamma ^{\mu }(1-\gamma _{5})l]\bigg )\nonumber \\&+\frac{G_{F}}{\sqrt{2}}\bigg (V_{cb}[\bar{c}\gamma _{\mu }(1-\gamma _{5})b] [\bar{l}\gamma ^{\mu }(1-\gamma _{5})\nu ]\nonumber \\&+V_{ub} [\bar{u}\gamma _{\mu }(1-\gamma _{5})b][\bar{l}\gamma ^{\mu }(1-\gamma _{5})\nu ] \bigg ), \end{aligned}$$

(37)

where $G_{F}$ and $V_{cs,cd,ub,cb}$ are Fermi constant and Cabibbo–Kobayashi–Maskawa (CKM) matrix element, respectively. Leptonic parts can be computed in perturbation theory while hadronic contributions are parametrized in terms of form factors.

The $B\rightarrow B^{\prime }$ form factors are parametrized in Eq. (19), and the helicity amplitudes of the vector current are related to these form factors through the following expressions:

$$\begin{aligned} H_{\frac{1}{2},0}^{V}&=-i\frac{\sqrt{Q_{-}}}{\sqrt{q^{2}}}\left( (M+M^{\prime })f_{1}-\frac{q^{2}}{M}f_{2}\right) ,\nonumber \\ H_{\frac{1}{2},1}^{V}&=i\sqrt{2Q_{-}}\left( -f_{1}+\frac{M+M^{\prime }}{M}f_{2}\right) ,\nonumber \\ H_{\frac{1}{2},0}^{A}&=-i\frac{\sqrt{Q_{+}}}{\sqrt{q^{2}}}\left( (M-M^{\prime })g_{1}+\frac{q^{2}}{M}g_{2}\right) ,\nonumber \\ H_{\frac{1}{2},1}^{A}&=i\sqrt{2Q_{+}}\left( -g_{1}-\frac{M-M^{\prime }}{M}g_{2}\right) , \end{aligned}$$

(38)

where $Q_{\pm }=2(P\cdot P^{\prime }\pm MM^{\prime })=2MM^{\prime }(\omega \pm 1)$. The parameter $\omega \equiv \frac{P\cdot P^{\prime }}{MM^{\prime }}=\frac{M^{2}+M^{\prime 2}-q^{2}}{2MM^{\prime }}$ ranges from 1 to $\omega _{\mathrm{max}}=\frac{1}{2}(\frac{M}{M^{\prime }}+\frac{M^{\prime }}{M})$. The M and $M^{\prime }$ is the mass for the initial and final baryon. The negative helicity amplitudes are derived as

$$\begin{aligned} H_{-\lambda ^{\prime },-\lambda _{W}}^{V}=H_{\lambda ^{\prime },\lambda _{W}}^{V}\quad \text {and}\quad H_{-\lambda ^{\prime },-\lambda _{W}}^{A}=-H_{\lambda ^{\prime },\lambda _{W}}^{A}. \end{aligned}$$

(39)

The helicity amplitudes for the left-handed current are obtained:

$$\begin{aligned} H_{\lambda ^{\prime },\lambda _{W}}=H_{\lambda ^{\prime }, \lambda _{W}}^{V}-H_{\lambda ^{\prime },\lambda _{W}}^{A}. \end{aligned}$$

(40)

The differential decay width for the $B\rightarrow B^{\prime }l\bar{\nu }$ decay is written as

$$\begin{aligned} \frac{\mathrm{d}\Gamma }{\mathrm{d}\omega }=\frac{\mathrm{d}\Gamma _{L}}{\mathrm{d}\omega }+ \frac{\mathrm{d}\Gamma _{T}}{\mathrm{d}\omega }, \end{aligned}$$

(41)

with the longitudinal and transverse polarizations:

$$\begin{aligned} \frac{\mathrm{d}\Gamma _{L}}{\mathrm{d}\omega }&=\frac{G_{F}^{2}|V_{CKM}|^{2}}{(2\pi )^{3}} \frac{q^{2}pM^{\prime }}{12M}(|H_{\frac{1}{2},0}|^{2}+|H_{-\frac{1}{2},0}|^{2}), \end{aligned}$$

(42)

$$\begin{aligned} \frac{\mathrm{d}\Gamma _{T}}{\mathrm{d}\omega }&=\frac{G_{F}^{2}|V_{CKM}|^{2}}{(2\pi )^{3}} \frac{q^{2}pM^{\prime }}{12M}(|H_{\frac{1}{2},1}|^{2}+|H_{-\frac{1}{2},-1}|^{2}), \end{aligned}$$

(43)

where $p=M^{\prime }\sqrt{\omega ^{2}-1}$ is the three-momentum of $B^{\prime }$ in the B rest frame. Integrating over the parameter $\omega$, we obtain the total decay width

$$\begin{aligned} \Gamma =\int _{1}^{\omega _{\mathrm{max}}}\mathrm{d}\omega \frac{\mathrm{d}\Gamma }{\mathrm{d}\omega }. \end{aligned}$$

(44)

One can also study the ratio of the longitudinal to transverse decay rates $\Gamma _{L}/\Gamma _{T}$.

It is also possible to express the differential decay width as

$$\begin{aligned} \frac{\mathrm{d}\Gamma }{\mathrm{d}q^{2}}=\frac{\mathrm{d}\Gamma _{L}}{\mathrm{d}q^{2}}+\frac{\mathrm{d}\Gamma _{T}}{\mathrm{d}q^{2}}, \end{aligned}$$

(45)

where $q^2$ is the lepton pair invariant mass. The polarized decay widths are given as

$$\begin{aligned} \frac{\mathrm{d}\Gamma _{L}}{\mathrm{d}q^{2}}&=\frac{G_{F}^{2}|V_{CKM}|^{2}}{(2\pi )^{3}}\frac{q^{2}p}{24M^{2}}(|H_{\frac{1}{2},0}|^{2}+|H_{-\frac{1}{2},0}|^{2}), \end{aligned}$$

(46)

$$\begin{aligned} \frac{\mathrm{d}\Gamma _{T}}{\mathrm{d}q^{2}}&=\frac{G_{F}^{2}|V_{CKM}|^{2}}{(2\pi )^{3}}\frac{q^{2}p}{24M^{2}}(|H_{\frac{1}{2},1}|^{2}+|H_{-\frac{1}{2},-1}|^{2}), \end{aligned}$$

(47)

where $p=\sqrt{Q_{+}Q_{-}}/2M$ and $Q_{\pm }=(M\pm M^{\prime })^{2}-q^{2}$. The total width is derived to be

$$\begin{aligned} \Gamma =\int _{0}^{(M-M^{\prime })^{2}}\mathrm{d}q^{2}\frac{\mathrm{d}\Gamma }{\mathrm{d}q^{2}}. \end{aligned}$$

(48)

4.2 Numerical results

For the numerical calculation, we will use the results for the Fermi constant and CKM matrix elements from the particle data group [2]:

$$\begin{aligned}&G_{F}=1.166\times 10^{-5}\;\mathrm{GeV}^{-2},\nonumber \\&|V_{ud}|=0.974,\quad |V_{us}|=0.225,\quad |V_{ub}|=0.00357,\nonumber \\&|V_{cd}|=0.225,\quad |V_{cs}|=0.974,\quad |V_{cb}|=0.0411. \end{aligned}$$

(49)

The integrated partial decay widths and the relevant branching ratios and the $\Gamma _{L}/\Gamma _{T}$ are given in Tables 16, 17, 18,19, 20 and 21, respectively.

For a comparison, we quote the experimental data on a few semileptonic D and B decays into different final state in the following [2]:

$$\begin{aligned} \mathcal{B}(D^+\rightarrow \bar{K}^0 e^+\nu _e)= & {} (8.82\pm 0.13)\%, \nonumber \\ \mathcal{B}(D^+\rightarrow \pi ^0 e^+\nu _e)= & {} (4.05\pm 0.18)\times 10^{-3}, \nonumber \\ \mathcal{B}(D^0\rightarrow K^- e^+\nu _e)= & {} (3.530\pm 0.028)\%, \nonumber \\ \mathcal{B}(D^0\rightarrow \pi ^- e^+\nu _e)= & {} (2.91\pm 0.04)\times 10^{-3}, \nonumber \\ \mathcal{B}(\Lambda _{c}^{+}\rightarrow \Lambda e^+\nu _e)= & {} (3.6\pm 0.4)\%, \nonumber \\ \mathcal{B}( B^0\rightarrow D^- \ell ^+\nu _\ell )= & {} (2.19\pm 0.12)\%, \nonumber \\ \mathcal{B}( B^0\rightarrow \pi ^- \ell ^+\nu _\ell )= & {} (1.45\pm 0.05)\times 10^{-4}. \end{aligned}$$

(50)

A few remarks are in order.

• When presenting the numerical result for branching fractions, we have used the lifetimes as given in Table 2, but as we have pointed out that there exist large uncertainties in the lifetimes. So we have also presented the results for decay widths.

• The $\Xi _{cc}^{++}\rightarrow \Xi _{c}^+l^+\nu _l$ and $\Xi _{cc}^{++}\rightarrow \Xi _{c}^{\prime +}l^+\nu _l$ are induced by the $c\rightarrow s$ transition. Their branching fractions, at a few percent level, are comparable to those of $D\rightarrow Ke^+\nu _e$.

• The branching ratio for $\Xi _{cc}^{++}\rightarrow \Lambda _{c}^+l^+\nu _l$ is suppressed due to the CKM matrix element $V_{cd}$, which is also comparable to those of the $D\rightarrow \pi e^+\nu _e$ mode.

• The branching ratios for $b\rightarrow c$ transitions are typically at the order $10^{-2}$ to $10^{-3}$, while the $b\rightarrow u$ transition is highly suppressed due to the smallness of $|V_{ub}|$.

• In the calculation carried above, we have neglected the form factors $f_{3}(q^{2})$ and $g_{3}(q^{2})$. For semileptonic decays, the contribution from $f_{3}$ or $g_{3}$ is proportional to $m_{l}$, thus it is safe to drop them if $l=e,\mu$. As for $l=\tau$, the transverse decay width $\mathrm{d}\Gamma _{T}/\mathrm{d}q^{2}$ in Eq. (43) remains unchanged, while the longitudinal decay width $\mathrm{d}\Gamma _{L}/\mathrm{d}q^{2}$ in Eq. (42) should be re-calculated:

  $$\begin{aligned} \frac{\mathrm{d}\Gamma _{L}}{\mathrm{d}q^{2}}= & {} \frac{G_{F}^{2}|V_{cb}|^{2}p\ q^{2}\ (1-\hat{m}_{l}^{2})^{2}}{384\pi ^{3}M^{2}}\nonumber \\&\times \left( (2+\hat{m}_{l}^{2})(|H_{-\frac{1}{2},0}|^{2} +|H_{\frac{1}{2},0}|^{2})\right. \nonumber \\&\left. +3\hat{m}_{l}^{2}(|H_{-\frac{1}{2},t}|^{2} +|H_{\frac{1}{2},t}|^{2})\right) , \end{aligned}$$

  (51)

  where $\hat{m}_{l}\equiv {m_{l}}/{\sqrt{q^{2}}}$ and $H_{\pm \frac{1}{2},t}$ are given by

  $$\begin{aligned} H_{\frac{1}{2},t}^{V}&=-i\frac{\sqrt{Q_{+}}}{\sqrt{q^{2}}}\left( (M-M^{\prime })f_{1}+\frac{q^{2}}{M}f_{3}\right) =H_{-\frac{1}{2},t}^{V},\nonumber \\ H_{\frac{1}{2},t}^{A}&=-i\frac{\sqrt{Q_{-}}}{\sqrt{q^{2}}}\left( (M+M^{\prime })g_{1}-\frac{q^{2}}{M}g_{3}\right) =-H_{-\frac{1}{2},t}^{A}. \end{aligned}$$

  (52)

Table 16 The cc sector: decay widths, branching ratios and the $\Gamma _{L}/\Gamma _{T}$ for semileptonic decays, with lepton mass neglected

Table 17 The bb sector: decay widths, branching ratios and the $\Gamma _{L}/\Gamma _{T}$ for semileptonic decays, with lepton mass neglected

Table 18 The bc sector with the c quark decay and an axial vector bc diquark in the initial state: decay widths, branching ratios and the $\Gamma _{L}/\Gamma _{T}$ for semileptonic decays, with lepton mass neglected

Table 19 The bc sector with the c quark decay and a scalar bc diquark in the initial state: decay widths, branching ratios and the $\Gamma _{L}/\Gamma _{T}$ for semileptonic decays, with lepton mass neglected. We have assumed $m_{B_{i}^{\prime }}=m_{B_{i}}$ and $\tau _{B_{i}^{\prime }}=\tau _{B_{i}}$, i.e. the only difference between $B_{i}^{\prime }\rightarrow B_{f}$ and $B_{i}\rightarrow B_{f}$ is the mixing coefficients

Table 20 The bc sector with the b quark decay and an axial vector bc diquark in the initial state: decay widths, branching ratios and the $\Gamma _{L}/\Gamma _{T}$ for semileptonic decays, with lepton mass neglected

Table 21 The bc sector with the b quark decay and a scalar bc diquark in the initial state: decay widths, branching ratios and the $\Gamma _{L}/\Gamma _{T}$ for semileptonic decays, with lepton mass neglected. We have assumed $m_{B_{i}^{\prime }}=m_{B_{i}}$ and $\tau _{B_{i}^{\prime }}=\tau _{B_{i}}$, i.e. the only difference between $B_{i}^{\prime }\rightarrow B_{f}$ and $B_{i}\rightarrow B_{f}$ is the mixing coefficients

4.3 SU(3) analysis

Recently, an analysis of weak decays of doubly heavy baryons based on flavor symmetry has become available in Ref. [73]. In the SU(3) symmetry limit, there exist a number of relations among these semileptonic decay widths, which we are going to examine in the following.

• cc sector

  $$\begin{aligned} \Gamma (\Xi _{cc}^{++}\rightarrow \Lambda _{c}^{+}l^{+}\nu )&=\Gamma (\Omega _{cc}^{+}\rightarrow \Xi _{c}^{0}l^{+}\nu ),\\ \Gamma (\Xi _{cc}^{++}\rightarrow \Xi _{c}^{+}l^{+}\nu )&=\Gamma (\Xi _{cc}^{+}\rightarrow \Xi _{c}^{0}l^{+}\nu ),\\ \Gamma (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{+}l^{+}\nu )&=\frac{1}{2}\Gamma (\Xi _{cc}^{+}\rightarrow \Sigma _{c}^{0}l^{+}\nu )\\&=\Gamma (\Omega _{cc}^{+}\rightarrow \Xi _{c}^{\prime 0}l^{+}\nu ),\\ \Gamma (\Xi _{cc}^{++}\rightarrow \Xi _{c}^{\prime +}l^{+}\nu )&=\Gamma (\Xi _{cc}^{+}\rightarrow \Xi _{c}^{\prime 0}l^{+}\nu )\\&=\frac{1}{2}\Gamma (\Omega _{cc}^{+}\rightarrow \Omega _{c}^{0}l^{+}\nu ),\\ \Gamma (\Xi _{cc}^{+}\rightarrow \Sigma _{c}^{0}l^{+}\nu )&=2\Gamma (\Omega _{cc}^{+}\rightarrow \Xi _{c}^{\prime 0}l^{+}\nu ), \end{aligned}$$

• bb sector

  $$\begin{aligned} \Gamma (\Xi _{bb}^{0}\rightarrow \Xi _{bc}^{+}l^{-}\bar{\nu })&=\Gamma (\Xi _{bb}^{-}\rightarrow \Xi _{bc}^{0}l^{-}\bar{\nu })\\&=\Gamma (\Omega _{bb}^{-}\rightarrow \Omega _{bc}^{0}l^{-}\bar{\nu }),\\ \Gamma (\Xi _{bb}^{-}\rightarrow \Lambda _{b}^{0}l^{-}\bar{\nu })&=\Gamma (\Omega _{bb}^{-}\rightarrow \Xi _{b}^{0}l^{-}\bar{\nu }),\\ \Gamma (\Xi _{bb}^{0}\rightarrow \Sigma _{b}^{+}l^{-}\bar{\nu })&=2\Gamma (\Xi _{bb}^{-}\rightarrow \Sigma _{b}^{0}l^{-}\bar{\nu })\\&=2\Gamma (\Omega _{bb}^{-}\rightarrow \Xi _{b}^{\prime 0}l^{-}\bar{\nu }), \end{aligned}$$

• bc sector with the c quark decay

  $$\begin{aligned} \Gamma (\Xi _{bc}^{+}\rightarrow \Lambda _{b}^{0}l^{+}\nu )&=\Gamma (\Omega _{bc}^{0}\rightarrow \Xi _{b}^{-}l^{+}\nu ),\\ \Gamma (\Xi _{bc}^{+}\rightarrow \Xi _{b}^{0}l^{+}\nu )&=\Gamma (\Xi _{bc}^{0}\rightarrow \Xi _{b}^{-}l^{+}\nu ),\\ \Gamma (\Xi _{bc}^{+}\rightarrow \Sigma _{b}^{0}l^{+}\nu )&=\frac{1}{2}\Gamma (\Xi _{bc}^{0}\rightarrow \Sigma _{b}^{-}l^{+}\nu )\\&=\Gamma (\Omega _{bc}^{0}\rightarrow \Xi _{b}^{\prime -}l^{+}\nu ),\\ \Gamma (\Xi _{bc}^{+}\rightarrow \Xi _{b}^{\prime 0}l^{+}\nu )&=\Gamma (\Xi _{bc}^{0}\rightarrow \Xi _{b}^{\prime -}l^{+}\nu )\\&=\frac{1}{2}\Gamma (\Omega _{bc}^{0}\rightarrow \Omega _{b}^{-}l^{+}\nu ), \end{aligned}$$

• bc sector with the b quark decay

  $$\begin{aligned} \Gamma (\Xi _{bc}^{+}\rightarrow \Xi _{cc}^{++}l^{-}\bar{\nu })&=\Gamma (\Xi _{bc}^{0}\rightarrow \Xi _{cc}^{+}l^{-}\bar{\nu })\\&=\Gamma (\Omega _{bc}^{0}\rightarrow \Omega _{cc}^{+}l^{-}\bar{\nu }),\\ \Gamma (\Xi _{bc}^{+}\rightarrow \Sigma _{c}^{++}l^{-}\bar{\nu })&=2\Gamma (\Xi _{bc}^{0}\rightarrow \Sigma _{c}^{+}l^{-}\bar{\nu })\\&=2\Gamma (\Omega _{bc}^{0}\rightarrow \Xi _{c}^{\prime +}l^{-}\bar{\nu }). \end{aligned}$$

Comparing the above equations predicted by SU(3) symmetry with the corresponding results in this work, we make the following remarks.

• SU(3) symmetry is respected very well in most cases, except for the following ones:

  $$\begin{aligned} \Gamma (\Xi _{cc}^{++}\rightarrow \Lambda _{c}^{+}l^{+}\nu )&= \Gamma (\Omega _{cc}^{+}\rightarrow \Xi _{c}^{0}l^{+}\nu ),\nonumber \\ \Gamma (\Xi _{bc}^{+}\rightarrow \Lambda _{b}^{0}l^{+}\nu )&= \Gamma (\Omega _{bc}^{0}\rightarrow \Xi _{b}^{-}l^{+}\nu ),\nonumber \\ \Gamma (\Xi _{bc}^{+}\rightarrow \Sigma _{b}^{0}l^{+}\nu )&= \Gamma (\Omega _{bc}^{0}\rightarrow \Xi _{b}^{\prime -}l^{+}\nu ),\nonumber \\ \Gamma (\Xi _{bc}^{+}\rightarrow \Xi _{b}^{\prime 0}l^{+}\nu )&= \frac{1}{2}\Gamma (\Omega _{bc}^{0}\rightarrow \Omega _{b}^{-}l^{+}\nu ),\nonumber \\ \Gamma (\Xi _{bc}^{0}\rightarrow \Sigma _{c}^{+}l^{-}\bar{\nu })&= \Gamma (\Omega _{bc}^{0}\rightarrow \Xi _{c}^{\prime +}l^{-}\bar{\nu }). \end{aligned}$$

  (53)

  These five relations are broken considerably: by more than 20% but still less than 50% using the definition of $(\mathrm{Max}[\Gamma _{\mathrm{LHS}},\Gamma _{\mathrm{RHS}}]-\mathrm{Min}[\Gamma _{\mathrm{LHS}},\Gamma _{\mathrm{RHS}}])/\mathrm{Max}[\Gamma _{\mathrm{LHS}},\Gamma _{\mathrm{RHS}}]$.

• Since the mass difference between the u and d quark has been neglected in this work, the isospin symmetry is well respected. But since the strange quark is much heavier, the SU(3) relations for the channels involving u, d quark and s quark can be sizably broken. All relations given in Eq. (53) are of this type.

• The first 4 relations in Eq. (53) involve the c quark decay but the last one involves the b quark decay. It indicates that the c quark decay modes tend to break SU(3) symmetry easily. This can be understood by the phase space of the c quark decay being smaller, and thus the decay amplitude is more sensitive to the mass of the initial and final baryons.

4.4 The loosely bounded diquark approximation and shape parameter uncertainty

In the above calculations, we have made the assumption that the two spectators, a heavy and a light quark, are treated as a system. Then baryons are composed of this loosely bounded system and the quark involved in the weak transition. We approximated this system as a heavy quark, and obtained the $\beta$ parameter in the light-front wave function by comparing the doubly heavy baryons with heavy quarkonia, and singly heavy baryons with heavy–light mesons.

From a phenomenological viewpoint, namely since the size of the loosely bounded system is mainly determined by the size of the light quark, it might also be applicable to derive the shape parameter $\beta$ under the approximation that the heavy–light spectator is treated a light system. Using these new parameters $\beta$, we have found that the form factors for the doubly charmed baryons are not significantly changed since the charm quark mass is not very large.

We show the form factors for the transition of $\Xi _{bbu}^0\rightarrow \Sigma _{buu}^+$ in Table 22, where for the left columns, $\beta _{\Xi _{bbu}^0}=1.472$ GeV and $\beta _{\Sigma _{buu}^{+}}=0.562$ GeV have been used; while the results in the right columns, $\beta _{\Xi _{bbu}^0}=0.562$ GeV and $\beta _{\Sigma ^+(buu)}=0.318$ GeV have been adopted. From this table, we can find that using the new parameters $\beta$, the form factors are tiny. This feature can be understood when we show the light-front wave functions in Fig. 3. The light-front wave function for the $\Xi ^0_{bbu}$ (dotted curves) and $\Sigma ^+_{buu}$(solid curves) are shown in this figure. In the left panel, we have used $\beta _{\Xi ^0_{bbu}}=1.472$ GeV and $\beta _{\Sigma ^+_{buu}}=0.562$ GeV; while in the right panel, the following parameters are used: $\beta _{\Xi ^0_{bbu}}=0.562$ GeV and $\beta _{\Sigma ^+_{buu}}=0.318$ GeV. Transition form factors can be viewed as the overlap of wave functions of $\Xi ^0_{bbu}$ and $\Sigma ^+_{buu}$, and apparently thus the left (right) panel leads to a larger(smaller) form factors. When showing these results, we have used $k_T^2=0.1 \mathrm{GeV}^2$, and we have found similar results for other transverse momentum $k_T$.

Table 22 Form factors $f_{1,2}$ and $g_{1,2}$ for the $\Xi _{bb}^{0}\rightarrow \Sigma _{b}^{+}$ process. For the left columns, $\beta _{\Xi _{bb}^0}=1.472$ GeV and $\beta _{\Sigma _{b}^{+}}=0.562$ GeV have been used; while the results in the right columns, $\beta _{\Xi _{bb}^0}=0.562$ GeV and $\beta _{\Sigma _{b}^{+}}=0.318$ GeV have been adopted. The fit formulas of (35) and (36) are adopted to access the $q^2$ distribution.

Fig. 3

Light-front wave functions for $\Xi _{bbu}^0$ (dotted curves) and $\Sigma ^+_{buu}$ (solid curves). Here x is the momentum fraction. In the left panel, we have used $\beta _{\Xi ^0_{bbu}}=1.472$ GeV and $\beta _{\Sigma ^+_{buu}}=0.562$ GeV; while in the right panel, the following parameters are used: $\beta _{\Xi _{bbu}^0}=0.562$ GeV and $\beta _{\Sigma ^+_{buu}}=0.318$ GeV. The form factor can be viewed as the overlap of wave functions of $\Xi _{bbu}^0$ and $\Sigma ^+_{buu}$, and thus the left (right) panel leads to a larger (smaller) form factors. When showing these results, we have used $k_T^2=0.1 \mathrm{GeV}^2$, and we have found similar results for other transverse momentum $k_T$

For the $B\rightarrow \pi$ transition, the form factors at $q^2=0$ are suppressed by ${\Lambda _\mathrm{QCD}}/m_b$ in the heavy quark limit, and for example we have [74]

$$\begin{aligned} F_1^{B\rightarrow \pi }(q^2=0)= (0.23\pm 0.05). \end{aligned}$$

(54)

Though a QCD analysis of $\Xi _{bbu}^0\rightarrow \Sigma ^+_{buu}$ transition is not available, we may expect similar power suppressions for these form factors, and the form factors might be of the order 0.1. Thus under the approximation of the two spectators as a loosely connected system, it may be reasonable to use the parameters $\beta _{\Xi ^0_{bbu}}=1.472$ GeV and $\beta _{\Sigma ^+_{buu}}=0.562$ GeV as an effective parameter.

5 Nonleptonic decays

Table 23 Partial decay widths (in units of GeV) and branching ratios for nonleptonic decays of the doubly charmed baryons

Table 24 Partial decay widths and branching ratios for nonleptonic decays of $\Xi _{bb}^{0}$ and $\Xi _{bb}^{-}$

Table 25 Partial decay widths and branching ratios for nonleptonic decays of $\Omega _{bb}^{-}$

In the following, we study two-body nonleptonic decays of doubly heavy baryons, $B\rightarrow B^{\prime }M$ with M as a pseudoscalar (P), vector (V) or axial vector (A) meson. As to a first systematic analysis, we only consider the tree current-current operators in the effective Hamiltonian, taking c quark decays as an example,

$$\begin{aligned} \mathcal{H}_{W}=\frac{G_{F}}{\sqrt{2}}V_{uq_{1}}V_{cq_{2}}^{*}(C_{1}O_{1}+C_{2}O_{2}), \end{aligned}$$

(55)

where $O_{1}=(\bar{q}_{2}c)_{V-A}(\bar{u}{q}_{1})_{V-A}$, $O_{2}=(\bar{u} c)_{V-A}(\bar{q}_{2}q_{1})_{V-A}$, $C_{i}(\mu )$ denote the corresponding Wilson coefficients, $q_{1,2}=d\ \mathrm{or}\ s$. It is similar for the $b\rightarrow c/u$ decays. In general, the transition amplitude of $B\rightarrow B^{\prime }M$ can be written as

$$\begin{aligned}&\mathcal{M}(B\rightarrow B^{\prime }P) =i\bar{u}_{B^{\prime }}(A+B\gamma _{5})u_{B},\nonumber \\&\mathcal{M}(B\rightarrow B^{\prime }V(A)) =\epsilon ^{*\mu }\bar{u}_{B^{\prime }}\nonumber \\&\quad \times \left( A_{1}\gamma _{\mu }\gamma _{5} +A_{2}\frac{P_{\mu }^{\prime }}{M}\gamma _{5}+B_{1}\gamma _{\mu }+B_{2}\frac{P_{\mu }^{\prime }}{M}\right) u_{B}, \end{aligned}$$

(56)

where $\epsilon ^{\mu }$ is the polarization vector of the final vector or axial vector mesons. In the heavy hadron decays, it has manifested that the factorization hypothesis works well in the heavy quark limit [75,76,77,78,79,80,81,82,83]. The above decay amplitudes in the factorization approach are expressed as

$$\begin{aligned} A&=-\lambda f_{P}(M-M^{\prime })f_{1}(m^{2}),\nonumber \\ B&=-\lambda f_{P}(M+M^{\prime })g_{1}(m^{2}),\nonumber \\ A_{1}&=-\lambda f_{V}m\left[ g_{1}(m^{2})+g_{2}(m^{2})\frac{M-M^{\prime }}{M}\right] ,\nonumber \\ A_{2}&=-2\lambda f_{V}mg_{2}(m^{2}),\nonumber \\ B_{1}&=\lambda f_{V}m\left[ f_{1}(m^{2})-f_{2}(m^{2})\frac{M+M^{\prime }}{M}\right] ,\nonumber \\ B_{2}&=2\lambda f_{V}mf_{2}(m^{2}), \end{aligned}$$

(57)

where $\lambda =\frac{G_{F}}{\sqrt{2}}V_{CKM}V_{q_{1}q_{2}}^{*}a_{1}$ with $a_{1}=C_{1}(\mu _{c})+C_{2}(\mu _{c})/3=1.07$ [84], $M(M')$ is the mass of the initial (final) baryon and m is the mass of the emitted meson. For the decay modes with an axial vector meson emitted, $A_{1,2}$ and $B_{1,2}$ in Eq. (57) are modified with the replacement of $f_{V}$ by $-f_{A}$. $f_{P,V,A}$ are the decay constants of pseudoscalar, vector and axial vector mesons, respectively, defined as

$$\begin{aligned} \langle P(P)|A_{\mu }|0\rangle&=-if_{P}P_{\mu },\nonumber \\ \langle V(P,\epsilon )|V_{\mu }|0\rangle&=f_{V}M_{V}\epsilon _{\mu }^{*}, \\ \langle A(P,\epsilon )|A_{\mu }|0\rangle&=f_{A}M_{A}\epsilon _{\mu }^{*}.\nonumber \end{aligned}$$

(58)

The decay width for $B\rightarrow B^{\prime }P$ is given as

$$\begin{aligned} \Gamma =\frac{p}{8\pi }\left( \frac{(M+M^{\prime })^{2}-m^{2}}{M^{2}}|A|^{2}+\frac{(M-M^{\prime })^{2}-m^{2}}{M^{2}}|B|^{2}\right) , \end{aligned}$$

(59)

where p is the magnitude of the three-momentum of the final-state particles in the rest frame of initial state. For $B\rightarrow B^{\prime }V(A)$ decay, the decay width is

$$\begin{aligned} \Gamma =\frac{p(E^{\prime }+M^{\prime })}{4\pi M}\left( 2(|S|^{2}+|P_{2}|^{2})+\frac{E^{2}}{m^{2}}(|S+D|^{2}+|P_{1}|^{2})\right) , \end{aligned}$$

(60)

where $E(E')$ is the energy of final-state meson (baryon), and

$$\begin{aligned} S&=-A_{1},\\ P_{1}&=-\frac{p}{E}\left( \frac{M+M^{\prime }}{E^{\prime }+M^{\prime }}B_{1}+B_{2}\right) ,\\ P_{2}&=\frac{p}{E^{\prime }+M^{\prime }}B_{1},\\ D&=-\frac{p^{2}}{E(E^{\prime }+M^{\prime })}(A_{1}-A_{2}). \end{aligned}$$

The values of the CKM matrix elements and the masses of the relevant mesons and baryons are taken from [2]. The decay constants are [26, 39, 69]

$$\begin{aligned}&f_{\pi } =130.4\;\mathrm{MeV},f_{\rho }=216\;\mathrm{MeV},f_{a_{1}}=238\;\mathrm{MeV},\nonumber \\&f_{K}=160\;\mathrm{MeV},f_{K^{*}}=210\;\mathrm{MeV},\nonumber \\&f_{D} =207.4\;\mathrm{MeV},f_{D^{*}}=220\;\mathrm{MeV},f_{D_{s}}=247.2\;\mathrm{MeV},\nonumber \\&f_{D_{s}^{*}}=247.2\;\mathrm{MeV}. \end{aligned}$$

(61)

Table 26 Partial decay widths and branching ratios for nonleptonic charm decays of the bottom–charm baryons with axial vector bc diquark

Table 27 Partial decay widths and branching ratios for nonleptonic charm decays of the bottom–charm baryons with scalar bc diquark

Table 28 Partial decay widths and branching ratios for nonleptonic decays: the bc sector with the b quark decay and an axial vector bc diquark in the initial state

Table 29 Partial decay widths and branching ratios for nonleptonic decays: the bc sector with the b quark decay and a scalar bc diquark in the initial state. We have assumed $m_{B_{i}^{\prime }}=m_{B_{i}}$ and $\tau _{B_{i}^{\prime }}=\tau _{B_{i}}$, i.e. the only difference between $B_{i}^{\prime }\rightarrow B_{f}$ and $B_{i}\rightarrow B_{f}$ is the mixing coefficients

The partial decay widths and branching ratios for the two-body nonleptonic modes of the doubly heavy flavor baryon decays are given in Tables 23, 24, 25, 26, 27, 28 and 29.

There are some remarks in the nonleptonic modes:

• As discussed before, the lifetimes of the doubly heavy flavor baryons are of great ambiguity in the theoretical predictions, especially for the baryons with charmed quark, since the significant non-perturbative contributions at the charm scale. Thus we show the decay widths for each decay mode, which is independent on the lifetime of the doubly heavy baryons. The branching fractions are obtained by the decay widths and the lifetimes shown in Table 2.

• In the charm decays of the doubly charmed baryons and bottom–charm baryons, the branching fractions of the Cabibbo-favored, singly Cabibbo-suppressed and doubly Cabibbo-suppressed processes are of the order of $10^{-2}$, $10^{-3}$ and $10^{-4}$, respectively, as expected as the cases in charmed meson and singly charmed baryon decays.

• In the bottom decays of the doubly bottom baryons and bottom–charm baryons, the branching fractions of $b\rightarrow c$ decays are of the order of $10^{-3}\sim 10^{-4}$, while those of $b\rightarrow u$ decays are suppressed by the CKM matrix element $|V_{ub}|$.

• For the bottom–charm baryons with the scalar or axial vector bc diquarks, only the lowest-lying states can decay weakly. As it is not clear which state is the lowest-lying one, we assume that the masses and lifetimes of the two sets of states are the same, $m_{B_{i}^{\prime }}=m_{B_{i}}$ and $\tau _{B_{i}^{\prime }}=\tau _{B_{i}}$. The only difference between $B_{i}^{\prime }\rightarrow B_{f}$ and $B_{i}\rightarrow B_{f}$ is the mixing coefficients in Tables 5 and 6. Our results would be useful for the studies in the future if the lowest-lying states are determined.

• The contributions from the form factors of $f_{3}(q^{2})$ and $g_{3}(q^{2})$ are neglected in the nonleptonic decays. For the modes with a pseudoscalar meson in the final state, the terms with $f_{3}$ or $g_{3}$ are proportional to $m_{P}^{2}/M^{2}$ in the heavy quark limit, with M as the mass of the initial-state baryon. No matter for the light pseudoscalar mesons $\pi$ or K in charm or bottom decays, or for the charmed mesons D or $D_{s}$ in bottom decays, these contributions are small and negligible. As to the processes with a vector or an axial vector meson in the final state, there is no contribution from $f_{3}$ or $g_{3}$ which is proportional to $q\cdot \epsilon ^{*}=0$.

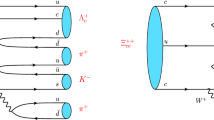
• Very recently, LHCb has observed $\Xi _{cc}^{++}$ in the final state of $\Lambda _{c}^{+}K^{-}\pi ^{+}\pi ^{+}$ with the significance of more than 12$\sigma$ [9]. The multi-body charmed hadron decays are usually dominated by the resonant contributions, since there are many resonances below the charm scale. The external W-emission contributions for this four-body process are $\Xi _{cc}^{++}$ decaying into (csu) states and a charged pion, followed by (csu) fragmented into $\Lambda _{c}^{+}K^{-}\pi ^{+}$. However, such contributions cannot be large. Only very high excited states of $\Xi _{c}$ can decay into $\Lambda _{c}^{+}K^{-}\pi ^{+}$. But the high excited states are more difficult to produce. The internal W-emission amplitudes can contribute to the four-body decay of $\Xi _{cc}^{++} \rightarrow \Lambda _{c}^{+}K^{-}\pi ^{+}\pi ^{+}$ [21], as seen in Fig. 4.

  There are many low-lying resonant contributions, for example $\Sigma _{c}^{++}(2455)$ and $\Sigma _{c}^{++}(2520)$ for $\Lambda _{c}^{+}\pi ^{+}$, $\overline{K}^{*0}$ and $(K\pi )_\mathrm{S-wave}$ for $K^{-}\pi ^{+}$. We can naively estimate such contributions. For the internal W-emission amplitudes, unlike the case in B meson decays where the non-factorizable contributions are color-suppressed and neglected, the non-factorizable contributions in charm decays are significantly enhanced due to the final-state interacting effects. Empirically, the effective Wilson coefficient in Eq. (57) is $|a_{2}^\mathrm{eff}(\mu _{c})|\sim 0.7$ as in D meson decays and in $\Lambda _{c}^{+}$ decays. With this value of $|a_{2}^\mathrm{eff}|$, we can obtain the branching fraction of $\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{++}(2455)\overline{K}^{*0}=4.1\%$, which is large enough for the experimental measurements. Considering the other resonant contributions, such as $\Sigma _{c}^{++}(2520)\overline{K}^{*0}$, $\Sigma _{c}^{++}(2455)(K\pi )_\mathrm{S-wave}$ and $\Sigma _{c}^{++}(2520)(K\pi )_\mathrm{S-wave}$, the branching fraction of $\Xi _{cc}^{++}\rightarrow \Lambda _{c}^{+}K^{-}\pi ^{+}\pi ^{+}$ could reach the order of $10\%$. Therefore, the internal W-emission contributions are essential to understand the discovery $\Xi _{cc}^{++}$ in the $\Xi _{cc}^{++}\rightarrow \Lambda _{c}^{+}K^{-}\pi ^{+}\pi ^{+}$ decay mode by LHCb.

6 Conclusions

In the past decades, heavy quark decays have played a very important role in extracting the CKM parameters in the standard model, understanding the mechanism for the CP violation, and in shaping our understanding of dynamics in strong interactions and factorization theorem. This, however, has only made use of weak decays of the ground state of the heavy mesons/baryons with a single heavy quark. Weak decays of the doubly heavy baryons are expected to provide equally important information.

Very recently, the LHCb collaboration has observed in the final state $\Lambda _c K^-\pi ^+\pi ^+$ a resonant structure that is identified as the doubly charmed baryon $\Xi _{cc}^{++}$. Such an important observation will undoubtedly promote the research on the hadron spectroscopy and also on the weak decays of the doubly heavy baryons. Inspired by this observation, we have investigated the decay processes of doubly heavy baryons $\Xi _{cc}^{++}$, $\Xi _{cc}^{+}$, $\Omega _{cc}^{+}$, $\Xi _{bc}^{(\prime )+}$, $\Xi _{bc}^{(\prime )0}$, $\Omega _{bc}^{(\prime )0}$, $\Xi _{bb}^{0}$, $\Xi _{bb}^{-}$ and $\Omega _{bb}^{-}$ and focused on the $1/2\rightarrow 1/2$ transition in this paper.

We have adopted a quark–diquark picture in the calculation of the transition form factors. At the quark level these transitions are induced by the weak decays of $c\rightarrow d/s$ or $b\rightarrow u/c$. We have derived the form factors of these transitions in the light-front approach and calculated the form factors for both scalar and axial vector diquarks. The obtained form factors are then applied to predict the partial widths for the semileptonic and nonleptonic decay of doubly heavy baryons. We find that a number of decay channels are sizable and can be examined in future measurements at experimental facilities like LHC, Belle II and CEPC. These results are also useful for a cross-check of $\Xi _{cc}^{++}$ and the search for other baryons.

This work can be regarded as a first step towards a comprehensive understanding of weak decays of doubly heavy baryons. The potential generalizations and improvements are given as follows.

• The $1/2\rightarrow 3/2$ transition:

  This work has focused on the $1/2\rightarrow 1/2$ transition, either the diquark spectator is a scalar or an axial vector system. When the diquark spectator is an axial vector, the final baryon may have spin 3 / 2. Such transitions will be calculated in the future.

• penguin dominated processes:

  The analysis of nonleptonic decay modes in this work are mainly dominated by tree-operators. Decay modes induced by penguin operators may have sizable branching fractions as shown in the heavy meson decays.

• Non-factorizable contributions:

  To give more precise predictions on branching ratios and more importantly the CP asymmetries, one has to reliably estimate the non-factorizable contributions.

• A comprehensive analysis from QCD:

  As we have discussed at the beginning of Sect. 3, it is a very crude approximation to adopt one heavy and one light quarks as a system to study the heavy to light transition, though this approximation greatly simplifies the calculation. Since the initial and final states contain heavy quark, soft and collinear degrees of freedom, a power counting analysis might be possible in the framework of soft-collinear effective theory.

Fig. 4

Dominant diagram of $\Xi _{cc}^{++}\rightarrow \Lambda _{c}^{+}K^{-}\pi ^{+}\pi ^{+}$