1 Introduction

Quite recently, the LHCb collaboration reported the discovery of a doubly charmed baryon \(\Xi _{cc}^{++}\) with the mass given as [1]

$$\begin{aligned} m_{\Xi _{cc}^{++}}=(3621.40\pm 0.72\pm 0.27\pm 0.14)\mathrm{MeV}. \end{aligned}$$
(1)

This discovery has already triggered great theoretical interest in the study of doubly heavy baryons from various aspects [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. Also after observing the first decay mode, \(\Xi _{cc}^{++}\rightarrow \Lambda _{c}^{+}K^{-}\pi ^{+}\pi ^{+}\), the LHCb collaboration is continuing the experimental analyses of doubly heavy baryon decays. This includes, but is not limited to, searches for the \(\Xi _{cc}^{+}\) and charmed-beauty \(\Xi _{bc}\) baryons [22]. Comprehensive theoretical studies on weak decays must be performed and the golden modes for discoveries must be derived in order to optimize the experimental resources. In our previous work [4], we have presented the calculation of 1/2 to 1/2 weak decays. It is generally anticipated that the 1/2 to 3/2 processes will also be important. For instance, it is very likely that the \(\Xi _{cc}^{++}\rightarrow \Lambda _{c}^{+}K^{-}\pi ^{+}\pi ^{+}\) comes from more than one intermediate \(1/2\rightarrow 3/2\) transition.

A doubly heavy baryon is composed of two heavy quarks and one light quark. Light flavor SU(3) symmetry arranges the doubly heavy baryons into the \(\varvec{3}\) representation. For spin-1/2 doubly heavy baryons, we have \(\Xi _{cc}^{++,+}\) and \(\Omega _{cc}^{+}\) in the cc sector, \(\Xi _{bb}^{0,-}\) and \(\Omega _{bb}^{-}\) in the bb sector. There are two sets of baryons for the bc sector depending on the symmetry property under interchange of b and c quarks. If it is symmetric under interchange of b and c quarks, this set is denoted by \(\Xi _{bc}^{+,0}\)and \(\Omega _{bc}^{0}\), while, for the antisymmetric case, the corresponding set is denoted by \(\Xi _{bc}^{\prime +,\prime 0}\) and \(\Omega _{bc}^{\prime 0}\).Footnote 1 In reality these two sets probably mix with each other, which is not taken into account in this work. Spin-3/2 doubly heavy baryons have the same flavor wave functions with but different spin structures from the spin-1/2 counterparts. The quantum numbers of low-lying doubly heavy baryons can be found in Table 1.

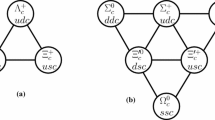
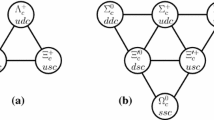
Table 1 Quantum numbers and quark content for the ground state of doubly heavy baryons. The \(S_{h}^{\pi }\) denotes the spin of the heavy quark system. The light quark q corresponds to u, d quark
Full size table

The decay final state of the \(\Xi _{cc}\) and \(\Omega _{cc}\) contains baryons with one charm quark and two light quarks. Light flavor SU(3) symmetry arranges them into the representations \(\varvec{3}\otimes \varvec{3}=\varvec{6}\oplus \bar{\varvec{3}}\), as can be seen from Fig. 1. The irreducible representation \(\bar{\varvec{3}}\) is composed of \(\Lambda _{c}^{+}\) and \(\Xi _{c}^{+,0}\), while the sextet is composed of \(\Sigma _{c}^{++,+,0}\), \(\Xi _{c}^{\prime +,\prime 0}\) and \(\Omega _{c}^{0}\). They all have spin 1/2, while, for the spin-3/2 sextet, we will denote them by \(\Sigma _{c}^{*++,*+,*0}\), \(\Xi _{c}^{\prime *+,\prime *0}\) and \(\Omega _{c}^{*0}\). The singly bottom baryons can be analyzed in a similar way.

Fig. 1
figure 1

Anti-triplets (a) and sextets (b) of charmed baryons with one charm quark and two light quarks. These are spin-1 / 2 baryons, while spin-3 / 2 baryons constitute another sextet

Full size image

To be explicit, we will investigate the following decay modes of doubly heavy baryons.

  • cc sector

    $$\begin{aligned} \Xi _{cc}^{++}(ccu)&\rightarrow \Sigma _{c}^{*+}(dcu)/\Xi _{c}^{\prime *+}(scu),\\ \Xi _{cc}^{+}(ccd)&\rightarrow \Sigma _{c}^{*0}(dcd)/\Xi _{c}^{\prime *0}(scd),\\ \Omega _{cc}^{+}(ccs)&\rightarrow \Xi _{c}^{\prime *0}(dcs)/\Omega _{c}^{*0}(scs), \end{aligned}$$

  • bb sector

    $$\begin{aligned} \Xi _{bb}^{0}(bbu)&\rightarrow \Sigma _{b}^{*+}(ubu)/\Xi _{bc}^{*+}(cbu),\\ \Xi _{bb}^{-}(bbd)&\rightarrow \Sigma _{b}^{*0}(ubd)/\Xi _{bc}^{*0}(cbd),\\ \Omega _{bb}^{-}(bbs)&\rightarrow \Xi _{b}^{\prime *0}(ubs)/\Omega _{bc}^{*0}(cbs), \end{aligned}$$

  • bc sector with c quark decay

    $$\begin{aligned} \Xi _{bc}^{+}(cbu)/\Xi _{bc}^{\prime +}(cbu)&\rightarrow \Sigma _{b}^{*0}(dbu)/\Xi _{b}^{\prime *0}(sbu),\\ \Xi _{bc}^{0}(cbd)/\Xi _{bc}^{\prime 0}(cbd)&\rightarrow \Sigma _{b}^{*-}(dbd)/\Xi _{b}^{\prime *-}(sbd),\\ \Omega _{bc}^{0}(cbs)/\Omega _{bc}^{\prime 0}(cbs)&\rightarrow \Xi _{b}^{\prime *-}(dbs)/\Omega _{b}^{*-}(sbs), \end{aligned}$$

  • bc sector with b quark decay

    $$\begin{aligned} \Xi _{bc}^{+}(bcu)/\Xi _{bc}^{\prime +}(bcu)&\rightarrow \Sigma _{c}^{*++}(ucu)/\Xi _{cc}^{*++}(ccu),\\ \Xi _{bc}^{0}(bcd)/\Xi _{bc}^{\prime 0}(bcd)&\rightarrow \Sigma _{c}^{*+}(ucd)/\Xi _{cc}^{*+}(ccd),\\ \Omega _{bc}^{0}(bcs)/\Omega _{bc}^{\prime 0}(bcs)&\rightarrow \Xi _{c}^{\prime *+}(ucs)/\Omega _{cc}^{*+}(ccs). \end{aligned}$$

In the above, the quark components have been explicitly shown in brackets, in which the quarks that participate in weak decay are placed first.

Fig. 2
figure 2

Feynman diagrams for baryon–baryon transitions in the diquark picture. \(P^{(\prime )}\) is the momentum of the incoming (outgoing) baryon, \(p_{1}^{(\prime )}\) is the initial (final) quark momentum, \(p_{2}\) is the diquark momentum and the cross mark denotes the weak interaction

Full size image

To deal with the dynamics in the decay, we will adopt the light-front approach, which has been widely used to study the properties of mesons [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]. Its application to the baryon sector can be found in Refs. [42,43,44,45,46], in which the two spectator quarks are viewed as a diquark. In this scheme, the role of the diquark system is similar to that of the antiquark in the meson case, as can be seen from Fig. 2. Following the same method, in this work we will study the \(1/2\rightarrow 3/2\) transition [46], where the spectator is a \(1^+\) diquark system.

The authors of Ref. [7] have investigated the doubly heavy baryon decays with the help of flavor SU(3) symmetry. Based on the available data, a great number of decay modes ranging from semileptonic decays to multi-body nonleptonic decays can be predicted. However, in the c quark decay, SU(3) symmetry breaking effects may be sizable and cannot be omitted. A quantitative study of SU(3) symmetry breaking effects will be conducted within the light-front approach.

The rest of the paper is arranged as follows. In Sect. 2, we will present briefly the framework of the light-front approach under the diquark picture, and flavor–spin wave functions will also be discussed. Numerical results are shown in Sect. 3, including the results for the form factors, predictions of semileptonic and nonleptonic decay widths, a detailed discussion of SU(3) symmetry, the error estimates and a comparison with the previous 1/2 to 1/2 results. A brief summary is given in the last section.

2 Theoretical framework

The theoretical framework for the \(1/2 \rightarrow 3/2\) transition will be briefly introduced in the first subsection, including the definitions of the states for spin-1/2 and spin-3/2 baryons, and the extraction of the form factors. More details can be found in [42, 46]. Flavor–spin wave functions will be given in the second subsection.

2.1 Light-front approach

In the framework of the light-front approach, the wave function of a \(1/2^{+}\) baryon with an axial-vector diquark is expressed as

$$\begin{aligned}&|\mathcal{B}(P,S=\frac{1}{2},S_{z})\rangle \nonumber \\&= \int \{d^{3}p_{1}\}\{d^{3}p_{2}\}2(2\pi )^{3}\delta ^{3}(\tilde{P}-\tilde{p}_{1}-\tilde{p}_{2})\nonumber \\&\quad \times \sum _{\lambda _{1}\lambda _{2}}\Psi ^{SS_{z}}(\tilde{p}_{1},\tilde{p}_{2},\lambda _{1},\lambda _{2})|Q(p_{1},\lambda _{1})\{di\}(p_{2},\lambda _{2})\rangle . \end{aligned}$$
(2)

Here

$$\begin{aligned}&\Psi ^{SS_{z}}(\tilde{p}_{1},\tilde{p}_{2},\lambda _{1},\lambda _{2})\nonumber \\&\quad = \frac{A}{\sqrt{2(p_{1}\cdot \bar{P}+m_{1}M_{0})}}\bar{u}(p_{1},\lambda _{1})\Gamma u(\bar{P},S_{z})\phi (x,k_{\perp }) \end{aligned}$$
(3)

with

(4)
$$\begin{aligned} \phi =4\left( \frac{\pi }{\beta ^{2}}\right) ^{3/4}\sqrt{\frac{e_{1}e_{2}}{x_{1}x_{2}M_{0}}}\exp \left( \frac{-\mathbf {k}^{2}}{2\beta ^{2}}\right) , \end{aligned}$$
(5)

and

$$\begin{aligned} A=\sqrt{\frac{3(m_{1}M_{0}+p_{1}\cdot \bar{P})}{3m_{1}M_{0}+p_{1}\cdot \bar{P}+2(p_{1}\cdot p_{2})(p_{2}\cdot \bar{P})/m_{2}^{2}}.} \end{aligned}$$
(6)

In analogy to the \(1/2^{+}\) baryon case, the \(3/2^{+}\) baryon state obeys an expression similar to Eq. (2), but with Eq. (3) replaced by

$$\begin{aligned}&\Psi ^{SS_{z}}(\tilde{p}_{1},\tilde{p}_{2},\lambda _{1},\lambda _{2})\nonumber \\&\quad =\frac{A^{\prime }}{\sqrt{2(p_{1}\cdot \bar{P}+m_{1}M_{0})}}\bar{u}(p_{1},\lambda _{1})\epsilon ^{\alpha *}(p_{2},\lambda _{2})u_{\alpha }(\bar{P},S_{z})\phi (x,k_{\perp }),\nonumber \\ \end{aligned}$$
(7)

where

$$\begin{aligned} A^{\prime }=\sqrt{\frac{3m_{2}^{2}M_{0}^{2}}{2m_{2}^{2}M_{0}^{2}+(p_{2}\cdot \bar{P})^{2}}}. \end{aligned}$$
(8)

With the help of Eqs. (2), (3) and (7), the transition matrix element can be derived to be

(9)

where

$$\begin{aligned} m_{1}=m_{Q},\quad m_{1}^{\prime }=m_{q},\quad m_{2}=m_{\{di\}}, \end{aligned}$$

and \(\varphi ^{(\prime )}=A^{(\prime )}\phi ^{(\prime )}\), Q (q) represents the quark b / c (u / d / s / c) in the initial (final) state, \(p_{1}\) (\(p_{1}^{\prime }\)) denotes its four-momentum, P (\(P^{\prime }\)) stands for the four-momentum of \(\mathcal{B}_{i}\) (\(\mathcal{B}_{f}\)). The form factors for the \(1/2\rightarrow 3/2\) transition are parameterized as

$$\begin{aligned}&\langle \mathcal{B}_{f}(P^{\prime },S^{\prime }=\frac{3}{2},S_{z}^{\prime })|\bar{q}\gamma ^{\mu }Q|\mathcal{B}_{i}(P,S=\frac{1}{2},S_{z})\rangle \nonumber \\&\quad = \bar{u}_{\alpha }(P^{\prime },S_{z}^{\prime })\Bigg [\gamma ^{\mu }P^{\alpha }\frac{f_{1}(q^{2})}{M}+\frac{f_{2}(q^{2})}{M^{2}}P^{\alpha }P^{\mu } \nonumber \\&\qquad +\frac{f_{3}(q^{2})}{MM^{\prime }}P^{\alpha }P^{\prime \mu }+f_{4}(q^{2})g^{\alpha \mu }\Bigg ]\gamma _{5}u(P,S_{z}), \end{aligned}$$
(10)
$$\begin{aligned}&\langle \mathcal{B}_{f}(P^{\prime },S^{\prime }=\frac{3}{2},S_{z}^{\prime })|\bar{q}\gamma ^{\mu }\gamma _{5}Q|\mathcal{B}_{i}(P,S=\frac{1}{2},S_{z})\rangle \nonumber \\&\quad = \bar{u}_{\alpha }(P^{\prime },S_{z}^{\prime })\Bigg [\gamma ^{\mu }P^{\alpha }\frac{g_{1}(q^{2})}{M}+\frac{g_{2}(q^{2})}{M^{2}}P^{\alpha }P^{\mu } \nonumber \\&\qquad +\frac{g_{3}(q^{2})}{MM^{\prime }}P^{\alpha }P^{\prime \mu }+g_{4}(q^{2})g^{\alpha \mu }\Bigg ]u(P,S_{z}). \end{aligned}$$
(11)

Here \(q=P-P^{\prime }\), and \(f_{i}\), \(g_{i}\) are the form factors.

These form factors \(f_{i}\) and \(g_{i}\) can be extracted in the following way [46]. Multiplying Eq. (9) by \(\bar{u}(P,S_{z})(\Gamma _{5}^{\mu \beta })_{i}u_{\beta }(P^{\prime },S_{z}^{\prime })\) with \((\Gamma _{5}^{\mu \beta })_{i}=\{\gamma ^{\mu }P^{\beta },P^{\prime \mu }P^{\beta },P^{\mu }P^{\beta },g^{\mu \beta }\}\gamma _{5}\), respectively, and taking the approximation \(P^{(\prime )}\rightarrow \bar{P}^{(\prime )}\) within the integral, and then summing over the polarizations in the initial and final states, one arrives at

(12)

with \((\bar{\Gamma }_{5}^{\mu \beta })_{i}=\{\gamma ^{\mu }\bar{P}^{\beta },\bar{P}^{\prime \mu }\bar{P}^{\beta },\bar{P}^{\mu }\bar{P}^{\beta },g^{\mu \beta }\}\gamma _{5}\).

Multiplying the difference of Eqs. (10) and (11) by the same factor \(\bar{u}(P,S_{z})(\Gamma _{5}^{\mu \beta })_{i}u_{\beta }(P^{\prime },S_{z}^{\prime })\), and also summing over the polarizations in the initial and final states, one arrives at

$$\begin{aligned} F_{i}= & {} \mathrm{Tr}\Bigg \{ u_{\beta }(P^{\prime },S_{z}^{\prime })\bar{u}_{\alpha }(P^{\prime },S_{z}^{\prime })\left[ \gamma ^{\mu }P^{\alpha }\frac{f_{1}(q^{2})}{M}\right. \nonumber \\&\left. +\frac{f_{2}(q^{2})}{M^{2}}P^{\alpha }P^{\mu }+\frac{f_{3}(q^{2})}{MM^{\prime }}P^{\alpha }P^{\prime \mu }+f_{4}(q^{2})g^{\alpha \mu }\right] \gamma _{5}\nonumber \\&\times u(P,S_{z})\bar{u}(P,S_{z})(\Gamma _{5}^{\mu \beta })_{i}\Bigg \}. \end{aligned}$$
(13)

The form factors \(f_{i}\) can then be extracted by equating Eqs. (12) and (13). With the same method, one can obtain the form factors \(g_{i}\).

2.2 Flavor–spin wave functions

In Sect. 2.1, the flavor–spin wave function was not taken into account. We consider first the initial state. For the doubly charmed baryons, the wave functions are given as

$$\begin{aligned} \mathcal {B}_{cc}=\frac{1}{\sqrt{2}}\left[ \left( -\frac{\sqrt{3}}{2}c^{1}(c^{2}q)_{S}+\frac{1}{2}c^{1}(c^{2}q)_{A}\right) +(c^{1}\leftrightarrow c^{2})\right] , \end{aligned}$$
(14)

with \(q=u\), d or s for \(\Xi _{cc}^{++}\), \(\Xi _{cc}^{+}\) or \(\Omega _{cc}^{+}\), respectively. It is similar for the doubly bottom baryons. For the bottom–charm baryons, there are two sets of states, with bc as a scalar or an axial-vector diquark. The wave functions of the bottom–charm baryons with an axial-vector bc diquark are

$$\begin{aligned} \mathcal {B}_{bc}&=-\frac{\sqrt{3}}{2}b(cq)_{S}+\frac{1}{2}b(cq)_{A}\nonumber \\&=-\frac{\sqrt{3}}{2}c(bq)_{S}+\frac{1}{2}c(bq)_{A}, \end{aligned}$$
(15)

while those with a scalar bc diquark are given as

$$\begin{aligned} \mathcal {B}_{bc}^{\prime }&=-\frac{1}{2}b(cq)_{S}-\frac{\sqrt{3}}{2}b(cq)_{A}=\frac{1}{2}c(bq)_{S}+\frac{\sqrt{3}}{2}c(bq)_{A}, \end{aligned}$$
(16)

with \(q=u\), d or s for \(\Xi _{bc}^{(\prime )+}\), \(\Xi _{bc}^{(\prime )0}\) or \(\Omega _{bc}^{(\prime )0}\), respectively. Note that the conventions for \(\mathcal{B}_{bc}^{(\prime )}\) in [23] are opposite to ours.

Table 2 Flavor–spin overlap factors. For the bc sector, \(\mathcal{B}_{bc}^{(\prime )}\) is defined with bc as a scalar or an axial-vector diquark
Full size table
Table 3 Flavor–spin overlap factors for the bc sector. \(\mathcal{B}_{bc}^{(1,2)}\) is defined with cq (\(q=u,d,s\)) as a scalar or an axial-vector diquark
Full size table

For the final state, the spin-3/2 baryon with quark content \(Qqq^{\prime }\) obeys

$$\begin{aligned} \mathcal{B}_{Qqq^{\prime }}^{*}=q(Qq^{\prime })_{A}=q^{\prime }(Qq)_{A}, \end{aligned}$$
(17)

while, for the Qqq baryon, an additional factor \(\sqrt{2}\) should be added. For the spin-3/2 baryon with quark content \(QQ^{\prime }q\), we have

$$\begin{aligned} \mathcal{B}_{QQ^{\prime }q}^{*}=Q(Q^{\prime }q)_{A}=Q^{\prime }(Qq)_{A}, \end{aligned}$$
(18)

while for the QQq baryon an additional factor \(\sqrt{2}\) should be added. Here the asterisk denotes that the baryon is spin-3/2 and \(q^{(\prime )}=u,d,s\).

Finally, the overlap factors are determined by taking the inner product of the flavor–spin wave functions in the initial and final states. The corresponding results are collected in Table 2.

Some comments on the bc sector are given now. It should be pointed out that the approximate mass eigenstates are those with distinct spin of the two lightest quarks, namely cq (\(q=u,d,s\)), because the hyperfine splittings between these are larger than the bc hyperfine splittings. The approximate mass eigenstates for the bc sector can be defined as \(\mathcal{B}_{bc}^{(1)}\equiv b(cq)_{S}\) and \(\mathcal{B}_{bc}^{(2)}\equiv b(cq)_{A}\); then it can be derived from Eqs. (15) and (16) that

$$\begin{aligned} \left( \begin{array}{c} \mathcal{B}_{bc}^{(1)}\\ \mathcal{B}_{bc}^{(2)} \end{array}\right) =\left( \begin{array}{cc} -\frac{\sqrt{3}}{2} &{} -\frac{1}{2}\\ \frac{1}{2} &{} -\frac{\sqrt{3}}{2} \end{array}\right) \left( \begin{array}{c} \mathcal{B}_{bc}\\ \mathcal{B}_{bc}^{\prime } \end{array}\right) . \end{aligned}$$
(19)

The mixing angle between these two bases can be read as \(5\pi /6\). The new overlap factors in the bc sector can now be readily derived via the mixing matrix given in Eq. (19) and the old overlap factors given in Table 2 as

$$\begin{aligned} \left( \begin{array}{c} \mathcal{B}_{bc}^{(1)}\rightarrow \mathcal{B}_{Q}^{*}\\ \mathcal{B}_{bc}^{(2)}\rightarrow \mathcal{B}_{Q}^{*} \end{array}\right) =\left( \begin{array}{cc} -\frac{\sqrt{3}}{2} &{} -\frac{1}{2}\\ \frac{1}{2} &{} -\frac{\sqrt{3}}{2} \end{array}\right) \left( \begin{array}{c} \mathcal{B}_{bc}\rightarrow \mathcal{B}_{Q}^{*}\\ \mathcal{B}_{bc}^{\prime }\rightarrow \mathcal{B}_{Q}^{*} \end{array}\right) , \end{aligned}$$
(20)

where \(\mathcal{B}_{Q}^{*}\) denotes a spin-3/2 singly heavy baryon in the final state. These new overlap factors can be found in Table 3.

3 Numerical results and discussions

All the inputs will be given in the first subsection. Numerical results for the form factors, semileptonic and nonleptonic decays will be shown subsequently. They are presented in this order: cc sector, bb sector, bc sector with the c quark decay, bc sector with the b quark decay, \(bc^{\prime }\) sector with the c quark decay, \(bc^{\prime }\) sector with the b quark decay. Some discussions will also be given.

Table 4 Masses (in units of GeV) and lifetimes (in units of fs) of doubly heavy baryons
Full size table
Table 5 The masses of baryons in the final states [23, 51]
Full size table

The variable \(\omega \) will be introduced

$$\begin{aligned} \omega \equiv v\cdot v^{\prime }=\frac{P\cdot P^{\prime }}{MM^{\prime }}, \end{aligned}$$
(21)

which can be easily changed to the squared momentum transfer \(q^{2}\), and vice versa.

The vectorial spinor for spin-3 / 2 baryon is given as

(22)

with \(v^{\alpha }=p^{\alpha }/m\), while its helicity eigenstate can be found in Eq. (20) of Ref. [47],

$$\begin{aligned} u^{\alpha }(p,\lambda )=\sum _{\lambda _{1},\lambda _{2}}\left\langle \frac{1}{2},\lambda _{1},1,\lambda _{2}|\frac{3}{2},\lambda \right\rangle \times u(p,\lambda _{1})\epsilon ^{\alpha }(p,\lambda _{2}). \end{aligned}$$
(23)

3.1 Inputs

The constituent quark masses are given as (in units of GeV) [33,34,35,36,37,38,39,40,41]

$$\begin{aligned} m_{u}=m_{d}=0.25,\quad m_{s}=0.37,\quad m_{c}=1.4,\quad m_{b}=4.8. \end{aligned}$$
(24)

The masses of the axial-vector diquarks are approximated by

$$\begin{aligned} m_{\{Qq\}}=m_{Q}+m_{q}. \end{aligned}$$
(25)

The shape parameters \(\beta \) in Eq. (5) are given as (in units of GeV) [28]

$$\begin{aligned} \beta _{u\{cq\}}= & {} \beta _{d\{cq\}}=0.470,\quad \beta _{s\{cq\}}=0.535,\quad \nonumber \\ \beta _{c\{cq\}}= & {} 0.753,\quad \beta _{b\{cq\}}=0.886, \nonumber \\ \beta _{u\{bq\}}= & {} \beta _{d\{bq\}}=0.562,\quad \beta _{s\{bq\}}=0.623,\quad \nonumber \\ \beta _{c\{bq\}}= & {} 0.886,\quad \beta _{b\{bq\}}=1.472, \end{aligned}$$
(26)

where \(q=u,d,s\).

The masses and lifetimes of the parent baryons are collected in Table 4 [1, 3, 23, 48,49,50]. Note that in Table 4 the masses and lifetimes of \(\mathcal{B}_{bc}\) and \(\mathcal{B}_{bc}^{\prime }\) are taken to be equal. Also note that we have taken a new value for the lifetime of \(\Omega _{cc}^{+}\), to be compared with our previous work [4], because according to Ref. [48], lifetimes of doubly charmed baryons should satisfy the following pattern:

$$\begin{aligned} \tau (\Xi _{cc}^{+})\sim \tau (\Omega _{cc}^{+})\ll \tau (\Xi _{cc}^{++}). \end{aligned}$$
(27)

The masses of the final state baryons are given in Table 5 [23, 51]. The Fermi constant and CKM matrix elements are given as [51]

$$\begin{aligned}&G_{F}=1.166\times 10^{-5}\ \mathrm{GeV}^{-2},\nonumber \\&|V_{ud}|=0.974,\quad |V_{us}|=0.225,\quad |V_{ub}|=0.00357,\nonumber \\&|V_{cd}|=0.225,\quad |V_{cs}|=0.974,\quad |V_{cb}|=0.0411. \end{aligned}$$
(28)

In the calculation of nonleptonic decays, the following mesons will be present in the final states: \(\pi ,\rho ,a_{1},K,K^{*},D,D^{*},D_{s},D_{s}^{*}\). Their masses can be found in Ref. [51], while their decay constants are given as follows [28, 41, 52]:

$$\begin{aligned} f_{\pi } =&130.4\ \mathrm{MeV},\quad f_{\rho }=216\ \mathrm{MeV},\quad f_{a_{1}}=238\ \mathrm{MeV},\quad \nonumber \\ f_{K}=&160\ \mathrm{MeV},\quad f_{K^{*}}=210\ \mathrm{MeV},\nonumber \\ f_{D} =&207.4\ \mathrm{MeV},\quad f_{D^{*}}=220\ \mathrm{MeV},\quad \nonumber \\ f_{D_{s}}=&247.2\ \mathrm{MeV},\quad f_{D_{s}^{*}}=247.2\ \mathrm{MeV}. \end{aligned}$$
(29)

The Wilson coefficients \(a_{1}=C_{1}(\mu _{c})+C_{2}(\mu _{c})/3=1.07\) [53] will be used.

3.2 Results for form factors

To access the \(q^2\)-distribution, the following single pole structure is assumed for the form factors:

$$\begin{aligned} F(q^{2})=\frac{F(0)}{1-\frac{q^{2}}{m_{\mathrm{pole}}^{2}}}, \end{aligned}$$
(30)

F(0) is the value of the form factors at \(q^{2}=0\), the corresponding numerical results predicted by the light-front approach are collected in Tables 6, 7, 8 and 9. For \(c\rightarrow d/s\) decays, \(m_{\mathrm{pole}}\) is respectively taken as 1.87, 1.97 GeV, while, for the \(b\rightarrow u/c\) decays, \(m_{\mathrm{pole}}\) is, respectively, taken as 5.28, 6.28 GeV. In practice, these quantities are given by the masses of D, \(D_{s}\), B and \(B_{c}\) mesons. The discussion for the validity of this assumption can be found in our previous work [41].

The physical form factors can be obtained by multiplying Eq. (30) by the corresponding overlap factor.

Table 6 Values of form factors at \(q^{2}=0\) for the cc sector. The single pole assumption in Eq. (30) will be adopted, and \(m_{\mathrm{pole}}\) is taken as \(1.87\ \mathrm{GeV}\)
Full size table
Table 7 Values of form factors at \(q^{2}=0\) for the bb sector
Full size table
Table 8 Same as Table 6 but for the \(bc^{(\prime )}\) sector with c quark decay
Full size table
Table 9 Same as Table 7 but for the \(bc^{(\prime )}\) sector with b quark decay
Full size table

3.3 Results for semileptonic decays

Helicity amplitudes are defined by \(H_{\lambda ^{\prime },\lambda _{W}}^{V}\equiv \langle \mathcal{B}_{f}^{*}(\lambda ^{\prime })|\bar{q}\gamma ^{\mu }Q|\mathcal{B}_{i}(\lambda )\rangle \epsilon _{W\mu }^{*}(\lambda _{W})\) and \(H_{\lambda ^{\prime },\lambda _{W}}^{A}\equiv \langle \mathcal{B}_{f}^{*}(\lambda ^{\prime })|\bar{q}\gamma ^{\mu }\gamma _{5}Q|\mathcal{B}_{i}(\lambda )\rangle \epsilon _{W\mu }^{*}(\lambda _{W})\), respectively, where \(\lambda =\lambda _{W}-\lambda ^{\prime }\) is understood. These helicity amplitudes are related to the form factors by the following expressions:

$$\begin{aligned} H_{3/2,1}^{V,A}= & {} \mp i\sqrt{2MM^{\prime }(\omega \mp 1)}f_{4}^{V,A}, \end{aligned}$$
(31)
$$\begin{aligned} H_{1/2,1}^{V,A}= & {} i\sqrt{\frac{2}{3}}\sqrt{MM^{\prime }(\omega \mp 1)}\left[ f_{4}^{V,A}-2(\omega \pm 1)f_{1}^{V,A}\right] , \nonumber \\\end{aligned}$$
(32)
$$\begin{aligned} H_{1/2,0}^{V,A}= & {} \pm i\frac{1}{\sqrt{q^{2}}}\frac{2}{\sqrt{3}}\sqrt{MM^{\prime }(\omega \mp 1)}\Big [(M\omega -M^{\prime })f_{4}^{V,A}\nonumber \\&\mp (M\mp M^{\prime })(\omega \pm 1)f_{1}^{V,A}\nonumber \\&+M^{\prime }(\omega ^{2}-1)f_{2}^{V,A}+M(\omega ^{2}-1)f_{3}^{V,A}\Big ], \end{aligned}$$
(33)

where the upper (lower) sign corresponds to V (A), \(f_{i}^{V}=f_{i}\) (\(f_{i}^{A}=g_{i}\)), \(\omega \) is defined in Eq. (21), and M (\(M^{\prime }\)) is the mass of the baryon in the initial (final) state. The remaining helicity amplitudes can be obtained by

$$\begin{aligned} H_{-\lambda ^{\prime },-\lambda _{W}}^{V,A}=\mp H_{\lambda ^{\prime },\lambda _{W}}^{V,A}. \end{aligned}$$
(34)

Partial differential decay widths are obtained:

$$\begin{aligned} \frac{{\text {d}}\Gamma _{T}}{{\text {d}}\omega }= & {} \frac{G_{F}^{2}}{(2\pi )^{3}}|V_{\mathrm{CKM}}|^{2}\frac{q^{2}M^{\prime 2}\sqrt{\omega ^{2}-1}}{12M}[|H_{1/2,1}|^{2}\nonumber \\&+|H_{-1/2,-1}|^{2}+|H_{3/2,1}|^{2}+|H_{-3/2,-1}|^{2}], \end{aligned}$$
(35)
$$\begin{aligned} \frac{{\text {d}}\Gamma _{L}}{{\text {d}}\omega }= & {} \frac{G_{F}^{2}}{(2\pi )^{3}}|V_{\mathrm{CKM}}|^{2}\frac{q^{2}M^{\prime 2}\sqrt{\omega ^{2}-1}}{12M}[|H_{1/2,0}|^{2}\nonumber \\&+|H_{-1/2,0}|^{2}]. \end{aligned}$$
(36)

Numerical results are collected in Tables 10, 11, 12, 13, 14 and 15. Some comments are given in Sect. 3.6.

Table 10 Semileptonic decays for the cc sector
Full size table
Table 11 Semileptonic decays for the bb sector
Full size table
Table 12 Semileptonic decays for the bc sector with c quark decay
Full size table
Table 13 Semileptonic decays for the bc sector with b quark decay
Full size table
Table 14 Semileptonic decays for the \(bc^{\prime }\) sector with c quark decay
Full size table
Table 15 Semileptonic decays for the \(bc^{\prime }\) sector with b quark decay
Full size table

3.4 Results for nonleptonic decays

For the nonleptonic processes, we are constrained: we may consider only those of a W boson emitted externally. For the process with a pseudoscalar meson in the final state, the decay width is obtained as

$$\begin{aligned} \Gamma =|\lambda |^{2}f_{P}^{2}\frac{M|\mathbf {P}^{\prime }|^{3}}{6\pi M^{\prime }}[(\omega -1)(B^{2}-2AB)+2A^{2}\omega ], \end{aligned}$$
(37)

with

$$\begin{aligned} \lambda\equiv & {} \frac{G_{F}}{\sqrt{2}}V_{cb}V_{q_{1}q_{2}}^{*}a_{1}, \end{aligned}$$
(38)
$$\begin{aligned} A= & {} (M-M^{\prime })\frac{g_{1}}{M}+\frac{g_{2}}{M^{2}}(P\cdot q)+\frac{g_{3}}{MM^{\prime }}(P^{\prime }\cdot q)+g_{4},\nonumber \\ \end{aligned}$$
(39)
$$\begin{aligned} B= & {} -(M+M^{\prime })\frac{f_{1}}{M}+\frac{f_{2}}{M^{2}}(P\cdot q)+\frac{f_{3}}{MM^{\prime }}(P^{\prime }\cdot q)+f_{4}.\nonumber \\ \end{aligned}$$
(40)
Table 16 Nonleptonic decays for the cc sector
Full size table

Here \(a_{1}\equiv C_{1}+C_{2}/3\).

For the process with a vector meson in the final state, the decay width is obtained:

$$\begin{aligned} \Gamma= & {} |\lambda |^{2}f_{V}^{2}m^{2}\frac{|\mathbf {P}^{\prime }|}{16\pi M^{2}}[|H_{1/2,1}|^{2}+|H_{-1/2,-1}|^{2}\nonumber \\&+|H_{3/2,1}|^{2}+|H_{-3/2,-1}|^{2} +|H_{1/2,0}|^{2}+|H_{-1/2,0}|^{2}].\nonumber \\ \end{aligned}$$
(41)

Note that in the above equations \(q^{2}=m^{2}\) is understood, where m is the mass of the meson.

All the corresponding results are collected in Tables 16, 17, 18, 19, 20 and 21. Some comments are given in Sect. 3.6.

Table 17 Nonleptonic decays for the bb sector
Full size table
Table 18 Nonleptonic decays for the bc sector with c quark decay
Full size table
Table 19 Nonleptonic decays for the bc sector with b quark decay
Full size table
Table 20 Nonleptonic decays for the \(bc^{\prime }\) sector with c quark decay
Full size table
Table 21 Nonleptonic decays for the \(bc^{\prime }\) sector with b quark decay
Full size table

3.5 SU(3) symmetry for semileptonic decays

According to flavor SU(3) symmetry, there exist the following relations among these semileptonic decay widths [7], which can also be readily rederived using the overlap factors given in Table 2.

  • cc sector

    $$\begin{aligned}&\frac{\Gamma (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{*+}l^{+}\nu )}{|V_{cd}|^{2}}\nonumber \\&\quad =\frac{\Gamma (\Xi _{cc}^{+}\rightarrow \Sigma _{c}^{*0}l^{+}\nu )}{2|V_{cd}|^{2}}=\frac{\Gamma (\Omega _{cc}^{+}\rightarrow \Xi _{c}^{\prime *0}l^{+}\nu )}{|V_{cd}|^{2}} \nonumber \\&\quad = \frac{\Gamma (\Xi _{cc}^{++}\rightarrow \Xi _{c}^{\prime *+}l^{+}\nu )}{|V_{cs}|^{2}}\nonumber \\&\quad =\frac{\Gamma (\Xi _{cc}^{+}\rightarrow \Xi _{c}^{\prime *0}l^{+}\nu )}{|V_{cs}|^{2}}=\frac{\Gamma (\Omega _{cc}^{+}\rightarrow \Omega _{c}^{*0}l^{+}\nu )}{2|V_{cs}|^{2}}, \end{aligned}$$
    (42)

  • bb sector

    $$\begin{aligned}&\Gamma (\Xi _{bb}^{0}\rightarrow \Sigma _{b}^{*+}l^{-}\bar{\nu })\nonumber \\&\quad =2\Gamma (\Xi _{bb}^{-}\rightarrow \Sigma _{b}^{*0}l^{-}\bar{\nu })=2\Gamma (\Omega _{bb}^{-}\rightarrow \Xi _{b}^{\prime *0}l^{-}\bar{\nu }),\nonumber \\&\Gamma (\Xi _{bb}^{0}\rightarrow \Xi _{bc}^{*+}l^{-}\bar{\nu })\nonumber \\&\quad =\Gamma (\Xi _{bb}^{-}\rightarrow \Xi _{bc}^{*0}l^{-}\bar{\nu }) =\Gamma (\Omega _{bb}^{-}\rightarrow \Omega _{bc}^{*0}l^{-}\bar{\nu }), \end{aligned}$$
    (43)

  • bc sector with the c quark decay

    $$\begin{aligned}&\frac{\Gamma (\Xi _{bc}^{+}\rightarrow \Sigma _{b}^{*0}l^{+}\nu )}{|V_{cd}|^{2}}=\frac{\Gamma (\Xi _{bc}^{0}\rightarrow \Sigma _{b}^{*-}l^{+}\nu )}{2|V_{cd}|^{2}}\nonumber \\&\quad =\frac{\Gamma (\Omega _{bc}^{0}\rightarrow \Xi _{b}^{\prime *-}l^{+}\nu )}{|V_{cd}|^{2}} \nonumber \\&\quad = \frac{\Gamma (\Xi _{bc}^{+}\rightarrow \Xi _{b}^{\prime *0}l^{+}\nu )}{|V_{cs}|^{2}}=\frac{\Gamma (\Xi _{bc}^{0}\rightarrow \Xi _{b}^{\prime *-}l^{+}\nu )}{|V_{cs}|^{2}}\nonumber \\&\quad =\frac{\Gamma (\Omega _{bc}^{0}\rightarrow \Omega _{b}^{*-}l^{+}\nu )}{2|V_{cs}|^{2}}, \end{aligned}$$
    (44)

  • bc sector with the b quark decay

    $$\begin{aligned}&\Gamma (\Xi _{bc}^{+}\rightarrow \Sigma _{c}^{*++}l^{-}\bar{\nu })=2\Gamma (\Xi _{bc}^{0}\rightarrow \Sigma _{c}^{*+}l^{-}\bar{\nu })\nonumber \\&\quad =2\Gamma (\Omega _{bc}^{0}\rightarrow \Xi _{c}^{\prime *+}l^{-}\bar{\nu }), \nonumber \\&\Gamma (\Xi _{bc}^{+}\rightarrow \Xi _{cc}^{*++}l^{-}\bar{\nu })=\Gamma (\Xi _{bc}^{0}\rightarrow \Xi _{cc}^{*+}l^{-}\bar{\nu })\nonumber \\&\quad =\Gamma (\Omega _{bc}^{0}\rightarrow \Omega _{cc}^{*+}l^{-}\bar{\nu }), \end{aligned}$$
    (45)

  • \(bc^{\prime }\) sector with the c quark decay

    $$\begin{aligned}&\frac{\Gamma (\Xi _{bc}^{\prime +}\rightarrow \Sigma _{b}^{*0}l^{+}\nu )}{|V_{cd}|^{2}}=\frac{\Gamma (\Xi _{bc}^{\prime 0}\rightarrow \Sigma _{b}^{*-}l^{+}\nu )}{2|V_{cd}|^{2}}\nonumber \\&\quad =\frac{\Gamma (\Omega _{bc}^{\prime 0}\rightarrow \Xi _{b}^{\prime *-}l^{+}\nu )}{|V_{cd}|^{2}}\nonumber \\&\quad = \frac{\Gamma (\Xi _{bc}^{\prime +}\rightarrow \Xi _{b}^{\prime *0}l^{+}\nu )}{|V_{cs}|^{2}}=\frac{\Gamma (\Xi _{bc}^{\prime 0}\rightarrow \Xi _{b}^{\prime *-}l^{+}\nu )}{|V_{cs}|^{2}}\nonumber \\&\quad =\frac{\Gamma (\Omega _{bc}^{\prime 0}\rightarrow \Omega _{b}^{*-}l^{+}\nu )}{2|V_{cs}|^{2}}, \end{aligned}$$
    (46)

  • \(bc^{\prime }\) sector with the b quark decay

    $$\begin{aligned}&\Gamma (\Xi _{bc}^{\prime +}\rightarrow \Sigma _{c}^{*++}l^{-}\bar{\nu })=2\Gamma (\Xi _{bc}^{\prime 0}\rightarrow \Sigma _{c}^{*+}l^{-}\bar{\nu })\nonumber \\&\quad =2\Gamma (\Omega _{bc}^{\prime 0}\rightarrow \Xi _{c}^{\prime *+}l^{-}\bar{\nu }), \nonumber \\&\Gamma (\Xi _{bc}^{\prime +}\rightarrow \Xi _{cc}^{*++}l^{-}\bar{\nu })=\Gamma (\Xi _{bc}^{\prime 0}\rightarrow \Xi _{cc}^{*+}l^{-}\bar{\nu })\nonumber \\&\quad =\Gamma (\Omega _{bc}^{\prime 0}\rightarrow \Omega _{cc}^{*+}l^{-} \bar{\nu }). \end{aligned}$$
    (47)

Also, we have compared the predictions of the light-front approach with those of SU(3) symmetry taking the cc and bb sectors as examples, which can be seen in Tables 22 and 23.

Table 22 Quantitative predictions of SU(3) symmetry breaking effects for semileptonic decays: the cc sector
Full size table
Table 23 Same as Table 22 but for the bb sector
Full size table

Some comments:

  • Note that the 1/2 to 3/2 process has completely the same SU(3) relations as the corresponding 1/2 to 1/2 case. This can be expected, because the spin-3/2 baryon has the same flavor wave function as the corresponding spin-1/2 baryon.

  • SU(3) predictions in the bc and \(bc^{\prime }\) sectors have completely the same form, as can be explained by the facts that they have the same set of final states and only the axial-vector diquark parts of the initial and final flavor–spin wave functions contribute to the overlap factors.

  • Many things can be read from Table 22. First of all, the SU(3) symmetry breaking effects in the \(c\rightarrow s\) processes (the last three channels) are much larger than those in the \(c\rightarrow d\) processes (the first three channels). Second, the SU(3) symmetry breaking effect is larger for the cs diquark case (the third or sixth channel) than for the cu / cd diquark cases (the first, second or fourth, fifth channels). Third, the isospin symmetry is respected well (the first, second or fourth, fifth channels). Of course, this can be attributed to the model parameters: we have taken the quark masses to satisfy \(m_{u} = m_{d} < m_{s}\) and the diquark masses to satisfy \(m_{cu} = m_{cd} < m_{cs}\).

  • Similar patterns can be found in Table 23. Note that the third channel in Table 22 and the third channel in Table 23 are related by the heavy quark symmetry \(c\rightarrow b\) and SU(3) symmetry \(d\rightarrow u\). However, a much smaller SU(3) symmetry breaking effect occurs in the bb sector (2%) than in the cc sector (6%). This is because the \(b\rightarrow u\) process has a much larger phase space than the \(c\rightarrow d\) process.

  • It is worth emphasizing again that the form factors listed in Tables 6, 7, 8 and 9 are not the physical form factors, because we do not consider the overlap factors. Of course, the overlap factors are considered when calculating the decay widths. Note, for example, that the processes \(\Xi _{bc}^{+}\rightarrow \Sigma _{b}^{*+}\) and \(\Xi _{bc}^{\prime +}\rightarrow \Sigma _{b}^{*+}\) are only different in their overlap factors. Also note that the decay width is proportional to the squared overlap factor. Then the decay widths for the approximate mass eigenstates \(\mathcal{B}_{bc}^{(1)}\equiv b(cq)_{S}\) and \(\mathcal{B}_{bc}^{(2)}\equiv b(cq)_{A}\), which are introduced at the end of Sect. 2, can be determined by the following equations:

    $$\begin{aligned}&\frac{\Gamma (\mathcal{B}_{bc}\rightarrow \mathcal{B}_{Q}^{*})}{|c(\mathcal{B}_{bc}\rightarrow \mathcal{B}_{Q}^{*})|^{2}}=\frac{\Gamma (\mathcal{B}_{bc}^{\prime }\rightarrow \mathcal{B}_{Q}^{*})}{|c(\mathcal{B}_{bc}^{\prime }\rightarrow \mathcal{B}_{Q}^{*})|^{2}}\nonumber \\&\quad =\frac{\Gamma (\mathcal{B}_{bc}^{(1)}\rightarrow \mathcal{B}_{Q}^{*})}{|c(\mathcal{B}_{bc}^{(1)}\rightarrow \mathcal{B}_{Q}^{*})|^{2}}=\frac{\Gamma (\mathcal{B}_{bc}^{(2)}\rightarrow \mathcal{B}_{Q}^{*})}{|c(\mathcal{B}_{bc}^{(2)}\rightarrow \mathcal{B}_{Q}^{*})|^{2}}, \end{aligned}$$
    (48)

    where \(c(X_{bc}\rightarrow \mathcal{B}_{Q}^{*})\) denotes the overlap factor and \(\mathcal{B}_{Q}^{*}\) is a spin-3/2 baryon in the final state.

    Some examples follow:

    $$\begin{aligned}&\Gamma (\Xi _{bc}^{(1)+}\rightarrow \Sigma _{b}^{*0}e^{+}\nu _{e})=\Gamma (\Xi _{bc}^{\prime +}\rightarrow \Sigma _{b}^{*0}e^{+}\nu _{e})\nonumber \\&\quad =3.30\times 10^{-15}\ \mathrm{GeV},\nonumber \\&\Gamma (\Xi _{bc}^{(2)+}\rightarrow \Sigma _{b}^{*0}e^{+}\nu _{e})=\Gamma (\Xi _{bc}^{+}\rightarrow \Sigma _{b}^{*0}e^{+}\nu _{e})\nonumber \\&\quad =1.10\times 10^{-15}\ \mathrm{GeV},\nonumber \\&\Gamma (\Xi _{bc}^{(1)+}\rightarrow \Sigma _{b}^{*0}\pi ^{+})=\Gamma (\Xi _{bc}^{\prime +}\rightarrow \Sigma _{b}^{*0}\pi ^{+})\nonumber \\&\quad =1.14\times 10^{-15}\ \mathrm{GeV},\nonumber \\&\Gamma (\Xi _{bc}^{(2)+}\rightarrow \Sigma _{b}^{*0}\pi ^{+})=\Gamma (\Xi _{bc}^{+}\rightarrow \Sigma _{b}^{*0}\pi ^{+})\nonumber \\&\quad =3.80\times 10^{-16},\ \mathrm{GeV} \end{aligned}$$
    (49)

    for c quark decay, and

    $$\begin{aligned}&\Gamma (\Xi _{bc}^{(2)+}\rightarrow \Sigma _{c}^{*++}e^{-}\bar{\nu }_{e})=4\Gamma (\Xi _{bc}^{+}\rightarrow \Sigma _{c}^{*++}e^{-}\bar{\nu }_{e})\nonumber \\&\quad =1.33\times 10^{-16}\ \mathrm{GeV},\nonumber \\&\Gamma (\Xi _{bc}^{(2)+}\rightarrow \Sigma _{c}^{*++}\pi ^{-})=4\Gamma (\Xi _{bc}^{+}\rightarrow \Sigma _{c}^{*++}\pi ^{-})\nonumber \\&\quad =3.28\times 10^{-18}\ \mathrm{GeV}, \end{aligned}$$
    (50)

    for b quark decay. The decay widths for \(\Xi _{bc}^{(1)+}\equiv b(cu)_{S}\) are absent for the case of b quark decay, because it cannot decay into a spin-3/2 baryon \(u(cu)_{A}\) or \(c(cu)_{A}\). [However, it contains the component of \(c(bu)_{A}\), so it can decay into a spin-3/2 baryon \(d(bu)_{A}\) or \(s(bu)_{A}\) with a certain probability, as can be seen from Eq. (49).].

3.6 Comparison

It will be beneficial to compare the results in this work with those in Ref. [4] and those in Ref. [41], which study the 1/2 to 1/2 doubly heavy baryon decays and the doubly heavy \(B_{c}\) meson decays, respectively. For the reader’s convenience, we list the corresponding results in Ref. [41] as follows:

$$\begin{aligned} \mathcal{B}(B_{c}\rightarrow B_{s}\bar{l}\nu )= & {} 1.51\times 10^{-2},\nonumber \\ \mathcal{B}(B_{c}\rightarrow B_{s}^{*}\bar{l}\nu )= & {} 1.96\times 10^{-2},\nonumber \\ \mathcal{B}(B_{c}\rightarrow B\bar{l}\nu )= & {} 1.04\times 10^{-3},\nonumber \\ \mathcal{B}(B_{c}\rightarrow B^{*}\bar{l}\nu )= & {} 1.34\times 10^{-3},\nonumber \\ \mathcal{B}(B_{c}\rightarrow B_{s}\pi )= & {} 4.1\times 10^{-2},\nonumber \\ \mathcal{B}(B_{c}\rightarrow B_{s}^{*}\pi )= & {} 2.0\times 10^{-2}. \end{aligned}$$
(51)

Some comments now follow:

  • We find that the result for the 1/2 to 3/2 process is roughly one order of magnitude smaller than the corresponding 1/2 to 1/2 case except for the \(\mathcal{B}_{bc}^{\prime }\) decays. Both the c quark and the b quark decays of \(\mathcal{B}_{bc}^{\prime }\) baryons are comparable to the corresponding 1/2 to 1/2 cases.

  • \(\mathcal{B}(H_{bc}\rightarrow H_{bs}l\nu )\sim 10^{-2}\) holds for the corresponding results in Refs. [4] and [41], while in this work, it ranges from \(10^{-3}\) to \(10^{-2}\). \(\mathcal{B}(H_{bc}\rightarrow H_{bd}l\nu )\sim 10^{-3}\) holds for the corresponding results in Refs. [4] and [41], while in this work, it ranges from \(10^{-4}\) to \(10^{-3}\). Here \(H_{bc}\) stands for the \(B_{c}\) meson or the \(\mathcal{B}_{bc}^{(\prime )}\) baryon.

  • \(\mathcal{B}(H_{bc}\rightarrow H_{bs}\pi )\sim 10^{-2}\) holds for the corresponding results in Refs. [4] and [41], while in this work it is roughly \(10^{-3}\). \(\mathcal{B}(H_{bc}\rightarrow H_{bd}\pi )\sim 10^{-3}\) holds for the corresponding results in Refs. [4] and [41], while in this work it is of order \(10^{-4}\).

3.7 Uncertainties

We will also investigate the dependence of the decay widths on the model parameters. Take the \(\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{*+}\) transition as an example. Varying the diquark mass \(m_{\{di\}}\), the shape parameters \(\beta _{i}\) and \(\beta _{f}\) for the initial and final baryons, and the parameter \(m_{\mathrm{pole}}\) in the single pole assumption by 10%, respectively, the corresponding error estimates are listed in Eq. (52). [\(m_{\{di\}}\), \(\beta _{i,f}\) and \(m_{\mathrm{pole}}\) are, respectively, given in Eqs. (25), (26) and (30).]

$$\begin{aligned}&\Gamma (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{*+}e^{+}\nu _{e}) \nonumber \\&\quad = (1.26\pm 0.26\pm 0.21\pm 0.25\pm 0.12)\times 10^{-15}\ \mathrm{GeV},\nonumber \\&\Gamma (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{*+}\pi ^{+}) \nonumber \\&\quad = (1.16\pm 0.08\pm 0.32\pm 0.04\pm 0.00)\times 10^{-15}\ \mathrm{GeV},\nonumber \\&\Gamma (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{*+}\rho ^{+}) \nonumber \\&\quad = (3.78\pm 0.81\pm 0.63\pm 0.79\pm 0.40)\times 10^{-15}\ \mathrm{GeV},\nonumber \\&\Gamma (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{*+}K^{+}) \nonumber \\&\quad = (4.97\pm 0.61\pm 0.17\pm 0.26\pm 0.18)\times 10^{-17}\ \mathrm{GeV},\nonumber \\&\Gamma (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{*+}K^{*+}) \nonumber \\&\quad = (1.60\pm 0.44\pm 0.59\pm 0.49\pm 0.25)\times 10^{-16}\ \mathrm{GeV}.\nonumber \\ \end{aligned}$$
(52)

For \(\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{+}\), the corresponding results are listed as follows:

$$\begin{aligned}&\Gamma (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{+}e^{+}\nu _{e}) \nonumber \\&\quad = (1.04\pm 0.04\pm 0.02\pm 0.11\pm 0.15)\times 10^{-14}\ \mathrm{GeV},\nonumber \\&\Gamma (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{+}\pi ^{+}) \nonumber \\&\quad = (5.75\pm 0.19\pm 0.35\pm 0.88\pm 0.02)\times 10^{-15}\ \mathrm{GeV},\nonumber \\&\Gamma (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{+}\rho ^{+}) \nonumber \\&\quad = (2.61\pm 0.08\pm 0.08\pm 0.29\pm 0.27)\times 10^{-14}\ \mathrm{GeV},\nonumber \\&\Gamma (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{+}K^{+}) \nonumber \\&\quad = (4.28\pm 0.15\pm 0.25\pm 0.66\pm 0.16)\times 10^{-16}\ \mathrm{GeV},\nonumber \\&\Gamma (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{+}K^{*+}) \nonumber \\&\quad = (1.39\pm 0.05\pm 0.02\pm 0.14\pm 0.22)\times 10^{-15}\ \mathrm{GeV}.\nonumber \\ \end{aligned}$$
(53)

Some comments now follow:

  • Equation (30) is also adopted for the \(\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{+}\) transitions for this time. In our previous work Ref. [4], the following fit formulas were adopted:

    $$\begin{aligned} F(q^{2})=\frac{F(0)}{1\mp \frac{q^{2}}{m_{\mathrm{fit}}^{2}}+\delta \left( \frac{q^{2}}{m_{\mathrm{fit}}^{2}}\right) ^{2}}. \end{aligned}$$
    (54)

    However, only a few percent is changed in Eq. (53) compared with our previous results in Ref. [4].

  • It can be seen that the variation in these parameters may cause a sizable change in the decay width, but the order of magnitude will not change.

4 Conclusions

In our previous work, we have performed the calculation of doubly heavy baryon weak decays for the 1/2 to 1/2 case. As a continuation, we investigate the 1/2 to 3/2 case in this work. The light-front approach under the diquark picture is once again adopted to extract the form factors. In Ref. [54], the same method was used to study bottom and charm baryon decays and reasonable results were obtained. The extracted form factors are then applied to predict the decay widths of semileptonic and nonleptonic decays. We find that the result for the 1/2 to 3/2 case is roughly one order of magnitude smaller than the corresponding 1/2 to 1/2 case, except for the \(\mathcal{B}_{bc}^{\prime }\) decays. For \(\mathcal{B}_{bc}^{\prime }\) baryons, both the c quark and the b quark decays are comparable to the corresponding 1/2 to 1/2 cases. SU(3) symmetry and sources of SU(3) symmetry breaking for semileptonic decays are discussed. The error estimates are also performed.

Recently, LHCb announced the discovery of \(\Xi _{cc}^{++}\) via the decay mode of \(\Xi _{cc}^{++}\rightarrow \Lambda _{c}^{+}K^{-}\pi ^{+}\pi ^{+}\), and very recently the lifetime of \(\Xi _{cc}^{++}\) was measured [55] and another decay mode \(\Xi _{cc}^{++}\rightarrow \Xi _{c}^{+}\pi ^{+}\) predicted by Ref. [3] was also found [56]. It is expected that more and more channels of \(\Xi _{cc}^{++}\) will be established in the next few years. According to the results of Ref. [4],

$$\begin{aligned} \mathcal{B}(\Xi _{cc}^{++}\rightarrow \Xi _{c}^{+}\pi ^{+})= & {} 7.14\times 10^{-2},\\ \mathcal{B}(\Xi _{cc}^{++}\rightarrow \Xi _{c}^{\prime +}\pi ^{+})= & {} 5.00\times 10^{-2}, \end{aligned}$$

it is very likely that the latter channel will also be found in the near future. In this work, its 1/2 to 3/2 counterpart is predicted to be

$$\begin{aligned} \mathcal{B}(\Xi _{cc}^{++}\rightarrow \Xi _{c}^{\prime *+}\pi ^{+})=1.02\times 10^{-2}, \end{aligned}$$

where \(\Xi _{c}^{\prime *+}\) decays via \(\Xi _{c}^{\prime *+}\rightarrow \Xi _{c}^{0}\pi ^{+}\) [51] and \(\Xi _{c}^{0}\) can be detected with charged final states.

So we suggest our experimental colleagues to search for the 1/2 to 1/2 process \(\Xi _{cc}^{++}\rightarrow \Xi _{c}^{\prime +}\pi ^{+}\) and its 1/2 to 3/2 counterpart \(\Xi _{cc}^{++}\rightarrow \Xi _{c}^{\prime *+}\pi ^{+}\).

It should be noted that the decay branching ratio is proportional to the lifetime of the initial baryon. However, as we have pointed out in Ref. [4], there exist large uncertainties in the lifetimes of these doubly heavy baryons. Our future work will aim to fix this problem.