Predictions for the neutrino parameters in the minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model

Abstract

We study the structure of the neutrino-mass matrix in the minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model, where three right-handed neutrinos are added to the Standard Model in order to obtain non-zero masses for the active neutrinos. Because of the $\hbox {U}(1)_{L_\mu -L_\tau }$ gauge symmetry, the structure of both Dirac and Majorana mass terms of neutrinos is tightly restricted. In particular, the inverse of the neutrino-mass matrix has zeros in the $(\mu ,\mu )$ and $(\tau ,\tau )$ components, namely, this model offers a symmetric realization of the so-called two-zero-minor structure in the neutrino-mass matrix. Due to these constraints, all the CP phases – the Dirac CP phase $\delta$ and the Majorana CP phases $\alpha _2$ and $\alpha _3$ – as well as the mass eigenvalues of the light neutrinos $m_i$ are uniquely determined as functions of the neutrino mixing angles $\theta _{12}$, $\theta _{23}$, and $\theta _{13}$, and the squared mass differences $\Delta m_{21}^2$ and $\Delta m_{31}^2$. We find that this model predicts the Dirac CP phase $\delta$ to be $\delta \simeq 1.59\pi$–$1.70\pi$ ($1.54\pi$–$1.78\pi$), the sum of the neutrino masses to be $\sum _{i}m_i \simeq 0.14$–0.22 eV (0.12–0.40 eV), and the effective mass for the neutrinoless double-beta decay to be $\langle m_{\beta \beta }\rangle \simeq 0.024$–0.055 eV (0.017–0.12 eV) at $1\sigma$ ($2\sigma$) level, which are totally consistent with the current experimental limits. These predictions can soon be tested in future neutrino experiments. Implications for leptogenesis are also discussed.

1 Introduction

A gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ symmetric extension of the Standard Model (SM), where $L_\mu$ and $L_\tau$ stand for the $\mu$ and $\tau$ numbers, respectively, has widely been considered so far, as it is one of the several possibilities of gauging an accidental U(1) symmetry in the SM [1,2,3,4]. An attractive feature of this class of models is that the muon $g-2$ anomaly [5,6,7,8] may be explained by the loop contribution of the $\hbox {U}(1)_{L_\mu -L_\tau }$ gauge boson if its mass lies around the weak scale or lower [9,10,11,12], though this possibility is severely restricted by the searches of the neutrino trident production process [13,14,15,16]. These models may also explain anomalies in flavor physics [15, 17] and offer promising candidates for dark matter in the Universe [18,19,20,21,22]. For other recent studies on gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ models, see Refs. [23,24,25,26,27,28,29,30,31,32,33,34,35].

On the other hand, neutrino oscillation data show that at least two of the active neutrinos have non-zero masses and there is sizable mixing among these neutrinos. This can be accounted for if we add right-handed neutrinos to the theory and couple them to the SM lepton and Higgs fields through the Yukawa couplings. After the Higgs field acquires a vacuum expectation value (VEV), these terms lead to the Dirac mass terms for the neutrinos. In addition, the right-handed neutrinos can have Majorana mass terms, and if these masses are much larger than the electroweak scale, then the smallness of the neutrino masses can naturally be explained by the seesaw mechanism [36,37,38,39].

In gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ models, however, the neutrino-mass structure is tightly restricted since the second and third generation leptons are charged under the $\hbox {U}(1)_{L_\mu -L_\tau }$ gauge symmetry [40,41,42,43,44]. In fact, in the $\hbox {U}(1)_{L_\mu -L_\tau }$ preserving limit, the Dirac mass matrix is diagonal, while in the Majorana mass matrix only the (e, e), $(\mu , \tau )$, and $(\tau , \mu )$ components can be non-zero. Such a simple structure cannot explain neutrino oscillation data, and therefore we need to break the $\hbox {U}(1)_{L_\mu -L_\tau }$ symmetry. To that end, one usually introduces a SM singlet scalar that has a non-zero $\hbox {U}(1)_{L_\mu -L_\tau }$ charge such that its VEV spontaneously breaks the $\hbox {U}(1)_{L_\mu -L_\tau }$ gauge symmetry and gives a mass to the $\hbox {U}(1)_{L_\mu -L_\tau }$ gauge boson. We, however, note that even though the $\hbox {U}(1)_{L_\mu -L_\tau }$ gauge symmetry is spontaneously broken, the structure of the neutrino-mass matrix is still highly constrained if we introduce just one $\hbox {U}(1)_{L_\mu -L_\tau }$-breaking scalar field and consider only renormalizable interactions. Therefore, it is interesting to study if this minimal setup can accommodate the neutrino-mass structure that is consistent with the present neutrino oscillation data.

In this paper, we consider this “minimal” gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model where three right-handed neutrinos and one $\hbox {U}(1)_{L_\mu -L_\tau }$-charged SM singlet scalar field are added to the SM. Then it turns out that the observed neutrino mixing structure can be obtained only when the $\hbox {U}(1)_{L_\mu -L_\tau }$-breaking scalar field has the $\hbox {U}(1)_{L_\mu -L_\tau }$ charge $\pm 1$. In this case, the $(\mu ,\mu )$ and $(\tau ,\tau )$ components of the Majorana mass matrix for the right-handed neutrinos remain zero even after the $\hbox {U}(1)_{L_\mu -L_\tau }$ symmetry is spontaneously broken. Because of this structure of the Majorana mass matrix together with the diagonal Dirac mass matrix, the inverse of the neutrino-mass matrix also has zeros in the $(\mu ,\mu )$ and $(\tau ,\tau )$ components [42, 45]. The minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model thus gives a concrete realization of a two-zero-minor model [46, 47]. Intriguingly, due to the condition that the $(\mu ,\mu )$ and $(\tau ,\tau )$ components in the inverse of the neutrino-mass matrix vanish, all the CP phases in the neutrino mixing matrix – the Dirac CP phase $\delta$ and the Majorana CP phases $\alpha _2$ and $\alpha _3$ – as well as the mass eigenvalues of the light neutrinos are uniquely determined as functions of the neutrino mixing angles $\theta _{12}$, $\theta _{23}$, and $\theta _{13}$, and the squared mass differences $\Delta m_{21}^2$ and $\Delta m_{31}^2$. As we shall see, this prediction is independent of the $\hbox {U}(1)_{L_\mu -L_\tau }$-symmetry breaking scale, and thus can be regarded as a generic prediction in the minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model. We find that the predicted values of the neutrino parameters are consistent with the present neutrino data and can be tested in future neutrino experiments. We also discuss the implications of our results for leptogenesis.

This paper is organized as follows. In Sect. 2, we introduce the minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model and examine the neutrino-mass structure in this model. We then show in Sect. 3 the predicted values of the Dirac CP phase $\delta$, the sum of the neutrino masses $\sum _{i}m_i$, and the effective mass for the neutrinoless double-beta decay $\langle m_{\beta \beta } \rangle$ using the neutrino mixing angles and the squared mass differences obtained in neutrino oscillation experiments. In Sect. 4, we discuss the implications for the leptogenesis. Finally, our conclusions are summarized in Sect. 5. This paper ends with two appendices which give further details of our analysis. In Appendix A, we present some miscellaneous formulas which are useful to study the neutrino structure in the minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model. In Appendix B, we perform similar analyses for the minimal gauged $\hbox {U}(1)_{L_e-L_\mu }$ and $\hbox {U}(1)_{L_e-L_\tau }$ models, and show that these minimal models fail to explain the observed neutrino oscillation data.

2 Neutrino-mass structure in the minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model

To begin with, we describe the minimal $\hbox {U}(1)_{L_\mu -L_\tau }$ model which we discuss in this paper. The model possesses a new U(1) gauge symmetry $\hbox {U}(1)_{L_\mu - L_\tau }$. Under this gauge symmetry, $\mu _{L,R}$ and $\nu _\mu$ have the $\hbox {U}(1)_{L_\mu - L_\tau }$ charge $+1$, $\tau _{L, R}$ and $\nu _\tau$ have the $\hbox {U}(1)_{L_\mu - L_\tau }$ charge $-1$, and the other SM fields have the zero $\hbox {U}(1)_{L_\mu - L_\tau }$ charge. We also introduce three right-handed neutrinos $N_e$, $N_\mu$, and $N_\tau$ to obtain non-zero neutrino masses. The $\hbox {U}(1)_{L_\mu - L_\tau }$ charges of these fields are 0, $+1$, and $-1$, respectively.¹

In the $(e, \mu , \tau )$ basis, the $\hbox {U}(1)_{L_\mu - L_\tau }$ charges of the Dirac Yukawa terms are

$$\begin{aligned} Q_{L_\mu - L_\tau }(\text {Dirac}): ~~ \begin{pmatrix} 0&{}\quad 1&{}\quad -1 \\ -1&{}\quad 0 &{}\quad -2 \\ 1 &{}\quad 2 &{}\quad 0 \end{pmatrix} ~, \end{aligned}$$

(1)

where the $(\alpha , \beta )$ entry in the above matrix represents the $\hbox {U}(1)_{L_\mu - L_\tau }$ charge of the fermion bilinear term $N_\alpha ^c L_\beta ^{}$, with $\alpha , \beta$ the flavor indices. For the Majorana mass terms of the right-handed neutrinos, on the other hand, we have

$$\begin{aligned} Q_{L_\mu - L_\tau }(\text {Majorana}): ~~ \begin{pmatrix} 0 &{}\quad 1 &{}\quad -1 \\ 1 &{}\quad 2 &{}\quad 0 \\ -1&{}\quad 0 &{}\quad -2 \\ \end{pmatrix} ~, \end{aligned}$$

(2)

where the $(\alpha , \beta )$ component indicates the $\hbox {U}(1)_{L_\mu - L_\tau }$ charge of the fermion bilinear term $N_\alpha N_\beta$. From Eq. (1), we find that the Dirac Yukawa matrix is always diagonal in the gauged $\hbox {U}(1)_{L_\mu - L_\tau }$ models – for the same reason, the charged-lepton Yukawa matrix is also diagonal. As long as renormalizable interactions are considered, this structure is not violated even if we introduce a $\hbox {U}(1)_{L_\mu - L_\tau }$-breaking scalar field. On the other hand, the charges of the Majorana mass matrix in Eq. (2) show that only the (e, e), $(\mu ,\tau )$, and $(\tau , \mu )$ components can have non-zero values in the $\hbox {U}(1)_{L_\mu - L_\tau }$-symmetric limit. As we mentioned above, with this simple structure, we cannot explain the required values of the neutrino mixing angles. We therefore introduce a scalar boson $\sigma$ which has a non-zero $\hbox {U}(1)_{L_\mu - L_\tau }$ charge, and couple it to right-handed neutrinos. After this scalar field develops a VEV, these couplings lead to Majorana mass terms of the right-handed neutrinos. If the scalar field has the $\hbox {U}(1)_{L_\mu - L_\tau }$ charge $\pm 1$, then the $(e,\mu )$, $(e, \tau )$, $(\mu ,e)$, and $(\tau , e)$ components in Eq. (2) can be induced after the scalar field acquires a VEV, while the $(\mu , \mu )$ and $(\tau , \tau )$ can be generated if the scalar has the $\hbox {U}(1)_{L_\mu - L_\tau }$ charge $\pm \,2$. In the latter case, however, the Majorana mass matrix becomes block-diagonal, which makes it unable to explain the observed neutrino mixing angles. We are thus left with the case where the scalar field has the $\hbox {U}(1)_{L_\mu - L_\tau }$ charge $\pm \,1$, and we take it to be $+\,1$ in the following discussion. We refer to this model as the minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model.

The interaction terms relevant to neutrino masses are then given by

$$\begin{aligned} \Delta \mathcal{L}&= -\lambda _e N_e^c (L_e \cdot H) -\lambda _\mu N_\mu ^c (L_\mu \cdot H) -\lambda _\tau N_\tau ^c (L_\tau \cdot H) \nonumber \\&\quad -\frac{1}{2}M_{ee} N_e^c N_e^c - M_{\mu \tau } N_\mu ^c N_\tau ^c - \lambda _{e\mu } \sigma N_e^c N_\mu ^c \nonumber \\&\quad - \lambda _{e\tau } \sigma ^* N_e^c N_\tau ^c +\text {h.c.} ~, \end{aligned}$$

(3)

where the dots indicate the contraction of the SU(2)$_L$ indices. After the Higgs field H and the singlet scalar $\sigma$ acquire VEVs $\langle H \rangle = v/\sqrt{2}$ and $\langle \sigma \rangle$,² respectively, these interaction terms lead to the neutrino-mass terms,

$$\begin{aligned} \mathcal{L}_\mathrm{mass}&= -(\nu _e, \nu _\mu , \nu _\tau ) \mathcal{M}_D \begin{pmatrix} N_e^c\\ N_\mu ^c\\ N_\tau ^c \end{pmatrix} \nonumber \\&\quad - \frac{1}{2}\left( N_e^c, N_\mu ^c, N_\tau ^c\right) \mathcal{M}_R \begin{pmatrix} N_e^c \\ N_\mu ^c \\ N_\tau ^c \end{pmatrix} +\text {h.c.} ~, \end{aligned}$$

(4)

where

$$\begin{aligned} \mathcal{M}_D= & {} \frac{v}{\sqrt{2}} \begin{pmatrix} \lambda _e &{}\quad 0&{}\quad 0\\ 0 &{}\quad \lambda _\mu &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \lambda _\tau \end{pmatrix}, \nonumber \\ \mathcal{M}_R= & {} \begin{pmatrix} M_{ee} &{} \lambda _{e\mu } \langle \sigma \rangle &{} \lambda _{e\tau } \langle \sigma \rangle \\ \lambda _{e\mu } \langle \sigma \rangle &{}\quad 0 &{}\quad M_{\mu \tau } \\ \lambda _{e\tau } \langle \sigma \rangle &{}\quad M_{\mu \tau } &{}\quad 0 \end{pmatrix}. \end{aligned}$$

(5)

The mass matrix for the light neutrinos is then given by [36,37,38,39]

$$\begin{aligned} \mathcal{M}_{\nu _L} \simeq - \mathcal{M}_D \mathcal{M}_R^{-1} \mathcal{M}_D^T ~. \end{aligned}$$

(6)

An explicit expression for $\mathcal{M}_{\nu _L}$ can be found in Appendix A.1. We can diagonalize this mass matrix by using a unitary matrix U (PMNS matrix [48]):

$$\begin{aligned} U^T \mathcal{M}_{\nu _L} U =\text {diag}(m_1, m_2, m_3) ~, \end{aligned}$$

(7)

which can be parametrized as

$$\begin{aligned} U= & {} \begin{pmatrix} c_{12} c_{13} &{} s_{12} c_{13} &{} s_{13} \mathrm{e}^{-i\delta } \\ -s_{12} c_{23} -c_{12} s_{23} s_{13} \mathrm{e}^{i\delta } &{} c_{12} c_{23} -s_{12} s_{23} s_{13} \mathrm{e}^{i\delta } &{} s_{23} c_{13}\\ s_{12} s_{23} -c_{12} c_{23} s_{13} \mathrm{e}^{i\delta } &{} -c_{12} s_{23} -s_{12} c_{23} s_{13} \mathrm{e}^{i\delta } &{} c_{23} c_{13} \end{pmatrix} \nonumber \\&\times \begin{pmatrix} 1 &{}\quad &{}\quad \\ &{}\quad \mathrm{e}^{i\frac{\alpha _{2}}{2}} &{}\quad \\ &{}\quad &{}\quad \mathrm{e}^{i\frac{\alpha _{3}}{2}} \end{pmatrix}, \end{aligned}$$

(8)

where $c_{ij} \equiv \cos \theta _{ij}$ and $s_{ij} \equiv \sin \theta _{ij}$ for $\theta _{ij} = [0, \pi /2]$, $\delta = [0, 2\pi ]$, and we have ordered $m_1<m_2$ without loss of generality. We follow the convention of the Particle Data Group [48], where $m_2^2-m_1^2\ll |m_3^2-m_1^2|$ and $m_1<m_2<m_3$ (Normal Ordering, NO) or $m_3<m_1<m_2$ (Inverted Ordering, IO).

If $m_i = 0$ ($i = 1$ or 3), then $\text {det}(\mathcal{M}_{\nu _L}) = 0$. As shown in Appendix A.1, in this case we cannot have desired mixing angles since $\mathcal{M}_{\nu _L}$ becomes block-diagonal. Thus, we focus on the $m_i \ne 0$ case, where we obtain from Eqs. (6) and (7)

$$\begin{aligned} \mathcal{M}_{\nu _L}^{-1}&= U \text {diag}\left( m_1^{-1}, m_2^{-1}, m_3^{-1}\right) U^T \nonumber \\&\simeq - \left( \mathcal{M}_D^{-1}\right) ^T \mathcal{M}_R \mathcal{M}_D^{-1} ~. \end{aligned}$$

(9)

We then notice that the $(\mu , \mu )$ and $(\tau , \tau )$ components of these terms vanish since $\mathcal{M}_D$ is diagonal and $\mathcal{M}_R$ has zeros in these components. This structure is sometimes called two-zero minor [46, 47]. For other previous studies of the two-zero minor structure, see Refs. [49, 50]. These two vanishing conditions then lead to

$$\begin{aligned} \frac{1}{m_1}V_{\mu 1}^2 + \frac{1}{m_2}V_{\mu 2}^2\,\mathrm{e}^{i\alpha _2} + \frac{1}{m_3}V_{\mu 3}^2\,\mathrm{e}^{i\alpha _3}&= 0 ~, \end{aligned}$$

(10)

$$\begin{aligned} \frac{1}{m_1}V_{\tau 1}^2 + \frac{1}{m_2}V_{\tau 2}^2\,\mathrm{e}^{i\alpha _2} + \frac{1}{m_3}V_{\tau 3}^2\,\mathrm{e}^{i\alpha _3}&= 0 ~, \end{aligned}$$

(11)

where the matrix V is defined by $U = V\cdot \text {diag}(1, e^{i\alpha _2/2}, e^{i\alpha _3/2})$. Notice that neither the $\hbox {U}(1)_{L_\mu - L_\tau }$-breaking singlet VEV $\langle \sigma \rangle$ nor Majorana masses $M_{ee}$ and $M_{\mu \tau }$ appear in these conditions explicitly. For this reason, the following discussions based on these equations have little dependence on the $\hbox {U}(1)_{L_\mu - L_\tau }$-symmetry breaking scale; it may be around the electroweak scale, or as large as $10^{(13-15)}$ GeV, which is a prime scale for the masses of right-handed neutrinos since small neutrino masses are explained with $\mathcal{O}(1)$ Yukawa couplings via the seesaw mechanism [36,37,38,39]. It follows from Eqs. (10) and (11) that

$$\begin{aligned} \mathrm{e}^{i\alpha _2}&=\frac{m_2}{m_1} R_2 (\delta ) ~, \quad \mathrm{e}^{i\alpha _3} =\frac{m_3}{m_1} R_3 (\delta ) ~, \end{aligned}$$

(12)

with³

$$\begin{aligned} R_2&\equiv \frac{(V_{\mu 1} V_{\tau 3} + V_{\mu 3} V_{\tau 1})V^*_{e2}}{(V_{\mu 2} V_{\tau 3}+ V_{\mu 3} V_{\tau 2}) V^*_{e1}} ~, \end{aligned}$$

(13)

$$\begin{aligned} R_3&\equiv \frac{(V_{\mu 1} V_{\tau 2} + V_{\mu 2} V_{\tau 1})V^*_{e3}}{(V_{\mu 2} V_{\tau 3}+ V_{\mu 3} V_{\tau 2}) V^*_{e1}} ~, \end{aligned}$$

(14)

where we have used $\widetilde{V}^T = V^{-1}$ and $\mathrm{det}V=1$ with $\widetilde{V}$ being the cofactor matrix of V.⁴ In Appendix A.2, we give explicit expressions for $R_2$ and $R_3$ in terms of neutrino oscillation parameters. By taking the absolute values of the equations in (12), we find

$$\begin{aligned} \frac{m_2}{m_1} = \frac{1}{|R_2(\delta )|} ~,\quad \frac{m_3}{m_1} = \frac{1}{|R_3(\delta )|} ~. \end{aligned}$$

(15)

Therefore, these mass ratios are given as functions of the Dirac CP phase $\delta$. Notice that $R_{2,3}^*(-\delta ) = R_{2,3}$ since $R_{2,3}$ contains a single CP phase $\delta$. As a consequence, $m_{2,3}/m_1$ are symmetric under the reflection $\delta \rightarrow -\delta$ (and $\pi + \delta \rightarrow \pi - \delta$) as we see below.

Fig. 1

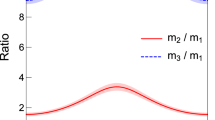
The mass ratios $m_2/m_1$ and $m_3/m_1$ as functions of the Dirac CP phase $\delta$, from Eq. (15). The bands show uncertainty coming from the 1$\sigma$ error in the neutrino mixing parameters. The thin dotted line corresponds to $m_{2,3}/m_1 = 1$

In Fig. 1, we plot the mass ratios $m_2/m_1$ and $m_3/m_1$ against the Dirac CP phase $\delta$ using Eq. (15). The bands show uncertainty coming from the 1$\sigma$ error in the neutrino mixing parameters. For input parameters of the neutrino mixing angles, we use $\sin ^2\theta _{12} = 2.97^{+0.17}_{-0.16}\times 10^{-1}$, $\sin ^2\theta _{13} = 2.15^{+0.07}_{-0.07}\times 10^{-2}$, and $\sin ^2\theta _{23} = 4.25^{+0.21}_{-0.15}\times 10^{-1}$ [51] (see Table 1).⁵ It is found that the resultant uncertainty mainly comes from the error in $\theta _{23}$. From this figure, we find that when $\delta \simeq 0,\, 2\pi$ the observed neutrino mixing angles are incompatible with the condition $m_1 < m_2$, and thus these regions are excluded. Moreover, around $\delta \simeq \pi$ we have $m_1< m_3 < m_2$, which disagrees with the possible neutrino-mass ordering: either $m_1<m_2< m_3$ or $m_3<m_1<m_2$ [48]. As a consequence, in the region where a consistent neutrino-mass ordering is obtained, the neutrino-mass ordering is always the Quasi-Degenerate Normal Ordering with $m_1\lesssim m_2 \lesssim m_3$, which is realized around $\delta \sim \pi /2$ and $3\pi /2$.

According to the recent global-fit analysis in Ref. [51], the NO is somewhat favored over IO at $\sim 2\sigma$ level. There are quite a few proposed experiments that may determine the neutrino-mass ordering at more than 3$\sigma$ level within a decade [54, 55], such as PINGU [56], ORCA [57], and JUNO [58, 59]. To confirm NO in these future experiments would be a first consistency check of our model.

Now that the mass ordering has been fixed, we determine $m_1$ and $\delta$ by using the above results. From the neutrino oscillation experiments, we can measure⁶

$$\begin{aligned} \delta m^2&\equiv m_2^2 - m_1^2 ~, \end{aligned}$$

(18)

$$\begin{aligned} \Delta m^2&\equiv m_3^2 -\left( m_2^2 + m_1^2\right) \Big /2. \end{aligned}$$

(19)

These quantities are related to the neutrino-mass ratios by

$$\begin{aligned}&\delta m^2 = m_1^2 \left( \frac{m_2^2}{m_1^2}-1 \right) = m_1^2\left( \frac{1}{\left| R_2(\delta )\right| ^2}-1\right) ~, \end{aligned}$$

(20)

$$\begin{aligned}&\Delta m^2 + \frac{\delta m^2}{2} = m_1^2 \left( \frac{m_3^2}{m_1^2}-1 \right) = m_1^2\left( \frac{1}{\left| R_3(\delta )\right| ^2}-1\right) . \end{aligned}$$

(16)

By solving these equations, we can determine $m_1$ and $\delta$. The observed values of $\delta m^2$ and $\Delta m^2$ are given by $\delta m^2 \simeq 7.37 \times 10^{-5}~\text {eV}^2$ and $\Delta m^2 \simeq 2.525 \times 10^{-3}~\text {eV}^2$, respectively [51]. This means that the right-hand side of Eq. (19) is much smaller than that in Eq. (20). From Fig. 1, we see that such a hierarchy can be realized only when $m_2^2/m_1^2 \simeq 1$, i.e., $|R_2 (\delta )| \simeq 1$. With the explicit formula of $R_2(\delta )$ in Eq. (A.3), this leads to

$$\begin{aligned} \cos \delta \simeq \frac{\cot 2\theta _{12} \cot 2\theta _{23}}{\sin \theta _{13}} ~. \end{aligned}$$

(21)

When the best-fit values of the mixing angles $\theta _{ij}$ are used, this leads to $\cos \delta \simeq 0.46$, which corresponds to $\delta \simeq 0.35\pi$ or $1.65\pi$. In Eq. (A.6) in Appendix A.3, we give a cubic equation whose solution gives an exact value of $\cos \delta$ as a function of the mixing angles $\theta _{ij}$ and the squared mass differences $\delta m^2$ and $\Delta m^2$. As discussed there, the solution (21) approximates the real solution of the cubic equation (A.6) at $\mathcal{O}(\delta m^2/\Delta m^2)$ level. By solving Eq. (A.6) numerically, we find $\cos \delta = 0.445$ for the best-fit values of $\theta _{ij}$, $\delta m^2$, and $\Delta m^2$, which means $\delta = 0.353\pi$ or $1.647\pi$, and justifies the expected accuracy of the approximated formula (21).⁷

From Eqs. (13) and (19), we obtain $m_1$ as a function of $\delta$. An explicit expression for $m_1$ is given in Appendix A.2. As noted above, $|R_{2,3} (\delta )|$ are symmetric with respect to the reflection $\delta \rightarrow -\delta$. This implies that $m_1$ is also symmetric under this reflection and thus depends only on $\cos \delta$ (not $\sin \delta$). As a result, even though there are two solutions for $\delta$, $m_1$ (and thus $m_{2,3}$ as well) is uniquely determined. Finally, by substituting the above results into Eq. (12), we determine the Majorana CP phases $\alpha _2$ and $\alpha _3$. Again, since $R^*_{2,3}(-\delta ) = R_{2,3} (\delta )$, we have $\alpha _{2,3} (-\delta ) = -\alpha _{2,3}(\delta )$, as seen in Fig. 7 in Appendix A.2.

In the next section, we discuss the predictions of the minimal gauged $\hbox {U}(1)_{L_\mu - L_\tau }$ model with the recent oscillation data. Before closing this section, let us give some general remarks.

• If the $\hbox {U}(1)_{L_\mu - L_\tau }$ symmetry breaking scale is much higher than the electroweak scale, we expect sizable quantum corrections to the neutrino-mass matrix. Such quantum corrections can be taken into account by using renormalization-group equations. Remarkably, it is found that the two-zero minor structure of $\mathcal{M}_{\nu _L}$ is preserved throughout the renormalization-group flow [46, 47]. To see this, we first note that below the right-handed neutrino-mass scale, which is around the $\hbox {U}(1)_{L_\mu - L_\tau }$ symmetry breaking scale in this model, right-handed neutrinos are integrated out to give the following dimension-five effective operator:

  $$\begin{aligned} \mathcal{L}_\mathrm{eff} = \frac{1}{2}C_{\alpha \beta } (L_\alpha \cdot H) (L_\beta \cdot H) +\text {h.c.}, \end{aligned}$$

  (22)

  where $C_{\alpha \beta }$ has the two-zero minor structure at the right-handed neutrino-mass scale. The renormalization-group equation of the Wilson coefficient $C_{\alpha \beta }$ at one-loop level is [60]

  $$\begin{aligned} \mu \frac{\mathrm{d}C}{\mathrm{d}\mu } = -\frac{3}{32\pi ^2}\left[ \left( Y_e^\dagger Y_e^{}\right) ^T C + C \left( Y_e^\dagger Y_e^{}\right) \right] +\frac{K}{16\pi ^2} C, \end{aligned}$$

  (23)

  with

  $$\begin{aligned} K = -3g_2^2 + 2 \mathrm{Tr} \left( 3 Y_u^\dagger Y_u^{} + 3Y_d^\dagger Y_d^{} + Y_e^\dagger Y_e^{} \right) + 2\lambda , \end{aligned}$$

  (24)

  where $Y_u$, $Y_d$, and $Y_e$ denote the up-type, down-type, and charged-lepton Yukawa matrices, respectively, $g_2$ is the SU(2)$_L$ gauge coupling, and $\lambda$ is the Higgs quartic coupling: $\mathcal{L}_\mathrm{quart} = -\frac{1}{2}\lambda (H^\dagger H)^2$. Now recall that the charged-lepton Yukawa matrix is diagonal in our model. In this case, the above equation can readily be solved as follows [61]:

  $$\begin{aligned} C(t) = I_K (t) \, \mathcal{I}(t)\, C(0) \,\mathcal{I}(t), \end{aligned}$$

  (25)

  where $t \equiv \ln (\mu /\mu _0)$ with $\mu _0$ being the initial scale, and

  $$\begin{aligned} I_K(t)&= \exp \left[ \frac{1}{16\pi ^2} \int _0^t K(t^\prime )\, \mathrm{d}t^\prime \right] , \nonumber \\ \mathcal{I}(t)&= \exp \left[ - \frac{3}{32\pi ^2} \int _0^t Y^\dagger _e Y_e^{}(t^\prime )\, \mathrm{d}t^\prime \right] . \end{aligned}$$

  (26)

  Note that $\mathcal{I}(t)$ is a diagonal matrix. Therefore, if $C_{\mu \mu }^{-1} (0) = C^{-1}_{\tau \tau } (0) = 0$, then $C_{\mu \mu }^{-1} (t) = C^{-1}_{\tau \tau } (t) = 0$, which proves that the two-zero minor structure of the Wilson coefficient C remains at low energies. As a result, the two-zero minor neutrino-mass structure in our model is robust against quantum corrections, even if the $\hbox {U}(1)_{L_\mu - L_\tau }$ symmetry breaking scale is much higher than the electroweak scale.

• By performing a similar analysis, we can study the minimal gauged $\hbox {U}(1)_{L_e- L_\mu }$ and $\hbox {U}(1)_{L_e- L_\tau }$ models. We again obtain two conditions, similar to Eqs. (10) and (11), which follow from the zero components in the inverse of the neutrino-mass matrix in each model. We, however, find that in these cases it is unable to find parameter space consistent with the observed values of the neutrino oscillation parameters, as demonstrated in Appendix B. We thus conclude that within the minimal approach discussed in this paper, the $\hbox {U}(1)_{L_\mu - L_\tau }$ case is the only possibility that offers a desirable neutrino-mass structure.

• If we go beyond the minimal model, we may obtain a different neutrino-mass structure in the presence of the $\hbox {U}(1)_{L_\mu - L_\tau }$ gauge symmetry. For example, Refs. [25, 33] discuss gauged $\hbox {U}(1)_{L_\mu - L_\tau }$ models where neutrino masses are radiatively induced at one-loop level. It turns out that the neutrino-mass matrices in these models have the form of the two-zero texture [62,63,64,65,66], which predicts IO for neutrino-mass spectrum. Thus, the determination of neutrino-mass hierarchy in future neutrino experiments allows us to distinguish this class of models from the minimal model, where NO is predicted as we have seen above.

3 Predictions for the neutrino parameters

Using the results obtained above, we now compute quantities relevant to neutrino experiments with the errors in the neutrino oscillation parameters taken into account. For input values, we use the values given in Ref. [51], which are summarized in Table 1. In particular, we take the three mixing angles and the two mass squared differences,

$$\begin{aligned} \theta _{12},~ \theta _{23},~ \theta _{13},~ \delta m^2,~ \Delta m^2, \end{aligned}$$

(27)

as input parameters, and evaluate the predicted values of the other parameters, including Dirac CP phase $\delta$, the absolute masses $m_i$, their sum $\sum _i m_i$, and the effective Majorana neutrino mass $\langle m_{\beta \beta } \rangle$. The prediction for the Majorana phases $\alpha _2$ and $\alpha _3$ is also presented in Appendix A.2.

Table 1 Input values for the neutrino oscillation parameters we use in this paper. We take them from Ref. [51]

Fig. 2

The prediction for the Dirac CP phase $\delta$ in the minimal gauged $\hbox {U}(1)_{L_\mu - L_\tau }$ model. The red lines show the CP phase $\delta$ against $\theta _{23}$. $\theta _{23}$ is varied in the 2$\sigma$ range, and the 1$\sigma$ range is in between the vertical thin dotted lines. The dark (light) red bands show the uncertainty coming from the 1$\sigma$ ($2\sigma$) errors in the parameters $\theta _{12}$, $\theta _{13}$, $\delta m^2$, and $\Delta m^2$. We also show the 1$\sigma$ (2$\sigma$) favored region of $\delta$ in the dark (light) horizontal green bands

In Fig. 2, we plot the Dirac CP phase $\delta$ as functions of $\theta _{23}$ in the red lines. We vary $\theta _{23}$ in the 2$\sigma$ renege, where the 1$\sigma$ range is in between the vertical thin dotted lines. The dark (light) red bands show the uncertainty coming from the 1$\sigma$ ($2\sigma$) errors in the other parameters $\theta _{12}$, $\theta _{13}$, $\delta m^2$, and $\Delta m^2$. We find that this uncertainty is dominated by the error in $\theta _{12}$. We also show the 1$\sigma$ (2$\sigma$) favored region of $\delta$ in the dark (light) horizontal green bands. As we discussed in the previous section, there are two solutions for $\delta$ for each value of $\theta _{23}$. Intriguingly, the upper line is right in the middle of the favored range of $\delta$; in particular, $\theta _{23} \simeq 41.5^\circ$ gives $\delta \simeq 1.6\pi$, both of which are within the $1\sigma$ allowed region. Consequently, this model predicts $\delta \simeq 1.59\pi$–$1.70\pi$ ($1.54\pi$–$1.78\pi$) within $1\sigma$ ($2\sigma$). Future neutrino experiments can test this prediction through precision measurements of $\theta _{23}$ and $\delta$ [67].

Fig. 3

a The prediction for the neutrino masses in the minimal gauged $\hbox {U}(1)_{L_\mu - L_\tau }$ model. The neutrino masses $m_i$ are shown as functions of $\theta _{23}$. The other four parameters ($\theta _{12}$, $\theta _{13}$, $\delta m^2$, and $\Delta m^2$) are fixed to their best-fit values. b The sum of the neutrino masses as a function of $\theta _{23}$. The dark (light) red band shows the uncertainty coming from the 1$\sigma$ ($2\sigma$) errors in the parameters $\theta _{12}$, $\theta _{13}$, $\delta m^2$, and $\Delta m^2$. The entire region is within the 2$\sigma$ range of $\theta _{23}$, while its 1$\sigma$ range is between the thin vertical dotted lines. We also show in the black dashed line the present limit imposed by the Planck experiment: $\sum _{i} m_i < 0.23$ eV (Planck TT+lowP+lensing+ext) [68]

Next, we evaluate the neutrino masses $m_i$, which are shown in Fig. 3a as functions of $\theta _{23}$. Here, the other parameters are fixed to be their best-fit values. We see that all of these masses are predicted to be $\gtrsim \sqrt{\Delta m^2} \simeq 5\times 10^{-2}$ eV. We also plot the sum of these neutrino masses as a function of $\theta _{23}$ in Fig. 3b, where the dark (light) red band shows the uncertainty coming from the 1$\sigma$ ($2\sigma$) errors in the parameters other than $\theta _{23}$. In this case, it turns out that the dominant contribution to the uncertainty (except for that from the error in $\theta _{23}$) comes from the error in $\theta _{13}$, though the error in $\Delta m^2$ also gives a sizable contribution. We also show in the black dashed line the present limit imposed by the Planck experiment: $\sum _{i} m_i < 0.23$ eV (Planck TT+lowP+lensing+ext) [68].⁸ From this figure, we find that a wide range of the parameter region predicts a value of $\sum _{i}m_i$ which is below the present limit, though a part of the parameter region has already been disfavored by the Planck limit. We, however, note that this bound relies on the standard cosmological history, and thus if some new physics effects modify the cosmological evolution, then this bound may significantly be relaxed. In any case, our model predicts a rather large value of the sum of the neutrino masses, $\sum _{i} m_i \simeq 0.14$–0.22 eV (0.12–0.40 eV) at $1\sigma$ ($2\sigma$), which may be probed in future cosmological observations.

These relatively large values of $m_i$ open up a possibility of testing this model in neutrinoless double-beta decay experiments. The rate of neutrinoless double-beta decay is proportional to the square of the effective Majorana neutrino mass $\langle m_{\beta \beta } \rangle$, which is given by

$$\begin{aligned} \langle m_{\beta \beta } \rangle&\equiv \left| \sum _{i} U_{ei}^2 m_i \right| \nonumber \\&= \left| c_{12}^2 c_{13}^2 m_1 + s_{12}^2 c_{13}^2 e^{i \alpha _2} m_2 + s_{13}^2 e^{i(\alpha _3 -2\delta )} m_3 \right| ~. \end{aligned}$$

(28)

It should be emphasized that, in the minimal gauged $\hbox {U}(1)_{L_\mu - L_\tau }$ model, not only the neutrino masses $m_i$ but also the Majorana phases $\alpha _{2,3}$ are uniquely determined as functions of the other neutrino oscillation parameters. Thus, the value of the effective mass $\langle m_{\beta \beta } \rangle$ is also predicted unambiguously. Note also that this quantity has reflection symmetry with respect to $\delta \rightarrow -\delta$ and thus depends only on $\cos \delta$. In Fig. 4, we show $\langle m_{\beta \beta } \rangle$ as a function of $\theta _{23}$, where the dark (light) red band shows the uncertainty coming from the 1$\sigma$ ($2\sigma$) errors in the parameters other than $\theta _{23}$. Currently, the KamLAND-Zen experiment gives the strongest bound on $\langle m_{\beta \beta } \rangle$: $\langle m_{\beta \beta } \rangle <0.061$–0.165 eV [69] where the uncertainty stems from the estimation of the nuclear matrix element for $^{136}$Xe. We also show in Fig. 4 the most severe bound from KamLAND-Zen, $\langle m_{\beta \beta } \rangle <0.061$ eV, in the black dashed line [69]. As can be seen, most parameter region predicts a value of $\langle m_{\beta \beta } \rangle$ lower than the strongest bound. At $1\sigma$ ($2\sigma$) level, this model predicts $\langle m_{\beta \beta }\rangle \gtrsim 0.024$ eV (0.017 eV)—this can be within the reach of future neutrinoless double-beta decay experiments [70].

Fig. 4

The prediction for the effective Majorana neutrino mass $\langle m_{\beta \beta } \rangle$ as a function of $\theta _{23}$ in the minimal gauged $\hbox {U}(1)_{L_\mu - L_\tau }$ model. The dark (light) red band shows the uncertainty coming from the 1$\sigma$ ($2\sigma$) errors in the parameters other than $\theta _{23}$. The entire region is within the 2$\sigma$ range of $\theta _{23}$, while its 1$\sigma$ range is between the thin vertical dotted lines. We also show the strongest limit from KamLAND-Zen, $\langle m_{\beta \beta } \rangle <0.061$ eV, in the black dashed line [69]

4 Implications for Leptogenesis

In this section, we discuss the implications of our results for the leptogenesis scenario [71], which is one of the most attractive mechanisms to explain the origin of the baryon asymmetry of the Universe. The minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model has three right-handed neutrinos coupled to the Standard Model leptons, and therefore it contains enough ingredients for the leptogenesis: the CP-violating decay of the right-handed neutrino in the early Universe can generate the lepton asymmetry, which is converted to the baryon asymmetry via the sphaleron process [72].

As we have seen in the previous sections, the light neutrino mass matrix $\mathcal{M}_{\nu _L} \simeq U^* \text {diag}(m_1, m_2, m_3) U^\dagger$ in the minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model is uniquely determined for a given set of neutrino oscillation parameters $\theta _{12},~ \theta _{23},~ \theta _{13},~ \delta m^2,~ \Delta m^2$, and $\text {sign}(\sin \delta )$. Therefore, the mass matrix of the right-handed neutrino, $\mathcal{M}_R \simeq - \mathcal{M}_D \mathcal{M}_{\nu _L}^{-1} \mathcal{M}_D$, is also tightly constrained, having only three additional free parameters, $\lambda _{e}$, $\lambda _\mu$ and $\lambda _\tau$. Note that these neutrino Yukawa couplings can be taken to be real and positive by field redefinitions. Therefore, there is no additional phase parameter in the model. By diagonalizing the masses of the right-handed neutrinos, we can rewrite the Lagrangian (3) as

$$\begin{aligned} \Delta \mathcal{L}&= -\sum _{i=1}^3 \sum _{\alpha =e,\mu ,\tau } \widehat{\lambda }_{i\alpha } \widehat{N}_i^c (L_\alpha \cdot H) \nonumber \\&\quad -\frac{1}{2}\sum _{i=1}^3M_i \widehat{N}_i^c \widehat{N}_i^c +\text {h.c.} ~, \end{aligned}$$

(29)

where $\widehat{N}_i^c$ are the right-handed neutrino fields in the basis where the masses are diagonalized, $\widehat{\lambda }_{i\alpha }$ are the neutrino Yukawa couplings in that basis, and $M_i$ are the masses which are taken to be real and positive. Explicitly, they are given by

$$\begin{aligned}&\mathcal{M}_R = \Omega ^* \text {diag}(M_1, M_2, M_3) \Omega ^\dagger , \quad \Omega ^\dagger \Omega = I, \end{aligned}$$

(30)

$$\begin{aligned}&\widehat{N}^c_i = \sum _{\alpha } \Omega _{\alpha i}^* N_\alpha ^c, \end{aligned}$$

(31)

$$\begin{aligned}&\widehat{\lambda }_{i\alpha } = \Omega _{\alpha i}\lambda _{\alpha }~~\text {(not summed)}. \end{aligned}$$

(32)

We emphasize again that both masses $M_i$ and the couplings $\widehat{\lambda }_{i\alpha }$ are completely determined by the three real parameters $\lambda _{e,\mu ,\tau }$ and the oscillation parameters $\theta _{12},~ \theta _{23},~ \theta _{13},~ \delta m^2, \Delta m^2$, $\text {sign}(\sin \delta )$.

One of the most important parameters in the leptogenesis scenario is the asymmetry parameter $\epsilon _1$, which represents the lepton asymmetry generated by the decay of the lightest right-handed neutrino. At the leading order, it is given by [73,74,75]

$$\begin{aligned}&\epsilon _1 = \frac{1}{8\pi } \frac{1}{ (\widehat{\lambda }\,\,\widehat{\lambda }^\dagger )_{11} } \sum _{j=2,3} \text {Im}\left[ \{(\widehat{\lambda }\,\,\widehat{\lambda }^\dagger )_{1j}\}^2 \right] f\left( \frac{M_j^2}{M_1^2}\right) , \end{aligned}$$

(33)

$$\begin{aligned}&f(x) = \sqrt{x}\left[ 1-(x+1)\ln \left( 1+\frac{1}{x}\right) -\frac{1}{x-1} \right] . \end{aligned}$$

(34)

Here, one can see that there is a correlation between the sign of the Dirac phase $\delta$ and the baryon asymmetry of the Universe. Suppose that the sign of the Dirac phase $\delta$ is flipped, $\delta \rightarrow -\delta$, while the other input oscillation parameters $\theta _{12},~ \theta _{23},~ \theta _{13},~ \delta m^2,~ \Delta m^2$ as well as the neutrino Yukawa couplings $\lambda _{e,\mu ,\tau }$ are fixed. As discussed in the previous sections, the Majorana phases then flip the sign, $\alpha _{2,3}\rightarrow -\alpha _{2,3}$, while the absolute masses of light neutrinos do not change, $m_i\rightarrow m_i$. Thus, the PMNS matrix transforms as $U\rightarrow U^*$. This then results in $\mathcal{M}_{\nu _L}\rightarrow \mathcal{M}_{\nu _L}^*$, leading to $\mathcal{M}_R\rightarrow \mathcal{M}_R^*$, $\Omega \rightarrow \Omega ^*$, $\widehat{\lambda }\rightarrow \widehat{\lambda }^*$, and eventually $\epsilon _1\rightarrow -\epsilon _1$. This means that, for a given input of oscillation parameters $\theta _{12},~ \theta _{23},~ \theta _{13},~ \delta m^2,~ \Delta m^2$ and the neutrino Yukawa couplings $\lambda _{e,\mu ,\tau }$, there is one-to-one correspondence between the sign of the Dirac phase $\delta$ and the sign of the baryon asymmetry of the Universe.

Fig. 5

The asymmetry parameter $\epsilon _1/\lambda ^2$ as a function of the diagonal neutrino Yukawa couplings, which are parametrized as $(\lambda _e,\lambda _\mu ,\lambda _\tau ) =\lambda (\cos \theta , \sin \theta \cos \phi , \sin \theta \sin \phi )$. The input oscillation parameters $(\theta _{12}, \theta _{23}, \theta _{13}, \delta m^2, \Delta m^2)$ are taken to be their best-fit values in Table 1, while the sign of the Dirac phase $\delta$ is taken to be negative, $\delta <0$ (or $\delta >\pi$)

Fig. 6

The sign of the asymmetry parameter $\epsilon _1$ and contours of the right-handed neutrino-mass ratios $M_2/M_1$ (left) and $M_3/M_1$ (right) in the $(\theta , \phi )$ plane, where the neutrino Yukawa couplings are parametrized as $(\lambda _e,\lambda _\mu ,\lambda _\tau ) =\lambda (\cos \theta , \sin \theta \cos \phi , \sin \theta \sin \phi )$. The input oscillation parameters $(\theta _{12}, \theta _{23}, \theta _{13}, \delta m^2, \Delta m^2)$ are taken to be their best-fit values in Table 1, while the sign of the Dirac phase $\delta$ is taken to be negative, $\delta <0$ (or $\delta >\pi$). The green cross corresponds to $\lambda _e = \lambda _\mu = \lambda _\tau$

In Fig. 5, we show the asymmetry parameter $\epsilon _1/\lambda ^2$ as a function of the neutrino Yukawa couplings, which are parametrized as $(\lambda _e,\lambda _\mu ,\lambda _\tau ) =\lambda (\cos \theta , \sin \theta \cos \phi , \sin \theta \sin \phi )$.⁹ Note that the parameter $\epsilon _1$ scales as $\epsilon _1\propto \lambda ^2$ in this parametrization, as shown in Eq. (33). The oscillation parameters $\theta _{12},~ \theta _{23},~ \theta _{13},~ \delta m^2,~ \Delta m^2$ are taken to be their best-fit values in Table 1. The sign of the Dirac phase $\delta$ is taken to be negative, $\delta <0$ (or $\delta >\pi$), as it is favored at 2$\sigma$ level. Note that the observed baryon asymmetry of the Universe requires $\epsilon _1<0$, because the sphaleron process predicts $n_B/n_L <0$ [76]. Surprisingly, negative $\epsilon _1$ is realized only in the limited regions of the parameter space. This is more clearly seen in Fig. 6, where we show the regions of $\epsilon _1<0$ in the $(\theta ,\phi )$ plane as red shaded areas. We also show the contours of the right-handed neutrino-mass ratios $M_{2}/M_1$ and $M_3/M_1$ in the left and right panels, respectively. As we see, the asymmetry parameter $\epsilon _1$ can be negative when some of the right-handed neutrinos are degenerate in mass—$M_1 \simeq M_2$ in the negative $\epsilon _1$ region around $\phi \simeq \pi /4$ while $M_2 \simeq M_3$ for $\theta \simeq \pi /2$ and $\phi \simeq 0, \pi /2$. In the latter regions, $\theta \simeq \pi /2$ and $\phi \simeq 0, \pi /2$, the lightest right-handed neutrino mass is much smaller than the other ones, and $\lambda _{e, \tau } \ll \lambda _\mu$ ($\lambda _{e, \mu } \ll \lambda _\tau$) for $\phi \simeq 0$ ($\phi \simeq \pi /2$). In these cases, the absolute value of the asymmetry parameter $|\epsilon _1|$ is found to be quite suppressed, and thus it is rather difficult to obtain a sizable value, say $|\epsilon _1| \gtrsim 10^{-6}$.¹⁰ Similarly, $|\epsilon _1|$ gets small for $\phi \simeq \pi /4$ and $\theta \ll \pi /4$. These observations further restrict the promising parameter region for leptogenesis to be $(\theta , \phi ) \simeq (\pi /4, \pi /4)$.

The final baryon asymmetry depends on the production mechanism of the right-handed neutrino. In the case of thermal leptogenesis, the predicted range of the lightest neutrino mass in the present model, $m_1\gtrsim 0.03~\text {eV}$, corresponds to the so-called strong wash-out region (see, e.g., [77]). Moreover, as we see from Fig. 6, around $(\theta , \phi ) \simeq (\pi /4, \pi /4)$, right-handed neutrino masses are close to each other. In this case, to properly estimate the net baryon asymmetry generated via the decay of right-handed neutrinos, we may need to include not only the contribution of the lightest right-handed neutrino but those of the other ones. Flavor effects [78,79,80] may also become important. A more detailed study will be given elsewhere [81].

5 Conclusions

We have studied the structure of the neutrino-mass matrix in the minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model. Because of the $\hbox {U}(1)_{L_\mu -L_\tau }$ gauge symmetry, the structure of both Dirac and Majorana mass terms of neutrinos is tightly restricted, which results in a two-zero minor structure of the neutrino-mass matrix. Because of this restriction, all the CP phases and the neutrino masses are uniquely determined. We find that this model gives the following prediction at $1\sigma$ ($2\sigma$) level:

• Dirac CP phase: $\delta \simeq 1.59\pi$–$1.70\pi$ ($1.54\pi$–$1.78\pi$),

• the sum of the neutrino masses: $\sum _{i}m_i \simeq 0.14$–0.22 eV (0.12–0.40 eV),

• the effective mass for the neutrinoless double-beta decay: $\langle m_{\beta \beta }\rangle \simeq 0.024$–0.055 eV (0.017–0.12 eV).

They are totally consistent with the current experimental limits, and hold independently of the $\hbox {U}(1)_{L_\mu -L_\tau }$ breaking scale and the Majorana mass scale. In this sense, the above predictions are the generic features of the minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model. Remarkably, these predictions can be tested in various neutrino experiments in the near future – regardless of the scale of the $\hbox {U}(1)_{L_\mu - L_\tau }$ symmetry breaking – which we believe sheds light on the gauge structure of physics beyond the Standard Model.

We have also discussed the implications of the minimal gauged $\hbox {U}(1)_{L_\mu - L_\tau }$ model for the leptogenesis scenario, and found that the correct sign of the baryon asymmetry of the Universe can be obtained only in the limited regions of the parameter space, as the right-handed neutrino-mass structure is also severely restricted in this model. In particular, the observed value of baryon asymmetry can be realized when right-handed neutrinos are degenerate in mass, which requires a further detailed study to assess the viability of leptogenesis in this model [81].

Appendices

Appendix

A Miscellaneous formulas

Here we give formulas that are useful for the study of the neutrino-mass structure in the minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model.

1.1 A.1 Neutrino-mass matrix $\mathcal{M}_{\nu _L}$

The light neutrino-mass matrix $\mathcal{M}_{\nu _L}$ in Eq. (6) can be expressed in terms of the Lagrangian parameters in Eq. (3) as¹¹

$$\begin{aligned} \mathcal{M}_{\nu _L}&= \frac{v^2}{2(M_{ee} M_{\mu \tau } - 2 \lambda _{e\mu } \lambda _{e\tau } \langle \sigma \rangle ^2)} \times \begin{pmatrix} -\lambda _e^2 M_{\mu \tau } &{} \lambda _e \lambda _\mu \lambda _{e\tau } \langle \sigma \rangle &{} \lambda _e \lambda _\tau \lambda _{e\mu } \langle \sigma \rangle \\ \lambda _e \lambda _\mu \lambda _{e\tau } \langle \sigma \rangle &{} - \frac{\lambda _\mu ^2 \lambda _{e\tau }^2 \langle \sigma \rangle ^2}{ M_{\mu \tau }} &{} \frac{\lambda _\mu \lambda _\tau (-M_{ee} M_{\mu \tau } +\lambda _{e\mu } \lambda _{e\tau } \langle \sigma \rangle ^2)}{M_{\mu \tau }} \\ \lambda _e \lambda _\tau \lambda _{e\mu } \langle \sigma \rangle &{} \frac{\lambda _\mu \lambda _\tau (-M_{ee} M_{\mu \tau } +\lambda _{e\mu } \lambda _{e\tau } \langle \sigma \rangle ^2)}{M_{\mu \tau }} &{} -\frac{\lambda _\tau ^2 \lambda _{e\mu }^2 \langle \sigma \rangle ^2}{M_{\mu \tau }} \end{pmatrix}.\quad \quad \quad \quad \quad \quad \quad \quad \quad \end{aligned}$$

(A.1)

The determinant of this mass matrix is given by

$$\begin{aligned} \text {det}\left( \mathcal{M}_{\nu _L}\right) =\frac{\lambda _e^2 \lambda _\mu ^2 \lambda _\tau ^2 v^6}{8 M_{\mu \tau } \left( M_{ee} M_{\mu \tau } -2\lambda _{e\mu } \lambda _{e\tau } \langle \sigma \rangle ^2 \right) }. \end{aligned}$$

(A.2)

We find that this determinant vanishes if and only if $\lambda _\nu = 0$ ($\nu = e$, $\mu$, or $\tau$). In this case, the mass matrix $\mathcal{M}_{\nu _L}$ is block-diagonal, and thus cannot reproduce the required neutrino mixing angles.

1.2 A.2 $R_2$ and $R_3$

The functions $R_2(\delta )$ and $R_3(\delta )$ defined in Eqs. (13) and (14), respectively, are expressed in terms of neutrino oscillation parameters as

$$\begin{aligned} R_2(\delta ) = -\frac{2\sin ^2\theta _{12}\cos 2\theta _{23} + \sin 2\theta _{12} \sin 2\theta _{23} \sin \theta _{13} e^{i\delta }}{2\cos ^2\theta _{12}\cos 2\theta _{23} - \sin 2\theta _{12} \sin 2\theta _{23} \sin \theta _{13} e^{i\delta }}, \nonumber \\ \end{aligned}$$

(A.3)

$$\begin{aligned}&R_3(\delta ) = - \frac{\sin \theta _{13} e^{2i\delta } \left[ 2\cos 2\theta _{12} \cos 2\theta _{23} \sin \theta _{13} -\sin 2\theta _{12} \sin 2\theta _{23} \left( e^{-i\delta }+\sin ^2 \theta _{13} e^{i\delta }\right) \right] }{\cos ^2 \theta _{13} \left[ 2\cos ^2\theta _{12}\cos 2\theta _{23} -\sin 2\theta _{12} \sin 2\theta _{23} \sin \theta _{13} e^{i\delta }\right] }. \end{aligned}$$

(A.4)

Using Eq. (19) together with Eq. (A.3), we find

$$\begin{aligned} m_1 = \delta m\biggl [ \frac{4s^4_{12} \cos ^2 2\theta _{23} + 4s^3_{12} c_{12}s_{13} \sin 4\theta _{23} \cos \delta + s^2_{13} \sin ^2 2\theta _{12} \sin ^2 2\theta _{23} }{2\left( 2\cos 2\theta _{12} \cos ^2 2\theta _{23} - s_{13} \sin 2\theta _{12} \sin 4\theta _{23} \cos \delta \right) } \biggr ]^{\frac{1}{2}} ~. \end{aligned}$$

(A.5)

This expression shows that $m_1$ depends only on $\cos \delta$ (not $\sin \delta$), as we have argued in Sect. 2.

Fig. 7

Majorana phases $\alpha _i$ as functions of $\delta$. We fix the other neutrino oscillation parameters to be their best-fit values. The green band depicts the 2$\sigma$ favored region of $\delta$ predicted in the minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model

Using Eqs. (12), (A.3), and (A.4), we determine the Majorana CP phases $\alpha _{2,3}$ as functions of $\delta$, and show them in Fig. 7. Here, we fix the other neutrino oscillation parameters to be their best-fit values. The green band depicts the 2$\sigma$ favored region of $\delta$ predicted in the minimal gauged $\hbox {U}(1)_{L_\mu -L_\tau }$ model. As can be seen, sizable Majorana CP phases are predicted in this model. In addition, we find $\alpha _{2,3} (-\delta ) = -\alpha _{2,3}(\delta )$ (or $\alpha _{2,3} (\pi -\delta ) = -\alpha _{2,3}(\pi + \delta )$), as discussed in Sect. 2.

1.3 A.3 Cubic equation for $\cos \delta$

Here, we show a cubic equation whose real solution in terms of x gives $\cos \delta$:

$$\begin{aligned}&s^2_{13} \bigl [ 4s^2_{13}\cos ^2 2\theta _{12} \cos ^2 2\theta _{23} -s_{13} \sin 4\theta _{12} \sin 4\theta _{23} (1+s_{13}^2) \,x \nonumber \\&\quad +\sin ^2 2\theta _{12} \sin ^2 2\theta _{23} \left( c^4_{13} + 4s^2_{13} \,x^2\right) \bigr ] \nonumber \\&\quad \times \bigl [ 2\left( 2\cos 2\theta _{12} \cos ^2 2\theta _{23} - s_{13} \sin 2\theta _{12} \sin 4\theta _{23} \,x \right) \bigr ] \nonumber \\&\quad -\epsilon \left[ 4s^4_{12} \cos ^2 2\theta _{23} + s^2_{13} \sin ^2 2\theta _{12} \sin ^2 2\theta _{23}\right. \nonumber \\&\quad \left. + 4s^3_{12} c_{12}s_{13} \sin 4\theta _{23} \, x \right] \nonumber \\&\quad \times \bigl [4\cos ^2 2\theta _{23} (c^4_{12} c^4_{13}-s^4_{13}\cos ^2 2\theta _{12}) - s_{13}\sin 4\theta _{23} \nonumber \\&\quad \times \{4c_{13}^4 c^3_{12} s_{12} -s^2_{13} \sin 4\theta _{12} (1+s^2_{13}) \} \, x \nonumber \\&\quad - 4 s^4_{13} \sin ^2 2 \theta _{12} \sin ^2 2\theta _{23} \, x^2 \bigr ] = 0 ~, \end{aligned}$$

(A.6)

where

$$\begin{aligned} \epsilon \equiv \frac{\delta m^2}{\Delta m^2 +{\delta m^2}/{2}}~. \end{aligned}$$

(A.7)

In the limit of $\epsilon \rightarrow 0$, the above equation leads to

$$\begin{aligned}&4s^2_{13}\cos ^2 2\theta _{12} \cos ^2 2\theta _{23} -s_{13} \sin 4\theta _{12} \sin 4\theta _{23} \left( 1+s_{13}^2\right) \,x \nonumber \\&\quad +\sin ^2 2\theta _{12} \sin ^2 2\theta _{23} \left( c^4_{13} + 4s^2_{13} \,x^2\right) =0 ~, \end{aligned}$$

(A.8)

or

$$\begin{aligned} 2\cos 2\theta _{12} \cos ^2 2\theta _{23} - s_{13} \sin 2\theta _{12} \sin 4\theta _{23} \,x = 0~. \end{aligned}$$

(A.9)

The discriminant of the quadratic Eq. (A.8) is given by

$$\begin{aligned} 8c_{13}^4 s_{13}^2 \sin ^2 2\theta _{12} \sin ^2 2\theta _{23} (\cos 4\theta _{12} + \cos 4\theta _{23}) ~, \end{aligned}$$

(A.10)

which is negative as $\cos 4\theta _{12} + \cos 4\theta _{23} \simeq -1.63 < 0$. Thus, Eq. (A.8) does not give a real solution. On the other hand, Eq. (A.9) gives

$$\begin{aligned} x = \frac{\cot 2\theta _{12} \cot 2\theta _{23}}{\sin \theta _{13}} ~, \end{aligned}$$

(A.11)

which agrees with Eq. (21). From the above derivation, we see that the solution (A.11) approximates the real solution of the cubic equation (A.6) with an accuracy of $\mathcal{O}(\epsilon ) = \mathcal{O}(\delta m^2/\Delta m^2)$.

B $\hbox {U}(1)_{L_e-L_\mu }$ and $\hbox {U}(1)_{L_e-L_\tau }$

In this section, we examine the neutrino-mass structure in the minimal gauged $\hbox {U}(1)_{L_e-L_\mu }$ and $\hbox {U}(1)_{L_e-L_\tau }$ models and show that it is unable to obtain a solution that is consistent with the observed values of the neutrino oscillation parameters.¹²

Fig. 8

The mass ratios $m_2/m_1$ and $m_3/m_1$ as functions of the Dirac CP phase $\delta$ for the gauged a $\hbox {U}(1)_{L_e-L_\mu }$ and b $\hbox {U}(1)_{L_e-L_\tau }$ models. The bands show uncertainty coming from the 1$\sigma$ error in the neutrino mixing parameters. The thin dotted line corresponds to $m_{2,3}/m_1 = 1$

1.1 B.1 $\hbox {U}(1)_{L_e-L_\mu }$

Following an analysis similar to that in Sect. 2, we find that the (e, e) and $(\mu , \mu )$ components in the inverse of the neutrino-mass matrix vanish in the minimal gauged $\hbox {U}(1)_{L_e-L_\mu }$ model. The corresponding two vanishing conditions are

$$\begin{aligned} \frac{1}{m_1}V_{e 1}^2 + \frac{1}{m_2}V_{e 2}^2\,\mathrm{e}^{i\alpha _2} + \frac{1}{m_3}V_{e 3}^2\,\mathrm{e}^{i\alpha _3}&= 0 ~, \end{aligned}$$

(B.1)

$$\begin{aligned} \frac{1}{m_1}V_{\mu 1}^2 + \frac{1}{m_2}V_{\mu 2}^2\,\mathrm{e}^{i\alpha _2} + \frac{1}{m_3}V_{\mu 3}^2\,\mathrm{e}^{i\alpha _3}&= 0 ~. \end{aligned}$$

(B.2)

Solving these equations, we have

$$\begin{aligned} \mathrm{e}^{i\alpha _2}&=\frac{m_2}{m_1} R_2^{e\mu } (\delta ) ~, \quad \mathrm{e}^{i\alpha _3} =\frac{m_3}{m_1} R_3^{e\mu } (\delta ) ~, \end{aligned}$$

(B.3)

with

$$\begin{aligned} R_2^{e\mu }&\equiv \frac{(V_{e 1} V_{\mu 3} + V_{e 3} V_{\mu 1})V^*_{\tau 2}}{(V_{e 2} V_{\mu 3}+ V_{e 3} V_{\mu 2}) V^*_{\tau 1}} ~, \end{aligned}$$

(B.4)

$$\begin{aligned} R_3^{e\mu }&\equiv \frac{(V_{e 1} V_{\mu 2} + V_{e 2} V_{\mu 1})V^*_{\tau 3}}{(V_{e 2} V_{\mu 3}+ V_{e 3} V_{\mu 2}) V^*_{\tau 1}} ~. \end{aligned}$$

(B.5)

In Fig. 8a, we plot the mass ratios $m_2/m_1$ and $m_3/m_1$ as functions of $\delta$. As we see from this figure, $m_2 < m_1$ is predicted for any value of $\delta$, and thus there is no solution which gives an allowed pattern of neutrino-mass spectrum.

1.2 B.2 $\hbox {U}(1)_{L_e-L_\tau }$

In this case, the (e, e) and $(\tau , \tau )$ components in $\mathcal{M}^{-1}_{\nu _L}$ are zero, which leads to

$$\begin{aligned} \frac{1}{m_1}V_{e 1}^2 + \frac{1}{m_2}V_{e 2}^2\,\mathrm{e}^{i\alpha _2} + \frac{1}{m_3}V_{e 3}^2\,\mathrm{e}^{i\alpha _3}&= 0 ~, \end{aligned}$$

(B.6)

$$\begin{aligned} \frac{1}{m_1}V_{\tau 1}^2 + \frac{1}{m_2}V_{\tau 2}^2\,\mathrm{e}^{i\alpha _2} + \frac{1}{m_3}V_{\tau 3}^2\,\mathrm{e}^{i\alpha _3}&= 0 ~. \end{aligned}$$

(B.7)

These equations read

$$\begin{aligned} \mathrm{e}^{i\alpha _2}&=\frac{m_2}{m_1} R_2^{e\tau } (\delta ) ~, \quad \mathrm{e}^{i\alpha _3} =\frac{m_3}{m_1} R_3^{e\tau } (\delta ) ~, \end{aligned}$$

(B.8)

with

$$\begin{aligned} R_2^{e\tau }&\equiv \frac{(V_{e 1} V_{\tau 3} + V_{e 3} V_{\tau 1})V^*_{\mu 2}}{(V_{e 2} V_{\tau 3}+ V_{e 3} V_{\tau 2}) V^*_{\mu 1}} ~, \end{aligned}$$

(B.9)

$$\begin{aligned} R_3^{e\tau }&\equiv \frac{(V_{e 1} V_{\tau 2} + V_{e 2} V_{\tau 1})V^*_{\mu 3}}{(V_{e 2} V_{\tau 3}+ V_{e 3} V_{\tau 2}) V^*_{\mu 1}} ~. \end{aligned}$$

(B.10)

Using these equations, we plot the mass ratios $m_2/m_1$ and $m_3/m_1$ as functions of $\delta$ in Fig. 8b. Again, $m_2 < m_1$ over the whole range of $\delta$, and thus this model cannot provide a desirable neutrino-mass ordering.