Distinguishing f(R) theories from general relativity by gravitational lensing effect

Abstract

The post-Newtonian formulation of a general class of f(R) theories is set up in a third-order approximation. It turns out that the information of a specific form of f(R) gravity is encoded in the Yukawa potential, which is contained in the perturbative expansion of the metric components. Although the Yukawa potential is canceled in the second-order expression of the effective refraction index of light, detailed analysis shows that the difference of the lensing effect between the f(R) gravity and general relativity does appear at the third order when $\sqrt{f''(0)/f'(0)}$ is larger than the distance $d_0$ to the gravitational source. However, the difference between these two kinds of theories will disappear in the axially symmetric spacetime region. Therefore only in very rare case the f(R) theories are distinguishable from general relativity by gravitational lensing effect in a third-order post-Newtonian approximation.

1 Introduction

Recently modified gravity theories have received increasingly attention in issues related to ”dark energy” [1,2,3], ”dark matter” [4,5,6,7], as well as non-trivial tests on gravity beyond general relativity (GR) [8]. Historically, Einstein’s GR is the simplest relativistic theory of gravity with correct Newtonian limit. To pursue new physics, Weyl and Eddington even began to consider modifying GR just after it was established [9, 10]. From the viewpoints of perturbutive quantum gravity, GR is non-renormalizable [11,12,13,14], while higher-order gravity theories might alleviate the problem. From the phenomenological viewpoints, there are many ways to modify GR, and some empirical approaches seem to have promising prospect, such as Dvali–Gabadadze–Porrati gravity [15], tensor-vector-scalar theory [16] and Einstein-Aether theory [17]. Among such extended theories, particular attention has been devoted to the so-called f(R)-gravity. This kind of theories is based on a generalization of the Einstein Hilbert Lagrangian to nonlinear functions f(R) of the Ricci scalar [18]. f(R)-gravity covers a lot of characteristics of higher-order gravity and is convenient to be operated. Hence, f(R) theories provide an ideal tool to study the possible extension of GR. f(R) theories of gravity can also be non-perturbatively quantized by loop quantum gravity approach [19, 20].

To confront f(R)-gravity with observations in Solar System, one can get constraints on the theories from different measurements, such as the EötWash experiment [21], the geodesic precession of gyroscopes measured by Gravity Probe B [22] and the precession of the binary pulsars PSR J0737-3039 [23]. At cosmological scales one would expect to employ f(R) theories to account for the problems of ”dark energy” [24,25,26] and ”dark matter” [27,28,29] needed in GR. If f(R) gravity could account for dark matter, besides matching the rotation curves of galaxy clusters, it should also match the measurements on gravitational lensing effect [30]. However, it is shown in [31] that, in a second-order post-Newtonian approximation, a rather general class of f(R) theories is indistinguishable from GR in gravitational lensing effect. Nevertheless, we will show in this paper that a class of f(R) theories is indeed distinguishable from GR in gravitational lensing effect in a third-order post-Newtonian approximation. However, the possibility to account for the dark matter problem with f(R) theory in lensing effect is highly suppressed due to this tiny third-order difference.

This paper is organized as follows. In Sect. 2, we briefly review the field equations of metric f(R)-gravity. In Sect. 3 the post-Newtonian approximation of a class of f(R) theories is formulated to the desired order. In Sect. 4 we introduce the gravitational lensing effect in metric theories of gravity and show how the f(R) gravity can be distinguishable from GR at third-order post-Newtonian approximation. The difference of the lensing reflection indices is discussed in an example. Finally, conclusions and remarks are given in Sect. 5. Throughout the paper, the metric tensor $g_{\mu \nu }$ takes the signature $(-,+,+,+)$.

2 Field equations of f(R) theory

In metric f(R) theories of gravity, the action of gravity coupled to matter fields is given by

$$\begin{aligned} S=\frac{1}{2\chi }{\int }f(R)\sqrt{-g} \mathrm {d}^{4}x+S_{M}, \end{aligned}$$

(2.1)

where g is the determinant of the metric tensor $g_{{\mu }{\nu }}$, $\chi =8{\pi }G/c^{4}$ with G and c being the Newtonian gravitational constant and the vacuum speed of light, respectively, $R=g^{{\mu }{\nu }}R_{{\mu }{\nu }}$ is the Ricci scalar, f(R) is a nonlinear function and $S_{M}$ is the standard matter action. The variation of action (2.1) with respect to the metric $g_{\mu {\nu }}$ yields the Euler–Lagrange equations

$$\begin{aligned}&f'(R)R_{\mu \nu }-\frac{1}{2}f(R)g_{\mu \nu }-\nabla _{\mu }\nabla _{\nu }f'(R)\nonumber \\&\quad +\,g_{\mu \nu }\square _gf'(R)={\chi }T_{\mu \nu }, \end{aligned}$$

(2.2)

where $\nabla _{\mu }$ is the covariant derivative for $g_{{\mu }{\nu }}$, $\square _g:=\nabla ^{\mu }\nabla _{\mu }$, and $T_{{\mu }{\nu }}=(-2c/\sqrt{-g})(\delta {S}_{M}/{\delta }{g}^{{\mu }{\nu }})$ is the energy momentum tensor of matter. Taking the trace of Eq. (2.2) we can get

$$\begin{aligned} 3\square _gf'(R)+f'(R)R-2f(R)={\chi }T, \end{aligned}$$

(2.3)

where T is the trace of $T_{{\mu }{\nu }}$. Using Eq. (2.3), we can rewrite Eq. (2.2) as

$$\begin{aligned} R_{\mu \nu }= & {} \frac{1}{f'(R)}\left( \frac{1}{3}g_{\mu \nu }f'(R)R-\frac{1}{6}f(R)g_{\mu \nu }\right. \nonumber \\&\left. +\nabla _{\mu }\nabla _{\nu }f'(R)+{\chi }(T_{\mu \nu }-\frac{1}{3}g_{\mu \nu }T)\right) . \end{aligned}$$

(2.4)

3 Post-Newtonian expansion

The matter constituents in the universe are usually well approximated by a perfect fluid with mass density $\rho$ and pressure p [32]. Hence we assume that the Newtonian potential U of the mass distribution, the typical velocities v and the pressure of the fluid obey such approximation respectively. In the post-Newtonian approximation, we can further expand the dynamical variables in the field equations perturbatively in powers of 1 / c, since we have the following order relation [33,34,35]:

$$\begin{aligned} \frac{U }{{{c}^{2}}}\sim \frac{{{v}^{2}}}{{{c}^{2}}}\sim \frac{p}{\rho {{c}^{2}}}\sim \Pi \sim O({2}), \end{aligned}$$

(3.1)

where $\Pi$ is the ratio of the energy density to the rest-mass density.

We consider the case that the gravitational field is weak and assume that in absence of a gravitational field the background space-time is flat [30]. We also assume that $f(0) = 0$, which neglects the contribution of a possible cosmological constant and excludes some form of f(R) theories, e.g, $f(R)=1/R$. Note that actually the contribution of a possible cosmological constant can be equivalently substituted by the corresponding contribution of an energy-momentum tensor. Moreover, the f(R) form which is unable to get weak field solution is useless here. In a weak field regime the metric tensor can be expanded about the Minkowski metric $\eta _{\mu \nu }$ in its Lorentzian coordinate system as

$$\begin{aligned} g_{{\mu }{\nu }}=\eta _{\mu \nu }+h_{\mu \nu }, \end{aligned}$$

(3.2)

where $|h_{\mu \nu }|\ll 1$. Up to third order the components of the metric tensor can be written as [31, 33, 36]:

$$\begin{aligned} \begin{aligned} {{g}_{00}}=&\,-1{{+}^{(2)}}{{h}_{00}}+O(4),\\ {{g}_{0i}}=&\,^{(3)}{{h}_{0i}}+O(5),\\ {{g}_{ij}}=&\,{{\delta }_{ij}}{{+}^{(2)}}{{h}_{ij}}+O(4),\\ \end{aligned} \end{aligned}$$

(3.3)

where the left upper index (n) means the order O(n). Using Eq. (3.3) we can get the components of the Ricci tensor:

$$\begin{aligned} \begin{aligned} {{R}_{00}}=&-\frac{1}{2} {{\nabla }^{2}}{^{(2)}}{h_{00}}+O(4),\\ {{R}_{0i}}=&\,\frac{1}{2}(-{{\nabla }^{2}}{^{(3)}}{h_{0i}} -\frac{1}{c}{^{(2)}h_{jj,0i}}\\&\quad +{^{(3)}h_{j0,ij}}+\frac{1}{c}{^{(2)}h_{ij,0j}})+O(5),\\ {{R}_{ij}}=&\,\frac{1}{2}(-{{\nabla }^{2}}{^{(2)}}{h_{ij}} +{^{(2)}h_{00,ij}}-{^{(2)}h_{kk,ij}}\\&\quad +{^{(2)}h_{ik,kj}}+{^{(2)}h_{kj,ki}})+O(4).\\ \end{aligned} \end{aligned}$$

(3.4)

Assuming f(R) to be analytic at $R = 0$, to the second order the Ricci scalar and thus f(R) and $f'(R)$ read, respectively,

$$\begin{aligned} \begin{aligned} R&=\,^{(2)}R+O(4),\\ f(R)&=f'{{(0)}^{(2)}}R+O(4),\\ f'(R)&=f'(0)+f''{{(0)}^{(2)}}R+O(4).\\ \end{aligned} \end{aligned}$$

(3.5)

To the leading order the components of the energy-momentum tensor of matter fields read

$$\begin{aligned} \begin{aligned}&{\chi {T}^{00}}=\chi {^{(-2)}}{T^{00}}+O(4),\\&{\chi {T}^{0i}}=\chi {^{(-1)}}{T^{0i}}+O(4),\\&{\chi {T}^{ij}}=O(4).\\ \end{aligned} \end{aligned}$$

(3.6)

Note that if $f''(0)=0$, Eq. (3.5) implies that $f'(R)$ is constant. Then Eq. (2.3) yields at the second order $^{(2)}R=-\chi ^{(2)}T_{00}/f'(0)$, which is consistent with the equation of GR at the same order. Thus in this approach, GR is nothing else but the first term of the Taylor expansion of a more general f(R) theory. As one can see from the action (2.1), we ask f(R) to carry the same dimension as R’s. Thus both $f'(R)$ and the term $f''(0) ^{(2)}R$ in Eq. (3.5) are dimensionless. Since the term $f''(0) ^{(2)}R$ is required to be of order O(2), the expansion of Eq. (3.5) will break down if $^{(2)}R {\ge }f'(0)/f''(0)$ [31].

To derive neat equations in the post-Newtonian approximation, we impose the gauge conditions [31, 36]

$$\begin{aligned}&g_{ij,j}-\frac{1}{2}(g_{jj}-g_{00})_{,i}-\frac{f'(R)_{,i}}{f'(R)}=O(4), \end{aligned}$$

(3.7)

$$\begin{aligned}&g_{0j,j}-\frac{1}{2c}g_{jj,0}-\frac{f'(R)_{,0}}{cf'(R)}=O(5). \end{aligned}$$

(3.8)

With the gauge conditions, we get from Eqs. (2.3) and (2.4)

$$\begin{aligned} {{\nabla }^{2(2)}}R&=-\frac{1}{3f''(0)}{{\chi }^{(-2)}}{{T}^{00}} +{{{\frac{f'(0)}{3f''(0)}}}{^{(2)}}R}, \end{aligned}$$

(3.9)

$$\begin{aligned} {{\nabla }^{2(2)}}{{h}_{00}}&=-{\frac{4 \chi }{3f'(0)}}{^{(-2)}{T}^{00}}+\frac{1}{3}{^{(2)}}R, \end{aligned}$$

(3.10)

$$\begin{aligned} {{\nabla }^{2(2)}}{{h}_{ij}}&=-\left( {\frac{2\chi }{3f'(0)}}{^{(-2)}{{T}^{00}}}+\frac{1}{3}{^{(2)}}R\right) {{\delta }_{ij}}, \end{aligned}$$

(3.11)

$$\begin{aligned} \nabla ^2{^{(3)}{h_{0i}}}&=\frac{2\chi }{f'(0)}{^{(-1)}T^{0i}} -\frac{1}{2c}{^{(2)}h_{00,0i}}. \end{aligned}$$

(3.12)

For the sake of physics and simplicity, we consider the case of $f'(0)>0$ and $f''(0)>0$ and define $\alpha ^2:=f'(0)/(3f''(0))$. Note that in this case the constant $1/f'(0)$ can be absorbed into the gravitational constant G if necessary. Then from Eq. (3.9) we can get [34, 36]

$$\begin{aligned} {^{(2)}R}=\frac{2\alpha ^2}{c^2}V(\varvec{x},t), \end{aligned}$$

(3.13)

with the Yukawa potential

$$\begin{aligned} V(\varvec{x},t):=\frac{G}{c^2}\int {\frac{{^{(-2)}T^{00}(\varvec{x}',t)}\mathrm {e}^{-\alpha \vert \varvec{x}-\varvec{x}' \vert }}{\vert \varvec{x}-\varvec{x}' \vert }} \mathrm {d}^3 x'. \end{aligned}$$

(3.14)

Note that the information of a specific form of f(R) gravity is encoded in the parameter $\alpha$ in the potential V, and we only consider the solution with $\alpha >0$. It should be noticed that, for the other solution with $\alpha <0$, the potential V would tend to be divergent at infinity.

It is easy to show by using Eq. (3.9) that Eq. (3.10) can be written as

$$\begin{aligned} {{\nabla }^{2(2)}}{{h}_{00}}=-{\frac{\chi }{f'(0)}} {^{(-2)}{{T}^{00}}}+\frac{f''(0)}{f'(0)}{{\nabla }^{2(2)}}R. \end{aligned}$$

(3.15)

Thus we get

$$\begin{aligned} {{\nabla }^{2}}\left( ^{(2)}{{h}_{00}}-\frac{1}{3\alpha {^2}}{^{(2)}}R\right) =-{\frac{\chi }{f'(0)}} {^{(-2)}{{T}^{00}}}. \end{aligned}$$

(3.16)

Using Eq. (3.13), the solution of Eq. (3.16) can be given by

$$\begin{aligned} {^{(2)}h_{00}(\varvec{x},t)}=\frac{2}{c^2}(U(\varvec{x},t)+\frac{1}{3}V(\varvec{x},t)), \end{aligned}$$

(3.17)

where the Newtonian potential U reads

$$\begin{aligned} U(\varvec{x},t):=\frac{G}{c^2}\int {\frac{{^{(-2)}T^{00}(\varvec{x}',t)}}{\vert \varvec{x}-\varvec{x}' \vert }} \mathrm {d}^3 x'. \end{aligned}$$

(3.18)

It is obvious that the Newtonian potential U remains unchanged for different forms of f(R) gravity. Similarly, the solution of Eq. (3.11) reads

$$\begin{aligned} {^{(2)}h_{ij}(\varvec{x},t)}=\frac{2\delta _{ij}}{c^2}(U(\varvec{x},t)-\frac{1}{3}V(\varvec{x},t)). \end{aligned}$$

(3.19)

From Eqs. (3.10) and (3.11), we have

$$\begin{aligned} {\nabla ^2 }(^{(2)}{h}_{00}-2^{(2)}{{h}_{ii}})= & {} -\frac{4 \chi }{3f'(0)} {^{(-2)}{T}^{00}}+\frac{1}{3}{^{(2)}}R\nonumber \\&+2\left( {\frac{2\chi }{3f'(0)}} {^{(-2)}{T}^{00}}+\frac{1}{3}{^{(2)}}R\right) \nonumber \\= & {} {^{(2)}R}. \end{aligned}$$

(3.20)

Using Eqs. (3.17) and (3.19), it is easy to see that

$$\begin{aligned} {\nabla ^2 }(^{(2)}{h}_{00}-2^{(2)}{{h}_{ii}})=\frac{2}{c^2}{\nabla ^2 }(V-U). \end{aligned}$$

(3.21)

Thus from Eq. (3.13) we have

$$\begin{aligned} V=\frac{1}{{\alpha }^2}{\nabla ^2 }(V-U). \end{aligned}$$

(3.22)

Then Eq. (3.17) can be written as

$$\begin{aligned} {^{(2)}h_{00}(\varvec{x},t)}=\frac{1}{c^2}{\nabla ^2 }\left( -\psi +\frac{2}{{3\alpha }^2}(V-U)\right) , \end{aligned}$$

(3.23)

where the potential $\psi$ is defined as

$$\begin{aligned} \begin{aligned} \psi (\varvec{x},t):=&-\frac{G}{c^2}\int {{^{(-2)}T^{00}(\varvec{x}',t)}\vert \varvec{x}-\varvec{x}' \vert } \mathrm {d}^3x', \end{aligned} \end{aligned}$$

(3.24)

such that ${\nabla ^2 }\psi =-2U$. Hence Eq. (3.12) can be written as

$$\begin{aligned} \nabla ^2\left( {^{(3)}h_{0i}}+\frac{1}{2c^3}\left( -\psi +\frac{2(V-U)}{3\alpha {^2}}\right) _{,0i}\right) =\frac{2{\chi }}{f'(0)}{^{(-1)}T^{0i}}. \end{aligned}$$

(3.25)

The solution of Eq. (3.25) reads

$$\begin{aligned} {^{(3)}h_{0i}(\varvec{x},t)}=\frac{1}{c^3}\left( -4 Y_i(\varvec{x},t)+\frac{1}{2}\psi (\varvec{x},t)_{,0i}+Z(\varvec{x},t)_{,0i}\right) , \end{aligned}$$

(3.26)

where

$$\begin{aligned} \begin{aligned} Y_i(\varvec{x},t):=&\frac{G}{c}\int {\frac{{^{(-1)}T^{0i}}(\varvec{x}',t)}{\vert \varvec{x}-\varvec{x}' \vert }} \mathrm {d}^3x',\\ Z(\varvec{x},t):=&\frac{1}{3\alpha {^2}}(U(\varvec{x},t)-V(\varvec{x},t)). \end{aligned} \end{aligned}$$

(3.27)

So up to third-order post-Newtonian approximation, the final form of the metric components reads

$$\begin{aligned} \begin{aligned} {g_{00}}&=-1+\frac{2}{c^2}U+\frac{2}{3c^2}V,\\ {g_{0i}}&=\frac{1}{c^3}\left( -4 Y_i+\frac{1}{2}\psi _{,0i}+Z_{,0i}\right) ,\\ {g_{ij}}&=\left( 1+\frac{2}{c^2}U-\frac{2}{3c^2}V\right) {\delta _{ij}}.\\ \end{aligned} \end{aligned}$$

(3.28)

In contrast, the metric components to the same order approximation in GR reads [33]

$$\begin{aligned} \begin{aligned} {g_{00}}&=-1+\frac{2}{c^2}U,\\ {g_{0i}}&=\frac{1}{c^3}\left( -4 Y_i+\frac{1}{2}\psi _{,0i}\right) ,\\ {g_{ij}}&=\left( 1+\frac{2}{c^2}U\right) {\delta _{ij}}.\\ \end{aligned} \end{aligned}$$

(3.29)

Hence the difference between the f(R) gravity and GR comes from the Yukawa-like potential V and $Z_{,0i}$. In the limit $f''(0) \rightarrow 0$, we get $\alpha \rightarrow \infty$ and $V \rightarrow 0$. Then the solution (3.28) of f(R) gravity goes back to (3.29) of GR. On the other hand, it is straightforward to see that, in the limit $f''(0) \rightarrow \infty$, we have $\alpha \rightarrow 0$ and hence get the most obvious departure of f(R) gravity from GR.

4 Gravitational lensing

A gravitational lens refers to a distribution of plates (such as a cluster of galaxies) between a distant source (a background galaxy) and an observer that is capable of bending the light from the source, as it travels towards the observer. The lensing effect can magnify and distort the image of the background source [37]. According to Fermat’s principle, the world line of a light should extremize its arrival time T with respect to an observer under the variation of $\gamma$. In metric theories of gravity, this principle implies that the world line of a light coincides with a null geodesic in the spacetime. In the Lorentzian coordinate system of the flat background spacetime, let $dl^2 = \delta _{ij} \mathrm {d}x^i d x^j$ be the spatial Euclidean line element. Up to a constant, the travel time of light on a null geodesic $\gamma$ is given by

$$\begin{aligned} T=\int _{\gamma } \mathrm {d}t\ \text {=}\int _{\gamma }\frac{\mathrm {d}t}{\mathrm {d}l}\mathrm {d}l\ \text {=}\ \frac{1}{c}\int _{\gamma }n\ \mathrm {d}l, \end{aligned}$$

(4.1)

where we defined the effective refraction index of light as

$$\begin{aligned} n:=c\frac{\mathrm {d}t}{\mathrm {d}l} \;. \end{aligned}$$

(4.2)

Then Eq. (4.1) takes the form similar to that of the propagation of a light through a medium in Newtonian space and time.

4.1 Second-order expansion

At the second-order post-Newtonian approximation, the only nonzero perturbative metric components are $h_{00}$ and $h_{ij}$ in Eqs. (3.17) and (3.19). For a null geodesic, we have [31, 38, 39]

$$\begin{aligned} \mathrm {d}{{s}^{2}}= & {} -(1-{}^{(2)}{{h}_{00}}){{c}^{2}}\text {d}{{t}^{2}}+({{\delta }_{ij}}\nonumber \\&+{}^{(2)}{{h}_{ij}})\mathrm {d}{{x}^{i}} \mathrm {d}{{x}^{j}}=0. \end{aligned}$$

(4.3)

Hence we can get

$$\begin{aligned} {{c}^{2}}\mathrm {d}{{t}^{2}}=\frac{{{\delta }_{ij}}+^{(2)}{{h}_{ij}}}{1{{-}^{(2)}}{{h}_{00}}} \mathrm {d}{{x}^{i}} \mathrm {d}{{x}^{j}}=\frac{1+^{(2)}h}{1-^{(2)}{{h}_{00}}}\mathrm {d}{{l}^{2}}, \end{aligned}$$

(4.4)

where h is defined such that Eq. (3.19) can be written as $^{(2)}{h}_{ij} = ^{(2)}h{\delta }_{ij}$. Using Eq. (4.2), we can obtain the effective index of refraction as

$$\begin{aligned} n=c\frac{\mathrm {d}t}{\mathrm {d}l}=\sqrt{\frac{1+{}^{(2)}h}{1-{}^{(2)}{{h}_{00}}}}, \end{aligned}$$

(4.5)

which at the second order reads

$$\begin{aligned} n=1+\frac{1}{2}{{(}^{(2)}}{{h}_{00}}{{+}^{(2)}}h). \end{aligned}$$

(4.6)

By Eqs. (3.17) and (3.19), it equals

$$\begin{aligned} n=1+\frac{2}{c^2}U(x,t), \end{aligned}$$

(4.7)

which illustrates that at second order, the effective refraction index n is only determined by the Newtonian potential U. As shown in Eqs. (3.28) and (3.29), the difference between f(R) gravity and GR comes from the potential V rather than U. Hence one cannot distinguish f(R) theories from GR at second-order approximation by the gravitational lensing effect [31].

4.2 Third-order expansion

We now consider the third-order post-Newtonian approximation which is needed in dealing with light rays in spacetime [33]. At the third-order expansion, the line element of the metric can be written as

$$\begin{aligned} \mathrm {d}{{s}^{2}}= & {} -(1-{}^{(2)}{{h}_{00}}){{c}^{2}}\text {d}{{t}^{2}}+({{\delta }_{ij}}+^{(2)}{{h}_{ij}}) \mathrm {d}{{x}^{i}} \mathrm {d}{{x}^{j}}\nonumber \\&+\,2^{(3)}{{h}_{0i}}c dtd{{x}^{i}}. \end{aligned}$$

(4.8)

For a null geodesic, by using Eq. (4.2) we have

$$\begin{aligned} 0= & {} -(1-{}^{(2)}{{h}_{00}}){n}^2+({{\delta }_{ij}}+^{(2)}{{h}_{ij}})\frac{\mathrm{d}{{x}^{i}} \mathrm {d}{{x}^{j}}}{{\mathrm {d}l}^2}\nonumber \\&+\,2^{(3)}{{h}_{0i}}\frac{\mathrm {d}{{x}^{i}}}{\mathrm {d}l}n. \end{aligned}$$

(4.9)

Thus we obtain

$$\begin{aligned} n=-\,\frac{{^{(3)}h_{0i}}}{-1+{^{(2)}h_{00}}}\frac{\mathrm {d}x^i}{\mathrm {d}l} \pm {F({^{(2)}h_{00}},{^{(2)}h},{^{(3)}h_{0i}})}, \end{aligned}$$

(4.10)

where

$$\begin{aligned} F:= & {} \sqrt{\frac{({^{(3)}h_{0i}}\mathrm {d}x^i)^2}{(1-{^{(2)}h_{00}})^2{\mathrm {d}l}^2} -\frac{(1+{^{(2)}h})({\mathrm {d}x^i}^2)}{(-1+{^{(2)}h_{00}}){\mathrm {d}l}^2}}\nonumber \\= & {} \sqrt{\frac{({^{(3)}h_{0i}}\mathrm {d}x^i)^2}{(1-{^{(2)}h_{00}})^2{\mathrm {d}l}^2} +\frac{1+{^{(2)}h}}{1-{^{(2)}h_{00}}}}. \end{aligned}$$

(4.11)

In the third-order approximation, Eq. (4.11) can be expressed as

$$\begin{aligned} F({^{(2)}h_{00}},{^{(2)}h},{^{(3)}h_{0i}})= & {} F|_{0,0,0}+\frac{\partial F}{\partial {^{(2)}h_{00}}}|_{(0,0,0)}{^{(2)}h_{00}}\nonumber \\&+\frac{\partial F}{\partial {^{(2)}h}}|_{(0,0,0)}{^{(2)}h}\nonumber \\&+\frac{\partial F}{\partial {^{(3)}h_{0i}}}|_{(0,0,0)}{^{(3)}h_{0i}}\nonumber \\&+{^{(4)}E({^{(2)}h_{00}},{^{(2)}h})}+O(5)\nonumber \\= & {} 1+\frac{1}{2} {^{(2)}h_{00}}+\frac{1}{2}{^{(2)}h}+O(4),\nonumber \\ \end{aligned}$$

(4.12)

where ${^{(4)}E({^{(2)}h_{00}},{^{(2)}h})}$ represents the expansion terms at fourth order. It is obvious that the − sign in front of the function F in Eq. (4.10) should be neglected, since otherwise the refraction index n would become negative. Hence Eq. (4.10) becomes

$$\begin{aligned} n= & {} -\frac{{^{(3)}h_{0i}}\frac{\mathrm {d}x^i}{\mathrm {d}l}}{-1+{^{(2)}h_{00}}}+\left( 1+\frac{1}{2} {^{(2)}h_{00}}+\frac{1}{2}{^{(2)}h}\right) \nonumber \\= & {} {^{(3)}h_{0i}}\frac{\mathrm {d}x^i}{\mathrm {d}t}\frac{n}{c}+\left( 1+\frac{1}{2} {^{(2)}h_{00}}+\frac{1}{2}{^{(2)}h}\right) . \end{aligned}$$

(4.13)

It is easy to see that Eq. (4.13) can be solved:

$$\begin{aligned} \begin{aligned} n&=1+\frac{1}{2} {^{(2)}h_{00}}+\frac{1}{2}{^{(2)}h}+\frac{1}{c}{^{(3)}h_{0i}}\frac{\mathrm {d}x^i}{dt}=n_2+\frac{1}{c}{^{(3)}h_{0i}}{u}^{i}, \end{aligned} \end{aligned}$$

(4.14)

where ${u}^{i}=\mathrm {d}x^i/dt$ is the components of the coordinate speed of light, and $n_2:=1+2U(x,t)/{c^2}$ is the refraction index at second order. Therefore, in a third-order post-Newtonian approximation, the effective refraction index of light is obviously dependent on the third-order metric components $h_{0i}$. From Eqs. (3.27), (3.28) and (3.29) one can see that, in contrast to the case of GR, in f(R) gravity $h_{0i}$ is effected also by the Yukawa potential V. Hence, f(R) theories are in principle distinguishable from GR by gravitational lensing effect in a third-order post-Newtonian approximation.

4.3 Differences: an example

Although the difference of lensing effect between f(R) gravity and GR is encoded in the third-order terms, it is still unclear whether the difference can actually be detected at this order and in which case the departure become most obvious. To answer these questions, we first recall from Eq. (4.14) that the difference at third-order effect is contained in the difference of the metric components $h_{0j}$ between f(R) gravity and GR, which reads

$$\begin{aligned} \Delta n:= & {} \frac{u^j}{c}\Delta n_j=\frac{u^j}{c^4}Z_{,0j}u^j\nonumber \\:= & {} \frac{1}{3\alpha {^2} c^4}(U(\varvec{x},t)-V(\varvec{x},t))_{,0j}. \end{aligned}$$

(4.15)

A straightforward calculation leads to

$$\begin{aligned} \Delta n_{j}= & {} \frac{ G}{c^5}\int {\frac{{^{(-2)}T^{00}(\varvec{x}',t)} v'_j }{\vert \varvec{x}-\varvec{x}' \vert } } g(\alpha \vert \varvec{x}-\varvec{x}' \vert ) \mathrm {d}^3 x' \nonumber \\&-\frac{G}{c{^5}}\int \frac{{^{(-2)}T^{00}(\varvec{x}',t)} v' \cdot (\varvec{x}-\varvec{x}')(\varvec{x}-\varvec{x}')_j}{\vert \varvec{x}-\varvec{x}' \vert ^{3}} \nonumber \\&\times h(\alpha \vert \varvec{x}-\varvec{x}' \vert ) \mathrm {d}^3 x', \end{aligned}$$

(4.16)

where

$$\begin{aligned} \begin{aligned} g(\alpha \vert \varvec{x}-\varvec{x}' \vert )&:=\frac{1}{3 \alpha ^2 \vert \varvec{x}-\varvec{x}' \vert ^2}\\&\quad \times \bigg (1-\mathrm {e}^{-\alpha \vert \varvec{x}-\varvec{x}' \vert } (1 + \alpha \vert \varvec{x}-\varvec{x}' \vert ) \bigg ),\\ h(\alpha \vert \varvec{x}-\varvec{x}' \vert )&:=\frac{1}{\alpha ^2 \vert \varvec{x}-\varvec{x}' \vert ^2} \left( \phantom {\left. \times \bigg (1+\alpha \vert \varvec{x}-\varvec{x}' \vert +\frac{1}{3}\alpha ^2 \vert \varvec{x}-\varvec{x}' \vert ^2 \bigg ) \right) }1-\mathrm {e}^{-\alpha \vert \varvec{x}-\varvec{x}'\vert }\right. \\&\quad \left. \times \bigg (1+\alpha \vert \varvec{x}-\varvec{x}' \vert +\frac{1}{3}\alpha ^2 \vert \varvec{x}-\varvec{x}' \vert ^2 \bigg ) \right) \end{aligned} \end{aligned}$$

(4.17)

are two monotone decreasing functions. Hence the lensing refraction indices of f(R) gravity and GR will have the biggest departure in the limit of $\alpha \rightarrow 0$, which reads

$$\begin{aligned} \Delta n_j\sim & {} \frac{G}{6c^5}\int {\frac{{^{(-2)}T^{00}(\varvec{x}',t)} v'_j }{\vert \varvec{x}-\varvec{x}' \vert } } \mathrm {d}^3 x'\nonumber \\&-\frac{G}{6c^5} \int { \frac{{^{(-2)}T^{00}(\varvec{x}',t)} v' \cdot (\varvec{x}-\varvec{x}')(\varvec{x}-\varvec{x}')_j}{\vert \varvec{x}-\varvec{x}' \vert ^3} } \mathrm {d}^3 x'\nonumber \\= & {} \frac{1}{6c^3} \psi _{,0i}. \end{aligned}$$

(4.18)

One may notice that this is nothing else but the potential $\psi _{,0i}$ appearing in the third-order post-Newtonian approximation of GR. Thus, in the case of the highest departure, the difference of the lensing refraction indices is at the same third order of GR.

By noticing that the functions g and h satisfy the relation

$$\begin{aligned} \frac{h(\alpha d)}{d^3}=-\frac{1}{d}\frac{\partial [g(\alpha d)/d]}{\partial d}, \end{aligned}$$

(4.19)

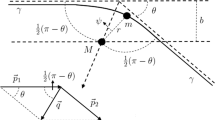
where $d=|\varvec{x}- \varvec{x}'|$, Eq. (4.16) can be further simplified. In terms of cylindrical coordinates $\{r,\theta ,z\}$, Eq. (4.16) can be written as

$$\begin{aligned} \Delta n_{j}= & {} \frac{ G}{c^5}\int {}r' \mathrm {d}r' \mathrm {d}z' \int {\frac{{^{(-2)}T^{00}(\varvec{x}',t)} v'_j }{\vert \varvec{x}-\varvec{x}' \vert } } g(\alpha \vert \varvec{x}-\varvec{x}' \vert ) \mathrm {d}\theta '\nonumber \\&+\frac{G}{c{^5}}\int {} r' \mathrm {d}r' \mathrm {d}z' \nonumber \\&\times \int {} \frac{{^{(-2)}T^{00}(\varvec{x}',t)} v' \cdot (\varvec{x}-\varvec{x}')(\varvec{x}-\varvec{x}')_j}{r r' sin(\theta ')} \frac{\mathrm {d}}{\mathrm {d}\theta '} \nonumber \\&\times \left( \frac{g(\alpha \vert \varvec{x}-\varvec{x}' \vert )}{\vert \varvec{x}-\varvec{x}' \vert } \right) \mathrm {d}\theta ' \nonumber \\= & {} \int {} r' \mathrm {d}r' \mathrm {d}z' \int {} \left( {^{(-2)}T^{00}(\varvec{x}',t)} v'_j \right. \nonumber \\&\left. - \frac{\mathrm {d}}{\mathrm {d}\theta '} \bigg (\frac{{^{(-2)}T^{00}(\varvec{x}',t)} v' \cdot (\varvec{x}-\varvec{x}')(\varvec{x}-\varvec{x}')_j}{r r' sin(\theta ')} \bigg ) \right) \nonumber \\&\times \frac{g(\alpha \vert \varvec{x}-\varvec{x}' \vert )}{\vert \varvec{x}-\varvec{x}' \vert } \mathrm {d}\theta ', \end{aligned}$$

(4.20)

where we used the identity $\mathrm {d}_{\theta '} |\varvec{x}- \varvec{x}'|=\mathrm {d}_{\theta '} \sqrt{r^2+r'^2-2 r r' \cos (\theta ') + (z-z')^2}=r r' \sin (\theta ')/|\varvec{x}- \varvec{x}'|$ and $\theta =0$.

In an axially symmetric spacetime, it is reasonable to consider the case that the velocities v of the gravitational sources are all tangent to the r–$\theta$ plane. Then from Eq. (4.20) one gets

$$\begin{aligned} \Delta n_r= & {} \int {} r' \mathrm {d}r' \mathrm {d}z' \int {} \Bigg ( {-^{(-2)}T^{00}(\varvec{x}',t)} v' \sin (\theta ')\nonumber \\&+ \frac{\mathrm {d}}{\mathrm {d}\theta '} \bigg (\frac{{^{(-2)}T^{00}(\varvec{x}',t)} (v' \sin (\theta ')r)(r - r' cos(\theta '))}{r r' \sin (\theta )} \bigg ) \Bigg ) \nonumber \\&\times \frac{g(\alpha \vert \varvec{x}-\varvec{x}' \vert )}{\vert \varvec{x}-\varvec{x}' \vert } \mathrm {d}\theta '\nonumber \\= & {} 0,\nonumber \\ \Delta n_\theta= & {} \int {} r' \mathrm {d}r' \mathrm {d}z' \int {} \Bigg ( {^{(-2)}T^{00}(\varvec{x}',t)} v' \cos (\theta ') \nonumber \\&+ \frac{\mathrm {d}}{\mathrm {d}\theta '} \bigg (\frac{{^{(-2)}T^{00}(\varvec{x}',t)} (v' \sin (\theta ')r)( - r' \sin (\theta '))}{r r' \sin (\theta ')} \bigg ) \Bigg ) \nonumber \\&\times \frac{g(\alpha \vert \varvec{x}-\varvec{x}' \vert )}{\vert \varvec{x}-\varvec{x}' \vert } \mathrm {d}\theta ' \nonumber \\= & {} 0. \end{aligned}$$

(4.21)

Therefore, in an axially symmetric spacetime region, which coincides in most cases with those of galaxies and compact objects, one cannot distinguish f(R) theories from GR by the lensing correction to the third-order term. This result suggests that there are few opportunities to distinguish f(R) theory from GR even in a third-order post-Newtonian approximation.

However, the difference $\Delta n$ will not vanish in a non-axially symmetrical spacetime region, thus one could detect the difference in principle. Since the potential appearing in Eq. (4.20) without function g are third-order post-Newtonian terms, the order of $\Delta n$ is determined by the order of the functions $g(\alpha d)$ (or $g(\alpha d)$ and $h(\alpha d)$, with the same order as shown in Fig. 1. It is shown that, for $\alpha \le {\frac{1}{d}}$, $\Delta n$ will be around $10^{-1}$ times the 3rd GR terms, and thus keeps the same third order. However, for $\alpha \ge \frac{10}{d}$, $\Delta n$ will be less than $10^{-2}$ times the third-order terms, and hence is indistinguishable with the fourth-order term. This estimation would approach the exact result for the spacetime region far away from the matter center. Then the functions g and h could be approximated by the values $g(\alpha d_0)$ and $h(\alpha d_0)$, where $d_0$ is the distance of the position to the matter center. Thus one could write the first-order approximation of (4.16) as

$$\begin{aligned} \begin{aligned} \Delta n_j \simeq&g(\alpha d_0)\frac{G }{c^5}\int _{c}{\frac{{^{(-2)}T^{00}(\varvec{x}',t)} v'_j }{\vert \varvec{x}-\varvec{x}' \vert } } \mathrm {d}^3 x'\\&\quad -h(\alpha d_0)\frac{G }{c{^5}}\int _{c}{ \frac{{^{(-2)}T^{00}} v' \cdot (\varvec{x}-\varvec{x}')(\varvec{x}-\varvec{x}')_j}{\vert \varvec{x}-\varvec{x}' \vert ^3} }\mathrm {d}^3 x',\\ \end{aligned} \end{aligned}$$

(4.22)

in which the whole integration is approximated by the integration of the region around the center where most part of the matter locate. Therefore, in highly non-axially symmetric spacetime region, it is possible to distinguish the lensing of GR from those of the f(R) theories satisfying $\alpha \le \frac{1}{d_0}$. It also requires that the measurement can approach the $10^{-1}$ precision of the third-order effect.

Fig. 1

The evaluation of the functions $g(\alpha d)$ and $h(\alpha d)$ respect to $\alpha d$

5 Concluding remarks

In this paper, the post-Newtonian approximation of a general class of f(R) theories is formulated up to third order. In the third-order expansion, the metric components contain not only the Newtonian potential U but also the Yukawa potential V together with the third order potentials. Note that f(R) theories can be transformed into generalized Brans–Dicke theories by suitable conformal transformations. Since the post-Newtonian formulation of Brans–Dicke gravity has been well studied [33], one can check the consistency of the post-Newtonian formulations between the two kinds of theories. It turns out that, in the limit of $\alpha \rightarrow 0$, our result (3.28) of f(R) gravity coincides with the result of Brans–Dicke gravity given in [33]. The proof will be presented in Appendix A.

In our post-Newtonian formulation, the information of a specific form of f(R) theories is contained in the Yukawa potential. While the Yukawa potential does not show in the second-order expression of the effective refraction index n of light, it does appear in the third-order expression of n. Therefore in principle we could distinguish f(R) gravity and GR. Moreover, detailed analysis shows that a series of f(R) forms, more specific, whose parameter $1/\alpha \sim \sqrt{f''(0)/f'(0)}$ is larger than the distance to the massive center, are distinguishable from GR by the gravitational lensing effect in a third-order post-Newtonian approximation. It should be noted that the conclusion that f(R) theories can lead to the gravitational lensing effect different from that of GR can also be obtained by the approach of Minkowski functionals [40]. Moreover, it should be pointed out that the third-order perturbations are also distinguishing f(R) theories from GR in view of the Birkhoff theorem [41]. However, it is shown in this paper that, in the axially symmetrical spacetime region, the gap term between these two kinds of theories vanishes and hence they are indistinguishable at third order.

One of the motivations for developing modified gravity theories is to account for the observed mass profiles in galaxies as well as clusters of galaxies without the inclusion of dark matter. The existence of dark matter in GR is confirmed by the observational data not only from the dynamical analysis, such as rotation curves in spiral galaxies [42] and velocity dispersions in early-type systems [43, 44], but also from gravitational lensing observations [45, 46]. Observations indicate that we need to take into account almost the same large amount of dark matter to explain the gravitational lensing effect as that for the dynamical data like the velocity dispersion or the temperature profile of the X-ray emitting intracluster medium [47, 48] in galaxy clusters or spiral galaxies. Up to now, certain f(R) theories are tested by the dynamical data in galaxy clusters and spiral galaxies [27,28,29, 49,50,51]. However, concerning the gravitational lensing observations, our results here show a disfavor of the attempts in this direction. For any f(R) form which could be weakly expanded, the lensing effect correction due to the f(R) will be at most of third order, which is at most $10^{-2}$ times of the leading order, i.e., the second-order post-Newtonian effect. Moreover, the fact that in axially symmetrical spacetime region there is no difference in lensing effect between these two kinds of theories strongly indicates that most of the lensing observations will not show the difference even at third order. Thus it is impossible to explain the lensing observations in the pure f(R) theories that we are considering without any dark matter involved. Actually there is already some evidence implying that f(R) theories without dark matter behave badly for galaxy clusters [52].

It is still possible to determine the parameter $\alpha ^2:=f'(0)/(3f''(0))$ though the precise observational results in non-axially symmetric system. Thus in near future, precise observations of lensing effect would be useful to distinguish certain f(R) theories from GR. It should be remarked that our result is only valid for the f(R) forms which could be weakly expanded. It is interesting to further study whether the dark matter content can be replaced by other unexpandable f(R) theories or other kinds of modified gravity.

Appendix A: PPN formalism

We will derive explicitly the third-order terms and get its limit of the largest effect in this appendix. Especially, we could get the limit of $\alpha \rightarrow 0$ and compare it to the result with the standard parametrized post-Newtonian (PPN) form.

First we will write out explicitly the third-order $g_{ij}$ term, more precisely, the $Z_{0i}$ term containing in the $g_{ij}$ expression. The other two terms $Y_i$ and $\psi _{,0i}$ is the usual potential in post-Newtonian form which reads

$$\begin{aligned} Y_i(\varvec{x},t)&:=\frac{G}{c}\int {\frac{{^{(-1)}T^{0i}}(\varvec{x}',t)}{\vert \varvec{x}-\varvec{x}' \vert }} \mathrm {d}^3x'=\,\frac{G}{c^2}\int {\frac{{^{(-2)}T^{00}(\varvec{x}',t)} v'_j }{\vert \varvec{x}-\varvec{x}' \vert } \mathrm {d}^3x}, \end{aligned}$$

(A1)

$$\begin{aligned} \psi _{,0i}&=Y_i-W_i, \end{aligned}$$

(A2)

where $W_i$ reads

$$\begin{aligned} W_i=\frac{G}{c{^2}}\int { \frac{{^{(-2)}T^{00}(\varvec{x}',t)} v' \cdot (\varvec{x}-\varvec{x}')(\varvec{x}-\varvec{x}')_j}{\vert \varvec{x}-\varvec{x}' \vert ^5} \mathrm {d}^3x}. \end{aligned}$$

(A3)

From (3.14) and (3.18), we have

$$\begin{aligned}&U(\varvec{x},t)_{,0j}:= \frac{G}{c^2}\int { \frac{{^{(-2)}T^{00}(\varvec{x}',t)} v'_j}{\vert \varvec{x}-\varvec{x}' \vert ^3} } \mathrm {d}^3 x'-\frac{3 G}{c^2}\int { \frac{{^{(-2)}T^{00}(\varvec{x}',t)} v' \cdot (\varvec{x}-\varvec{x}')(\varvec{x}-\varvec{x}')_j}{\vert \varvec{x}-\varvec{x}' \vert ^5} } \mathrm {d}^3 x',\end{aligned}$$

(A4)

$$\begin{aligned}&V(\varvec{x},t)_{,0j}=\frac{G}{c^2}\int {\frac{{^{(-2)}T^{00}(\varvec{x}',t)}\mathrm {e}^{-\alpha \vert \varvec{x}-\varvec{x}' \vert } v'_j (1 + \alpha \vert \varvec{x}-\varvec{x}' \vert )}{\vert \varvec{x}-\varvec{x}' \vert ^3}} \mathrm {d}^3 x' \nonumber \\&\qquad -\frac{3G}{c^2}\int {\frac{{^{(-2)}T^{00}(\varvec{x}',t)}\mathrm {e}^{-\alpha \vert \varvec{x}-\varvec{x}' \vert } v' \cdot (\varvec{x}-\varvec{x}')(\varvec{x}-\varvec{x}')_j (1 + \alpha \vert \varvec{x}-\varvec{x}' \vert )}{\vert \varvec{x}-\varvec{x}' \vert ^5}} \mathrm {d}^3 x'\nonumber \\&\quad -\frac{G}{c^2}\int {\frac{{^{(-2)}T^{00}(\varvec{x}',t)}\mathrm {e}^{-\alpha \vert \varvec{x}-\varvec{x}' \vert } \alpha ^2 v' \cdot (\varvec{x}-\varvec{x}') (\varvec{x}-\varvec{x}')_j}{\vert \varvec{x}-\varvec{x}' \vert ^3}} \mathrm {d}^3 x', \end{aligned}$$

(A5)

where $v'_j$ contributes the j components of the velocity at point $\varvec{x}'$.

Thus one get

$$\begin{aligned} \begin{aligned} Z_{0j}:=&\,\frac{G}{c^2}\int {\frac{{^{(-2)}T^{00}(\varvec{x}',t)} v'_j }{\vert \varvec{x}-\varvec{x}' \vert ^3} } \frac{1}{3\alpha ^2}(1-\mathrm {e}^{-\alpha \vert \varvec{x}-\varvec{x}' \vert } (1 + \alpha \vert \varvec{x}-\varvec{x}' \vert ))\\&\quad +\frac{{^{(-2)}T^{00}(\varvec{x}',t)} v' \cdot (\varvec{x}-\varvec{x}')(\varvec{x}-\varvec{x}')_j}{\alpha ^2 \vert \varvec{x}-\varvec{x}' \vert ^5}\\&\quad \times \left( \mathrm {e}^{-\alpha \vert \varvec{x}-\varvec{x}'\vert } \bigg (1+\alpha \vert \varvec{x}-\varvec{x}' \vert +\frac{1}{3}\alpha ^2 \vert \varvec{x}-\varvec{x}' \vert ^2 \bigg )-1 \right) \mathrm {d}^3 x'.\\ \end{aligned} \end{aligned}$$

(A6)

Then we are going to see the limit of $\alpha \rightarrow 0$. It is directly to see, $\lim _{\alpha \rightarrow 0}V=U$. Thus the limit of $g_{00}$ and $g_{ij}$ could be read off directly:

$$\begin{aligned}&g_{00}=-1+2\frac{U}{c^2} \frac{4}{3},&g_{ij}&=(1+2\frac{U}{c^2} \frac{2}{3}) \delta _{ij}. \end{aligned}$$

(A7)

And one could show that the limit of $\alpha \rightarrow 0$ leads to

$$\begin{aligned}&\lim _{\alpha \rightarrow 0} \frac{1}{3\alpha ^2}(1-\mathrm {e}^{-\alpha \vert \varvec{x}-\varvec{x}' \vert })=\frac{\vert \varvec{x}-\varvec{x}' \vert ^2}{6},\nonumber \\&\quad \lim _{\alpha \rightarrow 0} \frac{1}{\alpha ^2}\left( \mathrm {e}^{-\alpha \vert \varvec{x}-\varvec{x}'\vert } \bigg (1+\alpha \vert \varvec{x}-\varvec{x}' \vert +\frac{1}{3}\alpha ^2 \vert \varvec{x}-\varvec{x}' \vert ^2 \bigg ) \right) \nonumber \\&\quad =-\frac{\vert \varvec{x}-\varvec{x}' \vert ^2}{6}. \end{aligned}$$

(A8)

Thus for potential $Z_{0i}$ we simply get

$$\begin{aligned} Z_{0j}:= & {} \frac{G}{c^2}\int {\frac{{^{(-2)}T^{00}(\varvec{x}',t)} v'_j }{\vert \varvec{x}-\varvec{x}' \vert } } \mathrm {d}^3 x'\nonumber \\&\quad -\frac{G}{c{^2}} \int { \frac{{^{(-2)}T^{00}(\varvec{x}',t)} v' \cdot (\varvec{x}-\varvec{x}')(\varvec{x}-\varvec{x}')_j}{\vert \varvec{x}-\varvec{x}' \vert ^3} } \mathrm {d}^3 x'\nonumber \\= & {} \frac{1}{6}(Y_j-W_j). \end{aligned}$$

(A9)

Since from the standard PPN formalism in GR, we already know that

$$\begin{aligned} \begin{aligned} g_{0i}^{GR}:=&\frac{1}{c^3}(-4Y_j +1/2 \psi _{,0i})=\frac{1}{c^3}\left( -\frac{7}{2}Y_j-\frac{1}{2}W_j\right) , \end{aligned} \end{aligned}$$

(A10)

we have

$$\begin{aligned} \begin{aligned} g_{0i}:=&\frac{1}{c^3}\left( -\frac{10}{3}Y_j-\frac{2}{3}W_j\right) . \end{aligned} \end{aligned}$$

(A11)

After the redefinition of gravitational constant $G'=\frac{4}{3}G$ based on $g_{00}$, we get

$$\begin{aligned} {g_{00}}= & {} -1+\frac{2}{c^2}U,\nonumber \\ {g_{0i}}= & {} \frac{1}{c^3}\left( -\frac{5}{2}Y_j-\frac{1}{2}W_j\right) ,\\ {g_{ij}}= & {} \left( 1+\frac{1}{c^2}U\right) {\delta _{ij}},\nonumber \end{aligned}$$

(A12)

and one directly reads off $\gamma =0.5$ and $\alpha _1=\alpha _2=\zeta _1=\zeta =0$, respectively, which meets the result of this kind of f(R) form given by Will [33].