Seeking sterile neutrinos in Finslerian cosmology

Abstract

For the first time, to search for sterile neutrinos in the framework of Finler geometry, we constrain four cosmological models using the most stringent constraint we can provide so far. We find that the Finslerian massless sterile neutrino model can, respectively, give a better cosmological fit to data and alleviate the current $H_0$ tension more effectively than the other three models. For the Finslerian massless sterile neutrino model, we obtain the constraint $N_\mathrm{eff}=3.237^{+0.092}_{-0.185}$, which is consistent with $\Delta N_\mathrm{eff} > 0$ at the 1.03$\sigma$ confidence level (CL). This gives a very weak hint of massless sterile neutrinos and may imply the non-existence of massless sterile neutrinos in the Finslerian cosmological setting. For the Finslerian massive sterile neutrino model, we obtain the constraints $N_\mathrm{eff}=3.143^{+0.064}_{-0.066}$, which favors $\Delta N_\mathrm{eff} > 0$ at the 1.47$\sigma$ CL, and $m_{\nu , \mathrm{sterile}}^\mathrm{eff} < 0.121$ eV at the 2$\sigma$ CL which is much tighter than the Planck results. This very tight restriction appears to indicate the massive sterile neutrinos are also non-existent in the Finslerian scenarios. Consequently, one may conclude that the sterile neutrinos are possibly non-existent in the Finslerian universe. Our results are compatible with the recent results of the neutrino oscillation experiments implemented by the Daya Bay and MINOS collaborations and the cosmic ray one carried out by the IceCube collaboration.

1 Introduction

The recent precise measurements of the cosmic microwave background (CMB) anisotropies released by the Planck collaboration have demonstrated, once again, the high efficiency of the standard cosmological model, i.e., the cold dark matter (CDM) plus the cosmological constant $\Lambda$ scenario (hereafter $\Lambda$CDM) in describing the cosmological phenomena, and given the tightest constraints on the cosmological parameters up to now [1]. Nonetheless, in the train of the success of the $\Lambda$CDM model, some interesting tensions and anomalies emerge, which can be roughly divided into two classes, i.e., internal tensions existing in Planck CMB data and external tensions between Planck data and other astrophysical observations.

Under the assumption of $\Lambda$CDM, the most anomalous internal inconsistency existing in Planck CMB temperature and polarization angular spectra data may be exhibited in the constraints on the $A_L$ parameter (the amplitude of the lensing power relative to the physical value), which controls the amount of gravitational lensing in small-scale anisotropies. Specifically, the 95$\%$ limit of $A_L=1.15^{+0.13}_{-0.12}$ derived from Planck data is higher than the expected value $A_L=1$ in $\Lambda$CDM at more than $2\sigma$ CL [2]. Another evident internal discrepancy is that the constraint on the Thomson scattering optical depth parameter $\tau =0.055\,\pm ~0.009$ [2] obtained using Planck high-frequency-instrument (HFI) large angular-scale polarization data is lower than the value $\tau =0.099\pm 0.024$ [1] derived from full-range temperature power spectra and polarization data at small angular scales at the $1.7\sigma$ CL.

The external inconsistencies include two main tensions, namely the $\sigma _8$ (the amplitude of the root-mean-square density fluctuations) and $H_0$ (the Hubble constant) tensions. For the former case, assuming $\Lambda$CDM, the $\sigma _8$ parameter derived from Planck data is higher than the same quantity measured by several low redshift surveys including lensing, cluster counts and redshift space distortions (RSD) [2,3,4]. For instance, considering the parameter $S_8=\sigma _8\sqrt{\Omega _m/0.3}$ (where $\Omega _m$ is the matter density ratio today), the Planck result is higher than the recent result from the KiDS-450 cosmic shear survey [5] at about $2.3\sigma$ CL. For the latter case, the indirectly global measurement $H_0=66.93\pm 0.62$ km s$^{-1}$ Mpc$^{-1}$ derived by Planck collaboration (hereafter P15) [2] under the assumption of $\Lambda$CDM is lower than the directly local measurement $H_0=73.24\pm 1.74$ km s$^{-1}$ Mpc$^{-1}$ from Riess et al. 2016 (hereafter R16) [6] using the improved SNIa calibration techniques at over $3\sigma$ CL. Most recently, this strong tension has been confirmed in part by the H0LiCOW strong lensing survey which gives the value $H_0=71.9^{+2.4}_{-3.0}$ km s$^{-1}$ Mpc$^{-1}$ being higher than the prediction of Planck and more compatible with the R16’s result at $1\sigma$ CL [7].

To date, it is still unclear that these various tensions are originated from unknown observational systematics in different methods used for measurements, or possibly small deviations from $\Lambda$CDM indicating the underlying new physics at all. In order to alleviate or even solve these tensions, several extensions to the standard six-parameter $\Lambda$CDM model have been studied [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. Based on the fact that the solar and atmospheric neutrino oscillation experiments [23, 24] verified that the neutrinos have masses (see [25] for a recent review), massive neutrinos can potentially be one of the most appealing solution to relieve these tensions such as $\sigma _8$ and $H_0$ tensions, since the free-streaming neutrinos can suppress power in the clustering of matter at late times. More specifically, larger neutrino masses give a lower $\sigma _8$ and masses below 0.4 eV can provide an acceptable fit to the direct $H_0$ measurements (see [1] for details). Since the above-mentioned SK (Super-Kamiokande) and SNO (Sudbury Neutrino Observatory) experiments provide possible living space for extra sterile species, sterile neutrinos can also be used to alleviate these tensions and related work has been carried out in [3, 12, 26,27,28,29,30,31,32,33,34] by several authors. In general, sterile neutrinos include two subclasses, i.e., massless type corresponding to an extra parameter $N_\mathrm{eff}>3.046$ ($N_\mathrm{eff}$ is the effective number of relativistic degrees of freedom) in a specific cosmological model, and massive type corresponding to the addition of a new effective mass parameter $m_{\nu , \mathrm{sterile}}^\mathrm{eff}$ to the massless case.

Previous studies focus on using the sterile neutrinos to relieve tensions mentioned above in the framework of either dark energy models or modified theories of gravity [32]. Intriguingly, from a new geometrical perspective, one can also investigate the neutrino physics, search for the sterile neutrinos and study whether the sterile neutrinos can alleviate these tensions effectively. Finsler geometry [35,36,37], which takes Riemann geometry as its special case where the four-velocity vectors are treated as independent variables, opens a new prospect to understand the current cosmological acceleration. In history, E. Cartan first initiated the self-consistent Finsler geometry framework [38]. This new geometry keeps the properties of Riemann geometry, i.e., the isometric group is a Lie group on a Finslerian manifold, while it admits less Killing vectors than a Riemannian spacetime does. Generally, there are $n(n-1)/2+1$ independent Killing vectors in a n dimensional non-Riemannian Finslerian spacetime at most. Taking the simplest possible asymmetrical generalization of Riemannian metric into account, Randers [39] proposed the well-known Randers space, a subclass of Finslerian space. Subsequently, the Einstein–Finsler equations for the Cartan d-connection were introduced in 1950 [40]. In the context of Randers space, a generalized Friedmann–Robertson–Walker (FRW) cosmological scenario based on Finsler geometry has been studied carefully [41], and a modified dispersion relation of free particles has also been investigated [42].

Historically, the gravitational aspects in a Finslerian space were studied for a long time [43,44,45,46]. The gravitational field equations (GFEs) derived from a Riemannian osculating metric were presented in [47]. For such a metric, the FRW-like cosmological scenario and the anisotropies of the universe were also studied [41, 48]. However, their derived GFEs did not satisfy the Bianchi identity and the general covariance principle of Einstein’s gravity. Interestingly, the authors in [49,50,51] have overcome these difficulties and derived the corresponding modified Friedmann equations by constructing a Randers–Finsler space of approximate Berwald type, which is just an extension of the Riemannian space. Following the theoretical line, very attractively, we are motivated by searching for sterile neutrinos and exploring their potential in alleviating the current $H_0$ tension in the framework of Finsler geometry.

This study is structured as follows. In the next section, we introduce the Finslerian models. In Sect. 3, we describe the data and analysis method. In Sect. 4, we present our results, while we derive our conclusions in the final section.

2 Models

First of all, we review briefly the basic concepts and notions of the Finsler geometry [35]. We denote by $T_xM$ the tangent space located at a point x on a manifold M (i.e. $x\in M$), and by TM the tangent bundle of M. Every element of TM is characterized by a form (x, y), where $x\in M$ and $y\in T_xM$. The corresponding natural projection f: $TM\rightarrow M$ is defined as $f(x, y)\equiv x$. A Finsler structure is a function F: $TM\rightarrow [0,+\infty )$ with the following three properties:

• Regularity: F is $C^{\infty }$ on the entire slit tangent bundle $TM \setminus$0.

• Positive homogeneity: $F(x,\lambda y)=\lambda F(x, y)$ for all $\lambda >0$.

• Strong convexity: The $n\times n$ Hessian matrix $g_{\mu \nu }\equiv \frac{\partial }{\partial y^{\mu }}\frac{\partial }{\partial y^{\nu }}(\frac{1}{2}F^2)$ is positively definite at every point of $TM \setminus$0.

Chern [35] discovered that every Finsler manifold obeys a unique linear connection named the Chern connection, which is torsion-free and almost metric-compatible. The corresponding connection coefficients are expressed as

$$\begin{aligned} \Gamma ^{\alpha }_{~\mu \nu }=\gamma ^{\alpha }_{~\mu \nu }-g^{\alpha \lambda }\left( C_{\lambda \mu \beta }\frac{N^{\beta }_{~\nu }}{F}-C_{\mu \nu \beta }\frac{N^{\beta }_{~\lambda }}{F}+C_{\nu \lambda \beta }\frac{N^{\beta }_{~\mu }}{F}\right) , \end{aligned}$$

(1)

where $\gamma ^{\alpha }_{~\mu \nu }$ is the formal Christoffel symbols of the second kind with the same form of the Riemannian connection, $N^{\mu }_{~\nu }$ is defined as $N^{\mu }_{~\nu }\equiv \gamma ^{\mu }_{~\nu \alpha }y^{\alpha }-\frac{C^{\mu }_{~\nu \lambda }}{F}\gamma ^{\lambda }_{~\alpha \beta }y^{\alpha }y^{\beta }$ and $C_{\lambda \mu \nu }\equiv \frac{F}{4}\frac{\partial }{\partial y^{\lambda }}\frac{\partial }{\partial y^{\mu }}\frac{\partial }{\partial y^{\nu }}(F^2)$ is the so-called Cartan tensor considered as a deviation from the formal Riemannian manifold.

A Randers space is a special type of Finsler space and its Finsler structure can be written as

$$\begin{aligned} F(x,y)\equiv A(x,y)+B(x,y), \end{aligned}$$

(2)

where $A(x,y)\equiv \sqrt{\tilde{a}_{\mu \nu }y^{\mu }y^{\nu }}$ and $B(x,y)\equiv \tilde{b}_{\mu }(x)y^{\mu }$. The $\tilde{a}_{\mu \nu }$ and $\tilde{b}_{\mu }$ denote the components of a Riemannian metric and those of a 1-form, respectively. Throughout this study, the indices are lowered and raised by $g_{\mu \nu }$ and its inverse metric $g^{\mu \nu }$, and the lowering and raising of indices for the terms decorated with a tilde are implemented by $\tilde{a}_{\mu \nu }$ and its inverse $\tilde{a}^{\mu \nu }$ instead of the fundamental tensor.

To study the homogeneous and isotropic universe, we choose $\tilde{a}_{\mu \nu }$ as the standard FRW metric. Based on the cosmological principle and the condition [49,50,51,52] that a Randers space must satisfy when it is of Berwald type, we choose $\tilde{b}_{\mu }=(\tilde{b}_0,0,0,0)$, where $\tilde{b}_0$ denotes a very small constant. For the convenience of numerical analysis, we introduce two parameters as

$$\begin{aligned} \alpha \equiv \frac{A}{F}\left( \frac{B}{F}\tilde{a}_{00}\frac{y^0}{A}\frac{y^0}{A}-2\tilde{a}_{00}\frac{y^0}{A}\tilde{b}^{0}\right) , \end{aligned}$$

(3)

and

$$\begin{aligned} \beta \equiv \frac{A}{F}\left( \frac{B}{F}\tilde{a}_{ij}\frac{y^i}{A}\frac{y^j}{A}\right) , \end{aligned}$$

(4)

where two Latin indices “ i ” and “ j ” run from 1 to 3.

In a Finsler–Berwald FRW universe, utilizing Eqs. (3, 4) and combining the first Friedmann equation with the acceleration equation [49,50,51], the energy conservation equation can be written as

$$\begin{aligned}&\dot{\rho }\left( \frac{3\alpha }{4}+\frac{\beta }{12}+1\right) +\dot{p}\left( -\frac{3\alpha }{4}+\frac{\beta }{4}\right) \nonumber \\&\quad +\frac{\dot{a}}{a}\left[ \rho \left( \frac{3\alpha }{2}+\frac{\beta }{6}+2\right) +p\left( -\frac{3\alpha }{2}+\frac{\beta }{2}\right) \right. \nonumber \\&\quad \left. +\left( \rho +3p\right) \left( 1+\frac{\beta }{3}\right) \right] =0, \end{aligned}$$

(5)

where a, $\alpha$ and $\beta$ are the scale factor, effective time-component and space-component parameters, respectively. Notice that here “effective” denotes the physical quantities derived from the non-Riemannian Berwald space. Substituting the equation of state (EoS) $p_i=\omega _i\rho _i$ of each independent component i (where the constants $\omega _i=1/3, 0, -1, -1/3$ correspond to the effective radiation, non-relativistic matter, dark energy and effective curvature, respectively) into Eq. (7), one can express conveniently the effective energy density as

$$\begin{aligned} \rho _i\propto a^{-\frac{36(1+\omega _i)+18(1-\omega _i)\alpha +6(1+3\omega _i)\beta }{9(1-\omega _i)\alpha +(1+3\omega _i)\beta +12}}. \end{aligned}$$

(6)

For simplicity, we only consider the spatially flat Finslerian universe and consequently ignore the contribution from the effective curvature component in the following context. Combining the first Friedmann equation with Eq. (8), the squared dimensionless Hubble parameter of the base Finslerian model (hereafter F$\Lambda$), which is a two-parameter extension to the six-parameter standard cosmology, can be written as

$$\begin{aligned} E^2(a)= & {} \frac{9\alpha +\beta +12}{4(\alpha +1)(\beta +3)}\Omega _{m}a^{-\frac{6(3\alpha +\beta +6)}{9\alpha +\beta +12}}\nonumber \\&+\,\frac{9\alpha -\beta +6}{2(\alpha +1)(\beta +3)}\Omega _{de} a^{-\frac{6(3\alpha -\beta )}{9\alpha -\beta +6}}, \end{aligned}$$

(7)

where $\Omega _{m}$ and $\Omega _{de}$ are the present-day effective matter (baryons and dark matter) and dark energy density parameters, respectively. Note that, when $\alpha =\beta =0$, this model will reduce to the $\Lambda$CDM one.

In order to search for sterile neutrinos in the context of Finsler geometry using current cosmological observations, we concentrate on two Finslerian models, i.e., massless (hereafter Fs) and massive (hereafter Fms) sterile models. Meanwhile, as comparisons, we choose the $\Lambda$CDM and F$\Lambda$ models as reference models. Furthermore, we present the parameter spaces of two Finslerian sterile neutrino models considered in this analysis as follows:

• Fs Assuming the total mass of three active neutrinos $\Sigma m_\nu =0.06$ eV with a degenerate mass hierarchy and setting the effective number of relativistic species $N_\mathrm{eff}$ to be a free parameter being greater than 3.046, the Fs model based on the six-parameter $\Lambda$CDM cosmology can be characterized by the following 9-dimensional parameter space:

  $$\begin{aligned} \mathbf {P_1}= & {} \{\Omega _bh^2, \Omega _ch^2, 100\theta _{MC}, \tau , N_\mathrm{eff}, \alpha , \beta , \nonumber \\&\quad \mathrm {ln}(10^{10}A_s), n_s\}, \end{aligned}$$

  (8)

  where $\Omega _bh^2$ and $\Omega _ch^2$ denote, respectively, the baryon and CDM densities today, $\theta _{MC}$ is the ratio between the angular diameter distance and the sound horizon at the redshift of last scattering $z_\diamond$, $\tau$ is the Thomson scattering optical depth due to reionization, $\mathrm {ln}(10^{10}A_s)$ and $n_s$ are the amplitude and spectral index of the primordial power spectrum at the pivot scale $K_0=0.05$ Mpc$^{-1}$, respectively. Note that here h is related to the Hubble constant by $h\equiv H_0/(100\,\mathrm {km\,s^{-1}\,Mpc^{-1}})$.

• Fms Opening an extra sterile neutrino mass parameter based on the Fs model, the Fms model can be described by the following 10-dimensional parameter set:

  $$\begin{aligned} \mathbf {P_2}= & {} \{\Omega _bh^2, \Omega _ch^2, 100\theta _{MC}, \tau , N_\mathrm{eff}, m_{\nu , \mathrm{sterile}}^\mathrm{eff}, \nonumber \\&\quad \alpha , \beta , \mathrm {ln}(10^{10}A_s), n_s\}, \end{aligned}$$

  (9)

  where the parameter $m_{\nu , \mathrm{sterile}}^\mathrm{eff}$ is just a phenomenological characterization for the mass of extra sterile neutrinos. One can easily find that, because of Eqs. (8, 9), the Fs and Fms models are the three-parameter and four-parameter extensions to the standard $\Lambda$CDM model, respectively.

3 Observational data and analysis method

In this study, we employ the following observational datasets to place constraints on the above-mentioned four models including two reference and two Finslerian models.

• CMB: We utilize the temperature and polarization CMB angular power spectra data released by Planck 2015 [1]. This dataset consists of the large angular-scale temperature and polarization anisotropy measured by the Planck LFI experiment and the small-scale anisotropies measured by the Planck HFI one.

• BAO: To break the geometrical degeneracy between parameters to high precision, we use four baryonic acoustic oscillations (BAO) measurements containing the 6dFGS (six-degree-field galaxy survey) [53], SDSS-MGS (main galaxy sample) [54], and the latest BOSS-LOWZ and BOSS-CMASS surveys [55].

• SNIa: Since the Type Ia supernovae (SNIa) is theoretically regarded as a standard candle to explore the background evolution of the universe, we also use the largest SNIa sample “ Joint Light-curve Analysis ” (JLA) derived from the SNLS and SDSS catalogs in our analysis [56].

• Lensing: We also employ the full-mission Planck lensing data [57], which provide additional low redshift information and gives the most powerful measurement to date with a 2.5$\%$ constraint on the amplitude of the lensing potential power spectrum.

• $\mathbf {CC} + \mathbf {H_0}$: We also make use of the latest cosmic chronometers (CC) consisting of 30 data points covering in the redshift range $z \in [0.07, 1.97]$ (see [58, 59]). Meanwhile we adopt the direct local measurement of Hubble constant $H_0=73.24\pm 1.74$ km s$^{-1}$ Mpc$^{-1}$ as a complementary probe [6].

Using these cosmological datasets, we employ the Markov Chain Monte Carlo (MCMC) method to constrain the four models mentioned above. To infer the posterior probability distributions of different model parameters, we modify carefully the November 2016 version of the publicly MCMC package CosmoMC [60], which obeys a convergence diagnostic based on the Gelman and Rubin statistic, and Boltzmann code CAMB [61]. Note that we have included the full power spectrum in the CAMB code in our numerical analysis. To perform the Bayesian analysis, we choose the prior ranges for different parameters as follows: $\Omega _bh^2 \in [0.005, 0.1]$, $\Omega _ch^2 \in [0.001, 0.99]$, $100\theta _{MC} \in [0.5, 10]$, $\tau \in [0.01, 0.8]$, $N_\mathrm{eff} \in [3, 5]$ ($N_\mathrm{eff} \in [3.047, 5]$ for Fms model), $m_{\nu , \mathrm{sterile}}^\mathrm{eff} \in [0, 10]$, $\alpha \in [-3, 3]$, $\beta \in [-3, 3]$, $\mathrm {ln}[10^{10}A_s] \in [2, 4]$, $n_s \in [0.8, 1.2]$ and $H_0 \in [20, 100]$. In what follows, since our goal is searching for the sterile neutrinos in the framework of Finsler geometry and exploring the effects of different data combinations on the parameter estimations is beyond the scope of the present work, we just perform the most stringent constraint on the Finslerian models using the data combination CMB + BAO + SNIa + Lensing + CC + $H_0$, which is abbreviated as “ CBSLCH ” in the following context.

Table 1 The marginalized constraining results of different parameters in the $\Lambda$CDM, F$\Lambda$, Fs, and Fms models using the data combination CBSLCH, respectively. Note that we quote the 95$\%$ limits for the parameters which cannot be well constrained

Fig. 1

The 1-dimensional marginalized distributions and 2-dimensional contours for the parameters of the $\Lambda$CDM model by using the data combination CBSLCH

Fig. 2

The 1-dimensional marginalized distributions and 2-dimensional contours for the parameters of the F$\Lambda$ model by using the data combination CBSLCH

Fig. 3

The 1-dimensional marginalized distributions and 2-dimensional contours for the parameters of the Fs model by using the data combination CBSLCH

Fig. 4

The 1-dimensional marginalized distributions and 2-dimensional contours for the parameters of the Fms model by using the data combination CBSLCH

4 Results

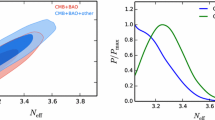
The results of our numerical analysis are presented in Table 1 utilizing the joint constraints from CBSLCH. The 1-dimensional marginalized distributions and 2-dimensional contours for the parameters of $\Lambda$CDM, F$\Lambda$, Fs and Fms models using the combined constraints CBSLCH are also exhibited in Figs. 1, 2, 3 and 4, respectively. It is clear that the Fs model gives a better cosmological fit than the other three models by an increase of $\Delta \chi ^2=-4.314$ with respect to F$\Lambda$ model at least. Comparing with $\Lambda$CDM and F$\Lambda$ models which yield a similar $\chi ^2_\mathrm{min}$, the Fms model does not fit very well with current data in light of the relatively large value of $\chi ^2_\mathrm{min}$. For three Finslerian models, we find that the constrained typical parameters $\alpha$ and $\beta$ are all compatible with zero at the 1$\sigma$ CL (see Table 1). This implies the effective Finslerian dark energy scenarios just deviate very slightly from $\Lambda$CDM based on the current data. Interestingly, the slightly negative best-fit values of $\beta$ are preferred for three Finslerian models when using the data combination CBSLCH. By adding the extra data combination BAO + SNIa + Lensing + CC + $H_0$ into Planck CMB data, the current $H_0$ tension has been reduced from 3.4$\sigma$ to 2.81$\sigma$ in the $\Lambda$CDM model (see Table 1). Furthermore, in the framework of Finsler geometry, this tension is reduced from 3.4$\sigma$ to 2.64$\sigma$, 1.87$\sigma$ and 2.32$\sigma$ for F$\Lambda$, Fs and Fms models, respectively. Especially, one can find that the Fs model relieve obviously the $H_0$ tension by considering a massless sterile neutrino in the base F$\Lambda$ model. In addition, using CBSLCH, we also find that the scale invariance of primordial power spectrum is strongly excluded in the Finslerian models, where the F$\Lambda$ model exhibits the largest discrepancy at the $11.35\sigma$ CL. However, this large inconsistency is reduced from $11.35\sigma$ to $9.41\sigma$ and $4.31\sigma$ when considering the massless and massive sterile neutrinos, respectively.

According to the previous studies [62, 63], the measurement of $\Delta N_\mathrm{eff}=N_\mathrm{eff}-3.046 > 0$ implies the existence of extra dark radiation component in our universe. In this study, we choose the fitting result of $\Delta N_\mathrm{eff} > 0$ as the evidence for the presence of massless sterile neutrinos. For the Fs model, from Table 1, we find that the constrained parameter $N_\mathrm{eff}=3.237^{+0.092}_{-0.185}$ is consistent with $\Delta N_\mathrm{eff} > 0$ at the 1.03$\sigma$ CL. This seems to indicate the non-existence of massless sterile neutrinos in the Finslerian cosmological setting. Varying simultaneously two effective parameters $N_\mathrm{eff}$ and $m_{\nu , \mathrm{sterile}}^\mathrm{eff}$ in the base F$\Lambda$ model, for the Fms model, we obtain the constraints $N_\mathrm{eff}=3.143^{+0.064}_{-0.066}$, which is in favor of $\Delta N_\mathrm{eff} > 0$ at the 1.47$\sigma$ CL, and $m_{\nu , \mathrm{sterile}}^\mathrm{eff} < 0.121$ eV at the 2$\sigma$ CL which is much tighter than the Planck results using the data combination CBL (CMB + BAO + Lensing) [1].

From Fig. 3, one can find that the parameter $N_\mathrm{eff}$ is positively correlated with parameters $n_s$, $H_0$ and $\sigma _8$, respectively. This indicates that larger effective number of relativistic species corresponds to larger spectral index, expansion rate of the universe and amplitude of matter fluctuations, which is consistent with the prediction of Planck under the assumption of $\Lambda$CDM [1]. However, in the Fms model, $N_\mathrm{eff}$ is highly degenerate with $\sigma _8$ (see Fig. 4) after considering the case of massive sterile neutrinos. Furthermore, although the effective sterile neutrino masses $m_{\nu , \mathrm{sterile}}^\mathrm{eff}$ are tighten to be very small at the $2\sigma$ CL, it is still anti-correlated with $H_0$ and $\sigma _8$, which implies that large masses of sterile neutrinos can increase the expansion rate of the universe and effects of matter clustering. In addition, one can also find that there exists a high degeneracy between $m_{\nu , \mathrm{sterile}}^\mathrm{eff}$ and $N_\mathrm{eff}$ as noted by Planck collaboration (see Fig. 32 in [1]).

Since one of our goals is to study the abilities of Finslerian sterile neutrino models in alleviating the current $H_0$ tension using the data combination CBSLCH, we are very interested in investigating the correlations between $H_0$ and other cosmological parameters. Meanwhile, for completeness, we also adopt $\Lambda$CDM and F$\Lambda$ models as comparisons. From Fig. 1, we find that $H_0$ is positively correlated with $n_s$, which implies that an increasing spectral index leads to a larger expansion rate of the universe. Interestingly, we also find that, using CBSLCH, the expansion rate $H_0$ in the F$\Lambda$ model is anti-correlated with the amplitude of matter fluctuations $\sigma _8$ being different from the consequences in the left three models. Furthermore, we find that $H_0$ is anti-correlated with $t_\mathrm{age}$ and $z_\mathrm{eq}$, respectively. This means that the larger the expansion rate is, the smaller the age of the universe and the redshift of matter–radiation equality are. Moreover, one can also find that two Finslerian sterile neutrino models amplify obviously the parameter spaces through adding extra parameters into the standard six-parameter cosmology.

To explore the impacts of the common parameter $N_\mathrm{eff}$ on other cosmological parameters in the Fs and Fms models is also attractive by using CBSLCH. From Fig. 5, interestingly, although the Fms model has one more parameter than the Fs one, it gives tighter constraints on different parameters than the Fs model does by utilizing the same data combination, especially in the $\tau -N_\mathrm{eff}$ plane. We find that the effective number of relativistic species $N_\mathrm{eff}$ is weakly positively correlated with the spectral index $n_s$, expansion rate of the universe and the amplitude of matter fluctuations $\sigma _8$, respectively, which give the same prediction by the Planck results (see Fig. 20 in [1]). Meanwhile, very attractively, the Finslerian universe gives a lower bound of $N_\mathrm{eff}=3.077$ at the $1\sigma$ CL in the presence of massive sterile neutrinos (see Figs. 4, 5), which is not the case in $\Lambda$CDM [1]. Furthermore, we also find that $N_\mathrm{eff}$ is anti-correlated with $t_\mathrm{age}$, which means that an increasing effective number of relativistic degree of freedom leads to a decreasing age of the universe. Additionally, we find that $N_\mathrm{eff}$ is weakly anti-correlated with $z_\mathrm{eq}$ in the Fms model, but this is not the case in the Fs one. For the Fms model, we are also of much interest in studying the correlations between the effective sterile neutrino masses $m_{\nu , \mathrm{sterile}}^\mathrm{eff}$ and other parameters such as $t_\mathrm{age}$ and $z_\mathrm{eq}$ (see Figs. 4, 6). We find that $m_{\nu , \mathrm{sterile}}^\mathrm{eff}$ is, respectively, positively and weakly positively correlated with $t_\mathrm{age}$ and $z_\mathrm{eq}$, which indicates that the larger sterile neutrino masses are, the larger the age of the universe and the redshift of matter–radiation equality are.

Fig. 5

The 2-dimensional marginalized contours of the Fs (red) and Fms (magenta) models in the planes of $\tau -N_\mathrm{eff}$, $n_s-N_\mathrm{eff}$, $H_0-N_\mathrm{eff}$, $\sigma _8-N_\mathrm{eff}$, $t_\mathrm{age}-N_\mathrm{eff}$ and $z_\mathrm{eq}-N_\mathrm{eff}$ by using the data combination CBSLCH, respectively

Fig. 6

The 2-dimensional marginalized contours of the Fms (magenta) model in the planes of $t_\mathrm{age}-m_{\nu , \mathrm{sterile}}^\mathrm{eff}$ and $z_\mathrm{eq}-m_{\nu , \mathrm{sterile}}^\mathrm{eff}$ by using the data combination CBSLCH, respectively

In order to characterize the details of different constrained parameters and compare conveniently with each other in four models, we also exhibit the 1-dimensional posterior distributions of them in Fig. 7. Combining Table 1 with Fig. 7, one can easily find that the Fs model gives a higher $H_0$ value and lower age of the universe than the left three models, and amplifies the ranges of different parameters by adding three extra parameters into $\Lambda$CDM (see also Fig. 8). Meanwhile the $\Lambda$CDM model gives a lower $H_0$ value and higher redshift of matter–radiation equality than the other three models. Interestingly, we also find that both the $\Lambda$CDM and the F$\Lambda$ models predict smaller spectral index and larger age of the universe than the left two models. Moreover, we find that both the F$\Lambda$ and the Fms models give higher values of the optical depth $\tau$ than the other two models, while both the F$\Lambda$ and the Fs models predict larger amplitudes of matter fluctuations than the left two models.

Fig. 7

The 1-dimensional posterior distributions of $\tau$, $n_s$, $H_0$, $\sigma _8$, $t_\mathrm{age}$ and $z_\mathrm{eq}$ in the $\Lambda$CDM (black), F$\Lambda$ (red), Fs (blue) and Fms (green) models by using the data combination CBSLCH, respectively

Fig. 8

The 2-dimensional marginalized contours of the $\Lambda$CDM (green), F$\Lambda$ (blue), Fs (red) and Fms (magenta) models in the planes of $n_s-H_0$, $\omega _m-H_0$, $t_\mathrm{age}-H_0$ and $z_\mathrm{eq}-H_0$ by using the data combination CBSLCH, respectively

5 Discussions and conclusions

Starting from a new geometrical perspective, our motivation is to search for the sterile neutrinos in the framework of Finsler geometry. Using the most stringent constraint we can provide so far, for the first time, we give the $68\%$ uncertainties of the effective number of relativistic degree of freedom for the Fs and Fms models, and $95\%$ upper bounds on the effective masses of sterile neutrinos in the Fms model, respectively. Specifically, for the Fs model, we obtain the constraint $N_\mathrm{eff}=3.237^{+0.092}_{-0.185}$, which is consistent with $\Delta N_\mathrm{eff} > 0$ at the 1.03$\sigma$ CL. This gives a very weak hint of massless sterile neutrinos and may imply the non-existence of massless sterile neutrinos in the Finslerian universe. For the Fms model, we obtain the constraints $N_\mathrm{eff}=3.143^{+0.064}_{-0.066}$ which is in favor with $\Delta N_\mathrm{eff} > 0$ at the 1.47$\sigma$ CL, and $m_{\nu , \mathrm{sterile}}^\mathrm{eff} < 0.121$ eV at the 2$\sigma$ CL which is much tighter than the Planck results using the data combination CBL [1]. This very tight restriction from the data combination CBSLCH appears to indicate the massive sterile neutrinos are also non-existent in the Finslerian cosmological setting. Furthermore, one may conclude that the sterile neutrinos are possibly non-existent in the Finslerian universe.

As a consequence, although our constraints provide very small living room for massive sterile neutrinos, to some extent, our results are in tension with the short-baseline neutrino oscillation experiments which prefer the light sterile neutrinos at around 1 eV [64,65,66,67]. However, our substantially tight constraints on the Fms model are compatible with the recent results of the neutrino oscillation experiments implemented by the Daya Bay and MINOS collaborations [68] and the cosmic ray experiment carried out by the IceCube collaboration [69], which both indicate no evidence of massive sterile neutrinos, respectively.

Using the data combination CBSLCH, we also find that: (1) the Fs model not only gives a better cosmological fit than the other three models, but also alleviates effectively the current $H_0$ tension between the local observation by R16 and the global measurement by the Planck satellite from 3.4$\sigma$ to 1.87$\sigma$. (2) The scale invariant Harrison–Zeldovich–Peebles (HZP) spectrum ($n_s=1$) [70,71,72] is strongly excluded in the Finslerian cosmological models, especially in the F$\Lambda$ model at the $11.35\sigma$ CL. Nonetheless, this large discrepancy is reduced from $11.35\sigma$ to $9.41\sigma$ and $4.31\sigma$ when considering the massless and massive sterile neutrinos, respectively. (3) Since the Fms model has one more parameter than the Fs one, it does not amplify the parameter spaces as expected but gives tighter constraints on the cosmological parameters than the Fs model does (see Figs. 5 and 8), which may imply that there exists either an unknown correlation between $N_\mathrm{eff}$ and $m_{\nu , \mathrm{sterile}}^\mathrm{eff}$ or underlying couplings between $m_{\nu , \mathrm{sterile}}^\mathrm{eff}$ and other physical parameters. (4) In the Fms model, there is still a high degeneracy between $m_{\nu , \mathrm{sterile}}^\mathrm{eff}$ and $N_\mathrm{eff}$ as noted by Planck collaboration in the $\Lambda$CDM model [1]. Meanwhile the larger sterile neutrino masses are, the larger the age of the universe and the redshift of matter–radiation equality are (see Fig. 6). (5) the Fs model predicts a lower value of the age of the universe than the left three models.

In the future, we will make a trial to investigate the abilities of different Finslerian models in relieving other tensions such as $\sigma _8$, $\tau$ and $A_L$ ones. It is worth noting that we just constrain the Finslerian models use the data combination CBSLCH and do not consider the constraining impacts of different data combinations on the correlations and degeneracies of cosmological parameters. Moreover, it is also interesting to place constraints on the effective Finslerian dark energy models by using other observational datasets such as weak gravitational lensing and Sunyaev–Zeldovich cluster counts.