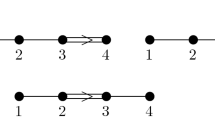
Appendix
In this appendix we present polynomials corresponding to the Lie algebra \(E_6\). The polynomials were calculated by using a certain program in Mathematica. We denote the variable z in bold and capital inside the polynomials for better readability:
$$\begin{aligned} \boxed {H_1}= & {} B_1^2 B_2^3 B_3^4 B_4^3 B_5^2 B_6^2 \mathbf Z ^{16} +16 B_1^2 B_2^3 B_3^4 B_4^3 B_5 B_6^2 \mathbf Z ^{15}\\&+\,120 B_1^2 B_2^3 B_3^4 B_4^2 B_5 B_6^2 \mathbf Z ^{14} +560 B_1^2 B_2^3 B_3^3 B_4^2 B_5 B_6^2 \mathbf Z ^{13}\\&+\,(1050 B_1^2 B_2^2 B_4^2 B_5 B_6^2 B_3^3 +770 B_1^2 B_2^3 B_4^2 B_5 B_6 B_3^3) \mathbf Z ^{12}\\&+(672 B_1 B_2^2 B_4^2 B_5 B_6^2 B_3^3 +3696 B_1^2 B_2^2 B_4^2 B_5 B_6 B_3^3) \mathbf Z ^{11}\\&+\,(3696 B_1 B_2^2 B_4^2 B_5 B_6 B_3^3 +4312 B_1^2 B_2^2 B_4^2 B_5 B_6 B_3^2) \mathbf Z ^{10}\\&+\,(8800 B_1 B_2^2 B_4^2 B_5 B_6 B_3^2 +2640 B_1^2 B_2^2 B_4 B_5 B_6 B_3^2) \mathbf Z ^9\\&+\,(660 B_1^2 B_2^2 B_4 B_6 B_3^2 +4125 B_1 B_2 B_4^2 B_5 B_6 B_3^2\\&+\,8085 B_1 B_2^2 B_4 B_5 B_6 B_3^2) \mathbf Z ^8 +(2640 B_1 B_2^2 B_4 B_6 B_3^2\\&+\,8800 B_1 B_2 B_4 B_5 B_6 B_3^2) \mathbf Z ^7 +(4312 B_1 B_2 B_4 B_6 B_3^2\\&+\,3696 B_1 B_2 B_4 B_5 B_6 B_3) \mathbf Z ^6 +(672 B_1 B_2 B_3 B_4 B_5\\&+\,3696 B_1 B_2 B_3 B_4 B_6) \mathbf Z ^5 +(1050 B_1 B_2 B_3 B_4\\&+\,770 B_1 B_2 B_3 B_6) \mathbf Z ^4 +560 B_1 B_2 B_3 \mathbf Z ^3\\&+\,120 B_1 B_2 \mathbf Z ^2+16 B_1 \mathbf Z +1, \end{aligned}$$
$$\begin{aligned} \boxed {H_2}= & {} B_1^3 B_2^6 B_3^8 B_4^6 B_5^3 B_6^4 \mathbf Z ^{30} +30 B_1^3 B_2^6 B_3^8 B_4^5 B_5^3 B_6^4 \mathbf Z ^{29}\\&+\,(120 B_1^3 B_2^6 B_4^5 B_5^2 B_6^4 B_3^8+315 B_1^3 B_2^6 B_4^5 B_5^3 B_6^4 B_3^7) \mathbf Z ^{28}\\&+\,(1050 B_1^3 B_2^5 B_4^5 B_5^3 B_6^4 B_3^7+2240 B_1^3 B_2^6 B_4^5 B_5^2 B_6^4 B_3^7\\&+\,770 B_1^3 B_2^6 B_4^5 B_5^3 B_6^3 B_3^7) \mathbf Z ^{27}+(1050 B_1^2 B_2^5 B_4^5 B_5^3 B_6^4 B_3^7\\&+\,9450 B_1^3 B_2^5 B_4^5 B_5^2 B_6^4 B_3^7+4200 B_1^3 B_2^6 B_4^4 B_5^2 B_6^4 B_3^7\\&+\,5775 B_1^3 B_2^5 B_4^5 B_5^3 B_6^3 B_3^7+6930 B_1^3 B_2^6 B_4^5 B_5^2 B_6^3 B_3^7) \mathbf Z ^{26}\\&+\,(10752 B_1^2 B_2^5 B_4^5 B_5^2 B_6^4 B_3^7+31500 B_1^3 B_2^5 B_4^4 B_5^2 B_6^4 B_3^7\\&+\,8316 B_1^2 B_2^5 B_4^5 B_5^3 B_6^3 B_3^7+59136 B_1^3 B_2^5 B_4^5 B_5^2 B_6^3 B_3^7\\&+\,23100 B_1^3 B_2^6 B_4^4 B_5^2 B_6^3 B_3^7+9702 B_1^3 B_2^5 B_4^5 B_5^3 B_6^3 B_3^6) \mathbf Z ^{25}\\&+\,(45360 B_1^2 B_2^5 B_4^4 B_5^2 B_6^4 B_3^7+92400 B_1^2 B_2^5 B_4^5 B_5^2 B_6^3 B_3^7\\&+\,249480 B_1^3 B_2^5 B_4^4 B_5^2 B_6^3 B_3^7+36750 B_1^3 B_2^5 B_4^4 B_5^2 B_6^4 B_3^6\\&+\,26950 B_1^2 B_2^5 B_4^5 B_5^3 B_6^3 B_3^6+8085 B_1^3 B_2^5 B_4^4 B_5^3 B_6^3 B_3^6\\&+\,107800 B_1^3 B_2^5 B_4^5 B_5^2 B_6^3 B_3^6+26950 B_1^3 B_2^6 B_4^4 B_5^2 B_6^3 B_3^6) \mathbf Z ^{24}\\&+\,(443520 B_1^2 B_2^5 B_4^4 B_5^2 B_6^3 B_3^7+94080 B_1^2 B_2^5 B_4^4 B_5^2 B_6^4 B_3^6\\&+\,16500 B_1^2 B_2^4 B_4^5 B_5^3 B_6^3 B_3^6+32340 B_1^2 B_2^5 B_4^4 B_5^3 B_6^3 B_3^6\\&+\,316800 B_1^2 B_2^5 B_4^5 B_5^2 B_6^3 B_3^6+1132560 B_1^3 B_2^5 B_4^4 B_5^2 B_6^3 B_3^6) \mathbf Z ^{23}\\&+\,(44100 B_1^2 B_2^4 B_4^4 B_5^2 B_6^4 B_3^6+44550 B_1^2 B_2^4 B_4^4 B_5^3 B_6^3 B_3^6\\&+\,202125 B_1^2 B_2^4 B_4^5 B_5^2 B_6^3 B_3^6+3256110 B_1^2 B_2^5 B_4^4 B_5^2 B_6^3 B_3^6\\&+\,242550 B_1^3 B_2^4 B_4^4 B_5^2 B_6^3 B_3^6+495000 B_1^3 B_2^5 B_4^3 B_5^2 B_6^3 B_3^6\\&+\,32340 B_1^3 B_2^5 B_4^4 B_5 B_6^3 B_3^6+177870 B_1^3 B_2^5 B_4^4 B_5^2 B_6^2 B_3^6\\&+\,1358280 B_1^3 B_2^5 B_4^4 B_5^2 B_6^3 B_3^5) \mathbf Z ^{22}+(2674100 B_1^2 B_2^4 B_4^4 B_5^2 B_6^3 B_3^6\\&+\,2182950 B_1^2 B_2^5 B_4^3 B_5^2 B_6^3 B_3^6+168960 B_1^2 B_2^5 B_4^4 B_5 B_6^3 B_3^6\\&+\,178200 B_1^3 B_2^5 B_4^3 B_5 B_6^3 B_3^6+711480 B_1^2 B_2^5 B_4^4 B_5^2 B_6^2 B_3^6\\&+\,23100 B_1^2 B_2^4 B_4^4 B_5^3 B_6^3 B_3^5+4928000 B_1^2 B_2^5 B_4^4 B_5^2 B_6^3 B_3^5\\&+\,1131900 B_1^3 B_2^4 B_4^4 B_5^2 B_6^3 B_3^5+1478400 B_1^3 B_2^5 B_4^3 B_5^2 B_6^3 B_3^5\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,830060 B_1^3 B_2^5 B_4^4 B_5^2 B_6^2 B_3^5) \mathbf Z ^{21}+(155232 B_1 B_2^4 B_4^4 B_5^2 B_6^3 B_3^6\\&+\,3234000 B_1^2 B_2^4 B_4^3 B_5^2 B_6^3 B_3^6+349272 B_1^2 B_2^4 B_4^4 B_5 B_6^3 B_3^6\\&+\,970200 B_1^2 B_2^5 B_4^3 B_5 B_6^3 B_3^6+853776 B_1^2 B_2^4 B_4^4 B_5^2 B_6^2 B_3^6\\&+\,9315306 B_1^2 B_2^4 B_4^4 B_5^2 B_6^3 B_3^5+7074375 B_1^2 B_2^5 B_4^3 B_5^2 B_6^3 B_3^5\\&+\,1559250 B_1^3 B_2^4 B_4^3 B_5^2 B_6^3 B_3^5+577500 B_1^3 B_2^5 B_4^3 B_5 B_6^3 B_3^5\\&+\,5082 B_1^2 B_2^4 B_4^4 B_5^3 B_6^2 B_3^5+3811500 B_1^2 B_2^5 B_4^4 B_5^2 B_6^2 B_3^5\\&+\,996072 B_1^3 B_2^4 B_4^4 B_5^2 B_6^2 B_3^5+1143450 B_1^3 B_2^5 B_4^3 B_5^2 B_6^2 B_3^5) \mathbf Z ^{20}\\&+\,(2069760 B_1^2 B_2^4 B_4^3 B_5 B_6^3 B_3^6+1478400 B_1 B_2^4 B_4^4 B_5^2 B_6^3 B_3^5\\&+\,4331250 B_1^2 B_2^3 B_4^4 B_5^2 B_6^3 B_3^5+21801780 B_1^2 B_2^4 B_4^3 B_5^2 B_6^3 B_3^5\\&+\,369600 B_1^2 B_2^4 B_4^4 B_5 B_6^3 B_3^5+3326400 B_1^2 B_2^5 B_4^3 B_5 B_6^3 B_3^5\\&+\,693000 B_1^3 B_2^4 B_4^3 B_5 B_6^3 B_3^5+11384100 B_1^2 B_2^4 B_4^4 B_5^2 B_6^2 B_3^5\\&+\,6225450 B_1^2 B_2^5 B_4^3 B_5^2 B_6^2 B_3^5+2439360 B_1^3 B_2^4 B_4^3 B_5^2 B_6^2 B_3^5\\&+\,508200 B_1^3 B_2^5 B_4^3 B_5 B_6^2 B_3^5) \mathbf Z ^{19}+(1559250 B_1 B_2^3 B_4^4 B_5^2 B_6^3 B_3^5\\&+\,3056130 B_1 B_2^4 B_4^3 B_5^2 B_6^3 B_3^5+14437500 B_1^2 B_2^3 B_4^3 B_5^2 B_6^3 B_3^5\\&+\,14314300 B_1^2 B_2^4 B_4^3 B_5 B_6^3 B_3^5+2032800 B_1 B_2^4 B_4^4 B_5^2 B_6^2 B_3^5\\&+\,8575875 B_1^2 B_2^3 B_4^4 B_5^2 B_6^2 B_3^5+28420210 B_1^2 B_2^4 B_4^3 B_5^2 B_6^2 B_3^5\\&+\,127050 B_1^2 B_2^4 B_4^4 B_5 B_6^2 B_3^5+3176250 B_1^2 B_2^5 B_4^3 B_5 B_6^2 B_3^5\\&+\,1372140 B_1^3 B_2^4 B_4^3 B_5 B_6^2 B_3^5+6338640 B_1^2 B_2^4 B_4^3 B_5^2 B_6^3 B_3^4\\&+\,2371600 B_1^2 B_2^4 B_4^4 B_5^2 B_6^2 B_3^4+711480 B_1^3 B_2^4 B_4^3 B_5^2 B_6^2 B_3^4) \mathbf Z ^{18}\\&+\,(5913600 B_1 B_2^3 B_4^3 B_5^2 B_6^3 B_3^5+1774080 B_1 B_2^4 B_4^3 B_5 B_6^3 B_3^5\\&+\,10187100 B_1^2 B_2^3 B_4^3 B_5 B_6^3 B_3^5+577500 B_1^2 B_2^4 B_4^2 B_5 B_6^3 B_3^5\\&+\,3811500 B_1 B_2^3 B_4^4 B_5^2 B_6^2 B_3^5+7470540 B_1 B_2^4 B_4^3 B_5^2 B_6^2 B_3^5\\&+\,32524800 B_1^2 B_2^3 B_4^3 B_5^2 B_6^2 B_3^5+18705960 B_1^2 B_2^4 B_4^3 B_5 B_6^2 B_3^5\\&+\,8731800 B_1^2 B_2^3 B_4^3 B_5^2 B_6^3 B_3^4+8279040 B_1^2 B_2^4 B_4^3 B_5 B_6^3 B_3^4\\&+\,4446750 B_1^2 B_2^3 B_4^4 B_5^2 B_6^2 B_3^4+16625700 B_1^2 B_2^4 B_4^3 B_5^2 B_6^2 B_3^4\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,711480 B_1^3 B_2^4 B_4^3 B_5 B_6^2 B_3^4) \mathbf Z ^{17}+(4527600 B_1 B_2^3 B_4^3 B_5 B_6^3 B_3^5\\&+\,18295200 B_1 B_2^3 B_4^3 B_5^2 B_6^2 B_3^5+5488560 B_1 B_2^4 B_4^3 B_5 B_6^2 B_3^5\\&+\,24901800 B_1^2 B_2^3 B_4^3 B_5 B_6^2 B_3^5+508200 B_1^2 B_2^4 B_4^2 B_5 B_6^2 B_3^5\\&+\,3880800 B_1 B_2^3 B_4^3 B_5^2 B_6^3 B_3^4+11884950 B_1^2 B_2^3 B_4^3 B_5 B_6^3 B_3^4\\&+\,2182950 B_1^2 B_2^4 B_4^2 B_5 B_6^3 B_3^4+2268750 B_1 B_2^3 B_4^4 B_5^2 B_6^2 B_3^4\\&+\,4446750 B_1 B_2^4 B_4^3 B_5^2 B_6^2 B_3^4+45530550 B_1^2 B_2^3 B_4^3 B_5^2 B_6^2 B_3^4\\&+\,1334025 B_1^2 B_2^4 B_4^2 B_5^2 B_6^2 B_3^4+18478980 B_1^2 B_2^4 B_4^3 B_5 B_6^2 B_3^4\\&+\,108900 B_1^3 B_2^4 B_4^2 B_5 B_6^2 B_3^4+1584660 B_1^2 B_2^4 B_4^3 B_5^2 B_6 B_3^4) \mathbf Z ^{16}\\&+\,(15937152 B_1 B_2^3 B_4^3 B_5 B_6^2 B_3^5+5588352 B_1 B_2^3 B_4^3 B_5 B_6^3 B_3^4\\&+\,3234000 B_1^2 B_2^3 B_4^2 B_5 B_6^3 B_3^4+34036496 B_1 B_2^3 B_4^3 B_5^2 B_6^2 B_3^4\\&+\,5808000 B_1^2 B_2^3 B_4^2 B_5^2 B_6^2 B_3^4+5808000 B_1 B_2^4 B_4^3 B_5 B_6^2 B_3^4\\&+\,53742416 B_1^2 B_2^3 B_4^3 B_5 B_6^2 B_3^4+6203600 B_1^2 B_2^4 B_4^2 B_5 B_6^2 B_3^4\\&+\,5588352 B_1^2 B_2^3 B_4^3 B_5^2 B_6 B_3^4+3234000 B_1^2 B_2^4 B_4^3 B_5 B_6 B_3^4\\&+\,15937152 B_1^2 B_2^3 B_4^3 B_5^2 B_6^2 B_3^3) \mathbf Z ^{15}+(108900 B_1^2 B_3^4 B_4^2 B_6^2 B_2^4\\&+\,1334025 B_1 B_3^4 B_4^2 B_5 B_6^2 B_2^4+508200 B_1^2 B_3^3 B_4^2 B_5 B_6^2 B_2^4\\&+\,2182950 B_1^2 B_3^4 B_4^2 B_5 B_6 B_2^4+1584660 B_1 B_3^4 B_4^2 B_5 B_6^3 B_2^3\\&+\,18295200 B_1 B_3^3 B_4^3 B_5^2 B_6^2 B_2^3+4446750 B_1 B_3^4 B_4^2 B_5^2 B_6^2 B_2^3\\&+\,5488560 B_1^2 B_3^3 B_4^2 B_5^2 B_6^2 B_2^3+45530550 B_1 B_3^4 B_4^3 B_5 B_6^2 B_2^3\\&+\,24901800 B_1^2 B_3^3 B_4^3 B_5 B_6^2 B_2^3+18478980 B_1^2 B_3^4 B_4^2 B_5 B_6^2 B_2^3\\&+\,3880800 B_1 B_3^4 B_4^3 B_5^2 B_6 B_2^3+4527600 B_1^2 B_3^3 B_4^3 B_5^2 B_6 B_2^3\\&+\,11884950 B_1^2 B_3^4 B_4^3 B_5 B_6 B_2^3+2268750 B_1 B_3^4 B_4^3 B_5^2 B_6^2 B_2^2) \mathbf Z ^{14}\\&+\,(577500 B_1^2 B_3^3 B_4^2 B_5 B_6 B_2^4+711480 B_1^2 B_3^4 B_4^2 B_6^2 B_2^3\\&+\,7470540 B_1 B_3^3 B_4^2 B_5^2 B_6^2 B_2^3+32524800 B_1 B_3^3 B_4^3 B_5 B_6^2 B_2^3\\&+\,16625700 B_1 B_3^4 B_4^2 B_5 B_6^2 B_2^3+18705960 B_1^2 B_3^3 B_4^2 B_5 B_6^2 B_2^3\\&+\,5913600 B_1 B_3^3 B_4^3 B_5^2 B_6 B_2^3+1774080 B_1^2 B_3^3 B_4^2 B_5^2 B_6 B_2^3\\&+\,8731800 B_1 B_3^4 B_4^3 B_5 B_6 B_2^3+10187100 B_1^2 B_3^3 B_4^3 B_5 B_6 B_2^3\\&+\,8279040 B_1^2 B_3^4 B_4^2 B_5 B_6 B_2^3+3811500 B_1 B_3^3 B_4^3 B_5^2 B_6^2 B_2^2\\&+\,4446750 B_1 B_3^4 B_4^3 B_5 B_6^2 B_2^2) \mathbf Z ^{13}+(711480 B_1 B_2^3 B_4^2 B_6^2 B_3^4\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,2371600 B_1 B_2^2 B_4^2 B_5 B_6^2 B_3^4+6338640 B_1 B_2^3 B_4^2 B_5 B_6 B_3^4\\&+\,1372140 B_1^2 B_2^3 B_4^2 B_6^2 B_3^3+2032800 B_1 B_2^2 B_4^2 B_5^2 B_6^2 B_3^3\\&+\,8575875 B_1 B_2^2 B_4^3 B_5 B_6^2 B_3^3 +28420210 B_1 B_2^3 B_4^2 B_5 B_6^2 B_3^3\\&+\,127050 B_1^2 B_2^2 B_4^2 B_5 B_6^2 B_3^3+3176250 B_1^2 B_2^3 B_4 B_5 B_6^2 B_3^3\\&+\,1559250 B_1 B_2^2 B_4^3 B_5^2 B_6 B_3^3 +3056130 B_1 B_2^3 B_4^2 B_5^2 B_6 B_3^3\\&+\,14437500 B_1 B_2^3 B_4^3 B_5 B_6 B_3^3 +14314300 B_1^2 B_2^3 B_4^2 B_5 B_6 B_3^3) \mathbf Z ^{12}\\&+\,(2439360 B_1 B_3^3 B_4^2 B_6^2 B_2^3+508200 B_1^2 B_3^3 B_4 B_6^2 B_2^3\\&+\,6225450 B_1 B_3^3 B_4 B_5 B_6^2 B_2^3+693000 B_1^2 B_3^3 B_4^2 B_6 B_2^3\\&+\,21801780 B_1 B_3^3 B_4^2 B_5 B_6 B_2^3+2069760 B_1^2 B_3^2 B_4^2 B_5 B_6 B_2^3\\&+\,3326400 B_1^2 B_3^3 B_4 B_5 B_6 B_2^3 +11384100 B_1 B_3^3 B_4^2 B_5 B_6^2 B_2^2\\&+\,1478400 B_1 B_3^3 B_4^2 B_5^2 B_6 B_2^2+4331250 B_1 B_3^3 B_4^3 B_5 B_6 B_2^2\\&+\,369600 B_1^2 B_3^3 B_4^2 B_5 B_6 B_2^2) \mathbf Z ^{11} +(1143450 B_1 B_3^3 B_4 B_6^2 B_2^3\\&+\,1559250 B_1 B_3^3 B_4^2 B_6 B_2^3+577500 B_1^2 B_3^3 B_4 B_6 B_2^3 \\&+\,3234000 B_1 B_3^2 B_4^2 B_5 B_6 B_2^3+7074375 B_1 B_3^3 B_4 B_5 B_6 B_2^3\\&+\,970200 B_1^2 B_3^2 B_4 B_5 B_6 B_2^3+996072 B_1 B_3^3 B_4^2 B_6^2 B_2^2\\&+\,5082 B_3^3 B_4^2 B_5 B_6^2 B_2^2+853776 B_1 B_3^2 B_4^2 B_5 B_6^2 B_2^2\\&+\,3811500 B_1 B_3^3 B_4 B_5 B_6^2 B_2^2+155232 B_1 B_3^2 B_4^2 B_5^2 B_6 B_2^2\\&+\,9315306 B_1 B_3^3 B_4^2 B_5 B_6 B_2^2+349272 B_1^2 B_3^2 B_4^2 B_5 B_6 B_2^2) \mathbf Z ^{10}\\&+\,(1478400 B_1 B_3^3 B_4 B_6 B_2^3+178200 B_1^2 B_3^2 B_4 B_6 B_2^3\\&+\,2182950 B_1 B_3^2 B_4 B_5 B_6 B_2^3+830060 B_1 B_3^3 B_4 B_6^2 B_2^2\\&+\,711480 B_1 B_3^2 B_4 B_5 B_6^2 B_2^2+1131900 B_1 B_3^3 B_4^2 B_6 B_2^2\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,23100 B_3^3 B_4^2 B_5 B_6 B_2^2+2674100 B_1 B_3^2 B_4^2 B_5 B_6 B_2^2\\&+\,4928000 B_1 B_3^3 B_4 B_5 B_6 B_2^2+168960 B_1^2 B_3^2 B_4 B_5 B_6 B_2^2) \mathbf Z ^9\\&+\,(495000 B_1 B_3^2 B_4 B_6 B_2^3+177870 B_1 B_3^2 B_4 B_6^2 B_2^2\\&+\,44100 B_1 B_3^2 B_4^2 B_5 B_2^2 +242550 B_1 B_3^2 B_4^2 B_6 B_2^2\\&+\,1358280 B_1 B_3^3 B_4 B_6 B_2^2+32340 B_1^2 B_3^2 B_4 B_6 B_2^2\\&+\,44550 B_3^2 B_4^2 B_5 B_6 B_2^2+3256110 B_1 B_3^2 B_4 B_5 B_6 B_2^2\\&+\,202125 B_1 B_3^2 B_4^2 B_5 B_6 B_2) \mathbf Z ^8\\&+\,(94080 B_1 B_3^2 B_4 B_5 B_2^2+1132560 B_1 B_3^2 B_4 B_6 B_2^2\\&+\,32340 B_3^2 B_4 B_5 B_6 B_2^2+443520 B_1 B_3 B_4 B_5 B_6 B_2^2\\&+\,16500 B_3^2 B_4^2 B_5 B_6 B_2+316800 B_1 B_3^2 B_4 B_5 B_6 B_2) \mathbf Z ^7\\&+\,(36750 B_1 B_3^2 B_4 B_2^2+45360 B_1 B_3 B_4 B_5 B_2^2\\&+\,26950 B_1 B_3^2 B_6 B_2^2+8085 B_3^2 B_4 B_6 B_2^2+249480 B_1 B_3 B_4 B_6 B_2^2\\&+\,107800 B_1 B_3^2 B_4 B_6 B_2+26950 B_3^2 B_4 B_5 B_6 B_2\\&+\,92400 B_1 B_3 B_4 B_5 B_6 B_2) \mathbf Z ^6+(31500 B_1 B_3 B_4 B_2^2\\&+\,23100 B_1 B_3 B_6 B_2^2+10752 B_1 B_3 B_4 B_5 B_2+9702 B_3^2 B_4 B_6 B_2\\&+\,59136 B_1 B_3 B_4 B_6 B_2+8316 B_3 B_4 B_5 B_6 B_2) \mathbf Z ^5\\&+\,(4200 B_1 B_3 B_2^2+9450 B_1 B_3 B_4 B_2+1050 B_3 B_4 B_5 B_2\\&+\,6930 B_1 B_3 B_6B_2 +5775 B_3 B_4 B_6 B_2) \mathbf Z ^4\\&+\,(2240 B_1 B_2 B_3+1050 B_2 B_4 B_3 +770 B_2 B_6 B_3) \mathbf Z ^3\\&+\,(120 B_1 B_2+315 B_3 B_2) \mathbf Z ^2+30 B_2 \mathbf Z +1,\\ \end{aligned}$$
$$\begin{aligned} \boxed {H_3}= & {} B_1^4 B_2^8 B_3^{12} B_4^8 B_5^4 B_6^6 \mathbf Z ^{42} +42 B_1^4 B_2^8 B_3^{11} B_4^8 B_5^4 B_6^6 \mathbf Z ^{41}\\&+\,(315 B_1^4 B_2^7 B_4^8 B_5^4 B_6^6 B_3^{11}+315 B_1^4 B_2^8 B_4^7 B_5^4 B_6^6 B_3^{11}\\&+\,231 B_1^4 B_2^8 B_4^8 B_5^4 B_6^5 B_3^{11}) \mathbf Z ^{40}\\&+\,(560 B_1^3 B_2^7 B_4^8 B_5^4 B_6^6 B_3^{11}+4200 B_1^4 B_2^7 B_4^7 B_5^4 B_6^6 B_3^{11}\\&+\,560 B_1^4 B_2^8 B_4^7 B_5^3 B_6^6 B_3^{11}+3080 B_1^4 B_2^7 B_4^8 B_5^4 B_6^5 B_3^{11}\\&+\,3080 B_1^4 B_2^8 B_4^7 B_5^4 B_6^5 B_3^{11}) \mathbf Z ^{39}\\&+\,(9450 B_1^3 B_2^7 B_4^7 B_5^4 B_6^6 B_3^{11}+9450 B_1^4 B_2^7 B_4^7 B_5^3 B_6^6 B_3^{11}\\&+\,6930 B_1^3 B_2^7 B_4^8 B_5^4 B_6^5 B_3^{11}+51975 B_1^4 B_2^7 B_4^7 B_5^4 B_6^5 B_3^{11}\\&+\,6930 B_1^4 B_2^8 B_4^7 B_5^3 B_6^5 B_3^{11}+11025 B_1^4 B_2^7 B_4^7 B_5^4 B_6^6 B_3^{10}\\&+\,8085 B_1^4 B_2^7 B_4^8 B_5^4 B_6^5 B_3^{10}+8085 B_1^4 B_2^8 B_4^7 B_5^4 B_6^5 B_3^{10}) \mathbf Z ^{38}\\&+\,(24192 B_1^3 B_2^7 B_4^7 B_5^3 B_6^6 B_3^{11}+133056 B_1^3 B_2^7 B_4^7 B_5^4 B_6^5 B_3^{11}\\&+\,133056 B_1^4 B_2^7 B_4^7 B_5^3 B_6^5 B_3^{11}+44100 B_1^3 B_2^7 B_4^7 B_5^4 B_6^6 B_3^{10}\\&+\,44100 B_1^4 B_2^7 B_4^7 B_5^3 B_6^6 B_3^{10}+32340 B_1^3 B_2^7 B_4^8 B_5^4 B_6^5 B_3^{10}\\&+\,407484 B_1^4 B_2^7 B_4^7 B_5^4 B_6^5 B_3^{10}+32340 B_1^4 B_2^8 B_4^7 B_5^3 B_6^5 B_3^{10}) \mathbf Z ^{37}\\&+\,(369600 B_1^3 B_2^7 B_4^7 B_5^3 B_6^5 B_3^{11}+36750 B_1^3 B_2^6 B_4^7 B_5^4 B_6^6 B_3^{10}\\&+\,200704 B_1^3 B_2^7 B_4^7 B_5^3 B_6^6 B_3^{10}+36750 B_1^4 B_2^7 B_4^6 B_5^3 B_6^6 B_3^{10}\\&+\,26950 B_1^3 B_2^6 B_4^8 B_5^4 B_6^5 B_3^{10}+1539384 B_1^3 B_2^7 B_4^7 B_5^4 B_6^5 B_3^{10}\\&+\,202125 B_1^4 B_2^6 B_4^7 B_5^4 B_6^5 B_3^{10}+202125 B_1^4 B_2^7 B_4^6 B_5^4 B_6^5 B_3^{10}\\&+\,1539384 B_1^4 B_2^7 B_4^7 B_5^3 B_6^5 B_3^{10}+26950 B_1^4 B_2^8 B_4^6 B_5^3 B_6^5 B_3^{10}\\&+\,148225 B_1^4 B_2^7 B_4^7 B_5^4 B_6^4 B_3^{10}+916839 B_1^4 B_2^7 B_4^7 B_5^4 B_6^5 B_3^9) \mathbf Z ^{36}\\&+\,(211680 B_1^3 B_2^6 B_4^7 B_5^3 B_6^6 B_3^{10}+211680 B_1^3 B_2^7 B_4^6 B_5^3 B_6^6 B_3^{10}\\&+\,1853280 B_1^3 B_2^6 B_4^7 B_5^4 B_6^5 B_3^{10}+1164240 B_1^3 B_2^7 B_4^6 B_5^4 B_6^5 B_3^{10}\\&+\,6044544 B_1^3 B_2^7 B_4^7 B_5^3 B_6^5 B_3^{10}+1164240 B_1^4 B_2^6 B_4^7 B_5^3 B_6^5 B_3^{10}\\&+\,1853280 B_1^4 B_2^7 B_4^6 B_5^3 B_6^5 B_3^{10}+853776 B_1^3 B_2^7 B_4^7 B_5^4 B_6^4 B_3^{10}\\&+\,853776 B_1^4 B_2^7 B_4^7 B_5^3 B_6^4 B_3^{10}+4527600 B_1^3 B_2^7 B_4^7 B_5^4 B_6^5 B_3^9\\&+\,1358280 B_1^4 B_2^6 B_4^7 B_5^4 B_6^5 B_3^9+1358280 B_1^4 B_2^7 B_4^6 B_5^4 B_6^5 B_3^9\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,4527600 B_1^4 B_2^7 B_4^7 B_5^3 B_6^5 B_3^9+996072 B_1^4 B_2^7 B_4^7 B_5^4 B_6^4 B_3^9) \mathbf Z ^{35}\\&+\,(396900 B_1^3 B_2^6 B_4^6 B_5^3 B_6^6 B_3^{10}+291060 B_1^2 B_2^6 B_4^7 B_5^4 B_6^5 B_3^{10}\\&+\,2182950 B_1^3 B_2^6 B_4^6 B_5^4 B_6^5 B_3^{10}+9168390 B_1^3 B_2^6 B_4^7 B_5^3 B_6^5 B_3^{10}\\&+\,9168390 B_1^3 B_2^7 B_4^6 B_5^3 B_6^5 B_3^{10}+2182950 B_1^4 B_2^6 B_4^6 B_5^3 B_6^5 B_3^{10}\\&+\,291060 B_1^4 B_2^7 B_4^6 B_5^2 B_6^5 B_3^{10}+1600830 B_1^3 B_2^6 B_4^7 B_5^4 B_6^4 B_3^{10}\\&+\,5336100 B_1^3 B_2^7 B_4^7 B_5^3 B_6^4 B_3^{10}+1600830 B_1^4 B_2^7 B_4^6 B_5^3 B_6^4 B_3^{10}\\&+\,13222440 B_1^3 B_2^6 B_4^7 B_5^4 B_6^5 B_3^9+8489250 B_1^3 B_2^7 B_4^6 B_5^4 B_6^5 B_3^9\\&+\,2546775 B_1^4 B_2^6 B_4^6 B_5^4 B_6^5 B_3^9+23654400 B_1^3 B_2^7 B_4^7 B_5^3 B_6^5 B_3^9\\&+\,8489250 B_1^4 B_2^6 B_4^7 B_5^3 B_6^5 B_3^9+13222440 B_1^4 B_2^7 B_4^6 B_5^3 B_6^5 B_3^9\\&+\,6225450 B_1^3 B_2^7 B_4^7 B_5^4 B_6^4 B_3^9+1867635 B_1^4 B_2^6 B_4^7 B_5^4 B_6^4 B_3^9\\&+\,1867635 B_1^4 B_2^7 B_4^6 B_5^4 B_6^4 B_3^9+6225450 B_1^4 B_2^7 B_4^7 B_5^3 B_6^4 B_3^9) \mathbf Z ^{34}\\&+\,(2069760 B_1^2 B_2^6 B_4^7 B_5^3 B_6^5 B_3^{10}+24147200 B_1^3 B_2^6 B_4^6 B_5^3 B_6^5 B_3^{10}\\&+\,2069760 B_1^3 B_2^7 B_4^6 B_5^2 B_6^5 B_3^{10}+11383680 B_1^3 B_2^6 B_4^7 B_5^3 B_6^4 B_3^{10}\\&+\,11383680 B_1^3 B_2^7 B_4^6 B_5^3 B_6^4 B_3^{10}+205800 B_1^3 B_2^6 B_4^6 B_5^3 B_6^6 B_3^9\\&+\,3773000 B_1^2 B_2^6 B_4^7 B_5^4 B_6^5 B_3^9+9240000 B_1^3 B_2^5 B_4^7 B_5^4 B_6^5 B_3^9\\&+\,37560600 B_1^3 B_2^6 B_4^6 B_5^4 B_6^5 B_3^9+82222140 B_1^3 B_2^6 B_4^7 B_5^3 B_6^5 B_3^9\\&+\,82222140 B_1^3 B_2^7 B_4^6 B_5^3 B_6^5 B_3^9+37560600 B_1^4 B_2^6 B_4^6 B_5^3 B_6^5 B_3^9\\&+\,9240000 B_1^4 B_2^7 B_4^5 B_5^3 B_6^5 B_3^9+3773000 B_1^4 B_2^7 B_4^6 B_5^2 B_6^5 B_3^9\\&+\,27544440 B_1^3 B_2^6 B_4^7 B_5^4 B_6^4 B_3^9+13280960 B_1^3 B_2^7 B_4^6 B_5^4 B_6^4 B_3^9\\&+\,6225450 B_1^4 B_2^6 B_4^6 B_5^4 B_6^4 B_3^9+41164200 B_1^3 B_2^7 B_4^7 B_5^3 B_6^4 B_3^9\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,13280960 B_1^4 B_2^6 B_4^7 B_5^3 B_6^4 B_3^9+27544440 B_1^4 B_2^7 B_4^6 B_5^3 B_6^4 B_3^9) \mathbf Z ^{33}\\&+\,(5588352 B_1^2 B_2^6 B_4^6 B_5^3 B_6^5 B_3^{10}+5588352 B_1^3 B_2^6 B_4^6 B_5^2 B_6^5 B_3^{10}\\&+\,30735936 B_1^3 B_2^6 B_4^6 B_5^3 B_6^4 B_3^{10}+5197500 B_1^2 B_2^5 B_4^7 B_5^4 B_6^5 B_3^9\\&+\,10187100 B_1^2 B_2^6 B_4^6 B_5^4 B_6^5 B_3^9+38981250 B_1^3 B_2^5 B_4^6 B_5^4 B_6^5 B_3^9\\&+\,28385280 B_1^2 B_2^6 B_4^7 B_5^3 B_6^5 B_3^9+63669375 B_1^3 B_2^5 B_4^7 B_5^3 B_6^5 B_3^9\\&+\,440527626 B_1^3 B_2^6 B_4^6 B_5^3 B_6^5 B_3^9+63669375 B_1^3 B_2^7 B_4^5 B_5^3 B_6^5 B_3^9\\&+\,38981250 B_1^4 B_2^6 B_4^5 B_5^3 B_6^5 B_3^9+28385280 B_1^3 B_2^7 B_4^6 B_5^2 B_6^5 B_3^9\\&+\,10187100 B_1^4 B_2^6 B_4^6 B_5^2 B_6^5 B_3^9+5197500 B_1^4 B_2^7 B_4^5 B_5^2 B_6^5 B_3^9\\&+\,7470540 B_1^2 B_2^6 B_4^7 B_5^4 B_6^4 B_3^9+28586250 B_1^3 B_2^5 B_4^7 B_5^4 B_6^4 B_3^9\\&+\,87268104 B_1^3 B_2^6 B_4^6 B_5^4 B_6^4 B_3^9+202848030 B_1^3 B_2^6 B_4^7 B_5^3 B_6^4 B_3^9\\&+\,202848030 B_1^3 B_2^7 B_4^6 B_5^3 B_6^4 B_3^9+87268104 B_1^4 B_2^6 B_4^6 B_5^3 B_6^4 B_3^9\\&+\,28586250 B_1^4 B_2^7 B_4^5 B_5^3 B_6^4 B_3^9+7470540 B_1^4 B_2^7 B_4^6 B_5^2 B_6^4 B_3^9\\&+\,11884950 B_1^3 B_2^6 B_4^6 B_5^4 B_6^5 B_3^8+11884950 B_1^4 B_2^6 B_4^6 B_5^3 B_6^5 B_3^8\\&+\,8715630 B_1^3 B_2^6 B_4^7 B_5^4 B_6^4 B_3^8+2614689 B_1^4 B_2^6 B_4^6 B_5^4 B_6^4 B_3^8\\&+\,8715630 B_1^4 B_2^7 B_4^6 B_5^3 B_6^4 B_3^8) \mathbf Z ^{32}+(24948000 B_1^2 B_2^5 B_4^6 B_5^4 B_6^5 B_3^9\\&+\,40748400 B_1^2 B_2^5 B_4^7 B_5^3 B_6^5 B_3^9+177031008 B_1^2 B_2^6 B_4^6 B_5^3 B_6^5 B_3^9\\&+\,467082000 B_1^3 B_2^5 B_4^6 B_5^3 B_6^5 B_3^9+467082000 B_1^3 B_2^6 B_4^5 B_5^3 B_6^5 B_3^9\\&+\,177031008 B_1^3 B_2^6 B_4^6 B_5^2 B_6^5 B_3^9+40748400 B_1^3 B_2^7 B_4^5 B_5^2 B_6^5 B_3^9\\&+\,24948000 B_1^4 B_2^6 B_4^5 B_5^2 B_6^5 B_3^9+18295200 B_1^2 B_2^5 B_4^7 B_5^4 B_6^4 B_3^9\\&+\,35858592 B_1^2 B_2^6 B_4^6 B_5^4 B_6^4 B_3^9+137214000 B_1^3 B_2^5 B_4^6 B_5^4 B_6^4 B_3^9\\&+\,60984000 B_1^2 B_2^6 B_4^7 B_5^3 B_6^4 B_3^9+224116200 B_1^3 B_2^5 B_4^7 B_5^3 B_6^4 B_3^9\\&+\,1339753968 B_1^3 B_2^6 B_4^6 B_5^3 B_6^4 B_3^9+224116200 B_1^3 B_2^7 B_4^5 B_5^3 B_6^4 B_3^9\\&+\,137214000 B_1^4 B_2^6 B_4^5 B_5^3 B_6^4 B_3^9+60984000 B_1^3 B_2^7 B_4^6 B_5^2 B_6^4 B_3^9\\&+\,35858592 B_1^4 B_2^6 B_4^6 B_5^2 B_6^4 B_3^9+18295200 B_1^4 B_2^7 B_4^5 B_5^2 B_6^4 B_3^9\\&+\,29106000 B_1^3 B_2^5 B_4^6 B_5^4 B_6^5 B_3^8+191866752 B_1^3 B_2^6 B_4^6 B_5^3 B_6^5 B_3^8\\&+\,29106000 B_1^4 B_2^6 B_4^5 B_5^3 B_6^5 B_3^8+21344400 B_1^3 B_2^5 B_4^7 B_5^4 B_6^4 B_3^8\\&+\,66594528 B_1^3 B_2^6 B_4^6 B_5^4 B_6^4 B_3^8+71148000 B_1^3 B_2^6 B_4^7 B_5^3 B_6^4 B_3^8\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,71148000 B_1^3 B_2^7 B_4^6 B_5^3 B_6^4B_3^8+66594528 B_1^4 B_2^6 B_4^6 B_5^3 B_6^4 B_3^8\\&+\,21344400 B_1^4 B_2^7 B_4^5 B_5^3 B_6^4 B_3^8) \mathbf Z ^{31}+(353089660 B_1^2 B_2^5 B_4^6 B_5^3 B_6^5 B_3^9\\&+\,247546530 B_1^2 B_2^6 B_4^5 B_5^3 B_6^5 B_3^9+707437500 B_1^3 B_2^5 B_4^5 B_5^3 B_6^5 B_3^9\\&+\,60555264 B_1^2 B_2^6 B_4^6 B_5^2 B_6^5 B_3^9+247546530 B_1^3 B_2^5 B_4^6 B_5^2 B_6^5 B_3^9\\&+\,353089660 B_1^3 B_2^6 B_4^5 B_5^2 B_6^5 B_3^9+111143340 B_1^2 B_2^5 B_4^6 B_5^4 B_6^4 B_3^9\\&+\,155636250 B_1^2 B_2^5 B_4^7 B_5^3 B_6^4 B_3^9+542666124 B_1^2 B_2^6 B_4^6 B_5^3 B_6^4 B_3^9\\&+\,1941993130 B_1^3 B_2^5 B_4^6 B_5^3 B_6^4 B_3^9+1941993130 B_1^3 B_2^6 B_4^5 B_5^3 B_6^4 B_3^9\\&+\,542666124 B_1^3B_2^6 B_4^6 B_5^2 B_6^4 B_3^9+155636250 B_1^3 B_2^7 B_4^5 B_5^2 B_6^4 B_3^9\\&+\,111143340 B_1^4 B_2^6 B_4^5 B_5^2 B_6^4 B_3^9+5478396 B_1^3 B_2^6 B_4^6 B_5^3 B_6^3 B_3^9\\&+\,20212500 B_1^2 B_2^5 B_4^6 B_5^4 B_6^5 B_3^8+110387200 B_1^2 B_2^6 B_4^6 B_5^3 B_6^5 B_3^8\\&+\,388031490 B_1^3 B_2^5 B_4^6 B_5^3 B_6^5 B_3^8+388031490 B_1^3 B_2^6 B_4^5 B_5^3 B_6^5 B_3^8\\&+\,110387200 B_1^3 B_2^6 B_4^6 B_5^2 B_6^5 B_3^8+20212500 B_1^4 B_2^6 B_4^5 B_5^2 B_6^5 B_3^8\\&+\,14822500 B_1^2 B_2^5 B_4^7 B_5^4 B_6^4 B_3^8+29052100 B_1^2 B_2^6 B_4^6 B_5^4 B_6^4 B_3^8\\&+\,253998360 B_1^3 B_2^5 B_4^6 B_5^4 B_6^4 B_3^8+8715630 B_1^3 B_2^6 B_4^5 B_5^4 B_6^4 B_3^8\\&+\,181575625 B_1^3 B_2^5 B_4^7 B_5^3 B_6^4 B_3^8+1554121926 B_1^3 B_2^6 B_4^6 B_5^3 B_6^4 B_3^8\\&+\,8715630 B_1^4 B_2^5 B_4^6 B_5^3 B_6^4 B_3^8+181575625 B_1^3 B_2^7 B_4^5 B_5^3 B_6^4 B_3^8\\&+\,253998360 B_1^4 B_2^6 B_4^5 B_5^3 B_6^4 B_3^8+29052100 B_1^4 B_2^6 B_4^6 B_5^2 B_6^4 B_3^8\\&+\,14822500 B_1^4 B_2^7 B_4^5 B_5^2 B_6^4 B_3^8+6391462 B_1^3 B_2^6 B_4^6 B_5^4 B_6^3 B_3^8\\&+\,6391462 B_1^4 B_2^6 B_4^6 B_5^3 B_6^3 B_3^8) \mathbf Z ^{30}+(651974400 B_1^2 B_2^5 B_4^5 B_5^3 B_6^5 B_3^9\\&+\,195592320 B_1^2 B_2^5 B_4^6 B_5^2 B_6^5 B_3^9+195592320 B_1^2 B_2^6 B_4^5 B_5^2 B_6^5 B_3^9\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,651974400 B_1^3 B_2^5 B_4^5 B_5^2 B_6^5 B_3^9+1644128640 B_1^2 B_2^5 B_4^6 B_5^3 B_6^4 B_3^9\\&+\,1075757760 B_1^2 B_2^6 B_4^5 B_5^3 B_6^4 B_3^9+3585859200 B_1^3 B_2^5 B_4^5 B_5^3 B_6^4 B_3^9\\&+\,292723200 B_1^2 B_2^6 B_4^6 B_5^2 B_6^4 B_3^9+1075757760 B_1^3 B_2^5 B_4^6 B_5^2 B_6^4 B_3^9\\&+\,1644128640 B_1^3 B_2^6 B_4^5 B_5^2 B_6^4 B_3^9+413887320 B_1^2 B_2^5 B_4^6 B_5^3 B_6^5 B_3^8\\&+\,356548500 B_1^2 B_2^6 B_4^5 B_5^3 B_6^5 B_3^8+1189465200 B_1^3 B_2^5 B_4^5 B_5^3 B_6^5 B_3^8\\&+\,356548500 B_1^3 B_2^5 B_4^6 B_5^2 B_6^5 B_3^8+413887320 B_1^3 B_2^6 B_4^5 B_5^2 B_6^5 B_3^8\\&+\,268939440 B_1^2 B_2^5 B_4^6 B_5^4 B_6^4 B_3^8+48024900 B_1^3 B_2^5 B_4^5 B_5^4 B_6^4 B_3^8\\&+\,133402500 B_1^2 B_2^5 B_4^7 B_5^3 B_6^4 B_3^8+672348600 B_1^2 B_2^6 B_4^6 B_5^3 B_6^4 B_3^8\\&+\,4320547560 B_1^3 B_2^5 B_4^6 B_5^3 B_6^4 B_3^8+4320547560 B_1^3 B_2^6 B_4^5 B_5^3 B_6^4 B_3^8\\&+\,48024900 B_1^4 B_2^5 B_4^5 B_5^3 B_6^4 B_3^8+672348600 B_1^3 B_2^6 B_4^6 B_5^2 B_6^4 B_3^8\\&+\,133402500 B_1^3 B_2^7 B_4^5 B_5^2 B_6^4 B_3^8+268939440 B_1^4 B_2^6 B_4^5 B_5^2 B_6^4 B_3^8\\&+\,35218260 B_1^3 B_2^5 B_4^6 B_5^4 B_6^3 B_3^8+180457200 B_1^3 B_2^6 B_4^6 B_5^3 B_6^3 B_3^8\\&+\,35218260 B_1^4 B_2^6 B_4^5 B_5^3 B_6^3 B_3^8+119528640 B_1^3 B_2^5 B_4^6 B_5^4 B_6^4 B_3^7\\&+\,398428800 B_1^3 B_2^6 B_4^6 B_5^3 B_6^4 B_3^7+119528640 B_1^4 B_2^6 B_4^5 B_5^3 B_6^4 B_3^7) \mathbf Z ^{29}\\&+\,(651974400 B_1^2 B_2^5 B_4^5 B_5^2 B_6^5 B_3^9+3585859200 B_1^2 B_2^5 B_4^5 B_5^3 B_6^4 B_3^9\\&+\,1075757760 B_1^2 B_2^5 B_4^6 B_5^2 B_6^4 B_3^9+1075757760 B_1^2 B_2^6 B_4^5 B_5^2 B_6^4 B_3^9\\&+\,3585859200 B_1^3 B_2^5 B_4^5 B_5^2 B_6^4 B_3^9+54573750 B_1^2 B_2^4 B_4^6 B_5^3 B_6^5 B_3^8\\&+\,1671169500 B_1^2 B_2^5 B_4^5 B_5^3 B_6^5 B_3^8+298045440 B_1^2 B_2^5 B_4^6 B_5^2 B_6^5 B_3^8\\&+\,298045440 B_1^2 B_2^6 B_4^5 B_5^2 B_6^5 B_3^8+1671169500 B_1^3 B_2^5 B_4^5 B_5^2 B_6^5 B_3^8\\&+\,54573750 B_1^3 B_2^6 B_4^4 B_5^2 B_6^5 B_3^8+24502500 B_1^2 B_2^4 B_4^6 B_5^4 B_6^4 B_3^8\\&+\,48024900 B_1^2 B_2^5 B_4^5 B_5^4 B_6^4 B_3^8+4609356210 B_1^2 B_2^5 B_4^6 B_5^3 B_6^4 B_3^8\\&+\,300155625 B_1^3 B_2^4 B_4^6 B_5^3 B_6^4 B_3^8+3054383640 B_1^2 B_2^6 B_4^5 B_5^3 B_6^4 B_3^8\\&+\,14283282150 B_1^3 B_2^5 B_4^5 B_5^3 B_6^4 B_3^8+300155625 B_1^3 B_2^6 B_4^4 B_5^3 B_6^4 B_3^8\\&+\,446054400 B_1^2 B_2^6 B_4^6 B_5^2 B_6^4 B_3^8+3054383640 B_1^3 B_2^5 B_4^6 B_5^2 B_6^4 B_3^8\\&+\,4609356210 B_1^3 B_2^6 B_4^5 B_5^2 B_6^4 B_3^8+48024900 B_1^4 B_2^5 B_4^5 B_5^2 B_6^4 B_3^8\\&+\,24502500 B_1^4 B_2^6 B_4^4 B_5^2 B_6^4 B_3^8+35218260 B_1^2 B_2^5 B_4^6 B_5^4 B_6^3 B_3^8\\&+\,117394200 B_1^2 B_2^6 B_4^6 B_5^3 B_6^3 B_3^8+607296690 B_1^3 B_2^5 B_4^6 B_5^3 B_6^3 B_3^8\\&+\,607296690 B_1^3 B_2^6 B_4^5 B_5^3 B_6^3 B_3^8+117394200 B_1^3 B_2^6 B_4^6 B_5^2 B_6^3 B_3^8\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,35218260 B_1^4 B_2^6 B_4^5 B_5^2 B_6^3 B_3^8+499167900 B_1^3 B_2^5 B_4^5 B_5^3 B_6^5 B_3^7\\&+\,186763500 B_1^2 B_2^5 B_4^6 B_5^4 B_6^4 B_3^7+56029050 B_1^3 B_2^5 B_4^5 B_5^4 B_6^4 B_3^7\\&+\,2655776970 B_1^3 B_2^5 B_4^6 B_5^3 B_6^4 B_3^7+2655776970 B_1^3 B_2^6 B_4^5 B_5^3 B_6^4 B_3^7\\&+\,56029050 B_1^4 B_2^5 B_4^5 B_5^3 B_6^4 B_3^7+186763500 B_1^4 B_2^6 B_4^5 B_5^2 B_6^4 B_3^7\\&+\,41087970 B_1^3 B_2^5 B_4^6 B_5^4 B_6^3 B_3^7+136959900 B_1^3 B_2^6 B_4^6 B_5^3 B_6^3 B_3^7\\&+\,41087970 B_1^4 B_2^6 B_4^5 B_5^3 B_6^3 B_3^7) \mathbf Z ^{28}+(4079910912 B_1^2 B_2^5 B_4^5 B_5^2 B_6^4 B_3^9\\&+\,323400000 B_1^2 B_2^4 B_4^5 B_5^3 B_6^5 B_3^8+2253071744 B_1^2 B_2^5 B_4^5 B_5^2 B_6^5 B_3^8\\&+\,323400000 B_1^3 B_2^5 B_4^4 B_5^2 B_6^5 B_3^8+11383680 B_1 B_2^5 B_4^6 B_5^3 B_6^4 B_3^8\\&+\,830060000 B_1^2 B_2^4 B_4^6 B_5^3 B_6^4 B_3^8+18476731056 B_1^2 B_2^5 B_4^5 B_5^3 B_6^4 B_3^8\\&+\,1778700000 B_1^3 B_2^4 B_4^5 B_5^3 B_6^4 B_3^8+1778700000 B_1^3 B_2^5 B_4^4 B_5^3 B_6^4 B_3^8\\&+\,4063973760 B_1^2 B_2^5 B_4^6 B_5^2 B_6^4 B_3^8+4063973760 B_1^2 B_2^6 B_4^5 B_5^2 B_6^4 B_3^8\\&+\,18476731056 B_1^3 B_2^5 B_4^5 B_5^2 B_6^4 B_3^8+830060000 B_1^3 B_2^6 B_4^4 B_5^2 B_6^4 B_3^8\\&+\,11383680 B_1^3 B_2^6 B_4^5 B_5 B_6^4 B_3^8+871627680 B_1^2 B_2^5 B_4^6 B_5^3 B_6^3 B_3^8\\&+\,766975440 B_1^2 B_2^6 B_4^5 B_5^3 B_6^3 B_3^8+2414513024 B_1^3 B_2^5 B_4^5 B_5^3 B_6^3 B_3^8\\&+\,766975440 B_1^3 B_2^5 B_4^6 B_5^2 B_6^3 B_3^8+871627680 B_1^3 B_2^6 B_4^5 B_5^2 B_6^3 B_3^8\\&+\,887409600 B_1^2 B_2^5 B_4^5 B_5^3 B_6^5 B_3^7+887409600 B_1^3 B_2^5 B_4^5 B_5^2 B_6^5 B_3^7\\&+\,50820000 B_1^2 B_2^4 B_4^6 B_5^4 B_6^4 B_3^7+99607200 B_1^2 B_2^5 B_4^5 B_5^4 B_6^4 B_3^7\\&+\,3252073440 B_1^2 B_2^5 B_4^6 B_5^3 B_6^4 B_3^7+622545000 B_1^3 B_2^4 B_4^6 B_5^3 B_6^4 B_3^7\\&+\,2075150000 B_1^2 B_2^6 B_4^5 B_5^3 B_6^4 B_3^7+19480302576 B_1^3 B_2^5 B_4^5 B_5^3 B_6^4 B_3^7\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,622545000 B_1^3 B_2^6 B_4^4 B_5^3 B_6^4 B_3^7+2075150000 B_1^3 B_2^5 B_4^6 B_5^2 B_6^4 B_3^7\\&+\,3252073440 B_1^3 B_2^6 B_4^5 B_5^2 B_6^4 B_3^7+99607200 B_1^4 B_2^5 B_4^5 B_5^2 B_6^4 B_3^7\\&+\,50820000 B_1^4 B_2^6 B_4^4 B_5^2 B_6^4 B_3^7+73045280 B_1^2 B_2^5 B_4^6 B_5^4 B_6^3 B_3^7\\&+\,21913584 B_1^3 B_2^5 B_4^5 B_5^4 B_6^3 B_3^7+1016898960 B_1^3 B_2^5 B_4^6 B_5^3 B_6^3 B_3^7\\&+\,1016898960 B_1^3 B_2^6 B_4^5 B_5^3 B_6^3 B_3^7+21913584 B_1^4 B_2^5 B_4^5 B_5^3 B_6^3 B_3^7\\&+\,73045280 B_1^4 B_2^6 B_4^5 B_5^2 B_6^3 B_3^7) \mathbf Z ^{27}+(356548500 B_1^2 B_2^4 B_4^5 B_5^2 B_6^5 B_3^8\\&+\,356548500 B_1^2 B_2^5 B_4^4 B_5^2 B_6^5 B_3^8+48024900 B_1 B_2^4 B_4^6 B_5^3 B_6^4 B_3^8\\&+\,94128804 B_1 B_2^5 B_4^5 B_5^3 B_6^4 B_3^8+5042614500 B_1^2 B_2^4 B_4^5 B_5^3 B_6^4 B_3^8\\&+\,1961016750 B_1^2 B_2^5 B_4^4 B_5^3 B_6^4 B_3^8+588305025 B_1^2 B_2^4 B_4^6 B_5^2 B_6^4 B_3^8\\&+\,27835512516 B_1^2 B_2^5 B_4^5 B_5^2 B_6^4 B_3^8+1961016750 B_1^3 B_2^4 B_4^5 B_5^2 B_6^4 B_3^8\\&+\,588305025 B_1^2 B_2^6 B_4^4 B_5^2 B_6^4 B_3^8+5042614500 B_1^3 B_2^5 B_4^4 B_5^2 B_6^4 B_3^8\\&+\,94128804 B_1^3 B_2^5 B_4^5 B_5 B_6^4 B_3^8+48024900 B_1^3 B_2^6 B_4^4 B_5 B_6^4 B_3^8\\&+\,264136950 B_1^2 B_2^4 B_4^6 B_5^3 B_6^3 B_3^8+4790284884 B_1^2 B_2^5 B_4^5 B_5^3 B_6^3 B_3^8\\&+\,880456500 B_1^2 B_2^5 B_4^6 B_5^2 B_6^3 B_3^8+880456500 B_1^2 B_2^6 B_4^5 B_5^2 B_6^3 B_3^8\\&+\,4790284884 B_1^3 B_2^5 B_4^5 B_5^2 B_6^3 B_3^8+264136950 B_1^3 B_2^6 B_4^4 B_5^2 B_6^3 B_3^8\\&+\,305613000 B_1^2 B_2^4 B_4^5 B_5^3 B_6^5 B_3^7+1669054464 B_1^2 B_2^5 B_4^5 B_5^2 B_6^5 B_3^7\\&+\,305613000 B_1^3 B_2^5 B_4^4 B_5^2 B_6^5 B_3^7+34303500 B_1^2 B_2^4 B_4^5 B_5^4 B_6^4 B_3^7\\&+\,1413304200 B_1^2 B_2^4 B_4^6 B_5^3 B_6^4 B_3^7+30824064054 B_1^2 B_2^5 B_4^5 B_5^3 B_6^4 B_3^7\\&+\,6565308750 B_1^3 B_2^4 B_4^5 B_5^3 B_6^4 B_3^7+6565308750 B_1^3 B_2^5 B_4^4 B_5^3 B_6^4 B_3^7\\&+\,3902976000 B_1^2 B_2^5 B_4^6 B_5^2 B_6^4 B_3^7+3902976000 B_1^2 B_2^6 B_4^5 B_5^2 B_6^4 B_3^7\\&+\,30824064054 B_1^3 B_2^5 B_4^5 B_5^2 B_6^4 B_3^7+1413304200 B_1^3 B_2^6 B_4^4 B_5^2 B_6^4 B_3^7\\&+\,34303500 B_1^4 B_2^5 B_4^4 B_5^2 B_6^4 B_3^7+25155900 B_1^2 B_2^4 B_4^6 B_5^4 B_6^3 B_3^7\\&+\,49305564 B_1^2 B_2^5 B_4^5 B_5^4 B_6^3 B_3^7+1445944500 B_1^2 B_2^5 B_4^6 B_5^3 B_6^3 B_3^7\\&+\,308159775 B_1^3 B_2^4 B_4^6 B_5^3 B_6^3 B_3^7+1027199250 B_1^2 B_2^6 B_4^5 B_5^3 B_6^3 B_3^7\\&+\,8951787306 B_1^3 B_2^5 B_4^5 B_5^3 B_6^3 B_3^7+308159775 B_1^3 B_2^6 B_4^4 B_5^3 B_6^3 B_3^7\\&+\,1027199250 B_1^3 B_2^5 B_4^6 B_5^2 B_6^3 B_3^7+1445944500 B_1^3 B_2^6 B_4^5 B_5^2 B_6^3 B_3^7\\&+\,49305564 B_1^4 B_2^5 B_4^5 B_5^2 B_6^3 B_3^7+25155900 B_1^4 B_2^6 B_4^4 B_5^2 B_6^3 B_3^7\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,8199664704 B_1^3 B_2^5 B_4^5 B_5^3 B_6^4 B_3^6) \mathbf Z ^{26}\\&+\,(409812480 B_1 B_2^4 B_4^5 B_5^3 B_6^4 B_3^8\\&+\,122943744 B_1 B_2^5 B_4^5 B_5^2 B_6^4 B_3^8+7991343360 B_1^2 B_2^4 B_4^5 B_5^2 B_6^4 B_3^8\\&+\,7991343360 B_1^2 B_2^5 B_4^4 B_5^2 B_6^4 B_3^8+122943744 B_1^2 B_2^5 B_4^5 B_5 B_6^4 B_3^8\\&+\,409812480 B_1^3 B_2^5 B_4^4 B_5 B_6^4 B_3^8+2253968640 B_1^2 B_2^4 B_4^5 B_5^3 B_6^3 B_3^8\\&+\,8611029504 B_1^2 B_2^5 B_4^5 B_5^2 B_6^3 B_3^8+2253968640 B_1^3 B_2^5 B_4^4 B_5^2 B_6^3 B_3^8\\&+\,599001480 B_1^2 B_2^4 B_4^5 B_5^2 B_6^5 B_3^7+599001480 B_1^2 B_2^5 B_4^4 B_5^2 B_6^5 B_3^7\\&+\,114345000 B_1 B_2^4 B_4^6 B_5^3 B_6^4 B_3^7+224116200 B_1 B_2^5 B_4^5 B_5^3 B_6^4 B_3^7\\&+\,19609868880 B_1^2 B_2^4 B_4^5 B_5^3 B_6^4 B_3^7+9158882040 B_1^2 B_2^5 B_4^4 B_5^3 B_6^4 B_3^7\\&+\,2858625000 B_1^3 B_2^4 B_4^4 B_5^3 B_6^4 B_3^7+1400726250 B_1^2 B_2^4 B_4^6 B_5^2 B_6^4 B_3^7\\&+\,59798117736 B_1^2 B_2^5 B_4^5 B_5^2 B_6^4 B_3^7+9158882040 B_1^3 B_2^4 B_4^5 B_5^2 B_6^4 B_3^7\\&+\,1400726250 B_1^2 B_2^6 B_4^4 B_5^2 B_6^4 B_3^7+19609868880 B_1^3 B_2^5 B_4^4 B_5^2 B_6^4 B_3^7\\&+\,224116200 B_1^3 B_2^5 B_4^5 B_5 B_6^4 B_3^7+114345000 B_1^3 B_2^6 B_4^4 B_5 B_6^4 B_3^7\\&+\,30187080 B_1^2 B_2^4 B_4^5 B_5^4 B_6^3 B_3^7+966735000 B_1^2 B_2^4 B_4^6 B_5^3 B_6^3 B_3^7\\&+\,17946116496 B_1^2 B_2^5 B_4^5 B_5^3 B_6^3 B_3^7+3421632060 B_1^3 B_2^4 B_4^5 B_5^3 B_6^3 B_3^7\\&+\,3421632060 B_1^3 B_2^5 B_4^4 B_5^3 B_6^3 B_3^7+2096325000 B_1^2 B_2^5 B_4^6 B_5^2 B_6^3 B_3^7\\&+\,2096325000 B_1^2 B_2^6 B_4^5 B_5^2 B_6^3 B_3^7+17946116496 B_1^3 B_2^5 B_4^5 B_5^2 B_6^3 B_3^7\\&+\,966735000 B_1^3 B_2^6 B_4^4 B_5^2 B_6^3 B_3^7+30187080 B_1^4 B_2^5 B_4^4 B_5^2 B_6^3 B_3^7\\&+\,439267752 B_1^3 B_2^5 B_4^5 B_5^3 B_6^2 B_3^7+16734009600 B_1^2 B_2^5 B_4^5 B_5^3 B_6^4 B_3^6\\&+\,5020202880 B_1^3 B_2^4 B_4^5 B_5^3 B_6^4 B_3^6+5020202880 B_1^3 B_2^5 B_4^4 B_5^3 B_6^4 B_3^6\\&+\,16734009600 B_1^3 B_2^5 B_4^5 B_5^2 B_6^4 B_3^6\\&+6754454784 B_1^3 B_2^5 B_4^5 B_5^3 B_6^3 B_3^6) \mathbf Z ^{25}\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,(557800320 B_1 B_2^4 B_4^5 B_5^2 B_6^4 B_3^8+1859334400 B_1^2 B_2^4 B_4^4 B_5^2 B_6^4 B_3^8\\&+\,557800320 B_1^2 B_2^5 B_4^4 B_5 B_6^4 B_3^8+3067901760 B_1^2 B_2^4 B_4^5 B_5^2 B_6^3 B_3^8\\&+\,3067901760 B_1^2 B_2^5 B_4^4 B_5^2 B_6^3 B_3^8+221852400 B_1^2 B_2^4 B_4^4 B_5^2 B_6^5 B_3^7\\&+\,2212838320 B_1 B_2^4 B_4^5 B_5^3 B_6^4 B_3^7+1985156250 B_1^2 B_2^3 B_4^5 B_5^3 B_6^4 B_3^7\\&+\,6097637700 B_1^2 B_2^4 B_4^4 B_5^3 B_6^4 B_3^7+520396800 B_1 B_2^5 B_4^5 B_5^2 B_6^4 B_3^7\\&+\,40830215370 B_1^2 B_2^4 B_4^5 B_5^2 B_6^4 B_3^7+40830215370 B_1^2 B_2^5 B_4^4 B_5^2 B_6^4 B_3^7\\&+\,6097637700 B_1^3 B_2^4 B_4^4 B_5^2 B_6^4 B_3^7+1985156250 B_1^3 B_2^5 B_4^3 B_5^2 B_6^4 B_3^7\\&+\,520396800 B_1^2 B_2^5 B_4^5 B_5 B_6^4 B_3^7+2212838320 B_1^3 B_2^5 B_4^4 B_5 B_6^4 B_3^7\\&+\,69877500 B_1 B_2^4 B_4^6 B_5^3 B_6^3 B_3^7+136959900 B_1 B_2^5 B_4^5 B_5^3 B_6^3 B_3^7\\&+\,16980581310 B_1^2 B_2^4 B_4^5 B_5^3 B_6^3 B_3^7+5281747240 B_1^2 B_2^5 B_4^4 B_5^3 B_6^3 B_3^7\\&+\,2862182400 B_1^3 B_2^4 B_4^4 B_5^3 B_6^3 B_3^7+855999375 B_1^2 B_2^4 B_4^6 B_5^2 B_6^3 B_3^7\\&+\,41763159900 B_1^2 B_2^5 B_4^5 B_5^2 B_6^3 B_3^7+5281747240 B_1^3 B_2^4 B_4^5 B_5^2 B_6^3 B_3^7\\&+\,855999375 B_1^2 B_2^6 B_4^4 B_5^2 B_6^3 B_3^7+16980581310 B_1^3 B_2^5 B_4^4 B_5^2 B_6^3 B_3^7\\&+\,136959900 B_1^3 B_2^5 B_4^5 B_5 B_6^3 B_3^7+69877500 B_1^3 B_2^6 B_4^4 B_5 B_6^3 B_3^7\\&+\,1220188200 B_1^2 B_2^5 B_4^5 B_5^3 B_6^2 B_3^7+1220188200 B_1^3 B_2^5 B_4^5 B_5^2 B_6^2 B_3^7\\&+\,18993314340 B_1^2 B_2^4 B_4^5 B_5^3 B_6^4 B_3^6+10676646750 B_1^2 B_2^5 B_4^4 B_5^3 B_6^4 B_3^6\\&+\,3890016900 B_1^3 B_2^4 B_4^4 B_5^3 B_6^4 B_3^6+38856294400 B_1^2 B_2^5 B_4^5 B_5^2 B_6^4 B_3^6\\&+\,10676646750 B_1^3 B_2^4 B_4^5 B_5^2 B_6^4 B_3^6+18993314340 B_1^3 B_2^5 B_4^4 B_5^2 B_6^4 B_3^6\\&+\,3913140 B_1^2 B_2^4 B_4^5 B_5^4 B_6^3 B_3^6+81523750 B_1^2 B_2^4 B_4^6 B_5^3 B_6^3 B_3^6\\&+\,16798204500 B_1^2 B_2^5 B_4^5 B_5^3 B_6^3 B_3^6+5039461350 B_1^3 B_2^4 B_4^5 B_5^3 B_6^3 B_3^6\\&+\,5039461350 B_1^3 B_2^5 B_4^4 B_5^3 B_6^3 B_3^6+16798204500 B_1^3 B_2^5 B_4^5 B_5^2 B_6^3 B_3^6\\&+\,81523750 B_1^3 B_2^6 B_4^4 B_5^2 B_6^3 B_3^6+3913140 B_1^4 B_2^5 B_4^4 B_5^2 B_6^3 B_3^6\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,1423552900 B_1^3 B_2^5 B_4^5 B_5^3 B_6^2 B_3^6) \mathbf Z ^{24}+(457380000 B_1 B_2^3 B_4^5 B_5^3 B_6^4 B_3^7\\&+\,896464800 B_1 B_2^4 B_4^4 B_5^3 B_6^4 B_3^7+4201797600 B_1 B_2^4 B_4^5 B_5^2 B_6^4 B_3^7\\&+\,5602905000 B_1^2 B_2^3 B_4^5 B_5^2 B_6^4 B_3^7+268939440 B_1 B_2^5 B_4^4 B_5^2 B_6^4 B_3^7\\&+\,32647658400 B_1^2 B_2^4 B_4^4 B_5^2 B_6^4 B_3^7+5602905000 B_1^2 B_2^5 B_4^3 B_5^2 B_6^4 B_3^7\\&+\,268939440 B_1^2 B_2^4 B_4^5 B_5 B_6^4 B_3^7+4201797600 B_1^2 B_2^5 B_4^4 B_5 B_6^4 B_3^7\\&+\,896464800 B_1^3 B_2^4 B_4^4 B_5 B_6^4 B_3^7+457380000 B_1^3 B_2^5 B_4^3 B_5 B_6^4 B_3^7\\&+\,1537683840 B_1 B_2^4 B_4^5 B_5^3 B_6^3 B_3^7+2515590000 B_1^2 B_2^3 B_4^5 B_5^3 B_6^3 B_3^7\\&+\,6940533600 B_1^2 B_2^4 B_4^4 B_5^3 B_6^3 B_3^7+402494400 B_1 B_2^5 B_4^5 B_5^2 B_6^3 B_3^7\\&+\,38328942960 B_1^2 B_2^4 B_4^5 B_5^2 B_6^3 B_3^7+38328942960 B_1^2 B_2^5 B_4^4 B_5^2 B_6^3 B_3^7\\&+\,6940533600 B_1^3 B_2^4 B_4^4 B_5^2 B_6^3 B_3^7+2515590000 B_1^3 B_2^5 B_4^3 B_5^2 B_6^3 B_3^7\\&+\,402494400 B_1^2 B_2^5 B_4^5 B_5 B_6^3 B_3^7+1537683840 B_1^3 B_2^5 B_4^4 B_5 B_6^3 B_3^7\\&+\,1075757760 B_1^2 B_2^4 B_4^5 B_5^3 B_6^2 B_3^7+3585859200 B_1^2 B_2^5 B_4^5 B_5^2 B_6^2 B_3^7\\&+\,1075757760 B_1^3 B_2^5 B_4^4 B_5^2 B_6^2 B_3^7+2561328000 B_1 B_2^4 B_4^5 B_5^3 B_6^4 B_3^6\\&+\,4802490000 B_1^2 B_2^3 B_4^5 B_5^3 B_6^4 B_3^6+14386125600 B_1^2 B_2^4 B_4^4 B_5^3 B_6^4 B_3^6\\&+\,48870138240 B_1^2 B_2^4 B_4^5 B_5^2 B_6^4 B_3^6+48870138240 B_1^2 B_2^5 B_4^4 B_5^2 B_6^4 B_3^6\\&+\,14386125600 B_1^3 B_2^4 B_4^4 B_5^2 B_6^4 B_3^6+4802490000 B_1^3 B_2^5 B_4^3 B_5^2 B_6^4 B_3^6\\&+\,2561328000 B_1^3 B_2^5 B_4^4 B_5 B_6^4 B_3^6+28131531120 B_1^2 B_2^4 B_4^5 B_5^3 B_6^3 B_3^6\\&+\,12664602720 B_1^2 B_2^5 B_4^4 B_5^3 B_6^3 B_3^6+6411081600 B_1^3 B_2^4 B_4^4 B_5^3 B_6^3 B_3^6\\&+\,45964195200 B_1^2 B_2^5 B_4^5 B_5^2 B_6^3 B_3^6+12664602720 B_1^3 B_2^4 B_4^5 B_5^2 B_6^3 B_3^6\\&+\,28131531120 B_1^3 B_2^5 B_4^4 B_5^2 B_6^3 B_3^6+4183502400 B_1^2 B_2^5 B_4^5 B_5^3 B_6^2 B_3^6\\&+\,1255050720 B_1^3 B_2^4 B_4^5 B_5^3 B_6^2 B_3^6+1255050720 B_1^3 B_2^5 B_4^4 B_5^3 B_6^2 B_3^6\\&+\,4183502400 B_1^3 B_2^5 B_4^5 B_5^2 B_6^2 B_3^6) \mathbf Z ^{23}\\&+\,(1400726250 B_1 B_2^3 B_4^5 B_5^2 B_6^4 B_3^7\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,3186932364 B_1 B_2^4 B_4^4 B_5^2 B_6^4 B_3^7+4669087500 B_1^2 B_2^3 B_4^4 B_5^2 B_6^4 B_3^7\\&+\,4669087500 B_1^2 B_2^4 B_4^3 B_5^2 B_6^4 B_3^7+3186932364 B_1^2 B_2^4 B_4^4 B_5 B_6^4 B_3^7\\&+\,1400726250 B_1^2 B_2^5 B_4^3 B_5 B_6^4 B_3^7+628897500 B_1 B_2^3 B_4^5 B_5^3 B_6^3 B_3^7\\&+\,1232639100 B_1 B_2^4 B_4^4 B_5^3 B_6^3 B_3^7+3421632060 B_1 B_2^4 B_4^5 B_5^2 B_6^3 B_3^7\\&+\,7703994375 B_1^2 B_2^3 B_4^5 B_5^2 B_6^3 B_3^7+369791730 B_1 B_2^5 B_4^4 B_5^2 B_6^3 B_3^7\\&+\,38630489436 B_1^2 B_2^4 B_4^4 B_5^2 B_6^3 B_3^7+7703994375 B_1^2 B_2^5 B_4^3 B_5^2 B_6^3 B_3^7\\&+\,369791730 B_1^2 B_2^4 B_4^5 B_5 B_6^3 B_3^7+3421632060 B_1^2 B_2^5 B_4^4 B_5 B_6^3 B_3^7\\&+\,1232639100 B_1^3 B_2^4 B_4^4 B_5 B_6^3 B_3^7+628897500 B_1^3 B_2^5 B_4^3 B_5 B_6^3 B_3^7\\&+\,3294508140 B_1^2 B_2^4 B_4^5 B_5^2 B_6^2 B_3^7+3294508140 B_1^2 B_2^5 B_4^4 B_5^2 B_6^2 B_3^7\\&+\,1200622500 B_1 B_2^3 B_4^5 B_5^3 B_6^4 B_3^6+2353220100 B_1 B_2^4 B_4^4 B_5^3 B_6^4 B_3^6\\&+\,4002075000 B_1^2 B_2^3 B_4^4 B_5^3 B_6^4 B_3^6+6556999680 B_1 B_2^4 B_4^5 B_5^2 B_6^4 B_3^6\\&+\,14707625625 B_1^2 B_2^3 B_4^5 B_5^2 B_6^4 B_3^6+76881768516 B_1^2 B_2^4 B_4^4 B_5^2 B_6^4 B_3^6\\&+\,14707625625 B_1^2 B_2^5 B_4^3 B_5^2 B_6^4 B_3^6+4002075000 B_1^3 B_2^4 B_4^3 B_5^2 B_6^4 B_3^6\\&+\,6556999680 B_1^2 B_2^5 B_4^4 B_5 B_6^4 B_3^6+2353220100 B_1^3 B_2^4 B_4^4 B_5 B_6^4 B_3^6\\&+\,1200622500 B_1^3 B_2^5 B_4^3 B_5 B_6^4 B_3^6+3447314640 B_1 B_2^4 B_4^5 B_5^3 B_6^3 B_3^6\\&+\,10017315000 B_1^2 B_2^3 B_4^5 B_5^3 B_6^3 B_3^6+27874845306 B_1^2 B_2^4 B_4^4 B_5^3 B_6^3 B_3^6\\&+\,80030488230 B_1^2 B_2^4 B_4^5 B_5^2 B_6^3 B_3^6+80030488230 B_1^2 B_2^5 B_4^4 B_5^2 B_6^3 B_3^6\\&+\,27874845306 B_1^3 B_2^4 B_4^4 B_5^2 B_6^3 B_3^6+10017315000 B_1^3 B_2^5 B_4^3 B_5^2 B_6^3 B_3^6\\&+\,3447314640 B_1^3 B_2^5 B_4^4 B_5 B_6^3 B_3^6+8519617260 B_1^2 B_2^4 B_4^5 B_5^3 B_6^2 B_3^6\\&+\,3843592830 B_1^2 B_2^5 B_4^4 B_5^3 B_6^2 B_3^6+1967099904 B_1^3 B_2^4 B_4^4 B_5^3 B_6^2 B_3^6\\&+\,13340250000 B_1^2 B_2^5 B_4^5 B_5^2 B_6^2 B_3^6+3843592830 B_1^3 B_2^4 B_4^5 B_5^2 B_6^2 B_3^6\\&+\,8519617260 B_1^3 B_2^5 B_4^4 B_5^2 B_6^2 B_3^6+2629630080 B_1^2 B_2^4 B_4^5 B_5^3 B_6^3 B_3^5\\&+\,788889024 B_1^3 B_2^4 B_4^4 B_5^3 B_6^3 B_3^5+2629630080 B_1^3 B_2^5 B_4^4 B_5^2 B_6^3 B_3^5) \mathbf Z ^{22}\\&+\,(1328096000 B_1 B_2^3 B_4^4 B_5^2 B_6^4 B_3^7+398428800 B_1 B_2^4 B_4^4 B_5 B_6^4 B_3^7\\&+\,1328096000 B_1^2 B_2^4 B_4^3 B_5 B_6^4 B_3^7+2191358400 B_1 B_2^3 B_4^5 B_5^2 B_6^3 B_3^7\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,4881115008 B_1 B_2^4 B_4^4 B_5^2 B_6^3 B_3^7+7304528000 B_1^2 B_2^3 B_4^4 B_5^2 B_6^3 B_3^7\\&+\,7304528000 B_1^2 B_2^4 B_4^3 B_5^2 B_6^3 B_3^7+4881115008 B_1^2 B_2^4 B_4^4 B_5 B_6^3 B_3^7\\&+\,2191358400 B_1^2 B_2^5 B_4^3 B_5 B_6^3 B_3^7+3123681792 B_1^2 B_2^4 B_4^4 B_5^2 B_6^2 B_3^7\\&+\,1138368000 B_1 B_2^3 B_4^4 B_5^3 B_6^4 B_3^6+3890016900 B_1 B_2^3 B_4^5 B_5^2 B_6^4 B_3^6\\&+\,10875161528 B_1 B_2^4 B_4^4 B_5^2 B_6^4 B_3^6+28921662000 B_1^2 B_2^3 B_4^4 B_5^2 B_6^4 B_3^6\\&+\,28921662000 B_1^2 B_2^4 B_4^3 B_5^2 B_6^4 B_3^6+10875161528 B_1^2 B_2^4 B_4^4 B_5 B_6^4 B_3^6\\&+\,3890016900 B_1^2 B_2^5 B_4^3 B_5 B_6^4 B_3^6+1138368000 B_1^3 B_2^4 B_4^3 B_5 B_6^4 B_3^6\\&+\,2752521200 B_1 B_2^3 B_4^5 B_5^3 B_6^3 B_3^6+5394941552 B_1 B_2^4 B_4^4 B_5^3 B_6^3 B_3^6\\&+\,10284615000 B_1^2 B_2^3 B_4^4 B_5^3 B_6^3 B_3^6+97828500 B_1^2 B_2^4 B_4^3 B_5^3 B_6^3 B_3^6\\&+\,10284615000 B_1 B_2^4 B_4^5 B_5^2 B_6^3 B_3^6+33718384700 B_1^2 B_2^3 B_4^5 B_5^2 B_6^3 B_3^6\\&+\,97828500 B_1 B_2^5 B_4^4 B_5^2 B_6^3 B_3^6+163830961008 B_1^2 B_2^4 B_4^4 B_5^2 B_6^3 B_3^6\\&+\,97828500 B_1^3 B_2^3 B_4^4 B_5^2 B_6^3 B_3^6+33718384700 B_1^2 B_2^5 B_4^3 B_5^2 B_6^3 B_3^6\\&+\,10284615000 B_1^3 B_2^4 B_4^3 B_5^2 B_6^3 B_3^6+97828500 B_1^2 B_2^4 B_4^5 B_5 B_6^3 B_3^6\\&+\,10284615000 B_1^2 B_2^5 B_4^4 B_5 B_6^3 B_3^6+5394941552 B_1^3 B_2^4 B_4^4 B_5 B_6^3 B_3^6\\&+\,2752521200 B_1^3 B_2^5 B_4^3 B_5 B_6^3 B_3^6+1138368000 B_1 B_2^4 B_4^5 B_5^3 B_6^2 B_3^6\\&+\,3890016900 B_1^2 B_2^3 B_4^5 B_5^3 B_6^2 B_3^6+10875161528 B_1^2 B_2^4 B_4^4 B_5^3 B_6^2 B_3^6\\&+\,28921662000 B_1^2 B_2^4 B_4^5 B_5^2 B_6^2 B_3^6+28921662000 B_1^2 B_2^5 B_4^4 B_5^2 B_6^2 B_3^6\\&+\,10875161528 B_1^3 B_2^4 B_4^4 B_5^2 B_6^2 B_3^6+3890016900 B_1^3 B_2^5 B_4^3 B_5^2 B_6^2 B_3^6\\&+\,1138368000 B_1^3 B_2^5 B_4^4 B_5 B_6^2 B_3^6+3123681792 B_1^2 B_2^4 B_4^4 B_5^2 B_6^4 B_3^5\\&+\,2191358400 B_1^2 B_2^3 B_4^5 B_5^3 B_6^3 B_3^5+4881115008 B_1^2 B_2^4 B_4^4 B_5^3 B_6^3 B_3^5\\&+\,7304528000 B_1^2 B_2^4 B_4^5 B_5^2 B_6^3 B_3^5+7304528000 B_1^2 B_2^5 B_4^4 B_5^2 B_6^3 B_3^5\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,4881115008 B_1^3 B_2^4 B_4^4 B_5^2 B_6^3 B_3^5+2191358400 B_1^3 B_2^5 B_4^3 B_5^2 B_6^3 B_3^5\\&+\,1328096000 B_1^2 B_2^4 B_4^5 B_5^3 B_6^2 B_3^5+398428800 B_1^3 B_2^4 B_4^4 B_5^3 B_6^2 B_3^5\\&+\,1328096000 B_1^3 B_2^5 B_4^4 B_5^2 B_6^2 B_3^5) \mathbf Z ^{21}\\&+\,(2629630080 B_1 B_2^3 B_4^4 B_5^2 B_6^3 B_3^7+788889024 B_1 B_2^4 B_4^4 B_5 B_6^3 B_3^7\\&+\,2629630080 B_1^2 B_2^4 B_4^3 B_5 B_6^3 B_3^7+8519617260 B_1 B_2^3 B_4^4 B_5^2 B_6^4 B_3^6\\&+\,3843592830 B_1 B_2^4 B_4^3 B_5^2 B_6^4 B_3^6+13340250000 B_1^2 B_2^3 B_4^3 B_5^2 B_6^4 B_3^6\\&+\,1967099904 B_1 B_2^4 B_4^4 B_5 B_6^4 B_3^6+3843592830 B_1^2 B_2^3 B_4^4 B_5 B_6^4 B_3^6\\&+\,8519617260 B_1^2 B_2^4 B_4^3 B_5 B_6^4 B_3^6+3447314640 B_1 B_2^3 B_4^4 B_5^3 B_6^3 B_3^6\\&+\,10017315000 B_1 B_2^3 B_4^5 B_5^2 B_6^3 B_3^6+27874845306 B_1 B_2^4 B_4^4 B_5^2 B_6^3 B_3^6\\&+\,80030488230 B_1^2 B_2^3 B_4^4 B_5^2 B_6^3 B_3^6+80030488230 B_1^2 B_2^4 B_4^3 B_5^2 B_6^3 B_3^6\\&+\,27874845306 B_1^2 B_2^4 B_4^4 B_5 B_6^3 B_3^6+10017315000 B_1^2 B_2^5 B_4^3 B_5 B_6^3 B_3^6\\&+\,3447314640 B_1^3 B_2^4 B_4^3 B_5 B_6^3 B_3^6+1200622500 B_1 B_2^3 B_4^5 B_5^3 B_6^2 B_3^6\\&+\,2353220100 B_1 B_2^4 B_4^4 B_5^3 B_6^2 B_3^6+6556999680 B_1^2 B_2^3 B_4^4 B_5^3 B_6^2 B_3^6\\&+\,4002075000 B_1 B_2^4 B_4^5 B_5^2 B_6^2 B_3^6+14707625625 B_1^2 B_2^3 B_4^5 B_5^2 B_6^2 B_3^6\\&+\,76881768516 B_1^2 B_2^4 B_4^4 B_5^2 B_6^2 B_3^6+14707625625 B_1^2 B_2^5 B_4^3 B_5^2 B_6^2 B_3^6\\&+\,6556999680 B_1^3 B_2^4 B_4^3 B_5^2 B_6^2 B_3^6+4002075000 B_1^2 B_2^5 B_4^4 B_5 B_6^2 B_3^6\\&+\,2353220100 B_1^3 B_2^4 B_4^4 B_5 B_6^2 B_3^6+1200622500 B_1^3 B_2^5 B_4^3 B_5 B_6^2 B_3^6\\&+\,3294508140 B_1^2 B_2^3 B_4^4 B_5^2 B_6^4 B_3^5+3294508140 B_1^2 B_2^4 B_4^3 B_5^2 B_6^4 B_3^5\\&+\,628897500 B_1 B_2^3 B_4^5 B_5^3 B_6^3 B_3^5+1232639100 B_1 B_2^4 B_4^4 B_5^3 B_6^3 B_3^5\\&+\,3421632060 B_1^2 B_2^3 B_4^4 B_5^3 B_6^3 B_3^5+369791730 B_1^2 B_2^4 B_4^3 B_5^3 B_6^3 B_3^5\\&+\,7703994375 B_1^2 B_2^3 B_4^5 B_5^2 B_6^3 B_3^5+38630489436 B_1^2 B_2^4 B_4^4 B_5^2 B_6^3 B_3^5\\&+\,369791730 B_1^3 B_2^3 B_4^4 B_5^2 B_6^3 B_3^5+7703994375 B_1^2 B_2^5 B_4^3 B_5^2 B_6^3 B_3^5\\&+\,3421632060 B_1^3 B_2^4 B_4^3 B_5^2 B_6^3 B_3^5+1232639100 B_1^3 B_2^4 B_4^4 B_5 B_6^3 B_3^5\\&+\,628897500 B_1^3 B_2^5 B_4^3 B_5 B_6^3 B_3^5+1400726250 B_1^2 B_2^3 B_4^5 B_5^3 B_6^2 B_3^5\\&+\,3186932364 B_1^2 B_2^4 B_4^4 B_5^3 B_6^2 B_3^5+4669087500 B_1^2 B_2^4 B_4^5 B_5^2 B_6^2 B_3^5\\&+\,4669087500 B_1^2 B_2^5 B_4^4 B_5^2 B_6^2 B_3^5+3186932364 B_1^3 B_2^4 B_4^4 B_5^2 B_6^2 B_3^5\\&+\,1400726250 B_1^3 B_2^5 B_4^3 B_5^2 B_6^2 B_3^5) \mathbf Z ^{20}+(4183502400 B_1 B_2^3 B_4^3 B_5^2 B_6^4 B_3^6\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,1255050720 B_1 B_2^3 B_4^4 B_5 B_6^4 B_3^6+1255050720 B_1 B_2^4 B_4^3 B_5 B_6^4 B_3^6\\&+\,4183502400 B_1^2 B_2^3 B_4^3 B_5 B_6^4 B_3^6+28131531120 B_1 B_2^3 B_4^4 B_5^2 B_6^3 B_3^6\\&+\,12664602720 B_1 B_2^4 B_4^3 B_5^2 B_6^3 B_3^6+45964195200 B_1^2 B_2^3 B_4^3 B_5^2 B_6^3 B_3^6\\&+\,6411081600 B_1 B_2^4 B_4^4 B_5 B_6^3 B_3^6+12664602720 B_1^2 B_2^3 B_4^4 B_5 B_6^3 B_3^6\\&+\,28131531120 B_1^2 B_2^4 B_4^3 B_5 B_6^3 B_3^6+2561328000 B_1 B_2^3 B_4^4 B_5^3 B_6^2 B_3^6\\&+\,4802490000 B_1 B_2^3 B_4^5 B_5^2 B_6^2 B_3^6+14386125600 B_1 B_2^4 B_4^4 B_5^2 B_6^2 B_3^6\\&+\,48870138240 B_1^2 B_2^3 B_4^4 B_5^2 B_6^2 B_3^6+48870138240 B_1^2 B_2^4 B_4^3 B_5^2 B_6^2 B_3^6\\&+\,14386125600 B_1^2 B_2^4 B_4^4 B_5 B_6^2 B_3^6+4802490000 B_1^2 B_2^5 B_4^3 B_5 B_6^2 B_3^6\\&+\,2561328000 B_1^3 B_2^4 B_4^3 B_5 B_6^2 B_3^6+1075757760 B_1 B_2^3 B_4^4 B_5^2 B_6^4 B_3^5\\&+\,3585859200 B_1^2 B_2^3 B_4^3 B_5^2 B_6^4 B_3^5+1075757760 B_1^2 B_2^4 B_4^3 B_5 B_6^4 B_3^5\\&+\,1537683840 B_1 B_2^3 B_4^4 B_5^3 B_6^3 B_3^5+402494400 B_1^2 B_2^3 B_4^3 B_5^3 B_6^3 B_3^5\\&+\,2515590000 B_1 B_2^3 B_4^5 B_5^2 B_6^3 B_3^5+6940533600 B_1 B_2^4 B_4^4 B_5^2 B_6^3 B_3^5\\&+\,38328942960 B_1^2 B_2^3 B_4^4 B_5^2 B_6^3 B_3^5+38328942960 B_1^2 B_2^4 B_4^3 B_5^2 B_6^3 B_3^5\\&+\,402494400 B_1^3 B_2^3 B_4^3 B_5^2 B_6^3 B_3^5+6940533600 B_1^2 B_2^4 B_4^4 B_5 B_6^3 B_3^5\\&+\,2515590000 B_1^2 B_2^5 B_4^3 B_5 B_6^3 B_3^5+1537683840 B_1^3 B_2^4 B_4^3 B_5 B_6^3 B_3^5\\&+\,457380000 B_1 B_2^3 B_4^5 B_5^3 B_6^2 B_3^5+896464800 B_1 B_2^4 B_4^4 B_5^3 B_6^2 B_3^5\\&+\,4201797600 B_1^2 B_2^3 B_4^4 B_5^3 B_6^2 B_3^5+268939440 B_1^2 B_2^4 B_4^3 B_5^3 B_6^2 B_3^5\\&+\,5602905000 B_1^2 B_2^3 B_4^5 B_5^2 B_6^2 B_3^5+32647658400 B_1^2 B_2^4 B_4^4 B_5^2 B_6^2 B_3^5\\&+\,268939440 B_1^3 B_2^3 B_4^4 B_5^2 B_6^2 B_3^5+5602905000 B_1^2 B_2^5 B_4^3 B_5^2 B_6^2 B_3^5\\&+\,4201797600 B_1^3 B_2^4 B_4^3 B_5^2 B_6^2 B_3^5+896464800 B_1^3 B_2^4 B_4^4 B_5 B_6^2 B_3^5\\&+\,457380000 B_1^3 B_2^5 B_4^3 B_5 B_6^2 B_3^5) \mathbf Z ^{19}\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,(1423552900 B_1 B_2^3 B_4^3 B_5 B_6^4 B_3^6+3913140 B_1^2 B_2^4 B_4^3 B_6^3 B_3^6\\&+\,3913140 B_2^3 B_4^4 B_5^2 B_6^3 B_3^6+81523750 B_1 B_2^2 B_4^4 B_5^2 B_6^3 B_3^6\\&+\,16798204500 B_1 B_2^3 B_4^3 B_5^2 B_6^3 B_3^6+5039461350 B_1 B_2^3 B_4^4 B_5 B_6^3 B_3^6\\&+\,5039461350 B_1 B_2^4 B_4^3 B_5 B_6^3 B_3^6+16798204500 B_1^2 B_2^3 B_4^3 B_5 B_6^3 B_3^6\\&+\,81523750 B_1^2 B_2^4 B_4^2 B_5 B_6^3 B_3^6+18993314340 B_1 B_2^3 B_4^4 B_5^2 B_6^2 B_3^6\\&+\,10676646750 B_1 B_2^4 B_4^3 B_5^2 B_6^2 B_3^6+38856294400 B_1^2 B_2^3 B_4^3 B_5^2 B_6^2 B_3^6\\&+\,3890016900 B_1 B_2^4 B_4^4 B_5 B_6^2 B_3^6+10676646750 B_1^2 B_2^3 B_4^4 B_5 B_6^2 B_3^6\\&+\,18993314340 B_1^2 B_2^4 B_4^3 B_5 B_6^2 B_3^6+1220188200 B_1 B_2^3 B_4^3 B_5^2 B_6^4 B_3^5\\&+\,1220188200 B_1^2 B_2^3 B_4^3 B_5 B_6^4 B_3^5+69877500 B_1 B_2^2 B_4^4 B_5^3 B_6^3 B_3^5\\&+\,136959900 B_1 B_2^3 B_4^3 B_5^3 B_6^3 B_3^5+16980581310 B_1 B_2^3 B_4^4 B_5^2 B_6^3 B_3^5\\&+\,855999375 B_1^2 B_2^2 B_4^4 B_5^2 B_6^3 B_3^5+5281747240 B_1 B_2^4 B_4^3 B_5^2 B_6^3 B_3^5\\&+\,41763159900 B_1^2 B_2^3 B_4^3 B_5^2 B_6^3 B_3^5+855999375 B_1^2 B_2^4 B_4^2 B_5^2 B_6^3 B_3^5\\&+\,2862182400 B_1 B_2^4 B_4^4 B_5 B_6^3 B_3^5+5281747240 B_1^2 B_2^3 B_4^4 B_5 B_6^3 B_3^5\\&+\,16980581310 B_1^2 B_2^4 B_4^3 B_5 B_6^3 B_3^5+136959900 B_1^3 B_2^3 B_4^3 B_5 B_6^3 B_3^5\\&+\,69877500 B_1^3 B_2^4 B_4^2 B_5 B_6^3 B_3^5+2212838320 B_1 B_2^3 B_4^4 B_5^3 B_6^2 B_3^5\\&+\,520396800 B_1^2 B_2^3 B_4^3 B_5^3 B_6^2 B_3^5+1985156250 B_1 B_2^3 B_4^5 B_5^2 B_6^2 B_3^5\\&+\,6097637700 B_1 B_2^4 B_4^4 B_5^2 B_6^2 B_3^5+40830215370 B_1^2 B_2^3 B_4^4 B_5^2 B_6^2 B_3^5\\&+\,40830215370 B_1^2 B_2^4 B_4^3 B_5^2 B_6^2 B_3^5+520396800 B_1^3 B_2^3 B_4^3 B_5^2 B_6^2 B_3^5\\&+\,6097637700 B_1^2 B_2^4 B_4^4 B_5 B_6^2 B_3^5+1985156250 B_1^2 B_2^5 B_4^3 B_5 B_6^2 B_3^5\\&+\,2212838320 B_1^3 B_2^4 B_4^3 B_5 B_6^2 B_3^5+221852400 B_1^2 B_2^4 B_4^4 B_5^2 B_6 B_3^5\\&+\,3067901760 B_1^2 B_2^3 B_4^4 B_5^2 B_6^3 B_3^4+3067901760 B_1^2 B_2^4 B_4^3 B_5^2 B_6^3 B_3^4\\&+\,557800320 B_1^2 B_2^3 B_4^4 B_5^3 B_6^2 B_3^4+1859334400 B_1^2 B_2^4 B_4^4 B_5^2 B_6^2 B_3^4\\&+\,557800320 B_1^3 B_2^4 B_4^3 B_5^2 B_6^2 B_3^4) \mathbf Z ^{18}\\&+\,(6754454784 B_1 B_2^3 B_4^3 B_5 B_6^3 B_3^6+16734009600 B_1 B_2^3 B_4^3 B_5^2 B_6^2 B_3^6\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,5020202880 B_1 B_2^3 B_4^4 B_5 B_6^2 B_3^6+5020202880 B_1 B_2^4 B_4^3 B_5 B_6^2 B_3^6\\&+\,16734009600 B_1^2 B_2^3 B_4^3 B_5 B_6^2 B_3^6+439267752 B_1 B_2^3 B_4^3 B_5 B_6^4 B_3^5\\&+\,30187080 B_1^2 B_2^4 B_4^3 B_6^3 B_3^5+30187080 B_2^3 B_4^4 B_5^2 B_6^3 B_3^5\\&+\,966735000 B_1 B_2^2 B_4^4 B_5^2 B_6^3 B_3^5+17946116496 B_1 B_2^3 B_4^3 B_5^2 B_6^3 B_3^5\\&+\,2096325000 B_1^2 B_2^2 B_4^3 B_5^2 B_6^3 B_3^5+2096325000 B_1^2 B_2^3 B_4^2 B_5^2 B_6^3 B_3^5\\&+\,3421632060 B_1 B_2^3 B_4^4 B_5 B_6^3 B_3^5+3421632060 B_1 B_2^4 B_4^3 B_5 B_6^3 B_3^5\\&+\,17946116496 B_1^2 B_2^3 B_4^3 B_5 B_6^3 B_3^5+966735000 B_1^2 B_2^4 B_4^2 B_5 B_6^3 B_3^5\\&+\,114345000 B_1 B_2^2 B_4^4 B_5^3 B_6^2 B_3^5+224116200 B_1 B_2^3 B_4^3 B_5^3 B_6^2 B_3^5\\&+\,19609868880 B_1 B_2^3 B_4^4 B_5^2 B_6^2 B_3^5+1400726250 B_1^2 B_2^2 B_4^4 B_5^2 B_6^2 B_3^5\\&+\,9158882040 B_1 B_2^4 B_4^3 B_5^2 B_6^2 B_3^5+59798117736 B_1^2 B_2^3 B_4^3 B_5^2 B_6^2 B_3^5\\&+\,1400726250 B_1^2 B_2^4 B_4^2 B_5^2 B_6^2 B_3^5+2858625000 B_1 B_2^4 B_4^4 B_5 B_6^2 B_3^5\\&+\,9158882040 B_1^2 B_2^3 B_4^4 B_5 B_6^2 B_3^5+19609868880 B_1^2 B_2^4 B_4^3 B_5 B_6^2 B_3^5\\&+\,224116200 B_1^3 B_2^3 B_4^3 B_5 B_6^2 B_3^5+114345000 B_1^3 B_2^4 B_4^2 B_5 B_6^2 B_3^5\\&+\,599001480 B_1^2 B_2^3 B_4^4 B_5^2 B_6 B_3^5+599001480 B_1^2 B_2^4 B_4^3 B_5^2 B_6 B_3^5\\&+\,2253968640 B_1 B_2^3 B_4^4 B_5^2 B_6^3 B_3^4+8611029504 B_1^2 B_2^3 B_4^3 B_5^2 B_6^3 B_3^4\\&+\,2253968640 B_1^2 B_2^4 B_4^3 B_5 B_6^3 B_3^4+409812480 B_1 B_2^3 B_4^4 B_5^3 B_6^2 B_3^4\\&+\,122943744 B_1^2 B_2^3 B_4^3 B_5^3 B_6^2 B_3^4+7991343360 B_1^2 B_2^3 B_4^4 B_5^2 B_6^2 B_3^4\\&+\,7991343360 B_1^2 B_2^4 B_4^3 B_5^2 B_6^2 B_3^4+122943744 B_1^3 B_2^3 B_4^3 B_5^2 B_6^2 B_3^4\\&+\,409812480 B_1^3 B_2^4 B_4^3 B_5 B_6^2 B_3^4) \mathbf Z ^{17}\\&+\,(8199664704 B_1 B_2^3 B_4^3 B_5 B_6^2 B_3^6+49305564 B_1^2 B_2^3 B_4^3 B_6^3 B_3^5\\&+\,25155900 B_1^2 B_2^4 B_4^2 B_6^3 B_3^5+25155900 B_2^2 B_4^4 B_5^2 B_6^3 B_3^5\\&+\,49305564 B_2^3 B_4^3 B_5^2 B_6^3 B_3^5+1445944500 B_1 B_2^2 B_4^3 B_5^2 B_6^3 B_3^5\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,1027199250 B_1 B_2^3 B_4^2 B_5^2 B_6^3 B_3^5+308159775 B_1 B_2^2 B_4^4 B_5 B_6^3 B_3^5\\&+\,8951787306 B_1 B_2^3 B_4^3 B_5 B_6^3 B_3^5+1027199250 B_1^2 B_2^2 B_4^3 B_5 B_6^3 B_3^5\\&+\,308159775 B_1 B_2^4 B_4^2 B_5 B_6^3 B_3^5+1445944500 B_1^2 B_2^3 B_4^2 B_5 B_6^3 B_3^5\\&+\,34303500 B_1^2 B_2^4 B_4^3 B_6^2 B_3^5+34303500 B_2^3 B_4^4 B_5^2 B_6^2 B_3^5\\&+\,1413304200 B_1 B_2^2 B_4^4 B_5^2 B_6^2 B_3^5+30824064054 B_1 B_2^3 B_4^3 B_5^2 B_6^2 B_3^5\\&+\,3902976000 B_1^2 B_2^2 B_4^3 B_5^2 B_6^2 B_3^5+3902976000 B_1^2 B_2^3 B_4^2 B_5^2 B_6^2 B_3^5\\&+\,6565308750 B_1 B_2^3 B_4^4 B_5 B_6^2 B_3^5+6565308750 B_1 B_2^4 B_4^3 B_5 B_6^2 B_3^5\\&+\,30824064054 B_1^2 B_2^3 B_4^3 B_5 B_6^2 B_3^5+1413304200 B_1^2 B_2^4 B_4^2 B_5 B_6^2 B_3^5\\&+\,305613000 B_1 B_2^3 B_4^4 B_5^2 B_6 B_3^5+1669054464 B_1^2 B_2^3 B_4^3 B_5^2 B_6 B_3^5\\&+\,305613000 B_1^2 B_2^4 B_4^3 B_5 B_6 B_3^5+264136950 B_1 B_2^2 B_4^4 B_5^2 B_6^3 B_3^4\\&+\,4790284884 B_1 B_2^3 B_4^3 B_5^2 B_6^3 B_3^4+880456500 B_1^2 B_2^2 B_4^3 B_5^2 B_6^3 B_3^4\\&+\,880456500 B_1^2 B_2^3 B_4^2 B_5^2 B_6^3 B_3^4+4790284884 B_1^2 B_2^3 B_4^3 B_5 B_6^3 B_3^4\\&+\,264136950 B_1^2 B_2^4 B_4^2 B_5 B_6^3 B_3^4+48024900 B_1 B_2^2 B_4^4 B_5^3 B_6^2 B_3^4\\&+\,94128804 B_1 B_2^3 B_4^3 B_5^3 B_6^2 B_3^4+5042614500 B_1 B_2^3 B_4^4 B_5^2 B_6^2 B_3^4\\&+\,588305025 B_1^2 B_2^2 B_4^4 B_5^2 B_6^2 B_3^4+1961016750 B_1 B_2^4 B_4^3 B_5^2 B_6^2 B_3^4\\&+\,27835512516 B_1^2 B_2^3 B_4^3 B_5^2 B_6^2 B_3^4+588305025 B_1^2 B_2^4 B_4^2 B_5^2 B_6^2 B_3^4\\&+\,1961016750 B_1^2 B_2^3 B_4^4 B_5 B_6^2 B_3^4+5042614500 B_1^2 B_2^4 B_4^3 B_5 B_6^2 B_3^4\\&+\,94128804 B_1^3 B_2^3 B_4^3 B_5 B_6^2 B_3^4+48024900 B_1^3 B_2^4 B_4^2 B_5 B_6^2 B_3^4\\&+\,356548500 B_1^2 B_2^3 B_4^4 B_5^2 B_6 B_3^4+356548500 B_1^2 B_2^4 B_4^3 B_5^2 B_6 B_3^4) \mathbf Z ^{16}\\&+\,(21913584 B_1 B_2^3 B_4^3 B_6^3 B_3^5+73045280 B_1^2 B_2^3 B_4^2 B_6^3 B_3^5\\&+\,73045280 B_2^2 B_4^3 B_5^2 B_6^3 B_3^5+21913584 B_2^3 B_4^3 B_5 B_6^3 B_3^5\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,1016898960 B_1 B_2^2 B_4^3 B_5 B_6^3 B_3^5+1016898960 B_1 B_2^3 B_4^2 B_5 B_6^3 B_3^5\\&+\,99607200 B_1^2 B_2^3 B_4^3 B_6^2 B_3^5+50820000 B_1^2 B_2^4 B_4^2 B_6^2 B_3^5\\&+\,50820000 B_2^2 B_4^4 B_5^2 B_6^2 B_3^5+99607200 B_2^3 B_4^3 B_5^2 B_6^2 B_3^5\\&+\,3252073440 B_1 B_2^2 B_4^3 B_5^2 B_6^2 B_3^5+2075150000 B_1 B_2^3 B_4^2 B_5^2 B_6^2 B_3^5\\&+\,622545000 B_1 B_2^2 B_4^4 B_5 B_6^2 B_3^5+19480302576 B_1 B_2^3 B_4^3 B_5 B_6^2 B_3^5\\&+\,2075150000 B_1^2 B_2^2 B_4^3 B_5 B_6^2 B_3^5+622545000 B_1 B_2^4 B_4^2 B_5 B_6^2 B_3^5\\&+\,3252073440 B_1^2 B_2^3 B_4^2 B_5 B_6^2 B_3^5+887409600 B_1 B_2^3 B_4^3 B_5^2 B_6 B_3^5\\&+\,887409600 B_1^2 B_2^3 B_4^3 B_5 B_6 B_3^5+871627680 B_1 B_2^2 B_4^3 B_5^2 B_6^3 B_3^4\\&+\,766975440 B_1 B_2^3 B_4^2 B_5^2 B_6^3 B_3^4+2414513024 B_1 B_2^3 B_4^3 B_5 B_6^3 B_3^4\\&+\,766975440 B_1^2 B_2^2 B_4^3 B_5 B_6^3 B_3^4+871627680 B_1^2 B_2^3 B_4^2 B_5 B_6^3 B_3^4\\&+\,11383680 B_1 B_2^2 B_4^3 B_5^3 B_6^2 B_3^4+830060000 B_1 B_2^2 B_4^4 B_5^2 B_6^2 B_3^4\\&+\,18476731056 B_1 B_2^3 B_4^3 B_5^2 B_6^2 B_3^4+4063973760 B_1^2 B_2^2 B_4^3 B_5^2 B_6^2 B_3^4\\&+\,4063973760 B_1^2 B_2^3 B_4^2 B_5^2 B_6^2 B_3^4+1778700000 B_1 B_2^3 B_4^4 B_5 B_6^2 B_3^4\\&+\,1778700000 B_1 B_2^4 B_4^3 B_5 B_6^2 B_3^4+18476731056 B_1^2 B_2^3 B_4^3 B_5 B_6^2 B_3^4\\&+\,830060000 B_1^2 B_2^4 B_4^2 B_5 B_6^2 B_3^4+11383680 B_1^3 B_2^3 B_4^2 B_5 B_6^2 B_3^4\\&+\,323400000 B_1 B_2^3 B_4^4 B_5^2 B_6 B_3^4+2253071744 B_1^2 B_2^3 B_4^3 B_5^2 B_6 B_3^4\\&+\,323400000 B_1^2 B_2^4 B_4^3 B_5 B_6 B_3^4+4079910912 B_1^2 B_2^3 B_4^3 B_5^2 B_6^2 B_3^3) \mathbf Z ^{15}\\&+\,(41087970 B_1 B_2^3 B_4^2 B_6^3 B_3^5+41087970 B_2^2 B_4^3 B_5 B_6^3 B_3^5\\&+\,136959900 B_1 B_2^2 B_4^2 B_5 B_6^3 B_3^5+56029050 B_1 B_2^3 B_4^3 B_6^2 B_3^5\\&+\,186763500 B_1^2 B_2^3 B_4^2 B_6^2 B_3^5+186763500 B_2^2 B_4^3 B_5^2 B_6^2 B_3^5\\&+\,56029050 B_2^3 B_4^3 B_5 B_6^2 B_3^5+2655776970 B_1 B_2^2 B_4^3 B_5 B_6^2 B_3^5\\&+\,2655776970 B_1 B_2^3 B_4^2 B_5 B_6^2 B_3^5+499167900 B_1 B_2^3 B_4^3 B_5 B_6 B_3^5\\&+\,35218260 B_1^2 B_2^3 B_4^2 B_6^3 B_3^4+35218260 B_2^2 B_4^3 B_5^2 B_6^3 B_3^4\\&+\,117394200 B_1 B_2^2 B_4^2 B_5^2 B_6^3 B_3^4+607296690 B_1 B_2^2 B_4^3 B_5 B_6^3 B_3^4\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,607296690 B_1 B_2^3 B_4^2 B_5 B_6^3 B_3^4+117394200 B_1^2 B_2^2 B_4^2 B_5 B_6^3 B_3^4\\&+\,48024900 B_1^2 B_2^3 B_4^3 B_6^2 B_3^4+24502500 B_1^2 B_2^4 B_4^2 B_6^2 B_3^4\\&+\,24502500 B_2^2 B_4^4 B_5^2 B_6^2 B_3^4+48024900 B_2^3 B_4^3 B_5^2 B_6^2 B_3^4\\&+\,4609356210 B_1 B_2^2 B_4^3 B_5^2 B_6^2 B_3^4+3054383640 B_1 B_2^3 B_4^2 B_5^2 B_6^2 B_3^4\\&+\,446054400 B_1^2 B_2^2 B_4^2 B_5^2 B_6^2 B_3^4+300155625 B_1 B_2^2 B_4^4 B_5 B_6^2 B_3^4\\&+\,14283282150 B_1 B_2^3 B_4^3 B_5 B_6^2 B_3^4+3054383640 B_1^2 B_2^2 B_4^3 B_5 B_6^2 B_3^4\\&+\,300155625 B_1 B_2^4 B_4^2 B_5 B_6^2 B_3^4+4609356210 B_1^2 B_2^3 B_4^2 B_5 B_6^2 B_3^4\\&+\,54573750 B_1 B_2^2 B_4^4 B_5^2 B_6 B_3^4+1671169500 B_1 B_2^3 B_4^3 B_5^2 B_6 B_3^4\\&+\,298045440 B_1^2 B_2^2 B_4^3 B_5^2 B_6 B_3^4+298045440 B_1^2 B_2^3 B_4^2 B_5^2 B_6 B_3^4\\&+\,1671169500 B_1^2 B_2^3 B_4^3 B_5 B_6 B_3^4+54573750 B_1^2 B_2^4 B_4^2 B_5 B_6 B_3^4\\&+\,3585859200 B_1 B_2^3 B_4^3 B_5^2 B_6^2 B_3^3+1075757760 B_1^2 B_2^2 B_4^3 B_5^2 B_6^2 B_3^3\\&+\,1075757760 B_1^2 B_2^3 B_4^2 B_5^2 B_6^2 B_3^3+3585859200 B_1^2 B_2^3 B_4^3 B_5 B_6^2 B_3^3\\&+\,651974400 B_1^2 B_2^3 B_4^3 B_5^2 B_6 B_3^3) \mathbf Z ^{14}+(119528640 B_1 B_2^3 B_4^2 B_6^2 B_3^5\\&+\,119528640 B_2^2 B_4^3 B_5 B_6^2 B_3^5+398428800 B_1 B_2^2 B_4^2 B_5 B_6^2 B_3^5\\&+\,35218260 B_1 B_2^3 B_4^2 B_6^3 B_3^4+35218260 B_2^2 B_4^3 B_5 B_6^3 B_3^4\\&+\,180457200 B_1 B_2^2 B_4^2 B_5 B_6^3 B_3^4+48024900 B_1 B_2^3 B_4^3 B_6^2 B_3^4\\&+\,268939440 B_1^2 B_2^3 B_4^2 B_6^2 B_3^4+268939440 B_2^2 B_4^3 B_5^2 B_6^2 B_3^4\\&+\,133402500 B_1 B_2 B_4^3 B_5^2 B_6^2 B_3^4+672348600 B_1 B_2^2 B_4^2 B_5^2 B_6^2 B_3^4\\&+\,48024900 B_2^3 B_4^3 B_5 B_6^2 B_3^4+4320547560 B_1 B_2^2 B_4^3 B_5 B_6^2 B_3^4\\&+\,4320547560 B_1 B_2^3 B_4^2 B_5 B_6^2 B_3^4+672348600 B_1^2 B_2^2 B_4^2 B_5 B_6^2 B_3^4\\&+\,133402500 B_1^2 B_2^3 B_4 B_5 B_6^2 B_3^4+413887320 B_1 B_2^2 B_4^3 B_5^2 B_6 B_3^4\\&+\,356548500 B_1 B_2^3 B_4^2 B_5^2 B_6 B_3^4+1189465200 B_1 B_2^3 B_4^3 B_5 B_6 B_3^4\\&+\,356548500 B_1^2 B_2^2 B_4^3 B_5 B_6 B_3^4+413887320 B_1^2 B_2^3 B_4^2 B_5 B_6 B_3^4\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,1644128640 B_1 B_2^2 B_4^3 B_5^2 B_6^2 B_3^3+1075757760 B_1 B_2^3 B_4^2 B_5^2 B_6^2 B_3^3\\&+\,292723200 B_1^2 B_2^2 B_4^2 B_5^2 B_6^2 B_3^3+3585859200 B_1 B_2^3 B_4^3 B_5 B_6^2 B_3^3\\&+\,1075757760 B_1^2 B_2^2 B_4^3 B_5 B_6^2 B_3^3+1644128640 B_1^2 B_2^3 B_4^2 B_5 B_6^2 B_3^3\\&+\,651974400 B_1 B_2^3 B_4^3 B_5^2 B_6 B_3^3+195592320 B_1^2 B_2^2 B_4^3 B_5^2 B_6 B_3^3\\&+\,195592320 B_1^2 B_2^3 B_4^2 B_5^2 B_6 B_3^3+651974400 B_1^2 B_2^3 B_4^3 B_5 B_6 B_3^3) \mathbf Z ^{13}\\&+\,(6391462 B_1 B_2^2 B_4^2 B_6^3 B_3^4+6391462 B_2^2 B_4^2 B_5 B_6^3 B_3^4\\&+\,8715630 B_1 B_2^2 B_4^3 B_6^2 B_3^4+253998360 B_1 B_2^3 B_4^2 B_6^2 B_3^4\\&+\,29052100 B_1^2 B_2^2 B_4^2 B_6^2 B_3^4+14822500 B_2 B_4^3 B_5^2 B_6^2 B_3^4\\&+\,29052100 B_2^2 B_4^2 B_5^2 B_6^2 B_3^4+14822500 B_1^2 B_2^3 B_4 B_6^2 B_3^4\\&+\,253998360 B_2^2 B_4^3 B_5 B_6^2 B_3^4+181575625 B_1 B_2 B_4^3 B_5 B_6^2 B_3^4\\&+\,8715630 B_2^3 B_4^2 B_5 B_6^2 B_3^4+1554121926 B_1 B_2^2 B_4^2 B_5 B_6^2 B_3^4\\&+\,181575625 B_1 B_2^3 B_4 B_5 B_6^2 B_3^4+20212500 B_1^2 B_2^3 B_4^2 B_6 B_3^4\\&+\,20212500 B_2^2 B_4^3 B_5^2 B_6 B_3^4+110387200 B_1 B_2^2 B_4^2 B_5^2 B_6 B_3^4\\&+\,388031490 B_1 B_2^2 B_4^3 B_5 B_6 B_3^4+388031490 B_1 B_2^3 B_4^2 B_5 B_6 B_3^4\\&+\,110387200 B_1^2 B_2^2 B_4^2 B_5 B_6 B_3^4+5478396 B_1 B_2^2 B_4^2 B_5 B_6^3 B_3^3\\&+\,111143340 B_1^2 B_2^3 B_4^2 B_6^2 B_3^3+111143340 B_2^2 B_4^3 B_5^2 B_6^2 B_3^3\\&+\,155636250 B_1 B_2 B_4^3 B_5^2 B_6^2 B_3^3+542666124 B_1 B_2^2 B_4^2 B_5^2 B_6^2 B_3^3\\&+\,1941993130 B_1 B_2^2 B_4^3 B_5 B_6^2 B_3^3+1941993130 B_1 B_2^3 B_4^2 B_5 B_6^2 B_3^3\\&+\,542666124 B_1^2 B_2^2 B_4^2 B_5 B_6^2 B_3^3+155636250 B_1^2 B_2^3 B_4 B_5 B_6^2 B_3^3\\&+\,353089660 B_1 B_2^2 B_4^3 B_5^2 B_6 B_3^3+247546530 B_1 B_2^3 B_4^2 B_5^2 B_6 B_3^3\\&+\,60555264 B_1^2 B_2^2 B_4^2 B_5^2 B_6 B_3^3+707437500 B_1 B_2^3 B_4^3 B_5 B_6 B_3^3\\&+\,247546530 B_1^2 B_2^2 B_4^3 B_5 B_6 B_3^3+353089660 B_1^2 B_2^3 B_4^2 B_5 B_6 B_3^3) \mathbf Z ^{12}\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,(66594528 B_1 B_2^2 B_4^2 B_6^2 B_3^4+21344400 B_1 B_2^3 B_4 B_6^2 B_3^4\\&+\,21344400 B_2 B_4^3 B_5 B_6^2 B_3^4+66594528 B_2^2 B_4^2 B_5 B_6^2 B_3^4\\&+\,71148000 B_1 B_2 B_4^2 B_5 B_6^2 B_3^4+71148000 B_1 B_2^2 B_4 B_5 B_6^2 B_3^4\\&+\,29106000 B_1 B_2^3 B_4^2 B_6 B_3^4+29106000 B_2^2 B_4^3 B_5 B_6 B_3^4\\&+\,191866752 B_1 B_2^2 B_4^2 B_5 B_6 B_3^4+137214000 B_1 B_2^3 B_4^2 B_6^2 B_3^3\\&+\,35858592 B_1^2 B_2^2 B_4^2 B_6^2 B_3^3+18295200 B_2 B_4^3 B_5^2 B_6^2 B_3^3\\&+\,35858592 B_2^2 B_4^2 B_5^2 B_6^2 B_3^3+60984000 B_1 B_2 B_4^2 B_5^2 B_6^2 B_3^3\\&+\,18295200 B_1^2 B_2^3 B_4 B_6^2 B_3^3+137214000 B_2^2 B_4^3 B_5 B_6^2 B_3^3\\&+\,224116200 B_1 B_2 B_4^3 B_5 B_6^2 B_3^3+1339753968 B_1 B_2^2 B_4^2 B_5 B_6^2 B_3^3\\&+\,224116200 B_1 B_2^3 B_4 B_5 B_6^2 B_3^3+60984000 B_1^2 B_2^2 B_4 B_5 B_6^2 B_3^3\\&+\,24948000 B_1^2 B_2^3 B_4^2 B_6 B_3^3+24948000 B_2^2 B_4^3 B_5^2 B_6 B_3^3\\&+\,40748400 B_1 B_2 B_4^3 B_5^2 B_6 B_3^3+177031008 B_1 B_2^2 B_4^2 B_5^2 B_6 B_3^3\\&+\,467082000 B_1 B_2^2 B_4^3 B_5 B_6 B_3^3+467082000 B_1 B_2^3 B_4^2 B_5 B_6 B_3^3\\&+\,177031008 B_1^2 B_2^2 B_4^2 B_5 B_6 B_3^3+40748400 B_1^2 B_2^3 B_4 B_5 B_6 B_3^3) \mathbf Z ^{11}\\&+\,(2614689 B_2^2 B_4^2 B_6^2 B_3^4+8715630 B_1 B_2^2 B_4 B_6^2 B_3^4\\&+\,8715630 B_2 B_4^2 B_5 B_6^2 B_3^4 +11884950 B_1 B_2^2 B_4^2 B_6 B_3^4\\&+\,11884950 B_2^2 B_4^2 B_5 B_6 B_3^4 +87268104 B_1 B_2^2 B_4^2 B_6^2 B_3^3\\&+\,7470540 B_2 B_4^2 B_5^2 B_6^2 B_3^3+28586250 B_1 B_2^3 B_4 B_6^2 B_3^3\\&+\,7470540 B_1^2 B_2^2 B_4 B_6^2 B_3^3+28586250 B_2 B_4^3 B_5 B_6^2 B_3^3\\&+\,87268104 B_2^2 B_4^2 B_5 B_6^2 B_3^3+202848030 B_1 B_2 B_4^2 B_5 B_6^2 B_3^3\\&+\,202848030 B_1 B_2^2 B_4 B_5 B_6^2 B_3^3+38981250 B_1 B_2^3 B_4^2 B_6 B_3^3\\&+\,10187100 B_1^2 B_2^2 B_4^2 B_6 B_3^3+5197500 B_2 B_4^3 B_5^2 B_6 B_3^3\\&+\,10187100 B_2^2 B_4^2 B_5^2 B_6 B_3^3+28385280 B_1 B_2 B_4^2 B_5^2 B_6 B_3^3\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,5197500 B_1^2 B_2^3 B_4 B_6 B_3^3+38981250 B_2^2 B_4^3 B_5 B_6 B_3^3\\&+\,63669375 B_1 B_2 B_4^3 B_5 B_6 B_3^3+440527626 B_1 B_2^2 B_4^2 B_5 B_6 B_3^3\\&+\,63669375 B_1 B_2^3 B_4 B_5 B_6 B_3^3+28385280 B_1^2 B_2^2 B_4 B_5 B_6 B_3^3\\&+\,30735936 B_1 B_2^2 B_4^2 B_5 B_6^2 B_3^2+5588352 B_1 B_2^2 B_4^2 B_5^2 B_6 B_3^2\\&+\,5588352 B_1^2 B_2^2 B_4^2 B_5 B_6 B_3^2) \mathbf Z ^{10}+(6225450 B_2^2 B_4^2 B_6^2 B_3^3\\&+\,13280960 B_1 B_2 B_4^2 B_6^2 B_3^3+27544440 B_1 B_2^2 B_4 B_6^2 B_3^3\\&+\,27544440 B_2 B_4^2 B_5 B_6^2 B_3^3+13280960 B_2^2 B_4 B_5 B_6^2 B_3^3\\&+\,41164200 B_1 B_2 B_4 B_5 B_6^2 B_3^3+205800 B_1 B_2^2 B_4^2 B_5 B_3^3\\&+\,37560600 B_1 B_2^2 B_4^2 B_6 B_3^3+3773000 B_2 B_4^2 B_5^2 B_6 B_3^3\\&+\,9240000 B_1 B_2^3 B_4 B_6 B_3^3+3773000 B_1^2 B_2^2 B_4 B_6 B_3^3\\&+\,9240000 B_2 B_4^3 B_5 B_6 B_3^3+37560600 B_2^2 B_4^2 B_5 B_6 B_3^3\\&+\,82222140 B_1 B_2 B_4^2 B_5 B_6 B_3^3+82222140 B_1 B_2^2 B_4 B_5 B_6 B_3^3\\&+\,11383680 B_1 B_2 B_4^2 B_5 B_6^2 B_3^2+11383680 B_1 B_2^2 B_4 B_5 B_6^2 B_3^2\\&+\,2069760 B_1 B_2 B_4^2 B_5^2 B_6 B_3^2+24147200 B_1 B_2^2 B_4^2 B_5 B_6 B_3^2\\&+\,2069760 B_1^2 B_2^2 B_4 B_5 B_6 B_3^2) \mathbf Z ^9+(1867635 B_2 B_4^2 B_6^2 B_3^3\\&+\,1867635 B_2^2 B_4 B_6^2 B_3^3+6225450 B_1 B_2 B_4 B_6^2 B_3^3\\&+\,6225450 B_2 B_4 B_5 B_6^2 B_3^3+2546775 B_2^2 B_4^2 B_6 B_3^3\\&+\,8489250 B_1 B_2 B_4^2 B_6 B_3^3+13222440 B_1 B_2^2 B_4 B_6 B_3^3\\&+\,13222440 B_2 B_4^2 B_5 B_6 B_3^3+8489250 B_2^2 B_4 B_5 B_6 B_3^3\\&+\,23654400 B_1 B_2 B_4 B_5 B_6 B_3^3+1600830 B_1 B_2^2 B_4 B_6^2 B_3^2\\&+\,1600830 B_2 B_4^2 B_5 B_6^2 B_3^2+5336100 B_1 B_2 B_4 B_5 B_6^2 B_3^2\\&+\,396900 B_1 B_2^2 B_4^2 B_5 B_3^2+2182950 B_1 B_2^2 B_4^2 B_6 B_3^2\\&+\,291060 B_2 B_4^2 B_5^2 B_6 B_3^2+291060 B_1^2 B_2^2 B_4 B_6 B_3^2\\&+\,2182950 B_2^2 B_4^2 B_5 B_6 B_3^2+9168390 B_1 B_2 B_4^2 B_5 B_6 B_3^2\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,9168390 B_1 B_2^2 B_4 B_5 B_6 B_3^2) \mathbf Z ^8+(996072 B_2 B_4 B_6^2 B_3^3\\&+\,1358280 B_2 B_4^2 B_6 B_3^3+1358280 B_2^2 B_4 B_6 B_3^3\\&+\,4527600 B_1 B_2 B_4 B_6 B_3^3 +4527600 B_2 B_4 B_5 B_6 B_3^3\\&+\,853776 B_1 B_2 B_4 B_6^2 B_3^2+853776 B_2 B_4 B_5 B_6^2 B_3^2\\&+\,211680 B_1 B_2 B_4^2 B_5 B_3^2+211680 B_1 B_2^2 B_4 B_5 B_3^2\\&+\,1164240 B_1 B_2 B_4^2 B_6 B_3^2+1853280 B_1 B_2^2 B_4 B_6 B_3^2\\&+\,1853280 B_2 B_4^2 B_5 B_6 B_3^2+1164240 B_2^2 B_4 B_5 B_6 B_3^2\\&+\,6044544 B_1 B_2 B_4 B_5 B_6 B_3^2) \mathbf Z ^7+(916839 B_2 B_4 B_6 B_3^3\\&+\,148225 B_2 B_4 B_6^2 B_3^2+36750 B_1 B_2^2 B_4 B_3^2\\&+\,36750 B_2 B_4^2 B_5 B_3^2+200704 B_1 B_2 B_4 B_5 B_3^2\\&+\,26950 B_1 B_2^2 B_6 B_3^2+202125 B_2 B_4^2 B_6 B_3^2\\&+\,202125 B_2^2 B_4 B_6 B_3^2+1539384 B_1 B_2 B_4 B_6 B_3^2\\&+\,26950 B_4^2 B_5 B_6 B_3^2+1539384 B_2 B_4 B_5 B_6 B_3^2\\&+\,369600 B_1 B_2 B_4 B_5 B_6 B_3) \mathbf Z ^6+(44100 B_1 B_2 B_4 B_3^2\\&+\,44100 B_2 B_4 B_5 B_3^2+32340 B_1 B_2 B_6 B_3^2+407484 B_2 B_4 B_6 B_3^2\\&+\,32340 B_4 B_5 B_6 B_3^2+24192 B_1 B_2 B_4 B_5 B_3\\&+\,133056 B_1 B_2 B_4 B_6 B_3\\&+\,133056 B_2 B_4 B_5 B_6 B_3) \mathbf Z ^5+(11025 B_2 B_4 B_3^2+8085 B_2 B_6 B_3^2\\&+\,8085 B_4 B_6 B_3^2+9450 B_1 B_2 B_4 B_3+9450 B_2 B_4 B_5 B_3\\&+\,6930 B_1 B_2 B_6 B_3\\&+\,51975 B_2 B_4 B_6 B_3+6930 B_4 B_5 B_6 B_3) \mathbf Z ^4+(560 B_1 B_2 B_3\\&+\,4200 B_2 B_4 B_3+560 B_4 B_5 B_3+3080 B_2 B_6 B_3\\&+\,3080 B_4 B_6 B_3) \mathbf Z ^3\\&+\,(315 B_2 B_3+315 B_4 B_3+231 B_6 B_3) \mathbf Z ^2+42 B_3 \mathbf Z +1, \end{aligned}$$
$$\begin{aligned} \boxed {H_4}= & {} B_1^3 B_2^6 B_3^8 B_4^6 B_5^3 B_6^4 \mathbf Z ^{30}\\&+\,30 B_1^3 B_2^5 B_3^8 B_4^6 B_5^3 B_6^4 \mathbf Z ^{29}+(120 B_1^2 B_2^5 B_4^6 B_5^3 B_6^4 B_3^8\\&+\,315 B_1^3 B_2^5 B_4^6 B_5^3 B_6^4 B_3^7) \mathbf Z ^{28}+(2240 B_1^2 B_2^5 B_4^6 B_5^3 B_6^4 B_3^7\\&+\,1050 B_1^3 B_2^5 B_4^5 B_5^3 B_6^4 B_3^7+770 B_1^3 B_2^5 B_4^6 B_5^3 B_6^3 B_3^7) \mathbf Z ^{27}\\&+\,(4200 B_1^2 B_2^4 B_4^6 B_5^3 B_6^4 B_3^7+9450 B_1^2 B_2^5 B_4^5 B_5^3 B_6^4 B_3^7\\&+\,1050 B_1^3 B_2^5 B_4^5 B_5^2 B_6^4 B_3^7+6930 B_1^2 B_2^5 B_4^6 B_5^3 B_6^3 B_3^7\\&+\,5775 B_1^3 B_2^5 B_4^5 B_5^3 B_6^3 B_3^7) \mathbf Z ^{26}+(31500 B_1^2 B_2^4 B_4^5 B_5^3 B_6^4 B_3^7\\&+\,10752 B_1^2 B_2^5 B_4^5 B_5^2 B_6^4 B_3^7+23100 B_1^2 B_2^4 B_4^6 B_5^3 B_6^3 B_3^7\\&+\,59136 B_1^2 B_2^5 B_4^5 B_5^3 B_6^3 B_3^7+8316 B_1^3 B_2^5 B_4^5 B_5^2 B_6^3 B_3^7\\&+\,9702 B_1^3 B_2^5 B_4^5 B_5^3 B_6^3 B_3^6) \mathbf Z ^{25}+(45360 B_1^2 B_2^4 B_4^5 B_5^2 B_6^4 B_3^7\\&+\,249480 B_1^2 B_2^4 B_4^5 B_5^3 B_6^3 B_3^7+92400 B_1^2 B_2^5 B_4^5 B_5^2 B_6^3 B_3^7\\&+\,36750 B_1^2 B_2^4 B_4^5 B_5^3 B_6^4 B_3^6+26950 B_1^2 B_2^4 B_4^6 B_5^3 B_6^3 B_3^6\\&+\,107800 B_1^2 B_2^5 B_4^5 B_5^3 B_6^3 B_3^6+8085 B_1^3 B_2^4 B_4^5 B_5^3 B_6^3 B_3^6\\&+\,26950 B_1^3 B_2^5 B_4^5 B_5^2 B_6^3 B_3^6) \mathbf Z ^{24}+(443520 B_1^2 B_2^4 B_4^5 B_5^2 B_6^3 B_3^7\\&+\,94080 B_1^2 B_2^4 B_4^5 B_5^2 B_6^4 B_3^6+1132560 B_1^2 B_2^4 B_4^5 B_5^3 B_6^3 B_3^6\\&+\,316800 B_1^2 B_2^5 B_4^5 B_5^2 B_6^3 B_3^6+32340 B_1^3 B_2^4 B_4^5 B_5^2 B_6^3 B_3^6\\&+\,16500 B_1^3 B_2^5 B_4^4 B_5^2 B_6^3 B_3^6) \mathbf Z ^{23}+(44100 B_1^2 B_2^4 B_4^4 B_5^2 B_6^4 B_3^6\\&+\,32340 B_1 B_2^4 B_4^5 B_5^3 B_6^3 B_3^6+495000 B_1^2 B_2^3 B_4^5 B_5^3 B_6^3 B_3^6\\&+\,242550 B_1^2 B_2^4 B_4^4 B_5^3 B_6^3 B_3^6+3256110 B_1^2 B_2^4 B_4^5 B_5^2 B_6^3 B_3^6\\&+\,202125 B_1^2 B_2^5 B_4^4 B_5^2 B_6^3 B_3^6+44550 B_1^3 B_2^4 B_4^4 B_5^2 B_6^3 B_3^6\\&+\,177870 B_1^2 B_2^4 B_4^5 B_5^3 B_6^2 B_3^6+1358280 B_1^2 B_2^4 B_4^5 B_5^3 B_6^3 B_3^5) \mathbf Z ^{22}\\&+\,(178200 B_1 B_2^3 B_4^5 B_5^3 B_6^3 B_3^6+168960 B_1 B_2^4 B_4^5 B_5^2 B_6^3 B_3^6\\&+\,2182950 B_1^2 B_2^3 B_4^5 B_5^2 B_6^3 B_3^6+2674100 B_1^2 B_2^4 B_4^4 B_5^2 B_6^3 B_3^6\\&+\,711480 B_1^2 B_2^4 B_4^5 B_5^2 B_6^2 B_3^6+1478400 B_1^2 B_2^3 B_4^5 B_5^3 B_6^3 B_3^5\\&+\,1131900 B_1^2 B_2^4 B_4^4 B_5^3 B_6^3 B_3^5+4928000 B_1^2 B_2^4 B_4^5 B_5^2 B_6^3 B_3^5\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,23100 B_1^3 B_2^4 B_4^4 B_5^2 B_6^3 B_3^5+830060 B_1^2 B_2^4 B_4^5 B_5^3 B_6^2 B_3^5) \mathbf Z ^{21}\\&+\,(970200 B_1 B_2^3 B_4^5 B_5^2 B_6^3 B_3^6+349272 B_1 B_2^4 B_4^4 B_5^2 B_6^3 B_3^6\\&+\,3234000 B_1^2 B_2^3 B_4^4 B_5^2 B_6^3 B_3^6+155232 B_1^2 B_2^4 B_4^4 B_5 B_6^3 B_3^6\\&+\,853776 B_1^2 B_2^4 B_4^4 B_5^2 B_6^2 B_3^6+577500 B_1 B_2^3 B_4^5 B_5^3 B_6^3 B_3^5\\&+\,1559250 B_1^2 B_2^3 B_4^4 B_5^3 B_6^3 B_3^5+7074375 B_1^2 B_2^3 B_4^5 B_5^2 B_6^3 B_3^5\\&+\,9315306 B_1^2 B_2^4 B_4^4 B_5^2 B_6^3 B_3^5+1143450 B_1^2 B_2^3 B_4^5 B_5^3 B_6^2 B_3^5\\&+\,996072 B_1^2 B_2^4 B_4^4 B_5^3 B_6^2 B_3^5+3811500 B_1^2 B_2^4 B_4^5 B_5^2 B_6^2 B_3^5\\&+\,5082 B_1^3 B_2^4 B_4^4 B_5^2 B_6^2 B_3^5) \mathbf Z ^{20}+(2069760 B_1 B_2^3 B_4^4 B_5^2 B_6^3 B_3^6\\&+\,693000 B_1 B_2^3 B_4^4 B_5^3 B_6^3 B_3^5+3326400 B_1 B_2^3 B_4^5 B_5^2 B_6^3 B_3^5\\&+\,369600 B_1 B_2^4 B_4^4 B_5^2 B_6^3 B_3^5+21801780 B_1^2 B_2^3 B_4^4 B_5^2 B_6^3 B_3^5\\&+\,4331250 B_1^2 B_2^4 B_4^3 B_5^2 B_6^3 B_3^5+1478400 B_1^2 B_2^4 B_4^4 B_5 B_6^3 B_3^5\\&+\,508200 B_1 B_2^3 B_4^5 B_5^3 B_6^2 B_3^5+2439360 B_1^2 B_2^3 B_4^4 B_5^3 B_6^2 B_3^5\\&+\,6225450 B_1^2 B_2^3 B_4^5 B_5^2 B_6^2 B_3^5+11384100 B_1^2 B_2^4 B_4^4 B_5^2 B_6^2 B_3^5) \mathbf Z ^{19}\\&+\,(14314300 B_1 B_2^3 B_4^4 B_5^2 B_6^3 B_3^5+14437500 B_1^2 B_2^3 B_4^3 B_5^2 B_6^3 B_3^5\\&+\,3056130 B_1^2 B_2^3 B_4^4 B_5 B_6^3 B_3^5+1559250 B_1^2 B_2^4 B_4^3 B_5 B_6^3 B_3^5\\&+\,1372140 B_1 B_2^3 B_4^4 B_5^3 B_6^2 B_3^5+3176250 B_1 B_2^3 B_4^5 B_5^2 B_6^2 B_3^5\\&+\,127050 B_1 B_2^4 B_4^4 B_5^2 B_6^2 B_3^5+28420210 B_1^2 B_2^3 B_4^4 B_5^2 B_6^2 B_3^5\\&+\,8575875 B_1^2 B_2^4 B_4^3 B_5^2 B_6^2 B_3^5+2032800 B_1^2 B_2^4 B_4^4 B_5 B_6^2 B_3^5\\&+\,6338640 B_1^2 B_2^3 B_4^4 B_5^2 B_6^3 B_3^4+711480 B_1^2 B_2^3 B_4^4 B_5^3 B_6^2 B_3^4\\&+\,2371600 B_1^2 B_2^4 B_4^4 B_5^2 B_6^2 B_3^4) \mathbf Z ^{18}+(577500 B_1 B_2^2 B_4^4 B_5^2 B_6^3 B_3^5\\&+\,10187100 B_1 B_2^3 B_4^3 B_5^2 B_6^3 B_3^5+1774080 B_1 B_2^3 B_4^4 B_5 B_6^3 B_3^5\\&+\,5913600 B_1^2 B_2^3 B_4^3 B_5 B_6^3 B_3^5+18705960 B_1 B_2^3 B_4^4 B_5^2 B_6^2 B_3^5\\&+\,32524800 B_1^2 B_2^3 B_4^3 B_5^2 B_6^2 B_3^5+7470540 B_1^2 B_2^3 B_4^4 B_5 B_6^2 B_3^5\\&+\,3811500 B_1^2 B_2^4 B_4^3 B_5 B_6^2 B_3^5+8279040 B_1 B_2^3 B_4^4 B_5^2 B_6^3 B_3^4\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,8731800 B_1^2 B_2^3 B_4^3 B_5^2 B_6^3 B_3^4+711480 B_1 B_2^3 B_4^4 B_5^3 B_6^2 B_3^4\\&+\,16625700 B_1^2 B_2^3 B_4^4 B_5^2 B_6^2 B_3^4+4446750 B_1^2 B_2^4 B_4^3 B_5^2 B_6^2 B_3^4) \mathbf Z ^{17}\\&+\,(4527600 B_1 B_2^3 B_4^3 B_5 B_6^3 B_3^5+508200 B_1 B_2^2 B_4^4 B_5^2 B_6^2 B_3^5\\&+\,24901800 B_1 B_2^3 B_4^3 B_5^2 B_6^2 B_3^5+5488560 B_1 B_2^3 B_4^4 B_5 B_6^2 B_3^5\\&+\,18295200 B_1^2 B_2^3 B_4^3 B_5 B_6^2 B_3^5+2182950 B_1 B_2^2 B_4^4 B_5^2 B_6^3 B_3^4\\&+\,11884950 B_1 B_2^3 B_4^3 B_5^2 B_6^3 B_3^4+3880800 B_1^2 B_2^3 B_4^3 B_5 B_6^3 B_3^4\\&+\,108900 B_1 B_2^2 B_4^4 B_5^3 B_6^2 B_3^4+18478980 B_1 B_2^3 B_4^4 B_5^2 B_6^2 B_3^4\\&+\,1334025 B_1^2 B_2^2 B_4^4 B_5^2 B_6^2 B_3^4+45530550 B_1^2 B_2^3 B_4^3 B_5^2 B_6^2 B_3^4\\&+\,4446750 B_1^2 B_2^3 B_4^4 B_5 B_6^2 B_3^4+2268750 B_1^2 B_2^4 B_4^3 B_5 B_6^2 B_3^4\\&+\,1584660 B_1^2 B_2^3 B_4^4 B_5^2 B_6 B_3^4) \mathbf Z ^{16}+(15937152 B_1 B_2^3 B_4^3 B_5 B_6^2 B_3^5\\&+\,3234000 B_1 B_2^2 B_4^3 B_5^2 B_6^3 B_3^4+5588352 B_1 B_2^3 B_4^3 B_5 B_6^3 B_3^4\\&+\,6203600 B_1 B_2^2 B_4^4 B_5^2 B_6^2 B_3^4+53742416 B_1 B_2^3 B_4^3 B_5^2 B_6^2 B_3^4\\&+\,5808000 B_1^2 B_2^2 B_4^3 B_5^2 B_6^2 B_3^4+5808000 B_1 B_2^3 B_4^4 B_5 B_6^2 B_3^4\\&+\,34036496 B_1^2 B_2^3 B_4^3 B_5 B_6^2 B_3^4+3234000 B_1 B_2^3 B_4^4 B_5^2 B_6 B_3^4\\&+\,5588352 B_1^2 B_2^3 B_4^3 B_5^2 B_6 B_3^4+15937152 B_1^2 B_2^3 B_4^3 B_5^2 B_6^2 B_3^3) \mathbf Z ^{15}\\&+\,(1584660 B_1 B_2^2 B_4^3 B_5 B_6^3 B_3^4+108900 B_2^2 B_4^4 B_5^2 B_6^2 B_3^4\\&+\,18478980 B_1 B_2^2 B_4^3 B_5^2 B_6^2 B_3^4+1334025 B_1 B_2^2 B_4^4 B_5 B_6^2 B_3^4\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,45530550 B_1 B_2^3 B_4^3 B_5 B_6^2 B_3^4+4446750 B_1^2 B_2^2 B_4^3 B_5 B_6^2 B_3^4\\&+\,2268750 B_1^2 B_2^3 B_4^2 B_5 B_6^2 B_3^4+2182950 B_1 B_2^2 B_4^4 B_5^2 B_6 B_3^4\\&+\,11884950 B_1 B_2^3 B_4^3 B_5^2 B_6 B_3^4+3880800 B_1^2 B_2^3 B_4^3 B_5 B_6 B_3^4\\&+\,508200 B_1 B_2^2 B_4^4 B_5^2 B_6^2 B_3^3+24901800 B_1 B_2^3 B_4^3 B_5^2 B_6^2 B_3^3\\&+\,5488560 B_1^2 B_2^2 B_4^3 B_5^2 B_6^2 B_3^3+18295200 B_1^2 B_2^3 B_4^3 B_5 B_6^2 B_3^3\\&+\,4527600 B_1^2 B_2^3 B_4^3 B_5^2 B_6 B_3^3) \mathbf Z ^{14}+(711480 B_2^2 B_4^3 B_5^2 B_6^2 B_3^4\\&+\,16625700 B_1 B_2^2 B_4^3 B_5 B_6^2 B_3^4+4446750 B_1 B_2^3 B_4^2 B_5 B_6^2 B_3^4\\&+\,8279040 B_1 B_2^2 B_4^3 B_5^2 B_6 B_3^4+8731800 B_1 B_2^3 B_4^3 B_5 B_6 B_3^4\\&+\,18705960 B_1 B_2^2 B_4^3 B_5^2 B_6^2 B_3^3+32524800 B_1 B_2^3 B_4^3 B_5 B_6^2 B_3^3\\&+\,7470540 B_1^2 B_2^2 B_4^3 B_5 B_6^2 B_3^3+3811500 B_1^2 B_2^3 B_4^2 B_5 B_6^2 B_3^3\\&+\,577500 B_1 B_2^2 B_4^4 B_5^2 B_6 B_3^3+10187100 B_1 B_2^3 B_4^3 B_5^2 B_6 B_3^3\\&+\,1774080 B_1^2 B_2^2 B_4^3 B_5^2 B_6 B_3^3+5913600 B_1^2 B_2^3 B_4^3 B_5 B_6 B_3^3) \mathbf Z ^{13}\\&+\,(711480 B_2^2 B_4^3 B_5 B_6^2 B_3^4+2371600 B_1 B_2^2 B_4^2 B_5 B_6^2 B_3^4\\&+\,6338640 B_1 B_2^2 B_4^3 B_5 B_6 B_3^4+1372140 B_2^2 B_4^3 B_5^2 B_6^2 B_3^3\\&+\,3176250 B_1 B_2 B_4^3 B_5^2 B_6^2 B_3^3+127050 B_1 B_2^2 B_4^2 B_5^2 B_6^2 B_3^3\\&+\,28420210 B_1 B_2^2 B_4^3 B_5 B_6^2 B_3^3+8575875 B_1 B_2^3 B_4^2 B_5 B_6^2 B_3^3\\&+\,2032800 B_1^2 B_2^2 B_4^2 B_5 B_6^2 B_3^3+14314300 B_1 B_2^2 B_4^3 B_5^2 B_6 B_3^3\\&+\,14437500 B_1 B_2^3 B_4^3 B_5 B_6 B_3^3+3056130 B_1^2 B_2^2 B_4^3 B_5 B_6 B_3^3\\&+\,1559250 B_1^2 B_2^3 B_4^2 B_5 B_6 B_3^3) \mathbf Z ^{12}+(508200 B_2 B_4^3 B_5^2 B_6^2 B_3^3\\&+\,2439360 B_2^2 B_4^3 B_5 B_6^2 B_3^3+6225450 B_1 B_2 B_4^3 B_5 B_6^2 B_3^3\\&+\,11384100 B_1 B_2^2 B_4^2 B_5 B_6^2 B_3^3+693000 B_2^2 B_4^3 B_5^2 B_6 B_3^3\\&+\,3326400 B_1 B_2 B_4^3 B_5^2 B_6 B_3^3+369600 B_1 B_2^2 B_4^2 B_5^2 B_6 B_3^3\\&+\,21801780 B_1 B_2^2 B_4^3 B_5 B_6 B_3^3+4331250 B_1 B_2^3 B_4^2 B_5 B_6 B_3^3\\&+\,1478400 B_1^2 B_2^2 B_4^2 B_5 B_6 B_3^3+2069760 B_1 B_2^2 B_4^3 B_5^2 B_6 B_3^2) \mathbf Z ^{11}\\&+\,(5082 B_1 B_2^2 B_4^2 B_6^2 B_3^3+1143450 B_2 B_4^3 B_5 B_6^2 B_3^3\\&+\,996072 B_2^2 B_4^2 B_5 B_6^2 B_3^3+3811500 B_1 B_2 B_4^2 B_5 B_6^2 B_3^3\\&+\,577500 B_2 B_4^3 B_5^2 B_6 B_3^3+1559250 B_2^2 B_4^3 B_5 B_6 B_3^3\\&+\,7074375 B_1 B_2 B_4^3 B_5 B_6 B_3^3+9315306 B_1 B_2^2 B_4^2 B_5 B_6 B_3^3\\&+\,853776 B_1 B_2^2 B_4^2 B_5 B_6^2 B_3^2+970200 B_1 B_2 B_4^3 B_5^2 B_6 B_3^2\\&+\,349272 B_1 B_2^2 B_4^2 B_5^2 B_6 B_3^2+3234000 B_1 B_2^2 B_4^3 B_5 B_6 B_3^2\\&+\,155232 B_1^2 B_2^2 B_4^2 B_5 B_6 B_3^2) \mathbf Z ^{10}+(830060 B_2 B_4^2 B_5 B_6^2 B_3^3\\&+\,23100 B_1 B_2^2 B_4^2 B_6 B_3^3+1478400 B_2 B_4^3 B_5 B_6 B_3^3\\ \end{aligned}$$
$$\begin{aligned} \phantom {\boxed {H_5}}&+\,1131900 B_2^2 B_4^2 B_5 B_6 B_3^3+4928000 B_1 B_2 B_4^2 B_5 B_6 B_3^3\\&+\,711480 B_1 B_2 B_4^2 B_5 B_6^2 B_3^2+178200 B_2 B_4^3 B_5^2 B_6 B_3^2\\&+\,168960 B_1 B_2 B_4^2 B_5^2 B_6 B_3^2+2182950 B_1 B_2 B_4^3 B_5 B_6 B_3^2\\&+\,2674100 B_1 B_2^2 B_4^2 B_5 B_6 B_3^2) \mathbf Z ^9+(1358280 B_2 B_4^2 B_5 B_6 B_3^3\\&+\,177870 B_2 B_4^2 B_5 B_6^2 B_3^2+44100 B_1 B_2^2 B_4^2 B_5 B_3^2\\&+\,44550 B_1 B_2^2 B_4^2 B_6 B_3^2+32340 B_2 B_4^2 B_5^2 B_6 B_3^2\\&+\,495000 B_2 B_4^3 B_5 B_6 B_3^2+242550 B_2^2 B_4^2 B_5 B_6 B_3^2\\&+\,3256110 B_1 B_2 B_4^2 B_5 B_6 B_3^2+202125 B_1 B_2^2 B_4 B_5 B_6 B_3^2) \mathbf Z ^8\\&+\,(94080 B_1 B_2 B_4^2 B_5 B_3^2+32340 B_1 B_2 B_4^2 B_6 B_3^2\\&+\,16500 B_1 B_2^2B_4 B_6 B_3^2+1132560 B_2 B_4^2 B_5 B_6 B_3^2\\&+\,316800 B_1 B_2 B_4 B_5 B_6 B_3^2 +443520 B_1 B_2 B_4^2 B_5 B_6 B_3) \mathbf Z ^7\\&+\,(36750 B_2 B_4^2 B_5 B_3^2 +8085 B_2 B_4^2 B_6 B_3^2+26950 B_1 B_2 B_4 B_6 B_3^2\\&+\,26950 B_4^2 B_5 B_6 B_3^2 +107800 B_2 B_4 B_5 B_6 B_3^2+45360 B_1 B_2 B_4^2 B_5 B_3\\&+\,249480 B_2 B_4^2 B_5 B_6 B_3 +92400 B_1 B_2 B_4 B_5 B_6 B_3) \mathbf Z ^6\\&+\,(9702 B_2 B_4 B_6 B_3^2 +31500 B_2 B_4^2 B_5 B_3+10752 B_1 B_2 B_4 B_5 B_3\\&+\,8316 B_1 B_2 B_4 B_6 B_3 +23100 B_4^2 B_5 B_6 B_3+59136 B_2 B_4 B_5 B_6 B_3) \mathbf Z ^5\\&+\,(4200 B_3 B_5 B_4^2 +1050 B_1 B_2 B_3 B_4+9450 B_2 B_3 B_5 B_4\\&+\,5775 B_2 B_3 B_6 B_4 +6930 B_3 B_5 B_6 B_4) \mathbf Z ^4+(1050 B_2 B_3 B_4\\&+\,2240 B_3 B_5 B_4 +770 B_3 B_6 B_4) \mathbf Z ^3+(315 B_3 B_4\\&+\,120 B_5 B_4) \mathbf Z ^2 +30 B_4 \mathbf Z +1, \end{aligned}$$
$$\begin{aligned} \boxed {H_5}= & {} B_1^2 B_2^3 B_3^4 B_4^3 B_5^2 B_6^2 \mathbf Z ^{16}\\&+\,16 B_1 B_2^3 B_3^4 B_4^3 B_5^2 B_6^2 \mathbf Z ^{15}+120 B_1 B_2^2 B_3^4 B_4^3 B_5^2 B_6^2 \mathbf Z ^{14}\\&+\,560 B_1 B_2^2 B_3^3 B_4^3 B_5^2 B_6^2 \mathbf Z ^{13}+(1050 B_1 B_2^2 B_4^2 B_5^2 B_6^2 B_3^3\\&+\,770 B_1 B_2^2 B_4^3 B_5^2 B_6 B_3^3) \mathbf Z ^{12}+(672 B_1 B_2^2 B_4^2 B_5 B_6^2 B_3^3\\&+\,3696 B_1 B_2^2 B_4^2 B_5^2 B_6 B_3^3) \mathbf Z ^{11}+(3696 B_1 B_2^2 B_4^2 B_5 B_6 B_3^3\\&+\,4312 B_1 B_2^2 B_4^2 B_5^2 B_6 B_3^2) \mathbf Z ^{10}+(2640 B_1 B_2 B_3^2 B_5^2 B_6 B_4^2\\&+\,8800 B_1 B_2^2 B_3^2 B_5 B_6 B_4^2) \mathbf Z ^9+(660 B_2 B_4^2 B_5^2 B_6 B_3^2\\&+\,8085 B_1 B_2 B_4^2 B_5 B_6 B_3^2+4125 B_1 B_2^2 B_4 B_5 B_6 B_3^2) \mathbf Z ^8\\&+\,(2640 B_2 B_4^2 B_5 B_6 B_3^2+8800 B_1 B_2 B_4 B_5 B_6 B_3^2) \mathbf Z ^7\\&+\,(4312 B_2 B_4 B_5 B_6 B_3^2+3696 B_1 B_2 B_4 B_5 B_6 B_3) \mathbf Z ^6\\&+\,(672 B_1 B_2 B_3 B_4 B_5+3696 B_2 B_3 B_4 B_6 B_5) \mathbf Z ^5\\&+\,(1050 B_2 B_3 B_4 B_5+770 B_3 B_4 B_6 B_5) \mathbf Z ^4\\&+\,560 B_3 B_4 B_5 \mathbf Z ^3 +120 B_4 B_5 \mathbf Z ^2 +16 B_5 \mathbf Z +1, \end{aligned}$$
$$\begin{aligned}\boxed {H_6}= & {} B_1^2 B_2^4 B_3^6 B_4^4 B_5^2 B_6^4 \mathbf Z ^{22}\\&+\,22 B_1^2 B_2^4 B_3^6 B_4^4 B_5^2 B_6^3 \mathbf Z ^{21}+231 B_1^2 B_2^4 B_3^5 B_4^4 B_5^2 B_6^3 \mathbf Z ^{20}\\&+\,(770 B_1^2 B_2^3 B_4^4 B_5^2 B_6^3 B_3^5+770 B_1^2 B_2^4 B_4^3 B_5^2 B_6^3 B_3^5) \mathbf Z ^{19}\\&+\,(770 B_1 B_2^3 B_4^4 B_5^2 B_6^3 B_3^5+5775 B_1^2 B_2^3 B_4^3 B_5^2 B_6^3 B_3^5\\&+\,770 B_1^2 B_2^4 B_4^3 B_5 B_6^3 B_3^5) \mathbf Z ^{18}+(8316 B_1 B_2^3 B_4^3 B_5^2 B_6^3 B_3^5\\&+\,8316 B_1^2 B_2^3 B_4^3 B_5 B_6^3 B_3^5+9702 B_1^2 B_2^3 B_4^3 B_5^2 B_6^3 B_3^4) \mathbf Z ^{17}\\&+\,(14784 B_1 B_2^3 B_4^3 B_5 B_6^3 B_3^5+26950 B_1 B_2^3 B_4^3 B_5^2 B_6^3 B_3^4\\&+\,26950 B_1^2 B_2^3 B_4^3 B_5 B_6^3 B_3^4+5929 B_1^2 B_2^3 B_4^3 B_5^2 B_6^2 B_3^4) \mathbf Z ^{16}\\&+\,(16500 B_1 B_2^2 B_4^3 B_5^2 B_6^3 B_3^4+90112 B_1 B_2^3 B_4^3 B_5 B_6^3 B_3^4\\&+\,16500 B_1^2 B_2^3 B_4^2 B_5 B_6^3 B_3^4+23716 B_1 B_2^3 B_4^3 B_5^2 B_6^2 B_3^4\\&+\,23716 B_1^2 B_2^3 B_4^3 B_5 B_6^2 B_3^4) \mathbf Z ^{15}+(72765 B_1 B_2^2 B_4^3 B_5 B_6^3 B_3^4\\&+\,72765 B_1 B_2^3 B_4^2 B_5 B_6^3 B_3^4+32670 B_1 B_2^2 B_4^3 B_5^2 B_6^2 B_3^4\\&+\,108900 B_1 B_2^3 B_4^3 B_5 B_6^2 B_3^4 +32670 B_1^2 B_2^3 B_4^2 B_5 B_6^2 B_3^4) \mathbf Z ^{14}\\&+\,(107800 B_1 B_2^2 B_4^2 B_5 B_6^3 B_3^4 +177870 B_1 B_2^2 B_4^3 B_5 B_6^2 B_3^4\\&+\,177870 B_1 B_2^3 B_4^2 B_5 B_6^2 B_3^4 +16940 B_1 B_2^2 B_4^3 B_5^2 B_6^2 B_3^3\\&+\,16940 B_1^2 B_2^3 B_4^2 B_5 B_6^2 B_3^3) \mathbf Z ^{13} +(379456 B_1 B_2^2 B_4^2 B_5 B_6^2 B_3^4\\&+\,45276 B_1 B_2^2 B_4^2 B_5 B_6^3 B_3^3 +5082 B_1 B_2^2 B_4^2 B_5^2 B_6^2 B_3^3\\ \end{aligned}$$
$$\begin{aligned}&+\,105875 B_1 B_2^2 B_4^3 B_5 B_6^2 B_3^3 +105875 B_1 B_2^3 B_4^2 B_5 B_6^2 B_3^3\\&+\,5082 B_1^2 B_2^2 B_4^2 B_5 B_6^2 B_3^3) \mathbf Z ^{12} +705432 B_1 B_2^2 B_3^3 B_4^2 B_5 B_6^2 \mathbf Z ^{11}\\&+\,(5082 B_1 B_2^2 B_4^2 B_6^2 B_3^3 +5082 B_2^2 B_4^2 B_5 B_6^2 B_3^3\\&+\,105875 B_1 B_2 B_4^2 B_5 B_6^2 B_3^3+105875 B_1 B_2^2 B_4 B_5 B_6^2 B_3^3\\&+\,45276 B_1 B_2^2 B_4^2 B_5 B_6 B_3^3+379456 B_1 B_2^2 B_4^2 B_5 B_6^2 B_3^2) \mathbf Z ^{10}\\&+\,(16940 B_1 B_2^2 B_4 B_6^2 B_3^3+16940 B_2 B_4^2 B_5 B_6^2 B_3^3\\&+\,177870 B_1 B_2 B_4^2 B_5 B_6^2 B_3^2 +177870 B_1 B_2^2 B_4 B_5 B_6^2 B_3^2\\&+\,107800 B_1 B_2^2 B_4^2 B_5 B_6 B_3^2) \mathbf Z ^9 +(32670 B_1 B_2^2 B_4 B_6^2 B_3^2\\&+\,32670 B_2 B_4^2 B_5 B_6^2 B_3^2+108900 B_1 B_2 B_4 B_5 B_6^2 B_3^2\\&+\,72765 B_1 B_2 B_4^2 B_5 B_6 B_3^2+72765 B_1 B_2^2 B_4 B_5 B_6 B_3^2) \mathbf Z ^8\\&+\,(23716 B_1 B_2 B_4 B_6^2 B_3^2 +23716 B_2 B_4 B_5 B_6^2 B_3^2\\&+\,16500 B_1 B_2^2 B_4 B_6 B_3^2+16500 B_2 B_4^2 B_5 B_6 B_3^2\\&+\,90112 B_1 B_2 B_4 B_5 B_6 B_3^2) \mathbf Z ^7+(5929 B_2 B_4 B_6^2 B_3^2\\&+\,26950 B_1 B_2 B_4 B_6 B_3^2 +26950 B_2 B_4 B_5 B_6 B_3^2\\&+\,14784 B_1 B_2 B_4 B_5 B_6 B_3) \mathbf Z ^6 +(9702 B_2 B_4 B_6 B_3^2 \\&+\,8316 B_1 B_2 B_4 B_6 B_3+8316 B_2 B_4 B_5 B_6 B_3) \mathbf Z ^5\\&+\,(770 B_1 B_2 B_3 B_6 +5775 B_2 B_3 B_4 B_6+770 B_3 B_4 B_5 B_6) \mathbf Z ^4\\&+\,(770 B_2 B_3 B_6+770 B_3 B_4 B_6) \mathbf Z ^3\\&+\,231 B_3 B_6 \mathbf Z ^2+22 B_6 \mathbf Z +1. \end{aligned}$$
It should be noted that five polynomials: \(H_1, H_2, H_4, H_5, H_6\) were found earlier (in a non-ordered form) in Ref. [48]. The biggest key polynomial \(H_3\) was not presented in Ref. [48]. We note that the “length” of the polynomial \(H_3\) is more than 5 / 8 of the total “length” of all polynomials.