Two component WIMP–FImP dark matter model with singlet fermion, scalar and pseudo scalar

Abstract

We explore a two component dark matter model with a fermion and a scalar. In this scenario the Standard Model (SM) is extended by a fermion, a scalar and an additional pseudo scalar. The fermionic component is assumed to have a global $\mathrm{U(1)}_\mathrm{DM}$ and interacts with the pseudo scalar via Yukawa interaction while a $\mathbb {Z}_2$ symmetry is imposed on the other component – the scalar. These ensure the stability of both dark matter components. Although the Lagrangian of the present model is CP conserving, the CP symmetry breaks spontaneously when the pseudo scalar acquires a vacuum expectation value (VEV). The scalar component of the dark matter in the present model also develops a VEV on spontaneous breaking of the $\mathbb {Z}_2$ symmetry. Thus the various interactions of the dark sector and the SM sector occur through the mixing of the SM like Higgs boson, the pseudo scalar Higgs like boson and the singlet scalar boson. We show that the observed gamma ray excess from the Galactic Centre as well as the 3.55 keV X-ray line from Perseus, Andromeda etc. can be simultaneously explained in the present two component dark matter model and the dark matter self interaction is found to be an order of magnitude smaller than the upper limit estimated from the observational results.

1 Introduction

The observational results from the satellite borne experiment WMAP [1] and more recently Planck [2] have now firmly established the presence of dark matter (DM) in the Universe. Their results reveal that more than 80% matter content of the Universe are in the form of mysterious unknown matter called the dark matter. Until now, only the gravitational interactions of DM have been manifested by most of its indirect evidences namely the flatness of rotation curves of spiral galaxies [3], gravitational lensing [4], the phenomena of the Bullet cluster [5] and other various colliding galaxy clusters etc. However, the particle nature of DM still remains an enigma. There are various ongoing dark matter direct detection experiments such as LUX [6], XENON-1T [7], $\text {PandaX-II}$ [8] etc. which have been trying to investigate the particle nature as well as the interaction type (spin dependent or spin independent) of DM with the visible sector by measuring the recoil energy of the scattered detector nuclei. However, the null results of these experiments have severely constrained the DM–nucleon spin independent scattering cross-section and thereby at present, $\sigma _\mathrm{SI}>2.2\times 10^{-46}$ cm$^2$ has been excluded by the LUX experiment [6] for the mass of a 50 GeV dark matter particle at 90% C.L. Similarly, for spin independent case, the present upper bound on DM–proton spin dependent scattering cross-section is $\sigma _\mathrm{SD} \sim 5\times 10^{-40}$ cm$^2$ [9, 10] for a dark matter of mass $\sim 20$–60 GeV. The DM–nucleon scattering cross-sections are approaching towards the regime of coherent neutrino–nucleon scattering cross-section and within next few years $\sigma _\mathrm{SI}$ may hit the “neutrino floor”. Therefore, it will be difficult to discriminate the DM signal from that of background neutrinos. However, if the DM is detected in direct detection experiments then that will be a “smoking gun signature” of the existence of a beyond Standard Model (BSM) scenario as the Standard Model of particle physics does not have any viable cold dark matter candidate.

Depending upon the production mechanism at the early Universe, the dark matter can be called thermal or non-thermal. In the former case, dark matter particles were in both kinetic and chemical equilibrium with other particles in the thermal soup at a very early epoch. However, the number density of DM became exponentially suppressed (or Boltzmann suppressed) as the temperature of the Universe drooped below the dark matter mass ($T_\mathrm{Universe}\lesssim M_\mathrm{DM}$) which resulted in a reduced interaction rate (interaction rate is directly proportional to number density). Decoupling of DM from the thermal bath occurred at around a temperature $\sim \frac{M_\mathrm{DM}}{20}$ when the DM interaction rate became subdominant compared to the expansion rate of the Universe. The corresponding temperature is known as the freeze-out temperature of DM. After decoupling DM became a thermal relic with a constant density known as its relic density. The Weakly Interacting Massive particle (WIMP) [11, 12] is the most favourite class for the thermal dark matter scenario. Some of the most studied WIMPs in the existing literature are neutralino [13], scalar singlet dark matter [14,15,16,17], inert doublet dark matter [18,19,20,21,22,23,24,25,26,27,28,29,30], singlet fermionic dark matter [31,32,33], hidden sector vector dark matter [34,35,36] etc.

On the other hand, in the non-thermal scenario, the interaction strengths of DM particles were so feeble that they never entered into thermal equilibrium with the other particles in the cosmic soup. As the Universe began to cool down, these types of particles were started to produce mainly from the decay of some heavy unstable particles at the early epoch. However, in principle they could also be produced from the annihilation of particles in the thermal bath, but in the present framework these annihilation channels are subdominant compared to the production from decay of heavy particles.¹ In this situation the DM relic density is generated from a different mechanism known as the “freeze-in” [37, 38] which is in a sense a opposite process to the usual freeze-out mechanism. DM particles of this type are often called Feebly Interacting Massive Particles or FIMPs. Sterile neutrinos produced from the decay of some heavy scalars [39,40,41] or gauge bosons [42] are a very good candidate of FIMP. Moreover, various FIMP type DM candidates in different extensions of the Standard Model have been studied in Refs. [43,44,45,46] and weakly coupled scenarios [47, 48].

Besides the direct detection searches for dark matter, another promising detection method of DM is to detect the annihilation or decay products of dark matter trapped in the heavy dense region of celestial objects namely core of the Sun, Galactic Centre (GC), dwarf galaxies etc. These secondary particles which can reveal the information about the particle nature of DM are gamma ray, neutrinos, charged cosmic rays including electrons, positrons, protons and antiprotons etc. This is known as the indirect detection of dark matter. Study of Fermi-LAT data [49] by independent groups [50,51,52,53,54,55,56,57,58,59,60] have observed an excess of gamma ray in the energy range 1–3 GeV, which can be interpreted as a result of dark matter annihilation in the region of GC. Detailed study of the excess by Calore et al. [60] also have reported that the gamma ray excess in 1–3 GeV energy range can be explained by dark matter annihilation into $b \bar{b}$ with annihilation cross-section ${\langle \sigma v\rangle }_{b \bar{b}}=1.76^{+0.28}_{-0.27} \times 10^{-26}~\mathrm{cm}^3\mathrm{s}^{-1}$ at GC having mass $49^{+6.4}_{-5.4}$ GeV. Excess in GC gamma ray can also be explained from point source considerations [61] or in terms of millisecond pulsars [62]. The study of dwarf spheroidals (dSphs) by Fermi-LAT and Dark Energy Survey (DES) provides a bound on the DM annihilation cross-section with DM mass, which is in agreement with the GC excess results for DM obtained from [63, 64]. Recent observations of 45 dwarf satellite galaxies by Fermi-LAT and DES collaboration [65] also do not exclude the possibility of DM origin of GC gamma ray excess. Different particle physics model for dark matter are explored in order to explain this 1–3 GeV gamma ray excess at GC [66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98]. Apart from the GC excess gamma ray, there is another observation of an unidentified 3.55 keV X-ray line from the study of 73 galaxy clusters by Bulbul et al. [99] and Boyarsky et al. [100] obtained from the XMM Newton observatory. This unknown X-ray line can be explained as a DM signal and several dark matter models are invoked to explain these phenomena [101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127]. There are also attempts claiming that this 3.55 keV line can have some astrophysical origin [128, 129]. The Hitomi collaboration [130] also suggest molecular interaction in nebula is responsible for this 3.55 keV signal which also requires further test to be confirmed. Study of colliding galaxy clusters can also provide valuable information for dark matter self interaction. An earlier attempt to calibrate the dark matter self interaction have been made by [131]. Recently an updated measurement for DM self interaction by Harvey et al. [132] have constrained DM self interaction from the observations of 72 galaxy cluster collisions. From their observations of spatial off set in collisions of different galaxy cluster, DM self interaction is found to be $\sigma /m<0.47$ cm$^2/$g with 95% confidence limit (C.L.). DM self interaction observation from Abell 3827 cluster performed by [133] also suggests that $\sigma /m\sim 1.5$ cm$^2/$g. A study of dark matter self interaction by Campbell et al. [134] has reported that a light DM of mass lesser than 0.1 GeV, whose production is followed by the freeze-in mechanism, can explain the self interaction results from Abell 3827 by [133].

Hence, the above results clearly indicate that both of these astrophysical signatures, GC excess (requires a heavier DM candidate) and DM self interaction (prefers a light DM), can be explained simultaneously with a multi component dark matter model.² Therefore, in order to explain the Galactic Centre gamma ray excess and DM self interaction bound from colliding galaxy clusters in a single framework of particle dark matter scenario, we propose a two component dark matter model where the Standard Model is extended by adding one extra singlet scalar and a fermion. An additional pseudo scalar is also introduced to the SM. The dark fermion has an additional global U(1)$_\mathrm{DM}$ symmetry which prevents its interaction with SM fermions. Although this dark fermion can interact with the pseudo scalar through a fermion pseudo scalar interaction involving $\gamma _5$ operator. The Lagrangian of the pseudo scalar is so chosen that there can be no explicit CP violation; the CP symmetry can only be spontaneously broken when the pseudo scalar acquires a non-zero VEV. We show that, in this model, the dark fermion can play the role of a WIMP type dark matter candidate. The other component, namely the singlet scalar (assumed to be lighter DM candidate), in the present two component model has a $\mathbb {Z}_2$ symmetry imposed on it to prevent its direct interaction with the SM particles. This light scalar field can be a viable FImP (denoted FImP instead of FIMP for being less massive) type dark matter candidate by assuming it has a sufficiently tiny interaction strength with other particles in the model. A study of thermal two component dark matter has been performed in the literature [136,137,138,139,140]. There is also work relating non-thermal multi component dark matter models explored to address the GC gamma ray excess or dwarf galaxy excess along with 3.55 keV X-ray results [90, 141]. However, our present work deals with a two different types of DM candidates, namely a WIMP (i.e., thermal DM) and a non-thermal DM candidate FImP. In order to compute the relic abundances of this “WIMP–FImP” system, we have solved a coupled Boltzmann equation involving both the dark fermion and singlet scalar and their self as well as mutual interactions. Since we are considering a WIMP type dark fermion which interacts with SM particles via a pseudo scalar mediator and FImP type singlet scalar, we show that our model can easily evade all the existing stringent bounds on the DM–nucleon spin independent scattering cross-sections. We find that besides satisfying the relic density criterion and other relevant experimental bounds, the annihilation of the dark fermion to the $b\bar{b}$ (through pseudo scalar mediator) final state at the Galactic Centre can explain the Fermi-LAT observed gamma ray excess while self interaction of light FImP dark matter is consistent with the upper bound on the DM self interaction required to explain the spatial offset in the collision of different galaxy clusters as obtained from [132, 133] and appears to be smaller by at least an order of magnitude. In addition, we show that within the existing framework of “WIMP–FImP” DM, the FImP dark matter component may also be able to explain the XMM Newton observed 3.55 keV X-ray anomaly from its decay to two photon final states via its tiny mixing with SM like Higgs boson.

The paper is organised as follows. The two component “WIMP–FImP” dark matter model is developed in Sect. 2. The multi component dark matter Boltzmann equation in the present model is addressed in Sect. 3. In Sect. 4 we provide the bounds from collider physics. Dark matter self interaction and bounds from the 3.55 keV X-ray are discussed in Sect. 5. Phenomenology of the two component dark matter model is explored in Sect. 6 along with direct detection measurements. The results for GC gamma ray excess and DM self interaction are presented in Sect. 7. Finally in Sect. 8 the paper is summarised with concluding remarks.

2 Two component dark matter model

The two component dark matter model having a fermionic component as well as a scalar component, considered in this work, is a renormalisable extension of the Standard Model (SM) by a real scalar field S, a singlet Dirac fermion $\chi$ and a pseudo scalar field $\Phi$. Therefore, in the present scenario the dark sector is composed of a Dirac fermion $\chi$ and a real scalar S. The Dirac fermion is a singlet under the SM gauge group and it has a global U(1)$_\mathrm{DM}$ charge. This prevents $\chi$ to couple with any Standard Model fermions which ensures its stability. On the other hand, we impose a discrete $\mathbb {Z}_2$ symmetry on the real scalar field S, which forbids the appearance of any term in the Lagrangian containing an odd number of S fields.³ The discrete symmetry $\mathbb {Z}_2$ breaks spontaneously when S gets a vacuum expectation value (VEV). Also, we have assumed that the Lagrangian is CP invariant and the CP symmetry is subjected to a spontaneous breaking when the pseudo scalar acquires a VEV. After the breaking of all the imposed symmetries (e.g. $\mathrm{SU}(2)_\mathrm{L} \times \mathrm{U}(1)_\mathrm{Y}$, $\mathbb {Z}_2$ and CP) of the Lagrangian through the VEVs of the scalar fields, the real components of H, $\Phi$ and S will mix among each other. The lightest one with suitable mass and sufficiently low values of the mixing angles with other scalars can serve as the FImP component of dark matter.

The Lagrangian of the model thus can be written as

$$\begin{aligned} \mathcal{L}= & {} \mathcal{L}_\mathrm{SM} + \mathcal{L}_\mathrm{DM} + \mathcal{L}_{\Phi } + \mathcal{L}_\mathrm{int}, \end{aligned}$$

(1)

where the Lagrangian for the SM particles including the usual kinetic term as well as the quadratic and quartic terms for the Higgs doublet H, is represented by $\mathcal {L}_\mathrm{SM}$. As mentioned above, the dark sector Lagrangian $\mathcal{L}_\mathrm{DM}$ has two parts namely the fermionic and the scalar, which are given by

$$\begin{aligned} \mathcal{L}_\mathrm{DM}= & {} {\bar{\chi }}(i\gamma ^\mu {\partial }_\mu - m)\chi + \mathcal{L}_S, \end{aligned}$$

(2)

with

$$\begin{aligned} \mathcal {L}_S = \frac{1}{2} (\partial _{\mu } S)(\partial ^{\mu } S) - \frac{{\mu }_S^2}{2} S^2- \frac{\lambda _S}{4} S^4. \end{aligned}$$

(3)

The Lagrangian $\mathcal{L}_\Phi$ for the pseudo scalar boson $\Phi$ is given by

$$\begin{aligned} \mathcal{L}_\Phi= & {} \frac{1}{2} (\partial _\mu \Phi )^2 - \frac{\mu _{\Phi }^2}{2} \Phi ^2- \frac{\lambda _{\Phi }}{4} \Phi ^4. \end{aligned}$$

(4)

Note that the above Lagrangian (Eq. (4)) does not have any term in odd power of $\Phi$. This is to make $\mathcal{L}_{\Phi }$ CP invariant. The interaction Lagrangian contains the Yukawa type term between pseudo scalar $\Phi$ and Dirac fermion $\chi$. In addition to that, it also contains all possible mutual interaction terms among the scalar fields H, $\Phi$ and S. The interaction Lagrangian is given as

$$\begin{aligned} \mathcal{L}_\mathrm{int}= & {} -\,i\,g\,\bar{\chi }\gamma _5\chi \,\Phi - V^{\prime }(H,\Phi ,S), \end{aligned}$$

(5)

where scalars and pseudo scalar mutual interaction terms are denoted by $V^{\prime }(H,\,S,\,\Phi )$. The expression of $V^{\prime }$ is given as

$$\begin{aligned} V^{\prime }(H,\,S,\,\Phi )= & {} {\lambda _{H\Phi }} H^\dagger H\,\Phi ^2 + {\lambda _{HS}} H^\dagger H\,S^2\nonumber \\&+ \lambda _{\Phi S} \Phi ^2\,S^2. \end{aligned}$$

(6)

Note that as in Eq. (5) we have a Yukawa term involving $\gamma _5$ only; hence the Lagrangian is CP invariant and does not contain any explicit CP symmetry breaking term. Moreover, it is also assumed in the model that the pseudo scalar $\Phi$ acquires a non-zero VEV. As a consequence of this assumption, the CP symmetry of the Lagrangian is broken spontaneously. In the present work the discrete $\mathbb {Z}_2$ symmetry is imposed on the scalar S; it has been broken spontaneously with a VEV $v_3$. This would result in domain walls in the Universe. One possible way to avoid such domain wall is to include a term $\sim |a|\exp ^{i\Phi _a} S$ in the Lagrangian, i.e., to break the $\mathbb {Z}_2$ symmetry explicitly as suggested in Ref. [142]. However, another way out to circumvent this problem requires the VEV $v_3$ to be small ([143] and the references therein). Such an approach to avoid the domain wall has been explored in the literature [114, 144]. In Ref. [114], it has been reported that the VEV of the scalar S considered in our work should be $v_3\le 10.7$ MeV to be consistent with CMB anisotropy measurements. Hence, we consider $v_3$ values within the above mentioned limit in our work to avoid the domain wall problem.

After the spontaneous symmetry breaking of the SM gauge symmetry, Higgs acquires a VEV, $v_1$ ($\sim$ 246 GeV) and the fluctuating scalar field about this minimum ($v_1$) is denoted by h. Denoting by $v_2$ the VEV of the pseudo scalar $\Phi$ and by $v_3$ the VEV that the singlet scalar S is assumed to acquire, we have

$$\begin{aligned} H = \frac{1}{\sqrt{2}} \left( \begin{array}{c} 0 \\ v_1 + h \end{array} \right) , \quad \Phi = v_2 + \phi , \quad S = v_3 +s. \end{aligned}$$

(7)

It is to be noted that the global U(1)$_\mathrm{DM}$ symmetry is conserved even after the spontaneous symmetry breaking.⁴ Let us consider the scalar potential term V

$$\begin{aligned} V= & {} \mu _{H}^2\,H^\dagger H + \lambda _{H}\,(H^\dagger H)^2 + \frac{\mu _{\Phi }^2}{2} \Phi ^2 + \frac{\lambda _{\Phi }}{4} \Phi ^4\nonumber \\&+ \frac{{\mu }_S^2}{2} S^2 + \frac{\lambda _S}{4} S^4\nonumber \\&+\, {\lambda _{H\Phi }} H^\dagger H\,\Phi ^2 + {\lambda _{HS}} H^\dagger H\,S^2 + \lambda _{\Phi S} \Phi ^2\,S^2. \end{aligned}$$

(8)

After symmetry breaking, the scalar potential Eq. (8) takes the following form:

$$\begin{aligned} V= & {} \dfrac{\mu _H^2}{2} (v_1 + h)^2 + \dfrac{\lambda _H}{4} (v_1 + h)^4 + \dfrac{\mu _\Phi ^2}{2} (v_2 + \phi )^2 \nonumber \\&+\, \dfrac{\lambda _\Phi }{4} (v_2 + \phi )^4 + \dfrac{\mu _S}{2} (v_3 + s)^2 + \dfrac{\lambda _S}{4} (v_3 + s)^4 \nonumber \\&+\, \dfrac{\lambda _{H\Phi }}{2} (v_1 + h)^2 (v_2 + \phi )^2 + \dfrac{\lambda _{HS}}{2} (v_1 + h)^2 (v_3 + s)^2 \nonumber \\&+\, \lambda _{\Phi S}(v_2 + \phi )^2 (v_3 + s)^2. \end{aligned}$$

(9)

Using the minimisation condition that

$$\begin{aligned} \left( \dfrac{\partial V}{\partial h}\right) ,\, \left( \dfrac{\partial V}{\partial \phi }\right) ,\, \left( \frac{\partial V}{\partial s} \right) \Bigg \vert _ {h = 0,\,\phi =0,\,s=0} =0, \end{aligned}$$

(10)

we obtain the three following conditions:

$$\begin{aligned}&\mu _H^2 + \lambda _H v_1^2 + \lambda _{H\Phi } v_2^2 + \lambda _{HS} v_3^2 = 0 , \nonumber \\&\mu _\Phi ^2 + \lambda _\Phi v_2^2 + \lambda _{H\Phi } v_1^2 + 2\lambda _{\Phi S} v_3^2 = 0 ,\nonumber \\&\mu _S^2 + \lambda _S v_3^2 + \lambda _{HS} v_1^2 + 2\lambda _{\Phi S} v_2^2 = 0. \end{aligned}$$

(11)

The mass matrix with respect to the h–$\phi$–s basis can now be constructed by evaluating $\frac{\partial ^2 V}{\partial h^2}$, $\frac{\partial ^2 V}{\partial \phi ^2}$, $\frac{\partial ^2 V}{\partial s^2}$, $\frac{\partial ^2 V}{{\partial h}{\partial \phi }}$, $\frac{\partial ^2 V}{{\partial h}{\partial s}}$, $\frac{\partial ^2 V}{{\partial s}{\partial \phi }}$ at $h=\phi =s=0$ and we obtain

$$\begin{aligned}&\mathcal {M}^2_\mathrm{scalar} = 2\,\left( \begin{array}{ccc} \lambda _H\,v_1^2 &{}\quad \lambda _{H\Phi }\,v_1\,v_2 &{}\quad \lambda _{HS}\,v_1\,v_3 \\ \lambda _{H\Phi }\,v_1\,v_2 &{}\quad \lambda _\Phi \,v_2^2 &{}\quad 2\lambda _{\Phi S}\,v_2\,v_3 \\ \lambda _{HS}\,v_1\,v_3 &{}\quad 2\lambda _{\Phi S}\,v_2\,v_3 &{}\quad \lambda _S\,v_3^2 \end{array} \right) .\nonumber \\ \end{aligned}$$

(12)

Diagonalising the symmetric mass matrix (Eq. (12)) by a unitary transformation we obtain the three eigenvectors $h_1$, $h_2$ and $h_3$, which represent three physical scalars. Each of the new eigenstates is a mixture of old basis states h, $\phi$ and s depending on the mixing angles $\theta _{12}$, $\theta _{23}$ and $\theta _{13}$, i.e.

$$\begin{aligned} \begin{pmatrix} h_1\\ h_2\\ h_3 \end{pmatrix}=U(\theta _{12}, \theta _{13}, \theta _{23}) \begin{pmatrix} h\\ \phi \\ s \end{pmatrix}, \end{aligned}$$

(13)

where $U(\theta _{12}, \theta _{23}, \theta _{13})$ is the usual PMNS matrix with the mixing angles $\theta _{12},\,\theta _{23},\,\theta _{13}$ and the complex phase $\delta =0$. In this work, we choose $h_1$ as the SM like Higgs boson which has been discovered few years ago by the LHC experiments [146, 147] at CERN. Therefore, throughout this work we keep the mass ($m_{1}$) of $h_1 \sim 125.5$ GeV.⁵ On the other hand as mentioned at the beginning of this section, we consider $h_2$ to be also heavy scalar and the lightest scalar $h_3$ to be a component of dark matter (FImP candidate). For simplicity, Eq. (13) can be rewritten as

$$\begin{aligned} \begin{pmatrix} h_1\\ h_2\\ h_3 \end{pmatrix}= \left( \begin{array}{ccc} a_{11}~~a_{12}~~a_{13} \\ a_{21}~~a_{22}~~a_{23} \\ a_{31}~~a_{32}~~a_{33} \end{array} \right) \begin{pmatrix} h\\ \phi \\ s \end{pmatrix}, \end{aligned}$$

(14)

where $a_{ij}$ are elements of PMNS matrix.

Further, in order to obtain a stable vacuum we have the following bounds on the quartic couplings derived following [148]:

$$\begin{aligned}&\lambda _H,\, \, \lambda _\Phi ,\,\, \lambda _S> 0 \nonumber \\&\lambda _{H\Phi } + \sqrt{\lambda _H \lambda _\Phi }> 0, \nonumber \\&\lambda _{HS} + \sqrt{\lambda _H \lambda _S}> 0 \nonumber \\&2\lambda _{\Phi S} + \sqrt{\lambda _\Phi \lambda _S} > 0, \end{aligned}$$

(15)

and

$$\begin{aligned}&\sqrt{2(\lambda _{H\Phi } + \sqrt{\lambda _H \lambda _\Phi }) (\lambda _{HS} + \sqrt{\lambda _H \lambda _S}) (2\lambda _{\Phi S} + \sqrt{\lambda _\Phi \lambda _S})}\nonumber \\&\quad +\,\sqrt{\lambda _H \lambda _\Phi \lambda _S} +\lambda _{H\Phi } \sqrt{\lambda _S} + \lambda _{HS} \sqrt{\lambda _\Phi } + 2\lambda _{\Phi S} \sqrt{\lambda _H}> 0. \nonumber \\ \end{aligned}$$

(16)

In this model the fermionic dark matter (WIMP DM candidate) has an interaction with the pseudo scalar $\Phi$, which should not be very large and be within the perturbative limit. For this purpose we consider $g\le 4\pi$ in our work.

It is to be noted that, in general, spontaneous CP violation does not occur when the singlet scalar acquires a VEV [149, 150]. However, in the present work, we consider a pseudoscalar field $\Phi$, which acquires a VEV $v_2$. Consequently this would result in mixing between scalar and pseudoscalar fields and hence CP is violated [142]. Although the Lagrangian in Eq. (5) is CP conserving, any mixing between scalar and pseudoscalar (terms with $\lambda _{H\Phi }$ and $\lambda _{\Phi S}$) would break the CP symmetry of the Lagrangian. Hence Eq. (5) is the source of CP violation in the model.

Fig. 1

Feynman diagrams for the fermionic dark matter $\chi$ and scalar dark matter $h_3$

3 Relic density

The relic densities for the two component dark matter considered in the paper are obtained by solving the coupled Boltzmann equations for each of the dark matter components and total DM relic abundance is given by adding up the relic densities of each of the components.

The Boltzmann equation for the fermionic component $\chi$ in the present model is given by

$$\begin{aligned} \frac{\mathrm{d}Y_{\chi }}{\mathrm{d}z}= & {} -\sqrt{\frac{\pi g_{\star }(T)}{45G}}\frac{m_{\chi }}{z^2} \left( \langle \sigma \mathrm{v} \rangle _{\bar{\chi } \chi \rightarrow x \bar{x}}\left( Y_\chi ^2 - (Y_\chi ^\mathrm{eq})^2 \right) \right. \nonumber \\&\left. + \langle \sigma \mathrm{v} \rangle _{\bar{\chi } \chi \rightarrow h_3h_3} \left( Y_\chi ^2 - \frac{(Y_\chi ^\mathrm{eq})^2}{(Y_{h_3}^\mathrm{eq})^2} Y_{h_3}^2 \right) \right) , \end{aligned}$$

(17)

where G is the gravitational constant. The fermionic dark matter in the present model follows the usual freeze-out mechanism and becomes a relic which behaves as a WIMP dark matter. However, evolution of the light dark matter $h_3$ is different. We assume that the mixings between the scalars $h_j, j=1$–3 are very small. Therefore the scalar $h_3$ is produced from the decay or annihilation of heavier particles such as Higgs or gauge bosons which never reaches thermal equilibrium (therefore becomes non-thermal in nature) and its production saturates as the Universe expands and cools down. This is also referred to as freeze-in production of the particle [37, 38] and the light dark matter resembles a FImP like DM. Hence the initial abundance of $h_3$, $Y_{h_3} =0$ in the present model. Thus Eq. (17) takes the form

$$\begin{aligned} \frac{\mathrm{d}Y_{\chi }}{\mathrm{d}z}= & {} -\sqrt{\frac{\pi g_{\star }(T)}{45G}}\frac{m_{\chi }}{z^2}\nonumber \\&\times \,\Bigg (\langle \sigma \mathrm{v} \rangle _{\bar{\chi } \chi \rightarrow x \bar{x}} \left( Y_\chi ^2 - (Y_\chi ^\mathrm{eq})^2 \right) +\langle \sigma \mathrm{v} \rangle _{\bar{\chi } \chi \rightarrow h_3h_3} Y_\chi ^2 \Bigg ),\nonumber \\ \end{aligned}$$

(18)

where $x=f,~W,~Z,~h_1,~h_2$, denotes the final state particles produced due to annihilation of the dark matter candidate $\chi$. The Boltzmann equation for the scalar component $h_3$ in the present framework is given by

$$\begin{aligned} \frac{\mathrm{d}Y_{h_{{}_{{}_3}}}}{\mathrm{d}z}= & {} -\frac{2M_{pl}z}{1.66 m^2} \frac{\sqrt{g_{\star }(T)}}{g_\mathrm{s}(T)}\Bigg (\sum _i\langle \Gamma _{h_{{}_{{}_i}} \rightarrow h_{{}_{{}_3}} h_{{}_{{}_3}}} \rangle \left( Y_{h_{{}_{{}_3}}} - {Y^{eq}_{h_{{}_{{}_i}}}}\right) \Bigg )\, \nonumber \\&-\, \frac{4 \pi ^2}{45} \frac{M_{pl} m}{1.66} \frac{\sqrt{g_{\star }(T)}}{z^2} \Bigg (\sum _{x = W, Z, f, h_1, h_2} \langle {\sigma \mathrm{v}}_{x\bar{x}\rightarrow h_{{}_{{}_3}} h_{{}_{{}_3}}} \rangle \nonumber \\&\times {({Y}^2_{h_3}} -{Y^{eq}_{x}\,^2)} -\langle {\sigma \mathrm{v}}_{\bar{\chi }\chi \rightarrow h_{{}_{{}_3}} h_{{}_{{}_3}}} \left( Y_\chi ^2 - \frac{(Y_\chi ^\mathrm{eq})^2}{(Y_{h_3}^\mathrm{eq})^2} Y_{h_3}^2 \right) \Bigg ).\nonumber \\ \end{aligned}$$

(19)

With $Y_{h_3} = 0$, Eq. (19) takes the form

$$\begin{aligned} \frac{\mathrm{d}Y_{h_{{}_{{}_3}}}}{\mathrm{d}z}= & {} -\frac{2M_{pl} z}{1.66 m^2} \frac{\sqrt{g_{\star }(T)}}{g_\mathrm{s}(T)} \Bigg (\sum _i\langle \Gamma _{h_{{}_{{}_i}} \rightarrow h_{{}_{{}_3}} h_{{}_{{}_3}}} \rangle \left( - {Y^{eq}_{h_{{}_{{}_i}}}}\right) \Bigg )\, \nonumber \\&-\,\frac{4 \pi ^2}{45} \frac{M_{pl} m}{1.66} \frac{\sqrt{g_{\star }(T)}}{z^2} \nonumber \\&\times \,\Bigg (\sum _{x = W, Z, f, h_1, h_2} \langle {\sigma \mathrm{v}}_{x\bar{x}\rightarrow h_{{}_{{}_3}} h_{{}_{{}_3}}} \rangle \,\,( -{Y^{eq}_{x}\,^2)} \nonumber \\&-\langle {\sigma \mathrm{v}}_{\bar{\chi } \chi \rightarrow h_{{}_{{}_3}} h_{{}_{{}_3}}} \rangle Y^2_{\chi } \Bigg ). \end{aligned}$$

(20)

In Eqs. (17)–(20), $Y_x=\frac{n_x}{S}$ is the comoving number density of dark matter candidate $x=\chi ,~h_3$ while $Y^{eq}_x$ is the equilibrium number density, $z=m/T$ where T is the photon temperature and S is the entropy of the Universe. $M_{pl}= 1.22\times 10^{19}$ GeV in Eqs. (19)–(20) denotes the Planck mass and the term $g_{\star }$ is expressed as [11]

$$\begin{aligned} \sqrt{{g_\star }(T)}= \frac{g_S(T)}{\sqrt{g_{\rho }(T)}} \left( 1+\frac{1}{3}\frac{\mathrm{d}~\mathrm{ln} g_S(T)}{\mathrm{d}~\mathrm{ln} T}\right) \end{aligned}$$

(21)

where $g_S$ and $g_{\rho }$ are the degrees of freedom corresponding to entropy and energy density of the Universe and written as [11]

$$\begin{aligned} S=g_S(T)\frac{2\pi ^2}{45}T^3,\quad \rho =g_{\rho }(T)\frac{\pi ^2}{30}T^4. \end{aligned}$$

(22)

Thermal average of various annihilation cross-sections ($\langle \sigma v \rangle$) and decay widths ($\langle \Gamma \rangle$) are given as

$$\begin{aligned} \langle \sigma \mathrm{v} \rangle _{aa\rightarrow bb}= & {} \frac{1}{8m_a^4\,T\,K_2^2(m_a/T)}\nonumber \\&\times \,\int _{4m_a^2}^\infty \mathrm{d}s~\sigma _{aa\rightarrow bb}(s)~(s-4m_a^2)\,\sqrt{s}\, K_1(\sqrt{s}/T)\nonumber \\ \langle \Gamma _{a\rightarrow bb} \rangle= & {} \Gamma _{a\rightarrow bb}\frac{K_1(z)}{K_2(z)}. \end{aligned}$$

(23)

In Eq. (23) $K_1$ and $K_2$ are modified Bessel functions and s represents the centre of momentum energy. Using Eqs. (18), (20) and (21)–(23) we solve for relic abundances of the dark matter candidates given as

$$\begin{aligned} \Omega _{j}h^2= 2.755 \times 10^8 \left( \frac{m_j}{GeV}\right) Y_j(T_0),j=\chi ,h_3, \end{aligned}$$

(24)

where $T_0$ is the present photon temperature and h is the Hubble parameter expressed in units of 100 km s$^{-1}$ Mpc$^{-1}$. It is to be noted that the relic densities of these two dark matter components must satisfy the condition for total dark matter density obtained from Planck [2] when added up, i.e.,

$$\begin{aligned} \Omega _{DM}h^2=\Omega _{\chi }h^2+\Omega _{h_3}h^2,\quad 0.1172\le \Omega _{DM}h^2 \le 0.1226. \end{aligned}$$

(25)

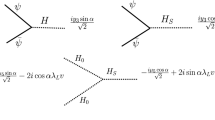
The expressions of different annihilation cross-sections and decay processes along with the relevant couplings are given in Appendix A. Feynman diagrams that contribute to the annihilations of $\chi$ along with the production of scalar dark matter $h_3$ via decay and annihilation channels are shown in Fig. 1. It is to be noted that the diagram $\chi \chi \rightarrow h_3 h_3$ will also contribute to the production of light scalar dark matter.

4 Bounds from collider physics

ATLAS and CMS have confirmed their observations of a Higgs like scalar with mass $\sim$ 125.5 GeV [146, 147]. In the present model described in Sect. 2, we introduced three scalar particles. As mentioned earlier we assume $h_1$ as the Higgs like scalar and $h_2$ to be the non-SM scalar (85 $\mathrm{GeV}\le m_2\le 110$ GeV), while $h_3$ is the light dark matter candidate. Since $h_1$ is the Higgs like scalar with mass $\sim$ 125.5 GeV, we expect it to satisfy the collider bounds on the signal strength of SM scalar. We define the signal strength as

$$\begin{aligned} R_1 = \frac{\sigma (pp\rightarrow h_1)}{\sigma ^\mathrm{SM}(pp\rightarrow h)} \frac{\mathrm{Br} (h_1 \rightarrow xx)}{\mathrm{Br}^\mathrm{SM}(h \rightarrow xx)}. \end{aligned}$$

(26)

In the above, $\sigma (pp\rightarrow h_1)$ defines the production cross-section of $h_1$ due to gluon fusion, while $\sigma ^\mathrm{SM}(pp\rightarrow h)$ is the same for SM Higgs. Similarly $\mathrm{Br} (h_1 \rightarrow xx)$ is defined as the decay branching ratio of $h_1$ into any final particle, and the same for SM Higgs is $\mathrm{Br}^\mathrm{SM}(h \rightarrow xx)$. The Higgs like scalar must satisfy the condition for SM Higgs signal strength $R_1\ge 0.8$ [151]. The branching ratio to any final state particle for $h_1$ is given as $\mathrm{Br} (h_1 \rightarrow xx)=\frac{\Gamma (h_1\rightarrow xx)}{\Gamma _1}$ (here $\Gamma (h_1\rightarrow xx)$ is the decay width of $h_1$ into final state particles and $\Gamma _1$ is the total decay width of $h_1$) and for the SM Higgs with mass 125.5 GeV it can be expressed as $\mathrm{Br}^\mathrm{SM}(h \rightarrow xx)=\frac{\Gamma (h\rightarrow xx)}{\Gamma _\mathrm{SM}}$, where $\Gamma _\mathrm{SM}$ is total decay width of Higgs. Hence, Eq. (26) can be written as

$$\begin{aligned} R_1=a_{11}^4\frac{\Gamma _\mathrm{SM}}{\Gamma _1}, \end{aligned}$$

(27)

where $\Gamma _1=a_{11}^2\Gamma _\mathrm{SM} + \Gamma ^{inv}_1$ is is the invisible decay width of $h_1$ into dark matter particles given as

$$\begin{aligned} R_2=a_{21}^4\frac{\Gamma '_\mathrm{SM}}{\Gamma _2} \end{aligned}$$

(28)

Similarly for $h_2$, the signal strength can be written as

$$\begin{aligned} R_2=a_{21}^4\frac{\Gamma '_{SM}}{\Gamma _2} \end{aligned}$$

(29)

with $\Gamma _2=a_{21}^2\Gamma '_\mathrm{SM}+\Gamma ^{inv}_2$ respectively where $\Gamma '_\mathrm{SM}$ is the total decay width of non-SM scalar of mass $m_2$ and $\Gamma ^{inv}_2=\Gamma _{h_2\rightarrow \chi \bar{\chi }} + \Gamma _{h_2\rightarrow h_3 h_3}$. The expression of invisible decay $\Gamma (h_i \rightarrow \chi \bar{\chi }),~i=1,2$, is

$$\begin{aligned}&\Gamma _{h_1 \rightarrow \chi \bar{\chi }}= \frac{m_1}{8\pi }g^2a_{21}^2 \left( 1-\frac{4m_{\chi }^2}{m_1^2}\right) ^{1/2},\nonumber \\&\Gamma _{h_2 \rightarrow \chi \bar{\chi }}=\frac{m_2}{8\pi }g^2a_{22}^2 \left( 1-\frac{4m_{\chi }^2}{m_2^2}\right) ^{1/2}, \end{aligned}$$

(30)

while the expression for $\Gamma _{h_j \rightarrow h_3 h_3},~j=1,2$, are given in Appendix A. The invisible decay branching ratio for the SM like Higgs is $Br_{inv}^{1}=\frac{\Gamma _1^{inv}}{\Gamma _1}$. We assume the invisible decay branching ratio to be small and impose the condition $Br_{inv}^{1}<0.2$ [152].

5 Dark matter self interaction

The study of dark matter self interaction has recently received attention and has been explored in the literature [131,132,133]. Dark matter, though primarily assumed to be collisionless in nature, is found to have self interaction from the observations of colliding galaxy clusters. A study of 72 colliding clusters by Harvey et al. [132] claims that the dark matter self interaction cross-section $\sigma _{DM}/m<0.47$ cm$^2/$g with 95% C.L. In the present model we proposed two dark matter candidates $\chi$ (WIMP like fermion) and a light scalar dark matter $h_3$ (FImP). In this work we will investigate whether any of these dark matter candidates can account for the observed dark matter self interaction cross-section. The study of dark matter self interaction by Campbell et al. [134] has reported that a light dark matter with mass below 0.1 GeV produced by the freeze-in mechanism can provide the required amount of dark matter self interaction cross-section (contact interaction) in order to explain the observations of Abell 3827 [133] with $\sigma _{DM}/m\sim 1.5$ cm$^2/$g, which is close to the bound obtained from [132]. Therefore in the present work, we investigate whether the FImP dark matter $h_3$ (produced via the freeze-in mechanism as mentioned earlier in Sect. 3) can account for the dark matter self interaction cross-section given by [132, 133]. The ratio to the self interaction cross-section with mass $m_3$ for the scalar dark matter candidate in the present model is given as [114]⁶

$$\begin{aligned} \frac{\sigma _{h_3}}{m_3}\simeq \frac{9\lambda _{S}^2}{2\pi m_3^3}, \end{aligned}$$

(31)

where the above expression of the self interaction is obtained by replacing the quartic coupling $\lambda _{3333}$ in terms of the coupling $\lambda _S$ for $h_3$ given in Appendix A. In Eq. (31) we have considered the contact interaction only and neglected the contributions from s-channel mediated diagrams since those are suppressed due to a small coupling with scalars $h_1$ and $h_2$ and also due to large mass terms in the propagator. It is to be noted that since in the present model we have two dark matter components, the self interaction cross-section for a particular component should be modified in accordance with the fractional contribution of that component towards the dark matter relic density. For the light DM component $h_3$ in the present model, this factor is $f_{h_3} = \frac{\Omega _{h_3}}{\Omega _\mathrm{DM}}$. Again, since the process of self interaction requires two dark matter particles to interact, the self interaction for the $h_3$ component should be modified by a factor $f_{h_3}^2$. We shall show in Sect. 6 that although the lighter component of DM has a smaller relic density, ($\Omega _{h_3}h^2\sim 0.1\Omega _{\chi }h^2$), the number density of $h_3$ is very high compared to that of $\chi$ resulting in a smaller fractional density $r_{\chi }=\frac{n_{\chi }}{n_{\chi }+n_{h_3}}\sim 10^{-6}$ for the heavier DM candidate. As a result the number of collisions will eventually be dominated by $h_3$ ($n_{h_3}^{coll}>>n_{\chi }^{coll}$). However, measurement of the dark matter self interaction is difficult and depends on several other factors. Our calculation shows that the self interaction of the heavier component $\chi$ is very small in comparison with that of $h_3$. Therefore, the lighter component with large self interaction will suffer significant change in its spatial distribution, while the same for $\chi$ will remain unaffected. However, in assessing the dark matter self interaction from the observational results (spatial offset as observed by [132]) of collisions of galaxy clusters, the mass distribution of dark matter (dark matter halo) in its totality has been considered (which in the present context signifies engaging both DM components of the model). Moreover, if the heavier component dominates the total contribution to the relic density (as presented in Sect. 7), it will share a large amount of mass of total DM halo. Then the gravitational effects between the DM components may affect the self interaction and the consequent observed spatial offset. Therefore, from the present study we may state that the effective self interaction ($\sim f_{h_3}^2 \frac{\sigma _{h_3}}{m_3}$) in our model is only an estimate and may be altered by these other factors. But this is for posterity.

5.1 3.55 keV X-ray emission and light dark matter candidate

Independent study of XMM Newton observatory data by Bulbul et al. [99] and Boyarsky et al. [100] has reported a 3.55 keV X-ray emission line from extragalactic spectrum. Such an observation cannot be explained by known astrophysical phenomena. Although the signal is not confirmed, if it yet would exist then such a signature can be explained by the decay of heavy dark matter candidates [115] or annihilation of light dark matter directly into the photon [90, 114]. The observations from the Hitomi collaboration [130] also suggest that the 3.55 keV X-ray line can be caused by charge exchange phenomena in a molecular nebula, which requires more sensitive observation to be confirmed. Since in the present framework we propose a light dark matter candidate $h_3$ to circumvent the self interaction property of dark matter, we further investigate whether it can also explain the 3.55 keV X-ray signal. For this purpose, we assume that the mass of the light FImP dark matter candidate $h_3$ is $m_3\sim$ 7.1 keV, which decays into a pair of photons.

Table 1 Constraints and chosen region of model parameters space for the two component dark matter model

The expression for the decay of $h_3$ into 3.55 keV X-rays is given as

$$\begin{aligned} \Gamma _{h_3 \rightarrow \gamma \gamma } = \left( \frac{\alpha _\mathrm{em}}{4 \pi }\right) ^2 |F|^2 \,\, a_{31}^2 \, \frac{ G_F m^3_{3}}{8 \sqrt{2} \pi }, \end{aligned}$$

(32)

where $G_F$ is the Fermi constant and $\alpha _\mathrm{em}\sim \frac{1}{137}$ is the fine structure constant. The loop factor F in Eq. (32) is

$$\begin{aligned} F = F_W(\beta _W) + \sum _fN_c Q_f^2 F_f(\beta _f), \end{aligned}$$

(33)

where

$$\begin{aligned}&\beta _W = \frac{4 m_W^2}{m^2_{3}}, \quad \beta _f = \frac{4 m_f^2}{m^2_{3}},\\&F_W(\beta ) = 2+3\beta +3 \beta (2-\beta ) f(\beta ),\\&F_f(\beta ) = -2\beta [1+(1-\beta )f(\beta )],\\&f(\beta ) = \arcsin ^2[\beta ^{-1/2}]. \end{aligned}$$

$N_c$ in the loop factor is the colour quantum number, while $Q_f$ denotes the charge of the fermion. It is to be noted that the decay width of $h_3$ must be in the range $2.5\times 10^{-29}~\mathrm{s^{-1}}\le f_{h_3}\Gamma _{h_3 \rightarrow \gamma \gamma } \le 2.5\times 10^{-28}~\mathrm{s^{-1}}$ in order to produce the required extragalactic X-ray flux obtained from Andromeda, Perseus etc. Since in the present model we have two dark matter components, the decay width of $h_3$ must be multiplied by a factor $f_{h_3}=\frac{\Omega _{h_3}}{\Omega _{DM}}$, the fractional contribution to the dark matter relic density by the $h_3$ component. Hence, in this work we will also test the viability of the light scalar dark matter candidate to explain the possible X-ray emission signal reported by [99, 100] along with DM self interaction results.

Fig. 2

The left panel (Fig. 2a) shows the changes in $f_{h_3}$ with mixing angle $\theta _{23}$. Figure 2b, c depicts the allowed values of the couplings $\lambda _{233}$ and $\lambda _{133}$ plotted against $\theta _{23}$

6 Calculations and results

In this section we test the viability of the present two component dark matter model scanning over a range of model parameter space. In Table 1, we tabulate the range of model parameter space and relevant constraints used in this work. Note that the coupling parameters $\lambda _{ij};~i,j=1$–$3~(i\ne j)$ are in agreement with the vacuum stability conditions mentioned earlier in Eq. (16) (Sect. 2) and also satisfy the perturbative unitarity condition. As we have mentioned earlier, $h_1$ is an SM like scalar and $h_2$ is a non-SM scalar; we take $v_1=246$ GeV and $v_2=500$ GeV in the present framework. We further assume two choices of $v_3=$ 6.5 MeV and 8.0 MeV. This choice is consistent with the previous studies of light scalar dark matter of mass $\sim$7.1 keV with bound 2.0 MeV $\le v_3 \le$ 10.0 MeV [90, 114]. We have also imposed the conditions on the signal strength and invisible decay branching ratio of the SM like scalar $h_1$ obtained from ATLAS and CMS at LHC ($R_1\ge 0.8$ and $Br_{inv}^{1}\le 0.2$). Using the range of the model parameter space tabulated in Table 1 we solve the three scalar mass matrix in order to find the mixing angles of the PMNS matrix and the $a_{ij};~i,j=1$–3, elements. These matrix elements are then used to calculate various couplings mentioned in Appendix A which are necessary in order to calculate the decay widths and annihilation cross-sections of the scalar dark matter candidate $h_3$. The coupling g ($\le 4\pi$, bound from the perturbative limit) between the pseudo scalar and the fermionic dark matter is also varied within the range mentioned in Table 1 to compute the annihilation cross-sections for fermionic dark matter. These decay widths and annihilation cross-sections of both dark matter candidates are then used to solve the coupled Boltzmann equations (18) and (20) and calculate the relic densities for each of the dark matter candidates satisfying the condition for total dark matter relic density, Eq. (25). In Fig. 2 we show the valid range of the model parameter space obtained using Table 1 and solving the coupled Boltzmann equations satisfying the condition $\Omega _{\chi }h^2+\Omega _{h_3}h^2=\Omega _{DM}h^2$ as given by the Planck satellite experiment. In Fig. 2a we plot the variation of the allowed mixing angle $\theta _{23}$ with the fractional relic density $f_{h_3}$ of the scalar dark matter in the present framework.⁷ The plotted blue and green shaded regions depicted in all the three figures of Fig. 2 correspond to the choice of $v_3=6.5\times 10^{-3}$ GeV and $8.0\times 10^{-3}$ GeV. The observation of Fig. 2a (in the $\theta _{23}$–$f_{h_3}$ plane) shows that the relic density contribution of the scalar dark matter component increases with the increase in $\theta _{23}$. It is to be noted that the maximum allowed range of $\theta _{23}$ depends on the choice of $v_3$ and we have found that for $v_3=6.5\times 10^{-3}$ GeV $\theta _{23}^\mathrm{max}\sim 2.8\times 10^{-13}$, while the same obtained with $v_3=8.0\times 10^{-3}$ GeV is $\theta _{23}^\mathrm{max}\sim 3.5\times 10^{-13}$. This variation of $\theta _{23}$ with $f_{h_3}$ shown in Fig. 2a is a direct consequence of the fact that the increase in $\theta _{23}$ also increases the value of $\lambda _{233}$, which is depicted in Fig. 2b. In Fig. 2b the variation of $\theta _{23}$ is plotted against $\lambda _{233}$. It is easily seen from Fig. 2b that when $\theta _{23}$ is small $\sim 10^{-16}$–$10^{-14}$, the value of $\lambda _{233}$ is very small. However, as $\theta _{23}$ increases further, there is a sharp increase in the value of $|\lambda _{233}|$. As a result the contribution from the decay channel $h_2 \rightarrow h_3 h_3$ enhances which then also increases the relic density contribution of the scalar $h_3$. From Fig. 2b we notice that the maximum allowed range of $\lambda _{233}$ is $\sim 5 \times 10^{-7}$ for both cases of $v_3$ considered in the work. Finally in Fig. 2c $\theta _{23}$ is plotted against $\lambda _{133}$ for the two values of $v_3$ mentioned above. From Fig. 2c we notice that $\lambda _{133}$ decreases steadily with enhancement in $\theta _{23}$ indicating a suppression in the contribution from $h_1$ (with $m_1\sim 125.5$ GeV) decay into pair of $h_3$. The allowed ranges of $\lambda _{133}$ for both values of $v_3$ lie within the range $5\times 10^{-8}$–$3.5\times 10^{-7}$. In the present work mass of $h_2$ is varied in the range 85–110 GeV (i.e., $m_2<m_1$) and the decay width is inversely proportional to the mass of decaying particle (see Appendix A for the expression). This indicates that the contribution of the non-SM scalar to the freeze-in production of FImP dark matter $h_3$ is significant compared to the same obtained from the SM like scalar when the coupling $\lambda _{233}$ is not small (i.e., $|\lambda _{233}|\sim \lambda _{133}$).

Fig. 3

The available model parameter space in the $\theta _{13}$–$\lambda _{133}$ plane is shown in the left panel (Fig. 3a), while in the right panel (Fig. 3b) the same region is depicted when $\theta _{23}$ is varied against $\theta _{13}$

Figure 3a depicts the allowed range of $\theta _{13}$ plotted against $\lambda _{133}$ for both values of $v_3$ considered in earlier plots of Fig. 2. We also use a similar colour scheme to indicate the values of $v_3$ satisfying the same conditions applied in order to plot Fig. 2. From Fig. 3a it can easily be observed that $\theta _{13}$ in the present model varies within the range $\sim 1.0-6.0\times 10^{-13}$ for both chosen values of $v_3=6.5\times 10^{-3}$ GeV and $v_3=8.0\times 10^{-3}$ GeV, respectively. It can also be noticed from the plots in Fig. 3a that $\lambda _{133}$ is proportional to the value of $\theta _{13}$. This reveals that the decay width $h_1 \rightarrow h_3 h_3$ increases with increase in $\theta _{13}$, which can enhance the freeze-in pair production of $h_3$ via $h_1$. In Fig. 3b we show the allowed model parameter space in $\theta _{23}$–$\theta _{13}$ plane for the same set of $v_3$ values and constraints used in earlier plots as well. Inspection of Fig. 3b reveals that, for smaller values of $\theta _{23}\sim 10^{-16}-10^{-14}$, $\theta _{13}$ maintains a value in range $\sim 3\times 10^{-13}-6\times 10^{-13}$ indicating that contribution in the relic density is mostly from the decay of $h_1$ into two $h_3$ scalars. However, as $\theta _{23}$ increases, the contribution of $h_2$ increases (due to an increase in $\lambda _{233}$), which reduces the value of $\theta _{13}$ (as well as $\lambda _{133}$) in order to maintain the total DM relic density by $h_3$ and to avoid overabundance of dark matter (when we add up the contribution of DM relic density obtained from the fermionic dark matter component $\chi$, i.e., $f_{h_3}+f_{\chi }=1$). It is to be mentioned that the mixing angle $\theta _{12}$ varies within the range $0.003\le \theta _{12}\le 0.183$ for the allowed model parameter space obtained using both sets of $v_3$ considered. Note that all the plots in Figs. 2 and 3 are in agreement with the constraints on the decay width of 7.1 keV scalar $h_3$ into X-ray, $2.5\times 10^{-29}$s$^{-1}\le f_{h_3}\Gamma _{h_3 \rightarrow \gamma \gamma }\le ~2.5\times 10^{-28}$s$^{-1}$. We have also found that the signal strength of $h_2$, i.e., $R_2$, in the present formalism is very small as regards it to be observed at the LHC experiments due to the smallness of mixing between the SM like scalar $h_1$ with $h_2$.

Fig. 4

Plots in Fig. 4a, b shows the $m_{\chi }$–$\Omega _{\chi }h^2$ parameter space for the set of parameters in Table 2 for the fermionic DM. The variation of $\Omega _{h_3}h^2$ (for the scalar DM $h_3$) with temperature T for the same set of parameter is shown in Fig. 4c

Table 2 Chosen parameter sets for the plots in Fig. 4a-c

So far, in this work, we have only discussed the available parameters for the two component dark matter model involving a fermion $\chi$ and a light scalar $h_3$ of mass $\sim 7.1$ keV in agreement with Planck dark matter relic density satisfying the condition $\Omega _{\chi }h^2+\Omega _{h_3}h^2=\Omega _{DM}h^2$ (Figs. 2 and 3). In Fig. 4a–b we show the $m_{\chi }$–$\Omega _{\chi }h^2$ plots, while in Fig. 4c the variation of the dark matter density $\Omega _{h_3}h^2$ for the light dark matter candidate $h_3$ ($m_3\sim 7.1$ keV) is plotted against the temperature T of the Universe. Instead of scanning over the full range of parameter space obtained from Figs. 2 and 3 (for two values of $v_3$), we consider two valid sets of parameters for the purpose of demonstration tabulated in Table 2. Therefore, the parameter sets in Table 2 are within the range of scans performed using Table 1 and also respects all other necessary conditions (such as vacuum stability, decay width of $h_3$, constraints from LHC etc.). The fermionic dark matter candidate can annihilate through s-channel annihilation mediated by the scalars $h_1$ and $h_2$ (see Fig. 1). The mixing between the SM like scalar $h_1$ and non-SM scalar $h_2$, given by $\theta _{12}$, is necessary to calculate the parameters $a_{ij},~i,j=1,2$, and different annihilations of the fermionic dark matter. Since in the present work the range of coupling $\lambda _{12}$ is large compared with other couplings $\lambda _{23}$ and $\lambda _{13}$, the parameters $a_{ij},~i,j=1,2$, will dominantly be determined by $\theta _{12}$. This is also justified by the plots in Fig. 3b where $\theta _{23}$ is varied with $\theta _{13}$, showing these mixing angles are very small. Therefore, we have chosen two values of $\theta _{12}$ for two sets of $v_3$ values given in Table 2. Note that we have also considered the same set of $v_3$ values of the light scalar S in our model along with $v_1=246$ GeV and $v_2=500$ GeV taken earlier in order to find the valid range parameter space obtained in Figs. 2 and 3. The shown $m_{\chi }$–$\Omega _{\chi }h^2$ plot in Fig. 4a corresponds to the set of parameters with $v_3=6.5\times 10^{-3}$ GeV and the same with the other set of parameters (for $v_3=8.0\times 10^{-3}$ GeV) is depicted in Fig. 4b. The red regions in both Fig. 4a and b are obtained by varying the coupling g within the range $0.01\le g\le 5.0$ and also varying the fermionic dark matter mass $m_{\chi }$ from 20 GeV to 200 GeV. From both Fig. 4a and b it can be observed that a very small region of parameter space (for the chosen sets in Table 2) lies below the total dark matter relic density bound given by Planck [2] (black horizontal line shown in both Fig. 4a and b). We have found that the relic density of fermionic dark matter becomes less abundant with respect to the total dark matter relic density near the resonances of SM like Higgs ($h_1$) and the non-SM scalar $h_2$ when its mass $m_{\chi }\sim m_{i}/2,~i=1,2$. Apart from that, there is also a region of parameter space with mass $\sim 100$–180 GeV (for $m_2=$ 102.5 GeV) and $\sim 100$–190 GeV (when $m_2=$ 107.2 GeV) where the condition $\Omega _{\chi }h^2<\Omega _{DM}h^2$ is satisfied. In this region the heavy fermionic dark matter annihilates into the scalars $h_1$ and $h_2$. Thus the dark matter annihilation cross-section gets enhanced which reduces the relic density $\Omega _{\chi }h^2$ of the fermionic dark matter candidate. The shaded blue horizontal regions shown in the plot Fig. 4a (Fig. 4b) are fractional contributions to the total DM relic density from the fermionic dark matter candidate $\chi$ with $f_{\chi }=0.54$ ($f_{\chi }=0.72$) where $f_{\chi }=\frac{\Omega _{\chi }}{\Omega _{DM}}$. In Fig. 4c we show the evolution of the relic density $\Omega _{h_3}h^2$ of the light scalar dark matter $h_3$ as a function of temperature T of the Universe with the same set of parameters as given in Table 2. The plot shown in red (blue) depicted in Fig. 4a (Fig. 4b) corresponds to the parameter set with $v_3=6.5\times 10^{-3}$ GeV ($v_3=8.0\times 10^{-3}$ GeV). Moreover, we have also satisfied the condition $f_{\chi }+f_{h_3}=1$ in the plots of Fig. 4c (in order to produce the total DM relic abundance obtained from the Planck results [2]) such that the fractional contribution of $h_3$ for each set of parameters in Table 2 is $f_{h_3}=1-f_{\chi }$, i.e., $f_{h_3}=0.46~(0.28)$ for the red (blue) plot depicted in Fig. 4c. It appears from the plots in Fig. 4c that the relic density of the light scalar dark matter is very small (as the initial abundance $Y_{h_3}=0$), increases gradually with decreasing temperature and finally saturates near $T\sim$ 10 GeV. The saturation of the relic density indicates that the production of $h_3$ ceases as the Universe expands and cools down due to a rapid decrease in the number density of decaying or annihilating particles. Therefore from Fig. 4a-c it can be concluded that the present model of two component dark matter with a WIMP (heavy fermion $\chi$) and a FImP (light scalar $h_3$) can successfully provide the observed dark matter relic density predicted by Planck satellite data.

6.1 Direct detection of dark matter

In this section we will investigate whether the allowed model parameter space is compatible with the results from direct detection of dark matter obtained from dark matter direct detection experiments. Direct detection experiments search for the evidence of dark matter–nucleon scattering and provide bounds on the dark matter–nucleon scattering cross-section. Dark matter candidates in the present model can undergo collisions with a detector nucleus and the recoil energy due to the scattering is calibrated. Since no such collision events have been observed yet by different dark matter direct detection experiments, these experiments provide an exclusion limit on the dark matter–nucleon scattering cross-section. The most stringent bound on the DM–nucleon spin independent (SI) cross-section is given by LUX [6], XENON-1T [7] and PandaX-II [8]. In the present model both dark matter components (WIMP and FImP) $\chi$ and $h_3$ can suffer spin independent (SI) elastic scattering with the detector nucleus. The fermionic dark matter $\chi$ in the present work can interact through pseudo scalar interaction via t-channel processes mediated by both $h_1$ and $h_2$. The expression of the spin independent scattering cross-section for the fermionic dark matter $\chi$ is

$$\begin{aligned} \sigma _{SI}^{\chi }=\frac{g^2}{\pi }m_r^2 \left( \frac{a_{11}a_{12}}{m_1^2}+\frac{a_{22}a_{21}}{m_2^2}\right) ^2 \lambda _p^2~v^2 \end{aligned}$$

(34)

where $\lambda _p$ is given as [153]

$$\begin{aligned} \lambda _p=\frac{m_p}{v_1}\left[ \sum _q f_q+ \frac{2}{9}\left( 1-\sum _q f_q\right) \right] \simeq 1.3\times 10^{-3}, \end{aligned}$$

(35)

and $m_r=\frac{m_{\chi }m_p}{m_{\chi }+m_p}$ denotes the reduced mass for the scattering. It is to be noted that due to the pseudo scalar interaction, the scattering cross-section of Eq. (34) is velocity suppressed and hence multiplied by a factor $v^2~$ with $v\sim 10^{-3}$ being the velocity of dark matter particle. We have found that this velocity suppressed scattering cross-section is way below the latest limit on DM–nucleon scattering given by direct detection experiments [6,7,8] DM direct search experiment. This finding is also in agreement with the results obtained in a different work by Ghorbani [85]. Moreover, since we have two dark matter components in the model, the effective scattering cross-section for the fermionic dark matter (i.e., WIMP candidate) will be rescaled by a factor proportional to the fractional number density $r_{\chi }=\frac{n_{\chi }}{n_{\chi }+n_{h_3}}$ ($n_x$ denotes the number density), i.e., $\sigma _{SI}^{'\chi }=r_{\chi }\sigma _{SI}^{\chi }$ (for further details see [87, 90]). The number density of both dark matter components $\chi$ and $h_3$ can be obtained from the expression of the individual relic density given in Eq. (24). In the present framework the fermionic dark matter candidate $\chi$ is $\sim 10^{6}$ times heavier than the scalar $h_3$ dark matter. For example if we consider that the contribution to the total relic density from $h_3$ is smaller with respect to that of the fermion $\chi$, having a value $\Omega _{h_3}h^2\sim 0.1\Omega _{\chi }h^2$, the number density of $h_3$ is $10^{6}$ times larger than that of $n_{\chi }$. This indicates that the rescaling factor $r_{\chi }\sim 10^{-6}$ and $r_{h_3}\sim 1$. Therefore the effective spin independent scattering cross-section $\sigma _{SI}^{'\chi }$ for the fermionic dark matter candidate is further suppressed by the rescaling factor $r_{\chi }<<1$ making it much smaller than the most sensitive dark matter direct detection limits obtained from experiments like LUX, PandaX-II. Similarly, for the scalar FImP dark matter candidate the effective spin independent direct detection cross-section is given as $\sigma _{SI}^{'h_3}= r_{h_3}\sigma _{SI}^{h_3}$ where

$$\begin{aligned} \sigma _{SI}^{h_3}=\frac{m_r^{'2}}{4\pi }\frac{f^2}{v_1^2}\frac{m_p^2}{m_3^2} \left( \frac{\lambda _{133}a_{11}}{m_1^2}+\frac{\lambda _{233}a_{21}}{m_2^2} \right) ^2, \end{aligned}$$

(36)

where $m'_r=\frac{m_{3}m_p}{m_{3}+m_p}$ and $f\sim$0.3 [154]. Since $m_3<<m_p$, $m'_r\sim m_3$ and Eq. (36) can be rewritten as

$$\begin{aligned} \sigma _{SI}^{h_3}=\frac{1}{4\pi }\frac{f^2}{v_1^2}m_p^2 \left( \frac{\lambda _{133}a_{11}}{m_1^2}+\frac{\lambda _{233}a_{21}}{m_2^2} \right) ^2. \end{aligned}$$

(37)

Since $h_3$ in the present model has very small interaction with the SM bath particles and never reaches equilibrium once being produced, the couplings $\lambda _{133}$ and $\lambda _{233}$ are very small ($\sim 10^{-7}$, as seen from Fig. 2b, c). We have found that though the number density of $h_3$ is high, $r_{h_3}\sim 1$ (as it is light), the effective scattering cross-section $\sigma _{SI}^{'h_3}\sim \sigma _{SI}^{h_3}$ is also very small as regards to being observed by any dark matter direct search experiments and it remains far below the most stringent limit given by LUX [6], XENON-1T [7] and PandaX-II [8] due to the smallness of the couplings $\lambda _{j33},~j=1,2$. Therefore, in the present scenario of the two component dark matter model (with a WIMP and a FImP), we do not expect any bound on the model parameter space from direct detection experimental constraints.

Table 3 Benchmark points for calculation of GC gamma ray excess plotted in Fig. 5 with fermionic dark matter $\chi$

7 Galactic Centre gamma ray excess and dark matter self interaction

An excess of gamma ray in the energy range 1–3 GeV has been obtained from the analysis of Fermi-LAT data [49] in the region of the Galactic Centre. Such an excess can be interpreted as a result of dark matter annihilation in the GC region. Dark matter particles can be trapped due to the immense gravitational pull of GC and also other astrophysical sites like dwarf galaxies, the Sun etc. These sites are rich with dark matter particles, which then undergo pair annihilation. Different particle physics models for dark matter are explored in order to provide a suitable explanation to this excess in gamma ray at GC as we have mentioned earlier in Sect. 1. An analysis of this 1–3 GeV GC excess of gamma rays by Calore, Cholis and Weniger (CCW) [60] using various galactic diffusion excess models suggests that Fermi-LAT data can be explained by dark matter annihilation at GC. Indeed, the $\gamma$-ray excess can be very well fitted with a dark matter of mass $49^{+6.4}_{-5.4}$ GeV, which annihilates into a pair of $b \bar{b}$ particles⁸ with annihilation cross-section ${\langle \sigma v\rangle }_{b \bar{b}}=1.76^{+0.28}_{-0.27} \times 10^{-26}~\mathrm{cm}^3\mathrm{s}^{-1}$. In this section we will investigate whether the WIMP like fermionic dark matter candidate $\chi$ can account for the observed GC gamma ray excess results. In addition, a self interaction study of the light scalar dark matter (FImP DM, mentioned earlier in Sect. 5) will also be addressed in this section. Before we explore the dark matter interpretation of GC gamma ray excess, a discussion is in order. The study of gamma ray signatures from dwarf galaxies by Fermi-LAT and DES [63, 64] also provides limits on the dark matter annihilation cross-sections into various annihilation modes. The limits on the dark matter annihilation cross-section into $b \bar{b}$ is consistent with the GC gamma ray excess analysis by CCW. However, apart from dark matter annihilation, the gamma ray excess at GC in the range 1–3 GeV can also be explained by various non-DM phenomena, such as a contribution from point sources near GC [61] or in terms of millisecond pulsars [62]. The study by Clark et al. [155] also rules out the idea that the point like sources are dark matter substructures. However, in a recent work the Fermi-LAT and DES collaborations have performed an analysis of $\gamma$-ray data with 45 confirmed dwarf spheroidals (dSphs) [65]. The analysis of gamma ray emission data from these dSphs by Fermi-LAT and DES provides a bound on the dark matter annihilation cross-section into different final channel particles ($b \bar{b}$ and $\tau \bar{\tau }$). Although their analysis [65] of the data does not show any significant excess at these sites (dSphs), the limits obtained on the DM annihilation cross-section in their analysis do not exclude the possibility of a DM interpretation of GC gamma ray excess either. Therefore in the present work, we will consider dark matter as the source to the gamma ray excess at the Galactic Centre observed by Fermi-LAT and test the viability of our model.

The expression for the differential gamma ray flux obtained in the region of the Galactic Centre for the fermionic dark matter candidate $\chi$ is

$$\begin{aligned} \frac{\mathrm{d}^2\Phi }{\mathrm{d}E \mathrm{d}\Omega }=\frac{{\langle \sigma {\mathrm{v}}\rangle }_f}{8\pi m_{\chi }^2}J \frac{\mathrm{d}N^{f}_{\gamma }}{\mathrm{d}E_{\gamma }}, \end{aligned}$$

(38)

performed over a solid angle $d\Omega$ for certain region of interest (ROI). From Eq. (38), it can be observed that the differential $\gamma$-ray flux depends on the thermal averaged annihilation cross-section ${\langle \sigma v\rangle }_f$ of dark matter into final state particles (fermions), and $\frac{\mathrm{d}N^{f}_{\gamma }}{\mathrm{d}E_{\gamma }}$ is the photon energy spectrum produced due to annihilation into fermions. In Eq. (38), the factor J, the astrophysical factor, depending on the dark matter density $\rho$, is expressed as

$$\begin{aligned} J=\int _\mathrm{los}\rho ^2(r(r',\theta ))\mathrm{d}r, \end{aligned}$$

(39)

as the line of sight integral where $r'=\sqrt{r_{\odot }^2+r^2-2r_{\odot }r\cos \theta }$ with r being the distance from the region of annihilation (GC) to Earth and $r_{\odot }=8.5$ kpc. The angle between line of sight and line from GC is denoted by $\theta$. In this work, we assume the dark matter distribution is spherically symmetric, following the Navarro–Frenk–White (NFW) [156] profile given as

$$\begin{aligned} \rho (r)=\rho _s\frac{(r/r_s)^{-\gamma }}{(1+r/r_s)^{3-\gamma }}. \end{aligned}$$

(40)

In the expression of the NFW halo profile $r_s=20$ kpc and $\rho _s$ is a typical scale density such that it produces the local dark matter density $\rho _{\odot }=0.4$ GeV cm$^{-3}$ at a distance $r_{\odot }$. The differential gamma ray flux is calculated using the ROI used by CCW [60] ($|l|\le 20^0$ and $2^0\le |b|\le 20^0$) for $\gamma =1.2$. The photon spectrum $\frac{dN^{f}_{\gamma }}{dE_{\gamma }}$ from the annihilation of dark matter is obtained from Cirelli [157]. In order to calculate the differential gamma ray flux obtained for the fermionic dark matter using Eqs. (38)–(40) and the specified ROI by CCW, we consider two benchmark points from the available model parameter space but with different values of $v_3$ (using the condition $v_3\le 10.7$ MeV to avoid the domain wall problem as mentioned earlier in Sect. 2). We have used different values of $v_3$ for benchmark points keeping the range of parameter space (given in Table 1) unchanged. Imposing other relevant conditions (relic density, direct detection etc.) we have observed that the nature of the plots and the physics discussed earlier in Sect. 6 do not alter and the conclusions remain same. Therefore the new set of benchmark points are in agreement with all the limits and constraints such as vacuum stability, LHC bounds, limits on the decay width of light scalar, dark matter relic density etc. The benchmark points are then used to calculate the gamma ray flux in this work is tabulated in Table 3. It is to be noted that since the dark matter candidate is a fermion, one may think that the annihilation cross-section will be velocity suppressed. However, in the present model, the fermion dark matter has a pseudo scalar type interaction which removes the velocity dependence of the dark matter annihilation cross-section [85]. In Fig. 5, we compare the GC gamma ray flux produced using benchmark points BP1 and BP2 tabulated in Table 3 with the results from CCW [60] for the GC gamma ray excess. It is to be noted that the annihilation cross-section for the fermionic dark matter $\chi$ into $b \bar{b}$, i.e., ${\langle \sigma v\rangle }_{b \bar{b}}$ will be multiplied by $f_{\chi }^2$ (since annihilation requires two dark matter candidates).⁹ Hence in order to produce the required flux for the excess of the GC gamma ray, the contribution to the relic density by the fermionic candidate $f_{\chi }$ should be large. In Fig. 5, the gamma ray flux obtained from BP1 (BP2) is plotted in green (blue) along with the data obtained from CCW [60]. From Fig. 5, it can be observed that the fermionic dark matter component $\chi$ (WIMP) in our model can account for the observed GC gamma ray excess results obtained by an analysis of the Fermi-LAT data. Moreover, from the benchmark points it can also be seen that the spin independent direct detection cross-section for the fermionic dark matter candidate calculated using Eqs. (34, 35) is very small and remains below the limits from the most stringent constraints on the DM–nucleon cross-section given by LUX [6], XENON-1T [7] etc.

Fig. 5

Comparison of the Fermi-LAT excess results from CCW [60] with the gamma ray flux obtained from benchmark points tabulated in Table 3

Table 4 Calculations of different observables for the scalar dark matter candidate for the same set of benchmark points given in Table 3

As we have mentioned earlier, we now investigate whether the light scalar dark matter $h_3$ can satisfy the condition for the dark matter self interaction with the same set of benchmark points. The relevant results for the scalar dark matter candidate $h_3$ for BP1 and BP2 are tabulated in Table 4. From Table 4, it can be easily seen that for both benchmark points, the effective self interaction cross-section of the light DM candidate $h_3$ remains below the observed limit $\sigma /m\le 0.47$ cm$^2/$g ($\sim \frac{1}{10}$ of the observed upper limit) obtained from the study by Harvey et al. [132]. However, as we have discussed in Sect. 5, it is to be noted that the result for the effective self interaction in this model is only an estimate and it may change significantly by the influence of other effects such as the gravitational interaction, the mass distribution etc. of dark matter. The self interaction for the light scalar DM candidate is calculated using Eq. (31) and it is then scaled by a factor $f^2_{h_3}$ to find the effective self interaction.

It can also be seen from Table 4 that the FImP like scalar DM can also explain the 3.55 keV X-ray emission as observed by the XMM Newton observatory if confirmed later as well. Calculation of DM–nucleon scattering cross-section for the scalar dark matter (using Eq. 37) also indicates that direct detection of the candidate is not possible at present, having a small $\sigma _{SI}^{'h_3}$ compared to the upper limit obtained LUX and other DM direct search experiments. Hence, at present, both dark matter candidates ($\chi$ and $h_3$) are beyond the reach of current direct DM search experiments with spin independent scattering cross-section lying far below the existing limits obtained from these experiments. This justifies our previous comments on the scattering cross-section for the dark matter particles with the detector nucleon discussed in Sect. 6.1.

8 Summary and conclusion

In this work we have explored the viability of a two component dark matter model with a fermionic dark matter that evolves thermally behaving like a WIMP and a non-thermal feebly interacting light singlet scalar dark matter which is produced via the freeze-in mechanism (FImP). The fermionic dark matter candidate $\chi$ interacts with the SM sector through a pseudo scalar particle $\Phi$ as the pseudo scalar acquires a non-zero VEV and thus the CP symmetry of the Lagrangian is broken spontaneously. Similarly the $\mathbb {Z}_2$ symmetry of the singlet scalar is also broken spontaneously when S is given a tiny non-zero VEV resulting in three physical scalars. However, the global $U(1)_\mathrm{DM}$ symmetry of the fermionic dark matter remains intact and provides us a stable dark WIMP like DM candidate. On the other hand the light scalar $h_3$ having a very small interaction with the SM sector also serves as a FImP dark matter candidate produced via the freeze-in mechanism. The $SU(2)_\mathrm{L}\times U(1)_\mathrm{Y}$ symmetry of the SM Higgs field is also broken spontaneously which provides mass to the SM particles. Hence, in the present model we have three scalars which mix with each other. We identify one of the physical scalars, $h_1$, to be SM like Higgs, $h_2$ as a non-SM Higgs and $h_3$ is the light scalar dark matter. We constrain the model parameter space by vacuum stability, unitarity, bounds from LHC results on the SM scalar etc. to solve for the coupled Boltzmann equation in the present framework such that the sum of the relic densities of these dark matter candidates satisfies the observed DM relic density by Planck. We test for the viability of the fermionic dark matter candidate in order to explain the GC gamma ray results obtained from the analysis of the Fermi-LAT data [49] by CCW [60]. We show that the excess of the GC gamma rays in the energy range 1–3 GeV can be obtained from the annihilation of fermionic dark matter, which produces the required amount of annihilation cross-section $\langle \sigma v\rangle _{b \bar{b}}$, having a mass $\sim$ 50 GeV. There is also a valid region for the fermionic dark matter candidate $\chi$ with mass ranging from 100–190 GeV. In addition, we investigate whether the light scalar dark matter candidate can account for dark matter self interaction. We found that the dark matter self interaction cross-section for the light scalar dark matter $h_3$ considered in the model is about ten times smaller than the observed upper limit obtained from galaxy cluster collisions results [132, 133]. Moreover, we also test for the viability of this light dark matter candidate to explain the possible 3.55 keV X-ray signal obtained from the study of extragalactic X-ray emission reported by Bulbul et al. [99]. Our study reveals that a light dark matter $m_3\sim 7.1$ keV in the present model can serve as a viable candidate that produces the required flux (in agreement with the condition for the decay width of $h_3 \rightarrow \gamma \gamma$) if confirmed by the observations of extragalactic X-ray search experiments and also consistent with the dark matter self interaction results. Both dark matter candidates in the present “WIMP–FImP” framework are insensitive to direct detection experimental bounds and the spin independent direct detection cross-section is far below the upper limit given by the LUX, PandaX-II DM direct search results. While this work is being completed, we came to know about a new work [158] on the analysis of the Fermi-LAT GC gamma ray excess for pseudo scalar interaction of dark matter using a different ROI ($15^0\times 15^0$) about GC with interstellar emission models (IEMs) and point sources. A detailed study of the results presented in [158] is beyond the scope of this work and we wish to test these results for pseudo scalar interactions in our model in a future work.

Appendix A

• Annihilation cross-section of fermion dark matter candidate $\chi$

  $$\begin{aligned} \sigma \mathrm{v}_{\bar{\chi } \chi \rightarrow f \bar{f}}= & {} N_c \frac{g^2}{32\pi } s\frac{m_f^2}{v_1^2}\left( 1-\frac{4m_f^2}{s}\right) ^{3/2}\\&\times \, F(s,m_1,m_2), \end{aligned}$$
  $$\begin{aligned} \sigma \mathrm{v}_{\bar{\chi } \chi \rightarrow W^+W^-}= & {} \frac{g^2}{64\pi } \left( 1-\frac{4m_W^2}{s}\right) ^{1/2} \left( \frac{m_W^2}{v_1}\right) ^2\\&\times \, \left( 2+\frac{(s-2m_W^2)^2}{4m_W^4}\right) F(s,m_1,m_2), \end{aligned}$$
  $$\begin{aligned} \sigma \mathrm{v}_{\bar{\chi } \chi \rightarrow ZZ}= & {} \frac{g^2}{128\pi } \left( 1-\frac{4m_Z^2}{s}\right) ^{1/2} \left( \frac{m_Z^2}{v_1}\right) ^2\\&\times \,\left( 2+\frac{(s-2m_Z^2)^2}{4m_Z^4}\right) F(s,m_1,m_2), \end{aligned}$$
  $$\begin{aligned}&F(s,m_1,m_2)\\&\quad = \left[ \frac{a_{12}^2a_{11}^2}{(s-m_1^2)^2+m_1^2\Gamma _1^2} + \frac{a_{21}^2a_{22}^2}{(s-m_2^2)^2+m_2^2\Gamma _2^2} \right. \\&\qquad \left. +\,a_{12}a_{11}a_{22}a_{21}\right. \\&\qquad \times \,\left. \frac{2(s-m_1^2)(s-m_2^2)+2m_1m_2\Gamma _1\Gamma _2}{[(s-m_1^2)^2+m_1^2\Gamma _1^2][(s-m_2^2)^2+m_2^2\Gamma _2^2]} \right] , \end{aligned}$$
  $$\begin{aligned}&\sigma \mathrm{v}_{\bar{\chi } \chi \rightarrow h_1h_1}\\&\quad = \frac{g^2}{32\pi } \left( 1-\frac{4m_1^2}{s}\right) ^{1/2} \left[ \frac{a_{12}^2\lambda _{111}^2}{(s-m_1^2)^2+m_1^2\Gamma _1^2} \right. \\&\quad \quad +\frac{a_{22}^2\lambda _{211}^2}{(s-m_2^2)^2+m_2^2\Gamma _2^2}\\&\quad \quad +\,\left. \frac{2a_{12}a_{22}\lambda _{111}\lambda _{211}((s-m_1^2) (s-m_2^2)+m_1m_2\Gamma _1\Gamma _2)}{[(s-m_1^2)^2+m_1^2\Gamma _1^2][(s-m_2^2)^2+m_2^2\Gamma _2^2]} \right] , \end{aligned}$$
  $$\begin{aligned}&\sigma \mathrm{v}_{\bar{\chi } \chi \rightarrow h_2h_2}\\&\quad = \frac{g^2}{32\pi } \left( 1-\frac{4m_2^2}{s}\right) ^{1/2} \left[ \frac{a_{12}^2\lambda _{122}^2}{(s-m_1^2)^2+m_1^2\Gamma _1^2} \right. \\&\quad \quad \left. +\frac{a_{22}^2\lambda _{222}^2}{(s-m_2^2)^2+m_2^2\Gamma _2^2}\right. \\&\quad \quad \left. +\frac{2a_{12}a_{22}\lambda _{122}\lambda _{222}((s-m_1^2) (s-m_2^2)+m_1m_2\Gamma _1\Gamma _2)}{[(s-m_1^2)^2+m_1^2\Gamma _1^2][(s-m_2^2)^2+m_2^2\Gamma _2^2]} \right] , \end{aligned}$$
  $$\begin{aligned}&\sigma \mathrm{v}_{\bar{\chi } \chi \rightarrow h_3h_3}\\&\quad = \frac{g^2}{32\pi } \left( 1-\frac{4m_3^2}{s}\right) ^{1/2} \left[ \frac{a_{12}^2\lambda _{133}^2}{(s-m_1^2)^2+m_1^2\Gamma _1^2} \right. \\&\quad \quad \left. +\frac{a_{22}^2\lambda _{233}^2}{(s-m_2^2)^2+m_2^2\Gamma _2^2}\right. \\&\quad \quad \left. +\frac{2a_{12}a_{22}\lambda _{133}\lambda _{233}((s-m_1^2) (s-m_2^2)+m_1m_2\Gamma _1\Gamma _2)}{[(s-m_1^2)^2+m_1^2\Gamma _1^2][(s-m_2^2)^2+m_2^2\Gamma _2^2]} \right] . \end{aligned}$$

• Decay and annihilation terms for scalar dark matter candidate $h_3$

  $$\begin{aligned} \Gamma _{h_{{}_{{}_j}}\rightarrow h_{{}_{{}_3}}h_{{}_{{}_3}}}= & {} \frac{\lambda ^2_{j33}}{8 \pi m_j} \sqrt{1-\frac{4m^2_3}{m^2_j}},\quad j=1,2, \end{aligned}$$
  $$\begin{aligned} \sigma _{f \bar{f}\rightarrow h_3 h_3}= & {} N_c\frac{1}{16\pi s}\sqrt{(s-{4m_3^2})(s-4m_f^2)}\\&\times \,\left( \frac{m_f}{v_1}\right) ^2 F'(s,m_1,m_2), \end{aligned}$$
  $$\begin{aligned} \sigma _{W^+W^-\rightarrow h_3 h_3}= & {} \frac{1}{18\pi s}\sqrt{\frac{s-{4m_3^2}}{s-4m_W^2}} \left( \frac{m_W^2}{v_1}\right) ^2\\&\times \,\left( 2+\frac{(s-2m_W^2)^2}{4m_W^4}\right) F'(s,m_1,m_2), \end{aligned}$$
  $$\begin{aligned} \sigma _{ZZ\rightarrow h_3 h_3}= & {} \frac{1}{18\pi s} \sqrt{\frac{s-{4m_3^2}}{s-4m_Z^2}} \left( \frac{m_Z^2}{v_1}\right) ^2\\&\times \,\left( 2+\frac{(s-2m_Z^2)^2}{4m_Z^4}\right) F'(s,m_1,m_2), \end{aligned}$$
  $$\begin{aligned}&F'(s,m_1,m_2)\\&\quad = \left[ \frac{a_{11}^2\lambda _{133}^2}{(s-m_1^2)^2+m_1^2\Gamma _1^2} + \frac{a_{21}^2\lambda _{233}^2}{(s-m_2^2)^2+m_2^2\Gamma _2^2} \right. \\&\qquad \left. +a_{11}\lambda _{133}a_{21}\lambda _{233}\right. \\&\qquad \times \,\left. \frac{ 2(s-m_1^2)(s-m_2^2)+2m_1m_2\Gamma _1\Gamma _2 }{[(s-m_1^2)^2+m_1^2\Gamma _1^2][(s-m_2^2)^2+m_2^2\Gamma _2^2]} \right] , \end{aligned}$$
  $$\begin{aligned} \sigma _{h_1h_1\rightarrow h_3h_3}= & {} \frac{1}{2\pi s} \sqrt{\frac{s-{4m_3^2}}{s-4m_1^2}}\\&\times \,\left( \lambda _{1133}+3\frac{\lambda _{111}\lambda _{133}}{(s-m_1^2)} +\frac{\lambda _{211}\lambda _{233}}{(s-m_2^2)}\right) ^2, \end{aligned}$$
  $$\begin{aligned} \sigma _{h_2h_2\rightarrow h_3h_3}= & {} \frac{1}{2\pi s} \sqrt{\frac{s-{4m_3^2}}{s-4m_2^2}}\\&\times \,\left( \lambda _{2233}+3\frac{\lambda _{222}\lambda _{233}}{(s-m_2^2)} +\frac{\lambda _{122}\lambda _{133}}{(s-m_1^2)}\right) ^2. \end{aligned}$$

• PMNS matrix with $\delta =0$

  $$\begin{aligned} U= & {} \left( \begin{array}{ccc} c_{13}c_{12} &{} s_{12}c_{13} &{} s_{13} \\ -s_{12}c_{23}-s_{23}s_{13}c_{12} &{} c_{23}c_{12}-s_{23}s_{13}s_{12} &{} s_{23}c_{13} \\ s_{23}s_{12}-s_{13}c_{23}c_{12} &{} -s_{23}c_{12}-s_{13}s_{12}c_{23}&{} c_{23}c_{13} \end{array} \right) . \end{aligned}$$

• Couplings between different physical scalars obtained from the expression of the potential

  $$\begin{aligned} -\lambda _{111}= & {} \lambda _H v_1 a_{11}^3+\lambda _{\Phi } v_2 a_{12}^3 +\lambda _{H\Phi }(v_2a_{11}^2a_{12}+v_1a_{11}a_{12}^2)\\&+\,\lambda _{HS} v_1a_{11}a_{13}^2+2\lambda _{\Phi S}v_2a_{12}a_{13}^2, \\ -\lambda _{222}= & {} \lambda _H v_1 a_{21}^3+\lambda _{\Phi } v_2 a_{22}^3 +\lambda _{H\Phi }(v_2a_{21}^2a_{22}+v_1a_{21}a_{22}^2)\\&+\,\lambda _{HS} v_1a_{21}a_{23}^2+2\lambda _{\Phi S}v_2a_{22}a_{23}^2, \\ -\lambda _{122}= & {} 3 \lambda _H v_1a_{11}a_{21}^2+ 3\lambda _{\Phi }v_2a_{12}a_{22}^2\\&+\,\lambda _{H\Phi }(v_2(a_{21}^2a_{12}+2a_{11}a_{21}a_{22})\\&+\,v_1(a_{11}a_{22} ^2+2a_{21}a_{12}a_{22}) \\&+\,\lambda _{HS}v_1(a_{11}a_{23}^2+2a_{21}a_{13}a_{23})\\&+\,2\lambda _{\Phi S}v_2(a_{12}a_{23}^2+2a_{22}a_{13}a_{23}), \\ -\lambda _{211}= & {} 3 \lambda _H v_1a_{11}^2a_{21}\\&+\, 3\lambda _{\Phi }v_2a_{12}^2a_{22} +\lambda _{H\Phi }(v_2(a_{11}^2a_{22}+2a_{11}a_{21}a_{12})\\&+\,v_1(a_{21}a_{12}^2 +2a_{11}a_{12}a_{22}) \\&+\,\lambda _{HS}v_1(a_{21}a_{13}^2+2a_{11}a_{13}a_{23})\\&+\,2\lambda _{\Phi S}v_2(a_{22}a_{31}^2+2a_{12}a_{13}a_{23}), \\ -\lambda _{133}= & {} 3 \lambda _H v_1a_{11}a_{31}^2\\&+\, 3\lambda _{\Phi }v_2a_{12}a_{32}^2 +\lambda _{H\Phi }(v_2(a_{31}^2a_{12}\\&+\,2a_{11}a_{31}a_{32})+v_1(a_{11}a_{32} ^2\\&+\,2a_{31}a_{12}a_{32})\\&+\,\lambda _{HS}v_1(a_{11}a_{33}^2+2a_{31}a_{13}a_{33})\\&+\,2\lambda _{\Phi S}v_2(a_{12}a_{33}^2+2a_{32}a_{13}a_{33}),\\ -\lambda _{233}= & {} 3\lambda _H v_1a_{21}a_{31}^2\\&+\,3\lambda _{\Phi }v_2a_{22}a_{32}^2 +\lambda _{H\Phi }(v_2(a_{31}^2a_{22}\\&+\,2a_{21}a_{31}a_{32})+v_1(a_{21}a_{32} ^2+2a_{31}a_{22}a_{32}) \\&+\,\lambda _{HS}v_1(a_{21}a_{33}^2+2a_{31}a_{23}a_{33})\\&+\,2\lambda _{\Phi S}v_2(a_{22}a_{33}^2\\&+\,2a_{32}a_{23}a_{33}), \\ -\lambda _{1133}= & {} \frac{3}{2}(\lambda _{H}a_{11}^2a_{31}^2)\\&+\,\frac{3}{2}(\lambda _{\Phi }a_{12}^2a_{32 } ^2)+\frac{3}{2}(\lambda _{S}a_{13}^2a_{33}^2) +\frac{\lambda _{H\Phi }}{2}\\&\times \,(a_{12}^2a_{31}^2+a_{11}^2a_{32}^2+4a_{11}a_{12}a_{31} a_{32}) \\&+\,\frac{\lambda _{HS}}{2}(a_{11}^2a_{33}^2+a_{13}^2a_{31}^2 +4a_{11}a_{13}a_{31}a_{ 33}) \\&+\,\lambda _{\Phi S}(a_{12}^2a_{33}^2+a_{13}^2a_{32}^2+ 4a_{12}a_{13}a_{32}a_{33}), \end{aligned}$$
  $$\begin{aligned} -\lambda _{2233}= & {} \frac{3}{2}(\lambda _{H}a_{21}^2a_{31}^2)+\frac{3}{2}(\lambda _{\Phi }a_{22}^2a_{32 } ^2)+\frac{3}{2}(\lambda _{S}a_{23}^2a_{33}^2)\\&+\,\frac{\lambda _{H\Phi }}{2}(a_{22}^2a_{31}^2+a_{21}^2a_{32}^2+4a_{21}a_{22}a_{31} a_{32}) \\&+\,\frac{\lambda _{HS}}{2}(a_{21}^2a_{33}^2+a_{23}^2a_{31}^2+4a_{21}a_{23}a_{31}a_{ 33})\\&+\,\lambda _{\Phi S}(a_{22}^2a_{33}^2+a_{23}^2a_{32}^2 +4a_{22}a_{23}a_{32}a_{33}), \\ -\lambda _{3333}= & {} \frac{1}{4}(\lambda _{H}a_{31}^4+\lambda _{\Phi }a_{32}^4+\lambda _{S}a_{33}^4) +\frac{\lambda _{H\Phi }}{2}a_{31}^2a_{32}^2\\&+\,\frac{\lambda _{HS}}{2}a_{31}^2a_{33}^2 +\lambda _{\Phi S}a_{32}^2a_{33}^2\sim \lambda _S/4. \end{aligned}$$