1 Introduction

The hints of lepton-flavour universality (LFU) violations in semileptonic B decays are among the most interesting deviations from the standard model (SM) reported by experiments in the last few years. The very recent result on the \(R_{K^*}\) ratio by LHCb [1] is only the last piece of a seemingly coherent set of results, involving different observables and different experiments, which started in 2003 with the BaBar results on \(R_{D^{(*)}}\) [2]. The evidence collected so far can naturally be grouped into two categories, according to the underlying quark-level transition:

  • deviations from \(\tau /(\mu ,e)\) universality in charged currents of the type \(b\rightarrow c \ell \bar{\nu }\) (observed in \(B \rightarrow D^* \ell \overline{\nu }\) and \(B \rightarrow D \ell \overline{\nu }\) decays [2,3,4]);

  • deviations from \(\mu /e\) universality in neutral currents of the type \(b\rightarrow s \ell \overline{\ell }\) (observed in \(B \rightarrow K^* \ell \overline{\ell }\) and \(B \rightarrow K \ell \overline{\ell }\) decays [1, 5]).

In both cases the combination of the results leads to evidence, exceeding the \(3\sigma \) level, for LFU contributions of non-SM origin, whose size is \(O(10\%)\) compared to the corresponding charged- or neutral-current SM amplitudes.Footnote 1

These deviations from the SM have triggered a series of theoretical speculations about possible new physics (NP) interpretations. In particular, attempts to provide a combined/coherent explanation for both charged- and neutral-current anomalies have been presented in Refs. [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. One of the puzzling aspects of the present anomalies is that they have been seen only in semileptonic B decays and are quite large compared to the corresponding SM amplitudes. On the contrary, no evidences of deviations from the SM have been seen so far in the precise (per-mil) tests of LFU performed in semileptonic K and \(\pi \) decays, in purely leptonic \(\tau \) decays, and in electroweak precision observables. The most natural assumption to address this apparent paradox is the hypothesis that the NP responsible for the breaking of LFU is coupled mainly to the third generation of quarks and leptons, with some small (but non-negligible) mixing with the light generations [14, 26, 28]. Within this paradigm, a motivated class of models are those based on a \(U(2)_q\times U(2)_\ell \) flavour symmetry acting on the light generations of SM fermions [29, 30], that turns out to be quite successful in addressing these anomalies while satisfying all existing bounds [26].

If NP is coupled mainly to third-generation fermions, it is very difficult to detect it in K decays, which necessarily imply a transition among light quarks and, in most cases, also imply light leptons in the final states. The only exception in this respect is provided by \(K\rightarrow \pi \nu \bar{\nu }\) decays, which involve third-generation leptons in the final state—the \(\tau \) neutrinos. As we will show in the following, this fact implies that \(K\rightarrow \pi \nu \bar{\nu }\) decays are a very sensitive probe of the most motivated models addressing the hints of LFU violations in B physics, as already pointed out in Refs. [18, 31] in specific models. On the one hand, \(\mathcal {B}(K\rightarrow \pi \nu \bar{\nu })\) could exhibit O(1) deviations from the SM predictions in a large area of the parameter space of such models. On the other hand, even in absence of large deviations, improved measurements (or constraints) on \(\mathcal {B}(K \rightarrow \pi \nu \bar{\nu })\) would provide a very valuable model-building information.

The paper is organised as follows: in Sect. 2 we briefly review the main formulae to evaluate \(\mathcal {B}(K\rightarrow \pi \nu \bar{\nu })\) within and beyond the SM. In Sect. 3 we discuss the effective field theory (EFT) approach to LFU violations based on the \(U(2)_q\times U(2)_\ell \) flavour symmetry and, in that framework, we analyse the possible impact on \(K\rightarrow \pi \nu \bar{\nu }\) decays. In Sect. 4 we focus in particular on the expected correlations between \(K\rightarrow \pi \nu \bar{\nu }\), the \(R_{D^{(*)}}\) anomaly, and \(B\rightarrow K^{(*)}\nu \bar{\nu }\), which turn out to be closely related observables (impact and constraints from other observables are briefly mentioned at the end of the section). The results are summarised in the conclusions.

2 The \(K\rightarrow \pi \nu \bar{\nu }\) decays

Here we briefly summarise the main steps to predict \(\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })\) and \(\mathcal {B}(K_L\rightarrow \pi ^0\nu \bar{\nu })\) within and beyond the SM, taking into account possible violations of LFU. The effective Lagrangian describing short-distance FCNC interactions of the type \(d_L^i\rightarrow d_L^j\nu \bar{\nu }\) is

$$\begin{aligned} \mathcal {L}_\mathrm{eff} = \frac{4 G_F}{\sqrt{2}}\frac{\alpha }{2\pi } V_{ti}^*V_{tj} C_{ij,\ell } \left( \bar{d}_L^i\gamma _\mu d_L^j\right) \left( \bar{\nu }_{\ell }\gamma ^\mu \nu _{\ell }\right) , \end{aligned}$$
(2.1)

where \(\alpha \) is the fine-structure constant, and \(V_{ij}\) are the elements of the CKM matrix. For \(s_L\rightarrow d_L\nu _\ell \bar{\nu }_\ell \), the Wilson coefficient in the SM reads

$$\begin{aligned} C^{\mathrm{SM}}_{sd,\ell } = -\frac{1}{s_\mathrm{w}^2}\left( X_\mathrm{t} + \frac{V_{cs}^*V_{cd}}{V_{ts}^*V_{td}} X_{c}^\ell \right) , \end{aligned}$$
(2.2)

where \(X_\mathrm{t}\) and \(X_{c}^\ell \) are the loop functions for the top and charm contributions, respectively, and \(s_\mathrm{w}\) is the sine of the weak mixing angle.

The branching ratio for \(K^+\rightarrow \pi ^+\nu \bar{\nu }\) in the SM, summing over the three neutrino species, can be written as [32]

$$\begin{aligned}&\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })_\mathrm{SM}= \frac{\kappa _+ (1+\Delta _\mathrm{em})}{3} \nonumber \\&\quad \times \sum _{\ell = e,\mu ,\tau } \left| \frac{V_{ts}^*V_{td}}{\lambda ^5}X_\mathrm{t} + \frac{V_{cs}^*V_{cd}}{\lambda }\left( \frac{X_c^\ell }{\lambda ^4} + \delta P_c^\ell \right) \right| ^2, \end{aligned}$$
(2.3)

where \(\lambda \) is the Cabibbo angle, \(\kappa _+ = (5.173\pm 0.025)\times 10^{-11}(\lambda /0.225)^8\), \(\Delta _\mathrm{em} = -0.003\) is a QED correction [33], and \(\delta P_{c,u}^\ell \approx 0.04\pm 0.02\) is the long-distance contribution from light quark loops [34]. The numerical value of the loop functions are \(X_\mathrm{t} = 1.481\pm 0.009\) and \(P_c = \frac{1}{3}\sum _\ell X_c^\ell /\lambda ^4 = 0.365 \pm 0.012\) [35].Footnote 2

Within the SM the CP-violating decay \(K_L\rightarrow \pi ^0\nu \bar{\nu }\) is lepton-flavour universal. However, in order to take into account possible violation of LFU beyond the SM, we can conveniently write its branching ratio as

$$\begin{aligned} \mathcal {B}(K_L \rightarrow \pi ^0\nu \bar{\nu })_\mathrm{SM} = \frac{\kappa _L}{3} \sum _{\ell = e,\mu ,\tau } \mathrm{Im}\left( \frac{V_{ts}^* V_{td}}{\lambda ^5}X_\mathrm{t}\right) ^2, \end{aligned}$$
(2.4)

where \(\kappa _L = (2.231\pm 0.013)\times 10^{-10} ( \lambda / 0.225)^8\).

In the class of NP models we will consider, the short-distance contributions to \(K \rightarrow \pi \nu \bar{\nu }\) amplitudes are still left-handed but lepton-flavour non-universal. The general expressions for the branching ratios in the presence of such non-standard contributions can simply be obtained replacing the function \(X_\mathrm{t}\) in (2.3) and (2.4) by

$$\begin{aligned} X\left( C_{sd,\ell }^{\mathrm{NP}}\right) = X_\mathrm{t }+ C_{sd,\ell }^{\mathrm{NP}}\, s^2_\mathrm{w}, \end{aligned}$$
(2.5)

where \(C^\mathrm{NP}_{sd,\ell }\) is the new physics contribution to the Wilson coefficient in (2.1).

Using the most recent determinations of the input parameters, the SM predictions for the two branching ratios are [37]

$$\begin{aligned}&\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })_\mathrm{SM} = (8.4\pm 1.0)\times 10^{-11}, \end{aligned}$$
(2.6)
$$\begin{aligned}&\mathcal {B}(K_L\rightarrow \pi ^0\nu \bar{\nu })_\mathrm{SM} = (3.4\pm 0.6)\times 10^{-11}. \end{aligned}$$
(2.7)

The dominant source of error in (2.6) and (2.7) comes from the uncertainty in the CKM matrix elements, and from the charm contribution.

The current experimental bounds are [38]

$$\begin{aligned}&\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })_\mathrm{exp} = 17.3^{+11.5}_{-10.5}\times 10^{-11}, \end{aligned}$$
(2.8)
$$\begin{aligned}&\mathcal {B}(K_L\rightarrow \pi ^0\nu \bar{\nu })_\mathrm{exp} \le 2.6\times 10^{-8}\quad (90\%\, \mathrm{CL}). \end{aligned}$$
(2.9)

The branching ratio of the charged mode is expected to be measured with a precision of 10%, relative to the SM prediction, by the on-going NA62 experiment at CERN [39]. A search for the challenging neutral mode at the SM level is the ultimate goal of the KOTO experiment at JPARC [40].

3 The EFT approach to LFU violations based on \(U(2)_q\times U(2)_\ell \)

As already anticipated, the B-physics anomalies observed so far point toward NP coupled mainly to the third generation of SM fermions with some small (but non-negligible) mixing with the light generations. In addition, all effects observed so far are well compatible with NP only involving left-handed currents. Left-handed four-fermion operators are also the most natural candidates to build a connection between anomalies in charged and neutral-current semileptonic processes. These observations have led to identify the EFT approach based on the \(U(2)_q\times U(2)_\ell \) flavour symmetry as a convenient framework (both successful and sufficiently general) to analyse B-physics anomalies and discuss possible correlations with other low-energy observables [14, 25, 26].

The EFT is based on the assumption that the first two generations of left-handed quarks and leptons transform as doublets of \(U(2)_q\times U(2)_\ell \), while the third generation and the right-handed fermions are singlets

$$\begin{aligned} Q&\equiv \left( q_L^1, q_L^2\right) \sim (\mathbf{2},\mathbf{1}),&q_L^3&\sim (\mathbf{1},\mathbf{1}), \end{aligned}$$
(3.1)
$$\begin{aligned} L&\equiv \left( \ell _L^1,\ell _L^2\right) \sim (\mathbf{1},\mathbf{2}),&\ell _L^3&\sim (\mathbf{1},\mathbf{1}). \end{aligned}$$
(3.2)

Motivated by the observed pattern of the quark mass matrices, it is further assumed that the leading breaking terms of this flavour symmetry are two spurion doublets, \(V_q \sim (\mathbf{2},\mathbf{1})\) and \(V_\ell \sim (\mathbf{1},\mathbf{2})\), which give rise to the mixing between the third generation and the other two [29] (additional sub-leading breaking terms are needed to generate the masses of the light generations and the corresponding mixing structures [29]).

This symmetry and symmetry-breaking pattern implies \(|V_{3i}| \approx |V_{i3}| \approx V_q^{(i)}\), up to model-dependent parameters of order one. As a starting point, it is convenient to work in the down-quark mass basis, where the left-handed singlet and doublet fields read

$$\begin{aligned} q_L^b&= \begin{pmatrix}V_{j3}^* u_L^j\\ b_L\end{pmatrix},&Q_L^i&= \begin{pmatrix} V_{ji}^* u_L^j\\ d_L^i\end{pmatrix},\quad (i = 1,2). \end{aligned}$$
(3.3)

In this basis, one can set

$$\begin{aligned} V_q \propto \left( V_{td}^*,V_{ts}^*\right) \equiv \hat{V}_q, \end{aligned}$$
(3.4)

with the proportionality constant real and of order one. In the lepton sector, the size of the spurion \(V_\ell \) is a free parameter, since it has no direct connection to the lepton Yukawa couplings.Footnote 3 Given that processes involving electrons are SM-like to a very high accuracy, we will assume \(V_\ell = (0,\epsilon _\ell )\) with \(|\epsilon _\ell | \ll 1\).

The choice of the down-quark mass basis to identify singlets and doublets of the (quark) flavour symmetry is somehow arbitrary. In particular, the singlets do not need to be aligned with bottom quarks. On general grounds we expect

$$\begin{aligned} q_{3L}&\equiv q_L^b + \theta _q e^{i\phi _q}\, {\hat{V}_q}^\dag \cdot Q_L~, \end{aligned}$$
(3.5)

where \(\theta _q e^{i\phi _q}\) is the complex O(1) parameter that controls this possible mis-alignment: \(\theta _{q}\rightarrow 0\) in the case of alignment to the down-quark mass basis, while \( \theta _q e^{i\phi _q} \rightarrow 1\) in the case of alignment to the up-quark mass basis. Given the absence of deviations from the SM in CP-violating observables, it is natural to expect \(\phi _q\) to be close to 0 or \(\pi \) (\(\theta _q \) is defined to be real and positive). Similarly, in the lepton sector we define

$$\begin{aligned} \ell _{3L} \equiv \ell _L^3 + V_\ell ^\dag \cdot L~. \end{aligned}$$
(3.6)

We shall describe NP effects through an EFT based on the following hypotheses:

  1. 1.

    the field content below the NP scale \(\Lambda > (G_F)^{-1/2}\) is the SM one;

  2. 2.

    the Lagrangian is invariant under the flavour symmetry \(U(2)_q\times U(2)_\ell \), apart from the breaking induced by the spurions \(V_q\) and \(V_\ell \);

  3. 3.

    NP is directly coupled only to left-handed quark and lepton singlets in flavour space (i.e. only operators containing only \(q_{3L}\) or \(\ell _{3L}\) fields are affected by tree-level matching conditions at the NP scale \(\Lambda \)).

Given these assumptions, we can identify only two independent operators of dimension six affected by NP and contributing to semileptonic decays at the tree level, namely the electroweak singlet and triplet current-current interactions,

$$\begin{aligned} \mathcal {L}_\mathrm{eff}= & {} -\frac{1}{\Lambda ^2}(\bar{q}_{3L} \gamma _\mu \sigma ^a q_{3L})(\bar{\ell }_{3L} \gamma ^\mu \sigma ^a \ell _{3L}) \nonumber \\&- \frac{c_{13}}{\Lambda ^2}(\bar{ q}_{3L} \gamma _\mu q_{3L})(\bar{ \ell }_{3L} \gamma ^\mu \ell _{3L}). \end{aligned}$$
(3.7)

The normalisation of the triplet operator in (3.7) has been chosen in order to generate a constructive interference with the SM in charged-current amplitudes, as suggested by \(b\rightarrow c \tau \bar{\nu }_\tau \) data. The overall scale of this operator defines the NP scale \(\Lambda \), while \(c_{13}\) denotes the ratio between the singlet and triplet Wilson coefficients.

4 Physical observables

4.1 The \(R_{D^{(*)}}\) anomaly

The averages of the \(\tau /\ell \) universality ratios (\(\ell ={\mu ,e}\)) in \(b\rightarrow c\) transitions measured by BaBar [2], Belle [3] and LHCb [4], are

$$\begin{aligned} R_{D^*}&\equiv \frac{\mathcal {B}(B\rightarrow D^* \tau \bar{\nu }_\tau )_\mathrm{exp}/\mathcal {B}(B\rightarrow D^* \tau \bar{\nu }_\tau )_\mathrm{SM}}{\mathcal {B}(B\rightarrow D^* \ell \bar{\nu }_\ell )_\mathrm{exp}/\mathcal {B}(B\rightarrow D^* \ell \bar{\nu }_\ell )_\mathrm{SM}}\nonumber \\&= 1.23\pm 0.07, \end{aligned}$$
(4.1)
$$\begin{aligned} R_{D}&\equiv \frac{\mathcal {B}(B\rightarrow D \tau \bar{\nu }_\tau )_\mathrm{exp}/\mathcal {B}(B\rightarrow D \tau \bar{\nu }_\tau )_\mathrm{SM}}{\mathcal {B}(B\rightarrow D \ell \bar{\nu }_\ell )_\mathrm{exp}/\mathcal {B}(B\rightarrow D \ell \bar{\nu }_\ell )_\mathrm{SM}} \nonumber \\&= 1.35\pm 0.16. \end{aligned}$$
(4.2)

These two results can be combined into a single observable that parametrises the violation of LFU in charged currents (assuming a purely left-handed structure):

$$\begin{aligned} R_{D^{(*)}} = 1.24\pm 0.07. \end{aligned}$$
(4.3)

Only the triplet operator in (3.7) contributes to \(b\rightarrow c\tau \bar{\nu }_{\tau }\) decays via the following effective interaction:

$$\begin{aligned} \mathcal {L}_{b\rightarrow c\tau \bar{\nu }_{\tau }}^\mathrm{NP}= & {} -\frac{2}{\Lambda ^2}\Big [V_{cb} + \theta _q e^{-i\phi _q} \left( V_{cs}V_{ts}^* + V_{cd}V_{td}^*\right) \Big ]\nonumber \\&\times (\bar{c}_L\gamma ^{\mu }b_{L})(\bar{\tau }_L\gamma _{\mu }\nu _{\tau })\,. \end{aligned}$$
(4.4)

The branching ratio for the processes \(B\rightarrow D^{(*)}\tau \bar{\nu }\) is then modified as follows by the triplet operator (using CKM unitarity and setting \(V_{tb} = 1\)):

$$\begin{aligned} \mathcal {B}(B\rightarrow D^{(*)}\tau \bar{\nu }) =&\, \mathcal {B}(B\rightarrow D^{(*)}\tau \bar{\nu })_\mathrm{SM}\nonumber \\&\times \left| 1 + R_0 \left( 1 - \theta _q e^{-i\phi _q} \right) \right| ^2 \end{aligned}$$
(4.5)

where we have defined

$$\begin{aligned} \displaystyle {R_0 = \frac{1}{\Lambda ^2}\frac{1}{\sqrt{2}G_F}}. \end{aligned}$$
(4.6)

In the limit where we neglect sub-leading terms suppressed by the small leptonic spurion, NP does not affect \(\mathcal {B}(B\rightarrow D^{(*)}\ell \bar{\nu })\) for the light leptons. This allows us to fix the overall scale of NP via the relation

$$\begin{aligned} \left[ R_{D^{(*)}}^{\tau /\mu }-1\right] \approx 2R_0(1-\theta _q \cos \phi _q) = 0.24\pm 0.07\,. \end{aligned}$$
(4.7)

The reference effective scale of NP, obtained for \(\theta _q \rightarrow 0\), is \(\Lambda _0 \approx 700\,\mathrm{GeV}\). Notice that higher scales of NP can be obtained if \(\theta _q =O(1)\) and \(\cos \phi _q < 0\), obtaining in this way a better compatibility with constraints from direct searches [41] and electroweak precision tests [42, 43]. On the other hand, the NP contribution to \(R_{D^{(*)}}\) vanishes in the case of alignment of the flavour symmetry to up-type quarks (\(\theta _q\rightarrow 1, \phi _q\rightarrow 0\)).

4.2 LFU-violating contributions to \(K\rightarrow \pi \nu \bar{\nu }\)

Fig. 1
figure 1

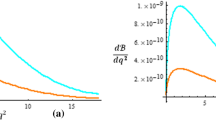
Left: allowed range for the real and imaginary parts of the NP Wilson coefficient \(C_{sd,\tau }^\mathrm{NP}\). Right: correlation between \(\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })\) and \(R_{D^{(*)}}\) for different values of the parameter \(\theta _q\) (with \(\phi _q = c_{13} = 0\)); the coloured regions are the experimental measurements at \(1\,\sigma \), the dark green band is the SM prediction

Full size image

The operators (3.7) contribute to \(s\rightarrow d\nu \bar{\nu }\) transitions through the term proportional to the \(V_q\) spurion in (3.5),

$$\begin{aligned} \mathcal {L}_{s\rightarrow d\nu \bar{\nu }}^\mathrm{NP} = \frac{1-c_{13}}{\Lambda ^2}\theta _q^2\, V_{ts}^*V_{td}(\bar{s}_L\gamma _\mu d_L)(\bar{\nu }_\tau \gamma _\mu \nu _\tau ). \end{aligned}$$
(4.8)

Neglecting, in first approximation, the NP contribution to \(s\rightarrow d\nu _\ell \bar{\nu }_\ell \) (\(\ell =e,\mu \)) amplitudes, we can write

$$\begin{aligned} \mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })= & {} 2\mathcal {B}(K^+\rightarrow \pi ^+\nu _e\bar{\nu }_e)_\mathrm{SM}\nonumber \\&+\, \mathcal {B}(K^+\rightarrow \pi ^+\nu _\tau \bar{\nu }_\tau )_\mathrm{SM}\nonumber \\&\times \left| 1 + \frac{R_0\, \theta _q^2(1-c_{13})}{(\alpha /\pi ) C_{sd,\tau }^\mathrm{SM,eff}} \right| ^2, \nonumber \\ \mathcal {B}(K_L \rightarrow \pi ^0 \nu \bar{\nu })= & {} 2\mathcal {B}(K_L \rightarrow \pi ^0 \nu _e\bar{\nu }_e)_\mathrm{SM} \nonumber \\&+\, \mathcal {B}(K_L \rightarrow \pi ^0 \nu _\tau \bar{\nu }_\tau )_\mathrm{SM}\nonumber \\&\times \left| 1 - \frac{R_0\, \theta _q^2(1-c_{13})}{(\alpha /\pi ) (X_\mathrm{t}/ s_\mathrm{w}^2) } \right| ^2, \end{aligned}$$
(4.9)

where \(C_{sd,\tau }^\mathrm{SM,eff} \approx -8.5 \times e^{0.11 i}\) includes also the long-distance contributions of (2.3).

The current allowed range from the experimental result (2.8) for the real and imaginary parts of the Wilson coefficient \(C_{sd,\tau }^\mathrm{NP}\) in a generic NP model is shown in Fig. 1 (left). In our case this translates into the constraint

$$\begin{aligned} \left| R_0\, \theta _q^2(1-c_{13})\right| \lesssim 0.1~. \end{aligned}$$
(4.10)

As expected, the constraint vanishes in the limit \(c_{13} \rightarrow 1\), where triplet and singlet NP contributions to \(s\rightarrow d\nu \bar{\nu }\) amplitudes cancel each other. However, it must be stressed that there is no symmetry reason to expect \(c_{13} = 1\). Even if \(c_{13} = 1\) holds as tree-level matching condition in the EFT (such as e.g. in the lepto-quark models of Refs. [18, 27]), one expects \(c_{13} \not = 1\) beyond the tree level [18]. For \(c_{13} \not = 1\) the result in (4.10) implies a severe constraint on the maximal value of \(\theta _q\), assuming (4.7) is satisfied. For \(|c_{13} - 1| \ll 1\) one finds \(|\theta _q | \lesssim 1/ |c_{13} - 1|\).

Expressing \(R_0\) in terms of the measured value of \(R_{D^{(*)}}\) (and the unknown parameters \(\theta _q\) and \(\phi _q\)) we can rewrite the previous expression as a relation between \(R_{D^{(*)}}\) and \(\mathcal {B}(K\rightarrow \pi \nu \bar{\nu })\) as follows:

$$\begin{aligned}&\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu }) \approx \mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })_\mathrm{SM} \nonumber \\&\quad \times \Big [ 1 - 14 \, [R_{D^{(*)}}-1]\theta ^2_q f_q + 165\, [R_{D^{(*)}}-1]^2\theta _q^4 f_q^2\Big ],\nonumber \\ \end{aligned}$$
(4.11)

where \(f_q \equiv (1-c_{13}) / (1-\theta _q\cos \phi _q)\), and where we neglected higher orders in \(R_0\) from (4.7). This correlation is shown in Fig. 1 (right), for different values of the free parameters. As can be seen, for \(\theta _q=O(1)\) the solution of the \(R_{D^{(*)}}\) anomaly can imply sizeable deviations in \(\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })\) compared to the SM. The dependence of \(\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })\) on the parameter \(\theta _q\), with \(R_{D^{(*)}}\) fixed as in (4.7), is shown by the blue lines in Fig. 2 (right) for the two values of the phase \(\phi _u = 0\) and \(\pi \), and for different values of the singlet contribution \(c_{13}\). Notice that for \(c_{13}>1\) the branching ratio is always enhanced with respect to the SM prediction.

The neutral mode \(K_L\rightarrow \pi ^0\nu \bar{\nu }\) is purely CP-violating and constrains only the imaginary part of the amplitude. The present bound on the NP Wilson coefficient from (2.9) is roughly 10 times weaker than the one from the \(K^+\) mode.

Fig. 2
figure 2

Left: correlation of \(\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })\) with \(\mathcal {B}(B^+\rightarrow K^{*+}\nu \bar{\nu })\), having imposed \(R_{D^{(*)}} = 1.25\). The red (blue) coloured region is for \(c_{13} = 0\) (\(c_{13} = 2\)). We also show isolines of \(\theta _q\), and the red star is the SM point. Right: branching ratios for \(K^+\rightarrow \pi ^+\nu \bar{\nu }\) and \(B^+\rightarrow K^{*+}\nu \bar{\nu }\), normalised to the SM values, as functions of \(\theta _q\). The solid (dashed) lines correspond to \(c_{13} = 0\), \(\phi _q = 0\) (\(c_{13} = 2\), \(\phi _q = \pi \))

Full size image

4.3 Correlations between \(B\rightarrow K^{(*)}\nu \bar{\nu }\) and \(K\rightarrow \pi \nu \bar{\nu }\)

Also \(b\rightarrow s\nu \bar{\nu }\) transitions are described by the Lagrangian (2.1), with \(C^\mathrm{SM}_{bs} = -X_\mathrm{t}/s_\mathrm{w}^2\approx -6.4\). Notice that the charm contribution is not relevant in this case. Both charged and neutral \(B\rightarrow K^{(*)}\nu \bar{\nu }\) decays set bounds on the new physics Wilson coefficient, with the stronger constraints coming from the \(B^+\) modes. In the SM, the branching ratios are [44]

$$\begin{aligned}&\mathcal {B}(B^+\rightarrow K^+\nu \bar{\nu })_\mathrm{SM} = 3.94\times 10^{-6}\left| \frac{V_{ts}V_{tb}^*}{0.04}\right| ^2, \end{aligned}$$
(4.12)
$$\begin{aligned}&\mathcal {B}(B^+\rightarrow K^{+*}\nu \bar{\nu })_\mathrm{SM} = 9.82\times 10^{-6}\left| \frac{V_{ts}V_{tb}^*}{0.04}\right| ^2, \end{aligned}$$
(4.13)

to be compared with the experimental bounds [38]

$$\begin{aligned} \mathcal {B}(B^+\rightarrow K^+\nu \bar{\nu })&\le 1.7\times 10^{-5}\quad @ 90\%\,\text { CL}, \end{aligned}$$
(4.14)
$$\begin{aligned} \mathcal {B}(B^+\rightarrow K^{+*}\nu \bar{\nu })&\le 4.0\times 10^{-5}\quad @ 90\%\,\text { CL}. \end{aligned}$$
(4.15)

In the presence of the operators of (3.7) the branching ratios are modified as follows:

$$\begin{aligned} \mathcal {B}(B\rightarrow K^{(*)}\nu \bar{\nu })= & {} \mathcal {B}(B\rightarrow K^{(*)}\nu \bar{\nu })_\mathrm{SM}\left[ \frac{2}{3} + \frac{1}{3}\right. \nonumber \\&\left. \times \left| 1 - \frac{\pi s_\mathrm{w}^2 R_0}{\alpha X_\mathrm{t}}\theta _q e^{i\phi _q}(1-c_{13})\right| ^2\right] .\nonumber \\ \end{aligned}$$
(4.16)

As for \(K\rightarrow \pi \nu \bar{\nu }\), we can obtain a direct connection to the charged-current anomaly expressing \(R_0\) in terms of \(R_{D^{(*)}}\):

$$\begin{aligned}&\mathcal {B}(B\rightarrow K^{(*)}\nu \bar{\nu }) \approx \mathcal {B}(B\rightarrow K^{(*)}\nu \bar{\nu })_\mathrm{SM}\nonumber \\&\quad \times \Big (1 {-}21 [R_{D^{(*)}}{-}1] \theta _q \cos \phi _q f_q {+}320 [R_{D^{(*)}}-1]^2 \theta _q^2 f_q^2\Big ).\nonumber \\ \end{aligned}$$
(4.17)

Figure 2 (right) shows the dependence of \(\mathcal {B}(B^+\rightarrow K^{*+}\nu \bar{\nu })\) on \(\theta _q\), with \(R_{D^{(*)}}\) fixed to the central value of the experimental measurement, and for two different values of \(\phi _q\) and \(c_{13}\).

The deviations from the SM expectations in the two FCNC neutrino modes are closely correlated, as described by the following relation:

$$\begin{aligned} \frac{ \Delta \mathcal {B}(K^+ \rightarrow \pi ^+\nu \bar{\nu }) }{ \Delta \mathcal {B}(B \rightarrow K^{(*)} \nu \bar{\nu }) } \approx&\frac{2}{3} \times \frac{\theta _q}{ \cos \phi _q} \nonumber \\&\times \frac{1 - 12\, [R_{D^{(*)}}-1] \theta ^2_q f_q}{1 - 15 [R_{D^{(*)}}-1]\, \frac{\theta _q f_q}{ \cos \phi _q} }, \end{aligned}$$
(4.18)

where \(\Delta \mathcal {B}= \frac{\mathcal {B}- \mathcal {B}_\mathrm{SM}}{\mathcal {B}_\mathrm{SM}}\), and as illustrated in Fig. 2. Notice that for small \(\theta _q\) this correlation does not depend on the measured value of \(R_{D^{(*)}}\). The constraints from \(B\rightarrow K^{(*)}\nu \bar{\nu }\) can severely limit the deviations in \(K\rightarrow \pi \nu \bar{\nu }\). This fact is well known in the literature, independently of the relation with the LFU B anomalies, see e.g. [45, 46]. If \(c_{13} <1\), the NP contributions interfere constructively with the SM amplitude in the first branching ratio, and destructively in the second one. As a consequence, in this case \(\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })\) is always suppressed, with deviations of up to \(-30\%\) with respect to the SM value. The opposite is true when \(c_{13}>1\). Also, the constraints are more stringent when \(\cos \phi _q\) is positive, since in this case the effective scale of new physics is lower. For negative \(\cos \phi _q\) and \(c_{13}>1\), in particular, the constraint from \(B\rightarrow K^{(*)}\nu \bar{\nu }\) becomes irrelevant, and large deviations can be expected in \(\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })\) [within the limits of (2.8)].

4.4 Constraints and connections to other observables

\(b\rightarrow s \ell ^+\ell ^-\). FCNC processes that involve the light generations of leptons are suppressed by the spurion \(V_\ell \) in our framework. While LFU violation in these modes is a general prediction following from (3.6), the exact size of these effects depends on the unknown parameter \(\epsilon _\ell \) (and, more generally, by the assumption on the breaking of the \(U(2)_\ell \) lepton-flavour symmetry). The NP contributions to the Wilson coefficients \(C_9\) and \(C_{10}\) of the semileptonic \(b\rightarrow s\mu ^+\mu ^-\) Lagrangian

$$\begin{aligned}&\mathcal {L}_\mathrm{eff}^{b\rightarrow s\mu \mu } = \frac{4G_F}{\sqrt{2}}\frac{\alpha }{4\pi }V_{tb}^*V_{ts}\nonumber \\&\quad \times \left[ C_{9,\mu } (\bar{b}_L\gamma _\mu s_L)(\bar{\mu }\gamma ^\mu \mu ) + C_{10,\mu }(\bar{b}_L\gamma _\mu s_L)(\bar{\mu }\gamma ^\mu \gamma _5 \mu )\right] \end{aligned}$$
(4.19)

read

$$\begin{aligned} C_{9,\mu }^\mathrm{NP} = -C_{10,\mu }^\mathrm{NP} = -\frac{\pi }{\alpha }R_0 \theta _q e^{i\phi _q} (1+c_{13})|\epsilon _\ell |^2~. \end{aligned}$$
(4.20)

Global fits of these Wilson coefficients, performed after the recent measurement of the LFU ratio \(R_{K^{*}}\) [1], in the case of NP coupled to left-handed currents only, yields \(C_{9,\mu }^\mathrm{NP} = -C_{10,\mu }^\mathrm{NP} = -0.64\pm 0.18\) [6,7,8,9,10]. From this result, fixing the overall scale of NP from (4.7), it follows that \(|\epsilon _\ell |\,(1+c_{13}) \approx 0.1\) up to an O(1) factor depending on \(\theta _q\) and \(\phi _q\). Since the sign of \(C_9^\mathrm{NP}\) must be negative to fit the \(b\rightarrow s\ell \bar{\ell }\) anomalies, it follows that \((1-c_{13}) \cos \phi _q > 0\).

\(b\rightarrow s \tau ^+\tau ^-\). FCNC decays of B mesons with a \(\tau ^+\tau ^-\) pair in the final state arise at leading order in the breaking of \(U(2)_q\times U(2)_\ell \). This implies that these processes can be directly related both to the \(R_{D^{(*)}}\) anomalies, and to the two neutrino modes discussed above. The current experimental limits on \(\mathcal {B}(B\rightarrow K\tau ^+\tau ^-)\) are four orders of magnitude larger than the corresponding SM prediction (which lies in the \(10^{-7}\) range). The Belle II experiment is expected to improve these limits by at least one order of magnitude, reaching the \(10^{-4}\) level [47]. While the value predicted in the SM would still be out of reach, this sensitivity could be interesting in the NP framework introduced above. The relevant NP Wilson coefficient are \(C_{9,\tau }^\mathrm{NP} = -C_{10,\tau }^\mathrm{NP} = C_{9,\mu }^\mathrm{NP}/|\epsilon _\ell |^2\), and the branching ratio depends quadratically on \(R_0 (1+c_{13})\) in the limit where the NP contribution is large. Setting \(R_{D^{(*)}}\) to the central value in (4.7), and imposing the constraints on \(\theta _q\) from \(\mathcal {B}\rightarrow K^{(*)}\nu \bar{\nu }\) and \(K\rightarrow \pi \nu \bar{\nu }\), one gets an enhancement of a factor \(10^{2}\div 10^{3}\) in \(\mathcal {B}(B\rightarrow K\tau ^+\tau ^-)\) if \(\left| \frac{1-c_{13}}{1+c_{13}}\right| \lesssim 20\%\) (which is a rather natural choice of parameters). Finally, it is interesting to note that the observation of \(b\rightarrow s\tau ^+\tau ^-\) transitions, together with \(s\rightarrow d\nu \bar{\nu }\) and \(b\rightarrow s\nu \bar{\nu }\), would allow to fix the three dimensionless parameters \(c_{13}\), \(\theta _q\), and \(\phi _q\) entering the Lagrangian (3.7), thus completely determining the leading free parameters of the EFT.

\(\tau \rightarrow K \nu \). The \(s\rightarrow u\) analogue of \(B\rightarrow D^{(*)}\tau \bar{\nu }\) is the tau decay \(\tau \rightarrow K \nu \), which is generated at tree-level in the SM, and gets a contribution from the charged-current interaction (3.7). The total branching ratio in the presence of NP can be written as

$$\begin{aligned} \mathcal {B}(\tau \rightarrow K\nu ) {=} \mathcal {B}(\tau \rightarrow K\nu )_\mathrm{SM}\left| 1 {-} R_0 \frac{V_{ub}V_{ts}}{\lambda } \theta _q (e^{i\phi }{-}\theta _q)\right| ^2. \end{aligned}$$
(4.21)

The measured value is \(\mathcal {B}(\tau \rightarrow K\nu )_\mathrm{exp} = (6.9\pm 0.1)\times 10^{-3}\), which has to be compared with the SM prediction \(\mathcal {B}(\tau \rightarrow K\nu )_\mathrm{SM} = (7.1\pm 0.1)\times 10^{-3}\). This translates into a loose bound on the scale of NP [\(R_0\theta _q(1-\theta _q) \lesssim 20\) for \(\phi _q = 0\)].

Loop effects. The running from the scale \(\Lambda \) to the electroweak scale, starting from the NP semileptonic Lagrangian (3.7), does generate non-vanishing contributions to four-quark and four-lepton operators. The contributions to \(K-\bar{K}\) and \(B_s-\bar{B}_s\) mixing, as well as to flavour-changing \(Zq\bar{q}\) interactions, are suppressed at least by the \(\tau \) mass, and turn out to be several orders of magnitude below present experimental constraints.

It is on the other hand well known that running effects due to quark loops, leading to purely leptonic operators [42, 43], are potentially more problematic because of precise constraints from leptonic \(\tau \) decays. In concrete models, additional UV contributions to the same effective operators will arise from the matching at the scale \(\Lambda \). These contributions can help satisfying the \(\tau \) decay constraints, but can also constitute a problem for meson mixing. On general grounds, satisfying all the constraints in a concrete UV completion that incorporates both the \(b\rightarrow c\tau \bar{\nu }\) and the \(b\rightarrow s\ell ^+\ell ^-\) anomalies is not straightforward. However, as shown in [26], this result can be achieved with a moderate tuning of parameters. Given the model-dependence of the radiative constraints, we do not take them into account in the present analysis whose main focus is on semileptonic decays.

5 Conclusions

Recent B-physics data hints toward violations of Lepton Flavour Universality in charged- and neutral-current semileptonic processes. The most natural explanation of these phenomena, if both will be confirmed as evidences of physics beyond the SM, is the hypothesis of a new interaction in the TeV range that couples mainly to third-generation fermions. If a CKM-like relation connects NP effects in B and K physics, it is natural to expect sizeable deviations from the SM in \(K\rightarrow \pi \nu \bar{\nu }\) decays, which are the only \(s\rightarrow d\) transitions that involve third-generation leptons in the final state.

To quantify possible NP effects in \(K\rightarrow \pi \nu \bar{\nu }\) decays in sufficiently general terms, being motivated by present B-physics anomalies, we have considered an EFT based on the hypothesis of a \(U(2)_q\times U(2)_\ell \) flavour symmetry acting on the light generations of left-handed fermions, broken in the quark sector by the small CKM-like spurion \(V_q\) connecting third and light generations (and similarly broken by a small spurion \(V_\ell \) in the lepton sector). We further assumed that NP is coupled only to the left-handed third-generation flavour singlets (\(q_{3L}\) and \(\ell _{3L}\)). Because of the freedom in the choice of the flavour basis, the spurions \(V_{q,\ell }\) can enter the definition of the flavour singlets with an arbitrary mixing parameter of order one. The latter control the communication of NP effects from processes with third-generation fermions only, to processes with light generations. This set-up is not the most general one compatible with the \(U(2)_q\times U(2)_\ell \) flavour symmetry, but it covers a wide class of the most motivated explicit models so far proposed to address B-physics anomalies.

In this framework, we focussed attention on semileptonic transitions involving only \(\tau \) leptons and \(\tau \) neutrinos. These processes are completely determined by four real parameters: the overall scale of the new interactions \(\Lambda \), the two model-dependent real (mixing) parameters \(\theta _q\) and \(\phi _q\) defining the (quark) flavour basis, and the relative strength of the electroweak-triplet and -singlet NP interactions \(c_{13}\). The measurement of the LFU ratios \(R_{D^{(*)}}\) can be used to fix the NP scale \(\Lambda \) in terms of \(\theta _q\) and \(\phi _q\). This allows one in turn to study the neutrino FCNC transitions \(K\rightarrow \pi \nu \bar{\nu }\) and \(B\rightarrow K^{(*)}\nu \bar{\nu }\), as well as \(B\rightarrow K^{(*)}\tau ^+\tau ^-\), as functions of the three remaining parameters naturally expected to be of O(1).

We have shown that, for natural values of the free parameters, sizeable and closely correlated deviations from the SM of both neutrino modes are expected. The electroweak-triplet operator alone necessarily causes a suppression of \(\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })\), due to the interference of NP with the SM amplitude which is always destructive. This suppression could be as large as \(30\%\), relative the SM value. If, on the other hand, also an electroweak singlet interaction is present, arbitrary modifications of \(\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })\) are possible. The strongest constraint on the allowed size of these deviations comes from the present bounds on \(\mathcal {B}(B\rightarrow K^{(*)}\nu \bar{\nu })\), which, however, do not exclude O(1) enhancements in \(\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })\), as illustrated in Fig. 2.

Order of magnitude enhancements of \(b\rightarrow s\tau ^+\tau ^-\) compared to the SM are possible in this class of NP models. However, these transitions are very challenging from the experimental point of view. In principle, the combined measurement of \(R_{D^{(*)}}\), \(\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })\), \(\mathcal {B}(B\rightarrow K^{(*)}\nu \bar{\nu })\), and \(\mathcal {B}(B\rightarrow K\tau ^+\tau ^-)\) would allow one to completely determine the leading parameters of the EFT. The correlation with other observables is less straightforward: violations of \(\mu /e\) universality in \(b\rightarrow s\ell \bar{\ell }\) transitions are a natural prediction of this framework; however, their size and the correlation with NP effects in the neutrino modes are controlled by additional free parameters.

Summarising, \(K\rightarrow \pi \nu \bar{\nu }\) decays could be significantly affected by the non-standard LFU-violating interactions hinted by present B-physics data. The forthcoming measurement of \(\mathcal {B}(K^+\rightarrow \pi ^+\nu \bar{\nu })\) by the NA62 experiment at CERN will provide an important insight on this class of NP models. The general expectation is a sizeable deviation from the SM, which, however, could result also into a significant suppression. Should a deviation from the SM prediction be observed in this channel, its correlation with NP effects in \(\mathcal {B}(B\rightarrow K^{(*)}\nu \bar{\nu })\) and, possibly, \(\mathcal {B}(B\rightarrow K\tau ^+\tau ^-)\), would allow one to reveal the flavour structure of this new interaction.