Charged-Higgs on $R_{D^{(*)}}$, $\tau$ polarization, and FBA

Abstract

We study the influence of a charged-Higgs on the excess of branching fraction ratio, $R_M = BR(\bar{B} \rightarrow M \tau \bar{\nu }_\tau )/BR(\bar{B} \rightarrow M \ell \bar{\nu }_\ell )$ $(M=D, D^*)$, in a generic two-Higgs-doublet model. In order to investigate the lepton polarization, the detailed decay amplitudes with lepton helicity are given. When the charged-Higgs is used to resolve excesses, it is found that two independent Yukawa couplings are needed to explain the $R_D$ and $R_{D^*}$ anomalies. We show that when the upper limit of $BR(B_c\rightarrow \tau \bar{\nu }_\tau )<30\%$ is included, $R_D$ can be significantly enhanced while $R_{D^*}<0.27$. With the $BR(B_c\rightarrow \tau \bar{\nu }_\tau )$ constraint, we find that the $\tau$-lepton polarizations can be still affected by the charged-Higgs effects, where the standard model (SM) predictions are obtained: $P^\tau _{D} \approx 0.324$ and $P^\tau _{D^*}\approx -0.500$, and they can be enhanced to be $P^\tau _{D} \approx 0.5$ and $P^\tau _{D^*}\approx -0.41$ by the charged-Higgs. The integrated lepton forward–backward asymmetry (FBA) is also studied, where the SM result is $\bar{A}^{D^{(*)},\tau }_{FB}\approx -0.359(0.064)$, and they can be enhanced (decreased) to be $\bar{A}^{D^{(*)},\tau }_{FB}\approx -0.33 (0.02)$.

1 Introduction

The exclusive semileptonic $\bar{B} \rightarrow D^{(*)} \tau \bar{\nu }_\tau$ decay has drawn a lot of attention since the BaBar collaboration reported evidence for an excess in the ratio of branching ratios (BRs) [1, 2], which is defined by

$$\begin{aligned} R_{D^{(*)}} =\frac{BR(\bar{B}\rightarrow D^{(*)} \tau \bar{\nu })}{BR(\bar{B}\rightarrow D^{(*)} \ell \bar{\nu })}. \end{aligned}$$

(1)

Intriguingly, a similar excess was also reported by Belle [3,4,5] and LHCb [6]. The averaged results from the heavy flavor averaging group (HFAG) now are given by [7]

$$\begin{aligned} R_D= & {} 0.403 \pm 0.04 \pm 0.024, \nonumber \\ R_{D^*}= & {} 0.310 \pm 0.015 \pm 0.008, \end{aligned}$$

(2)

where the standard model (SM) predictions are: $R^\mathrm{SM}_D \approx 0.300$ [8, 9] and $R^\mathrm{SM}_{D^*}\approx 0.252$ [10]. Inspired by the unexpected measurements, many implications and speculations were studied in the literature [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58].

In addition to the branching fraction ratio, Belle recently showed the measurement of $\tau$ polarization in the $\bar{B} \rightarrow D^* \tau \bar{\nu }_{\tau }$ decay:

$$\begin{aligned} P^{\tau }_{D^*} = \frac{\Gamma ^{h=+}_{D^*} - \Gamma ^{h=-}_{D^*}}{\Gamma ^{h=+}_{D^*} + \Gamma ^{h=-}_{D^*}}=-0.38\pm 0.51^{+0.21}_{-0.16}, \end{aligned}$$

(3)

where $\Gamma ^{\pm }_{D^*}$ denotes the partial decay rate with a $\tau$-lepton helicity of $h=\pm$, and the SM result is $P^{\tau }_{D^*} \approx -0.500$. Although the errors in the current observation are still large, any significant deviations from the SM results can indicate the new physics [18, 62]. Based on the current experimental indications and from a phenomenological viewpoint, we investigate the impacts of a charged-Higgs on the semileptonic B decays in a generic two-Higgs-doublet model (THDM) [12, 59, 60].

Without imposing extra global symmetry, it is well known that the flavor-changing neutral currents (FCNCs) in the THDM can be induced at the tree level. The related couplings can be severely constrained by $\Delta F=2$ processes, such as K–$\bar{K}$, $B_q$–$\bar{B}_q$ ($q=d,s$), and D–$\bar{D}$ mixings. However, these constraints occur in down-type quarks and the first two generations of up-type quarks. The top-quark-involving effects may not have serious bounds. Thus, with the constraints from the Higgs precision measurements, the BR for the $t\rightarrow c h$ process can be of the order of $10^{-4}-10^{-3}$ [61]. It was found that the same FCNC coupling in the quark sector can help to resolve $R_D$ and $R_{D^*}$ excesses by the charged-Higgs mediation [12, 59]. In addition, the tree-level FCNCs in the lepton sector not only can resolve the muon $g-2$ anomaly, but also can provide a large BR to the lepton-flavor violating process, such as $h\rightarrow \tau \mu$, for which the details can be found in our previous work [60].

In this study, we revisit the charged-Higgs Yukawa couplings to the $\bar{B}\rightarrow (D,D^*)\tau \nu _{\tau }$ processes in the generic THDM. In order to naturally suppress the FCNCs at the tree level, we adopt the so-called Cheng–Sher ansatz [63] in the quark and lepton sectors, where the Yukawa couplings are formulated by $Y_{ij} \propto \sqrt{m_i m_j}/v$. For the semileponic B decays, the main uncertainty is from the hadronic $\bar{B} \rightarrow D^{(*)}$ transition form factors. In order to restrain the influence of hadronic effects, we take the values of form factors so that the BRs for $\bar{B}\rightarrow D^{(*)} \ell \bar{\nu }_\ell$ ($\ell =e,\mu$) can fit the experimental data within $2\sigma$ errors. Although the charged-Higgs also contributes to the light lepton channels, due to the suppression of $m_\ell /v$, its effects are small to the $\bar{B}\rightarrow D^{(*)} \ell \bar{\nu }_\ell$ decays. It is found that we need at least two new parameters to explain the $R_{D}$ and $R_{D^*}$ excesses; one is from quark sector, and the other is from the lepton sector. The conclusion is different from that shown in [12], in which only one parameter was required to explain the excesses. However, when the upper limit of $BR(B_c \rightarrow \tau \bar{\nu }_\tau )< 30\%$ obtained in [52, 53] is taken into account, the allowed parameter space is strictly constrained. It will be seen that $R_{D}$ can be significantly enhanced while the change of $R_{D^*}$ is minor and can be only up to around 0.27.

In addition to the ratios of branching fractions, we also investigate the influence of the charged-Higgs on the lepton-helicity asymmetries, and lepton forward–backward asymmetries (FBAs). We find that $\tau$ polarizations in the $\bar{B}\rightarrow (D, D^*) \tau \bar{\nu }_\tau$ decays are sensitive to the charged-Higgs effects. For the FBA, the $\bar{B}\rightarrow D^* \tau \bar{\nu }_\tau$ process is more sensitive to the charged-Higgs effects.

The paper is organized as follows. In Sect. 2, we briefly introduce the charged Higgs Yukawa couplings to the quarks and leptons in the generic THDM. We formulate the decay amplitudes with the lepton-helicity states, the differential branching ratios, the lepton polarizations, and the lepton FBAs for $\bar{B}\rightarrow (D, D^*) \ell \bar{\nu }_\ell$ in Sect. 3. The numerical estimations and discussions are given in Sect. 4. A summary is shown in Sect. 5.

2 Charged-Higgs Yukawa Couplings in the THDM

To obtain the scalar couplings to the quarks and leptons in the model, the Yukawa sector is written as [60, 68]

$$\begin{aligned} -\mathcal{L}_Y= & {} \bar{Q}_L Y^d_1 D_R H_1 + \bar{Q}_L Y^{d}_2 D_R H_2 \nonumber \\&+\, \bar{Q}_L Y^u_1 U_R \tilde{H}_1 + \bar{Q}_L Y^{u}_2 U_R \tilde{H}_2 \nonumber \\&+ \, \bar{L} Y^\ell _1 \ell _R H_1 + \bar{L} Y^{\ell }_2 \ell _R H_2 + H.c., \end{aligned}$$

(4)

where the flavor indices are suppressed, $Q^T_L=(u, d)_L$ and $L^T = (\nu , \ell )_L$ are the $SU(2)_L$ quark and lepton doublets, respectively, $Y^f_{1,2}$ are the Yukawa matrices, $\tilde{H}_2 = i\tau _2 H^*_2$ with $(i\tau _{2})_{11(22)} =0$ and $(i\tau _2)_{12(21)} =1(-1)$, and the Higgs doublets are usually taken as

$$\begin{aligned} H_i= & {} \left( \begin{array}{c} \phi ^+_i \\ (v_i+\phi _i +i \eta _i)/\sqrt{2} \\ \end{array} \right) \end{aligned}$$

(5)

with $v_i$ being the VEV of $H_i$. Equation (4) can recover the type II THDM if $Y^{d,\ell }_2$ and $Y^{u}_{1}$ vanish. Since $\phi _1$ and $\phi _2$ are two CP-even scalars, and they mix, we can introduce a mixing $\alpha$ angle to describe their physical states. The CP-odd and charged scalars are composed of $\eta _{1,2}$ and $\phi ^\pm _{1,2}$, respectively; therefore, the mixing angle only depends on the ratio of $v_1$ and $v_2$. Hence, the relations between the physical and weak scalar states are expressed as

$$\begin{aligned} h= & {} -s_\alpha \phi _1 + c_\alpha \phi _2, \nonumber \\ H= & {} c_\alpha \phi _1 + s_\alpha \phi _2, \nonumber \\ H^\pm (A)= & {} -s_\beta \phi ^\pm _1 (\eta _1) + c_\beta \phi ^\pm _2 (\eta _2), \end{aligned}$$

(6)

where h is the SM-like Higgs while H, A, and $H^\pm$ are new particles in the THDM, $c_\alpha (s_\alpha )= \cos \alpha (\sin \alpha )$, $c_\beta = \cos \beta = v_1/v$, and $s_\beta = \sin \beta = v_2/v$.

Using Eqs. (4) and (5), the quark and charged lepton mass matrices can be written as

$$\begin{aligned} \mathbf{M}^{f}= \frac{v}{\sqrt{2}}\left( c_\beta Y^{f}_1 + s_\beta Y^{f}_2 \right) . \end{aligned}$$

(7)

We can diagonalize $\mathbf{M}^{f}$ by introducing unitary matrices $V^f_L$ and $V^f_R$ via $\mathbf{m}^f_\mathrm{dia} = V^f_L \mathbf{M}^f V^{f \dagger }_R$. Accordingly, the charged Higgs Yukawa couplings to fermions can be found to be [60]

$$\begin{aligned} -\mathcal{L}^{H^\pm }_Y= & {} \sqrt{2} \bar{d}_L \mathbf{V}^\dagger \left[ - \frac{ \cot \beta }{v } \mathbf{m_u} + \frac{\mathbf{X}^u}{ s_\beta } \right] u_R H^- \nonumber \\&+\, \sqrt{2} \bar{u}_L \mathbf{V}\left[ - \frac{ \tan \beta }{v } \mathbf{m_d} + \frac{\mathbf{X}^d}{ c_\beta } \right] d_R H^+ \nonumber \\&+\, \sqrt{2} \bar{\nu }_L \left[ -\frac{\tan \beta }{v } \mathbf{m_\ell } + \frac{\mathbf{X}^\ell }{ c_\beta } \right] \ell _R H^+ + H.c., \end{aligned}$$

(8)

where $\mathbf{V}$ denotes the Cabibbo–Kobayashi–Maskawa (CKM), and $\mathbf{X^f}$ is defined by

$$\begin{aligned} \mathbf{X^u}= V^u_L \frac{Y^u_1}{\sqrt{2}} V^{u\dagger }_R, \ \mathbf{X^d}= V^d_L \frac{Y^d_2}{\sqrt{2}} V^{d\dagger }_R, \ \mathbf{X^\ell }= V^\ell _L \frac{Y^\ell _2}{\sqrt{2}} V^{\ell \dagger }_R. \end{aligned}$$

(9)

From Eq. (8), it can be seen that $X^{f}_{ij}$ dictates not only FCNCs but also violation of lepton universality; in addition, the effects of $X^{d}$ and $X^{\ell }$ can be further enhanced with a large value of $\tan \beta$, i.e., $c_\beta \ll 1$. Although the $Y^{f}_1$ and $Y^{f}_2$ Yukawa matrices basically are arbitrary free parameters, since they are related to the fermion masses, in order to show the mass-dependence effects, we further adopt the Cheng–Sher ansatz for $X^{f}_{ij}$ as $X^{f}_{ij} = \sqrt{m^f_i m^f_j}/v\, \chi ^{f}_{ij}$ [63], where $X^{f}_{ij}$ now are suppressed by $\sqrt{m^f_i m^f_j}/v$, and $\chi ^{f}_{ij}$ are the free parameters.

Before we further discuss the effective interactions mediated by the charged Higgs for the $b\rightarrow c \ell \bar{\nu }_\ell$ process, we analyze the effect of $\mathbf{X}^{u}$ associated with the CKM matrix, such as $(\mathbf{V}^\dagger \mathbf{X^u})_{bc}$ in Eq. (8). If we assume that $\mathbf{X^{u}}$ is a diagonal matrix, it can be clearly seen that $(\mathbf{V}^\dagger \mathbf{X^u})_{bc} = V^*_{cb} X^u_{cc}$. With the Cheng–Sher ansatz, the charged Higgs Yukawa couplings are then suppressed by $m_c/v$. Due to the fact that there is no significant $\tan \beta$ enhancement, the contribution is expected to be small. However, if $X^{u}_{ij}$ with $i\ne j$ are allowed, $(\mathbf{V}^\dagger \mathbf{X^u})_{bc}$ can be simplified as

$$\begin{aligned} (\mathbf{V}^\dagger \mathbf{X^u})_{bc}&= V^*_{ub} X^u_{uc} + V^*_{cb} X^u_{cc} + V^*_{tb} X^u_{tc}, \nonumber \\&\approx \frac{\sqrt{m_t m_c}}{v} \chi ^u_{tc}, \end{aligned}$$

(10)

where we have taken $|V_{ub}|< |V_{cb}| \ll V_{tb} \approx 1$ and the Cheng–Sher relation. With the approximation $\sqrt{m_t m_c}/v \sim V_{cb}$, it can be seen that $\chi ^u_{tc}\sim O(1)$ indicates a large coupling at the b–c–$H^\pm$ vertex and could help to resolve the excesses. A similar situation also occurs in the $(\mathbf{V X^d})_{cb}$, which can be expressed as $(\mathbf{V X^d})_{cb}/c_\beta \approx \sqrt{m_b m_s}\chi ^{d}_{sb}/v$. Since $\chi ^d_{sb}$ can be limited by the $\Delta B =2$ process via the mediation of neutral scalar bosons at the tree level, we can ignore its contribution. Hence, we focus on the influence of $\chi ^{u}_{tc}$.

3 Phenomenological formulations

Combining the SM and $H^\pm$ contributions, the effective Hamiltonian for $b\rightarrow c \ell \bar{\nu }_{\ell }$ is written as

$$\begin{aligned} H_\mathrm{eff}= & {} \frac{G_F}{\sqrt{2}} V_{cb} \left[ (\bar{c} b)_{V-A} (\bar{\ell }\nu )_{V-A}\right. \nonumber \\&\left. +\, C^{\ell }_L (\bar{c} b)_{S-P} (\bar{\ell }\nu )_{S-P}+ C^{\ell }_R (\bar{c} b)_{S+P} (\bar{\ell }\nu )_{S-P} \right] ,\nonumber \\ \end{aligned}$$

(11)

where $(\bar{f}' f)_{V\pm A}=\bar{f}' \gamma ^\mu (1\pm \gamma _5) f$, $(\bar{f}' f)_{S\pm P}=\bar{f}' (1\pm \gamma _5) f$, and the coefficients from the charged Higgs with $g^2/(8 m^2_W) = 1/(2v^2)$ are given by

$$\begin{aligned} C^{\ell }_L\approx & {} - \frac{m_c m_\ell }{m^2_{H^\pm }} \left( 1- \frac{\chi ^{\ell }_{\ell \ell } }{s_\beta }\right) \left( 1 - \sqrt{\frac{m_t}{m_c}} \frac{ \chi ^{u}_{ct} }{c_\beta V_{cb} } \right) , \end{aligned}$$

(12)

$$\begin{aligned} C^{\ell }_R\approx & {} - \frac{ m_b m_\ell \tan ^2\beta }{m^2_{H^\pm }} \left( 1 - \frac{\chi ^{\ell }_{\ell \ell } }{s_\beta }\right) . \end{aligned}$$

(13)

It can be seen that without $\chi ^{\ell }_{\ell \ell }$ and $\chi ^u_{ct}$, both $C^\ell _{L}$ and $C^\ell _R$ are negative and correspond to the type-II THDM; as a result, they are destructive contributions to the SM [1]. In addition to the sign issue, we also need to adjust $C^\ell _R + C^\ell _L$ and $C^\ell _R - C^\ell _L$ so that $R_D$ and $R_{D^*}$ can be explained at the same time. In order to demonstrate the effects of the generic THDM, we will discuss the situations with and without $\chi ^{\ell }_{\ell \ell }$ and $\chi ^u_{ct}$ after we introduce the differential decay rates for the $\bar{B}\rightarrow (D, D^*) \ell \bar{\nu }_\ell$ decays.

To calculate the exclusive semileptonic B decays, we parametrize the $B\rightarrow (D, D^*)$ transition form factors as

$$\begin{aligned} \langle D(p_2)|\bar{c} \gamma ^{\mu } b | \bar{B}(p_1)\rangle= & {} F_1(q^2)\left[ P^{\mu }-\frac{P\cdot q}{q^2}q^{\mu } \right] \nonumber \\&+\,F_0(q^2)\frac{P\cdot q }{q^2}q^{\mu }, \nonumber \\ \langle D(p_2)| \bar{c} b |\overline{B}(p_1) \rangle= & {} ({m_B+m_D}) F_S(q^2), \end{aligned}$$

(14)

$$\begin{aligned}&\langle D^*(p_2,\epsilon )|\overline{c}\gamma ^{\mu }b|\overline{B}(p_1)\rangle = \frac{V(q^2)}{m_B+m_{D^*}}\epsilon ^{\mu \nu \rho \sigma } \epsilon ^*_{\nu }P_{\rho }q_{\sigma }, \nonumber \\&\quad \langle D^*(p_2,\epsilon )|\overline{c}\gamma ^{\mu }\gamma _5 b|\overline{B}(p_1)\rangle \nonumber \\&\quad =2im_{D^*} A_0(q^2)\frac{\epsilon ^*\cdot q}{q^2}q^{\mu }+i(m_B+m_{D^*})A_1(q^2)\nonumber \\&\qquad \times \left[ \epsilon ^*_{\mu } -\frac{\epsilon ^*\cdot q}{q^2}q^{\mu } \right] -iA_2(q^2)\frac{\epsilon ^*\cdot q}{m_B+m_{D^*}}\nonumber \\&\qquad \times \left[ P^{\mu }-\frac{P\cdot q }{q^2}q^{\mu } \right] , \nonumber \\&\langle D^*(p_2, \epsilon )| \overline{c} \gamma _5 b |\overline{B}(p_1) \rangle = -i \epsilon ^* \cdot q F_P(q^2), \end{aligned}$$

(15)

where $\epsilon ^{0123}=1$, $P=p_1+p_2$, $q=p_1-p_2$; $\epsilon$ is the polarization vector of $D^*$ meson, and $\epsilon \cdot \epsilon ^* =-1$. Using the equations of motion and , we obtain the relationships

$$\begin{aligned} F_S(q^2)\approx & {} \frac{m_B-m_D}{m_b(\mu )-m_c (\mu )} F_0(q^2), \nonumber \\ F_P(q^2)\approx & {} \frac{2 m_{D^*}}{m_b (\mu )+m_c(\mu )} A_0(q^2), \end{aligned}$$

(16)

where $m_{b,c}(\mu )$ are the current quark masses at the $\mu$ scale. According to the interactions in Eq. (11), the decay amplitudes for $\bar{B}\rightarrow (D, D^*) \ell \bar{\nu }_\ell$ are then

$$\begin{aligned} A_{D}= & {} \frac{G_F}{\sqrt{2}} V_{cb} \left[ F_1 \left( P^\mu -\frac{P\cdot q}{q^2}q^\mu \right) (\bar{\ell }\nu )_{V-A} \right. \nonumber \\&+ \left. \left( m_\ell F_0 \frac{P\cdot q}{q^2} + (C^{\ell }_R + C^{\ell }_L)(m_B + m_D) F_S \right) (\bar{\ell }\nu )_{S-P}\right] , \nonumber \\ A^L_{D^*}= & {} -i \frac{G_F}{\sqrt{2}} V_{cb} \left\{ \epsilon ^*\cdot q \left( (C^{\ell }_R -C^{\ell }_L) F_P + 2 A_0 \frac{m_{D^*} m_\ell }{q^2}\right) (\bar{\ell }\nu )_{S-P} \right. \nonumber \\&+ \left[ (m_B + m_{D^*}) A_1 \left( \epsilon ^*_\mu (L) - \frac{\epsilon ^*\cdot q}{q^2} q_\mu \right) \right. \nonumber \\&\left. -\, \frac{A_2 \epsilon ^*\cdot q}{m_B + m_D} \left( P_\mu -\frac{P\cdot q}{q^2}q_\mu \right) \right] (\bar{\ell }\nu )_{V-A}, \nonumber \\ A^{T}_{D^*}= & {} \frac{G_F}{\sqrt{2}} V_{cb} \left[ \frac{V}{m_B + m_{D^*}} \varepsilon _{\mu \nu \rho \sigma } \epsilon ^*_\nu (T) P^\rho q^\sigma \right. \nonumber \\&\left. -\, i (m_B + m_{D^*})A_1 \epsilon ^*_\mu (T) \right] (\bar{\ell }\nu )_{V-A}, \end{aligned}$$

(17)

where we have suppressed the $q^2$-dependence in the form factors, and $A^L_{D^*}$ and $A^T_{D^*}$ denote the longitudinal and transverse components of $D^*$-meson, respectively. It can be seen that the charged Higgs only affects the longitudinal part.

In order to derive the differential decay rate with a specific lepton helicity, we set the coordinates of various kinematic variables in the rest frame of $\ell \bar{\nu }$ invariant mass as

$$\begin{aligned} q= & {} (\sqrt{q^2}, 0 , 0, 0),~ p_{M} = ( E_{M}, 0, 0, p_M),\nonumber \\ E_{M}= & {} \frac{1}{2\sqrt{q^2}}(m^2_B -q^2 - m^2_{M}), \end{aligned}$$

(18)

$$\begin{aligned} p_{M}= & {} \frac{\sqrt{\lambda _M}}{2\sqrt{q^2}},\nonumber \\ p_{\nu }= & {} (E_\nu , p_\nu \sin \theta _\ell \cos \phi , p_\nu \sin \theta _\ell \sin \phi , p_\nu \cos \theta _\ell ),\nonumber \\ p_{\ell }= & {} (E_\ell , - \mathbf {p}_{\nu }), \nonumber \\ \epsilon (L)= & {} \frac{1}{m_{D^*}}( p_{D^*},0,0, E_{D^*}),~\epsilon (\pm )\nonumber \\= & {} \frac{1}{\sqrt{2}} (0, \mp 1, - i,0), ~ p_{\ell }=p_{\nu }=\frac{q^2 -m^2_\ell }{2\sqrt{q^2}}, \end{aligned}$$

(19)

where $\theta _\ell$ is the polar angle of a neutrino with respect to the moving direction of M meson in the $q^2$ rest frame, and the components of $\vec {p}_{\ell }$ can be obtained from $\vec {p}_{\nu }$ by using $\pi -\theta _\ell$ and $\phi + \pi$ instead of $\theta _\ell$ and $\phi$. Since the SM neutrino is left-handed, if we neglect its small mass, its helicity can be fixed to be negative; therefore, we focus on the helicity amplitudes of a charged lepton. Accordingly, the charged lepton-helicity amplitudes for the $\bar{B} \rightarrow D \ell \bar{\nu }_{\ell }$ decay can be derived as

$$\begin{aligned} A^{L, h=+}_{D}= & {} \frac{G_F V_{cb}}{\sqrt{2}} \left( 2 m_\ell \beta _\ell \frac{\sqrt{\lambda _{D}}}{\sqrt{q^2}} F_1 \cos \theta _\ell - 2\beta _\ell \sqrt{q^2} X^{0\ell }_{D}\right) ,\nonumber \\ \end{aligned}$$

(20)

$$\begin{aligned} A^{L, h=-}_{D}= & {} \frac{G_F V_{cb}}{\sqrt{2}} \left( -2 \beta _{\ell } \sqrt{\lambda _{D}} F_1 \sin \theta _\ell \right) , \end{aligned}$$

(21)

$$\begin{aligned} X^{0\ell }_D= & {} \frac{m^2_B - m^2_D}{q^2} m_\ell F_0 + (m_B + m_D) \left( C^{\ell }_R + C^{\ell }_L\right) F_S, \nonumber \\ \end{aligned}$$

(22)

where $\beta _{\ell } = (1 - m^2_\ell /q^2)^{1/2}$, $h= +(-)$ denotes the positive (negative) helicity of a charged lepton, and the detailed spinor states and derivations of $(\bar{\ell }\nu )_{V-A}$ and $(\bar{\ell }\nu )_{S-P}$ with polarized leptons are given in the appendix. Although the D meson does not carry spin degrees of freedom, in order to use similar notation to that in the $\bar{B} \rightarrow D^* \ell \bar{\nu }_\ell$ decay, we put an extra index L in $A^{L, h=\pm }_D$.

With the same approach, we can obtain the helicity amplitudes for the $\bar{B}\rightarrow D^* \ell \bar{\nu }_\ell$ decay. Since the $D^*$ meson is a vector boson and carries spin degrees of freedom, we separate the lepton-helicity amplitudes into longitudinal (L) and transverse (T) parts to show the information for each $D^*$ polarization. Thus, the helicity amplitudes for $\bar{B}\rightarrow D^* \ell \bar{\nu }_\ell$ with the $D^*$ longitudinal polarization are found to be

$$\begin{aligned} A^{L,h=+}_{D^*}= & {} -i\frac{G_F V_{cb}}{\sqrt{2}} \left( 2 m_\ell \beta _\ell h^0_{D^*} \cos \theta _\ell - 2 \beta _\ell \frac{\sqrt{\lambda _{D^*}}}{ \sqrt{q^2} } X^{0\ell }_{D^*}\right) ,\nonumber \\ \end{aligned}$$

(23)

$$\begin{aligned} A^{L,h=-}_{D^*}= & {} -i\frac{G_F V_{cb}}{\sqrt{2}} \left( -2\sqrt{q^2} \beta _\ell h^0_{D^*} \sin \theta _\ell \right) , \end{aligned}$$

(24)

$$\begin{aligned} h^0_{D^*}(q^2)= & {} \frac{ 1}{2 m_{D^*} \sqrt{q^2}}\left[ \phantom {\left. -\frac{{\lambda _{D^*} }}{m_B+m_{D^*}}A_2\right] }(m_B^2-m_{D^*}^2-q^2)(m_B+m_{D^*})A_1 \right. \nonumber \\&\left. -\,\frac{{\lambda _{D^*} }}{m_B+m_{D^*}}A_2\right] , \nonumber \\ X^{0\ell }_{D^*}= & {} m_\ell A_0 + \frac{q^2}{2m_D^* } (C^\ell _R - C^\ell _L) F_P. \end{aligned}$$

(25)

It can be seen that the formulas of $A^{L,h=\pm }_{D^*}$ are similar to those of $A^{L, h=\pm }_{D}$. The decay amplitudes with the $D^*$ transverse polarizations are given by

$$\begin{aligned} A^{T=\pm , h=+}_{D^*}= & {} i\frac{G_F V_{cb}}{\sqrt{2}} \left[ -\sqrt{2} m_{\ell } \beta _{\ell } \sin \theta _\ell e^{\mp i \phi } \right] h^{\pm }_{D^*}, \end{aligned}$$

(26)

$$\begin{aligned} A^{T=\pm , h=-}_{D^*}= & {} \mp i \frac{G_F V_{cb}}{\sqrt{2}} \left[ -\sqrt{2} \sqrt{q^2} \beta _\ell (1\mp \cos \theta _\ell ) e^{\mp i \phi } \right] h^{\pm }_{D^*}, \nonumber \\ h^{\pm }_{D^*}= & {} \frac{\sqrt{\lambda _{D^*}} }{m_B + m_{D^*}} V \mp (m_B + m_{D^*} ) A_1. \end{aligned}$$

(27)

Since the scalar charged Higgs cannot affect the transverse parts, the $A^{T=\pm , h=\pm }_{D^*}$ are only from the SM contributions. According to these helicity amplitudes, it can be clearly seen that due to angular-momentum conservation, the $A^{L, h=+}_{D}$ and $A^{L(T), h=+}_{D^*}$, which come from $\bar{\ell }\gamma _\mu (1-\gamma _5)\nu$, are chiral suppression and proportional to $m_\ell$. The charged lepton in $\bar{\ell }(1-\gamma _5) \nu$ prefers the $h=+$ state and in principle has no chiral suppression; however, in our case, chiral suppression exists and is from the charged-Higgs Yukawa couplings due to the Cheng–Sher ansatz.

Including the three-body phase space, the differential decay rates with lepton helicity and $D^*$ polarization as a function of $q^2$ and $\cos \theta _\ell$ can be obtained:

$$\begin{aligned} \frac{d\Gamma ^{h=\pm }_{D}}{dq^2 d\cos \theta _\ell }= & {} \frac{\sqrt{\lambda _{D}}}{512 \pi ^3 m^3_B} \beta ^2_{\ell }\, |A^{L,h=\pm }_{D}|^2 , \nonumber \\ \frac{d\Gamma ^{L(T), h=\pm }_{D^*}}{dq^2 d\cos \theta _\ell }= & {} \frac{\sqrt{\lambda _{D^*}}}{512 \pi ^3 m^3_B} \beta ^2_{\ell }\, |A^{L(T),h=\pm }_{D^*}|^2 . \end{aligned}$$

(28)

The differential decay rates, which integrate out the polar $\theta _\ell$ angle, are shown in the appendix. In addition to the branching fraction ratios $R_D$ and $R_{D^*}$, based on Eq. (28), we can also study the lepton-helicity asymmetry [13, 18, 62] (see also Refs. [64, 65]) and the FBA [66, 67]. Helicity asymmetry can be defined by

$$\begin{aligned} P^{\ell }_{M}&= \frac{\Gamma ^{h= +}_M - \Gamma ^{h=-}_M}{ \Gamma ^{h= +}_M + \Gamma ^{h=-}_M }, \end{aligned}$$

(29)

where $M=D, D^*$ and $\Gamma ^{h=\pm }_{D^*}=\sum _{\lambda =L,\pm } \Gamma ^{\lambda ,h=\pm }_{D^*}$ have summed all $D^*$ polarizations. From Eqs. (51) and (53), the lepton-helicity asymmetries for $\bar{B}\rightarrow (D, D^{*}) \ell \bar{\nu }_\ell$ with charged Higgs effects can be found to be

$$\begin{aligned} P^{\ell }_{D}= & {} \frac{\int ^{q^2_\mathrm{max}}_{m^2_\ell } dq^2 \sqrt{\lambda _D} \beta ^4_\ell \left[ \frac{2}{3} \left( m^2_{\ell } -2 q^2 \right) \lambda _D F^2_1 /q^2 + 2 m^2_\ell q^2 |X^{0\ell }_D|^2\right] }{\int ^{q^2_\mathrm{max}}_{m^2_\ell } dq^2 \sqrt{\lambda _D} \beta ^4_\ell \left[ \frac{2}{3} \left( m^2_{\ell }+ 2 q^2 \right) \lambda _D F^2_1/q^2 + 2 m^2_\ell q^2 |X^{0\ell }_D|^2\right] }, \end{aligned}$$

(30)

$$\begin{aligned} P^{\ell }_{D^*}= & {} \frac{\int ^{q^2_\mathrm{max}}_{m^2_\ell } dq^2 \sqrt{\lambda _{D^*}} \beta ^4_\ell \left[ \frac{2}{3} (m^2_\ell -2 q^2) \left( \sum _{\lambda =L,\pm } |h^{\lambda }_{D^*}|^2\right) + 2(m^2_\ell /q^2) \lambda _{D^*} |X^{0\ell }_{D^*}|^2 \right] }{\int ^{q^2_\mathrm{max}}_{m^2_\ell } dq^2 \sqrt{\lambda _{D^*}} \beta ^4_\ell \left[ \frac{2}{3} (m^2_\ell + 2 q^2) \left( \sum _{\lambda =L,\pm } |h^{\lambda }_{D^*}|^2\right) + 2(m^2_\ell /q^2) \lambda _{D^*} |X^{0\ell }_{D^*}|^2 \right] }. \end{aligned}$$

(31)

The lepton FBA can be defined by

$$\begin{aligned} A^{M,\ell }_{FB} (q^2)&= \frac{\int ^{1}_{0} dz (d\Gamma _M/dq^2dz) - \int ^{0}_{-1} dz (d\Gamma _M/dq^2dz)}{\int ^{1}_{0} dz (d\Gamma _M/dq^2dz) + \int ^{0}_{-1} dz (d\Gamma _M/dq^2dz)}, \end{aligned}$$

(32)

where $z=\cos \theta _\ell$, and $\Gamma _M$ denotes the total partial decay rate for the $\bar{B}\rightarrow M \ell \bar{\nu }_\ell$ decay. Accordingly, the FBAs mediated by the charged Higgs and W-boson in $\bar{B} \rightarrow (D, D^*) \ell \bar{\nu }_\ell$ are obtained:

$$\begin{aligned} A^{D,\ell }_{FB} (q^2)= & {} - \frac{2 m_{\ell } \sqrt{\lambda _D} F_1 X^0_D}{H^+_D + H^-_D}, \nonumber \\ A^{D^*, \ell }_{FB} (q^2)= & {} \frac{1}{\sum _{\lambda =L,\pm } (H^{\lambda , +}_{D^*} +H^{\lambda , -}_{D^*})}\nonumber \\&\times \,\left[ -2 m_\ell \frac{\sqrt{\lambda _{D^*}}}{\sqrt{q^2}} h^0_{D^*} X^0_{D^*} +4 q^2 \sqrt{\lambda _{D^*}} A_1 V \right] . \nonumber \\ \end{aligned}$$

(33)

From Eq. (33), it can be seen that the FBAs in the $A^{D,\ell }_{FB}$ and the longitudinal part of $A^{D^*,\ell }_{FB}$ depend on $m_\ell$ and are chiral suppressed. Due to $m_\tau /m_b \sim 0.4$, which is not highly suppressed, we expect $\bar{B} \rightarrow D \tau \bar{\nu }_\tau$ to have a sizable FBA. Moreover, since $A^{D^*,\ell }_{FB}$ does not vanish in the chiral limit, it can be sizable in a light charged lepton mode. Basically, the observations of the tau polarization and FBA rely on tau-lepton reconstruction, where the kinematic information is from its decay products; however, since the final state in a tau decay at least involves one invisible neutrino, it is experimentally challenging to measure the polarization and FBA. Instead of a $\tau$ reconstruction, an approach using the kinematics of visible particles in $\tau$ decays has recently been proposed by the authors in [69], where the tau polarization and FBA can be extracted from an angular asymmetry of visible particles in a tau decay. Accordingly, it is shown that the $\tau \rightarrow \pi \nu _\tau$ decay is the most sensitive channel. Based on this new approach, a statistical precision of $10\%$ can be achieved at Belle II with an integrated luminosity of 50 ab$^{-1}$. The detailed analysis can be found in [69].

Fig. 1

Contours for $R_D$ (dashed) and $R_{D^*}$ (solid) as a function of $\chi ^{u}_{ct}$ and a $\chi ^{\ell }_{\tau \tau }$ with $\tan \beta =40$, b $\tan \beta$ with $\chi ^{\ell }_{\tau \tau }=4$, where we have fixed $m_{H^\pm }=400$ GeV

4 Numerical analysis and discussions

4.1 Roles of the $\chi ^{\ell }_{\tau \tau }$ and $\chi ^{u}_{ct}$ parameters

Before presenting the detailed numerical analysis, we first discuss the influence of $\chi ^{\ell }_{\ell \ell }$ and $\chi ^{u}_{ct}$ on the $C^{\ell }_{R}$ and $C^\ell _{L}$. From Eqs. (22) and (25), it can be seen that the $\bar{B}\rightarrow (D, D^*) \ell \bar{\nu }_\ell$ decays are related to $C^\ell _R + C^\ell _L$ and $C^\ell _R - C^\ell _L$, respectively. If the charged-Higgs can resolve the anomalies, the main effects then are on the $\tau \bar{\nu }_\tau$ modes due to the lepton mass-dependent Yukawa couplings. In the following study, we concentrate on the $\bar{B}\rightarrow (D, D^*) \tau \bar{\nu }_\tau$ decays. Since the measured $R_{D}$ and $R_{D^*}$ are somewhat higher than the SM predictions, the $H^\pm$ effects should constructively interfere with the SM contributions. Thus, we have to require $C^\tau _R \pm C^\tau _L >0$. Furthermore, from Eq. (23), the charged-Higgs contribution is associated with the $\sqrt{\lambda _{D^*}}$ factor, which represents $|\vec {p}_{D^*}|$ and decreases while $q^2$ increases; as a result, the $H^\pm$ effects on the $BR(\bar{B}\rightarrow D^* \tau \bar{\nu }_\tau )$ are not as sensitive as those on the $BR(\bar{B}\rightarrow D \tau \bar{\nu }_\tau )$. Therefore, to simultaneously enhance $R_D$ and $R_{D^*}$ through the mediation of the charged-Higgs, we conclude $C^{\tau }_R - C^{\tau }_L> C^{\tau }_{R} + C^{\tau }_L > 0$; that is, $C^{\tau }_R> 0 > C^\tau _L$. We note that $C^{\ell }_{R,L}$ from other scalar boson can in general be much larger than the SM contributions, so the interference effects are not important. Since the $H^\pm$ couplings are proportional to the $m_\ell \tan \beta /v$, even with a large $\tan \beta$ case, the effects are naturally limited. Hence, our discussions can be only applied to the charged-Higgs-like case.

Following the analysis above, we now discuss the roles of $\chi ^{\ell }_{\tau \tau }$ and $\chi ^u_{ct}$ in the $C^\tau _R$ and $C^\tau _L$. From Eq. (13), it can be seen that without $\chi ^{\ell }_{\tau \tau }$, $C^\tau _R < 0$. In other words, we need $\chi ^{\ell }_{\tau \tau }$ to tune the sign of $C^\tau _R$ from negative to positive. According to Eq. (12), if we take $C^\tau _R >0$ and ignore the $\chi ^u_{ct}$ factor, the sign of $C^\tau _L$ is positive, which disfavors our earlier conclusion. Hence, we need $\chi ^u_{ct}$ to flip the positive $C^\tau _L$ to make it negative. In addition to the signs of $C^\tau _R$ and $C^\tau _L$, their magnitudes are also an important issue. The charged-Higgs Yukawa couplings generally depend on the fermion mass, with the exception of the top-quark, and the couplings are suppressed by the $m_f/v$. To enhance the involved Yukawa couplings, we adopt a scenario with a large value of $\tan \beta$.

4.2 Numerical analysis of $R_{D^{(*)}}$ and constraint from $B_c \rightarrow \tau \bar{\nu }_\tau$

To estimate the physical quantities of the exclusive semileptonic B decays, we use the $B\rightarrow M$ form factors, which were calculated based on the heavy quark effective theory (HQET) and shown in [22, 70]. The corrections of $\mathcal{O}(\Lambda _\mathrm{QCD}/m_{b,c})$ and $\mathcal{O}(\alpha _s)$ to the form factors can be found in [71]. Most phenomena of interest in this work are related to the ratios of squared decay amplitudes, where $V_{cb}$ is canceled and the influence from the uncertainties of form factors is mild. In order to fix the parameters in the $B\rightarrow M$ transition form factors, we adopt the parameter values of the form factors so that the BRs for $\bar{B} \rightarrow (D, D^*) \ell \bar{\nu }_{\ell }$ in the SM satisfy the experimental data within $1\sigma$ errors. With $V_{cb}=3.93\times 10^{-2}$ and the form factors in [22, 70], we get the BRs for $B^- \rightarrow D^{(*)} \ell \bar{\nu }_\ell$ in the SM as

$$\begin{aligned} BR(B^- \rightarrow D \ell \bar{\nu }_\ell )\approx & {} 2.26\, [2.16] \% ~~~\text {HQET [RQM]}, \nonumber \\ BR(B^- \rightarrow D^{*} \ell \bar{\nu }_\ell )\approx & {} 5.58\, [5.81] \% ~~~\text {HQET [RQM]}, \end{aligned}$$

(34)

where the experimental data are $BR^\mathrm{exp}(B^- \rightarrow D \ell \bar{\nu }_\ell )=(2.27 \pm 0.11)\%$ and $BR^\mathrm{exp}(B^- \rightarrow D^{*} \ell \bar{\nu }_\ell )=(5.69 \pm 0.19)\%$ [73]. For comparison, we also show the results using the form factors calculated in the framework of relativistic quark models (RQM) [72]. Using the same values of $V_{cb}$ and form factors, the BRs for $B^- \rightarrow (D, D^{*}) \tau \nu _{\tau }$ in the SM can be straightforwardly calculated to be

$$\begin{aligned} BR(B^- \rightarrow D \tau \bar{\nu }_\tau )\approx & {} 0.69\, [0.63]\% ~~~\text {HQET [RQM]}, \nonumber \\ BR(B^- \rightarrow D^{*} \tau \bar{\nu }_\tau )\approx & {} 1.43\, [1.42]\% ~~~\text {HQET [RQM]}, \end{aligned}$$

(35)

where the experimental values are $BR^\mathrm{exp}(B^- \rightarrow D \tau \bar{\nu }_\tau ) = (0.77 \pm 0.25)\%$ and $BR^\mathrm{exp}(B^- \rightarrow D^{*} \tau \bar{\nu }_\tau ) = (1.88 \pm 0.20)\%$ [73]. It can be seen that the $\tau \bar{\nu }_\tau$ measurements are somewhat larger than the theoretical estimations. The resulting ratios $R_D$ and $R_{D^*}$ and tau polarizations in the SM are given by

$$\begin{aligned} R_D&\approx 0.307,\, \quad R_{D^*} \approx 0.257, \end{aligned}$$

(36)

$$\begin{aligned} P^{\tau (\mu )}_D&\approx 0.324(-0.962), \quad P^{\tau (\mu )}_{D^*} \approx -0.513 (-0.986). \end{aligned}$$

(37)

The obtained values of $R_{D,D^*}$ are close to those values shown in [8,9,10]. We will use the form factors to estimate the $\tau$ polarizations and FBAs.

Fig. 2

The legend is the same as that in Fig. 1, and the upper limit of $BR(B_c \rightarrow \tau \bar{\nu }_\tau )< 30\%$ is included

In order to present the charged-Higgs influence on the ratios $R_{D,D^*}$, we adopt the formulas parametrized as [10]

$$\begin{aligned} R_D\approx & {} R^\mathrm{SM}_D \left[ 1+ 1.5 Re(C^\tau _R + C^\tau _L) +1.0 |C^\tau _R + C^\tau _L|^2 \right] ,\nonumber \\ \end{aligned}$$

(38)

$$\begin{aligned} R_{D^*}\approx & {} R^\mathrm{SM}_{D^*} \left[ 1+ 0.12 Re(C^\tau _R - C^\tau _L ) + 0.05 |C^\tau _R - C^\tau _L|^2 \right] .\nonumber \\ \end{aligned}$$

(39)

Accordingly, we show the contours for $R_D$ and $R_{D^*}$ as a function of $\chi ^{\ell }_{\tau \tau }$ and $\chi ^{u}_{ct}$ in Fig. 1(a) and of $\tan \beta$ and $\chi ^{u}_{ct}$ in Fig. 1(b), where we fix $\tan \beta =40$ and $\chi ^{\ell }_{\tau \tau } =4$ in the plots, respectively, and $m_{H^\pm }=400$ GeV in both plots is used. For clarity, we use two limits, $\chi ^{u}_{ct}=0$ and $\chi ^{\ell }_{\tau \tau }=0$, to concretely show their importance in the following discussions. With $\chi ^u_{ct}=0$, we obtain $R_{D^*} \sim 0.3$ when $\chi ^{\ell }_{\tau \tau } \sim 15$; however, the corresponding value of $R_D$ has been larger than 1. In such case, the values of $C^\tau _R$ and $C^\tau _L$ are: $C^\tau _R\sim 1.79 \gg C^\tau _L \sim 0$. Since $B^- \rightarrow D \tau \bar{\nu }_\tau$ is sensitive to $C^\tau _R + C^\tau _L$, when we require $R_{D^*} \sim 0.3$, it can be expected that $R_{D}$ will be significantly enhanced. With $\chi ^{\ell }_{\tau \tau }=0$, we obtain $R_D \sim 0.35$ with $\chi ^u_{ct}\sim 1$, but $R_{D^*} \sim 0.24$, where $C^\tau _{R, L}\sim (-0.13, 0.24)$, which disfavors the earlier conclusion with $C^\tau _{R}>0$ and $C^\tau _L < 0$. Based on these two limits, it is clear that neither $\chi ^{u}_{ct}$ nor $\chi ^\ell _{\tau \tau }$ can singly resolve the $R_D$ and $R_{D^*}$ anomalies at the same time. From Fig. 1(a), it can be seen that by properly adjusting both $\chi ^{u}_{ct}$ and $\chi ^\ell _{\tau \tau }$, the $R_D$ and $R_{D^*}$ excesses can be explained together.

In addition to the $B^-\rightarrow D^{(*)} \tau \bar{\nu }_\tau$ decay, the effective Hamiltonian in Eq. (11) also contributes to the $B_c \rightarrow \tau \bar{\nu }_\tau$ process [52, 53], where the allowed upper limit, which is obtained from the difference between the SM prediction and the experimental measurement in $B_c$ meson lifetime, is $BR(B_c^- \rightarrow \tau \bar{\nu }_\tau ) < 30 \%$ [53]. We express the BR for $B_c \rightarrow \tau \bar{\nu }_\tau$ as [53]

$$\begin{aligned} BR(B_c \rightarrow \tau \bar{\nu }_\tau )= & {} \tau _{B_c} \frac{m_{Bc} m^2_\tau f^2_{B_c} G_F^2 |V_{cb}|^2}{8 \pi } \left( 1 - \frac{m_\tau ^2}{m_{B_c}^2} \right) ^2\nonumber \\&\times \,\left| 1 + \frac{m^2_{B_c}}{m_\tau (m_b + m_c)} \epsilon _P \right| ^2, \end{aligned}$$

(40)

where $f_{B_c}$ is the $B_c$ decay constant, $\epsilon _{P}=C^\tau _R - C^\tau _L$, and the SM result is $BR^\mathrm{SM}(B_c \rightarrow \tau \bar{\nu }_\tau )\approx 2.2\%$. As pointed out by the authors in Refs. [52, 53], due to the enhancement factor $m^2_{B_c}/m_\tau (m_b +m_c) \sim 3.6$, the obtained upper limit on $BR(B_c\rightarrow \tau \bar{\nu }_\tau )$ will exclude most of the parameter space for $R_{D^*} > R^\mathrm{SM}_{D^*}$. In order to demonstrate the strict constraint, we show the contours for $BR(B_c\rightarrow \tau \bar{\nu }_\tau )$ and $R_{D^{(*)}}$ in Fig. 2, where the gray area is excluded by the upper limit of $BR(B_c^- \rightarrow \tau \bar{\nu }_\tau )$. It can be clearly seen that when the constraint from $B_c \rightarrow \tau \bar{\nu }_\tau$ is included, $R_{D}\sim 0.39$ is still allowed; however, $R_{D^*}$ becomes less than 0.28 when $\tan \beta =40$ is used. Since $R_{D^*}$ is limited by the $B_c \rightarrow \tau \bar{\nu }_\tau$ constraint, hereafter, we just show the range of $R_{D^*}=[0.25,0.27]$.

4.3 $\tau$ polarization and FBA

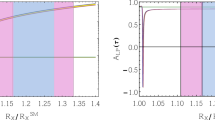
The Belle collaboration recently reported the measurement of $\tau$ polarization in the $\bar{B}\rightarrow D^* \tau \bar{\nu }_\tau$ decay. If the $R_D$ and $R_{D^*}$ excesses originate from the new physics, the $\tau$ polarization can also be influenced. To understand the charged-Higgs contributions, according to Eq. (31), we plot the contours for $P^\tau _{D}$ (dashed) and $P^\tau _{D^*}$ (solid) as a function of $\chi ^u_{ct}$ and $\chi ^\ell _{\tau \tau }$ with $\tan \beta =40$ in Fig. 3a, and the dependence of $\chi ^{u}_{ct}$ and $\tan \beta$ with $\chi ^{\ell }_{\tau \tau }=4$ is shown in Fig. 3b, where the bounded areas denote the ranges of $R_{D}=[0.31,0.39]$ (red) and $R_{D^*}=[0.25,0.27]$ (blue). From the numerical analysis, it can be seen that $P^\tau _{D}$ and $P^\tau _{D^*}$ are more sensitive to $\chi ^u_{ct}$ and $\chi ^{\ell }_{\tau \tau }$, and they can be enhanced from 0.3 to 0.5 and $\sim -0.5$ to $\sim -0.41$, respectively.

Fig. 3

Contours for $P^\tau _D$ (dashed) and $P^\tau _{D^*}$ (solid) as a function of $\chi ^{u}_{ct}$ and a $\chi ^{\ell }_{\tau \tau }$ with $\tan \beta =40$, b $\tan \beta$ with $\chi ^{\ell }_{\tau \tau }=4$, where we have fixed $m_{H^\pm }=400$ GeV. The bounded areas denote the ranges of $R_{D}=[0.31,0.39]$ (red) and $R_{D^*}=[0.25,0.27]$ (blue)

Fig. 4

The legend is the same as that in Fig. 3, but for FBA, defined in Eq. (41)

Finally, we show the numerical results for the FBA. Since the $\tau$ lepton FBAs have not yet been observed, to demonstrate the charged-Higgs contributions, we adopt the integrated FBAs, which are defined by

$$\begin{aligned} \bar{A}^{D,\tau }_{FB}= & {} - \frac{\int ^{(m_B -m_D)^2}_{m^2_\tau } dq^2 \left( 2 m^2_{\tau } \lambda _D \beta ^4_\tau F_1 X^{0\tau }_D \right) }{ \int ^{(m_B -m_D)^2}_{m^2_\tau } dq^2 \sqrt{\lambda _D } \beta ^4_\tau (H^+_D + H^-_D)}, \nonumber \\ \bar{A}^{D^*, \tau }_{FB}= & {} \frac{ \int ^{(m_B -m_{D^*})^2}_{m^2_\tau } dq^2 \sqrt{\lambda _{D^*} } \beta ^4_\tau \!\left( \!-2 m_\tau \frac{\sqrt{\lambda _{D^*}}}{\sqrt{q^2}} h^0_{D^*} X^{0\tau }_{D^*} \!+\!4 q^2 \sqrt{\lambda _{D^*}} A_1 V \!\right) }{\int ^{(m_B -m_{D^*})^2}_{m^2_\tau } dq^2 \sqrt{\lambda _{D^*} } \beta ^4_\tau \sum _{\lambda =L,\pm } (H^{\lambda , +}_{D^*} +H^{\lambda , -}_{D^*})}. \nonumber \\ \end{aligned}$$

(41)

The contours for $\bar{A}^{D,\tau }_{FB}$ and $\bar{A}^{D^*,\tau }_{FB}$ as a function of $\chi ^{u}_{ct}$ and $\chi ^{\ell }_{\tau \tau }$ with $\tan \beta =40$ are shown in Fig. 4a, whereas the contours with $\chi ^{\ell }_{\tau \tau }=4$ as a function of $\chi ^{u}_{ct}$ and $\tan \beta$ are given in Fig. 4b. From the plots, it can be seen that $\bar{A}^{D^*,\tau }_{FB}$ is more sensitive to the charged Higgs effects. The sign of $\bar{A}^{D^*,\tau }_{FB}$ in general can be changed in different parameter space; however, when the $BR(B_c\rightarrow \tau \bar{\nu }_\tau )$ constraint is included, its sign can be only positive. Moreover, the magnitude of $\bar{A}^{D^*,\tau }_{FB}$ is smaller than that of $\bar{A}^{D,\tau }_{FB}$. These behaviors can be understood from Eq. (41), in which the first and second terms in the numerator are opposite in sign and are from the $D^*$ longitudinal and transverse parts, respectively. Although the first term is proportional to $m_\ell$, when $m_\ell = m_\tau$, the contribution from the first becomes compatible with that of the second so that the sign can be flipped. The results with some chosen benchmarks of $(\chi ^u_{ct}, \chi ^\ell _{\ell \ell })$ are given in Table 1. For comparisons, we also show the values of $R_D$, $R_{D^*}$, $P^\tau _D$, and $P^\tau _{D^*}$ in the table.

Table 1 Values of integrated FBA, $R_{D(D^*)}$, and $P^\tau _{D(D^*)}$ with and without charged-Higgs effects in some chosen benchmarks of $(\chi ^u_{ct}, \chi ^\ell _{\ell \ell })$, where we have fixed $m_{H^\pm }=400$ GeV and $\tan \beta =40$

5 Summary

We studied the charged-Higgs $H^\pm$ effects on the $\bar{B} \rightarrow ( D, D^*) \ell \bar{\nu }_{\ell }$ decays in a generic two-Higgs-doublet model. In order to parametrize the new $H^\pm$ Yukawa couplings to the quarks and leptons, we employ the Cheng–Sher ansatz. Accordingly, the third-generation b-quark and $\tau$-lepton related processes are dominant and can then be enhanced using a scheme with large $\tan \beta$. Based on this study, it can be seen that two parameters ($\chi ^u_{ct}$ & $\chi ^\ell _{\tau \tau }$) are required to explain the $R_{D}$ and $R_{D^*}$ excesses. However, when the constraint from the $B_c \rightarrow \tau \bar{\nu }_\tau$ decay with $BR(B_c\rightarrow \tau \bar{\nu }_\tau ) < 30\%$ is applied, $R_{D}$ can be still significantly enhanced while $R_{D^*}$ can only have a slight change. The $\tau$ polarizations in the $\bar{B} \rightarrow (D, D^*) \tau \bar{\nu }_\tau$ decays were calculated, and it was found that they are sensitive to the $H^\pm$ effects. The integrated $\tau$-lepton forward–backward asymmetries were studied. We found that the asymmetry of $\bar{B} \rightarrow D^* \tau \bar{\nu }_\tau$ is more sensitive to the $H^\pm$ effects. Although the sign of $\bar{A}^{D^*,\tau }_{FB}$ can be reversed in some parameter space, when the constraint from $B_c\rightarrow \tau \bar{\nu }_\tau$ is included, the sign is only positive.

Appendix

In order to derive the charged lepton-helicity amplitudes in the $\bar{B}\rightarrow M \ell \bar{\nu }_\ell$ decay, we need the specific spinor states of a charged lepton and neutrino in the $q^2$ rest frame. Let $p=(E, \vec {p})$ be the four-momentum of a spin-1/2 particle, the solutions of the Dirac equation for positive and negative energy are expressed as

$$\begin{aligned} u_{\pm } (p)= & {} \frac{1}{\sqrt{E+m} } \left( \begin{array}{c} \sqrt{E+m} \chi _{\pm } ( \vec {p}) \\ \vec {\sigma }\cdot \vec {p} \chi _{\pm }(\vec {p}) \end{array} \right) , \nonumber \\ v_{\pm } (p)= & {} \frac{1}{\sqrt{E+m} } \left( \begin{array}{c} \vec {\sigma }\cdot \vec {p} \chi _{\mp }(\vec {p}) \\ \sqrt{E+m} \chi _{\mp } ( \vec {p}) \end{array} \right) , \end{aligned}$$

(42)

where the ± indices in $\chi$ are the eigenvalues of $\vec {\sigma }\cdot \vec {p} /|\vec {p}|$, and $+/-$ denote the left-/right-handed states, respectively. If the spatial momentum of a particle is taken as $\vec {p}= p(\sin \theta \cos \phi , \sin \theta \sin \phi , \cos \theta )$, the eigenstates of $\vec {\sigma } \cdot \vec {p}$ can be found to be

$$\begin{aligned} \chi _+ (\vec {p}) = \left( \begin{array}{c} \cos \frac{\theta }{2} \\ e^{i\phi } \sin \frac{\theta }{2}\end{array} \right) , \quad \chi _{-}(\vec {p})= \left( \begin{array}{c} \sin \frac{\theta }{2} \\ - e^{i\phi } \cos \frac{\theta }{2}\end{array} \right) . \end{aligned}$$

(43)

With the Pauli–Dirac representation of the $\gamma$-matrices, which are defined by

$$\begin{aligned} \gamma ^0 = \left( \begin{array}{cc} \mathbf{1} &{} 0 \\ 0 &{} -\mathbf{1} \end{array} \right) , \quad \gamma ^i = \left( \begin{array}{cc} 0 &{} \sigma ^i \\ -\sigma ^i &{} 0\end{array} \right) , \quad \gamma _5=\gamma ^5 = \left( \begin{array}{cc} 0 &{} \mathbf{1} \\ \mathbf{1} &{} 0 \end{array} \right) , \end{aligned}$$

(44)

we get $\bar{\ell }_{u_\pm } [...] (1-\gamma _5) \nu _{v_+} = 2 \bar{\ell }_{u_\pm } [...] \nu _{v_{+}}$ and $\bar{\ell }[...] (1-\gamma _5) \nu _{v_+}=0$ when $m_\nu =0$ is applied, in which $[...] =\{ 1, \gamma ^\mu , \sigma ^{\mu \nu } \}$.

For simplifying the derivations of $\bar{\ell }_{u_{\pm }} [...] (1-\gamma _5) \nu _{v_+}$, we define some useful polarization vectors:

$$\begin{aligned} |\vec {P}| \epsilon ^\mu _X&\equiv P^\mu - \frac{P\cdot q }{q^2} q^\mu , \quad \epsilon ^\mu _X \epsilon _{X \mu } =-1, \nonumber \\ \frac{E_{D^*}}{m_{D^*}} \epsilon ^\mu _Z&\equiv \epsilon ^\mu (L) - \frac{\epsilon \cdot q }{q^2} q^\mu , \quad \sqrt{\frac{\lambda _{D^*}}{2}} e^\mu _{D^*}(T) \equiv \varepsilon ^{\mu \nu \rho \sigma } \epsilon _\nu (T) P_\rho q_\sigma \end{aligned}$$

(45)

with $|\vec {P}|= \sqrt{\lambda _M}/\sqrt{q^2}$. According to the chosen coordinates in the $q^2$ rest frame, the leptonic current associated with a specific charged lepton helicity can be derived as follows: for the $B\rightarrow D$ case, we get

(46)

with $\beta _\ell = \sqrt{1 - m^2_\ell /q^2}$. For the $B\rightarrow D^*$ case, the $D^*$ longitudinal parts are obtained:

(47)

(48)

while the two $D^*$ transverse parts are, respectively, given by

(49)

(50)

The differential decay rates shown in Eq. (28) are functions of $q^2$ and $\theta _{\ell }$. After integrating out the polar angle, the differential decay rate with each lepton helicity as a function of $q^2$ can be obtained as follows: For the $\bar{B} \rightarrow D \ell \bar{\nu }_\ell$ decay, they can be shown:

$$\begin{aligned} \frac{d \Gamma ^{h=\pm }_{D}}{dq^2 }&= \frac{G^2_F |V_{cb}|^2 \sqrt{\lambda _D} \beta ^4_\ell }{256 \pi ^3 m^3_B} H^{\pm }_{D}, \end{aligned}$$

(51)

$$\begin{aligned} H^+_{D}&= \frac{2 m^2_\ell }{3 q^2 }\lambda _D F^2_1 + 2 m^2_\ell q^2 |X^0_D|^2, ~ H^-_{D} =\frac{4}{3} \lambda _D F^2_1 \,; \end{aligned}$$

(52)

and for the $\bar{B}\rightarrow D^* \ell \nu _\ell$ decay, they are expressed as

$$\begin{aligned}&\frac{d \Gamma ^{\lambda , h=\pm }_{D^*}}{dq^2 } = \frac{G^2_F |V_{cb}|^2 \sqrt{\lambda _{D^*}} \beta ^4_\ell }{256 \pi ^3 m^3_B} H^{\lambda , \pm }_{D^*}, \end{aligned}$$

(53)

$$\begin{aligned}&H^{L,+}_{D^*} = \frac{2 m^2_\ell }{3 } |h^0_{D^*}|^2 + \frac{2 m^2_\ell }{q^2} \lambda _{D^*} |X^0_{D^*}|^2, ~ H^{L,-}_{D^*} =\frac{4 q^2 }{3} |h^0_{D^*}|^2, \end{aligned}$$

(54)

$$\begin{aligned}&H^{T=\pm ,+}_{D^*} = \frac{2 m^2_\ell }{3 } |h^{\pm }_{D^*}|^2, \quad H^{T=\pm ,-}_{D^*} = \frac{4 q^2 }{3 } |h^{\pm }_{D^*}|^2. \end{aligned}$$

(55)