Kinetically modified non-minimal inflation with exponential frame function

Abstract

We consider supersymmetric (SUSY) and non-SUSY models of chaotic inflation based on the $\phi ^n$ potential with $n=2$ or 4. We show that the coexistence of an exponential non-minimal coupling to gravity $f_\mathcal{R}=\mathrm{e}^{c_\mathcal{R}\phi ^{p}}$ with a kinetic mixing of the form $f_{\mathrm{K}}=c_{\mathrm{K}}f_\mathcal{R}^m$ can accommodate inflationary observables favored by the Planck and Bicep2/Keck Array results for $p=1$ and 2, $1\le m\le 15$ and $2.6\times 10^{-3}\le r_{\mathcal {R}\mathrm{K}}=c_\mathcal{R}/c_{\mathrm{K}}^{p/2}\le 1,$ where the upper limit is not imposed for $p=1$. Inflation is of hilltop type and it can be attained for subplanckian inflaton values with the corresponding effective theories retaining the perturbative unitarity up to the Planck scale. The supergravity embedding of these models is achieved employing two chiral gauge singlet supefields, a monomial superpotential and several (semi)logarithmic or semi-polynomial Kähler potentials.

1 Introduction

In a recent paper [1, 2] we show that the consideration of a monomial potential of the type

$$\begin{aligned} V_{\mathrm{CI}}(\phi )=\lambda ^2\phi ^n/2^{n/2}, \end{aligned}$$

(1.1)

for the inflaton $\phi$ in conjunction with a non-minimal coupling function

$$\begin{aligned} f_\mathcal{R}(\phi )=1+c_\mathcal{R}\phi ^{n/2}, \end{aligned}$$

(1.2)

between $\phi$ and the Ricci scalar $\mathcal {R}$, and a non-minimal kinetic mixing of the form

$$\begin{aligned} f_{\mathrm{K}}(\phi )=c_{\mathrm{K}}f_\mathcal{R}^m, \end{aligned}$$

(1.3)

gives rise to a novel type of non-minimal (chaotic) inflation (nMI) [3,4,5,6,7,8,9,10,11,12,13,14,15,16] named kinetically modified. The inflationary observables of these models can become impressively compatible with the latest data [17, 18] provided that the parameter $r_{\mathcal {R}\mathrm{K}}=c_\mathcal{R}/c_{\mathrm{K}}^{n/4}$ is adjusted to natural values. Most notably, the resulting tensor-to-scalar ratio not only respects the upper bound imposed by Planck [17] but also can be confined in the $1\sigma$ margin of the Bicep2/Keck Array data [18]. Moreover, the corresponding effective theories are stable against corrections from higher order terms and unitarity safe up $r_{\mathcal {R}\mathrm{K}}\le 1$ and any n—cf. Ref. [19,20,21]. In short, the simple, predictive and well-motivated models based on $V_{\mathrm{CI}}$ of Eq. (1.1), which are by now observationally [17] excluded in their minimal form for $n\ge 2$, can be totally revitalized and probed in the near future [22] within our scheme at the cost of two more parameters (m and $r_{\mathcal {R}\mathrm{K}}$) for fixed n.

Trying to test the applicability of our proposal, we here continue developing SUSY and non-SUSY inflationary models relied on the same structure. Namely, we keep $V_{\mathrm{CI}}$ in Eq. (1.1) and the functional dependence of $f_{\mathrm{K}}$ on $f_\mathcal{R}$ in Eq. (1.3) whereas we replace the polynomial $f_\mathcal{R}$ in Eq. (1.2) with an exponential one introducing one more parameter p, i.e., we here adopt

$$\begin{aligned} f_\mathcal{R}(\phi )=\mathrm{e}^{c_\mathcal{R}\phi ^{p}}\quad \hbox {with }c_\mathcal{R}>0. \end{aligned}$$

(1.4)

More specifically, we present inflationary solutions employing $n=2$ and 4 in Eq. (1.1), $p=1$ and 2 in Eq. (1.4) and various m’s in Eq. (1.3). The emerging models are drastically different from the original ones in Ref. [1, 2]—see also Refs. [23,24,25]—since they support exclusively inflation of hilltop type [26]. However, they share similar observational and theoretical advantages with the initial ones.

Our scheme can be also incarnated in the context of Supergravity (SUGRA) by adopting two chiral superfields, a monomial superpotential, W, and various Kähler potentials, K, which may cooperate with it. In particular, we specify ten different K’s using two possible functional forms for the inflaton field and two possible stabilization methods [9,10,11,12, 27, 28] for the accompanying field. A common feature of all these K’s is the presence of a shift-symmetric term for taming [29,30,31,32,33,34,35,36,37,38] the well-known $\eta$ problem of inflation within SUGRA—such continuous symmetries appear naturally at tree-level due to the underlying discrete modular symmetries of the full string theory as pointed out in Ref. [39, 40]. The non-minimal gravitational coupling and kinetic mixing of the inflaton arise as violations of this shift symmetry—for similar attempts see Ref. [41,42,43].

The exponential frame function and kinetic mixing are used for the dilaton in the low-energy effective string theories—see Ref. [44, 45] where mostly negative $c_\mathcal{R}$’s are considered. The resulting potential has the form $\phi ^n\mathrm{e}^{-2c_\mathcal{R}\phi ^p}$ and resembles the one met in the models of logamediate inflation [46, 47]. However, the non-minimal kinetic mixing and gravitational coupling in Eqs. (1.3) and (1.4) make the canonically normalized inflaton in our case drastically different from $\phi$ and so, the inflationary dynamics is clearly distinguishable from those models. In the SUGRA framework only some subclasses of the set of models introduced here are investigated in Refs. [29, 30, 38]. Most notably, in Ref. [38] the cases with $n=1, 3/2, 2$, $m=1$ and $p=1,2$ are investigated adopting one of the K’s suggested here. The consideration of $n=4$ and $m>1$ together with the variety of K’s and the analysis of the small-field behavior of the models consist our main novelties in the present work.

Below we first, in Sect. 2, establish our setting in a non-SUSY framework and then, in Sect. 3, we outline its possible implementations in SUGRA. The resulting inflationary models are tested against observations in Sect. 4. Our conclusions are finally summarized in Sect. 5. Throughout the text, we use units where the reduced Planck scale $m_{\mathrm{P}}= 2.433\times 10^{18}~{\mathrm{GeV}}$ is set to be unity, the subscript of type , z denotes derivation with respect to (w.r.t.) the field z and charge conjugation is denoted by a star ($^*$).

2 Non-SUSY framework

According to its definition [1, 2], kinetically modified nMI is formulated in the Jordan frame (JF) where the action of $\phi$ is given by

$$\begin{aligned} \mathsf{S} = \int \mathrm{d}^4 x \sqrt{-\mathfrak {g}} \left( -\frac{1}{2}f_\mathcal{R}\mathcal {R}+\frac{1}{2}f_{\mathrm{K}}g^{\mu \nu } \partial _\mu \phi \partial _\nu \phi - V_{\mathrm{CI}}(\phi )\right) ,\nonumber \\ \end{aligned}$$

(2.1)

where the involved functions $V_{\mathrm{CI}},f_{\mathrm{K}}$ and $f_\mathcal{R}$ are defined in Eqs. (1.1), (1.3) and (1.4), respectively. Furthermore, $\mathfrak {g}$ is the determinant of the background Friedmann–Robertson–Walker metric $g^{\mu \nu }$ with signature $(+,-,-,-)$. The vacuum expectation value (v.e.v) of $\phi$ is $\langle {\phi } \rangle =0$, and the validity of ordinary Einstein gravity at low energies is guaranteed since $\langle {f_\mathcal{R}} \rangle =1$.

By performing a conformal transformation [3, 4, 7] according to which we define the Einstein frame (EF) metric $\widehat{ g}_{\mu \nu }=f_\mathcal{R}\,g_{\mu \nu }$ we can write $\mathsf{S}$ in the EF as follows:

$$\begin{aligned} \mathsf{S}= \int \mathrm{d}^4 x \sqrt{-\widehat{\mathfrak {g}}}\left( -\frac{1}{2} \widehat{\mathcal {R}}+\frac{1}{2}\widehat{ g}^{\mu \nu } \partial _\mu {\widehat{\phi }}\partial _\nu {\widehat{\phi }}-{\widehat{V}}_{\mathrm{CI}}({\widehat{\phi }})\right) , \nonumber \\ \end{aligned}$$

(2.2)

where hat is used to denote quantities defined in the EF. The EF canonically normalized field ${\widehat{\phi }}$ and potential ${\widehat{V}}_{\mathrm{CI}}$ are given as functions of the initial field, $\phi$, through the relations

$$\begin{aligned} \frac{\mathrm{d}{\widehat{\phi }}}{\mathrm{d}\phi }= & {} J=\sqrt{\frac{f_{\mathrm{K}}}{f_\mathcal{R}}+{3\over 2}\left( {f_\mathcal{R,\phi }\over f_\mathcal{R}}\right) ^2}\nonumber \\= & {} \sqrt{{c_{\mathrm{K}}\over f_\mathcal{R}^{1-m}}+\frac{3}{2}p^2c_\mathcal{R}^2\phi ^{2(p-1)}}\quad \hbox {and}\nonumber \\ {\widehat{V}}_{\mathrm{CI}}= & {} \frac{V_{\mathrm{CI}}}{f_\mathcal{R}^2}={\lambda ^2\phi ^n\over 2^{\frac{n}{2}} \mathrm{e}^{2c_\mathcal{R}\phi ^p}} \end{aligned}$$

(2.3)

where Eqs. (1.1) and (1.4) are considered. The resulting ${\widehat{V}}_{\mathrm{CI}}$ represents an almost Gaussian profile clearly distinguishable from its shape in the models of the pure [3, 4, 7, 8] or kinetically modified [1, 2, 23,24,25] nMI where an almost flat plateau emerges in EF—see Sect. 4.2 too. The parametrization of $f_{\mathrm{K}}$ in Eq. (1.3) assists us to simplify the derived J in Eq. (2.3). However, the variation of m allows us to scan a very wide range of the parametric space.

To determine transparently it, we perform a rescaling $\phi ={\tilde{\phi }}/\sqrt{c_{\mathrm{K}}}$. Then Eq. (2.1) preserves its form replacing $\phi$ with ${\tilde{\phi }}$ and $f_{\mathrm{K}}$ with $f_\mathcal{R}^m$ where $f_\mathcal{R}$ and ${\widehat{V}}_{\mathrm{CI}}$ take, respectively, the forms

$$\begin{aligned}&f_\mathcal{R}=\mathrm{e}^{r_{\mathcal {R}\mathrm{K}}{\tilde{\phi }}^{p}} \quad \hbox {and} \quad {\widehat{V}}_{\mathrm{CI}}=2^{-n/2}\lambda ^2f_\mathcal{R}^{-2}{\tilde{\phi }}^{n}c_{\mathrm{K}}^{n/2}\nonumber \\&\quad \hbox {with }r_{\mathcal {R}\mathrm{K}}=c_\mathcal{R}c_{\mathrm{K}}^{-p/2}. \end{aligned}$$

(2.4)

Therefore, we expect that our scenario depends only on $r_{\mathcal {R}\mathrm{K}}$ and $\lambda ^2/c_{\mathrm{K}}^{n/2}$ for fixed n, p and m.

3 Supergravity framework

The inflationary model introduced above (in the non-SUSY framework) can be also implemented in the context of SUGRA as established in Sect. 3.1 and verified in Sect. 3.2.

3.1 Possible embeddings

In Sect. 3.1.1 we outline the basics of the SUGRA regime. Then we specify a variety of logarithmic or semi-logarithmic—in Sect. 3.1.2—and semi-polynomial—in Sect. 3.1.3—K’s obeying a number of enhanced symmetries pointed out in Sect. 3.1.4.

3.1.1 The general set-up

The SUGRA versions of our model can be easily constructed if we use two gauge singlet chiral superfields, i.e., $z^{\alpha }=\Phi , S$, with $\Phi$ (${\alpha }=1$) and S (${\alpha }=2)$ being the inflaton and a “stabilizer” field, respectively. The EF action for $z^{\alpha }$’s within SUGRA [9,10,11,12] can be written as

$$\begin{aligned} \mathsf{S}=\int \mathrm{d}^4x \sqrt{-\widehat{ \mathfrak {g}}}\left( -\frac{1}{2}\widehat{\mathcal {R}}+K_{{\alpha }{\bar{\beta }}} \widehat{ g}^{\mu \nu }\partial _\mu z^{\alpha }\partial _\nu z^{*{\bar{\beta }}}-\widehat{V}\right) \nonumber \\ \end{aligned}$$

(3.1a)

where summation is taken over the scalar fields $z^{\alpha }$, denoted by the same superfield symbol, $K_{{\alpha }{\bar{\beta }}}=K_{,z^{\alpha }z^{*{\bar{\beta }}}}$ and $K^{{\alpha }{\bar{\beta }}}K_{{\bar{\beta }}\gamma }=\delta ^{\alpha }_{\gamma }$. Also $\widehat{V}$ is the EF F–term SUGRA potential given by

$$\begin{aligned}&\widehat{V}=\mathrm{e}^{K}\left( K^{{\alpha }{\bar{\beta }}}(D_{\alpha }W) (D^*_{\bar{\beta }}W^*)-3{\vert W\vert ^2}\right) \nonumber \\&\quad \hbox {with } D_{\alpha }W=W_{,z^{\alpha }} +K_{,z^{\alpha }}W. \end{aligned}$$

(3.1b)

Defining the inflationary trajectory by the constraints

$$\begin{aligned} S=\Phi -\Phi ^*=0, \quad \hbox {or} \quad s=\bar{s}=\theta =0 \end{aligned}$$

(3.2)

if we express $\Phi$ and S according to the parametrization

$$\begin{aligned} \Phi = {\phi | \mathrm{e}^{i \theta }}/{\sqrt{2}} \quad \hbox {and} \quad S=(s +i \bar{s})/\sqrt{2}, \end{aligned}$$

(3.3)

we can derive $V_\mathrm{CI}$ in Eq. (1.1), in the flat limit, by the superpotential

$$\begin{aligned} W=\lambda S\Phi ^{n/2}, \end{aligned}$$

(3.4)

since $V_{\mathrm{CI}}=|W_{,S}|^2$. The form of W can be uniquely determined if we impose an R symmetry, under which S and $\Phi$ have charges 1 and 0, and a global U(1) symmetry with assigned charges $-1$ and 2 / n for S and $\Phi$. The latter is violated though in the proposed K’s below. The same W is considered also in Ref. [38]. Here we focus on $n=2$ and 4, which are mainly encountered in concrete particle models. E.g., for $n=2$ this W is employed in the first paper in Refs. [13, 14] and for $n=4$ this W is adopted in Refs. [48, 49] and the last paper in Refs. [9,10,11,12].

On the other hand, ${\widehat{V}}_{\mathrm{CI}}$ in Eq. (2.3) can be derived from Eq. (3.1b) by conveniently choosing K. The consideration of S facilitates this aim, since only one term from $\widehat{V}$ survives along the path in Eq. (3.2), which reads

$$\begin{aligned} {\widehat{V}}_{\mathrm{CI}}=\widehat{V}(\theta =s=\bar{s}=0)=\mathrm{e}^{K}K^{SS^*}\, |W_{,S}|^2. \end{aligned}$$

(3.5)

The selected K’s should incorporate $f_\mathcal{R}$ in Eq. (1.4) and $f_{\mathrm{K}}$ in Eq. (1.3). To this end we introduce the functions

$$\begin{aligned}&F_\mathcal{R}(\Phi )=\exp F_{p}(\Phi ) \quad \hbox {with }F_{p}(\Phi )= 2^{p/2}c_\mathcal{R}\Phi ^{p}\ \hbox {and} \nonumber \\&\qquad F_{\mathrm{K}}=(\Phi -\Phi ^*)^2. \end{aligned}$$

(3.6a)

Here $F_\mathcal{R}$ is an holomorphic function reducing to $f_\mathcal{R}$, along the path in Eq. (3.2), and $F_{\mathrm{K}}$ is a real function which assists us to incorporate the non-canonical kinetic mixing generating by $f_{\mathrm{K}}$ in Eq. (1.3). Indeed, $F_{\mathrm{K}}$ lets intact ${\widehat{V}}_{\mathrm{CI}}$, since it vanishes along the trajectory in Eq. (3.2), but it contributes to the normalization of $\Phi$. For the same reason, terms of the form $k_\mathrm{KK}F_{\mathrm{K}}^2+k_{S\mathrm K}|S|^2F_{\mathrm{K}}$ are practically irrelevant in our analysis and are not included for simplicity in the expression of the K’s given below. We also include in K’s the typical kinetic term for S, in terms of the functions

$$\begin{aligned} F_{1S}=|S|^2-k_S{|S|^4} \quad \hbox {or} \quad F_{2S}=1+|S|^2/N_{S}, \end{aligned}$$

(3.6b)

where we consider the next-to-minimal term in $F_{1S}$ for stability reasons [9,10,11,12]. Alternatively, we can assume that S is a nilpotent superfield [50,51,52] and the second term in the definition of $F_{1S}$ can be avoided.

3.1.2 (Semi)logarithmic Kähler  potentials

The conventional embedding of a non-minimal coupling within SUGRA is realized [9,10,11,12] using a logarithmic K which includes it in its argument. Applying this recipe in our case we arrive at

$$\begin{aligned} K_1= & {} -3\ln ((F_\mathcal{R}+F_\mathcal{R}^*)/2-F_{1S}/3\nonumber \\&+\,c_{\mathrm{K}}(F_\mathcal{R}+F_\mathcal{R}^*)^mF_{\mathrm{K}}/6\cdot 2^m), \end{aligned}$$

(3.7a)

where we can easily recognize the similarities with the K’s introduced in Ref. [1, 2]. Using the reasoning of Ref. [25] and insisting on integer prefactors for the logarithms, to avoid any relevant tuning, we can enumerate six other semi-logarithmic K’s which yield identical results, i.e.,

$$\begin{aligned} K_2= & {} -3\ln ((F_\mathcal{R}+F_\mathcal{R}^*)/2 - F_{1S}/3)\nonumber \\&-\,c_{\mathrm{K}}(F_\mathcal{R}+F_\mathcal{R}^*)^{m-1}F_{\mathrm{K}}/2^m,\end{aligned}$$

(3.7b)

$$\begin{aligned} K_3= & {} -2\ln ((F_\mathcal{R}+F_\mathcal{R}^*)/2\nonumber \\&+c_{\mathrm{K}}(F_\mathcal{R}+F_\mathcal{R}^*)^mF_{\mathrm{K}}/2^{m+2})+F_{1S},\end{aligned}$$

(3.7c)

$$\begin{aligned} K_4= & {} -2\ln ((F_\mathcal{R}+F_\mathcal{R}^*))/2)\nonumber \\&-\,c_{\mathrm{K}}(F_\mathcal{R}+F_\mathcal{R}^*)^{m-1}F_{\mathrm{K}}/2^m+F_{1S},\end{aligned}$$

(3.7d)

$$\begin{aligned} K_5= & {} -2\ln ((F_\mathcal{R}+F_\mathcal{R}^*)/2\nonumber \\&+\,c_{\mathrm{K}}(F_\mathcal{R}+F_\mathcal{R}^*)^mF_{\mathrm{K}}/2^{m+2})+N_{S}\ln F_{2S},\end{aligned}$$

(3.7e)

$$\begin{aligned} K_6= & {} -2\ln ((F_\mathcal{R}+F_\mathcal{R}^*)/2)\nonumber \\&-\,c_{\mathrm{K}}(F_\mathcal{R}+F_\mathcal{R}^*)^{m-1}F_{\mathrm{K}}/2^m+N_{S}\ln F_{2S}, \end{aligned}$$

(3.7f)

$$\begin{aligned} K_7= & {} -2\ln (F_\mathcal{R}+F_\mathcal{R}^*)/2\nonumber \\&+\,N_{S}\ln (-c_{\mathrm{K}}(F_\mathcal{R}+F_\mathcal{R}^*)^{m-1}F_{\mathrm{K}}/2^mN_{S}+F_{2S}).\nonumber \\ \end{aligned}$$

(3.7g)

Namely, $K_2$ is constructed placing $F_{\mathrm{K}}$ outside the argument of the logarithm. If we do the same for $F_{1S}$ we can obtain two others K’s, $K_3$ and $K_4$. Moreover, if we employ $N_{S}\ln F_{2S}$ instead of $F_{1S}$ to stabilize S [27, 28], we can obtain $K_5$ and $K_6$ which have the form of $K_3$ and $K_4$ correspondingly. Furthermore, allowing the term including $F_{\mathrm{K}}$ to share the same logarithmic argument with $F_{2S}$ we can obtain $K=K_7$.

3.1.3 Semi-polynomial Kähler  potentials

Due to the exponential factor in Eq. (3.1b), ${\widehat{V}}_{\mathrm{CI}}$ in Eq. (2.3) can be obtained by semi-polynomial K’s too—in contrast to Ref. [1, 2] where only logarithmic K’s are suited. Indeed, we seek the following:

$$\begin{aligned} K_8=-F_{p}-F_{p}^*-c_{\mathrm{K}}(F_\mathcal{R}+F_\mathcal{R}^*)^{m-1}F_{\mathrm{K}}/2^m+F_{1S}.\nonumber \\ \end{aligned}$$

(3.8a)

For $m=c_{\mathrm{K}}=1$, $c_\mathcal{R}=b/\sqrt{2}$ [$c_\mathcal{R}=b^2/2$] and $p=1$ [$p=2$], $K_8$ recovers the K’s adopted in Ref. [38]—no higher order term in $F_{1S}$ is considered there. For the same m and $c_{\mathrm{K}}$, $c_\mathcal{R}=3\xi /2$ and $p=2$, $K_8$ also yields one of the K’s used in Ref. [29, 30] in conjunction with a generalized version of W in Eq. (3.4) for $n=2$. Employing the alternative kinetic terms for S we can construct two other K’s:

$$\begin{aligned} K_9= & {} -F_{p}-F_{p}^*-c_{\mathrm{K}}(F_\mathcal{R}+F_\mathcal{R}^*)^{m-1}F_{\mathrm{K}}/2^m\nonumber \\&+\,N_{S}\ln F_{2S}, \end{aligned}$$

(3.8b)

$$\begin{aligned} K_{10}= & {} -F_{p}-F_{p}^*\nonumber \\&+\,N_{S}\ln (-c_{\mathrm{K}}(F_\mathcal{R}+F_\mathcal{R}^*)^{m-1}F_{\mathrm{K}}/2^mN_{S}+F_{2S}),\nonumber \\ \end{aligned}$$

(3.8c)

where the structure of the terms beyond $F_{p}$ and $F_{p}^*$ is this adopted in Eqs. (3.7f) and (3.7g).

3.1.4 Enhanced symmetries

For $r_{\mathcal {R}\mathrm{K}}\ll 1$, our models are completely natural in the ’t Hooft sense because, in the limits $c_\mathcal{R}\rightarrow 0$ and $\lambda \rightarrow 0$, $K_i$ with $i=1,\ldots ,4$ and 8 enjoy the following enhanced symmetries:

$$\begin{aligned} \Phi \rightarrow \Phi ^*,\quad \Phi \rightarrow \Phi +c \quad \hbox {and} \quad S \rightarrow \mathrm{e}^{i\varphi } S, \end{aligned}$$

(3.9a)

where c and $\varphi$ are real numbers. In the same limit, $K_i$ with $i=5, 6, 7, 9$ and 10 enjoy even more interesting enhanced symmetries:

$$\begin{aligned} \Phi \rightarrow \Phi ^*,\quad \Phi \rightarrow \Phi +c \quad \hbox {and} \quad \frac{S}{\sqrt{N_{S}}}\rightarrow \frac{a S/\sqrt{N_{S}}+b}{-b^*S/\sqrt{N_{S}}+a^*}\nonumber \\ \end{aligned}$$

(3.9b)

with $|a|^2+|b|^2=1$. In other words, the theory exhibits a $SU(2)_S/U(1)$ enhanced symmetry for the above considered K’s. Thanks to the shift symmetry shown in Eqs. (3.9a) and (3.9b) the operation of $F_{\mathrm{K}}$ is suitably balanced as emphasized in Refs. [1, 2, 23,24,25]. On the one hand, its coefficient dominates $K_{\Phi \Phi ^*}$, but on the other hand, it does not influence ${\widehat{V}}_{\mathrm{CI}}$ letting its shape intact. On the contrary, $(F_\mathcal{R}+F_\mathcal{R}^{*})/2$ affects only ${\widehat{V}}_{\mathrm{CI}}$ without impact on $K_{\Phi \Phi ^*}$ (for $c_{\mathrm{K}}\gg c_\mathcal{R}$).

3.2 The inflaton and its potential

We verify below—see Sect. 3.2.1—that W and K’s proposed above reproduce ${\widehat{V}}_{\mathrm{CI}}$ in Eq. (2.3). In the region where our models are well defined for any p with $r_{\mathcal {R}\mathrm{K}}\le 1$—see Sect. 4.1.5—J in Eq. (2.3) is practically obtained too. Then, in Sect. 3.2.3, we estimate the SUGRA frame function and analyze, in Sect. 3.2.2, the stability of the inflationary path and the possibly arising radiative corrections.

3.2.1 Tree-level EF computation

Along the trough in Eq. (3.2), the matrix with elements $K_{{\alpha }{\bar{\beta }}}$ for the K’s in Eqs. (3.7a)–(3.8c) is diagonal with non-vanishing elements $K_{\Phi \Phi ^*}$ and $K_{SS^*}$. In particular, we obtain

$$\begin{aligned}&K_{\Phi \Phi ^*}\nonumber \\&={\left\{ \begin{array}{ll} J^2, &{}\hbox {for }K=K_i \hbox { with }i=1,2,\\ J^2-p^2c_\mathcal{R}^2\phi ^{2(p-1)}/2, &{}\hbox {for } K=K_i \hbox { with }i=3,\ldots ,7,\\ J^2-3p^2c_\mathcal{R}^2\phi ^{2(p-1)}/2, &{}\hbox {for }K=K_i \hbox { with }i=8,9,10, \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.10)

where J is given by Eq. (2.3). These differences in the normalization of ${\widehat{\phi }}$ in the two latter cases have negligible impact on the results during nMI for $r_{\mathcal {R}\mathrm{K}}\le 1$ and any i or $i=1,\ldots ,7$ and any $r_{\mathcal {R}\mathrm{K}}$. A crucial ramification is implied only to the domains where the corresponding effective theories preserve the perturbative unitarity up to $m_{\mathrm{P}}$ for $p=1$—see Sect. 4.1.5. Moreover, we get

$$\begin{aligned} K_{SS^*}= {\left\{ \begin{array}{ll} 1/f_\mathcal{R}\\ 1 \end{array}\right. } \quad \hbox {for } K= {\left\{ \begin{array}{ll} K_i&{}\hbox {with }i=1,2,\\ K_{i}&{}\hbox {with }i=3,\ldots ,10. \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.11)

Upon substitution of $K^{SS^*}=1/K_{SS^*}$ and

$$\begin{aligned} \mathrm{e}^K={\left\{ \begin{array}{ll} f_\mathcal{R}^{-3}\\ f_\mathcal{R}^{-2}\end{array}\right. } \quad \hbox {for }K={\left\{ \begin{array}{ll} K_i&{}\quad \hbox {with }i=1,2,\\ K_{i}&{}\quad \hbox {with }i=3,\ldots ,10 , \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.12)

into Eq. (3.5) we easily deduce that ${\widehat{V}}_{\mathrm{CI}}$ in Eq. (2.3) is recovered.

A reliable extraction of the inflationary observables requires the accurate determination of the canonically normalized inflaton. This is done inserting Eqs. (3.10) and (3.11) in the second term of the right-hand side (r.h.s.) of Eq. (3.1a), which is written as

$$\begin{aligned} K_{{\alpha }{\bar{\beta }}}{\dot{z}}^{\alpha }{\dot{z}}^{*{\bar{\beta }}}= & {} {K_{\Phi \Phi ^*}\over 2}\bigg ({\dot{\phi }}^2+\phi ^2{\dot{\theta }}^2 \bigg ) +\frac{K_{SS^*}}{2}\bigg (\dot{s}^2+\dot{\bar{s}}^2\bigg )\nonumber \\\simeq & {} \frac{1}{2}\bigg ({\dot{\widehat{\phi }}}^2+{\dot{\widehat{\theta }}}^{~2}+{\dot{\widehat{s}}}^2+{\dot{\widehat{\bar{s}}}}^{~2}\bigg ), \end{aligned}$$

(3.13a)

where the dot denotes derivation w.r.t. the cosmic time, t and the EF canonically normalized (hatted) fields can be expressed in terms of the initial (unhatted) ones via the relations

$$\begin{aligned} \frac{\mathrm{d}{\widehat{\phi }}}{\mathrm{d}\phi }=\sqrt{K_{\Phi \Phi ^*}},\quad \widehat{\theta } =\sqrt{K_{\Phi \Phi ^*}}\phi \theta \quad \hbox {and}\quad (\widehat{s},\widehat{\bar{s}})=\sqrt{K_{SS^*}}(s,\bar{s}).\nonumber \\ \end{aligned}$$

(3.13b)

The spinors $\psi _\Phi$ and $\psi _S$ associated with S and $\Phi$ are normalized similarly, i.e., $\widehat{\psi }_{S}=\sqrt{K_{SS^*}}\psi _{S}$ and $\widehat{\psi }_{\Phi }=\sqrt{K_{\Phi \Phi ^*}}\psi _{\Phi }$, from which we can derive the mass eigenstates $\widehat{\psi }_{\pm }\simeq (\widehat{\psi }_{S}\pm \widehat{\psi }_{\Phi })/\sqrt{2}$—see below.

3.2.2 Frame function

Limiting ourselves along the inflationary trajectory in Eq. (3.2) we can define the function $\Omega$ via the relation

$$\begin{aligned}&{\Omega /N}=-\mathrm{e}^{-K/N},\nonumber \\&\quad \hbox {where } N={\left\{ \begin{array}{ll} 3, &{}\hbox {for }K=K_i \hbox { with }i=1,2,\\ 2, &{}\hbox {for }K=K_i \hbox { with }i=3,\ldots ,10.\end{array}\right. }\qquad \qquad \end{aligned}$$

(3.14)

If we perform the inverse of the conformal transformation described in Eqs. (2.1) and (2.2) along the lines of Ref. [23] we end up with the JF potential $V_{\mathrm{CI}}=\Omega ^2{\widehat{V}}_{\mathrm{CI}}/N^2$ in Eq. (1.1) with the function $-\Omega /N=f_\mathcal{R}$ acting as a frame function. Moreover, the conventional Einstein gravity at the SUSY vacuum, $\langle {S} \rangle =\langle {\Phi } \rangle =0$, is recovered since $-\langle {\Omega } \rangle /N=1$.

3.2.3 Stability and one-loop radiative corrections

Contrary to the non-SUSY case where the inflaton appears uncoupled in Eq. (2.2), here it coexists obligatorily with other scalars and fermions which construct the two chiral supermultiplets—for possible ramifications of the non-SUSY nMI due to the presence of couplings between the inflaton with other fields see Ref. [13, 14]. Therefore, we have to verify that the inflationary direction in Eq. (3.2) is stable w.r.t. the fluctuations of the non-inflaton fields. To this end, we construct the mass spectrum of the scalars taking into account the canonical normalization of the various fields in Eq. (3.13a). In the limit $f_\mathcal{R}>1$, we find the expressions of the masses squared $\widehat{m}^2_{\chi ^{\alpha }}$ (with $\chi ^{\alpha }=\theta$ and s) arranged in Table 1. These results approach rather well the quite lengthy, exact expressions taken into account in our numerical computation and are valid for any $r_{\mathcal {R}\mathrm{K}}$. From these findings we can easily confirm that $\widehat{m}^2_{\chi ^{\alpha }}\gg {\widehat{H}}_{\mathrm{CI}}^2={\widehat{V}}_{\mathrm{CI}}/3$ during nMI provided that $k_S>1/6f_\mathcal{R}$ for $K=K_i$ with $i=1$ and 2 or $k_S>0.2$ for $K=K_i$ with $i=3,4$ and 8 or $0<N_{S}<6$ for $K=K_i$ with $i=5,6, 7, 9$ and 10. This means that the fields $\chi ^{\alpha }$ rapidly roll towards zero and stay there during nMI.

Table 1 Mass-squared spectrum for $K=K_i$ with $i=1,\ldots ,10$ along the inflationary trajectory in Eq. (3.2) for $\phi \ll 1$

Inserting the derived mass spectrum in the well-known Coleman–Weinberg formula [53], we can find the one-loop radiative corrections, $\Delta {\widehat{V}}_{\mathrm{CI}}$ to ${\widehat{V}}_{\mathrm{CI}}$. It can be verified that our results are immune from $\Delta {\widehat{V}}_{\mathrm{CI}}$, provided that the renormalization group mass scale $\Lambda$—involved in this formula—, is determined by requiring $\Delta {\widehat{V}}_{\mathrm{CI}}(\phi _\star )=0$ or $\Delta {\widehat{V}}_{\mathrm{CI}}(\phi _{\mathrm{f}})=0$. The possible dependence of our results on the choice of $\Lambda$ can be totally avoided if we confine ourselves to $k_S\sim (0.5-1.5)$ in $K_i$ with $i=1,\ldots ,4$ or $0<N_{S}<6$ in $K_i$ with $i=5,6$ and 7 resulting in $\Lambda \simeq (0.9-9)\times 10^{-5}$—cf. Refs. [13, 14, 23]. Under these circumstances, our results can be reproduced by using exclusively ${\widehat{V}}_{\mathrm{CI}}$ in Eq. (2.3).

4 Inflation analysis

A successful inflationary scenario has to be compatible with a number of criteria which are outlined in Sect. 4.1. We then test our models against these constraints, first numerically in Sect. 4.2 and then (semi)analytically in Sect. 4.3.

4.1 Inflationary constraints

The analysis of nMI can be carried out exclusively in the EF using the standard slow-roll approximation keeping in mind the dependence of $\widehat{\phi }$ on $\phi$—given by Eq. (2.3) in both the SUSY and non-SUSY set-up. Working this way, we outline in the following a number of observational and theoretical requirements which we impose in our investigation—see, e.g., Ref. [47, 54, 55].

4.1.1 Inflationary e-foldings

The number of e-foldings that the pivot scale $k_\star =0.05/\mathrm{Mpc}$ experiences during nMI, has to be enough to resolve the horizon and flatness problems of standard big bang cosmology, i.e., [7, 17]

$$\begin{aligned} {\widehat{N}_\star }= & {} \int _{{\widehat{\phi }}_\mathrm{f}}^{{\widehat{\phi }}_\star }\, \mathrm{d}{\widehat{\phi }}\, \frac{\widehat{V}_\mathrm{CI}}{\widehat{V}_\mathrm{CI,{\widehat{\phi }}}} \simeq 61.3+\frac{1}{2}\ln \left( {{\widehat{V}}_{\mathrm{CI}}(\phi _\star )\over {\widehat{V}}_{\mathrm{CI}}(\phi _{\mathrm{f}})^{1/2}}{f_\mathcal{R}(\phi _\star )\over g_\mathrm{rh*}^{1/6}}\right) \nonumber \\&+\, \frac{1-3w_\mathrm{rh}}{12(1+w_\mathrm{rh})}\ln \frac{\pi ^2g_\mathrm{rh*}T_{\mathrm{rh}}^4}{30{\widehat{V}}_{\mathrm{CI}}(\phi _{\mathrm{f}})f_\mathcal{R}(\phi _{\mathrm{f}})^2} \end{aligned}$$

(4.1)

where we assumed that nMI is followed in turn by an oscillatory phase, with mean equation-of-state parameter $w_\mathrm{rh}$ [56], radiation and matter domination. Also $T_{\mathrm{rh}}$ is the reheat temperature after nMI, with energy-density effective number of degrees of freedom $g_\mathrm{rh*}=106.75$, which corresponds to the Standard Model spectrum. Since, for low values of $\phi$, our inflationary potentials can be well approximated by a $\phi ^n$ potential we compute $w_\mathrm{rh}$ [54,55,56] from the formula

$$\begin{aligned} w_\mathrm{rh} = \frac{n-2}{n+2} \quad \Rightarrow \quad w_\mathrm{rh}={\left\{ \begin{array}{ll}0,&{}\hbox {for }n=2,\\ 1/3,&{}\hbox {for }n=4.\end{array}\right. } \end{aligned}$$

(4.2)

Note that, for $n=4$, ${\widehat{N}_\star }$ turns out to be independent of $T_{\mathrm{rh}}$—cf. Refs. [23, 25]. For $n=2$ we take $T_{\mathrm{rh}}=4.1\times 10^{-10}$. In Eq. (4.1) $\phi _\star ~[{\widehat{\phi }}_{\star }]$ is the value of $\phi ~[{\widehat{\phi }}]$ when $k_\star$ crosses outside the inflationary horizon, and $\phi _{\mathrm{f}}~[\widehat{\phi }_\mathrm{f}]$ is the value of $\phi ~[{\widehat{\phi }}]$ at the end of nMI, which can be found, in the slow-roll approximation, from the condition

$$\begin{aligned}&\mathsf{max}\{\widehat{\epsilon }({\widehat{\phi }}),|\widehat{\eta }({\widehat{\phi }})|\}\simeq 1,\quad \hbox {where } \widehat{\epsilon }=\frac{1}{2}\left( \frac{\widehat{V}_\mathrm{CI,{\widehat{\phi }}}}{\widehat{V}_\mathrm{CI}}\right) ^2 \hbox { and} \nonumber \\&\qquad \widehat{\eta }={\widehat{V}_\mathrm{CI,{\widehat{\phi }}{\widehat{\phi }}}\over \widehat{V}_\mathrm{CI}}. \end{aligned}$$

(4.3)

4.1.2 Normalization of the power spectrum

The amplitude $A_{\mathrm{s}}$ of the power spectrum of the curvature perturbation generated by $\phi$ at the pivot scale $k_\star$ to be consistent with data [57] must obey

$$\begin{aligned} \sqrt{A_\mathrm{s}}= & {} \frac{1}{2\sqrt{3}\, \pi } \; \frac{\widehat{V}_\mathrm{CI}({\widehat{\phi }}_{\star })^{3/2}}{|\widehat{V}_\mathrm{CI,{\widehat{\phi }}}({\widehat{\phi }}_{\star })|}\nonumber \\= & {} \frac{|J(\phi _\star )|}{2\sqrt{3}\, \pi } \; \frac{\widehat{V}_\mathrm{CI}(\phi _\star )^{3/2}}{|\widehat{V}_\mathrm{CI,\phi }(\phi _\star )|}\simeq 4.627\times 10^{-5}, \end{aligned}$$

(4.4)

where we assume that no other contributions to the observed curvature perturbation exists. This is ensured from the heaviness of the non-inflaton fields checked in Sect. 3.2.3.

4.1.3 Inflationary observables

The remaining inflationary observables (the spectral index $n_{\mathrm{s}}$, its running $a_{\mathrm{s}}$, and the tensor-to-scalar ratio r) must be in agreement with the fitting of the Planck, Baryon Acoustic Oscillations (BAO) and Bicep2/Keck Array data [17, 18] with $\Lambda$CDM$+r$ model, i.e.,

$$\begin{aligned} \mathsf{(a)}\ n_{\mathrm{s}}=0.968\pm 0.009 \quad \hbox {and} \quad \mathsf{(b)}\ r\le 0.07, \end{aligned}$$

(4.5)

at 95$\%$ confidence level (c.l.) with $|a_{\mathrm{s}}|\ll 0.01$. Although compatible with Eq. (4.5b) all data taken by the Bicep2/Keck Array CMB polarization experiments up to and including the 2014 observing season (BK14) [18] seem to favor r’s of order 0.01 since $r= 0.028^{+0.025}_{-0.025}$ at 68$\%$ c.l. has been reported. These inflationary observables are estimated through the relations:

$$\begin{aligned}&\mathsf{(a)}\quad n_{\mathrm{s}}=\, 1-6\widehat{\epsilon }_\star \ +\ 2\widehat{\eta }_\star ,\nonumber \\&\mathsf{(b)}\quad a_{\mathrm{s}}=\,\frac{2}{3}\left( 4\widehat{\eta }_\star ^2-(n_{\mathrm{s}}-1)^2\right) -2\widehat{\xi }_\star \nonumber \\&\hbox {and} \quad \mathsf{(c)} \quad r=16\widehat{\epsilon }_\star , \end{aligned}$$

(4.6)

where $\widehat{\xi }={\widehat{V}_\mathrm{CI,{\widehat{\phi }}} \widehat{V}_\mathrm{CI,{\widehat{\phi }}{\widehat{\phi }}{\widehat{\phi }}}/\widehat{V}_\mathrm{CI}^2}$ and the variables with subscript $\star$ are evaluated at $\phi =\phi _\star$. For a direct comparison of our findings with the observational outputs in Refs. [17, 18], we also compute $r_{0.002}=16\widehat{\epsilon }({\widehat{\phi }}_{0.002})$ where ${\widehat{\phi }}_{0.002}$ is the value of ${\widehat{\phi }}$ when the scale $k=0.002/\mathrm{Mpc}$, which undergoes $\widehat{N}_{0.002}={\widehat{N}_\star }+3.22$ e-foldings during nMI, crosses outside the horizon of nMI.

4.1.4 Tuning of the initial conditions

In all cases ${\widehat{V}}_{\mathrm{CI}}$ in Eq. (2.3) develops a local maximum

$$\begin{aligned}&{\widehat{V}}_{\mathrm{CI}}(\phi _\mathrm{max})=2^{-n(2+p)/2p}\lambda ^2 \left( \frac{epc_\mathcal{R}}{n}\right) ^{n/p} \nonumber \\&\quad \hbox {at }\phi _\mathrm{max}=\frac{1}{\sqrt{c_{\mathrm{K}}}}\left( \frac{n}{2pr_{\mathcal {R}\mathrm{K}}}\right) ^{1/p}, \end{aligned}$$

(4.7)

giving rise to a stage of hilltop [26] nMI. In a such case we are forced to assume that nMI occurs with $\phi$ rolling from the region of the maximum down to smaller values. Therefore, a mild tuning of the initial conditions is required which can be quantified defining [58,59,60,61] the quantity

$$\begin{aligned} \Delta _{\mathrm{max}} \star =\left( \phi _\mathrm{max} - \phi _\star \right) /\phi _\mathrm{max}. \end{aligned}$$

(4.8)

The naturalness of the attainment of nMI increases with $\Delta _{\mathrm{max}} \star$ and it is maximized when $\phi _\mathrm{max}\gg \phi _\star$ or $\Delta _{\mathrm{max}} \star \simeq 1$. This is facilitated as $r_{\mathcal {R}\mathrm{K}}$ and p decrease and n increases.

4.1.5 Effective field theory

Our inflationary scenario becomes stable against corrections of higher order non-renormalizable terms if we impose two additional theoretical constraints—keeping in mind that ${\widehat{V}}_{\mathrm{CI}}(\phi _{\mathrm{f}})\le {\widehat{V}}_{\mathrm{CI}}(\phi _\star )$:

$$\begin{aligned} \mathsf{(a)}\ {\widehat{V}}_{\mathrm{CI}}(\phi _\star )^{1/4}\le \Lambda _{\mathrm{UV}}\quad \hbox {and} \quad \mathsf{(b)}\ \phi _\star \le \Lambda _{\mathrm{UV}}, \end{aligned}$$

(4.9)

where $\Lambda _{\mathrm{UV}}$ is the ultraviolet (UV) cut-off scale. Below we show that, in the non-SUSY regime, $\Lambda _{\mathrm{UV}}=1$ (in units of $m_{\mathrm{P}}$) for $p=1$ and any $r_{\mathcal {R}\mathrm{K}}$ or $p>1$ and $r_{\mathcal {R}\mathrm{K}}\le 1$. As a consequence, no concerns regarding the validity of the effective theory arise although $c_{\mathrm{K}}$ (or $c_\mathcal{R}$) may take relatively large values for $\phi <1$—see Sects. 4.2 and 4.3. The origin of this nice behavior is the fact that the EF (canonically normalized) inflaton,

$$\begin{aligned}&\widehat{\delta {\phi }}=\langle {J} \rangle \delta {\phi }\quad \hbox {with }\delta {\phi }=\phi -\langle {\phi } \rangle ,\nonumber \\&\quad \hbox {and }\langle {J} \rangle ={\left\{ \begin{array}{ll} \sqrt{c_{\mathrm{K}}+3c_\mathcal{R}^2/2},&{}\hbox {for }p=1,\\ \sqrt{c_{\mathrm{K}}},&{}\hbox {for }p>1, \end{array}\right. } \end{aligned}$$

(4.10)

does not coincide with $\delta {\phi }$ at the vacuum of the theory—contrary to the pure nMI [19,20,21] with $n>2$—for $c_{\mathrm{K}}\gg 1$ and any p or even for $c_{\mathrm{K}}\ll 1, c_\mathcal{R}\gg 1$ and $p=1$.

To clarify further this point we analyze the small-field behavior of our models in the EF. We restrict ourselves to the (n, p)’s which support acceptable inflationary solutions, shown in Sect. 4.2. Although the expansions about $\langle {\phi } \rangle = 0$, presented below, are not valid during nMI, we consider $\Lambda _{\mathrm{UV}}$ extracted this way as the overall cut-off scale of the theory, since the reheating phase realized via oscillations about $\langle {\phi } \rangle =0$ is an unavoidable stage of the inflationary dynamics. Namely, we focus on the second term in the r.h.s. of Eq. (2.2) for $\mu =\nu =0$ and we expand it about $\langle {\phi } \rangle =0$ in terms of ${\widehat{\phi }}$. Our result can be written as

$$\begin{aligned} J^2 {\dot{\phi }}^2\simeq {\dot{{\widehat{\phi }}}}^2\cdot {\left\{ \begin{array}{ll} 1 + \dfrac{2 \sqrt{2}(m-1)r_{\mathcal {R}\mathrm{K}}{\widehat{\phi }}}{(2 + 3r_{\mathcal {R}\mathrm{K}}^2)^{3/2}} + \dfrac{2 (m-1)^2r_{\mathcal {R}\mathrm{K}}^2{\widehat{\phi }}^2}{(2 + 3r_{\mathcal {R}\mathrm{K}}^2)^2} + \dfrac{2 \sqrt{2} (m-1)^3r_{\mathcal {R}\mathrm{K}}^3{\widehat{\phi }}^3}{3 (2 + 3r_{\mathcal {R}\mathrm{K}}^2)^{5/2}},&{}\hbox {for } p=1 , \\ 1+(m-1)r_{\mathcal {R}\mathrm{K}}{\widehat{\phi }}^2 + (m-1)^2r_{\mathcal {R}\mathrm{K}}^2{\widehat{\phi }}^4/2,&{}\hbox {for } p=2. \end{array}\right. } \end{aligned}$$

(4.11a)

The form of the expansions above for $p=1$ can be specified in the two following regimes:

$$\begin{aligned} J^2 {\dot{\phi }}^2\simeq {\dot{{\widehat{\phi }}}}^2\cdot {\left\{ \begin{array}{ll} 1 +(m-1)r_{\mathcal {R}\mathrm{K}}{\widehat{\phi }}+ (m-1)^2r_{\mathcal {R}\mathrm{K}}^2{\widehat{\phi }}^2/2 + (m-1)^3r_{\mathcal {R}\mathrm{K}}^3{\widehat{\phi }}^3/6,&{}\hbox {for} \quad r_{\mathcal {R}\mathrm{K}}\ll 1\\ 1 +\dfrac{1}{r_{\mathcal {R}\mathrm{K}}^2}\left( \dfrac{2}{3}\sqrt{\dfrac{2}{3}} (m-1){\widehat{\phi }}- \dfrac{2}{9}(m-1)^2{\widehat{\phi }}^2 +\dfrac{2}{27}\sqrt{\dfrac{2}{3}}(m-1)^3{\widehat{\phi }}^3\right) ,&{}\quad \hbox {for } r_{\mathcal {R}\mathrm{K}}\gg 1. \end{array}\right. } \end{aligned}$$

(4.11b)

We remark that no $r_{\mathcal {R}\mathrm{K}}$ appears in the denominators for $r_{\mathcal {R}\mathrm{K}}\ll 1$ and no $r_{\mathcal {R}\mathrm{K}}$ appears in the nominators for $r_{\mathcal {R}\mathrm{K}}\gg 1$ and so $\Lambda _{\mathrm{UV}}=1$. Note also that as $r_{\mathcal {R}\mathrm{K}}$ approaches unity, $m-1$ must not exceed unity by a lot. We impose conservatively the global bound $m\le 15$—see Sect. 4.2.

Expanding similarly ${\widehat{V}}_{\mathrm{CI}}$, see Eq. (2.3), in terms of ${\widehat{\phi }}$ we have

$$\begin{aligned} {\widehat{V}}_{\mathrm{CI}}\simeq \frac{\lambda ^2{\widehat{\phi }}^n}{(2c_{\mathrm{K}})^{n/2}}\cdot {\left\{ \begin{array}{ll} 1 - 2r_{\mathcal {R}\mathrm{K}}{\widehat{\phi }}+ 2r_{\mathcal {R}\mathrm{K}}^2{\widehat{\phi }}^2 - 4r_{\mathcal {R}\mathrm{K}}^3{\widehat{\phi }}^3/3 + 2r_{\mathcal {R}\mathrm{K}}^4{\widehat{\phi }}^4/3,&{}\hbox {for }(n,p)=(2,1) ,\\ 1 - 2r_{\mathcal {R}\mathrm{K}}{\widehat{\phi }}^2 + 2r_{\mathcal {R}\mathrm{K}}^2{\widehat{\phi }}^4-4r_{\mathcal {R}\mathrm{K}}^6{\widehat{\phi }}^3/3,&{}\hbox {for }(n,p)=(2,2) ,\\ 1 - 2r_{\mathcal {R}\mathrm{K}}{\widehat{\phi }}+ 2r_{\mathcal {R}\mathrm{K}}^2{\widehat{\phi }}^2 - 4r_{\mathcal {R}\mathrm{K}}^3{\widehat{\phi }}^3/3 + (2r_{\mathcal {R}\mathrm{K}}^4{\widehat{\phi }}^4)/3,&{}\hbox {for }(n,p)=(4,1),\\ 1 - 2r_{\mathcal {R}\mathrm{K}}{\widehat{\phi }}^2 + 2r_{\mathcal {R}\mathrm{K}}^2{\widehat{\phi }}^4-4r_{\mathcal {R}\mathrm{K}}^6{\widehat{\phi }}^3/3,&{}\hbox {for }(n,p)=(4,2). \end{array}\right. } \end{aligned}$$

(4.11c)

For $p=2$ the expansions above are valid for any $r_{\mathcal {R}\mathrm{K}}$ whereas for $p=1$ these are convenient only for $r_{\mathcal {R}\mathrm{K}}\ll 1$. For $r_{\mathcal {R}\mathrm{K}}\gg 1$ and $p=1$, ${\widehat{V}}_{\mathrm{CI}}$ may be expanded as follows:

$$\begin{aligned} {\widehat{V}}_{\mathrm{CI}}\simeq \frac{2\lambda ^2{\widehat{\phi }}^n}{(2c_{\mathrm{K}})^{n/2}}\cdot {\left\{ \begin{array}{ll} (27 - 18 \sqrt{6}{\widehat{\phi }}+ 36{\widehat{\phi }}^2- 8 \sqrt{6}{\widehat{\phi }}^3+8{\widehat{\phi }}^4)/81 r_{\mathcal {R}\mathrm{K}}^2+\mathcal{O}(r_{\mathcal {R}\mathrm{K}}^{-4}),&{}\hbox {for }(n,p)=(2,1) , \\ 2(27 - 18 \sqrt{6}{\widehat{\phi }}+ 36{\widehat{\phi }}^2- 8 \sqrt{6}{\widehat{\phi }}^3)/243r_{\mathcal {R}\mathrm{K}}^4+\mathcal{O}(r_{\mathcal {R}\mathrm{K}}^{-5}),&{}\hbox {for }(n,p)=(4,1).\end{array}\right. } \end{aligned}$$

(4.11d)

We conclude again that $\Lambda _{\mathrm{UV}}=1$ independently from m for the ranges of p and $r_{\mathcal {R}\mathrm{K}}$ mentioned below Eq. (4.9)—note that the expressions above for $p=2$ can be easily extended to all $p>1$.

Taking into account Eq. (3.10) we infer that the results above are also valid for our SUGRA models with $p>1$, since $\langle {K_{\Phi \Phi ^*}} \rangle =\langle {J^2} \rangle$. When $p=1$, we obtain $\langle {K_{\Phi \Phi ^*}} \rangle =\langle {J^2} \rangle =c_{\mathrm{K}}+3c_\mathcal{R}/2$ for $K=K_i$ with $i=1,2$, $\langle {K_{\Phi \Phi ^*}} \rangle =c_{\mathrm{K}}+c_\mathcal{R}$ for $K=K_i$ with $i=3,\ldots ,7$ and $\langle {K_{\Phi \Phi ^*}} \rangle =c_{\mathrm{K}}$ for $K=K_i$ with $i=8,9,10$. Therefore, for $p=1$ and $i=1,2$, the expansions of $K_{\Phi \Phi ^*}\dot{\phi }^2$ and ${\widehat{V}}_{\mathrm{CI}}$ coincide with those given for $J^2\dot{\phi }^2$ and ${\widehat{V}}_{\mathrm{CI}}$ above. For $p=1$ and $i=3,\ldots ,7$, expansions similar to the ones obtained in the non-SUSY case can be extracted, leading to identical conclusions. On the contrary, for $p=1$ and $i=8,9,10$ the expansions for any $r_{\mathcal {R}\mathrm{K}}$ coincide with the expansions above for $r_{\mathcal {R}\mathrm{K}}\ll 1$. Therefore, in the last case, naturalness implies $r_{\mathcal {R}\mathrm{K}}\le 1$. In other words, for $p=1$ there is a theoretical discrimination between our SUGRA models based on the (semi)logarithmic and semi-polynomial K’s.

Our overall conclusion is that our models respect the perturbative unitarity up to $m_{\mathrm{P}}$ for $r_{\mathcal {R}\mathrm{K}}\le 1$ and $p>1$. For

$p=1$ the non-SUSY models and the SUGRA ones for $K=K_i$ with $i=1,\ldots ,7$ are unitarity safe up to $m_{\mathrm{P}}$ for any $r_{\mathcal {R}\mathrm{K}}$, whereas the SUGRA models relying on $K=K_i$ with $i=8,9,$ or 10 require still $r_{\mathcal {R}\mathrm{K}}\le 1$. On the other hand, m has to be of order unity for $r_{\mathcal {R}\mathrm{K}}$ approaching 1.

Fig. 1

Allowed curves in the $n_{\mathrm{s}}-r_{0.002}$ plane for a $n=2$, $p=1$ and $m=1, 3, 6,$ and 12, b $n=2$, $p=2$ and $m=5,7,10$ and 15, c $n=4$, $p=1$ and $m=2,3,5$ and 10, d $n=4$, $p=2$ and $m=3,4,6$ and 12 with the $r_{\mathcal {R}\mathrm{K}}$ values indicated on the curves. The conventions adopted for the various lines are shown in the plots. The marginalized joint $68\%$ [$95\%$] regions from Planck, BAO and BK14 data are depicted by the dark [light] shaded areas. The allowed $r_{\mathcal {R}\mathrm{K}}^\mathrm{min}$, $r_{\mathcal {R}\mathrm{K}}^\mathrm{max}$ and $r_{0.002}^\mathrm{min}$ values in each plot are listed in the table. The values in curly brackets correspond to the SUSY models with $K=K_i$ where $i=8,9$ and 10. In these cases the allowed curves are limited to values $r_{\mathcal {R}\mathrm{K}}\le 1$

4.2 Numerical results

The SUSY version of our models, which employs W in Eq. (3.4) and one of the K’s in Eqs. (3.7a)–(3.8c), is described by the following parameters:

$$\begin{aligned} \lambda ,\>n,\>p,\>m,\>c_\mathcal{R},\>c_{\mathrm{K}}\>\hbox {and}\>\>k_S\>\hbox {or}\>N_{S}, \end{aligned}$$

(4.12)

for the K’s given by Eqs. (3.7a)–(3.7d) and (3.8a) or Eqs. (3.7e)–(3.7g), (3.8b) and (3.8c), respectively. Obviously, the non-SUSY models do not depend on the two last parameters which control only $\widehat{m}_{s}^2$ in Table 1 and let intact the inflationary predictions provided that these are selected so that $\widehat{m}_{s}^2>{\widehat{H}}_{\mathrm{CI}}^2$. Recall that we use $T_{\mathrm{rh}}=4.1\times 10^{-9}$ throughout and ${\widehat{N}_\star }$ is computed self-consistently with n via Eqs. (4.2) and (4.1). Our result is ${\widehat{N}_\star }\simeq (50-52)$ for $n=2$ and ${\widehat{N}_\star }=(55-58)$ for $n=4$. Note finally that, for fixed n, p and m, J and ${\widehat{V}}_{\mathrm{CI}}$ in Eq. (2.3) are functions of $r_{\mathcal {R}\mathrm{K}}=c_\mathcal{R}/c_{\mathrm{K}}^{p/2}$ and $\lambda /c_{\mathrm{K}}^{n/4}$ and not $c_\mathcal{R}$, $c_{\mathrm{K}}$ and $\lambda$ as naively expected—see Sect. 2.

The confrontation of the parameters above with observations is implemented numerically substituting J and ${\widehat{V}}_{\mathrm{CI}}$ in Eqs. (4.1), (4.3), and (4.4), and extracting the inflationary observables as functions of $n, p, m, r_{\mathcal {R}\mathrm{K}}, \lambda /c_{\mathrm{K}}^{n/4}$ and $\phi _\star$. The two latter parameters can be determined by fulfilling Eqs. (4.1) and (4.4). We then compute the predictions of the models applying Eq. (4.6) for every selected n, p, m and $r_{\mathcal {R}\mathrm{K}}$, taking into account the available data in Eq. (4.5). From Eqs. (2.3) and (3.10) we see that the obtained results are precisely valid for the non-SUSY models and the SUSY ones for $K=K_i$ with $i=1,2$. However, as emphasized in Sect. 3.2, these are practically identical for any i and the $r_{\mathcal {R}\mathrm{K}}$’s which ensure the validity of the corresponding effective theories up to $m_{\mathrm{P}}$—see Sect. 4.1.5.

We start the presentation of our results by comparing the outputs of our models against the observational data [17, 18] in the $n_{\mathrm{s}}-r_{0.002}$ plane—see Fig. 1. We depict the theoretically allowed values for (i) $(n,p)=(2,1)$ and $m=1,3,6$ and 12 in Fig. 1a, (ii) $(n,p)=(2,2)$ and $m=5,7,10$ and 15 in Fig. 1b, (iii) $(n,p)=(4,1)$ and $m=2,3,5$ and 10 in Fig. 1c, and (iv) $(n,p)=(4,2)$ and $m=3,4,6$ and 12 in Fig. 1d. The conventions adopted for the various lines are shown in the plots and the variation of $r_{\mathcal {R}\mathrm{K}}$ is shown along each of them. In particular, we use double dot-dashed, dashed, solid and dot-dashed lines for each (n, p) with increasing m. For $m=1$ we confirm the findings of Ref. [38] according to which the lines move to the left increasing n with fixed p. Indeed, for $n=2$ and $p=m=1$ the double dot-dashed curve lies inside the observationally favored (light gray) region as seen from Fig. 1a. For $n=4$ and $p=m=1$, however, the corresponding line lies entirely outside (and to the left of) the allowed region. For this reason we plot the line with $m=2$, which displays an observationally acceptable segment as shown in Fig. 1c. On the contrary, the lines with the same p and $m>1$ have the tendency to move to the right for increasing n, as can be inferred comparing the position of the dashed lines in Fig. 1a, c. This fact indicates that the kinetic mixing introduced in Eq. (1.3) plays a key role for the observational viability of the models.

In all plots of Fig. 1, we observe that for low enough $r_{\mathcal {R}\mathrm{K}}$—i.e. $r_{\mathcal {R}\mathrm{K}}\le 0.0001$—the various lines converge to the $(n_{\mathrm{s}},r_{0.002})$’s obtained within the minimal chaotic inflation defined for $c_\mathcal{R}=0$, i.e., $(n_{\mathrm{s}},r_{0.002})\simeq (0.962,0.14)$ in Fig. 1a, b and $(n_{\mathrm{s}},r_{0.002})\simeq (0.949,0.25)$ (not shown in the plots) in Fig. 1c, d. Increasing $r_{\mathcal {R}\mathrm{K}}$ we can determine a minimal $r_{\mathcal {R}\mathrm{K}}$, $r_{\mathcal {R}\mathrm{K}}^\mathrm{min}$, for which the various lines enter the $95\%$ c.l. observationally allowed region. For $r_{\mathcal {R}\mathrm{K}}>r_{\mathcal {R}\mathrm{K}}^\mathrm{min}$ the various lines cover the marginalized joint $95\%$ c.l. regions, turn to the left and mostly cross outside them. On each line we can also define a maximal $r_{\mathcal {R}\mathrm{K}}$, $r_{\mathcal {R}\mathrm{K}}^\mathrm{max}$, which obviously correspond to a minimal $r_{0.002}$, $r_{0.002}^\mathrm{min}$. We have $r_{\mathcal {R}\mathrm{K}}^\mathrm{max}=1$, if the theory ceases to be unitarity safe beyond this value, as for $(n, p, m)=(2,2,15)$ and (4, 2, 12). Otherwise, $r_{\mathcal {R}\mathrm{K}}^\mathrm{max}$ is the $r_{\mathcal {R}\mathrm{K}}$ value for which the corresponding lines cross outside the $95\%$ c.l. observationally allowed corridors. More specifically, the $r_{\mathcal {R}\mathrm{K}}^\mathrm{min}$, $r_{\mathcal {R}\mathrm{K}}^\mathrm{max}$ and $r_{0.002}^\mathrm{min}$ values for each line are accumulated in the table shown below the plots. Note that, if we employ $K=K_i$ with $i=8,9$ or 10 for the SUSY implementation of our models, the dot-dashed line in Fig. 1a and the solid and dot-dashed lines in Fig. 1c have to be terminated at $r_{\mathcal {R}\mathrm{K}}^\mathrm{max}=1$ and the relevant $r_{\mathcal {R}\mathrm{K}}^\mathrm{max}$ and $r_{0.002}^\mathrm{min}$ values are displayed in curly brackets.

Fig. 2

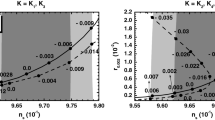
Allowed (lightly gray and gray shaded) regions in the $m-r_{\mathcal {R}\mathrm{K}}$ plane for a $(n, p)=(2, 1)$, b $(n, p)=(2, 2)$, c $(n, p)=(4, 1)$ and d $(n, p)=(4, 2)$. For $p=1$ the allowed regions in the panels a and b are extended to the whole lined region for the non-SUSY models and the SUGRA ones employing $K=K_i$ with $i=1,\ldots ,7$. The conventions adopted for the various lines are also shown. The allowed ranges of m, $r_{\mathcal {R}\mathrm{K}}$, r and $\Delta _{\mathrm{max}} \star$ along the thick solid lines in the plots are listed in the table. The limiting values obtained imposing $r_{\mathcal {R}\mathrm{K}}\le 1$ for $p=1$ are indicated in curly brackets

Enforcing the constraints of Sect. 4.1 we delineate in Fig. 2a–d the allowed regions of our models for $(n,p)=(2,1), (2,2), (4,1)$ and (4, 2), respectively, by varying continuously $r_{\mathcal {R}\mathrm{K}}$ and m. The conventions adopted for the various lines are also shown in each plot. In particular, the dashed line originates from the restriction $r_{\mathcal {R}\mathrm{K}}\le 1$, and the dot-dashed and thin lines come from the lower and upper bounds on $n_{\mathrm{s}}$ and r, respectively—see Eq. (4.5). The lined regions in Fig. 2a, b are allowed in the non-SUSY regime and in the SUSY one for $K=K_i$ with $i=1,\ldots ,7$ since in this case $r_{\mathcal {R}\mathrm{K}}$ is unbounded as shown in Sect. 4.1.5. If we use, though, the $K_i$’s with $i=8,9$ and 10 then only the lightly gray shaded regions are allowed. In Fig. 2c, d where $p=2$ the upper bound on $r_{\mathcal {R}\mathrm{K}}$ is applied in both cases and so the gray shaded regions are allowed. Fixing $n_{\mathrm{s}}$ to its central value in Eq. (4.5) we obtain the thick solid lines along which the various parameters of the models range as shown in the table displayed below the relevant plots. Let us clarify that the maximal r and $\Delta _{\mathrm{max}} \star$ values corresponds to the minimal $r_{\mathcal {R}\mathrm{K}}$ occurring at the intersection point of the thick and thin solid lines whereas the minimal r and $\Delta _{\mathrm{max}} \star$ values corresponding to the maximal $r_{\mathcal {R}\mathrm{K}}$ are localized at the junction of the thick solid line either with the dashed line, if the constraint $r_{\mathcal {R}\mathrm{K}}\le 1$ is applied, or with the right vertical axis at the maximal m set by hand—see Sect. 4.1.5.

Fig. 3

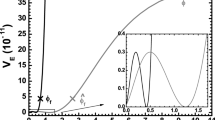
The inflationary potential ${\widehat{V}}_{\mathrm{CI}}$ as a function of $\phi$ for $\phi >0$ and $(n,p,m, r_{\mathcal {R}\mathrm{K}})=(2,1,6,0.04)$ (gray line), $(n,p,m, r_{\mathcal {R}\mathrm{K}})=(2,2,12,0.005)$ (dark gray line), $(n,p,m, r_{\mathcal {R}\mathrm{K}})=(4,1,3, 0.15)$ (black line), or $(n,p,m, r_{\mathcal {R}\mathrm{K}})=(4,2,6, 0.01)$ (light gray line). The values of $\phi _\star =1$, $\phi _{\mathrm{f}}$ and $\phi _\mathrm{max}$ are also indicated in each case and listed together with the corresponding inflationary observables in the table

From our findings in the figures above we infer that as p increases the allowed regions have considerably shrunk regardless of the range of the validity of the effective theory. Indeed, from Fig. 1 we see that the curves in Fig. 1b, d, where $p=2$, move to the left w.r.t. their position in Fig. 1a, c, where $p=1$, and the required m’s increase. This fact can be understood by Eq. (4.7) where we see that increasing p, $\phi _{\mathrm{max}}$ (and $\Delta _{\mathrm{max}} \star$) decreases sharply (due to the relevant exponent) reducing, thereby, the viable space of successful nMI. From the same formula we infer that $\phi _{\mathrm{max}}$ decreases also as $r_{\mathcal {R}\mathrm{K}}$ increases for fixed m and p. This is the origin of the turn to the left of the various lines in Fig. 1. Similar behavior is observed in Fig. 1-(b) of Ref. [25] for $n>0$ (in the notation of that reference) where hilltop solutions are exhibited too. Contrary to that set-up, though, hilltop nMI is solely attained here. The relevant parameter $\Delta _{\mathrm{max}} \star$, for central $n_{\mathrm{s}}$, can be as large as $75\%$ and remains larger than $18\%$ for $r_{\mathcal {R}\mathrm{K}}\ge 1$. That is, the required tuning is not severe. Actually, this is milder than the one obtained within the models of F-term hybrid inflation [58,59,60,61] where $\Delta _{\mathrm{max}} \star \le 0.3$. The hilltop solutions are extensively utilized there for reducing $n_{\mathrm{s}}$ in the range of Eq. (4.5). Moreover, our models are testable by the forthcoming experiments [22] searching for primordial gravity waves since $r\gtrsim 0.0059$ for $r_{\mathcal {R}\mathrm{K}}\ge 1$ and $r\gtrsim 6\times 10^{-4}$ without the latter restriction. In summary, $a_{\mathrm{s}}$ is confined in the range $-(5$–$6)\times 10^{-4}$ and so, consistency with the fitting of data with the $\Lambda$CDM+r model [17] is certainly maintained.

We complete our numerical analysis by studying the structure of ${\widehat{V}}_{\mathrm{CI}}$ as a function of $\phi$. This is visualized in Fig. 3, where we depict ${\widehat{V}}_{\mathrm{CI}}$ (gray, dark gray, black and light gray line) versus $\phi$ for $\phi _\star =1$ and $(n,p,m,r_{\mathcal {R}\mathrm{K}})=(2,1,6,0.04)$, $(2,2,15,5\times 10^{-3})$, (4, 1, 3, 0.15) and (4, 2, 6, 0.01), respectively, resulting in $n_{\mathrm{s}}=0.968$. The extracted values of the relevant parameters and observables are accommodated in the table below the plot and compared with our semi-analytical estimates in Sect. 4.3.2. As anticipated in Sect. 2, and contrary to the picture in Refs. [1, 2, 23,24,25]—cf. Fig. 2 of Refs. [23, 25]—, ${\widehat{V}}_{\mathrm{CI}}$ possesses a clear maximum, which does not upset, though, the realization of nMI since $\phi _{\mathrm{max}}\gg {\widehat{\phi }}_{\star }$ with $\Delta _{\mathrm{max}} \star \ge 0.3$. The relatively high r values encountered here are associated with ${\widehat{\phi }}_{\star }\gg 1$ in accordance with the Lyth bound [62,63,64]. However, this fact does not invalidate our scenario, from the point of view of the effective theory, since $\phi _\star =1$ saturating Eq. (4.9b). This is accomplished selecting conveniently $c_{\mathrm{K}}$ as explained in Sect. 4.3. Actually, the $c_{\mathrm{K}}$’s shown in the table of Fig. 3 coincide with the lowest possible $c_{\mathrm{K}}$’s since we employ the maximal possible $\phi _\star$, $\phi _\star =1$.

Note, finally, that no attractor is pinned down in our setting (even for $c_\mathcal{R}\gg c_{\mathrm{K}}$) and no acceptable inflationary solutions are detected for $m=0$ in contrast to the findings of Refs. [1, 2, 23]. As opposed to the situation in Refs. [1, 2, 24, 25] also, the $m=1$ case, which simplifies the $K_i$’s with $i=2,4,6,7,8,9$ and 10 is rather limited here—see Fig. 2.

4.3 (Semi)analytical results

With our numerical solutions in hand, we can now derive some (semi)analytic expressions which allow us to obtain a satisfactory understanding of our numerics. We focus on the solutions with $r_{\mathcal {R}\mathrm{K}}\ll 1$, of which consist the bulk of our findings, which are more natural in the sense of the discussion in Sect. 3.1.4 and ensure r’s of order 0.01, consistently with the $95\%$ c.l. region of BK14 data—see Sect. 4.1.3. Under this basic assumption, J is well approximated by

$$\begin{aligned} J\simeq \sqrt{{c_{\mathrm{K}}}{f_\mathcal{R}^{m-1}}}. \end{aligned}$$

(4.13)

Obviously, J is n independent and for $m=1$ it becomes $\phi$ independent too, leading, thereby, to exceptionally simple analytic results—see below. Employing Eq. (4.13) the slow-roll parameters in Eq. (4.3) can be calculated for any m as follows:

$$\begin{aligned} \widehat{\epsilon }=\frac{( n - 2pc_\mathcal{R}\phi ^p)^2}{2c_{\mathrm{K}}\phi ^2f_\mathcal{R}^{m-1}}\quad \hbox {and}\quad \widehat{\eta }=\frac{2 n^2 - n (2 +(7 + m)pc_\mathcal{R}\phi ^p)+2pc_\mathcal{R}\phi ^p (2 +p(c_\mathcal{R}(3 + m)\phi ^p-2))}{2c_{\mathrm{K}}\phi ^2f_\mathcal{R}^{m-1}}. \end{aligned}$$

(4.14)

Expanding $\widehat{\epsilon }$ and $\widehat{\eta }$ for $\phi \ll 1$ we can convince ourselves that $\phi _{\mathrm{f}}\ll \phi _\star$. Indeed, Eq. (4.3) is saturated at the maximal $\phi$ value, $\phi _{\mathrm{f}}$, from the following two values:

$$\begin{aligned} \phi _{1\mathrm f}\simeq {\left\{ \begin{array}{ll} n\bigg ( D_1+ \sqrt{8 + D_1^2}\bigg )/4\sqrt{c_{\mathrm{K}}},&{}\hbox {for } p=1,\\ n/\sqrt{c_{\mathrm{K}}}\sqrt{2 + Dr_{\mathcal {R}\mathrm{K}}},&{}\hbox {for } p=2, \end{array}\right. } \end{aligned}$$

(4.15a)

with $D_1=(n(1-m)-4)r_{\mathcal {R}\mathrm{K}}$, $D=n (8 + (m-1) n)$ and

$$\begin{aligned} \phi _{2\mathrm f}\simeq {\left\{ \begin{array}{ll} \bigg ( n D_2 + \sqrt{n}\sqrt{16 (n-1) + n D_2^2}\bigg )/4 \sqrt{c_{\mathrm{K}}},&{}\hbox {for } p=1,\\ \sqrt{n(n-1)}/\sqrt{c_{\mathrm{K}}}\sqrt{1 +(4+ D)r_{\mathcal {R}\mathrm{K}}},&{}\hbox {for } p=2,\end{array}\right. }\nonumber \\ \end{aligned}$$

(4.15b)

with $D_2=(m-9+2n(1-m))r_{\mathcal {R}\mathrm{K}}$. Here $\phi _{1\mathrm f}$ and $\phi _{2\mathrm f}$ are such that $\widehat{\epsilon }(\phi _{1\mathrm f})\simeq 1$ and $\widehat{\eta }(\phi _{2\mathrm f})\simeq 1$.

Moreover, Eq. (4.4) is written as

$$\begin{aligned} \sqrt{A_{\mathrm{s}}}=\frac{\lambda f_\mathcal{R}(\phi _\star )^{(m-3)/2}\sqrt{c_{\mathrm{K}}}\phi _\star ^{1 + n/2}}{2^{1+{n\over 4}}\sqrt{3}\pi (n-2pc_\mathcal{R}\phi _\star ^p)}. \end{aligned}$$

(4.16)

Finally, ${\widehat{N}_\star }$ can be computed from Eq. (4.1) as follows:

$$\begin{aligned} {\widehat{N}_\star }\simeq \int _{\phi _{\mathrm{f}}}^{\phi _\star }\mathrm{d}\phi \,\frac{c_{\mathrm{K}}\phi \mathrm{e}^{(m-1)c_\mathcal{R}\phi ^p}}{n - 2pc_\mathcal{R}\phi ^p}. \end{aligned}$$

(4.17)

Table 2 Comparison between the numerical and analytic results for $p=m=\phi _\star =1$ and two different sets of input and output parameters of our model

The implementation of the integration obliges us to single out two cases, one for $m=1$ studied in Sect. 4.3.1 and one for $m\ne 1$ investigated in Sect. 4.3.2.

4.3.1 Analytic results for $p=m=1$

As shown in Fig. 2, there is a tiny slice of the allowed parameter space where $p=m=1$ for both $n=2$ and 4. In this case J becomes $\phi$ independent and ${\widehat{\phi }}$ is related to $\phi$ by the simple expression ${\widehat{\phi }}=\sqrt{c_{\mathrm{K}}}\phi$. Moreover, the integration of Eq. (4.17) gets simplified with the result

$$\begin{aligned} {\widehat{N}_\star }=\int _{\phi _{\mathrm{f}}}^{\phi _\star }\frac{\mathrm{d}\phi \, c_{\mathrm{K}}\phi }{n - 2 c_\mathcal{R}\phi }\simeq \frac{c_{\mathrm{K}}}{2c_\mathcal{R}}\left( \frac{n}{2c_\mathcal{R}}\ln \frac{n}{n - 2c_\mathcal{R}\phi _\star }-\phi _\star \right) ,\nonumber \\ \end{aligned}$$

(4.18)

where we take into account that $\phi _\star \gg \phi _{\mathrm{f}}$. Equation (4.18) can be solved w.r.t. $\phi _\star$ yielding

$$\begin{aligned} \phi _\star \simeq n(1+W_0(y_\star ))/{2c_\mathcal{R}}\quad \hbox {with }y_\star =-\mathrm{e}^{-(1+4r_{\mathcal {R}\mathrm{K}}^2{\widehat{N}_\star }/n)}.\nonumber \\ \end{aligned}$$

(4.19)

Here $W_0$ is the Lambert W or product logarithmic function [65]. Obviously there is a lower bound on $c_{\mathrm{K}}$ for every $r_{\mathcal {R}\mathrm{K}}$ above which Eq. (4.9b) is fulfilled. Indeed, from Eq. (4.19) we have

$$\begin{aligned} \phi _\star \le 1\ \Rightarrow \ c_{\mathrm{K}}\ge n^2(1+W_0(y_\star ))^2/{4r_{\mathcal {R}\mathrm{K}}^2} \end{aligned}$$

(4.20)

and so, our proposal can be stabilized against corrections from higher order terms, despite the fact that ${\widehat{\phi }}_{\star }\gg 1$. From Eq. (4.16) we can also derive a constraint on $\lambda /c_{\mathrm{K}}^{n/4}$, i.e.,

$$\begin{aligned} \lambda= & {} -2^{2 +{3 n}/{4}}n^{-{n/2}}\sqrt{3A_{\mathrm{s}}}\pi c_{\mathrm{K}}^{n/4} f_\mathcal{R}(\phi _\star ) W_0(y_\star )\nonumber \\&\times \,(r_{\mathcal {R}\mathrm{K}}/(1 + W_0(y_\star )))^{(2 +n)/2}. \end{aligned}$$

(4.21)

Upon substitution of Eq. (4.19) into Eq. (4.6) we find the following expressions which ensure that $n_{\mathrm{s}}$ and r drop as $r_{\mathcal {R}\mathrm{K}}$ increases: for n fixed—cf. Fig. 1. Namely

$$\begin{aligned} n_{\mathrm{s}}= & {} 1 - 4r_{\mathcal {R}\mathrm{K}}^2\frac{2+nW_0^2(y_\star )}{n(1+W_0(y_\star ))^2}\nonumber \\\simeq & {} 1 - \frac{2 + n}{2{\widehat{N}_\star }} \,{+}\, \frac{4}{3}\left( \frac{2}{n}\right) ^{\frac{1}{2}} \frac{n-1}{{\widehat{N}_\star }^\frac{1}{2}}r_{\mathcal {R}\mathrm{K}}- \frac{2}{9 n}(10 \,{+}\, 11 n)r_{\mathcal {R}\mathrm{K}}^2\nonumber \\&+\,\frac{8 \sqrt{2}}{135 n^\frac{3}{2}}(11 n-23){\widehat{N}_\star }^{\frac{1}{2}}r_{\mathcal {R}\mathrm{K}}^3,\end{aligned}$$

(4.22a)

$$\begin{aligned} a_{\mathrm{s}}= & {} 32\frac{W_0(y_\star )}{n^2}\frac{2-nW_0(y_\star )}{(1+W_0(y_\star ))^4}r_{\mathcal {R}\mathrm{K}}^4\simeq -\frac{2+ n}{2{\widehat{N}_\star }^2} \nonumber \\&+\,\frac{2 \sqrt{2} (n-1)}{3 (n {\widehat{N}_\star }^3)^\frac{1}{2}} r_{\mathcal {R}\mathrm{K}}+ \frac{4 \sqrt{2} (23 - 11 n)}{135(n^3{\widehat{N}_\star })^\frac{1}{2}} r_{\mathcal {R}\mathrm{K}}^3, \end{aligned}$$

(4.22b)

$$\begin{aligned} r= & {} 32r_{\mathcal {R}\mathrm{K}}^2\frac{W_0^2(y_\star )}{(1+W_0(y_\star ))^2}\simeq \frac{4 n}{{\widehat{N}_\star }} -\frac{32 \sqrt{2n}}{3({\widehat{N}_\star })^\frac{1}{2}}r_{\mathcal {R}\mathrm{K}}\nonumber \\&+\,\frac{176}{9} r_{\mathcal {R}\mathrm{K}}^2 -\frac{704(2{\widehat{N}_\star })^\frac{1}{2}}{135\sqrt{n}}r_{\mathcal {R}\mathrm{K}}^3. \end{aligned}$$

(4.22c)

To appreciate the validity of our analytic estimates, we test them against our numerical ones. We use two sets of input parameters (for $n=2$ and 4) and we present in Table 2 their response by applying our numerical procedure (first five columns to the right of the leftmost three ones) or using the formulas above (next five columns). We see that the results are quite close to each other.

4.3.2 Semi-analytic results for $m\ne 1$

Contrary to the situation in Refs. [1, 2, 24, 25] the $m=1$ case is not the central one in the allowed areas—see Fig. 2. As a consequence the purely analytic verification above of our numerical results has to be extended to other m’s too.

Table 3 The coefficients $c^{(n,p)}_{jN}$ in Eq. (4.25) for $(n,p)=(2,1), (2,2), (4,1)$ and (4, 2)

Using the estimation of J in Eq. (4.13) we can extract ${\widehat{\phi }}$ as function of $\phi$

$$\begin{aligned} {\widehat{\phi }}= & {} \frac{1}{\sqrt{(m-1)r_{\mathcal {R}\mathrm{K}}}}\nonumber \\&\cdot \,{\left\{ \begin{array}{ll} 2(f_\mathcal{R}^{(m-1)/2}-1)/\sqrt{(m-1)r_{\mathcal {R}\mathrm{K}}},&{} \hbox {for }p=1,\\ \sqrt{\pi /2}\, {\mathrm{erfi}}\bigg (\sqrt{(m-1)c_{\mathrm{K}}r_{\mathcal {R}\mathrm{K}}}\phi /\sqrt{2}\bigg ),&{} \hbox {for }p=2,\end{array}\right. }\nonumber \\ \end{aligned}$$

(4.23)

where ${\mathrm{erfi}}$ is the imaginary error function [65]. As we see in the table of Fig. 3, the attainment of nMI requires ${\widehat{\phi }}_{\star }\gg 1$, whereas Eq. (4.9b) dictates $\phi _\star \le 1$. Eq. (4.23) ensures that both requirements above can be met since ${\widehat{\phi }}$ is increasing function of $c_{\mathrm{K}}$ for fixed $\phi$. Indeed, changing iteratively $c_{\mathrm{K}}\gg 1$ for fixed $\phi _\star \le 1$ we may obtain any possible ${\widehat{\phi }}_{\star }\gg 1$.

Taking into account that $\phi _\star \gg \phi _{\mathrm{f}}$, ${\widehat{N}_\star }$ can be computed from Eq. (4.1) as follows:

$$\begin{aligned} {\widehat{N}_\star }= {\left\{ \begin{array}{ll} -\frac{1}{2 r_{\mathcal {R}\mathrm{K}}^2} \left( \frac{f_\mathcal{R}(\phi _\star )^{m-1}}{m-1}+\mathrm{e}^{m-1}\mathrm{Ei}((m-1) (c_\mathcal{R}\phi _\star -1))\right) +N_0^{(2,1)},&{}\hbox {for }(n,p)=(2,1),\\ -\frac{\mathrm{e}^{(m-1)/2}}{8r_{\mathcal {R}\mathrm{K}}}\mathrm{Ei}((m-1)(2c_\mathcal{R}\phi _\star ^2-1)/2)+N_0^{(2,2)},&{} \hbox {for }(n,p)=(2,2),\\ -\frac{1}{2 r_{\mathcal {R}\mathrm{K}}^2}\left( \frac{f_\mathcal{R}(\phi _\star )^{m-1}}{m-1}+2\mathrm{e}^{2(m-1)}\mathrm{Ei}((m-1) (c_\mathcal{R}\phi _\star -2))\right) +N_0^{(4,1)},&{} \hbox {for }(n,p)=(4,1),\\ -\frac{\mathrm{e}^{m-1}}{8r_{\mathcal {R}\mathrm{K}}}\mathrm{Ei}((m-1)(c_\mathcal{R}\phi _\star ^2-1))+N_0^{(4,2)},&{} \hbox {for }(n,p)=(4,2), \end{array}\right. } \end{aligned}$$

(4.24a)

where $\mathrm{Ei}$ is the integral exponential function [65] and $N_0^{(n,p)}$ is a constant term which reads

$$\begin{aligned} N_0^{(n,p)}= \frac{1}{8(m-1) r_{\mathcal {R}\mathrm{K}}^2}\cdot {\left\{ \begin{array}{ll} 4(1 + \mathrm{e}^{m - 1}(m-1) \mathrm{Ei}(1 - m)),&{}\hbox {for }(n,p)=(2,1),\\ \mathrm{e}^{(m - 1)/2}(m-1)r_{\mathcal {R}\mathrm{K}}\mathrm{Ei}((1 - m)/2),&{} \hbox {for }(n,p)=(2,2),\\ 4(1 + 2\mathrm{e}^{2(m - 1)}(m-1) \mathrm{Ei}(2 - 2m)),&{} \hbox {for }(n,p)=(4,1),\\ \mathrm{e}^{m - 1}(m-1) \mathrm{Ei}(1 - m),&{} \hbox {for }(n,p)=(4,2). \end{array}\right. } \end{aligned}$$

(4.24b)

Table 4 Input and output parameters as found applying our semi-analytical estimates

Since ${\widehat{N}_\star }$ depends on $\phi _\star$ in a rather complicate way, it is not doable to solve analytically the equations above w.r.t. $\phi _\star$ and derive formulas for the minimal possible $c_{\mathrm{K}}$, and the observables $n_{\mathrm{s}}, a_{\mathrm{s}}$ and r as functions of ${\widehat{N}_\star }$—cf. Eqs. (4.20), (4.22a)–(4.22c). This difficulty persists even if we expand ${\widehat{N}_\star }$ in (convergent) series of $r_{\mathcal {R}\mathrm{K}}\ll 1$. Indeed, doing so we obtain the following expressions:

$$\begin{aligned} {\widehat{N}_\star }= & {} \frac{1}{8}c_{\mathrm{K}}\phi _\star ^2\sum _{j=0}^5r_{\mathcal {R}\mathrm{K}}^j\nonumber \\&\cdot \,{\left\{ \begin{array}{ll} 2c_{jN}^{(2,1)}c_{\mathrm{K}}^{j/2}\phi _\star ^j,&{} \hbox {for }(n,p)=(2,1),\\ 2c_{jN}^{(2,2)}c_{\mathrm{K}}^{j}\phi _\star ^{2j},&{} \hbox {for }(n,p)=(2,2),\\ c_{jN}^{(4,1)}c_{\mathrm{K}}^{j/2}\phi _\star ^{j},&{} \hbox {for }(n,p)=(4,1),\\ c_{jN}^{(4,2)}c_{\mathrm{K}}^{j}\phi _\star ^{2j},&{} \hbox {for }(n,p)=(4,2), \end{array}\right. } \end{aligned}$$

(4.25)

where the coefficients $c_{jN}^{(n,p)}$ are arranged in Table 3 with $c_{0N}^{(n,p)}=1$ for any (n, p). The difficulty related to the derivation of $\phi _\star$ in terms of ${\widehat{N}_\star }$ can be overcome by fixing $\phi _\star$ to a specific value and find (numerically) the corresponding $c_{\mathrm{K}}$ in order to obtain the required ${\widehat{N}_\star }$ by Eq. (4.1). This is possible since nMI can be realized for any $\phi _\star \le 1$ selecting conveniently $c_{\mathrm{K}}$ for given n, p, m and $r_{\mathcal {R}\mathrm{K}}$. We verified that Eq. (4.25) with fixed ${\widehat{N}_\star }$ exhibits unique real and positive solutions $c_{\mathrm{K}}=c_{1\mathrm{K}}$ for $\phi _\star =1$. Substituting these values for $c_{\mathrm{K}}$ and $\phi _\star$ into Eqs. (4.14) and (4.6) we can obtain relatively simple expressions for the inflationary observables as functions of $c_{1\mathrm{K}}$. Namely, we get

$$\begin{aligned} n_{\mathrm{s}}\simeq & {} 1-\frac{n(2+n)}{f_{1\mathcal R}^{m-1}c_{1\mathrm{K}}} - \frac{(m-5)n+4(p-1)p}{f_{1\mathcal R}^{m-1}c_{1\mathrm{K}}^{1-p/2}} r_{\mathcal {R}\mathrm{K}}\nonumber \\&+\,\frac{2(m-3)p^2}{c_{1\mathrm{K}}^{1-p}f_{1\mathcal R}^{m-1}}r_{\mathcal {R}\mathrm{K}}^2,\end{aligned}$$

(4.26a)

$$\begin{aligned} a_{\mathrm{s}}\simeq & {} \frac{2 pc_{1\mathrm{K}}^{p/2}r_{\mathcal {R}\mathrm{K}}-n}{c_{1\mathrm{K}}^{2}f_{1\mathcal R}^{2(m-1)}} ( 2 n (2 + n)+c_{1\mathrm{K}}^p\nonumber \\&\times (16 + 5 n + m ((m-6) n + 8 (p-1)) - 16 p) p^2r_{\mathcal {R}\mathrm{K}}^2 \nonumber \\&-pc_{1\mathrm{K}}^{p/2} ( 8 + n (12 + n - m (4 + n))\nonumber \\&-\, 12 p +(m-5) n p + 4 p^2)r_{\mathcal {R}\mathrm{K}}\nonumber \\&-\, 2p^3 c_{1\mathrm{K}}^{3 p/2} (m-3) (m-1) r_{\mathcal {R}\mathrm{K}}^3), \end{aligned}$$

(4.26b)

$$\begin{aligned} r\simeq & {} \frac{8}{c_{1\mathrm{K}}f_{1\mathcal R}^{m-1}}( n-2pc_{1\mathrm{K}}^{p/2}r_{\mathcal {R}\mathrm{K}})^2\nonumber \\&\quad \hbox {with }f_{1\mathcal R}=f_\mathcal{R}(\phi =1)=\mathrm{e}^{c_\mathcal{R}}. \end{aligned}$$

(4.26c)

From the expressions above we deduce that $n_{\mathrm{s}}$ and r decrease as $r_{\mathcal {R}\mathrm{K}}$ increases for fixed n and m, in accordance with the behavior of the curves in Fig. 1. Finally, from Eq. (4.16) we can find $\lambda _1$ corresponding to $c_{1\mathrm{K}}$ from the formula

$$\begin{aligned} \lambda _1=2^{1 + n/4}\sqrt{3A_{\mathrm{s}}}\pi f_{1\mathcal R}^{(3-m)/2}(n - 2pc_\mathcal{R})/\sqrt{c_{1\mathrm{K}}}. \end{aligned}$$

(4.27)

In this result we are not able to recover the proportionality of $\lambda$ on $c_{\mathrm{K}}^{n/4}$ as in Eq. (4.21), since $\phi _\star$ is not expressed in terms of $c_{\mathrm{K}}$ as in Eq. (4.19).

To qualify our semi-analytic treatment we compare its outputs with the numerical ones for the inputs used in Fig. 3. Our findings are displayed in Table 4 and are in good agreement with the values evaluated numerically and exposed in the table of Fig. 3. This is improved especially for small $r_{\mathcal {R}\mathrm{K}}$’s, which ensure more accurate convergence of the expansions in Eq. (4.25).

5 Conclusions

Following the strategy in Refs. [1, 2, 23,24,25] we proposed a class of SUSY and non-SUSY models which support hilltop inflation compatible with observations. The main novelty of our present proposal is the consideration of an exponential non-minimal coupling to gravity in Eq. (1.4) apart from the potential in Eq. (1.1) and the non-canonical kinetic mixing in Eq. (1.3) already used in Ref. [1, 2]. This setting can be elegantly implemented in SUGRA too, employing a bilinear (for $n=2$) or a linear–quadratic (for $n=4$) superpotential term—see Eq. (3.4)—and one of the Kähler potentials given in Eqs. (3.7a)–(3.8c). Prominent in all cases is the role of a shift-symmetric quadratic function $F_{\mathrm{K}}$ in Eq. (3.6a) which remains invisible in the SUGRA scalar potential while dominates mostly the canonical normalization of the inflaton. We specified two functional forms for the inflaton in the K’s, one logarithmic in Eqs. (3.7a)–(3.7g) and one polynomial in Eqs. (3.8a)–(3.8c), and two stabilization mechanisms for the non-inflaton field, one with a higher order term in Eqs. (3.7a)–(3.7d) and (3.8a), and one leading to a $SU(2)_S/U(1)$ symmetric Kähler manifold in Eqs. (3.7e)–(3.7g), (3.8b) and (3.8c). The only discrimination between those models arises for $p=1$ and regards the domain where the effective theory is valid up to $m_{\mathrm{P}}$.

In summary, our inflationary setting depends essentially on five free parameters (n, p, m, $\lambda /c_{\mathrm{K}}^{n/4}$ and $r_{\mathcal {R}\mathrm{K}}$), which were constrained to natural values, imposing a number of observational and theoretical restrictions. In particular, we investigated two pairs of n and p values ($n=2, 4$ and $p=1, 2$) allowing m to vary from 0 to 15. Therefore, the extra parameter, p, w.r.t. those used in Ref. [1, 2] assists us to enlarge the allowed parametric space and increases the naturalness of our proposal. Confining, e.g., $r_{\mathcal {R}\mathrm{K}}$ to the range $(2.6\times 10^{-3}$–1), where the upper bound does not apply to the $p=1$ case in the non-SUSY models and the SUSY ones for $K=K_i$ with $i=1,\ldots ,7$, we succeeded to reproduce the present data for $n_{\mathrm{s}}=0.968$, negligibly small $|a_{\mathrm{s}}|$ and mostly observationally reachable r’s in the foreseen future—see the table of Fig. 2. In all cases, $\lambda /c_{\mathrm{K}}^{n/4}$ is computed enforcing Eq. (4.4) and ${\widehat{V}}_{\mathrm{CI}}$ develops a maximum, which does not disturb, though, the implementation of hilltop nMI since the relevant tuning is mostly rather low. Our inflationary setting can be attained with subplanckian values of the initial (non-canonically normalized) inflaton requiring large $c_{\mathrm{K}}$’s and without causing any problem with the perturbative unitarity. It is gratifying that our scheme remains intact from radiative corrections and the inflationary quantities can be estimated analytically for $p=m=1$ and semi-analytically for the remaining cases.

Let us, finally, remark that the inflaton in our present regime was identified with a gauge singlet field. However, our models can be also realized very economically by a Higgs-inflaton, as in Refs. [15, 16, 23,24,25]. That is, the inflaton could be represented by a Higgs field involved in the breakdown of a SUSY grand unified theory. We expect that the results of such a possibility will be similar to those displayed here for $n=4$. The details of this investigation, though, could be the aim of a forthcoming publication.