Relativistic scattering of fermions in quaternionic quantum mechanics

Abstract

In this article, we propose a quaternionic version of the Dirac equation in the presence of scalar and vector potentials. It has been shown that in complex limit of such an equation, the complex version of this equation can be covered. After setting a quaternionic form for the Dirac delta potential, scattering due to the considered interaction has been studied. Wave functions and discontinuity conditions of the problem considered have been derived in detail. Using the continuity equation, we have found a constraint implying the conservation law of the probability current.

1 Introduction

The mathematical structure of quantum mechanics, one of the fundamental pillars of modern physics of the description of new aspects of nature, consists of Hilbert spaces defined over the field of complex numbers. Physicists have witnessed that the underlying foundations of the theory are enormously successful in describing different quantal phenomena [1,2,3,4,5,6]. For the first time quantum theory was extended to include the field of quaternions by Hamilton [7, 8].

Mathematically the quaternions can be expressed by extending complex numbers in the following form:

$$\begin{aligned} Q = {q_1} + i{q_2} + j{q_3} + k{q_4}, \end{aligned}$$

(1.1)

where i, j and k are imaginary units and $q_l$, $l=1,2,3,4$ are real. The imaginary units are interrelated by

$$\begin{aligned} ij = - ji = k, \quad jk = - kj = i, \quad ki = - ik = j, \end{aligned}$$

(1.2)

which signals the non-commutative character of the field of quaternions with respect to the multiplication.

Quaternions have a representation similar to complex numbers as follows:

$$\begin{aligned} \begin{aligned}&Q = {Q_\mathrm{a}} + j{Q_\mathrm{b}},\\&{Q_\mathrm{a}} = {q_1} + i{q_2},\\&{Q_\mathrm{b} } = {q_3} - i{q_4}, \end{aligned} \end{aligned}$$

(1.3)

and the conjugation of quaternion is defined as

$$\begin{aligned} {\bar{Q} }= {q_1} - i{q_2} - j{q_3} - k{q_4}. \end{aligned}$$

(1.4)

Having appropriate mathematical tools using quaternions [9, 10], a lot of efforts have been made to reconstruct quantum mechanics in terms of quaternion functions during the past few decades such as those by Kaneno [11], Finkelstein and Jauch [12, 13], Emch[14], Horwitz and Biedenharn [15], De Leo [16,17,18,19,20], to name a few; maybe the best-known person in this research field is Adler [21,22,23,24,25,26]. In recent times, scattering for non-relativistic and spinless quantum particles has been studied in [27,28,29] in the presence of a quaternionic Dirac delta potential in the direction proposed by De Leo [20]. Motivated by the above progress, in this article, we want to investigate the relativistic scattering of fermions in the presence of scalar and vector potentials. In order to do this, we investigate the quaternionic version of the Dirac equation in Sect. 2. In Sect. 3 we introduce the scattering potential and present related calculations. We derive the reflection and transmission coefficients to establish the conservation of the current probability in Sect. 4, and finally in Sect. 5 we present the conclusion of our work.

2 Quaternionic version of the Dirac equation

According to the rules of quaternionic quantum mechanics we should write the Dirac equation in terms of an anti-hermitian operator; this version of the Dirac equation [20] in the presence of a quaternionic vector and scalar potential can be written as

$$\begin{aligned} \frac{{\partial \Psi ({\varvec{r}},t)}}{{\partial t}}= & {} - \left[ {\varvec{ \alpha . \nabla }} + {\varvec{\beta }}\left( i(m + {S_a}({\varvec{r}}))\right. \right. \nonumber \\&\left. \left. + j{S_b}({\varvec{r}}) \right) + i{V_a}({\varvec{r}}) + j{V_b}({\varvec{r}}) \right] \Psi ({\varvec{r}},t), \end{aligned}$$

(2.1)

where we have used $\hbar = c = 1$ and supposed that ${S_\mathrm{a}}({\varvec{r}}),{V_\mathrm{a}}({\varvec{r}})$ are real functions and ${S_\mathrm{b}}({\varvec{r}}),{V_\mathrm{b}}({\varvec{r}})$ are complex functions in Eq. (2.1). Let us test Eq. (2.1) carefully. In the complex limit this equation must recover the famous Dirac equation. In order to check this important point, we set ${S_\mathrm{b}}({\varvec{r}}),{V_\mathrm{b}}({\varvec{r}}) \rightarrow 0$. By using this condition, Eq. (2.1) turns into

$$\begin{aligned} i\frac{{\partial \Psi ({\varvec{r}},t)}}{{\partial t}} = \left[ { \varvec{\alpha . P} + {\varvec{\beta }}\left( {m + {S_\mathrm{a}}({\varvec{r}})} \right) + {V_\mathrm{a}}({\varvec{r}})} \right] \Psi ({\varvec{r}},t). \end{aligned}$$

(2.2)

Equation (2.2) is the complex version of the Dirac equation [30, 31]. In Eqs. (2.1) and (2.2) ${\varvec{\alpha }}$ and $\varvec{\beta }$ are defined by the Pauli and unity matrices as follows:

$$\begin{aligned}&\varvec{ \alpha } = \left( \begin{array}{ll} \varvec{ 0} &{}\quad {\varvec{ \sigma } }\\ {\varvec{ \sigma } }&{}\quad \varvec{ 0} \end{array}\right) \nonumber \\&{\varvec{\beta }} = \left( \begin{array}{ll} {\varvec{1}}&{}\quad {\varvec{0}}\\ {\varvec{0}}&{}\quad {{\varvec{ - 1}}} \end{array}\right) . \end{aligned}$$

(2.3)

Setting the wave function $\Psi ({\varvec{r}},t) = \Phi ({\varvec{r}}){e^{ - iEt}}$, we get to the eigenvalue form of Eq. (2.1):

$$\begin{aligned} \Phi ({\varvec{r}})iE= & {} \left[ { \varvec{\alpha . \nabla }} + {\varvec{\beta }}\left( {i(m + {S_a}({\varvec{r}})) + j{S_b}({\varvec{r}})} \right) + i{V_a}({\varvec{r}})\right. \nonumber \\&\left. + j{V_b}({\varvec{r}}) \right] \Phi ({\varvec{r}}). \end{aligned}$$

(2.4)

$\Phi ({\varvec{r}})$ is a spinor with two components, up and down, that we denote ${\Phi ^ + }({\varvec{r}})$ and ${\Phi ^ - }({\varvec{r}})$, respectively. By some calculation and setting $i{S_\mathrm{a}}({\varvec{r}}) + j{S_\mathrm{b}}({\varvec{r}}) = i{V_\mathrm{a}}({\varvec{r}}) + j{V_\mathrm{b}}({\varvec{r}})$, we can find a connection between these two components:

$$\begin{aligned}&{\Phi ^ + }(x)iE= {\sigma _x}\frac{{\mathrm{d}{\Phi ^ - }(x)}}{{\mathrm{d}x}}\nonumber \\&\quad + \left( {im + 2(i{S_\mathrm{a}}(x) + j{S_\mathrm{b}}(x))} \right) {\Phi ^ + }(x),\end{aligned}$$

(2.5)

$$\begin{aligned}&{\Phi ^ - }(x)iE = {\sigma _x}\frac{{\mathrm{d}{\Phi ^ + }(x)}}{{\mathrm{d}x}} - im{\Phi ^ - }(x), \end{aligned}$$

(2.6)

where the interaction direction has been considered in the x-direction. The quaternionic wave function components are in the form of $\Phi ^{\pm } (x) = \phi ^{\pm } _\mathrm{a} (x) + j \phi ^{\pm } _\mathrm{b} (x)$ where $\phi ^{\pm } _\mathrm{a} (x)$ and $\phi ^{\pm } _\mathrm{b} (x)$ are the complex functions. Considering such a form of the wave function components in Eq. (2.6) yields

$$\begin{aligned} \phi ^{-} _\mathrm{a} (x)&= \frac{\sigma _x}{i(E+m)} \frac{\mathrm{d} \phi ^{+} _\mathrm{a} (x)}{\mathrm{d}x}, \end{aligned}$$

(2.7)

$$\begin{aligned} \phi ^{-} _\mathrm{b} (x)&= \frac{\sigma _x}{i(E-m)} \frac{\mathrm{d} \phi ^{+} _\mathrm{b} (x)}{\mathrm{d}x}. \end{aligned}$$

(2.8)

Substitution of Eqs. (2.7) and (2.8) into Eq. (2.5) provides a system of coupled differential equations,

$$\begin{aligned} \frac{\mathrm{d}^2 \phi ^{+} _\mathrm{a} (x)}{\mathrm{d}x^2}&+ \left( p^2 -2(E+m)S_\mathrm{a} (x)\right) \phi ^{+} _\mathrm{a} (x) \nonumber \\&-2i (E+m) S^*_\mathrm{b} (x) \phi ^{+} _\mathrm{b} (x) = 0, \end{aligned}$$

(2.9)

$$\begin{aligned} \frac{\mathrm{d}^2 \phi ^{+} _\mathrm{b} (x)}{\mathrm{d}x^2}&+ \left( -p^2 -2(E-m)S_\mathrm{a} (x)\right) \phi ^{+} _\mathrm{b} (x) \nonumber \\&+2i (E-m) S_\mathrm{b} (x) \phi ^{+} _\mathrm{a} (x) = 0, \end{aligned}$$

(2.10)

where $p^2 = E^2 - m^2$ and $*$ means the complex conjugation. Now, we are in a position to investigate scattering states due to the quaternionic Dirac delta potential.

3 Investigation of quaternionic Dirac delta scattering

The interaction which we want to study consists of a Dirac delta function with a quaternion coefficient

$$\begin{aligned} S_\mathrm{a}(x) + j S_\mathrm{b} (x) = (V_\mathrm{a} + j iV_\mathrm{b}) \delta (x), \end{aligned}$$

(3.1)

where $V_\mathrm{a}$ and $V_\mathrm{b}$ are real constants. Inserting Eq. (3.1) into Eqs. (2.9) and (2.10) and taking an integral in the neighborhood of $x=0$ result in the discontinuity condition of the wave function components,

$$\begin{aligned}&\left. \frac{\mathrm{d} \phi ^{+} _\mathrm{a}}{\mathrm{d}x} \right| _{x=0^+} - \left. \frac{\mathrm{d} \phi ^{+} _\mathrm{a}}{\mathrm{d}x} \right| _{x=0^-} \nonumber \\&\quad = 2(E+m) (V_\mathrm{a} \phi ^{+} _\mathrm{a} (0) + V_\mathrm{b} \phi ^{+} _\mathrm{b} (0)), \end{aligned}$$

(3.2)

$$\begin{aligned}&\left. \frac{\mathrm{d} \phi ^{+} _\mathrm{b}}{\mathrm{d}x} \right| _{x=0^+} - \left. \frac{\mathrm{d} \phi ^{+} _\mathrm{b}}{\mathrm{d}x} \right| _{x=0^-}\nonumber \\&\quad = 2(E-m) ( V_\mathrm{a} \phi ^{+} _\mathrm{a} (0) + V_\mathrm{b} \phi ^{+} _\mathrm{b} (0)). \end{aligned}$$

(3.3)

We would like to assume that the particles are coming from region I $(x<0)$. After experiencing the scattering potential at the origin, some of them will be reflected into region I and the others will be transmitted into region II $(x>0)$. For the free particles we have

$$\begin{aligned} \phi ^{+} _\mathrm{a} (x)&= c_1 e^{ipx} + c_2 e^{-ipx},\end{aligned}$$

(3.4)

$$\begin{aligned} \phi ^{+} _\mathrm{b} (x)&= c_3 e^{px} + c_4 e^{-px}, \end{aligned}$$

(3.5)

where the coefficients are complex constants in general. Therefore, according to our assumption as regards the particles, the physical wave functions can be written as

$$\begin{aligned} \phi ^{+} _{\mathrm{I}} (x)&= e^{ipx} + r e^{-ipx} + j e^{px},\end{aligned}$$

(3.6)

$$\begin{aligned} \phi ^{+} _{\mathrm{II}} (x)&= t e^{ipx} + j \tilde{t} e^{-px}, \end{aligned}$$

(3.7)

in which the coefficients will be determined using continuity and discontinuity conditions of the wave functions at $x=0$.

Continuity of the wave functions necessitates

$$\begin{aligned} 1 + r&= t, \end{aligned}$$

(3.8)

$$\begin{aligned} \tilde{r}&= \tilde{t}. \end{aligned}$$

(3.9)

Using discontinuity of derivatives of the wave functions results in

$$\begin{aligned} ip (t-1+r) = 2(E+m)(V_\mathrm{a} t + V_\mathrm{b} \tilde{t}), \end{aligned}$$

(3.10)

$$\begin{aligned} -p(\tilde{t} + \tilde{r}) = 2 (E-m)(V_\mathrm{a} t + V_\mathrm{b} \tilde{t}). \end{aligned}$$

(3.11)

The coefficients can be derived by solving the system of equations (3.8), (3.9), (3.10) and (3.11). After solving the system of equations we have

$$\begin{aligned} r&= -\frac{i (m+E) V_\mathrm{a}}{i (m+E) V_\mathrm{a}+(E-m) V_\mathrm{b}+p},\end{aligned}$$

(3.12)

$$\begin{aligned} t&= \frac{(E-m) V_\mathrm{b}+p}{i (m+E) V_\mathrm{a}+(E-m) V_\mathrm{b}+p},\end{aligned}$$

(3.13)

$$\begin{aligned} \tilde{r}&= \tilde{t} = -\frac{(E-m) V_\mathrm{a}}{i (m+E) V_\mathrm{a}+(E-m) V_\mathrm{b}+p}. \end{aligned}$$

(3.14)

In the next section, the conservation law of probability will be studied.

4 Reflection and transmission coefficients

In quaternionic quantum mechanics, similar to the complex version, we have the continuity equation

$$\begin{aligned} \frac{{\partial \rho }}{{\partial t}} + {\varvec{\nabla }.\varvec{J}} = 0, \end{aligned}$$

(4.1)

where

$$\begin{aligned} \rho&= {\bar{\Psi } }\Psi , \end{aligned}$$

(4.2)

$$\begin{aligned} {{\varvec{J}}}&= {\Psi ^\dag } {\varvec{\alpha }} \Psi . \end{aligned}$$

(4.3)

To check the conservation law of probability we need to calculate the currents of each of the regions. To derive the currents of each region, we need the spinor form of the wave function of each region. This form of the wave functions can be obtained using Eqs. (2.7) and (2.8):

$$\begin{aligned} \Phi _I (x)&= \begin{pmatrix} e^{ipx} + r e^{-ipx} + j \tilde{r} e^{px}\\ \sigma _x p \left( \frac{e^{ipx} - r e^{-ipx}}{E+m} + j \frac{\tilde{r} e^{px}}{i(E-m)} \right) \end{pmatrix},\end{aligned}$$

(4.4)

$$\begin{aligned} \Phi _{\mathrm{II}} (x)&= \begin{pmatrix} t e^{ipx} + j \tilde{t} e^{-px}\\ \sigma _x p \left( \frac{t e^{ipx}}{E+m} - j \frac{\tilde{t} e^{-px}}{i(E-m)} \right) \end{pmatrix}. \end{aligned}$$

(4.5)

It is straightforward to prove that by using the definition $J_x = \Psi ^\dagger \alpha _x \Psi$, we derive the constraint

$$\begin{aligned} |r|^2 + |t|^2 = 1. \end{aligned}$$

(4.6)

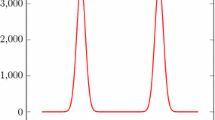
Details of the derivation of Eq. (4.6) are presented in the appendix. We plotted treatments of the reflection and transmission coefficients in Fig. 1, considering $m=1$, ${V_\mathrm{a} } = {V_\mathrm{b} } = 0.5$.

Fig. 1

Treatments of the reflection and transmission coefficients in terms of energy. For this plot we have set $m=1$, ${V_\mathrm{a} } = {V_\mathrm{b} } = 0.5$ and the energy $\in [1, 4]$

Furthermore, in Figs. 2 and 3, different numerical values for elements of the considered potential have been assumed and effects of these elements on reflection $\left( |r|^2\right)$, transmission $\left( |t|^2\right)$ coefficients have been plotted.

Fig. 2

Effects of different values of $V_\mathrm{a}$ on the coefficients. The constants in this figure are $m=1$ and $V_\mathrm{b}=0.5$

Fig. 3

Effects of different values of $V_\mathrm{b}$ on the coefficients. The constants in this figure are $m=1$ and $V_\mathrm{a}=0.5$

As can be understood from Figs. 2 and 3, the effects of $V_\mathrm{a}$ on the reflection and transmission coefficients are stronger than $V_\mathrm{b}$.

5 Conclusion

In this article the quaternionic form of the Dirac equation was studied. Because of the non-commutative nature of the quaternions, the derivation of the wave function in the formalism considered is different from the usual one. In this study a quaternionic Dirac delta potential was considered. We have shown how such a potential provided a discontinuity condition for the derivative of the wave functions. Using boundary conditions, we were able to find explicit form of reflection and transmission coefficients. The conservation law of probability was checked. The correctness of the results was checked and proved as we expected from ordinary quantum mechanics. Furthermore, in some plots, the effects of the elements of the quaternionic Dirac delta potential on the reflection and transmission coefficients were depicted.

Appendix

In this section details of the derivation of Eq. (4.6) are mentioned. In order to be brief in the calculations, we will indicate them in a compact form.

At the first step, we are going to derive the current of probability of region I. Using the definition of the probability current we have

$$\begin{aligned} J_{\mathrm{I}}=&\Psi ^ \dagger \alpha _x \Psi , \nonumber \\ =&\left( e^{-ipx} + r^*e^{ipx} - e^{px} \tilde{r}^*j,\right. \nonumber \\&\times \left. \sigma _x p \left( \frac{e^{-ipx} - r^*e^{ipx}}{E+m} + \frac{\tilde{r}^*e^{px}}{i(E-m)}j \right) \right) \begin{pmatrix} 0 &{} \sigma _x \\ \sigma _x &{} 0 \end{pmatrix}\nonumber \\&\times \begin{pmatrix} e^{ipx} + r e^{-ipx} + j \tilde{r} e^{px}\\ \sigma _x p \left( \frac{e^{ipx} - r e^{-ipx}}{E+m} + j \frac{\tilde{r} e^{px}}{i(E-m)} \right) \end{pmatrix}. \end{aligned}$$

(6.1)

It should be noted that the spinor of a wave function is a quaternion and since the coefficients are complex constants, their order and j, the imaginary unit, is important. Hence in the daggered form of the spinor we are faced with a reversed order in Eq. (6.1). Proceeding in the matrix multiplication form we have

$$\begin{aligned} J_{\mathrm{I}} =&\left( \overbrace{e^{-ipx} + r^*e^{ipx}}^{A_1} \overbrace{- e^{px} \tilde{r}^*j}^{A_2}, \right. \nonumber \\&\times \left. \sigma _x p \left( \underbrace{\frac{e^{-ipx} - r^*e^{ipx}}{E+m}}_{A_3} \underbrace{+ \frac{\tilde{r}^*e^{px}}{i(E-m)}j}_{A_4} \right) \right) \nonumber \\&\times \begin{pmatrix} p \left( \overbrace{\frac{e^{ipx} - r e^{-ipx}}{E+m}}^{B_1} + \overbrace{j \frac{\tilde{r} e^{px}}{i(E-m)}}^{B_2} \right) \\ \sigma _x\left( \underbrace{e^{ipx} + r e^{-ipx}}_{B_3} + \underbrace{j \tilde{r} e^{px}}_{B_4} \right) \end{pmatrix},\end{aligned}$$

(6.2)

$$\begin{aligned} J_{\mathrm{I}} =&A_1 B_1 + A_1 B_2 + A_2 B_1 + A_2 B_2 + A_3 B_3 \nonumber \\&+ A_3 B_4 + A_4 B_3 + A_4 B_4. \end{aligned}$$

(6.3)

To avoid complicity of the multiplication of Eq. (6.2), we have

$$\begin{aligned} A_1 B_1&= \frac{p}{E+m} \left( 1- r e^{-2ipx} + r^*e^{2ipx} - |r|^2 \right) , \end{aligned}$$

(6.4a)

$$\begin{aligned} A_1 B_2&=j \frac{p}{i(E-m)} \left( \tilde{r} e^{px(1+i)} + r \tilde{r} e^{px (1-i)} \right) , \end{aligned}$$

(6.4b)

$$\begin{aligned} A_2 B_1&= j \frac{p}{(E+m)} \left( -\tilde{r} e^{px(1+i)} + r \tilde{r} e^{px (1-i)} \right) , \end{aligned}$$

(6.4c)

$$\begin{aligned} A_2 B_2&= \frac{p}{i(E-m)} \left( |\tilde{r}|^2 e^{2px} \right) , \end{aligned}$$

(6.4d)

$$\begin{aligned} A_3 B_3&= \frac{p}{E+m} \left( 1 + r e^{-2ipx} - r^*e^{2ipx} - |r|^2 \right) , \end{aligned}$$

(6.4e)

$$\begin{aligned} A_3 B_4&= j \frac{p}{(E+m)} \left( \tilde{r} e^{px(1+i)} - r \tilde{r} e^{px (1-i)} \right) , \end{aligned}$$

(6.4f)

$$\begin{aligned} A_4 B_3&= -j \frac{p}{i(E-m)} \left( \tilde{r} e^{px(1+i)} + r \tilde{r} e^{px (1-i)} \right) , \end{aligned}$$

(6.4g)

$$\begin{aligned} A_4 B_4&= -\frac{p}{i(E-m)} \left( |\tilde{r}|^2 e^{2px} \right) . \end{aligned}$$

(6.4h)

With the help of Eqs. (6.3)–(6.4h), we can find the probability current of the region I:

$$\begin{aligned} J_{\mathrm{I}} = \frac{2p}{E+m} (1-|r|^2). \end{aligned}$$

(6.5)

In the same manner, we can find the probability current of region II:

$$\begin{aligned} J_{\mathrm{II}} = \frac{2p}{E+m} |t|^2. \end{aligned}$$

(6.6)

Since there is no sink or source for the particles, we have

$$\begin{aligned} J_{\mathrm{I}} = J_{\mathrm{II}} \Rightarrow |r|^2 + |t|^2 =1. \end{aligned}$$

(6.7)