Innermost stable circular orbit of Kerr-MOG black hole

Abstract

We study the innermost stable circular orbit (ISCO) of the metric of the Kerr black hole in modified gravity (Kerr-MOG black hole), which is one of the exact solutions of the field equation of modified gravity in the strong gravity regime. The Kerr-MOG metric is constructed; it is the commonly known Kerr metric in Boyer–Lindquist coordinates by adding a repulsive term like the Yukawa force, which is explained in quantum gravity. In this paper, we numerically calculate the circular orbit of a photon and the ISCO of a test particle of Kerr-MOG black holes.

1 Introduction

General relativity (GR) is a well-established theory to predicting many cosmological phenomena in the solar system and the universe. Especially it predicts a black hole, which is one of the astronomically most surprising phenomena. However, the interior of the black hole and some other astronomical observations are not explained by GR. An example in particular is the strange phenomenon of galaxy rotation curves found by the study of Zwicky, Rubin and collaborators [1,2,3,4]. Zwicky was the first to theoretically and formally postulate an unknown form of matter, called dark matter. Rubin found that Einstein’s theory cannot explain the rotation curve of a spiral galaxy. This phenomenon is an important clue for the existence of dark matter. However, dark matter has not been discovered by experimental observation so far. A theory for this phenomenon without invoking the concept of dark matter may be necessary. First of all, modified Newtonian dynamics (MOND) was proposed by Milgrom [5] by altering the “inverse-square” law of gravity in the scalar field of Newtonian gravity. This fits some observations and the weak-field approximation like the solar system but MOND has limited capability to explain the phenomena at a large scale, such as the rotation curve of our galaxy of the spiral region from $\sim$0.2  kpc out to $\sim$200 kpc and the velocity dispersion profiles of globular clusters [6, 7].

A scalar–tensor–vector gravity (STVG) theory was proposed by Moffat [8]. STVG was referred to as the modified gravity theory (MOG), developed to explain the discordance between the general relativity at large scale and many astronomical observations such as the dynamics of galaxies, galaxy rotation curves, bullet clusters, the amount of luminous matter in these galaxies and the accelerating universe [8,9,10]. The MOG theory is the field theory which is an addition of a scalar action, vector action and matter action, thereby modifying the Einstein–Hilbert action. Moffat also obtained the metric of Kerr modified gravity (Kerr-MOG) of a black hole by combining the MOG theory with the Kerr geometry [11]. This metric is an alternative metric in strong gravity and an exact solution for a rotating black hole. He also theoretically showed observational methods for the black hole shadow of the Kerr-MOG case [12]. The research for the shadow of the black hole at our galactic center is in progress by the Event Horizon Telescope (EHT) [13]. EHT observed the shadow of a black hole by studying the dynamics near the black hole such as particles or photons around the accretion disk. Most of all, movement of a particle or photon by strongly curved spacetime is a relevant subject. In particular, circular motions of timelike or lightlike geodesics are important because they give information on the geometric framework around non-rotating or rotating black holes. For instance, there is the minimum radius of a trajectory that is able to maintain a stable circular orbit which does not enter the event horizon of a black hole; this is called an innermost stable circular orbit (ISCO) [14]. In the accretion disk theory [15], the ISCO is regarded as one of the rotating black hole’s important features like the event horizon, ergosphere, etc. ISCO is believed to be the inner edge of an accretion disc orbiting a black hole. Iron line profiles for black holes are determined by the photons that are emitted near the ISCO [16]. The radius of the ISCO is 6M (M is the total mass of a black hole) in the case of the Schwarzschild black hole, while the radius of ISCO for a Kerr black hole depends on the intrinsic angular momentum a, the well-known Kerr parameter. As an example, the ISCO of the extreme rotating black hole, which has the intrinsic angular momentum of a Kerr black hole, which is M $(a=M)$; we have M in the co-rotating and 9M in the counter-rotating cases where $G_{N}=c=1$ in the case of the Schwarzschild and Kerr metric [17]. ISCOs assist the study which finds the shape of thin disks and Penrose processes at the ergosphere as well as properties in the vicinity of the black hole. Furthermore, an ISCO that is closely related to a black hole shadow helps the research investigation by EHT.

In this paper, we numerically calculate the trajectories of null and timelike geodesics of a t and $\phi$ coordinate system, comparing the Kerr-MOG metric with the Kerr metric. In particular, we study the circular orbit of a photon and ISCO of a test particle of Kerr-MOG black holes analytically. We obtain two analytic expressions of the energy E and the angular momentum L of a photon and a test particle in a circular orbit for the Kerr-MOG metric, using a method due to Refs. [18, 19]. According to the method, we also numerically calculate the circular orbit of the photon and ISCO of the test particle of the Kerr-MOG case and analyze the result and will show how to vary them by the parameter $\alpha$, which is related to Newton’s gravitational constant.

2 Field equation of MOG and Kerr-MOG metric

The field equation of MOG is given by [8, 11]

$$\begin{aligned} G_{\mu \nu } = -8\pi GT_{\phi \mu \nu }, \end{aligned}$$

(1)

where it is postulated that $G=G_{N}(1+\alpha )$, $\partial _{\nu }G=0$, where $G_{N}$ is Newton’s gravitational constant and G is rewritten as the parameter $\alpha$. Furthermore, the canonical energy-momentum tensor of matter $T_{M\mu \nu }=0$ and the energy-momentum tensor for the vector field $\phi _{\mu }$ are induced by

$$\begin{aligned} T_{\phi \mu \nu } = -\frac{1}{4\pi }\Big (B_{\mu }^{\sigma }B_{\nu \sigma } - \frac{1}{4}g_{\mu \nu }B^{\sigma \beta }B_{\sigma \beta }\Big ), \end{aligned}$$

(2)

where $B_{\mu \nu } = \partial _{\mu }\phi _{\nu } - \partial _{\nu }\phi _{\mu }$ and $\phi _{\mu }$ is for the vector field with the source charge $Q = \sqrt{\alpha G_{N}}M$. Moreover, the vacuum field equations are

$$\begin{aligned}&\nabla _{\nu }B^{\mu \nu } = \frac{1}{\sqrt{-g}}\partial {_\nu }\big (\sqrt{-g}B^{\mu \nu }\big ) = 0, \nonumber \\&\nabla _{\sigma }B_{\mu \nu } + \nabla _{\mu }B_{\nu \sigma } + \nabla _{\nu }B_{\sigma \mu } = 0, \end{aligned}$$

(3)

where $\nabla _{\nu }$ is in regard to the metric tensor $g_{\mu \nu }$. The Kerr-MOG black hole is a static and axisymmetric solution of the gravitational field equations. The Kerr-MOG metric in Boyer–Lindquist coordinates is

$$\begin{aligned} \mathrm{d}s^{2}= & {} \frac{\varDelta }{\rho ^{2}}(\mathrm{d}t - a\sin ^{2}{\theta }\mathrm{d}\phi )^{2} \nonumber \\&-\frac{\sin ^{2}\theta }{\rho ^{2}}[(r^{2}+a^{2})\mathrm{d}\phi - a\mathrm{d}t]^{2} - \frac{\rho ^{2}}{\varDelta }\mathrm{d}r^{2} - \rho ^{2}\mathrm{d}\theta ^{2},\nonumber \\ \end{aligned}$$

(4)

where

$$\begin{aligned}&\varDelta = r^{2}-2G_{N}(1+\alpha )Mr+a^{2}+M^{2}G_{N}^{2}\alpha (1+\alpha ),\nonumber \\&\rho ^{2}=r^2+a^{2}\cos ^{2}{\theta }. \end{aligned}$$

(5)

The Kerr-MOG metric has two horizons known as the outer horizon $(r_{+})$ and the inner horizon $(r_{-})$ like a Kerr black hole determined by $\varDelta =0$. The two horizons are also called the event horizon and the Cauchy horizon, respectively. They are given by

$$\begin{aligned} r_{\pm }=G_{N} (1+\alpha ) M \left[ 1 \pm \sqrt{1-\frac{a^{2}}{G_{N}^{2}(1+\alpha )^{2}M^{2}} - \frac{\alpha }{1+\alpha }} \right] .\nonumber \\ \end{aligned}$$

(6)

3 Total energy of Kerr-MOG metric in circular orbit

To find the circular orbit in any metric one considers the effective potential for the motion of a massive particle or photon [14,15,16,17,18,19,20,21,22,23,24,25,26,27]. We approach the problem by solving ISCO by the well-developed method different from the one that Moffat has proposed [11, 18, 19]. We investigate the behavior of a test particle or a photon in the equatorial plane ($\theta =\pi /2$). The covariant components of the Kerr-MOG metric are

$$\begin{aligned}&g_{tt}= \frac{\varDelta -a^{2}}{r^{2}},\quad g_{t\phi }= \frac{a}{r^{2}}{[(r^{2}+a^{2})-\varDelta ]},\quad g_{rr}= -\frac{r^{2}}{\varDelta },\nonumber \\&g_{\theta \theta }=-r^{2},\quad g_{\phi \phi }= -\frac{1}{r^2} [(r^{2}+a^{2})^{2}-a^{2}\varDelta ]. \end{aligned}$$

(7)

Because of the property of stationarity- and axis symmetry for the Kerr-MOG metric, we consider two conserved quantities to be the specific energy E and the specific angular momentum L for constant motion of the test particle with rest mass $\mu$. We use the Lagrangian. The Lagrangian is

$$\begin{aligned} L = \frac{1}{2}g_{\mu \nu } \dot{x}^{\mu }\dot{x}^{\nu }. \end{aligned}$$

(8)

The Euler–Lagrange equation by solving the geodesic equation with respect to the affine parameter gives the equation for t and $\phi$ as well as the radial equation,

$$\begin{aligned}&\dot{t} = \frac{-Eg_{\phi \phi } - Lg_{t\phi }}{g_{t\phi }^{2} - g_{tt}g_{\phi \phi }}, \end{aligned}$$

(9)

$$\begin{aligned}&\dot{\phi } = \frac{Eg_{t\phi } + Lg_{tt}}{g_{t\phi }^{2} - g_{tt}g_{\phi \phi }}, \end{aligned}$$

(10)

$$\begin{aligned}&\dot{r}^{2} = \frac{1}{r^2} \Bigg [E^{2}r^{2} - (L^{2}-a^{2}E^{2})\nonumber \\&\qquad \quad +\bigg (\frac{2M_{\alpha }}{r}-\frac{\beta ^{2}}{r^{2}}\bigg )(L-aE)^{2} - \varDelta \mu \Bigg ], \end{aligned}$$

(11)

where

$$\begin{aligned} M_{\alpha } = G_{N}(1+\alpha )M ,\quad \beta ^{2} = M^2G_{N}^{2}\alpha (1+\alpha ). \end{aligned}$$

(12)

For convenience of the calculations, we use the above notations.

4 Circular orbit of a photon of Kerr-MOG black hole

We can obtain circular orbits of photons in Kerr-MOG geometry, setting the finite rest mass of a particle at zero; i.e., $\mu =0$. The radial equation (11) becomes

$$\begin{aligned} \dot{r}^{2}= & {} \frac{1}{r^2} \Bigg [E^{2}r^{2} - (L^{2}-a^{2}E^{2})+ \bigg (\frac{2M_{\alpha }}{r} -\frac{\beta ^{2}}{r^{2}}\bigg )\nonumber \\&\times (L-aE)^{2}\Bigg ]. \end{aligned}$$

(13)

We consider the impact parameter D to easily distinguish the geodesic,

$$\begin{aligned} D = \frac{L}{E}. \end{aligned}$$

(14)

We can also introduce the condition regarding the principal null geodesics [18,19,20,21, 28]:

$$\begin{aligned} D = a \end{aligned}$$

(15)

and thus Eq. (14) becomes $L=aE$. Substituting $L=aE$ into Eqs. (9), (10) and (11), they become

$$\begin{aligned}&\dot{t} = \frac{r^{2}+a^{2}}{\varDelta } E, \end{aligned}$$

(16)

$$\begin{aligned}&\dot{\phi } = \frac{a}{\varDelta } E, \end{aligned}$$

(17)

$$\begin{aligned}&\dot{r} = \pm E. \end{aligned}$$

(18)

Because the radial coordinate is described at constant ratio corresponding to the affine parameter, we take

$$\begin{aligned}&\frac{\mathrm{d}t}{\mathrm{d}r} = \frac{\dot{t}}{\dot{r}} = \frac{r^{2}+a^{2}}{\varDelta }, \end{aligned}$$

(19)

$$\begin{aligned}&\frac{\mathrm{d}\phi }{\mathrm{d}r} = \frac{\dot{\phi }}{\dot{r}} =\frac{a}{\varDelta }. \end{aligned}$$

(20)

When $a^{2}<M^{2}$, Eqs. (19) and (20) can be integrated to give

$$\begin{aligned}&t = r + \left( M_{\alpha }^{2} + \frac{M_{\alpha }^{2}}{\sqrt{M_{\alpha }^{2} - a^{2}}}\right) \ln {\bigg |\frac{r}{r_{+}} - 1\bigg |}+\bigg (M_{\alpha }^{2} \nonumber \\&\quad -\frac{M_{\alpha }^{2}}{\sqrt{M_{\alpha }^{2} - a^{2}}}\bigg )\ln {\bigg |\frac{r}{r_{+}} - 1\bigg |}, \end{aligned}$$

(21)

$$\begin{aligned}&\phi = \frac{a}{2\sqrt{M_{\alpha }^{2} - a^{2}}}\ln {\bigg |\frac{r-r_{+}}{r-r_{-}}\bigg |}. \end{aligned}$$

(22)

Fig. 1

The trajectory of a photon in the case of the Kerr black hole with $a=0.8$ (in the figure, we set $M=1$). The trajectory of a photon is plotted by the solid line, two horizons are illustrated by the dashed circles and the ring singularity is shown by short dot circle. In the (x, y)-plane, $x=\sqrt{r^{2}+a^{2}}\cos \phi$ and $y=\sqrt{r^{2}+a^{2}}\sin \phi$. As a photon approaches the Kerr black hole, it has a discontinuous orbit at the outer and inner horizons ($r_{+}=1.6$ and $r_{-}=0.4$). That is, the motion of the photon reverses at the horizons (see the left panel); thereafter, it is bending to the ring singularity

Fig. 2

The trajectory of the photon in the case of the Kerr-MOG black hole with $a=0.8$ and $\alpha =0.5$. As a photon approaches the Kerr-MOG black hole, it has a discontinuous orbit at the outer and inner horizons ($r_{+}=2.4274$ and $r_{-}=0.5726$). Consequently, the trajectory of the photon is similar to the Kerr black hole for horizons but the photon is bending rapidly to the ring singularity compared to the Kerr black hole

Fig. 3

The trajectory of a photon in the case of the Kerr-MOG black hole with $a=0.8$ and $\alpha =9$. As a photon approaches the ring singularity from the inner horizon, the trajectory of a photon explicitly shows that the photon is bending rapidly to the singularity compared to the case shown in Fig. 2

Like the Kerr black hole, Eqs. (21) and (22) show the motion of t and $\phi$ as r approaches $r_{+}$ and $r_{-}$. They also show null geodesics of the equatorial plane. Figures 1 and 2 describe the trajectory of an incoming a photon in the (x, y)-plane where $x=\sqrt{r^{2} + a^{2}}\cos {\phi }$ and $y=\sqrt{r^{2}+a^{2}}\sin {\phi }$. They have null geodesics in a Kerr black hole with intrinsic angular momentum $a=0.8M$ and a Kerr-MOG black hole with $a=0.8M$ and parameter $\alpha =0.5$. Since the horizons of the Kerr-MOG black hole are greater than the horizons of the Kerr black hole, the scale of the dynamics is different, as shown in Figs. 1 and 2. We explain the properties of the expanded horizons of the Kerr-MOG black hole in the next section in detail. Figure 3 clearly shows that the photon of the Kerr-MOG black hole is bending rapidly to the ring singularity compared to the case of a Kerr black hole when the photon shifts from the inner horizon into the singularity. But because the trajectory of a photon is discontinuous at the horizons the coordinate $\phi$ and t are not ‘good’ coordinates. The reason for the discontinuous orbit is that the radial motion for t is infinite at the two horizons (see the left panel of the Figs. 1 and 2). In other words, there is the coordinate singularity that is not an intrinsic singularity at two horizons. This problem can be resolved by a coordinate transformation such as the Kruskal coordinate transformation.

However, because we want to obtain a circular orbit we consider the critical value of the impact parameter $D_{c}$. In the case of $D=D_{c}$ the geodesic equation shows an unstable circular orbit of radius $r_{c}$. For $D<D_{c}$, the photon arrives near the black hole from infinity and crosses both horizons and falls into the singularity. (For $D>D_{c}$, two types of orbits can be obtained such as a photon arriving near the black hole from infinity and having perihelion distances greater than $r_{c}$ or aphelion distances less than $r_{c}$. Then the photon falls into the singularity at $r=0$ and $\theta =\frac{\pi }{2}$.) [18].

The radial equation is obtained at $\dot{r}=0$ and $\partial \dot{r}/\partial r=0$ as follows:

$$\begin{aligned} E^2 + \left( \frac{2M_{\alpha }}{r_{c}^{3}}-\frac{\beta ^{2}}{r_{c}^{4}}\right) (L-aE)^{2} - (L^{2}-a^{2}E^{2})\left( \frac{1}{r_{c}^{2}}\right) = 0\nonumber \\ \end{aligned}$$

(23)

and

$$\begin{aligned} \left( -\frac{6M_{\alpha }}{r_{c}^{4}}+\frac{4\beta ^{2}}{r_{c}^{5}}\right) (L-aE)^{2} + (L^{2}-a^{2}E^{2})\left( \frac{2}{r_{c}^{2}}\right) = 0.\nonumber \\ \end{aligned}$$

(24)

Substituting $D_{c}=\frac{L}{E}$ in Eqs. (23) and (24), we obtain

$$\begin{aligned} r_{c}^{4} - (D_{c}^{2}-a^{2})r_{c}^{2}+ 2M_{\alpha }(D_{c}-a)^{2}r_{c} - \beta ^{2}(D_{c}-a)^{2} = 0\nonumber \\ \end{aligned}$$

(25)

and

$$\begin{aligned} (D_{c}+a)r_{c}^{2} - 3M_{\alpha }(D_{c}-a)r_{c} + 2\beta ^{2}(D_{c}-a) = 0. \end{aligned}$$

(26)

We get solutions of the quadratic formula with respect to $r_{c}$ and $D_{c}$ in Eqs. (25) and (26), respectively, as follows:

$$\begin{aligned} D_{c}= & {} \frac{1}{(2M_{\alpha }r_{c}-\beta ^{2}-r_{c}^{2})}\Big [a(2M_{\alpha }r_{c}-\beta ^{2}) \nonumber \\&\pm \, \{(a(2M_{\alpha }r_{c}-\beta ^{2}))^{2}-(2M_{\alpha }r_{c}-\beta ^{2}-r_{c}^{2})\nonumber \\&\times \, (r_{c}^{4}+a^{2}r_{c}^{2}+2M_{\alpha }a^{2}r_{c} -\beta ^{2}a^{2}) \}^{\frac{1}{2}} \Big ] \end{aligned}$$

(27)

and

$$\begin{aligned} r_{c}= & {} \frac{1}{2(D_{c}+a)} \Big [3M_{\alpha }(D_{c}-a) \pm \{(3M_{\alpha }(D_{c}-a))^{2} \nonumber \\&-4(2\beta ^{2}(D_{c}-a)(D_{c}+a)) \}^{\frac{1}{2}} \Big ]. \end{aligned}$$

(28)

The values of the negative part of Eq. (27) and the positive part of Eq. (28) correspond to the prograde circular photon orbit. Also, their opposite values are corresponding to a retrograde circular photon orbit.

Therefore, we investigate the prograde and retrograde circular photon orbit outside the event horizon except for the circular photon orbit inside the inner horizon. A circular photon orbit of a Kerr-MOG black hole can be found numerically where we adopt $M=1$. Figure 4 shows the circular photon orbit of the Kerr-MOG black holes with respect to the intrinsic angular momentum a and parameter $\alpha$. We address a prograde circular orbit. The circular photon orbit of the Kerr black hole converges to 1 and is equal to the event horizon when $a=1$ but there are circular photon orbits of Kerr-MOG black holes at $a=1$. Thus, for rapidly spinning black holes $(a>1)$, there are always the circular photon orbits of the Kerr-MOG case. A Kerr black hole with $a=0.95$ has the radius of the circular photon orbit $r_{c}=1.386$ and the impact parameter $D_{c}=2.582$ for the null geodesics, while a Kerr-MOG black hole with $a=0.95$ and $\alpha =9$ has the radius of the circular photon orbit $r_{c}=20.007$ and the impact parameter $D_{c}=21.0097$. In Ref. [11], the photosphere is given by (Figs. 5 and 6)

$$\begin{aligned} r_\mathrm{ps} = \frac{3}{2}G_{N}(1+\alpha )M\left( 1+\sqrt{1-\frac{8\alpha }{9(1+\alpha )}}\right) . \end{aligned}$$

(29)

Fig. 4

Circular photon orbit of the Kerr black hole and the Kerr-MOG black hole. The solid line is the case of the Kerr black hole. A circular photon orbit is plotted on some intrinsic angular momentum a and parameter $\alpha$. In particular, it has a value greater than 3, different from the Schwarzschild metric, when a is zero. Moreover, the circular photon orbit of an extreme Kerr black hole ($a=1$) has 1 but the Kerr-MOG black hole shows $r_{c}>1$

Fig. 5

The trajectory of a test particle of the Kerr black hole with $a=0.8$. The trajectory of a test particle is plotted by the solid line, two horizons are illustrated by the dashed circles and the ring singularity is shown by a short dot circle

We consider the non-rotating case $a=0$, like the Schwarzschild-MOG black hole. Comparing this with a circular photon orbit of the Kerr-MOG, we obtain the same result ($r_\mathrm{ps}=21.7082$, $r_{c}=21.7082$) numerically in the case of $a=0$ and $\alpha$. We demonstrate that the photon circular orbit of Kerr-MOG black hole obeys the same results as the case of the Schwarzschild-MOG black hole for all values of parameter $\alpha$ when $a=0$. That is, Fig. 7 shows that the two lines overlap and increase as $\alpha$.

5 Innermost stable circular orbit (ISCO) of a test particle of Kerr-MOG black hole

Fig. 6

The trajectory of a test particle of the Kerr-MOG black hole with $a=0.8$ and $\alpha =0.5$. As a test particle approaches the two horizons, it is bending rapidly to the ring singularity comparing with Kerr black hole

Fig. 7

$r_\mathrm{ps}$ is photosphere or photon circular orbit of the Schwarzschild-MOG black hole and $r_{c}$ is the photon circular orbit of a Kerr-MOG black hole when $a=0$. For the two cases, the solutions coincide for all values of $\alpha$

The null geodesics of coordinate t and $\phi$ are ‘bad’ coordinates. Nevertheless, the null geodesics of coordinates t and $\phi$ are a valuable tool to study a spacetime diagram of the light-cone structure, like the Penrose diagram, by describing the conformal geometry of a black hole of coordinate t and $\phi$. Thus, we study timelike geodesics of the coordinates t and $\phi$ of the Kerr and the Kerr-MOG black hole.

For simplicity, we consider a a test particle of zero angular momentum. Thus, we set $L=0$ and $E=1$ and can avoid the complexity of the geodesic equations [18,19,20,21]. From Eq. (9), we obtain

$$\begin{aligned}&\dot{t} = \frac{1}{\varDelta r^{2}} [(r^{2}+a^{2})^{2}-a^{2}\varDelta ], \end{aligned}$$

(30)

$$\begin{aligned}&\dot{\phi } = \frac{a}{\varDelta r^{2}} [(r^{2}+a^{2})-\varDelta ], \end{aligned}$$

(31)

$$\begin{aligned}&\dot{r^{2}} = \left( \frac{2M_{\alpha }}{r}-\frac{\beta ^{2}}{r^{2}}\right) \left( 1+\frac{a^{2}}{r^{2}}\right) . \end{aligned}$$

(32)

The radial motions of the trajectory of the test particle are expressed by differentiating of the coordinate t and $\phi$ with respect to r:

$$\begin{aligned} \frac{\mathrm{d}t}{\mathrm{d}r}= & {} \frac{\dot{t}}{\dot{r}} = \frac{1}{\varDelta r^{2}} [(r^{2}+a^{2})^{2}-a^{2}\varDelta ]\nonumber \\&\times \,\Bigg [\bigg (\frac{2M_{\alpha }}{r} -\frac{\beta ^{2}}{r^{2}}\bigg )\bigg (1+\frac{a^{2}}{r^{2}}\bigg )\Bigg ]^{-\frac{1}{2}}, \end{aligned}$$

(33)

$$\begin{aligned} \frac{\mathrm{d}\phi }{\mathrm{d}r}= & {} \frac{\dot{\phi }}{\dot{r}} = \frac{a}{\varDelta r^{2}}(2M_{\alpha }r-\beta ^{2})\Bigg [\bigg (\frac{2M_{\alpha }}{r}-\frac{\beta ^{2}}{r^{2}}\bigg ) \nonumber \\&\times \,\bigg (1+\frac{a^{2}}{r^{2}}\bigg )\Bigg ]^{-\frac{1}{2}}. \end{aligned}$$

(34)

We numerically calculate $\mathrm{d}t/\mathrm{d}r$ and $\mathrm{d}\phi /\mathrm{d}r$ where we adopt $M=1$. Figures 5 and 6 illustrate orbits of the test particles of the Kerr and Kerr-MOG black holes in the (x, y)-plane where $x=\sqrt{r^{2} + a^{2}}\cos {\phi }$ and $y=\sqrt{r^{2}+a^{2}}\sin {\phi }$. They have timelike geodesics of a Kerr black hole with intrinsic angular momentum $a=0.8$ and Kerr-MOG black hole with $a=0.8$ and parameter $\alpha =0.5$. The trajectories of the test particles of the Kerr and Kerr-MOG black holes are described by the solid line. The horizons are described by the broken lines. Since the two horizons of the Kerr-MOG black hole are greater than the horizons of the Kerr black hole with parameter $\alpha$, the trajectory of the test particle is different from the case of the Kerr black hole. It is bending rapidly to the singularity. To obtain ISCO of a test particle around the Kerr-MOG black hole, we study timelike geodesics $(\mu =1)$ of the circular orbit of the test particle. We will use the reciprocal radius $u(=1/r)$ and $x=L-aE$ as independent variables and we consider $\dot{r}=0$ and $\partial \dot{r}/\partial r=0$. The radial equations are

$$\begin{aligned}&E^2-(x^{2}+2aEx)u^{2} +(2M_{\alpha }-\beta ^{2}u)x^{2}u^{3}\nonumber \\&\quad -(1+a^{2}u^{2}-2M_{\alpha }u+\beta ^2u^{2})=0 \end{aligned}$$

(35)

and

$$\begin{aligned}&-(x^{2}+2aEx)u^{2} +3M_{\alpha }x^{2}u^{3}-2\beta ^{2}x^{2}u^{4}\nonumber \\&\quad -(a^{2}u^{2}-M_{\alpha }u+\beta ^2u^{2})=0. \end{aligned}$$

(36)

Subtracting Eq. (36) from Eq. (35), we take

$$\begin{aligned} E^{2} = 1-M_{\alpha }u + M_{\alpha }x^{2}u^{3}-\beta ^{2}x^{2}u^{4} \end{aligned}$$

(37)

and from Eq. (36), we obtain

$$\begin{aligned} 2aExu = x^2 [3M_{\alpha }u - 2\beta ^{2}u^{2} - 1 ]u -(a^{2}u - M_{\alpha }) - \beta ^{2}u.\nonumber \\ \end{aligned}$$

(38)

We also can derive the quadratic equation for x from combining Eq. (37) with Eq. (38) and eliminating E,

$$\begin{aligned}&x^4u^2 [(3M_{\alpha }u-1)^{2} - 4a^{2}M_{\alpha }u^{3} + 4\beta ^{4}u^{4} \nonumber \\&\quad -4\beta ^{2}u^{2}(3M_{\alpha }u-1) + 4a^{2}\beta ^{2}u^{4} ] +(a^{2}u - M_{\alpha })^{2} + \beta ^{4}u^{2}\nonumber \\&\quad + 2\beta ^{2}u(a^{2}u-M_{\alpha })-2x^{2}u [(3M_{\alpha }u-1)(a^{2}u-M_{\alpha })\nonumber \\&\quad + 2a^{2}u - 2Ma^{2}u^{2} - 2\beta ^2u^{2}(a^{2}u - M_{\alpha })+\beta ^{2}u(3M_{\alpha }u-1)\nonumber \\&\quad - 2\beta ^{4}u^{3} ] = 0. \end{aligned}$$

(39)

The discriminant $\frac{1}{4}(b^{2}-4ac)$ of this equation is

$$\begin{aligned} 4a^{2}u^{3}(M_{\alpha } - \beta ^{2}u)\varDelta _{u}^{2}, \end{aligned}$$

(40)

where

$$\begin{aligned} \varDelta _{u} = a^{2}u^{2} - 2M_{\alpha }u + 1 +\beta ^{2}u^{2}. \end{aligned}$$

(41)

We take

$$\begin{aligned} x^{2}u^{2} = \frac{Q_{\pm }\varDelta _{u}-Q_{+}Q_{-}}{Q_{+}Q_{-}} = \frac{1}{Q_{\mp }}(\varDelta _{u} - Q_{\mp }), \end{aligned}$$

(42)

where

$$\begin{aligned}&Q_{+}Q_{-} = (3M_{\alpha }u - 2\beta ^2u^{2}-1)^{2} - 4a^{2}u^{3}(M_{\alpha } - \beta ^{2}u),\nonumber \\ \end{aligned}$$

(43)

$$\begin{aligned}&Q_{\pm } = 1 + 2\beta ^{2}u^{2} - 3M_{\alpha }u \pm 2a\sqrt{(M_{\alpha } - \beta ^{2}u)u^{3}}, \end{aligned}$$

(44)

and

$$\begin{aligned} \varDelta _{u} - Q_{\mp } = u\Big [a\sqrt{u} \pm \sqrt{(M_{\alpha } - \beta ^{2}u)}\Big ]^{2}. \end{aligned}$$

(45)

Therefore, the solution of the quadratic equation for x can be found:

$$\begin{aligned} x = - \frac{a\sqrt{u} \pm \sqrt{(M_{\alpha } - \beta ^{2}u)}}{\sqrt{uQ_{\mp }}}. \end{aligned}$$

(46)

Equation (46) shows that the upper sign in the foregoing equation refers to the counter-rotating orbit; on the other hand, the lower sign refers to the co-rotating orbit. We will use the lower sign to find ISCO of Kerr-MOG. The equation of energy E can be derived by substituting Eq. (46) in Eq. (37), with Eq. (12);

$$\begin{aligned} E= & {} \frac{1}{\sqrt{Q_{\mp }}}\Bigg [1 - 2G_{N}(1+\alpha )Mu + M^{2}G_{N}^2\alpha (1+\alpha )u^{2}\nonumber \\&\mp \, a\sqrt{ [G_{N}(1+\alpha )M - M^{2}G_{N}^{2}\alpha (1+\alpha )u ]u^{3}}\Bigg ]. \end{aligned}$$

(47)

According to $x = L-aE$, we find

$$\begin{aligned} L= & {} \mp \frac{\sqrt{G_{N}M(1+\alpha )-M^{2}G_{N}^2\alpha (1+\alpha )u}}{\sqrt{uQ_{\mp }}}\Bigg [a^{2}u^{2} + 1 \nonumber \\&\pm \frac{a\sqrt{u^{3}}}{\sqrt{G_{N}M(1+\alpha )-M^{2}G_{N}^2\alpha (1+\alpha )u}} \Bigg [2G_{N}M(1 \nonumber \\&+\, \alpha )-M^{2}G_{N}^2\alpha (1+\alpha )u ] \Bigg ]. \end{aligned}$$

(48)

We easily find the Kerr metric when $\alpha$ is zero,

$$\begin{aligned} E = \frac{1}{\sqrt{Q_{\mp }}}\Big [1 - 2G_{N}Mu \mp a\sqrt{G_{N}Mu^{3}}\Big ]. \end{aligned}$$

(49)

Fig. 8

Radius of stable circular orbit and energy E of a function of r. For $\alpha =9$, $a=0.95$, there is a minimum point at ISCO $r=38.672$ and energy E is a function of r. For $\alpha =0.5$, $a=0.95$, there is a minimum point of the effective potential equal to ISCO at $r=4.328$

Fig. 9

Comparing ISCOs of the Schwarzschild-MOG and Kerr black holes when $a=0$, two values coincide for all values of $\alpha$

Fig. 10

Event horizons (EH) and ISCOs of the Kerr-MOG black holes. The difference between ISCO and the outer horizon (EH) of Kerr-MOG black hole increases as parameter $\alpha$ increases

We have

$$\begin{aligned} L = \mp \frac{\sqrt{G_{N}M}}{\sqrt{uQ_{\mp }}}\Big [a^{2}u^{2} + 1 \pm 2a\sqrt{G_{N}Mu^{3}}\Big ]. \end{aligned}$$

(50)

Thus, we obtain numerical values of the ISCOs of Kerr-MOG black holes from Eq. (49) where we adopt $M=1$. Differentiating E for radius r leaves us with zero, that is,

$$\begin{aligned} \frac{\mathrm{d}E}{\mathrm{d}r} = 0. \end{aligned}$$

(51)

Fig. 11

ISCOs of Kerr-MOG black holes. ISCOs are plotted on some intrinsic angular momentum a and parameter $\alpha$. The solid line is the case of the Kerr black hole. The ISCO of the Kerr black hole converges to 1 at $a=1$, while the ISCO of the Kerr-MOG case is not. Thus, for rapidly spinning black holes $(a>1)$, there is an ISCO in the Kerr-MOG case

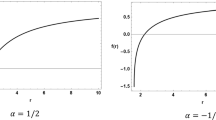
By the condition of Eq. (51), the radius of the ISCO is obtained at a minimum value of E. Figure 8 shows some examples of the minimum point of the energy of test particles having the radius of an ISCO of the Kerr-MOG black hole when $\alpha$ is 9 and a is 0.95 and when $\alpha$ is 0.5 and a is 0.95. In the case of a Kerr black hole, the radius of the ISCO depends on the intrinsic angular momentum a of the black hole. However, the radius of the ISCO of the Kerr-MOG black hole depends on a and the parameter $\alpha$, which is related to the gravitational constant G. In Fig. 9, there is the ISCO of the Schwarzschild-MOG black hole in Ref. [14] and we numerically calculate it by differentiating the critical energy ($\mathrm{d}\varepsilon _{0}/\mathrm{d}r$). We demonstrate that ISCOs of Kerr-MOG black holes lead to the same result as ISCOs of Schwarzschild-MOG black holes when $a=0$. Therefore, the two values for ISCOs of Kerr-MOG ($a=0$) and Schwarzschild-MOG black holes coincide for $\alpha$. Figure 10 shows that event horizons and ISCOs of Kerr-MOG black holes are proportional to the parameter $\alpha$. It shows that the difference between event horizon and ISCO of the Kerr-MOG black hole gradually increases as the parameter $\alpha$ increases. In the Fig. 10, the outer horizons for $a=0.5$ and $a=0.95$ show a slight difference. In Fig. 11, Comparing the Kerr with the Kerr-MOG black hole, the ISCO of the Kerr-MOG black hole is always greater than the ISCO of the Kerr black hole. In the case of a co-rotating orbit, the ISCO of the Kerr black hole converges to 1 and is equal to the event horizon when $a=1$, while the ISCO of the Kerr-MOG black hole is not. Thus, for rapidly spinning black holes $(a>1)$, there are ISCOs for the Kerr-MOG black holes. Figure 12 shows the curves for ISCOs of high values of parameter $\alpha$. The radius of the ISCO increases as the parameter $\alpha$ increases.

The Kerr-MOG ISCO can help in the study of comparing black hole shadows of the Kerr-MOG case with the astronomical observation of supermassive black holes like SgA* at the center of the Milky Way. It also can be expected to radiate more around a black hole as the difference between the ISCO and the event horizon of the black hole increases.

Fig. 12

ISCOs of Kerr-MOG black holes with large values of $\alpha$. The radii of the ISCOs decrease with increasing values of a and increase as $\alpha$ increases

6 Conclusions

In this paper, we investigated the rotating black hole in modified gravity theory, called the Kerr-MOG black hole. We have shown the trajectory of null and timelike geodesics of coordinates t and $\phi$ for the Kerr-MOG black hole. In particular, we have calculated conserved quantities for a photon and a test particle of Kerr-MOG black holes by using a well-established method [18, 19] and numerically computed the radius of the ISCO in a Kerr-MOG black hole. We also investigated the phenomena determined by the parameter $\alpha$ by comparing with the ISCO of the Kerr black hole. Thus, the following properties can be discovered:

• 1. For the Kerr-MOG black hole, the radius of the ISCO depends on parameter $\alpha$ as well as intrinsic angular momentum a.

• 2. The difference between the ISCO of the Kerr-MOG black hole and event horizon increases as the parameter $\alpha$ increases.

• 3. The ISCO of the Kerr black hole converges to 1 at $a=1$, while the ISCO of Kerr-MOG does not. Thus, for rapidly spinning black holes $(a>1)$, there are ISCOs of Kerr-MOG black holes.

• 4. Because the ring singularity of Kerr-MOG black hole does not change by $\alpha$ and two horizons have larger radii than the horizons of the Kerr black hole, trajectories of a photon and a test particle are bending rapidly to the singularity compared with a Kerr black hole.