1 Introduction

In recent years great interest has arisen in the study of higher order curvature theories of gravity [1,2,3,4]. Among all these higher curvature theories of gravity, the most widely studied theory of gravity is known as Einstein–Gauss–Bonnet (EGB) gravity. The Lagrangian of EGB gravity is the particular form of Lagrangian of Lovelock theory [5]. In a 4-dimensional vacuum theory of gravity, the most general Lovelock theory is a combination of the zeroth and first Euler density; in other words, general relativity (GR) with a cosmological constant. Also, it has been observed that the second Euler density is known as the Gauss–Bonnet combination, which is a topological invariant in 4 dimensions and does not contribute to the dynamical equations of the motion if included in the action [6]. Further, a simple and natural way to make a GB combination dynamical in 4-dimensional theory is to couple it to a dynamical scalar field. The perturbation method has been used to see the effects of the GB coupling term \(\alpha >0\) on the dynamical instability of non-static anisotropic fluid spheres [7]. The thermal aspects of a gravitating source in 5D EGB theory of gravity have been explored in detail by coupling the heat transport equation with the dynamical equations [8]. Boulware and Deser [4] have formulated the static black hole exact solutions in greater than or equal to 5-dimensional theories of gravity with a 4-dimensional GB term modifying the usual Einstein–Hilbert action [9].

Several LTB-like solutions Einstein field equations have been explored in higher order theories of gravity, which include the higher derivative curvature terms in their action. The higher curvature correction to the action has a great effect on the topological structure of the singularity appearing during the gravitational collapse of massive star [10]. In EGB theory of gravity with \(\alpha >0\), there exists a massive, naked and un-central singularity only in 5D, while such a singularity is disallowed in \(D\ge 6\) [11]. It has been the subject of great interest for many theoretical physicists to explore the slowly rotating BH solutions in Gauss–Bonnet theory of gravity. However, due to the nonlinearity of the field equations in GB gravity, it is very hard to obtain the exact analytic rotating black hole solutions in the framework of this theory. Therefore by introducing a small angular momentum as a perturbation into a rotating system, some BH solutions have been investigated in the past [12, 13]. Also, such slowly rotating BHs solutions exist in the EGB theory with an AdS term [14]. Using the linear order of the rotation parameter \(\textit{a}\), the slowly rotating charged/uncharged BHs solutions in AdS third order Lovelock gravity have been investigated in [15], which have some interesting physical features.

During the most recent decade AdS BHs and especially their thermodynamics have attracted the attention of many researchers due to AdS/CFT duality. In the AdS EGB gravity, the thermodynamical relations such temperature and entropy of the charged BHs get no corrections from the rotation parameter \(\textit{a}\) [16]. Zou et al. [17] have explored the thermodynamics of GB–Born–Infeld BHs in AdS space. Also, they have calculated the mass, temperature, entropy and heat of the resulting BHs. In third order Lovelock AdS gravity, the thermodynamic and conserved quantities of BHs with flat horizons are independent of the Lovelock coefficients [18]. Such interests in higher order theories of gravity have motivated us to study the gravitational collapse of a perfect fluid in EGB with the LTB model.

The stars are composed of some nuclear matter and gravitational collapse is the phenomenon in which the stars are continuously gravitating and attracted towards their centers due to the gravitational interaction of its particles. According to the singularity theorem [19], space-time singularities are generated during the continual gravitational collapse of massive stars. During the recent decades, it has been an interesting problem in astronomy and astrophysics to determine the final fate of gravitational collapse. In this connection, Oppenheimer and Snyder [20] were the pioneers who found the black hole as the end state of the dust collapse by using the static Schwarzschild space-time as an exterior space-time and a Friedmann like solution as an interior spacetime. Later on this work was extended with a positive and negative cosmological constant [21, 22]. Several authors [23,24,25,26,27,28,29,30,31,32,33] have discussed the phenomena of gravitational collapse using the dissipative and viscous fluid in general relativity. The lack of analytical consequences has lead to unproven conjectures namely, the cosmic censorship conjecture (CCC) [34], the hoop conjecture (HC) [35], and Seifert’s conjecture [36]. Oppenheimer and Snyder [20] considered a homogeneous spherical star with zero rotation and vanishing internal pressure under these ideal conditions, the cloud collapses simultaneously to a space-time singularity, which is enclosed by an event horizon. Further, it is interesting to study the gravitational collapse of stars with some realistic matter and geometry.

Recently, Jhingan and Ghosh [37], have studied the dust spherical collapse in 5 dimensions with GB term. They found the exact solutions in closed form with the marginally bound conditions. In this paper, we extended the work of Jhingan and Ghosh [37], to the case of a perfect fluid with marginally bound conditions. The paper has been arranged as follows: in Sect. 2, we present the exact solution of the field equation. Section 3 deals with a singularity analysis. In the last section, we summarize the results of the paper.

2 Exact solution of field equations in Einstein Gauss–Bonnet gravity

Here, the required 5D gravitational action is

$$\begin{aligned} S = \int \mathrm{d}^5 x \sqrt{-g} \left[ \frac{1}{2\kappa ^2_{5}}(R+\alpha L_\mathrm{GB})\right] +S_\mathrm{matter}, \end{aligned}$$
(1)

where R and \(\kappa _{5} \equiv \sqrt{8 \pi G_{5}} \), \(\alpha \) are the Ricci scalar, the gravitational constant in 5D, and the Gauss–Bonnet coupling constant, respectively. In this case the Gauss–Bonnet Lagrangian is

$$\begin{aligned} L_\mathrm{GB} = R^2 -4R_{\mu \nu } R^{\mu \nu } +R_{\mu \nu \gamma \lambda } R^{\mu \nu \gamma \lambda }. \end{aligned}$$
(2)

The above action appears as the low-energy limit of heterotic super-string theory [4] and \(\alpha \) is the inverse string tension, which is usually taken as positive finite, so we restrict ourselves to the case when \(\alpha \ge 0 \). The variation of the action (1) yields the following form of the equations of motion in Einstein Gauss–Bonnet gravity:

$$\begin{aligned} G_{\mu \nu } + \alpha H_{\mu \nu } = T_{\mu \nu }, \end{aligned}$$
(3)

where \(G_{\mu \nu }=R_{\mu \nu } - \frac{1}{2} g_{\mu \nu }R\) is the Einstein tensor and

$$\begin{aligned} H_{\mu \nu }= & {} 2[RR_{\mu \nu } -2 R_{\mu \alpha } R^{\alpha }_{\nu } -2R^{\alpha \beta } R_{\mu \alpha \nu \beta }+R^{\alpha \beta \gamma }_{\mu } R_{\nu \alpha \beta \gamma }]\nonumber \\&-\frac{1}{2} g_{\mu \nu } L_\mathrm{GB} \end{aligned}$$
(4)

is the Lanczos tensor. The stress-energy tensor for a perfect fluid is

$$\begin{aligned} T_{\mu \nu }=\Big ( \rho (r,t) +p(r,t)\Big )V_{\mu }V_{\nu }+p g_{\mu \nu } , \end{aligned}$$
(5)

where \(V_{\mu }= \delta ^{t}_{\mu }\) is the 5D velocity, \(\rho (r,t)\) is the energy density and p(r, t) is the isotropic pressure due to the fluid distribution in the interior region of a star. The LTB metric with co-moving coordinates in the 5D case [37,38,39,40] is

$$\begin{aligned} \mathrm{d}s^2 = -\mathrm{d}t^2 +B^2 \mathrm{d}r^2 + C^2 \mathrm{d}\Omega ^2_{3}, \end{aligned}$$
(6)

where \(B=B(r,t)\) and \(C=C(r,t)\), and \(\mathrm{d}\Omega ^2_{3} = (\mathrm{d}\theta ^2 +\sin ^2\theta (\mathrm{d}\phi ^2+\sin ^2\phi \mathrm{d}\psi ^2))\).

The set of independent field equations in Einstein–Gauss–Bonnet gravity for the metric (6) and stress-energy tensor (5) are

$$\begin{aligned}&\frac{12(C^{'2} -B^{2} (1+{\dot{C}}^2))}{C^{3} B^{5}} \Bigg (C{'} B{'} +B^{2} \dot{C} \dot{B} -B C''\Bigg )\alpha \nonumber \\&\quad - \frac{3}{B^3 C^2}\Bigg (B^3 (1+ \dot{C}^2)\nonumber \\&\quad +B^2C \dot{C} \dot{B} + C C' B' -B(CC'' +C^{'2})\Bigg ) = -\rho ,\end{aligned}$$
(7)
$$\begin{aligned}&-12 \alpha \Bigg (\frac{1}{C^3} -\frac{C^{'2}}{B^2C^3}+\frac{\dot{C}^2}{C^3}\Bigg )\ddot{C}\nonumber \\&\quad +3\frac{C^{'2}}{B^2C^2}-\frac{3\Bigg (1+ \dot{C}^2+C \ddot{C}\Bigg )}{C^2} = p,\end{aligned}$$
(8)
$$\begin{aligned}&\frac{4 \alpha }{B^4 C^2}\Bigg [-2B\Bigg (B'C'+B^2\dot{B} \dot{C}-BC''\Bigg )\ddot{C}\nonumber \\&\quad +B\Bigg (C^{'2} -B^2 (1+\dot{C}^2)\Bigg )\ddot{B}+2\Bigg (\dot{B}C'-B\dot{C}'\Bigg )\Bigg ]\nonumber \\&\quad -\frac{1}{B^3C^2}\Bigg [B^3\Bigg (1+\dot{C}^2+2C\ddot{C}\Bigg )+B^2C\Bigg (2\dot{C}\dot{B}+C\ddot{B}\Bigg )\nonumber \\&\quad +2CC'B'-2B\Bigg (CC''+C^{'2}\Bigg )\Bigg ]= p, \end{aligned}$$
(9)
$$\begin{aligned} \frac{12 \alpha }{B^5C^3}\Bigg (\dot{B}C'-B\dot{C}'\Bigg )\Bigg (B^2\Bigg (1+\dot{C}^2\Bigg )-C^{'2}\Bigg )-3 \frac{B \dot{C}'-\dot{B}C'}{B^3C} =0, \end{aligned}$$

where a dot \( =\partial _t\) and a prime \(=\partial _r\). After some simplification Eq. (10) yields two families of solutions in the following form:

$$\begin{aligned} B(t,r)= & {} \frac{C'}{Z},\end{aligned}$$
(10)
$$\begin{aligned} B(t,r)= & {} {\pm } \frac{2\sqrt{\alpha }C'}{\left( C^2 + 4 \alpha (\dot{C}^2 +1)\right) ^{1/2}}, \end{aligned}$$
(11)

where \(Z=Z(r)\) is a function of integration. The solution for B(r, t) in Eq. (10) is similar to 5D-LTB solution [38,39,40], while the solution in Eq. (11) is trivial for \(\alpha \rightarrow 0\), hence we take the non-trivial form of B(r, t) given in Eq. (10). Now Eq. (8) with Eq. (10) gives

$$\begin{aligned} \frac{\ddot{C}}{C}=\frac{\dot{C}^2 - (Z^2-1)+\frac{C^2p}{3}}{4 \alpha (Z^2 -1 -\dot{C}^2)-C^2}. \end{aligned}$$
(12)

Now we have to solve the above equation analytically for C(r, t), this requires that we have to integrate the above twice with respect to t. Since this equation involves the unknown function p(r, t), when we try to integrate Eq. (12), we cannot get the exact solution because there is the unknown function p(r, t); to get rid of it, we try to make it at least independent of t. To this end, we apply the conservation of the energy-momentum tensor which makes it independent of r. But our purpose is to make it independent of t, and for this purpose we take p(t) as a polynomial in t, then after some simplification, we make it constant (as in [41]). This whole procedure is explained as follows.

The conservation of the energy-momentum tensor gives

$$\begin{aligned} \frac{\partial p}{\partial r}=0,\quad \Rightarrow p=p(t). \end{aligned}$$
(13)

We consider p as a polynomial in t as given by [41]

$$\begin{aligned} p(t)=p_0\left( \frac{t}{T}\right) ^{-c}, \end{aligned}$$
(14)

where T is the constant time introduced in the problem due to physical reasons by re-scaling of \(t;~p_0\) and c are positive constants. Further, for the integration of Eq. (12), we take \(c=0\) in Eq. (14), so that

$$\begin{aligned} p(t)=p_0. \end{aligned}$$
(15)

There are many other choices for p(t), so Eq. (14) is not always a unique choice for p(t). For example it can be treated with \(c\ne 0\), but such choices do not provide the results in closed form which reduce to a 5D dimensional perfect fluid collapse in the limit \(\alpha \rightarrow 0\) [33, 39, 40], and we do not recover the results of 5D dust collapse in Einstein–Gauss–Bonnet gravity as \(p\rightarrow 0\) [37]. That is why we have taken the pressure as constant which is a better choice in the present situation. Further, some other choice of p(t), as defined in Refs. [41, 42], may produce interesting numerical results but such solutions may be considered explicitly in a future investigation by taking an anisotropic fluid.

Using the above equation in Eq. (12) and intergrading, one get

$$\begin{aligned} \dot{C}^2\left[ 1-4 \alpha \left( \frac{Z^2 -1}{C^2}\right) \right]= & {} (Z^2 -1)+\frac{\zeta }{C^2}-\frac{1}{6}C^2p_0\nonumber \\&-2 \alpha \frac{\dot{C}^4}{C^2}. \end{aligned}$$
(16)

where \(\zeta =\zeta (r)\), is integration function and assumed as a mass function. Equation (16) is the main equation of the system. By using Eqs. (10) and (16) into Eq. (7), we get

$$\begin{aligned} \zeta ' =\frac{2}{3}C^3C' (\rho +p_0). \end{aligned}$$
(17)

The integration of the above equation yields

$$\begin{aligned} \zeta (r)=\frac{2}{3}\int (\rho +p_0)C^3 \mathrm{d}C. \end{aligned}$$
(18)

Here, we have used \(\zeta (0)=0\). The validity of the energy conditions is necessarily a requirement for a physically reasonable energy-momentum tensor. The energy conditions for a perfect fluid in this case are the following:

$$\begin{aligned}&{NEC}:\rho +p_0\ge 0,\end{aligned}$$
(19)
$$\begin{aligned}&{WEC}:\rho \ge 0, \quad \rho +p_0\ge 0,\end{aligned}$$
(20)
$$\begin{aligned}&{SEC}:\rho +p_0\ge 0, \quad \rho +3p_0\ge 0. \end{aligned}$$
(21)
Fig. 1
figure 1

This graph shows the validity of null energy condition for \(p_0>0\), \(\zeta '(r)>0\)

Full size image
Fig. 2
figure 2

This graph shows the validity of weak energy condition

Full size image
Fig. 3
figure 3

This graph shows the validity of null energy condition for \(p_0>0\)

Full size image

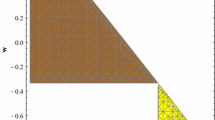
From Eq. (17), we see that, for \(\zeta '(r)>0\), \(C>0\) and \(C'>0\), one gets \(\rho +p_0>0\) and the null energy condition is valid as shown in Fig. 1. Using Eq. (11), the marginally bound condition \(Z=1\), \(\dot{C}<0\), \(\dot{C'}<0\) along with the above mentioned conditions in the field equations (8) and (10), we get \(\rho \ge 0\) as shown in Fig. 2. Also, the field equations (8), (10) and (15) along with the above mentioned conditions yield \(\rho +3p_0\ge 0\) as shown in Fig. 3. Hence null, weak and strong energy conditions are valid with restrictions on C and its derivatives.

In the limit \(\alpha \rightarrow 0\), Eq. (16) gives the 5D perfect fluid solutions [39, 40]

$$\begin{aligned} \dot{C}^2 = Z^2 -1+\frac{\zeta }{C^2}-\frac{1}{6}C^2p_0. \end{aligned}$$
(22)

Now the above equation yields three solutions: hyperbolic, parabolic, and elliptic solutions if \(Z > 1\), \(Z = 1\) or \(Z< 1\), respectively [39, 40]. For simplicity, we take \(Z = 1\), which is the marginally bound case. In order to proceed, we write Eq. (16), in the following simplified form:

$$\begin{aligned} \dot{C}^2= & {} (Z^2 -1)- \frac{C^2}{4 \alpha }\nonumber \\&\times \left( 1{\mp } \sqrt{\left[ 1 + \frac{16 \alpha ^2}{C^4}(Z^2 -1)^2 -\frac{4}{3} \alpha p_0+\frac{8 \alpha \zeta }{C^4}\right] }\right) ,\nonumber \\ \end{aligned}$$
(23)

corresponding to \({\mp }\) sign in Eq. (23), there are two families of solutions. In the limit \(\alpha \rightarrow 0\) for the minus solution, we get a \(5D-LTB\) solution [40]; however, no results are available in the literature if one applies the limit \(\alpha \rightarrow 0\) to the plus branch solution; yet such solutions are very interesting as these provide the contribution of pure Gauss–Bonnet terms, here we discuss both these solutions and their singularity structure explicitly.

2.1 Minus branch solution

Maeda [43] found the LTB models near the region \(r \sim 0\), in the framework of EGB without finding an explicit solution. Also, Jhingan and Ghosh [37] explored \(5D-LTB-EGB\) gravitational collapse with dust matter as the source of gravity. In this work, we determine the exact solution of the \(5D-LTB\) model in EGB gravity with a perfect fluid in closed form to see the effect of pressure on the final fate of gravitational collapse. Hence, we consider the minus branch solution with the marginally bound case, \(Z=1\). Integrating Eq. (23), we have

$$\begin{aligned}&t_\varsigma (r)-t=\frac{\sqrt{\alpha }}{2\sqrt{2}} \tan ^{-1}\nonumber \\&\quad \times \left[ \frac{3C^2(1-\frac{4}{3} \alpha p_0) -\sqrt{C^4(1-\frac{4}{3} \alpha p_0) +8 \alpha \zeta }}{2\sqrt{2}C(1-\frac{4}{3} \alpha p_0)[\sqrt{C^4(1-\frac{4}{3} \alpha p_0)+8 \alpha \zeta }-C^2]^{1/2}}\right] \nonumber \\&\quad +\sqrt{\frac{\alpha C^2(1-\frac{4}{3} \alpha p_0)^2}{\sqrt{C^4(1-\frac{4}{3} \alpha p_0)+8 \alpha \zeta }-C^2}}, \end{aligned}$$
(24)

where \(t_\varsigma (r)\) is a function of integration, which is related to the time of formation of the singularity. Without loss of generality, we consider \(t=0\), r coincides with the area radius,

$$\begin{aligned} C(0,r)=r. \end{aligned}$$
(25)

The above two equations lead to

$$\begin{aligned} t_\varsigma= & {} \frac{\sqrt{\alpha }}{2\sqrt{2}}\tan ^{-1}\nonumber \\&\times \left[ \frac{3(1-\frac{4}{3}\alpha p_0)-\sqrt{1-\frac{4}{3}\alpha p_0+8 \alpha \tilde{\zeta }}}{2 \sqrt{2}(1-\frac{4}{3}\alpha p_0)[\sqrt{1-\frac{4}{3}\alpha p_0+8 \alpha \tilde{\zeta }}-1]^{1/2}}\right] \nonumber \\&+\sqrt{\frac{\alpha (1-\frac{4}{3}\alpha p_0)^2}{\sqrt{1-\frac{4}{3}\alpha p_0+8 \alpha \tilde{\zeta }}-1}} , \end{aligned}$$
(26)

where \(\tilde{\zeta }=\zeta /r^4\). It is the time of formation of a singularity which is affected by pressure and \(\alpha \).

The Kretschmann scalar \(K=R_{\mu \nu \gamma \lambda }R^{\mu \nu \gamma \lambda },\) given (6) with Eq. (10), takes the following form:

$$\begin{aligned} K = 12 \frac{\ddot{C}^2}{C^2} +12 \frac{\dot{C^4}}{C^4} +4 \frac{\ddot{C'}^2}{C^{'2}}+12 \frac{\dot{C^2}\dot{C^{'2}}}{C^{'2} C^2}. \end{aligned}$$
(27)

It is finite on the initial data surface. From the field equations the energy density is

$$\begin{aligned} \rho (t, r) = \frac{3 \zeta '}{2C^3 C'}-p_0. \end{aligned}$$
(28)

Hence, it is clear that if \(\zeta '\) is finite and strictly positive in the entire domain, then \(\rho \rightarrow \infty \) when \(C'=0\) and \(C=0\). The shell crossing and shell focusing singularities occur for \(C'=0\) and \(C=0\), respectively [37]. Also, the Kretschmann scalar diverges at \(t=t_{c}(r)\), this implies the existence of a curvature singularity [19]. Using Eq. (24), the shell focusing singularity curve is

$$\begin{aligned} t_{c}(r)=t_{\varsigma }(r)+\frac{\pi \sqrt{\alpha }}{4 \sqrt{2}}. \end{aligned}$$
(29)

The trapped surfaces are surfaces whose outward normals are null,

$$\begin{aligned} g^{\mu \nu } C_{,\mu }C_{,\nu } = - \dot{C^2}+\frac{C^{'2}}{B^2} = 0. \end{aligned}$$
(30)

Now Eqs. (16) and (30) yield the horizon radius

$$\begin{aligned} C(t_{AH}(r), r)= \frac{1}{\sqrt{p_0}}\sqrt{\sqrt{6p_0(\zeta -2 \alpha )+9}-3}. \end{aligned}$$
(31)

In the above equation, the location of apparent horizons is affected by \(\alpha \) and \(p_0\). Simplifying Eqs. (24) and (29), we get the horizon curve

$$\begin{aligned}&t_{c}(r)-t=\frac{\pi \sqrt{\alpha }}{4\sqrt{2}}+\sqrt{\frac{\alpha C^2(1-\frac{4}{3} \alpha p_0)^2}{\sqrt{C^4(1-\frac{4}{3}\alpha p_0)+8 \alpha \zeta }-C^2}}\nonumber \\&\quad +\frac{\sqrt{\alpha }}{2\sqrt{2}}\tan ^{-1}\left[ \frac{3C^2(1-\frac{4}{3}\alpha p_0)-\sqrt{C^4(1-\frac{4}{3}\alpha p_0)+8 \alpha \zeta }}{2\sqrt{2}C(1-\frac{4}{3}\alpha p_0)[\sqrt{C^4(1-\frac{4}{3}\alpha p_0) +8 \alpha \zeta }-C^2]^{1/2}}\right] .\nonumber \\ \end{aligned}$$
(32)

Now combining Eqs. (31) and (32), we get

$$\begin{aligned}&t_{c}(r)-t_{AH}(r)=\frac{\pi \sqrt{\alpha }}{4\sqrt{2}}\nonumber \\&\quad +\sqrt{\frac{\alpha (Q-3)(1-\frac{4}{3}\alpha p_0)^2}{\sqrt{(Q-3)^2 (1-\frac{4}{3}\alpha p_0)+8 \alpha {p_0}^2 \zeta }-(Q-3)}}+\frac{\sqrt{\alpha }}{2\sqrt{2}}\tan ^{-1}\nonumber \\&\quad \times \left[ \frac{3(Q-3)(1-\frac{4}{3} \alpha p_0)-\sqrt{(Q-3)^2(1-\frac{4}{3} \alpha p_0)+8\alpha {p_0}^2 \zeta }}{2\sqrt{2 (Q-3)(1-\frac{4}{3} \alpha p_0)[(Q-3)^2(1-\frac{4}{3} \alpha p_0)+8\alpha {p_0}^2 \zeta -(Q-3)]^{1/2}}}\right] ,\nonumber \\ \end{aligned}$$
(33)

where \(Q=\sqrt{6p_0\zeta -12\alpha p_0+9}\).

It is to be noted that, for \(\alpha >0\), the time difference between the formation of central singularity and apparent horizon is affected by the pressure. We would like to mention that all the results reduced to the dust case [37], when \(p_0=0\).

2.2 Plus branch solution

The plus branch solution of Eq. (23) when subjected to the marginally bound condition is given by

$$\begin{aligned} t_c(r)-t(r)= & {} \frac{1}{2}\log \left| 8\alpha \zeta \left| -\frac{\sqrt{\alpha }}{2\sqrt{2}} \log \right| C^{2}(1-\frac{4}{3}\alpha p_{0})\right. \nonumber \\&\left. -\sqrt{C^{4}(1-\frac{4}{3}\alpha p_{0})+8\alpha \zeta }+\sqrt{2}C(1-\frac{4}{3}\alpha p_{0})\right. \nonumber \\&\left. \times \left( \sqrt{\sqrt{C^{4}(1-\frac{4}{3}\alpha p_{0})+8\alpha \zeta }+C^{2}}\right) \right| \nonumber \\&+ \sqrt{\frac{\alpha C^2(1-\frac{4}{3} \alpha p)^2}{\sqrt{C^4(1-\frac{4}{3} \alpha p)+8 \alpha \zeta }-C^2}}. \end{aligned}$$
(34)

After applying the same procedure as in the previous case, we get

$$\begin{aligned} t_c(r)-t_{AH}= & {} \frac{1}{2}\log \Bigg |8\alpha \zeta \left| +\frac{\sqrt{\alpha }}{2\sqrt{2}} \log \right| \frac{1}{p_{0}}\Bigg [(Q-3)\nonumber \\&\times \left( 1-\frac{4}{3}\alpha p_{0}\right) +\sqrt{(Q-3)^{2}\left( 1-\frac{4}{3}\alpha p_{0}\right) +8\alpha \zeta }\nonumber \\&+\sqrt{2(Q-3)}\left( 1-\frac{4}{3}\alpha p_{0}\right) \nonumber \\&\times \Bigg (\sqrt{\sqrt{(Q-3)^{4}\left( 1-\frac{4}{3}\alpha p_{0}\right) +8\alpha \zeta }+(Q-3)}\Bigg )\Bigg ]\Bigg |\nonumber \\&+ \sqrt{\frac{\alpha (Q-3)\left( 1-\frac{4}{3} \alpha p_0\right) ^2}{\sqrt{(Q-3)^{2}\left( 1-\frac{4}{3} \alpha p_0\right) +8 \alpha \zeta }+(Q-3)}}.\nonumber \\ \end{aligned}$$
(35)

This implies that horizons form after the formation of a singularity, hence the singularity is uncovered due to the absence of event horizons, and the end state of gravitational collapse is a naked singularity.

3 Summary and conclusion

The Einstein–Gauss–Bonnet theory of gravity is the low-energy limit of supersymmetric string theory [44]. Here, we have investigated the exact solution of the field equations in the frame work of EGB theory with LTB model which enclosed the inhomogeneous perfect fluid in 5D. In order to do so, the marginally bound condition has been imposed on the dynamical equation. The conservation of the energy-momentum tensor implies that \(\frac{\partial p}{\partial r}=0,\) which produces the result \(p=p(t)\). Further, it has been taken as a constant, \(p_0\), by using some physical assumptions as given by Eq. (14). The procedure along with marginally bound condition enables us to integrate the differential equation Eq. (8) analytically in closed form. It has been found that the resulting solution implies the spherical inhomogeneous prefect fluid gravitational collapse. The coupling constant \(\alpha \) has direct effect on the resulting singularity and the end state of gravitational collapse is reversed. For \(\alpha > 0\), there exists a naked singularity. The time formation of singularity and horizons is deeply affected by the pressure term. The presence of pressure also reduces the total matter density of the gravitating system.

The position of the apparent horizon in the space-time is affected by the factor \(2 \alpha \) and the pressure \(p_0\). Due to the presence of second order curvature corrections in EGB gravity the out product collapse is a massive naked singularity, which is not admissible in \(5D-LTB\). The prediction as regards the regular initial data has been made that it results in the formation of a massive naked singularity, and that is in contradiction to CCC. The singularity in this case is weaker as compared to the corresponding \(5D-LTB\); therefore the existence of a naked singularity in the present case is not a serious contradiction of CCC. According to the Seifert conjecture [9] when a strictly positive finite amount of matter undergoes gravitational contraction, then one point is always hidden, which is a counterexample to the Seifert conjecture. It has been investigated that singularities are formed rather than horizons in the marginally bound case \((Z(r)=1)\), hence no BH is formed, and hence they must violate HC. In other words the present analysis is a counterexample to all three conjectures. But this analysis does not provide serious threats to CCC.