Two Higgs bosons near 125 GeV in the NMSSM: beyond the narrow width approximation

Abstract

In the next-to-minimal supersymmetric (NMS) Standard Model (SM), it is possible for either one of the additional singlet-like scalar and pseudoscalar Higgs bosons to be almost degenerate in mass with the $\sim$ $125$ GeV SM-like Higgs state. In the real NMSSM (rNMSSM), when the mass difference between two scalar states is comparable to their individual total decay widths, the quantum mechanical interference, due to the relevant diagonal as well as off-diagonal terms in the propagator matrix, between them can become sizeable. This possibility invalidates usage of the narrow width approximation (NWA) to compute the cross section for the production of a di-photon pair with a given invariant mass via resonant Higgs boson(s) in the gluon fusion process at the Large Hadron Collider (LHC). When, motivated by the baryon asymmetry of the universe, CP-violating (CPV) phases are explicitly invoked in the Higgs sector of the NMSSM, all the interaction eigenstates mix to give five CP-indefinite physical Higgs bosons. In this scenario, the interference effects due to the off-diagonal terms in the Higgs mass matrix that mix the pseudoscalar-like state with the SM-like one can also become significant, when these two are sufficiently mass-degenerate. We perform a detailed analysis, in both the real and complex NMSSM, of these interference effects, when the full propagator matrix is taken into account, in the production of a photon pair with an invariant mass near 125 GeV through gluon fusion. We find that these effects can account for up to $\sim$ $40$% of the total cross section for certain model parameter configurations. We also investigate how such mutually interfering states contributing to the $\sim$ $125$ GeV signal observed at the LHC can be distinguished from a single resonance.

1 Introduction

The discovery of a Higgs boson [1, 2] at the LHC provides convincing evidence of spontaneous electro-weak (EW) symmetry breaking (SB) through the Higgs mechanism. It is also intriguing that the subsequent measurements of its properties have shown their remarkable agreement with the expectations from the SM of particle physics. These measurements include the signal rates and coupling strengths in the various Higgs boson production and decay channels that have so far been analysed, as well as its spin and parity. However, the shortcomings of the standard Higgs mechanism, including primarily the stability of the mass of the Higgs boson against large quantum corrections, need to be addressed properly in order to completely understand the dynamics of EWSB. Putting this together with other unresolved issues in the SM, such as its inability to explain the mass of neutrinos, the nature of dark matter (DM) and the large baryon asymmetry of the universe, compel us to believe that the elementary particle spectrum could be richer than the minimal one embedded in the SM.

Supersymmetry (SUSY), proposed originally as a remedy for some of the above problems faced by the SM, presents an appealing explanation for the stability of the Higgs mass, while providing also a natural candidate for DM. However, its minimal manifestation, known as the minimal supersymmetric Standard Model (MSSM), is becoming increasingly constrained by the LHC measurements of the Higgs boson properties, besides becoming more and more fine-tuned in explaining null searches for its own direct signatures (i.e., of sparticle states). The MSSM is also troubled by issues arising purely from naturalness considerations, like the presence of a quadratic Lagrangian term with a new mass parameter, $\mu$, which is phenomenologically required to lie at the EW scale but has no theoretical ground to do so [3, 4]. The NMSSM was proposed to take care of this so-called $\mu$-problem through the introduction of a new singlet scalar superfield [5,6,7,8]. The presence of this superfield leads to two additional neutral Higgs mass eigenstates in the NMSSM (see, e.g., [9, 10] for reviews) compared to the MSSM. When all the parameters in the Higgs and sfermion sectors are assumed to be real and hence CP-conserving (CPC), one of these two additional states is a scalar and the other a pseudoscalar. With five neutral Higgs bosons in total, the real NMSSM (rNMSSM) provides some unique possibilities for collider phenomenology.

In multi-Higgs models like the MSSM and NMSSM, the observed signature near 125 GeV can in principle be explained in terms of a single Higgs resonance or, alternatively, two or more Higgs resonances that cannot be individually resolved by the experiment as yet. In the MSSM, the possibility of the two scalars both lying near 125 GeV is ruled out by the fact that such a mass for one of the scalars generally necessitates the other scalar to be essentially decoupled, and hence much heavier or lighter (see, e.g., [11]). In the rNMSSM, in contrast, it is still a plausible scenario, as discussed in [12,13,14,15,16]. The alternative possibility of a pair of $\sim$ $125$ GeV scalar and pseudoscalar has also been studied in [17].

In the NMSSM, to address the baryonic asymmetry of the universe, CP-violation can be invoked directly and explicitly in the Higgs sector at the tree level, unlike in the MSSM, where it is only radiatively induced into the Higgs sector beyond the Born approximation. This is done by taking the Higgs sector trilinear couplings to be complex parameters, hence we refer to this version of the model as the complex NMSSM (cNMSSM) here. For non-zero CPV phases of these parameters, instead of the distinct CP-even and CP-odd Higgs bosons, the model contains five CP-indefinite neutral states. This CP mixing in the Higgs sector can get additional contributions from the complex Higgs–sfermion–sfermion couplings as well as the phases in the neutralino–chargino sector, as in the CPV MSSM. Consequently, depending on the sizes of these phases, the mass spectrum and production/decay rates of the Higgs states can get considerably modified compared to the CPC case [18], similarly to the MSSM [19,20,21,22,23,24,25,26,27,28,29]. The phenomenology of a single CPV Higgs boson near 125 GeV in the cNMSSM has been studied for a variety of possible underlying scenarios in [18, 30, 31]. The specific case of two mass-degenerate Higgs resonances near 125 GeV within the cNMSSM has also been considered in [32], where it was shown that these can give a better fit to the LHC Run-I data, performed using the program HiggsSignals [33], compared to a single resonance.

In all the above-mentioned analyses of two $\sim$ $125$ GeV Higgs bosons in the NMSSM, it was assumed that each of them is produced on-shell and decays subsequently into any of the observed final states. However, for very strong mass degeneracy, it is possible that the two Higgs states produced in gluon fusion oscillate into each other before they decay. This could be perceived as being facilitated through quantum corrections of the propagator with two different mass eigenstates at the two ends. Such effects, coming into play beyond a Breit–Wigner (BW) resonance, in general contexts as well as in specific scenarios like the CPC MSSM, have been considered in some studies [34,35,36,37]. The specific case of the CPV MSSM with one-loop effects in the full propagator was treated in [26].

The purpose of the present work is to explore this possibility of quantum mechanical interference between two Higgs states near 125 GeV in the NMSSM, both real and complex. We shall demonstrate here that the inclusion of such effects enhances the span of the model solutions mimicking the LHC observation. We shall then investigate possible ways to identify signatures of such a coupled system of Higgs bosons through a shape study of the profile of the resonance in the invariant mass distribution of the di-photon decay products. The analysis is carried out by first performing numerical scans of the model parameter space to identify specific Benchmark Points (BPs) where two of the Higgs bosons are degenerate with mass around 125 GeV, within the uncertainty allowed by present LHC measurements. For these BPs, we then calculate the cross section for the production of a di-photon pair with invariant mass near 125 GeV via Higgs resonance(s) in the gluon fusion process at the LHC, using a Monte Carlo (MC) integration code developed in-house. This cross section is calculated assuming three different approaches: the full Higgs propagator matrix in the amplitude; only diagonal terms in the propagator matrix; for the two Higgs bosons individually without any mutual interference. A comparison of these three cross sections shows significant effects of interference, with the full propagator case deviating by up to about 38% compared to the sum of the two individual Higgs boson contributions, along with a hint of a distortion in the line-shape of the differential distribution.

The article is organised as follows. In the next section we will briefly revisit the Higgs sector of the NMSSM. In Sect. 3 we will derive the analytical expression for the cross section that includes the full Higgs propagator matrix. In Sect. 4 we will provide details of our methodology for the numerical analysis. In Sect. 5 we will discuss the results of our analysis and in Sect. 6 we will present our conclusions.

2 The NMSSM Higgs sector

The NMSSM is defined by the superpotential

$$\begin{aligned} W_\mathrm{NMSSM}= & {} h_u\, \widehat{Q} \cdot \widehat{H}_u\; \widehat{U}^c_R + h_d\, \widehat{H}_d \cdot \widehat{Q}\; \widehat{D}^c_R + h_e\, \widehat{H}_d \cdot \widehat{L}\; \widehat{E}_R^c\nonumber \\&+ \lambda \widehat{S} \widehat{H}_u \cdot \widehat{H}_d + \frac{\kappa }{3}\ \widehat{S}^3, \end{aligned}$$

(1)

where $y_u$, $y_d$ and $y_e$ are the quark and lepton Yukawa coupling constants, $\hat{Q}$ and $\hat{L}$ are the left-handed quark and lepton doublet superfields, $\hat{U}$, $\hat{D}$ and $\hat{E}$ are the right-handed up-type, down-type and electron-type singlet superfields, respectively, and the charge conjugation is denoted by the superscript c. Furthermore, $\hat{H}_u$ and $\hat{H}_d$ in the above superpotential are $SU(2)_L$ Higgs doublet superfields with opposite hypercharge, $Y = \pm 1$, as in the MSSM, and $\hat{S}$ is a Higgs singlet superfield. Here, $\lambda$ and $\kappa$ are dimensionless trilinear coupling constants.

The fourth term on the right hand side of Eq. (1) replaces the Higgs-higgsino mass term, $\mu \hat{H}_u \hat{H}_d$, present in the MSSM superpotential. The Higgs singlet superfield acquires a non-zero vacuum expectation value (VEV), $v_s$, after EWSB. This $v_s$ is naturally of the order of the SUSY-breaking scale $M_\mathrm{SUSY}$ (herein operationally defined as $M_\mathrm{SUSY}^2 = \frac{m^2_{\tilde{t}_1} + m^2_{\tilde{t}_2}}{2}$, where $m_{\tilde{t}_1}$ and $m_{\tilde{t}_2}$ are the physical masses of the two stops), thus solving the $\mu$-problem of the MSSM by generating an effective $\mu$-term,

$$\begin{aligned} \mu _{\mathrm{eff}} \equiv \lambda \langle \hat{S} \rangle = \lambda v_s. \end{aligned}$$

(2)

The absence of a $\mu \hat{H}_u \hat{H}_d$ term, however, results in a $U(1)_\mathrm{PQ}$ symmetry, which is explicitly broken here by the last term in Eq. (1), thus introducing instead a discrete $Z_3$ symmetry and making the NMSSM superpotential scale-invariant as well.

The Higgs potential, derived from the above superpotential, is given as

$$\begin{aligned} V_0= & {} {| \lambda (H_u^+ H_d^- - H_u^0 H_d^0 ) + \kappa S^2 |}^2 \nonumber \\&+ (m_{H_u}^2 + {| \mu + \lambda S |}^2 ) ({| H_u^0 |}^2 + {| H_u^+ |}^2 ) \nonumber \\&+ (m_{H_d}^2 + {| \mu + \lambda S |}^2 ) ({| H_d^0 |}^2 + {| H_d^- |}^2 ) \nonumber \\&+ \frac{g^2}{4} ({| H_u^0 |}^2 + {| H_u^+ |}^2 - {| H_d^0 |}^2 - {| H_d^- |}^2 )^2 \nonumber \\&+ \frac{g_2^2}{2} {| H_u^+ H_d^{0*} + H_u^0 H_d^{-*} |}^2 + m_S^2 {| S |}^2 \nonumber \\&+ [ \lambda A_{\lambda } (H_u^+ H_d^- - H_u^0 H_d^0 ) S + \frac{1}{3} \kappa A_{\kappa } S^3 + \mathrm{h.c.}], \end{aligned}$$

(3)

where $g_1$ and $g_2$ are the $U(1)_Y$ and $SU(2)_L$ gauge coupling constants, respectively, and $g^2 = \frac{g_1^2+g_2^2}{2}$. Here, $A_{\lambda }$ and $A_{\kappa }$ are soft SUSY-breaking Higgs trilinear couplings, while $m_{H_d}$, $m_{H_u}$ and $m_S$ denote the soft Higgs masses. The fields $H_d$, $H_u$ and S are expanded about their respective VEVs, $v_d$, $v_u$ and $v_s$, as

$$\begin{aligned} H_d^0= & {} \left( \begin{array}{c} \frac{1}{\sqrt{2}}(v_d+H_{dR}+iH_{dI}) \\ H_d^- \end{array} \right) ,\nonumber \\ H_u^0= & {} e^{i \phi _u} \left( \begin{array}{c} H_d^+ \\ \frac{1}{\sqrt{2}}(v_u+H_{uR}+iH_{uI}) \end{array} \right) ,\nonumber \\ S^0= & {} \frac{e^{i \phi _s}}{\sqrt{2}}(v_s+S_R+iS_I). \end{aligned}$$

(4)

For correct EWSB, the $V_0$, rewritten in terms of these expanded fields, should have a minimum at non-vanishing $v_d$, $v_u$ and $v_s$, implying

$$\begin{aligned} \langle \frac{\delta V_0}{\delta \theta }\rangle = 0~~~ {\mathrm{for}}~~~ \theta = H_{dR}, H_{uR}, S_R, H_{dI}, H_{uI}, S_I, \end{aligned}$$

(5)

which leads to six ‘tadpole conditions’ (see, e.g., [31]).

Taking the second derivative of $V_0$ at the vacuum yields the tree-level $6 \times 6$ neutral Higgs mass matrix-squared, $\mathcal{M}^2_0$, in the basis $\mathrm{H}^T = (H_{dR},H_{uR},S_R,H_{dI},H_{uI},S_I)$. It can be expressed in the general form

$$\begin{aligned} \mathcal{M}_0^2 = \left( \begin{array}{c|c} \mathcal{M}_S^2 &{} \mathcal{M}_{SP}^2 \\ \\ \hline &{} \\ \left( \mathcal{M}_{SP}^2\right) ^T &{} \mathcal{M}_P^2 \end{array} \right) , \end{aligned}$$

(6)

where the $3 \times 3$ block $\mathcal{M}_S^2$ corresponds to the CP-even interaction states ($H_{dR}$, $H_{uR}$, $S_R$), the $3 \times 3$ block $\mathcal{M}_P^2$ to the CP-odd states ($H_{dI}$, $H_{uI}$, $S_I$), while $\mathcal{M}_{SP}^2$ is responsible for mixing between the CP-even and -odd states.

In the rNMSSM, where all the Higgs sector trilinear coupling parameters are real, $\mathcal{M}_{SP}^2$ is a null matrix. One can therefore simply rotate only the submatrix $\mathcal{M}_P^2$ to isolate the massless Nambu–Goldstone boson field, G, which can then be dropped to yield a $5 \times 5$ mass matrix $\mathcal{M}_0^{'2}$. This mass matrix receives higher order corrections, $\Delta \mathcal{M}^2$, from various sectors of the model, and thus gets modified as

$$\begin{aligned} \mathcal{M}_H^2 = \mathcal{M}_0^{'2} + \Delta \mathcal{M}^2. \end{aligned}$$

(7)

The most dominant of these corrections can be found in [9, 38]. Some further two-loop corrections have been calculated in [39, 40]. After the inclusion of these corrections, the submatrices $\mathcal{M}_S^2$ and $\mathcal{M}_P^{'2}$ are separately diagonalised to obtain the three CP-even mass eigenstates, $H_{1,2,3}$ (with $m_{H_1}< m_{H_2} < m_{H_3}$), and the two CP-odd physical Higgs bosons, $A_{1,2}$ (with $m_{A_1} < m_{A_2}$).

On the other hand, one can also invoke CP-violation explicitly by assuming $\lambda \equiv | \lambda | e^{i \phi _{\lambda }}$, $\kappa \equiv | \kappa | e^{i \phi _{\kappa }}$, $A_{\lambda } \equiv | A_{\lambda } | e^{i \phi _{A_{\lambda }}}$ and $A_{\kappa } \equiv | A_{\kappa } | e^{i \phi _{A_{\kappa }}}$. This leads to non-zero entries in the $\mathcal{M}_{SP}^2$ submatrix, implying that the CP-even and CP-odd interaction eigenstates also mix mutually. In this cNMSSM, the G state is first separated out through a rotation of the entire $\mathcal{M}^2_0$ by $\mathcal{R}^G$,

$$\begin{aligned}&\left( H_{dR},H_{uR},S_R,H_I,S_I,G \right) ^T \nonumber \\&\quad = \mathcal{R}^G \left( H_{dR},H_{uR},S_R,H_{dI},H_{uI},S_I \right) ^T, \end{aligned}$$

(8)

and dropped before calculating the higher order corrections to the resulting $\mathcal{M}_0^{'2}$. The complete expressions for the tree-level $\mathcal{M}_0^{'2}$ and the dominant one-loop contributions to $\Delta \mathcal{M}^2$ from the (s)quark and gauge sectors in the cNMSSM were studied in [41,42,43,44] in the renormalisation group equations-improved effective potential approach. The corrections from the gaugino sector were added in [31] and, more inclusively, in [45]. In the Feynman diagrammatic approach, the complete one-loop Higgs mass matrix was derived in [30] and the $\mathcal {O}(\alpha _t \alpha _s)$ contributions to it were calculated recently in [46].

The physical Higgs mass eigenstates of the cNMSSM are then obtained from the interaction states through another rotation by $\mathcal{R}^H$,

$$\begin{aligned} \left( H_1,H_2,H_3,H_4,H_5 \right) ^T = \mathcal{R}^H \left( H_{dR},H_{uR},S_R,H_I,S_I \right) ^T, \end{aligned}$$

(9)

resulting in the diagonalised squared mass matrix,

$$\begin{aligned}&\mathrm{diag} ( m_{H_1}^2,m_{H_2}^2,m_{H_3}^2,m_{H_4}^2,m_{H_5}^2 ) \nonumber \\&\quad = \mathcal{R}^H [ \mathcal{R}^G \mathcal{M}_H^2 {(\mathcal{R}^G )}^T ] {(\mathcal{R}^H)}^T. \end{aligned}$$

(10)

Here $H_1$, $H_2$, $H_3$, $H_4$ and $H_5$ are the five neutral CP-indefinite Higgs bosons, ordered in terms of increasing mass.

Note here that only the physical phase combination $\phi _{\lambda }-\phi _{\kappa }+\phi _u-2\phi _s$ appears in the cNMSSM Higgs sector at the tree-level, as the other possible phase combinations involving $\phi _{A_\lambda }$ and $\phi _{A_\kappa }$ are determined by it, up to a twofold ambiguity, through the tadpole conditions. Beyond this level, the CPV phases of the gaugino mass parameters, $M_{1,2,3}$, and of the soft trilinear couplings, $A_{\tilde{f}}$, of the Higgs boson to the sfermions also get radiatively induced into this sector.

3 Di-photon production via gluon fusion

We now turn our attention to the process under scrutiny, i.e., di-photon production from gluon fusion via Higgs states at the LHC. The squared amplitude for the $gg \rightarrow H \rightarrow \gamma \gamma$ process, with H collectively denoting the five neutral CP-indefinite Higgs bosons, can be written as [47]

$$\begin{aligned} {\mid \mathcal{M} \mid }^2 = \sum _{\lambda , \sigma =\pm } \mathcal{M}_{P \lambda } \mathcal{M}_{P \lambda }^* \left| D_H(\hat{s})\right| ^2 \mathcal{M}_{D \sigma } \mathcal{M}_{D \sigma }^*, \end{aligned}$$

(11)

where $\lambda , \sigma = \pm 1$ are the gluon and photon helicities, respectively, and $D_H(\hat{s})$ is the Higgs boson propagator, with ${\hat{s}}$ being the squared center-of-mass (CM) energy of the incoming gluons. The amplitude for the production part is given as

$$\begin{aligned} \mathcal{M}_{P \lambda } {=} \sum _{i=1-5}\mathcal{M}_{P_i \lambda }{=}\sum _{i=1-5}\frac{\alpha _s m_{H_i}^2}{4 \pi v} \{ S_i^g(m_{H_i}) + i \lambda P_i^g(m_{H_i}) \}, \end{aligned}$$

(12)

where the scalar and pseudoscalar form-factors are [48]

$$\begin{aligned}&S_i^g(m_{H_i}) = 2\sum _q g_{H_i qq}^S \tau _q \{ 1+(1-\tau _q) f(\tau _q) \} \nonumber \\&\quad - \sum _{\tilde{q}} \frac{m_Z^2 \tau _{\tilde{q}}}{m_{\tilde{q}}^2} g_{H_i {\tilde{q}}{\tilde{q}}} \{1-\tau _{\tilde{q}} f(\tau _{\tilde{q}}) \},\end{aligned}$$

(13)

$$\begin{aligned}&P_i^g(m_{H_i}) = 2\sum _q g_{H_i qq}^P \tau _q f(\tau _q), \end{aligned}$$

(14)

with $\tau _x = 4m_x^2/m_{H_i}^2~(x=q,\tilde{q})$ and the loop function being

$$\begin{aligned}&f(\tau ) = \mathrm{arcsin^2}(1/\sqrt{\tau }),~\tau \ge 1;\nonumber \\&f(\tau ) = -\frac{1}{4}\left\{ \mathrm{ln}\left( \frac{1+\sqrt{1-\tau }}{1-\sqrt{1-\tau }}\right) -i\pi \right\} ^2,~\tau < 1. \end{aligned}$$

(15)

Note that $g^{S,P}_{H_i qq}$ and $g^{S}_{H_i {\tilde{q}}{\tilde{q}}}$ in Eq. (13) are the couplings of $H_i$ to quarks q and squarks $\tilde{q}$, respectively, which depend on the elements of the Higgs mixing matrix, $\mathcal{R}^H$, noted in Eq. (10) above. The exact forms of these couplings can be found in [44].

The amplitude for the decay part is similarly given as

$$\begin{aligned} \mathcal{M}_{D \sigma }= & {} \sum _{i=1-5} \mathcal{M}_{D_i \sigma }\nonumber \\ {}= & {} \sum _{i=1-5}\frac{\alpha _{em} m_{H_i}^2}{4 \pi v} \{ S_i^{\gamma }(m_{H_i}) + i \sigma P_i^{\gamma }(m_{H)i})\}, \end{aligned}$$

(16)

with the form-factors being

$$\begin{aligned} S_i^\gamma (m_{H_i})= & {} 2\sum _f N_\mathrm{cf} e_q^2 g_{H_i qq}^S \tau _q \{ 1+(1-\tau _q) f(\tau _q) \}\nonumber \\&- \sum _{\tilde{f}} N_\mathrm{cf} e_{\tilde{q}}^2 \frac{M_Z^2}{M_{\tilde{q}}^2} g_{H_i {\tilde{q}}{\tilde{q}}} \tau _{\tilde{q}} \{1-\tau _{\tilde{q}} f(\tau _{\tilde{q}}) \} \nonumber \\&- g_{H_i WW}\{2+3\tau _W+3\tau _W(2-\tau _W)f(\tau _W) \}\nonumber \\&- \frac{M_Z^2}{2M_{H^\pm }^2} g_{H_i H^+ H^-} \tau _{H^\pm }\{1-\tau _{H^\pm }f(\tau _{H^\pm }) \} \nonumber \\&+ 2\sum _{{\tilde{\chi }}_{j=1,2}^\pm } \frac{M_W}{M_{{\tilde{\chi }}_j^\pm }} g_{H_i {{\tilde{\chi }}_j^+}{{\tilde{\chi }}_j^-}}^S \tau _{{\tilde{\chi }}_j^\pm } \{ 1+(1-\tau _{{\tilde{\chi }}_j^\pm }) f(\tau _{{\tilde{\chi }}_j^\pm }) \},\end{aligned}$$

(17)

$$\begin{aligned} P_i^\gamma (m_{H_i})= & {} 2\sum _f N_\mathrm{cf} e_q^2 g_{H_i qq}^P \tau _q f(\tau _q)\nonumber \\&+ 2\sum _{{\tilde{\chi }}_{j=1,2}^\pm } \frac{M_W}{M_{{\tilde{\chi }}_j^\pm }} g_{H_i {{\tilde{\chi }}_j^+}{{\tilde{\chi }}_j^-}}^P \tau _{{\tilde{\chi }}_j^\pm } f(\tau _{{\tilde{\chi }}_j^\pm }), \end{aligned}$$

(18)

where $N_\mathrm{cf} = 3,1$ is the colour factor for (s)quarks and charged (s)leptons, respectively, with $e_f$ being the corresponding electric charge. Finally, the full propagator in Eq. (11) is a $5\times 5$ matrix,¹ given as

$$\begin{aligned}&D_H(\hat{s}) = \hat{s}\nonumber \\&\left( \begin{array}{@{}ccccc@{}} \mathrm{m_{11}} &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{12}(\hat{s}) &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{13}(\hat{s}) &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{14}(\hat{s}) &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{15}(\hat{s}) \\ i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{21}(\hat{s}) &{} \mathrm{m_{22}} &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{23}(\hat{s}) &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{24}(\hat{s}) &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{25}(\hat{s}) \\ i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{31}(\hat{s}) &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{32}(\hat{s}) &{} \mathrm{m_{33}} &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{34}(\hat{s}) &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{35}(\hat{s}) \\ i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{41}(\hat{s}) &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{42}(\hat{s}) &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{43}(\hat{s}) &{} \mathrm{m_{44}} &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{45}(\hat{s}) \\ i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{51}(\hat{s}) &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{52}(\hat{s}) &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{53}(\hat{s}) &{} i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{54}(\hat{s}) &{} \mathrm{m_{55}} \\ \end{array}\right) ^{-1},\nonumber \\ \end{aligned}$$

(19)

where $\mathrm{m}_{ii} \equiv \hat{s}-m_{H_i}^2 +i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{ii}(\hat{s})$, with ${{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{ij}(\hat{s})$ being the absorptive parts of the Higgs self-energies, for $i,\,j=1 - 5$. The diagonal absorptive parts are equivalent to the widths of the corresponding Higgs states, $\Gamma _{H_i}$. The explicit expressions for ${{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{ij}(\hat{s})$ are given in the Appendix. Note here that in our numerical analysis we will only focus on $H_1$ and $H_2$ having masses very close to 125 GeV. This implies that essentially the propagator matrix elements with $i,\,j=1 - 2$ are the only ones that contribute to the production of the di-photon pair with invariant mass near 125 GeV, assuming that the remaining three Higgs bosons are relatively heavy. Moreover, in the case of the rNMSSM, since the CP-even–odd mixing terms in the Higgs mass matrix vanish, it is sufficient for our purpose to consider only the $3\times 3$ propagator matrix corresponding to the CP-even states instead of the complete one above.

When the splitting between the Higgs boson masses is much larger than the sizes of the absorptive parts in Eq. (19), the NWA can be applied to the ith Higgs boson propagator as

$$\begin{aligned} \left| D_{ii}(\hat{s})\right| ^2{=}{\left| \frac{1}{\hat{s} - m_{H_i}^2 + i m_{H_i} {\Gamma }_{H_i}} \right| ^2} \rightarrow \frac{\pi }{m_{H_i} {\Gamma }_{H_i}} \delta (\hat{s} - m_{H_i}^2), \end{aligned}$$

(20)

so that the partonic cross section becomes

$$\begin{aligned}&\hat{\sigma }(gg \rightarrow H \rightarrow \gamma \gamma ) = \frac{1}{1024 \pi \hat{s}} \sum _{i=1-5}\nonumber \\&\times \left( \sum _{\lambda =\pm } {\left| \mathcal{M}_{P_i \lambda }\right| }^2 {\times } \frac{\pi }{m_{H_i} {\Gamma }_{H_i}} \delta (\hat{s} - m_{H_i}^2) {\times } \sum _{\sigma =\pm } {\left| \mathcal{M}_{D_i \sigma }\right| }^2 \right) .\nonumber \\ \end{aligned}$$

(21)

The total cross-section for the process $pp \rightarrow H \rightarrow \gamma \gamma$ is then written as

$$\begin{aligned} \sigma _{pp}^{\gamma \gamma }= & {} \int _{0}^{1} \mathrm{d}x_2 \int _{0}^{1} \mathrm{d}x_1~~ \hat{\sigma }(gg \rightarrow H \rightarrow \gamma \gamma )~~ g(x_1) g(x_2) \nonumber \\= & {} \int _{0}^{1} dx_2 \int _{0}^{1} \mathrm{d}x_1 \frac{g(x_1) g(x_2)}{1024 \pi \hat{s}} \sum _{i=1-5}\nonumber \\\times & {} \left( \sum _{\lambda =\pm } {\left| \mathcal{M}_{P_i \lambda }\right| }^2 \frac{\pi }{m_{H_i} {\Gamma }_{H_i}} \delta (\hat{s} - m_{H_i}^2) \sum _{\sigma =\pm } {\left| \mathcal{M}_{D_i \sigma }\right| }^2 \right) ,\nonumber \\ \end{aligned}$$

(22)

where $g(x_1)$ and $g(x_2)$ are the parton distribution functions (PDFs) of the two gluons. By substituting $x_2$ in the above equation as

$$\begin{aligned}&\hat{s} = x_1 x_2 s \implies x_1 x_2 = \frac{\hat{s}}{s}\nonumber \\&\quad \equiv \tau \implies x_2 = \frac{\tau }{x_1} \implies dx_2 = \frac{d \tau }{x_1}, \end{aligned}$$

(23)

where s is the total CM energy of the pp system, and performing the integration over $d\tau$, one gets

$$\begin{aligned} \sigma _{pp}^{\gamma \gamma }= & {} \int _{\frac{m_{H_i}^2}{s}}^{1} \mathrm{d}x_1~\frac{1}{1024 s m_{H_i}^3 \Gamma _{H_i}} \sum _{i=1-5}\nonumber \\&\times \left( \sum _{\lambda =\pm } {\left| \mathcal{M}_{P_i \lambda }\right| }^2 \sum _{\sigma =\pm } {\left| \mathcal{M}_{D_i \sigma }\right| }^2 \right) \frac{g(x_1) g\left( {\frac{m_{H_i}^2}{s~x_1}}\right) }{x_1}.\nonumber \\ \end{aligned}$$

(24)

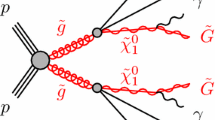
In contrast, when two (or more) Higgs bosons of the model are almost degenerate in mass near a given ${\hat{s}}$, the sizes of the corresponding absorptive parts can become comparable to their mass difference. As a result, the ith Higgs state can undergo resonant transition to the jth state through quantum corrections, as shown in Fig. 1. In such a scenario, the NWA is no longer valid, and the total cross section is given as

$$\begin{aligned} \sigma _{pp}^{\gamma \gamma }= & {} \int _{0}^{1} \mathrm{d}\tau \int _{\tau }^{1} \frac{\mathrm{d}x_1}{x_1} \frac{g(x_1) g(\tau /x_1)}{1024 \pi \hat{s}^3} \sum _{i,j=1-5} \nonumber \\&\times \left\{ \sum _{\lambda =\pm } {\left| \mathcal{M}_{P_i \lambda }\right| }^2 \left| D_{ij}(\hat{s})\right| ^2 \sum _{\sigma =\pm } {\left| \mathcal{M}_{D_j \sigma }\right| }^2 \right\} , \end{aligned}$$

(25)

where $\left| D_{ij}(\hat{s})\right| ^2$ is the propagator matrix given in Eq. (19). From the above equation, one obtains the differential cross section (recall that $\tau = \frac{\hat{s}}{s}$) as

$$\begin{aligned} \frac{\mathrm{d}\sigma _{pp}^{\gamma \gamma }}{\mathrm{d}\sqrt{\hat{s}}}= & {} \int _{\tau }^{1} \frac{2\sqrt{\hat{s}}}{s} \frac{\mathrm{d}x_1}{x_1} \frac{g(x_1) g(\hat{s}/s x_1)}{1024 \pi \hat{s}^3} \sum _{i,j=1-5}\nonumber \\&\times \left\{ \sum _{\lambda =\pm } {\left| \mathcal{M}_{P_i \lambda }\right| }^2 \left| D_{ij}(\hat{s})\right| ^2 \sum _{\sigma =\pm } {\left| \mathcal{M}_{D_j \sigma }\right| }^2 \right\} . \end{aligned}$$

(26)

Fig. 1

Illustration of the effect of mixing in the propagator induced by quantum corrections

4 Numerical analysis

We first performed numerical scanning of the parameter space of the NMSSM, requiring $H_1$ and $H_2$ to lie within the 123–127 GeV range.² Our first scan corresponded to the rNMSSM, wherein sufficient mass degeneracy near 125 GeV between the two lightest scalars can generally be obtained for large values of the couplings $\lambda$ and $\kappa$ and a relatively small $\tan \beta$, which results in maximal mixing between the doublet- and singlet-like states, as noted in some earlier studies [12,13,14]. In the rNMSSM, while it is also possible for $A_1$ to lie near 125 GeV [17], it does not mix with the SM-like $H_1$ when the coupling parameters are all real. Therefore, the corresponding off-diagonal absorptive parts in the propagator matrix given in Eq. (19) are zero. When the complex phases are turned on though, all the Higgs states become CP-indefinite, and any of the off-diagonal terms in the full $5 \times 5$ propagator matrix can be non-zero and contribute to the interference effects. Therefore, either one of the scalar-singlet-like and pseudoscalar-singlet-like states can have strong mass degeneracy with the $\sim$ $125$ GeV SM-like state and interfere with it.

As stated earlier, at the tree level, only the phase combination $\phi _{\lambda }-\phi _{\kappa }+\phi _u-2\phi _s$ appears in the Higgs sector of the cNMSSM. Furthermore, several studies [30, 43, 44] have shown that, out of all the individual phases, including those appearing beyond the Born approximation, the phase $\phi _\kappa$ is virtually unconstrained by the measurements of the fermion Electric Dipole Moments (EDMs). Therefore, after setting all the other phases to $0^\circ$, we performed two separate parameter space scans of the cNMSSM also, with the value of $\phi _\kappa$ fixed to $3^\circ$ in one and to $10^\circ$ in the other. In Table 1 we list the scanned ranges of the free parameters (input at the EW scale), which assume the following universality conditions:

$$\begin{aligned} M_0 \equiv M_{Q_{1,2,3}} = M_{U_{1,2,3}} = M_{D_{1,2,3}} = M_{L_{1,2,3}} = M_{E_{1,2,3}}; \nonumber \\ M_{1/2} \equiv 2M_1 = M_2 = \frac{1}{3}M_3;~~~ A_0 \equiv A_{\tilde{t}} = A_{\tilde{b}} = A_{\tilde{\tau }}, \nonumber \end{aligned}$$

where $M_{Q_{1,2,3}},\,M_{U_{1,2,3}},\,M_{D_{1,2,3}} ,\,M_{L_{1,2,3}}$ and $M_{E_{1,2,3}}$ are the soft masses of the sfermions, $M_{1,2,3}$ those of the gauginos and $A_{\tilde{t},\tilde{b},\tilde{\tau }}$ the soft trilinear couplings. These ranges are consistent across the three scans and correspond to the parameter space region that was noted to yield maximally mass-degenerate $H_1$ and $H_2$ in a previous study [32], where more details about the scanning methodology can also be found. It was additionally pointed out in that study that for larger values of $\phi _\kappa$ it gets increasingly difficult to obtain both $H_1$ and $H_2$ near 125 GeV in the cNMSSM.

Table 1 NMSSM parameters and their scanned ranges

For each parameter space input point generated by the scanning algorithm, the masses as well as branching ratios (BRs) of the Higgs bosons were calculated with the public code NMSSMCALC v2.00 [48]. The Supersymmetric Les Houches Accord [49, 50] output file produced by NMSSMCALC for a scanned point was then passed to HiggsBounds v4.3.1 [51,52,53,54] to check for the consistency of each Higgs boson with the direct Higgs search results from LEP, Tevatron and LHC. We further made sure that a point only got through the scan if it satisfied the limits from measurements of the EDMs, computed intrinsically by NMSSMCALC. Finally, the CMS and ATLAS collaborations have performed measurements of the total width of the $h_\mathrm{obs}$ by analysing its off-shell production and subsequent decays in the ZZ and $W^+ W^-$ channels [55,56,57]. The most recent observed 95% confidence level upper limit for the two channels combined is 13 MeV. Therefore, we also require each of the $H_1$ and $H_2$ in a given scan to observe this constraint, unless stated otherwise for exceptional scenarios, which may well be plausible, as such a limit presumes an underlying BW resonance for the signal [58, 59], which is not the case here.

Fig. 2

Points obtained from the parameter scans of the rNMSSM (top) and of the cNMSSM with $\phi _\kappa = 3^\circ$ (bottom left) and with $\phi _\kappa = 10^\circ$ (bottom right). For all the points shown, $\Delta m$ (colour map) is always smaller than $\Gamma _{H_1}$ (x-axis) and/or $\Gamma _{H_2}$ (y-axis)

Fig. 3

Distribution of the differential cross section as a function of the di-photon invariant mass (assumed equal to $\sqrt{\hat{s}}$) for the three benchmark points in the rNMSSM. The red, green and blue curves correspond to the Cases 1, 2 and 3, respectively, discussed in the text

Next, from the points collected in each scan, we selected BPs satisfying certain specific criteria, which will be explained later. In order to perform the numerical calculation of the cross sections for these BPs, we implemented the expressions given in Eqs. (25) and (26) in a locally developed fortran program. This code is linked to the LAPACK package v3.6.0 [60] for propagator matrix inversion, as well as to a locally modified version of the VEGAS routine [61] to perform the 2-dimensional numerical integration. As a test of the reliability of our results, for a given model point, we calculated the cross section in the NWA for each of the two Higgs bosons with our code and compared it with the gluon fusion cross section computed using the publicly available code SusHi v1.6.0 [62,63,64] multiplied by its di-photon BRs obtained from NMSSMCALC. We found that the two results agreed within 5% or better in all cases. The various Higgs boson couplings for a given parameter space point, needed for the calculation of the absorptive parts of the propagator matrix as well as of the production and decay form-factors in our code, were also obtained from NMSSMCALC.

Note that our program calculates the total cross section only at the Leading Order (LO), since implementing Higher Order (HO) corrections, e.g., as included in SusHi, is a highly involved task beyond the scope of this work, which is aimed at comparing the effects of including the full propagator against the simplest approach of two separate BWs on the total cross section. In fact, since these HO corrections apply only to the production process, they should have exactly the same impact in both approaches, hence including their effect is simply tantamount to rescaling the cross section by a ‘k factor’ (defined as $k_\mathrm{HO}\equiv \sigma _\mathrm{HO} / \sigma _\mathrm{LO}$, with HO implying the perturbative order at which the cross section is to be evaluated), which can be obtained from a dedicated public tool. For a few test points corresponding to the rNMSSM, using SusHi, we thus also estimated the Next-to-Next-to-LO (NNLO) factor, $k_\mathrm{NNLO}$, by calculating the gluon-fusion cross section at both LO and NNLO in QCD. We found this $k_\mathrm{NNLO}$ to always lie very close to 3 for both $H_1$ and $H_2$. However, since SusHi is not yet compatible with the cNMSSM, the k factor cannot be estimated exactly for the points corresponding to the cNMSSM. Therefore, for an approximate evaluation of the NNLO cross section in our discussion below, we will multiply the LO cross section obtained with our tool for a given point, both in the real and the complex NMSSM, with a constant $k_\mathrm{NNLO}=3$. (In fact, for an almost decoupled SUSY sector, as is generally the case here, the k factor is indeed a constant for a SM-like $\sim$ $125$ GeV Higgs boson, which can be obtained from, e.g., [65].)

Finally, we used the CT10 [66] PDF set for gluons in our cross section calculation, with renormalisation/factorisation scale set to the $h_\mathrm{obs}$ mass, i.e., 125 GeV. We have, however, verified that the gross features of our analysis are independent of the choice of the PDF set as well as of the fixed numerical inputs for the SM and NMSSM parameters, for which the default NMSSMCALC values were retained.

5 Results and discussion

In Fig. 2 we show those points obtained from the three scans for which $\Delta m\equiv m_{H_2}-m_{H_1}$ is smaller than one (or both) of the widths, $\Gamma _{H_1}$ and $\Gamma _{H_2}$, of the two lightest Higgs bosons. The top panel corresponds to the rNMSSM, while the bottom panels to the cNMSSM with $\phi _\kappa = 3^\circ$ (left) and with $\phi _\kappa = 10^\circ$ (right). We note in the figure that, given the parameter space in Table 1, for the vast majority of points, $\Gamma _{H_1}$ and $\Gamma _{H_2}$ tend to lie within 3–4 MeV of each other in the rNMSSM. For $\phi _\kappa = 3^\circ$, the size of splitting between $\Gamma _{H_1}$ and $\Gamma _{H_2}$ can range from very small to fairly large across the points collected. However, for $\phi _\kappa = 10^\circ$, no points appear along the diagonal for $\Gamma _{H_1/H_2} > 6$ MeV in the bottom right frame, as the splitting between these two widths starts growing beyond this value.

From each of these scans we selected a few BPs to study the cross section for the production of a di-photon pair with an invariant mass, $\mathcal{M}_{\gamma \gamma }$, near 125 GeV via resonant Higgs boson(s) in gluon fusion at the LHC with $\sqrt{s}=14$ TeV. More specifically, we studied the distributions, with respect to the partonic CM energy $\sqrt{\hat{s}}$ (which is the same as $\mathcal{M}_{\gamma \gamma }$ at LO), of the differential cross section, calculated such that:

Table 2 Values of the input parameters for all the selected BPs. All dimensionful parameters are in units of GeV

Case 1 The $m_{11}$ and $m_{22}$ terms in the propagator matrix, Eq. (19), each contribute alternatively to two amplitudes, which are squared and then summed, implying two independent Higgs boson resonances;

Case 2 Both $m_{11}$ and $m_{22}$ contribute to the amplitude which is then squared, thus allowing for interference between $H_1$ and $H_2$ but without any mixing effects;

Case 3 Besides $m_{11}$ and $m_{22}$, the off-diagonal terms $i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{12}$ and $i{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{21}$ also contribute to the amplitude before squaring, leading to additional interference effects arising from the mixing of the two Higgs states.

Table 3 The masses and total widths of $H_1$ and $H_2$ in the selected BPs. Also listed for each BP is the cross section for the $pp\rightarrow H \rightarrow \gamma \gamma$ process calculated in the three different ways considered

The distributions obtained for the Cases 1, 2 and 3 (colour-coded in red, green and blue, respectively) are plotted in Fig. 3 for each of the three selected BPs corresponding to the rNMSSM, with the integrated cross section for each curve also given in the legend. For these distributions, a $\mathcal{M}_{\gamma \gamma }$ bin width of 2 MeV has been used. As noted above, $\Gamma _{H_1}\sim \Gamma _{H_2}$ for most of the points in the rNMSSM. Therefore, in order to illustrate the dependence of the interference effects on the mass difference and relative widths of the two Higgs bosons, we selected BP1 such that $\Delta m \sim \Gamma _{H_1/H_2}$, BP2 such that $\Delta m < \Gamma _{H_1/H_2}$ and BP3 with $\Delta m \ll \Gamma _{H_1/H_2}$. One sees, going from the top panel to the bottom right one in the figure, that these effects are always positive and grow larger as $\Delta m$ decreases compared to $\Gamma _{H_1/H_2}$, as expected. Also, the interference effects due to the mixing terms in the propagators matrix (Case 3) are notably larger than those due only to the diagonal terms (Case 2) for each of the three BPs. The deviation in the total cross section with the full propagator matrix compared to the Case 1 for BP3 at an inclusive level is about 38%, clearly indicating that the interference effects can be quite sizeable. We point out here that although the BP3 represents maximal enhancement of these effects among all the points collected in our scans, it is possible that they can be even slightly larger for certain other parameter combinations in the vicinity of this BP. Note also that the total integrated cross section (obtained at NNLO in QCD, as mentioned earlier) is generally consistent with the fiducial one, as estimated for the SM-like Higgs boson near 125 GeV [67], or measured by the ATLAS and CMS collaborations for $h_\mathrm{obs}$ at $\sqrt{s}=13$ TeV.³

The values of the input parameters for all the selected BPs can be found in Table 2, and the masses and widths of $H_1$ and $H_2$ as well as the total cross sections corresponding to the three Cases for each of the BPs are given in Table 3.

The enhancement in the interference effects for a larger difference between $\Delta m$ and $\Gamma _{H_1}\sim \Gamma _{H_2}$ is further confirmed by the distributions shown in the top panels of Fig. 4 for BP4 and BP5, in the cNMSSM with $\phi _\kappa =3^\circ$. For both these BPs, the interference is again constructive, as in the rNMSSM. It is, however, also possible for the interference to be destructive in this scenario. This is the case for BP6, shown in the bottom left panel of the figure, for which the cumulative cross section is smaller for Case 2 compared to Case 1. Turning on the mixing terms in the propagator matrix further contributes negatively to lower the cross section, although the overall effect is hardly per cent level for this particular parameter space point.

Fig. 4

As in Fig. 3, for the BPs corresponding to the cNMSSM with $\phi _\kappa = 3^\circ$

Fig. 5

As in Fig. 3, for the BPs corresponding to the cNMSSM with $\phi _\kappa = 10^\circ$

For BPs 4–6 above, the $H_1$ and $H_2$ are scalar-like, which is the case for almost all the points obtained in the scan for this scenario. We note here that the singlet-like Higgs boson near 125 GeV is classified as scalar (pseudoscalar)-like if its coupling to the gauge bosons are significantly larger (smaller) than those of the singlet-like $H_3$, which itself also lies fairly close in mass.⁴ While one of the main reasons for considering the cNMSSM was to explore the possibility of interference of a $\sim$ $125$ GeV pseudoscalar-like Higgs boson with the SM-like one, only a handful of such points were found by our scan, wherein the widths of the $H_1$ and $H_2$ are always relatively small.

BP7 in Fig. 4 illustrates the scenario with a pseudoscalar-like $H_2$, with its total width, as well as that of the SM-like $H_1$, being smaller than 3 MeV. An intriguing feature of this point is that, while the overall interference effect is positive for Case 2, enhancing the cross section compared to Case 1, it becomes negative when the complete propagator matrix is included. The destructive interference here is much stronger than in BP6 above and has the desirable consequence of bringing the total cross section down to a level consistent with the LHC measurements noted earlier. The reason why the cross section for Case 1 for this point is considerably higher than that seen for the other BPs so far can be ascribed to the fact that the $H_1$ is much more SM-like here compared to the points where the scalar-like $H_2$ gets closer in mass to it owing to large singlet–doublet mixing.

Fig. 6

Convolution of the distributions 1 and 3 for BP10 with Gaussians of width 1 GeV (top) and 300 MeV (bottom). An integrated luminosity of 300 fb$^{-1}$ is assumed in the left panels and of 1000 fb$^{-1}$ in the right panels

In Fig. 5 we display the distributions for the five BPs selected in the cNMSSM with $\phi _\kappa =10^\circ$. As noted from the corresponding scatter plot above, this value of $\phi _\kappa$ allows for a much larger splitting between $\Gamma _{H_1}$ and $\Gamma _{H_2}$, compared particularly to the rNMSSM. This makes it possible to test the impact of interference when $\Delta m$, instead of being smaller than both the widths, lies somewhere in between them. Thus, for each of these points $\Gamma _{H_{1}}<3$ MeV and $\Gamma _{H_{2}}>10$ MeV, with $\Delta m$ varying from about 9.5 MeV for BP8 to 2 MeV for BP11. While the behaviour of the interference is similar to what has been observed earlier, i.e., it grows larger as the gap between $\Delta m$ and $\Gamma _{H_2}$ increases, its overall size remains comparatively small, reaching about 9% for BP10, for which $\Delta m$ is only slightly larger than $\Gamma _{H_1}$. However, when $\Delta m$ is lowered below $\Gamma _{H_1}$ also, as in BP11, the interference effects get reduced instead of continuing to grow. BP12 is another example of mutually opposite contributions to the interference effects from the diagonal and off-diagonal elements of the Higgs propagator matrix. As opposed to BP7 though, here the negative interference comes from the diagonal elements in the propagator matrix, while the mixing effects contribute positively to again raise the cross section slightly for Case 3.

Fig. 7

Top The differential distributions for TP1 without convolution (left) and after convolution with a Gaussian of width 1 GeV for an integrated luminosity of $300~\mathrm{fb^{-1}}$ (right). Bottom TP1 distributions after convolution with a Gaussian of width 300 MeV for an integrated luminosity of $300~\mathrm{fb^{-1}}$ (left) and $1000~\mathrm{fb^{-1}}$ (right)

A closer look at the curves for BP6 and BP10 above reveals very small kinks near $m_{H_1}$ in addition to tall peaks near $m_{H_2}$. These kinks result from the large splitting between the $\Gamma _{H_1}$ and $\Gamma _{H_2}$, coupled with the fact that $\Delta m$, while still being sufficiently smaller than the $\Gamma _{H_2}$ to cause notable interference effects, is larger than the bin size of 2 MeV adopted for plotting the distribution. Thus, for these points not only does the values of the inclusive (i.e., integrated) cross section change between the respective Cases 1 and 3, but also the shape of the distribution for the exclusive (i.e., differential) one. However, a bin width of 2 MeV is about three orders of magnitude smaller than the current experimental $\mathcal{M}_{\gamma \gamma }$ resolution of around 1 GeV [70]. Evidently, any differences between their shapes corresponding to each of the three Cases for a given BP, which could prove crucial for mutually distinguishing them and hence unraveling the interference effects, would not appear had a realistic bin width of 1 GeV been used. It is nevertheless interesting to study whether these differences persist to some extent once the differential distributions are convolved with a Gaussian distribution emulating detector effects. We performed the convolution using the ListConvolve function [71] in Mathematica by supplying the differential distribution data for a point as a list, as well as specifying the mean and width of the Gaussian.

Fig. 8

As in Fig. 7, for the TP2

Fig. 9

As in Fig. 7, for the TP3

In the top frames of Fig. 6 we display the result of the convolution of the distributions corresponding to Cases 1 and 3 for BP10 with a Gaussian of width (resolution) 1 GeV, which is also used as the size of the $\mathcal{M}_{\gamma \gamma }$ bins for first reproducing these distributions with our MC integrator. We use two prospective integrated luminosities at the LHC: 300 fb$^{-1}$ (left), which is expected by the end of the machine run in standard configuration; and 1000 fb$^{-1}$ (right), foreseen for the High-Luminosity (HL) LHC option [72].⁵ It is worth appreciating in the figures that, while the kinks have expectedly disappeared and the distributions are smoother, there exists some marginal scope at the LHC to distinguish at the differential level the simplistic scenario generally assumed (Case 1) and the one rigorously predicted (Case 3), as the difference in the heights of the red and blue curves is not constant for all the bins in $\sqrt{\hat{s}}$. However, evidently this requires knowledge of additional model inputs (e.g., the Higgs boson couplings) as such difference could also be generated by a different point in the parameter space. This difference is even more pronounced in the bottom panels of the figure, which correspond to the convolution with a Gaussian of resolution 300 MeV (clearly an unrealistic value at present, yet potentially within the reach of a detector upgrade). In fact, the histograms referring to these two predictions could eventually be statistically separable, again though, with the aforementioned caveat that one ought to have established additional model parameters elsewhere.

The difficulty to separate the Cases 1 and 3 for BP10 (as it would be for all other BPs) with present machine and detector conditions at the LHC is ultimately related to the enforcement of the $\Gamma _{H_1/H_2}< 13$ MeV constraint from off-shell Higgs measurements in our selection of the BPs. We therefore consider a Test Point (TP) 1, where this constraint is dismissed and only the milder $\Gamma _{h_\mathrm{obs}}< 41$ MeV constraint, as obtained from a global fit to the on-shell Higgs boson signal strength measurements [73], is imposed. This is all the more important in light of the fact that some critiques have been drawn about the model-independence of such a measurement, see, e.g., [74, 75], or its stability against theoretical uncertainties [76, 77].⁶ The top right frame of Fig. 7 shows the convoluted distributions 1 and 3 for TP1 with a Gaussian of 1 GeV width, illustrating again the fact that also in this case there exists some scope in separating the Cases 1 and 3, even for current di-photon mass resolutions, so long that sufficient luminosity is accrued. The bottom frames of the figure illustrate that this scope gets further enriched if the mass resolution is improved to 300 MeV.

In fact, one could ignore constraints on the total width altogether in order to estimate the minimal mass splitting that could be potentially detectable. While this exercise may appear academic (i.e., to dismiss a crucial experimental constraint), it is worth noting that the current procedures adopted to extract the Higgs boson properties inevitably work with the underlying assumption that only one resonance is produced around 125 GeV. This implies that the allowed intrinsic widths of a pairs of degenerate Higgs states need not relate directly to the currently fitted value.

In Figs. 8 and 9 we thus display the distributions of Cases 1 and 3 for two more TPs, 2 and 3, respectively, convolved, again, with Gaussians of 1 GeV and 300 MeV widths for two prospective integrated luminosities. In both these TPs, the $H_1$ is very wide, $\mathcal {O}$(100) MeV, while $\Gamma _{H_2}$ is a few 10s of MeVs, as seen in Table 4.⁷ But since $\Gamma _{H_1} - \Delta m$ is only about 70 MeV for TP2, while it is larger than half of $\Gamma _{H_1}$ for TP3, the interference effects are highly enhanced for the latter (about 46%) compared to the former ($\sim$ $30$%). These figures more effectively bring home the point that a very large $\Gamma _{H_1}$ (as noticeable in the top-left frames) does not impact significantly the quality of the fit to what, in the end, looks like a single object shape (as visible in the other three frames). Though, clearly, the difference between the Cases 1 and 3 is much more pronounced here than for TP1 (and all the BPs). This difference may potentially be established experimentally within the next few years, more likely so the wider (one of) the Higgs states.

Table 4 Higgs boson masses and widths as well as the $pp\rightarrow H \rightarrow \gamma \gamma$ cross sections corresponding to the three Cases for the three selected TPs

Table 5 Values of the input parameters for the three TPs considered. All dimensionful parameters are in units of GeV

6 Conclusions

In summary, we have scrutinised in detail the proton–proton to di-photon process, through which a 125 GeV resonance consistent with the SM Higgs boson has been discovered at the LHC. Indeed, this is the signature for which the Higgs mass resolution is highest amongst all those accessible at the CERN collider. Measurements of its cross section, at both the inclusive and exclusive level, however, do not exclude the possibility of non-SM explanations. Amongst these, particularly intriguing are those invoking two Higgs bosons produced via gluon fusion, with such a small mass difference that they cannot be resolved by the experimental apparatus. This scenario can emerge only in non-minimal realisations of SUSY, such as the NMSSM, wherein (unlike the MSSM) two coexisting Higgs bosons can contribute to the 125 GeV signal (in $\gamma \gamma$ as well as other final states). In this case, an accurate treatment is required of the propagation of the two states, which not only goes beyond the NWA but also allows for full interference between these. Hence, we have studied the quantitative impact of interference between two Higgs states near 125 GeV, with and without mixing effects, relative to the simplistic approach where the two resonant objects are treated independently of each other. For a full treatment, including the possibility of complex couplings as well, we have considered both real and complex NMSSM.

Our analysis involved scanning of the parameter space of the model for finding possible solutions consistent not only with the LHC exclusion limits on the additional Higgs bosons but also with the constraints from EDM measurements. These scans further collected only model solutions yielding two Higgs bosons with masses lying within the uncertainty of the measurements of the 125 GeV resonance. This was followed by a dedicated computation, performed with the help of a locally developed MC program, producing both integrated and differential cross sections for the full process $pp(gg)\rightarrow H_1,H_2\rightarrow \gamma \gamma$. We have found that the aforementioned interference effects can be sizeable, with some of the selected BPs providing a difference of around 40% in inclusive rates between the standard approach consisting in treating the two resonances as separate BW functions and the full propagator one including all non-trivial quantum effects.

We then considered the possibility of a shape analysis of the emerging profile, which could reveal the presence of multiple resonances, assuming realistic, current and prospective, di-photon mass resolutions of the LHC detectors. This revealed some long-term potential to see the difference between the generally exploited simplistic case of assuming two separate resonances and the one where the two nearly mass-degenerate states interfere due to the inclusion of the complete propagator matrix in the amplitude calculation. These differences are in fact more visible with a smaller di-photon mass resolution and a larger data sample, both of which can only be achieved with upgraded detectors and/or machine. Finally, in attempting to distinguish the two approaches, we have also noted a tension in the underlying dynamics. Any distortion effect of a single BW shape can only be exploited when the mass difference is sufficiently larger than the assumed width of the bins (which should naturally be consistent with the available experimental mass resolution) in the distribution of the differential cross section. However, a larger mass difference leads to smaller interference effects.

Appendix

The absorptive part of the Higgs propagator matrix can be written as

$$\begin{aligned} {{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{ij}(s)= & {} {{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{ij}^{ff}(s) +{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{ij}^{VV}(s) +{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{ij}^{HV}(s) \nonumber \\&+{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{ij}^{HH}(s) +{{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{ij}^{\tilde{f} \tilde{f}}(s). \end{aligned}$$

(A.1)

We reproduce here the expressions for the individual contributions from [26], where those to vector bosons as well as associated Higgs and vector boson pairs were derived using the Pinch Technique [78,79,80,81,82,83,84,85], which ensures their linear dependence on s. These two contributions are given as

$$\begin{aligned} {{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{ij}^{VV}(s)= & {} \frac{g^2 g_{H_iVV} g_{H_jVV} \delta _V \beta _V}{128\pi m_W^2} \nonumber \\&\times \{ -4m_V^2(2 s-3m_V^2) +2m_V^2(m_{H_i}^2+m_{H_j}^2) \nonumber \\&+m_{H_i}^2m_{H_j}^2 \}~ \Theta (s-4m_V^2), \end{aligned}$$

(A.2)

with $\beta _V=\sqrt{1-4\kappa _V}$ and $\delta _W=2,~\delta _Z=1$, and

$$\begin{aligned} {{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{ij}^{HV}(s)= & {} \frac{g^2}{64\pi m_W^2} \sum _{k=1-5} g_{H_i H_k Z} g_{H_j H_k Z}~ \lambda ^{1/2}\Bigl (1,\kappa _Z,\kappa _{H_k}\Bigr )\nonumber \\&\times \Bigg \{ -4 s m_Z^2+ (m_Z^2-m_{H_k}^2)^2 \nonumber \\&+(m_Z^2-m_{H_k}^2)(m_{H_i}^2+m_{H_j}^2) +m_{H_i}^2 m_{H_j}^2 \Bigg \}~\nonumber \\&\times \Theta (s-(m_Z+m_{H_k})^2) \nonumber \\&+\frac{g^2}{32\pi m_W^2}{\mathfrak {R}}\mathrm{e} (g_{H_i H^+ W^-} g_{H_j H^+ W^-}^*)~ \lambda ^{1/2}\nonumber \\&\times (1,\kappa _W,\kappa _{H^\pm })\Bigg \{ -4\hat{s} m_W^2+ (m_W^2-m_{H^\pm }^2)^2 \nonumber \\&+(m_W^2-m_{H^\pm }^2)(m_{H_i}^2+m_{H_j}^2) +m_{H_i}^2 m_{H_j}^2\Bigg \}~\nonumber \\&\times \Theta (s-(m_W+m_{H^\pm })^2). \end{aligned}$$

(A.3)

The contribution from loops of Higgs boson pairs reads

$$\begin{aligned} {{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{ij}^{HH}(s)= & {} \frac{v^2}{16\pi }\sum _{k\ge l=1-5} \frac{S_{ij;kl}}{1+\delta _{kl}} g_{H_i H_k H_l} g_{H_j H_k H_l}~ \lambda ^{1/2}\nonumber \\&\times (1,\kappa _{H_k},\kappa _{H_l})~ \Theta (s-(m_{H_k}+m_{H_{H_l}})^2),\nonumber \\ \end{aligned}$$

(A.4)

where the symmetry factor $S_{ij;kl}$ is equal to 2 for $i=j$ and $k\ne l$, or $i\ne j$ and $k=l$, to 4 for $i=j$ and $k=l$, and to 1 otherwise.

Finally, the loops of fermions (omitting the QCD K-factors) and sfermions give

$$\begin{aligned} {{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{ij}^{ff}(s)= & {} \frac{s}{8\pi } \sum _{f,f^\prime } g_f^2 \Delta _{ff^\prime } N_\mathrm{cf} ~\lambda ^{1/2}(1,\kappa _f,\kappa _{f^\prime }) \nonumber \\&\times \{ (1-\kappa _f-\kappa _{f^\prime }) (g_{H_i f \bar{f}^\prime }^S g_{H_j f \bar{f}^\prime }^{S*}\nonumber \\&+g_{H_i f \bar{f}^\prime }^P g_{H_j f \bar{f}^\prime }^{P*}) \nonumber \\&-2\sqrt{\kappa _f \kappa _{f^\prime }} (g_{H_i f \bar{f}^\prime }^S g_{H_j f \bar{f}^\prime }^{S*} -g_{H_i f \bar{f}^\prime }^P g_{H_j f \bar{f}^\prime }^{P*})\}\nonumber \\&\times \Theta (s-(m_f+m_{f^\prime })^2), \end{aligned}$$

(A.5)

where $g_f=\frac{gm_f}{2m_W}$, $\Delta _{ff^\prime }=\delta _{ff^\prime }~(f,f^\prime =t,b,c,s,\tau ,\mu )$, $\frac{4}{1+\delta _{ff^\prime }}~(f,f^\prime =\tilde{\chi }_{1,2,3,4,5}^0)$, 1 $(f,f^\prime =\tilde{\chi }_{1,2}^+)$, $\lambda (x,y,z)=x^2+y^2+z^2-2(xy+yz+zx)$ and $\kappa _x=\frac{m_x^2}{\hat{s}}$, and

$$\begin{aligned} {{\mathfrak {I}}\mathrm{m}\hat{\Pi }}_{ij}^{\tilde{f} \tilde{f}}(s)= & {} \frac{v^2}{16\pi } \sum _{\tilde{f}} \sum _{k,l=1-2} N_\mathrm{cf} g_{H_i \tilde{f}_k \tilde{f}_l^*} g_{H_j f_k \tilde{f}_l^*}^*~ \lambda ^{1/2}\nonumber \\&\times (1,\kappa _{\tilde{f}_k},\kappa _{\tilde{f}_l})\Theta (s-(m_{\tilde{f}_k}+m_{\tilde{f}_l})^2). \end{aligned}$$

(A.6)