1 Introduction

Recent observations strongly suggest that the universe is undergoing an accelerated expansion in the present epoch [1, 2]. The matter content responsible for such a certain stage of evolution of the universe is popularly referred to as “dark energy” (DE), which accounts for almost \(70\%\) of the current energy budget of the universe. In this regard, various DE models have been proposed to match with recent observed data and the \(\Lambda \)CDM model is the most simplest one in this series. But this model suffers from some other problems which are known as the “fine tuning” problem [3], “coincidence” problem [4] and the “age” problem [5]. To overcome these issues, it is quite natural to think for some alternative possibilities to explain the origin and nature of DE. Models with scalar fields (both the canonical and non-canonical scalar field) play a major role in current description of the evolution of the universe. Motivated by the scalar field theories, over the last decade, numerous DE models were explored, which include quintessence, K-essence, phantom, tachyon, chaplygin gas and so on (for review see [6] and the references therein). However, we do not yet have a concrete and satisfactory DE model.

As mentioned before, the cosmological observations also indicate that the observed cosmic acceleration is a recent phenomenon. So, in the absence of DE or when its effect is subdominant, the same model should have decelerated phase in the early epoch of matter era to allow the formation of structure (as gravity holds matter together) in the universe. For this reason, a cosmological model requires both a decelerated and an accelerated phase of expansion to describe the whole evolution history of the universe. In this context, the deceleration parameter plays an important role, which is defined as

$$\begin{aligned} q=-\frac{a{\ddot{a}}}{{\dot{a}}^2} \end{aligned}$$
(1)

where a(t) is the scale factor of the universe. For an accelerating universe, \({\ddot{a}}>0\), i.e., \(q<0\) and vice versa. The most popular way of achieving such a scenario is to consider a parametrization for the deceleration parameter as a function of the scale factor (a) or the redshift (z) or the cosmic time (t) (see Refs. [7,8,9,10,11,12,13,14,15,16,17,18,19]). It should be noted that, for most of these parametrizations, the q-parametrization diverges in the far future and others are valid at low redshift (i.e., \(z<<1\)) [10,11,12,13,14,15]. Also such parametric methods may be misleading as to the true nature of dark energy due to the assumed parametric form. The non-parametric method is more advantageous than the parametric method in the literature, since it avoids parametrizing cosmological quantities and finds the evolution of our universe directly from observational data [20,21,22,23,24]. However, such approaches also have drawbacks [25]. Till now, there is no well-motivated theoretical model of the universe which can describe the entire evolution history of the universe. So, it is reasonable to adopt a parametric approach to measure the transition from a decelerating to an accelerating phase of the universe. In addition to this, the parametric approach also helps to improve efficiency of the future cosmological surveys. Motivated by these facts, in the present work, we have chosen a special form of deceleration parameter in such a way that q(z) will provide the desired property for sign flip from a decelerating to an accelerating phase. The properties of this parametrization are mentioned in Sect. 2. The constraints on the model parameters of our toy model have also been obtained using the SNIa, BAO and CMB datasets. We have also reconstructed the redshift evolutions of q(z) and the total EoS parameter and have compared their evolution behaviors with other well-known models, such as \(q\propto z\) [8], \(q\propto \frac{z}{1+z}\) [11,12,13,14,15] and \(\Lambda \)CDM, to study the different properties of this model. We have shown that for this choice of q(z), the present model describes the evolution of the universe from an early decelerated phase (where matter dominates over DE) to an accelerated phase (where DE dominates over matter) at the current epoch for each dataset.

Another important kinematical quantity, related to the expansion of the universe, is the jerk parameter (the dimensionless third derivative of the scale factor a(t) with respect to cosmic time t), which is defined as [26,27,28,29]

$$\begin{aligned} j=\frac{\frac{\mathrm{d}^3a}{\mathrm{d}t^3}}{aH^3}, \end{aligned}$$
(2)

and in terms of q

$$\begin{aligned} j={\left[ q(2q+1) + (1+z)\frac{\mathrm{d}q}{\mathrm{d}z}\right] }, \end{aligned}$$
(3)

which will be useful when the parametric form of q(z) is given. A powerful feature of the jerk parameter is that for the standard \(\Lambda \)CDM model \(j= 1\) (constant) always, which provides a simple test for departure from the \(\Lambda \)CDM scenario. It deserves mention here that Sahni et al. [30] and Alam et al. [31] drew attention to the importance of j for discriminating various models of dark energy, because any deviation from 1 in the value of j would favor a dynamical dark energy model, instead of the \(\Lambda \)CDM model. In this paper, we have also investigated the evolution of j for the present parametrized model.

The present paper is organized as follows. The basic equations for the phenomenological DE model are presented in the next section. We then try to obtain some accelerating solutions for this toy model using a specific parametrization of q(z). In Sect. 3, we obtain the observational constraints on these model parameters using various datasets and present our results. Finally, in Sect. 4, there is a brief conclusion as regards the results obtained in this work.

2 Basic equations and solutions

Let us consider a spatially flat, homogeneous and isotropic FRW universe

$$\begin{aligned} \mathrm{d}s^2 = \mathrm{d}t^2 - a^2(t)[\mathrm{d}r^2 + r^2 \mathrm{d}{\Omega }^2] \end{aligned}$$
(4)

composed of two perfect fluids, namely ordinary matter with negligible pressure and canonical scalar field (as a candidate of dark energy). In this case, the Einstein field equations become (choosing \(8\pi G=c=1\))

$$\begin{aligned} 3H^{2}=\rho _{m} + \rho _{\phi }, \end{aligned}$$
(5)
$$\begin{aligned} 2{\dot{H}} + 3H^{2}=-p_{\phi }, \end{aligned}$$
(6)

where \(H=\frac{\dot{a}}{a}\) is the Hubble parameter and \(\rho _{m}\) is the matter energy density. Here, \(\rho _{\phi }\) and \(p_{\phi }\) are the contributions of the scalar field to the energy density and pressure, respectively, and are given by

$$\begin{aligned}&\rho _{\phi }=\frac{1}{2}{\dot{\phi }}^{2} + V(\phi ),\end{aligned}$$
(7)
$$\begin{aligned}&p_{\phi }=\frac{1}{2}{\dot{\phi }}^{2} - V(\phi ), \end{aligned}$$
(8)

where an overhead dot denotes a derivative with respect to the cosmic time t and \(V(\phi )\) is the potential associated with the scalar field \(\phi \).

Also, the conservation equations for the scalar field and matter field read

$$\begin{aligned} {\dot{\rho }}_{\phi } + 3H(\rho _{\phi }+p_{\phi })=0, \end{aligned}$$
(9)
$$\begin{aligned} {\dot{\rho }}_{m} + 3H\rho _{m}=0. \end{aligned}$$
(10)

Now one can easily solve the above equation to find the energy density for the normal matter as

$$\begin{aligned} \rho _{m}=\rho _{m0}(1+z)^{3} \end{aligned}$$
(11)

where \(\rho _{m0}\) is an integration constant (which represents the matter energy density at the present epoch) and z is the redshift parameter, defined as \(z=\frac{1}{a}-1\).

The corresponding equation of state (EoS) parameter is now given by

$$\begin{aligned} \omega _{\phi }=\frac{p_{\phi }}{\rho _{\phi }}=-\frac{(2{\dot{H}}+3H^2)}{(3H^2 -\rho _{m})}, \end{aligned}$$
(12)

which further leads to

$$\begin{aligned} \omega _{\phi }=\frac{2q -1}{3 - 3\Omega _{m0}(1+z)^{3} {\left( \frac{H_{0}}{H}\right) }^{2} } \end{aligned}$$
(13)

where \(\Omega _{m0}=\frac{\rho _{m0}}{3H^2_{0}}\) is the matter density parameter at the present epoch.

From Eqs. (5) and (6), one can obtain

$$\begin{aligned} \frac{\ddot{a}}{a}=-\frac{1}{6}{\left( \rho _{m}+\rho _{\phi }+3p_{\phi }\right) }, \end{aligned}$$
(14)

and the present model will provide acceleration (\({\ddot{a}}>0\)) only if

$$\begin{aligned} \omega _\mathrm{tot}=\frac{p_{\phi }}{\rho _{m}+\rho _{\phi }}=-\frac{(2{\dot{H}} + 3H^{2})}{3H^{2}}<-\frac{1}{3} \end{aligned}$$
(15)

where \(\omega _\mathrm{tot}\) denotes the effective or total EoS parameter.

Now, out of Eqs. (5), (6), (9) and (10), only three are independent equations with four unknown parameters, namely, H, \(\rho _{m}\), \(\phi \) and \(V(\phi )\). Thus, in order to solve the system of equations we need an additional input.

It is well known that the parametrization of the deceleration parameter q plays an important role in describing the nature of the expansion rate of the universe. In general, q can be parametrized as

$$\begin{aligned} q(z)=q_{0} + q_{1}X(z) \end{aligned}$$
(16)

where \(q_{0}\), \(q_{1}\) are real numbers and X(z) is a function of redshift z. In fact, various functional forms of X(z) have been proposed in the literature [7,8,9,10,11,12,13,14,15,16,17,18,19], which can provide a satisfactory solution to some of the cosmological problems. However, as mentioned earlier, some of these parametrizations lose their prediction capability regarding the future evolution of the universe and others are valid for \(z<<1\) only. In Ref. [19] the authors have considered a divergence-free parametrization of q to study the whole expansion history of the universe. The authors have shown that such a model is more consistent with the current observational constraints for some restrictions on model parameters. Hence, search is still on for an appropriate functional form of q(z) that will fit well in dealing with cosmological challenges. Motivated by these facts, in this present work, we propose a parametrization of the deceleration parameter, which is given by

$$\begin{aligned} q(z)=q_{0} + q_{1}\left( \frac{\ln (N+z)}{1+z}-\kappa \right) \end{aligned}$$
(17)

where \(q_{0}\), \(q_{1}\), N and \(\kappa \) are arbitrary model parameters. The system of equations is closed now. It is straightforward to see that q(z) has the following limiting cases:

$$\begin{aligned} {q(z)} = \left\{ \begin{array}{l@{\quad }l} q_{0}-q_{1}\kappa ,&{} \mathrm{for} \, z\rightarrow +\infty \, (\mathrm{early~epoch}),\\ q_0 +q_{1}(\ln N -\kappa ), &{} \mathrm{for}\, z=0 \,\,(\mathrm{present~epoch}).\\ \end{array}\right. \nonumber \\ \end{aligned}$$
(18)

Clearly, one can realize the history of the cosmic evolution with this new parametrization. Similarly, at low redshift (\(z<<1\)), the form of q(z) turns out to be

$$\begin{aligned} q(z) = q_{0} + q_{1}{\left( \frac{\ln N}{(1+z)}+\frac{z}{N(1+z)}-\kappa \right) }. \end{aligned}$$
(19)

Now, we try to reproduce different well-known forms of q(z) from Eq. (19) for various choices of \(\kappa \).

  1. (i)

    For \(\kappa =\ln N\), one can easily obtain the expression for q(z):

    $$\begin{aligned}&q(z) = q_{0} + {\tilde{q}}_{1}{\left( \frac{z}{1+z}\right) },\quad \mathrm{where}\quad {\tilde{q}}_{1} = q_{1}{\left( \frac{1}{N} - \ln N \right) },\nonumber \\ \end{aligned}$$
    (20)

    which is similar to the well-known parametrization of q(z) used by several authors [11,12,13,14,15].

  2. (ii)

    For \(\kappa =0\), q(z) reduces to

    $$\begin{aligned}&q(z) = q_{0} + \frac{q_{1}z + q_{2}}{N(1+z)} \end{aligned}$$
    (21)

    where \(q_{2}=q_{1}N\ln N\). Note that the above form of the deceleration parameter is similar to the parametrization of \(q(z) = \frac{1}{2} + \frac{q_{1}z + q_{2}}{(1+z)^{\epsilon }}\), where \(\epsilon \) is an arbitrary constant. A similar form of deceleration parameter has been used by many authors with \(\epsilon =2\) [9, 10], where they have shown that \(q(z) = \frac{1}{2} + \frac{q_{1}z + q_{2}}{(1+z)^{2}}\).

  3. (iii)

    Similarly, for \(\kappa =\frac{1}{N}\), we obtain

    $$\begin{aligned}&q(z) = q_{0} + \frac{{q}^{*}_{1}}{1+z},\quad \mathrm{where}\quad {q}^{*}_{1} = \frac{q_{1}}{N}{\left( N\ln N -1\right) },\nonumber \\ \end{aligned}$$
    (22)

    which is similar to the form of \(q(z) = \frac{1}{2} + \frac{{q}_{1}}{(1+z)^{\epsilon }}\) for \(\epsilon =1\) and the appropriate choices of \(q_{0}\), \(q_{1}\) and N [14].

Therefore, the new parametrization of q(z), given by Eq. (19), covers a wide range of other popular theoretical models [as given in Eqs. (20), (21) and (22)] for \(z<<1\) and different choices of \(\kappa \).

However, for our analysis, in the present work, we have considered the parametrization of q(z),

$$\begin{aligned} q(z)=q_{0} + q_{1}\left( \frac{\ln (N+z)}{1+z}-\ln N\right) ,\quad N>1\quad (\mathrm{Model}~1), \end{aligned}$$
(23)

which can be derived from Eq. (17) by replacing \(\kappa =\mathrm{ln}N\). The reason for making this choice is that at \(z=0\) (i.e., at present epoch), the second term in Eq. (23) vanishes and \(q_{0}\) provides the present value of q(z).

In general, \(q_{1}\) is another model parameter which characterizes the evolution of q(z). To ensure the matter dominated epoch i.e., \(q = \frac{1}{2}\) at the high z, one can constrain \(q_{0}-q_{1}\ln N=\frac{1}{2}\) for this parametrization. In this case, Eq. (23) reduces to

$$\begin{aligned} q(z)=q_{0} + \frac{2q_{0}-1}{2\ln N}\left( \frac{\ln (N+z)}{1+z}-\ln N\right) . \end{aligned}$$
(24)

In that case, the three parameter parametrization reduces to two parameter parametrization, namely \(q_{0}\) and N. Since we are interested in obtaining a viable dynamical dark energy model and we cannot ignore the importance of the two parameters \(q_{0}\) and \(q_{1}\) to probe the evolutionary history of the universe. For this reason, in this work, we consider the two parameter (\(q_{0},q_{1}\))-phase space with their proper physical interpretation. We can now easily constrain them using the available observational data, so that the above mentioned toy model can explain the present evolution of the universe more precisely.

The Hubble parameter and the deceleration parameter are related by the following equation:

$$\begin{aligned} H(z)=H_{0}\mathrm{exp}{\left( \int ^{z}_{0} \frac{1+q(z^{\prime })}{1+z^{\prime }}\mathrm{d}z^{\prime }\right) } \end{aligned}$$
(25)

where \(H_{0}\) is the present value of the Hubble parameter. With the help of Eqs. (23) and (25), we have obtained the expression for the Hubble parameter H:

$$\begin{aligned} H(z)=H_{0}N^{\frac{q_{1}N}{N-1}}(1+z)^{\alpha } (N+z)^{-\frac{q_{1}(N+z)}{(1+z)(N-1)}} \end{aligned}$$
(26)

where \(\alpha ={\left( 1+q_{0}+\frac{q_{1}}{N-1} -q_{1}\ln N\right) }\).

For this model, the expressions for the EoS parameter \(\omega _{\phi }\) can easily be obtained [using Eqs. (13), (23) and (26)]:

$$\begin{aligned} \omega _{\phi }(z)=\frac{2q_{0} - 1 + 2q_{1}\left( \frac{\ln (N+z)}{1+z}-\ln N\right) }{3-3\Omega _{m0}N^{\frac{-2q_{1}N}{N-1}}(1+z)^{3-2\alpha } (N+z)^{\frac{2q_{1}(N+z)}{(1+z)(N-1)}}}. \end{aligned}$$
(27)

It is evident from Eq. (27) that the EoS parameter \(\omega _{\phi }(z)\) at low redshift reduces to

$$\begin{aligned} \omega _{\phi }(z)=\frac{2q_{0}-1}{(3-3\Omega _{m0})} + \frac{2{\tilde{q}}_{1}}{(3-3\Omega _{m0})}{\left( \frac{z}{1+z}\right) }, \end{aligned}$$
(28)

which is similar to the CPL parametrization of \(\omega _{\phi }(z)\) given by \(\omega _{\phi }(z)=\omega _{0} + \omega _{1}{\left( \frac{z}{1+z}\right) }\), and which has been frequently used for many cosmological analyses [32, 33].

Now, using Eqs. (15) and (26), the total EoS parameter is obtained:

$$\begin{aligned} \omega _\mathrm{tot}(z)= & {} -1+\frac{2(1+z)}{3H}\frac{\mathrm{d}H}{\mathrm{d}z}= -1 + \frac{2}{3}\Big [1+q(z)\Big ]\nonumber \\= & {} -\frac{1}{3}{\left[ 1-2q_{0}+2q_{1}\mathrm{ln}N - 2q_{1}\frac{\mathrm{ln}(N+z)}{1+z}\right] }. \end{aligned}$$
(29)

For the present model, the cosmic jerk parameter j(z) can be obtained [using Eqs. (3) and (23)],

$$\begin{aligned} j(z)=q_{0}+q_{1}{\left( \frac{1}{N+z}-\ln N\right) } + 2{\left[ q_{0}+q_{1}{\left( \frac{\ln (N+z)}{1+z}-\ln N\right) }\right] }^2 \end{aligned}$$
(30)

with \(j_{0}=j(z=0)=q_{0}+2q^2_{0} + \frac{q_{1}}{N}(1-N\ln N)\).

In the remaining part of this paper, the possibility of having a transition of the expansion of the universe from a decelerated to an accelerated one is investigated. It is seen from Eq. (23) that the functional form of q(z) depends crucially on the values of the model parameters, namely, \(q_{0}\), \(q_{1}\) and N. So, in principle one can choose these parameters arbitrarily and study the functional behavior of q(z) to confront it with the observational dataset. But, in this work, we first constrain the model parameters (\(q_{0},q_{1}\)) for some specific values of N and, using various observational datasets and with the best-fit values obtained, we then try to reconstruct q(z), \(\omega _\mathrm{tot}(z)\) and j(z). We have also checked that the present analysis is consistent with the observational datasets for higher values of N (\(N>2\)) as well. Interestingly, we have also found that, for \(N=2\), the logarithmic form of q(z) [as given in Eq. (23)] is similar to the divergence-free parametrization of the dark energy EoS parameter [34].

For a comprehensive analysis, we have also compared our theoretical model with the following well-known models (for details, see Sect. 3.3).

  1. (i)

    Firstly, we have considered the linear redshift parametrization of q(z), which has the following functional form [8]:

    $$\begin{aligned}&q(z)=q_{0}+q_{1}z\quad (\mathrm{Model}~2) \end{aligned}$$
    (31)

    where \(q_{0}\) and \(q_{1}\) represent the present value and the first derivative of q(z), respectively. In this case, H(z) evolves as

    $$\begin{aligned}&H(z)=H_{0}(1+z)^{(1+q_{0}-q_{1})}e^{q_{1}z}. \end{aligned}$$
    (32)
  2. (ii)

    Secondly, we have considered a q-parametrization of the following functional form [11,12,13,14,15]:

    $$\begin{aligned}&q(z)=q_{0}+\frac{q_{1}z}{1+z}\quad (\mathrm{Model}~3). \end{aligned}$$
    (33)

    For this model, the Hubble parameter can be obtained:

    $$\begin{aligned}&H(z)=H_{0}(1+z)^{(1+q_{0}+q_{1})}e^{-\frac{q_{1}z}{1+z}}. \end{aligned}$$
    (34)
  3. (iii)

    Next, we have considered a flat \(\Lambda \)CDM model. The corresponding form of q(z) is given by

    $$\begin{aligned} q(z)= & {} -1+\frac{3}{2{\left[ 1+\frac{\Omega _{\Lambda 0}}{\Omega _{m0}}(1+z)^{-3}\right] }}\quad \nonumber \\&(\Lambda \mathrm{CDM~model}) \end{aligned}$$
    (35)

    where \(\Omega _{\Lambda 0}+\Omega _{m0}=1\). In this case, the solution for H(z) can be obtained:

    $$\begin{aligned} H(z)=H_{0}[\Omega _{m0}(1+z)^{3} + (1-\Omega _{m0})]^{\frac{1}{2}}. \end{aligned}$$
    (36)

For each of these models (Models 1, 2 and 3), we have performed a statistical analysis to constrain the parameters (\(q_{0},q_{1}\)) of the models and with the best-fit values of these parameters, the evolution of various relevant cosmological parameters have been studied.

3 Observational constraints and results

In this section, we describe the observational datasets and the statistical analysis method that will be used to put constraints on the various parameters of the model presented in the previous section and then discuss the results obtained in this analysis. In this work, we have used the recent observational datasets from the type Ia supernova (SNIa), baryon acoustic oscillation (BAO) and the cosmic microwave background (CMB) radiation observations.

3.1 Type Ia supernova data

In the present work, the 31 binned distance modulus data sample of the recent joint lightcurve analysis has been utilized [35]. For this dataset, the \(\chi ^{2}\) is defined as (for more details see [36])

$$\begin{aligned} \chi ^{2}_\mathrm{SNIa}=A(p)-\frac{{B}^2(p)}{C}-\frac{2\mathrm{ln}10}{5C}B(p)-Q \end{aligned}$$
(37)

where

$$\begin{aligned} A(p)= & {} \sum _{\alpha ,\beta }(\mu ^{th}-\mu ^{obs})_{\alpha }(\mathcal{C}ov)^{-1}_{\alpha \beta }(\mu ^{th}-\mu ^{obs})_{\beta },\end{aligned}$$
(38)
$$\begin{aligned} B(p)= & {} \sum _{\alpha }(\mu ^{th}-\mu ^{obs})_{\alpha }\sum _{\beta }(\mathcal{C}ov)^{-1}_{\alpha \beta }, \end{aligned}$$
(39)
$$\begin{aligned} C= & {} \sum _{\alpha ,\beta }(\mathcal{C}ov)^{-1}_{\alpha \beta }, \end{aligned}$$
(40)

and the \(``\mathcal{C}ov\)” is the \(31\times 31\) covariance matrix of the binned data sample. Here, Q is a constant that does not depend on the model parameter p and hence has been ignored. Also, \(\mu ^{th}\) and \(\mu ^{obs}\) represent the theoretical and observed distance modulus, respectively.

3.2 BAO/CMB data

Next, we have considered baryon acoustic oscillation (BAO) [37,38,39,40] and cosmic microwave background (CMB) [41] radiation measurement dataset to obtain the BAO/CMB constraints on the model parameters. For BAO data, the results from the WiggleZ Survey [37], SDSS Galaxy sample [38, 39] and 6dF Galaxy Survey [40] datasets have been adopted. Also, the CMB measurement considered is derived from the Planck2015 observations [41]. One can look into Refs. [42], where the required datasets are given in a tabular form. The details of the methodology for obtaining the BAO/CMB constraints on the model parameters are available in Ref. [42], where the \(\chi ^2\) function is defined as

$$\begin{aligned} \chi ^2_\mathrm{BAO/CMB} = X^{T}C^{-1}X. \end{aligned}$$
(41)

Here, X and \(C^{-1}\) are the transformation matrix and the inverse covariance matrix, respectively [42].

Fig. 1
figure 1

\(1\sigma \) (solid line) and \(2\sigma \) (dashed line) confidence level contours in (\(q_{0}\), \(q_{1}\)) plane have been shown for different choices of N. In each panel, the large dot indicates the best-fit values of \(q_{0}\) and \(q_{1}\) arising from the analysis of SNIa + BAO/CMB dataset

Full size image

To constrain cosmological parameters from a joint analysis of the SNIa and BAO/CMB datasets, we compute

$$\begin{aligned} \chi ^{2}=\chi ^2_\mathrm{SNIa}+\chi ^2_\mathrm{BAO/CMB}. \end{aligned}$$
(42)

The best fit corresponds to the model parameters for which the above \(\chi ^{2}\) is minimum. In this work, we have minimized \(\chi ^{2}\) with respect to the model parameters \(q_{i}\) (where \(i=0,1\)) to estimate their best-fit values. For this purpose, we have fixed the parameter N to some constant value. From \(\chi ^{2}\), one can also compute the total likelihood function L, which is given by

$$\begin{aligned} {L}(q_{i})=e^{-\frac{\chi ^{2}_{T}(q_{i})}{2}} = {L}_\mathrm{SNIa}(q_{i})\times {L}_\mathrm{BAO/CMB}(q_{i}) \end{aligned}$$
(43)

where \({L}_\mathrm{SNIa}(q_{i})=e^{-\frac{\chi ^{2}_\mathrm{SNIa}(q_{i})}{2}}\) and \({L}_\mathrm{BAO/CMB}(q_{i})=e^{-\frac{\chi ^{2}_\mathrm{BAO/CMB}(q_{i})}{2}}\) are the likelihood functions of the SNIa and BAO/CMB datasets respectively.

3.3 Results of the data analysis

Figure 1 shows the \(1\sigma \) and \(2\sigma \) contours in the \(q_{0}\)–\(q_{1}\) plane for the logarithm parametrization given by Eq. (23). We have found that the best-fit values of the free parameters (\(q_{0}\) and \(q_{1}\)) for the SNIa + BAO/CMB dataset are well fitted in the \(1\sigma \) confidence contour.

In particular, the \(\chi ^{2}\) analysis is done by fixing the parameter N to some constant value and the best-fit values of \(q_{0}\) and \(q_{1}\) are presented in Table 1. Using those best-fit values of \(q_{0}\) and \(q_{1}\), we have then reconstructed the deceleration parameter q(z) and the results are plotted in Fig. 2. It is evident from Fig. 2 that q(z) favors the past deceleration \((q>0)\) and recent acceleration \((q<0)\) of the universe. This is essential for the structure formation of the universe.

Table 1 Results of statistical analysis (within \(1\sigma \) confidence level) for Model 1 by considering different values of N. Here, \(\chi ^{2}_\mathrm{min}\) denotes the minimum value of \(\chi ^{2}\). For this analysis we have considered SNIa + BAO/CMB dataset
Full size table
Fig. 2
figure 2

The deceleration parameter q(z) is reconstructed for the parametrization given by Eq. (23) using different values of N, as indicated in the each panel. The central thick line (black) represents the best-fit curve, while the dashed and dotted contours represent the \(1\sigma \) and \(2\sigma \) confidence level, respectively. In each panel, the orange, red and magenta lines represent the trajectory of q for Models 2 and 3 and the \(\Lambda \)CDM model (with \(\Omega _{\Lambda 0}=0.73\)), respectively. Also, the horizontal thin line indicates \(q(z) = 0\)

Full size image
Fig. 3
figure 3

Evolution of q(z) is shown up to \(z>-1\) for various models using the best-fit values of \(q_{0}\) and \(q_{1}\) arising from the joint analysis of SNIa + BAO/CMB dataset (see Tables 1, 2)

Full size image
Fig. 4
figure 4

The reconstructed total EoS parameter \(\omega _\mathrm{tot}(z)\) for the best-fit model by considering different values of N, as indicated in the panel (see also Table 1)

Full size image
Fig. 5
figure 5

The evolution of j(z) with respect to redshift z is shown using the best-fit values of \(q_{0}\) and \(q_{1}\) for different values of N, as indicated in the frame. The horizontal thick line (magenta) indicates \(j = 1\) (constant) for a \(\Lambda \)CDM model

Full size image

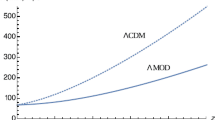
In this work, we have also obtained the best-fit values of the transition redshift (\(z_{t}\)) within \(1\sigma \) errors for the SNIa + BAO/CMB dataset and presented them in Table 3. These results are found to be consistent with the results obtained by many authors by different considerations [14, 19]. For comparison, the corresponding curves for Models 2 and 3 and the \(\Lambda \)CDM model are also plotted in Fig. 2, which shows that the evolution of q(z) is not always compatible with Model 2 for different choices of N. It is also clear from Fig. 2 that the best-fit values of \(q_{0}\) and \(z_{t}\) are in good agreement with the standard \(\Lambda \)CDM model (within \(2\sigma \) errors) and the Model 3 (within \(1\sigma \) confidence level) if we increase the value of N. From Fig. 3, it is seen that as z approaches \(-1\), the evolution of q(z) deviates from that of \(\Lambda \)CDM model. Such a behavior of q(z) may be an outcome of the choice “\(\kappa =\ln N\)” made in Eq. (23). As mentioned earlier, the choice of \(\kappa =\ln N\) was made such that \(q_{0}\) provides the present value of deceleration parameter. Some other choice of \(\kappa \) may as well be made so as to make the \(\Lambda \)CDM model consistent in the far future and thus this needs more detailed analysis. The best-fit evolution of the total EoS parameter \(\omega _\mathrm{tot}\) as a function of z, given by Eq. (29), is shown in Fig. 4, which indicates that \(\omega _\mathrm{tot}\) attains the required value of \(-\frac{1}{3}\) at \(z<1\) (or, at \(z<1.4\) for \(N=2\)) and remains greater than \(-1\) up to the current epoch (i.e., \(z=0\)) for the combined (SNIa + BAO/CMB) dataset. This result is consistent with the recent observational results. On the other hand, Fig. 5 clearly shows the departure of j, given by Eq. (30), from the flat \(\Lambda \)CDM model (\(j = 1\)) for the best-fit model. It is seen from Fig. 5 that, for the best-fit model, the present value of j is greater than 1 for \(N=3,4\) and 5, while for \(N=2\), j is less than 1 (see also Table 3). So, the present model (with \(j\ne 1\) and \(q_{0}<0\)) clearly indicates that a dynamical DE is more likely to be responsible for the current acceleration.

Table 2 Results of statistical analysis (within \(1\sigma \) confidence level) for Model 2 and 3 by considering SNIa + BAO/CMB dataset
Full size table
Table 3 Best-fit values of \(z_{t}\) and \(j_{0}\) (within \(1\sigma \) errors) for Model 1 by considering different values of N. Here, \(z_{t}\) is the transition redshift and \(j_{0}\) is the present value of j. For this analysis we have considered SNIa + BAO/CMB dataset
Full size table

For statistical comparison of Model 1 with Models 2 and 3, two model selection criteria have been used, the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). The AIC is defined as [43]

$$\begin{aligned} \mathrm{AIC}=-2\mathrm{ln}L_\mathrm{max} + 2g \end{aligned}$$
(44)

and the BIC is defined as [44]

$$\begin{aligned} \mathrm{BIC}=-2\mathrm{ln}L_\mathrm{max} + g\mathrm{ln}k \end{aligned}$$
(45)

where \(L_\mathrm{max}\) is the maximum likelihood (equivalently, minimum of \(\chi ^2\)) obtained for the model, g is the number of free parameters in that model and k is the number of data points used for the data analysis. If the magnitude of the differences between the AIC (\(\triangle \)AIC) of the two models (or \(\triangle \)BIC) is less than 2, then the toy model under consideration (here, Model 1) is strongly favored by the reference model (here, Models 2 and 3). On the other hand, if the magnitude of \(\triangle \)AIC or \(\triangle \)BIC is greater than 10, then the models strongly disfavor each other. As mentioned earlier, the statistical analysis is done by fixing the parameter N to some constant. Because of this, all the three models (Models 1, 2 and 3) have same number of degrees of freedom, and thus \(\triangle \)AIC or \(\triangle \)BIC will be same. Now for Model 1 in comparison with the Model 2 and 3, the \(\triangle \)AIC (or \(\triangle \)BIC) values are given by

$$\begin{aligned} \triangle \mathrm{AIC}=\chi ^{2}_\mathrm{min}(\mathrm{Model}~1) - \chi ^{2}_\mathrm{min}(\mathrm{Model}~2) \end{aligned}$$

and

$$\begin{aligned} \triangle \mathrm{AIC}=\chi ^{2}_\mathrm{min}(\mathrm{Model}~1) - \chi ^{2}_\mathrm{min}(\mathrm{Model}~3). \end{aligned}$$

Now, it is clear from Tables 1 and 2 that, for Model 3, the \(\triangle \)AIC (or \(\triangle \)BIC) is less than 2 for each choices of N. Hence, the present reconstructed model is highly consistent with Model 3.

4 Conclusions

In the present work, we have studied the dynamics of accelerating scenario within the framework of scalar field model. Here, we have considered one specific parameterization of the deceleration parameter q(z) and from this we have found analytical solutions for various cosmological parameters. As we have seen before, the new parametrization of q(z) is similar to the well-known parametrization of q(z) for appropriate choices of \(q_{0}\), \(q_{1}\) and N. We have also compared our theoretical model with three different popular models, such as \(q\propto z\) [see Eq. (31)], \(q\propto \frac{z}{1+z}\) [see Eq. (33)] and \(\Lambda \)CDM [see Eq. (35)], to draw a direct comparison between them. In what follows, we have summarized the main results of our analysis.

The observational data analysis by \(\chi ^{2}\)-minimization technique have also been analyzed for this model using the SNIa + BAO/CMB dataset. From this analysis, we have obtained the bounds on the arbitrary parameters \(q_{0}\) and \(q_{1}\) within \(1\sigma \) and \(2\sigma \) confidence levels. It has been found that q(z) shows exactly the behavior which is desired, a deceleration for high z limit whereas an acceleration for the low z limit. This is essential to explain both the observed growth of structure at the early epoch and the late-time cosmic acceleration measurements. It should be noted that, for the present model, the values of the transition redshift \(z_{t}\) with \(1\sigma \) errors are consistent with the values obtained by many authors from different scenarios [14, 19]. For this model, the jerk parameter j is found to be evolving, which indicates a tendency of deviation of the universe from the standard \(\Lambda \)CDM model. These results make the present work worthy of attention. The present model also provides an analytical solution for the EoS parameter \(\omega _{\phi }(z)\). Interestingly, it has been found that the EoS parameter reduces to the well-known CPL parametrization of \(\omega _{\phi }(z)\) for low z [32, 33]. To obtain more physical insight regarding the evolution of \(\omega _{\phi }(z)\), we have plotted the reconstructed total EoS parameter in Fig. 4 and the resulting scenarios agree very well with the observational results at the present epoch.

As discussed earlier, this particular choice of q(z) is quite arbitrary and we have made this assumption to close the system of equations. Since the nature of the universe is still a mystery, therefore the idea to parameterize q(z) is a simple approach to study the transition of the universe from decelerated to accelerated expansion phase and also opens up possibilities for future studies regarding the nature of dark energy. Definitely, the addition of more observational datasets in the present work may help us to obtain more precise constraints on the expansion history of the universe and the present work is one preliminary step in that direction.