1 Introduction

In conformally flat spacetimes, the Weyl tensor vanishes [1] and one of its interesting features is that the Maxwell field equations are equivalent to the flat spacetime [2, 3]. As of such conformally flat spacetimes one finds the Robertson–Walker cosmological metrics [4,5,6,7], the Einstein–de Sitter spacetime [8] and the Mannheim solution [9]. The Levi-Civita–Bertotti–Robinson (LBR) conformally flat solution to the Einstein–Maxwell field equations in the context of general relativity is given by (\(G=1=4\pi \epsilon _{0}\))

$$\begin{aligned} \mathrm{d}s^{2}=\frac{Q^{2}}{r^{2}}\left( -\mathrm{d}t^{2}+\mathrm{d}r^{2}+r^{2}\mathrm{d}\Omega ^{2}\right) , \end{aligned}$$
(1)

which was found in [10,11,12,13] and has been interpreted as the spacetime outside a static, massless, charged particle by Lovelock [14, 15]. According to Lovelock, in order to avoid the naked singularity, one has to assume that \(Q<2r_\mathrm{s}\) in which \(r_\mathrm{s}\) stands for the Schwarzschild radius of the particle [14, 15]. This, however, implies that the singularity cannot be avoided. Alternatively, Dolan in [16] has shown that the solution (1) is not spherically symmetric and therefore the physical singularity at \(r=0\) can be avoided [15]. Recently in [15], by excluding \(r=0\) from a spherically symmetric spacetime, Gron and Johannesen have constructed the LBR spacetime without encountering the physical singularity at \(r=0\). In this effort they have established a timelike thin shell of radius Q and mass \(M=Q\) with flat Minkowski spacetime inside and the LBR solution outside the shell. Inspired by Refs. [15, 17, 18], in this work we shall assess the stability of the thin shell introduced in [15]. To do so, since the outside spacetime, i.e., Eq. (1), is conformally flat, first we give a general formalism for constructing thin shells in conformally flat bulks in R-gravity together with their stability and then we will investigate the specific thin shell mentioned above. Let us add that the stability of thin shells against a linear perturbation have already been introduced and studied in the literature [19,20,21,22,23,24].

Furthermore, the Mannheim metric [9] in Einstein’s theory of gravity,

$$\begin{aligned} \mathrm{d}s^{2}=-\left( 1-2\eta R\right) \mathrm{d}T^{2}+\frac{\mathrm{d}R^{2}}{1-2\eta R}+R^{2}\mathrm{d}\Omega ^{2}, \end{aligned}$$
(2)

which has been considered for the gravity at large distances [25,26,27] is also conformally flat. Here, \(\eta <0\) is called the Rindler acceleration, which was estimated by Carloni, Grumiller and Preis to be upper bounded, i.e., \(\left| \eta \right| \le 9\times 10^{-10}\,\mathrm{m/s}^{2}\) in SI units [26]. In [26] the authors considered a classical test on general relativity in the solar system by considering the spacetime outside the sun to be of the form of

$$\begin{aligned} \mathrm{d}s^{2}= & {} -\left( 1-\frac{2M}{R}-2\eta R-\Lambda R^{2}\right) \mathrm{d}T^{2}\nonumber \\&+\,\frac{\mathrm{d}R^{2}}{1-\frac{2M}{R}-2\eta R-\Lambda R^{2}}+R^{2}\mathrm{d}\Omega ^{2} \end{aligned}$$
(3)

in which M is the solar mass and \(\Lambda \) is the cosmological constant; but it was set to zero in their calculations. For the details of their test we suggest the reader to look at Ref. [26]. To see the conformally flatness of the Mannheim spacetime first we impose the transformation \(R=\frac{1-e^{-2x}}{2\eta }\), which yields

$$\begin{aligned} \mathrm{d}s^{2}=e^{-2x}\left( -\mathrm{d}T^{2}+\frac{\mathrm{d}x^{2}}{\eta ^{2}}+\frac{\sinh ^{2}x}{ \eta ^{2}}\mathrm{d}\Omega ^{2}\right) , \end{aligned}$$
(4)

followed by a second transformation expressed as

$$\begin{aligned} r=\frac{e^{\eta t}}{\eta }\sinh x \end{aligned}$$
(5)

and

$$\begin{aligned} t=\frac{e^{\eta t}}{\eta }\cosh x. \end{aligned}$$
(6)

These lead to the Mannheim metric becoming

$$\begin{aligned} \mathrm{d}s^{2}=\frac{4}{\eta ^{2}\left( r+t\right) ^{2}}\left( -\mathrm{d}t^{2}+\mathrm{d}r^{2}+r^{2}\mathrm{d}\Omega ^{2}\right) , \end{aligned}$$
(7)

which is manifestly conformally flat. We note that, unlike the LBR the conformal factor of the Mannheim metric is time t and space r dependent. We would like to add that, although (7) is the conformally flat form of the Mannheim metric, in the last part of the paper we consider the thin shell in the Mannheim spacetime in the standard spherically symmetric form (2). Hence, the organization of the paper is as follows. In Sect. 2 we give the formalism of the constructing of thin shells in conformally flat spacetime and in the same section we study the stability of such thin shells with the explicit example of LBR spacetime. In Sect. 3 we work on the thin shell in the Mannheim spacetime in its spherically symmetric form (2) and its stability. We conclude our paper in Sect. 4.

2 Thin shell formalism in conformally flat bulk

In \(3+1\)-dimensional spacetime in standard general relativity, i.e., R-gravity, we consider a timelike spherical thin shell defined by \(\digamma =r-a\left( \tau \right) =0\) in which r is the spherical radial coordinate and \(\tau \) is the proper time measured by an observer located on the shell. We consider the spacetime inside and outside the shell to be two distinct conformally flat spacetimes given by

$$\begin{aligned} \mathrm{d}s_{i}^{2}=\frac{-\mathrm{d}t_{i}^{2}+\mathrm{d}r_{i}^{2}+r_{i}^{2}\left( \mathrm{d}\theta _{i}^{2}+\sin ^{2}\theta _{i}\mathrm{d}\phi _{i}^{2}\right) }{\psi _{i}\left( r\right) ^{2}} \end{aligned}$$
(8)

in which \(\psi _{i}\left( r\right) \) is a function of r only. In (8) a subscript i stands for 1 and 2, which refer to inside (\(r<a\)) and outside (\(r>a\)) the shell, respectively. For smooth matching one has to apply the so-called Israel junction conditions. In accordance with these conditions, at the shell’s place we set \(r_{1}=r_{2}=a,\) \(\psi _{1}\left( a\right) =\psi _{2}\left( a\right) =\psi \left( a\right) ,\) \(\theta _{1}=\theta _{2}=\theta \), \(\phi _{1}=\phi _{2}=\phi \) and the times are related via

$$\begin{aligned} \frac{-\dot{t}_{1}^{2}+\dot{a}_{1}^{2}}{\psi _{1}\left( a\right) ^{2}}=\frac{ -\dot{t}_{2}^{2}+\dot{a}_{2}^{2}}{\psi _{2}\left( a\right) ^{2}}=-1. \end{aligned}$$
(9)

Herein, a dot stands for the derivative with respect to the proper time \( \tau \). This setup guarantees that the induced metric on both sides of the thin shell are identical and given by

$$\begin{aligned} \mathrm{d}s_\mathrm{TS}^{2}=-\mathrm{d}\tau ^{2}+\frac{a^{2}}{\psi \left( a\right) ^{2}}\left( \mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\phi ^{2}\right) . \end{aligned}$$
(10)

Next to Israel’s condition is the Einstein equation on the shell, which can be expressed as (\(G=1\))

$$\begin{aligned} \left[ K_{m}^{n}\right] -\left[ K\right] \delta _{m}^{n}=-8\pi S_{m}^{n} \end{aligned}$$
(11)

where \(\left[ K_{m}^{n}\right] =K_{m\left( 2\right) }^{n}-K_{m\left( 1\right) }^{n}\), \(\left[ K\right] =\) \(\left[ K_{m}^{m}\right] \) and \( S_{m}^{n}=\mathrm{diag}\left( -\sigma ,p_{\theta },p_{\phi }\right) \) is the energy-momentum tensor of the matter source presented on the shell. The components of the extrinsic curvature tensor \(K_{mn\left( 1,2\right) }\) are defined by

$$\begin{aligned} K_{mn\left( 1,2\right) }=-n_{\gamma \left( 1,2\right) }\left( \frac{\partial ^{2}x^{\gamma }}{\partial y^{m}\partial y^{n}}+\Gamma _{\alpha \beta }^{\gamma }\frac{\partial x^{\alpha }}{\partial y^{m}}\frac{\partial x^{\beta }}{\partial y^{n}}\right) , \end{aligned}$$
(12)

in which \(x^{\alpha }=\left\{ t,r,\theta ,\phi \right\} \) and \(y^{m}=\left\{ \tau ,\theta ,\phi \right\} \) are the coordinate systems describing the embedding bulk spacetimes and the embedded thin shell. Here, \(n_{\gamma \left( 1,2\right) }\) are the normal four-vectors on both sides of the thin shell which are geometrically pointing from inside toward outside the shell and given by

$$\begin{aligned} n_{\gamma \left( 1,2\right) }=\frac{1}{\sqrt{\frac{\partial \digamma }{ \partial x_{\left( 1,2\right) }^{\alpha }}\frac{\partial \digamma }{\partial x_{\left( 1,2\right) }^{\beta }}g_{\left( 1,2\right) }^{\alpha \beta }}} \frac{\partial \digamma }{\partial x_{\left( 1,2\right) }^{\gamma }}, \end{aligned}$$
(13)

in which \(\digamma \) was introduced above. Our explicit calculations reveal that

$$\begin{aligned} n_{\gamma \left( 1,2\right) }=\left( -\frac{\dot{a}}{\psi ^{2}\left( a\right) },\frac{\sqrt{\psi ^{2}\left( a\right) +\dot{a}^{2}}}{\psi ^{2}\left( a\right) },0,0\right) , \end{aligned}$$
(14)

and consequently the nonzero components of the mixed extrinsic curvature are obtained as follows:

$$\begin{aligned} K_{\tau \left( 1,2\right) }^{\tau }=\frac{\psi \left( a\right) \ddot{a} -\left( 2\dot{a}^{2}+\psi ^{2}\left( a\right) \right) \psi _{1,2}^{\prime }\left( a\right) }{\psi \left( a\right) \sqrt{\psi ^{2}\left( a\right) +\dot{ a}^{2}}}, \end{aligned}$$
(15)

and

$$\begin{aligned} K_{\theta \left( 1,2\right) }^{\theta }= & {} K_{\phi \left( 1,2\right) }^{\phi } \nonumber \\= & {} \frac{\sqrt{\psi ^{2}\left( a\right) +\dot{a}^{2}}\left( \psi \left( a\right) -a\psi _{1,2}^{\prime }\left( a\right) \right) }{a\psi \left( a\right) }. \end{aligned}$$
(16)

We note that \(\psi \left( a\right) \) is continuous at the location of the thin shell but \(\psi ^{\prime }\left( a\right) \) is not, therefore, \( \psi _{1}\left( a\right) =\psi _{2}\left( a\right) =\psi \left( a\right) \) but \(\psi _{1}^{\prime }\left( a\right) \ne \psi _{2}^{\prime }\left( a\right) \) and one has to keep them with the proper subindices. Furthermore, applying these to (11) one finds

$$\begin{aligned} \sigma =\frac{\sqrt{\psi ^{2}\left( a\right) +\dot{a}^{2}}\left( \psi _{2}^{\prime }\left( a\right) -\psi _{1}^{\prime }\left( a\right) \right) }{ 4\pi \psi \left( a\right) } \end{aligned}$$
(17)

and

$$\begin{aligned} p=p_{\theta }=p_{\phi }=-\frac{\left( 3\dot{a}^{2}+2\psi ^{2}\left( a\right) \right) \left( \psi _{2}^{\prime }\left( a\right) -\psi _{1}^{\prime }\left( a\right) \right) }{8\pi \psi \left( a\right) \sqrt{\psi ^{2}\left( a\right) + \dot{a}^{2}}}\nonumber \\ \end{aligned}$$
(18)

in which a prime stands for the derivative with respect to \(r_{1}\) for \(\psi _{1}^{\prime }\) and \(r_{2}\) for \(\psi _{2}^{\prime }\). We note also that if the thin shell is at equilibrium at \(a=a_{0}\) with no velocity and acceleration, the energy density and lateral pressure reduce to

$$\begin{aligned} \sigma _{0}=\frac{1}{4\pi }\left( \psi _{2}^{\prime }\left( a_{0}\right) -\psi _{1}^{\prime }\left( a_{0}\right) \right) \end{aligned}$$
(19)

and

$$\begin{aligned} p_{0}=-\sigma _{0}. \end{aligned}$$
(20)

Let us add that with \(\psi _{2}^{\prime }\left( a_{0}\right) \ge \psi _{1}^{\prime }\left( a_{0}\right) \) we get \(\sigma _{0}\ge 0\) and with the identity \(p_{0}+\sigma _{0}=0\) the weak energy conditions are satisfied on the shell.

2.1 Dynamic thin shell and stability

To get further for a dynamic thin shell one has to consider an equation of state which in our case is assumed to be a linear gas–fluid with the relation

$$\begin{aligned} p=w\sigma \end{aligned}$$
(21)

between p and \(\sigma \) in which w is a constant (in the sequel we shall give a physical interpretation to w). Considering this equation of state together with (17) and (18) one finds

$$\begin{aligned} \frac{\left( \left( 3+2w\right) \dot{a}^{2}+2\left( 1+w\right) \psi ^{2}\left( a\right) \right) \left( \psi _{2}^{\prime }\left( a\right) -\psi _{1}^{\prime }\left( a\right) \right) }{\psi \left( a\right) \sqrt{\psi ^{2}\left( a\right) +\dot{a}^{2}}}=0,\nonumber \\ \end{aligned}$$
(22)

which follows upon considering that \(\psi _{2}^{\prime }\left( a\right) \ne \psi _{1}^{\prime }\left( a\right) \) admits an equation of motion for the thin shell given by

$$\begin{aligned} \dot{a}^{2}+\frac{2\left( 1+w\right) }{\left( 3+2w\right) }\psi ^{2}\left( a\right) =0. \end{aligned}$$
(23)

This is a one-dimensional equation of motion with potential

$$\begin{aligned} V\left( a\right) =\frac{2\left( 1+w\right) }{\left( 3+2w\right) }\psi ^{2}\left( a\right) \end{aligned}$$
(24)

and energy \(E=0.\) Referring to (23), we comment that a dynamic and stable thin shell requires \(V\left( a\right) <0\) and \(V^{\prime \prime }\left( a\right) >0\) in some interval for a respectively. This is important to note that \(V^{\prime \prime }\left( a\right) =\frac{\mathrm{d}^{2}V\left( a\right) }{ \mathrm{d}a^{2}}.\) Imposing \(V\left( a\right) <0\) one finds \(-\frac{3}{2}<w<-1\) and at exact \(w=-1\) the potential \(V\left( a\right) \) vanishes. Consequently \( \dot{a}=0\), which is the equilibrium case mentioned above. Upon posing the stability condition, i.e., \(V^{\prime \prime }\left( a\right) >0\), we find \(\psi ^{\prime }\left( a\right) ^{2}+\psi \left( a\right) \psi ^{\prime \prime }\left( a\right) <0\) for a within the interval as \(V\left( a\right) <0\).

2.2 Applications

2.2.1 LBR spacetime

Gron and Johannesen in Ref. [15] have considered LBR spacetime to be the solution of the Einstein field equations in empty space outside a timelike spherically symmetric thin shell whose inside spacetime is flat. Considering the conformally flat expression of the LBR solution, the line element inside and outside of the shell can be expressed by (8) provided

$$\begin{aligned} \psi _{1}\left( r_{1}\right) =1 \end{aligned}$$
(25)

and

$$\begin{aligned} \psi _{2}\left( r_{2}\right) =\frac{r_{2}}{a}. \end{aligned}$$
(26)

The energy density and lateral pressures are given by

$$\begin{aligned} \sigma =\frac{\sqrt{1+\dot{a}^{2}}}{4\pi a} \end{aligned}$$
(27)

and

$$\begin{aligned} p=p_{\theta }=p_{\phi }=-\frac{3\dot{a}^{2}+2}{8\pi a\sqrt{1+\dot{a}^{2}}}, \end{aligned}$$
(28)

and the one-dimensional potential of the thin shell becomes

$$\begin{aligned} V\left( a\right) =\frac{2\left( 1+w\right) }{\left( 3+2w\right) }, \end{aligned}$$
(29)

which is a constant. To have the formation of the thin shell as a possibility one has to impose \(-\frac{3}{2}<w<-1\) and upon solving (23) with \(\psi \left( a\right) =1\) one finds

$$\begin{aligned} a=\pm \sqrt{-\frac{2\left( 1+w\right) }{\left( 3+2w\right) }}\tau +a_{0}, \end{aligned}$$
(30)

which is the radius of the thin shell in terms of the proper time \(\tau .\) Finally, we observe that the radius of the shell either increases or decreases with a constant rate. Also in the case when \(w=-1,\) one finds \(\dot{ a}^{2}=0\), which is the equilibrium state. To finalize our assessment let us add a note on what we call a in our calculations: it is nothing but the charge of the thin shell, i.e., \(Q>0\). Having time-dependent a results in a time dependent electric charge on the shell. Therefore the Maxwell electric field two-form reads

$$\begin{aligned} \mathbf {F=}\frac{Q\left( t\right) }{r^{2}}\mathrm{d}t\wedge \mathrm{d}r. \end{aligned}$$
(31)

Furthermore, the Maxwell field equations become

$$\begin{aligned} d\left( \mathbf {F}\right) =0 \end{aligned}$$
(32)

and

$$\begin{aligned} d\left( ^{\bigstar }\mathbf {F}\right) =\left. ^{\bigstar }\mathbf {J},\right. \end{aligned}$$
(33)

where \(\mathbf {\bigstar }\) implies the dual fields and \(\mathbf {J=-}\left. ^{\bigstar }\left( ^{\bigstar }\mathbf {J}\right) \right. \) is the electric current one-form. The first integrability condition (32) is identically satisfied but (33) explicitly yields an electric current given by

$$\begin{aligned} \mathbf {J=-}\frac{\dot{Q}}{Q^{2}}\mathrm{d}r. \end{aligned}$$
(34)

This is a radial current outward / inward from / to the shell for \(\dot{Q}<0\) / \(>0.\) If we assume that the charge is only on the shell then the only possibility is \(\dot{Q}<0\). Hence, the radius of the thin shell decreases according to

$$\begin{aligned} \dot{a}=\dot{Q}=-\sqrt{-\frac{2\left( 1+w\right) }{\left( 3+2w\right) }} \end{aligned}$$
(35)

provided \(-\frac{3}{2}<w<-1.\)

In general when the inner spacetime is flat irrespective of the outer metric the thin shell obeys the same equation of motion as of (23) with \(\psi \left( a\right) =1\). In other words, suppose \(\psi _{1}\left( r_{1}\right) =1\); then according to the Israel first condition \(\psi _{2}\left( a\right) =1\). This implies that the thin shell experiences the same potential as (29) and follows the same path as LBR given in (30).

3 Thin shell in Mannheim’s spacetime

In this section we construct a timelike spherically symmetric thin shell with the Mannheim metric as the outer spacetime and flat Minkowski as the inner spacetime. Hence, we define the timelike hyperplane as \( \digamma =r-a\left( \tau \right) =0\) with the line-elements

$$\begin{aligned} \mathrm{d}s_{i}^{2}=-f_{i}\mathrm{d}t_{i}^{2}+\frac{1}{f_{i}}\mathrm{d}r_{i}^{2}+r_{i}^{2}\left( \mathrm{d}\theta _{i}^{2}+\sin ^{2}\theta _{i}\mathrm{d}\phi _{i}^{2}\right) , \end{aligned}$$
(36)

in which \(f_{1}=1\) and \(f_{2}=1-2\eta r\) in which \(\eta <0.\) Without going through the details, using the definitions of normal four-vector and second fundamental form of the shell given in (13) and (12) together with the Israel junction conditions we get

$$\begin{aligned} n_{\gamma \left( 1,2\right) }=\left( -\dot{a},\frac{\sqrt{f_{1,2}\left( a\right) +\dot{a}^{2}}}{f_{1,2}\left( a\right) },0,0\right) , \end{aligned}$$
(37)
$$\begin{aligned} K_{\tau \left( 1,2\right) }^{\tau }=\frac{2\ddot{a}+f_{1,2}^{\prime }}{2 \sqrt{f_{1,2}\left( a\right) +\dot{a}^{2}}}, \end{aligned}$$
(38)
$$\begin{aligned} K_{\theta \left( 1,2\right) }^{\theta }=K_{\phi \left( 1,2\right) }^{\phi }= \frac{\sqrt{f_{1,2}\left( a\right) +\dot{a}^{2}}}{a}, \end{aligned}$$
(39)
$$\begin{aligned} \sigma =\frac{1}{4\pi }\left( \frac{\sqrt{f_{1}\left( a\right) +\dot{a}^{2}} }{a}-\frac{\sqrt{f_{2}\left( a\right) +\dot{a}^{2}}}{a}\right) , \end{aligned}$$
(40)

and

$$\begin{aligned} p= & {} p_{\theta }=p_{\phi } \nonumber \\= & {} \frac{1}{16\pi }\left( -\sigma +\frac{2\ddot{a}+f_{2}^{\prime }}{\sqrt{ f_{2}\left( a\right) +\dot{a}^{2}}}-\frac{2\ddot{a}+f_{1}^{\prime }}{\sqrt{ f_{1}\left( a\right) +\dot{a}^{2}}}\right) . \end{aligned}$$
(41)

At the equilibrium point \(a=a_{0}\), which is defined as \(\dot{a}=\ddot{a}=0\), one finds

$$\begin{aligned} \sigma _{0}=\frac{1}{4\pi }\left( \frac{\sqrt{f_{1}\left( a_{0}\right) }}{ a_{0}}-\frac{\sqrt{f_{2}\left( a_{0}\right) }}{a_{0}}\right) \end{aligned}$$
(42)

and

$$\begin{aligned} p_{0}=\frac{1}{2}\left( -\sigma _{0}+\frac{1}{8\pi }\left( \frac{ f_{2}^{\prime }\left( a_{0}\right) }{\sqrt{f_{2}\left( a_{0}\right) }}-\frac{ f_{1}^{\prime }\left( a_{0}\right) }{\sqrt{f_{1}\left( a_{0}\right) }} \right) \right) . \end{aligned}$$
(43)

The energy conservation can be directly found from the explicit form of \( \sigma \) and p, which reads

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}a}+\frac{2}{a}\left( p+\sigma \right) =0. \end{aligned}$$
(44)

To find the dynamic equation of the thin shell we use (40) to find

$$\begin{aligned} \dot{a}^{2}+V\left( a\right) =0 \end{aligned}$$
(45)

in which

$$\begin{aligned} V\left( a\right) =\frac{f_{1}+f_{2}}{2}-\frac{\left( f_{1}-f_{2}\right) ^{2} }{\left( 8\pi a\sigma \right) ^{2}}-\left( 2\pi a\sigma \right) ^{2}. \end{aligned}$$
(46)

Next, we consider again a linear equation of state as \(p=\omega \sigma \) for the matter presented on the shell in which \(\omega =v_{s}^{2}\) in which \( v_{s}\) is the speed of sound. Therefore to keep our analysis physical in this part we impose \(0<\omega \le 1.\) Upon plugging the equation of state in (44) one finds

$$\begin{aligned} \sigma =\frac{C}{8\pi a^{2\left( \omega +1\right) }} \end{aligned}$$
(47)

in which \(C>0\) is an integration constant. Moreover, the one-dimensional potential (46) after setting \(f_{1}=1\) and \(f_{2}=1-2H_{\Lambda }r\) becomes

$$\begin{aligned} V\left( a\right) =1-a\eta -\frac{4\eta ^{2}}{C^{2}}a^{4\left( \omega +1\right) }-\frac{C^{2}}{16a^{2\left( 2\omega +1\right) }}. \end{aligned}$$
(48)

Introducing

$$\begin{aligned} \tilde{a}=aC^{\frac{-1}{1+2\omega }} \end{aligned}$$
(49)

and

$$\begin{aligned} \tilde{\eta }=\eta C^{\frac{1}{1+2\omega }}, \end{aligned}$$
(50)

one can absorb the constant C and the potential reduces to

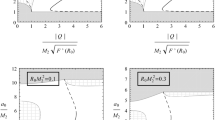
$$\begin{aligned} V\left( \tilde{a}\right) =1-\tilde{a}\tilde{\eta }-4\tilde{\eta }^{2}\tilde{a} ^{4\left( \omega +1\right) }-\frac{1}{16\tilde{a}^{2\left( 2\omega +1\right) }}. \end{aligned}$$
(51)

For \(0<\omega \le 1\) this potential, in both limits, i.e., \(\tilde{a} \rightarrow 0\) and \(\tilde{a}\rightarrow \infty ,\) diverges to \(-\infty \) and only one maximum occurs at \(\tilde{a}=\left( -\frac{1}{8\tilde{\eta }} \right) ^{\frac{1}{3+4\omega }}.\) This reveals that the potential cannot confine the thin shell and therefore the motion of the thin shell ends up either by collapsing or evaporation. In contrast, if we relax the value of \( \omega ,\) for \(-1<\omega <-\frac{1}{2}\) we find one maximum at \(\tilde{a} =\left( -\frac{1}{8\tilde{\eta }}\right) ^{\frac{1}{3+4\omega }}\) and one minimum at \(\tilde{a}=\left( \frac{2\omega +1}{16\tilde{\eta }\left( \omega +1\right) }\right) ^{\frac{1}{3+4\omega }}.\) In Fig. 1 we plot \(V\left( \tilde{a}\right) \) in terms of \(\tilde{a}\) for \(\omega =-0.95\) and various values for \(\tilde{\eta }.\) As displayed in Fig. 1 for constant \(\omega \) increasing the magnitude of \(\tilde{\eta }\) increases the deepness of the potential well. Also since the total energy of the thin shell is zero it is confined between the two roots of the potential, which we call turning points (Fig. 1). Note that this kind of motion occurs due to the nature of the potential. For instance if such a thin shell forms at the outer turning point with initial velocity zero, it moves down the potential well toward the inner turning point and returns to its initial point. Hence, an oscillation forms between the two turning points, from which one concludes that the thin shell is confined or stable.

Fig. 1
figure 1

Plot of \(V\left( \tilde{a}\right) \) versus \(\tilde{a}\) for \(\omega =-0.95\) and \(\tilde{\eta }=-0.55,-0.65,\) and \(-0.75\) from top to bottom. The turning points for green (dash-dot) curve are also shown

Full size image

4 Conclusion

We aimed to investigate the stability of a charged thin shell of radius \(a=Q\) with inside and outside metrics as the flat Minkowski and LBR metrics, respectively. This structure has been proposed by Gron and Johannesen in [15]. To that end, however, we started with a generic thin shell in conformally flat bulk spacetime in R-gravity. We presented the general conditions to be satisfied in order to have a thin shell supported by matter with a linear equation of state to be formed and remaining stable. In particular we considered the case constructed in [15] and we have shown that it cannot be stable. For a more general case, we also found that it cannot be stable. Following our assessment on the stability of the thin shells in conformally flat bulks, we considered a spherically symmetric thin shell with inside metric to be the flat Minkowski and outside to be the Mannheim metric but in a standard spherical coordinate representation. The connection of this specific case to our general case is the fact that the Mannheim metric is also conformally flat. We observed that with a linear equation of state i.e., \(p=\omega \sigma \) and \(0<\omega \le 1\), the thin shell is not stable. However, by considering \(-1<\omega <-\frac{1}{2}\) and finely tuned \(\tilde{\eta }\), the thin shell may be confined or stable. Finally let us add that in all our considerations we assumed the matter presented on the shell to be a perfect fluid with a linear equation of state. More general equations of state remain open for further study.