1 Introduction

Various astronomical and cosmological observations of the last decade, including CMB studies [1], supernovae [2, 3] and large scale structure [4], have provided a picture of the universe with accelerating expansion. This profound mystery leads us to the prospect that either about \(70\%\) of the universe is made up of a substance known as dark energy[5], about which we have almost no knowledge at all, or that General Relativity (GR) is modified at cosmological scales [6,7,8]. A simple candidate for the dark energy is the cosmological constant with the equation of state (EoS) parameter \(\omega = -1\). However, the cosmological constant model is subject to the fine-tuning and coincidence problems [9]. In order to solve these problems, various dynamical dark energy models have been proposed: quintessence [10, 11], phantom [12, 13] and quintom [14,15,16]. Because the quintessence type of matter could not give the possibility that \(\omega < -1\), extended paradigms (i.e. phantom and quintom) were proposed [17]. Beside this unknown-nature dark energy, a second way, concerning various gravitational modification theories like f(R), f(T) and scalar-tensor theories, has been addressed. One of the modifications of the matter part of the Einstein–Hilbert action is f(T) gravity as an extension of teleparallel gravity. Teleparallel Gravity (TG), demonstrably equivalent to general relativity, was initially introduced by Einstein for the sake of unifying gravity and electromagnetism. In TG we use the Weitzenböck connection instead of the Levi-Civita connection, so we have torsion in lieu of curvature only. The field equations in this theory are second-order differential equations, while for the generalized f(R) theory they are of fourth order, thus it is simpler to analyze and elaborate the cosmic evolution [18].

The actions of this context are likely to contain several scalar fields, but it is normally assumed that only one of these fields remains dynamical for a long period. We always see the coupling function of f(R) and also f(T) in the form of a function; that is, \(F(\varphi ) f(R)\) or \(F(\varphi ) f(T)\), depending upon the scalar field only. The motivation for the nonminimal coupling, \(F(\varphi )R\) in which \(F(\varphi )= \frac{1}{2} \left( \frac{1}{8\pi G} - \xi \varphi ^2 \right) \), in the gravitational Lagrangian comes from many directions. However, this explicit nonminimal coupling was originally introduced in the context of classical radiation problems [19], and also it is required by renormalizability in curved spacetime [20]. For different values of \(\xi \), we have the following table (Table 1).

Table 1 Special values of the dimensionless coupling constant, \((\xi )\), in the nonminimal coupling and their names
Full size table

However, the values of \(\xi \) in renormalizable theories depend upon the class of theory [56, 57]. A nonzero \(\xi \) is generated by first loop corrections even if it is absent in the classical action [21, 22]. A nonminimal coupling term is expected at high curvatures [23], and it has been argued that classicalization of the universe in quantum cosmology indeed requires \(\xi \ne 0\). Moreover, the nonminimal coupling can solve potential problems of primordial nucleosynthesis [24] and the absence of pathologies in the propagation of \(\varphi \)-waves seems to require conformal coupling for all nongravitational scalar fields [25]. Any attempt to formulate quantum field theory on a curved spacetime necessarily leads to modifying the Hilbert–Einstein action. This means adding terms containing nonlinear invariants of the curvature tensor or nonminimal couplings between matter and the curvature originating in the perturbative expansion [26, 27].

Now, let us take the incomplete action

$$\begin{aligned} S = \int d^4x \sqrt{-g} \left[ F(\varphi )R+ \cdots \right] \end{aligned}$$

into account. Eliminating the accelerating term under integration by parts, the corresponding point-like Lagrangian reads

$$\begin{aligned} L = 6 a {\dot{a}}^2 F - 6K a F+{\underline{\underline{{{6 a}^{2} {\dot{a}} F^{\prime } {\dot{\varphi }}}}}}+ \cdots , \end{aligned}$$
(1)

where \(K=0, \pm 1\). Here we assume the signs (+ - - -) for the FRW metric components. On the other hand, in f(T) gravity, pursuant to the torsion form, we have no accelerating term, so in this case, we do not have the last term in (1) in which the derivative of the scalar field couples with the scale factor and its derivative. Maybe it is worth to note what happens when we insert a term as \(U\left( \varphi , \varphi _{,\mu }\varphi ^{,\mu } \right) g(T)\) in the actions of f(T) gravity. As mentioned in the first paragraph of the introduction, the “Teleparallel” case is equivalent to General Relativity (TEGR). Altogether, in many cases, the authors construct the actions of f(T) gravity by replacing the torsion instead of curvature (for example, see [41, 59]). However, when the nonminimal coupling is switched on, the resulting theory exhibits different behavior. Hence, the last term in (1) is the inspiration for adding such a term. The main purpose of the present work is to answer the aforementioned question by having recourse to the Noether symmetry approach.

Symmetries play a substantial role in theoretical physics. It can safely be said that Noether symmetries are a powerful implement both to select models at a fundamental level and to find exact solutions for specific Lagrangians. In the literature, applications of the Noether symmetry in generalized theories of gravity have been abundantly studied (for example see [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50]). Beside this useful approach, another lucrative approach, the Beyond Noether Symmetry approach (B.N.S. approach), has recently been presented as an innovation [51]. The B.N.S. approach may carry more conserved currents than the Noether symmetry approach. Furthermore, sometimes the Noether symmetry approach fails to achieve the purpose. In such cases, utilizing the B.N.S. approach is the first option. Also, with this new procedure, solving an ordinary differential equation system, comprising field equations and conserved currents, is a paved road.

The Noether theorem states that, for a given Lagrangian L, defined on the tangent space of configurations, \(TQ\equiv \{q_{i},{\dot{q}}_{i}\}\), if the Lie derivative of the Lagrangian L, dragged along a vector field \(\mathbf{X}\),

$$\begin{aligned} \mathbf{X}=\alpha ^{i}(q)\frac{\partial }{\partial q^{i}}+{\dot{\alpha }}^{i}(q)\frac{\partial }{\partial {\dot{q}}^{i}},\end{aligned}$$
(2)

where a dot means a derivative with respect to t, vanishes [52],

$$\begin{aligned} {\mathfrak {L}}_{\mathbf{X}}L=\mathbf{X}_{\mu }L^{\mu }=\alpha ^{i}(q)\frac{\partial L}{\partial q^{i}}+{\dot{\alpha }}^{i}(q)\frac{\partial L}{\partial {\dot{q}}^{i}}= 0, \end{aligned}$$
(3)

then \(\mathbf{X}\) is a symmetry for the dynamics and it generates the following conserved quantity (constant of motion):

$$\begin{aligned} \Sigma _{0}=\alpha ^{i}\frac{\partial L}{\partial {\dot{q}}^{i}}. \end{aligned}$$
(4)

Alternatively, utilizing the Cartan one-form

$$\begin{aligned} \theta _{L}\equiv \frac{\partial L}{\partial {\dot{q}}^{i}}\mathrm{d}q^{i}\end{aligned}$$
(5)

and defining the inner derivative

$$\begin{aligned} i_{\mathbf{X}}\theta _{L}=\langle \theta _{L},\mathbf{X}\rangle \end{aligned}$$
(6)

we get

$$\begin{aligned} i_{\mathbf{X}} \theta _{L} = \Sigma _{0}, \end{aligned}$$
(7)

provided that (3) holds. Equation (7) is coordinate independent. Using a point transformation, the vector field \(\mathbf{X}\) is rewritten as

$$\begin{aligned} {\tilde{{\varvec{\mathrm{X}}}}} = \left( i_{\mathbf {X}}{\mathrm{d}Q}^{k} \right) {\frac{\partial }{\partial Q^{k}}}+\left[ {\frac{\mathrm{d}}{\mathrm{d}Q^{k}}}\left( i_{{\mathbf {X}}} \mathrm{d}Q^{k} \right) \right] {\frac{\partial }{\partial {\dot{Q}}^{k}}} . \end{aligned}$$
(8)

If \(\mathbf{X}\) is a symmetry, so is \({\tilde{{\mathbf {X}}}}\) (i.e. \({\tilde{{\mathbf {X}}}} L =0\)), and a point transformation is chosen such that

$$\begin{aligned} i_{\mathbf{X}} \mathrm{d}Q^{1} = 1 , \qquad i_{\mathbf{X}} \mathrm{d}Q^{i} = 0 \qquad (i \ne 1) . \end{aligned}$$
(9)

It follows that

$$\begin{aligned} {\tilde{{\mathbf {X}}}} = \frac{\partial }{\partial Q^{1}} , \qquad \frac{\partial L}{\partial Q^{1}} = 0; \end{aligned}$$
(10)

therefore, \(\,{Q^{1}}\) is a cyclic coordinate and the dynamics can be reduced. However, the change of coordinates is not unique and a clever choice would be advantageous [53]. The structure of the paper is as follows. In Sect. 2 we introduce the model and extract the point-like lagrangian and field equations. In Sect. 3 we present the Noether symmetries, invariants and exact solutions of the model. Moreover, by data analysis, we demonstrate that the observational data corroborate our findings. In Sect. 4 we sum up the graceful results obtained.

2 The model

Regarding the points mentioned in the second and third paragraphs of the introduction (1), we want to investigate the following gravitational action in the context of extended gravity:

$$\begin{aligned} S= & {} \int d^4x e \bigg [ f(\varphi )T {\underbrace{{{-} U\left( \varphi ,\varphi _{,\mu }\varphi ^{,\mu } \right) g(T)}}_\mathbf{The Unusual Term }} \nonumber \\&- \frac{\omega (\varphi )}{2}\varphi _{,\mu } \varphi ^{,\mu } + V(\varphi ) \bigg ], \end{aligned}$$
(11)

where \(e=\det (e_{\nu }^{i})=\sqrt{-g}\) with \(e_{\nu }^{i}\) being a vierbein (tetrad) basis, \(f(\varphi )\) is the generic function describing the coupling between the scalar field and scalar torsion T, \(\varphi _{,\mu }\) indicates the covariant derivative of \(\varphi \), \(U\left( \varphi ,\varphi _{,\mu }\varphi ^{,\mu } \right) \) is the unknown coupling function which we hypothesize, in general, to depend upon the scalar field and gradients of it. This function is coupled with an unknown function of torsion g(T). Here, \(\omega (\varphi )\) and \(V(\varphi )\) are the coupling function and scalar potential, respectively. Note that the scalars here are caused by conformal symmetry [58]. We presume that the geometry of spacetime is described by the flat FRW metric, which is consistent with the present cosmological observations. The line element of flat FRW background can be written as

$$\begin{aligned} \mathrm{d}s^2 = \mathrm{d}t^2 - a^2(t) \left[ \mathrm{d}x^2 + \mathrm{d}y^2 + \mathrm{d}z^2\right] , \end{aligned}$$
(12)

where the scale factor a is a function of time. With this background geometry, the scalar torsion takes the form \(T=-6{\dot{a}}^2/{a^2}\). First, for simplifying the action, we set the following form by assuming that two main parts of U are separable:

$$\begin{aligned} U\left( \varphi ,\varphi _{,\mu }\varphi ^{,\mu } \right) =h(\varphi ) \Phi ({\dot{\varphi }}) = h(\varphi ) {\dot{\varphi }}, \end{aligned}$$
(13)

where \(h(\varphi )\) is an unknown function of the scalar field \(\varphi \), and the dot represents a differentiation with respect to t. We cannot present any physical argument behind such a choice for the unknown function \(\Phi ({\dot{\varphi }})\), it rather relies on the fact that it works fairly well and the Hessian determinant turns out to be zero through this choice of function after finding the other unknown coupling functions via the Noether approach. Moreover, speaking of the last term in (1) and the points mentioned in the introduction, it is better we fit the second main part as \({\dot{\varphi }}\) at first. Using (11), (13), and the Lagrange method of undetermined coefficients, the action (11) can be written as

$$\begin{aligned} S= & {} \int d^4x e \bigg [ f(\varphi )T - h(\varphi ){\dot{\varphi }} g(T)\nonumber \\&-\lambda \left( T + 6 \frac{{\dot{a}}^2}{a^2} \right) - \frac{\omega (\varphi )}{2} {\dot{\varphi }}^2 + V(\varphi ) \bigg ], \end{aligned}$$
(14)

where the Lagrange multiplier \(\lambda \) is derived by varying the action (14) with respect to T

$$\begin{aligned} \lambda = f - h{\dot{\varphi }}g^{\tau }, \end{aligned}$$
(15)

in which the \(\tau \) denotes a differentiation with respect to the torsion T. So, the point-like Lagrangian corresponding to the action (11) becomes

$$\begin{aligned} L \!= \!fTa^{3}\!-\!h{\dot{\varphi }}ga^3\!-\! (f\!-\!h{\dot{\varphi }}g^{\tau })[Ta^3\!+\!6{\dot{a}}^2a]\!-\!\frac{1}{2}\omega {\dot{\varphi }}^2 a^3\!+\!Va^3.\nonumber \\ \end{aligned}$$
(16)

Hence, the Euler–Lagrange equations for the scale factor a would be

$$\begin{aligned}&4\left( \frac{\ddot{a}}{a}\right) \left( f - h {\dot{\varphi }} g^{\tau } \right) + 2\left( \frac{\dot{a}}{a} \right) ^2 \left( f - h{\dot{\varphi }} g^{\tau } \right) \nonumber \\&\quad +\, 4 \left( \frac{\dot{a}}{a} \right) \left( f^{\prime }{\dot{\varphi }}-hg^{\tau } \ddot{\varphi }-hg^{\tau \tau } {\dot{\varphi }}\dot{T}-h^{\prime }g^{\tau } {\dot{\varphi }}^2 \right) \nonumber \\&\quad +\,\left( Tg^{\tau }-g \right) h{\dot{\varphi }}-\frac{1}{2}\omega {\dot{\varphi }}^2 +V=0, \end{aligned}$$
(17)

where the prime indicates a derivative with respect to \(\varphi \). For the scalar field, \(\varphi \), the Euler–Lagrange equation takes the following form:

$$\begin{aligned}&12h g^{\tau } \left( \frac{\ddot{a}}{a} \right) \left( \frac{\dot{a}}{a} \right) +6h g^{\tau } \left( \frac{\dot{a}}{a} \right) ^3 \nonumber \\&\quad +\,6 \left( \frac{\dot{a}}{a} \right) ^2 \left( f^{\prime } +h g^{\tau \tau } \dot{T} \right) -3\left( \frac{\dot{a}}{a} \right) \left( hg-h g^{\tau }T+\omega {\dot{\varphi }} \right) \nonumber \\&\quad +\,h g^{\tau \tau }T \dot{T} - \omega \ddot{\varphi }-\frac{1}{2}\omega ^{\prime } {\dot{\varphi }}^2 - V^{\prime } =0, \end{aligned}$$
(18)

which is the Klein–Gordon equation. The energy function which is the \(\left( {\begin{array}{c}0\\ 0\end{array}}\right) \)-Einstein equation, associated with the point-like Lagrangian (16), is found as

$$\begin{aligned} \left( 12h g^{\tau } {\dot{\varphi }} -6f \right) \left( \frac{\dot{a}}{a}\right) ^2 -\frac{1}{2}\omega {\dot{\varphi }}^2 -V=0. \end{aligned}$$
(19)

The Euler–Lagrange equation for the torsion scalar T reads

$$\begin{aligned} a^3 h {\dot{\varphi }}g^{\tau \tau } \left( T + 6\frac{\dot{a}^2}{a^2} \right) =0. \end{aligned}$$
(20)

From Eq. (20), there are three possibilities: (1) \(g^{\tau \tau } = 0\), implying linearity for g(T), which is not interesting, for we have the linear form of torsion in the action (11), (2) \({\dot{\varphi }}=0\), which leads to the constant scalar field, so it is not suitable, and (3) the possibility of

$$\begin{aligned} T = - 6 \frac{\dot{a}^2}{a^2}, \end{aligned}$$

which is the definition of the scalar torsion for flat FRW.

3 Exact solutions via the Noether symmetry approach and data analysis

In this section, we utilize the Noether symmetry approach for solving Eqs. (17)–(20). The configuration space of the point-like Lagrangian (16) is \(Q=\{a, \varphi , T\}\) whose tangent space is \(TQ = \{a, \dot{a}, \varphi , {\dot{\varphi }}, T, \dot{T}\}\). The existence of the Noether symmetry implies the existence of a vector field \(\mathbf{X}\),

$$\begin{aligned} \mathbf{X} = \alpha \frac{\partial }{\partial a}+\beta \frac{\partial }{\partial \varphi } +\gamma \frac{\partial }{\partial T} + \alpha _{,t} \frac{\partial }{\partial \dot{a}}+\beta _{,t} \frac{\partial }{\partial {\dot{\varphi }}}+\gamma _{,t} \frac{\partial }{\partial \dot{T}}, \end{aligned}$$
(21)

where

$$\begin{aligned}&y = y (a, \varphi , T)\\&\quad \longrightarrow y_{,t} = \dot{a} \frac{\partial y}{\partial a}+ {\dot{\varphi }} \frac{\partial y}{\partial \varphi }+\dot{T} \frac{\partial y}{\partial T}; \quad y \in \{\alpha , \beta , \gamma \}, \end{aligned}$$

such that

$$\begin{aligned}&\mathfrak {L}_{\mathbf{X}}L =0\\&\quad \rightarrow \alpha \frac{\partial L}{\partial a}+\beta \frac{\partial L}{\partial \varphi } + \gamma \frac{\partial L}{\partial T}+ \alpha _{,t} \frac{\partial L}{\partial \dot{a}}+\beta _{,t} \frac{\partial L}{\partial {\dot{\varphi }}} +\gamma _{,t} \frac{\partial L}{\partial \dot{T}} =0. \end{aligned}$$

This condition yields the following system of linear partial differential equations:

$$\begin{aligned} \frac{\partial \alpha }{\partial b} = 0, \quad \frac{\partial \alpha }{\partial T} = 0, \quad \frac{\partial \beta }{\partial a} =0, \quad \frac{\partial \beta }{\partial T} = 0, \end{aligned}$$
(22)
$$\begin{aligned} 3 \alpha V+\beta a V^{\prime }=0, \end{aligned}$$
(23)
$$\begin{aligned} 2af \left( \frac{\partial \alpha }{\partial a}\right) +\alpha f+a\beta f^{\prime } = 0, \end{aligned}$$
(24)
$$\begin{aligned} 2a \omega \left( \frac{\partial \beta }{\partial \varphi }\right) +3 \alpha \omega +a \beta \omega ^{\prime } = 0, \end{aligned}$$
(25)
$$\begin{aligned}&6 \alpha h g^{\tau }+ 6a\beta h^{\prime } g^{\tau }+12ah g^{\tau } \left( \frac{\partial \alpha }{\partial a}\right) \nonumber \\&\quad +\,6hag^{\tau } \left( \frac{\partial \beta }{\partial \varphi }\right) +6ah \gamma g^{\tau \tau }=0, \end{aligned}$$
(26)
$$\begin{aligned}&\left( aTh g^{\tau }-ahg \right) \left( \frac{\partial \beta }{\partial \varphi }\right) +aTh \gamma g^{\tau \tau }\nonumber \\&\quad +\,3\alpha Th g^{\tau }+\beta aT g^{\tau } h^{\prime }-3\alpha hg-\beta h^{\prime }ga =0. \end{aligned}$$
(27)
Fig. 1
figure 1

Plot a indicates the scale factor a(t) versus time t at the time range [0.0006, 13.816], while plot b shows the scale factor a(t) versus redshift z at the redshift range [0, 7]

Full size image

This system of linear partial differential equations can be solved by using the separation of variables. Hence, one may obtain

$$\begin{aligned}&f(\varphi )=f_{0}\varphi ^n, \quad h(\varphi )=h_{0}\varphi ^{n-1}, \quad V(\varphi )= V_{0} \varphi ^{n},\nonumber \\&g(T)=(-6 T)^{1/n},\quad \omega (\varphi )= \omega _{0} \varphi ^{n-2}, \quad \alpha =\alpha _{0} a,\nonumber \\&\beta = \beta _{0} \varphi , \quad \gamma = 0, \end{aligned}$$
(28)

in which \(f_{0}\), \(\omega _{0}\), \(V_{0}\), \(h_{0}\), \(\alpha _{0}\), and \(\beta _{0}\) are constants of integration and \(\beta _{0}=-3\alpha _{0}/n\) and \(h_{0}=nf_{0}\). This solution holds for \(n = 2\), only. Of course, \(n=2\) is of a physical nature as well, because the common form of \(f(\varphi )\) can be given by the nonminimal coupling as \(f(\varphi ) = \frac{1}{2} \left( \frac{1}{8\pi G} - \xi \varphi ^2 \right) \), however, certain grand-unified theories lead to a polynomial coupling of the form \(1+\xi \varphi ^2+\zeta \varphi ^4\), but on the other hand \(\omega \) must be dimensionless, so n should be equal to 2. According to (28) and (21), the symmetry generator turns out to be

$$\begin{aligned} \mathbf{X} = a \frac{\partial }{\partial a}+ \frac{-3}{2} \varphi \frac{\partial }{\partial \varphi }+\dot{a}\frac{\partial }{\partial \dot{a}}+\frac{-3}{2} {\dot{\varphi }}\frac{\partial }{\partial {\dot{\varphi }}}. \end{aligned}$$
(29)

Hence the corresponding conserved current is found to be

$$\begin{aligned} \mathbf{I} = 3 \alpha _{0} a^2 \varphi \left( 2f_{0}\varphi \dot{a}-4 f_{0}a{\dot{\varphi }}+\frac{\omega _{0}}{2}a{\dot{\varphi }} \right) . \end{aligned}$$
(30)

The form of g(T) has been specified (see Eq. (28)) and \(\gamma =0\), and on the other hand, regarding the third option in Eq. (20), it is an ineffective shot to tow T in Q. Therefore, the configuration space reduces to two \(Q=\{a, \varphi \}\). This means we can rewrite the point-like Lagrangian (16) free of T by substituting the form of the torsion T. Now, by assuming that \(\mathbf{X}\) is a symmetry, we seek point transformations on the vector field \(\mathbf{X}\) such that

$$\begin{aligned} i_{\mathbf{X}}\mathrm{d}z =1, \end{aligned}$$
(31)
$$\begin{aligned} i_{\mathbf{X}} \mathrm{d}p=0, \end{aligned}$$
(32)

whereas \(i: (a,\varphi ) \longrightarrow (z,p)\) in which \(z=z(a,\varphi )\) and \(p=p(a,\varphi )\). Here z is a cyclic variable. If we were to keep T, then it had to be mapped to itself, i.e. \(i: (a,\varphi , T) \rightarrow (z, p, T)\). Solving Eqs. (31)–(32) leads to

$$\begin{aligned} p=a^{3/2} \varphi , \qquad \qquad z=a^{3/2} \varphi + \ln (a). \end{aligned}$$
(33)

So, the corresponding inverse transformations are

$$\begin{aligned} a(p,z)=\exp (z-p), \qquad \varphi (p,z)=p \exp \left( \frac{3}{2} (p-z) \right) . \end{aligned}$$
(34)

It is clear that the choices in Eq. (33) are arbitrary, as more general conditions are possible. The point-like Lagrangian (16) can be rewritten in terms of cyclic variables by (34) as

$$\begin{aligned} \mathcal {L }=\frac{\dot{p}^2}{2} \left( \frac{3}{4}p+1 \right) -p \left( \frac{3}{8}\dot{p} \dot{z}-V_{0}p \right) , \end{aligned}$$
(35)

in which we put \(\omega _{0}=1\) and \(f_{0} = 3/32\) or equivalently \(h_{0}=3/16\). The Euler–Lagrange equations relevant to (35) are

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \left( p \dot{p} \right) =0, \end{aligned}$$
(36)
$$\begin{aligned} \frac{3}{8} p \ddot{z}-\ddot{p} \left( 1+\frac{3}{4}p \right) -\frac{3}{8}\dot{p}^2 -2 V_{0}p=0. \end{aligned}$$
(37)

Note that Eq. (36) is equivalent to \(\mathbf{I}\), which is given by Eq. (30), so rewriting Eq. (30) in terms of cyclic variables does not add a new equation (i.e. \(\mathbf{I} \equiv \mathrm{d}(p\dot{p})/\mathrm{d}t\)). The Hamiltonian constraint reads

$$\begin{aligned} \frac{1}{2}\dot{p}^2 \left( \frac{3}{4}p+1 \right) -\frac{3}{8}\dot{z} \dot{p} p + V_{0} p^2=0. \end{aligned}$$
(38)

One can write a ‘constant’ in the right side of Eq. (38) instead of zero, as in general, we have \(E_{L}=const.\) Solving Eqs. (36)–(38) leads to

$$\begin{aligned} p(t)= \sqrt{2\left( c_{1}t+c_{2} \right) }, \end{aligned}$$
(39)
$$\begin{aligned} z(t)= & {} \frac{2}{3} \ln \left( \left| c_{1}t+c_{2} \right| \right) +\frac{8}{3}V_{0}t^2 \nonumber \\&+\left( c_{3}-\frac{16}{3}\frac{V_{0}c_{2}}{c_{1}} \right) t+\sqrt{2\left( c_{1}t+c_{2} \right) } +c_{4}, \end{aligned}$$
(40)

where the \(\{c_{i}\), \(i = 1,\ldots ,4\}\), are constants of integration. Doing inverse transformations by the use of Eq. (34) give the solutions of Eqs. (17)–(19) and \(\mathbf{I}=0\) (see Eq. (30)):

Fig. 2
figure 2

Plots a and b indicate the temperature T(t) and \( t \times H(t)\) versus redshift z at the redshift range [0, 3.5], respectively

Full size image
Fig. 3
figure 3

Plot a indicates the deceleration parameter q(t) versus time t at the time range [1, 13.816], while plot b shows the deceleration parameter q(t) versus redshift z at the redshift range [0, 3.5]

Full size image
Fig. 4
figure 4

Plot a indicates the scalar field \(\varphi (t)\) versus time t at the time range [0.0006, 13.816] and plot b shows coupling function \(U(\varphi , \varphi _{\mu } \varphi ^{\mu })\), \(h(\varphi )\) and the scalar potential \(V(\varphi )\) versus time t at the same time range

Full size image
$$\begin{aligned} a(t)\!=\!\left( c_{1} t\!+\!c_{2}\right) ^{2/3} \exp \left( \frac{8}{3}V_{0}t^2 \!+\!\left[ c_{3}\!-\!\frac{16}{3}\frac{V_{0}c_{2}}{c_{1}} \right] t\!+\!c_{4}\right) , \end{aligned}$$
(41)
$$\begin{aligned} \varphi (t) = \frac{\exp \left( -4V_{0} t^2 - \frac{3}{2} \left[ c_{3}-\frac{16}{3} \frac{V_{0}c_{2}}{c_{1}}\right] t-\frac{3}{2}c_{4} \right) }{\sqrt{2(c_{1}t+c_{2})}}. \end{aligned}$$
(42)

Therefore, these solutions carry two conserved currents, \(E_{L}\) (Eq. (19)) and \(\mathbf{I}\) (Eq. (30)), which correspond to two symmetry generators \(\mathbf{X}_{1}=\partial / \partial t\) and \(\mathbf{X}\) (Eq. (29)), respectively.

For illustrating the descriptions of late-time-accelerated expansion from the perspective of the studied model, we single out the constants

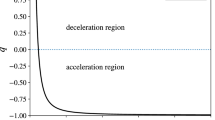
$$\begin{aligned}&c_{1} = 1, \quad c_{2} = 0.6068, \quad c_{3} = -0.0162, \nonumber \\&\quad c_{4} = - 1.8340, \quad V_{0} = 0.0006. \end{aligned}$$
(43)

We present five figures with data analysis with the time unit 1 Gyr \(\equiv \) \(\mathbf {1}\). The behavior of the scale factor a versus time and redshift in Fig. 1 imply, first, the scale factor with increasing nature expressing initially the decelerated and then accelerated expansion of the universe (see Fig. 1a); second, the scale factor versus redshift plot, 1b, confirms that the present value of the scale factor is exactly 1 (i.e. \((z_{0},a_{0})=(0,1)\)), so, from Fig. 1a we learn that the age of the universe is \(t_{0} = 13.816\) Gyr. As usual, ignoring a small variation of the prefactor, we consider that the CMBR temperature falls as \(a^{-1}\); then its present value is \(T_{0} = 2.725\) K (see Fig. 2a). The evolution of the Hubble parameter (not presented) gives its present value, \(H_{0} = 7.238 \times 10^{-11}\) year \(^{-1}\) \(\equiv 70.82\) km s\(^{-1}\) Mpc\(^{-1}\). It is a nice result, as the recent observational data show \(H_{0} = 72.25 \pm 2.38\) km s\(^{-1}\) Mpc\(^{-1}\) [60]. Therefore \(H_{0} \times t_{0} = 1\), which fits the observational data with high precision, as plotted in Fig. 2b. Figure 3a indicates the deceleration parameter, \(q = -(a \ddot{a}) / \dot{a}^2\), versus time. It shows its passing from negative to positive values, which corresponds first to decelerating universe, \(q > 0\), then to accelerating universe, \(q < 0\), and its present value is \(q_{0}= -1\), as we expect. Obviously, \(q=0\) renders the inflection point (i.e. shifting from decelerated to accelerated expansion in Fig. 1a. So, at redshift \(z_{\mathrm {acce.}}=0.712\) or equivalently \(t_{\mathrm {acce.}}=6.198\) Gyr acceleration started (see Fig. 3b). It coincides with the astrophysical data, for the observational data concede that at redshift \(z_{\mathrm {acce.}}<1\) or, equivalently, at about half the age of the universe acceleration commenced. It is well known that the scalar field must decrease with time. As Fig. 4a shows, our scalar field is consistent with this physical point. Figure 4b indicates the manners of the scalar potential \(V(\varphi )\), coupling function \(U(\varphi , \varphi _{,\mu }\varphi ^{,\mu })\) and \(h(\varphi )\) versus time. The behavior of the scalar potential is admissible (i.e. detractive in face of time). Considering the action (11), we found that the terms U and V have different signs. So, by applying the minus sign of U we learn that both V and U are positive and have subtractive behaviors versus time. A marked difference between the two is that U falls more sharply than V. It is obvious that h has a narrow band around zero, and this restricts the behavior of U. In addition, all these three functions turn out to be almost constant with a little difference from that of the present time. Before terminating this section, we would like to investigate the Om-diagnostic analysis.

In Fig. 5 we show the Om-diagnostic parameter versus redshift. The Om-diagnostic is an important geometrical diagnostic proposed by Sahni et al. [54], in order to classify the different dark energy (DE) models. The Om-diagnostic parameter is able to distinguish dynamical DE from the cosmological constant in a robust manner both with and without reference to the value of the matter density. It is defined as [55]

$$\begin{aligned} Om(z) \equiv \frac{\left[ \frac{H(z)}{H_{0}}\right] ^2 -1}{\left( 1+z \right) ^3 -1}. \end{aligned}$$
(44)

For dark energy with a constant equation of state (EoS) \(\omega \), it reads

$$\begin{aligned} Om(z) = \Omega _{m0} + (1-\Omega _{m0}) \frac{(1+z)^{3(1+\omega )}-1}{(1+z)^{3}-1}, \end{aligned}$$
(45)

so \(Om(z) = \Omega _{m0}\) corresponds to the \(\Lambda \)CDM model, therefore the regions \(Om(z) > \Omega _{m0}\) and \(Om(z) < \Omega _{m0}\) correspond with quintessence (\(\omega > -1\)) and phantom (\(\omega < -1\)), respectively. Figure 5 indicates phase crossing from quintessence (\(Om(z) \gtrsim 0.3\)) to phantom (\(Om(z) \lesssim 0.3\)). Hence, now we are in the phantom phase.

Fig. 5
figure 5

The plot indicates the Om-diagnostic versus redshift z at the redshift range [0.07 , 7]

Full size image

4 Conclusion

Owing to the facts mentioned in the introduction (1), we applied the term \(U(\varphi , \varphi _{,\mu }\varphi ^{,\mu })g(T)\) within a generic action in f(T) gravity context in FRW background spacetime. Because the resulting system was overdetermined, for simplifying the action we did a suitable choice for the unknown function \(U=h(\varphi ){\dot{\varphi }}\) by assuming the separation of two main parts. Then by applying the Noether symmetry approach and using a cyclic variables method, we could obtain nice results, as our data analysis showed deep results compatible with observational data.

In a nutshell, some of our noteworthy findings were as follows.

  1. 1.

    The present value of the scale factor \(a_{0} = 1\) (i.e. \((z_{0},a_{0})=(0,1)\)), so the present value of temperature may be found to be \(T_{0} = 2.725\) K.

  2. 2.

    The age of the universe is \(t_{0} = 13.816\) Gyr.

  3. 3.

    The resulting model can give a late-time-accelerated expansion. The universe before entering the accelerated expansion epoch, became a victim of a Friedmann-like matter dominated era for quite a long time. Thus, acceleration dawns at the redshift value \(z_{\mathrm {acce.}}=0.712\), which is equivalent to \(t_{\mathrm {acce.}} = 6.198\) Gyr, that is, about half the age of the universe.

  4. 4.

    The present value of the Hubble parameter is \(H_{0} = 7.238 \times 10^{-11}\) year\(^{-1}\) or equivalently \(H_{0}=70.82\) km s\(^{-1}\) Mpc\(^{-1}\).

  5. 5.

    We have \(H_{0} \times t_{0} = 1\).

  6. 6.

    The present value of the deceleration parameter is \(q_{0}= -1\).

  7. 7.

    The Om-diagnostic parameter shows phase crossing from a quintessence to a phantom phase.

The added extra function, \(U(\varphi , \varphi _{,\mu }\varphi ^{,\mu })\), is affected like the scalar potential \(V(\varphi )\) with the difference that U decayed more sharply than V. Moreover, around the present time, their values are negligibly different.

Considering the deep results compatible with astrophysical and observational data, we conclude that entering such a term, \(U\left( \varphi ,\varphi _{,\mu }\varphi ^{,\mu } \right) g(T)\), to the scope of the actions of f(T) gravity, not only has no anomalous effect (at least in the case studied) but it may give desired results.