What do we know about cosmography

Abstract

In the present paper, we investigate the cosmographic problem using the bias–variance trade-off. We find that both the z-redshift and the $y=z/(1+z)$-redshift can present a small bias estimation. It means that the cosmography can describe the supernova data more accurately. Minimizing risk, it suggests that cosmography up to the second order is the best approximation. Forecasting the constraint from future measurements, we find that future supernova and redshift drift can significantly improve the constraint, thus having the potential to solve the cosmographic problem. We also exploit the values of cosmography on the deceleration parameter and equation of state of dark energy w(z). We find that supernova cosmography cannot give stable estimations on them. However, much useful information was obtained, such as that the cosmography favors a complicated dark energy with varying w(z), and the derivative ${\text {d}}w/{\text {d}}z <0$ for low redshift. The cosmography is helpful to model the dark energy.

1 Introduction

Cosmic accelerating expansion is a landmark cosmological discovery of recent decades. Till now, a number of dynamical mechanisms have been proposed to explain this mysterious cosmological phenomenon. However, its natural essence is still not known to us. The theoretical attempts include dark energy, or modified gravity, or violation of cosmological principle. The first paradigm is based on the belief that an exotic cosmic component called dark energy probably exists in the form of the cosmological constant [1] or scalar field [2, 3] and possesses a negative pressure to drive the cosmic acceleration. The modified gravities do not need an exotic component but a modification to the theory of general relativity [4, 5]. Violation of the cosmological principle is usually in the form of the inhomogeneous Lemaître–Tolman–Bondi void model [6,7,8].

Different from the above dynamical templates, cosmic kinematics is a more moderate approach in understanding this acceleration. It only highlights a homogeneous and isotropic universe at the large scale. In this family, kinematic parameters independent of the cosmic dynamical models become very essential. For example, the scale factor a(t) directly describes how the universe evolves over time. The deceleration factor can immediately map the decelerating or accelerating expansion of the universe. Collecting some kinematic parameters, the authors in Refs. [9, 10] created the cosmography via a Taylor expansion of the luminosity distance over the redshift z. Mathematically, this expansion should be performed near a small quantity, i.e. a low redshift. Using the standard theory of complex variables, Cattoën and Visser [11] demonstrated that the convergence radius of Taylor expansion over redshift z is at most $|z|=1$. For high redshift, $z>1$, it fails to reach convergence. Nevertheless, many observations focus on the high-redshift region. For example, the supernova in a joint light-curve analysis (JLA) compilation can span the redshift region up to 1.3; the cosmic microwave background (CMB) even can retrospect to the very early universe at $z \sim 1100$. To legitimate the expansion at high redshift, they introduced an improved redshift parametrization $y=z/(1+z)$ [11]. Thus, cosmography in the y-based expansion is mathematically safe and useful, because of $0<y<1$, even for the high redshift. Later, some other methods of redshift were also proposed [12].

When confronted with observational data, the cosmography study encounters some difficulties. Initially, the SNIa data were used to fit with the cosmography [13, 14]. Then some auxiliary data sets [15] were also considered. The output indicated that fewer series truncation lead to smaller errors but a worse estimation; and more terms lead to more accurate approximation but bigger errors. That is, cosmography is in the dilemma between accuracy and precision. The crisis naturally turns around the question of where the “sweet spot” is, i.e., the most optimized series truncation. In previous work [13, 15, 16], one found that estimation up to the snap term is meaningless in the light of the F-test. For the y-redshift, it presents bigger errors of the parameters [13]. In spite of different observational data sets being used, most of the results were consistent. Recent work [17] investigated the cosmography using the baryon acoustic oscillations (BAO) only. From the simulated Euclid-like BAO survey, one found that future BAO observation also favored a best cosmography with a jerk term. Because it only requires the homogeneity and isotropy of the universe, cosmography was frequently used to deduce or test the cosmological models. Recently, it was used to test the $\Lambda$CDM model [18], but it turned out that the parameter $j_0 \ne 1$ is ambiguous for different orders of expansion; it is not enough for a test. Reconstructing dark energy in f(R) gravities, one found that there exist extra free parameters, which cannot be constrained by the cosmography. The analysis was based on the mock data generated by a unified error of magnitude $\sigma _{\mu }=0.15$. In the following, we will test the constraint of these mock data with flat errors. Following the work in Ref. [18], these mock data were generated assuming the same redshift distribution as the Union 2.1 catalog [19], but under the fiducial model from the best-fit ones by JLA data.

Although the cosmography has been widely investigated, we still are left with a lot of questions. On the one hand, we do not present a repetitive work using more data, but numerically excavate more detailed information as regards the accuracy and precision in the convergence problem. The new approach we use is the bias–variance trade-off. Moreover, we will try to investigate whether future measurement can solve the serious convergence issue. On the other hand, before the use of cosmography, we should make certain what information it can provide and what it cannot provide.

Although many types of observational data were used to fit the cosmography, our goal in this paper is to understand the convergence problem from another side, i.e., the geometric or dynamical measurement. Future surveys with high-precision may present a different constraint. To understand the above questions, we need the help of a future WFIRST-like supernova observation and a dynamical survey of the redshift drift. Different from the geometric measurement, the redshift drift is desirable to measure the secular variation of $\dot{a}(t)$ [20]. In contrast, geometric observation usually measures the integral of $\dot{a}(t)$. Interestingly, this concept is also independent of any cosmological model, requiring only the Friedmann–Robertson–Walker universe. Taking advantage of the capacity of E-ELT [21,22,23], numerous works agreed that this future probe could provide an excellent contribution to understand the cosmic dynamics, such as the dark energy [24, 25] or modified gravity models [26]. More importantly, it can be extended to test the fundamental Copernican principle [27] and the cosmic acceleration [28]. However, studies of the redshift drift on kinematics have been scarce.

This paper is organized as follows: In Sect. 2, we introduce the cosmography. In Sect. 3 we present the observational data. According to the goals introduced above, we analyze the problem of cosmography in Sect. 4, and explore its values in Sect. 5. Finally, in Sect. 6 a conclusion is drawn and a discussion presented.

2 Cosmography

Cosmography is an artful combination of kinematic parameters via the Taylor expansion with the hypotheses of large-scale homogeneity and isotropy. In this framework, the introduction of the cosmographic parameters of interest is appropriate.

The Hubble parameter

$$\begin{aligned} H(t)= + \frac{1}{a}\frac{\mathrm{d}a}{\mathrm{d}t} \end{aligned}$$

(1)

accurately connects the cosmological models with observational data.

The deceleration parameter

$$\begin{aligned} q(t)= - \frac{1}{a}\frac{\mathrm{d}^2a}{\mathrm{d}t^2}\left[ \frac{1}{a} \frac{\mathrm{d}a}{\mathrm{d}t}\right] ^{-2} \end{aligned}$$

(2)

directly represents the decelerating or accelerating expansion of the universe.

The jerk parameter

$$\begin{aligned} j(t)= + \frac{1}{a} \frac{\mathrm{d}^3a}{\mathrm{d}t^3}\left[ \frac{1}{a} \frac{\mathrm{d}a}{\mathrm{d}t}\right] ^{-3} \end{aligned}$$

(3)

and the snap parameter

$$\begin{aligned} s(t)= + \frac{1}{a} \frac{\mathrm{d}^4a}{\mathrm{d}t^4} \left[ \frac{1}{a} \frac{\mathrm{d}a}{\mathrm{d}t}\right] ^{-4} \end{aligned}$$

(4)

are often used as a geometrical diagnostic of dark energy models [29, 30]. An important feature should be announced: it is that jerk has been a traditional tool to test the spatially flat cosmological constant dark energy model in which $j(z)=1$ all time.

The lerk parameter

$$\begin{aligned} l(t)= + \frac{1}{a}\frac{\mathrm{d}^5 a}{\mathrm{d}t^5} \left[ \frac{1}{a} \frac{\mathrm{d}a}{\mathrm{d}t}\right] ^{-5} \end{aligned}$$

(5)

is an higher order parameter to indicate the cosmic expansion.

With the above preparation, the Hubble parameter in cosmography can be expressed as [9, 14]

$$\begin{aligned} H(z)= & {} H_0 + \frac{\mathrm{d}H}{\mathrm{d}z}\Big |_{z=0} z + \frac{1}{2!}\frac{\mathrm{d}^2H}{\mathrm{d}z^2}\Big |_{z=0} z^2\nonumber \\&+ \frac{1}{3!}\frac{\mathrm{d}^3H}{\mathrm{d}z^3}\Big |_{z=0} z^3 + \cdots \nonumber \\= & {} H_0\left[ 1 + (1+q_0) z +\frac{1}{2}(-q_0^2+j_0)z^2\right. \nonumber \\&+\, \frac{1}{6}(3q_0^2+3q_0^3-4 q_0 j_0-3 j_0 -s_0)z^3 \nonumber \\&+\, \frac{1}{24}(-12q_0^2-24q_0^3-15q_0^4+32q_0 j_0 +25 q_0^2 j_0 \nonumber \\&\left. +\, 7 q_0 s_0 + 12 j_0-4 j_0^2+ 8 s_0 + l_0) z^4 \phantom {\frac{1}{6}}\right] + \cdots \end{aligned}$$

(6)

where the subscript “0” indicates that cosmographic parameters are evaluated at the present epoch. According to the differential relations with the Hubble parameter, the luminosity distance in the study of cosmography can be conveniently expressed as [11, 14]

$$\begin{aligned} d_L^{\text {cos}}(z) = z + {\mathcal {C}}_1 z^2 + {\mathcal {C}}_2 z^3 + {\mathcal {C}}_3 z^4 + {\mathcal {C}}_4 z^5, \end{aligned}$$

(7)

where

$$\begin{aligned} {\mathcal {C}}_1= & {} \frac{1}{2}(1-q_0) , \nonumber \\ {\mathcal {C}}_2= & {} -\frac{1}{6}(1- q_0-3q_0^2+ j_0) , \nonumber \\ {\mathcal {C}}_3= & {} \frac{1}{24}(2-2 q_0-15q_0^2-15 q_0^3+5 j_0+10 q_0 j_0 +s_0) ,\nonumber \\ {\mathcal {C}}_4= & {} \frac{1}{120}(-6+6q_0+81q_0^2+165q_0^3+105q_0^4 \nonumber \\&+\,10j_0^2-27j_0-110q_0 j_0-105q_0^2 j_0-15q_0 s_0 \nonumber \\&-\,11s_0-l_0). \end{aligned}$$

(8)

As introduced above, cosmography at high redshift, $z>1$, fails to converge. To solve this trouble, a y-redshift hence introduced [11]

$$\begin{aligned} y = \frac{z}{1+z}. \end{aligned}$$

(9)

For the new redshift, we can simplify it as $y=1-a(t)$. Obviously, it is $0<y<1$ for the current observational data. One benefit from the y-redshift is that it can extend the expansion to the high redshift region. This is important for the study of cosmography. The reason is that the model of cosmography in Eq. (7) is theoretically valid for redshift $z<1$. With the import of the y-redshift, many observational data, such as supernova with higher redshift and even CMB, can be used to fit and study the cosmography. For example, it is reduced to $y=0.56$ for the supernova at maximum redshift $z=1.3$ in the JLA compilation. Moreover, its value is $y=0.999$ which guarantees the safe use of the early CMB data. As described in Ref. [11], it even can extrapolate back to the big bang. The other physical significance is y-redshift also can bring us back to the future universe, but breaks down at $y=-1$. In the y-redshift space, the luminosity distance is

$$\begin{aligned} d_L^{\text {cos}}(y) = y + {\mathcal {C}}_1 y^2 + {\mathcal {C}}_2 y^3 + {\mathcal {C}}_3 y^4 + {\mathcal {C}}_4 y^5, \end{aligned}$$

(10)

with

$$\begin{aligned} {\mathcal {C}}_1= & {} \frac{1}{2}(3-q_0) \nonumber \\ {\mathcal {C}}_2= & {} \frac{1}{6}(11-5 q_0+3q_0^2- j_0) \nonumber \\ {\mathcal {C}}_3= & {} \frac{1}{24}(50- 26q_0+21 q_0^2-15 q_0^3-7 j_0+10 q_0 j_0 +s_0) \nonumber \\ {\mathcal {C}}_4= & {} \frac{1}{120}(274-154q_0+141q_0^2-135q_0^3+105q_0^4 \nonumber \\&+\,10j_0^2-47j_0+90q_0 j_0-105q_0^2 j_0-15q_0 s_0 \nonumber \\&+\,9s_0-l_0). \end{aligned}$$

(11)

In the following analysis, one test we should do is concerned with the improvement of the y-redshift.

In our cosmographic study, we need the help of the dynamical redshift drift. The story should start from the redshift.

In an expanding universe, we observe at time $t_0$ a signal emitted by a source at $t_{\mathrm {em}}$. The source’s redshift can be represented through the cosmic scale factor

$$\begin{aligned} z(t_0) = \frac{a(t_0)}{a(t_{\mathrm {em}})} -1. \end{aligned}$$

(12)

Over the observer’s time interval $\Delta t_0$, the source’s redshift becomes

$$\begin{aligned} z(t_0+\Delta t_0) = \frac{a(t_0+\Delta t_0)}{a(t_{\mathrm {em}}+\Delta t_{\mathrm {em}})}-1, \end{aligned}$$

(13)

where $\Delta t_{\mathrm {em}}$ is the time interval-scale for the source to emit another signal. It should satisfy $\Delta t_{\mathrm {em}} = \Delta t_0 / (1+z)$. As a consequence, the observed redshift variation of the source is

$$\begin{aligned} \Delta z=\frac{a(t_0+\Delta t_0)}{a(t_{\mathrm {em}}+\Delta t_{\mathrm {em}})} - \frac{a(t_0)}{a(t_{\mathrm {em}})}. \end{aligned}$$

(14)

Taking the first order approximation with Eq. (14), the physical interpretation of redshift drift can be exposed thus:

$$\begin{aligned} \Delta z \approx \left[ \frac{\dot{a}(t_0) - \dot{a}(t_{\mathrm {em}})}{a(t_{\mathrm {em}})} \right] \Delta t_0, \end{aligned}$$

(15)

where a dot denotes the derivative with respect to cosmic time. Obviously, we should note that the secular redshift drift monitors the variation of $\dot{a}$ during the evolution of the universe. For the distance measurement, it commonly extracts information content via the integral of a variant of $\dot{a}$. Theoretically, the Hubble parameter, a function of $\dot{a}$, may be more effective in probing the cosmic expansion. However, its acquisition in observational cosmology currently is indirect from the differential ages of galaxies [31,32,33], from the BAO peaks in the galaxy power spectrum [34, 35], or from the BAO peaks using the Ly$\alpha$ forest of quasars (QSOs) [36]. For the redshift drift, we note that it is a direct measurement of the cosmic expansion and can become true via multiple methods [37].

In terms of the Hubble parameter $H(z)=\dot{a}(t_{\mathrm {em}})/a(t_{\mathrm {em}})$, we simplify Eq. (15) to

$$\begin{aligned} \frac{\Delta z}{\Delta t_0}=(1+z)H_0 - H(z). \end{aligned}$$

(16)

What we should highlight is its independence of any prior and dark energy model. With regard to this unique advantage, many analyses have demonstrated that the redshift drift is not only able to provide much stronger constraints on the dynamical cosmological models [26, 38], but also to solve some crucial cosmological problems [39, 40]; it even allows us to test the Copernican principle [27]. Observationally, it is convenient to probe the spectroscopic velocity drift

$$\begin{aligned} \frac{\Delta \upsilon }{\Delta t_0} = \frac{c}{1+z} \frac{\Delta z}{\Delta t_0}, \end{aligned}$$

(17)

which is of the order of several cm s$^{-1}$ year$^{-1}$. The signal is naturally accumulated with an increase of observational time $\Delta t_0$.

A Taylor expansion tells us that the redshift drift should be

$$\begin{aligned} \frac{\Delta \upsilon }{\Delta t_0}= & {} \frac{\Delta \upsilon }{\Delta t_0}\Big |_{z=0} + \frac{\mathrm{d}}{\mathrm{d}z}\left( \frac{\Delta \upsilon }{\Delta t_0}\right) \Big |_{z=0} z \nonumber \\&+\,\frac{1}{2!} \frac{\mathrm{d}^2 }{\mathrm{d}z^2}\left( \frac{\Delta \upsilon }{\Delta t_0}\right) \Big |_{z=0} z^2 + \cdots \end{aligned}$$

(18)

Using the Taylor series of Hubble parameter in Eq. (6), we can put Eq. (18) into practice,

$$\begin{aligned} \frac{\Delta \upsilon }{\Delta t_0} (z)= & {} c H_0 \left[ -q_0 z + \frac{1}{2} (2q_0 +q_0^2 -j_0) z^2\right. \nonumber \\&+\,\frac{1}{6} (-6q_0 -6q_0^2 -3q_0^3 +4q_0j_0 + 6j_0 +s_0)z^3 \nonumber \\&+\, \frac{1}{24}(24q_0+36q_0^2+36q_0^3+15q_0^4-48q_0 j_0 \nonumber \\&\left. -25q_0^2 j_0- 7q_0 s_0-36j_0+4j_0^2-12s_0-l_0)z^4 \right] .\nonumber \\ \end{aligned}$$

(19)

For the y-redshift, it is simplified to

$$\begin{aligned} \frac{\Delta \upsilon }{\Delta t_0} (y)= & {} cH_0 \left[ -q_0 y + \frac{1}{2} (q_0^2-j_0) y^2 \right. \nonumber \\&+\,\frac{1}{6}(-3q_0^3+4q_0 j_0 +s_0) y^3 \nonumber \\&\left. +\,\frac{1}{24}(15q_0^4-25q_0^2 j_0+ 4j_0^2-7q_0 s_0-l_0) y^4 \right] .\nonumber \\ \end{aligned}$$

(20)

Recently, a Taylor expansion of the redshift drift was also provided in the varying speed of light cosmology [41]. One can reduce it from the non-mainstream scenario to the classical case. In this paper, we mainly use it to provide a numerical constraint on the cosmography, to test its constraint power on the cosmic kinematics.

3 Observational data

In this section, we introduce the related data in our calculation. Current data we use are the canonical distance modulus from JLA compilation. In order to test whether future SNIa observation can alleviate or terminate the tiresome convergence problem, we produce some mock data by the Wide-Field InfraRed Survey Telescope-Astrophysics Focused Telescope Assets (WFIRST-AFTA).¹ The dynamical redshift drift is forecast by the E-ELT. The parameters can be estimated through a Markov chain Monte Carlo method, by modifying the publicly available code “CosmoMC [42]. As introduced in Sect. 2, the cosmography is independent of dynamical models. Therefore, we fix the background variables, and we relax the cosmographic parameters as free parameters in our calculation.

3.1 Current supernova

One important reason of why the supernova data were widely used is its extremely plentiful resource. In this paper, we use the latest supernova JLA compilation of 740 data set from the SDSS and SNLS [43]. The data are usually presented as tabulated distance modulus with errors. In this catalog, the redshift spans $z<1.3$, and about 98.9% of the samples are in the redshift region $z<1$. In our calculation, we also consider the whole covariance matrix.

3.2 Future supernova

In the study of cosmology, forecasting the constraint of future observations on the cosmological model is quite useful for theoretical research. Estimation of the uncertainty of the observational variable is a core matter. In a previous cosmography study, one usually uses several mock data from a conceptual telescope or satellite [15], or extrapolation from current observational data [44]. To be more reliable, in the present paper, we plan to use a current program. The WFIRST-2.4 not only stores tremendous potential on some key scientific programs, but also enables one to make a survey with more supernovae in a more uniform redshift distribution. One of its scientific issues is to measure the cosmic expansion history. According to the updated report by the Science Definition Team [45], we obtain 2725 SNIa over the region $0.1<z<1.7$ with a bin $\Delta z=0.1$ of the redshift.

The photometric measurement error per supernova is $\sigma _{\text {meas}} = 0.08$ magnitudes. The intrinsic dispersion in luminosity is assumed to be $\sigma _{\text {int}} = 0.09$ magnitudes (after correction/matching for light-curve shape and spectral properties). The other contribution to the statistical errors is gravitational lensing magnification, $\sigma _{\text {lens}} = 0.07 \times z$ mags. The overall statistical error in each redshift bin is then

$$\begin{aligned} \sigma _{\text {stat}} = [(\sigma _{\text {meas}})^2 + (\sigma _{\text {int}})^2 + (\sigma _{\text {lens}})^2]^{1/2}/\sqrt{N_i}, \end{aligned}$$

(21)

where $N_i$ is the number of supernova in the ith redshift bin. According to the estimation, a systematic error per bin is

$$\begin{aligned} \sigma _{\text {sys}} = 0.01 (1+z)/1.8. \end{aligned}$$

(22)

Therefore, the total error per redshift bin is

$$\begin{aligned} \sigma _{\text {tot}} = [(\sigma _{\text {stat}})^2 + (\sigma _{\text {sys}})^2]^{1/2}. \end{aligned}$$

(23)

In our simulation, the fiducial models are taken from the best-fit values by current supernova on the cosmographic models. We should note that although we have considered the various error sources, it is still difficult to provide the total covariance matrix of future WFIRST-like current supernova data. It may inevitably underestimate the errors of cosmographic parameters. However, this forecast is helpful for us in our study of whether future observation can improve the convergence problem.

3.3 Redshift drift

As suggested by Loeb [37], the redshift drift probe can come true via the wavelength shift of the QSO Ly$\alpha$ absorption lines, emission spectra of galaxies, and some other radio techniques. There, the ground-based largest optical/near-infrared telescope E-ELT will provide a continuous monitor from the Ly$\alpha$ forest in the spectra of high-redshift QSOs [46]. These spectra are not only immune from the noise of the peculiar motions relative to the Hubble flow, but also they have a large number of lines in a single spectrum [47]. According to the capability of E-ELT, the uncertainties of the velocity drift can be modeled as [21, 47]

$$\begin{aligned} \sigma _{\Delta \upsilon } = 1.35 \left( \frac{S/N}{2370} \right) ^{-1}\left( \frac{N_{{\text {QSO}}}}{30} \right) ^{-1/2}\left( \frac{1+z_{{\text {QSO}}}}{5} \right) ^{q} {\mathrm {cm/s}},\nonumber \\ \end{aligned}$$

(24)

with $q=-1.7$ for $2<z<4$, or $q=-0.9$ for $z>4$, where the signal-to-noise ratio S / N is assumed as 3000, the number of QSOs $N_{{\text {QSO}}}=30$ and $z_{{\text {QSO}}}$ is the redshift at $2<z<5$. Following previous work [23, 24, 26, 38], we can obtain the mock data assumed to be uniformly distributed among the redshift bins: $z_{{\text {QSO}}}= [2.0, \, 2.8, \, 3.5, \, 4.2, \, 5.0]$ under the fiducial model from the best-fit ones by JLA data. With no specific declaration, the observational time is set as 10 years.

4 Problem of the cosmography

The convergence problem has always been a top priority in the study of cosmography. According to the requirement of a Taylor expansion, we will, respectively, perform a related calculation for data at $z<1$ and $y<1$. In this section, we will analyze the convergence issue in current observational data, and forecast the constraint of future measurement. To ensure the physical meaning of the constraint, we should apply a prior on the Hubble parameter,

$$\begin{aligned} H(z) >0, \end{aligned}$$

in our calculation for both the z-redshift and the y-redshift.

Fig. 1

Constraints on cosmographic parameters in the 4 order from the JLA compilation for redshift $z<1$

4.1 Convergence issue in current data

Using the JLA compilation, we obtain the cosmographic parameters up to the fourth order. We show the corresponding results in Figs. 1, 2 and 3 and Table 1.

For the z-redshift, we can roughly distinguish the data and cosmographic models by residuals in Fig. 3. On the one hand, most of the data locate at the low redshift, and fit well with the models. On the other hand, some of the data at high redshift present a little bigger residual with the cosmographic models. Thus, more low-z data make the cosmography study more precise. From the constraints in Table 1, we note that all of the constraints on the parameter $q_0$ in $1\sigma$ confidence level are negative, which shows a recent accelerating expansion. However, some recent work has tried to find a slowing down of the acceleration. Moreover, this novel phenomenon has attracted much attention [48,49,50,51,52,53], including the recent work of [54]. Using the dark energy parameterizations, one found that the cosmic acceleration may already have peaked, and the expansion may be slowing down from the deceleration parameter being $q_0>0$. In recent work [55, 56], a model-independent analysis on this interesting subject was presented, using the powerful Gaussian processes technique. It was found that no slowing down is detected within $2\sigma$ C.L. from current data. Moreover, we analyzed the inconsistency in Ref. [56]. We further deduced what physical condition should be satisfied by the observational data [57]. These results are consistent with the cosmographic constraint from JLA data.

Fig. 2

Constraints on cosmographic parameters in the fourth order from the JLA compilation for y-redshift

Fig. 3

Residuals between the cosmographic distance modulus with different orders and the observational SNIa data. The vertical coordinates $\Delta \mu (z) = \mu ^{\text {cos}} (z) - \mu ^{\text {obs}} (z)$ denotes the residuals

Comparison between Figs. 1 and 2 shows that degeneracies among the parameters in the y-redshift are similar to the z-redshift. The difference is that it provides much bigger errors on some parameters. Taking the parameter $l_0$ as an example, we find that its absolute value shows an increasing trend. Moreover, its relative error in the y-redshift 2478.44/2056.97 is also bigger than that of the z-redshift 158.08/149.54. This is consistent with the result in previous work, namely, the y-redshift brings about worse constraints.

Table 1 Constrained cosmographic parameters by the JLA compilation and mock data within $1\sigma$ confidence level

In recent years, much work has focused on the question of which series truncation fits the data best. In previous work [13, 15, 16], one introduced the F-test to find the answer, by favoring one model, and assessing the other alternative model. Although it showed that expansion up to the jerk term is a better description for the observational luminosity distance, the cosmographic problem is still vague. It is difficult for us to escape from the maze of cosmography in the accuracy and precision. We should underline that a small error does not mean a credible description, and a large error is not necessarily a bad thing. For further analysis of this issue, we recommend the bias–variance trade-off [58]; we have

$$\begin{aligned} {\text {risk}}= & {} {\text {bias}}^2 + {\text {variance}} \nonumber \\= & {} \sum _{i=1}^N [\mu ^{\text {cos}}(z_i) - \tilde{\mu }(z_i)]^2 + \sum _{i=1}^N \sigma ^2 (\mu ^{\text {cos}}(z_i)) \end{aligned}$$

(25)

where $\mu ^{\text {cos}}(z_i)$ is the reconstructed cosmographic distance modulus in different series truncations, $\tilde{\mu }(z_i)$ is the fiducial value, $\sigma (\mu ^{\text {cos}}(z_i))$ is the uncertainty of reconstruction. Obviously, the bias–variance trade-off can reveal more detailed information. The term bias$^2$ describes its accuracy (about the deviation from the true values), the variance conveys the precision (about the errors) of the constraint. Theoretically, minimizing risk corresponds to a balance between bias and variance. In cosmology, this promising approach has been widely utilized to find an effective way of obtaining information as regards the dark energy equation of state w(z) [59, 60]. In order to investigate the influence from fiducial model on the risk, we respectively consider the fiducial $\Lambda$CDM model with $\Omega _m=0.305$ and wCDM model with $w=-1.027$ in the combination of JLA and complementary probes [43].

4.1.1 Accuracy

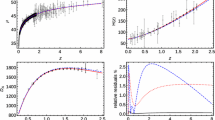
Accuracy is a deviation from the true value, which can be expressed by the bias square. In Fig. 4 we show the bias$^2$ of current data at the basis of fiducial $\Lambda$CDM model. First, we find that all of the bias are small, which indicates that the cosmographic models fit well with the JLA data. It implies that cosmography is sufficiently accurate to describe the observational JLA data. This is not difficult to understand; about 99% of the JLA data are at low redshift. Thus, application of the JLA data in cosmology would be a very useful strategy. Second, we see that bias square slightly increases for higher order. Finally, importantly, we find that the z-redshift and y-redshift both favor the second order, which indicates that expansion up to the jerk term is in best agreement with the true values.

Fig. 4

Bias square in the z-redshift and y-redshift of the JLA compilation with different cosmographic series truncations at the basis of fiducial $\Lambda$CDM model

4.1.2 Precision

Precision is usually statistic, and it represents errors. Variance, the set of errors, is independent of the fiducial model. In Fig. 5, we plot the variance of the cosmographic model in the z-redshift and y-redshift. First, variances at low order in these two redshift spaces are both small, almost zero. It indicates that current observational data can present a precise measurement on the parameters $q_0$ and $j_0$. Second, we note that variance at the third order starts to increase rapidly, especially for the y-redshift, which means that current data cannot give a physical measurement on the $s_0$ term, even higher orders. However, it has enough information for us to infer that the universe will continue to accelerate or slow down. Third, we should admit that variance in the y-redshift space at the fourth order is larger than that of the z-redshift.

Fig. 5

Variance in the z-redshift and y-redshift of the JLA compilation with different cosmographic series truncations

4.1.3 Risk

Risk is used to balance the bias square and variance, and to find which series truncation is the best description of the observational data. Due to the model dependence of the bias square, in this section we also investigate the influence of different fiducial models on the final risk analysis. In Fig. 6, we plot the risk for fiducial $\Lambda$CDM model and wCDM model. From the comparison between two panels, we first find that risk affected by the fiducial model is so little. They both favor the idea that cosmography up to the $j_0$ term is a better choice to describe current JLA data. This consequence is consistent with our previous work via the F-test [15]. It also proves that the risk analysis is a stable and scientific tool to analyze the convergence problem.

From the bias–variance trade-off, we conclude that the JLA data is so precise that the cosmographic model at z-redshift and y-redshift both can present an estimation with high accuracy. Of course, the introduction of the y-redshift can improve the cosmography study to a higher-redshift region, even to the early epoch. With its help, the past universe can be understood more objectively. Meanwhile, the risk analysis is also stable. The effects of the redshift parameter and fiducial model are not significant.

Fig. 6

Risk with different cosmographic series truncations in diverse fiducial models. The panel (a) is for the $\Lambda$CDM model, and the panel (b) is for the wCDM model

4.2 Forecasting

The above analysis shows that cosmography at high order suffers from an unphysical estimation, i.e., a large variance. We anticipate that future observation is able to give tighter constraints on the cosmography, with the improvement of observational precision, thus leading to a relaxation of the convergence problem. In this section, we forecast the constraint from future WFIRST and redshift drift on cosmography. In order to test the constraint from the mock distance modulus with flat errors $\sigma _{\mu }=0.15$, we also generate some data following the work in Ref. [18]. The comparison in Table 1 shows that future measurements can improve the constraints. For example, compared with $\sigma _{l_0} = 2478.44$ from the JLA sample, the redshift drift gives a more robust constraint on the parameters, e.g., $\sigma _{l_0} = 1299.17$, almost improving by double than current JLA data. Due to future measurements mainly focusing on the high-redshift region, we make a comparison of the variance for the y-redshift in Fig. 7. On the one hand, we find that all the future observations can improve the constraints at low order with high significant. Especially, the redshift drift can present an error $\sigma _{q_0} \sim 10^{-5}$ for the first order model. On the other hand, the future observations, including the mock data with $\sigma _{\mu }=0.15$ all improve the constraint at high order dramatically. Variances in these cases are much smaller than current data. Thus, we can see that the bias-trade off is effective to estimate the cosmographic problem. The future observations also have the potential to solve the cosmographic problem.

Fig. 7

Variance for different cosmographic series truncations in the y-redshift by current and future observations

Fig. 8

Cosmographic distance modulus, Hubble parameter and deceleration parameter with different orders in the y-redshift

5 Values of the cosmography

In previous work, cosmography has been widely used to reconstruct some special cosmological parameters, because of its model independence. In this section, we are interested in investigating its values to report what information we can obtain from the cosmography, and what we cannot get.

5.1 Deceleration parameter

The deceleration parameter is important for its sharp sense on the cosmic expansion. Especially, its negative (positive) sign immediately indicates the accelerating (decelerating) expansion. However, it is not an observable quantity temporarily. Most studies were performed in multiform parameterized q(z). Therefore, a model-independent analysis is appreciated.

In the right panel of Fig. 8, we plot the reconstructed deceleration factor over y-redshift using the best-fit values of supernova data. We find that the q(y) in various series truncations are quite different. They strongly depend on the order of Taylor expansion. Therefore, it is difficult to obtain a model-independent and stable estimation on the deceleration parameter via cosmography.

In order to find the reason why we cannot obtain a stable estimation of the deceleration parameter, we also compare the cosmographic distance modulus and Hubble parameter for different orders. For the distance modulus, they are almost indistinguishable at all redshifts, which indicates that cosmography fit well with the observational data. However, for the Hubble parameter, we can only obtain a relatively stable estimation at low redshift $y < 0.2$. For high redshift, they gradually deviate from each other. When we extract the information of the deceleration parameter, we only can obtain a similar estimation at redshift $y \approx 0.1$. This comparison tells us that despite the cosmographic models fitting well with the data, their contradictions become more and more prominent, with our increasing requirement on the cosmic expansion study. Therefore, it is difficult to obtain a more detailed expansion history via cosmography.

In fact, Fig. 8 implies that a dynamical measurement may be useful to solve this contradiction. In our previous work [15], we found that inclusion of Hubble parameter data can lead to stronger constraints on the cosmographic parameters. In Ref. [61], the authors also showed that the distance indicator cannot directly measure $q_0$ with both accuracy and precision. However, the redshift drift possibly does it. Therefore, it is reasonable for us to anticipate that inclusion of the dynamical redshift drift could present a much more stable evaluation on cosmic expansion history.

Fig. 9

Cosmographic EoS for different orders with matter density $\Omega _m=0.25,$ 0.30 and 0.35, respectively

Fig. 10

Derivative of dark energy EoS ${\text {d}}w/{\text {d}}z$ for different cosmographic orders with varying parameter $\Omega _m$ from 0.25 to 0.35

5.2 Dark energy equation of state

In previous work, cosmography was often used to reconstruct the dynamical cosmological model. For example, with two cosmographic parameters $(q_{0}, j_{0})$, one can derive the constant equation of state (EoS) dark energy model [62],

$$\begin{aligned} \Omega _{m}(q_{0}, j_{0})= & {} \frac{2 (j_{0} - q_{0} - 2 q_{0}^{2})}{1 + 2 j_{0} - 6 q_{0}}, \nonumber \\ w_{0}(q_{0}, j_{0})= & {} \frac{1 + 2 j_{0} - 6 q_{0}}{-3 + 6 q_{0}}. \end{aligned}$$

(26)

However, it needs a background model. In order to get an undamaged map of dark energy, our study is concerned with the normal cosmological model,

$$\begin{aligned} H^2(z)= & {} H_0^2 \left[ \Omega _m (1+z)^3\right. \nonumber \\&\left. +\,(1-\Omega _m)\exp \left[ 3\int _0^z \frac{1+w(z)}{1+z}\right] \mathrm{d}z\right] . \end{aligned}$$

(27)

In our analysis, we do not impose any style of dark energy, but the common w(z). Solving Eq. (27), we obtain

$$\begin{aligned} 1 + w(z)=\frac{1}{3} \frac{[H^2(z) - H^2_0 \Omega _m (1+z)^3]' (1+z)}{H^2(z)-H^2_0 \Omega _m (1+z)^3}, \end{aligned}$$

(28)

where the prime denotes the derivative with respect to redshift z. For Eq. (28), we note that the denominator may be zero for $H(z)^2=H_0^2 \Omega _m (1+z)^3$. This case may lead to a singularity in the EoS reconstruction. In Fig. 9, we plot the reconstruction of dark energy with different cosmographic series. In order to investigate the influence of matter density parameter, we relax parameter $\Omega _m$ from 0.25 to 0.35. On the one hand, we find that cosmography has all favored a cosmological constant EoS recently. On the other hand, however, a reliable estimation of w(z) is difficult to obtain. In addition, we find that w(z) at redshift $z \sim 0.8$ shows a sharp change, independent of the matter density parameter.

Usually, it is difficult to determine the EoS constant or varying model independently. A model-independent analysis of the derivative of EoS can be studied using the cosmography

$$\begin{aligned} w' = \frac{{\text {d}} w}{{\text {d}} z}. \end{aligned}$$

(29)

In Fig. 10, we plot the derivative $w' (z)$ by cosmography with different series. We also consider the parameter $\Omega _m$ in a wide region. At first, we find that $w'(z=0)$ is not zero in different cosmographic models. This indicates that a constant EoS dark energy model may be inappropriate. Moreover, $w'(z)$ at low redshift are generally negative. Thus, the cosmography may suggest a varying EoS and more complicated dark energy candidate. A linear EoS like $w(z)=w_0 + w_a z$ may be improper. According to the above picture, we infer that cosmography may favor a dark energy with $w(z) = -1 +w_a z + w_b z^2 + \cdots$, where $w_a <0$ and $w_b \ne 0$. However, an accurate determination on the derivative $w'(z)$ needs more data to join in, because it also strongly depends on the cosmographic series truncation.

6 Conclusion and discussion

In the present paper, we analyze the problem of cosmography using the bias–variance trade-off, and investigate its values.

To solve the convergence issue in cosmography, an improved redshift $y=z/(1+z)$ was introduced. Using the bias–variance trade-off, we find that the y-redshift produces bigger variances at high orders. For the low cosmographic order (i.e., first and second order), y-redshift does not bring about bigger errors, but a nearly identical variance as z-redshift. For the JLA data, we find that most of them are distributed in the low-redshift region with high precision. Therefore, the z-redshift is sufficiently accurate to describe the data. Although the y-redshift does not present a smaller bias than the z-redshift for the JLA data, it still can ensure the correctness of cosmography at high redshift.

Minimizing risk, it suggests that expansion up to the $j_0$ term is the best choice for current supernova data, regardless of the z-redshift or y-redshift. We also test the influence of the fiducial model on risk analysis. The comparison demonstrates that it is trivial. Although a previous F-test also obtained a similar result, our paper is not a repeated work using more data. Our analysis finds a deeper insight in the convergence issue. First, it not only can tell us the convergence problem is in the accuracy or the precision, but also can provide us more objective information about how serious the divergence problem is. Because if the crux lies in the accuracy, the convergence problem maybe still cannot be solved even though more data were included. Second, in previous work, most focus was on the pursuit of a “sweet spot”, which has masked the physical meaning of the y-redshift. In our study, we not only find it is influenced by the distribution of data, but also forecast whether future observations can solve the convergence problem. Our analysis in Fig. 8 and Sect. 5.1 also indicates that the dynamical measurement is a potential clue to solve this problem.

Our forecast finds that future WFIRST and redshift drift can significantly improve the constraints. Therefore, inclusion of dynamical measurement such as Hubble parameter data, redshift drift, etc. may be able to improve the constraint in accuracy and precision with high significance. As studied in our previous work [15], inclusion of the H(z) data can lead to stronger constraints on the cosmographic parameters. This discovery is helpful to understand or solve the convergence issue of supernova data. This is because a dynamical probe like the canonical redshift drift can provide direct measurement to the cosmic expansion history. While distance measurement is geometric. As studied in Ref. [63], the luminosity distance determines the EoS w through a multiple integral relation that smears out much information. For the redshift drift, it not only directly measures the change of Hubble parameter, but also can be realized via multiple wavebands and methods [37, 64]. Moreover, it is immune from extra systematic errors, and does not need photometric calibration, etc. Recently, a test in German Vacuum Tower Telescope demonstrates that the Laser Frequency Combs also have an advantage with long-term calibration precision, accuracy to realize the redshift drift experiment [65].

Our investigation also promotes the study of the values of cosmography. In previous work, most attention were focus on a special model. However, our analysis presents an almost undamaged map of dark energy. It breaks the limitation of extrapolation to other models. Setting the dark energy w(z) as free, we find that cosmography cannot give reliable estimations on q(z) and w(z). However, we find that it does not favor a constant EoS, but a complicated w(z), such as $w(z) = -1 +w_a z + w_b z^2 + \cdots$, where $w_a <0$ and $w_b \ne 0$. These estimations are useful for modeling the dark energy.

Cosmography has been an useful tool with great potential to study the cosmology. For the dark energy, it was usually reconstructed by parametrization, such as the Chevallier–Polarski–Linder [66, 67], Jassal–Bagla–Padmanabhan [68]; or the non-parameterization, such as the Gaussian processes [55, 69], principal component analysis [60, 70]. Cosmography is another model-independent method to assess dark energy models. Moreover, cosmography has also been widely used in another fields, such as to test the power of supernova data [71]. Therefore, we have to say that cosmography is an important method to study the cosmology. Our study provides a straightforward and scientific reference. Of course, we will also devote ourselves to improving the cosmography study in our future work. We would like to study the influence of the inclusion of BAO and CMB data on cosmography. Throughout previous work, we find that many different observational data or combinations favor the best cosmography to second order. In our future work, we will also be interested in exploring their subtle relations to further understand the cosmography. Moreover, we also have an interest in improving the cosmographic problem by proposing some other physical redshift.