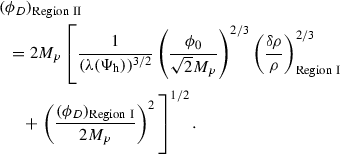COSMOS-$e'$-soft Higgsotic attractors

Abstract

In this work, we have developed an elegant algorithm to study the cosmological consequences from a huge class of quantum field theories (i.e. superstring theory, supergravity, extra dimensional theory, modified gravity, etc.), which are equivalently described by soft attractors in the effective field theory framework. In this description we have restricted our analysis for two scalar fields – dilaton and Higgsotic fields minimally coupled with Einstein gravity, which can be generalized for any arbitrary number of scalar field contents with generalized non-canonical and non-minimal interactions. We have explicitly used $R^2$ gravity, from which we have studied the attractor and non-attractor phases by exactly computing two point, three point and four point correlation functions from scalar fluctuations using the In-In (Schwinger–Keldysh) and the $\delta \mathcal{N}$ formalisms. We have also presented theoretical bounds on the amplitude, tilt and running of the primordial power spectrum, various shapes (equilateral, squeezed, folded kite or counter-collinear) of the amplitude as obtained from three and four point scalar functions, which are consistent with observed data. Also the results from two point tensor fluctuations and the field excursion formula are explicitly presented for the attractor and non-attractor phase. Further, reheating constraints, scale dependent behavior of the couplings and the dynamical solution for the dilaton and Higgsotic fields are also presented. New sets of consistency relations between two, three and four point observables are also presented, which shows significant deviation from canonical slow-roll models. Additionally, three possible theoretical proposals have presented to overcome the tachyonic instability at the time of late time acceleration. Finally, we have also provided the bulk interpretation from the three and four point scalar correlation functions for completeness.

1 Introduction

The inflationary paradigm is a theoretical proposal which attempts to solve various long-standing issues with standard Big Bang cosmology and has been studied earlier in various works [1,2,3,4,5,6,7,8,9,10,11,12]. But apart from the success of this theoretical framework it is important to note that no single model exists till now using which one can explain the complete evolution history of the universe and also one is unable to break the degeneracy between various cosmological parameters computed from various models of inflation [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. It is important to note that we have the vacuum energy contribution generated by the trapped Higgs field in a metastable vacuum state which mimics the role of an effective cosmological constant in effective theory. At the later stages of the universe such a vacuum contribution dominates over other contents and correspondingly the universe expands in an exponential fashion. But using such metastable vacuum state it is not possible to explain the tunneling phenomenon and also impossible to explain the end of inflation. To serve both of the purposes the effective potential for inflation should have a flat structure. Due to such a specific structure the effective potential for inflation satisfies the flatness or slow-roll condition using which one can easily determine the field value corresponding to the end of inflation. There are various classes of models in existence in the cosmological literature where one has derived such a specific structure of inflation [14, 34,35,36,37,38,39]. For example, the Coleman–Weinberg effective potential serves this purpose [40, 41]. Now if we consider the finite temperature contributions in the effective potential [42, 43] then such thermal effects need to localize the inflaton field to small expectation values at the beginning of inflation. The flat structure of the effective potential for inflation is such that the scalar inflaton field slowly rolls down in the valley of potential during which the scale factor varies exponentially and then inflation ends when the scalar inflaton field goes to the non-slow-rolling region by violating the flatness condition. At this epoch inflaton field evolves to the true minimum very fast and then it couples to the matter content of the universe and reheats our universe via subsequent oscillations about the minimum of the slowly varying effective potential for inflation. This class of models is a very successful theoretical probe through which it is possible to explain the characteristic and amplitude of the spectrum of density fluctuations with high statistical accuracy ($2\sigma$ CL from Planck 2015 data [44,45,46]) and at late times these perturbations act as the seeds for the large scale structure formation, which we observe at the present epoch. Apart from this huge success of the inflationary paradigm in the slowly varying regime it is important to mention that these density fluctuations generated from various classes of successful models were unfortunately large enough to explain the physics of standard Grand Unified Theory (GUT) with well-known theoretical frameworks and also it is not possible to explain the observed isotropy of the Cosmic Microwave Background Radiation (CMBR) at small scales during the inflationary epoch. The only physical possibility is that the self interactions of the inflaton field and the associated couplings to other matter field contents would be sufficiently small to possibly satisfy these cosmological and particle physics constraints. But the prime theoretical challenge at this point is that for such a setup it is impossible to achieve thermal equilibrium at the end of inflation. Consequently, it is not at all possible to localize the scalar inflaton field near zero Vacuum Expectation Value (VEV), $\langle \phi \rangle =\langle 0|\phi |0\rangle =0,$ where $|0\rangle$ is the corresponding vacuum state in quasi-de Sitter space time. Therefore, a sufficient amount of expansion will not be obtained from this prescribed setup. Here it is important to note that, for a broad category of effective potentials, the inflaton field evolves with time very slowly compared to the Hubble scale following slow-roll conditions and satisfies all of the observational constraints [44,45,46] computable from various inflationary observables from this setup. However, apart from the success of the slow-roll inflationary paradigm the density fluctuations or more precisely the scalar component of the metric perturbations restricts the coupling parameters to be sufficiently small and allows huge fine-tuning in the theoretical setup. This is obviously a not recommendable prescription from a model builder’s point of view. Additionally, all these classes of models are not ruled out completely by the present observed data (Planck 2015 and other joint data sets [44,45,46,47]), as they are degenerate in terms of the determination of inflationary observables and associated cosmological parameters in precision cosmology. There are various ideas existing in the cosmological literature which can drive inflation. These are:

• Category I: In this class of models, inflation is driven through a field theory which involves a very high energy physics phenomenon. Example: string theory and its supergravity extensions [13, 15,16,17, 19, 22, 23, 25, 48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82], various supersymmetric models [14, 34,35,36,37,38,39], etc.

• Category II: In this case, inflation is driven by changing the mathematical structure of the gravitational sector. This can be done using the following ways:

  • 1. Introducing higher derivative terms of the form of f(R), where R is the Ricci scalar [83,84,85,86]. Example: the Starobinsky inflationary framework, which is governed by the model [83] $f(R)=aR+bR^2$, where the coefficients a and b are given by $a=M^2_p$ and $b=1/6M^2$. If we set $a=0$ and $b=1/6M^2=\alpha$ then we can get back the theory of scale free gravity in this context. In this paper we will explore the cosmological consequences from the scale free theory of gravity.

  • 2. Introducing higher derivative terms of the form of Gauss–Bonnet gravity coupled with a scalar field in a non-minimal fashion, where the contribution in the effective action can be expressed as [87, 88]

    $$\begin{aligned} S_{GB}= & {} \int \mathrm{d}^4x\sqrt{-g}~f(\phi )[R_{\mu \nu \alpha \beta }R^{\mu \nu \alpha \beta }\nonumber \\&-\,4R_{\mu \nu }R^{\mu \nu }+R^2], \end{aligned}$$

    (1.1)

    where $f(\phi )$ is the inflaton dependent coupling which can be treated as the non-minimal coupling in the present context. This is also an interesting possibility which we have not explored in this paper. Here one cannot consider the Gauss–Bonnet term in the gravity sector in 4D without coupling to other matter fields, as in 4D the Gauss–Bonnet term is a topological surface term.

  • 3. Another possibility is to incorporate the effect of non-minimal coupling of the inflaton field and the gravity sector [89,90,91]. The simplest example is $f(\phi )R$ gravity theory. For Higgs inflation [89], $f(\phi )=(1+\xi \phi ^2)$, where $\xi$ is the non-minimal coupling of the Higgs field. Here one can consider a more complicated possibility as well by considering a non-canonical interaction between inflaton and f(R) gravity by allowing an $f(\phi )f(R)$ term in the 4D effective action [92]. For the construction of the effective potential we have considered this possibility.

  • 4. One can also consider the other possibility, where higher derivative non-local terms can be incorporated in the gravity sector [93,94,95,96,97,98,99,100,101,102]. For example one can consider the possibilities $Rf_{1}(\Box )R$, $R_{\mu \nu }f_{2}(\Box )R^{\mu \nu }$, $R_{\mu \nu \alpha \beta }f_{3}(\Box )R^{\mu \nu \alpha \beta }$, $Rf_{4}(\Box )\nabla _{\mu }\nabla _{\nu }\nabla _{\alpha }\nabla _{\beta }R^{\mu \nu \alpha \beta }$, $R_{\mu }^{\nu \alpha \beta }f_{5}(\Box )\nabla _{\alpha }\nabla _{\beta }\nabla _{\nu }\nabla _{\rho }\nabla _{\lambda }\nabla _{\gamma }R^{\mu \rho \lambda \gamma }$, $R^{\mu \nu \alpha \beta }f_{6}(\Box )\nabla _{\alpha }\nabla _{\beta }\nabla _{\nu }\nabla _{\mu }\nabla _{\lambda }\nabla _{\gamma }\nabla _{\eta }\nabla _{\xi }R^{\lambda \gamma \eta \xi }$, where $\Box$ is defined as $\Box =\frac{1}{\sqrt{-g}}\partial _{\mu }[\sqrt{-g}~g^{\mu \nu }\partial _{\nu }]$; it is the d’Alembertian operator in 4D and the $f_{i}(\Box )\forall i=1,2,\ldots ,6$ are analytic entire functions containing higher derivatives up to infinite order. This is itself a very complicated possibility which we have not explored in this paper.

• Category III: In this case, inflation is driven by changing the mathematical structure of both the gravitational and the matter sector of the effective theory. One of the examples is to use Jordan–Brans–Dicke (JBD) gravity theory [103, 104] along with extended inflationary models which includes non-canonical interactions. By adjusting the value of the Brans–Dicke parameters one can study the observational consequences from this setup. Instead of Jordan–Brans–Dicke (JBD) gravity theory one can also use non-local gravity or many other complicated possibilities.

Fig. 1

Representative schematic diagram of attractor and non-attractor phase of soft Higgsotic inflation

In this paper, we consider the possibility of the soft inflationary paradigm in an Einstein frame, where a chaotic Higgsotic potential is coupled to a dilaton via exponential type of potential, which is appearing through the conformal transformation from Jordan to Einstein frame in the metric within the framework of scale free $\alpha R^2$ gravity. Here it is important to mention that, in the case of a soft inflationary model, the dilaton exponential potential is multiplied by a coupling constant of the Higgsotic theory which mimics the role of an effective coupling constant and its value always decreases with the field value. One can generalize this idea for any arbitrary matter interactions which is also described by generalized $P(X,\phi )$ theory [105, 106] (see Appendix 10.1 for more details). In this context also it is important to specify that one can treat the field dependent couplings in the simple effective potentials or maybe in generalized $P(X,\phi )$ functionals, entailing a decaying behavior with dilaton field value as it contains an overall exponential factor which is coming from the dilaton potential itself in an Einstein frame. This is a very interesting feature from the point of view of RG flow in QFT as the field dependent coupling in an Einstein frame captures the effect of field flow (energy flow). In this context instead of solving directly the RGE for the effective coupling, we solve the dynamical equations for the fields and the effective coupling for power-law and exponential attractors. Due to the similarities in the two techniques here one can arrive at the conclusion that in cosmology solving a dynamical attractor problem in the presence of effective coupling in an Einstein frame mimics the role of solving RGE in QFT. Thus due to the exponential suppression in the effective coupling in an Einstein frame it is naturally expected from the prescribed framework that for suitable choices of the model parameters soft cosmological constraints can be obtained [107, 108]. As in this prescribed framework the dilaton exponential coupling plays a very significant role, one can ask the very crucial question of its theoretical origin. Obviously there are various sources in existence from which one can derive exponential effective couplings or more precisely the effective potentials for dilaton. These possibilities are:

• Source I: One of the sources for dilaton exponential potential is string theory, appearing in the Category I. Specifically, superstring theory and low energy supergravity models are the theoretical possibilities in string theory [109,110,111,112,113,114,115,116,117,118] where dilaton exponential potential appears in the gravity part of the action in a Jordan frame and after a conformal transformation in the Einstein frame such dilaton effective potential is coupled with the matter sector. The most important example is the $\alpha$-attractor which mimics a class of inflationary models in $\mathcal{N}=1$ supergravity in 4D. For details see Refs. [119,120,121,122,123,124,125,126,127,128,129].

• Source II: Another possible source of the dilaton exponential potential is coming from a modified gravity theory framework such as f(R) gravity [83,84,85,86], $f(\phi )f(R)$ gravity [89,90,91,92] and Jordan–Brans–Dicke theory [103, 104] in the Jordan frame, which appear in the Category II (1 and 3) and Category III. After transforming the theory in the Einstein frame via conformal transformation one can derive the dilaton exponential potential.

In Fig 1a–c, we have shown the diagrammatic representation of attractor and non-attractor phases of soft Higgsotic inflation. In these representative diagrams we have shown the steps followed during the computation. In this work we have addressed the following important points through which it is possible to understand the underlying cosmological consequences from the proposed setup. These issues are:

• Transition from scale free gravity to scale dependent gravity have discussed and its impact on the solutions in the attractor and non-attractor regime of inflation have also discussed.

• Explicit calculation of the $\delta \mathcal{N}$ formalism is presented by considering the effect up to second-order perturbation in the solution of the field equation in attractor regime. Additionally deviation in the consistency relation between the non-Gaussian amplitude for four point and three point scalar correlation function a.k.a. Suyama–Yamaguchi relation is presented to explicitly show the consequences from attractor and non-attractor phase.

• Additionally, new sets of consistency relations are presented in attractor and non-attractor phases of inflation to explicitly show the deviation from the results obtained from a canonical single field slow-roll model.

• Detailed numerical estimations are given for all the inflationary observables for attractor and non-attractor phases of inflation which confronts well Planck 2015 data. Additionally, constraints on reheating is also presented for attractor and non-attractor phase.

• Bulk interpretation are given in terms of S, T and U channel contribution for all the individual terms obtained from three and four point correlation function.

• Scale dependent behaviors of the non-minimal coupling between inflaton field and additional dilaton field are given in an Einstein frame for power-law and exponential types of attractor.

• Three possible theoretical proposals have presented to overcome the tachyonic instability [130,131,132,133,134] at the time of late time acceleration in a Jordan frame and due to this fact the structure of the effective potentials changes in an Einstein frame as well. These proposals are inspired by:

  • I. Non-BPS D-brane in superstring theory [23, 135,136,137,138,139,140].

  • II. An alternative situation where we switch on the effects of additional quadratic mass term in the effective potential.

  • III. Also we have considered a third option where we switch on the effect of non-minimal coupling between scale free $\alpha R^2$ gravity and the inflaton field.

Now before going to the further technical details let us clearly mention the underlying assumptions to understand the background physical setup of this paper:

• 1. We have restricted our analysis up to monomial $\phi ^4$ model and due to the structural similarity with Higgs potential at the scale of inflation we have identified monomial $\phi ^4$ model as Higgsotic model in the present context.

• 2. To investigate the role of scale free theory of gravity, as an example we have used $\alpha R^2$ gravity. But the present analysis can be generalized to any class of f(R) gravity models.

• 3. In the matter sector we allow only simplest canonical kinetic term which are minimally coupled with $\alpha R^2$ gravity sector. For such canonical slow-roll models the effective sound speed $c_\mathrm{S}=1$. But for completeness one can consider a most generalized version of $P(X,\phi )$ models, where $X=-\frac{1}{2}g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu }\phi$ and the effective sound speed $c_\mathrm{S}<1$ for such models. For example one can consider the following structure [56, 105]:

  $$\begin{aligned} P(X,\phi )=-\frac{1}{f(\phi )}\sqrt{1-2Xf(\phi )}+\frac{1}{f(\phi )}-V(\phi ),\nonumber \\ \end{aligned}$$

  (1.2)

  which is exactly similar to the DBI model. But here one can implement our effective Higgsotic models in $V(\phi )$ instead of choosing the fixed structure of the DBI potential in UV and IR regime. Here one can choose [56] $f(\phi )\approx \frac{g}{\phi ^4}$, which is known as the throat factor in string theory. In string theory g is the parameter which depends on the flux number. But other choices for $f(\phi )$ are also allowed for the general class of $P(X,\phi )$ theories which follows the above structure. Similarly one can consider the following structure of $P(X,\phi )$ for tachyon and Gtachyon models given by [23, 141]

  $$\begin{aligned}&\text {For Tachyon:}\quad P(X,\phi )=-V(\phi )\sqrt{1-2X\alpha ^{\prime }},\end{aligned}$$

  (1.3)
  $$\begin{aligned}&\text {For GTachyon:}\quad P(X,\phi )=-V(\phi )(1-2X\alpha ^{\prime })^{q}\nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (1/2<q<2), \end{aligned}$$

  (1.4)

  where $\alpha ^{\prime }$ is the Regge slope. Here we consider the most simple canonical form, $P(X,\phi )=X-V(\phi )$, where $V(\phi )$ is the effective potential for the monomial $\phi ^4$ model considered here for our computation.

• 4. As a choice of the initial condition or precisely as the choice of vacuum state we restrict our analysis using Bunch–Davies vacuum. If we relax this assumption, then we can generalize the results for $\alpha$ vacua as well.

• 5. During our computation we have restricted ourselves up to the minimal interaction between the $\alpha R^2$ gravity and matter sector. Here one can consider the possibility of non-minimal interaction between $\alpha R^2$ gravity and matter sector.

• 6. During the implementation of the In-In formalism [2] to compute three and four point correlation function we have use the fact that the additional dilaton field $\Psi$ is fixed at Planckian field value to get the non-attractor behavior of the present setup. One can relax this assumption and can redo the analysis of the In-In formalism to compute three and four point correlation function without freezing the dilaton field $\Psi$ and also use the attractor behavior of the model to simplify the results.

• 7. During the computation of correlation functions using a semi classical method, via the $\delta \mathcal{N}$ formalism [23, 142,143,144,145,146], we have restricted up to second-order contributions in the solution of the field equation in FLRW background and also neglected the contributions from the back reaction for all type of effective Higgsotic models derived in an Einstein frame. For completeness, one can relax these assumptions and redo the analysis by taking care of all such contributions.

• 8. In this work we have neglected the contribution from the loop effects (radiative corrections) in all of the effective Higgsotic interactions (specifically in the self couplings) derived in the Einstein frame. After switching on all such effects one can investigate the numerical contribution of such terms and comment on the effects of such terms in precision cosmology measurement.

• 9. We have also neglected the interactions between gauge fields and Higgsotic scalar field in this paper. One can consider such interactions by breaking conformal invariance of the U(1) gauge field in the presence of time dependent coupling $f(\phi (\eta ))$ to study the features of primordial magnetic field through inflationary magnetogenesis [147,148,149].

The plan of this paper is as follows:

• In Sect. 2, we start our discussion with $f(R)=\alpha R^2$ gravity where a scalar field is minimally coupled with the gravity sector and contains only canonical kinetic term. Next in the matter sector we choose a very simple monomial model of potential, $V(\phi )=\frac{\lambda }{4}\phi ^4$, which can be treated as a Higgs like potential as at the scale of inflation, the contribution from the VEV of Higgs is almost negligible.

• Further, in Sect. 3, we provide the field equations in a Jordan frame written in a spatially flat FLRW background. Next, we perform a conformal transformation in the metric to the Einstein frame and introduce a new dilaton field. Further, we derive the field equations in an Einstein frame and try to solve them for two dynamical attractor features: a power-law solution, and exponential solution. However, the second case give rise to tachyonic behavior which can be resolved by considering-I. non-BPS D-brane in superstring theory, II. via switching on the effect of quadratic term in the effective potential and III. by introducing a non-minimal coupling between matter and $\alpha R^2$ gravity sector.

• Next, in Sect. 4, using two dynamical attractors, power-law and exponential solution, we study the cosmological constraints in the presence of two fields. We study the constraints from primordial density perturbation, by deriving the expressions for two point function and the present inflationary observables in Sect. 4.2. Further, we repeat the analysis for tensor modes and also comment on the future observables – the amplitude of the tensor fluctuations and tensor-to-scalar ratio in Sect. 4.3. Additionally, in Sect. 4.4, we study the constraint for the reheating temperature. Finally, in Sects. 5.1 and 5.2, we derive the expression for the inflaton and the non-minimal coupling at horizon crossing, during reheating and at the onset of inflation for the two above mentioned dynamical cosmological attractors.

• Further, in Sect. 6, we have explored the cosmological solutions beyond attractor regime. Here we restrict ourselves at spatially flat FLRW background and made cosmological predictions from this setup in Sect. 7.1. To serve this purpose we have used the ADM formalism using which we compute two point functions and associated present observables using the Bunch–Davies initial condition for scalar fluctuations in Sects. 7.2.1 and 7.2.2. Further, in Sects. 7.3.1 and 7.3.2, we repeat the procedure for tensor fluctuations as well where we have computed two point function and the associated future observables. We also derive a few sets of consistency relations in this context which are different from the usual single field slow-roll models. Further, in Sect. 7.4, we derive the constraints on reheating temperature in terms of observables and the number of e-foldings.

• Next, in Sects. 8.1.1 and 8.1.2, as a future probe, we compute the expression for three point function and the bispectrum of scalar fluctuations using the In-In formalism for the non-attractor case and the $\delta \mathcal{N}$ formalism for the attractor case. Further, we derive the result for a non-Gaussian amplitude $f^{\mathrm{{loc}}}_{\mathrm{NL}}$ for equilateral and squeezed limit triangular shape configuration. Also we give a bulk interpretation of each of the momentum dependent terms appearing in the expression for the three point scalar correlation function in terms of S, T and U channel contributions. Further, for the consistency check we freeze the additional field $\Psi$ in the Planck scale and redo the analysis of the $\delta \mathcal{N}$ formalism. Here we show that the expression for the three point non-Gaussian amplitude is slightly different as expected for the single field case. Further, in Sects. 8.1.1 and 8.1.2, we compare the results obtained from the In-In formalism and $\delta \mathcal{N}$ formalism for the non attractor phase, where the additional field $\Psi$ is fixed in Planck scale. Finally, we give a theoretical bound on the scalar three point non-Gaussian amplitude.

• Finally, in Sects. 8.2.1 and 8.2.2, as an additional future probe, we have also computed the expression for the four point function and the trispectrum of scalar fluctuations using the In-In formalism for the non-attractor case and $\delta \mathcal{N}$ formalism for the attractor case. Further, we derive the results for non-Gaussian amplitude $g^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$ for equilateral, counter-collinear or folded kite and squeezed limit shape configuration from the In-In formalism. Further we give a bulk interpretation of each of the momentum dependent terms appearing in the expression for the four point scalar correlation function in terms of S, T and U channel contributions. In the attractor phase following the prescription of $\delta \mathcal{N}$ formalism we also derive the expressions for the four point non-Gaussian amplitude $g^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$. Next we have shown that the consistency relation connecting three and four point non-Gaussian amplitude aka Suyama–Yamaguchi relation is modified in the attractor phase and further given an estimate of the amount of deviation. Further, for the consistency check we freeze the additional field $\Psi$ in Planck scale and redo the analysis of the $\delta \mathcal{N}$ formalism. Here we show that the four point non-Gaussian amplitude is slightly different as expected for the single field case. Finally, we give a theoretical bound on the scalar four point non-Gaussian amplitude.

2 Model building from scale free gravity

To describe the theoretical setup let us start with the total action of f(R) gravity coupled minimally along with a scalar inflaton field $\phi$:

$$\begin{aligned} S=\int \mathrm{d}^{4}x\sqrt{-g}\left[ f(R)-\frac{g^{\mu \nu }}{2} (\partial _{\mu }\phi )(\partial _{\nu }\phi )-V(\phi )\right] \end{aligned}$$

(2.1)

where in general f(R) can be an arbitrary function of the Ricci scalar R. For example one can choose a generic form given by [150, 151]

$$\begin{aligned} f(R)=\sum ^{\infty }_{n=1}a_{n}R^{n}, \end{aligned}$$

(2.2)

where $a_{n}\forall n$ are the expansion coefficients for the above mentioned generic expansion. Here one can note down the following features of this generic choice of the expansion:

• 1. If we set $a_{1}= M^2_p/2,~ a_{n}= 0 \forall n>1,$ then one can get back the well-known Einstein–Hilbert action (GR) in Jordan frame: $f(R)=M^2_p R/2$. In this particular case Jordan frame and Einstein frame are exactly the same because the conformal factor for the frame transformation is unity. This directly implies that no dilaton potential appears due to the frame transformation from Jordan to Einstein frame. But since in this paper we are specifically interested in the effects of modified gravity sector, the higher powers of R are more significant in the above mentioned generic expansion of f(R) gravity.

• 2. If we set, $a_{1}= a=M^{2}_{p}/2,~ a_{2}= b=\alpha ,~ a_{n}= 0 \forall n>2,$ then one can get back the specific structure of the very well-known Starobinsky model: $f(R)=aR+bR^2=M^2_p R/2+\alpha R^2$. Here one can treat the $\alpha R^2$ term as an additional quantum correction to the Einstein gravity.

• 3. One can also set $a_{1}= a=M^{2}_{p}/2,~~a_{n}= \alpha \forall n\ge 2,$ then one can get back the specific structure $f(R)=M^2_p R/2+\alpha R^n$, which describes the situation where the Einstein–Hilbert gravity action is modified by the monomial powers of R. Here also one can treat the $\alpha R^n$ term as an additional quantum correction to the Einstein gravity.

• 4. In our computation we set $a_{1}= a=0,~ a_{2}= b=\alpha ,~ a_{n}= 0\forall n>2,$ which is known as scale free gravity in a Jordan frame: $f(R)=\alpha R^{2}$, where $\alpha$ is a dimensionless scale free coefficient. For this type of theory if we perform the conformal transformation from Jordan to Einstein frame then we will induce a constant term in the effective potential and this can be interpreted as the 4D cosmological constant using which one can fix the scale of the theory for early and late universe. But in our computation we introduce an additional scalar field in the action in a Jordan frame, which we identified to be the inflaton. After a conformal transformation in an Einstein frame we get an effective potential which is coming from the interaction between the dilaton exponential potential and the inflationary potential as appearing in a Jordan frame. We will show that here the two fields, dilaton and inflaton form dynamical attractors using which one can very easily solve this two-field complicated model in the context of cosmology.

Next we will discuss the structure of the inflational as appearing in Eq. (2.1). Generically in 4D effective theory the effective potential can be expressed as

$$\begin{aligned} V(\phi )= & {} \underbrace{V_{\mathrm{{ren}}}(\phi )}_{\mathrm{{Renormalizable}}~\mathrm{{part}}}+ \underbrace{\sum ^{\infty }_{\delta =5}J_{\delta }(g)\frac{\phi ^{\delta }}{M^{\delta -4}_p}}_{\mathrm{{Non}}\text {-}\mathrm{{renormalizable}}~\mathrm{{part}}}\nonumber \\= & {} \sum ^{\infty }_{\delta =0}C_{\delta }(g)\frac{\phi ^{\delta }}{M^{\delta -4}_p}, \end{aligned}$$

(2.3)

where $J_{\delta }(g)$ and $C_{\delta }(g)$ are the Wilson coefficients in effective theory. Here g stands for the scale of theory and the dependences of the Wilson coefficients on the scale can be exactly computed for a full UV complete theory using renormalization group equations. In this paper a similar scale dependence on the couplings we will calculate using dynamical attractor method in an Einstein frame, which exactly mimics the role of solving renormalization group equations in the context of cosmology. As written here, the total effective potential is made by renormalizable (relevant operators) and non-renormalizable (irrelevant operators) part, which can be obtained by heavy degrees of freedom from a known UV complete theory. In our computation we just concentrate on the renormalizable part of the action, which can be recast as

$$\begin{aligned} V(\phi )=\sum ^{4}_{\delta =0}C_{\delta }(g)\frac{\phi ^{\delta }}{M^{\delta -4}_p}. \end{aligned}$$

(2.4)

Next to get the Higgslike monomial structure of the potential we set $C_{3}(g)=0,$ as in this paper our prime motivation is to look into only Higgsotic potentials. Consequently we get

$$\begin{aligned} V(\phi )=C_{0}+C_{2}(g)M^2_p\phi ^2+C_{4}(g)\phi ^4. \end{aligned}$$

(2.5)

To get the Higgsotic structure of the potential one should set

$$\begin{aligned} C_{0}(g)=\frac{\lambda }{4}v^4,\quad C_{2}(g)=-\frac{\lambda }{2}v^2,\quad C_{4}(g)=\frac{\lambda }{4}. \end{aligned}$$

(2.6)

Here v is the VEV of the field $\phi$. Consequently, one can write the potential in the following simplified form:

$$\begin{aligned} V(\phi )=\frac{\lambda }{4}(\phi ^2-v^2)^2. \end{aligned}$$

(2.7)

Now we consider a situation where scale of inflation as well as the field value are very much larger than the VEV of the field. This assumption is pretty consistent with inflation with Higgs field. Consequently, in our case the final simplified monomial form of the Higgsotic potential is given by

$$\begin{aligned} V(\phi )=\frac{\lambda }{4}\phi ^{4}. \end{aligned}$$

(2.8)

Further varying Eq. (2.1) with respect to the metric and using Eqs. (2.2) and (2.8) the equation of motion (modified Einstein equation) for the $\alpha R^2$ scale free gravity can be written as

$$\begin{aligned} \tilde{G}_{\mu \nu }:=\alpha [\{R_{\mu \nu }+2 (g_{\mu \nu }\Box -\nabla _{\mu }\nabla _{\nu })\}+G_{\mu \nu }]R=T_{\mu \nu }\nonumber \\ \end{aligned}$$

(2.9)

where the D’Alembertian operator is defined as $\Box =g^{\alpha \beta }\nabla _{\alpha }\nabla _{\beta }=g^{\alpha \beta } \nabla _{\alpha }\partial _{\beta }=\frac{1}{\sqrt{-g}}\partial _{\alpha }(\sqrt{-g} g^{\alpha \beta }\partial _{\beta })$ and the energy-momentum stress tensor can be expressed as

$$\begin{aligned} T_{\mu \nu }= & {} -\frac{2}{\sqrt{-g}}\frac{\delta (\sqrt{-g}\mathcal{L}_{M})}{\delta g^{\mu \nu }}\nonumber \\= & {} \partial _{\mu }\phi \partial _{\nu }\phi -g_{\mu \nu } \left( \frac{1}{2}g^{\alpha \beta }\partial _{\alpha } \phi \partial _{\beta }\phi +\frac{\lambda }{4}\phi ^{4}\right) . \end{aligned}$$

(2.10)

Here it is important to note that the Einstein tensor is defined as $G_{\mu \nu }:=R_{\mu \nu }-\frac{g^{\mu \nu }}{2}R$. Now after taking the trace of Eq. (2.9) we get $R\Box R=\frac{T}{6\alpha },$ where the trace of the energy-momentum tensor is characterized by the symbol $T=T_{\mu }^{\mu }$. In this modified gravity picture we have $\nabla ^{\mu }\tilde{G}_{\mu \nu }=4\alpha [\nabla _{\mu },\Box ]R\ne 0$ where we use $\nabla ^{\mu }R_{\mu \nu }=\frac{g^{\mu \nu }}{2}\nabla ^{\mu }R$, which directly follows from the Bianchi identity $\nabla ^{\mu }G_{\mu \nu }=0$. Now varying Eq. (2.1) with respect to the field $\phi$ we get the following equation of motion in curved space-time:

$$\begin{aligned} \Box \phi= & {} -V^{\prime }(\phi )=-\lambda \phi ^{3} \Longrightarrow \frac{1}{\sqrt{-g}}\partial _{\alpha }\left( \sqrt{-g} g^{\alpha \beta }\partial _{\beta }\phi \right) \nonumber \\= & {} -\lambda \phi ^{3}. \end{aligned}$$

(2.11)

Further assuming the flat ($k=0$) FLRW background metric the Friedmann equations can be written from Eq. (2.9) as

$$\begin{aligned}&H^{2}=\left( \frac{\dot{a}}{a}\right) ^2=\frac{\rho _{\phi }}{6\alpha R}+\frac{R}{2}-\left( \frac{\dot{R}}{R}\right) H,\end{aligned}$$

(2.12)

$$\begin{aligned}&2\dot{H}+3H^{2}=2\left( \frac{\ddot{a}}{a}\right) +\left( \frac{\dot{a}}{a}\right) ^{2}\nonumber \\&~~~~~~~~~~~~~~~~~~~=-\frac{p_{\phi }}{2\alpha R} -2\left( \frac{\dot{R}}{R}\right) H-\frac{\ddot{R}}{R}+\frac{R}{4}, \end{aligned}$$

(2.13)

where we have assumed the energy-momentum tensor can be described by a perfect fluid as $T^{\mu }_{\nu }=\hbox {diag}(-\rho _{\phi },p_{\phi },p_{\phi },p_{\phi })$ where the energy density $\rho _{\phi }$ and the pressure density $p_{\phi }$ can be expressed for the scalar field $\phi$ as

$$\begin{aligned} \rho _{\phi }=\frac{\dot{\phi }^2}{2}+\frac{\lambda }{4}\phi ^{4},\quad p_{\phi }=\frac{\dot{\phi }^2}{2}-\frac{\lambda }{4}\phi ^{4}. \end{aligned}$$

(2.14)

Similarly the field equation for the scalar field $\phi$ in the flat ($k=0$) FLRW background can be recast as

$$\begin{aligned} \ddot{\phi }+3H\dot{\phi }+\lambda \phi ^{3}=0. \end{aligned}$$

(2.15)

In the flat ($k=0$) FLRW background we have the following expressions:

$$\begin{aligned} R= & {} 6(\dot{H}+2H^2),\quad \dot{R}=6(\ddot{H}+4H\dot{H}),\nonumber \\ \ddot{R}= & {} 6(\dddot{H}+4\dot{H}^2+4H\ddot{H}). \end{aligned}$$

(2.16)

Substituting these results in Eqs. (2.12) and (2.13) the Friedmann equations can be recast in the Jordan frame as

$$\begin{aligned} 2H(\ddot{H}+3H\dot{H})-\dot{H}^2= & {} \frac{\rho _{\phi }}{18\alpha },\end{aligned}$$

(2.17)

$$\begin{aligned} 9\dot{H}(\dot{H}+H^{2})+6H\ddot{H}+\dddot{H}= & {} -\frac{p_{\phi }}{6\alpha }. \end{aligned}$$

(2.18)

In the slow-roll regime ($\dot{\phi }^2/2\ll \frac{\lambda }{4}\phi ^{4}$) the energy density $\rho _{\phi }$ and the pressure density $p_{\phi }$ can be approximated by $\rho _{\phi }\approx \frac{\lambda }{4}\phi ^{4},~ p_{\phi }\approx -\frac{\lambda }{4}\phi ^{4}$. Consequently Eqs. (2.15), (2.17) and (2.18) can be recast as

$$\begin{aligned} 3H\dot{\phi }+\lambda \phi ^{3}\approx & {} 0,\end{aligned}$$

(2.19)

$$\begin{aligned} 2H(\ddot{H}+3H\dot{H})-\dot{H}^2\approx & {} \frac{V(\phi )}{18\alpha },\end{aligned}$$

(2.20)

$$\begin{aligned} 9\dot{H}(\dot{H}+H^{2})+6H\ddot{H}+\dddot{H}\approx & {} -\frac{V(\phi )}{6\alpha }, \end{aligned}$$

(2.21)

where $V(\phi )=\frac{\lambda }{4}\phi ^4$. Further combining Eqs. (2.20) and (2.21) we get $\dddot{H}= 3\dot{H}(3H^{2}-4\dot{H})$. For further analysis one can also define the following sets of slow-roll parameters in a Jordan frame:

$$\begin{aligned} \epsilon _{H}= & {} -\frac{\dot{H}}{H^{2}},\quad \delta _{H}=-\frac{\ddot{H}}{H^{3}}= \left( \frac{\dot{\epsilon _{H}}}{H}-2\epsilon ^{2}_{H}\right) ,\nonumber \\ \gamma _{H}= & {} -\frac{\dddot{H}}{H^{4}}=3\epsilon _{H}\left( 3+4\epsilon _{H}\right) ,\quad \eta _{H}= -\frac{\ddot{\phi }}{H\dot{\phi }}. \end{aligned}$$

(2.22)

Further using these new sets of parameters in Eqs. (2.20) and (2.21) can be recast into the following simplified form:

$$\begin{aligned} 2\delta _{H}+\frac{\gamma _{H}}{12}+\frac{21}{4}\epsilon _{H}\approx -\frac{V(\phi )}{18\alpha H^{4}}=-\frac{\lambda \phi ^{4}}{72\alpha H^{4}}. \end{aligned}$$

(2.23)

However, solving this two-field problem in the presence of scale free gravity is itself very complicated for the following reasons:

• Complication I: First of all, for a given structure of inflationary potential in a Jordan frame (here it is the Higgsotic potential as mentioned earlier) it is impossible to solve directly the dynamical equations (2.20), (2.21) and (2.23) due its complicated coupled structural form.

• Complication II: One can use various solution Ansatzes to get approximated numerical results, but this is also dependent on the structure of the inflaton potential in a Jordan frame and how one can able to implement initial condition (starting point) of inflation for arbitrary structure of the effective potential.

• Complication III: In connection with the implementation of the initial condition and to check the sufficient condition for inflation in this complicated field theoretical setup one needs to define the expression for number of e-foldings in terms of effective potentials. But this cannot be very easy in the present context as the field equations are coupled.

Due to these huge number of difficulties in a Jordan frame we transform the total action into the Einstein frame using a conformal transformation. After transforming the Jordan frame action into the Einstein frame in the present context we need the solve a two interacting field problem in the presence of Einstein gravity. There are several ways one can solve this problem. These possibilities are:

• Solution I: the first solution to this problem is to follow the well-known approach to solving two-field models of inflation by following the method of curvature and isocurvature perturbation in the semiclassical $\delta \mathcal{N}$ formalism. For more accurate results one can also solve directly the Mukhanov–Sasaki equation for this two-field model and directly treat fluctuations quantum mechanically. Since this methodology has been discussed in various earlier works, we will not discuss this issue in this paper. See Refs. [152,153,154,155,156] fore more details.

• Solution II: a second way of solving this problem is to use dynamical attractor mechanism in the present context where the two fields are connected through specific relations, which can be obtained by solving dynamical field equations in cosmology. This is equivalent to solving renormalization group equations in the context of quantum field theory as the dynamical attractor solution of two fields captures the effects of all the energy scale. In our computation we explore the possibility of two dynamical attractors:

  • 1. Power-law attractor

  • 2. Exponential attractor

  Here they have different cosmological consequences. But they originate from the Higgsotic structure of the effective potential which we will discuss in the next section in detail.

• Solution III: a final possibility is to freeze the dilaton field in the Planck scale or in the vicinity, so that one can absorb it in the effective couplings in the Higgsotic theory. This is identified as the non-attractor phase in the context of cosmology. The physical justification for such possibilities can also be explained from the UV behavior of the 4D effective theory, which is known as the UV completion of the effective theory. According to this proposal we have two sectors in the theory:

  • 1. Hidden sector: the hidden sector is made up of a heavy field (in our case dilaton) which lies around the UV cutoff of the effective theory, which is the Planck scale. We are not able to probe directly this sector. But we can visualize how its imprints on the low energy effective theory.

  • 2. Visible sector: the visible sector is made up of a light field (in our case inflaton) which one can probe directly. For present discussion the visible sector is important to explain the cosmological evolution.

  Usually in such a prescription one integrates the heavy fields and finally gets an effective theory in the visible sector. Here we use the fact that such a procedure mimics the role of freezing the heavy dilaton field near the Planck scale. The only difference is that in the case of freezing the dilaton field we only concentrate on the Higgsotic potential. But the integration of the heavy field allows for all relevant and irrelevant operators. However, by applying a similar argument one can look into only the renormalizable Higgsotic part of the total effective potential. Additionally, it is important to note that at late times the dynamical picture is completely opposite where the inflaton field freezes in the vicinity of the Planck scale and the dynamical contribution for late time acceleration comes from the dilaton field. In a simpler way one can interpret this physical prescription as the competitive dynamical description of the two fields. During inflation the Higgsotic field wins the game and at late times the dilaton serves the same purpose. More precisely, within this prescription dynamic features transfer from dilaton to Higgsotic field (or any scalar inflaton) during inflation and at late times a completely opposite situation appears, where a similar transfer takes place from inflaton to dilaton field.

In this paper we explore the possibility of Solution II and Solution III in detail in the next section. For completeness we briefly review also Solution I in the appendix.

3 Soft attractor: a two-field approach

In the present context let us introduce a scale dependent mode $\Psi$, which can be written in terms of a no scale dilaton mode $\Theta$ as

$$\begin{aligned} \Theta= & {} f^{\prime }(R)M^{-2}_{p}=2\alpha R~M^{-2}_{p}=\mathrm{e}^{\sqrt{\frac{2}{3}}\frac{\Psi }{M_p}} \end{aligned}$$

(3.1)

which mimics the role of a Lagrange multiplier and arises in the Jordan frame without space-time derivatives. In terms of the newly introduced no scale dilaton mode $\Theta$ the total action of the theory (see Eq. (2.1)) can be recast as

$$\begin{aligned} S= & {} \int \mathrm{d}^{4}x \sqrt{-g}\left\{ \frac{M^{2}_{p}}{2}\Theta R-\frac{M^{4}_{p}}{8\alpha }\Theta ^{2}\right. \nonumber \\&\left. -\,\frac{g^{\mu \nu }}{2} (\partial _{\mu }\phi )(\partial _{\nu }\phi )- \frac{\lambda }{4}\phi ^{4}\phantom {\frac{M^{2}_{p}}{2}}\right\} . \end{aligned}$$

(3.2)

To study the behavior of the proposed $R^2$ theory of gravity here we introduce the following conformal transformation (C.T.) in the metric from Jordan frame to the Einstein frame:

$$\begin{aligned}&g_{\mu \nu }\xrightarrow {\mathrm{{C.T.}}}\tilde{g}_{\mu \nu }=\Omega ^{2}g_{\mu \nu }, \quad g^{\mu \nu }\xrightarrow {\mathrm{{C.T.}}}\tilde{g}^{\mu \nu }=\Omega ^{-2}g^{\mu \nu },\nonumber \\&\quad \sqrt{-g}\xrightarrow {\mathrm{{C.T.}}}\sqrt{-\tilde{g}}=\Omega ^{4}\sqrt{-g}, \end{aligned}$$

(3.3)

which satisfies the condition $g_{\mu \nu }g^{\nu \beta }=\tilde{g}_{\mu \kappa }\tilde{g}^{\kappa \beta }=\delta _{\mu }^{\beta }$. In the present context the conformal factor $\Omega$ is given by

$$\begin{aligned} \Omega =\sqrt{\Theta }=\mathrm{e}^{\frac{\sqrt{2}}{2\sqrt{3}}\frac{\Psi }{M_p}}. \end{aligned}$$

(3.4)

With this proposed C.T. in the metric the Ricci curvature scalar in the Jordan frame (R) is related to the Einstein frame ($\tilde{R}$) as

$$\begin{aligned} R=\Omega ^{2}[\tilde{R}+6\widetilde{\Box }\mathrm{ln}~ \Omega -6\tilde{g}^{\mu \nu }\tilde{\partial }_{\mu }\mathrm{ln}~ \Omega ~\tilde{\partial }_{\nu }\mathrm{ln}~\Omega ] \end{aligned}$$

(3.5)

where $\tilde{\partial }_{\mu }= \frac{\partial }{\partial \tilde{x}^{\mu }}$ and $\widetilde{\Box }\mathrm{ln}~ \Omega \equiv \frac{1}{\sqrt{-\tilde{g}}}\partial _{\alpha }(\sqrt{-\tilde{g}} \tilde{g}^{\alpha \beta }\partial _{\beta }\mathrm{ln}~ \Omega )$. After doing C.T. the total action can be recast in the Einstein frame as¹:

$$\begin{aligned} S~~\underrightarrow{\mathrm{{C.T.}}}~~\tilde{S}= & {} \int \mathrm{d}^{4}x \sqrt{-\tilde{g}}\left[ \frac{M^{2}_{p}}{2}\tilde{R}+ \frac{\tilde{g}^{\mu \nu }}{2}\tilde{\partial }_{\mu } \Psi \tilde{\partial }_{\nu }\Psi \right. \nonumber \\&\left. +\,\frac{\tilde{g}^{\mu \nu }}{2}\tilde{\partial }_{\mu } \phi \tilde{\partial }_{\nu }\phi -\tilde{W}(\phi ,\Psi )\phantom {\frac{M^{2}_{p}}{2}}\right] \end{aligned}$$

(3.6)

where after applying C.T. the total potential can be recast as

$$\begin{aligned} \tilde{W}(\phi ,\Psi )=\frac{\frac{M^{4}_{p}}{8\alpha }\mathrm{e}^{2\sqrt{\frac{2}{3}}\frac{\Psi }{M_p}}+\frac{\lambda }{4}\phi ^{4}}{\Omega ^4} =V_0 \left[ 1+\frac{2\alpha \lambda (\Psi )}{M^{4}_{p}}\phi ^{4}\right] \nonumber \\ \end{aligned}$$

(3.8)

where $V_0=M^{4}_{p}/8\alpha$ exactly mimics the role of the cosmological constant and the effective matter coupling ($\lambda (\Psi )$) in the potential sector is given by $\lambda (\Psi )=\frac{\lambda }{\Omega ^4}=\lambda \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}$. Now varying Eq. (3.7) with respect to the metric the field equations can be expressed as

$$\begin{aligned} \tilde{\mathcal{G}}_{\mu \nu }:=\left( \tilde{R}_{\mu \nu }-\frac{\tilde{g}_{\mu \nu }}{2} \tilde{R}\right) =\tilde{T}_{\mu \nu }(\phi ,\Psi ) \end{aligned}$$

(3.9)

where the energy-momentum tensor $\tilde{T}_{\mu \nu }(\phi , \Psi )$ for the dilaton–inflaton coupled theory can be expressed as

$$\begin{aligned} \tilde{T}_{\mu \nu }(\phi ,\Psi )= & {} -\frac{2}{\sqrt{-\tilde{g}}} \frac{\delta \left( \sqrt{-\tilde{g}}\mathcal{L}(\phi ,{\Psi })\right) }{\delta \tilde{g}^{\mu \nu }}\\= & {} \tilde{\partial }_{\mu }\phi \tilde{\partial }_{\nu }\phi +\tilde{\partial }_{\mu }\Psi \tilde{\partial }_{\nu }\Psi -\tilde{g}_{\mu \nu } \left( \frac{1}{2}\tilde{g}^{\alpha \beta } \tilde{\partial }_{\alpha }\phi \tilde{\partial }_{\beta }\phi \nonumber \right. \\&\left. +\,\frac{1}{2}\tilde{g}^{\alpha \beta } \tilde{\partial }_{\alpha }\Psi \tilde{\partial }_{\beta }\Psi +\tilde{W}(\phi ,\Psi )\right) . \end{aligned}$$

Here for the matter part of the action the following property holds between the Einstein frame and Jordan frame energy-momentum tensor: $\tilde{T}_{\mu \nu }(\phi ,\Psi )\supset \tilde{T}_{\mu \nu }=-\frac{2}{\sqrt{-\tilde{g}}}\frac{\delta (\sqrt{-\tilde{g}}\mathcal{L}_{M})}{\delta \tilde{g}^{\mu \nu }} =\frac{T_{\mu \nu }}{\Omega ^{2}}$, which implies that using the perfect fluid assumption one can write $\tilde{T}^{\mu }_{\nu }=\hbox {diag}(-\tilde{\rho }_{\phi }, \tilde{p}_{\phi },\tilde{p}_{\phi },\tilde{p}_{\phi })=\frac{1}{\Omega ^4} \hbox {diag}(-\rho _{\phi },p_{\phi },p_{\phi },p_{\phi })=\frac{T^{\mu }_{\nu }}{\Omega ^4}$. Assuming the flat ($k=0$) FLRW background metric in an Einstein frame the Friedmann equations can be written from Eq. (3.9) as²:

$$\begin{aligned} \tilde{H}^2= & {} \left( \frac{\mathrm{d}\ln a}{\mathrm{d}\tilde{t}}\right) ^{2}=\frac{\tilde{\rho }}{3M^2_p},\end{aligned}$$

(3.10)

$$\begin{aligned} \frac{\mathrm{d}\tilde{H}}{\mathrm{d}\tilde{t}}+\tilde{H}^2= & {} \left( \frac{\mathrm{d}^{2} a}{\mathrm{d}\tilde{t}^{2}}\right) =-\frac{\left( \tilde{\rho } +3\tilde{p}\right) }{6M^{2}_p} \end{aligned}$$

(3.11)

where the effective energy density ($\tilde{\rho }$) and the effective pressure ($\tilde{p}$) can be written in an Einstein frame as

$$\begin{aligned} \tilde{\rho }= & {} \left( \frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}\right) ^2 +\left( \frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}\right) ^2+\tilde{W}(\phi ,\Psi ),\nonumber \\ \tilde{p}= & {} \left( \frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}\right) ^2 +\left( \frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}\right) ^2-\tilde{W}(\phi ,\Psi ). \end{aligned}$$

(3.12)

Additionally, the Hubble parameter in the Einstein frame ($\tilde{H}$) can be expressed as its Jordan frame (H) counterpart as $\tilde{H}=\frac{1}{\Omega }\left[ H+\frac{1}{2}\frac{\mathrm{d}\ln \Omega ^2}{\mathrm{d}t}\right] = \mathrm{e}^{-\frac{1}{\sqrt{6}}\frac{\Psi }{M_p}} \left\{ H+\frac{\dot{\Psi }}{\sqrt{6}M_p}\right\}$. Also the Klein–Gordon field equations for the inflaton field $\phi$ and the new field $\Psi$ can be written in the flat ($k=0$) FLRW background as

$$\begin{aligned}&\frac{\mathrm{d}^{2}\phi }{\mathrm{d}\tilde{t}^{2}}+3\tilde{H}\frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}+ \partial _{\phi }\tilde{W}(\phi ,\Psi )=0\end{aligned}$$

(3.13)

$$\begin{aligned}&\frac{\mathrm{d}^{2}\Psi }{\mathrm{d}\tilde{t}^{2}}+3\tilde{H} \frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}+\partial _{\Psi }\tilde{W}(\phi ,\Psi )=0. \end{aligned}$$

(3.14)

Now in the slow-roll regime the field equations are approximated by

$$\begin{aligned}&3\tilde{H}\frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}+\lambda (\Psi )\phi ^3=0\end{aligned}$$

(3.15)

$$\begin{aligned}&3\tilde{H}\frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}- \frac{\lambda (\Psi )\phi ^4}{\sqrt{6} M_p}=0,\end{aligned}$$

(3.16)

$$\begin{aligned}&\tilde{H}^2=\frac{\tilde{W}(\phi ,\Psi )}{3M^2_p}= \frac{V_0}{3M^2_p}\left[ 1+\frac{2\alpha \lambda (\Psi )}{M^{4}_{p}}\phi ^{4}\right] . \end{aligned}$$

(3.17)

To study the behavior of the proposed model let us consider two cases, where the dynamical features are characterized by

• 1. Case I: power-law solution,

• 2. Case II: exponential solution.

which we discuss in the next subsection.

3.1 Case I: Power-law solution

We consider here large $\alpha$, small $V_0(\approx 0)$ with $\lambda >0$ with effective potential

$$\begin{aligned} \tilde{W}(\phi ,\Psi ) \approx \frac{\lambda (\Psi )}{4}\phi ^{4}=\frac{\lambda }{4}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}\phi ^{4}\quad (\hbox {for Case~I}).\nonumber \\ \end{aligned}$$

(3.18)

Consequently the field equations can be recast as

$$\begin{aligned}&3\tilde{H}\frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}+\lambda \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}\phi ^3=0,\end{aligned}$$

(3.19)

$$\begin{aligned}&3\tilde{H}\frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}-\frac{\lambda \phi ^4}{\sqrt{6} M_p}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}=0,\end{aligned}$$

(3.20)

$$\begin{aligned}&\tilde{H}^2=\frac{\lambda }{12M^2_p}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}\phi ^{4}. \end{aligned}$$

(3.21)

This is the case where the cosmological constant $V_0$ or more precisely the parameter $\alpha$ will not appear in the final solution. The cosmological solutions of Eqs. (3.19)–(3.21) are given by³:

$$\begin{aligned}&\hbox {Case I}\nonumber \\&\Psi -\Psi _0\approx \frac{2\sqrt{2}M_p}{\sqrt{3}} \ln \left( \frac{a}{a_0}\right) =\frac{\sqrt{3}M_p}{\sqrt{2}} \ln \left( \frac{t}{t_0}\right) \nonumber \\&\quad =-\frac{9}{2\sqrt{6}M_p}(\phi ^2-\phi ^2_0),\end{aligned}$$

(3.22)

$$\begin{aligned}&a\approx a_0\left( \frac{t}{t_0}\right) ^{3/4},\end{aligned}$$

(3.23)

$$\begin{aligned}&\mathcal{N}(\phi )-\mathcal{N}(\phi _0)=\frac{1}{M^{2}_{p}}\int ^{\phi }_{\phi _0}\mathrm{d}\phi \frac{\tilde{V}(\phi )}{\partial _{\phi }\tilde{V}(\phi )}=\frac{\phi ^2- \phi ^2_0}{8M^{2}_{p}}\nonumber \\&\quad \approx -\frac{5}{9}\ln \left( \frac{a}{a_0}\right) =-\frac{5}{12}\ln \left( \frac{t}{t_0}\right) . \end{aligned}$$

(3.24)

Fig. 2

Behavior of the inflationary potential for a $V_0\approx 0$ and $\lambda >0$ (Case I) and b $V_0\ne 0$ and $\lambda <0$ (Case II). In a the inflaton rolls down from a large field value and inflation ends at $\phi _{f}\approx 1.09~{ M_p}$. On the other hand in b the inflaton field rolls down from a small field value and the inflation ends at the field value $\phi _{f}=2.88~\alpha ^{1/8}~M_p$, where the lower bound on the parameter $\alpha$ is $\alpha \ge 2.51\times 10^{7}$, which is consistent with Planck 2015 data [44,45,46]

3.2 Case II: Exponential solution

We consider small $\alpha$, large $V_0$ with $\lambda <0$ with effective potential

$$\begin{aligned} \tilde{W}(\phi ,\Psi )\approx & {} \frac{M^{4}_{p}}{8\alpha }+ \frac{\lambda (\Psi )}{4}\phi ^{4}\nonumber \\= & {} \frac{M^{4}_{p}}{8\alpha }-\frac{\lambda }{4}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}\phi ^{4}\quad (\hbox {for Case II}). \end{aligned}$$

(3.25)

Here to avoid any confusion we have taken out the signature of the coupling $\lambda$ outside in the expression for the effective potential for $\lambda <0$ case.

Finally the field equations can be expressed as

$$\begin{aligned}&3\tilde{H}\frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}- \lambda \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}\phi ^3=0\end{aligned}$$

(3.26)

$$\begin{aligned}&3\tilde{H}\frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}+ \frac{\lambda \phi ^4}{\sqrt{6} M_p}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}} \frac{\Psi }{M_p}}=0,\end{aligned}$$

(3.27)

$$\begin{aligned}&\tilde{H}^2=\frac{M^{2}_{p}}{24\alpha }- \frac{\lambda }{12M^2_p}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}} \frac{\Psi }{M_p}}\phi ^{4}. \end{aligned}$$

(3.28)

The cosmological solutions of Eqs. (3.26)–(3.28) are given by

$$\begin{aligned}&\text {Case II}\nonumber \\&\Psi -\Psi _0\approx \frac{2\sqrt{2}M_p}{\sqrt{3}}\ln \left( \frac{a}{a_0}\right) =\frac{M^{2}_{p}}{3\sqrt{\alpha }} (t-t_0)\nonumber \\&\quad =-\frac{1}{2\sqrt{6}M_p}(\phi ^2-\phi ^2_0), \end{aligned}$$

(3.29)

$$\begin{aligned}&a\approx a_0\exp \left[ \frac{M_p}{2\sqrt{6\alpha }}(t-t_0)\right] ,\end{aligned}$$

(3.30)

$$\begin{aligned}&\mathcal{N}(\phi )-\mathcal{N}(\phi _0)=\frac{1}{M^{2}_{p}} \int ^{\phi }_{\phi _0}\mathrm{d}\phi \frac{\tilde{V}(\phi )}{\partial _{\phi }\tilde{V}(\phi )}\nonumber \\&\quad =-\frac{M^2_p}{16\alpha \lambda (\Psi )}\left( \frac{1}{\phi ^2_0}-\frac{1}{\phi ^2}\right) \nonumber \\&\quad =-\frac{M^2_p}{16\alpha \lambda (\Psi )\phi ^2_0} \left[ 1-\frac{1}{1-\frac{8M^2_p}{\phi ^2_0}\ln \left( \frac{a}{a_0}\right) }\right] \nonumber \\&\quad \approx \frac{M^4_p}{2\alpha \lambda (\Psi ) \phi ^4_0}\ln \left( \frac{a}{a_0}\right) \nonumber \\&\quad \approx \frac{M^5_p}{4\alpha ^{3/2}\lambda (\Psi )\sqrt{6} \phi ^4_0}(t-t_0). \end{aligned}$$

(3.31)

This is the specific case where the cosmological constant is explicitly appearing in the potential. To end inflation we need to fulfill an extra requirement that $\lambda <0$ and this will finally led to massless tachyonic solution. In Fig. 2a, b we have shown the behavior of the inflationary potential for the two cases, 1. $V_0\approx 0$ and $\lambda >0$, 2. $V_0\ne 0$ and $\lambda <0$.

Figure 2a implies that the inflaton rolls down from a large field value and inflation ends at $\phi _{f}\approx 1.09~{ M_p}$. Also the potential has a global minimum at $\phi =0$, around which field is start to oscillate and take part in reheating. On the other hand in Fig. 2b the inflaton field rolls down from a small field value and the inflation ends at the field value $\phi _{f}=2.88~\alpha ^{1/8}~M_p$, where the lower bound on the parameter $\alpha$ is, $\alpha \ge 2.51\times 10^{7}$, which is consistent with Planck 2015 data [44,45,46]. Within this prescription it is possible to completely destroy the effect of cosmological constant at the end of inflationary epoch. But within this setup to explain the particle production during reheating and also explain the late time acceleration of our universe we need additional features in the total effective potential in scale free $\alpha R^2$ gravity theory. It is a general notion that the reheating phenomenon can only be explained if the effective potential has a local minimum and a remnant contribution (vacuum energy or equivalent to cosmological constant) in the total effective potential finally produce the observed energy density at the present epoch as given by⁴ $\rho _{\mathrm{now}}\approx 10^{-47}~\mathrm{GeV}^{4}$, which is necessarily required to explain the late time acceleration of the universe. Now here one can ask a very relevant question: if we include some additional features to the effective Higgsotic potential, which also can be treated as a massless tachyonic potential, then how one can interpret the justifiability as well as the behavior of effective field theory framework around the minimum of the potential which will significantly control the dynamical behavior in the context of cosmology? The most probable answer to this very significant question can be described in various ways. In the present context to get a stable minimum (vacuum) of the derived effective Higgsotic potential in an Einstein frame here we discuss a few physical possibilities:

• Choice I: The first possible solution of the mentioned problem is motivated from non-BPS D-brane in superstring theory. In this prescription the effective potential have a pair of global extrima at the field value, $\phi _{\mathrm{extrema}}=\phi =\pm \phi _{V}$ for the non-BPS D-brane within the framework of superstring theory [23, 135,136,137,138,139,140]. Additionally, it is important to note that here a one parameter $(\gamma )$ family of global extrima exists at the field value, $\phi =\phi _{V}~\mathrm{e}^{i\gamma }$ for the brane–antibrane system. Here $\phi _{V}$ is identified to be the field value where the reheating phenomenon occurs. At this specified field value of the minimum the brane tension of the D-brane configuration which is exactly canceled by the negative contribution as appearing in the expression for effective potential in an Einstein frame. Here for the sake of simplicity we relax a little bit the constraints as appearing exactly in Case II. To explore the behavior of the derived effective potential here we have allowed both of the signatures of the coupling parameter $\lambda$. This directly implies the following constraint condition:

  $$\begin{aligned} -\frac{\lambda }{4}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}} \frac{\Psi }{M_p}}\phi ^{4}_{V}+\varvec{\Theta }_{p}= & {} 0\quad (\hbox {for }\lambda <0),\end{aligned}$$

  (3.32)
  $$\begin{aligned} \frac{\lambda }{4}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}} \frac{\Psi }{M_p}}\phi ^{4}_{V}+\varvec{\Theta }_{p}= & {} 0 \quad (\hbox {for }\lambda >0), \end{aligned}$$

  (3.33)

  where $\varvec{\Theta }_{p}$ is the above mentioned additional contribution and in the context of superstring theory this is given by

  $$\begin{aligned} \varvec{\Theta }_{p}=\left\{ \begin{array}{ll} \sqrt{2}(2\pi )^{-p}g^{-1}_{\mathrm{s}} &{} \text {for non-BPS Dp-brane},\\ 2(2\pi )^{-p}g^{-1}_{\mathrm{s}} &{} \text {for non-BPS Dp}{-}\bar{D}\text {p brane pair}, \end{array} \right. \nonumber \\ \end{aligned}$$

  (3.34)

  with string coupling constant $g_{\mathrm{s}}$. This implies that the inflaton energy density vanishes at the minimum of the tachyon type of the derived effective potential and in this connection the remnant energy contribution is given by $V_0=M^4_{p}/8\alpha$, which serves the explicit role of cosmological constant in the context of late time acceleration of the universe. In this case considering the additional contribution as mentioned above the total effective potential can be modified as

  $$\begin{aligned}&\hbox {v}1{:}\ \tilde{W}(\phi ,\Psi )=\frac{M^{4}_{p}}{8\alpha }- \frac{\lambda }{4}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}} \frac{\Psi }{M_p}}(\phi ^4-\phi ^{4}_{V})\nonumber \\&\qquad (\text {for }\lambda <0),\end{aligned}$$

  (3.35)
  $$\begin{aligned}&\hbox {v}2{:}\ \tilde{W}(\phi ,\Psi )=\frac{M^{4}_{p}}{8\alpha }+ \frac{\lambda }{4}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}} \frac{\Psi }{M_p}}(\phi ^4-\phi ^{4}_{V})\nonumber \\&\qquad (\text {for }\lambda >0). \end{aligned}$$

  (3.36)

  Here to avoid any confusion we have taken out the signature of the coupling $\lambda$ outside in the expression for the effective potential for the $\lambda <0$ case. In the present context the field equations can be expressed as

  $$\begin{aligned} \text {For v1:}\&3\tilde{H}\frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}- \lambda \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}\phi ^3=0,\end{aligned}$$

  (3.37)
  $$\begin{aligned}&3\tilde{H}\frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}+ \frac{\lambda (\phi ^4-\phi ^4_V)}{\sqrt{6}M_p} \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}=0,\end{aligned}$$

  (3.38)
  $$\begin{aligned}&\tilde{H}^2=\frac{M^{2}_{p}}{24\alpha }- \frac{\lambda }{12M^2_p}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}} \frac{\Psi }{M_p}}(\phi ^4-\phi ^{4}_{V}).\nonumber \\ \end{aligned}$$

  (3.39)
  $$\begin{aligned} \text {For v2:}\&3\tilde{H}\frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}+\lambda \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}\phi ^3=0,\end{aligned}$$

  (3.40)
  $$\begin{aligned}&3\tilde{H}\frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}- \frac{\lambda (\phi ^4-\phi ^4_V)}{\sqrt{6} M_p}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}=0,\end{aligned}$$

  (3.41)
  $$\begin{aligned}&\tilde{H}^2=\frac{M^{2}_{p}}{24\alpha }+ \frac{\lambda }{12M^2_p}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}} \frac{\Psi }{M_p}}(\phi ^4-\phi ^{4}_{V}).\nonumber \\ \end{aligned}$$

  (3.42)

  The solutions of Eqs. (3.37)–(3.42) are given by

  $$\begin{aligned}&\text {Choice~I(v1)} \nonumber \\&\Psi -\Psi _0\approx \frac{2\sqrt{2}M_p}{\sqrt{3}}\ln \left( \frac{a}{a_0}\right) =\frac{M^{2}_{p}}{3\sqrt{\alpha }}(t-t_0)\nonumber \\&\quad =-\frac{1}{2\sqrt{6}M_p}\left[ (\phi ^2 -\phi ^2_0) +\phi ^4_V\left( \frac{1}{\phi ^2}-\frac{1}{\phi ^2_0}\right) \right] ,\end{aligned}$$

  (3.43)
  $$\begin{aligned}&a\approx a_0\exp \left[ \frac{M_p}{2\sqrt{6\alpha }} (t-t_0)\right] ,\end{aligned}$$

  (3.44)
  $$\begin{aligned}&\mathcal{N}(\phi )-\mathcal{N}(\phi _0)= \frac{1}{M^{2}_{p}}\int ^{\phi }_{\phi _0}\mathrm{d}\phi \frac{\tilde{V}(\phi )}{\partial _{\phi }\tilde{V}(\phi )}\nonumber \\&\quad \approx -\left( \frac{M^2_{p}}{16\alpha \lambda (\Psi )}+ \frac{\phi ^4_{V}}{8M^2_p}\right) \left( \frac{1}{\phi ^2_0}- \frac{1}{\phi ^2}\right) \nonumber \\&\quad \approx \left( \frac{M^4_{p}}{2\alpha \lambda (\Psi )}+ \frac{\phi ^4_{V}}{\phi ^2_0}\right) \ln \left( \frac{a}{a_0}\right) , \end{aligned}$$

  (3.45)
  $$\begin{aligned}&{\text {Choice~I(v2)}}\nonumber \\&\Psi -\Psi _0\approx \frac{2\sqrt{2}M_p}{\sqrt{3}} \ln \left( \frac{a}{a_0}\right) =\frac{M^{2}_{p}}{3\sqrt{\alpha }} (t-t_0)\nonumber \\&\quad =-\frac{1}{2\sqrt{6}M_p}\left[ (\phi ^2-\phi ^2_0)+ \phi ^4_V\left( \frac{1}{\phi ^2}-\frac{1}{\phi ^2_0}\right) \right] , \end{aligned}$$

  (3.46)
  $$\begin{aligned}&a\approx a_0~\exp \left[ \frac{M_p}{2\sqrt{6\alpha }} (t-t_0)\right] ,\end{aligned}$$

  (3.47)
  $$\begin{aligned}&\mathcal{N}(\phi )-\mathcal{N}(\phi _0)= \frac{1}{M^{2}_{p}}\int ^{\phi }_{\phi _0}\mathrm{d}\phi \frac{\tilde{V}(\phi )}{\partial _{\phi }\tilde{V}(\phi )}\nonumber \\&\quad \approx \left( \frac{M^2_{p}}{16\alpha \lambda (\Psi )}- \frac{\phi ^4_{V}}{8M^2_p}\right) \left( \frac{1}{\phi ^2_0}- \frac{1}{\phi ^2}\right) \nonumber \\&\quad \approx \left( \frac{M^4_{p}}{2\alpha \lambda (\Psi )}- \frac{\phi ^4_{V}}{\phi ^2_0}\right) \ln \left( \frac{a}{a_0}\right) . \end{aligned}$$

  (3.48)

  In Fig. 3a, b we have shown the variation of the potential with respect to the inflaton field for both cases. For Fig. 3a the inflaton can roll down in both ways. Firstly, it can roll down to a global minimum at the field value $\phi _{V}=0$ from higher to lower field value and take part in particle production procedure during reheating. On the other hand, in the same picture the inflaton can also roll down from higher to lower field value in an opposite fashion. In that case the inflaton goes up to the zero energy level of the effective potential and cannot explain the thermal history of the early universe in a proper sense. It is also important to note that in this picture the position of the maximum of the effective potential in the Einstein frame is around the field value, $\phi _{V}=0.42~M_p$. Figure 3b is the case where the signature of the coupling $\lambda$ is positive. Also the behavior of the effective potential is completely opposite compared to the situation arising in Fig. 3a. In this case the inflaton field can be able to roll down to higher to lower field value or lower to higher field value. But in both cases the inflaton field settles down to a local minimum at, $\phi _{\mathrm{min}}=\phi _{V}=0.42~M_p$ and within the vicinity of this point it will produce particles via reheating. In the two situations the lower bound on the parameter $\alpha$ is fixed at, $\alpha \ge 2.51\times 10^{7}$, which is perfectly consistent with Planck 2015 data [44,45,46].

• Choice II: It is possible to explain the reheating as well as the light time cosmic acceleration once we switch on the effect of mass like quadratic term in the effective potential. In such a case the modified effective potential in an Einstein frame can be written as

  $$\begin{aligned} \text {v1:}\quad \tilde{W}(\phi ,\Psi )= & {} \frac{M^{4}_{p}}{8\alpha }+\left( \frac{m^{2}_{c}}{2} \phi ^2-\frac{\lambda }{4}\phi ^{4}\right) \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}\nonumber \\&\quad (\text {for } m^{2}_{c}>0,\lambda <0),\end{aligned}$$

  (3.49)
  $$\begin{aligned} \text {v2:}\quad \tilde{W}(\phi ,\Psi )= & {} \frac{M^{4}_{p}}{8\alpha }- \left( \frac{m^{2}_{c}}{2}\phi ^2-\frac{\lambda }{4}\phi ^{4}\right) \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}\nonumber \\&\quad (\text {for } m^{2}_{c}<0,\lambda >0). \end{aligned}$$

  (3.50)

  Here to avoid any confusion we have taken out the signature of the coupling $\lambda$ outside in the expression for the effective potential for $\lambda <0$ case. In this context during inflation the inflaton field satisfies the constraint $\phi \gg \sqrt{\frac{2}{|\lambda |}}|m_{c}|$. After inflation when reheating starts, the field satisfies $\phi \ll \sqrt{\frac{2}{|\lambda |}}|m_{c}|$. Finally at the field value $\phi =\sqrt{\frac{2}{|\lambda |}}|m_{c}|$ the remnant energy $V_0=M^4_{p}/8\alpha$ serves the purpose of explaining the late time acceleration of the universe. In the present context the field equations can be expressed as

  $$\begin{aligned} \text {For v1:}\&3\tilde{H}\frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}} +(m^{2}_{c}\phi -\lambda \phi ^{3})\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}} \frac{\Psi }{M_p}}=0,\end{aligned}$$

  (3.51)
  $$\begin{aligned}&3\tilde{H}\frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}- \frac{2\sqrt{2}\left( \frac{m^{2}_{c}}{2}\phi ^2-\frac{\lambda }{4} \phi ^{4}\right) }{\sqrt{3} M_p}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}} \frac{\Psi }{M_p}}=0,\end{aligned}$$

  (3.52)
  $$\begin{aligned}&\tilde{H}^2=\frac{M^{2}_{p}}{24\alpha }+ \frac{\left( \frac{m^{2}_{c}}{2}\phi ^2-\frac{\lambda }{4}\phi ^{4}\right) }{3M^2_p}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}. \end{aligned}$$

  (3.53)
  $$\begin{aligned} \text {For v2:}\&3\tilde{H}\frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}-(m^{2}_{c}\phi - \lambda \phi ^{3})\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}=0,\end{aligned}$$

  (3.54)
  $$\begin{aligned}&3\tilde{H}\frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}+ \frac{2\sqrt{2}\left( \frac{m^{2}_{c}}{2}\phi ^2- \frac{\lambda }{4}\phi ^{4}\right) }{\sqrt{3} M_p} \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}=0,\end{aligned}$$

  (3.55)
  $$\begin{aligned}&\tilde{H}^2=\frac{M^{2}_{p}}{24\alpha }- \frac{\left( \frac{m^{2}_{c}}{2}\phi ^2-\frac{\lambda }{4}\phi ^{4}\right) }{3M^2_p}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}.\nonumber \\ \end{aligned}$$

  (3.56)

  The solutions of Eqs. (3.51)–(3.56) are given by

  $$\begin{aligned}&{\text {Choice~II(v1)}} \nonumber \\&\Psi -\Psi _0\approx \frac{2\sqrt{2}M_p}{\sqrt{3}}\ln \left( \frac{a}{a_0}\right) =\frac{M^{2}_{p}}{3\sqrt{\alpha }}(t-t_0)\nonumber \\&\quad =-\frac{1}{2\sqrt{6}M_p}\left[ (\phi ^2 -\phi ^2_0) +\frac{m^{2}_{c}}{\lambda }\ln \left( \frac{m^2_{c}-\lambda \phi ^{2}}{m^2_{c}-\lambda \phi ^{2}_0}\right) \right] ,\nonumber \\ \end{aligned}$$

  (3.57)
  $$\begin{aligned}&a\approx a_0~\exp \left[ \frac{M_p}{2\sqrt{6\alpha }}(t-t_0)\right] ,\end{aligned}$$

  (3.58)
  $$\begin{aligned}&\mathcal{N}(\phi )-\mathcal{N}(\phi _0)=\frac{M^4_p}{16m^{2}_{c}(\Psi )\alpha } \ln \left( \frac{\phi ^2(m^2_{c}-\lambda \phi ^2_0)}{\phi ^2_0(m^2_{c}-\lambda \phi ^2)}\right) \nonumber \\&\quad \approx \frac{M^4_p}{16m^{2}_{c}(\Psi )\alpha } \ln \left( \frac{\left[ 1-\frac{8M^2_p}{\phi ^2_0}\ln \left( \frac{a}{a_0}\right) \right] (m^2_{c}-\lambda \phi ^2_0)}{\left( m^2_{c}-\lambda \phi ^2_0 \left[ 1-\frac{8M^2_p}{\phi ^2_0}\ln \left( \frac{a}{a_0}\right) \right] \right) }\right) ,\nonumber \\ \end{aligned}$$

  (3.59)
  $$\begin{aligned}&{\text {Choice~II(v2)}}\nonumber \\&\Psi -\Psi _0\approx \frac{2\sqrt{2}M_p}{\sqrt{3}}\ln \left( \frac{a}{a_0}\right) =\frac{M^{2}_{p}}{3\sqrt{\alpha }}(t-t_0)\nonumber \\&\quad =-\frac{1}{2\sqrt{6}M_p}\left[ (\phi ^2 -\phi ^2_0)+ \frac{m^{2}_{c}}{\lambda }\ln \left( \frac{m^2_{c}-\lambda \phi ^{2}}{m^2_{c}-\lambda \phi ^{2}_0}\right) \right] ,\nonumber \\ \end{aligned}$$

  (3.60)
  $$\begin{aligned}&a\approx a_0~\exp \left[ \frac{M_p}{2\sqrt{6\alpha }}(t-t_0)\right] ,\end{aligned}$$

  (3.61)
  $$\begin{aligned}&\mathcal{N}(\phi )-\mathcal{N}(\phi _0)=\frac{M^4_p}{16m^{2}_{c}(\Psi )\alpha } \ln \left( \frac{\phi ^2_0(m^2_{c}-\lambda \phi ^2)}{\phi ^2(m^2_{c}-\lambda \phi ^2_0)}\right) \nonumber \\&\quad \approx \frac{M^4_p}{16m^{2}_{c}(\Psi )\alpha }\ln \left( \frac{\left( m^2_{c}-\lambda \phi ^2_0 \left[ 1-\frac{8M^2_p}{\phi ^2_0}\ln \left( \frac{a}{a_0}\right) \right] \right) }{\left[ 1-\frac{8M^2_p}{\phi ^2_0}\ln \left( \frac{a}{a_0}\right) \right] (m^2_{c}-\lambda \phi ^2_0)}\right) ,\nonumber \\ \end{aligned}$$

  (3.62)

  The behavior of the effective potential in an Einstein frame is plotted in Fig. 4a, b, where the inflaton field is rolling down from a large field to lower value or the lower to larger field value and after inflation take part in particle production and reheating. Here the two situations both are completely equivalent to the previous choice of the effective potentials as discussed earlier. Here the only difference is the scale of inflation, which is surely different compared to the previously mentioned scientific scenario. Additionally, it is noted that for both cases the effective potential can be able to generate VEV at the field value $\phi =2.5~M_p$, which will finally take part to explain the particle production and reheating mechanism. In both of the situations the lower bound on the parameter $\alpha$ of the scale free gravity is fixed at, $\alpha \ge 2.51\times 10^{7}$, which is perfectly consistent with Planck 2015 data and other available joint constraints [44,45,46].

• Choice III: In third option it is also possible to explain the reheating as well as the late time cosmic acceleration once we switch on the effect of non-minimal coupling between, $f(R)=\alpha R^2$ gravity sector and the matter field sector. In that case the total effective action is modified in a Jordan frame as

  $$\begin{aligned} S= & {} \int \mathrm{d}^{4}x\sqrt{-g}\left[ \frac{\alpha }{2} (1+\xi \phi ^2)R^2+\frac{g^{\mu \nu }}{2} (\partial _{\mu }\phi )(\partial _{\nu }\phi )\right. \nonumber \\&\left. -\,\frac{\lambda }{4}(\phi ^2-\phi ^2_{V})^2\right] \end{aligned}$$

  (3.63)

  where $\xi$ represents the non-minimal coupling parameter and $\phi _{V}$ represents the VEV of the field $\phi$ in this context. After performing conformal transformation, the effective action in the Einstein frame can be written as

  $$\begin{aligned} S ~~\underrightarrow{\mathrm{C.T.}}~~\tilde{S}= & {} \int \mathrm{d}^{4}x \sqrt{-\tilde{g}}\left[ \frac{M^{2}_{p}}{2}\tilde{R}+ \frac{\tilde{g}^{\mu \nu }}{2}\tilde{\partial }_{\mu }\Psi \tilde{\partial }_{\nu }\Psi \right. \nonumber \\&\left. +\,\frac{\tilde{g}^{\mu \nu }}{2}\tilde{\partial }_{\mu }\phi \tilde{\partial }_{\nu }\phi -\tilde{W}(\phi ,\Psi )\right] \end{aligned}$$

  (3.64)

  where after applying C.T. the total modified effective action can be written as

  $$\begin{aligned} \tilde{W}(\phi ,\Psi )=\frac{M^{4}_{p}}{8\alpha }+\frac{\frac{\lambda }{4}(\phi ^2 -\phi ^2_{V})^2}{(1+\xi \phi ^2)^2} \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}. \end{aligned}$$

  (3.65)

  In the present context the field equations can be expressed as

  $$\begin{aligned}&3\tilde{H}\frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}+\frac{\lambda \phi (1+\xi \phi ^2_{V})(\phi ^2-\phi ^2_{V})}{(1+\xi \phi ^2)^3} \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}=0,\end{aligned}$$

  (3.66)
  $$\begin{aligned}&3\tilde{H}\frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}- \frac{\lambda (\phi ^2-\phi ^2_{V})^2}{\sqrt{6} M_p(1+\xi \phi ^2)^2} \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}=0,\end{aligned}$$

  (3.67)
  $$\begin{aligned}&\tilde{H}^2=\frac{M^{2}_{p}}{24\alpha }+ \frac{\frac{\lambda }{4}(\phi ^2-\phi ^2_{V})^2}{3M^2_p(1+\xi \phi ^2)^2}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}. \end{aligned}$$

  (3.68)

  The solutions of Eqs. (3.66)–(3.68) are given by:

  $$\begin{aligned}&{\text {Choice~III}}\nonumber \\&\Psi -\Psi _0\approx \frac{2\sqrt{2}M_p}{\sqrt{3}}\ln \left( \frac{a}{a_0}\right) =\frac{M^{2}_{p}}{3\sqrt{\alpha }}(t-t_0)\nonumber \\&\quad =-\frac{1}{2\sqrt{6}M_p}\frac{\left[ (\phi ^2-\phi ^2_0)\left( 1+\frac{\xi }{2} \left( \phi ^2 +\phi ^2_0 -2\phi ^2_{V}\right) \right) +2\phi ^2_{V}\ln \left( \frac{\phi }{\phi _0}\right) \right] }{\left( 1+\xi \phi ^2_{V}\right) },\nonumber \\ \end{aligned}$$

  (3.69)
  $$\begin{aligned}&a\approx a_0~\exp \left[ \frac{M_p}{2\sqrt{6\alpha }}(t-t_0)\right] ,\end{aligned}$$

  (3.70)
  $$\begin{aligned}&\mathcal{N}(\phi )-\mathcal{N}(\phi _0)=\frac{1}{M^{2}_{p}}\int ^{\phi }_{\phi _0}\mathrm{d}\phi \frac{\tilde{V}(\phi )}{\partial _{\phi }\tilde{V}(\phi )}\nonumber \\&\quad =\frac{M^2_p}{16\phi ^2_{V}\alpha \lambda (\Psi )(1+\xi \phi ^2_{V})} \ln \left( \frac{\phi ^2_{0}(\phi ^{2}-\phi ^{2}_{V})}{\phi ^2(\phi ^{2}_{0}-\phi ^{2}_{V})}\right) \nonumber \\&\quad =\frac{M^2_p}{16\phi ^2_{V}\alpha \lambda (\Psi )(1+\xi \phi ^2_{V})}\nonumber \\&\qquad \times \ln \left( \frac{\left( \phi ^2_0 \left[ 1-\frac{8M^2_p}{\phi ^2_0} \ln \left( \frac{a}{a_0}\right) \right] -\phi ^{2}_{V}\right) }{ \left[ 1-\frac{8M^2_p}{\phi ^2_0}\ln \left( \frac{a}{a_0}\right) \right] \left( \phi ^{2}_{0}-\phi ^{2}_{V}\right) }\right) , \end{aligned}$$

  (3.71)

  In Fig. 5, we have shown the behavior of the effective potential with respect to inflaton field in the presence of non-minimal coupling parameter, $\xi =M^{-2}_{p}$ and $\xi =10^{-8}~M^{-2}_{p}$ depicted by red and blue colored curves, respectively. For both of the cases we have taken the self interacting coupling parameter $\lambda >0$. Also it is important to mention here that if we decrease the strength of the non-minimal coupling parameter then the effective potential becomes steeper. For both situations the inflaton field can roll down from higher to lower or lower to higher field values and finally settle down to a local minimum at $\phi _{V}=M_p$.

Fig. 3

Behavior of the modified effective potential for case II with a Choice I(v1): $V_0\ne 0$, $\lambda <0$, b Choice I(v2): $V_0\ne 0$, $\lambda >0$, where $M_p=2.43\times 10^{18}~\hbox {GeV}$

Fig. 4

Behavior of the modified effective potential for case II with a Choice II(v1): $V_0\ne 0$, $\lambda <0$, $m^{2}_{c}>0$ and $\phi \ll \sqrt{\frac{2}{|\lambda |}}|m_{c}|$, b Choice II(v2): $V_0\ne 0$, $\lambda >0$, $m^{2}_{c}<0$ and $\phi \ll \sqrt{\frac{2}{|\lambda |}}|m_{c}|$, where $M_p=2.43\times 10^{18}~\hbox {GeV}$

Fig. 5

Behavior of the modified effective potential in presence of non-minimal coupling in $R^2$ gravity for case II with Choice III: $V_0\ne 0$, $\lambda >0$, $\xi =M^{-2}_{p}$ (red), $10^{-8}~M^{-2}_{p}$ (blue), where $M_p=2.43\times 10^{18}~\hbox {GeV}$

4 Constraints on inflation with soft attractors

Here we require the following constraints to study the inflationary paradigm in the attractor regime:

4.1 Number of e-foldings

To get a sufficient amount of inflation from the proposed setup (for both Case I and Case II), necessarily

$$\begin{aligned} |\mathcal{N}(\phi _0)-\mathcal{N}(\phi _f)|\approx \left| \ln \left( \frac{a_f}{a_0}\right) \right| \gtrsim 50-70. \end{aligned}$$

(4.1)

which is a necessary quantity to be able to solve the horizon problem associated with standard big-bang cosmology. The subscripts ‘f’ and ‘0’ physically signify the final and initial values of the inflationary epoch. Further using Eqs. (3.24) and (3.31) the field value at the end of inflation can be explicitly computed for the above mentioned two cases as

$$\begin{aligned} \begin{array}{lll} \phi _f \sim \left\{ \begin{array}{ll} \phi _{0} \left[ 1-\frac{480M^{2}_{p}}{\phi ^{2}_{0}}\right] ^{1/2} &{} \quad \text {for Case I}\\ \frac{\phi _0}{\left[ 1+\frac{960\alpha \lambda (\Psi _f)\phi ^2_0}{M^{2}_p}\right] ^{1/2}} &{}\quad \text {for Case II}. \end{array} \right. \end{array} \end{aligned}$$

(4.2)

Here it is important to mention the following facts:

• For Case I the expression for the field associated with the end of inflation $\phi _{f}$ is completely fixed by the value initial field value $\phi _0$. Here no information for the field dependent coupling $\lambda (\psi _f)=\lambda (\Psi =\Psi _f)$ is required for this case as the expression for $\phi _f$ is independent of the dilaton field dependent coupling.

• For Case II the expression for the field associated with the end of inflation $\phi _{f}$ is fixed by the value initial field value $\phi _0$ as well as by the field dependent coupling $\lambda (\psi _f)=\lambda (\Psi =\Psi _f)$.

4.2 Primordial density perturbation

4.2.1 Two point function

The next observational constraint comes from the imprints of density perturbations through scalar fluctuations. Such fluctuations in CMB map directly implies that⁵:

$$\begin{aligned} \frac{\delta \rho }{\rho }<\left( \frac{\delta \rho }{\rho }\right) _{\mathrm{cr}}=\sqrt{A_\mathrm{S}}\sim 10^{-5} \end{aligned}$$

(4.3)

measured on the horizon crossing scales, where $\delta \rho$ is the perturbation in the density $\rho$. Additionally, it is important to note that $A_\mathrm{S}$, represents the amplitude of the scalar power spectrum. Also in the present context for both cases one can write

$$\begin{aligned} \left[ \sigma \frac{\delta \rho }{\rho }\right] _{t_1}= \left[ \sigma \frac{\delta \rho }{\rho }\right] _{t_2} \end{aligned}$$

(4.4)

where the parameter $\sigma$ is the parameter in the present context, which can be expressed in terms of equation parameter as, $\sigma = 1+\frac{2}{3(1+w)},~ w=\frac{p}{\rho }$. It is important to note that $(t_{1},t_{2})$ represent the times when the perturbation first left and re-entered the horizon, respectively. At time $t_{1}$, Eq. (3.12) perfectly hold good in the present context. On the other hand at time $t=t_2$ the representative parameter $\sigma$ take the value, $\sigma =3/2$ and $\sigma =5/3$ during the radiation- and matter-dominated epochs, respectively. For the potential dominated inflationary epoch, $w\approx -1$ and consequently one can write the following constraint condition:

$$\begin{aligned} \left( \frac{\delta \rho }{\rho }\right) _{t_{2}}\approx \left( \left( 1-\frac{1}{\sigma }\right) \frac{\delta \rho }{\rho }\right) _{t_{1}}. \end{aligned}$$

(4.5)

Further using Eq. (3.12) and approximated equation of motion in slow-roll regime of fluctuation in the total energy density or equivalently in the scalar modes can be written as

$$\begin{aligned} \delta \rho= & {} \dot{\phi }\delta {\dot{\phi }}+\dot{\Psi }\delta {\dot{\Psi }} -3\tilde{H}\left( \dot{\phi }\delta {\phi }+\dot{\Psi }\delta {\Psi }\right) \nonumber \\\approx & {} -2\tilde{H}\left( \dot{\phi }\delta {\phi }+\dot{\Psi }\delta {\Psi }\right) . \end{aligned}$$

(4.6)

where we use the symbol as $\dot{~}~\equiv \mathrm{d}/\mathrm{d}\tilde{t}$ and one can write down, $\delta \dot{\phi }\approx \tilde{H}\delta \phi$, $\delta \dot{\Psi }\approx \tilde{H}\delta \Psi$, $\delta \phi \approx \tilde{H}$, $\delta \Psi \approx \tilde{H}$, and finally the fractional density contrast can be expressed as

$$\begin{aligned} \left( \frac{\delta \rho }{\rho }\right) _{t_{2}}= \left( \frac{\tilde{H}^2 (|\dot{\phi }|+|\dot{\Psi }|)}{\dot{\phi }^2 +\dot{\Psi }^2}\mathcal{C}\right) _{t_{1}} \end{aligned}$$

(4.7)

with the following constraint on the parameter $\mathcal{C}$ as given by, $\mathcal{C}\sim \mathcal{O}(1)$ and it serves the purpose of a normalization constant in this context. Then we get the two physically acceptable situations for both of the cases which can be written as

$$\begin{aligned}&{\text {Region~I}}{:}\quad |\dot{\phi }|<|\dot{\Psi }|\Rightarrow \frac{\delta \rho }{\rho }\approx \frac{\tilde{H}^2}{|\dot{\Psi }|}\approx \frac{\sqrt{\tilde{W}_\mathrm{h}}}{2\sqrt{2}M^2_p},\end{aligned}$$

(4.8)

$$\begin{aligned}&{\text {Region~II}}{:}\quad |\dot{\phi }|>|\dot{\Psi }|\Rightarrow \frac{\delta \rho }{\rho }\approx \frac{\tilde{H}^2}{|\dot{\phi }|}\approx \frac{\tilde{W}^{3/2}_\mathrm{h}}{M^3_p(\partial _{\phi }\tilde{W})_\mathrm{h}}.\nonumber \\ \end{aligned}$$

(4.9)

Here one can interpret the results as

• In Region I, the amplitude of the density fluctuation at the horizon crossing is only controlled by the scale of inflation and the magnitude of the dilaton dependent effective coupling parameter $\lambda (\Phi _\mathrm{h})$.

• In Region II, the amplitude of the density fluctuation at the horizon crossing is given by

  $$\begin{aligned} \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~II}}}= \frac{2}{\left( \sqrt{\epsilon _{\tilde{W}}}\right) _\mathrm{h}}\left( \frac{\delta \rho }{\rho }\right) _{{\mathrm{{Region~I}}}}. \end{aligned}$$

  (4.10)

  This implies that contribution from the first slow-roll parameter, as given by $\epsilon _{\tilde{W}}=\frac{M^2_p}{2} \left( \frac{\partial _{\phi }\tilde{W}}{\tilde{W}}\right)$, controls the magnitude of the amplitude of density perturbation apart from the effect from the scale of inflation and the magnitude of the dilaton dependent effective coupling parameter $\lambda (\Phi _\mathrm{h})$.

4.2.2 Present observables

Further using the approximate equations of motion the fractional density contrast for the above mentioned two cases can be written as

$$\begin{aligned}&{\text {Case~I}}{:}\ \frac{\delta \rho }{\rho } \sim \left\{ \begin{array}{ll} \frac{\phi ^2_0}{4M^2_p}\sqrt{\frac{\lambda (\Psi _\mathrm{h})}{2}} \left[ 1-\frac{2\sqrt{6}M_p}{9\phi ^2_0}(\Psi _\mathrm{h} - \Psi _0)\right] &{}\quad \text {for Region I}\\ \frac{\phi ^3_0\sqrt{\lambda (\Psi _\mathrm{h})}}{8M^3_p} \left[ 1-\frac{2\sqrt{6}M_p}{9\phi ^2_0}(\Psi _\mathrm{h} - \Psi _0)\right] ^{3/2} &{}\quad \text {for Region II}. \end{array} \right. \end{aligned}$$

(4.11)

$$\begin{aligned}&{\text {Case~II}}{:}\ \frac{\delta \rho }{\rho } \sim \left\{ \begin{array}{ll} \frac{1}{8\sqrt{\alpha }}\left[ 1+\frac{2\phi ^2_0\alpha \lambda (\Psi _\mathrm{h})}{M^4_p}\left\{ 1-\frac{2\sqrt{6}M_p}{\phi ^2_0}(\Psi _\mathrm{h}-\Psi _0) \right\} ^2\right] ^{1/2}&{}\quad \text {for Region I}\\ \frac{M^3_p}{\lambda (\Psi _\mathrm{h})(8\alpha )^{3/2}\phi ^3_0 \left[ 1-\frac{2\sqrt{6}M_p}{\phi ^2_0}(\Psi _\mathrm{h} -\Psi _0)\right] ^{3/2}} &{}\quad \text {for Region II}. \end{array} \right. \end{aligned}$$

(4.12)

Here one can interpret the results as

• In Region I and Region II of Case I, the amplitudes of the density fluctuation at the horizon crossing are related by

  $$\begin{aligned}&\left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~II}}} =\frac{\phi _0}{\sqrt{2}M_p}\left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~I}}}\nonumber \\&\qquad \times \left[ 1-\frac{2\sqrt{6}M_p}{9\phi ^2_0}(\Psi _\mathrm{h} - \Psi _0)\right] ^{1/2}\nonumber \\&\quad \approx \frac{\phi _0}{\sqrt{2}M_p}\left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~I}}}. \end{aligned}$$

  (4.13)

  This implies that if we know the field value at the starting point of inflation then one can directly quantify the amplitude of density perturbation. Most importantly, if inflation starts from the vicinity of the Planck scale i.e. $\phi _0 \sim \sqrt{2}M_p\sim \mathcal{O}(M_p)$ then by evaluating the amplitude of the density perturbation in Region I one can easily quantify the amplitude of the density perturbation in Region II. In this setup within the range $50<\mathcal{N}_{f/h}<70$, we get

  $$\begin{aligned} \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~I}}}\sim \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~II}}}\sim 2.2\times 10^{-9}, \end{aligned}$$

  (4.14)

  which is consistent with Planck 2015 data. But if inflation starts at the following field value, $\phi _0=\sqrt{2}\Delta ~M_p$, where the parameter $\Delta \gtrless 1$ then one ca write the following relationship between the amplitude of the density perturbation in Region I and Region II as

  $$\begin{aligned}&\left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~II}}}=\Delta \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~I}}}\nonumber \\&\qquad \times \left[ 1-\frac{\sqrt{6}}{9\Delta ^2M_p}(\Psi _\mathrm{h} - \Psi _0)\right] ^{1/2}\nonumber \\&\quad \approx \Delta \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~I}}}. \end{aligned}$$

  (4.15)

  This implies that for $\Delta \gtrless 1$ we get

  $$\begin{aligned} \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~II}}}\gtrless & {} \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~I}}}. \end{aligned}$$

  (4.16)

  In this case for Region I we get

  $$\begin{aligned} \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~I}}}\sim 2.2\times 10^{-9}, \end{aligned}$$

  (4.17)

  then for Region II we get

  $$\begin{aligned} \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~I}}}\gtrless 2.2\times 10^{-9}. \end{aligned}$$

  (4.18)

  This implies that for $\Delta \gtrless 1$ in Region II we get tightly constrained result for the amplitude for the density perturbation.

• In Region I and Region II of Case II, the amplitude of the density fluctuation at the horizon crossing are related by

  $$\begin{aligned} \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~II}}} \approx \frac{M^3_p}{\sqrt{8}\alpha \lambda (\Psi _\mathrm{h})\phi ^3_0}\left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~I}}}. \end{aligned}$$

  (4.19)

  This implies that if we know the field value at the starting point of inflation, the dilaton field dependent coupling at the horizon crossing $\lambda (\Psi _\mathrm{h})$ and the coupling of scale free gravity $\alpha$, then one can directly quantify the amplitude of density perturbation. Most importantly, if inflation starts from the vicinity of the Planck scale i.e. $\phi _0 \sim \mathcal{O}(M_p)$ and we have an additional constraint:

  $$\begin{aligned} \lambda (\Psi _\mathrm{h})\sim \frac{1}{\sqrt{8}\alpha }, \end{aligned}$$

  (4.20)

  then by evaluating the amplitude of the density perturbation in the Region I one can easily quantify the amplitude of the density perturbation in Region II. Here one can also consider an equivalent constraint:

  $$\begin{aligned} \phi _0 \sim \left( \frac{1}{\sqrt{8}\alpha \lambda (\Psi _\mathrm{h})}\right) ^{1/3}~M_p. \end{aligned}$$

  (4.21)

  For both situations in the present setup within the range $50<\mathcal{N}_{f/h}<70$, we get

  $$\begin{aligned} \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~I}}}\sim \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~II}}}\sim 2.3\times 10^{-9}, \end{aligned}$$

  (4.22)

  which is also consistent with Planck 2015 data. But if inflation starts at the field value $\phi _0=\Delta ~M_p$, where the parameter $\Delta \gtrless 1$, and we define

  $$\begin{aligned} \Gamma =\left( \frac{1}{\sqrt{8}\alpha \lambda (\Psi _\mathrm{h})\Delta ^3}\right) , \end{aligned}$$

  (4.23)

  where the parameter $\Gamma \gtrless 1$, then one can write the following relationship between the amplitude of the density perturbation in Region I and Region II as

  $$\begin{aligned} \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~II}}}= \Gamma \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~I}}}. \end{aligned}$$

  (4.24)

  This implies that for $\Delta \gtrless 1$ and $\Gamma \gtrless 1$ we get

  $$\begin{aligned} \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~II}}} \gtrless \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~I}}}. \end{aligned}$$

  (4.25)

  In this case for Region I we get

  $$\begin{aligned} \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~I}}}\sim 2.3\times 10^{-9}, \end{aligned}$$

  (4.26)

  then for Region II we get

  $$\begin{aligned} \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{{Region~I}}}\gtrless 2.3\times 10^{-9}. \end{aligned}$$

  (4.27)

  This implies that for $\Delta \gtrless 1$ and $\Gamma \gtrless 1$ in Region II we get a tightly constrained result for the amplitude for the density perturbation.

Table 1 Inflationary observables and model constraints in the light of Planck 2015 data [44,45,46] for the dynamical attractors considered in Case I and Case II

Fig. 6

Plot for running of the running of spectral index $\kappa _\mathrm{S}=\mathrm{d}^2n_\mathrm{S}/\mathrm{d}^2\ln k$ vs. running of the spectral index $\beta _\mathrm{S}=\mathrm{d}n_\mathrm{S}/\mathrm{d}\ln k$ for scalar modes. Here for Case I and Case II we have drawn green and pink colored lines. We also draw the background of the confidence contours obtained from various joint constraints [44,45,46]

In this context the scalar spectral tilt can be written at the horizon crossing as⁶

$$\begin{aligned} n_\mathrm{S}-1=\left( \frac{\mathrm{d}\ln A_\mathrm{S}}{\mathrm{d}f}\right) _\mathrm{h} \approx \left\{ \begin{array}{ll} -\frac{3}{\left( \mathcal{N}_{f/h}+1\right) } &{}\quad \text {for Case I},\\ -\frac{3}{\mathcal{N}_{f/h}} &{}\quad \text {for Case II}. \end{array} \right. \nonumber \\ \end{aligned}$$

(4.30)

Further using Eq. (4.29) the running of the scalar spectral tilt can be computed as

$$\begin{aligned} \beta _\mathrm{S}=\left( \frac{\mathrm{d}n_\mathrm{S}}{\mathrm{d}f}\right) _\mathrm{h} \approx \left\{ \begin{array}{ll} \frac{3}{\left( \mathcal{N}_{f/h}+1\right) ^2} &{}\quad \text {for Case I},\\ \frac{3}{\mathcal{N}^{2}_{f/h}}&{}\quad \text {for Case II}, \end{array} \right. \end{aligned}$$

(4.31)

and

$$\begin{aligned} \kappa _\mathrm{S}=\left( \frac{\mathrm{d}\beta _\mathrm{S}}{\mathrm{d}f}\right) _\mathrm{h} \approx \left\{ \begin{array}{ll} -\frac{6}{\left( \mathcal{N}_{f/h}+1\right) ^3} &{}\quad \text {for Case I},\\ -\frac{6}{\mathcal{N}^{3}_{f/h}}&{}\quad \text {for Case II}. \end{array} \right. \end{aligned}$$

(4.32)

Finally combining Eqs. (4.29), (4.30) and (4.31) we get the following consistency relation for both Case I and Case II:

$$\begin{aligned} \beta _\mathrm{S}=\frac{\left( n_\mathrm{S}-1\right) ^2}{3} =3\left( -\frac{\kappa _\mathrm{S}}{6}\right) ^{2/3}. \end{aligned}$$

(4.28)

This is obviously a new consistency relation for the present Higgsotic model of inflation and it is also consistent with Planck 2015 data [44,45,46]. In Table 1 we have shown the numerical estimations of the inflationary observables for the Higgsotic attractors depicted in Case I and Case II within the range $50<\mathcal{N}_{f/h}<70$.

In Fig. 6, we have plotted the running of the spectral tilt for scalar perturbation ($\kappa _\mathrm{S}=\mathrm{d}^2n_\mathrm{S}/\mathrm{d}^2\ln k$) vs. spectral tilt for scalar perturbation ($n_\mathrm{S}$) in the light of Planck 2015 data along with various joint constraints. Here it is important to note that for Case I and Case II the Higgsotic models are shown by the green and pink colored lines. Also the big circle, intermediate size circle and small circle represent the representative points in $(\kappa _\mathrm{S},n_\mathrm{S})$ 2D plane for the numbers of e-foldings $\mathcal{N}_{f/h}=70$, $\mathcal{N}_{f/h}=60$ and $\mathcal{N}_{f/h}=50$, respectively. To represent the present status as well as statistical significance of the Higgsotic model for the dynamical attractors as depicted in Case I and Case II, we have drawn the $1\sigma$ and $2\sigma$ confidence contours from Planck+WMAP+BAO 2015 joint data sets [44,45,46]. It is clear from Fig. 6 that, for Case I we cover the range $0.59\times 10^{-3}<\beta _\mathrm{S}=\frac{\mathrm{d}n_\mathrm{S}}{\mathrm{d}\ln k}<1.16\times 10^{-3}$ and $-1.65\times 10^{-5}>\kappa _\mathrm{S}=\frac{\mathrm{d}^2n_\mathrm{S}}{\mathrm{d}^2\ln k}>-4.56\times 10^{-5}$ in the $(\kappa _\mathrm{S},\beta _\mathrm{S})$ 2D plane. Similarly for Case II we cover the range $0.62\times 10^{-3}<\beta _\mathrm{S}=\frac{\mathrm{d}n_\mathrm{S}}{\mathrm{d}\ln k}<1.20\times 10^{-3}$ and $-1.78\times 10^{-5}>\kappa _\mathrm{S}=\frac{\mathrm{d}^2n_\mathrm{S}}{\mathrm{d}^2\ln k}>-4.80\times 10^{-5}$ in the $(\kappa _\mathrm{S},\beta _\mathrm{S})$ 2D plane.

Fig. 7

Variation of the tensor-to-scalar ratio r with respect to a coupling parameter $\lambda (\Psi _\mathrm{h})$ (Case I) and b scale free parameter $\alpha$ (Case II). For both plots the dotted region is disfavored by Planck 2015 data along with BICEP2+Keck Array joint constraint [44,45,46]

Fig. 8

r vs. $n_\mathrm{S}$ plot for Case I and Case II in the background of confidence contours obtained from Planck TT+low P, Planck TT+low P+BKP, Planck TT+low P+BKP+BAO joint data sets

4.3 Primordial tensor modes and future observables

In terms of the number of e-foldings ($\mathcal{N}$) the most useful parametrization of the primordial scalar and tensor power spectrum or equivalently the tensor-to-scalar ratio can be written near the horizon crossing $\mathcal{N}_\mathrm{h}=\mathcal{N}(\phi _\mathrm{h})$ as

$$\begin{aligned} r(\mathcal{N})=\frac{8}{M^{2}_{p}}\left( \frac{\mathrm{d}\phi }{\mathrm{d}\mathcal{N}}\right) ^2=r(\mathcal{N}_\mathrm{h})\mathrm{e}^{\left( \mathcal{N}-\mathcal{N}_\mathrm{h}\right) \left\{ A_\mathrm{h}+B_\mathrm{h}\left( \mathcal{N}-\mathcal{N}_\mathrm{h}\right) \right\} }\nonumber \\ \end{aligned}$$

(4.33)

where in the slow-roll regime of inflation the tensor-to-scalar ratio $r(\mathcal{N}_\mathrm{h})$ can be written in terms of the inflationary potential as

$$\begin{aligned} r=r(\mathcal{N}_\mathrm{h})\approx 8M^{2}_{p}\left( \frac{V^{\prime }_\mathrm{h}}{V_\mathrm{h}}\right) ^2 =\left\{ \begin{array}{ll} \frac{128M^{2}_{p}}{\phi ^2_\mathrm{h}} &{}\quad \text {for Case I},\\ \frac{512\alpha ^2\lambda ^{2}(\Psi _\mathrm{h})\phi ^{6}_\mathrm{h}}{M^6_p}&{}\quad \text {for Case II}, \end{array} \right. \nonumber \\ \end{aligned}$$

(4.34)

and the symbols $A_\mathrm{h}$, $B_\mathrm{h}$ and $C_\mathrm{h}$ are expressed in terms of the inflationary observables at horizon crossing as $A_\mathrm{h}=n_{\mathrm{T}}-n_\mathrm{S}+1,~ B_\mathrm{h}=\frac{1}{2}(\beta _{\mathrm{T}}-\beta _\mathrm{S})$. In the above parametrization $A_\mathrm{h}\gg B_\mathrm{h}$ i.e. $\beta _\mathrm{S}-2(n_\mathrm{S}-1)\gg \beta _{\mathrm{T}}-2n_{\mathrm{T}}$ is always required for convergence of the Taylor expansion. Using this assumption the relationship between field excursion, $\Delta \phi =\phi _\mathrm{h} -\phi _f$ and tensor-to-scalar ratio $r(\mathcal{N}_\mathrm{h})$ can be computed as

$$\begin{aligned} \frac{|\Delta \phi |}{M_p}\approx & {} \sqrt{\frac{r(\mathcal{N}_\mathrm{h})}{8}} \mathrm{e}^{-\frac{A^{2}_\mathrm{h}}{2B_\mathrm{h}}}\sqrt{\frac{2\pi }{B_\mathrm{h}}}\left| \mathrm{erfi}\left( \frac{A_\mathrm{h}}{\sqrt{2B_\mathrm{h}}} \right) \right. \nonumber \\&-\,\left. \mathrm{erfi}\left( \frac{A_\mathrm{h}}{\sqrt{2B_\mathrm{h}}} -\sqrt{\frac{B_\mathrm{h}}{8}}\mathcal{N}_{f/h}\right) \right| . \end{aligned}$$

(4.35)

Now the scale of inflation is connected with the tensor-to-scalar ratio in the following fashion:

$$\begin{aligned} {V^{1/4}_\mathrm{h}}= & {} \left( \frac{3}{2}\pi ^2 A_\mathrm{S} r(f_\mathrm{h})\right) ^{1/4}\nonumber \\ M_p\sim & {} 7.9\times 10^{-3}~M_p \times \left( \frac{r(f_\mathrm{h})}{0.11}\right) ^{1/4}. \end{aligned}$$

(4.36)

Substituting Eq. (4.36) in Eq. (4.35) we compute the relationship between field excursion and the scale of inflation as

$$\begin{aligned} \frac{|\Delta \phi |}{M_p}\approx & {} \sqrt{\frac{V_\mathrm{h}}{6\pi M^{4}_{p}A_\mathrm{S} B_\mathrm{h}}} \mathrm{e}^{-\frac{A^{2}_\mathrm{h}}{2B_\mathrm{h}}}\left| \mathrm{erfi}\left( \frac{A_\mathrm{h}}{\sqrt{2B_\mathrm{h}}} \right) \right. \nonumber \\&\left. -\,\mathrm{erfi}\left( \frac{A_\mathrm{h}}{\sqrt{2B_\mathrm{h}}} -\sqrt{\frac{B_\mathrm{h}}{8}}\mathcal{N}_{f/h}\right) \right| . \end{aligned}$$

(4.37)

Also using Eq. (4.36) the tensor-to-scalar ratio can be written as

$$\begin{aligned} r=r(\mathcal{N}_\mathrm{h}) =\left\{ \begin{array}{ll} \frac{\lambda (\Psi _\mathrm{h})\phi ^4_\mathrm{h}}{(2\times 10^{-2} M_p)^4} &{}\quad \text {for Case I},\\ \frac{1}{\alpha (2.4\times 10^{-2})^4} &{}\quad \text {for Case II}. \end{array} \right. \end{aligned}$$

(4.38)

Further using Eqs. (4.34) and (4.38) we get the following constraints from the primordial tensor perturbation:

$$\begin{aligned} \phi _\mathrm{h} =\left\{ \begin{array}{ll} \frac{0.17 M_p}{\root 6 \of {\lambda (\Psi _\mathrm{h})}} &{} \quad \text {for Case I},\\ \frac{4.25 M_p}{\alpha ^{1/2}\root 3 \of {\lambda (\Psi _\mathrm{h})}}&{} \quad \text {for Case II}. \end{array} \right. \end{aligned}$$

(4.39)

Consequently the model parameters of the prescribed theory can be recast in terms of the tensor-to-scalar ratio as

$$\begin{aligned} \lambda (\Psi _\mathrm{h})= & {} 9.358\times 10^{-15}\times \left( \frac{r}{0.11}\right) ^3\quad \text {for Case I},\end{aligned}$$

(4.40)

$$\begin{aligned} \alpha= & {} 2.740\times 10^{7}\times \left( \frac{r}{0.11}\right) ^{-1}\quad \text {for Case II}. \end{aligned}$$

(4.41)

To satisfy the upper bound of the tensor-to-scalar ratio as obtained from Planck 2015 + BICEP2 + Keck Array i.e. $r\sim 0.11$ [44,45,46], Eqs. (4.40) and (4.41) give the upper bound of the model parameters $\lambda (\Psi _\mathrm{h})$ and $\alpha$, respectively.

In Fig. 7a, b, we have shown the variation of tensor-to-scalar ratio r with respect to field dependent coupling parameter $\lambda (\Psi _\mathrm{h})$ for Case I and scale free parameter $\alpha$ for Case II. For both plots the dotted region is disfavored by Planck 2015 data along with BICEP2+Keck Array joint constraint.

In Fig. 8, we have plotted the tensor-to-scalar ratio (r) vs. spectral tilt for scalar perturbation ($n_\mathrm{S}$) in the light of Planck data along with various joint constraints. Here it is important to note that for Case I and Case II the Higgsotic models are shown by the green and pink colored lines. Also the big circle, intermediate size circle and small circle represent the representative points in $(r,n_\mathrm{S})$ 2D plane for the numbers of e-foldings, $\mathcal{N}_{f/h}=70$, $\mathcal{N}_{f/h}=60$ and $\mathcal{N}_{f/h}=50$, respectively. To represent the present status as well as the statistical significance of the Higgsotic model for the dynamical attractors as depicted in Case I and Case II, we have drawn the $1\sigma$ and $2\sigma$ confidence contours from Planck TT+low P, Planck TT+low P+BKP, Planck TT+low P+BKP+BAO joint data sets [44,45,46] in Fig. 8. It is clearly visualized from Fig. 8 that for Case I we cover the range $0.941<n_\mathrm{S}<0.958$ and $0.07<r<0.11$ in the $(r,n_\mathrm{S})$ 2D plane for the effective field dependent coupling constrained within the window $5.956\times 10^{-15}<\lambda (\Psi _\mathrm{h})<9.358\times 10^{-15}$. Similarly for Case II we cover the range $0.940<n_\mathrm{S}<0.957$ and $0.056<r<0.09$, in the $(r,n_\mathrm{S})$ 2D plane for the effective scale of the Higgsotic potential constrained within the window $5.382\times 10^{7}>\alpha >3.349\times 10^{7}$. Additionally, it is important to mention here that the area bounded by the parallel vertical green lines and the pink lines represent the allowed parameter space in the $(r,n_\mathrm{S})$ 2D plane for the two Higgsotic dynamical attractors as depicted in Case I and Case II.

4.4 Reheating

To get successful amount of reheating from the proposed setup we consider the fact that reheating to commence at the end of slow rolling of the inflaton, $\ddot{\phi }\approx 3\tilde{H}\dot{\phi }$. This condition translates into the following physical constraint for Case I and Case II:

$$\begin{aligned} \partial _{\phi \phi }\left( \sqrt{\tilde{W}}\right) =\frac{3}{2M^{2}_{p}}\sqrt{\tilde{W}}. \end{aligned}$$

(4.42)

Further using this constraint in Eq. (4.2) the inflaton field value at the end of inflation can be computed for Case I and Case II as

$$\begin{aligned} \phi _f \sim \left\{ \begin{array}{ll} \sqrt{\frac{6}{5}}~M_p &{}\quad \text {for Case I},\\ \frac{\phi _0}{\left[ 1+\frac{270\phi ^2_0}{M^{2}_p}\right] ^{1/2}} &{}\quad \text {for Case II}. \end{array} \right. \end{aligned}$$

(4.43)

Additionally, it is important to mention here that the slow-roll approximation in Eqs. (6.3)–(6.5) is only valid when the following constraint is satisfied, $\tilde{W}\ge \frac{\partial _{\phi }\tilde{W}}{\sqrt{6}}M_p$. For our present setup this condition translates into the following constraint for Case I and Case II:

$$\begin{aligned}&\text {Case~I:}\quad \phi _{\mathrm{inf}}\ge \frac{2\sqrt{6}}{3}~M_p,\end{aligned}$$

(4.44)

$$\begin{aligned}&\text {Case~II:}\quad \phi _{\mathrm{inf}}\le \left( \frac{4\sqrt{2}}{3\sqrt{3}}\right) ^{1/3}~M_p, \end{aligned}$$

(4.45)

where $\phi _{\mathrm{inf}}$ represent the field value of the inflaton during inflation. Here it is important to note that, once the $\dot{\phi }$ term becomes dominant, the slow-roll condition is not valid. In such a case we need to solve the equation of motions with large inflaton kinetic terms where $|\ddot{\phi }/3\tilde{H}\dot{\phi }|\sim \mathcal{O}(1)$. This also implies that when the $\dot{\phi }^2$ contribution is dominant in the energy density, the slow-roll approximation for the inflaton field completely breaks down and reheating starts.

Further we assume that to occur successful reheating in the proposed framework it is important to convert energy from the potential energy density to radiation. Consequently one can write the following expression for the reheating temperature:

$$\begin{aligned} T_{\mathrm{{RH}}}=\left( \frac{30\rho _f}{\pi ^2 g_*}\right) ^{1/4}\approx \left( \frac{30\tilde{W}_f}{\pi ^2 g_*}\right) ^{1/4}>T_{\mathrm{{RH}},\min }\sim \mathcal{E}~\mathrm{GeV}\nonumber \\ \end{aligned}$$

(4.46)

where $g_*$ is the effective number of particle species and $\mathcal{E}$ is a parameter which is different for different models of inflation. In this context successful reheating does not require instant transition to a radiation-dominated universe after inflation. The inflaton decay can occur much later than the end of inflation, and formation of a fully thermalized radiation bath can take even longer. This implies that very large value of $\mathcal{E}$ is not allowed in the present context, which is consistent with various supersymmetric models of inflation. Equivalently Eq. (4.46) can be translated for Case I and Case II as

$$\begin{aligned}&\text {Case I:}\quad \lambda (\Psi _f)=\lambda \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi _f}{M_p}}>\left( \frac{5\pi ^2 g_*\mathcal{E}^4}{54}\right) \nonumber \\&\qquad \times \, (4.12\times 10^{-19})^4,\end{aligned}$$

(4.47)

$$\begin{aligned}&\text {Case II:}\quad \alpha <\left( \frac{15}{4\pi ^2 g_*\mathcal{E}^4}\right) \times (4.12\times 10^{-19})^{-4}. \end{aligned}$$

(4.48)

One can interpret the results obtained in this section as follows.

• For Case I we get a lower bound on the field dependent coupling $\lambda (\Psi _f)$, which is expressed in terms of the effective number of particle $g_*$ and the parameter $\mathcal{E}$.

• Similarly for Case II we get an upper bound on the scale free gravity coupling $\alpha$, which is also expressed in terms of the effective number of particle $g_*$ and the parameter $\mathcal{E}$.

• For a given value of $g_*$ and $\mathcal{E}$ one can explicitly determine the respective bounds on the coupling parameters. For an example one can fix $g_* \sim 100$ in the present context.

5 Cosmological solutions from soft attractors

5.1 Solutions for the inflaton

To study the inflationary constraints and the cosmological consequences from our proposed setup here we first express the value of the inflaton field at the onset of inflation, the horizon, reheating and including the density perturbation conditions as given by

$$\begin{aligned}&\text {Case~I}\nonumber \\&\phi _0>\phi _\mathrm{h}=\sqrt{\frac{6}{5}}~M_p \left[ 1+\frac{5}{27}\mathcal{N}_{f/h} \right] ^{1/2},\end{aligned}$$

(5.1)

$$\begin{aligned}&\phi _0<\phi _{\mathrm{{RH}}}=T_{\mathrm{{RH}},\min }\times \left( \frac{\pi ^2 g_* \lambda (\Psi _0)}{120}\right) ^{1/4}, \end{aligned}$$

(5.2)

$$\begin{aligned}&\phi _0>\phi _{D}=\left\{ \begin{array}{ll} 2M_p\left[ \left( \frac{\delta \rho }{\rho }\right) _{\mathrm{cr}} \sqrt{\frac{2}{\lambda (\Psi _\mathrm{h})}}+ \left( \frac{\phi _0}{2M_p}\right) ^2-\frac{3}{10}-\frac{20}{9}\mathcal{N}_{f/h}\right] ^{1/2}&{}\quad \text {for Region I},\\ 2M_p\left[ \left( \frac{\delta \rho }{\rho }\right) ^{2/3}_{\mathrm{cr}}\frac{1}{(\lambda (\Psi _\mathrm{h}))^{3/2}}+ \left( \frac{\phi _0}{2M_p}\right) ^2-\frac{3}{10}-\frac{20}{9}\mathcal{N}_{f/h}\right] ^{1/2}&{}\quad \text {for Region II}, \end{array} \right. \end{aligned}$$

(5.3)

$$\begin{aligned}&\text {Case~II}\nonumber \\&\phi _0>\phi _\mathrm{h}=M_p \left[ \frac{\left( \frac{\phi _0}{M_p}\right) ^2}{1+270\left( \frac{\phi _0}{M_p}\right) ^2}+8\mathcal{N}_{f/h}\right] ^{1/2},\end{aligned}$$

(5.4)

$$\begin{aligned}&\phi _0>\phi _{\mathrm{{RH}}}=M_p~\root 4 \of {\frac{4}{\lambda (\Psi _0)}}\left[ \frac{\pi ^2 g_*}{30}\left( \frac{T_{\mathrm{{RH}},\min }}{M_p}\right) ^4-\frac{1}{8\alpha }\right] ^{1/4},\end{aligned}$$

(5.5)

$$\begin{aligned}&\phi _0>\phi _{D}=\left\{ \begin{array}{ll} M_p\left[ \frac{1}{\sqrt{2\alpha \lambda (\Psi _\mathrm{h})}} \left\{ 64\alpha \left( \frac{\delta \rho }{\rho }\right) ^2_{\mathrm{cr}}-1\right\} ^{1/2} +\frac{270\left( \frac{\phi _0}{M_p}\right) ^{4}}{1+270\left( \frac{\phi _0}{M_p}\right) ^{2}}-16 \mathcal{N}_{f/h}\right] ^{1/2}&{}\quad \text {for Region I},\\ M_p\left[ \frac{1}{(8\alpha )^{3/2}\lambda (\Psi _\mathrm{h}) \left( \frac{\phi _0}{M_p}\right) }\left( \frac{\delta \rho }{\rho }\right) ^{-1}_{\mathrm{cr}} +\frac{270\left( \frac{\phi _0}{M_p}\right) ^{4}}{1+270\left( \frac{\phi _0}{M_p}\right) ^{2}}-16\mathcal{N}_{f/h}\right] ^{1/2}&{}\quad \text {for Region II}. \end{array} \right. \end{aligned}$$

(5.6)

The physical interpretation of the obtained results are given now:

• For Case I the field value at the horizon crossing is completely specified by the number of e-foldings, which is lying within the window, $50<\mathcal{N}_{f/h}=\mathcal{N}_{cmb}<70$. On the other hand for Case II field value at the horizon crossing is specified by two parameters – (A) the number of e-foldings and (B) the field value at the starting point of inflation (initial condition).

• For Case I the field value during the time of reheating is specified by three parameters – (A) the minimum value of the reheating temperature, (B) the value of the field dependent coupling parameter at the starting point of inflation, and (C) the effective number of degrees of freedom $g_*$. For Case II to determine the field value at the time of reheating we need to know additionally the numerical value of the scale free gravity parameter $\alpha$.

• For Case I the field value during the density perturbation is specified by four parameters – (A) the value of the density contrast or more precisely the amplitude of the scalar perturbation, (B) the value of the field dependent coupling parameter at the horizon crossing and at the starting point of inflation, and (C) the number of e-foldings. For Case II to determine the field value during the density perturbation we need to know additionally the numerical value of the scale free gravity parameter $\alpha$. For Case I one can express the solution for Region II in terms of Region I as

  

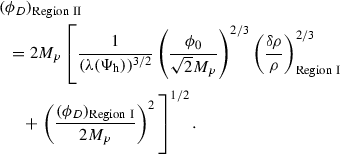  (5.7)

  Similarly for Case II one can express the solution for Region II in terms of Region I as

  $$\begin{aligned} (\phi _{D})_{\mathrm{{Region~II}}}= & {} 2M_p\left[ \frac{1}{8\alpha ^{1/2}} \frac{\phi ^2_0}{M^2_p}\left( \frac{\delta \rho }{\rho }\right) ^{-1}_{\mathrm{{Region~I}}}\right. \nonumber \\&\left. +\left( \frac{(\phi _D)_{\mathrm{{Region~I}}}}{M_p}\right) ^2 -\frac{1}{\sqrt{2\alpha \lambda (\Psi _\mathrm{h})}}\right. \nonumber \\&\times \,\left. \left\{ 64\alpha \left( \frac{\delta \rho }{\rho } \right) ^{2}_{\mathrm{{Region~I}}}-1\right\} \right] ^{1/2}. \end{aligned}$$

  (5.8)

5.2 Solutions for field dependent coupling $\lambda (\Psi )$

Now let us describe the behavior of the running or the scale dependence of the field dependent coupling $\lambda (\Psi )$ in the above mentioned two cases as

$$\begin{aligned}&{\text {Case~I}}\nonumber \\&\lambda (\Psi )=\lambda (\Psi _0)\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}M_p} \left( \Psi -\Psi _0\right) }=\lambda (\Psi _0)\mathrm{e}^{\frac{1}{3M^2_p} \left( \phi ^2-\phi ^2_0\right) }\nonumber \\&\quad ~~~~~~=\lambda (\Psi _0) \left( \frac{t_0}{t}\right) ^2,\end{aligned}$$

(5.9)

$$\begin{aligned}&{\text {Case~II}} \nonumber \\&\lambda (\Psi )= \lambda (\Psi _0) \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}M_p}\left( \Psi -\Psi _0\right) }=\lambda (\Psi _0) \mathrm{e}^{\frac{3}{M^2_p}\left( \phi ^2-\phi ^2_0\right) }\nonumber \\&\quad ~~~~~~=\lambda (\Psi _0)\mathrm{e}^{-\frac{2\sqrt{2}M_p}{3\sqrt{3\alpha }}(t-t_0)}. \end{aligned}$$

(5.10)

Further using Eqs. (4.39), (5.1) and (5.4) we get the following constraint on the field dependent coupling $\lambda (\Psi _\mathrm{h})$ at horizon crossing:

$$\begin{aligned} \lambda (\Psi _\mathrm{h})=\left\{ \begin{array}{ll} \lambda \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi _\mathrm{h}}{M_p}}=\frac{1.4\times 10^{-5}}{\left[ 1+\frac{5}{27}\alpha _{f/h}\right] ^{3}} &{}\quad \text {for Case I},\\ -\lambda \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi _\mathrm{h}}{M_p}} =-\frac{77~M_p}{\alpha ^{3/2}\left[ \frac{\left( \frac{\phi _0}{M_p} \right) ^2}{1+270\left( \frac{\phi _0}{M_p}\right) ^2}+8\alpha _{f/h}\right] ^{3/2}}. &{}\quad \text {for Case II}. \end{array} \right. \nonumber \\ \end{aligned}$$

(5.11)

Similarly using Eq. (5.11) the field dependent coupling $\lambda (\Psi _0)$ can be expressed in terms of the number of e-foldings as

$$\begin{aligned} \lambda (\Psi _0) =\left\{ \begin{array}{ll} \lambda \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi _0}{M_p}}=\frac{1.4\times 10^{-5}\times \mathrm{e}^{-\frac{2}{5}\left[ 1+\frac{5}{27} \alpha _{f/h}\right] }}{\left[ 1+\frac{5}{27}\alpha _{f/h} \right] ^{3}}\mathrm{e}^{\frac{\phi ^2_0}{3M^2_p}} &{}\quad \text {for Case I},\\ -\lambda \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}} \frac{\Psi _0}{M_p}}=-\frac{77~M_p\times \mathrm{e}^{-\frac{1}{3}\left[ \frac{\left( \frac{\phi _0}{M_p} \right) ^2}{1+270\left( \frac{\phi _0}{M_p}\right) ^2} +8\alpha _{f/h}\right] }}{\alpha ^{3/2}\left[ \frac{ \left( \frac{\phi _0}{M_p}\right) ^2}{1+270\left( \frac{\phi _0}{M_p}\right) ^2}+8\alpha _{f/h}\right] ^{3/2}} \mathrm{e}^{\frac{\phi ^2_0}{3M^2_p}}. &{}\quad \text {for Case II}. \end{array} \right. \end{aligned}$$

(5.12)

Additionally, we get the following constraint condition on the ratio of the couplings at the horizon crossing and at the starting point of inflation:

$$\begin{aligned} \frac{\lambda (\Psi _\mathrm{h})}{\lambda (\Psi _0)}\mathrm{e}^{\frac{\phi ^2_0}{3M^2_p}} =\left\{ \begin{array}{ll} \mathrm{e}^{\frac{2}{5}\left[ 1+\frac{5}{27}\alpha _{f/h}\right] } &{} \quad \text {for Case I},\\ \mathrm{e}^{\frac{1}{3}\left[ \frac{\left( \frac{\phi _0}{M_p}\right) ^2}{1+270\left( \frac{\phi _0}{M_p}\right) ^2}+8\alpha _{f/h}\right] } &{}\quad \text {for Case II}. \end{array} \right. \end{aligned}$$

(5.13)

6 Beyond soft attractor: a single field approach

In this section our prime objective is to analyze the non-attractor phase of inflation. For this purpose let us start with the Klein–Gordon field equations for the inflaton field $\phi$ and dilaton field $\Psi$, which can be written in the flat ($k=0$) FLRW background as

$$\begin{aligned}&\frac{\mathrm{d}^{2}\phi }{\mathrm{d}\tilde{t}^{2}}+3\tilde{H} \frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}+\partial _{\phi } \tilde{W}(\phi ,\Psi )=0\nonumber \\&\quad \Rightarrow \frac{\mathrm{d}^{2}\phi }{\mathrm{d}\tilde{t}^{2}} +3\tilde{H}\frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}+\lambda (\Psi )\phi ^3=0,\end{aligned}$$

(6.1)

$$\begin{aligned}&\frac{\mathrm{d}^{2}\Psi }{\mathrm{d}\tilde{t}^{2}} +3\tilde{H}\frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}+ \partial _{\Psi }\tilde{W}(\phi ,\Psi )=0\nonumber \\&\quad \Rightarrow \frac{\mathrm{d}^{2}\Psi }{\mathrm{d}\tilde{t}^{2}} +3\tilde{H}\frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}-\frac{\lambda (\Psi )\phi ^4}{\sqrt{6} M_p}=0. \end{aligned}$$

(6.2)

Now in the slow-roll approximation regime the field equations are approximated by

$$\begin{aligned}&3\tilde{H}\frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}+\lambda (\Psi )\phi ^3=0\end{aligned}$$

(6.3)

$$\begin{aligned}&3\tilde{H}\frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}} -\frac{\lambda (\Psi )\phi ^4}{\sqrt{6} M_p}=0,\end{aligned}$$

(6.4)

$$\begin{aligned}&\tilde{H}^2=\frac{\tilde{W}(\phi ,\Psi )}{3M^2_p} =\frac{V_0}{3M^2_p}\left[ 1+\frac{2\alpha \lambda (\Psi )}{M^{4}_{p}}\phi ^{4}\right] . \end{aligned}$$

(6.5)

During the non-attractor phase of inflation we assume that the $\phi$ field is the only dynamical field controlling the scenario and at that time the $\Psi$ field freezes at the Planck scale. On the other hand, at late times the dynamical contribution comes from the $\Psi$ field and the inflaton field $\phi$ freezes at Planck scale. Assuming this fact the general behavior during the inflationary epoch is governed by

$$\begin{aligned} a= & {} a_i\exp \left[ -\frac{1}{20M^5_p}(\phi ^5 -\phi ^5_b) -\frac{\sqrt{3\pi }}{16\alpha \bar{\lambda }}\left\{ \mathrm{Erf}\left[ \frac{\phi }{\sqrt{3}M_p} \right] \right. \right. \nonumber \\&\left. \left. -\mathrm{Erf}\left[ \frac{\phi _i}{\sqrt{3}M_p}\right] \right\} \right] , \end{aligned}$$

(6.6)

$$\begin{aligned} t-t_i\approx & {} -\frac{3}{2\bar{\lambda }\sqrt{2\alpha }}\left[ \frac{\sqrt{3\pi }}{2}\left\{ \mathrm{Erf}\left[ \frac{\phi }{\sqrt{3}M_p} \right] -\mathrm{Erf}\left[ \frac{\phi _i}{\sqrt{3}M_p}\right] \right\} \right. \nonumber \\&\left. +\frac{\alpha \bar{\lambda }}{5M^5_p}(\phi ^5-\phi ^5_b)\right] , \end{aligned}$$

(6.7)

where the ‘i’ subscript is used to describe the boundary/initial condition within the prescribed setup. It is important to note that in Eqs. (6.6) and (6.7) we introduce the new symbol $\bar{\lambda }$, which signifies the value of the self coupling at the freezing value of the dilaton field ${\varvec{\Psi }}\sim \mathcal{O}(M_p)$ during inflation, i.e.

$$\begin{aligned} \bar{\lambda }=\lambda ({{\varvec{\Psi }}})=\lambda \exp \left[ -\frac{2\sqrt{2}}{\sqrt{3}}\right] . \end{aligned}$$

(6.8)

On the other hand at late time the inflaton field get its VEV at $\phi \sim \mathcal{O}(M_p)$ and correspondingly the self coupling $\hat{\lambda }$ at late time is defined as

$$\begin{aligned} \hat{\lambda }\equiv \frac{\lambda }{4}\hat{\mathbf{\phi }}^{4}\sim \frac{\lambda }{4}M^{4}_{p}. \end{aligned}$$

(6.9)

Here the obtained results can be interpreted as follows:

• The solution for the scale factor a(t) and inflaton field $\phi (t)$ admits a quasi de Sitter behavior in the presence of an additional contribution coming from error functions.

• For the large value of the product $\alpha \lambda$ one can further neglect the contributions from the error function. In that case one can get back the exact de Sitter behavior in the present context.

For further analysis let us introduce the following Hubble flow functions in an Einstein frame:

$$\begin{aligned} \tilde{\epsilon }_{H}= & {} -\frac{1}{\tilde{H}^2}\frac{\mathrm{d}\tilde{H}}{\mathrm{d}\tilde{t}}, \quad \tilde{\eta }_{H}=-\frac{1}{\tilde{H}} \left( \frac{\frac{\mathrm{d}^{2}\phi }{\mathrm{d}\tilde{t}^2}}{\frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}}\right) . \end{aligned}$$

(6.10)

The flow functions in the Einstein frame can be expressed in terms of the Jordan frame Hubble flow functions as

$$\begin{aligned} \tilde{\epsilon }_{H}= & {} \epsilon _{H}\frac{\left[ 1-\frac{1}{2H^{2}\epsilon _{H}} \frac{\mathrm{d}^{2}\ln \Omega ^{2}}{\mathrm{d}t^{2}}+\frac{1}{H\epsilon _{H}}\frac{\mathrm{d}\ln \Omega ^2}{\mathrm{d}t} -\frac{1}{4}\left( \frac{\mathrm{d}\ln \Omega ^{2}}{\mathrm{d}t}\right) ^{2}\right] }{\left[ 1+\frac{1}{2H}\frac{\mathrm{d}\ln \Omega ^{2}}{\mathrm{d}t}\right] ^{2}},\nonumber \\ \tilde{\eta }_{H}= & {} \eta _{H}\frac{\left[ 1+\frac{1}{2H\eta _{H}}\frac{\mathrm{d}\ln \Omega ^2}{\mathrm{d}t}\right] }{\left[ 1+\frac{1}{2H}\frac{\mathrm{d}\ln \Omega ^2}{\mathrm{d}t}\right] }. \end{aligned}$$

(6.11)

Further we introduce potential flow functions in an Einstein frame for the Higgs field $\phi$ as

$$\begin{aligned} \tilde{\epsilon }_{\tilde{W}}= & {} \frac{M^{2}_{p}}{2}(\partial _{\phi } \ln \tilde{W}(\phi ,{\varvec{\Psi }}))^{2}\, =\frac{32\alpha ^{2}\bar{\lambda }^{2}\phi ^{6}}{M^{6}_{p}\left[ 1+\frac{2\alpha \bar{\lambda }}{M^{4}_{p}}\phi ^{4}\right] ^{2}},\end{aligned}$$

(6.12)

$$\begin{aligned} \tilde{\eta }_{\tilde{W}}= & {} {M^{2}_{p}}\frac{\partial _{\phi \phi }\tilde{W}(\phi ,{\varvec{\Psi }})}{\tilde{W}(\phi ,{\varvec{\Psi }})}\, =\frac{24\alpha \bar{\lambda }\phi ^{2}}{M^{2}_{p}\left[ 1+\frac{2\alpha \bar{\lambda }}{M^{4}_{p}}\phi ^{4}\right] },\end{aligned}$$

(6.13)

$$\begin{aligned} \tilde{\xi }^{2}_{\tilde{W}}= & {} M^{4}_{p} \frac{(\partial _{\phi }\ln \tilde{W}(\phi ,{\varvec{\Psi }}))(\partial _{\phi \phi \phi } \tilde{W}(\phi ,{\varvec{\Psi }}))}{(\tilde{W}(\phi ,{\varvec{\Psi }}))^{2}}\nonumber \\= & {} \frac{384\alpha ^{2}\bar{\lambda }^{2}\phi ^{4}}{M^{4}_{p} \left[ 1+\frac{2\alpha \bar{\lambda }}{M^{4}_{p}}\phi ^{4}\right] ^{2}},\end{aligned}$$

(6.14)

$$\begin{aligned} \tilde{\sigma }^{3}_{\tilde{W}}= & {} M^{6}_{p} \frac{(\partial _{\phi }\ln \tilde{W}(\phi ,{\varvec{\Psi }}))^{2} (\partial _{\phi \phi \phi \phi }\tilde{W}(\phi ,{\varvec{\Psi }}))}{(\tilde{W}(\phi ,{\varvec{\Psi }}))^{3}}\nonumber \\= & {} \frac{3072\alpha ^{3}\bar{\lambda }^{3}\phi ^{6}}{M^{6}_{p} \left[ 1+\frac{2\alpha \bar{\lambda }}{M^{4}_{p}}\phi ^{4}\right] ^{3}}, \end{aligned}$$

(6.15)

where we assume that the dilaton field $\Psi$ freezes at the field value ${\varvec{\Psi }}$ during inflation. For further numerical estimation during inflation we fix the freezing value of dilaton field ${\varvec{\Psi }}\sim \mathcal{O}(M_p)$. During inflation the potential is characterized by

$$\begin{aligned} \tilde{W}(\phi ,{\varvec{\Psi }})= & {} \tilde{U}({\varvec{\Psi }})+\tilde{V}(\phi )=V_0 \left[ 1+\frac{2\alpha \lambda ({\varvec{\Psi }})}{M^{4}_{p}}\phi ^{4}\right] \nonumber \\= & {} V_0+\frac{\bar{\lambda }}{4}\phi ^{4}. \end{aligned}$$

(6.16)

On the other hand in an Einstein frame the potential and Hubble flow functions are connected through the following relations:

$$\begin{aligned}&\tilde{\epsilon }_{H}\approx \tilde{\epsilon }_{\tilde{W}} =\frac{32\alpha ^{2}\bar{\lambda }^{2}\phi ^{6}}{M^{6}_{p} \left[ 1+\frac{2\alpha \bar{\lambda }}{M^{4}_{p}}\phi ^{4}\right] ^{2}},\nonumber \\&\tilde{\eta }_{H}\approx \tilde{\eta }_{\tilde{W}}-\tilde{\epsilon }_{\tilde{W}} =\frac{24\alpha \bar{\lambda }\phi ^{2}}{M^{2}_{p}\left[ 1+\frac{2\alpha \bar{\lambda }}{M^{4}_{p}}\phi ^{4}\right] } -\frac{32\alpha ^{2}\bar{\lambda }^{2} \phi ^{6}}{M^{6}_{p}\left[ 1+\frac{2\alpha \bar{\lambda }}{M^{4}_{p}}\phi ^{4}\right] ^{2}}.\nonumber \\ \end{aligned}$$

(6.17)

Table 2 Inflaton field value at the end, horizon crossing and starting point of inflation

Table 3 Inflationary observables and model constraints in the light of Planck 2015 data

7 Constraints on inflation beyond soft attractor

7.1 Number of e-foldings

In the present context the total number of e-foldings is defined as

$$\begin{aligned} \mathcal{N}_{\mathrm{total}}=\mathcal{N}(t_{e},t_{i})=\int ^{t_{e}}_{t_{i}}H ~\mathrm{d}t=\mathcal{N}_{cmb}+\Delta \mathcal{N} \end{aligned}$$

(7.1)

where $\mathcal{N}_{cmb}$ and $\Delta \mathcal{N}$ are defined as

$$\begin{aligned} \mathcal{N}_{cmb}= & {} \mathcal{N}(t_{e},t_{cmb})=\int ^{t_{e}}_{t_{cmb}}H ~\mathrm{d}t,\nonumber \\ \Delta \mathcal{N}= & {} \mathcal{N}(t_{cmb},t_{i})=\int ^{t_{cmb}}_{t_{i}}H ~\mathrm{d}t. \end{aligned}$$

(7.2)

Further substituting the explicit form of the potential presented in this paper, the number of e-foldings can be recast as

$$\begin{aligned} \mathcal{N}_{\mathrm{total}}\approx & {} -\frac{1}{M^2_p} \int ^{\phi _{e}}_{\phi _{i}}\frac{\tilde{W}(\phi , {\varvec{\Psi }})}{\partial _{\phi }\tilde{W}(\phi ,{\varvec{\Psi }})} ~\mathrm{d}\phi \nonumber \\= & {} \frac{M^{2}_{p}}{16\alpha \bar{\lambda }}\left\{ \frac{1}{\phi ^2_e} -\frac{1}{\phi ^2_i}\right\} -\frac{1}{8M^2_p}(\phi ^2_e-\phi ^2_i),\end{aligned}$$

(7.3)

$$\begin{aligned} \mathcal{N}_{cmb}\approx & {} -\frac{1}{M^2_p} \int ^{\phi _{e}}_{\phi _{cmb}}\frac{\tilde{W}(\phi , {\varvec{\Psi }})}{\partial _{\phi }\tilde{W}(\phi ,{\varvec{\Psi }})} ~\mathrm{d}\phi \nonumber \\= & {} \frac{M^{2}_{p}}{16\alpha \bar{\lambda }} \left\{ \frac{1}{\phi ^2_e}-\frac{1}{\phi ^2_{cmb}}\right\} -\frac{1}{8M^2_p}(\phi ^2_e-\phi ^2_{cmb}), \end{aligned}$$

(7.4)

where superscript e, cmb and i denote the values of the inflaton field evaluated at the end of inflation, horizon crossing and starting point of inflation, respectively.

In the present context the field value of the inflaton at the inflation is determined from the condition $\epsilon _{\tilde{W}}(\phi _{e})=1=|\eta _{\tilde{W}}(\phi _{e})|$. Further substituting Eqs. (6.12) and (6.13) in the inflaton field value at the end of inflation can be computed as $\phi _{e}=3\sqrt{2}~M_{p}$. Now the expression for the inflaton field value at the horizon crossing is given by

$$\begin{aligned} \phi _{cmb}= & {} \frac{M_{p}}{2}\sqrt{\frac{\mathcal{A}_{cmb}}{\alpha \bar{\lambda }}} \left[ 1+\sqrt{1+\frac{8\alpha \bar{\lambda }}{\mathcal{A}^{2}_{cmb}}}\right] ^{\frac{1}{2}}\nonumber \\\approx & {} \frac{M_p}{2}\sqrt{\frac{2\mathcal{A}_{cmb}}{\alpha \bar{\lambda }}} \approx 2M_{p}\sqrt{\mathcal{N}_{cmb}} \end{aligned}$$

(7.5)

where we use the following constraint condition: $\sqrt{1+\frac{8\alpha \bar{\lambda }}{\mathcal{A}^{2}_{cmb}}}\approx 1+\frac{4\alpha \bar{\lambda }}{\mathcal{A}^{2}_{cmb}}+\cdots \sim \mathcal{O}(1)$ as $\alpha \bar{\lambda }/\mathcal{A}^2_{cmb}\ll 1$. Here the parameter $\mathcal{A}_{cmb}$ is defined as

$$\begin{aligned} \mathcal{A}_{cmb}= & {} \alpha \bar{\lambda }\left( 16\mathcal{N}_{cmb}+36\right) \nonumber \\= & {} 16\alpha \bar{\lambda }\mathcal{N}_{cmb}\left[ 1+\frac{9}{4\mathcal{N}_{cmb}}\right] \approx 16\alpha \bar{\lambda }\mathcal{N}_{cmb}. \end{aligned}$$

(7.6)

Similarly using Eqs. (7.5 and (7.6) in Eq. (7.3) the expression for the inflaton field value at the starting point of inflation is given by

$$\begin{aligned} \phi _{i}= & {} \frac{M_{p}}{2}\sqrt{\frac{\mathcal{A}_{\mathrm{total}}}{\alpha \bar{\lambda }}} \left[ 1+\sqrt{1+\frac{8\alpha \bar{\lambda }}{\mathcal{A}^{2}_{\mathrm{total}}}}\right] ^{\frac{1}{2}}\nonumber \\\approx & {} \frac{M_{p}}{2}\sqrt{\frac{\mathcal{A}_{\mathrm{total}}}{\alpha \bar{\lambda }}}\approx 2M_p\sqrt{\mathcal{N}_{\mathrm{total}}} \end{aligned}$$

(7.7)

where we use a similar constraint to the one mentioned above, i.e. $\sqrt{1+\frac{8\alpha \bar{\lambda }}{\mathcal{A}^{2}_{\mathrm{total}}}}\approx 1+\frac{4\alpha \bar{\lambda }}{\mathcal{A}^{2}_{\mathrm{total}}}+\cdots \sim \mathcal{O}(1)$ as $\alpha \bar{\lambda }/\mathcal{A}^2_{\mathrm{total}}\ll 1$. Here the parameter $\mathcal{A}_{\mathrm{total}}$ is defined as

$$\begin{aligned} \mathcal{A}_{\mathrm{total}}= & {} \alpha \bar{\lambda }\left( 16\mathcal{N}_{\mathrm{total}}+36\right) \nonumber \\= & {} 16\alpha \bar{\lambda }\mathcal{N}_{\mathrm{total}}\left[ 1+\frac{9}{4\mathcal{N}_{\mathrm{total}}}\right] \approx 16\alpha \bar{\lambda }\mathcal{N}_{\mathrm{total}}. \end{aligned}$$

(7.8)

In Table 2 we have given an estimate of the inflaton field value at horizon crossing ($\phi _{cmb}$) and starting point of inflation ($\phi _i$) for different values of $\mathcal{N}_{cmb}$ within the window $50\le \mathcal{N}_{cmb}\le 70$ (Table 3).

7.2 Primordial density perturbation

In the present context it is important to note that the perturbations to the homogeneous FLRW metric are described by the well known ADM formalism. The line element in the ADM formalism after cosmological perturbation takes the following simplified form:

$$\begin{aligned} \mathrm{d}s^2= N^2\mathrm{d}t^2 + g_{ij} (\mathrm{d}x^i + N^i \mathrm{d}t)(\mathrm{d}x^j + N^j \mathrm{d}t), \end{aligned}$$

(7.9)

where $g_{ij}$ is the induced spatial metric on the three surface labeled by time coordinate t, and N, $N_i$ are the time dependent lapse and shift functions, respectively. To do further analysis in the present computation one needs to make a proper choice of gauge to fix the diffeomorphism invariance of the theory of soft inflation originating from extended theories of gravity. A convenient choice is the synchronous gauge, defined by imposing the conditions $N=1,~N^i=0$. The perturbed metric in synchronous gauge has the mathematical structure $g_{ij}=a^2(t)[(1+2\zeta (t,\mathbf{x}))\delta _{ij}+\gamma _{ij}]$, $\gamma _{ii}=0$, where $\zeta (t,\mathbf{x})$ and $\gamma _{ij}$ are the scalar and tensor perturbations in the metric, respectively. Here to proceed we need to make a specific gauge choice to fix the diffeomorphism invariance of the inflationary theory. Additionally, it is important to mention here that, for the computation the inflationary correlation functions, it is more convenient to choose the gauge, $\delta \phi (t,\mathbf{x})= 0$, where the inflaton is homogeneous and the scalar perturbations are also appearing in the metric. Our focus will be on computing the two and three point functions for the scalar fluctuation at late time, when the modes of interest have exited the horizon.

7.2.1 Two point function

To compute the two point function for the scalar fluctuation we start with the second-order action for the curvature perturbation as given by

$$\begin{aligned} S^{(2)}_{\zeta }\approx \int \mathrm{d}^{4}x ~a^3~M^2_p\epsilon \left[ \dot{\zeta }^2 - \frac{1}{a^2}(\partial _{i}\zeta )^2 \right] . \end{aligned}$$

(7.10)

Next we introduce a new variable $v(\eta ,\mathbf{x})$, which is defined as $v(\eta ,\mathbf{x})=z~\zeta (\eta ,\mathbf{x})~M_p$. In general the parameter z is defined as $z =a\sqrt{2\epsilon }$. Now in terms of $v(\eta ,\mathbf{x})$ the second-order action for the curvature perturbation can be recast as

$$\begin{aligned} S^{(2)}_{\zeta }\approx \int \mathrm{d}^{3}x~ \mathrm{d}\eta ~\left[ v^{'2} -(\partial _{i}v)^2\frac{1}{a^2}(\partial _{i}\zeta )^2-m^{2}_{\mathrm{{eff}}}(\eta )v^2 \right] ,\nonumber \\ \end{aligned}$$

(7.11)

where the effective mass parameter $m_{\mathrm{{eff}}}(\eta )$ is defined as $m^{2}_{\mathrm{{eff}}}(\eta )=-\frac{1}{z}\frac{\mathrm{d}^2z}{\mathrm{d}\eta ^2}$. During inflation the scale factor and the parameter z can be expressed in terms of the conformal time $\eta$ as, $a(\eta )=-\frac{1}{H\eta }$ and $z =a\sqrt{2\epsilon }= -\sqrt{2\epsilon }/H\eta$ where $\epsilon$ is the Hubble slow-roll parameter defined earlier. But for simplicity one can neglect the contribution from $\epsilon$ in the leading order for the quasi-de Sitter case as it is sufficiently small in the slow-roll regime. Now further taking the Fourier transform,

$$\begin{aligned} v(\eta ,\mathbf{x})=\int \frac{\mathrm{d}^3k}{(2\pi )^3}~v_\mathbf{k}(\eta )~\mathrm{e}^{i\mathbf{k}.\mathbf{x}}, \end{aligned}$$

(7.12)

one can write down the equation of motion for the scalar fluctuation as

$$\begin{aligned} v^{\prime \prime }_\mathbf{k}+(k^2+m^{2}_{\mathrm{{eff}}}(\eta ))v_\mathbf{k}=0. \end{aligned}$$

(7.13)

Here it is important to note that for the de Sitter and quasi-de Sitter case the effective mass parameter can be expressed as $m^{2}_{\mathrm{{eff}}}(\eta ) = -\frac{2}{\eta ^2}$. Finally, considering the behavior of the mode function in the subhorizon regime and superhorizon regime one can write the expression in the de Sitter case with Bunch–Davies vacuum as

$$\begin{aligned} \zeta (\eta ,\mathbf{k})= & {} \frac{v_\mathbf{k}(\eta )}{z~M_p}= \frac{iH}{2~M_p\sqrt{\epsilon _{H}}~k^{\frac{3}{2}}}~\mathrm{e}^{- i(k\eta +\pi )}(1+ik\eta ).\nonumber \\ \end{aligned}$$

(7.14)

At the horizon crossing taking the late time limit one can write down the following expression for the two point function for scalar fluctuation:

$$\begin{aligned} \langle \zeta (\mathbf{k}) \zeta (\mathbf{q})\rangle =(2\pi )^3\delta ^{(3)}(\mathbf{k}+\mathbf{q})P_{\zeta }(k_*)\frac{1}{k^3}, \end{aligned}$$

(7.15)

where $P_{\zeta }(k_*)$ is known as the power spectrum at the horizon crossing for scalar fluctuations and it is defined as

$$\begin{aligned} P_{\zeta }(k_*)=\frac{H^2}{4~M^2_p\epsilon ^{*}_H}. \end{aligned}$$

(7.16)

For simplicity one can further define the amplitude of the power spectrum $\mathcal{P}_\mathrm{S}(\mathcal{N}_{cmb})$ at the horizon crossing as

$$\begin{aligned} \mathcal{P}_\mathrm{S}(\mathcal{N}_{cmb})=\frac{1}{2\pi ^2}P_{\zeta }(k_*)=\frac{H^2}{8\pi ^2~M^2_p\epsilon ^*_H}. \end{aligned}$$

(7.17)

Fig. 9

Plot for running of the running of spectral index $\kappa _\mathrm{S}=\mathrm{d}^2n_\mathrm{S}/\mathrm{d}^2\ln k$ vs. running of the spectral index $\beta _\mathrm{S}=\mathrm{d}n_\mathrm{S}/\mathrm{d}\ln k$ for scalar modes. Here for the non-attractor phase of inflation we have drawn a blue colored line. We also draw the background of confidence contours obtained from various joint constraints [44,45,46]

7.2.2 Present observables

Applying slow-roll approximation in the present context the inflationary observables i.e. power spectrum, spectral tilt, running and running of the running of the tilt for scalar modes from our model at horizon crossing ($\mathcal{N}=\mathcal{N}_{cmb}$) can be computed as

$$\begin{aligned} \mathcal{P}_\mathrm{S}(\mathcal{N}_{cmb})= & {} \frac{\tilde{W}(\phi _{cmb}, {\varvec{\Psi }})}{24\pi ^{2}M^{4}_{p}\epsilon ^{*}_{\tilde{W}}}\nonumber \\= & {} \frac{1}{393216\pi ^{2}\alpha ^{3}\bar{\lambda }^{2}\mathcal{N}^{3}_{cmb}} [1+32\alpha \bar{\lambda }\mathcal{N}^{2}_{cmb}]^{3},\nonumber \\\end{aligned}$$

(7.18)

$$\begin{aligned} n_\mathrm{S}(\mathcal{N}_{cmb})= & {} 1+\left( \frac{\mathrm{d}\ln \mathcal{P}_\mathrm{S}}{\mathrm{d}\mathcal{N}}\right) _{\mathcal{N}_{cmb}} \approx 1-\frac{3}{\mathcal{N}_{cmb}},\end{aligned}$$

(7.19)

$$\begin{aligned} \alpha _\mathrm{S}(\mathcal{N}_{cmb})= & {} \left( \frac{\mathrm{d}n_\mathrm{S}}{\mathrm{d}\mathcal{N}}\right) _{\mathcal{N}_{cmb}} \approx \frac{3}{\mathcal{N}^{2}_{cmb}}, \nonumber \\ \kappa _\mathrm{S}(\mathcal{N}_{cmb})= & {} \left( \frac{\mathrm{d}\alpha _\mathrm{S}}{\mathrm{d}\mathcal{N}}\right) _{\mathcal{N}_{cmb}} \approx -\frac{6}{\mathcal{N}^{3}_{cmb}}, \end{aligned}$$

(7.20)

where ${\varvec{\Psi }}$ represents the freezing value of $\Psi$ field at Planck scale.

In Fig. 9, we have plotted running of the running of spectral tilt for scalar perturbation ($\kappa _\mathrm{S}=\mathrm{d}^2n_\mathrm{S}/\mathrm{d}^2\ln k$) vs. running of the spectral index $\beta _\mathrm{S}=\mathrm{d}n_\mathrm{S}/\mathrm{d}\ln k$ in the light of Planck data along with various joint constraints. Here it is important to note that for the non-attractor phase of inflation the Higgsotic models are shown by the blue colored line. Also the big circle, intermediate size circle and small circle represent the representative points in $(\kappa _\mathrm{S},\beta _\mathrm{S})$ 2D plane for the numbers of e-foldings $\mathcal{N}_{cmb}=70$, $\mathcal{N}_{cmb}=60$ and $\mathcal{N}_{cmb}=50$, respectively. To represent the present status as well as the statistical significance of the Higgsotic model for the non-attractor phase of inflation, we have drawn the $1\sigma$ and $2\sigma$ confidence contours from Planck+WMAP+BAO joint data sets [44,45,46]. It is clear from Fig. 9 that for the non-attractor phase of inflation we cover the range $0.6\times 10^{-3}<\beta _\mathrm{S}=\frac{\mathrm{d}n_\mathrm{S}}{\mathrm{d}\ln k}<1.2\times 10^{-3}$ and $-1.8\times 10^{-5}>\kappa _\mathrm{S}=\frac{\mathrm{d}^2n_\mathrm{S}}{\mathrm{d}^2\ln k}>-4.8\times 10^{-5}$ in the $(\kappa _\mathrm{S},\beta _\mathrm{S})$ 2D plane.

7.3 Primordial tensor modes

7.3.1 Two point function

To compute the expression for the two point function for the tensor fluctuation here we start with the second-order action for the spin-2 graviton:

$$\begin{aligned} S^{(2)}_{\gamma }\approx \int \mathrm{d}^{4}x ~a^3~\frac{M^2_p}{8}\left[ \dot{\gamma }_{ij}\dot{\gamma }_{ij} - \frac{1}{a^2}(\partial _{m}\gamma _{ij})^2 \right] . \end{aligned}$$

(7.21)

In terms of conformal time in the present context the second-order action for the tensor fluctuation can be recast as

$$\begin{aligned} S^{(2)}_{\gamma }\approx \int \mathrm{d}^{3}x~\mathrm{d}\eta ~a^2~\frac{M^2_p}{8}\left[ \gamma ^{'2}_{ij} - (\partial _{m}\gamma _{ij})^2 \right] . \end{aligned}$$

(7.22)

In Fourier space one can further decompose the graviton $\gamma _{ij}(\eta ,\mathbf{x})$ as

$$\begin{aligned} \gamma _{ij}(\eta ,\mathbf{x})=\sum _{\lambda =\times ,+}\int \frac{\mathrm{d}^3 k}{(2\pi )^{\frac{3}{2}}}\epsilon ^{\lambda }_{ij}(k)~\gamma _{\lambda }(\eta ,\mathbf{k})~\mathrm{e}^{i\mathbf{k}.\mathbf{x}}, \end{aligned}$$

(7.23)

where $\epsilon ^{\lambda }_{ij}$ is the polarization tensor, which satisfies the following property: $\epsilon ^{\lambda }_{ii}=k^{i}\epsilon ^{\lambda }_{ij}=0,~ \sum _{i,j}\epsilon ^{\lambda }_{ij}\epsilon ^{\lambda ^{\prime }}_{ij} =2\delta _{\lambda \lambda ^{\prime }}$. Similar to the scalar fluctuation here we also define a new variable $u_{\lambda }(\eta ,\mathbf{k})$ in Fourier space as $u_{\lambda }(\eta ,\mathbf{k}) =\frac{a}{\sqrt{2}}~M_p~\gamma _{\lambda }(\eta ,\mathbf{k})= -\frac{1}{\sqrt{2}H\eta }~M_p~\gamma _{\lambda }(\eta ,\mathbf{k})$. Using $u_{\lambda }(\eta ,\mathbf{k})$ one can further write down the second-order action for the graviton as

$$\begin{aligned} S^{(2)}_{\gamma }\approx & {} \int \mathrm{d}^{3}x~\mathrm{d}\eta ~a^2~\frac{M^2_p}{4}\nonumber \\&\times \left[ u^{'2}_{\lambda }(\eta ,\mathbf{k}) -\left( k^2-\frac{a^{\prime \prime }}{a}\right) (u_{\lambda }(\eta ,\mathbf{k}))^2 \right] . \end{aligned}$$

(7.24)

Fig. 10

r vs. $n_\mathrm{S}$ plot for the non-attractor phase of inflation for Higgsotic model in the background of confidence contours obtained from Planck TT+low P, Planck TT+low P+BKP, Planck TT+low P+BKP+BAO joint data sets

From this action one can find the mode equation for the tensor fluctuation as

$$\begin{aligned} u^{\prime \prime }_{\lambda }(\eta ,\mathbf{k})+\left( k^2-\frac{a^{\prime \prime }}{a}\right) u_{\lambda }(\eta ,\mathbf{k})=0. \end{aligned}$$

(7.25)

It is important to mention here that for the de Sitter case we have $\frac{a^{\prime \prime }}{a}=\frac{2}{\eta ^2}$. Further considering the behavior of the solution in the superhorizon and subhorizon regimes for the Bunch–Davies vacuum we get

$$\begin{aligned} u_{\lambda }(\eta ,\mathbf{k})= & {} \frac{1}{i\eta \sqrt{2}~ k^{\frac{3}{2}}}~\mathrm{e}^{-i(k\eta +\pi )}~(1+ik\eta ). \end{aligned}$$

(7.26)

At the horizon crossing taking the late time limit one can write down the following expression for the two point function for scalar fluctuation:

$$\begin{aligned} \langle h(\eta ,\mathbf{k}) h(\eta ,\mathbf{q})\rangle= & {} \sum _{\lambda ,\lambda ^{\prime }} \langle h_{\lambda }(\eta ,\mathbf{k})h_{\lambda ^{\prime }}(\eta ,\mathbf{q})\rangle \nonumber \\= & {} (2\pi )^3\delta ^{(3)}(\mathbf{k}+\mathbf{q})P_\mathrm{h}(k,\eta ), \end{aligned}$$

(7.27)

where $P_\mathrm{h}(k_*)$ is known as the power spectrum at the horizon crossing for tensor fluctuations and it is defined as

$$\begin{aligned} P_\mathrm{h}(k_*)=\frac{4H^2}{M^2_p}. \end{aligned}$$

(7.28)

For simplicity one can further define the amplitude of the power spectrum $\mathcal{P}_{\mathrm{T}}(\mathcal{N}_{cmb})$ at the horizon crossing as

$$\begin{aligned} \mathcal{P}_{\mathrm{T}}(\mathcal{N}_{cmb})=\frac{1}{2\pi ^2}P_\mathrm{h}(k_*)=\frac{2H^2}{\pi ^2~M^2_p}. \end{aligned}$$

(7.29)

7.3.2 Future observables

Applying slow-roll approximation in the present context the future inflationary observables i.e. power spectrum, spectral tilt, running and running of the running of the tilt for tensor modes from our model at horizon crossing ($\mathcal{N}=\mathcal{N}_{cmb}$) can be computed as

$$\begin{aligned}&\mathcal{P}_{\mathrm{T}}(\mathcal{N}_{cmb})=\frac{2\tilde{W}(\phi _{cmb},{\varvec{\Psi }})}{3\pi ^{2}M^{4}_{p}}\nonumber \\&~~~~~~~~~~~~~~~\quad =\frac{1}{12\pi ^{2}\alpha }\left[ 1+32\alpha \bar{\lambda }\mathcal{N}^{2}_{cmb}\right] ,\end{aligned}$$

(7.30)

$$\begin{aligned}&n_{\mathrm{T}}(\mathcal{N}_{cmb})=\left( \frac{\mathrm{d}\ln \mathcal{P}_{\mathrm{T}}}{\mathrm{d}\mathcal{N}}\right) _{\mathcal{N}_{cmb}} = \frac{64\alpha \bar{\lambda }\mathcal{N}_{cmb}}{\left[ 1+32\alpha \bar{\lambda }\mathcal{N}^{2}_{cmb}\right] },\nonumber \\&\alpha _{\mathrm{T}}(\mathcal{N}_{cmb})=\left( \frac{\mathrm{d}n_{\mathrm{T}}}{\mathrm{d}\mathcal{N}}\right) _{\mathcal{N}_{cmb}} = \frac{64\alpha \bar{\lambda }\left[ 1-32\alpha \bar{\lambda }\mathcal{N}^{2}_{cmb}\right] }{\left[ 1+32\alpha \bar{\lambda }\mathcal{N}^{2}_{cmb}\right] ^2},\end{aligned}$$

(7.31)

$$\begin{aligned}&\kappa _{\mathrm{T}}(\mathcal{N}_{cmb})=\left( \frac{\mathrm{d}\alpha _{\mathrm{T}}}{\mathrm{d}\mathcal{N}}\right) _{\mathcal{N}_{cmb}}= -2048\alpha ^2 \bar{\lambda }^2 \mathcal{N}_{cmb}\nonumber \\&\qquad \times \left[ \frac{\mathcal{N}_{cmb}\left[ 1+32\alpha \bar{\lambda }\mathcal{N}^{2}_{cmb}\right] ^2+4 \left[ 1-1024\alpha ^2 \bar{\lambda }^2 \mathcal{N}^{4}_{cmb}\right] }{\left[ 1+32\alpha \bar{\lambda }\mathcal{N}^{2}_{cmb}\right] ^4}\right] ,\nonumber \\\end{aligned}$$

(7.32)

$$\begin{aligned}&r(\mathcal{N}_{cmb}) =\frac{\mathcal{P}_{\mathrm{T}}(\mathcal{N}_{cmb})}{\mathcal{P}_\mathrm{S}(\mathcal{N}_{cmb})}= 16\epsilon ^{*}_{\tilde{W}} = \frac{32768\alpha ^{2}\bar{\lambda }^{2}\mathcal{N}^{3}_{cmb}}{\left[ 1+32\alpha \bar{\lambda }\mathcal{N}^{2}_{cmb}\right] ^{2}}. \end{aligned}$$

(7.33)

In Fig. 10, we have plotted the tensor-to-scalar ratio (r) vs. spectral tilt for scalar perturbation ($n_\mathrm{S}$) in the light of Planck data along with various joint constraints. Here it is important to note that the non-attractor phase of inflation for Higgsotic model is shown by the green and pink colored lines. Also the big circle, intermediate size circle and small circle represent the representative points in $(r,n_\mathrm{S})$ 2D plane for the number of e-foldings, $\mathcal{N}_{cmb}=70$, $\mathcal{N}_{cmb}=60$ and $\mathcal{N}_{cmb}=50$, respectively. To represent the present status as well as the statistical significance of the Higgsotic model in its non-attractor phase, we have drawn the $1\sigma$ and $2\sigma$ confidence contours from Planck TT+low P, Planck TT+low P+BKP, Planck TT+low P+BKP+BAO joint data sets [44,45,46] in Fig. 10. It is clear from Fig. 10 that we cover the range $0.94<n_\mathrm{S}<0.96$ and $0.06<r<0.11$ in the $(r,n_\mathrm{S})$ 2D plane.

Now to derive the constraints on the model parameters $\alpha$ and $\bar{\lambda }$ we use Eq. (7.18) and Eq. (7.33), which can be recast as

$$\begin{aligned} \alpha\approx & {} \frac{1}{(96\pi ^{2}\mathcal{P}_\mathrm{S}(\mathcal{N}_{cmb}))^{1/3}\bar{\lambda }^{2/3}\times 16\mathcal{N}_{cmb}},\end{aligned}$$

(7.34)

$$\begin{aligned} \bar{\lambda }\approx & {} (96\pi ^{2}\mathcal{P}_\mathrm{S}(\mathcal{N}_{cmb}))\left[ \frac{r(\mathcal{N}_{cmb})}{128\mathcal{N}_{cmb}}\right] ^{3/2}. \end{aligned}$$

(7.35)

Further substituting Eq. (7.35) on Eq. (7.34) finally we get

$$\begin{aligned} \alpha\approx & {} \frac{1}{12\pi ^{2}\mathcal{P}_\mathrm{S}(\mathcal{N}_{cmb})r(\mathcal{N}_{cmb})}. \end{aligned}$$

(7.36)

In terms of the number of e-foldings ($\mathcal{N}$) the most useful parametrization of the primordial scalar and tensor power spectrum or equivalently for the tensor-to-scalar ratio can be written near the horizon crossing $\mathcal{N}=\mathcal{N}_{cmb}$ as

$$\begin{aligned} r(\mathcal{N})= & {} \frac{\mathcal{P}_{\mathrm{T}}(\mathcal{N})}{\mathcal{P}_\mathrm{S}(\mathcal{N})}=r(\mathcal{N}_{cmb})\exp [(\mathcal{N}-\mathcal{N}_{cmb})\{A(\mathcal{N}_{cmb})\nonumber \\&+\,B(\mathcal{N}_{cmb})(\mathcal{N}-\mathcal{N}_{cmb}) +C(\mathcal{N}_{cmb})(\mathcal{N}-\mathcal{N}_{cmb})^2\}]\nonumber \\ \end{aligned}$$

(7.37)

where the symbols $A(\mathcal{N}_{cmb})$, $B(\mathcal{N}_{cmb})$ and $C(\mathcal{N}_{cmb})$ are expressed in terms of the inflationary observables at horizon crossing as $A(\mathcal{N}_{cmb})=n_{\mathrm{T}}(\mathcal{N}_{cmb})-n_\mathrm{S}(\mathcal{N}_{cmb})+1$, $B(\mathcal{N}_{cmb})=\frac{1}{2}(\alpha _{\mathrm{T}}(\mathcal{N}_{cmb})-\alpha _\mathrm{S}(\mathcal{N}_{cmb}))$, $C(\mathcal{N}_{cmb})=\frac{1}{6}(\kappa _{\mathrm{T}}(\mathcal{N}_{cmb})-\kappa _\mathrm{S}(\mathcal{N}_{cmb}))$. In the above parametrization, $A(\mathcal{N}_{cmb})\gg B(\mathcal{N}_{cmb})\gg C(\mathcal{N}_{cmb})$ is always required for convergence of the Taylor expansion. For the time being to make the computation simpler let us assume that the term involving the coefficient of the quadratic term $B(\mathcal{N}_{cmb})$ and cubic term $C(\mathcal{N}_{cmb})$ is negligibly small compared to the leading-order term $A(\mathcal{N}_{cmb})$ as appearing in the exponent of the above mentioned parametrization. Using this assumption the relation between field excursion and tensor-to-scalar ratio can be computed as

$$\begin{aligned} \frac{|\Delta \phi |}{M_p}\approx & {} \frac{2}{A(\mathcal{N}_{cmb})}\sqrt{\frac{r(\mathcal{N}_{cmb})}{8}} \left[ 1-\mathrm{e}^{-\Delta \mathcal{N}\left( \frac{A(\mathcal{N}_{cmb})}{2}\right) }\right] \nonumber \\\approx & {} \sqrt{\frac{r(\mathcal{N}_{cmb})}{8}}\Delta \mathcal{N} \end{aligned}$$

(7.38)

and finally using the above relation from our $R^2$ gravity model we get

$$\begin{aligned} r(\mathcal{N}_{cmb})\approx & {} 8\left( \frac{|\Delta \phi |}{M_p \Delta \mathcal{N}}\right) ^{2} \approx 32\left( \frac{\left[ \sqrt{\mathcal{N}_{\mathrm{total}}}-\sqrt{\mathcal{N}_{cmb}}\right] }{\Delta \mathcal{N}}\right) ^{2}\nonumber \\= & {} \frac{32}{\left[ \sqrt{\mathcal{N}_{\mathrm{total}}}+\sqrt{\mathcal{N}_{cmb}}\right] ^2}. \end{aligned}$$

(7.39)

For our prescribed model $|\Delta \phi |\approx 1.2 ~\mathrm{M}_{p}$ and $\Delta \mathcal{N}=10$ is fixed by Planck 2015 observation. Substituting these values in the relation stated in Eq. (7.39), the upper bound of the tensor-to-scalar ratio at the scale of horizon crossing computed from our setup as $r(\mathcal{N}_{cmb})\lesssim 0.11$. Now in the present context using Eq. (7.19) we can express the number of e-foldings at the horizon crossing as

$$\begin{aligned} \mathcal{N}_{cmb}=\frac{3}{1-n_\mathrm{S}(\mathcal{N}_{cmb})} \end{aligned}$$

(7.40)

and substituting in Eq. (7.20) we get the following sets of consistency relations for scalar modes from our analysis:

$$\begin{aligned} \alpha _\mathrm{S}(\mathcal{N}_{cmb})\approx & {} \frac{\left( 1-n_\mathrm{S}(\mathcal{N}_{cmb})\right) ^{2}}{3},\end{aligned}$$

(7.41)

$$\begin{aligned} \kappa _\mathrm{S}(\mathcal{N}_{cmb})\approx & {} -\frac{2\left( 1-n_\mathrm{S}(\mathcal{N}_{cmb})\right) ^{3}}{9} \end{aligned}$$

(7.42)

and combining Eqs. (7.41) and (7.42) we finally get

$$\begin{aligned} 1-n_\mathrm{S}(\mathcal{N}_{cmb})+\frac{3\kappa _\mathrm{S}(\mathcal{N}_{cmb})}{2\alpha _\mathrm{S}(\mathcal{N}_{cmb})}\approx 0. \end{aligned}$$

(7.43)

Similarly from tensor modes we get the following sets of consistency relations from our model:

$$\begin{aligned} r(\mathcal{N}_{cmb}) \approx 16\epsilon ^{*}_{\tilde{W}}= & {} \frac{884736\alpha ^{2}\bar{\lambda }^{2}}{\left( 1-n_\mathrm{S}(\mathcal{N}_{cmb})\right) ^{3} \left[ 1+\frac{288\alpha \bar{\lambda }}{\left( 1-n_\mathrm{S}(\mathcal{N}_{cmb})\right) ^2}\right] ^2}\nonumber \\= & {} \frac{884736\alpha ^{2}\bar{\lambda }^{2}}{\left( 3\alpha _\mathrm{S}(\mathcal{N}_{cmb}) \right) ^{3/2}\left[ 1+\frac{96\alpha \bar{\lambda }}{\alpha _\mathrm{S}(\mathcal{N}_{cmb})}\right] ^2} \nonumber \\= & {} -\frac{196608\alpha ^{2}\bar{\lambda }^{2}}{\kappa _\mathrm{S}(\mathcal{N}_{cmb})\left[ 1+\frac{288\alpha \bar{\lambda }}{\left\{ -\frac{9}{2} \kappa _\mathrm{S}(\mathcal{N}_{cmb})\right\} ^{2/3}}\right] ^2}\nonumber \\= & {} \frac{24n^{2}_{\mathrm{T}}(\mathcal{N}_{cmb})}{1-n_\mathrm{S}(\mathcal{N}_{cmb})}. \end{aligned}$$

(7.44)

It is important to mention here that in the present context the usual consistency relation for single field slow-roll inflation,

$$\begin{aligned} r(\mathcal{N}_{cmb})=-8n_{\mathrm{T}}(\mathcal{N}_{cmb}) \end{aligned}$$

(7.45)

violates and after doing the analysis we found a completely new consistency relation as presented in Eq. (7.44). In the case of usual slow-roll single field inflationary setup the tensor spectral tilt, $n_{\mathrm{T}}(\mathcal{N}_{cmb})<0$ always. But for the prescribed setup Eq. (7.31), Eq. (7.35) and Eq. (7.36) suggest that $\bar{\lambda }>0,\alpha >0$ always imply $n_{\mathrm{T}}(\mathcal{N}_{cmb})>0$. Further using Eq. (7.39) in Eq. (7.44) we get the following constraint relationship:

$$\begin{aligned} \frac{|\Delta \phi |}{M_p}\approx & {} 2\left[ \sqrt{\mathcal{N}_{\mathrm{total}}}-\sqrt{\mathcal{N}_{cmb}}\right] \nonumber \\= & {} \sqrt{\frac{3}{1-n_\mathrm{S}(\mathcal{N}_{cmb})}}n_{\mathrm{T}}(\mathcal{N}_{cmb})\nonumber \\&\times \left[ \mathcal{N}_{\mathrm{total}} -\frac{3}{1-n_\mathrm{S}(\mathcal{N}_{cmb})}\right] . \end{aligned}$$

(7.46)

7.4 Reheating

The above results provide limits on the reheating temperature $T_{\mathrm{reh}}$, defined as the initial temperature of the homogeneous radiation dominated universe. In general, the reheating temperature $T_{\mathrm{reh}}$ is related to the energy density $\rho _{\mathrm{reh}}$ through the following expression:

$$\begin{aligned} \rho _{\mathrm{reh}}= & {} \frac{\pi ^{2}}{30}g_\mathrm{eff}(T_{\mathrm{reh}})T^{4}_{\mathrm{reh}} \Rightarrow T_{\mathrm{reh}}\nonumber \\= & {} \left( \frac{30}{\pi ^{2}g_\mathrm{eff}(T_{\mathrm{reh}})}\right) ^{1/4}\rho ^{1/4}_{\mathrm{reh}}\nonumber \\\approx & {} \left( \frac{30}{\pi ^{2}g_\mathrm{eff}(T_{\mathrm{reh}})}\right) ^{1/4}V^{1/4}_{\mathrm{reh}} \end{aligned}$$

(7.47)

where $g_\mathrm{eff}(T_{\mathrm{reh}})$ is the effective number of relativistic degrees of freedom present in the thermal bath at the temperature $T=T_{\mathrm{reh}}$ and $V_{\mathrm{reh}}$ represents the scale of reheating at $\phi =\phi _{\mathrm{reh}}$ given by the expression $V_{\mathrm{reh}}=V(\phi =\phi _{\mathrm{reh}})=V_0\left[ 1+\frac{2\alpha \bar{\lambda }}{M^{4}_{p}}\phi ^{4}_{\mathrm{reh}}\right]$. Counting all degrees of freedom of the Standard Model and the dilaton degrees of freedom, one has $g_\mathrm{eff}(T_{\mathrm{reh}})=107.75$. To find the reheating constraint from our prescribed setup let us introduce the number of e-foldings at the time of reheating defined as

$$\begin{aligned} \mathcal{N}_{\mathrm{reh}}= & {} \int ^{t_{e}}_{t_{\mathrm{reh}}} H~\mathrm{d}t=\mathcal{N}_{\mathrm{total}}-\overline{\Delta \mathcal{N}}\nonumber \\\approx & {} -\frac{1}{M^2_p}\int ^{\phi _{e}}_{\phi _{\mathrm{reh}}} \frac{\tilde{W}(\phi ,{\varvec{\Psi }})}{\partial _{\phi } \tilde{W}(\phi ,{\varvec{\Psi }})}~\mathrm{d}\phi \nonumber \\= & {} \frac{M^{2}_{p}}{16\alpha \bar{\lambda }}\left\{ \frac{1}{\phi ^2_e}- \frac{1}{\phi ^2_{\mathrm{reh}}}\right\} -\frac{1}{8M^2_p}\left( \phi ^2_e- \phi ^2_{\mathrm{reh}}\right) . \end{aligned}$$

(7.48)

For the sake of clarity let us express the interval $\overline{\Delta \mathcal{N}}$ as

$$\begin{aligned} \overline{\Delta \mathcal{N}}= & {} \int ^{t_{e}}_{t_{i}} H~dt-\int ^{t_{e}}_{t_{\mathrm{reh}}} H~dt=\int ^{t_{\mathrm{reh}}}_{t_{i}} H~dt\nonumber \\= & {} \mathcal{N}_{\mathrm{total}}-\mathcal{N}_{\mathrm{reh}}=\Delta \mathcal{N}-\left( \mathcal{N}_{\mathrm{reh}}-\mathcal{N}_{cmb}\right) \nonumber \\\Rightarrow & {} \Delta \mathcal{N}-\overline{\Delta \mathcal{N}}=\mathcal{N}_{\mathrm{reh}}-\mathcal{N}_{cmb}\nonumber \\= & {} \frac{M^{2}_{p}}{16\alpha \bar{\lambda }} \left\{ \frac{1}{\phi ^2_{cmb}}-\frac{1}{\phi ^2_{\mathrm{reh}}}\right\} -\frac{1}{8M^2_p}\left( \phi ^2_{cmb}-\phi ^2_{\mathrm{reh}}\right) .\nonumber \\ \end{aligned}$$

(7.49)

Finally using the last step of Eq. (7.49) the field value during reheating can be expressed as

$$\begin{aligned} \phi _{\mathrm{reh}}= & {} \frac{M_{p}}{2}\sqrt{\frac{\mathcal{M}_{\mathrm{reh}}}{\alpha \bar{\lambda }}} \left[ 1+\sqrt{1+\frac{8\alpha \bar{\lambda }}{\mathcal{M}^{2}_{\mathrm{reh}}}}\right] ^{\frac{1}{2}} \approx \frac{M_p}{2}\sqrt{\frac{\mathcal{M}_{\mathrm{reh}}}{\alpha \bar{\lambda }}}\nonumber \\\approx & {} 2M_{p}\sqrt{\left( \Delta \mathcal{N}-\overline{\Delta \mathcal{N}}\right) }\approx 2M_{p}\sqrt{\mathcal{N}_{\mathrm{reh}}-\mathcal{N}_{cmb}}\nonumber \\ \end{aligned}$$

(7.50)

where

$$\begin{aligned} \mathcal{M}_{\mathrm{reh}}= & {} \alpha \bar{\lambda }\left[ 16\left( \Delta \mathcal{N}-\overline{\Delta \mathcal{N}}\right) +8\mathcal{N}_{cmb}\right] -\frac{1}{4\mathcal{N}_{cmb}}\nonumber \\\approx & {} 16\alpha \bar{\lambda }\left( \Delta \mathcal{N}-\overline{\Delta \mathcal{N}}\right) . \end{aligned}$$

(7.51)

Using Eq. (7.51) finally we get the scale of reheating in terms of the number of e-foldings as

$$\begin{aligned} V_{\mathrm{reh}}\approx & {} V_0[1+32\alpha \bar{\lambda }(\Delta \mathcal{N}-\overline{\Delta \mathcal{N}})^{2}]\nonumber \\= & {} V_0[1+32\alpha \bar{\lambda }(\mathcal{N}_{\mathrm{reh}}-\mathcal{N}_{cmb})^{2}]. \end{aligned}$$

(7.52)

Further substituting Eq. (7.52) in Eq. (7.47) the reheating temperature can be expressed in terms of the number of e-foldings and scale of inflation in the context of our proposed model as

$$\begin{aligned} T_{\mathrm{reh}}\approx & {} \left( \frac{30}{\pi ^{2}g_\mathrm{eff}(T_{\mathrm{reh}})}\right) ^{1/4} V^{1/4}_{0}[1+32\alpha \bar{\lambda }(\Delta \mathcal{N}-\overline{\Delta \mathcal{N}})^{2}]^{1/4}\nonumber \\= & {} \left( \frac{30}{\pi ^{2}g_\mathrm{eff}(T_{\mathrm{reh}})}\right) ^{1/4} \left( \frac{1}{8\alpha }+4\bar{\lambda }\left( \mathcal{N}_{\mathrm{reh}}-\mathcal{N}_{cmb}\right) ^{2}\right) ^{1/4}~M_p\nonumber \\= & {} \left[ \frac{45\pi ^{2}\mathcal{P}_\mathrm{S}(\mathcal{N}_{cmb})r(\mathcal{N}_{cmb})}{g_\mathrm{eff}(T_{\mathrm{reh}})} \left\{ 1+2\left[ \frac{r(\mathcal{N}_{cmb})}{128\mathcal{N}^{3}_{cmb}}\right] ^{1/2}\right. \right. \nonumber \\&\times \left. \left. \left( \mathcal{N}_{\mathrm{reh}}-\mathcal{N}_{cmb}\right) ^{2}\phantom {\frac{30}{\pi ^{2}g_\mathrm{eff}(T_{\mathrm{reh}})}}\right\} \right] ^{1/4}M_p. \end{aligned}$$

(7.53)

8 Future probe: primordial non-Gaussianity

8.1 Three point function

8.1.1 Using the In-In formalism

Here we discuss the constraint on the primordial three point scalar correlation function in the non-attractor regime of soft inflation. In general one can write down the following expressions for the three point function of the scalar fluctuation: [2, 157,158,159,160,161,162,163,164,165,166,167,168,169]:

$$\begin{aligned} \langle \zeta (\mathbf{k}_1)\zeta (\mathbf{k}_2)\zeta (\mathbf{k}_3)\rangle =(2\pi )^3\delta ^{(3)}(\mathbf{k}_1+{} \mathbf{k}_2+\mathbf{k}_3)B(k_1,k_2,k_3).\nonumber \\ \end{aligned}$$

(8.1)

In our computation we choose the Bunch–Davies vacuum state and for single field soft slow-roll inflation we get the following expression for the bispectrum:

$$\begin{aligned}&B(k_1,k_2,k_3)\approx \frac{\tilde{W}^2(\phi _{cmb}, {\varvec{\Psi }})}{288(\epsilon ^*_{\tilde{W}})^2M^6_p (k_1k_2k_3)^3}\nonumber \\&\quad \times \left[ 2(3\epsilon ^*_{\tilde{W}}- \eta ^{*}_{\tilde{W}})\sum ^{3}_{i=1}k^3_i +\epsilon ^*_{\tilde{W}}\left( -\sum ^{3}_{i=1}k^3_i\right. \right. \nonumber \\&\quad \left. \left. +\sum ^{3}_{i,j=1,i\ne j}k_i k^2_j+\frac{8}{K}\sum ^{3}_{i,j=1,i> j}k^2_i k^2_j\right) \right] , \end{aligned}$$

(8.2)

where $K=k_1+k_2+k_3=\sum ^{3}_{i=1}k_i$,and the potential flow functions in an Einstein frame can be expressed in terms of number of e-foldings $\mathcal{N}_{cmb}$ as

$$\begin{aligned} \tilde{\epsilon }_{\tilde{W}}= & {} \left[ \frac{M^{2}_{p}}{2}(\partial _{\phi } \ln \tilde{W}(\phi ,{\varvec{\Psi }}))^{2}\right] _{\phi =\phi _{cmb}}\nonumber \\= & {} \frac{32\alpha ^{2}\bar{\lambda }^{2}\phi ^{6}_{cmb}}{M^{6}_{p} \left[ 1+\frac{2\alpha \bar{\lambda }}{M^{4}_{p}}\phi ^{4}_{cmb}\right] ^{2}} =\frac{2048\alpha ^{2}\bar{\lambda }^{2}\mathcal{N}^3_{cmb}}{\left[ 1+32\alpha \bar{\lambda }\mathcal{N}^2_{cmb}\right] ^{2}},\end{aligned}$$

(8.3)

$$\begin{aligned} \tilde{\eta }_{\tilde{W}}= & {} \left[ {M^{2}_{p}} \frac{\partial _{\phi \phi }\tilde{W}(\phi ,{\varvec{\Psi }})}{\tilde{W}(\phi ,{\varvec{\Psi }})}\right] _{\phi =\phi _{cmb}} =\frac{24\alpha \bar{\lambda }\phi ^{2}_{cmb}}{M^{2}_{p}\left[ 1+\frac{2\alpha \bar{\lambda }}{M^{4}_{p}}\phi ^{4}_{cmb}\right] }\nonumber \\= & {} \frac{96\alpha \bar{\lambda }\mathcal{N}_{cmb}}{\left[ 1+32\alpha \bar{\lambda }\mathcal{N}^2_{cmb}\right] }. \end{aligned}$$

(8.4)

In the present context one can parameterize non-Gaussianity phenomenologically via a non-linear correction to a Gaussian perturbation $\zeta _{g}$ in position space as [2]

$$\begin{aligned} \zeta (\mathbf{x})=\zeta _{g}(\mathbf{x})+\frac{3}{5}f^{\mathrm{{loc}}}_{\mathrm{NL}}[\zeta ^2_{g}(\mathbf{x})-\langle \zeta ^2_{g}(\mathbf{x})\rangle ]+\cdots , \end{aligned}$$

(8.5)

where $\cdots$ represents higher-order non-Gaussian contributions. This definition is local in real space and therefore called local non-Gaussianity. In the case of local non-Gaussianity, the amplitude of the bispectrum from the three point function is defined as [2]

$$\begin{aligned}&f^{\mathrm{{loc}}}_{\mathrm{NL}}(k_1,k_2,k_3)\nonumber \\&\quad =\frac{5}{6}\frac{B(k_1,k_2,k_3)}{\left[ P_{\zeta }(k_1)P_{\zeta }(k_2)+P_{\zeta }(k_2) P_{\zeta }(k_3)+P_{\zeta }(k_1)P_{\zeta }(k_3)\right] }.\nonumber \\ \end{aligned}$$

(8.6)

Further substituting the expression for the bispectrum and power spectrum the non-Gaussianity amplitude can be expressed as

$$\begin{aligned}&f^{\mathrm{{loc}}}_{\mathrm{NL}}(k_1,k_2,k_3) \approx \frac{5}{12}\frac{1}{\sum ^{3}_{i=1}k^3_i} \left[ 2(3\epsilon ^*_{\tilde{W}}-\eta ^{*}_{\tilde{W}}) \sum ^{3}_{i=1}k^3_i\right. \nonumber \\&\quad \left. +\epsilon ^*_{\tilde{W}}\left( -\sum ^{3}_{i=1}k^3_i+\sum ^{3}_{i,j=1,i\ne j}k_i k^2_j+\frac{8}{K}\sum ^{3}_{i,j=1,i> j}k^2_i k^2_j\right) \right] .\nonumber \\ \end{aligned}$$

(8.7)

Fig. 11

Representative S, T and U channel Feynman–Witten diagram for bulk interpretation of three point scalar correlation function in the presence of graviton exchange contribution. In all the diagrams the graviton is propagating on the bulk and the end points of the scalars are attached to the boundary at $z=0$. More precisely the wavy line denotes the bulk-to-bulk graviton propagator, the solid lines represent the bulk-to-boundary propagators for the scalar field and the dashed line denotes background represented by $\partial _{z}{\bar{\phi }}$

To give the bulk interpretation of the obtained results for scalar three point correlation function here we start with the graviton propagator which can be computed from the second-order fluctuation in $\delta g_{\mu \nu }$ for the canonical scalar field action minimally coupled with Einstein gravity. In this context we choose a gauge $\delta g_{zz}=0=\delta g_{zi}$, which is equivalent to choosing $N^i =0, N=1$ in the ADM formalism. After choosing this gauge we get

$$\begin{aligned}&G_{ij;kl}(z_1,\mathbf{y}_{1};z_2,\mathbf{y}_{2})=\int \frac{\mathrm{d}^3\mathbf{k}}{(2\pi )^3}\mathrm{e}^{i\mathbf{k}.(\mathbf{y}_1-\mathbf{y}_2)}\nonumber \\&\quad \times \int ^{\infty }_{0}q\mathrm{d}q\frac{J_{\frac{3}{2}} (qz_1)J_{\frac{3}{2}}(qz_2)}{2\sqrt{z_1z_2}}\Delta _{ijkl}, \end{aligned}$$

(8.8)

where $\Delta _{ijkl}$ is defined as $\Delta _{ijkl}=P_{ik}P_{jl}+P_{il}P_{jk}-P_{ij}P_{kl}$. Here $P_{ij}$ is the projection operator in momentum space, which is defined as $P_{ij}=(\delta _{ij}+k_i k_j/q^2)$. Further one can also write down the expression for the transverse part of the graviton propagator from this computation:

$$\begin{aligned}&\bar{G}_{ij;kl}(z_1,\mathbf{y}_{1};z_2,\mathbf{y}_{2})= \int \frac{\mathrm{d}^3\mathbf{k}}{(2\pi )^3}\mathrm{e}^{i\mathbf{k}.(\mathbf{y}_1-\mathbf{y}_2)}\nonumber \\&\quad \times \int ^{\infty }_{0}q\mathrm{d}q\frac{J_{\frac{3}{2}}(qz_1) J_{\frac{3}{2}}(qz_2)}{2\sqrt{z_1z_2}}\bar{\Delta }_{ijkl}, \end{aligned}$$

(8.9)

where $\bar{\Delta }_{ijkl}$ is defined as $\bar{\Delta }_{ijkl}=\bar{P}_{ik}\bar{P}_{jl}+\bar{P}_{il}\bar{P}_{jk}-\bar{P}_{ij}\bar{P}_{kl}$. Here $\bar{P}_{ij}$ is the transverse part of the projection operator in momentum space, which is defined as $\bar{P}_{ij}=(\delta _{ij}-k_i k_j/q^2)$. Similarly the longitudinal part of the graviton propagator can be expressed as

$$\begin{aligned} \hat{G}_{ij;kl}(z_1,\mathbf{y}_{1};z_2,\mathbf{y}_{2})= & {} G_{ij;kl}(z_1,\mathbf{y}_{1};z_2,\mathbf{y}_{2})\nonumber \\&-\,\bar{G}_{ij;kl}(z_1,\mathbf{y}_{1};z_2,\mathbf{y}_{2}). \end{aligned}$$

(8.10)

Consequently in the bulk the on-shell action can be written as a sum of transverse and longitudinal contributions as

$$\begin{aligned} S^\mathrm{Bulk}_{\mathrm{{on}}\text {-}\mathrm{{shell}}} =-\frac{3M^2_p}{2\Lambda }(Z_{\mathrm{{tr}}}+Z_{\mathrm{long}}), \end{aligned}$$

(8.11)

where $\Lambda$ is the cosmological constant. In this context the transverse contribution $Z_{\mathrm{{tr}}}$ and longitudinal contribution $Z_{\mathrm{long}}$ are defined as

$$\begin{aligned} Z_{\mathrm{{tr}}}= & {} \int \mathrm{d}z_{1}\mathrm{d}z_{2}\mathrm{d}^{3}{} \mathbf{y}_1 \mathrm{d}^{3}{} \mathbf{y}_2 T_{mn}(z_1,\mathbf{y}_1)\nonumber \\&\times \bar{G}_{mn;kl}(z_1,\mathbf{y}_{1};z_2,\mathbf{y}_{2})T_{kl}(z_1,\mathbf{y}_1),\end{aligned}$$

(8.12)

$$\begin{aligned} Z_{\mathrm{long}}= & {} -\int \frac{\mathrm{d}z}{z^2}\int \mathrm{d}^3\mathbf{y}\left[ T_{zk}(z,\mathbf{y})\partial ^{-2}T_{zk}(z,\mathbf{y})\phantom {\frac{1}{2}}\right. \nonumber \\&+\,\frac{z}{2}\partial _{k}T_{zk}(z,\mathbf{y})\partial ^{-2}T_{zz}(z,\mathbf{y})\nonumber \\&+\left. \frac{1}{4}\partial _{k}T_{zk}(z,\mathbf{y})(\partial ^{-2})^2\partial _{m}T_{zm}(z,\mathbf{y})\right] . \end{aligned}$$

(8.13)

Finally one can write down the following simplified expression:

$$\begin{aligned}&S^\mathrm{Bulk}_{\mathrm{{on}}\text {-}\mathrm{{shell}}}= -\frac{3M^2_p}{2\Lambda }\sqrt{2\epsilon }(2\pi )^3\delta ^{(3)}(\mathbf{k}_1+\mathbf{k}_2+\mathbf{k}_3)\prod ^{3}_{n=1}\phi _{0}(k_{n})\nonumber \\&\quad \times \left[ -\sum ^{3}_{i=1}k^3_i+\sum ^{3}_{i,j=1,i\ne j}k_i k^2_j+\frac{8}{K}\sum ^{3}_{i,j=1,i> j}k^2_i k^2_j\right] .\nonumber \\ \end{aligned}$$

(8.14)

Further taking the derivatives with respect to the background field value $\phi _0$ and choosing the gauge $\zeta =-H\delta \phi /\dot{\phi }$, one can write down the following expression for the scalar three point function:

$$\begin{aligned}&\langle \zeta (\mathbf{k}_1)\zeta (\mathbf{k}_2)\zeta (\mathbf{k}_3)\rangle =(2\pi )^3\delta ^{(3)}(\mathbf{k}_1+\mathbf{k}_2+\mathbf{k}_3)\nonumber \\&\quad \times \,\frac{H^4}{32(\epsilon ^*_{H})^2M^4_p}\frac{1}{(k_1k_2k_3)^3}\left[ 2(2\epsilon ^*_{H}-\eta ^*_{H})\sum ^{3}_{i=1}k^3_i\right. \nonumber \\&\quad \left. +\,\epsilon ^*_{H}\left( -\sum ^{3}_{i=1}k^3_i+\sum ^{3}_{i,j=1,i\ne j}k_i k^2_j+\frac{8}{K}\sum ^{3}_{i,j=1,i> j}k^2_i k^2_j\right) \right] ,\nonumber \\ \end{aligned}$$

(8.15)

which can be expressed in terms of the effective potentials using the Friedman equations and using the relation between Hubble and potential dependent slow-roll parameters. The representative S, T and U channel Feynman–Witten diagrams for bulk interpretation of the three point scalar correlation function in the presence of graviton exchange is shown in shown in Fig. 11a–c. In these diagrams we have explicitly shown that the graviton is propagating on the bulk and the end points of the scalars are attached to the boundary at $z=0$. Additionally, it is important to note that the dashed line represents background denoted by $\partial _{z}{\bar{\phi }}$ in all of the representative diagrams. Here $\bar{\phi }$ is the background field value. More precisely the wavy line denotes the bulk-to-bulk graviton propagator, the solid lines represent the bulk-to-boundary propagators for the scalar field. In our computation all the representative diagrams are important to explain the total three point scalar correlation function.

Table 4 Constraint on scalar three point non-Gaussian amplitude from equilateral and squeezed configuration

To analyze the shape of the bispectrum here we further consider two limiting configurations – the equilateral limit and the squeezed limit. In these limits, the final simplified results are appended below:

Fig. 12

Representative diagram for equilateral non-Gaussian three point amplitude vs. product of the parameters $\alpha \bar{\lambda }$ in four different regions for $\mathcal{N}_{cmb}=50$ (red), $\mathcal{N}_{cmb}=60$ (blue) and $\mathcal{N}_{cmb}=70$ (green)

Fig. 13

Representative 3D diagram for equilateral non-Gaussian three point amplitude vs. the model parameters $\alpha$ and $\bar{\lambda }$ for $\mathcal{N}_{cmb}=60$ in two different angular views

Fig. 14

Representative diagram for squeezed non-Gaussian three point amplitude vs. product of the parameters $\alpha \bar{\lambda }$ in four different regions for $\mathcal{N}_{cmb}=50$ (red), $\mathcal{N}_{cmb}=60$ (blue) and $\mathcal{N}_{cmb}=70$ (green)

Fig. 15

Representative 3D diagram for squeezed non-Gaussian three point amplitude vs. the model parameters $\alpha$ and $\bar{\lambda }$ for $\mathcal{N}_{cmb}=60$ in two different angular views

• 1. Equilateral limit configuration: For this case we have $|\mathbf{k}_1|=|\mathbf{k}_2|=|\mathbf{k}_3|=k$ and the bispectrum for scalar fluctuation can be written as

  $$\begin{aligned} B(k,k,k) \approx \frac{\tilde{W}^2(\phi _{cmb},{\varvec{\Psi }})}{288(\epsilon ^*_{\tilde{W}})^2M^6_p}\frac{1}{k^6}\left[ 29\epsilon ^*_{\tilde{W}}-6\eta ^*_{\tilde{W}} \right] . \end{aligned}$$

  (8.16)

  In this case the non-Gaussian amplitude for bispectrum can be expressed as

  $$\begin{aligned} f^{\mathrm{{equil}}}_{\mathrm{NL}}=f^{\mathrm{{loc}}}_{\mathrm{NL}}(k,k,k) \approx \frac{5}{36} \left[ 29\epsilon ^*_{\tilde{W}}-6\eta ^*_{\tilde{W}} \right] . \end{aligned}$$

  (8.17)

• 2. Squeezed limit configuration: For this case we have $k_{1}\approx k_{2}(=k_{\mathrm{L}})\gg k_{3}(=k_\mathrm{S})$, where $k_{i}=|\mathbf{k_{i}}|\forall i=1,2,3$. Here $k_{\mathrm{L}}$ and $k_\mathrm{S}$ represent momentum for long and short modes respectively. Consequently the bispectrum for scalar fluctuation for arbitrary vacuum can be expressed as

  $$\begin{aligned}&B(k_{\mathrm{L}},k_{\mathrm{L}},k_\mathrm{S})\approx \frac{\tilde{W}^2(\phi _{cmb}, {\varvec{\Psi }})}{288(\epsilon ^*_{\tilde{W}})^2M^6_p} \frac{1}{k^3_Lk^3_\mathrm{S}}\nonumber \\&\quad \times \left[ 4(4\epsilon ^*_{\tilde{W}}-\eta ^*_{\tilde{W}}) +10\epsilon ^*_{\tilde{W}}\left( \frac{k_\mathrm{S}}{k_{\mathrm{L}}}\right) ^2\right. \nonumber \\&\quad -\left. (2\eta ^*_{\tilde{W}}-\epsilon ^*_{\tilde{W}})\left( \frac{k_\mathrm{S}}{k_{\mathrm{L}}}\right) ^3\right] . \end{aligned}$$

  (8.18)

  In this case the non-Gaussian amplitude for bispectrum can be expressed as

  $$\begin{aligned} f^{\mathrm{{sq}}}_{\mathrm{NL}}= & {} f^{\mathrm{{loc}}}_{\mathrm{NL}}(k_{\mathrm{L}},k_{\mathrm{L}},k_\mathrm{S}) \approx \frac{5}{12}\left[ 4(4\epsilon ^*_{\tilde{W}}-\eta ^*_{\tilde{W}}) \phantom {\frac{1}{2}\left( \frac{k_\mathrm{S}}{k_{\mathrm{L}}}\right) ^3}\right. \nonumber \\&\left. +\,10\epsilon ^*_{\tilde{W}}\left( \frac{k_\mathrm{S}}{k_{\mathrm{L}}} \right) ^2-(2\eta ^*_{\tilde{W}}-\epsilon ^*_{\tilde{W}}) \left( \frac{k_\mathrm{S}}{k_{\mathrm{L}}}\right) ^3\right] .\nonumber \\ \end{aligned}$$

  (8.19)

In Table 4, we give the numerical estimates and constraints on the three point non-Gaussian amplitude from equilateral and squeezed configuration. Here all the obtained results are consistent with the two point constraints as well as with the Planck 2015 data.

In Fig. 12, we have shown the features of non-Gaussian amplitude from three point function in equilateral limit configuration in four different scanning regions of the product of the two parameters $\alpha \bar{\lambda }$ in the $(f^{\mathrm{{equil}}}_{\mathrm{NL}},\alpha \bar{\lambda })$ 2D plane for the number of e-foldings $50<\mathcal{N}_{cmb}<70$. Physical explanation of the obtained features are appended following:

• Region I: Here for the parameter space $0.0001<\alpha \bar{\lambda }<0.001$ the non-Gaussian amplitude lying within the window $0.06<f^{\mathrm{{equil}}}_{\mathrm{NL}}<0.11.$ Further if we increase the numerical value of $\alpha \bar{\lambda }$, then the magnitude of the non-Gaussian amplitude saturates and we get the maximum value for $\mathcal{N}_{cmb}=50$, $|f^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.11$.

• Region II: Here for the parameter space $0.00001<\alpha \bar{\lambda }<0.0001$ the non-Gaussian amplitude lying within the window $0.01<f^{\mathrm{{equil}}}_{\mathrm{NL}}<0.08$. In this region we get the maximum value for $\mathcal{N}_{cmb}=50$, $|f^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.08$. Additionally, it is important to note that in this case for $\alpha \bar{\lambda }=0.00004$ the lines obtained for $\mathcal{N}_{cmb}=50$, $\mathcal{N}_{cmb}=60$ and $\mathcal{N}_{cmb}=70$ cross each other.

• Region III: Here for the parameter space $0.000001<\alpha \bar{\lambda }<0.00001$ the non-Gaussian amplitude lying within the window $-0.004<f^{\mathrm{{equil}}}_{\mathrm{NL}}<0.02$. In this region we get the maximum value for $\mathcal{N}_{cmb}=70$, $|f^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.02$. Additionally, it is important to note that in this case for $0.000003\le \alpha \bar{\lambda }\le 0.000006$ the lines obtained for $\mathcal{N}_{cmb}=50$, $\mathcal{N}_{cmb}=60$ and $\mathcal{N}_{cmb}=70$ cross the zero line of non-Gaussian amplitude and a transition takes place from negative to positive values of $f^{\mathrm{{equil}}}_{\mathrm{NL}}$.

• Region IV: Here for the parameter space $0.0000001<\alpha \bar{\lambda }<0.000001$ the non-Gaussian amplitude lying within the window $-0.0001<f^{\mathrm{{equil}}}_{\mathrm{NL}}<-0.0029$. In this region we get the maximum value for $\mathcal{N}_{cmb}=60$, $|f^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.0029$.

Further combining the contribution from Region I, Region II, Region III and Region IV we finally get the following constraint on the three point non-Gaussian amplitude in the equilateral limit configuration:

$$\begin{aligned}&\text {Region~I}+\text {Region~II}+\text {Region~III}+ \text {Region~IV}{:}\nonumber \\&\quad -0.0001<f^{\mathrm{{equil}}}_{\mathrm{NL}}<0.11 \end{aligned}$$

(8.20)

for the following parameter space:

$$\begin{aligned}&\text {Region~I}+\text {Region~II}+\text {Region~III}+ \text {Region~IV}{:}\nonumber \\&\quad 0.0000001<\alpha \bar{\lambda }<0.001. \end{aligned}$$

(8.21)

In this analysis we get the following maximum value of the three point non-Gaussian amplitude in the equilateral limit configuration as given by

$$\begin{aligned} |f^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.11. \end{aligned}$$

(8.22)

To visualize these constraints more clearly we have also presented $(f^{\mathrm{{equil}}}_{\mathrm{NL}},\alpha ,\bar{\lambda })$ 3D plot in Fig. 13a, b, for two different angular orientations as given by Angle I and Angle II. From the representative surfaces it is clearly observed the behavior of three point non-Gaussian amplitude in the equilateral limit for the variation of two fold parameter $\alpha$ and $\bar{\lambda }$ and the results are consistent with the obtained constraints in 2D analysis. Here all the obtained results are consistent with the two point constraints and the Planck 2015 data.

In Fig. 14, we have shown the features of non-Gaussian amplitude from three point function in squeezed limit configuration in four different scanning regions of the product of the two parameters $\alpha \bar{\lambda }$ in the $(f^{\mathrm{{sq}}}_{\mathrm{NL}},\alpha \bar{\lambda })$ 2D plane for the number of e-foldings $50<\mathcal{N}_{cmb}<70$. Physical explanation of the obtained features are appended following:

• Region I: Here for the parameter space $0.0001<\alpha \bar{\lambda }<0.001$ the non-Gaussian amplitude lying within the window $0.09<f^{\mathrm{{sq}}}_{\mathrm{NL}}<0.16$. Further if we increase the numerical value of $\alpha \bar{\lambda }$, then the magnitude of the non-Gaussian amplitude saturates and we get maximum value for $\mathcal{N}_{cmb}=50$, $|f^{\mathrm{{sq}}}_{\mathrm{NL}}|_{\max }\sim 0.16$.

• Region II: Here for the parameter space $0.00001<\alpha \bar{\lambda }<0.0001$ the non-Gaussian amplitude lying within the window $0.01<f^{\mathrm{{sq}}}_{\mathrm{NL}}<0.12$. In this region we get the maximum value for $\mathcal{N}_{cmb}=50$, $|f^{\mathrm{{sq}}}_{\mathrm{NL}}|_{\max }\sim 0.12$. Additionally, it is important to note that in this case for $\alpha \bar{\lambda }=0.00004$ the lines obtained for $\mathcal{N}_{cmb}=50$, $\mathcal{N}_{cmb}=60$ and $\mathcal{N}_{cmb}=70$ cross each other.

• Region III: Here for the parameter space $0.000001<\alpha \bar{\lambda }<0.00001$ the non-Gaussian amplitude lying within the window $-0.01<f^{\mathrm{{sq}}}_{\mathrm{NL}}<0.03$. In this region we get the maximum value for $\mathcal{N}_{cmb}=70$, $|f^{\mathrm{{sq}}}_{\mathrm{NL}}|_{\max }\sim 0.03$. Additionally, it is important to note that in this case for $0.000003\le \alpha \bar{\lambda }\le 0.000006$ the lines obtained for $\mathcal{N}_{cmb}=50$, $\mathcal{N}_{cmb}=60$ and $\mathcal{N}_{cmb}=70$ cross the zero line of non-Gaussian amplitude and a transition takes place from negative to positive values of $f^{\mathrm{{sq}}}_{\mathrm{NL}}$.

• Region IV: Here for the parameter space $0.0000001<\alpha \bar{\lambda }<0.000001$ the non-Gaussian amplitude lying within the window $-0.0005<f^{\mathrm{{sq}}}_{\mathrm{NL}}<-0.006.$ In this region we get the maximum value for $\mathcal{N}_{cmb}=60$, $|f^{\mathrm{{sq}}}_{\mathrm{NL}}|_{\max }\sim 0.006$.

Further combining the contribution from Region I, Region II, Region III and Region IV we finally get the following constraint on the three point non-Gaussian amplitude in the squeezed limit configuration:

$$\begin{aligned}&\text {Region~I}+\text {Region~II}+\text {Region~III}+ \text {Region~IV}{:}\nonumber \\&\quad -0.0005<f^{\mathrm{{sq}}}_{\mathrm{NL}}<0.16 \end{aligned}$$

(8.23)

for the following parameter space:

$$\begin{aligned}&\text {Region~I}+\text {Region~II}+\text {Region~III}\nonumber \\&\quad +\,\text {Region~IV}{:}\quad 0.0000001<\alpha \bar{\lambda }<0.001. \end{aligned}$$

(8.24)

To visualize these constraints more clearly we have also presented $(f^{\mathrm{{sq}}}_{\mathrm{NL}},\alpha ,\bar{\lambda })$ 3D plot in Fig. 15a, b, for two different angular orientations as given by Angle I and Angle II. From the representative surfaces it is clearly observed the behavior of three point non-Gaussian amplitude in the squeezed limit for the variation of two fold parameter $\alpha$ and $\bar{\lambda }$ and the results are consistent with the obtained constraints in 2D analysis. Here all the obtained results are consistent with the two point constraints and the Planck 2015 data.

Fig. 16

Diagrammatic representation of $\delta N$ formalism

8.1.2 Using $\delta \mathcal{N}$ formalism

A. Basic methodology: In this section our prime objective is to use $\delta \mathcal{N}$ formalism to compute the three point and four point correlation functions in the attractor regime. Here $\mathcal{N}$ signifies the number of e-foldings as we have defined earlier. In this formalism the dominant contribution comes from only on the perturbations of the scalar field trajectories with respect to the field value at the initial hypersurface $\phi , \Psi$ and the velocity $\dot{\phi }, \dot{\Psi }$. This can be realized by providing two initial conditions on both of them on the initial hypersurface. More specifically, in the present context, we have assumed that the evolution of the universe is governed in a unique fashion after the value of the scalar field achieved at $\phi =\phi _*$ and $\Psi =\Psi _*$, where it mimics the role of a standard clock in inflationary cosmology. Here the value of its velocity $\dot{\phi }_*$ and $\dot{\Psi }_*$ is completely insignificant. Let us mention that only in this case $\delta \mathcal{N}$ is equal to the final value of the comoving curvature perturbation $\zeta$, which is conserved at the epoch $t\ge t_*$. In Fig. 16, we have shown the schematic diagram of the $\delta \mathcal{N}$ formalism.

For further computation we assume that on large scales the dynamical behavior which permits us to ignore time derivatives appearing in the cosmological perturbation theory, the horizon volume will evolve in such a way as accords with a perfectly self contained universe. As a result the scalar curvature perturbation can be expressed beyond linear order in cosmological perturbation theory as

$$\begin{aligned} \zeta= & {} \delta \mathcal{N}= \left[ \mathcal{N}_{,\phi }\delta \phi +\mathcal{N}_{,\Psi }\delta \Psi \right] +\frac{1}{2!}\left[ \mathcal{N}_{,\phi \phi }\delta \phi \delta \phi \right. \nonumber \\&+\left. \left( \mathcal{N}_{,\phi \Psi }+\mathcal{N}_{,\Psi \phi }\right) \delta \phi \delta \Psi +N_{,\Psi \Psi }\delta \Psi \delta \Psi \right] \nonumber \\&+\frac{1}{3!}\left[ \mathcal{N}_{,\phi \phi \phi }\delta \phi \delta \phi \delta \phi +\left( \mathcal{N}_{,\phi \Psi \Psi }+\mathcal{N}_{,\Psi \phi \Psi }\right. \right. \nonumber \\&+\left. \left. \mathcal{N}_{,\Psi \Psi \phi }\right) \delta \phi \delta \Psi \delta \Psi \right. \nonumber \\&\left. +\left( \mathcal{N}_{,\phi \phi \Psi }+N_{,\phi \Psi \phi }+\mathcal{N}_{,\Psi \phi \phi }\right) \delta \phi \delta \phi \delta \Psi \right. \nonumber \\&+\left. \mathcal{N}_{,\Psi \Psi \Psi }\delta \Psi \delta \Psi \delta \Psi \right] +\cdots , \end{aligned}$$

(8.25)

where we use the following notations for simplicity:

$$\begin{aligned} \mathcal{N}_{,\phi }= & {} \partial _{\phi }\mathcal{N},\quad \mathcal{N}_{,\Psi }=\partial _{\Psi }\mathcal{N},\end{aligned}$$

(8.26)

$$\begin{aligned} \mathcal{N}_{,\phi \phi }= & {} \partial ^2_{\phi }\mathcal{N},\quad \mathcal{N}_{,\Psi \Psi }=\partial ^2_{\Psi }\mathcal{N},\nonumber \\ N_{,\phi \Psi }= & {} \partial _{\phi }\partial _{\Psi }\mathcal{N},\quad \mathcal{N}_{,\Psi \phi }=\partial _{\Psi }\partial _{\phi }\mathcal{N},\end{aligned}$$

(8.27)

$$\begin{aligned} \mathcal{N}_{,\phi \phi \phi }= & {} \partial ^3_{\phi }\mathcal{N},\quad \mathcal{N}_{,\Psi \Psi \Psi }=\partial ^3_{\Psi }\mathcal{N},\nonumber \\ \mathcal{N}_{,\phi \phi \Psi }= & {} \partial _{\phi }\partial _{\phi }\partial _{\Psi }\mathcal{N},\quad \mathcal{N}_{,\phi \Psi \phi }=\partial _{\phi }\partial _{\Psi }\partial _{\phi }\mathcal{N},\end{aligned}$$

(8.28)

$$\begin{aligned} \mathcal{N}_{,\Psi \phi \phi }= & {} \partial _{\Psi }\partial _{\phi }\partial _{\phi }\mathcal{N},\quad \mathcal{N}_{,\phi \Psi \Psi }=\partial _{\phi }\partial _{\Psi }\partial _{\Psi }\mathcal{N},\end{aligned}$$

(8.29)

$$\begin{aligned} \mathcal{N}_{,\Psi \phi \Psi }= & {} \partial _{\Psi }\partial _{\phi }\partial _{\Psi }\mathcal{N},\quad \mathcal{N}_{,\Psi \Psi \phi }=\partial _{\Psi }\partial _{\Psi }\partial _{\phi }\mathcal{N}. \end{aligned}$$

(8.30)

Here we use the notation, $\partial _{\phi }=\partial /\partial \phi$ and $\partial _{\Psi }=\partial /\partial \Psi$ to denote the partial derivatives. But here we have to point that in attractor regime both the fields $\phi$ and $\Psi$ are connected with each other, which we have already pointed out earlier in this paper.

Further the curvature perturbation can be recast as

$$\begin{aligned} \zeta= & {} \delta \mathcal{N}= 2\mathcal{N}_{,\phi }\delta \phi +\left\{ 2\mathcal{N}_{,\phi \phi }-\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}(\phi )}~\mathcal{N}_{,\phi }\right\} \delta \phi \delta \phi \nonumber \\&+\left\{ \frac{4}{3}\mathcal{N}_{,\phi \phi \phi }-2\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}(\phi )}\mathcal{N}_{,\phi \phi }\right. \nonumber \\&\left. +\left( \frac{5}{3}\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^2(\phi )}-\frac{1}{6}\frac{\mathcal{V}^{\prime \prime }(\phi )}{\mathcal{V}(\phi )}\right) \mathcal{N}_{,\phi }\right\} \delta \phi \delta \phi \delta \phi +\cdots ,\nonumber \\ \end{aligned}$$

(8.31)

which implies that if we compute $\mathcal{N}_{,\phi }$, $\mathcal{N}_{,\phi \phi }$ and $\mathcal{N}_{,\phi \phi \phi }$, then one can determine the curvature perturbation and also compute the three and four point functions using Eq. (8.31). The detailed computation of the field derivatives of $\mathcal{N}$ are explicitly given in the Appendix for all the derived effective potentials.

B. Generalized convention for field solution: In $\delta N$ formalism to compute $\mathcal{N}_{,\phi }$, $\mathcal{N}_{,\phi \phi }$ and $\mathcal{N}_{,\phi \phi \phi }$ we start with the background equation of motion for the $\phi$ field:

$$\begin{aligned} \ddot{\phi }+3\tilde{H}\dot{\phi }+\partial _{\phi }\tilde{W}(\phi ,\Psi )=0, \end{aligned}$$

(8.32)

where the effective potential $\tilde{W}(\phi ,\Psi )$ is given by

$$\begin{aligned} \tilde{W}(\phi ,\Psi )=\left\{ \begin{array}{ll} \frac{\lambda }{4}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}\phi ^{4} &{}\quad \text {for Case I}\\ \frac{M^{4}_{p}}{8\alpha }-\frac{\lambda }{4}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}\phi ^{4}&{}\quad \text {for Case II}\\ \frac{M^{4}_{p}}{8\alpha }-\frac{\lambda }{4}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}(\phi ^4-\phi ^{4}_{V})&{} \quad \text {for Case~II}+\text {Choice~I(v1)}\\ \frac{M^{4}_{p}}{8\alpha }+\frac{\lambda }{4}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}(\phi ^4-\phi ^{4}_{V}) &{}\quad \text {for Case~II}+\text {Choice~I(v2)}\\ \frac{M^{4}_{p}}{8\alpha }+\left( \frac{m^{2}_{c}}{2}\phi ^2- \frac{\lambda }{4}\phi ^{4}\right) \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}&{}\quad \text {for Case~II}+\text {Choice~II(v1)}\\ \frac{M^{4}_{p}}{8\alpha }-\left( \frac{m^{2}_{c}}{2}\phi ^2- \frac{\lambda }{4}\phi ^{4}\right) \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}&{} \quad \text {for Case~II}+\text {Choice~II(v2)}\\ \frac{M^{4}_{p}}{8\alpha }+\frac{\frac{\lambda }{4}(\phi ^2 -\phi ^2_{V})^2}{(1+\xi \phi ^2)^2}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}&{} \quad \text {for Case~II}+\text {Choice~III}. \end{array} \right. \end{aligned}$$

(8.33)

Here it is important to note that the exact connecting relations between the $\Psi$ field and the inflaton field $\phi$ is given by

$$\begin{aligned} \Psi -\Psi _{0} =-\frac{1}{2\sqrt{6}M_p}\times \left\{ \begin{array}{ll} 9(\phi ^2-\phi ^2_0)&{}\quad \text {for Case I}\\ (\phi ^2 -\phi ^2_0)&{}\quad \text {for Case II}\\ \left[ (\phi ^2 -\phi ^2_0)+\phi ^4_V\left( \frac{1}{\phi ^2}- \frac{1}{\phi ^2_0}\right) \right] &{} \quad \text {for Case~II} +\text {Choice~I(v1)}\\ \left[ (\phi ^2-\phi ^2_0)+\phi ^4_V\left( \frac{1}{\phi ^2}- \frac{1}{\phi ^2_0}\right) \right] &{}\quad \text {for Case~II} +\text {Choice~I(v2)}\\ \left[ (\phi ^2 -\phi ^2_0)+\frac{m^{2}_{c}}{\lambda }\ln \left( \frac{m^2_{c}-\lambda \phi ^{2}}{m^2_{c}- \lambda \phi ^{2}_0}\right) \right] &{}\quad \text {for Case~II} +\text {Choice~II(v1)}\\ \left[ (\phi ^2 -\phi ^2_0)+\frac{m^{2}_{c}}{\lambda }\ln \left( \frac{m^2_{c}-\lambda \phi ^{2}}{m^2_{c}- \lambda \phi ^{2}_0}\right) \right] &{}\quad \text {for Case~II} +\text {Choice~II(v2)}\\ \frac{1}{(1+\xi \phi ^2_{V})}\left[ (\phi ^2 -\phi ^2_0) \left( 1+\frac{\xi }{2}(\phi ^2 +\phi ^2_0 -2\phi ^2_{V})\right) \right. \\ \left. +2\phi ^2_{V}\ln \left( \frac{\phi }{\phi _0}\right) \right] &{}\quad \text {for Case~II}+\text {Choice~III}. \end{array} \right. \end{aligned}$$

(8.34)

It is obvious from the structural form of the effective potential for all these cases that the general analytical solution for the inflaton field $\phi$ is too much complicated. To simplify the job here we consider a particular solution of the following form:

$$\begin{aligned} \phi =\phi _{\mathrm{L}}\propto \exp (\mathcal{Y}Ht)\quad (\hbox {i.e. }\phi =\phi _{\mathrm{L}}(\mathcal{N})=\phi _{*}\exp (-\mathcal{Y}\mathcal{N})).\nonumber \\ \end{aligned}$$

(8.35)

Here we assume that $\mathcal{Y}$ is a time independent quantity. Further our prime motivation is to obtain a more generalized version of the solution for FLRW cosmological background up to the consistent second order in cosmological perturbations around the prescribed particular solution. During our computation we also assume that the boundary between the attractor phase and the non attractor phase is determined by the field value $\phi =\phi _{*}=\phi (\mathcal{N}_{cmb})=\phi _{cmb}$, which in cosmological literature identified to be the field value associated at the pivot scale.

To proceed further here we define a theoretical perturbative parameter which accounts the deviation from the actual inflaton field value compared to the field value after perturbation:

$$\begin{aligned} \Delta _{\mathrm{{part}}}\equiv \phi -\phi _0 -\phi _{\mathrm{L}}=\sum ^{\infty }_{n=1}\Delta _{n}, \end{aligned}$$

(8.36)

where in general $\phi _0$ is the VEV of the inflaton field $\phi$. Here we assume that the parameter can take into account the difference between the true FLRW background solution and the proposed reference solution to solve the background Eq. (8.32) in the physical domain where cosmological perturbation theory is valid. Additionally we claim that to validate the cosmological perturbation theory in the preferred physical domain, the infinite series sum should be convergent. Consequently in the present context we only look into $\Delta _{1}$ and $\Delta _{2}$, which are the general linearized and second-order solution within cosmological perturbation theory for the background field equations. We also neglect all the higher-order contribution in the perturbative regime of the solution as they are very small.

C. Linearized perturbative solution: Before proceed further in this section let us clearly mention that here we use the following Ansatz to derive the results for linearized solution in the perturbative regime.

In this case we assume that at the equation of motion level in the linear regime of perturbation theory there is no contribution from effective potential which contains quadratic structure or more complicated than that in terms of field $\phi$. In our calculation we treat all such contributions to be the back reactions and in the linear perturbative regime of the solution our claim is such effects are small and largely suppressed. In this paper the derived effective potentials for all these cases are also complicated and to get a preferred analytical solution in the linearized perturbative regime we use this Ansatz. Here we get

$$\begin{aligned}{}[\partial _{\phi }\tilde{W}]_{\phi =\phi _0+\phi _{\mathrm{L}}+\Delta _1}\approx 0, \end{aligned}$$

(8.37)

which is valid for all types of derived potentials in the present context. Now let us consider the linearized perturbative solution $\Delta _{1}$ in this section. Consequently in the leading order of cosmological perturbation the background linearized version of the equation of motion takes the following form using the prescribed Ansatz:

$$\begin{aligned} \ddot{\Delta }_{1}+ & {} 3H\dot{\Delta }_{1}+\phi _{\mathrm{L}}\left\{ \mathcal{Y}^2H^2\left( 1-2tH\epsilon _{H}\right) -2\mathcal{Y}H^2\epsilon _{H}\right. \nonumber \\+ & {} \left. 3H^2\mathcal{Y}(1-tH\epsilon _{H})\right\} =0, \end{aligned}$$

(8.38)

where $\epsilon _{H}$ is the Hubble slow-roll parameter, $\epsilon _{H}=-\dot{H}/H^2$. The exact analytical solution of the Eq. (8.38) is given by

$$\begin{aligned} \Delta _{1}= & {} \mathbf{D}_{2}-\frac{1}{3H}{} \mathbf{D}_{1}\mathrm{e}^{-3Ht}+\frac{1}{\mathcal{Y}(3+\mathcal{Y})^2}\phi _* \mathrm{e}^{H\mathcal{Y}t}\nonumber \\&\times \,[-\mathcal{Y}(3+\mathcal{Y})^2 +\epsilon _{H}(-9+\mathcal{Y}(3+\mathcal{Y})\nonumber \\&\times \,\{-2+H(3+2\mathcal{Y})t\})]. \end{aligned}$$

(8.39)

Here $\mathbf{D}_{1}$ and $\mathbf{D}_{2}$ are dimensionful arbitrary integration constants which can be determined by imposing the appropriate boundary condition. Additionally, it is important to note that in the present context this solution is valid in the case of the quasi-de Sitter case also where the Hubble parameter H is not exactly constant.

D. Second-order perturbative solution: Here we have considered the effect from the second-order cosmological perturbation, $\Delta _2$. It is important to note that during the computation here we also follow the same Ansatz, which we have already introduced in the last section. As a result, including the contribution from the slow-roll correction, the perturbative second-order background equation of motion takes the following simplified form:

$$\begin{aligned}&\ddot{\Delta }_{2}+3H\dot{\Delta }_{2}+\phi _{\mathrm{L}}\{\mathcal{Y}^2H^2(1-2tH\epsilon _{H})-2\mathcal{Y}H^2\epsilon _{H}\nonumber \\&\quad +\,3H^2\mathcal{Y}(1-tH\epsilon _{H})\}=\Sigma _\mathrm{S}. \end{aligned}$$

(8.40)

Here it is important to note that in Eq. (8.40), $\Sigma _\mathrm{S}$ is the source contribution which is coming from the linear-order perturbation $\Delta _1$. In this paper $\Sigma _\mathrm{S}$ can be expressed for all derived effective potentials as

$$\begin{aligned} \Sigma _\mathrm{S}=\left\{ \begin{array}{ll} \Lambda _{c}\mathrm{e}^{\frac{3((\Delta _1+\phi _{\mathrm{L}})^2 -\phi ^2_0)}{M^2_p}}(\Delta _1+\phi _{\mathrm{L}})^{4} &{} \quad \text {for Case I}\\ \frac{M^{3}_{p}}{8\alpha }-\Lambda _{c}\mathrm{e}^{\frac{( (\Delta _1+\phi _{\mathrm{L}})^2-\phi ^2_0)}{3M^2_p}}(\Delta _1+\phi _{\mathrm{L}})^{4}&{} \quad \text {for Case II}\\ \frac{M^{3}_{p}}{8\alpha }-\Lambda _{c}\mathrm{e}^{\frac{ \left[ ((\Delta _1+\phi _{\mathrm{L}})^2 -\phi ^2_0)+ \phi ^4_V\left( \frac{1}{(\Delta _1+\phi _{\mathrm{L}})^2}- \frac{1}{\phi ^2_0}\right) \right] }{3M^2_p}} ((\Delta _1+\phi _{\mathrm{L}})^4-\phi ^{4}_{V})&{} \quad \text {for Case~II}+\text {Choice~I(v1)}\\ \frac{M^{3}_{p}}{8\alpha }+\Lambda _{c}\mathrm{e}^{\frac{ \left[ ((\Delta _1+\phi _{\mathrm{L}})^2 -\phi ^2_0)+\phi ^4_V \left( \frac{1}{(\Delta _1+\phi _{\mathrm{L}})^2}-\frac{1}{\phi ^2_0}\right) \right] }{3M^2_p}}\left( (\Delta _1+\phi _{\mathrm{L}})^4-\phi ^{4}_{V}\right) &{} \quad \text {for Case~II}+\text {Choice~I(v2)}\\ \frac{M^{3}_{p}}{8\alpha }+\left( \frac{m^{2}_{c}}{2M_p} (\Delta _1+\phi _{\mathrm{L}})^2\right. \\ \quad \left. -\Lambda _{c}(\Delta _1+\phi _{\mathrm{L}})^{4}\right) \mathrm{e}^{\frac{\left[ ((\Delta _1+\phi _{\mathrm{L}})^2 -\phi ^2_0) +\frac{m^{2}_{c}}{\lambda }\ln \left( \frac{m^2_{c}- \lambda (\Delta _1+\phi _{\mathrm{L}})^{2}}{m^2_{c}-\lambda \phi ^{2}_0}\right) \right] }{3M^2_p}}&{}\quad \text {for Case~II}+\text {Choice~II(v1)}\\ \frac{M^{3}_{p}}{8\alpha }-\left( \frac{m^{2}_{c}}{2 M_p} (\Delta _1+\phi _{\mathrm{L}})^2\right. \\ \quad \left. -\Lambda _{c}(\Delta _1+\phi _{\mathrm{L}})^{4}\right) \mathrm{e}^{\frac{\left[ ((\Delta _1+\phi _{\mathrm{L}})^2 -\phi ^2_0) +\frac{m^{2}_{c}}{\lambda }\ln \left( \frac{m^2_{c}- \lambda (\Delta _1+\phi _{\mathrm{L}})^{2}}{m^2_{c}-\lambda \phi ^{2}_0}\right) \right] }{3M^2_p}}&{}\quad \text {for Case~II}+\text {Choice~II(v2)}\\ \frac{M^{3}_{p}}{8\alpha }+\frac{\Lambda _{c} ((\Delta _1+\phi _{\mathrm{L}})^2 -\phi ^2_{V})^2}{(1+\xi (\Delta _1+\phi _{\mathrm{L}})^2)^2}\mathrm{e}^{\frac{\left[ ((\Delta _1+\phi _{\mathrm{L}})^2 -\phi ^2_0 )\left( 1+\frac{\xi }{2}((\Delta _1+\phi _{\mathrm{L}})^2+\phi ^2_0 -2\phi ^2_{V})\right) +2\phi ^2_{V}\ln \left( \frac{(\Delta _1+\phi _{\mathrm{L}})}{\phi _0}\right) \right] }{3M^2_p(1+\xi \phi ^2_{V})}} &{}\quad \text {for Case~II}+\text {Choice~III}, \end{array} \right. \end{aligned}$$

(8.41)

where we define a new parameter:

$$\begin{aligned} \Lambda _{c}=\frac{\lambda }{4M_p}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi _0}{M_p}}. \end{aligned}$$

(8.42)

From the complicated mathematical structure of the source function $\Sigma _\mathrm{S}$ it is clear that, using it, it is not possible to solve second-order perturbation equations. To solve this problem one can simplify the source function in the following way:

$$\begin{aligned} \Sigma _\mathrm{S}\approx \left\{ \begin{array}{ll} \Lambda _{c}\phi ^4_{\mathrm{L}}\left( 1+4\frac{\Delta _1}{\phi _{\mathrm{L}}}\right) &{} \quad \text {for Case I}\\ \beta -\Lambda _{c}\phi ^4_{\mathrm{L}}\left( 1+4\frac{\Delta _1}{\phi _{\mathrm{L}}}\right) &{}\quad \text {for Case II}\\ \beta -\Lambda _{c}\left( \phi ^4_{\mathrm{L}}\left( 1+4\frac{\Delta _1}{\phi _{\mathrm{L}}}\right) - \phi ^{4}_{V}\right) &{}\quad \text {for Case~II}+\text {Choice~I(v1)}\\ \beta +\Lambda _{c}\left( \phi ^4_{\mathrm{L}}\left( 1+4\frac{\Delta _1}{\phi _{\mathrm{L}}}\right) -\phi ^{4}_{V}\right) &{}\quad \text {for Case~II}+\text {Choice~I(v2)}\\ \beta +\left( \frac{M_{c}}{2}\phi ^2_{\mathrm{L}}\left( 1+2\frac{\Delta _1}{\phi _{\mathrm{L}}}\right) -\Lambda _{c}\phi ^4_{\mathrm{L}}\left( 1+4\frac{\Delta _1}{\phi _{\mathrm{L}}}\right) \right) &{} \quad \text {for Case~II}+\text {Choice~II(v1)}\\ \beta -\left( \frac{M_{c}}{2}\phi ^2_{\mathrm{L}}\left( 1+2\frac{\Delta _1}{\phi _{\mathrm{L}}}\right) -\Lambda _{c}\phi ^4_{\mathrm{L}}\left( 1+4\frac{\Delta _1}{\phi _{\mathrm{L}}}\right) \right) &{}\quad \text {for Case~II}+\text {Choice~II(v2)}\\ \beta +\Gamma _\xi \left\{ 1+\Theta _{\xi }\frac{\Delta _1}{\phi _{\mathrm{L}}}\right\} &{}\quad \text {for Case~II}+\text {Choice~III}, \end{array} \right. \end{aligned}$$

(8.43)

where $\beta ,M_c$ and $\Gamma _c$ are defined as

$$\begin{aligned} \beta= & {} \frac{M^{3}_{p}}{8\alpha },\quad M_c=\frac{m^2_c}{M_p},\nonumber \\ \Gamma _\xi= & {} \Lambda _{c}(\phi ^2_{\mathrm{L}}-\phi ^2_V)^2(1+2\xi \phi ^2_{\mathrm{L}}),\nonumber \\ \Theta _{\xi }= & {} 4\phi ^2_{\mathrm{L}}\left( \xi +\frac{1}{\phi ^2_{\mathrm{L}}-\phi ^2_V}\right) . \end{aligned}$$

(8.44)

The representative solutions of Eq. (8.40) for various sources are given in the Appendix.

D. Implementation of $\delta \mathcal{N}$ at the final hypersurface: Using the results derived in the previous two sections here our prime objective is to explicitly compute the expression for the cosmological scalar perturbations in terms of the number of e-folds, $\delta \mathcal{N}$, which we have already introduced earlier. In the present context the truncated version of the background solution of the inflaton field $\phi$ corrected up to the second-order cosmological perturbations around the reference trajectory, $\phi _{\mathrm{L}}\propto \mathrm{e}^{-\mathcal{Y}\mathcal{N}}$ or $\phi _{\mathrm{L}}\propto \mathrm{e}^{\mathcal{Y}Ht}$, is generically given by for all the various physical cases are

$$\begin{aligned} \phi (\mathcal{N})= & {} \phi _0+\frac{\phi _*}{1+\hat{\Delta }_{1}(\mathcal{N}=0)+\hat{\Delta }_{2}(\mathcal{N}=0)}\nonumber \\&\times \,(\mathrm{e}^{-\mathcal{Y}\mathcal{N}}+\hat{\Delta }_{1}(\mathcal{N})+\hat{\Delta }_{2}(\mathcal{N})), \end{aligned}$$

(8.45)

or equivalently one can write

$$\begin{aligned} \phi (t)= & {} \phi _0+\frac{\phi _*}{1+\hat{\Delta }_{1}(t=0)+ \hat{\Delta }_{2}(t=0)}\nonumber \\&\times \,(\mathrm{e}^{\mathcal{Y}Ht}+\hat{\Delta }_{1}(t)+\hat{\Delta }_{2}(t)). \end{aligned}$$

(8.46)

But for the sake of simplicity we use Eq. (8.45) as we want to implement the methodology of the $\delta \mathcal{N}$ formalism. Additionally, it is important to mention that the symbol $\hat{}$ is introduced in the present context to rescale the integration constants and the perturbative solutions by the field value $\phi _*$ i.e. ${\Delta }_1=\phi _* \hat{\Delta }_1$, ${\Delta }_2=\phi _* \hat{\Delta }_2$. Expressions for the perturbative solutions $\Delta _{1}(\mathcal{N}=0)$ and $\Delta _{2}(\mathcal{N}=0)$ are explicitly written in the appendix.

In the present context all of the sets of scaled integration constants parameterize different trajectories and for our computation we set $\phi (0,\hat{\mathbf{W}}_{k})=\phi _*,$ where $\hat{\mathbf{W}}_{k}$ is defined as the collection of all integration constants in a specific situation as defined as $\hat{\mathbf{W}}_{k} =[\hat{\mathbf{W}}_{1},\hat{\mathbf{W}}_{2},\hat{\mathbf{W}}_{3},\hat{\mathbf{W}}_{4}]=[\hat{\mathbf{D}}_1, \hat{\mathbf{D}}_2, \hat{\mathbf{D}}_3, \hat{\mathbf{D}}_4]$. Further inverting Eq. (8.45), for a specified set of values of the constants $\hat{\mathbf{W}}_{k}$, we have obtained the following simplified expression for $\delta \mathcal{N}$ as an implicit function of the inflaton field $\phi$, the additional field $\Psi$ and $\hat{\mathbf{W}}_{k}$:

$$\begin{aligned}&\delta \mathcal{N}(\phi ,\Psi ,\hat{\mathbf{W}}_{k})=\mathcal{N}(\phi +\delta \phi ,\Psi +\delta \Psi ,\hat{\mathbf{W}}_{k})-\mathcal{N}(\phi ,\Psi , 0)\nonumber \\&\quad =\sum ^{2}_{\alpha =1}\sum ^{4}_{k=0}\sum _{n,m} \frac{1}{n!m!}\partial ^{n}_{\phi ^n_{\alpha }}\partial ^{m}_{\hat{\mathbf{W}}^m_{k}}\left\{ \mathcal{N}(\phi _{\alpha },0)\right\} ~\delta \phi ^n_{\alpha }~\hat{\mathbf{W}}^m_{k}.\nonumber \\ \end{aligned}$$

(8.47)

For this computation we have introduced the shift of the inflaton field $\phi$, additional field $\Psi$ and the number of e-foldings $\mathcal{N}$ as $\phi \rightarrow \phi +\delta \phi$, $\Psi \rightarrow \Psi +\delta \Psi$, $\mathcal{N}\rightarrow \mathcal{N}+\delta \mathcal{N}$, in the two sides of Eq. (8.45), to compute the analytical expression for $\delta \mathcal{N}$ in an iterative way from our present setup. Additionally, it is important to note that in this present context $\phi$ field and $\Psi$ field are not independent. They are related via Eq. (8.34), as we have already mentioned earlier. In the present setup, we have already obtained the second-order perturbative solutions of the scalar inflaton field trajectories around the particular reference solution, $\phi _{\mathrm{L}}=\phi _* \mathrm{e}^{\mathcal{Y}Ht}=\phi _* \mathrm{e}^{-\mathcal{Y}\mathcal{N}}$, as we have already pointed out earlier. Additionally important to note that if we neglect the sub dominant contribution of the form $\Delta _{1}\propto \mathrm{e}^{\mathcal{Y}Ht}$, then the analysis only holds true only at the sufficiently late time epochs. This directly implies that in this computation if we use such assumption then we choose the initial time in such a way that it is very close to the final time for the number of e-folds $\mathcal{N}\le 1$. To serve this purpose the simplest possibility is to choose the initial time epoch is infinitesimally close to the time scale at $\phi =\phi _{*}=\phi (\mathcal{N}_{cmb})=\phi _{cmb}$.

For the sake of simplicity one can further assume that the final expression for curvature perturbation in $\delta \mathcal{N}$ formalism is independent of the coefficients $\hat{\mathbf{W}}_{k}$ at $\mathcal{N}=0$ for which the following constraints holds true perfectly, $\partial ^{m}_{\hat{\mathbf{W}}_{k}}\mathcal{N}=0~~~\forall m=1,\ldots ,\infty$. Consequently we get the following simplified expression:

$$\begin{aligned} \zeta =\delta \mathcal{N}= & {} \sum ^{2}_{\alpha =1}\sum _{n}\frac{1}{n!}\partial ^{n}_{\phi ^n_{\alpha }}\left\{ \mathcal{N}(\phi _{\alpha },0)\right\} ~\delta \phi ^n_{\alpha }\nonumber \\= & {} 2\mathcal{N}_{,\phi }\delta \phi +\left\{ 2\mathcal{N}_{,\phi \phi }-\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}(\phi )}~\mathcal{N}_{,\phi }\right\} \delta \phi \delta \phi \nonumber \\&+\left\{ \frac{4}{3}\mathcal{N}_{,\phi \phi \phi }-2\frac{\mathcal{V}^{\prime \prime }(\phi )}{\mathcal{V}(\phi )}\mathcal{N}_{,\phi \phi }\right. \nonumber \\&+\left. \left( \frac{5}{3}\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^2(\phi )}-\frac{1}{6}\frac{\mathcal{V}^{\prime \prime }(\phi )}{\mathcal{V}(\phi )}\right) \mathcal{N}_{,\phi }\right\} \delta \phi \delta \phi \delta \phi +\cdots ,\nonumber \\ \end{aligned}$$

(8.48)

where the function $\mathcal{V}(\phi )$ we have explicitly defined earlier for all the derived effective potentials. Here $\cdots$ corresponds to the higher-order contributions, which are very much small compared to the leading-order contributions appearing from cosmological perturbation theory for scalar fluctuations.

Next we take the derivatives of both sides of Eq. (8.45) and further set the following two constraints, $\mathcal{N}=0,~~~ \hat{\mathbf{W}}_k=0 ~~\forall k$, at the final stage of the calculation. Our next task is to derive the analytical expression for the inflaton fluctuation $\delta \phi _*$ and the coefficients $\hat{\mathbf{W}}_{k}$, which are generated via quantum fluctuations on the flat slice of $\delta \phi$. To implement this computational technique let us consider the evolution of fluctuation in the inflaton field $\delta \phi$ on super horizon scales. The field fluctuation or more precisely the shift in the inflaton field $\phi$ can be expressed as

$$\begin{aligned} \delta \phi (\mathcal{N})= & {} \sum ^{2}_{i=1}\delta \phi _{i}(\mathcal{N})=\phi _* \sum ^{2}_{i=1}\hat{\Delta }_{i}(\mathcal{N}), \end{aligned}$$

(8.49)

where the subscript “1” and “2” signify the linear and second-order solution appearing from cosmological perturbation. Additionally, it is important to note that both the solutions $\hat{\Delta }_{1}(\mathcal{N})$ and $\hat{\Delta }_{2}(\mathcal{N})$ contain the growing and decaying mode characteristics. Further imposing the appropriate boundary condition from the end of the non-attractor region, where the number of e-folds $\mathcal{N}=0$, we get the following expression for the shift in the inflaton field from linear-order and second-order cosmological perturbation at $\phi =\phi _*$ as

$$\begin{aligned} \delta \phi _{*}=\delta \phi (0)= & {} \sum ^{2}_{i=1}\delta \phi _{i*}=\phi _* \sum ^{2}_{i=1}\hat{\Delta }_{i}(0)\nonumber \\= & {} \phi _*(\hat{\Delta }_{1}(0)+\hat{\Delta }_{2}(0)). \end{aligned}$$

(8.50)

See the appendix for more details. Now in the present context as we have started our computation from the reference solution $\phi \propto \mathrm{e}^{-\mathcal{Y}\mathcal{N}}$, using this relationship one can write down the explicit expression for the number of e-folds in terms of the inflaton field value as $\mathcal{N}(\phi )=\frac{1}{\mathcal{Y}}\ln \left( \frac{\phi _*}{\phi }\right)$, which is consistent with the boundary condition that at $\phi =\phi _*$ the number of e-folds is $\mathcal{N}=0$ in the present case. Using these result at $\phi =\phi _{*}$ one can write down the following expression for the curvature perturbation using the $\delta \mathcal{N}$ formalism as

$$\begin{aligned} \zeta= & {} \delta \mathcal{N} =\mathcal{A}(\phi _*)\delta \phi _*+\mathcal{B}(\phi _*)\delta \phi _*\delta \phi _*\nonumber \\&+\,\mathcal{C}(\phi _*)\delta \phi _*\delta \phi _*\delta \phi _*+\cdots , \end{aligned}$$

(8.51)

where $\mathcal{A}(\phi _*)$, $\mathcal{B}(\phi _*)$ and $\mathcal{C}(\phi _*)$ is defined as

$$\begin{aligned} \mathcal{A}(\phi _*)= & {} -\frac{2}{\mathcal{Y}\phi _*},\end{aligned}$$

(8.52)

$$\begin{aligned} \mathcal{B}(\phi _*)= & {} \left\{ \frac{2}{\mathcal{Y} \phi ^2_*}+\left( \frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}(\phi )}\right) _{*}~\frac{1}{\mathcal{Y}\phi _*}\right\} ,\end{aligned}$$

(8.53)

$$\begin{aligned} \mathcal{C}(\phi _*)= & {} \left\{ -\frac{2}{\mathcal{Y} \phi ^3_*}\frac{4}{3}-2\left( \frac{\mathcal{V}^{\prime \prime }(\phi )}{\mathcal{V}(\phi )}\right) _{*}\frac{1}{\mathcal{Y} \phi ^2_*} -\left( \frac{5}{3}\left( \frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^2(\phi )}\right) _*\right. \right. \nonumber \\&-\left. \left. \frac{1}{6}\left( \frac{\mathcal{V}^{\prime \prime }(\phi )}{\mathcal{V}(\phi )}\right) _*\right) \frac{1}{\mathcal{Y}\phi _*}\right\} . \end{aligned}$$

(8.54)

Explicit forms of $\mathcal{B}(\phi _*)$ and $\mathcal{C}(\phi _*)$ are written in the appendix for all the derived effective potentials.

Next we decompose the product of the fluctuation in the inflaton field $\delta \phi _*\delta \phi _*$ and $\delta \phi _*\delta \phi _*\delta \phi _*$ into two parts which comes from linear and second-order cosmological perturbation in the following way:

$$\begin{aligned} \delta \phi _*\delta \phi _*= & {} \delta \phi (0)\delta \phi (0)= \sum ^{2}_{i=1}\sum ^{2}_{j=1}\delta \phi _{i*}\delta \phi _{j*}\nonumber \\= & {} \phi ^2_{*}\sum ^{2}_{i=1}\sum ^{2}_{j=1}\hat{\Delta }_{i}(0)\hat{\Delta }_{j}(0),\end{aligned}$$

(8.55)

$$\begin{aligned} \delta \phi _*\delta \phi _*\delta \phi _*= & {} \delta \phi (0)\delta \phi (0)\delta \phi (0)\nonumber \\= & {} \sum ^{2}_{i=1}\sum ^{2}_{j=1}\sum ^{2}_{k=1}\delta \phi _{i*} \delta \phi _{j*}\delta \phi _{k*}\nonumber \\= & {} \phi ^3_{*}\sum ^{2}_{i=1}\sum ^{2}_{j=1} \sum ^{2}_{k=1}\hat{\Delta }_{i}(0)\hat{\Delta }_{j}(0)\hat{\Delta }_{k}(0), \end{aligned}$$

(8.56)

and we write down the following expression for the curvature perturbation using the $\delta \mathcal{N}$ formalism:

$$\begin{aligned} \zeta= & {} \delta \mathcal{N}=\phi _*\mathcal{A}(\phi _*)\sum ^{2}_{i=1}\hat{\Delta }_{i}(0)\nonumber \\&+\,\phi ^2_*\mathcal{B}(\phi _*)\sum ^{2}_{i=1}\sum ^{2}_{j=1}\hat{\Delta }_{i}(0)\hat{\Delta }_{j}(0)\nonumber \\&+\,\phi ^3_*\mathcal{C}(\phi _*)\sum ^{2}_{i=1}\sum ^{2}_{j=1}\sum ^{2}_{k=1}\hat{\Delta }_{i}(0)\hat{\Delta }_{j}(0)\hat{\Delta }_{k}(0)+\cdots \nonumber \\ {}= & {} \phi _*\mathcal{A}(\phi _*)\left( \hat{\Delta }_{1}(0)+\hat{\Delta }_{2}(0)\right) \nonumber \\&+\,\phi ^2_*\mathcal{B}(\phi _*)\left( \hat{\Delta }^2_{1}(0)+\hat{\Delta }^2_{2}(0)+2\hat{\Delta }_{1}(0)\hat{\Delta }_{2}(0)\right) \nonumber \\&+\,\phi ^3_*\mathcal{C}(\phi _*)\left( \hat{\Delta }^3_{1}(0)+\hat{\Delta }^3_{2}(0)+3\hat{\Delta }^2_{1}(0)\hat{\Delta }_{2}(0)\right. \nonumber \\&\left. +\,3\hat{\Delta }_{1}(0)\hat{\Delta }^2_{2}(0)\right) +\cdots . \end{aligned}$$

(8.57)

Further using a local configuration in momentum space one can define the non-Gaussian amplitude associated with the three point function using the $\delta \mathcal{N}$ formalism as [142]:

$$\begin{aligned} f^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{5}{6}\frac{B(k_1,k_2,k_3)}{\left[ P_{\zeta }(k_1)P(k_2)+P_{\zeta }(k_2)P_{\zeta }(k_3) +P_{\zeta }(k_3)P_{\zeta }(k_1)\right] }\nonumber \\= & {} \frac{5}{6}\frac{\mathcal{N}_{,IJ}\mathcal{N}_{,I}\mathcal{N}_{,J}}{(\mathcal{N}_{,K}\mathcal{N}_{,K})^2}, \end{aligned}$$

(8.58)

Here $B(k_1,k_2,k_3)$ is the bispectrum and $P_{\zeta }(k)$ is the power spectrum for scalar perturbations. Here I, J, K are the field configuration indices i.e. $I,J,K=\phi ,\Psi$. In terms of the inflaton field $\Phi$ and additional field $\Psi$ we get the following simplified expression for the non-Gaussian amplitude associated with the three point function:

$$\begin{aligned} f^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{5}{6}\left[ \frac{\mathcal{N}_{,\phi \phi }\mathcal{N}_{,\phi }\mathcal{N}_{,\phi } +\mathcal{N}_{,\Psi \Psi }\mathcal{N}_{,\Psi }\mathcal{N}_{,\Psi }+\left( \mathcal{N}_{,\phi \Psi }+\mathcal{N}_{,\Psi \phi }\right) \mathcal{N}_{,\phi }\mathcal{N}_{,\Psi }}{(\mathcal{N}_{,\phi }\mathcal{N}_{,\phi }+\mathcal{N}_{,\Psi }\mathcal{N}_{,\Psi })^2}\right] _{*}. \end{aligned}$$

(8.59)

Now as the $\Psi$ field can be expressed in terms of $\phi$ field, using this crucial fact we get the following result of non-Gaussian amplitude in the attractor regime as

$$\begin{aligned} f^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{5}{6}\left[ \frac{\left( 1+\frac{2}{\mathcal{V}^2(\phi )}+\frac{1}{\mathcal{V}^4(\phi )}\right) }{\left( 1+\frac{1}{\mathcal{V}^2(\phi )}\right) ^2 }\frac{\mathcal{N}_{,\phi \phi }}{\mathcal{N}^2_{,\phi }} -\frac{\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}}{\left( 1+\frac{1}{\mathcal{V}^2(\phi )}\right) }\frac{1}{\mathcal{N}_{,\phi }}\right] _{*}.\nonumber \\ \end{aligned}$$

(8.60)

Further substituting the explicit form of the function $\mathcal{V}(\phi )$ and $\mathcal{N}_{,\phi }$, $\mathcal{N}_{,\phi \phi }$ for all derived effective potentials at $\phi =\phi _*$ we get

$$\begin{aligned} f^{\mathrm{{loc}}}_{\mathrm{NL}}=\frac{5\mathcal{Y}}{6}\left[ \mathcal{G}_{1}(\phi _*)+\mathcal{G}_{2}(\phi _*)\phi _*\right] , \end{aligned}$$

(8.61)

where the functions $\mathcal{G}_{1}(\phi _*)$ and $\mathcal{G}_{2}(\phi _*)$ are defined in the appendix.

Here it is important to note that the exact momentum dependence will not be calculable using the semi classical techniques used in $\delta \mathcal{N}$ formalism in the attractor regime of cosmological perturbations. But to know the exact momentum dependence of the non-Gaussian amplitude obtained from the three point function of the scalar curvature fluctuation it is always useful to follow exact quantum mechanical techniques used in In-In formalism as discussed earlier part of this section. In the case of the In-In formalism we freeze the value of the additional field $\Psi$ at the Planck scale and perform the calculation in the non-attractor regime of perturbation theory. But to get the correct estimate one can claim that the results obtained using the two techniques should match at the horizon crossing iff we freeze the value of the $\Psi$ field at the Planck scale in the $\delta \mathcal{N}$ formalism. This is also a strong information from the observational point of view, as by Planck and the other future observations trying to probe the value of non-Gaussianity at this scale. In this work, we have done both calculations for three point function for scalar curvature fluctuation by following semi classical and quantum mechanical techniques. In the case of the In-In formalism we have computed the results we use two physical shape configurations or templates- equilateral and squeezed to analyze the non-Gaussian amplitude obtained from the three point function for scalar curvature fluctuation by freezing the value of the additional $\Psi$ field at the Planck scale. Now to implement the equality between two results at the horizon crossing we have to fix the value of the additional field $\Psi$ in the $\delta \mathcal{N}$ formalism also. After freezing the value of $\Psi$ in all derived effective potentials we get the following result for curvature perturbation in terms of $\delta \mathcal{N}$ at $\phi =\phi _*$:

$$\begin{aligned} \zeta =\delta \mathcal{N}= & {} \phi _*\mathcal{D}(\phi _*)\sum ^{2}_{i=1}\hat{\Delta }_{i}(0)\nonumber \\&+\,\phi ^2_*\mathcal{E}(\phi _*)\sum ^{2}_{i=1}\sum ^{2}_{j=1}\hat{\Delta }_{i}(0)\hat{\Delta }_{j}(0)\nonumber \\&+\,\phi ^3_*\mathcal{F}(\phi _*)\sum ^{2}_{i=1}\sum ^{2}_{j=1}\sum ^{2}_{k=1}\hat{\Delta }_{i}(0)\hat{\Delta }_{j}(0)\hat{\Delta }_{k}(0)+\cdots \nonumber \\= & {} \phi _*\mathcal{D}(\phi _*)\left( \hat{\Delta }_{1}(0)+\hat{\Delta }_{2}(0)\right) +\phi ^2_*\mathcal{E}(\phi _*)\nonumber \\&\times \left( \hat{\Delta }^2_{1}(0)+\hat{\Delta }^2_{2}(0)+2\hat{\Delta }_{1}(0)\hat{\Delta }_{2}(0)\right) \nonumber \\&+\,\phi ^3_*\mathcal{F}(\phi _*)\left( \hat{\Delta }^3_{1}(0)+\hat{\Delta }^3_{2}(0)\right. \nonumber \\&\left. +\,3\hat{\Delta }^2_{1}(0)\hat{\Delta }_{2}(0)+3\hat{\Delta }_{1}(0)\hat{\Delta }^2_{2}(0)\right) +\cdots ,\nonumber \\ \end{aligned}$$

(8.62)

where the new functions $\mathcal{D}(\phi _*)$, $\mathcal{E}(\phi _*)$ and $\mathcal{F}(\phi _*)$ are defined as

$$\begin{aligned} \mathcal{D}(\phi _*)= & {} \left( \mathcal{N}_{,\phi }\right) _*=-\frac{1}{\mathcal{Y}\phi _*},\quad \mathcal{E}(\phi _*)=\frac{1}{2}\left( \mathcal{N}_{,\phi \phi }\right) _*=\frac{1}{2\mathcal{Y} \phi ^2_*},\nonumber \\ \mathcal{F}(\phi _*)= & {} \frac{1}{6}\left( \mathcal{N}_{,\phi \phi \phi }\right) _*=-\frac{1}{3\mathcal{Y} \phi ^3_*}. \end{aligned}$$

(8.63)

After freezing the value $\Psi$ in the Planck scale in the non-attractor regime of cosmological perturbation theory we get the following expression for the non-Gaussian amplitude from three point scalar curvature fluctuation:

$$\begin{aligned} f^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{5}{6}\left[ \frac{\mathcal{N}_{,\phi \phi }}{\mathcal{N}_{,\phi }}\right] _{*}=\frac{5}{6}\mathcal{Y}. \end{aligned}$$

(8.64)

Now further we use the general momentum dependent result at the horizon crossing and also use two different templates to equate with the results obtained from $\delta \mathcal{N}$ formalism and finally we get the following expression for the unknown factor $\mathcal{Y}$:

$$\begin{aligned} \mathcal{Y}\approx & {} \frac{1}{2\sum ^{3}_{i=1}k^3_i} \left[ 2(3\epsilon ^*_{\tilde{W}}-\eta ^{*}_{\tilde{W}})\sum ^{3}_{i=1}k^3_i +\epsilon ^*_{\tilde{W}}\left( -\sum ^{3}_{i=1}k^3_i\right. \right. \nonumber \\&+\left. \left. \sum ^{3}_{i,j=1,i\ne j}k_i k^2_j+\frac{8}{K}\sum ^{3}_{i,j=1,i> j}k^2_i k^2_j\right) \right] . \end{aligned}$$

(8.65)

However, it is crucial to note that without freezing the value of the addition field $\Psi$ in the Planck scale in the non-attractor regime of cosmological perturbation theory one can perform the exact quantum mechanical In-In calculation where the solution of the $\Psi$ field is related to the inflaton field $\phi$ and finally match with the results obtained from the $\delta \mathcal{N}$ formalism. In this paper we have not computed this in the case of the In-In formalism and we also hope to generalize this methodology in the attractor regime as well in the near future.

Next we use the two physical templates for the shape configurations – equilateral and squeezed – to determine the functional form of the unknown factor $\mathcal{Y}$, which is appearing in the $\delta \mathcal{N}$ formalism. In this context we get

• 1. Equilateral limit configuration:

  $$\begin{aligned} \mathcal{Y}\approx \frac{1}{6} \left[ 29\epsilon ^*_{\tilde{W}}-6\eta ^*_{\tilde{W}} \right] . \end{aligned}$$

  (8.66)

• 2. Squeezed limit configuration:

  $$\begin{aligned} \mathcal{Y}\approx & {} \frac{1}{2}\left[ 4(4\epsilon ^*_{\tilde{W}}-\eta ^*_{\tilde{W}}) +10\epsilon ^*_{\tilde{W}}\left( \frac{k_\mathrm{S}}{k_{\mathrm{L}}}\right) ^2\right. \nonumber \\&\left. -\,(2\eta ^*_{\tilde{W}}-\epsilon ^*_{\tilde{W}})\left( \frac{k_\mathrm{S}}{k_{\mathrm{L}}}\right) ^3\right] , \end{aligned}$$

  (8.67)

which are correct results of the unknown factor $\mathcal{Y}$ at the level of three point function computed from scalar curvature perturbation.

8.2 Four point function

8.2.1 Using the In-In formalism

Here we discuss the constraint on the primordial four point scalar correlation function in the non-attractor regime of soft inflation. In general one can write down the following expressions for the four point function of the scalar fluctuation [170,171,172,173,174,175]:

$$\begin{aligned} \langle \zeta (\mathbf{k}_1)\zeta (\mathbf{k}_2)\zeta (\mathbf{k}_3)\zeta (\mathbf{k}_4)\rangle= & {} (2\pi )^3\delta ^{(3)}(\mathbf{k}_1+\mathbf{k}_2+\mathbf{k}_3+\mathbf{k}_4)\nonumber \\&\times \, T(k_1,k_2,k_3,k_4). \end{aligned}$$

(8.68)

In our computation we choose Bunch–Davies vacuum state and for single field soft slow-roll inflation we get the following expression for the trispectrum:

$$\begin{aligned}&T(k_1,k_2,k_3,k_4)\approx \frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{216M^{12}_p(\epsilon ^*_{\tilde{W}})^2}\frac{1}{(k_1 k_2 k_3k_4)^3}\nonumber \\&\quad \times \left[ \hat{G}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)+\hat{G}^{S}(\mathbf{k}_1,\mathbf{k}_3,\mathbf{k}_2,\mathbf{k}_4)\right. \nonumber \\&\quad +\,\hat{G}^{S}(\mathbf{k}_1,\mathbf{k}_4,\mathbf{k}_3,\mathbf{k}_2)-\hat{W}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)\nonumber \\&\quad -\,\hat{W}^{S}(\mathbf{k}_1,\mathbf{k}_3,\mathbf{k}_2,\mathbf{k}_4)-\hat{W}^{S}(\mathbf{k}_1,\mathbf{k}_4,\mathbf{k}_3,\mathbf{k}_2)\nonumber \\&\quad -\,2\left\{ \hat{R}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)+\hat{R}^{S}(\mathbf{k}_1,\mathbf{k}_3,\mathbf{k}_2,\mathbf{k}_4)\right. \nonumber \\&\quad \left. \left. +\,\hat{R}^{S}(\mathbf{k}_1,\mathbf{k}_4,\mathbf{k}_3,\mathbf{k}_2)\right\} \right] , \end{aligned}$$

(8.69)

where the momentum dependent functions $\hat{G}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,{} \mathbf{k}_4)$, $\hat{W}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)$ and $\hat{R}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)$ are defined in the appendix.

Here it is important to mention that our derived result consists of the three following parts:

• 1. First of all, we have the contribution from contact interaction term $\hat{R}^{S}$, which appears due to the longitudinal graviton S-channel propagator:

  $$\begin{aligned}&R^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)=16(2\pi )^3\delta ^{(3)}(\mathbf{k}_1+\mathbf{k}_2+\mathbf{k}_3+\mathbf{k}_4)\nonumber \\&\quad \times \left[ \prod ^{4}_{I=1}\phi (\mathbf{k}_{I})\right] \hat{R}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4). \end{aligned}$$

  (8.70)

• 2. Next we have the contribution from the terms like $\hat{W}^{S}$, which comes from the contribution which appears due to the transverse graviton propagator:

  $$\begin{aligned} \widetilde{W}= & {} \int \mathrm{d}z_1 \mathrm{d}^3\mathbf{x}_1\int \mathrm{d}z_2 \mathrm{d}^3\mathbf{x}_2T_{i^{\prime }j^{\prime }}(z_1,\mathbf{x}_1)\delta ^{i^{\prime }i }\delta ^{j^{\prime }j }\nonumber \\&\times \,\tilde{G}_{ij,kl}(z_1,\mathbf{x}_1;z_2,\mathbf{x}_2)\delta ^{kk^{\prime \prime }} \delta ^{ll^{\prime \prime }}T_{k^{\prime \prime }l^{\prime \prime }}(z_2,\mathbf{x}_2),\nonumber \\ \end{aligned}$$

  (8.71)

  where the transverse graviton Green’s function $\tilde{G}_{ij,kl}(z_1,\mathbf{x}_1;z_2,\mathbf{x}_2)$ is given by

  $$\begin{aligned}&\tilde{G}_{ij,kl}(z_1,\mathbf{x}_1;z_2,\mathbf{x}_2) =\int \frac{\mathrm{d}^3\mathbf{k }}{(2\pi )^3}~\mathrm{e}^{i\mathbf{k}.(\mathbf{x}_1-\mathbf{x}_2)}\int ^{\infty }_{0}\mathrm{d}p^2\nonumber \\&\quad \times \frac{1}{4}\left[ \frac{J_{\frac{3}{2}}(pz_1) J_{\frac{3}{2}}(pz_2)}{\sqrt{z_1z_2}(\mathbf{k}^2+p^2)}\left( \widetilde{P}_{ik} \widetilde{P}_{jl}+\widetilde{P}_{il} \widetilde{P}_{jk}-\widetilde{P}_{ij}\widetilde{P}_{kl}\right) \right] .\nonumber \\ \end{aligned}$$

  (8.72)

  Here $\widetilde{P}_{ij}$ is the transverse traceless projector onto the directions perpendicular to $\mathbf{k}$ as given by $\widetilde{P}_{ij}=\left( \delta _{ij}-\frac{k_ik_j}{k^2}\right)$, and $J_{\frac{3}{2}}(x)$ is the Bessel function with characteristic index 3 / 2, which can be expressed in terms of the following simplified form:

  $$\begin{aligned} J_{\frac{3}{2}}(x)= & {} \sqrt{\frac{2}{\pi x}}\left( \frac{\sin x}{x}-\cos x\right) \nonumber \\= & {} \sqrt{\frac{2}{\pi x}}\frac{(1-ix)~\mathrm{e}^{ix}-(1+ix)~\mathrm{e}^{-ix}}{2ix}. \end{aligned}$$

  (8.73)

  Additionally in the present context the expression for the stress tensor $T_{ij}(z,\mathbf{x})$ in terms of scalar field inflaton fluctuation $\delta \phi (z,\mathbf{x})$ is given by the following simplified expression:

  $$\begin{aligned} T_{ij}(z,\mathbf{x})= & {} 2(\partial _{i}\delta \phi )(\partial _{j}\delta \phi )\nonumber \\&-\,\delta _{ij}[(\partial _{z}\delta \phi )^2+ \eta ^{kl}(\partial _{k}\delta \phi )(\partial _{l}\delta \phi )]. \end{aligned}$$

  (8.74)

  Here it is important to mention that two different insertions of the stress tensor correspond to two different values of the radial variable $z=(z_1,z_2)$, which we finally integrate out. Finally, for the S-channel contribution substituting for $\delta \phi$ in Fourier space we get the following expression for the transverse graviton propagator:

  $$\begin{aligned}&\widetilde{W}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4) =16(2\pi )^3\delta ^{(3)}(\mathbf{k}_1+\mathbf{k}_2+\mathbf{k}_3+\mathbf{k}_4)\nonumber \\&\quad \times \left[ \prod ^{4}_{I=1}\phi (\mathbf{k}_{I})\right] \times k^{i}_{1}k^{j}_{2}k^{k}_{3}k^{l}_{4}\left( \widetilde{P}_{ik} \widetilde{P}_{jl}+\widetilde{P}_{il}\widetilde{P}_{jk}- \widetilde{P}_{ij}\widetilde{P}_{kl}\right) \nonumber \\&\quad \,\times \Theta (k_1,k_2,k_3,k_4), \end{aligned}$$

  (8.75)

  where $\Theta (k_1,k_2,k_3,k_4)$ and the transverse projector along with the appropriate index contraction in momentum direction is defined as

  $$\begin{aligned}&\Theta (k_1,k_2,k_3,k_4)\nonumber \\&\quad =-\frac{2k_1k_2(k_1+k_2)^2((k_1+k_2)^2-k^2_3-k^2_4-4k_3k_4)}{(\hat{K}-2(k_3+k_4))^2\hat{K}^2((k_1+k_2)^2-K^2_s)}\nonumber \\&\qquad \times \left( \frac{3}{2(k_1+k_2)} -\frac{1}{\hat{K}}-\frac{1}{\hat{K}-2(k_3+k_4)} -\frac{k_1+k_2}{2k_1k_2}\right. \nonumber \\&\qquad \left. +\frac{k_1+k_2}{K^2_s-(k_1+k_2)^2}-\frac{k_1+k_2}{k^2_3+k^2_4+4k_3k_4-(k_1+k_2)^2}\right) \nonumber \\&\qquad +\,(1,2\leftrightarrow 3,4)\nonumber \\&\qquad +\,\frac{K^3_s(K^2_s-k^2_1-k^2_2-4k_1k_2) (K^2_s-k^2_3-k^2_4-4k_3k_4)}{(K^2_s-k^2_1-k^2_2-2k_1k_2)^2 (K^2_s-k^2_3-k^2_4-2k_3k_4)^2},\nonumber \\ \end{aligned}$$

  (8.76)
  $$\begin{aligned}&k^{i}_{1}k^{j}_{2}k^{k}_{3}k^{l}_{4} \left( \widetilde{P}_{ik}\widetilde{P}_{jl}+ \widetilde{P}_{il}\widetilde{P}_{jk}- \widetilde{P}_{ij}\widetilde{P}_{kl}\right) \nonumber \\&\quad =\left[ \mathbf{k}_1.\mathbf{k}_3+\frac{(\mathbf{k}_1.(\mathbf{k}_1+\mathbf{k}_2))(\mathbf{k}_3.(\mathbf{k}_3+\mathbf{k}_4))}{|\mathbf{k}_1+\mathbf{k}_2|^2}\right] \nonumber \\&\qquad \times \left[ \mathbf{k}_2.\mathbf{k}_4+\frac{(\mathbf{k}_2. (\mathbf{k}_1+\mathbf{k}_2))(\mathbf{k}_4.(\mathbf{k}_3+\mathbf{k}_4))}{|\mathbf{k}_1+\mathbf{k}_2|^2}\right] \nonumber \\&\qquad +\left[ \mathbf{k}_1.\mathbf{k}_4+\frac{(\mathbf{k}_1.(\mathbf{k}_1+\mathbf{k}_2))(\mathbf{k}_4.(\mathbf{k}_3+\mathbf{k}_4))}{|\mathbf{k}_1+\mathbf{k}_2|^2}\right] \nonumber \\&\qquad \times \left[ \mathbf{k}_2.\mathbf{k}_3+\frac{(\mathbf{k}_2.(\mathbf{k}_1+\mathbf{k}_2))(\mathbf{k}_3.(\mathbf{k}_3+\mathbf{k}_4))}{|\mathbf{k}_1+\mathbf{k}_2|^2}\right] \nonumber \\&\qquad -\left[ \mathbf{k}_1.\mathbf{k}_2-\frac{(\mathbf{k}_1.(\mathbf{k}_1+\mathbf{k}_2))(\mathbf{k}_2.(\mathbf{k}_3+\mathbf{k}_4))}{|\mathbf{k}_1+\mathbf{k}_2|^2}\right] \nonumber \\&\qquad \times \left[ \mathbf{k}_3.\mathbf{k}_4-\frac{(\mathbf{k}_3.(\mathbf{k}_1+\mathbf{k}_2))(\mathbf{k}_4.(\mathbf{k}_3+\mathbf{k}_4))}{|\mathbf{k}_1+\mathbf{k}_2|^2}\right] . \end{aligned}$$

  (8.77)

  where $K_s$ is defined as the norm of the total momentum required for graviton exchange in S-channel, $K_s=|\mathbf{k}_1+\mathbf{k}_2|=|-(\mathbf{k}_3+\mathbf{k}_4)|=|\mathbf{k}_3+\mathbf{k}_4|$. Finally substituting all these expressions in Eq. (8.75) we get the following simplified expression for the S-channel contribution in transverse graviton propagator:

  $$\begin{aligned} \widetilde{W}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)= & {} 16(2\pi )^3\delta ^{(3)}(\mathbf{k}_1+\mathbf{k}_2+\mathbf{k}_3+\mathbf{k}_4)\nonumber \\&\times \left[ \prod ^{4}_{I=1}\phi (\mathbf{k}_{I})\right] \hat{W}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4),\nonumber \\ \end{aligned}$$

  (8.78)

  where $\hat{W}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)$ is defined as

  $$\begin{aligned} \hat{W}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)= & {} k^{i}_{1}k^{j}_{2}k^{k}_{3}k^{l}_{4} (\widetilde{P}_{ik}\widetilde{P}_{jl}+\widetilde{P}_{il}\widetilde{P}_{jk}\nonumber \\&-\,\widetilde{P}_{ij}\widetilde{P}_{kl})\Theta (k_1,k_2,k_3,k_4).\nonumber \\ \end{aligned}$$

  (8.79)

  Here it is important to note that the contribution from the T and U-channel can be obtained by replacing the following momenta:

  $$\begin{aligned} T\text {-}\mathrm{channel}{:}\quad \mathbf{k}_{2}&\leftrightarrow&\mathbf{k}_{3},\end{aligned}$$

  (8.80)
  $$\begin{aligned} U\text {-}\mathrm{channel}{:}\quad \mathbf{k}_{2}&\leftrightarrow&\mathbf{k}_{4}. \end{aligned}$$

  (8.81)

  The representative S, T and U channel diagrams for bulk interpretation of the four point scalar correlation function in presence of graviton exchange is shown in shown in Fig. 17a–c. In these diagrams we have explicitly shown that the graviton is propagating on the bulk and the end points of the scalars are attached to the boundary at $z=0$. In or computation all the representative diagrams are important to explain the total four point scalar correlation function.

• 3. Additionally, the extra contributions $\hat{G}^{S}$ appear due to integrating out the metric perturbation.

Fig. 17

Representative S, T and U channel diagram for bulk interpretation of four point scalar correlation function in the presence of graviton exchange contribution. In all the diagrams the graviton is propagating on the bulk and the end points of the scalars are attached to the boundary at $z=0$

In the present context, including the contribution from four point function one can parameterize non-Gaussianity phenomenologically via a non-linear correction to a Gaussian perturbation $\zeta _{g}$ in position space as

$$\begin{aligned} \zeta (\mathbf{x})= & {} \zeta _{g}(\mathbf{x})+\frac{3}{5}f^{\mathrm{{loc}}}_{\mathrm{NL}}\left[ \zeta ^2_{g}(\mathbf{x})-\langle \zeta ^2_{g}(\mathbf{x})\rangle \right] \nonumber \\&+\,\frac{9}{25}g^{\mathrm{{loc}}}_{\mathrm{NL}}\zeta ^3_{g}(\mathbf{x})+\cdots , \end{aligned}$$

(8.82)

where $\cdots$ represents higher-order non-Gaussian contributions. In the case of local non-Gaussianity, the amplitude of the bispectrum from the three point function is defined as [159, 170]

$$\begin{aligned} T(k_1,k_2,k_3,k_4)= & {} \left[ \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}\sum _{j<p,i\ne j,p}P_{\zeta }(k_{ij})P_{\zeta }(k_j)P_{\zeta }(k_p)\right. \nonumber \\&+\left. \frac{54}{25}g^{\mathrm{{loc}}}_{\mathrm{NL}}\sum _{i<j<p}P_{\zeta }(k_{i})P_{\zeta }(k_j)P_{\zeta }(k_p)\right] ,~~~~~\nonumber \\ \end{aligned}$$

(8.83)

where $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}=\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}(k_1,k_2,k_3,k_4)$ and $g^{\mathrm{{loc}}}_{\mathrm{NL}}=g^{\mathrm{{loc}}}_{\mathrm{NL}}(k_1,k_2,k_3,k_4)$. Here additionally it is important to note that the connecting relation between the non-Gaussian parameter $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $g^{\mathrm{{loc}}}_{\mathrm{NL}}$ can be expressed as

$$\begin{aligned} g^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \mathcal{N}_{\mathrm{{NORM}}}\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}, \end{aligned}$$

(8.84)

where $\mathcal{N}_{\mathrm{{NORM}}}$ is defined as the appropriate normalization factor. In general the values of the normalization factor are different in different shape configurations. Further using Eq. (8.84) in Eq. (8.83) we get the following simplified expression for the non-Gaussian parameter $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $g^{\mathrm{{loc}}}_{\mathrm{NL}}$ as obtained from the four point scalar function:

$$\begin{aligned} \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{T(k_1,k_2,k_3,k_4)}{\left[ \sum _{j<p,i\ne j,p}P_{\zeta }(k_{ij})P_{\zeta }(k_j)P_{\zeta }(k_p)+\frac{54}{25}\mathcal{N}_{\mathrm{{NORM}}}\sum _{i<j<p}P_{\zeta }(k_{i})P_{\zeta }(k_j)P_{\zeta }(k_p)\right] },\end{aligned}$$

(8.85)

$$\begin{aligned} g^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{\mathcal{N}_{\mathrm{{NORM}}}T(k_1,k_2,k_3,k_4)}{\left[ \sum _{j<p,i\ne j,p}P_{\zeta }(k_{ij})P_{\zeta }(k_j)P_{\zeta }(k_p)+\frac{54}{25}\mathcal{N}_{\mathrm{{NORM}}}\sum _{i<j<p}P_{\zeta }(k_{i})P_{\zeta }(k_j)P_{\zeta }(k_p)\right] }. \end{aligned}$$

(8.86)

Additionally, it is important to note that in the non-attractor regime of soft inflation the model exactly similar to the single field slow-roll model of inflation, where it is a well-known fact that the non-Gaussian parameter $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $f^{\mathrm{{loc}}}_{\mathrm{NL}}$ are connected via the following constraint relationship:

$$\begin{aligned} \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}=\frac{36}{25}(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2, \end{aligned}$$

(8.87)

which is commonly known as the Suyama–Yamaguchi consistency relation. If this relation perfectly holds true in the present context, then one can easily gets

$$\begin{aligned} \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}\approx & {} \frac{36}{144}\frac{1}{\left( \sum ^{3}_{i=1}k^3_i\right) ^2} \left[ 2(3\epsilon ^*_{\tilde{W}}-\eta ^{*}_{\tilde{W}})\sum ^{3}_{i=1}k^3_i\right. \nonumber \\&+\left. \epsilon ^*_{\tilde{W}}\left( -\sum ^{3}_{i=1}k^3_i+\sum ^{3}_{i,j=1,i\ne j}k_i k^2_j+\frac{8}{K}\sum ^{3}_{i,j=1,i> j}k^2_i k^2_j\right) \right] ^2.\nonumber \\ \end{aligned}$$

(8.88)

from which one can find the following expression for the normalization factor:

$$\begin{aligned}&\mathcal{N}_{\mathrm{{NORM}}}=\frac{25}{54}\nonumber \\&\quad \times \,\frac{\left[ \frac{25T(k_1,k_2,k_3,k_4)}{36(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2}-\sum _{j<p,i\ne j,p}P_{\zeta }(k_{ij})P_{\zeta }(k_j)P_{\zeta }(k_p)\right] }{\sum _{i<j<p}P_{\zeta }(k_{i})P_{\zeta }(k_j)P_{\zeta }(k_p)}.\nonumber \\ \end{aligned}$$

(8.89)

Here it is very easy to observe that the normalization factor is different for different shapes.

But in general always the connecting relationship between the non-Gaussian parameters $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $f^{\mathrm{{loc}}}_{\mathrm{NL}}$ or more precisely the Suyama–Yamaguchi consistency relation does not perfectly hold true as the cosmological perturbation during the inflationary epoch is subject to quantum mechanical interference effects at the time of horizon crossing and such prescriptions does not satisfy a simple type of parameterization in terms of momentum independent-coefficients in Fourier space. In that specific case one can write down the connecting relation between the non-Gaussian parameter $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $g^{\mathrm{{loc}}}_{\mathrm{NL}}$ as

$$\begin{aligned} g^{\mathrm{{loc}}}_{\mathrm{NL}}= f(k_1,k_2,k_3,k_4,k_{12},k_{14},k_{13})\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}, \end{aligned}$$

(8.90)

where one can choose the momentum dependent function $f(k_1,k_2,k_3,k_4,k_{12},k_{14},k_{13})$ as

$$\begin{aligned}&f(k_1,k_2,k_3,k_4,k_{12},k_{14},k_{13})\nonumber \\&\quad =\frac{64}{\hat{K}^3}\sum _{i<j,m\ne i,j}k^3_ik^3_j\left( \frac{1}{k^3_{im}}+\frac{1}{k^3_{jm}}\right) , \end{aligned}$$

(8.91)

which is motivated from the choice of the shape function for trispectrum.

In this situation we get the following simplified expression for the non-Gaussian parameter $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $g^{\mathrm{{loc}}}_{\mathrm{NL}}$ as obtained from the four point scalar function:

$$\begin{aligned} \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{T(k_1,k_2,k_3,k_4)}{\left[ \sum _{j<p,i\ne j,p}P_{\zeta }(k_{ij})P_{\zeta }(k_j)P_{\zeta }(k_p)+\frac{54}{25}f(k_1,k_2,k_3,k_4,k_{12},k_{14},k_{13})\sum _{i<j<p}P_{\zeta }(k_{i})P_{\zeta }(k_j)P_{\zeta }(k_p)\right] },\end{aligned}$$

(8.92)

$$\begin{aligned} g^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{f(k_1,k_2,k_3,k_4,k_{12},k_{14},k_{13})T(k_1,k_2,k_3,k_4)}{\left[ \sum _{j<p,i\ne j,p}P_{\zeta }(k_{ij})P_{\zeta }(k_j)P_{\zeta }(k_p)+\frac{54}{25}f(k_1,k_2,k_3,k_4,k_{12},k_{14},k_{13})\sum _{i<j<p}P_{\zeta }(k_{i})P_{\zeta }(k_j)P_{\zeta }(k_p)\right] }. \end{aligned}$$

(8.93)

In this context we denote the angle between two momentum vectors as

$$\begin{aligned}&\cos \theta _{12}=\cos \theta _{34}\equiv \cos \theta _3,\end{aligned}$$

(8.94)

$$\begin{aligned}&\cos \theta _{23}=\cos \theta _{14}\equiv \cos \theta _1,\end{aligned}$$

(8.95)

$$\begin{aligned}&\cos \theta _{13}=\cos \theta _{24}\equiv \cos \theta _2, \end{aligned}$$

(8.96)

which satisfy the constraint condition $\sum ^{4}_{i<j=1}\cos \theta _{ij}=-2$ and can be equivalently written as $\sum ^{3}_{\alpha =1}\cos \theta _{\alpha }=\cos \theta _1 + \cos \theta _2 + \cos \theta _3 =-1$. This is an outcome of conservation of momentum. Additionally here,

$$\begin{aligned} k_{14}= & {} k_{23}=|\mathbf{k}_{1}+\mathbf{k}_{4}|=|\mathbf{k}_{2}+\mathbf{k}_{3}|\nonumber \\= & {} \sqrt{k^2_1+k^2_4+2k_1k_4\cos \theta _1}\nonumber \\= & {} \sqrt{k^2_2+k^2_3+2k_2k_3\cos \theta _1}, \end{aligned}$$

(8.97)

$$\begin{aligned} k_{24}= & {} k_{13}=|\mathbf{k}_{2}+\mathbf{k}_{4}|=|\mathbf{k}_{1}+\mathbf{k}_{3}|\nonumber \\= & {} \sqrt{k^2_2+k^2_4+2k_2k_4\cos \theta _2}\nonumber \\= & {} \sqrt{k^2_1+k^2_3+2k_1k_3\cos \theta _2}, \end{aligned}$$

(8.98)

$$\begin{aligned} k_{34}= & {} k_{12}=|\mathbf{k}_{3}+\mathbf{k}_{4}|=|\mathbf{k}_{1}+\mathbf{k}_{2}|\nonumber \\= & {} \sqrt{k^2_3+k^2_4+2k_3k_4\cos \theta _3}\nonumber \\= & {} \sqrt{k^2_1+k^2_2+2k_1k_2\cos \theta _3}. \end{aligned}$$

(8.99)

Let us now concentrate on the following limiting configurations for the trispectrum to analyze the shape properly from the obtained results:

Fig. 18

Representative diagram for equilateral non-Gaussian three point amplitude vs. product of the parameters $\alpha \bar{\lambda }$ in four different regions for $\mathcal{N}_{cmb}=50$ (red), $\mathcal{N}_{cmb}=60$ (blue) and $\mathcal{N}_{cmb}=70$ (green)

Fig. 19

Representative 3D diagram for equilateral non-Gaussian three point amplitude vs. the model parameters $\alpha$ and $\bar{\lambda }$ for $\mathcal{N}_{cmb}=60$ in two different angular views

Fig. 20

Representative diagram for equilateral non-Gaussian three point amplitude vs. product of the parameters $\alpha \bar{\lambda }$ in four different regions for $\mathcal{N}_{cmb}=50$ (red), $\mathcal{N}_{cmb}=60$ (blue) and $\mathcal{N}_{cmb}=70$ (green)

Fig. 21

Representative 3D diagram for equilateral non-Gaussian three point amplitude vs. the model parameters $\alpha$ and $\bar{\lambda }$ for $\mathcal{N}_{cmb}=60$ in two different angular views

Fig. 22

Representative diagram for equilateral non-Gaussian three point amplitude vs. product of the parameters $\alpha \bar{\lambda }$ in four different regions for $\mathcal{N}_{cmb}=50$ (red), $\mathcal{N}_{cmb}=60$ (blue) and $\mathcal{N}_{cmb}=70$ (green)

Fig. 23

Representative 3D diagram for equilateral non-Gaussian three point amplitude vs. the model parameters $\alpha$ and $\bar{\lambda }$ for $\mathcal{N}_{cmb}=60$ in two different angular views

Fig. 24

Representative diagram for equilateral non-Gaussian three point amplitude vs. product of the parameters $\alpha \bar{\lambda }$ in four different regions for $\mathcal{N}_{cmb}=50$ (red), $\mathcal{N}_{cmb}=60$ (blue) and $\mathcal{N}_{cmb}=70$ (green)

• 1. Equilateral limit configuration: For this case we have

  $$\begin{aligned} |\mathbf{k}_1|=|\mathbf{k}_2|=|\mathbf{k}_3|=k=k_i\quad \forall i=1,2,3,4, \end{aligned}$$

  (8.100)

  and this implies

  $$\begin{aligned} k_{ij}= & {} |k_{i}+k_{j}|=\sqrt{2}k\sqrt{1+\cos \theta _{ij}}\nonumber \\= & {} \sqrt{2}k\sqrt{1+\cos \theta _{\alpha }},\nonumber \\&\quad \forall (i,j=1,2,3,4)~\hbox {with }i<j, \alpha =1,2,3.\nonumber \\ \end{aligned}$$

  (8.101)

  Additionally in the equilateral limit configuration, $\theta =\theta _{\alpha }\forall \alpha =1,2,3$. Further using the constraint condition as stated in Eq. (8.105), we get

  $$\begin{aligned} \cos \theta =\cos \theta _{i}=-\frac{1}{3}\quad \forall i=1,2,3, \end{aligned}$$

  (8.102)

  and further using these results the trispectrum for scalar fluctuation can be written as

  $$\begin{aligned} T(k,k,k,k)\approx & {} \frac{3H^6}{8M^6_p (\epsilon ^*_{\tilde{W}})^2}\frac{1}{k^{12}}\left[ \hat{G}^{S}(\mathbf{k},\mathbf{k},\mathbf{k},\mathbf{k})\right. \nonumber \\&-\left. \hat{W}^{S}(\mathbf{k},\mathbf{k},\mathbf{k},\mathbf{k})-2\hat{R}^{S}(\mathbf{k},\mathbf{k},\mathbf{k},\mathbf{k})\right] ,\nonumber \\ \end{aligned}$$

  (8.103)

  where the momentum dependent functions $\hat{G}^{S}(\mathbf{k},\mathbf{k},\mathbf{k},{} \mathbf{k})$, $\hat{W}^{S}(\mathbf{k},\mathbf{k},\mathbf{k},\mathbf{k})$ and $\hat{R}^{S}(\mathbf{k},\mathbf{k},\mathbf{k},\mathbf{k})$ in the equilateral limit configuration are defined as

  $$\begin{aligned} \hat{G}^{S}(\mathbf{k},\mathbf{k},\mathbf{k},\mathbf{k})= & {} 0, \end{aligned}$$

  (8.104)
  $$\begin{aligned} \hat{R}^{S}(\mathbf{k},\mathbf{k},\mathbf{k},\mathbf{k})= & {} -\frac{1}{48}k^3,\end{aligned}$$

  (8.105)
  $$\begin{aligned} \hat{W}^{S}(\mathbf{k},\mathbf{k},\mathbf{k},\mathbf{k})= & {} 0, \end{aligned}$$

  (8.106)

  where we use $\hat{K}=4k$. Also the momentum dependent functions $A_{1}(\mathbf{k},\mathbf{k},\mathbf{k},\mathbf{k})$, $A_{2}(\mathbf{k},\mathbf{k},\mathbf{k},\mathbf{k})$ and $A_{3}(\mathbf{k},\mathbf{k},{} \mathbf{k},\mathbf{k})$ are defined as

  $$\begin{aligned} A_{1}(\mathbf{k},\mathbf{k},\mathbf{k},\mathbf{k})= & {} -\frac{7}{24}k^4,\quad A_{2}(\mathbf{k},\mathbf{k},\mathbf{k},\mathbf{k})=\frac{1}{4}k^5,\nonumber \\ A_{3}(\mathbf{k},\mathbf{k},\mathbf{k},\mathbf{k})= & {} \frac{7}{3}k^6. \end{aligned}$$

  (8.107)

  Substituting Eqs. (8.104) and (8.105) and Eq. (8.106) in Eq. (8.103), we get the following simplified expression for the trispectrum for scalar fluctuation:

  $$\begin{aligned} T(k,k,k,k)= & {} \frac{H^6}{64M^6_p (\epsilon ^*_H)^2}\frac{1}{k^9} \approx \frac{\tilde{W}^3(\phi _{cmb}, {\varvec{\Psi }})}{1728M^{12}_p (\epsilon ^*_{\tilde{W}})^2}\frac{1}{k^9}.\nonumber \\ \end{aligned}$$

  (8.108)

  Now if we assume that the non-Gaussian parameter $\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}$ and $f^{\mathrm{{equil}}}_{\mathrm{NL}}$ are connected through the Suyama–Yamaguchi consistency relation, then in the equilateral limiting configuration we get the following expression for the four point non-Gaussian parameter:

  $$\begin{aligned} \tau ^{\mathrm{{equil}}}_{\mathrm{NL}}\approx & {} \frac{1}{36} \left[ 29\epsilon ^*_{\tilde{W}}-6\eta ^*_{\tilde{W}} \right] ^2. \end{aligned}$$

  (8.109)

  In this limiting configuration the normalization factor $\mathcal{N}_{\mathrm{{NORM}}}$, which connects the two non-Gaussian parameters $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $g^{\mathrm{{loc}}}_{\mathrm{NL}}$, computed from four point function is

  $$\begin{aligned} \mathcal{N}_{\mathrm{{NORM}}}\approx & {} \left\{ \frac{9\epsilon ^*_H}{ \left[ 29\epsilon ^*_{\tilde{W}}-6\eta ^*_{\tilde{W}} \right] ^2}-\frac{9\sqrt{3}}{8}\right\} . \end{aligned}$$

  (8.110)

  Consequently the non-Gaussian parameter $g^{\mathrm{{loc}}}_{\mathrm{NL}}$ can be expressed as

  $$\begin{aligned} g^{\mathrm{{equil}}}_{\mathrm{NL}}\approx & {} \frac{\left\{ \frac{9\epsilon ^*_{\tilde{W}}}{\left[ 29\epsilon ^*_{\tilde{W}}-6\eta ^*_{\tilde{W}} \right] ^2}-\frac{9\sqrt{3}}{8}\right\} \epsilon ^*_H}{\left[ \frac{9\sqrt{3}}{8}+\frac{162}{25}\left\{ \frac{9\epsilon ^*_H}{\left[ 29\epsilon ^*_{\tilde{W}}-6\eta ^*_{\tilde{W}} \right] ^2}-\frac{9\sqrt{3}}{8}\right\} \right] }, \end{aligned}$$

  (8.111)

  or equivalently one can write the expression for the non-Gaussian parameter $g^{\mathrm{{loc}}}_{\mathrm{NL}}$ as

  $$\begin{aligned} g^{\mathrm{{equil}}}_{\mathrm{NL}}\approx & {} \frac{1}{36}\left\{ 9\epsilon ^*_{\tilde{W}}-\frac{9\sqrt{3}}{8}\left[ 29\epsilon ^*_{\tilde{W}}-6\eta ^*_{\tilde{W}} \right] ^2\right\} , \end{aligned}$$

  (8.112)

  as we have assumed the Suyama–Yamaguchi consistency relation perfectly holds true. Here it is important to mention that the results obtained from Eqs. (8.111) and (8.112) are perfectly consistent as in the leading order the two predict similar magnitudes, proportional to the slow-roll parameter $\epsilon ^*_H$ or $\epsilon ^*_{\tilde{W}}$. In Figs. 18 and 22, we have shown the features of the non-Gaussian amplitude from the four point scalar function $\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}$ and $g^{\mathrm{{equil}}}_{\mathrm{NL}}$ in the equilateral limit configuration in four different scanning regions of the product of the two parameters $\alpha \bar{\lambda }$ in the $(\tau ^{\mathrm{{equil}}}_{\mathrm{NL}},\alpha \bar{\lambda })$ and $(g^{\mathrm{{equil}}}_{\mathrm{NL}},\alpha \bar{\lambda })$ 2D plane for the number of e-foldings $50<\mathcal{N}_{cmb}<70$ (Figs. 19, 20, 21, 22, 24). The physical explanation of the obtained features are:

  • Region I: Here for the parameter space $0.0001<\alpha \bar{\lambda }<0.001$ the non-Gaussian amplitude lying within the window $0.006<\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}<0.016$, $-0.004<g^{\mathrm{{equil}}}_{\mathrm{NL}}<-0.023$. Further if we increase the numerical value of $\alpha \bar{\lambda }$, then the magnitude of the non-Gaussian amplitude saturates and we get the maximum value for $\mathcal{N}_{cmb}=50$, $|\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.016$, $|g^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.023$.

  • Region II: Here for the parameter space $0.00001<\alpha \bar{\lambda }<0.0001$ the non-Gaussian amplitude lies within the window $0.001<\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}<0.009$, $0.002<g^{\mathrm{{equil}}}_{\mathrm{NL}}<-0.011$. In this region we get maximum value for $\mathcal{N}_{cmb}=50$, $|\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.009$, $|g^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.011$. Additionally, it is important to note that in this case for $\alpha \bar{\lambda }=0.00004$ the lines obtained for $\mathcal{N}_{cmb}=50$, $\mathcal{N}_{cmb}=60$ and $\mathcal{N}_{cmb}=70$ cross each other.

  • Region III: Here for the parameter space $0.000001<\alpha \bar{\lambda }<0.00001$ the non-Gaussian amplitude lies within the window $0.00002<\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}<0.00062$, $0.0001<g^{\mathrm{{equil}}}_{\mathrm{NL}}<0.0017$. In this region we get the maximum value for $\mathcal{N}_{cmb}=70$, $|\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.00062$, $|g^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.0017$. Additionally, it is important to note that in this case for $0.000003\le \alpha \bar{\lambda }\le 0.000006$ the lines obtained for $\mathcal{N}_{cmb}=50$, $\mathcal{N}_{cmb}=60$ and $\mathcal{N}_{cmb}=70$ cross each other and then show increasing behavior.

  • Region IV: Here for the parameter space $0.0000001<\alpha \bar{\lambda }<0.000001$ the non-Gaussian amplitude lies within the window $10^{-6}<\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}<0.000012$, $2\times 10^{-6}<g^{\mathrm{{equil}}}_{\mathrm{NL}}<0.00011$. In this region we get the maximum value for $\mathcal{N}_{cmb}=60$, $|\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.000012$, $|g^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.00011$.

  Further combining the contribution from Region I, Region II, Region III and Region IV we finally get the following constraint on the four point non-Gaussian amplitude in the equilateral limit configuration:

  $$\begin{aligned}&\text {Region~I}+\text {Region~II}+\text {Region~III}+ \text {Region~IV}{:}\nonumber \\&\quad 10^{-6}<\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}<0.016, \quad -0.023<g^{\mathrm{{equil}}}_{\mathrm{NL}}<0.002\nonumber \\ \end{aligned}$$

  (8.113)

  for the following parameter space:

  $$\begin{aligned}&\text {Region~I}+\text {Region~II}+\text {Region~III}+ \text {Region~IV}{:}\nonumber \\&\quad 0.0000001<\alpha \bar{\lambda }<0.001. \end{aligned}$$

  (8.114)

  In this analysis we get the following maximum value of the three point non-Gaussian amplitude in the equilateral limit configuration:

  $$\begin{aligned} |\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.016,\quad |g^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.002. \end{aligned}$$

  (8.115)

  To visualize these constraints more clearly we have also presented $(\tau ^{\mathrm{{equil}}}_{\mathrm{NL}},\alpha ,\bar{\lambda })$ and $(g^{\mathrm{{equil}}}_{\mathrm{NL}},\alpha ,\bar{\lambda })$ 3D plots in Figs. 19a, b, 23a, b for two different angular orientations: Angle I and Angle II. From the representative surfaces the behavior is clearly observed of three point non-Gaussian amplitude in the equilateral limit for the variation of two fold parameters $\alpha$ and $\bar{\lambda }$ and the results are consistent with the obtained constraints in 2D analysis. Here all the obtained results are consistent with the two point and three point constraints as well as with the Planck 2015 data [44,45,46]. But as we have already pointed that if we relax the assumption of holding the Suyama–Yamaguchi consistency relation in the present context of discussion, then using Eq. (8.105) one can write down the expression for momentum dependent function $f(k,k,k,k,\frac{2}{\sqrt{3}}k,\frac{2}{\sqrt{3}}k,\frac{2}{\sqrt{3}}k)$ in the equilateral limiting configuration as, $f\left( k,k,k,k,\frac{2}{\sqrt{3}}k,\frac{2}{\sqrt{3}}k,\frac{2}{\sqrt{3}}k\right) =\frac{9\sqrt{3}}{2}$, using which we get the following simplified expression for the non-Gaussian parameter $\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}$ and $g^{\mathrm{{equil}}}_{\mathrm{NL}}$ as obtained from the four point scalar function in equilateral limiting configuration:

  $$\begin{aligned} \tau ^{\mathrm{{equil}}}_{\mathrm{NL}}= & {} \frac{50\sqrt{3}}{6507}\epsilon ^*_H\approx \frac{50\sqrt{3}}{6507}\epsilon ^*_{\tilde{W}},\nonumber \\ g^{\mathrm{{equil}}}_{\mathrm{NL}}= & {} \frac{25}{241}\epsilon ^*_H\approx \frac{25}{241}\epsilon ^*_{\tilde{W}}. \end{aligned}$$

  (8.116)

  In Figs. 20 and 24, without assuming the Suyama–Yamaguchi consistency relation we have shown the features of non-Gaussian amplitude from four point scalar function $\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}$ and $g^{\mathrm{{equil}}}_{\mathrm{NL}}$ in equilateral limit configuration in four different scanning region of the product of the two parameters $\alpha \bar{\lambda }$ in the $(\tau ^{\mathrm{{equil}}}_{\mathrm{NL}},\alpha \bar{\lambda })$ and $(g^{\mathrm{{equil}}}_{\mathrm{NL}},\alpha \bar{\lambda })$ 2D plane for the number of e-foldings $50<\mathcal{N}_{cmb}<70$. Physical explanations of the obtained features are:

  • Region I: Here for the parameter space $0.0001<\alpha \bar{\lambda }<0.001$ the non-Gaussian amplitude lies within the window $0.00028<\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}<0.00052$, $0.0022<g^{\mathrm{{equil}}}_{\mathrm{NL}}<0.004$. Further if we increase the numerical value of $\alpha \bar{\lambda }$, then the magnitude of the non-Gaussian amplitude saturates and we get the maximum value for $\mathcal{N}_{cmb}=50$, $|\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.00052$, $|g^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.004$.

  • Region II: Here for the parameter space $0.00001<\alpha \bar{\lambda }<0.0001$ the non-Gaussian amplitude lies within the window $0.00005<\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}<0.00042$, $0.0005<g^{\mathrm{{equil}}}_{\mathrm{NL}}<0.0033$. In this region we get the maximum value for $\mathcal{N}_{cmb}=50$, $|\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.00042$, $|g^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.0033$. Additionally, it is important to note that in this case for $\alpha \bar{\lambda }=0.00004$ the lines obtained for $\mathcal{N}_{cmb}=50$, $\mathcal{N}_{cmb}=60$ and $\mathcal{N}_{cmb}=70$ cross each other.

  • Region III: Here for the parameter space $0.000001<\alpha \bar{\lambda }<0.00001$ the non-Gaussian amplitude lying within the window $0.00001<\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}<0.00014$, $0.00008<g^{\mathrm{{equil}}}_{\mathrm{NL}}<0.0014$. In this region we get the maximum value for $\mathcal{N}_{cmb}=70$, $|\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.00014$, $|g^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.0014$. Additionally, it is important to note that in this case for $0.000003\le \alpha \bar{\lambda }\le 0.000006$ the lines obtained for $\mathcal{N}_{cmb}=50$, $\mathcal{N}_{cmb}=60$ and $\mathcal{N}_{cmb}=70$ cross each other and then show increasing behavior.

  • Region IV: Here for the parameter space $0.0000001<\alpha \bar{\lambda }<0.000001$ the non-Gaussian amplitude lying within the window $10^{-7}<\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}<7\times 10^{-6}$, $5\times 10^{-8}<g^{\mathrm{{equil}}}_{\mathrm{NL}}<0.000052$. In this region we get the maximum value for $\mathcal{N}_{cmb}=60$, $|\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 7\times 10^{-6}$, $|g^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.000052$.

  Further combining the contribution from Region I, Region II, Region III and Region IV we finally get the following constraint on the four point non-Gaussian amplitude in the equilateral limit configuration:

  $$\begin{aligned}&\text {Region~I}+\text {Region~II}+\text {Region~III}+ \text {Region~IV}{:}\nonumber \\&\quad 10^{-7}<\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}<0.00052,\quad 5\times 10^{-8}<g^{\mathrm{{equil}}}_{\mathrm{NL}}<0.004\nonumber \\ \end{aligned}$$

  (8.117)

  for the following parameter space:

  $$\begin{aligned}&\text {Region~I}+\text {Region~II}+\text {Region~III}+ \text {Region~IV}{:}\nonumber \\&\quad 0.0000001<\alpha \bar{\lambda }<0.001. \end{aligned}$$

  (8.118)

  In this analysis we get the following maximum value of the three point non-Gaussian amplitude in the equilateral limit configuration:

  $$\begin{aligned} |\tau ^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.00052,\quad |g^{\mathrm{{equil}}}_{\mathrm{NL}}|_{\max }\sim 0.004. \end{aligned}$$

  (8.119)

  To visualize these constraints more clearly we have also presented $(\tau ^{\mathrm{{equil}}}_{\mathrm{NL}},\alpha ,\bar{\lambda })$ and $(g^{\mathrm{{equil}}}_{\mathrm{NL}},\alpha ,\bar{\lambda })$ 3D plot in Figs. 21a, b, 25a, b for two different angular orientations: Angle I and Angle II. From the representative surfaces it is clearly observed the behavior of three point non-Gaussian amplitude in the equilateral limit for the variation of two fold parameter $\alpha$ and $\bar{\lambda }$ and the results are consistent with the obtained constraints in 2D analysis. Here all the obtained results are consistent with the two point and three point constraints as well as with the Planck 2015 data [44,45,46].

• 2. Counter-collinear or folded kite limiting configuration: For this case we have the situation where the magnitude of the sum of the two momenta is taken to be zero, which implies

  $$\begin{aligned}&k_{ij}=|k_{i}+k_{j}|=\sqrt{k^2_i+k^2_j+2k_ik_j\cos \theta _{ij}}\rightarrow 0,\nonumber \\&\quad \forall (i,j=1,2,3,4)\hbox { with }i<j, \end{aligned}$$

  (8.120)

which implies $\cos \theta _{ij}\rightarrow -\frac{(k^2_i+k^2_j)}{2k_ik_j},\forall (i,j=1,2,3,4)\hbox { with }i<j,$ and this satisfies $\sum ^{4}_{i<j=1}\frac{(k^2_i+k^2_j)}{k_ik_j}\rightarrow 4$. In the present context, we identify this situation as the counter-collinear limiting configuration as in this case for each momentum there is another associated momentum which has equal magnitude along with opposite direction. In this specific case one can construct a quadrilateral which is formed by the momentum vectors participating in this limit using two fold ways. From the analysis it is observed that if by our choice on the momenta they are of the same order in magnitude then the counter-collinear configurations are adjacent. Sometimes in the literature this is identified as the folded kite limiting configuration. On the contrary, here one can also choose the momenta in such a way that the counter-collinear configurations are on the opposite sides of the quadrilateral formed in the present context. But both situations are specifically dual configurations to each other. Consequently, the mathematical structure of the local trispectrum for scalar fluctuation simplifies in the counter-collinear or folded kite limiting configuration. In this limit here we actually take

$$\begin{aligned} k_{12}\ll k_{1}\approx k_{2},k_{3}\approx k_{4}. \end{aligned}$$

(8.121)

Consequently we have $\cos \theta _1=\cos \theta _2,$ $\cos \theta _3=-1.$ In this case the trispectrum for scalar fluctuation can be written as

$$\begin{aligned}&T(k_1,k_1,k_3,k_3)\approx \frac{\tilde{W}^3(\phi _{cmb}, {\varvec{\Psi }})}{216M^{12}_p (\epsilon ^*_{\tilde{W}})^2}\frac{1}{(k_1 k_3 )^6}\nonumber \\&\quad \times \left[ \frac{9}{4}\frac{k^3_1k^3_3}{k^3_{12}} \sin ^2\alpha _1\sin ^2\alpha _3\cos 2\chi _{12,34}+\cdots \right] , \end{aligned}$$

(8.122)

where in the counter-collinear or folded kite limiting configuration contribution from the momentum dependent functions $\hat{W}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)$ and $\hat{R}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)$ are finite but the contributions are sub dominant for which one can easily neglect this part compared to the graviton exchange contribution. Here the graviton exchange contribution in the counter-collinear or folded kite limiting configuration is defined as

$$\begin{aligned}&\hat{G}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)\nonumber \\&\quad =\left[ \frac{9}{4}\frac{k^3_1k^3_3}{k^3_{12}}\sin ^2\alpha _1\sin ^2\alpha _3\cos 2\chi _{12,34}+\cdots \right] \end{aligned}$$

(8.123)

where in counter-collinear or folded kite limiting configuration we have used additionally the following results:

$$\begin{aligned} S(\mathbf{k}_1,\mathbf{k}_2)\approx & {} \frac{3}{2}k_1,\quad S(\mathbf{k}_3,\mathbf{k}_4)\approx \frac{3}{2}k_3, \end{aligned}$$

(8.124)

and for the polarization sum we use

$$\begin{aligned}&\sum _{s=+,\times }\epsilon ^{s}_{ij}(\mathbf{k}_{12})\epsilon ^{s}_{lm}(\mathbf{k}_{34})k^{i}_{1}k^{j}_{2}k^{l}_{3}k^{m}_{4}\nonumber \\&\quad =k^2_1k^2_3\sin ^2\alpha _1\sin ^2\alpha _3\cos 2\chi _{12,34}. \end{aligned}$$

(8.125)

Here we have to mention that

$$\begin{aligned}&\epsilon ^{+}_{ij}=\mathbf{a}_{i}{} \mathbf{a}_{j}-\bar{\mathbf{a}}_{i}\bar{\mathbf{a}}_{j},\quad \epsilon ^{\times }_{ij}=\mathbf{a}_{i}{} \mathbf{a}_{j}+\bar{\mathbf{a}}_{i}\bar{\mathbf{a}}_{j},\end{aligned}$$

(8.126)

$$\begin{aligned}&\epsilon ^{+}_{ij}(\mathbf{k}_{12})k^{i}_{1}k^{j}_{2} =k_{1}k_{2}\sin \alpha _{1}\sin \alpha _{2}\cos (\beta _{1}+\beta _{2}),\end{aligned}$$

(8.127)

$$\begin{aligned}&\epsilon ^{+}_{ij}(\mathbf{k}_{34})k^{l}_{3}k^{m}_{4} =k_{3}k_{4}\sin \alpha _{3}\sin \alpha _{4}\cos (\beta _{1}+\beta _{2})\end{aligned}$$

(8.128)

$$\begin{aligned}&\epsilon ^{\times }_{ij}(\mathbf{k}_{12})k^{i}_{1}k^{j}_{2} =k_{1}k_{2}\sin \alpha _{1}\sin \alpha _{2}\sin (\beta _{1}+\beta _{2}),\end{aligned}$$

(8.129)

$$\begin{aligned}&\epsilon ^{\times }_{ij}(\mathbf{k}_{34})k^{l}_{3}k^{m}_{4} =k_{3}k_{4}\sin \alpha _{3}\sin \alpha _{4}\sin (\beta _{1}+\beta _{2}),\end{aligned}$$

(8.130)

$$\begin{aligned}&\frac{\sin \alpha _{2}}{\sin \alpha _{1}}=\frac{k_1}{k_2}\approx 1,\quad \frac{\sin \alpha _{4}}{\sin \alpha _{3}}=\frac{k_3}{k_4}\approx 1,\end{aligned}$$

(8.131)

$$\begin{aligned}&\beta _{2}-\beta _{1}=\pi ,\quad \beta _{4}-\beta _{3}=\pi ,\quad \beta _{1}-\beta _{3}=\chi _{12,34},\nonumber \\ \end{aligned}$$

(8.132)

and we use the following coordinate to parameterize the momentum vector:

$$\begin{aligned} \mathbf{k}_{i}=k_{i}\left( \sin \alpha _{i}\cos \beta _{i}, \sin \alpha _{i}\sin \beta _{i},\cos \alpha _{i}\right) \quad \forall i=(1,2,3,4),\nonumber \\ \end{aligned}$$

(8.133)

where

$$\begin{aligned} \alpha _{i}\equiv & {} \cos ^{-1}(\hat{\mathbf{k}}_{i}.\hat{\mathbf{k}}_{12})\quad \forall i=(1,2,3,4),\end{aligned}$$

(8.134)

$$\begin{aligned} \beta _{i}\equiv & {} \cos ^{-1}(\hat{\mathbf{k}}_{i}.\mathbf{a})\quad \forall i=(1,2,3,4). \end{aligned}$$

(8.135)

Now if we assume that the non-Gaussian parameter $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $f^{\mathrm{{loc}}}_{\mathrm{NL}}$ are connected through the Suyama–Yamaguchi consistency relation, then in the counter-collinear or folded kite limiting configuration we get the following expression for the four point non-Gaussian parameter:

$$\begin{aligned} \tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}\approx & {} \frac{36}{144}\frac{1}{(2k^3_1+k^3_3)^2} \left[ 2(3\epsilon ^*_{\tilde{W}}-\eta ^{*}_{\tilde{W}})(2k^3_1+k^3_3) \phantom {\frac{8k^2_1}{(2k_1+k_3)}}\right. \nonumber \\&\left. +\,\epsilon ^*_{\tilde{W}}\left( -(2k^3_1+k^3_3) +2(k^3_1+k_1k_3(k_1+k_3))\phantom {\frac{8k^2_1}{(2k_1+k_3)}}\right. \right. \nonumber \\&\left. \left. +\,\frac{8k^2_1}{(2k_1+k_3)}(k^2_1+2k^2_3)\right) \right] ^2. \end{aligned}$$

(8.136)

In this limiting configuration the normalization factor $\mathcal{N}_{\mathrm{{NORM}}}$, which connects the two non-Gaussian parameters $\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}$ and $g^{\mathrm{{foldkite}}}_{\mathrm{NL}}$, computed from four point function, is

$$\begin{aligned} \mathcal{N}_{\mathrm{{NORM}}}=\frac{25}{54}\left[ \frac{\Delta _{1}-\Delta _{2}}{\Delta _{3}}\right] , \end{aligned}$$

(8.137)

where the momentum dependent factors $\Delta _{1}$, $\Delta _{2}$ and $\Delta _{3}$ are defined as

$$\begin{aligned} \Delta _{1}\approx & {} \frac{\frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{54M^{12}_p (\epsilon ^*_{\tilde{W}})^2}\frac{(2k^3_1+k^3_3)^2}{(k_1 k_3 )^6}\left[ \frac{9}{4}\frac{k^3_1k^3_3}{k^3_{12}}\sin ^2\alpha _1\sin ^2\alpha _3\cos 2\chi _{12,34}+\cdots \right] }{\left[ 2(3\epsilon ^*_{\tilde{W}}-\eta ^{*}_{\tilde{W}})\left( 2k^3_1+k^3_3\right) +\epsilon ^*_{\tilde{W}}\left( -\left( 2k^3_1+k^3_3\right) +2\left( k^3_1+k_1k_3(k_1+k_3)\right) +\frac{8k^2_1(k^2_1+2k^2_3)}{(2k_1+k_3)}\right) \right] ^{2}}, \end{aligned}$$

(8.138)

$$\begin{aligned} \Delta _{2}= & {} \sum _{j<p,i\ne j,p}P_{\zeta }(k_{ij})P_{\zeta }(k_j)P_{\zeta }(k_p)\nonumber \\\approx & {} \frac{\tilde{W}^3 (\phi _{cmb},{\varvec{\Psi }})}{1728 M^{12}_{p}(\epsilon ^*_{\tilde{W}})^3} \left[ \frac{4}{k^{3}_{12}k^{3}_{1}k^{3}_{3}}+\frac{1}{k^{3}_{13}k^{3}_{3}} \left( \frac{3}{k^3_1}+\frac{1}{k^3_3}\right) \right. \nonumber \\&\left. +\,\frac{1}{k^{3}_{23}}\left( \frac{1}{k^3_1}+\frac{1}{k^3_3}\right) ^2\right] ,\end{aligned}$$

(8.139)

$$\begin{aligned} \Delta _{3}= & {} \sum _{i<j<p}P_{\zeta }(k_{i})P_{\zeta }(k_j)P_{\zeta }(k_p)\nonumber \\\approx & {} \frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{864 M^{12}_{p}(\epsilon ^*_{\tilde{W}})^3} \frac{1}{k^3_1k^3_3}\left( \frac{1}{k^3_1}+\frac{1}{k^3_3}\right) , \end{aligned}$$

(8.140)

Consequently the non-Gaussian parameter $g^{\mathrm{{loc}}}_{\mathrm{NL}}$ can be expressed as

$$\begin{aligned} g^{\mathrm{{foldkite}}}_{\mathrm{NL}}\approx & {} \frac{25}{216}\left[ \frac{\Delta _{1}-\Delta _{2}}{\Delta _{3}}\right] \frac{1}{(2k^3_1+k^3_3)^2}\nonumber \\&\times \left[ 2(3\epsilon ^*_{\tilde{W}}-\eta ^{*}_{\tilde{W}}) (2k^3_1+k^3_3)\phantom {\frac{8k^2_1}{(2k_1+k_3)}}\right. \nonumber \\&+\,\epsilon ^*_{\tilde{W}}\left( -(2k^3_1+k^3_3) +2(k^3_1+k_1k_3(k_1+k_3))\phantom {\frac{8k^2_1}{(2k_1+k_3)}}\right. \nonumber \\&\left. \left. +\,\frac{8k^2_1}{(2k_1+k_3)}(k^2_1+2k^2_3)\right) \right] ^2. \end{aligned}$$

(8.141)

In Figs. 26 and 28, we have shown the features of non-Gaussian amplitude from four point scalar function $\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}$ and $g^{\mathrm{{foldkite}}}_{\mathrm{NL}}$ in the folded kite limit configuration in four different scanning regions of the product of the two parameters $\alpha \bar{\lambda }$ in the $(\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}},\alpha \bar{\lambda })$ and $(g^{\mathrm{{foldkite}}}_{\mathrm{NL}},\alpha \bar{\lambda })$ 2D plane for the number of e-foldings $50<\mathcal{N}_{cmb}<70$ (Figs. 27, 29). Physical explanation of the obtained features are appended following:

• Region I: Here for the parameter space $0.0001<\alpha \bar{\lambda }<0.001$ the non-Gaussian amplitude lying within the window $0.0025<\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}<0.0085$, $0.014<g^{\mathrm{{foldkite}}}_{\mathrm{NL}}<0.038$. Further if we increase the numerical value of $\alpha \bar{\lambda }$, then the magnitude of the non-Gaussian amplitude saturates and we get the maximum value for $\mathcal{N}_{cmb}=50$, $|\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}|_{\max }\sim 0.0085$, $|g^{\mathrm{{foldkite}}}_{\mathrm{NL}}|_{\max }\sim 0.038$.

• Region II: Here for the parameter space $0.00001<\alpha \bar{\lambda }<0.0001$ the non-Gaussian amplitude lying within the window $0.0002<\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}<0.0048$, $0.001<g^{\mathrm{{foldkite}}}_{\mathrm{NL}}<0.023$. In this region we get the maximum value for $\mathcal{N}_{cmb}=50$, $|\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}|_{\max }\sim 0.0048$, $|g^{\mathrm{{foldkite}}}_{\mathrm{NL}}|_{\max }\sim 0.023$. Additionally it is important to note that in this case for $\alpha \bar{\lambda }=0.00004$ the lines obtained for $\mathcal{N}_{cmb}=50$, $\mathcal{N}_{cmb}=60$ and $\mathcal{N}_{cmb}=70$ cross each other.

• Region III: Here for the parameter space $0.000001<\alpha \bar{\lambda }<0.00001$ the non-Gaussian amplitude lying within the window $0.000018<\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}<0.001$,  $0.0001<g^{\mathrm{{foldkite}}}_{\mathrm{NL}}<0.001$. In this region we get the maximum value for $\mathcal{N}_{cmb}=70$, $|\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}|_{\max }\sim 0.00062$, $|g^{\mathrm{{foldkite}}}_{\mathrm{NL}}|_{\max }\sim 0.001$. Additionally, it is important to note that in this case for $0.000001\le \alpha \bar{\lambda }\le 0.000006$ the lines obtained for $\mathcal{N}_{cmb}=50$, $\mathcal{N}_{cmb}=60$ and $\mathcal{N}_{cmb}=70$ show increasing, decreasing and further increasing behavior.

• Region IV: Here for the parameter space $0.0000001<\alpha \bar{\lambda }<0.000001$ the non-Gaussian amplitude lying within the window $10^{-6}<\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}<0.000014,$ $2\times 10^{-6}<g^{\mathrm{{foldkite}}}_{\mathrm{NL}}<0.000066$. In this region we get the maximum value for $\mathcal{N}_{cmb}=60$, $|\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}|_{\max }\sim 0.000014$, $|g^{\mathrm{{foldkite}}}_{\mathrm{NL}}|_{\max }\sim 0.000066$.

Further combining the contribution from Region I, Region II, Region III and Region IV we finally get the following constraint on the four point non-Gaussian amplitude in the equilateral limit configuration:

$$\begin{aligned}&\text {Region~I}+\text {Region~II}+\text {Region~III}+ \text {Region~IV}{:}\nonumber \\&\quad 10^{-6}<\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}<0.016,\quad -0.023<g^{\mathrm{{foldkite}}}_{\mathrm{NL}}<0.002\nonumber \\ \end{aligned}$$

(8.142)

for the following parameter space:

$$\begin{aligned}&\text {Region~I}+\text {Region~II}+\text {Region~III}+ \text {Region~IV}{:}\nonumber \\&\quad 0.0000001<\alpha \bar{\lambda }<0.001. \end{aligned}$$

(8.143)

In this analysis we get the following maximum value of the three point non-Gaussian amplitude in the equilateral limit configuration as given by

$$\begin{aligned} |\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}|_{\max }\sim 0.016,\quad |g^{\mathrm{{foldkite}}}_{\mathrm{NL}}|_{\max }\sim 0.002. \end{aligned}$$

(8.144)

To visualize these constraints more clearly we have also presented $(\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}},\alpha ,\bar{\lambda })$ and $(g^{\mathrm{{foldkite}}}_{\mathrm{NL}},\alpha ,\bar{\lambda })$ 3D plot in Figs. 19a, b, 23a, b for two different angular orientations: Angle I and Angle II. From the representative surfaces it is clearly observed the behavior of scalar four point non-Gaussian amplitude in the folded kite limit for the variation of two fold parameter $\alpha$ and $\bar{\lambda }$ and the results are consistent with the obtained constraints in 2D analysis. Here all the obtained results are consistent with the two point and three point constraints as well as with the Planck 2015 data [44,45,46].

But as we have already pointed that if we relax the assumption of holding the Suyama–Yamaguchi consistency relation in the present context of discussion, then using Eq. (8.105) one can write down the expression for momentum dependent function $f(k_1,k_1,k_3,k_3,k_{12},k_{13},k_{23})$ in the equilateral limiting configuration as

$$\begin{aligned}&f(k_1,k_1,k_3,k_3,k_{12},k_{13},k_{23})\nonumber \\&\quad =\frac{8}{(k_1+k_3)^3}\left[ (k^6_1 +k^6_3) \left( \frac{1}{k^3_{13}}+\frac{1}{k^3_{23}}\right) \right. \nonumber \\&\qquad \left. +\,2k^3_1 k^3_3\left( \frac{2}{k^3_{12}}+\frac{1}{k^3_{13}} +\frac{1}{k^3_{23}}\right) \right] , \end{aligned}$$

(8.145)

using which we get the following simplified expression for the non-Gaussian parameter $\tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}$ and $g^{\mathrm{{foldkite}}}_{\mathrm{NL}}$ as obtained from the four point scalar function in equilateral limiting configuration as

$$\begin{aligned} \tau ^{\mathrm{{foldkite}}}_{\mathrm{NL}}\approx & {} \frac{\frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{216M^{12}_p (\epsilon ^*_{\tilde{W}})^2}\frac{1}{(k_1 k_3 )^6}\left[ \frac{9}{4}\frac{k^3_1k^3_3}{k^3_{12}}\sin ^2\alpha _1\sin ^2\alpha _3\cos 2\chi _{12,34}+\cdots \right] }{\left[ \Delta _{2}+\frac{54}{25}\frac{8}{(k_1+k_3)^3}\left\{ (k^6_1 +k^6_3)\left( \frac{1}{k^3_{13}}+\frac{1}{k^3_{23}}\right) +2k^3_1 k^3_3\left( \frac{2}{k^3_{12}}+\frac{1}{k^3_{13}}+\frac{1}{k^3_{23}}\right) \right\} \Delta _{3}\right] },\end{aligned}$$

(8.146)

$$\begin{aligned} g^{\mathrm{{foldkite}}}_{\mathrm{NL}}\approx & {} \frac{\frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{216M^{12}_p (\epsilon ^*_{\tilde{W}})^2}\frac{1}{(k_1 k_3 )^6}\left[ \frac{9}{4}\frac{k^3_1k^3_3}{k^3_{12}}\sin ^2\alpha _1\sin ^2\alpha _3\cos 2\chi _{12,34}+\cdots \right] }{\left[ \frac{\Delta _{2}}{\frac{8}{(k_1+k_3)^3}\left\{ (k^6_1 +k^6_3)\left( \frac{1}{k^3_{13}}+\frac{1}{k^3_{23}}\right) +2k^3_1 k^3_3\left( \frac{2}{k^3_{12}}+\frac{1}{k^3_{13}}+\frac{1}{k^3_{23}}\right) \right\} }+\frac{54}{25}\Delta _{3}\right] }. \end{aligned}$$

(8.147)

• 3. Squeezed limiting configuration: For this case we have $k_{1}\approx k_{2}\approx k_{3}(=k_{\mathrm{L}})\gg k_{4}(=k_\mathrm{S})$, where $k_{i}=|\mathbf{k_{i}}|\forall i=1,2,3.$ Here $k_{\mathrm{L}}$ and $k_\mathrm{S}$ represent momentum for long and short modes respectively. In this case one can write, $\cos \theta _{i}=-\frac{1}{2}\left( 1+\frac{k_\mathrm{S}}{k_{\mathrm{L}}}\right) ,~\forall ~i=(1,2,3),$ which gives an estimate of the factor $k_\mathrm{S}/k_{\mathrm{L}}$ in the squeezed limit configuration and this estimate we will use for future computation.

In this case the trispectrum for scalar fluctuation can be written as

$$\begin{aligned}&T(k_{\mathrm{L}},k_{\mathrm{L}},k_{\mathrm{L}},k_\mathrm{S})\approx \frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{216M^{12}_p (\epsilon ^*_{\tilde{W}})^2}\frac{1}{k^6_Lk^3_\mathrm{S}}\nonumber \\&\quad \times \left[ \frac{9}{4}\frac{1}{\left( 1-\frac{k_\mathrm{S}}{k_{\mathrm{L}}}\right) ^{\frac{3}{2}}}\sin ^2\alpha _1\sin ^2\alpha _3\cos 2\chi _{12,34}\right] . \end{aligned}$$

(8.148)

where in the squeezed limiting configuration contribution from the momentum dependent functions $\hat{W}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)$ and $\hat{R}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)$ vanishes in leading order in slow-roll and negligibly small but finite contribution comes from the graviton exchange term. Here the graviton exchange contribution in squeezed limiting configuration defined as

$$\begin{aligned} \hat{G}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)= & {} \frac{\frac{9}{4}k^6_{\mathrm{L}}}{\left( 1-\frac{k_\mathrm{S}}{k_{\mathrm{L}}}\right) ^{\frac{3}{2}}}\sin ^2\alpha _1\sin ^2\alpha _3\cos 2\chi _{12,34},\nonumber \\ \end{aligned}$$

(8.149)

where in squeezed limiting configuration we have used additionally the following results:

$$\begin{aligned} S(\mathbf{k}_1,\mathbf{k}_2)\approx \frac{3}{2}k_{\mathrm{L}}\approx S(\mathbf{k}_3,\mathbf{k}_4), \end{aligned}$$

(8.150)

and for the polarization sum we use the same results that we have used in the case of counter-collinear limit. Additionally here we have

$$\begin{aligned} \frac{\sin \alpha _{2}}{\sin \alpha _{1}}=\frac{k_{\mathrm{L}}}{k_{\mathrm{L}}}\approx 1,\quad \frac{\sin \alpha _{4}}{\sin \alpha _{3}}=\frac{k_{\mathrm{L}}}{k_\mathrm{S}}\gg 1. \end{aligned}$$

(8.151)

Now if we assume that the non-Gaussian parameter $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $f^{\mathrm{{loc}}}_{\mathrm{NL}}$ are connected through the Suyama–Yamaguchi consistency relation, then in the case where $k_{1}\sim k_{2} \sim k_{3}\approx k_{\mathrm{L}}$, we get the following expression for the four point non-Gaussian parameter:

$$\begin{aligned} \tau ^{\mathrm{{sq}}}_{\mathrm{NL}} \approx \frac{1}{36} \left[ 29\epsilon ^*_{\tilde{W}}-6\eta ^{*}_{\tilde{W}}\right] ^2. \end{aligned}$$

(8.152)

In this limiting configuration the normalization factor $\mathcal{N}_{\mathrm{{NORM}}}$, which connects the two non-Gaussian parameters $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $g^{\mathrm{{loc}}}_{\mathrm{NL}}$, computed from four point function, is

$$\begin{aligned} \mathcal{N}_{\mathrm{{NORM}}}=\frac{25}{54}\left[ \frac{\Delta _{1}-\Delta _{2}}{\Delta _{3}}\right] , \end{aligned}$$

(8.153)

where the momentum dependent factors $\Delta _{1}$, $\Delta _{2}$ and $\Delta _{3}$ are defined as

$$\begin{aligned} \Delta _{1}= & {} \frac{25 T(k_1,k_1,k_3,k_3)}{36(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2}\nonumber \\\approx & {} \frac{\frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{6M^{12}_p (\epsilon ^*_{\tilde{W}})^2}\frac{1}{k^6_Lk^3_\mathrm{S}} \left[ \frac{9}{4}\frac{1}{\left( 1-\frac{k_\mathrm{S}}{k_{\mathrm{L}}}\right) ^{\frac{3}{2}}} \sin ^2\alpha _1\sin ^2\alpha _3\cos 2\chi _{12,34}\right] }{ \left[ 29\epsilon ^*_{\tilde{W}}-6\eta ^*_{\tilde{W}}\right] ^2}\nonumber \\ ,\end{aligned}$$

(8.154)

$$\begin{aligned} \Delta _{2}= & {} \sum _{j<p,i\ne j,p}P_{\zeta }(k_{ij})P_{\zeta }(k_j) P_{\zeta }(k_p)\nonumber \\= & {} \frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{1728 M^{12}_{p}(\epsilon ^*_{\tilde{W}})^3}\frac{6}{k^6_{\mathrm{L}}} \left( \frac{1}{k^3_{\mathrm{L}}}+\frac{1}{k^3_\mathrm{S}}\right) \frac{1}{\left( 1-\frac{k_\mathrm{S}}{k_{\mathrm{L}}}\right) ^{\frac{3}{2}}},\end{aligned}$$

(8.155)

$$\begin{aligned} \Delta _{3}= & {} \sum _{i<j<p}P_{\zeta }(k_{i})P_{\zeta }(k_j)P_{\zeta }(k_p)\nonumber \\= & {} \frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{1728 M^{12}_{p} (\epsilon ^*_{\tilde{W}})^3}\frac{1}{k^6_{\mathrm{L}}}\left( \frac{1}{k^3_{\mathrm{L}}}+ \frac{3}{k^3_\mathrm{S}}\right) . \end{aligned}$$

(8.156)

Consequently the non-Gaussian parameter $g^{\mathrm{{loc}}}_{\mathrm{NL}}$ can be expressed as

$$\begin{aligned} g^{\mathrm{{sq}}}_{\mathrm{NL}}\approx \frac{25}{1944}\left[ \frac{\Delta _{1}-\Delta _{2}}{\Delta _{3}}\right] \left[ 29\epsilon ^*_{\tilde{W}}-6\eta ^{*}_{\tilde{W}}\right] ^2. \end{aligned}$$

(8.157)

In Figs. 30 and 32, we have shown the features of non-Gaussian amplitude from four point scalar function $\tau ^{\mathrm{{sq}}}_{\mathrm{NL}}$ and $g^{\mathrm{{sq}}}_{\mathrm{NL}}$ in squeezed limit configuration in four different scanning regions of product of the two parameters $\alpha \bar{\lambda }$ in the $(\tau ^{\mathrm{{sq}}}_{\mathrm{NL}},\alpha \bar{\lambda })$ and $(g^{\mathrm{{sq}}}_{\mathrm{NL}},\alpha \bar{\lambda })$ 2D plane for the number of e-foldings $50<\mathcal{N}_{cmb}<70$ (Fig. 31). Physical explanations of the obtained features are:

• Region I: Here for the parameter space $0.0001<\alpha \bar{\lambda }<0.001$ the non-Gaussian amplitude lying within the window $0.01<\tau ^{\mathrm{{sq}}}_{\mathrm{NL}}<0.021$,  $0.05<g^{\mathrm{{sq}}}_{\mathrm{NL}}<0.095$. Further if we increase the numerical value of $\alpha \bar{\lambda }$, then the magnitude of the non-Gaussian amplitude saturates and we get the maximum value for $\mathcal{N}_{cmb}=50$, $|\tau ^{\mathrm{{sq}}}_{\mathrm{NL}}|_{\max }\sim 0.021$, $|g^{\mathrm{{sq}}}_{\mathrm{NL}}|_{\max }\sim 0.095$.

• Region II: Here for the parameter space $0.00001<\alpha \bar{\lambda }<0.0001$ the non-Gaussian amplitude lying within the window $0.002<\tau ^{\mathrm{{sq}}}_{\mathrm{NL}}<0.017$,  $0.01<g^{\mathrm{{sq}}}_{\mathrm{NL}}<0.075$. In this region we get maximum value for $\mathcal{N}_{cmb}=50$, $|\tau ^{\mathrm{{sq}}}_{\mathrm{NL}}|_{\max }\sim 0.017$, $|g^{\mathrm{{sq}}}_{\mathrm{NL}}|_{\max }\sim 0.075$. Additionally, it is important to note that in this case for $\alpha \bar{\lambda }=0.00004$ the lines obtained for $\mathcal{N}_{cmb}=50$, $\mathcal{N}_{cmb}=60$ and $\mathcal{N}_{cmb}=70$ cross each other.

• Region III: Here for the parameter space $0.000001<\alpha \bar{\lambda }<0.00001$ the non-Gaussian amplitude lying within the window $-0.0008<\tau ^{\mathrm{{sq}}}_{\mathrm{NL}}<0.0042$,  $-0.0008<g^{\mathrm{{sq}}}_{\mathrm{NL}}<0.02$. In this region we get the maximum value for $\mathcal{N}_{cmb}=70$, $|\tau ^{\mathrm{{sq}}}_{\mathrm{NL}}|_{\max }\sim 0.0042$, $|g^{\mathrm{{sq}}}_{\mathrm{NL}}|_{\max }\sim 0.02$. Additionally, it is important to note that in this case for $0.000001\le \alpha \bar{\lambda }\le 0.000006$ the lines obtained for $\mathcal{N}_{cmb}=50$, $\mathcal{N}_{cmb}=60$ and $\mathcal{N}_{cmb}=70$ show increasing, decreasing and further increasing behavior.

• Region IV: Here for the parameter space $0.0000001<\alpha \bar{\lambda }<0.000001$ the non-Gaussian amplitude lying within the window $-0.00005<\tau ^{\mathrm{{sq}}}_{\mathrm{NL}}<-0.00058$,  $-0.0001<g^{\mathrm{{sq}}}_{\mathrm{NL}}<-0.0027$. In this region we get the maximum value for $\mathcal{N}_{cmb}=60$, $|\tau ^{\mathrm{{sq}}}_{\mathrm{NL}}|_{\max }\sim 0.00058$, $|g^{\mathrm{{sq}}}_{\mathrm{NL}}|_{\max }\sim 0.0027$.

Fig. 25

Representative 3D diagram for equilateral non-Gaussian three point amplitude vs. the model parameters $\alpha$ and $\bar{\lambda }$ for $\mathcal{N}_{cmb}=60$ in two different angular views

Fig. 26

Representative diagram for equilateral non-Gaussian three point amplitude vs. product of the parameters $\alpha \bar{\lambda }$ in four different regions for $\mathcal{N}_{cmb}=50$ (red), $\mathcal{N}_{cmb}=60$ (blue) and $\mathcal{N}_{cmb}=70$ (green)

Fig. 27

Representative 3D diagram for equilateral non-Gaussian three point amplitude vs. the model parameters $\alpha$ and $\bar{\lambda }$ for $\mathcal{N}_{cmb}=60$ in two different angular views

Fig. 28

Representative diagram for equilateral non-Gaussian three point amplitude vs. product of the parameters $\alpha \bar{\lambda }$ in four different regions for $\mathcal{N}_{cmb}=50$ (red), $\mathcal{N}_{cmb}=60$ (blue) and $\mathcal{N}_{cmb}=70$ (green)

Fig. 29

Representative 3D diagram for equilateral non-Gaussian three point amplitude vs. the model parameters $\alpha$ and $\bar{\lambda }$ for $\mathcal{N}_{cmb}=60$ in two different angular views

Fig. 30

Representative diagram for equilateral non-Gaussian three point amplitude vs. product of the parameters $\alpha \bar{\lambda }$ in four different regions for $\mathcal{N}_{cmb}=50$ (red), $\mathcal{N}_{cmb}=60$ (blue) and $\mathcal{N}_{cmb}=70$ (green)

Fig. 31

Representative 3D diagram for equilateral non-Gaussian three point amplitude vs. the model parameters $\alpha$ and $\bar{\lambda }$ for $\mathcal{N}_{cmb}=60$ in two different angular views

Fig. 32

Representative diagram for equilateral non-Gaussian three point amplitude vs. product of the parameters $\alpha \bar{\lambda }$ in four different regions for $\mathcal{N}_{cmb}=50$ (red), $\mathcal{N}_{cmb}=60$ (blue) and $\mathcal{N}_{cmb}=70$ (green)

Fig. 33

Representative 3D diagram for equilateral non-Gaussian three point amplitude vs. the model parameters $\alpha$ and $\bar{\lambda }$ for $\mathcal{N}_{cmb}=60$ in two different angular views

Further combining the contribution from Region I, Region II, Region III and Region IV we finally get the following constraint on the four point non-Gaussian amplitude in the equilateral limit configuration:

$$\begin{aligned}&\text {Region~I}+\text {Region~II}+\text {Region~III}+ \text {Region~IV}{:}\nonumber \\&\quad 10^{-6}<\tau ^{\mathrm{{sq}}}_{\mathrm{NL}}<0.016,\quad -0.023<g^{\mathrm{{sq}}}_{\mathrm{NL}}<0.002\nonumber \\ \end{aligned}$$

(8.158)

for the following parameter space:

$$\begin{aligned}&\text {Region~I}+\text {Region~II}+\text {Region~III}+ \text {Region~IV}{:}\nonumber \\&\quad 0.0000001<\alpha \bar{\lambda }<0.001. \end{aligned}$$

(8.159)

In this analysis we get the following maximum value of the three point non-Gaussian amplitude in the equilateral limit configuration:

$$\begin{aligned} |\tau ^{\mathrm{{sq}}}_{\mathrm{NL}}|_{\max }\sim 0.021,\quad |g^{\mathrm{{sq}}}_{\mathrm{NL}}|_{\max }\sim 0.095. \end{aligned}$$

(8.160)

To visualize these constraints more clearly we have also presented $(\tau ^{\mathrm{{sq}}}_{\mathrm{NL}},\alpha ,\bar{\lambda })$ and $(g^{\mathrm{{sq}}}_{\mathrm{NL}},\alpha ,\bar{\lambda })$ 3D plot in Figs. 31a, b, 33a, b for two different angular orientations: Angle I and Angle II. From the representative surfaces it is clearly observed the behavior of scalar four point non-Gaussian amplitude in the squeezed limit for the variation of two fold parameter $\alpha$ and $\bar{\lambda }$ and the results are consistent with the obtained constraints in 2D analysis. Here all the obtained results are consistent with the two point and three point constraints as well as with the Planck 2015 data [44,45,46].

For the sake of simplicity one can further neglect all the contribution from the very small factor $k_\mathrm{S}/k_{\mathrm{L}}$ and finally write the following expression for the trispectrum in the squeezed limiting configuration as

$$\begin{aligned} T(k_{\mathrm{L}},k_{\mathrm{L}},k_{\mathrm{L}},k_\mathrm{S})\approx 3\left( \tau ^{\mathrm{{sq}}}_{\mathrm{NL}}+\frac{54}{25}g^{\mathrm{{sq}}}_{\mathrm{NL}}\right) P_{\zeta }(k_\mathrm{S})P^2_{\zeta }(k_{\mathrm{L}}),\nonumber \\ \end{aligned}$$

(8.161)

which implies that in the squeezed limiting configuration if we neglect the contribution from very small term $k_\mathrm{S}/k_{\mathrm{L}}$ then the trispectrum contributes equally to the four point non-Gaussian parameter $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $g^{\mathrm{{loc}}}_{\mathrm{NL}}$. So if we now assume that the Suyama–Yamaguchi relation perfectly holds true in the present context i.e. Eq. (8.152) is completely correct then using Eq. (8.161) one can find the following expression for the four point non-Gaussian parameter $g^{\mathrm{{loc}}}_{\mathrm{NL}}$:

$$\begin{aligned} g^{\mathrm{{sq}}}_{\mathrm{NL}}\approx & {} 6\epsilon ^*_{\tilde{W}}\sin ^2\alpha _1\sin ^2\alpha _3\cos 2\chi _{12,34}\nonumber \\&-\,\frac{1}{36} \left[ 29\epsilon ^*_{\tilde{W}}-6\eta ^*_{\tilde{W}}\right] ^2, \end{aligned}$$

(8.162)

where we have used the approximation, $(1+\cos \theta _3)\approx \frac{1}{2}\left( 1-\frac{k_\mathrm{S}}{k_{\mathrm{L}}}\right) \approx \frac{1}{2}$, due to the smallness of the momentum ratio $k_\mathrm{S}/k_{\mathrm{L}}$ as it is much smaller than unity.

But as we have already pointed that if we relax the assumption of holding the Suyama–Yamaguchi consistency relation in the present context of discussion, then using Eq. (8.105) one can write down the expression for momentum dependent function in the squeezed limiting configuration as

$$\begin{aligned}&f\left( k_{\mathrm{L}},k_{\mathrm{L}},k_{\mathrm{L}},k_\mathrm{S},k_{\mathrm{L}}\sqrt{1-\frac{k_\mathrm{S}}{k_{\mathrm{L}}}}, k_{\mathrm{L}}\sqrt{1-\frac{k_\mathrm{S}}{k_{\mathrm{L}}}},k_{\mathrm{L}}\sqrt{1-\frac{k_\mathrm{S}}{k_{\mathrm{L}}}}\right) \nonumber \\&\quad \approx \frac{\frac{128}{9}\left( 1+\frac{k^3_\mathrm{S}}{k^3_{\mathrm{L}}}\right) }{\left( 1+\frac{k_\mathrm{S}}{3k_{\mathrm{L}}}\right) ^3}\frac{1}{\left( 1-\frac{k_\mathrm{S}}{k_{\mathrm{L}}}\right) ^{\frac{3}{2}}}, \end{aligned}$$

(8.163)

using which we get the following simplified expression for the non-Gaussian parameter $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $g^{\mathrm{{loc}}}_{\mathrm{NL}}$ as obtained from the four point scalar function in squeezed limiting configuration as

$$\begin{aligned} \tau ^{\mathrm{{sq}}}_{\mathrm{NL}}\approx & {} \frac{\frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{216M^{12}_p (\epsilon ^*_{\tilde{W}})^2}\frac{1}{k^9_{\mathrm{L}}}\frac{\sin ^3\alpha _4}{\sin ^3\alpha _3}\left[ \frac{9}{4}\frac{1}{\left( 1-\frac{\sin \alpha _3}{\sin \alpha _4}\right) ^{\frac{3}{2}}}\sin ^2\alpha _1\sin ^2\alpha _3\cos 2\chi _{12,34}\right] }{\left[ \Delta _2+\frac{54}{25}\frac{128}{9}\left( 1+\frac{\sin ^3\alpha _3}{\sin ^3\alpha _4}\right) \frac{1}{\left( 1+\frac{\sin \alpha _3}{3\sin \alpha _4}\right) ^3}\frac{1}{\left( 1-\frac{\sin \alpha _3}{\sin \alpha _4}\right) ^{\frac{3}{2}}}\Delta _3\right] },\end{aligned}$$

(8.164)

$$\begin{aligned} g^{\mathrm{{sq}}}_{\mathrm{NL}}\approx & {} \frac{\frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{216M^{12}_p (\epsilon ^*_{\tilde{W}})^2}\frac{1}{k^9_{\mathrm{L}}}\frac{\sin ^3\alpha _4}{\sin ^3\alpha _3}\left[ \frac{9}{4}\frac{1}{\left( 1-\frac{\sin \alpha _3}{\sin \alpha _4}\right) ^{\frac{3}{2}}}\sin ^2\alpha _1\sin ^2\alpha _3\cos 2\chi _{12,34}\right] }{\left[ \frac{\Delta _2}{\frac{128}{9}\left( 1+\frac{\sin ^3\alpha _3}{\sin ^3\alpha _4}\right) \frac{1}{\left( 1+\frac{\sin \alpha _3}{3\sin \alpha _4}\right) ^3}\frac{1}{\left( 1-\frac{\sin \alpha _3}{\sin \alpha _4}\right) ^{\frac{3}{2}}}}+\frac{54}{25}\Delta _3\right] }. \end{aligned}$$

(8.165)

Further if we neglect the contribution from very small term $k_\mathrm{S}/k_{\mathrm{L}}$ then the four point non-Gaussian parameter $\tau ^{\mathrm{{sq}}}_{\mathrm{NL}}$ and $g^{\mathrm{{sq}}}_{\mathrm{NL}}$ can be expressed as

$$\begin{aligned} \tau ^{\mathrm{{sq}}}_{\mathrm{NL}}\approx & {} \frac{\frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{216M^{12}_p (\epsilon ^*_{\tilde{W}})^2}\frac{1}{k^9_{\mathrm{L}}}\frac{\sin ^3\alpha _4}{\sin ^3\alpha _3}\left[ \frac{9}{4}\sin ^2\alpha _1\sin ^2\alpha _3\cos 2\chi _{12,34}\right] }{\left[ \Delta _2+\frac{54}{25}\frac{128}{9}\Delta _3\right] },\end{aligned}$$

(8.166)

$$\begin{aligned} g^{\mathrm{{sq}}}_{\mathrm{NL}}\approx & {} \frac{\frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{216M^{12}_p (\epsilon ^*_{\tilde{W}})^2}\frac{1}{k^9_{\mathrm{L}}}\frac{\sin ^3\alpha _4}{\sin ^3\alpha _3}\left[ \frac{9}{4}\sin ^2\alpha _1\sin ^2\alpha _3\cos 2\chi _{12,34}\right] }{\left[ \frac{9}{128}\Delta _2+\frac{54}{25}\Delta _3\right] },\nonumber \\ \end{aligned}$$

(8.167)

where the momentum dependent factors can be approximated by

$$\begin{aligned}&f\left( k_{\mathrm{L}},k_{\mathrm{L}},k_{\mathrm{L}},k_\mathrm{S},k_{\mathrm{L}},k_{\mathrm{L}},k_{\mathrm{L}}\right) \approx \frac{128}{9},\end{aligned}$$

(8.168)

$$\begin{aligned}&\Delta _{2}=\frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{1728 M^{12}_{p}(\epsilon ^*_{\tilde{W}})^3}\frac{6}{k^6_{\mathrm{L}}}\left( \frac{1}{k^3_{\mathrm{L}}}+\frac{1}{k^3_\mathrm{S}}\right) \frac{1}{\left( 1-\frac{k_\mathrm{S}}{k_{\mathrm{L}}}\right) ^{\frac{3}{2}}},\end{aligned}$$

(8.169)

$$\begin{aligned}&\Delta _{3}=\frac{\tilde{W}^3(\phi _{cmb},{\varvec{\Psi }})}{1728 M^{12}_{p}(\epsilon ^*_{\tilde{W}})^3}\frac{3}{k^6_Lk^3_\mathrm{S}}, \end{aligned}$$

(8.170)

Table 5 Constraint on scalar four point non-Gaussian amplitude from equilateral, folded kite and squeezed configuration with assuming Suyama–Yamaguchi consistency relation

Table 6 Constraint on scalar four point non-Gaussian amplitude from equilateral configuration without assuming Suyama–Yamaguchi consistency relation

In Table 5, we give the numerical estimates and constraints on the four point non-Gaussian amplitude from equilateral configuration with assuming Suyama–Yamaguchi consistency relation. Also in Table 6, we give the numerical estimates and constraints on the four point non-Gaussian amplitude from equilateral configuration without assuming Suyama–Yamaguchi consistency relation. Here all the obtained results are consistent with the two point and three point constraints as well as with the Planck 2015 data [44,45,46].

8.2.2 Using $\delta \mathcal{N}$ formalism

In this section using the prescription of $\delta \mathcal{N}$ formalism in the attractor regime of cosmological perturbation we derive the expression for the non-Gaussian amplitudes associated with the four point function of scalar curvature fluctuation as

$$\begin{aligned} \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{\mathcal{N}_{,JI}\mathcal{N}_{,JK}\mathcal{N}_{,I}\mathcal{N}_{,K}}{\left( \mathcal{N}_{,M}\mathcal{N}_{,M}\right) ^3},\end{aligned}$$

(8.171)

$$\begin{aligned} g^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{25}{54}\frac{\mathcal{N}_{,IJK}\mathcal{N}_{,I}\mathcal{N}_{,J}\mathcal{N}_{,K}}{\left( \mathcal{N}_{,M}\mathcal{N}_{,M}\right) ^3}. \end{aligned}$$

(8.172)

Further writing the expressions for the non-Gaussian amplitudes in terms of the inflaton field $\phi$ and the additional field $\Psi$ we get

$$\begin{aligned} \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{1}{\left( \mathcal{N}_{,\phi }\mathcal{N}_{,\phi }+\mathcal{N}_{,\Psi }\mathcal{N}_{,\Psi }\right) ^3_{*}}\nonumber \\&\times \left[ \left( \mathcal{N}_{,\phi \phi }\mathcal{N}_{,\phi \phi }+\mathcal{N}_{,\Psi \phi }\mathcal{N}_{,\Psi \phi }\right) \mathcal{N}_{,\phi }\mathcal{N}_{,\phi }\right. \nonumber \\&\left. +\left( \mathcal{N}_{,\Psi \Psi }\mathcal{N}_{,\Psi \Psi }+\mathcal{N}_{,\phi \Psi }\mathcal{N}_{,\phi \Psi }\right) \mathcal{N}_{,\Psi }\mathcal{N}_{,\Psi }\right. \nonumber \\&\left. +2\left( \mathcal{N}_{,\phi \phi }\mathcal{N}_{,\phi \Psi }+\mathcal{N}_{,\Psi \Psi }\mathcal{N}_{,\Psi \phi }\right) \mathcal{N}_{,\phi }\mathcal{N}_{,\Psi }\right] _{*},\end{aligned}$$

(8.173)

$$\begin{aligned} g^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{25}{54}\frac{1}{\left( \mathcal{N}_{,\phi }\mathcal{N}_{,\phi }+\mathcal{N}_{,\Psi }\mathcal{N}_{,\Psi }\right) ^3_{*}}\nonumber \\&\times \left[ \mathcal{N}_{,\phi \phi \phi }\mathcal{N}_{,\phi }\mathcal{N}_{,\phi }\mathcal{N}_{,\phi }+\mathcal{N}_{,\Psi \Psi \Psi }\mathcal{N}_{,\Psi }\mathcal{N}_{,\Psi }\mathcal{N}_{,\Psi }\right. \nonumber \\&\left. +\left( \mathcal{N}_{,\phi \phi \Psi }+\mathcal{N}_{,\Psi \phi \phi }+\mathcal{N}_{,\phi \Psi \phi }\right) \mathcal{N}_{,\phi }\mathcal{N}_{,\phi }\mathcal{N}_{,\Psi }\right. \nonumber \\&\left. +\left( \mathcal{N}_{,\phi \Psi \Psi }+\mathcal{N}_{,\Psi \Psi \phi }+\mathcal{N}_{,\Psi \phi \Psi }\right) \mathcal{N}_{,\phi }\mathcal{N}_{,\Psi }\mathcal{N}_{,\Psi }\right] _{*}.\nonumber \\ \end{aligned}$$

(8.174)

Now we already know that in the attractor regime cosmological perturbation, solution for the additional field $\Psi$ can be expressed in terms of the inflaton field $\phi$ and using this fact the expression for the non-Gaussian amplitudes associated with the four point function of scalar curvature fluctuation can be recast as

$$\begin{aligned} \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \left[ X_{1}(\phi )~\frac{\mathcal{N}_{,\phi \phi }\mathcal{N}_{,\phi \phi }}{\left( \mathcal{N}_{,\phi }\mathcal{N}_{,\phi }\right) ^2}+X_2(\phi )~\frac{\mathcal{N}_{,\phi \phi }}{\mathcal{N}^3_{,\phi }}\right. \nonumber \\&\left. +\,X_3(\phi )~\frac{1}{\mathcal{N}_{,\phi }\mathcal{N}_{,\phi }}\right] _{*},\end{aligned}$$

(8.175)

$$\begin{aligned} g^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{25}{54}\left[ X_{4}(\phi )\frac{\mathcal{N}_{,\phi \phi \phi }}{\mathcal{N}_{,\phi }\mathcal{N}_{,\phi }\mathcal{N}_{,\phi }}+X_{5}(\phi )\frac{\mathcal{N}_{,\phi \phi }}{\mathcal{N}_{,\phi }\mathcal{N}_{,\phi }\mathcal{N}_{,\phi }}\right. \nonumber \\&\left. +\,X_{6}(\phi )\frac{1}{\mathcal{N}_{,\phi }\mathcal{N}_{,\phi }}\right] _{*}. \end{aligned}$$

(8.176)

where the new functions $X_{1}(\phi ),\ldots ,X_{6}(\phi )$ are defined as

$$\begin{aligned} X_{1}(\phi )= & {} f(\phi )\left( 1+\frac{2}{\mathcal{V}^2(\phi )}+\frac{2}{\mathcal{V}^4(\phi )}+\frac{1}{\mathcal{V}^6(\phi )}\right) ,~\nonumber \\ X_{2}(\phi )= & {} -3f(\phi )\left( \frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}+\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^5(\phi )}\right) ,\nonumber \\ X_{3}(\phi )= & {} f(\phi )\left( \frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^6(\phi )}+\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^4(\phi )}\right) ,\nonumber \\ X_{4}(\phi )= & {} f(\phi )\left( 1+\frac{3}{\mathcal{V}^2(\phi )}+\frac{3}{\mathcal{V}^4(\phi )}+\frac{1}{\mathcal{V}^6(\phi )}\right) ,\nonumber \\ X_{5}(\phi )= & {} -3f(\phi )\left( \frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^7(\phi )}+2\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^5(\phi )}+\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}\right) ,\nonumber \\ X_{6}(\phi )= & {} -f(\phi )\left( \frac{\mathcal{V}^{\prime \prime }(\phi )}{\mathcal{V}^3(\phi )}-2\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^4(\phi )}-3\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^8(\phi )}-5\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^6(\phi )}\right) .\nonumber \\ \end{aligned}$$

(8.177)

where $f(\phi )=\left( 1+\frac{1}{\mathcal{V}^2(\phi )}\right) ^{-3}$. Further substituting the explicit form of the function $\mathcal{V}(\phi )$ and $\mathcal{N}_{,\phi }$, $\mathcal{N}_{,\phi \phi }$, $\mathcal{N}_{,\phi \phi \phi }$ for all derived effective potentials at $\phi =\phi _*$ we get

$$\begin{aligned} \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \mathcal{Y}^2\left[ X_{1}(\phi _{*})+X_2(\phi _{*})\phi _*+X_3(\phi _{*})\phi ^2_*\right] ,\end{aligned}$$

(8.178)

$$\begin{aligned} g^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{25}{54}\mathcal{Y}^2\left[ 2X_{4}(\phi _{*})+X_{5}(\phi _{*})\phi _*+X_{6}(\phi _{*})\phi ^2_*\right] .\nonumber \\ \end{aligned}$$

(8.179)

Now we comment on the consistency relation between the non-Gaussian parameters derived from four point and three point scalar correlation function in the attractor regime of inflation. To establish this connection we start with Eqs. (8.64), (8.178) and (8.179) and finally get new set of consistency relations:

$$\begin{aligned} \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{36}{25}(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2\left[ X_{1}(\phi _{*})+X_2(\phi _{*})\phi _*+X_3(\phi _{*})\phi ^2_*\right] ,\nonumber \\ \end{aligned}$$

(8.180)

$$\begin{aligned} g^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{10}{27}(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2\left[ 2X_{4}(\phi _{*})+X_{5}(\phi _{*})\phi _*+X_{6}(\phi _{*})\phi ^2_*\right] . \nonumber \\ \end{aligned}$$

(8.181)

$$\begin{aligned} g^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{125}{486}\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}\frac{\left[ 2X_{4}(\phi _{*})+X_{5}(\phi _{*}) \phi _*+X_{6}(\phi _{*})\phi ^2_*\right] }{\left[ 2X_{4}(\phi _{*})+X_{5}(\phi _{*})\phi _*+X_{6}(\phi _{*})\phi ^2_*\right] }.\nonumber \\ \end{aligned}$$

(8.182)

It is a very well-known fact that in the non-attractor regime, where the additional field $\Psi$ is frozen in the Planck scale Suyama–Yamaguchi consistency relation [176,177,178] holds true, which states:

$$\begin{aligned} \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}=\frac{36}{25}(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2. \end{aligned}$$

(8.183)

Further using this results one can estimate the deviation in the Suyama–Yamaguchi consistency relation if we go from attractor regime to non-attractor regime of cosmological perturbation as

$$\begin{aligned} |\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}|= & {} |[ \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}|_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}- \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}|_{\mathrm{{attractor}}}]\nonumber \\= & {} \frac{36}{25}(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2|_{\mathrm{{non}}\text {-}\mathrm{{attractor}}} |\{1-Q_{\mathrm{{corr}}}\}|, \end{aligned}$$

(8.184)

where the correction factor $Q_{\mathrm{{corr}}}$ can be written as

$$\begin{aligned} Q_{\mathrm{{corr}}}=\frac{(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2|_{\mathrm{{attractor}}}}{(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2|_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}}\left[ X_{1}(\phi _{*}) +X_2(\phi _{*})\phi _*+X_3(\phi _{*})\phi ^2_*\right] .\nonumber \\ \end{aligned}$$

(8.185)

Here we need to point out a few crucial issues:

• First of all, to estimate the magnitude of the deviation factor $Q_{\mathrm{{corr}}}$ we need to concentrate on two physical situations, I. Super Planckian field regime and II. Sub Planckian field regime.

• In the super Planckian field regime the deviation factor $Q_{\mathrm{{corr}}}$ can be expressed as

$$\begin{aligned} Q_{\mathrm{{corr}}}=\Delta _{f}\times \left\{ \begin{array}{ll} \left( 1-\frac{18M^2_p}{81\phi ^2_*}-\frac{72M^4_p}{6561\phi ^4_*}- \frac{3888M^8_p}{43046721\phi ^8_*}+\cdots \right) &{} \quad \text {for Case I}\\ \left( 1-\frac{18M^2_p}{\phi ^2_*}-\frac{72M^4_p}{\phi ^4_*}- \frac{3888M^8_p}{\phi ^8_*}+\cdots \right) &{} \quad \text {for Case II}\\ \left( 1-\frac{18M^2_p}{\phi ^2_*\left( 1-\frac{\phi ^4_V}{\phi ^4_*}\right) ^2}-\frac{72M^4_p}{\phi ^4_*\left( 1- \frac{\phi ^4_V}{\phi ^4_*}\right) ^4} -\frac{3888M^8_p}{\phi ^8_*\left( 1-\frac{\phi ^4_V}{\phi ^4_*}\right) ^8}+\cdots \right) &{} \quad \text {for Case~II}+\text {Choice~I}\\ \left( 1-\frac{18M^2_p}{\phi ^2_*\left( 1-\frac{m^2_c}{m^2_c-\lambda \phi ^2_*}\right) ^2}-\frac{72M^4_p}{\phi ^4_*\left( 1-\frac{m^2_c}{m^2_c-\lambda \phi ^2_*}\right) ^4} -\frac{3888M^8_p}{\phi ^8_*\left( 1-\frac{m^2_c}{m^2_c- \lambda \phi ^2_*}\right) ^8}+\cdots \right) &{}\quad \text {for Case~II}+\text {Choice~II}\\ \left( 1-\frac{18M^2_p}{\phi ^2_*\left( 1+\xi (\phi ^ 2_*-\phi ^2_V)+ \frac{\phi ^2_V}{\phi ^2_*}\right) ^2}-\frac{72M^4_p}{\phi ^4_* \left( 1+\xi (\phi ^2_*-\phi ^2_V)+\frac{\phi ^2_V}{\phi ^2_*}\right) ^4}\right. &{}\\ \quad \left. -\frac{3888M^8_p}{\phi ^8_*\left( 1+\xi (\phi ^2_*-\phi ^2_V)+ \frac{\phi ^2_V}{\phi ^2_*}\right) ^8}+\cdots \right) &{}\quad \text {for Case~II}+\text {Choice~III}. \end{array} \right. \end{aligned}$$

(8.186)

where the factor $\Delta _{f}$ is defined as

$$\begin{aligned} \Delta _{f}=\frac{(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2|_{\mathrm{{attractor}}}}{(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2|_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}}. \end{aligned}$$

(8.187)

Now to give a proper estimate of the deviation in the magnitude of the amplitude of non-Gaussian parameter computed from four point function in terms of the three point non-Gaussian amplitude for the time being we assume that the results obtained from the attractor and non-attractor formalism is almost at the same order of magnitude. In that case we have $\Delta _f \sim \mathcal{O}(1)$. Consequently the deviation factor can be recast as

$$\begin{aligned} Q_{\mathrm{{corr}}}\sim \Delta _f(1-J_{\mathrm{{corr}}})\sim 1-J_{\mathrm{{corr}}}, \end{aligned}$$

(8.188)

where the correction factor $J_{\mathrm{{corr}}}\ll 1$ is highly suppressed in the super Planckian region of the perturbation theory, but those small corrections are important as precision measurement is concerned in the context of cosmology. In the case of our derived effective potentials we get the following approximate expressions for the correction factor:

$$\begin{aligned} J_{\mathrm{{corr}}}\sim \left\{ \begin{array}{ll} \left( \frac{18M^2_p}{81\phi ^2_*}+\frac{72M^4_p}{6561\phi ^4_*}+ \frac{3888M^8_p}{43046721\phi ^8_*}+\cdots \right) &{}\quad \text {for Case I}\\ \left( \frac{18M^2_p}{\phi ^2_*}+\frac{72M^4_p}{\phi ^4_*}+ \frac{3888M^8_p}{\phi ^8_*}+\cdots \right) &{} \quad \text {for Case II}\\ \left( \frac{18M^2_p}{\phi ^2_*\left( 1-\frac{\phi ^4_V}{\phi ^4_*} \right) ^2}+\frac{72M^4_p}{\phi ^4_*\left( 1-\frac{\phi ^4_V}{\phi ^4_*}\right) ^4} +\frac{3888M^8_p}{\phi ^8_*\left( 1-\frac{\phi ^4_V}{\phi ^4_*} \right) ^8}+\cdots \right) &{}\quad \text {for Case~II}+\text {Choice~I}\\ \left( \frac{18M^2_p}{\phi ^2_*\left( 1-\frac{m^2_c}{m^2_c- \lambda \phi ^2_*}\right) ^2}+\frac{72M^4_p}{\phi ^4_* \left( 1-\frac{m^2_c}{m^2_c-\lambda \phi ^2_*}\right) ^4} \right. &{}\\ \quad \left. +\frac{3888M^8_p}{\phi ^8_*\left( 1-\frac{m^2_c}{m^2_c-\lambda \phi ^2_*}\right) ^8}+\cdots \right) &{}\quad \text {for Case~II}+\text {Choice~II}\\ \left( \frac{18M^2_p}{\phi ^2_*\left( 1+\xi (\phi ^2_*-\phi ^2_V)+ \frac{\phi ^2_V}{\phi ^2_*}\right) ^2}+\frac{72M^4_p}{\phi ^4_* \left( 1+\xi (\phi ^2_*-\phi ^2_V)+\frac{\phi ^2_V}{\phi ^2_*}\right) ^4}\right. &{}\\ \quad \left. +\frac{3888M^8_p}{\phi ^8_*\left( 1+\xi (\phi ^2_*- \phi ^2_V)+\frac{\phi ^2_V}{\phi ^2_*}\right) ^8}+\cdots \right) &{}\quad \text {for Case~II}+\text {Choice~III}. \end{array} \right. \end{aligned}$$

(8.189)

Further using this results one can estimate the deviation in the Suyama–Yamaguchi consistency relation if we go from attractor regime to non-attractor regime of cosmological perturbation as

$$\begin{aligned} |\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}|= & {} \frac{36}{25}(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2|_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}|\left\{ 1-\Delta _{f}(1-J_{\mathrm{{corr}}})\right\} |\nonumber \\\sim & {} \frac{36}{25}(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2|_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}|J_{\mathrm{{corr}}}|. \end{aligned}$$

(8.190)

Also the fractional change can be expressed as

$$\begin{aligned} \left| \frac{\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}}{(\tau ^{\mathrm{{loc}}}_{\mathrm{NL}})_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}}\right| _{\phi _*\gg M_p}= & {} |1-\Delta _{f}(1-J_{\mathrm{{corr}}})|\sim |J_{\mathrm{{corr}}}|.\nonumber \\ \end{aligned}$$

(8.191)

So it is clear that $|J_{\mathrm{{corr}}}|$ captures the effect of the deviation in the Suyama–Yamaguchi consistency relation which are very small and highly suppressed in the super Planckian regime of inflation. But as far as precision cosmology is concerned, this small effect is also very useful to discriminate between all derived effective models considered in this paper. If in the near future Planck or any other observational probe detects the signature of primordial non-Gaussianity with high statistical significance then one can also further comment on the significance of attractors and non-attractors in the context of early universe cosmology.

• In the sub Planckian field regime the deviation factor $Q_{\mathrm{{corr}}}$ can be expressed as

$$\begin{aligned} Q_{\mathrm{{corr}}}=\Delta _{f}\times \left\{ \begin{array}{ll} \left( 1+\frac{19683}{8}\frac{\phi ^6_*}{M^6_p}+\cdots \right) &{} \quad \text {for Case I}\\ \left( 1+\frac{1}{216}\frac{\phi ^6_*}{M^6_p}+\cdots \right) &{} \quad \text {for Case II}\\ \left( 1+\frac{1}{216}\frac{\phi ^6_*}{M^6_p} \left( 1-\frac{\phi ^4_V}{\phi ^4_*}\right) ^6+\cdots \right) &{} \quad \text {for Case~II}+\text {Choice~I}\\ \left( 1+\frac{1}{216}\frac{\phi ^6_*}{M^6_p} \left( 1-\frac{m^2_c}{m^2_c-\lambda \phi ^2_*}\right) ^6+\cdots \right) &{}\quad \text {for Case~II}+\text {Choice~II}\\ \left( 1+\frac{1}{216}\frac{\phi ^6_*}{M^6_p} \left( 1+\xi (\phi ^2_*-\phi ^2_V)+\frac{\phi ^2_V}{\phi ^2_*}\right) ^6+\cdots \right) &{}\quad \text {for Case~II}+\text {Choice~III}. \end{array} \right. \end{aligned}$$

(8.192)

where the factor $\Delta _{f}$ is defined earlier, which is $\Delta _f \sim \mathcal{O}(1)$. Consequently the deviation factor can be recast as

$$\begin{aligned} Q_{\mathrm{{corr}}}\sim \Delta _f(1+C_{\mathrm{{corr}}})\sim 1+C_{\mathrm{{corr}}}, \end{aligned}$$

(8.193)

where the correction factor $C_{\mathrm{{corr}}}\ll 1$ is suppressed in the sub Planckian region of the perturbation theory, but those small corrections are important as precision measurement is concerned in the context of cosmology. In the case of our derived effective potentials we get the following approximate expressions for the correction factor:

$$\begin{aligned} C_{\mathrm{{corr}}}\sim \Delta _{f}\times \left\{ \begin{array}{ll} \left( \frac{19683}{8}\frac{\phi ^6_*}{M^6_p}+\cdots \right) &{} \quad \text {for Case I}\\ \left( \frac{1}{216}\frac{\phi ^6_*}{M^6_p}+\cdots \right) &{} \quad \text {for Case II}\\ \left( \frac{1}{216}\frac{\phi ^6_*}{M^6_p} \left( 1-\frac{\phi ^4_V}{\phi ^4_*}\right) ^6+\cdots \right) &{} \quad \text {for Case~II}+\text {Choice~I}\\ \left( 1+\frac{1}{216}\frac{\phi ^6_*}{M^6_p} \left( 1-\frac{m^2_c}{m^2_c-\lambda \phi ^2_*}\right) ^6+\cdots \right) &{}\quad \text {for Case~II}+\text {Choice~II}\\ \left( \frac{1}{216}\frac{\phi ^6_*}{M^6_p} \left( 1+\xi (\phi ^2_*-\phi ^2_V)+\frac{\phi ^2_V}{\phi ^2_*}\right) ^6+\cdots \right) &{}\quad \text {for Case~II}+\text {Choice~III}. \end{array} \right. \end{aligned}$$

(8.194)

Further using this results one can estimate the deviation in the Suyama–Yamaguchi consistency relation if we go from attractor regime to non-attractor regime of the cosmological perturbation as

$$\begin{aligned} |\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}|= & {} \frac{36}{25}(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2|_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}| \{1-\Delta _{f}(1+C_{\mathrm{{corr}}})\}|\nonumber \\\sim & {} \frac{36}{25}(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2 |_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}|C_{\mathrm{{corr}}}|. \end{aligned}$$

(8.195)

Also the fractional change can be expressed as

$$\begin{aligned} \left| \frac{\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}}{(\tau ^{\mathrm{{loc}}}_{\mathrm{NL}})_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}}\right| _{\phi _*\ll M_p}= & {} |1-\Delta _{f}(1+C_{\mathrm{{corr}}})|\sim |C_{\mathrm{{corr}}}|.\nonumber \\ \end{aligned}$$

(8.196)

So it is clear that $|C_{\mathrm{{corr}}}|$ captures the effects of the deviation in the Suyama–Yamaguchi consistency relation which are very small and suppressed in the sub Planckian regime of inflation.

• From the study of sub Planckian and super Planckian regime it is evident that when $\Delta _{f}\sim \mathcal{O}(1)$ i.e. the non-Gaussian amplitude obtained from three point function in attractor and non-attractor regime for all the derived effective potentials are of the same order then the deviation from Suyama–Yamaguchi consistency relation is very small. The only difference is in the sub Planckian case this correction is greater than unity and on the other hand in the super Planckian case this correction factor is less than unity. But since we are interested in the precision cosmological measurement, such small but distinctive corrections will play a significant role in discriminating between the classes of effective models of inflation derived in this paper.

• Finally, if we relax the assumption that the deviation factor, $\Delta _{f} \ne 1$, then one can consider the following two situations-

  • 1. First we consider, $\Delta _{f}\gg 1$. In this case in the super Planckian and sub Planckian regime we get the following results for the deviation in the Suyama–Yamaguchi consistency relation:

    $$\begin{aligned}&|\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}|_{\phi _*\gg M_p} =\frac{36}{25}(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2|_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}|\Delta _{f}(1-J_{\mathrm{{corr}}})|.\nonumber \\ \end{aligned}$$

    (8.197)
    $$\begin{aligned}&|\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}|_{\phi _*\ll M_p} =\frac{36}{25}(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2|_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}|\Delta _{f}(1+C_{\mathrm{{corr}}})|.\nonumber \\ \end{aligned}$$

    (8.198)

    Also the fractional change in the Suyama–Yamaguchi consistency relation can be expressed as

    $$\begin{aligned}&\left| \frac{\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}}{(\tau ^{\mathrm{{loc}}}_{\mathrm{NL}})_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}}\right| _{\phi _*\gg M_p}=|\Delta _{f}(1-J_{\mathrm{{corr}}})|,\nonumber \\&\left| \frac{\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}}{(\tau ^{\mathrm{{loc}}}_{\mathrm{NL}})_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}}\right| _{\phi _*\ll M_p}= |\Delta _{f}(1+C_{\mathrm{{corr}}})|.\nonumber \\ \end{aligned}$$

    (8.199)

    In this specific situation the deviation factor is large and consequently one can achieve a maximum amount of violation in the Suyama–Yamaguchi consistency relation. Here the results of the super Planckian and sub Planckian field values differ due to the presence of the correction factors $J_{\mathrm{{corr}}}$ and $C_{\mathrm{{corr}}}$. Here both $J_{\mathrm{{corr}}}<1$ and $C_{\mathrm{{corr}}}<1$, but for model discrimination such small corrects are significant as mentioned earlier.

  • 2. Next we consider, $\Delta _{f}\ll 1$. In this case in the super Planckian and sub Planckian regime we get the following results for the deviation in the Suyama–Yamaguchi consistency relation:

    $$\begin{aligned} |\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}|_{\phi _*\gg M_p}= & {} \frac{36}{25}(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2|_{\mathrm{{non}}\text {-}\mathrm{{attractor}}} |1-\Delta _{f}|.\nonumber \\ \end{aligned}$$

    (8.200)
    $$\begin{aligned} |\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}|_{\phi _*\ll M_p}= & {} \frac{36}{25}(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2 |_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}|1-\Delta _{f}|.\nonumber \\ \end{aligned}$$

    (8.201)

    Also the fractional change in the Suyama–Yamaguchi consistency relation can be expressed as

    $$\begin{aligned}&\left| \frac{\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}}{(\tau ^{\mathrm{{loc}}}_{\mathrm{NL}})_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}}\right| _{\phi _*\gg M_p}=|1-\Delta _{f}|,\nonumber \\&\left| \frac{\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}}{(\tau ^{\mathrm{{loc}}}_{\mathrm{NL}})_{\mathrm{{non}}\text {-}\mathrm{{attractor}}}}\right| _{\phi _*\ll M_p}=|1-\Delta _{f}|. \end{aligned}$$

    (8.202)

    In this specific situation deviation factor is small and consequently one can achieve very small amount of violation in Suyama–Yamaguchi consistency relation. Here the results of the super Planckian and sub Planckian field value are almost the same as we have neglected the terms $\Delta _{f}J_{\mathrm{{corr}}}\ll 1$ and $\Delta _{f}C_{\mathrm{{corr}}}\ll 1$.

Now to derive the results of non-Gaussian amplitudes in the non-attractor regime using the $\delta \mathcal{N}$ formalism we need to freeze the value of the additional field $\Psi$ in the Planck scale. If we do this job then the expression for the four point non-Gaussian amplitude computed from scalar fluctuation can be expressed as

$$\begin{aligned} \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \left[ \frac{\mathcal{N}_{,\phi \phi }\mathcal{N}_{,\phi \phi }}{\left( \mathcal{N}_{,\phi }\mathcal{N}_{,\phi }\right) ^2}\right] _{*}=\mathcal{Y}^2,\nonumber \\ g^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{25}{54}\left[ \frac{\mathcal{N}_{,\phi \phi \phi }}{\mathcal{N}_{,\phi }\mathcal{N}_{,\phi }\mathcal{N}_{,\phi }}\right] _{*}=\frac{25}{108}\mathcal{Y}^2. \end{aligned}$$

(8.203)

In this case we also derive the modified consistency relation between the four point and three point non-Gaussian amplitude for scalar fluctuations as

$$\begin{aligned} g^{\mathrm{{loc}}}_{\mathrm{NL}}= & {} \frac{25}{108}\tau ^{\mathrm{{loc}}}_{\mathrm{NL}},\quad \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}=\frac{972}{625}(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2. \end{aligned}$$

(8.204)

This implies that the well-known Suyama–Yamaguchi consistency relation also is violated in this context and the amount of violation is given by

$$\begin{aligned} |\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}|= & {} |(\tau ^{\mathrm{{loc}}}_{\mathrm{NL}})_{\delta \mathcal{N }}-(\tau ^{\mathrm{{loc}}}_{\mathrm{NL}})_{\mathrm{{In}}\text {-}\mathrm{{In}}}|\nonumber \\= & {} \frac{36}{25}((f^{\mathrm{{loc}}}_{\mathrm{NL}})^2)_{\mathrm{{In}}\text {-}\mathrm{{In}}}\left| \frac{27}{25}W_f-1\right| , \end{aligned}$$

(8.205)

where the factor $W_{f}$ is defined by

$$\begin{aligned} W_f = \frac{(f^{\mathrm{{loc}}}_{\mathrm{NL}})^2)_{\delta \mathcal{N }}}{((f^{\mathrm{{loc}}}_{\mathrm{NL}})^2)_{\mathrm{{In}}\text {-}\mathrm{{In}}}}. \end{aligned}$$

(8.206)

Also the fractional change is given by

$$\begin{aligned} \left| \frac{\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}}{(\tau ^{\mathrm{{loc}}}_{\mathrm{NL}})_{\mathrm{{In}}\text {-}\mathrm{{In}}}}\right| =\left| \frac{27}{25}W_f-1\right| . \end{aligned}$$

(8.207)

Now if we claim that at the horizon crossing non-Gaussian amplitudes obtained from the $\delta \mathcal{N}$ and In-In formalism are of the same order then in that case we get $W_f\sim \mathcal{O}(1)$. Consequently the deviation in the Suyama–Yamaguchi consistency relation can be recast as

$$\begin{aligned} |\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}|=|(\tau ^{\mathrm{{loc}}}_{\mathrm{NL}})_{\delta \mathcal{N }}-(\tau ^{\mathrm{{loc}}}_{\mathrm{NL}})_{\mathrm{{In}}\text {-}\mathrm{{In}}}|\sim \frac{72}{625}((f^{\mathrm{{loc}}}_{\mathrm{NL}})^2)_{\mathrm{{In}}\text {-}\mathrm{{In}}}.\nonumber \\ \end{aligned}$$

(8.208)

Consequently the fractional deviation is given by $\left| \frac{\Delta \tau ^{\mathrm{{loc}}}_{\mathrm{NL}}}{(\tau ^{\mathrm{{loc}}}_{\mathrm{NL}})_{\mathrm{{In}}\text {-}\mathrm{{In}}}}\right| \sim \frac{2}{25}$.

9 Conclusion

To summarize, in the present article, we have addressed the following points:

• Firstly we have started our discussion with a specific class of modified theory of gravity, aka f(R) gravity where a single matter (scalar field) is minimally coupled with the gravity sector. For simplicity we consider the case where the matter field contains only canonical kinetic term. To build effective potential from this toy setup of modified gravity in 4D we choose $f(R)=\alpha R^2$ gravity.

• Next to start with in the matter sector we choose a very simple model of potential, $V(\phi )=\frac{\lambda }{4}\phi ^4$, where $\phi$ is a real scalar field and $\lambda$ is a real parameter of the monomial model. This type of potential can be treated as a Higgs like potential as the structure of Higgs potential is given by $V(H)=\frac{\lambda }{4}(H^{\dagger }H-V^2)$, where $\lambda$ is Yukawa coupling, H is the Higgs SU(2) doublet and $\langle 0|H|0\rangle =\mathcal{V}\sim 125~\mathrm{GeV}$ is the VEV of the Higgs field. Now one can write the Higgs SU(2) doublet as $H ^{\dagger }=(\phi ~~ 0)$ and the corresponding Higgs potential can be recast as $V(\phi )=\frac{\lambda }{4}(\phi ^2-\mathcal{V}^2)^2$. Now at the scale of inflation, which is at $\mathcal{O}(10^{16}~\mathrm{GeV})$, contribution from the VEV is almost negligible and consequently one can recast the Higgs potential in the monomial form, $V(\phi )\approx \frac{\lambda }{4}\phi ^4$. The only difference is in the case of Higgs where $\lambda$ is the Yukawa coupling and in the case of a general monomial model $\lambda$ is a free parameter of the theory. Due to the similar structural form of the potential we call the general $\phi ^4$ monomial model as Higgsotic potential.

• Further, we provide the field equations in a spatially flat FLRW background, which are extremely complicated to solve for this setup. To simplify, next we perform a conformal transformation in the metric and write down the model action in the transformed Einstein frame. Next, we derive the field equations in a spatially flat FLRW background and try to solve them for two dynamical attractor features: I. a power-law solution and II. an exponential solution. However, the second case gives rise to tachyonic behavior which can be resolved by considering the non-BPS D-brane in superstring theory, considering the effect of mass like quadratic term in the effective potential and considering the effect of non-minimal coupling between $f(R)=\alpha R^2$ scale free gravity sector and the matter field sector.

• Next, using two dynamical attractors, a power-law and an exponential solution, we have studied the cosmological constraints in the presence of two fields in an Einstein frame. We have studied the constraints from primordial density perturbation, by deriving the expressions for two point function and the present observables-amplitude of power spectrum for density perturbations, corresponding spectral tilt and associated running and running of the running for inflation. We have repeated the analysis for tensor modes and also comment on the future observables – the amplitude of the tensor fluctuations, associated tilt and running, and the tensor-to-scalar ratio. We also provide a modified formula for the field excursion in terms of the tensor-to-scalar ratio, scale of inflation and the number of e-foldings. Further, we have compared our model with Planck 2015 data and constrain the parameter $\alpha$ of the scale free gravity and non-minimal coupling parameter $\lambda (\Psi _\mathrm{h})$. Additionally, we have studied the constraint for the reheating temperature. Finally, we derive the expression for the inflaton and the coupling parameter at horizon crossing, during reheating and at the onset of inflation which are very useful to study the scale dependent behavior. Most importantly, in the present context one can interpret such scale dependence as an outcome of RG flow in the usual Quantum Field Theory.

• Further, we have explored the cosmological solutions beyond attractor regime. We have shown that this possibility can be achieved if we freeze the field value of the dilaton field in Einstein frame. This possibility can be treated as a single field model where an additional field freezes at a certain field value, which we fix at the reduced Planck scale. To serve this purpose we have used the ADM formalism and computed the two point function and associated present inflationary observables using Bunch–Davies initial condition for scalar fluctuations. We have repeated the procedure for tensor fluctuations as well. In the non-attractor regime, we have also derived a modified version of the field excursion formula in terms of the tensor-to-scalar ratio, scale of inflation and the number of e-foldings. We have also derived few sets of consistency relations in this context which are different from the usual single field slow-roll models. For example, instead of getting $r=-8n_{\mathrm{T}}$ here we get $r=\frac{24n^2_{\mathrm{T}}}{1-n_\mathrm{S}}$ at horizon crossing scale. Further, we derive the constraints on the reheating temperature in terms of inflationary observables and the number of e-foldings.

• Next, as a future probe, we have computed the expression for three point function and the bispectrum of scalar fluctuations using the In-In formalism for the non-attractor case and $\delta \mathcal{N}$ formalism for the attractor case. Following the fact that the local Ansatz for curvature perturbation perfectly holds true, we have derived the results for non-Gaussian amplitude $f^{\mathrm{{loc}}}_{\mathrm{NL}}$ for equilateral limit and squeezed limit triangular shape configuration. We also give a bulk interpretation of each of the momentum dependent terms appearing in the expression for the three point scalar correlation function in terms of S, T and U channel contributions. It is important to note that in the attractor phase, since we have started with various proposals of the effective potentials, as mentioned earlier, we have found various non-trivial features up to second-order perturbation in the $\delta \mathcal{N}$ formalism. Further, for the consistency check we freeze the dilaton field in the Planck scale and redo the analysis of $\delta \mathcal{N}$ formalism. By doing this we have found that the expression for the three point non-Gaussian amplitude is slightly different as expected for the single field case. Further, we compare the results obtained from the In-In formalism and $\delta \mathcal{N}$ formalism for the non-attractor phase, where the dilaton field is fixed in Planck scale. Here, finally, we give a theoretical bound on the scalar three point non-Gaussian amplitude computed from equilateral and squeezed limit configurations. The obtained results are consistent with the Planck 2015 data.

• Finally, as an additional future probe, we have also computed the expression for the four point function as well as the trispectrum of scalar fluctuations using the In-In formalism for the non-attractor case and the $\delta \mathcal{N}$ formalism for the attractor case. We have derived the results for non-Gaussian amplitude $g^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$ for equilateral limit, counter-collinear or folded kite limit and squeezed limit shape configuration from the In-In formalism. Further we have given the bulk interpretation of each of the momentum dependent terms appearing in the expression for the four point scalar correlation function. We have identified the S, T and U channel contributions in momentum space from our computation. In our computation we have considered the contribution from contact interaction term, scalar and graviton exchange. In the attractor phase following the prescription of the $\delta \mathcal{N}$ formalism we also derive the expressions for the four point non-Gaussian amplitude $g^{\mathrm{{loc}}}_{\mathrm{NL}}$ and $\tau ^{\mathrm{{loc}}}_{\mathrm{NL}}$. Next we have shown that the consistency relation connecting three and four point non-Gaussian amplitude aka Suyama–Yamaguchi relation is modified in the attractor phase and further given an estimate of the amount of deviation. Further, for the consistency check we freeze the dilaton field in the Planck scale and redo the analysis of the $\delta \mathcal{N}$ formalism. By doing this we have found that the expression for the four point non-Gaussian amplitude is slightly different as expected for the single field case. Next we have also shown that the exact numerical deviation of the consistency relation is of the order of 2 / 25 by assuming non-Gaussian three point amplitude for attractor and non-attractor phase are of the same order of magnitude. Further, we compare the results obtained from the In-In formalism and $\delta \mathcal{N}$ formalism for the non-attractor phase, where the dilaton field is fixed in the Planck scale. Here, finally, we give a theoretical bound on the scalar four point non-Gaussian amplitude computed from equilateral, folded kite and squeezed limit configurations. The obtained results are consistent with the Planck 2015 data.

The future prospects of our work are appended below:

• We have restricted our analysis up to monomial $\phi ^4$ model and due to the structural similarity with Higgs potential at the scale of inflation we have identified monomial $\phi ^4$ model as Higgsotic model in the present context.

• To investigate the role of scale free theory of gravity, as an example we have used $\alpha R^2$ gravity. But the present analysis can be generalized to any class of f(R) gravity models and other class of higher derivative gravity models.

• In the matter sector for completeness one can consider most generalized version of $P(X,\phi )$ models, where $X=-\frac{1}{2}g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu }\phi$. DBI is one of the examples of $P(X,\phi )$ model which can be implemented in the matter sector instead of simple canonical kinetic contribution.

• In this work, we have not given any three point computation and found point scalar correlation function and representative non-Gaussian amplitudes using the In-In formalism in the attractor regime in the presence of both fields, $\phi$ and $\Psi$, for all classes of Higgsotic models. In near future we are planning to present the detailed calculation on this important issue.

• Generation of primordial magnetic field through inflationary magnetogenesis is one of the important issues in the context of primordial cosmology, which we have not explored yet from our setup. One can consider such interactions by breaking conformal invariance of the U(1) gauge field in the presence of time dependent coupling $f(\phi (\eta ))$ to study the features of primordial magnetic field through inflationary magnetogenesis. We have also a future plan to address this issue.

• In this work we have restricted our analysis within the class of Higgsotic models. For completeness in the future we will extend this idea to all class of potentials allowed by the presently available observed Planck data. We will also include the effects of various types of non-minimal and non-canonical interactions in the present setup.

• In the same direction one can also carry forward the present analysis in the context of various types of higher derivative gravity setup and comment on the constraints on the primordial non-Gaussianity, reheating and generation of primordial magnetic field through inflationary magnetogenesis for completeness. Also one can consider the possibility of non-minimal interaction between $\alpha R^2$ gravity and matter sector. In future we will investigate the possibility of appearing new consistency relations in the presence of higher derivative gravity setup and will give proper estimate of the amount of violation from Suyama–Yamaguchi consistency relation.

• During the computation of correlation functions using semi classical method, via the $\delta \mathcal{N}$ formalism, we have restricted up to second-order contributions in the solution of the field equation in FLRW background and also neglected the contributions from the back reaction for all type of effective Higgsotic models derived in an Einstein frame. For more completeness, one can relax these assumptions and redo the analysis by taking care of all such contributions. Additionally, we have a future plan to extend the semi classical computation of the $\delta \mathcal{N}$ formalism of cosmological perturbation theory in a more sophisticated way and will redo the analysis in the present context.

• In this work, we also have not investigated the possibility of getting dark matter and dark energy constraints from the present up. Most importantly the present structure of interactions in the Einstein frame shows that the two fields, $\phi$ and $\Psi$, are coupled and due to this fact if we want to explain the possibility of dark matter and dark energy together; from this setup it is very clear that they are coupled. But this is not very clear at the level of analytics and detailed calculations. Here one can also investigate these possibilities from this setup.

• In this work we have not investigated the contribution from the loop effects (radiative corrections) in all of the effective Higgsotic interactions (specifically in the self couplings) derived in the Einstein frame. After switching on all such effects one can investigate the specific numerical contribution of such terms and comment on the effects of such terms in precision cosmology measurement.

• Here one can generalize the results for $\alpha$ vacua and study its cosmological consequences for all types of derived potential in the present context.

• In the present context one can also study the quantum entanglement between the Bell pairs, which can be created through the Bell inequality violation in cosmology [179,180,181].

Appendix

1.1 Effective Higgsotic models for generalized $P(X,\phi )$ theory

In this section, to give a broad overview of the effective Higgsotic models let us start with a general f(R) theory in the gravity sector and generalized $P(X,\phi )$ theory in the matter sector. The representative actions in a Jordan frame is given by

$$\begin{aligned} S=\int \mathrm{d}^{4}x \sqrt{-g}\left[ f(R)+P(X,\phi )\right] , \end{aligned}$$

(10.1)

where $P(X,\phi )$ is a arbitrary function of single scalar field $\phi$ and the kinetic term $X=-\frac{1}{2}g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu }\phi$. In general f(R) is any arbitrary function of R. But for our purpose we choose $f(R)=\alpha R^2$ to study the consequences from scale free gravity. From this representative action one can write down the field equations in a spatially flat FLRW background as

$$\begin{aligned}&H^{2}=\left( \frac{\dot{a}}{a}\right) ^2=\frac{\rho _{\phi }}{6\alpha R}+\frac{R}{2}-\left( \frac{\dot{R}}{R}\right) H,\end{aligned}$$

(10.2)

$$\begin{aligned}&2\dot{H}+3H^{2}=2\left( \frac{\ddot{a}}{a}\right) + \left( \frac{\dot{a}}{a}\right) ^{2}\nonumber \\&\qquad =-\frac{p_{\phi }}{2\alpha R} -2\left( \frac{\dot{R}}{R}\right) H-\frac{\ddot{R}}{R}+\frac{R}{4} \end{aligned}$$

(10.3)

where for generalized $P(X,\phi )$ theory pressure $p_{\phi }$ and density $\rho _{\phi }$ can be written as

$$\begin{aligned} p_{\phi }=P(X,\phi ),\quad \rho _{\phi }=2XP_{,X}(X,\phi )-P(X,\phi ). \end{aligned}$$

(10.4)

Here the effective speed of sound parameter $c_\mathrm{S}$ is defined as

$$\begin{aligned} c_\mathrm{S}=\sqrt{\frac{P_{,X}(X,\phi )}{P_{,X}(X,\phi )+2XP_{,XX}(X,\phi )}}. \end{aligned}$$

(10.5)

If we choose the following functional form of $P(X,\phi )$:

$$\begin{aligned} P(X,\phi )=-\frac{1}{f(\phi )}\sqrt{1-2Xf(\phi )}+\frac{1}{f(\phi )}-V(\phi ), \end{aligned}$$

(10.6)

as pointed out earlier, then we get the following simplified expression for $p_{\phi }$ and density $\rho _{\phi }$:

$$\begin{aligned} p= & {} \frac{1}{f(\phi )}(1-c_\mathrm{S})-V(\phi ),\nonumber \\ \rho= & {} \frac{1}{f(\phi )}\left( \frac{1}{c_\mathrm{S}}-1\right) +V(\phi ). \end{aligned}$$

(10.7)

Also one can consider any arbitrary slow-roll effective potential but for our purpose we choose monomial Higgsotic model, $V(\phi )=\frac{\lambda }{4}\phi ^4$ in the Jordan frame.

In the present context let us introduce a scale dependent mode $\Psi$, which can be written in terms of a no scale dilaton mode $\Theta$ as $\Theta = f^{\prime }(R)M^{-2}_{p}=2\alpha R~M^{-2}_{p}=\mathrm{e}^{\sqrt{\frac{2}{3}}\frac{\Psi }{M_p}}=\Omega ^2$, which plays the role of a Lagrange multiplier and arises in the Jordan frame without space-time derivatives. Here $\Omega$ is the conformal factor of the conformal transformation that we perform from Jordan frame to Einstein frame.

In terms of the newly introduced no scale dilaton mode $\Theta$ the total action of the theory (see Eq. (2.1)) can be recast as

$$\begin{aligned} S=\int \mathrm{d}^{4}x \sqrt{-g}\left\{ \frac{M^{2}_{p}}{2}\Theta R-\frac{M^{4}_{p}}{8\alpha }\Theta ^{2}+P(X,\phi )\right\} . \end{aligned}$$

(10.8)

After doing C.T. the total action can be recast in the Einstein frame as

$$\begin{aligned} S~~\underrightarrow{\mathrm{{C.T.}}}~~ \tilde{S} =\int \mathrm{d}^{4}x \sqrt{-\tilde{g}}\left[ \frac{M^{2}_{p}}{2}\tilde{R}+G(\tilde{X},\phi ,\Psi )\right] \end{aligned}$$

(10.9)

where after applying C.T. the functional $G(\tilde{X},\phi ,\Psi )$ is defined in an Einstein frame as

$$\begin{aligned} G(\tilde{X},\phi ,\Psi )=\frac{1}{\Omega ^4}\left[ P(\tilde{X},\phi )-\frac{M^{4}_{p}}{8\alpha }\mathrm{e}^{2\sqrt{\frac{2}{3}}\frac{\Psi }{M_p}}\right] . \end{aligned}$$

(10.10)

Here $\tilde{X}$ is the kinetic term after a conformal transformation, which is defined as $\tilde{X}=-\frac{1}{2}\tilde{g}^{\mu \nu }\tilde{\partial }_{\mu }\phi \tilde{\partial }_{\nu }\phi$. Now in the case of the specific form of $P(X,\phi )$ as stated in Eq. (10.6) after a conformal transformation we get

$$\begin{aligned} G(\tilde{X},\phi ,\Psi )= & {} \frac{1}{\Omega ^4} \left[ -\frac{1}{f(\phi )}\sqrt{1-2\tilde{X}f(\phi )}+\frac{1}{f(\phi )}\right. \nonumber \\&\left. -V(\phi )-\frac{M^{4}_{p}}{8\alpha }\mathrm{e}^{2\sqrt{\frac{2}{3}}\frac{\Psi }{M_p}}\right] . \end{aligned}$$

(10.11)

Here the total potential can be recast as

$$\begin{aligned} \tilde{W}(\phi ,\Psi )= & {} \frac{\frac{M^{4}_{p}}{8\alpha } \mathrm{e}^{2\sqrt{\frac{2}{3}}\frac{\Psi }{M_p}}+V(\phi )+ \frac{1}{f(\phi )}}{\Omega ^4}\nonumber \\= & {} V_0 \left[ 1+\left( \frac{8\alpha }{M^{4}_{p}}V(\phi )+ \frac{1}{f(\phi )}\right) \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}\right] ,\nonumber \\ \end{aligned}$$

(10.12)

where $V_0=M^{4}_{p}/8\alpha$, exactly mimics the role of cosmological constant as mentioned earlier.

In the case of Higgsotic model we can rewrite the total potential as

$$\begin{aligned} \tilde{W}(\phi ,\Psi )= & {} \frac{\frac{M^{4}_{p}}{8\alpha } \mathrm{e}^{2\sqrt{\frac{2}{3}}\frac{\Psi }{M_p}}+ \frac{\lambda }{4}\phi ^{4}+\frac{1}{f(\phi )}}{\Omega ^4}\nonumber \\= & {} V_0\left[ 1+\frac{2\alpha \lambda (\Psi )}{M^{4}_{p}}\phi ^{4} +\frac{1}{f(\phi )}\mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}\right] .\nonumber \\ \end{aligned}$$

(10.13)

Here the effective matter coupling ($\lambda (\Psi )$) in the potential sector is given by

$$\begin{aligned} \lambda (\Psi )=\frac{\lambda }{\Omega ^4}=\lambda \mathrm{e}^{-\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p}}. \end{aligned}$$

(10.14)

The rest of the computation is exactly similar to what we have performed earlier, only the structure of the total effective potential changes.

Here it is important to note that apart from f(R) gravity one can consider various other possibilities. To give a clear picture about various classes of two-field attractor models one can consider the following 4D effective action in an Einstein frame:

$$\begin{aligned} S=\int \mathrm{d}^{4}x\sqrt{-g}\left[ \frac{M^2_p}{2}R+J(X,Y,\phi ,\Psi )\right] . \end{aligned}$$

(10.15)

where $J(X,Y,\phi ,\Psi )$ is the general functional of the two fields $\phi$ and $\Psi$: the following specific mathematical structure:

$$\begin{aligned} J(X,Y,\phi ,\Psi )=\mathrm{e}^{-\frac{c_{1}\Psi }{M_p}}X+Y-W(\phi ,\Psi ). \end{aligned}$$

(10.16)

Here $c_{1}$ and $c_{2}$ characterize the effective coupling constant in 4D, which are different for various types of source theories. In the EFT setup these are identified as the Wilson coefficients. Additionally, it is important to note that the kinetic terms for the $\phi$ and $\Psi$ field are defined as $X= -\frac{g^{\mu \nu }}{2}\partial _{\mu }\phi \partial _{\nu }\phi$ and $Y=-\frac{g^{\mu \nu }}{2}\partial _{\mu }\Psi \partial _{\nu }\Psi$. Here $W(\phi ,\Psi )$ is the 4D effective potential, which is given by the following expression:

$$\begin{aligned} W(\phi ,\Psi )=\mathrm{e}^{-\frac{c_{2}\Psi }{M_p}}V(\phi ). \end{aligned}$$

(10.17)

This is a non-separable form of the two-field effective potential where one can treat $V(\phi )$ as usual inflaton field and $\mathrm{e}^{-\frac{c_{2}\Psi }{M_p}}$ as the dilaton exponential coupling.

This type of effective theory can be derived from the following class of models:

• 1. Type I: Consider an action in a Jordan frame where the scalar field $\Phi$ is non-minimally coupled with the gravity sector as given by

  $$\begin{aligned} S= & {} \int \mathrm{d}^4 x\sqrt{-g}\left[ f_1(\Phi )R-f_2(\Phi ) g^{\mu \nu }\partial _{\mu }\Phi \partial _{\nu }\Phi \right. \nonumber \\&\left. -\,U(\Phi )+X-V(\phi )\right] . \end{aligned}$$

  (10.18)

  Here $f_{1}(\Phi )$ is the non-minimal coupling and $f_{2}(\Phi )$ is the non-canonical interaction. This type of theories include the following subclass of models:

  • Jordan Brans Dicke (JBD) theory: In this case we have

    $$\begin{aligned}&f_1(\Phi )=\frac{\Phi }{16\pi },\quad f_2(\Phi )=\frac{\omega }{16\pi \Phi },\quad U(\Phi )= 0,\nonumber \\&\quad c_{1}=\frac{c_2}{2},\quad c_{2}=\sqrt{\frac{8}{2\omega +3}},\end{aligned}$$

    (10.19)
    $$\begin{aligned}&\Psi =M_p\sqrt{\omega +\frac{3}{2}}\ln \left( \frac{\Phi }{2M^2_p}\right) . \end{aligned}$$

    (10.20)

    Here $\omega$ is the JBD parameter and for power-law inflation $\omega >1/2$.

  • Induced gravity theory: In this case we have

    $$\begin{aligned}&f_1(\Phi )=\frac{g_1}{2}\Phi ^2,\quad f_2(\Phi )=\frac{1}{2},\nonumber \\&\quad U(\Phi )= \frac{\lambda }{8}(\Phi ^2-g^2_2)^2,\nonumber \\&\quad c_{1}=\frac{c_2}{2},\quad c_{2}=\sqrt{\frac{16g_1}{6g_1+1}},\end{aligned}$$

    (10.21)
    $$\begin{aligned}&\Psi =M_p\sqrt{6+\frac{1}{g_1}}\ln \left( \frac{\sqrt{g_1}\Phi }{M_p}\right) . \end{aligned}$$

    (10.22)

    Here $g_1$ and $g_2$ are coupling constants. For power-law inflation $g_{1}<1/2$.

  • Non-minimally coupled theory: In this case we have

  $$\begin{aligned}&f_1(\Phi )=\frac{M^2_p}{2}-\frac{\xi }{2}\Phi ^2,\quad f_2(\Phi )=\frac{1}{2},\quad U(\Phi )=0,\nonumber \\&\quad c_{1}=\frac{c_2}{2},\quad c_{2}=\sqrt{\frac{3\xi M^2_p}{2(6\xi M^2_p+1)}}, \end{aligned}$$

  (10.23)

$$\begin{aligned}&\Psi =\left\{ \begin{array}{ll} \sqrt{6}M_p\left\{ \mathrm{tan}^{-1}\left[ \frac{\sqrt{6}\xi \Phi }{\xi \left( 6\xi +\frac{1}{M^2_p}\right) \Phi ^2-1}\right] \right. &{}\\ \left. -\sqrt{1+\frac{1}{6\xi M^2_p}}~\mathrm{sin}^{-1} \left[ \sqrt{\xi \left( 6\xi +\frac{1}{M^2_p}\right) }\Phi \right] \phantom {\left[ \frac{\sqrt{6}\xi \Phi }{\xi \left( 6\xi +\frac{1}{M^2_p}\right) \Phi ^2-1}\right] }\right\} &{}\quad \text {for }{\xi \ne 1/6}\\ \frac{M_p}{\sqrt{6}}~\mathrm{sin}^{-1}\left[ \sqrt{6} \frac{\Phi }{M^2_p}\right] &{}\quad \text {for } {\xi =1/6}. \end{array} \right. \nonumber \\ \end{aligned}$$

(10.24)

After doing the conformal transformation in an Einstein frame one can derive the required form of the effective action from all these models.

• 2. Type II: Consider an action in a Jordan frame where the scalar field $\Phi$ is minimally coupled with the f(R) gravity sector as given by

  $$\begin{aligned} S=\int \mathrm{d}^4 x \sqrt{-g}\left[ f(R)+X-V(\phi )\right] . \end{aligned}$$

  (10.25)

  Here f(R) is an arbitrary functional of the Ricci scalar R. After doing the conformal transformation in an Einstein frame one can derive the required form of the effective action.

• 3. Type III: Consider a $4+D$ dimensional Kaluza–Klein theory with an additional scalar field. This type of theories includes the following subclass of models:

  • Extra dimensional theory-I: In this case the inflaton is introduced in the 4D effective action in a Jordan frame:

    $$\begin{aligned} S= & {} \int \mathrm{d}^4x\sqrt{-g}\left[ \frac{M^2_p}{2} \left\{ \Phi ^2R+4\left( 1-\frac{1}{D}\right) \right. \right. \nonumber \\&\left. \left. \times \, g^{\mu \nu } \partial _{\mu }\Phi \partial _{\nu }\Phi \right\} -U(\Phi )+X-V(\phi )\phantom {\frac{M^2_p}{2}}\right] .\nonumber \\ \end{aligned}$$

    (10.26)

    In this case we have

    $$\begin{aligned}&c_{1}=\frac{c_2}{2},\quad c_{2}=\sqrt{\frac{8D}{D+2}},\nonumber \\&\quad \Psi =M_p\sqrt{2\left( 1+\frac{2}{D}\right) }\ln (\Phi ). \end{aligned}$$

    (10.27)

    But from this type of model no power-law inflationary solutions are possible.

  • Extra dimensional theory-II: In this case the inflaton is introduced in the $4+D$ dimensional action in a Jordan frame as given by

    $$\begin{aligned} S=\int \mathrm{d}^{4+D}x\sqrt{-g_{4+D}}\left[ \frac{1}{2\kappa ^2_{4+D}}R+X-V(\phi )\right] .\nonumber \\ \end{aligned}$$

    (10.28)

    Here $g_{4+D}$ is the determinant of the $4+D$ dimensional metric and $\kappa ^2_{4+D}$ is the $4+D$ dimensional gravitational coupling constant. In this case also we have

    $$\begin{aligned}&c_{1}=0,\quad c_{2}=\sqrt{\frac{2D}{D+2}},\nonumber \\&\quad \Psi =M_p\sqrt{2\left( 1+\frac{2}{D}\right) }\ln (\Phi ). \end{aligned}$$

    (10.29)

    From this type of model power-law inflationary solutions are possible for all extra D dimensions.

• 4. Type IV: Consider an action in a Jordan frame from superstring theory in 10 dimension with fixed Kalb–Ramond background. In this case the scalar field $\Phi$ is non-minimally coupled with the gravity sector:

  $$\begin{aligned} S=\int \mathrm{d}^4 x \sqrt{-g}\left[ \mathrm{e}^{-2\Phi }R+4g^{\mu \nu }\partial _{\mu }\Phi \partial _{\nu }\Phi +X-V(\phi )\right] .\nonumber \\ \end{aligned}$$

  (10.30)

  In this case $\Phi$ is known as the dilaton field. But from this type of model no power-law inflationary solutions are possible. Here additionally we have two classes of the solutions: Class I:

  $$\begin{aligned} c_{1}=\frac{c_2}{2},\quad c_{2}=2\sqrt{2},\quad \Psi =\frac{M_p}{\sqrt{2}}\left( 6\ln b-\frac{\Phi }{2}\right) .\nonumber \\ \end{aligned}$$

  (10.31)

  Class II:

  $$\begin{aligned} c_{1}=c_2,\quad c_{2}=-\sqrt{6},\quad \Psi =\frac{M_p}{\sqrt{2}}\left( 2\ln b+\frac{\Phi }{2}\right) .\nonumber \\ \end{aligned}$$

  (10.32)

1.2 Dynamical dilaton at late times

After the completion of the phase of reheating, the total system enters the radiation dominated stage, at the beginning of which the total energy density is governed by Eq. (7.47). At that stage, the scalar inflaton fields have almost settled down in one of the potential valleys of the derived EFT potentials and get its VEV for the proposed model in $R^2$ gravity setup in an Einstein frame. To make the computation simpler we also assume that at the level of perturbations the dilaton field $\Psi$ is almost decoupled from the Standard Model fields and the only dynamical field present in the model at late times. Henceforth, we will treat $\Psi$ as a dynamical field minimally coupled to the $R^2$ gravity in a conformally transformed Einstein frame and also assume that the $\Psi$ field is non-interacting with other matter degrees of freedom and radiation content of the universe at late times. During this epoch the total potential is characterized by the following expression:

$$\begin{aligned} \tilde{W}(\hat{ \phi },\Psi )= & {} V_0 \left[ 1+\frac{2\alpha \lambda (\Psi )}{M^{4}_{p}}\hat{\mathbf{\phi }}^{4}\right] \nonumber \\= & {} V_0+ \underbrace{\hat{\lambda } \exp \left[ -\frac{2\sqrt{2}}{\sqrt{3}}\frac{\Psi }{M_p} \right] }_{\mathrm{{Dominant~at~late~time}}}, \end{aligned}$$

(10.33)

where $V_0$ is defined as $V_0=\frac{M^{4}_{p}}{8\alpha }$, and the VEV of the inflaton field $\phi$ is denoted by the symbol $\hat{\phi }$. Here one can set $\hat{\phi }\sim \mathcal{O}(M_p)$ for the proposed model at late time scale.

Once the contribution of the inflaton scalar field $\phi$ gets its VEV the corresponding energy density $\rho _{m}\equiv \rho _{\phi }=\mathrm{Constant}$. Now in the present context to characterize the features of late time acceleration of the universe let us introduce equation of state parameter $w_{\mathbf{X}}(=w_{\Psi })$, which is defined as

$$\begin{aligned} w_\mathbf{X}=\frac{p_{\mathbf{X}}}{\rho _{\mathbf{X}}}=\frac{\left( \frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}\right) ^2 -\tilde{W}(\hat{\phi },\Psi )}{\left( \frac{\mathrm{d}\Psi }{\mathrm{d}\tilde{t}}\right) ^2 +\tilde{W}(\hat{\phi },\Psi )} \end{aligned}$$

(10.34)

and the continuity equation in the present context can be written as

$$\begin{aligned} \frac{\mathrm{d}\rho _\mathbf{X}}{\mathrm{d}\tilde{t}}+3\tilde{H}(1+w_\mathbf{X})\rho _\mathbf{X}=0. \end{aligned}$$

(10.35)

For the qualitative analysis of the prescribed system in the Einstein frame and in order to compare with present day observations, we introduce the following sets of dimensionless density parameters and shifted equation of state parameter:

$$\begin{aligned}&\Omega _\mathbf{X}\equiv \Omega _{\Psi }=\frac{\rho _\mathbf{X}}{3\tilde{H}^{2}M^{2}_{p}},\quad \Omega _m \equiv \Omega _{\phi }=\frac{\rho _m}{3\tilde{H}^{2}M^{2}_{p}},\nonumber \\&\quad \Omega _r \equiv \frac{\rho _r}{3\tilde{H}^{2}M^{2}_{p}},\end{aligned}$$

(10.36)

$$\begin{aligned}&\Delta _\mathbf{X} \equiv \Delta _{\Psi }=1+w_{\Psi }=1+w_\mathbf{X},\nonumber \\&\Delta _{m}\equiv \Delta _{\phi }=1+w_{\phi }=1+w_{m}. \end{aligned}$$

(10.37)

In order to transform the cosmological equations into a simplified autonomous system, we define the following dimensionless auxiliary variables for the study of present dynamical system at late time scale:

$$\begin{aligned}&x\equiv \frac{\dot{\Psi }}{\sqrt{6}\tilde{H}M_p},\quad y\equiv \frac{\dot{\tilde{W}}(\hat{\phi },\Psi )}{\sqrt{3}\tilde{H}M_p},\nonumber \\&\quad \Theta \equiv -M_p\partial _{\Psi }\ln \tilde{W}(\hat{\phi },\Psi ),\nonumber \\&\quad \Sigma \equiv \frac{\tilde{W}(\hat{\phi },\Psi ) \partial _{\Psi \Psi }\tilde{W}(\hat{\phi },\Psi )}{(\partial _{\Psi }\tilde{W}(\hat{\phi },\Psi ))^{2}} \end{aligned}$$

(10.38)

which can be recast in the autonomous form as

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}\mathcal{N}}= & {} \frac{x}{2}(\Omega _r-3y^2-3)+\frac{3x^3}{2} +\sqrt{\frac{3}{2}}y^2\Theta ,\nonumber \\ \frac{\mathrm{d}y}{\mathrm{d}\mathcal{N}}= & {} \frac{y}{2}(3x^2-\sqrt{6}x\Theta +3+\Omega _r) -\frac{3 y^3}{2}, \nonumber \\ \frac{\mathrm{d} \Theta }{\mathrm{d}\mathcal{N}}= & {} -\frac{\sqrt{6}}{2} \Theta ^2 (\Sigma -1)x,\nonumber \\ \frac{\mathrm{d} \Omega _r}{\mathrm{d}\mathcal{N}}= & {} -\Omega _r(1-3(x^2 -y^2)-\Omega _r),\nonumber \\ \frac{\mathrm{d} \Omega _m}{\mathrm{d}\mathcal{N}}= & {} \Omega _m(3(x^2 -y^2)+\Omega _r), \end{aligned}$$

(10.39)

together with an additional constraint condition, $\Omega _X+\Omega _r+\Omega _m=x^2+y^2+\Omega _m +\Omega _r=1$. Also using these dimensionless variables Eqs. (10.34) and (10.36) can be recast as

$$\begin{aligned} w_{X}\equiv & {} \frac{p_{X}}{\rho _{X}}=\frac{ x^2-y^2}{ x^2+y^2}=\frac{x^2-y^2}{\Omega _X}=\frac{w_\mathrm{eff}-\frac{\Omega _r}{3}}{\Omega _X}, \nonumber \\ \Omega _{X}\equiv & {} \frac{\rho _{X}}{3\tilde{H}^2M^{2}_{p}} = x^2+y^2. \end{aligned}$$

(10.40)

One can also define the total effective equation of state as

$$\begin{aligned} w_\mathrm{eff}\equiv & {} \frac{p_\mathrm{eff}}{\rho _\mathrm{eff}}=\frac{p_\mathbf{X}+p_m+p_r}{\rho _{ X}+\rho _m+\rho _r}\nonumber \\= & {} \frac{p_{\varvec{\Psi }}+p_{\phi }+p_r}{\rho _{ \Psi }+\rho _{\phi }+\rho _r} = x^2 -y^2 +\frac{\Omega _r}{3}. \end{aligned}$$

(10.41)

For an accelerated expansion effective equation of state satisfy the following constraint, $w_\mathrm{eff}<-1/3$. Using this methodology mentioned in this section one can study the constraints on the model from late time acceleration which is beyond the scope of our discussion in this paper.

1.3 Details of the $\delta \mathcal{N}$ formalism

1.3.1 Useful field derivatives of $\mathcal{N}$

To simplify the calculation for $\delta \mathcal{N}$ let us consider all these possibilities to write down the infinitesimal change in $\Psi$ field in terms of the inflaton field $\phi$:

$$\begin{aligned}&\text {Case~I}{:}\quad \delta \Psi =-\frac{9\phi }{\sqrt{6}M_p}~\delta \phi ,\end{aligned}$$

(10.42)

$$\begin{aligned}&\text {Case~II}{:}\quad \delta \Psi =-\frac{\phi }{\sqrt{6}M_p}~\delta \phi ,\end{aligned}$$

(10.43)

$$ \begin{aligned}&\text {Case~II}+\text {Choice~I}(\text {v1} \& \text {v}2){:}\nonumber \\&\quad \delta \Psi =-\frac{\phi }{\sqrt{6}M_p}~\delta \phi \left[ 1-\frac{\phi ^4_V}{\phi ^4}\right] ,\end{aligned}$$

(10.44)

$$ \begin{aligned}&\text {Case~II}+\text {Choice~II}(\text {v}1 \& \text {v}2){:}\nonumber \\&\quad \delta \Psi =-\frac{\phi }{\sqrt{6}M_p}~\delta \phi \left[ 1-\frac{m^2_c}{(m^2_c-\lambda \phi ^2)}\right] ,\end{aligned}$$

(10.45)

$$\begin{aligned}&\text {Case~II}+\text {Choice~III}{:}\nonumber \\&\quad \delta \Psi = -\frac{\phi }{\sqrt{6}M_p}~\delta \phi \left[ 1+\frac{\xi }{2}(\phi ^2+\phi ^2_0-2\phi ^2_V)\right. \nonumber \\&\quad \left. +\frac{\xi }{2}(\phi ^2-\phi ^2_0)+\frac{\phi ^2_V}{\phi ^2}\right] . \end{aligned}$$

(10.46)

Combining all these possibilities one can write the following expression:

$$\begin{aligned} \delta \Psi= & {} \mathcal{V}(\phi )~\delta \phi , \end{aligned}$$

(10.47)

where we introduce a function $\mathcal{V}(\phi )$, which can be written as

$$ \begin{aligned} \mathcal{V}(\phi )=-\frac{\phi }{\sqrt{6}M_p}\times \left\{ \begin{array}{ll} 9 &{}\quad \text {for Case I}\\ 1&{}\quad \text {for Case II}\\ \left[ 1-\frac{\phi ^4_V}{\phi ^4}\right] &{}\quad \text {for Case~II}+\text {Choice~I} (\text {v}1 \& \text {v}2)\\ \left[ 1-\frac{m^2_c}{(m^2_c-\lambda \phi ^2)}\right] &{} \quad \text {for Case~II}+\text {Choice~II}(\text {v}1 \& \text {v}2)\\ \left[ 1+\frac{\xi }{2}(\phi ^2+\phi ^2_0-2\phi ^2_V) +\frac{\xi }{2}(\phi ^2-\phi ^2_0)+\frac{\phi ^2_V}{\phi ^2}\right] &{}\quad \text {for Case II}+\text {Choice~III}. \end{array} \right. \end{aligned}$$

(10.48)

This additionally implies that one can write down the following differential operator for the $\Psi$ field:

$$\begin{aligned} \partial _{\Psi }= & {} \frac{1}{\mathcal{V}(\phi )}~\partial _{\phi }, \partial ^2_{\Psi }=\left[ \frac{1}{\mathcal{V}^2(\phi )}~\partial ^2_{\phi }-\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}\partial _{\phi }\right] ,\nonumber \\ \partial ^3_{\Psi }= & {} \left[ \frac{1}{\mathcal{V}^3(\phi )}~\partial ^3_{\phi }-3\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^4(\phi )}~\partial ^2_{\phi }+3\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^5(\phi )}~\partial _{\phi }\right] ,\end{aligned}$$

(10.49)

$$\begin{aligned} \partial _{\phi }\partial _{\Psi }= & {} \left[ \frac{1}{\mathcal{V}(\phi )}~\partial ^2_{\phi }-\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^2(\phi )}~\partial _{\phi }\right] ,~~ \partial _{\Psi }\partial _{\phi }=\frac{1}{\mathcal{V}(\phi )}~\partial ^2_{\phi },\end{aligned}$$

(10.50)

$$\begin{aligned} \partial _{\phi }\partial _{\phi }\partial _{\Psi }= & {} \left[ \frac{1}{\mathcal{V}(\phi )}~\partial ^3_{\phi }-2\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^2(\phi )}~\partial ^2_{\phi }\right. \nonumber \\&\left. -\left( \frac{\mathcal{V}^{\prime \prime }(\phi )}{\mathcal{V}^2(\phi )}-2\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^3(\phi )}\right) \partial _{\phi }\right] ,\nonumber \\ \partial _{\phi }\partial _{\Psi }\partial _{\phi }= & {} \left[ \frac{1}{\mathcal{V}(\phi )}~\partial ^3_{\phi }-\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^2(\phi )}~\partial ^2_{\phi }\right] ,\end{aligned}$$

(10.51)

$$\begin{aligned} \partial _{\Psi }\partial _{\phi }\partial _{\phi }= & {} \frac{1}{\mathcal{V}(\phi )}~\partial ^3_{\phi },\nonumber \\ \partial _{\phi }\partial _{\Psi }\partial _{\Psi }= & {} \left[ \frac{1}{\mathcal{V}^2(\phi )}~\partial ^{3}_{\phi }-3\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}~\partial ^{2}_{\phi }+3~\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^4(\phi )}~\partial _{\phi }\right] ,\nonumber \\ \end{aligned}$$

(10.52)

$$\begin{aligned} \partial _{\Psi }\partial _{\phi }\partial _{\Psi }= & {} \left[ \frac{1}{\mathcal{V}^2(\phi )}~\partial ^{3}_{\phi }-2\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}~\partial ^{2}_{\phi }+2~\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^4(\phi )}~\partial _{\phi }\right] ,\nonumber \\ \partial _{\Psi }\partial _{\Psi }\partial _{\phi }= & {} \left[ \frac{1}{\mathcal{V}^2(\phi )}~\partial ^{3}_{\phi }-\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}~\partial ^{2}_{\phi }\right] , \end{aligned}$$

(10.53)

where $'$ is defined as the partial derivative with respect to the field $\phi$ i.e. $'=\partial _{\phi }$.

Consequently one can write

$$\begin{aligned} \mathcal{N}_{,\Psi }= & {} \frac{1}{\mathcal{V}(\phi )}~\partial _{\phi }\mathcal{N}=\frac{1}{\mathcal{V}(\phi )}~\mathcal{N}_{,\phi },\nonumber \\ \mathcal{N}_{,\Psi \Psi }= & {} \left[ \frac{1}{\mathcal{V}^2(\phi )}~ \partial ^2_{\phi }-\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}\partial _{\phi }\right] \mathcal{N}\nonumber \\= & {} \left[ \frac{1}{\mathcal{V}^2(\phi )}~\mathcal{N}_{,\phi \phi }- \frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}~\mathcal{N}_{,\phi }\right] ,\end{aligned}$$

(10.54)

$$\begin{aligned} \mathcal{N}_{,\phi \Psi }= & {} \left[ \frac{1}{\mathcal{V}(\phi )}~\partial ^2_{\phi }-\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^2(\phi )}~\partial _{\phi }\right] \mathcal{N}\nonumber \\= & {} \left[ \frac{1}{\mathcal{V}(\phi )}~\mathcal{N}_{,\phi \phi }-\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^2(\phi )}~\mathcal{N}_{,\phi }\right] ,\nonumber \\ \mathcal{N}_{,\Psi \phi }= & {} \frac{1}{\mathcal{V}(\phi )}~\partial ^2_{\phi }~\mathcal{N}=\frac{1}{\mathcal{V}(\phi )}~\mathcal{N}_{,\phi \phi },\end{aligned}$$

(10.55)

$$\begin{aligned} \mathcal{N}_{,\Psi \Psi \Psi }= & {} \left[ \frac{1}{\mathcal{V}^3(\phi )}~\partial ^3_{\phi }-3\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^4(\phi )}~\partial ^2_{\phi }+3\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^5(\phi )}~\partial _{\phi }\right] \mathcal{N}\nonumber \\= & {} \left[ \frac{1}{\mathcal{V}^3(\phi )}~\mathcal{N}_{,\phi \phi \phi }-3\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^4(\phi )}~\mathcal{N}_{,\phi \phi }+3\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^5(\phi )}~\mathcal{N}_{,\phi }\right] ,\nonumber \\ \end{aligned}$$

(10.56)

$$\begin{aligned} \mathcal{N}_{,\phi \phi \Psi }= & {} \left[ \frac{1}{\mathcal{V}(\phi )}~\partial ^3_{\phi }-2\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^2(\phi )}~\partial ^2_{\phi }\right. \nonumber \\&\left. -\left( \frac{\mathcal{V}^{\prime \prime }(\phi )}{\mathcal{V}^2(\phi )}-2\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^3(\phi )}\right) \partial _{\phi }\right] ~\mathcal{N},\nonumber \\= & {} \left[ \frac{1}{\mathcal{V}(\phi )}~\mathcal{N}_{,\phi \phi \phi }-2\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^2(\phi )}~\mathcal{N}_{,\phi \phi }\right. \nonumber \\&\left. -\left( \frac{\mathcal{V}^{\prime \prime }(\phi )}{\mathcal{V}^2(\phi )}-2\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^3(\phi )}\right) ~\mathcal{N}_{,\phi }\right] ,\end{aligned}$$

(10.57)

$$\begin{aligned} \mathcal{N}_{,\phi \Psi \phi }= & {} \left[ \frac{1}{\mathcal{V}(\phi )}~\partial ^3_{\phi }-\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^2(\phi )}~\partial ^2_{\phi }\right] ~\mathcal{N}\nonumber \\= & {} \left[ \frac{1}{\mathcal{V}(\phi )}~\mathcal{N}_{,\phi \phi \phi }-\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^2(\phi )}~\mathcal{N}_{,\phi \phi }\right] ,\end{aligned}$$

(10.58)

$$\begin{aligned} N_{,\Psi \phi \phi }= & {} \frac{1}{\mathcal{V}(\phi )}~\partial ^3_{\phi }~\mathcal{N}=\frac{1}{\mathcal{V}(\phi )}~\mathcal{N}_{,\phi \phi \phi }, \end{aligned}$$

(10.59)

$$\begin{aligned} \mathcal{N}_{,\phi \Psi \Psi }= & {} \left[ \frac{1}{\mathcal{V}^2(\phi )}~\partial ^{3}_{\phi }-3\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}~\partial ^{2}_{\phi }+3~\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^4(\phi )}~\partial _{\phi }\right] \mathcal{N}\nonumber \\= & {} \left[ \frac{1}{\mathcal{V}^2(\phi )}~\mathcal{N}_{,\phi \phi \phi }-3\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}~\mathcal{N}_{,\phi \phi }\right. \nonumber \\&\left. +3~\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^4(\phi )}~\mathcal{N}_{,\phi }\right] , \end{aligned}$$

(10.60)

$$\begin{aligned} \mathcal{N}_{,\Psi \phi \Psi }= & {} \left[ \frac{1}{\mathcal{V}^2(\phi )}~\partial ^{3}_{\phi }-2\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}~\partial ^{2}_{\phi }+2~\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^4(\phi )}~\partial _{\phi }\right] \mathcal{N}\nonumber \\= & {} \left[ \frac{1}{\mathcal{V}^2(\phi )}~\mathcal{N}_{,\phi \phi \phi }-2\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}~\mathcal{N}_{,\phi \phi }\right. \nonumber \\&\left. +2~\frac{\mathcal{V}^{'2}(\phi )}{\mathcal{V}^4(\phi )}~\mathcal{N}_{,\phi }\right] ,\end{aligned}$$

(10.61)

$$\begin{aligned} \mathcal{N}_{,\Psi \Psi \phi }= & {} \left[ \frac{1}{\mathcal{V}^2(\phi )}~\partial ^{3}_{\phi }-\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}~\partial ^{2}_{\phi }\right] \nonumber \\ \mathcal{N}= & {} \left[ \frac{1}{\mathcal{V}^2(\phi )}~\mathcal{N}_{,\phi \phi \phi }-\frac{\mathcal{V}^{\prime }(\phi )}{\mathcal{V}^3(\phi )}~\mathcal{N}_{,\phi \phi }\right] . \end{aligned}$$

(10.62)

1.3.2 Second-order perturbative solution with various source

If we neglect the quadratic slow-roll corrections then the solution of Eq. (8.40) takes the following form for all different cases considered here:

$$\begin{aligned}&\text {For~Case~I}{:}\nonumber \\&\Delta _2=\mathbf{D}_{4}+\frac{1}{27H^3} \left[ \frac{27\phi _* H \mathrm{e}^{H\mathcal{Y}t}}{\mathcal{Y}^2(3+\mathcal{Y})^3}\{-\mathcal{Y}(3+\mathcal{Y})^2\right. \nonumber \\&\quad \times \,(4\Lambda _c \phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y}))\nonumber \\&\quad +\,\epsilon _H(4\Lambda _c \phi ^3_{\mathrm{L}}(-18+\mathcal{Y}(3+\mathcal{Y})(-6+Ht(3+2\mathcal{Y})))\nonumber \\&\quad +\,H^2\mathcal{Y}(3+\mathcal{Y})(-9+\mathcal{Y}(3+\mathcal{Y})(-2+Ht(3+2\mathcal{Y}))))\}\nonumber \\&\quad +\,9H^2\Lambda _c\phi ^3_{\mathrm{L}} t(\phi _{\mathrm{L}}+4\mathbf{D}_2)\nonumber \\&\quad \left. +\,\mathrm{e}^{-3Ht}(4\Lambda _c \phi ^3_{\mathrm{L}}(1+3Ht)\mathbf{D}_1-9H^2\mathbf{D}_3)\right] .\end{aligned}$$

(10.63)

$$\begin{aligned}&\text {For Case II}{:}\nonumber \\&\Delta _2=\mathbf{D}_{4}+\frac{1}{27H^3}\left[ \frac{27\phi _* H \mathrm{e}^{H\mathcal{Y}t}}{\mathcal{Y}^2(3+\mathcal{Y})^3}\right. \nonumber \\&\quad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( -4\Lambda _c \phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H\left( -4\Lambda _c \phi ^3_{\mathrm{L}}(-18+\mathcal{Y}(3+\mathcal{Y})(-6+Ht(3+2\mathcal{Y})))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. +H^2\mathcal{Y}(3+\mathcal{Y})(-9+\mathcal{Y}(3+\mathcal{Y})(-2+Ht(3+2\mathcal{Y})))\right) \right\} \right. \nonumber \\&\quad \left. +9H^2 t\left( \beta -\Lambda _c\phi ^3_{\mathrm{L}} \left( \phi _{\mathrm{L}}+4\mathbf{D}_2\right) \right) \right. \nonumber \\&\quad \left. -\mathrm{e}^{-3Ht}\left( 4\Lambda _c \phi ^3_{\mathrm{L}}(1+3Ht)\mathbf{D}_1+9H^2\mathbf{D}_3\right) \right] .\end{aligned}$$

(10.64)

$$\begin{aligned}&\text {For Case II}+\text {Choice I(v1)}{:}\nonumber \\&\Delta _2=\mathbf{D}_{4}+\frac{1}{27H^3}\left[ \frac{27\phi _* H \mathrm{e}^{H\mathcal{Y}t}}{\mathcal{Y}^2(3+\mathcal{Y})^3}\right. \nonumber \\&\quad \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( -4\Lambda _c \phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H\left( -4\Lambda _c \phi ^3_{\mathrm{L}}(-18+\mathcal{Y}(3+\mathcal{Y})(-6+Ht(3+2\mathcal{Y})))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. +H^2\mathcal{Y}(3+\mathcal{Y})(-9+\mathcal{Y}(3+\mathcal{Y})(-2+Ht(3+2\mathcal{Y})))\right) \right\} \right. \nonumber \\&\quad \left. +9H^2t\left( \beta +\Lambda _c\phi ^4_V-\Lambda _c\phi ^3_{\mathrm{L}} \left( \phi _{\mathrm{L}}+4\mathbf{D}_2\right) \right) \right. \nonumber \\&\quad \left. -\mathrm{e}^{-3Ht}\left( 4\Lambda _c \phi ^3_{\mathrm{L}}(1+3Ht)\mathbf{D}_1+9H^2\mathbf{D}_3\right) \right] . \end{aligned}$$

(10.65)

$$\begin{aligned}&\text {For Case II}+\text {Choice~I(v2)}{:}\nonumber \\&\Delta _2=\mathbf{D}_{4}+\frac{1}{27H^3}\left[ \frac{27\phi _* H \mathrm{e}^{H\mathcal{Y}t}}{\mathcal{Y}^2(3+\mathcal{Y})^3}\right. \nonumber \\&\quad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( 4\Lambda _c \phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H\left( 4\Lambda _c \phi ^3_{\mathrm{L}}(-18+\mathcal{Y}(3+\mathcal{Y})(-6+Ht(3+2\mathcal{Y})))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. +H^2\mathcal{Y}(3+\mathcal{Y})(-9+\mathcal{Y}(3+\mathcal{Y})(-2+Ht(3+2\mathcal{Y})))\right) \right\} \right. \nonumber \\&\quad \left. +9H^2 t\left( \beta -\Lambda _c\phi ^4_V+\Lambda _c\phi ^3_{\mathrm{L}} \left( \phi _{\mathrm{L}}+4\mathbf{D}_2\right) \right) \right. \nonumber \\&\quad \left. +\mathrm{e}^{-3Ht}\left( 4\Lambda _c \phi ^3_{\mathrm{L}}(1+3Ht)\mathbf{D}_1-9H^2\mathbf{D}_3\right) \right] .\end{aligned}$$

(10.66)

$$\begin{aligned}&\text {For Case II}+\text {Choice~II(v1)}{:}\nonumber \\&\Delta _2=\mathbf{D}_{4}+\frac{1}{54H^3}\left[ \frac{54\phi _* H \mathrm{e}^{H\mathcal{Y}t}}{\mathcal{Y}^2(3+\mathcal{Y})^3} \right. \nonumber \\&\quad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( M_c\phi _{\mathrm{L}}-4\Lambda _c\phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H \left( (4\Lambda _c \phi ^3_{\mathrm{L}}-M_c\phi _{\mathrm{L}} )(18-\mathcal{Y}(3+\mathcal{Y})(-6+Ht(3+2\mathcal{Y})))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. +H^2\mathcal{Y}(3+\mathcal{Y})(-9+\mathcal{Y}(3+\mathcal{Y})(-2+Ht(3+2\mathcal{Y})))\right) \right\} \right. \nonumber \\&\quad \left. +9H^2t\left( 2\beta +\phi _{\mathrm{L}}(M_c(\phi _{\mathrm{L}}+2\mathbf{D}_2)-\Lambda _c\phi ^2_{\mathrm{L}}(\phi _{\mathrm{L}}+4\mathbf{D}_2))\right) \right. \nonumber \\&\quad \left. +\mathrm{e}^{-3Ht}\left( 2\phi _{\mathrm{L}}(M_c-4\Lambda _c\phi ^2_{\mathrm{L}})(1+3Ht)\mathbf{D}_1-18H^2\mathbf{D}_3\right) \right] .\nonumber \\ \end{aligned}$$

(10.67)

$$\begin{aligned}&\text {For Case II}+\text {Choice~II(v2)}{:}\nonumber \\&\Delta _2=\mathbf{D}_{4}+\frac{1}{54H^3}\left[ \frac{54\phi _* H \mathrm{e}^{H\mathcal{Y}t}}{\mathcal{Y}^2(3+\mathcal{Y})^3}\right. \nonumber \\&\quad \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( -M_c\phi _{\mathrm{L}}+4\Lambda _c\phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H \left( (-4\Lambda _c \phi ^3_{\mathrm{L}}+M_c\phi _{\mathrm{L}} )(18-\mathcal{Y}(3+\mathcal{Y})(-6+Ht(3+2\mathcal{Y})))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. +H^2\mathcal{Y}(3+\mathcal{Y})(-9+\mathcal{Y}(3+\mathcal{Y})(-2+Ht(3+2\mathcal{Y})))\right) \right\} \right. \nonumber \\&\quad \left. +9H^2t\left( 2\beta +\phi _{\mathrm{L}}(-M_c(\phi _{\mathrm{L}}+2\mathbf{D}_2)+\Lambda _c\phi ^2_{\mathrm{L}}(\phi _{\mathrm{L}}+4\mathbf{D}_2))\right) \right. \nonumber \\&\quad \left. -\mathrm{e}^{-3Ht}\left( 2\phi _{\mathrm{L}}(M_c-4\Lambda _c\phi ^2_{\mathrm{L}})(1+3Ht)\mathbf{D}_1+18H^2\mathbf{D}_3\right) \right] .\end{aligned}$$

(10.68)

$$\begin{aligned}&\text {For Case III}{:}\nonumber \\&\Delta _2=\mathbf{D}_{4}+\frac{1}{27H^3\phi _{\mathrm{L}}}\left[ \frac{27\phi _* H \mathrm{e}^{H\mathcal{Y}t}}{\mathcal{Y}^2(3+\mathcal{Y})^3} \right. \nonumber \\&\quad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( \Gamma _{\xi }\Theta _{\xi }+H^2\phi _{\mathrm{L}}\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H\left( \Gamma _{\xi }\Theta _{\xi }(-18+\mathcal{Y}(3+\mathcal{Y})(-6+Ht(3+2\mathcal{Y})))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. +H^2\phi _{\mathrm{L}}\mathcal{Y}(3+\mathcal{Y})(-9+\mathcal{Y}(3+\mathcal{Y})(-2+Ht(3+2\mathcal{Y})))\right) \right\} \right. \nonumber \\&\quad \left. +9H^2t\left( \phi _{\mathrm{L}}(\beta +\Gamma _{\xi })+\Gamma _{\xi }\Theta _{\xi }\mathbf{D}_2\right) \right. \nonumber \\&\quad \left. +\mathrm{e}^{-3Ht}\left( \Gamma _{\xi }\Theta _{\xi }(1+3Ht)\mathbf{D}_1-9H^2\phi _{\mathrm{L}} \mathbf{D}_3\right) \right] . \end{aligned}$$

(10.69)

Here $\mathbf{D}_{3}$ and $\mathbf{D}_{4}$ are dimensionful arbitrary integration constants which can be determined by imposing the appropriate boundary condition.

1.3.3 Expressions for perturbative solutions in final hypersurface

Neglecting the contribution from the quadratic slow-roll term and taking up to linear-order term in slow-roll we get the following result:

$$\begin{aligned} \Delta _{1}(\mathcal{N}=0)= & {} \mathbf{D}_{2}-\frac{1}{3H}\mathbf{D}_{1}+\frac{1}{\mathcal{Y}(3+\mathcal{Y})^2}\phi _* \left[ -\mathcal{Y}(3+\mathcal{Y})^2\right. \nonumber \\&\left. -2\epsilon _{H}\left( -9+\mathcal{Y}(3+\mathcal{Y})\right) \right] . \end{aligned}$$

(10.70)

Similarly if we neglect the quadratic slow-roll corrections then the solution of $\Delta _{2}(N=0)$ takes the following form for all different cases considered here:

$$\begin{aligned}&\text {For Case I}{:}\nonumber \\&\Delta _2(\mathcal{N}=0)=\mathbf{D}_{4}+\frac{1}{27H^3}\left[ \frac{27\phi _* H}{\mathcal{Y}^2(3+\mathcal{Y})^3} \right. \nonumber \\&\quad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( 4\Lambda _c \phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H\left( -4\Lambda _c \phi ^3_{\mathrm{L}}(18+6\mathcal{Y}(3+\mathcal{Y}))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. -H^2\mathcal{Y}(3+\mathcal{Y})(9+2\mathcal{Y}(3+\mathcal{Y}))\right) \right\} \right. \nonumber \\&\quad \left. +\left( 4\Lambda _c \phi ^3_{\mathrm{L}}\mathbf{D}_1-9H^2\mathbf{D}_3\right) \phantom {\frac{27\phi _* H}{\mathcal{Y}^2(3+\mathcal{Y})^3}}\right] .\end{aligned}$$

(10.71)

$$\begin{aligned}&\text {For Case II}{:}\nonumber \\&\Delta _2(\mathcal{N}=0)=\mathbf{D}_{4}+\frac{1}{27H^3}\left[ \frac{27\phi _* H }{\mathcal{Y}^2(3+\mathcal{Y})^3}\right. \nonumber \\&\quad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( -4\Lambda _c \phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H\left( 4\Lambda _c \phi ^3_{\mathrm{L}}(18+6\mathcal{Y}(3+\mathcal{Y}))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. -H^2\mathcal{Y}(3+\mathcal{Y})(9+2\mathcal{Y}(3+\mathcal{Y}))\right) \right\} \right. \nonumber \\&\quad \left. -\left( 4\Lambda _c \phi ^3_{\mathrm{L}}\mathbf{D}_1+9H^2\mathbf{D}_3\right) \right] .\end{aligned}$$

(10.72)

$$\begin{aligned}&\text {For Case II}+\text {Choice~I(v1)}{:}\nonumber \\&\Delta _2(\mathcal{N}=0)=\mathbf{D}_{4}+\frac{1}{27H^3}\left[ \frac{27\phi _* H }{\mathcal{Y}^2(3+\mathcal{Y})^3}\right. \nonumber \\&\quad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( -4\Lambda _c \phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H\left( 4\Lambda _c \phi ^3_{\mathrm{L}}(18+6\mathcal{Y}(3+\mathcal{Y}))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. -H^2\mathcal{Y}(3+\mathcal{Y})(9+2\mathcal{Y}(3+\mathcal{Y}))\right) \right\} \right. \nonumber \\&\quad \left. -\left( 4\Lambda _c \phi ^3_{\mathrm{L}}\mathbf{D}_1+9H^2\mathbf{D}_3\right) \right] .\end{aligned}$$

(10.73)

$$\begin{aligned}&\text {For Case II}+\text {Choice~I(v2)}{:}\nonumber \\&\Delta _2(\mathcal{N}=0)=\mathbf{D}_{4}+\frac{1}{27H^3}\left[ \frac{27\phi _* H }{\mathcal{Y}^2(3+\mathcal{Y})^3}\right. \nonumber \\&\quad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( 4\Lambda _c \phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H\left( -4\Lambda _c \phi ^3_{\mathrm{L}}(18+6\mathcal{Y}(3+\mathcal{Y}))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. -H^2\mathcal{Y}(3+\mathcal{Y})(9+2\mathcal{Y}(3+\mathcal{Y}))\right) \right\} \right. \nonumber \\&\quad \left. +\left( 4\Lambda _c \phi ^3_{\mathrm{L}}\mathbf{D}_1-9H^2\mathbf{D}_3\right) \right] .\end{aligned}$$

(10.74)

$$\begin{aligned}&\text {For Case II}+\text {Choice II(v1)}{:}\nonumber \\&\Delta _2(\mathcal{N}=0)=\mathbf{D}_{4}+\frac{1}{54H^3}\left[ \frac{54\phi _* H }{\mathcal{Y}^2(3+\mathcal{Y})^3}\right. \nonumber \\&\quad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( M_c\phi _{\mathrm{L}}-4\Lambda _c\phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H \left( (4\Lambda _c \phi ^3_{\mathrm{L}}-M_c\phi _{\mathrm{L}} )(18+6\mathcal{Y}(3+\mathcal{Y}))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. -H^2\mathcal{Y}(3+\mathcal{Y})(9+2\mathcal{Y}(3+\mathcal{Y})))\right) \right\} \right. \nonumber \\&\quad \left. +\left( 2\phi _{\mathrm{L}}(M_c-4\Lambda _c\phi ^2_{\mathrm{L}})\mathbf{D}_1-18H^2\mathbf{D}_3\right) \right] .\end{aligned}$$

(10.75)

$$\begin{aligned}&\text {For Case II}+\text {Choice II(v2)}{:}\nonumber \\&\Delta _2(\mathcal{N}=0)=\mathbf{D}_{4}+\frac{1}{54H^3}\left[ \frac{54\phi _* H }{\mathcal{Y}^2(3+\mathcal{Y})^3}\right. \nonumber \\&\quad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( -M_c\phi _{\mathrm{L}}+4\Lambda _c\phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H \left( (-4\Lambda _c \phi ^3_{\mathrm{L}}+M_c\phi _{\mathrm{L}} )(18+6\mathcal{Y}(3+\mathcal{Y}))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. -H^2\mathcal{Y}(3+\mathcal{Y})(9+2\mathcal{Y}(3+\mathcal{Y}))\right) \right\} \right. \nonumber \\&\quad \left. -\left( 2\phi _{\mathrm{L}}(M_c-4\Lambda _c\phi ^2_{\mathrm{L}})\mathbf{D}_1+18H^2\mathbf{D}_3\right) \right] . \end{aligned}$$

(10.76)

$$\begin{aligned}&\text {For Case III}{:}\nonumber \\&\Delta _2(\mathcal{N}=0)=\mathbf{D}_{4}+\frac{1}{27H^3\phi _{\mathrm{L}}}\left[ \frac{27\phi _* H }{\mathcal{Y}^2(3+\mathcal{Y})^3}\right. \nonumber \\&\quad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( \Gamma _{\xi }\Theta _{\xi }+H^2\phi _{\mathrm{L}}\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H\left( -\Gamma _{\xi }\Theta _{\xi }(18+6\mathcal{Y}(3+\mathcal{Y}))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. -H^2\phi _{\mathrm{L}}\mathcal{Y}(3+\mathcal{Y})(9+2\mathcal{Y}(3+\mathcal{Y}))\right) \right\} \right. \nonumber \\&\quad \left. +\left( \Gamma _{\xi }\Theta _{\xi }{} \mathbf{D}_1-9H^2\phi _{\mathrm{L}} \mathbf{D}_3\right) \right] . \end{aligned}$$

(10.77)

1.3.4 Shift in the inflaton field due to $\delta \mathcal{N}$

Analytical expression for the shift in the inflaton field from linear-order and second-order cosmological perturbation theory can be written up to considering the contributions from the first-order slow-roll contribution as

$$\begin{aligned}&\delta \phi _{1}(\mathcal{N}=0)=\delta \phi _{1*}=\phi _* \hat{\Delta }_{1}(\mathcal{N}=0)=\phi _*\hat{\mathbf{D}}_{2}\nonumber \\&\quad -\,\frac{\phi _*}{3H}\hat{\mathbf{D}}_{1}+\frac{\phi _*}{\mathcal{Y}(3+\mathcal{Y})^2}\left[ -\mathcal{Y}(3+\mathcal{Y})^2\right. \nonumber \\&\quad \left. +\,\epsilon _{H}\left( -9+\mathcal{Y}(3+\mathcal{Y})\left\{ -2+H(3+2\mathcal{Y})t\right\} \right) \right] .\end{aligned}$$

(10.78)

$$\begin{aligned}&\text {For Case I}{:}\nonumber \\&\delta \phi _{2}(\mathcal{N}=0)=\delta \phi _{2*}=\phi _* \hat{\Delta }_{2}(\mathcal{N}=0)\nonumber \\&\quad =\phi _*\hat{\mathbf{D}}_{4}+\frac{\phi _*}{27H^3}\left[ \frac{27H}{\mathcal{Y}^2(3+\mathcal{Y})^3} \right. \nonumber \\&\qquad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( 4\Lambda _c \phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\qquad \left. \left. +\epsilon _H\left( -4\Lambda _c \phi ^3_{\mathrm{L}}(18+6\mathcal{Y}(3+\mathcal{Y}))\right. \right. \right. \nonumber \\&\qquad \left. \left. \left. -H^2\mathcal{Y}(3+\mathcal{Y})(9+2\mathcal{Y}(3+\mathcal{Y}))\right) \right\} \right. \nonumber \\&\quad \left. +\left( 4\Lambda _c \phi ^3_{\mathrm{L}}\hat{\mathbf{D}}_1-9H^2\hat{\mathbf{D}}_3\right) \right] .\end{aligned}$$

(10.79)

$$\begin{aligned}&\text {For Case II}{:}\nonumber \\&\delta \phi _{2}(\mathcal{N}=0)=\delta \phi _{2*}=\phi _* \hat{\Delta }_{2}(\mathcal{N}=0)\nonumber \\&\quad =\phi _*\hat{\mathbf{D}}_{4}+\frac{\phi _*}{27H^3}\left[ \frac{27H }{\mathcal{Y}^2(3+\mathcal{Y})^3}\right. \nonumber \\&\qquad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( -4\Lambda _c \phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\qquad \left. \left. +\epsilon _H\left( 4\Lambda _c \phi ^3_{\mathrm{L}}(18+6\mathcal{Y}(3+\mathcal{Y}))\right. \right. \right. \nonumber \\&\qquad \left. \left. \left. -H^2\mathcal{Y}(3+\mathcal{Y})(9+2\mathcal{Y}(3+\mathcal{Y}))\right) \right\} \right. \nonumber \\&\quad \left. -\left( 4\Lambda _c \phi ^3_{\mathrm{L}}\hat{\mathbf{D}}_1+9H^2\hat{\mathbf{D}}_3\right) \right] . \end{aligned}$$

(10.80)

$$\begin{aligned}&\text {For Case II}+\text {Choice~I(v1)}{:}\nonumber \\&\delta \phi _{2}(\mathcal{N}=0)=\delta \phi _{2*}=\phi _* \hat{\Delta }_{2}(\mathcal{N}=0)\nonumber \\&\quad =\phi _*\hat{\mathbf{D}}_{4}+\frac{\phi _*}{27H^3}\left[ \frac{27H }{\mathcal{Y}^2(3+\mathcal{Y})^3}\right. \nonumber \\&\qquad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( -4\Lambda _c \phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H\left( 4\Lambda _c \phi ^3_{\mathrm{L}}(18+6\mathcal{Y}(3+\mathcal{Y}))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. -H^2\mathcal{Y}(3+\mathcal{Y})(9+2\mathcal{Y}(3+\mathcal{Y}))\right) \right\} \right. \nonumber \\&\quad \left. -\left( 4\Lambda _c \phi ^3_{\mathrm{L}}\hat{\mathbf{D}}_1+9H^2\hat{\mathbf{D}}_3\right) \right] .\end{aligned}$$

(10.81)

$$\begin{aligned}&\text {For Case II}+\text {Choice~I(v2)}{:}\nonumber \\&\delta \phi _{2}(\mathcal{N}=0)=\delta \phi _{2*}=\phi _* \hat{\Delta }_{2}(\mathcal{N}=0)\nonumber \\&\quad =\phi _*\hat{\mathbf{D}}_{4}+\frac{\phi _*}{27H^3}\left[ \frac{27H }{\mathcal{Y}^2(3+\mathcal{Y})^3}\right. \nonumber \\&\qquad \times \left. \left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( 4\Lambda _c \phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\quad \left. \left. +\epsilon _H\left( -4\Lambda _c \phi ^3_{\mathrm{L}}(18+6\mathcal{Y}(3+\mathcal{Y}))\right. \right. \right. \nonumber \\&\quad \left. \left. \left. -H^2\mathcal{Y}(3+\mathcal{Y})(9+2\mathcal{Y}(3+\mathcal{Y}))\right) \right\} \right. \nonumber \\&\quad \left. +\left( 4\Lambda _c \phi ^3_{\mathrm{L}}\hat{\mathbf{D}}_1-9H^2\hat{\mathbf{D}}_3\right) \right] . \end{aligned}$$

(10.82)

$$\begin{aligned}&\text {For Case II}+\text {Choice~II(v1)}{:}\nonumber \\&\Delta _2(\mathcal{N}=0)=\phi _*\hat{\mathbf{D}}_{4}+\frac{\phi _*}{54H^3}\left[ \frac{54 H }{\mathcal{Y}^2(3+\mathcal{Y})^3}\left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( M_c\phi _{\mathrm{L}}-4\Lambda _c\phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\qquad \left. \left. +\epsilon _H \left( (4\Lambda _c \phi ^3_{\mathrm{L}}-M_c\phi _{\mathrm{L}} )(18+6\mathcal{Y}(3+\mathcal{Y}))-H^2\mathcal{Y}(3+\mathcal{Y})(9+2\mathcal{Y}(3+\mathcal{Y})))\right) \right\} +\left( 2\phi _{\mathrm{L}}(M_c-4\Lambda _c\phi ^2_{\mathrm{L}})\hat{\mathbf{D}}_1-18H^2\hat{\mathbf{D}}_3\right) \right] . \end{aligned}$$

(10.83)

$$\begin{aligned}&\text {For Case II}+\text {Choice II(v2)}{:}\nonumber \\&\delta \phi _{2}(\mathcal{N}=0)=\delta \phi _{2*}=\phi _* \hat{\Delta }_{2}(\mathcal{N}=0)=\phi _*\hat{\mathbf{D}}_{4}+\frac{\phi _*}{54H^3}\left[ \frac{54 H }{\mathcal{Y}^2(3+\mathcal{Y})^3}\left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( -M_c\phi _{\mathrm{L}}+4\Lambda _c\phi ^3_{\mathrm{L}}+H^2\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\qquad \left. \left. +\epsilon _H \left( (-4\Lambda _c \phi ^3_{\mathrm{L}}+M_c\phi _{\mathrm{L}} )(18+6\mathcal{Y}(3+\mathcal{Y}))-H^2\mathcal{Y}(3+\mathcal{Y})(9+2\mathcal{Y}(3+\mathcal{Y}))\right) \right\} -\left( 2\phi _{\mathrm{L}}(M_c-4\Lambda _c\phi ^2_{\mathrm{L}})\hat{\mathbf{D}}_1+18H^2\hat{\mathbf{D}}_3\right) \right] .\end{aligned}$$

(10.84)

$$\begin{aligned}&\text {For~Case~III}{:}\nonumber \\&\delta \phi _{2}(\mathcal{N}=0)=\delta \phi _{2*}=\phi _* \hat{\Delta }_{2}(\mathcal{N}=0) =\phi _*\hat{\mathbf{D}}_{4}+\frac{\phi _*}{27H^3\phi _{\mathrm{L}}}\left[ \frac{27 H }{\mathcal{Y}^2(3+\mathcal{Y})^3}\left\{ -\mathcal{Y}(3+\mathcal{Y})^2\left( \Gamma _{\xi }\Theta _{\xi }+H^2\phi _{\mathrm{L}}\mathcal{Y}(3+\mathcal{Y})\right) \right. \right. \nonumber \\&\qquad \times \left. \left. +\epsilon _H\left( -\Gamma _{\xi }\Theta _{\xi }(18+6\mathcal{Y}(3+\mathcal{Y})) -H^2\phi _{\mathrm{L}}\mathcal{Y}(3+\mathcal{Y})(9+2\mathcal{Y}(3+\mathcal{Y}))\right) \right\} +\left( \Gamma _{\xi }\Theta _{\xi }\hat{\mathbf{D}}_1-9H^2\phi _{\mathrm{L}} \hat{\mathbf{D}}_3\right) \right] . \end{aligned}$$

(10.85)

1.3.5 Various useful constants for $\delta \mathcal{N}$

For the derived effective potentials $\mathcal{B}(\phi _*)$ and $\mathcal{C}(\phi _*)$ can be recast as

$$ \begin{aligned} \mathcal{B}(\phi _*) =\left\{ \begin{array}{ll} \frac{3}{\mathcal{Y}\phi ^2_*}&{}\quad \text {for Case I } \& \text { II}\\ \frac{1}{\mathcal{Y} \phi ^2_*}\frac{\left( 3+\frac{\phi ^4_V}{\phi ^4_*}\right) }{\left( 1-\frac{\phi ^4_V}{\phi ^4_*}\right) } &{}\quad \text {for Case II}+\text {Choice~I}(\text {v}1 \& \text {v}2)\\ \frac{1}{\mathcal{Y} \phi ^2_*}\left\{ 3-\frac{2\lambda m^2_c \phi ^2_*}{(m^2_c-\lambda \phi ^2_*)^2\left( 1-\frac{m^2_c}{(m^2_c-\lambda \phi ^2_*)}\right) }\right\} &{}\quad \text {for Case II}+\text {Choice~II}(\text {v}1 \& \text {v}2)\\ \frac{2}{\mathcal{Y}\phi ^2_*}\left\{ 2+\frac{1+\xi (3\phi ^2_*-\phi ^2_V) -\frac{\phi ^2_V}{\phi ^2_*}}{1+\xi (\phi ^2_*-\phi ^2_V)+ \frac{\phi ^2_V}{\phi ^2_*}}\right\} &{}\quad \text {for Case II}+\text {Choice~III}, \end{array} \right. \end{aligned}$$

(10.86)

$$ \begin{aligned} \mathcal{C}(\phi _*)\approx \left\{ \begin{array}{ll} -\frac{19}{3}\frac{1}{\mathcal{Y} \phi ^3_*} &{}\quad \text {for Case I } \& \text {II}\\ -\frac{1}{\mathcal{Y} \phi ^3_*}\left\{ \frac{8}{3}+\frac{2 \left( 1+2\frac{\phi ^4_V}{\phi ^4_*}\right) }{\left( 1- \frac{\phi ^4_V}{\phi ^4_*}\right) }-\frac{5}{3} \frac{\left( 1+3\frac{\phi ^4_V}{\phi ^4_*}\right) ^2}{\left( 1-\frac{\phi ^4_V}{\phi ^4_*}\right) ^2}\right\} &{} \quad \text {for Case II}+\text {Choice I}(\text {v}1 \& \text {v}2)\\ -\frac{1}{\mathcal{Y}\phi ^3_*}\left\{ \frac{8}{3}+ \frac{2\left( 1-\frac{m^2_c}{m^2_c-\lambda \phi ^2_*}-\frac{2\lambda m^2_c\phi ^2_*}{(m^2_c-\lambda \phi ^2_*)^2}\right) }{\left( 1-\frac{m^2_c}{m^2_c-\lambda \phi ^2_*}\right) }\right. \\ \left. +\left( \frac{5}{3}\frac{\left( 1-\frac{m^2_c}{m^2_c- \lambda \phi ^2_*}-\frac{2\lambda m^2_c\phi ^2_*}{(m^2_c-\lambda \phi ^2_*)^2}\right) ^2}{\left( 1-\frac{m^2_c}{m^2_c-\lambda \phi ^2_*}\right) ^2} +\frac{1}{6}\frac{\left( \frac{6m^2_c\lambda \phi _*}{(m^2_c-\lambda \phi ^2_*)^2}+\frac{8\lambda ^2 m^2_c\phi ^3_*}{(m^2_c-\lambda \phi ^2_*)^3}\right) }{\left( 1-\frac{m^2_c}{m^2_c-\lambda \phi ^2_*}\right) }\right) \right\} &{}\quad \text {for Case II}+\text {Choice II}(\text {v}1 \& \text {v}2)\\ -\frac{1}{\mathcal{Y} \phi ^3_*}\left\{ \frac{8}{3}+\frac{2\left( 1+\xi (3\phi ^2_*-\phi ^2_V)-\frac{\phi ^2_V}{\phi ^2_*}\right) }{1+\xi (\phi ^2_*-\phi ^2_V)+\frac{\phi ^2_V}{\phi ^2_*}}\right. \\ \left. +\left( \frac{5}{3}\frac{\left( 1+\xi (3\phi ^2_*-\phi ^2_V)-\frac{\phi ^2_V}{\phi ^2_*}\right) ^2}{(1+\xi (\phi ^2_*-\phi ^2_V)+\frac{\phi ^2_V}{\phi ^2_*})^2} -\frac{1}{6}\frac{\left( 6\xi \phi ^2_*+2\frac{\phi ^2_V}{\phi ^2_*}\right) }{\left( 1+\xi (\phi ^2_*-\phi ^2_V)+\frac{\phi ^2_V}{\phi ^2_*}\right) }\right) \right\} &{}\quad \text {for Case II}+\text {Choice III}. \end{array} \right. \end{aligned}$$

(10.87)

Additionally the constants $\mathcal{G}_{1}(\phi _*)$ and $\mathcal{G}_{2}(\phi _*)$, as appearing in the expression for $f^{\mathrm{{loc}}}_{\mathrm{NL}}$, are defined as

$$ \begin{aligned} \mathcal{G}_{1}(\phi _*)=\left\{ \begin{array}{ll} \left( 1+\frac{6M^2_p}{81\phi ^2_*}\right) ^{-2} \left( 1+\frac{12M^2_p}{81\phi ^2_*}+\frac{36M^4_p}{6561\phi ^4_*}\right) &{}\quad \text {for Case I}\\ \left( 1+\frac{6M^2_p}{\phi ^2_*}\right) ^{-2} \left( 1+\frac{12M^2_p}{\phi ^2_*}+\frac{36M^4_p}{\phi ^4_*}\right) &{} \quad \text {for Case II}\\ \left( 1+\frac{6M^2_p}{\phi ^2_*\left( 1-\frac{\phi ^4_V}{\phi ^4_*}\right) ^2}\right) ^{-2} \left( 1+\frac{12M^2_p}{\phi ^2_*\left( 1-\frac{\phi ^4_V}{\phi ^4_*}\right) ^2}+\frac{36M^4_p}{\phi ^4_*\left( 1-\frac{\phi ^4_V}{\phi ^4_*}\right) ^4}\right) &{}\quad \text {for Case II}+\text {Choice~I}(\text {v}1 \& \text {v}2)\\ \left( 1+\frac{6M^2_p}{\phi ^2_*\left( \frac{m^2_c}{m^2_c-\lambda \phi ^2_*}\right) ^2}\right) ^{-2} \left( 1+\frac{12M^2_p}{\phi ^2_*\left( 1-\frac{m^2_c}{m^2_c-\lambda \phi ^2_*}\right) ^2}+\frac{36M^4_p}{\phi ^4_*\left( 1-\frac{m^2_c}{m^2_c-\lambda \phi ^2_*}\right) ^4}\right) &{}\text {for Case II}+\text {Choice~II}(\text {v}1 \& \text {v}2)\\ \left( 1+\frac{6M^2_p}{\phi ^2_*\left( 1+\xi (\phi ^2_*-\phi ^2_V)+\frac{\phi ^2_V}{\phi ^2_*}\right) ^2}\right) ^{-2} \left( 1+\frac{12M^2_p}{\phi ^2_*\left( 1+\xi (\phi ^2_*-\phi ^2_V)+\frac{\phi ^2_V}{\phi ^2_*}\right) ^2}+\frac{36M^4_p}{\phi ^4_*\left( 1+\xi (\phi ^2_*-\phi ^2_V)+\frac{\phi ^2_V}{\phi ^2_*}\right) ^4}\right) &{}\quad \text {for Case II}+\text {Choice~III} \end{array} \right. \end{aligned}$$

(10.88)

and

$$ \begin{aligned} \mathcal{G}_{2}(\phi _*)=\left\{ \begin{array}{ll} \left( 1+\frac{6M^2_p}{81\phi ^2_*}\right) ^{-1}\frac{6M^2_p}{81\phi ^3_*} &{}\quad \text {for Case I}\\ \left( 1+\frac{6M^2_p}{\phi ^2_*}\right) ^{-1}\frac{6M^2_p}{\phi ^3_*}&{} \quad \text {for Case II}\\ \left( 1+\frac{6M^2_p}{\phi ^2_*\left( 1-\frac{\phi ^4_V}{\phi ^4_*}\right) ^2}\right) ^{-1}\frac{6M^2_p\left( 1+3\frac{\phi ^4_V}{\phi ^4_*}\right) }{\phi ^3_*\left( 1-\frac{\phi ^4_V}{\phi ^4_*}\right) ^3}~~~~~ &{}\quad \text {for Case II}+\text {Choice~I}(\text {v}1 \& \text {v}2)\\ \left( 1+\frac{6M^2_p}{\phi ^2_*\left( \frac{m^2_c}{m^2_c-\lambda \phi ^2_*}\right) ^2}\right) ^{-1}\frac{6M^2_p\left( 1-\frac{m^2_c}{m^2_c-\lambda \phi ^2_*}-\frac{2\lambda m^2_c\phi ^2_*}{(m^2_c-\lambda \phi ^2_*)^2}\right) }{\phi ^3_*\left( \frac{m^2_c}{m^2_c-\lambda \phi ^2_*}\right) ^3}~~~~~ &{}\quad \text {for Case II}+\text {Choice~II}(\text {v}1 \& \text {v}2)\\ \left( 1+\frac{6M^2_p}{\phi ^2_*\left( 1+\xi (\phi ^2_*-\phi ^2_V)+\frac{\phi ^2_V}{\phi ^2_*}\right) ^2}\right) ^{-1}\frac{6M^2_p\left( 1+\xi (3\phi ^2_*-\phi ^2_V)-\frac{\phi ^2_V}{\phi ^2_*}\right) }{\phi ^3_*\left( 1+\xi (\phi ^2_*-\phi ^2_V)+\frac{\phi ^2_V}{\phi ^2_*}\right) ^3} &{}\quad \text {for Case II}+\text {Choice III}. \end{array} \right. \end{aligned}$$

(10.89)

1.4 Momentum dependent functions in four point function

Momentum dependent functions $\hat{G}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)$, $\hat{W}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)$ and $\hat{R}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)$ as appearing in four point function are defined as

$$\begin{aligned}&\hat{G}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)=\frac{S(\tilde{\mathbf{k}},\mathbf{k}_1,\mathbf{k}_2)S(\tilde{\mathbf{k}},\mathbf{k}_3,\mathbf{k}_4)}{|\mathbf{k}_1+\mathbf{k}_2|^3}\left[ \left\{ \mathbf{k}_1.\mathbf{k}_3+\frac{\left[ \mathbf{k}_1.(\mathbf{k}_1+\mathbf{k}_2)\right] \left[ \mathbf{k}_3.(\mathbf{k}_3+\mathbf{k}_4)\right] }{|\mathbf{k}_1+\mathbf{k}_2|^2}\right\} \right. \nonumber \\&\quad \left. \times \left\{ \mathbf{k}_2.\mathbf{k}_4+\frac{\left[ \mathbf{k}_2.(\mathbf{k}_1+\mathbf{k}_2)\right] \left[ \mathbf{k}_4.(\mathbf{k}_3+\mathbf{k}_4)\right] }{|\mathbf{k}_1+\mathbf{k}_2|^2}\right\} +\left\{ \mathbf{k}_1.\mathbf{k}_4+\frac{\left[ \mathbf{k}_1.(\mathbf{k}_1+\mathbf{k}_2)\right] \left[ \mathbf{k}_4.(\mathbf{k}_3+\mathbf{k}_4)\right] }{|\mathbf{k}_1+\mathbf{k}_2|^2}\right\} \right. \nonumber \\&\quad \left. \times \left\{ \mathbf{k}_2.\mathbf{k}_3+\frac{\left[ \mathbf{k}_2.(\mathbf{k}_1+\mathbf{k}_2)\right] \left[ \mathbf{k}_3.(\mathbf{k}_3+\mathbf{k}_4)\right] }{|\mathbf{k}_1+\mathbf{k}_2|^2}\right\} -\left\{ \mathbf{k}_1.\mathbf{k}_2+\frac{\left[ \mathbf{k}_1.(\mathbf{k}_1+\mathbf{k}_2)\right] \left[ \mathbf{k}_2.(\mathbf{k}_3+\mathbf{k}_4)\right] }{|\mathbf{k}_1+\mathbf{k}_2|^2}\right\} \right. \nonumber \\&\quad \left. \times \left\{ \mathbf{k}_3.\mathbf{k}_4+\frac{\left[ \mathbf{k}_3.(\mathbf{k}_3-\mathbf{k}_4)\right] \left[ \mathbf{k}_4.(\mathbf{k}_3-\mathbf{k}_4)\right] }{|\mathbf{k}_1+\mathbf{k}_2|^2}\right\} \right] \end{aligned}$$

(10.90)

with

$$\begin{aligned} S(\tilde{\mathbf{k}},\mathbf{k}_1,\mathbf{k}_2)= & {} \left[ K-\frac{1}{K}\sum _{i>j}k_ik_j-\frac{1}{K^2}\prod ^{3}_{i=1}k_i\right] _{\tilde{\mathbf{k}}=-(\mathbf{k}_1+\mathbf{k}_2)} \end{aligned}$$

(10.91)

and

$$\begin{aligned} \hat{R}^{S}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)= & {} \sum ^{3}_{n=1}\frac{1}{\hat{K}^{n}}A_{n}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4), \end{aligned}$$

(10.92)

where

$$\begin{aligned} \hat{K}=k_1+k_2+k_3+k_4=\sum ^{4}_{i=1}k_i=K+k_4, \end{aligned}$$

(10.93)

and the momentum dependent functions $A_{1}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)$, $A_{2}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)$ and $A_{3}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)$ are defined as

$$\begin{aligned}&A_{1}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)=\left[ \frac{(\mathbf{k}_3.\mathbf{k}_4)((\mathbf{k}_1.\mathbf{k}_2)(k^2_1+k^2_2)+2k^2_1k^2_2)}{8|\mathbf{k}_1+\mathbf{k}_2|^2}\right. \nonumber \\&\quad \left. +(1,2\leftrightarrow 3,4)\right] \nonumber \\&\quad -\frac{(k^2_1k^2_4(\mathbf{k}_2.\mathbf{k}_3)+k^2_1k^2_3(\mathbf{k}_2.\mathbf{k}_4)+k^2_2k^2_4(\mathbf{k}_1.\mathbf{k}_3)+k^2_1k^2_4(\mathbf{k}_2.\mathbf{k}_3))}{2|\mathbf{k}_1+\mathbf{k}_2|^2}\nonumber \\&\quad -\frac{((\mathbf{k}_1.\mathbf{k}_2)(k^2_1+k^2_2)+2k^2_1k^2_2)((\mathbf{k}_3.\mathbf{k}_4)(k^2_3+k^2_4)+2k^2_3k^2_4)}{8|\mathbf{k}_1+\mathbf{k}_2|^4},\nonumber \\ \end{aligned}$$

(10.94)

$$\begin{aligned}&A_{2}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)=-\frac{\left[ k_3k_4(k_3+k_4)((\mathbf{k}_1.\mathbf{k}_2)(k^2_1+k^2_2)+2k^2_1k^2_2)(k_3k_4+\mathbf{k}_3.\mathbf{k}_4)+(3,4\leftrightarrow 1,2) \right] }{8|\mathbf{k}_{1}+\mathbf{k}_{2}|^4}\nonumber \\&\qquad -\frac{1}{2|\mathbf{k}_1+\mathbf{k}_2|^2}\left[ k^2_1k^2_4(\mathbf{k}_2.\mathbf{k}_3)(k_2+k_3)+k^2_1k^2_3(\mathbf{k}_2.\mathbf{k}_4)(k_2+k_4)+k^2_2k^2_4(\mathbf{k}_1.\mathbf{k}_3)(k_1+k_3)+k^2_2k^2_3(\mathbf{k}_1.\mathbf{k}_4)(k_1+k_4)\right] \nonumber \\&\qquad +\left\{ \frac{(\mathbf{k}_1.\mathbf{k}_2)}{8|\mathbf{k}_1+\mathbf{k}_2|^2}\left[ ((k_1+k_2)((\mathbf{k}_3.\mathbf{k}_4)(k^2_3+k^2_4)+2k^2_3k^2_4)+k_3k_4(k_3+k_4)(k_3k_4+\mathbf{k}_3.\mathbf{k}_4))\right] +(1,2\leftrightarrow 3,4)\right\} , \end{aligned}$$

(10.95)

$$\begin{aligned}&A_{3}(\mathbf{k}_1,\mathbf{k}_2,\mathbf{k}_3,\mathbf{k}_4)=-\frac{k_1k_2k_3k_4(k_1+k_2)(k_3+k_4)(k_1k_2+\mathbf{k}_1.\mathbf{k}_2)(k_3k_4+\mathbf{k}_3.\mathbf{k}_4)}{4|\mathbf{k}_1+\mathbf{k}_2|^4}\nonumber \\&\qquad -\frac{k_1k_2k_3k_4(k_1k_4(\mathbf{k}_2.\mathbf{k}_3)+k_1k_3(\mathbf{k}_2.\mathbf{k}_4)+k_2k_4(\mathbf{k}_1,\mathbf{k}_3)+k_2k_3(\mathbf{k}_1,\mathbf{k}_4))}{|\mathbf{k}_1+\mathbf{k}_2|^2}\nonumber \\&\qquad +\frac{\left[ k_3k_4(k_3+k_4)((\mathbf{k}_1.\mathbf{k}_2)(k^2_1+k^2_2)+2k^2_1k^2_2)(k_3k_4+\mathbf{k}_3.\mathbf{k}_4)+(3,4\leftrightarrow 1,2) \right] }{2|\mathbf{k}_{1}+\mathbf{k}_{2}|^2}\nonumber \\&\qquad +\frac{3k_1k_2k_3k_4(k_1k_2+\mathbf{k}_1.\mathbf{k}_2)(k_3k_4+\mathbf{k}_3.\mathbf{k}_4)}{4|\mathbf{k}_1+\mathbf{k}_2|^2}. \end{aligned}$$

(10.96)

$$\begin{aligned}&\hat{W}^{S}(\mathbf{k}_1,\mathbf{k}_3,\mathbf{k}_2,\mathbf{k}_4) =-\frac{2|\mathbf{k}_1+\mathbf{k}_2|^3\hat{G}^{S}(\mathbf{k}_1,\mathbf{k}_3,\mathbf{k}_2,\mathbf{k}_4)}{S(\tilde{\mathbf{k}},\mathbf{k}_1,\mathbf{k}_2)S(\tilde{\mathbf{k}},\mathbf{k}_3,\mathbf{k}_4)}\left[ \left\{ \frac{k_1k_2(k_1+k_2)^2((k_1+k_2)^2-k^2_3-k^2_4-k_3k_4)}{(\hat{K}-2(k_3+k_4))^2\hat{K}^2((k_1+k_2)^2-|\mathbf{k}_1+\mathbf{k}_2|^2)}\right. \right. \nonumber \\&\quad \left. \left. \times \left( -\frac{k_1+k_2}{2k_1k_2}-\frac{k_1+k_2}{k^2_3+k^2_4+4k_3k_4-(k_1+k_2)^2}+\frac{k_1+k_2}{|\mathbf{k}_1+\mathbf{k}_2|^2-(k_1+k_2)^2}\right. \right. \right. \nonumber \\&\quad \left. \left. \left. +\frac{1}{\hat{K}-2(k_1+k_2)}-\frac{1}{\hat{K}}+\frac{3}{2(k_1+k_2)}\right) +(1,2\leftrightarrow 3,4)\right\} \right. \nonumber \\&\quad \left. -\frac{|\mathbf{k}_1+\mathbf{k}_2|^3(|\mathbf{k}_1+\mathbf{k}_2|^2-k^2_1-k^2_2-4k_1k_2)(|\mathbf{k}_1+\mathbf{k}_2|^2-k^2_3-k^2_4-4k_3k_4)}{2(|\mathbf{k}_1+\mathbf{k}_2|^2-k^2_1-k^2_2-2k_1k_2)(|\mathbf{k}_1+\mathbf{k}_2|^2-k^2_3-k^2_4-2k_3k_4)}\right] . \end{aligned}$$

(10.97)