1 Introduction

It is predicted by general relativity (GR) that in the presence of a mass distribution, light is deflected. However, it was not entirely a new prediction by Einstein, in fact, Newton had obtained a similar result by a different set of assumptions. In 1936, Einstein [1] noted that if a star (lens), the background star (source) and the observer are highly aligned then the image obtained by the deflection of light of a background star due to another star can be highly magnified. He also noted that optical telescopes at that time were not sufficiently capable to resolve the angular separation between images.

In 1963, the discovery of quasars at high redshift gave the actual observation to the gravitational lensing effects. Quasars are central compact light emitting regions which are extremely luminous. When a galaxy appears between the quasar and the observer, the resulting magnification of images would be large and hence well separated images are obtained. This effect was named macro-lensing. The first example of gravitational lensing was discovered (the quasar QSO 0957 + 561) in 1979 [2].

The weak field theory of gravitational lensing is based on the first order expansion of the smallest deflection angle. It has been developed by several authors such as Klimov [3], Liebes [4], Refsdal [5], Bourassa [6,7,8], and Kantowski [9]. They were succeeded in explaining astronomical observations up to now (for more details see [10]).

Due to a highly curved space-time by a black hole (BH), the weak field approximation is no longer valid. Ellis and Virbhadra obtained the lens equation by studying the strong gravitational fields [11]. They analyzed the lensing of the Schwarzchild BH with an asymptotically flat metric. They found two infinite sets of faint relativistic images with the primary and secondary images. Fritelli et al. [12] obtained exact lens equation and they compared them with the results of Virbhadra and Ellis. By using the strong field approximation, Bozza et al. [13] gave analytical expressions for the magnification and positions of the relativistic images.

From recent observational measurements, we can see that our Universe is dominated by a mysterious form of energy called “Dark Energy”. This kind of energy is responsible for the accelerated expansion of our Universe [14, 15]. Dark energy acts as a repulsive gravitational force so that usually it is modeled as an exotic fluid. One can consider a fluid with an equation of state in which the state parameter w(t) depends on the ratio of the pressure p(t) and its energy density \(\rho (t)\), such as \(w(t) = \frac{p(t)}{\rho (t)}\). So far, a wide variety of dark energy models with dynamical scalar fields have been proposed as alternative models to the cosmological constant. Such scalar field models include quintessence [16,17,18,19], k-essence [20], quintom [21, 22], phantom dark energy [23] and others.

Quintessence is a candidate of dark energy which is represented by an exotic kind of scalar field that is varying with respect to the cosmic time. The solution for a spherically symmetric space-time geometry surrounded by a quintessence matter was derived by Kiselev [16]. There is little work focused on studying the Kiselev black hole (KBH). Thermodynamics and phase transition of the Reissner–Nordström BH surrounded by quintessence are given in [17, 18, 24]. The thermodynamics of the Reissner–Nordström–de Sitter black hole surrounded by quintessence has been investigated by one of us [18] and has led to the notion of two thermodynamic volumes. The properties of a charged BH surrounded by the quintessence were studied in [18, 25]. New solutions that generalize the Nariai horizon to asymptotically de Sitter-like solutions surrounded by quintessence have been determined in [18]. The detailed study of the photon trajectories around the charged BH surrounded by the quintessence is given in [26]. Recently, Younas et al. worked on the strong gravitational lensing by Schwarzschild-like BH surrounded by quintessence [27].

We will extend that work by adding a charge Q (charged KBH). We will consider the lensing phenomenon only for the case of non-degenerate horizons. By computing the null geodesics, we examine the behavior of light around a charged KBH. We analyze the circular orbits (photon region) for photons. Furthermore, we observe how both the quintessence and the charge parameters affects the light trajectories of massless particles (photons), when they are strongly deflected due to the charged KBH. We will not restrict the investigation to the analytically tractable cases \(w_{q}=-1/3\) and \(w_{q}=-2/3\), as some work did [25, 26, 28]; rather, we will consider the full range of the quintessence parameter \(w_q\) and we will rely partly on the work done by one of us [18].

The paper is structured as follows: in Sect. 2, we study the charged KBH geometry and we derive the basic equations for null geodesics. Additionally, in that section we write down the basic equations for null geodesics in charged Kiselev space-time along with the effective potential and the horizons. In Sect. 3, the analytical solution of the trajectory equation is obtained via the perturbation technique. Section 4 is devoted to the study of the lens equation to derive the bending angle. The strong field approximation of the lens equation is discussed as well. Finally, we provide a conclusion in Sect. 6.

Throughout this paper, we adopt the natural system of units where \(c = G = 1\) and the metric convention is \((+,-,-,-)\).

2 Basic equations for null geodesics in charged Kiselev space-time

The geometry of a charged KBH surrounded by quintessence is given by [16]

$$\begin{aligned} \mathrm{d}s^{2}=f(r)\mathrm{d}t^{2}-\frac{1}{f(r)}\mathrm{d}r^{2}-r^{2}\mathrm{d}\theta ^{2}-r^{2}\sin ^{2}\theta \mathrm{d}\phi ^{2}, \end{aligned}$$
(1)

where

$$\begin{aligned} f(r)=1-\frac{2M}{r}-\frac{\sigma }{r^{3w_{q}+1}}+\frac{Q^{2}}{r^{2}}. \end{aligned}$$
(2)

Here, M is the mass of the BH, \(w_{q}\) is the quintessence state parameter (having range between \(-1\le w_{q} <-1/3\)), \(\sigma \) is a positive normalization factor and Q is the charge of the BH. The equation of state for the quintessence matter with isotropic negative pressure \(p_{q}\) is linear of the form

$$\begin{aligned} p_{q}=w_{q}\rho _{q}<0, \end{aligned}$$
(3)

where \(\rho _{q}\) is the energy density given by (taking \(G=\hbar =1\))

$$\begin{aligned} \rho _{q}=-\frac{3w_{q}\sigma }{8\pi r^{3(1+w_{q})}}>0. \end{aligned}$$
(4)

For a detailed metric derivation and a discussion of its properties, we refer the reader to the original paper by Kiselev [16]. For a further discussion see [17, 18]. Note that not all the values of \(w_q\) are manageable to find analytically solutions to the trajectory equation (see Sect. 2). However, the cosmological constant case, corresponding to \(w_q=-1\), and the case \(w_q=-2/3\) are relatively simple.

2.1 Horizons in charged Kiselev black hole

In order to study the trajectories of photons near the space-time (1), one has to understand where the horizons are located for the charged KBH. In order to find the horizons, we require \(f(r)=0\), which depends on four parameters \(M,Q^2,w_{q}\) and \(\sigma \). It has become custom to fix \(M,Q^2\) and \(w_{q}\) [17, 18] and investigate the properties of these BHs upon constraining the values of \(\sigma \) in terms of \(M,Q^2\) and \(w_{q}\). We proceed the same way in this work.

Fig. 1
figure 1

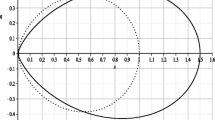
Plots of \(y=1-2Mu+Q^2 u^2\) (dashed line), \(y=\sigma u^{3w_q+1}\) (continuous line), and \(y=(2-6Mu+4Q^2 u^2)/[3(w_q+1)]\) (dotted line) versus \(u\equiv 1/r\) for a \(Q^2/M^2\le 1\), \(-1\le w_q<-1/3\), and \(\sigma <\sigma _1\) (7); b \(Q^2/M^2>1\), \(-1\le w_q<-1/3\), and \(\sigma _2<\sigma <\sigma _1\) (8). Here \(u_\mathrm{ch}=1/r_\mathrm{ch}\), \(u_\mathrm{eh}=1/r_\mathrm{eh}\), \(u_\mathrm{ah}=1/r_\mathrm{ah}\). The points of intersection of the dashed parabola and the continuous line provide the locations of the three horizons (11): (\(u_\mathrm{ch},u_\mathrm{eh},u_\mathrm{ah}\)). The point of intersection of the dotted parabola and the continuous line provides the only local maximum value (18) of the potential \(V_\text {eff}\) (16) for \(u_\mathrm{ch}<u<u_\mathrm{eh}\), which is the location of the photon sphere: \(u_{ps}\)

Full size image

We are only interested in the case where the BH has three distinct horizons: a cosmological horizon \(r_\mathrm{ch}\), an event horizon \(r_\mathrm{eh}\), and an inner horizon \(r_\mathrm{ah}\) with \(r_\mathrm{ch}>r_\mathrm{eh}>r_\mathrm{ah}\) and

$$\begin{aligned}&f<0\quad \text {for}\quad 0<r<r_\mathrm{ah},\nonumber \\&f>0\quad \text {for}\quad r_\mathrm{eh}<r<r_\mathrm{ch},\nonumber \\&f<0\quad \text {for}\quad r>r_\mathrm{ch}. \end{aligned}$$
(5)

The photon paths are all confined in the region

$$\begin{aligned} r_\mathrm{eh}\le r\le r_\mathrm{ch}, \end{aligned}$$
(6)

where \(f\ge 0\).

For \(M,Q^2\) and \(w_{q}\) fixed, the constraints for having three positive distinct roots of \(f(r)=0\) depend on the ratio \(Q^2/M^2\). There will be three distinct horizons if [18]

$$\begin{aligned}&\frac{Q^2}{M^2}\le 1\quad \text {and}\quad \sigma <\sigma _1\equiv \frac{2(Q^2u_1-M)}{(3w_q+1)u_1^{3w_q}},\\&\text {where}\nonumber \\&u_1=-\frac{\sqrt{9w_q^2M^2+(1-9w_q^2)Q^2}+3w_q M}{(1-3w_q)Q^2},\nonumber \end{aligned}$$
(7)

or if [18]

$$\begin{aligned}&\frac{Q^2}{M^2}>1\quad \text {and}\quad \sigma _2\equiv \frac{2(Q^2u_2-M)}{(3w_q+1)u_2^{3w_q}}<\sigma <\sigma _1,\\&\text {where}\nonumber \\&u_2=\frac{\sqrt{9w_q^2M^2+(1-9w_q^2)Q^2}-3w_q M}{(1-3w_q)Q^2}.\nonumber \end{aligned}$$
(8)

In Ref. [18] it was shown that under the above constraints (7) and (8) we have

$$\begin{aligned}&u_2>u_1>0,\quad \sigma _1>\sigma _2>0,\end{aligned}$$
(9)
$$\begin{aligned}&r_\mathrm{ch}>r_\mathrm{eh}>\frac{Q^2}{M}>r_\mathrm{ah}>0. \end{aligned}$$
(10)

Introducing the variable \(u=1/r\), the horizon equation becomes \(f(r)=f(u)=0\), yielding the values of the three horizons. This equation takes the following form (\(-2\le 3w_q+1<0\)):

$$\begin{aligned} 1-2Mu+Q^2 u^2 = \sigma u^{3w_q+1}. \end{aligned}$$
(11)

Figure 1, which is a plot of the parabola \(y=1-2Mu+Q^2 u^2\) and the curve \(y=\sigma u^{3w_q+1}\), shows the existence of three distinct horizons for \(Q^2/M^2\le 1\) and \(Q^2/M^2>1\). In the remaining part of this work we assume that the constraints (7) and (8) are satisfied.

2.2 Equations of motion for a photon

In the presence of a spherically symmetric gravitational field, we can confine the photon orbits in the equatorial plane by taking \(\theta =\pi /2\). Therefore, the Lagrangian for a photon traveling in a charged KBH space-time will be given by

$$\begin{aligned} \mathcal {L}=f(r)\dot{t}^{2}-\frac{1}{f(r)}\dot{r}^{2}-r^{2}\dot{\phi }^{2}, \end{aligned}$$
(12)

where the dot represents the derivative with respect to the affine parameter \(\lambda \) for null geodesics. The Euler–Lagrange equations for null geodesics yield

$$\begin{aligned}&\dot{t}\equiv \frac{\mathrm{d}t}{\mathrm{d}\lambda }=\frac{E}{f(r)},\end{aligned}$$
(13)
$$\begin{aligned}&\dot{\phi }\equiv \frac{\mathrm{d}\phi }{\mathrm{d}\lambda }=\frac{L}{r^{2}}. \end{aligned}$$
(14)

In the above equations, E and L are constants known as the energy and angular momentum per unit mass. Using the condition for null geodesics \(g_{\mu \nu }u^{\mu }u^{\nu }=0\), we obtain the equation of motion for photons

$$\begin{aligned} \dot{r}= & {} L\sqrt{\displaystyle \frac{1}{b^{2}}-\frac{f(r)}{r^{2}}}, \ \ \ \text {where} \ \ \ b\equiv \Big |\frac{L}{E}\Big |. \end{aligned}$$
(15)

Here, b is the impact parameter which is a perpendicular line to the ray of light converging at the observer from the center of the charged KBH. Further, photons experience a gravitational force in the presence of the gravitational field. This force can be expressed via the effective energy potential which is given by (\(\dot{r}^2+V_\text {eff}=E^2\))

$$\begin{aligned} V_\text {eff}=\frac{L^2}{r^{2}}~f(r)=\frac{L^2}{r^{2}}\Big (1-\frac{2M}{r} -\frac{\sigma }{r^{3w_{q}+1}}+\frac{Q^{2}}{r^{2}}\Big ). \end{aligned}$$
(16)

In the left hand side of the above equation, the first term corresponds to a centrifugal potential, the second term represents the relativistic correction, the third term is due to the presence of the quintessence field while the fourth term appears due to the presence of electric charge. The terms appearing with positive (negative) signs correspond to repulsive (attractive) force fields.

In terms of u, \(V_\text {eff}\) reads

$$\begin{aligned} V_\text {eff}=L^2(u^2-2Mu^3+Q^2u^4-\sigma u^{3w_q+3}). \end{aligned}$$
(17)

Since \(f(u_\mathrm{eh})=f(u_\mathrm{ch})=0\) and, by (5), \(f>0\) for \(u_\mathrm{ch}<u<u_\mathrm{eh}\) (\(u_\mathrm{ch}=1/r_\mathrm{ch}\), \(u_\mathrm{eh}=1/r_\mathrm{eh}\)), using (16) we see that \(V_\text {eff}(u_\mathrm{eh})=V_\text {eff}(u_\mathrm{ch})=0\) and \(V_\text {eff}>0\) for \(u_\mathrm{ch}<u<u_\mathrm{eh}\) too. In the non-extremal case, in which we are interested, this implies that the potential \(V_\text {eff}\) may have only an odd number of extreme values between the two horizons \(u_\mathrm{ch}\) and \(u_\mathrm{eh}\); that is, \(n+1\) local maxima and n local minima with \(n\in \mathbb {N}\). These extreme values are determined by the constraint \(dV_\text {eff}/du=0\), which reads (\(-2\le 3w_q+1<0\))

$$\begin{aligned} \frac{2}{3(w_q+1)}-\frac{6Mu}{3(w_q+1)}+\frac{4Q^2u^2}{3(w_q+1)}=\sigma u^{3w_q+1}. \end{aligned}$$
(18)

In absolute value, the slope of the parabola on the l.h.s. of (18) is larger than that of the parabola on the l.h.s. of (11) [recall \(-1\le w_q<-1/3\)]. Thus, referring to Fig. 1, the parabola on the l.h.s. of (18) intersects the curve \(y=\sigma u^{3w_q+1}\) at one and only one point between the two horizons \(u_\mathrm{ch}\) and \(u_\mathrm{eh}\), which provides the point at which the potential \(V_\text {eff}\) has a local maximum and is, by this fact, the location of the photon sphere \(u_{ps}\).

Therefore there is no stable closed orbit for the photons. If \(E^2=V_\text {eff max}\), the photons describe unstable circular orbits. If \(E^2<V_\text {eff max}\), the motion will be confined between the event horizon and the smaller root of \(V_\text {eff}=E^2\) or between the cosmological horizon and the larger root of \(V_\text {eff}=E^2\). If \(E^2>V_\text {eff max}\), the motion will be confined between the event and cosmological horizons.

In (16), if we take \(Q=0\), the effective potential reduces to the KBH effective potential,

$$\begin{aligned} V^\text {K}_\text {eff}= & {} \frac{L^{2}}{r^{2}}\Big (1-\frac{2M}{r} -\frac{\sigma }{r^{3w_{q}+1}}\Big ). \end{aligned}$$
(19)

When we take \(\sigma =0\), (16) reduces to the Reissner–Nordström BH effective potential for photons,

$$\begin{aligned} V^\text {R}_\text {eff}= & {} \frac{L^{2}}{r^{2}}\Big (1-\frac{2M}{r} +\frac{Q^{2}}{r^{2}}\Big ). \end{aligned}$$
(20)

Further, when \(\sigma =Q=0\), the effective potential for the Schwarzschild BH is given by

$$\begin{aligned} V^\text {S}_\text {eff}= & {} \frac{L^{2}}{r^{2}}\Big (1-\frac{2M}{r}\Big ). \end{aligned}$$
(21)
Fig. 2
figure 2

Effective potential \({V}_\text {eff}\) is shown as a function of distance r for non-extreme case at different values of quintessence parameter \(\sigma \) with a fixed value of the charge Q. The first upper curve for \(V^\text {R}_\text {eff}\), the second curve for \(V^\text {S}_\text {eff}\) and the fourth curve for \(V^\text {K}_\text {eff}\) are taken as a reference. The third, fifth and sixth curves are the non-extreme case of charged Kiselev black hole effective potential \(V_\text {eff}\)

Full size image
Fig. 3
figure 3

Effective potential \({V}_\text {eff}\) is shown as a function of distance r for non-extreme case at a different values of charge Q with constant value of quintessence parameter \(\sigma \). First upper curve for \(V^\text {R}_\text {eff}\), second curve for \(V^\text {S}_\text {eff}\) and fifth curve for \(V^\text {K}_\text {eff}\) are taken as a reference. Third and fourth curves are the non-extreme case of charged Kiselev black hole effective potential \(V_\mathrm{eff}\)

Full size image

In Figs. 2 and 3, the effective potential \(V_\text {eff}\), i.e. Eq. (16), is plotted to study the behavior of photons near a charged KBH for the non-extreme case where \(0<\sigma <0.17\) and \(0<Q<1\). We observe that in each curve, there are no minima. In these graphs each curve corresponds to the maximum value \(V_\text {max}\), which means that, for photons, only an unstable circular orbit exists. In these two figures, the effective potentials of Kiselev (19), Reissner–Nordström (20) and Schwartzschild (21) black holes are displayed as references. In Fig. 2 (Fig. 3), the quintessence parameter \(\sigma \) is varying (fixed) and the charge Q is fixed (varying). Both graphs are reciprocal to each other. We observe that by increasing the value of \(\sigma \) (Q), the photon has more (less) possibility to fall into the black hole.

2.3 The u–\(\phi \) trajectory equation

In terms of \(u=1/r\), we rewrite (15) as

$$\begin{aligned} \dot{u}^2=L^2u^4\Big (\frac{1}{b^2}-u^2f\Big ). \end{aligned}$$
(22)

Combining this with (14) we obtain the following equations:

$$\begin{aligned} \Big (\frac{\mathrm{d}u}{\mathrm{d}\phi }\Big )^2&=\ \frac{1}{b^2}-u^2f,\nonumber \\&=\ \frac{1}{b^2}+\sigma u^{3w_q+3}-u^2+2Mu^3-Q^2u^4, \end{aligned}$$
(23)
$$\begin{aligned} \frac{\mathrm{d}^2u}{\mathrm{d}\phi ^2}+u&=\ u(1-f)-\frac{u^2}{2}\frac{\mathrm{d}f}{\mathrm{d}u},\nonumber \\&=\ \frac{3(w_q+1)\sigma }{2}~u^{3w_q+2}+3Mu^2-2Q^2u^3.\nonumber \\ \end{aligned}$$
(24)

3 Solution to the trajectory equation

The presence of a cosmological horizon does not make sense to investigate the photon paths beyond it as is the case beyond the event horizon. The usual bending formula [29], developed for asymptotically flat solutions, no longer applies. The bending angle may be derived upon integrating either (23) or (24). The usually used approach is that of Ishak and Rindler [30]. In the problems treated so far, \(\sigma \) is zero, so the approach consists in integrating

$$\begin{aligned} \frac{\mathrm{d}^2u}{\mathrm{d}\phi ^2}+u=0,\quad \text {with}\quad u(\phi =\pi /2)=b=R, \end{aligned}$$

which yields \(u_0=\sin \phi /R\), then construct by a perturbation approach a solution to

$$\begin{aligned} \frac{\mathrm{d}^2u}{\mathrm{d}\phi ^2}+u=3Mu^2-2Q^2u^3, \end{aligned}$$
(25)

of the form \(u=u_0+u_1\), where in (25) the terms in \(u^n\) with \(n>1\) are seen as perturbations in the limit \(u\rightarrow 0\).

The approach described above does not hold if \(\sigma \ne 0\) and \(-1\le w_q<-1/3\); since \(-1\le 3w_q+2<1\), the term proportional to \(\sigma \) in (24) is rather a leading term in the limit \(u\rightarrow 0\). In the presence of quintessence, one should first solve

$$\begin{aligned} \frac{\mathrm{d}^2u_0}{\mathrm{d}\phi ^2}+u_0=\frac{3(w_q+1)\sigma }{2}~u_0^{3w_q+2}, \end{aligned}$$
(26)

or

$$\begin{aligned} \frac{\mathrm{d}^2u_0}{\mathrm{d}\phi ^2}=\frac{3(w_q+1)\sigma }{2}~u_0^{3w_q+2} \end{aligned}$$
(27)

(with \(-1\le w_q<-1/3\)) as if \(M=0\) and \(Q=0\), then by a perturbation approach one solves (24). Unfortunately, Eqs. (26) and (27) are not tractable analytically except in the cases \(w_q=-1\) and \(w_q=-2/3\).

In the tractable case \(w_q=-2/3\), Eq. (26) reduces to

$$\begin{aligned} \frac{\mathrm{d}^2u_0}{\mathrm{d}\phi ^2}+u_0-\frac{\sigma }{2}=0, \end{aligned}$$
(28)

and it possesses the particular solution

$$\begin{aligned} u_0=c \sin \phi +\frac{\sigma }{2}. \end{aligned}$$
(29)

Since (24) is not equivalent to (23), from which it has been derived, one determines c from the reduced expression of (23) upon taking \(M=0\) and \(Q=0\):

$$\begin{aligned} \Big (\frac{\mathrm{d}u_0}{\mathrm{d}\phi }\Big )^2=\frac{1}{b^2}+\sigma u_0-u_0^2. \end{aligned}$$
(30)

Substituting (29) into (30), we obtain

$$\begin{aligned} c=\frac{\sqrt{1+\tfrac{b^2\sigma ^2}{4}}}{b} \end{aligned}$$
(31)

and

$$\begin{aligned} u_0=\frac{\sqrt{1+\tfrac{b^2\sigma ^2}{4}}}{b}~\sin \phi +\frac{\sigma }{2}. \end{aligned}$$
(32)

Figure 4 shows the real path that the light follows and the path that the light would follow in empty space (\(\sigma =0,M=0,Q=0\)) for the same value of the physical ratio \(b=L/E\) of the angular momentum and energy. From that figure, it is obvious that in empty space \(c=1/b\), which is the same expression as the one Eq. (31) reduces to on setting \(\sigma =0\).

Fig. 4
figure 4

The diagram shows the real curved path the photons follow versus the fictitious free straight path they would follow in empty space if carrying the same angular momentum L and same energy E. Here \(\phi +\varphi =\pi /2\) and \(\tan \psi =r \sqrt{f} \,|\mathrm{d}\phi /\mathrm{d} r|=u \sqrt{f} \,|\mathrm{d}\phi /\mathrm{d} u|\) (40)

Full size image

If quintessence is the unique acting force (\(M=0\) and \(Q=0\)), the minimum distance of approach \(r_n\), as shown in Fig. 4, corresponds to \(\phi =\pi /2\) and is derived from (32) by

$$\begin{aligned} r_n=\frac{2}{2c+\sigma }=\frac{b}{\sqrt{1+\tfrac{b^2\sigma ^2}{4}} +\tfrac{b\sigma }{2}}<b. \end{aligned}$$
(33)

This can be derived directly from the definition of \(r_n\), which is the nearest distance from the light path to the lens. This is such that the r.h.s. of (23) is 0, yielding the same expression as in (33).

In bending-angle problems the parameter b is assumed to be large to allow for series expansions in powers of 1 / b. Since quintessence is not supported observationally, we make the statement that \(\sigma \ll 1\), which we will make clearer in the next section (Eq. (47)).

All authors who worked on the bending angle in a de Sitter-like geometry draw a similar figure as Fig. 4, but they make no distinction between b and \(r_{n}\); rather, they use loosely a common notation R for b and \(r_{n}\). This remains more or less justified as far as quintessence is not taken into consideration where one may write \(b \gtrsim r_{n}\). As we mentioned earlier, in bending-angle problems the parameter b is assumed to be large to allow for series expansions in powers of 1 / b, so in the presence of quintessence, one has to further assume \(b\sigma =\tfrac{L\sigma }{E}\ll 1\) (Eq. (47)) in order to have \(b \gtrsim r_{n}\). In the presence of quintessence, corrections in the expression of \(r_n\) are needed: if \(\sigma \ll 1\) and \(b\sigma \ll 1\) we obtain to the first order in 1 / b (see Eq. (39) for further orders of approximation)

$$\begin{aligned} u_n=\frac{1}{r_n}= \frac{1}{b}\left[ 1+\frac{b\sigma }{2}+\frac{b^2\sigma ^2}{8}+\mathcal {O} (b^4\sigma ^4)\right] . \end{aligned}$$
(34)

Now, substituting \(u=u_0+u_1\) into (24) reduces to (\(w_q=-2/3\))

$$\begin{aligned} \frac{\mathrm{d}^2u_1}{\mathrm{d}\phi ^2}+u_1=3Mu_0^2-2Q^2u_0^3, \end{aligned}$$

where \(u_0\) is given by (32). A particular exact solution is

$$\begin{aligned} u_1=\frac{3M\sigma ^2}{4}-\frac{Q^2\sigma ^3}{4}+cC_1+c^2C_2+c^3C_3, \end{aligned}$$
(35)

where c is given by (31) and the coefficients (\(C_1,C_2,C_3\)) are related to the coefficients (\(B_1,B_2,B_3\)), which were first evaluated in Ref. [26], by \(C_1=B_1-\sin \phi \), \(C_2=B_2\), and \(C_3=B_3\). We have

$$\begin{aligned} C_1&= M \bigg ( \tfrac{ 3 \sigma \pi }{4} \cos \phi - \tfrac{3}{2} \phi \sigma \cos \phi + \tfrac{3}{2} \sigma \sin \phi \bigg )\nonumber \\&\quad +Q^2\bigg ( \tfrac{3}{4} \phi \sigma ^2 \cos \phi - \tfrac{3}{8} \pi \sigma ^2 \cos \phi - \tfrac{3}{4} \sigma ^2 \sin \phi \bigg ),\nonumber \\ C_2&= M \bigg ( \tfrac{3}{2} + \tfrac{1}{2} \cos 2 \phi \big ) - Q^2 \big ( \tfrac{ 3 \sigma }{2} + \tfrac{ \sigma }{2} \cos 2 \phi \bigg ),\nonumber \\ C_3&= Q^2 \bigg ( \tfrac{3}{4} \phi \cos \phi - \tfrac{ 3}{8} \pi \cos \phi -\tfrac{9}{16} \sin \phi - \tfrac{1}{16} \sin 3 \phi \bigg ). \end{aligned}$$
(36)

Under the constraints \(\sigma \ll 1\) and \(b\sigma \ll 1\), expansions of the r.h.s. of (36) and of \(u_0\) (32) yield

$$\begin{aligned} u&= \tfrac{1}{b} \bigg [\sin \phi +\tfrac{1}{2}b\sigma +\tfrac{\sin \phi }{8} b^2\sigma ^2+\mathcal {O}(b^4 \sigma ^4)\bigg ]\nonumber \\&\quad +\tfrac{M}{b^2} \bigg [\tfrac{3}{2}+\tfrac{1}{2} \cos 2\phi +\big (\tfrac{3}{4} \pi \cos \phi -\tfrac{3}{2} \phi \cos \phi +\tfrac{3}{2} \sin \phi \big ) b\sigma \nonumber \\&\quad +\big (\tfrac{9}{8}+\tfrac{1}{8} \cos 2\phi \big ) b^2\sigma ^2+\mathcal {O}(b^3 \sigma ^3)\bigg ]\nonumber \\&\quad +\tfrac{Q^2}{b^3}\bigg [\tfrac{3}{4} \phi \cos \phi -\tfrac{3}{8} \pi \cos \phi -\tfrac{9}{16} \sin \phi -\tfrac{1}{16} \sin 3\phi \nonumber \\&\quad -\big (\tfrac{3}{2}+\tfrac{1}{2} \cos 2\phi \big ) b\sigma +\mathcal {O}(b^2 \sigma ^2)\bigg ], \end{aligned}$$
(37)
$$\begin{aligned} u_0\simeq \tfrac{1}{b} \bigg [\sin \phi +\tfrac{1}{2}b\sigma +\tfrac{\sin \phi }{8} b^2\sigma ^2\bigg ]. \end{aligned}$$
(38)

For (37) to hold it is sufficient that the products \(M\sigma \,b\sigma \) and \(Q^2\sigma ^2\,b\sigma \) remain much smaller than unity. This conclusion is easily derived from the requirement that \(u_1/u_0\ll 1\).

As to the minimum distance \(r_n=1/u_n\), this is given by [setting \(\phi =\pi /2\) in (37)]

$$\begin{aligned} u_n&= \frac{1}{b} [1+\tfrac{1}{2}b\sigma +\tfrac{1}{8} b^2\sigma ^2+\mathcal {O}(b^4 \sigma ^4)]\nonumber \\&\quad +\frac{M}{b^2} [1+\tfrac{3}{2} b\sigma +b^2\sigma ^2+\mathcal {O}(b^3 \sigma ^3)]\nonumber \\&\quad -\frac{Q^2}{b^3}[\tfrac{1}{2}+ b\sigma +\mathcal {O}(b^2 \sigma ^2)]. \end{aligned}$$
(39)

We see that the mass M contributes to the second order while \(Q^2\) contributes to the third order of the series expansion in powers of 1 / b.

Fig. 5
figure 5

The symbols I, L, O, and S denote the image, lens (black hole), observer, and source, respectively. The angles \(\phi \) and \(\psi \), \(r_{\text {min}}\), and r are those defined in Fig. 4. The angles \(\beta \) and \(\theta \) are the angular positions of the source and image, and \(\alpha =(\phi _s-\phi _o)+(\psi _o-\psi _s)\) is the deflection angle. The image location \(\theta \) is the angle \(\angle \,\text {IOL}\), which is by definition \(\psi _o=\theta \)

Full size image

4 Lens equation: bending angle

The expression of the angle \(\psi \) defined as the angle the direction \(\phi \) makes with the light path at r, as depicted in Fig. 4, is given by [31]

$$\begin{aligned} \tan \psi =r \sqrt{f} \Big |\frac{\mathrm{d}\phi }{\mathrm{d} r}\Big |=u \sqrt{f} \Big |\frac{\mathrm{d}\phi }{\mathrm{d} u}\Big |, \end{aligned}$$

or, preferably, by [32]

$$\begin{aligned} \sin \psi = bu\sqrt{f(u)}. \end{aligned}$$
(40)

A series expansion of \(\phi \) may be determined upon reversing the expansion (37). This is a cumbersome work which we will avoid in this section. Rather, we will rely on (40) and on the integral form of \(\phi \) (23),

$$\begin{aligned} \phi =\int \frac{\mathrm{d}u}{\sqrt{\frac{1}{b^2}-u^2f}}, \end{aligned}$$
(41)

to determine the deflection angle \(\alpha \).

Figure 5 depicts a light path along with the locations of the lens (L: black hole), observer (O), source (S), and image (I). The observer sees the image along the direction OI, which is tangent to the light path at O. The angles \(\beta \) and \(\theta \) are the angular positions of the source and image. The image location \(\theta \) is the angle \(\angle \,\text {IOL}\), which is by definition \(\psi _o=\theta \). The distances from the lens to the observer and to the source are denoted by \(r_o=1/u_o\) and \(r_s=1/u_s\), respectively. The nearest distance from the light path to the lens, denoted by \(r_n=1/u_n\), is such that the r.h.s. of (23) is 0, yielding

$$\begin{aligned} \frac{1}{b^2}=u_n^2f(u_n). \end{aligned}$$
(42)

In the special case \(w_{q}=-2/3\), we obtain \(1/b^2=u_n(u_n-2Mu_n^2+Q^2u_n^3-\sigma )\) a series solution of which is given by (39). In this section, instead of b, we will employ \(u_n\) as an independent parameter around which we expand the deflection angle \(\alpha \).

Let F(u) denote the function on the r.h.s. of (23),

$$\begin{aligned} F(u)=u_n^2f(u_n)-u^2f(u), \end{aligned}$$
(43)

where we have used (42). From Fig. 5, we see that the deflection angle \(\alpha \) is given by

$$\begin{aligned} \alpha =\int _{u_o}^{u_n}\frac{\mathrm{d}u}{\sqrt{F}} +\int _{u_s}^{u_n}\frac{\mathrm{d}u}{\sqrt{F}}+\psi _o-\psi _s, \end{aligned}$$
(44)

where the sum of the first two terms is, according to Fig. 5, the integral form of the angle \(\angle \,\text {SLO}=\phi _s-\phi _o\). Equivalently, Eq. (44) is brought to the form

$$\begin{aligned} \alpha =2\int _{0}^{u_n}\frac{\mathrm{d}u}{\sqrt{F}} - \int _{0}^{u_o}\frac{\mathrm{d}u}{\sqrt{F}} - \int _{0}^{u_s}\frac{\mathrm{d}u}{\sqrt{F}}+\psi _o-\psi _s.\nonumber \\ \end{aligned}$$
(45)

By Fig. 5 and Eq. (40) we have \(\psi _o=\arcsin (bu_o\sqrt{f(u_o)})\) and \(\psi _s=\pi -\arcsin (bu_s\sqrt{f(u_s)})\). Using (42) in these expressions we arrive at

$$\begin{aligned} \alpha&=2\int _{0}^{u_n}\frac{\mathrm{d}u}{\sqrt{u_n^2f(u_n)-u^2f(u)}} -\pi \nonumber \\&\quad - \int _{0}^{u_o}\frac{\mathrm{d}u}{\sqrt{u_n^2f(u_n)-u^2f(u)}}- \int _{0}^{u_s}\frac{\mathrm{d}u}{\sqrt{u_n^2f(u_n)-u^2f(u)}}\nonumber \\&\quad +\arcsin \bigg (\frac{u_o}{u_n}\sqrt{\frac{f(u_o)}{f(u_n)}}\bigg ) +\arcsin \bigg (\frac{u_s}{u_n}\sqrt{\frac{f(u_s)}{f(u_n)}}\bigg ). \end{aligned}$$
(46)

The first line in (46) is the expression of the deflection angle we would have obtained had we assumed the observer and the source to be at spatial infinity (\(u_o\equiv 0\) and \(u_s\equiv 0\)). The four last terms in (46) are corrections added to the asymptotically flat expression of the deflection angle. From now on, we assume that the independent parameters (\(u_o\ll 1,u_s\ll 1,u_n\ll 1\)) are small compared to unity but are not 0.

Another important parameter is \(\sigma \). Since quintessence has not been observed in the cosmos, it is legitimate to assume \(\sigma \ll 1\); rather, we assume

$$\begin{aligned} \sigma \ll \min (u_o,u_s)<\max (u_o,u_s)\ll u_n\ll 1, \end{aligned}$$
(47)

considering thus quintessence as a perturbation to the Reissner–Nordström black hole (the constraint \(\max (u_o,u_s)\ll u_n\) is satisfied by definition of \(u_n\)). The evaluation of (46) consists in determining the series expansion of its r.h.s. in powers of the independent parameters (\(\sigma \ll 1,u_o\ll 1,u_s\ll 1,u_n\ll 1\)).

We will not assume the location of the observer to correspond to \(\phi _o=\pi /2\), as some authors did [26, 33], for this introduces a wrong term [34] in the series expansionFootnote 1 of \(\alpha \).

5 Strong deflection limit

5.1 Case \(w_{q}=-2/3\)

Conditions (47) being observed, we find in the case \(w_{q}=-2/3\)

$$\begin{aligned} \alpha&= 4 M u_n+[(15 \pi -16)M^2 -3 \pi Q^2] \frac{u_n^2}{4}\nonumber \\&\quad -\frac{M (1+M u_n) (u_o^2+u_s^2)}{u_n}\nonumber \\&\quad +\bigg \{\frac{(3 \pi -4)M}{2}+[(88-15 \pi )M^2 -(16-3 \pi ) Q^2]\frac{u_n}{4} \nonumber \\&\quad -\frac{M^2 (u_o+u_s)}{2}-\frac{2 M (u_o^2+u_s^2)}{4u_n^2}-\frac{M (u_o+u_s)}{2 u_n}\bigg \} \sigma .\nonumber \\ \end{aligned}$$
(48)

In the first line we recognize the expression of the deflection angle for the Reissner–Nordström black hole as determined in Ref. [35] (in Eq. (2.8) of Ref. [35], \(\gamma =1\) corresponds to Reissner–Nordström black hole and to obtain the first line in (48) from Eq. (2.8) of Ref. [35] insert \(r_++r_-=2M\), \(r_+r_-=Q^2\), and \(r_+^2+r_-^2=4M^2-2Q^2\), where \(r_-<r_+\) are the two horizons). The second line in (48) is a correction to the deflection angle for the Reissner–Nordström black hole when the observer and the source are at large, but finite, distances from the lens. Notice that this correction up to the power 2 in \(u_o\) and \(u_s\) does not depend on the charge of the black hole. The remaining terms, proportional to \(\sigma \), are corrections due to quintessence.

The power series in the r.h.s. of (48) has been determined as follows. The series expansions of the arcsin terms in (46) in powers of (\(\sigma ,u_o,u_s,u_n\)) is straightforward; the series expansion of the first line in (46) has been done in Appendix A of Ref. [35]. In this work we show how to derive the series expansion of the first term in the second line of (46); the series expansion of the second term is obtained by mere substitution \(u_o\leftrightarrow u_s\). In all calculations the series expansions are obtained in the order given in (47); that is, we first expand with respect to \(\sigma \) to order 1, then expand with respect to (\(u_o,u_s\)) to order 2, and finally we expand with respect to \(u_n\) to order 2 too. In the final expansion (48) we have kept all the terms with order not exceeding 2.

Set \(u=u_ox\) and \(0\le x\le 1\). The first term in the second line of (46) becomes

$$\begin{aligned} u_o\int _{0}^{1}\frac{\mathrm{d}x}{\sqrt{u_n^2f(u_n)-u_o^2x^2f(u_ox)}}, \end{aligned}$$
(49)

yielding in the case \(w_{q}=-2/3\)

$$\begin{aligned}&\frac{u_o}{\sqrt{u_n^2f(u_n)-u_o^2x^2f(u_ox)}}\simeq \Big (M+\frac{15 M^2 \sigma }{4}-\frac{3 Q^2 \sigma }{4}\Big )u_o\nonumber \\&\quad +\frac{u_o \sigma }{2 u_n^2}+ (3 M^2-Q^2)~\frac{u_n u_o}{2}+\frac{(2+3 M \sigma )u_o}{2 u_n}, \end{aligned}$$
(50)

where the integration over x is straightforward.

5.2 Case for all \(-1\le w_{q}< -1/3\)

In this section, we will obtain the general expression for the deflection angle for any value of \(w_{q}\). For simplicity, let us introduce a new constant

$$\begin{aligned} \gamma =3(w_{q}+1), \end{aligned}$$
(51)

which makes Eq. (23) easier to handle. Now, all the exponents in u in (23) are positive or zero. Since \(-1\le w_{q}< -1/3\), the new constant lies between \(0\le \gamma < 2\). Now, let us compute each term of Eq. (46) separately. For the sake of simplicity we will denote each term of (46) as follows:

$$\begin{aligned} I_{1}&=\int _{0}^{u_n}\frac{\mathrm{d}u}{\sqrt{u_n^2f(u_n)-u^2f(u)}}, \end{aligned}$$
(52)
$$\begin{aligned} I_{2}&=- \int _{0}^{u_o}\frac{\mathrm{d}u}{\sqrt{u_n^2f(u_n)-u^2f(u)}}\nonumber \\&\quad - \int _{0}^{u_s}\frac{\mathrm{d}u}{\sqrt{u_n^2f(u_n)-u^2f(u)}}, \end{aligned}$$
(53)
$$\begin{aligned} I_{3}&=\arcsin \bigg (\frac{u_o}{u_n}\sqrt{\frac{f(u_o)}{f(u_n)}}\bigg ) +\arcsin \bigg (\frac{u_s}{u_n}\sqrt{\frac{f(u_s)}{f(u_n)}}\bigg ), \end{aligned}$$
(54)

so that Eq. (46) can be expressed as

$$\begin{aligned} \alpha =2I_{1}-\pi +I_{2}+I_{3}. \end{aligned}$$
(55)

The final expression for \(\alpha \) needs to be separated in three ranges of \(\gamma \): (i) \(\gamma =0\) , (ii) \(0<\gamma \le 1\) and (iii) \(1<\gamma <2\). In the following sections, we will follow the same idea as in Sect. 5.1 to compute all these terms for any \(\gamma \).

5.2.1 Computing \(I_{1}\)

Let \(u=u_{n}x\) with \(0\le x \le 1\). First, we expand the integrand of \(I_{1}\) up to first order in \(\sigma \) and then up to second order in \(u_{n}\). By doing that, for \(0\le \gamma \le 1\) the expansion of the integrand of (52) takes the form

$$\begin{aligned}&\frac{u_n}{\sqrt{u_n^2f(u_n)-u_n^2x^2f(u_nx)}}\nonumber \\&\quad \simeq \frac{3 \sigma u_{n}^{\gamma } \left( x^{\gamma }-1\right) \left( Q^2 (x+1)^2 \left( x^2+1\right) -5 M^2 \left( x^2+x+1\right) ^2\right) }{4 (1-x)^{3/2} (x+1)^{7/2}}\nonumber \\&\qquad +\frac{u_{n}^2 \left( 3 M^2 \left( x^2+x+1\right) ^2-Q^2 (x+1)^2 \left( x^2+1\right) \right) }{2 \sqrt{1-x} (x+1)^{5/2}}\nonumber \\&\qquad +\frac{1}{\sqrt{1-x^2}} -\frac{3 M \sigma \left( x^2+x+1\right) u_{n}^{\gamma -1} \left( x^{\gamma }-1\right) }{2 (1-x)^{3/2} (x+1)^{5/2}}\nonumber \\&\qquad +\frac{M u_{n} \left( x^2+x+1\right) }{\sqrt{1-x} (x+1)^{3/2}}-\frac{\sigma u_{n}^{\gamma -2} \left( x^{\gamma }-1\right) }{2 \left( 1-x^2\right) ^{3/2}}, \end{aligned}$$
(56)

and for \(1<\gamma <2\)

$$\begin{aligned}&\frac{u_n}{\sqrt{u_n^2f(u_n)-u_n^2x^2f(u_nx)}}\nonumber \\&\quad \simeq \frac{u_{n}^2 \left( 3 M^2 \left( x^2+x+1\right) ^2-Q^2 (x+1)^2 \left( x^2+1\right) \right) }{2 \sqrt{1-x} (x+1)^{5/2}}\nonumber \\&\qquad +\,\frac{1}{\sqrt{1-x^2}} -\frac{3 M \sigma \left( x^2+x+1\right) u_{n}^{\gamma -1} \left( x^{\gamma }-1\right) }{2 (1-x)^{3/2} (x+1)^{5/2}}\nonumber \\&\qquad +\,\frac{M u_{n} \left( x^2+x+1\right) }{\sqrt{1-x} (x+1)^{3/2}}+\frac{\sigma u_{n}^{\gamma -2}(1-x^{\gamma })}{2 \left( 1-x^2\right) ^{3/2}}. \end{aligned}$$
(57)

Integration over x will depend on \(\gamma \) so that it is not possible to write down an explicit result for \(I_{1}\) for a general \(\gamma \). Therefore, for \(0\le \gamma \le 1\), we can write \(I_{1}\) as follows:

(58)

Note that \(\displaystyle \lim _{\gamma \rightarrow 0}\Gamma ((\gamma +1)/2)/\Gamma (\gamma /2)=0\) and \(\displaystyle \lim _{\gamma \rightarrow 0}\Gamma ((\gamma +1)/2)/(\gamma \Gamma (\gamma /2))=\sqrt{\pi }/2\) are finite, so that the above expression is well defined for \(\gamma =0\). Now, for the range \(1<\gamma < 2\), the integral becomes

$$\begin{aligned} I_{1}\simeq & {} \int _0^1 -\frac{3 M \sigma \left( x^2+x+1\right) u_{n}^{\gamma -1} \left( x^{\gamma }-1\right) }{2 (1-x)^{3/2} (x+1)^{5/2}} \, \mathrm{d}x\nonumber \\&+u_{n}^2 \left( \left( \frac{15 \pi }{8}-2\right) M^2-\frac{3 \pi Q^2}{8}\right) +2 M u_{n}\nonumber \\&+\frac{\sqrt{\pi } \sigma \, \Gamma \left( \frac{\gamma +1}{2}\right) u_{n}^{\gamma -2}}{2 \, \Gamma \left( \frac{\gamma }{2}\right) }+\frac{\pi }{2}. \end{aligned}$$
(59)

5.2.2 Computing \(I_{2}\)

First, we will compute the first term of \(I_{2}\) and then we can directly use that result to compute the second term of \(I_{2}\) by changing \(u_{o}\) for \(u_{s}\). As we did before, we set \(u=u_o x \) and expand up to first order in \(\sigma \) and then up to second order in \(u_{0}\). Finally, we need to take expansions up to second order in \(u_{n}\). The integrand of the first term of \(I_{2}\) is then expanded as follows:

$$\begin{aligned}&\frac{u_o}{\sqrt{u_n^2f(u_n)-u_o^2x^2f(u_ox)}}\simeq {\left\{ \begin{array}{ll} \frac{5}{4} M \sigma u_{o} \left( 7 M^2-3 Q^2\right) +\frac{1}{4} M u_{o} \left( -35 M^2 \sigma +15 Q^2 \sigma +4\right) \\ +\frac{3 \sigma u_{o} \left( 5 M^2-Q^2\right) }{4 u_{n}}+\frac{u_{o} \left( -15 M^2 \sigma +3 Q^2 \sigma +4\right) }{4 u_{n}}-\frac{1}{2} u_{o} u_{n} \left( Q^2-3 M^2\right) , &{} \gamma =0,\\ \frac{u_{o} \left( -15 M^2 \sigma u_{o}^{\gamma } x^{\gamma }+3 Q^2 \sigma u_{o}^{\gamma } x^{\gamma }+4\right) }{4 u_{n}}+\frac{3}{4} \sigma u_{o} \left( 5 M^2-Q^2\right) u_{n}^{\gamma -1}+M u_{o}\\ -\frac{1}{2} u_{o} u_{n} \left( Q^2-3 M^2\right) +\frac{1}{2} \sigma u_{o} (3 M u_{n}+1) u_{n}^{\gamma -3},&{} 0<\gamma< 1,\\ \big (M+\frac{15 M^2 \sigma }{4}-\frac{3 Q^2 \sigma }{4}\big )u_o +\frac{u_o \sigma }{2 u_n^2}+ (3 M^2-Q^2)~\frac{u_n u_o}{2}+\frac{(2+3 M \sigma )u_o}{2 u_n},&{} \gamma = 1,\\ -\frac{1}{2} u_{o} u_{n} \left( Q^2-3 M^2\right) +\frac{1}{2} \sigma u_{o} (3 M u_{n}+1) u_{n}^{\gamma -3}+M u_{o}+\frac{u_{o}}{u_{n}}, &{} 1<\gamma <2. \end{array}\right. } \end{aligned}$$
(60)

Therefore, by integrating over x and then compute the second integral by changing \(u_{o}\) by \(u_{s}\) we arrive at

$$\begin{aligned} I_{2}\simeq {\left\{ \begin{array}{ll} -\frac{1}{2} u_{n} \left( 3 M^2-Q^2\right) (u_{o}+u_{s})-M (u_{o}+u_{s})-\frac{u_{o}+u_{s}}{u_{n}}, &{} \gamma =0,\\ \frac{3 (u_{0}^{1+\gamma }+u_{s}^{1+\gamma })\sigma \left( 5 M^2-Q^2 \right) }{4 (\gamma +1) u_{n}}-\frac{3}{4} \sigma \left( 5 M^2-Q^2\right) (u_{o}+u_{s}) u_{n}^{\gamma -1}\\ -\frac{1}{2} u_{n} \left( 3 M^2-Q^2\right) (u_{o}+u_{s})+\frac{3 M \sigma (u_{o}^{\gamma +1}+u_{s}^{\gamma +1}) }{2 (\gamma +1) u_{n}^2}-\frac{3}{2} M \sigma (u_{o}+u_{s}) u_{n}^{\gamma -2}-M (u_{o}+u_{s})\\ +\frac{\sigma \left( u_{o}^{\gamma +1}+u_{s}^{\gamma +1}\right) }{2 (\gamma +1) u_{n}^3}-\frac{1}{2} \sigma (u_{o}+u_{s}) u_{n}^{\gamma -3}-\frac{u_{o}+u_{s}}{u_{n}},&{} 0<\gamma<1,\\ -\frac{1}{2} u_{n} \left( 3 M^2-Q^2\right) (u_{o}+u_{s})-\frac{3}{4} \sigma \left( 5 M^2-Q^2\right) (u_{o}+u_{s})-\frac{3 M \sigma (u_{o}+u_{s})}{2 u_{n}}\\ -M (u_{o}+u_{s})-\frac{\sigma (u_{o}+u_{s})}{2 u_{n}^2}-\frac{u_{s}+u_{0}}{u_n},&{} \gamma = 1,\\ -\frac{1}{2} u_{n} \left( 3 M^2-Q^2\right) (u_{o}+u_{s}) -\frac{3}{2} M \sigma (u_{o}+u_{s}) u_{n}^{\gamma -2}-M (u_{o}+u_{s})\\ -\frac{1}{2} \sigma (u_{o}+u_{s}) u_{n}^{\gamma -3}-\frac{u_{o}+u_{s}}{u_{n}},&{} 1<\gamma <2. \end{array}\right. } \end{aligned}$$
(61)

5.2.3 Computing \(I_{3}\)

By expanding the term \(I_{3}\) as we did before, i.e., first up to first order in \(\sigma \), then up to second order in \(u_o\) and finally up to second order in \(u_{n}\) we find

$$\begin{aligned} I_{3}\simeq {\left\{ \begin{array}{ll} -\frac{u_{n} \left( 3 M^2-Q^2\right) \left( M \sigma u_{o}+\sigma -2 u_{o}^2\right) }{4 u_{o}}+\frac{M \left( u_{o}^2 \left( 29 M^2 \sigma -13 Q^2 \sigma +8\right) -8 M u_{o}^3-4 M \sigma u_{o}-4 \sigma \right) }{8 u_{o}}\\ \frac{u_{o}^2 \left( 9 M^2 \sigma -Q^2 \sigma +8\right) -8 M u_{o}^3-4 M \sigma u_{o}-4 \sigma }{8 u_{o} u_{n}} -\frac{3 M \sigma u_{o} (M u_{o}-1)}{4 u_{n}^2}, &{} \gamma =0,\\ -\frac{3}{4} M^2 \sigma u_{n} u_{o}^{\gamma -1}-\frac{21 M^2 \sigma u_{o}^{\gamma +1}}{8 u_{n}}-\frac{1}{2} M^2 \sigma u_{o}^{\gamma }-\frac{3}{2} M^2 \sigma u_{o}^2 u_{n}^{\gamma -2}-M^2 u_{o}^2+\frac{15}{4} M^2 \sigma u_{o} u_{n}^{\gamma -1}\\ +\frac{3}{2} M^2 u_{o} u_{n}-\frac{1}{2} M \sigma u_{o}^{\gamma -1}-\frac{3 M \sigma u_{o}^{\gamma +1}}{4 u_{n}^2}-\frac{M \sigma u_{o}^{\gamma }}{2 u_{n}}-\frac{1}{2} M \sigma u_{o}^2 u_{n}^{\gamma -3}-\frac{M u_{o}^2}{u_{n}}+\frac{3}{2} M \sigma u_{o} u_{n}^{\gamma -2}\\ +M u_{o}+\frac{1}{4} Q^2 \sigma u_{n} u_{o}^{\gamma -1}+\frac{5 Q^2 \sigma u_{o}^{\gamma +1}}{8 u_{n}}-\frac{3}{4} Q^2 \sigma u_{o} u_{n}^{\gamma -1}-\frac{1}{2} Q^2 u_{o} u_{n} -\frac{\sigma u_{o}^{\gamma -1}}{2 u_{n}}\\ +\frac{1}{2} \sigma u_{o} u_{n}^{\gamma -3}+\frac{u_{o}}{u_{n}},&{} 0<\gamma< 1,\\ u_{o} \left( \frac{13 M^2 \sigma }{4}+M-\frac{3 Q^2 \sigma }{4}\right) +u_{n} \left( \frac{1}{4} \sigma \left( Q^2-3 M^2\right) +\frac{1}{2} u_{o} \left( 3 M^2-Q^2\right) \right) -M^2 u_{o}^2-\frac{M \sigma }{2}\\ +\frac{1}{u_n^2}\Big (\frac{\sigma u_{o}}{2}-\frac{1}{2} M \sigma u_{o}^2\Big )-\frac{1}{u_n}\Big ( \frac{\sigma }{2}-u_{o} (M \sigma +1)\Big ),&{} \gamma = 1,\\ -M^2 u_o^2+\frac{3}{2} M^2 u_o u_n-\frac{M u_o^2}{u_n}+\frac{1}{2} \sigma u_o u_n^{\gamma -3}+M u_o-\frac{1}{2} Q^2 u_o u_n-\frac{\sigma u_o^{\gamma -1}}{2 u_n}+\frac{u_o}{u_n}+\frac{3}{2} M \sigma u_{o} u_{n}^{\gamma -2}, &{} 1<\gamma <2. \end{array}\right. } \end{aligned}$$
(62)

5.2.4 Computing \(\alpha \)

Now, we have all the ingredients to find the final expression for \(\alpha \) for a general \(\gamma \). If we replace all the terms computed before in (55), for \(\gamma =0\) we find

$$\begin{aligned} \alpha= & {} \frac{1}{{u_{n}}}\Bigg [- M (u_{o}^2+u_{s}^2+\sigma ) +\frac{1}{8} \sigma (u_{o}+u_{s})\nonumber \\&\times \left( 9 M^2-Q^2\right) -\frac{\sigma }{2 }\Big (\frac{1}{u_{o}}+\frac{1}{u_{s}}\Big )\Bigg ]\nonumber \\&+\frac{1}{8} M \sigma (u_{s}+u_0) \left( 29 M^2-13 Q^2\right) \nonumber \\&+u_{n}^2 \Big ( \big (\frac{15 \pi }{4}-4\big ) M^2-\frac{3 \pi Q^2}{4}\Big )-M^2(u_{o}^2+ u_{s}^2+\sigma )\nonumber \\&+u_{n} \left( \frac{1}{2} M \left( (Q^2-3 M^2) \sigma +8\right) +\frac{\sigma \left( Q^2-3 M^2\right) }{4 }\right. \nonumber \\&\times \left. \Big (\frac{1}{u_{o}}+\frac{1}{u_{s}}\Big )\right) -\frac{M \sigma }{2 }\Big (\frac{1}{u_{o}}+\frac{1}{u_{s}}\Big ) \nonumber \\&-\frac{3}{4u_{n}^2} M \sigma \left( M (u_{o}^2+ u_{s}^2)-u_{s} -u_{o}\right) , \end{aligned}$$
(63)

for \(0<\gamma < 1\) we get

$$\begin{aligned}&\alpha =-3 M \sigma u_{n}^{\gamma -1}\nonumber \\&\quad \times \int _0^1 \frac{\left( x^2+x+1\right) \left( x^{\gamma }-1\right) \left( 5 M u_{n} \left( x^2+x+1\right) +2 (x+1)\right) }{2 (1-x)^{3/2} (x+1)^{7/2}} \, \mathrm{d}x \nonumber \\&\quad -\,\frac{M \left( M \sigma u_{o}^{\gamma }+2 M u_{o}^2+\sigma u_{o}^{\gamma -1}\right) }{2}\nonumber \\&-\,\frac{M \left( M \sigma u_{s}^{\gamma }+2 M u_{s}^2+\sigma u_{s}^{\gamma -1}\right) }{2}\nonumber \\&\quad +\,u_{n} \left( 4M+\frac{(Q^2 - 3 M^2)\sigma u_{o}^{\gamma -1}}{4}+\frac{(Q^2 - 3 M^2)\sigma u_{s}^{\gamma -1}}{4}\right) \nonumber \\&\quad -\, \frac{M \sigma u_{n}^{\gamma -3}}{2}(u_{o}^2+ u_{s}^2)\nonumber \\&\quad +\,u_{n}^2 \left( \Big (\frac{15 \pi }{4}-4\Big ) M^2-\frac{3 \pi Q^2}{4}\right) -\frac{3 (\gamma -1) M \sigma (u_o^{\gamma +1}+u_s^{\gamma +1})}{4 (\gamma +1) u_n^2}\nonumber \\&\quad +\,\frac{3 \sqrt{\pi } Q^2 \sigma \left( \sqrt{\pi } \gamma \, \Gamma \left( \frac{\gamma }{2}\right) -2 (2 \gamma +1) \, \Gamma \left( \frac{\gamma +1}{2}\right) \right) u_n^{\gamma }}{4 \gamma \, \Gamma \left( \frac{\gamma }{2}\right) }\nonumber \\&\quad -\,\frac{1}{u_{n}}\Big [\frac{\sigma [3 (7 \gamma -3) M^2+(1-5 \gamma ) Q^2] (u_o^{\gamma +1}+u_s^{\gamma +1})}{8 (\gamma +1)}\nonumber \\&\quad +\,\frac{1}{2} \sigma (u_o^{\gamma -1}+u_s^{\gamma -1})+\frac{1}{2} M \sigma \left( u_o^{\gamma }+u_s^{\gamma }\right) +M (u_o^2+u_s^2)\Big ]\nonumber \\&\quad +\,\frac{1}{2} \sigma u_n^{\gamma -2} \Big (\frac{2 \sqrt{\pi }\, \Gamma \big (\frac{\gamma +1}{2}\big )}{\Gamma \left( \frac{\gamma }{2}\right) }-3 M^2 (u_o^2+u_s^2)\Big ). \end{aligned}$$
(64)

Finally, for \(1<\gamma <2\) we find that the deflection angle becomes

$$\begin{aligned} \alpha= & {} -3 M \sigma u_{n}^{\gamma -1}\int _0^1 \frac{ (x^2+x+1) (x^{\gamma }-1)}{ (1-x)^{3/2} (x+1)^{5/2}} \, \mathrm{d}x\nonumber \\&+\,u_{n}^2 \Big [\Big (\frac{15 \pi }{4}-4\Big ) M^2-\frac{3 \pi Q^2}{4}\Big ]\nonumber \\&-\,M (u_{o}^2+u_{s}^2)(M+u_n^{-1})+4 M u_{n}\nonumber \\&+\,\Big [\frac{\sqrt{\pi }\, \Gamma \big (\frac{\gamma +1}{2}\big ) u_{n}^{\gamma -2}}{ \,\Gamma \big (\frac{\gamma }{2}\big )}-\frac{1}{2} (u_{o}^{\gamma -1}+ u_{s}^{\gamma -1})u_n^{-1}\Big ]\sigma .\nonumber \\ \end{aligned}$$
(65)

We see from (63)–(65), as was the case with (48) corresponding to \(\gamma =1\), that the corrections to the deflection angle for the Reissner–Nordström black hole (in the absence of quintessence) when the observer and the source are at large, but finite, distances (\(r_o=1/u_o,r_s=1/u_s\)) from the lens do not depend on the charge up to \(u_o^2\) and \(u_s^2\). All these corrections do not depend on \(\sigma \) and are symmetric functions of (\(u_o,u_s\)), so they are easily recognized in Eqs. (63) to (65) and (48). Corrections due to quintessence are all functions of \(\sigma \). Setting \(\sigma =0\) in any one of the equations (63) to (65) and (48) yields the deflection angle for the Reissner–Nordström black hole.

All integrals over x in Eqs. (63) to (65) do converge and could be given in closed forms, however, for some values of \(\gamma \) only. For instance, for \(\gamma =3/2\) the integral in (65) is given in terms of the complete elliptic integral E(m) and the complete elliptic integral of the first kind K(m)

$$\begin{aligned} \int _0^1 \frac{(x^2+x+1)(x^{3/2}-1)}{ (1-x)^{3/2} (x+1)^{5/2}} \, \mathrm{d}x=\frac{2}{3}-\frac{7E(1/2)}{\sqrt{2}}\\+\frac{5\sqrt{2}K(1/2)}{3}. \end{aligned}$$

How quintessence affects the deflection angle can be seen from the coefficient \(C_{\sigma }\) of \(\sigma \) in Eqs. (63)–(65), and (48). For instance, in (65) we have

$$\begin{aligned} C_{\sigma }\equiv \frac{\sqrt{\pi }\, \Gamma \big (\frac{\gamma +1}{2}\big ) u_{n}^{\gamma -2}}{ \,\Gamma \big (\frac{\gamma }{2}\big )}-\frac{1}{2} (u_{o}^{\gamma -1}+ u_{s}^{\gamma -1})u_n^{-1}. \end{aligned}$$
(66)

For fixed (\(u_0,\,u_s,\,u_n\)) satisfying (47), the coefficient \(C_{\sigma }\) has a smooth variation for \(1\le \gamma <2\). This follows from the series expansions of \(C_{\sigma }\) in the vicinity of \(\gamma =2\) and \(\gamma =1\), respectively:

$$\begin{aligned}&C_{\sigma }=\frac{\pi }{2}-\frac{1}{2 u_n}(u_o+u_s)+\mathcal {O}(\gamma -2),\end{aligned}$$
(67)
$$\begin{aligned}&C_{\sigma }=-\frac{1}{2 u_n}~\ln \Big (\frac{u_o u_s}{4 u_n^2}\Big )(\gamma -1)+\mathcal {O}(\gamma -1)^2. \end{aligned}$$
(68)

By (47), the second term in (67) is neglected with respect to the first term, so the coefficient \(C_{\sigma }\) varies roughly between 0 (68) and some factor of \(\pi \) for \(1\le \gamma <2\). Thus, for \(\gamma \) larger than unity, the effect of quintessence almost disappears and the values of the deflection angle are not very sensitive to variations in the values of \(\gamma \).

6 Conclusion

The motion of photons around black holes is one of the most studied problems in black hole physics. The behavior of light near black holes is important to study the structure of space-time near black holes. In particular, if the light returns after circling around the black hole to the observer, it cause a gravitational lens phenomenon. Light passing by the black hole will be deflected by angle which can be large or small depending on its distance from the black hole.

In present paper, we have extended our previous work for the Kiselev black hole by including the effects of the electric charge. This extra parameter enriches the structure of space-time with an additional horizon. By solving the geodesic equations, we have obtained the null geodesic structure for this black hole. Moreover, the lens equation provides the information as regards the bending angle. For a general \(w_q\), we managed to find an analytical expression for the bending angle in the strong deflection limit considering quintessence as a perturbation to the Reissner–Nordström. Since this geometry is non-asymptotically flat, one needs to be very careful to compute the bending angle since the standard approach, i.e. using the bending formula (see [29]), cannot be applied any more.

Instead of this approach, by using perturbation techniques and series expansions (assuming some physical conditions on the parameters), we directly integrate Eq. (23) for all \(w_q\) to find the bending angle. The final expression of the bending angle in the strong limit Eqs. (63) to (65) and (48) contain some corrections to the deflection angle obtained by a Reissner–Nordström black hole, which are proportional to the normalization parameter \(\sigma \), as well as corrections due to the finiteness of the distances of the source and observer to the lens.

It is instructive to compare the results of deflection in the presence of quintessence with those in the presence of phantom fields. In Ref. [35] light paths of normal and phantom Einstein–Maxwell-dilaton black holes have been investigated. It was emphasized that, in the presence of phantom fields, light rays are more deflected than in the normal case. Adopting the Bozza formalism [36], the authors of Ref. [37] have shown that the lensing properties of the phantom field black hole are quite similar to that of the electrically charged Reissner–Norström black hole, i.e., the deflection angle and angular separation increase with the phantom constant. A similar approach was adopted in [38] to study lensing by a regular phantom black hole. These authors have demonstrated that the deflection angle does not depend on the phantom field parameter in the weak field limit, whereas the strong deflection limit coefficients are slightly different form that of Schwarzschild black hole (see also [39]). In our case, \(C_{\sigma }\) (66) is positive for \(1<\gamma <2\). This means that the deflection angle is a bit larger if quintessence is present.

As future work, one can also study the lensing for other interesting configurations such as Nariai BHs, ultra cold BHs, and also for rotating black holes surrounded by quintessence matter. This type of work might be important to study highly redshifted galaxies, quasars, supermassive black holes, exoplanets and dark matter candidates, etc.