Gravitational waves from pulsars in the context of magnetic ellipticity

Abstract

In one of our previous articles we have considered the role of a time dependent magnetic ellipticity on the pulsars’ braking indices and on the putative gravitational waves these objects can emit. Since only nine of more than 2000 known pulsars have accurately measured braking indices, it is of interest to extend this study to all known pulsars, in particular as regards gravitational wave generation. To do so, as shown in our previous article, we need to know some pulsars’ observable quantities such as: periods and their time derivatives, and estimated distances to the Earth. Moreover, we also need to know the pulsars’ masses and radii, for which we are adopting current fiducial values. Our results show that the gravitational wave amplitude is at best $h \sim 10^{-28}$. This leads to a pessimistic prospect for the detection of gravitational waves generated by these pulsars, even for Advanced LIGO and Advanced Virgo, and the planned Einstein Telescope, if the ellipticity has a magnetic origin.

1 Introduction

It is well known that, besides compact binaries, rapidly rotating neutron stars are promising sources of gravitational waves (GWs) which could be detected in a near future by advanced LIGO (aLIGO) and advanced VIRGO (AdV), and also by the planned Einstein Telescope (ET). These sources generate continuous GWs whether or not they are perfectly symmetric around their rotation axis, i.e., they show some equatorial ellipticity.

It is worth stressing that the equatorial ellipticity is an extremely relevant parameter since the GW amplitude is directly proportional to it. Therefore, if the ellipticity be extremely small, i.e., $\varepsilon \ll 10^{-5}$, the GW amplitude will also be extremely small, implying that the detection of such continuous GWs generated by pulsars may be unattainable (see, [1, 2]) with current technology. For comparison, some authors argue that an acceptable upper limit for the ellipticity would be around $\varepsilon \sim 10^{-6}$ (see, e.g., [3]). An important mechanism for producing asymmetries is the development of non-axisymmetric instabilities in rapidly rotating neutron stars driven by the gravitational emission reaction or by nuclear matter viscosity (see, e.g., [4], and the references therein).

We explore, in the present paper, some consequences of an ellipticity generated by the magnetic dipole of the pulsars themselves. It is well known that, for strong magnetic fields ($\sim$10$^{12}$ to $10^{15}$ G), the equilibrium configuration of a neutron star can be distorted due to the magnetic pressure. Therefore, both rotation and magnetic field combined can produce a flattened equilibrium star. However, star rotation and strong magnetic field may not be sufficient for GW emission, other effects must be associated with it, such as the pulsar’s precession (see, e.g., [5]).

The main goal of the present paper is to extend our previous study where the role of ellipticity of magnetic origin ($\varepsilon _{\mathrm{B}}$) was considered [6]. Since in that paper we were also interested in braking indices, which are until now accurately measured for only nine pulsars, we had restricted that study exclusively for those very pulsars.

However, $\varepsilon _{\mathrm{B}}$ does not depend on the pulsar braking index; maybe it is the other way around. In fact, $\varepsilon _{\mathrm{B}}$ is mostly associated to both the pulsar period (P) and its time derivative ($\dot{P}$), for a given value of mass, radius and moment of inertia. Therefore, it is straightforward to extend the $\varepsilon _{\mathrm{B}}$ calculation for all pulsars with known P and $\dot{P}$. Consequently, with $\varepsilon _{\mathrm{B}}$ in hands, we can calculate the GW amplitudes for all pulsars with known P, $\dot{P}$, and their distances to the Earth. In this regard it is worth mentioning that the distance to these sources has been established, although there are observational uncertainties in its determination, which are not taken into account in the present paper. A putative uncertainty in one order of magnitude in distance would mean this very uncertainty in the GW amplitude.

To do so this paper is organized as follows: Sect. 2 is devoted to a brief procedure description which is conducted by a basic set of equations. In Sect. 3 we present the calculations and discuss the results obtained. Finally, in Sect. 4 we summarize the main conclusions and make remarks about them.

2 Basic equations

In Ref. [6] we consider in detail how to relate $\varepsilon _{\mathrm{B}}$ to P and $\dot{P}$. In addition, the basic equations used for calculating the amplitude of the putative GWs generated by pulsars are also presented. All those equations are used to calculate the relevant quantities of this present paper. Therefore, here we are only providing the main steps for deriving these relevant equations.

Recall that the equatorial ellipticity is given by (see e.g., [7])

$$\begin{aligned} \varepsilon =\frac{I_{xx}-I_{yy}}{I_{zz}}, \end{aligned}$$

(1)

where $I_{xx}$, $I_{yy}$, $I_{zz}$ are the moment of inertia with respect to the rotation axis (hereafter simply denoted I), z, and along the directions perpendicular to it.

Regarding the ellipticity of magnetic origin, it was shown by different authors [8,9,10] to be given by

$$\begin{aligned} \varepsilon _\mathrm{B} = \kappa \frac{B_0^2 R^4}{G M^2}\sin ^2\phi , \end{aligned}$$

(2)

where $B_0$ is the dipole magnetic field, R and M are the radius and the mass of the star, respectively, $\phi$ is the angle between the rotation and magnetic dipole axes, whereas $\kappa$ is the distortion parameter, which depends on both the star equation of state (EoS) and the magnetic field configuration (see e.g., [10]).

Regarding the GW amplitude, one finds in the literature the following equation:

$$\begin{aligned} h^{\mathrm{SD}} = \left( \frac{5}{2}\frac{G}{c^3}\frac{I}{r^2}\frac{\mid \dot{f}_\mathrm{rot}\mid }{f_\mathrm{rot}}\right) ^{1/2} \end{aligned}$$

(3)

(see, e.g., [11]) where one considers the whole contribution to $\dot{f}_\mathrm{rot}$ to be due to GW emission, i.e., we have the spin-down limit. This equation must be modified to take into account the magnetic braking (see [1, 2]). This can be done by writing

$$\begin{aligned} \dot{\bar{f}}_\mathrm{rot} = \eta \dot{f}_\mathrm{rot}, \end{aligned}$$

(4)

where $\dot{\bar{f}}_\mathrm{rot}$ can be interpreted as the part of $\dot{f}_\mathrm{rot}$ related to the GW emission brake. Consequently, the GW amplitude is given by

$$\begin{aligned} h^2 = \frac{5}{2}\frac{G}{c^3}\frac{I}{r^2}\frac{\mid \dot{\bar{f}}_{rot}\mid }{f_{rot}} = \frac{5}{2}\frac{G}{c^3}\frac{I}{r^2}\frac{\mid \dot{f}_\mathrm{rot}\mid }{f_\mathrm{rot}} \, \eta . \end{aligned}$$

(5)

On the other hand, the GWs amplitude can also be written as follows:

$$\begin{aligned} h = \frac{16\pi ^2G}{c^4} \frac{I\varepsilon f_\mathrm{rot}^2}{r} \end{aligned}$$

(6)

(see, e.g., [7]). By combining the two equations above one can obtain $\varepsilon _{\mathrm{B}}$ in terms of P, $\dot{P}$ (observable quantities), $\eta$ and I, namely

$$\begin{aligned} \varepsilon = \sqrt{\frac{5}{512\pi ^4} \frac{c^5}{G}\frac{\dot{P}P^3}{I}\eta }. \end{aligned}$$

(7)

Still concerning $\eta$, as discussed in detail by [6], it can be also be interpreted as the fraction of the rotation power ($\dot{E}_{\mathrm{rot}}$) emitted in the form of GWs ($\dot{E}_{\mathrm{GW}}$), or yet, the efficiency for GW generation. Obviously, part of the rotation power is emitted in the form of electromagnetic radiation through magnetic dipole emission ($\dot{E}_{\mathrm{d}}$).

Also, in [6] an useful equation is shown relating $\eta$ to the pulsar dipole magnetic field, which is derived by recalling that the magnetic brake is related to P and $\dot{P}$, i.e.

$$\begin{aligned} \bar{B}_0\sin ^2\phi = \frac{3 I c^3}{4 \pi ^2 R^6} P \dot{P} \end{aligned}$$

(8)

where $\bar{B}_0$ would be the magnetic field if the breaking is purely magnetic. Since pulsars might also emit GWs, $B_0 < \bar{B}_0$ is a reasonable assumption. Thus, the equation relating $\eta$ to the pulsar dipole magnetic field reads (see [6] for details)

$$\begin{aligned} \eta = 1 - \left( \frac{B_0}{\bar{B}_0} \right) ^2. \end{aligned}$$

(9)

By substituting this last expression into Eq. (2), one obtains

$$\begin{aligned} \varepsilon _\mathrm{B} = \frac{3Ic^3}{4\pi ^2GM^2R^2}P\dot{P} \left( 1 - \eta \right) \kappa . \end{aligned}$$

(10)

In addition, by combining this equation with Eq. (7), one has

$$\begin{aligned} \eta = \frac{288}{5}\frac{I^3c}{GM^4R^4}\frac{\dot{P}}{P}\left( 1-\eta \right) ^2 \kappa ^2. \end{aligned}$$

(11)

Since $\varepsilon$ and $\eta \ll 1$, one can readily obtain the following useful equations:

$$\begin{aligned} \varepsilon _\mathrm{B} \simeq \frac{3Ic^3}{4\pi ^2GM^2R^2}P\dot{P}\kappa \end{aligned}$$

(12)

and

$$\begin{aligned} \eta \simeq \frac{288}{5}\frac{I^3c}{GM^4R^4}\frac{\dot{P}}{P} \kappa ^2. \end{aligned}$$

(13)

Now, we are ready to calculate $\varepsilon _{\mathrm{B}}$, $\eta$ and the GW amplitudes for all pulsars with known P, $\dot{P}$, and estimated distances to the Earth, for given values of M, R, I and $\kappa$. The next section is devoted to such an issue as well as the corresponding discussion of the results.

Fig. 1

The P–$\dot{P}$ diagram for radio pulsars obtained from the ATNF Pulsar Catalog (http://www.atnf.csiro.au/people/pulsar/psrcat/)

Fig. 2

Correlation between the magnetic ellipticity and the period for all pulsars with known P, $\dot{P}$

Fig. 3

Ellipticity histogram for the 1964 pulsars of Table 1 for $k=10$

3 Calculations and discussions

The table with the necessary parameters used for the calculation of $\varepsilon _{\mathrm{B}}$, $\eta$ and h as well as the adopted criteria for the selection of the pulsars can be found in the appendix. Figure 1 is made with columns 2 and 3 of this very table, in which the pulsars’ periods and their corresponding time derivatives (spin-down rate) are shown. Although being a well-known diagram, it will be very useful for the discussions of the subsequent results. It is easily distinguishable two pulsar populations: the millisecond pulsars in the lower left (with periods $P<10^{-2}\,\mathrm {s}$), composed of very old pulsars, and another class of isolated pulsars with periods $10^{-1}<P<10^1\,\mathrm {s}$, composed of younger pulsars which have already depleted a respectful fraction of their rotation power.

On the last three columns of Table 1, we present the results of our calculations, namely, $\varepsilon _{\mathrm{B}}$, $\eta$ and h. In order to perform these calculations, we also need to provide values for M, R, I and $\kappa$. For the first three parameters, we are adopting fiducial values, namely, $M = 1.4 M_{\odot }$, $R = 10\, \mathrm{km}$, and $I = 10^{38} \mathrm{kg\,m^{2}}$. Regarding the distortion parameter $\kappa$, as already mentioned, it depends on the EoS and on the magnetic field configuration. In particular, we choose $\kappa = 10$, but values as high as $\kappa = 1000$ could be considered, although they are probably unrealistic (see, e.g., [10] for a brief discussion).

From Eq. (12), we find that $\varepsilon _{\mathrm{B}}$ is extremely small ($\sim$10$^{-19}$ to $10^{-15}$) for the millisecond pulsars of Table 1, even when the extremely optimistic case in which $\kappa \sim 1000$ is considered. Moreover, the ellipticity distribution assumes values of the order of $\sim$ $10^{-10}$ for the slowest pulsars. In Fig. 2 we present $\log \varepsilon _{\mathrm{B}}$ versus P for $\kappa = 10$ for all pulsars of Table 1. The ellipticity for different values of $\kappa$, since $\varepsilon _{\mathrm{B}} \propto \kappa$, can be readily obtained.

An interesting histogram can also be made from Table 1, namely, the number of pulsars for a $\log \varepsilon _{\mathrm{B}}$ bin (see Fig. 3). The high number of pulsars concentrated around $\sim$10$^{-10} (10^{-8})$ for $k = 10 \,(1000)$ is worth noticing.

Fig. 4

Correlation between the efficiency and the period for all pulsars with known P, $\dot{P}$

Fig. 5

Histogram of the efficiencies (or the spin-down ratio) for the 1964 pulsars of Table 1 for $k=10$

A similar analysis can be made for $\eta$ by means of Eq. (13). In Fig. 4 we present $\log \eta$ versus P for $\kappa = 10$ for all pulsars of Table 1. Notice that $\eta$ is also extremely small, even if one consider $\kappa = 1000$. Also, an histogram for the number of pulsars for $\log \eta ^{1/2}$ can be seen in Fig. 5. This quantity ($\eta ^{1/2}$) is equivalent to the ratio $h/h^\mathrm{{SD}}$, i.e., the spin-down ratio. One may notice a peak in the $\eta$ histogram at $10^{-16}$ to $10^{-15}$ for the pulsars of Table 1. As for $\varepsilon _{\mathrm{B}}$, $\eta$ for different values of $\kappa$ can easily be obtained, since $\eta \propto \kappa ^2$. Thus, even for $\kappa = 1000$ the peak in the histogram would be around $10^{-12}$–$10^{-11}$. Before proceeding, it is worth stressing that the two pulsar populations mentioned above also clearly appear in Figs. 2, 3, 4 and 5.

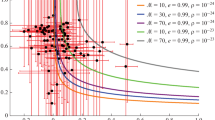
These extremely small values of $\varepsilon _{\mathrm{B}}$ and $\eta$ have very important consequences as regards the detectability of GWs generated by the pulsars, if the ellipticity is mainly due to the magnetic dipole of the pulsars themselves. Our calculations show that the GW amplitudes for most of these pulsars are at best seven orders of magnitude smaller than those obtained by assuming the spin-down limit (SD); see Fig. 6. Notice that, even considering an extremely optimistic case, the value of the ellipticity is at best $\varepsilon _{\mathrm{B}} \sim 10^{-5}$ (for PSR J1846-0258) and the corresponding efficiency $\eta \sim 10^{-8}$. Thus, the GW amplitude even in this case would be four orders of magnitude lower than the amplitude obtained by assuming the spin-down limit ($\eta =1$).

Fig. 6

Histogram of the amplitude of GWs for all pulsars with known P, $\dot{P}$

Still regarding Fig. 5, a recent result from the searches for GWs from 200 pulsars by using the aLIGO first observation run data (see Fig. 4 of [12]) presents a similar distribution for $h/h^\mathrm{{SD}}$, but displaced by some orders of magnitude. The high ellipticity values they found should be considered as upper limits since no continuous GW has been detected. In our present work, as already mentioned, we have considered that the ellipticity is caused exclusively by magnetic dipole and showed that such a mechanism alone could not generate a much strong star deformation. In our view, another mechanism or other mechanisms should be associated to the magnetic field to make possible those putative high ellipticities, e.g., high precession and/or non-conventional EoS.

For a matter of comparison, some authors argue that a fiducial upper limit for the ellipticity would be around $\varepsilon \sim 10^{-6}$, considering asymmetries supported by anisotropic stress built up during the crystallization period of the crust (see, e.g., [3], and references therein).

Finally, since the predicted GW amplitudes are extremely small for all pulsars of Table 1, and thousands of years of observing time would be needed, even advanced detectors such as aLIGO and AdV, and the planned ET would not be able to detect these pulsars, if the ellipticity is of magnetic dipole origin.

4 Conclusions and final remarks

In this paper, we extend our previous studies [6] in which we considered the role of magnetic ellipticity on the braking index and on the pulsar distortion. It is well known that, for strong magnetic fields ($\sim$10$^{12}$ to $10^{15}$ G), the equilibrium configuration of a neutron star can be distorted by magnetic tension. Such magnetic fields could not generate enough deformation to lead to high values of ellipticity. The presence of a magnetic field exceeding the magnetar strength ($\sim$10$^{16}$ G) could account for an ellipticity of $\sim$10$^{-4}$. Recall that much higher values of magnetic fields could violate the Virial Theorem and disrupt the star equilibrium (see, e.g., [13]).

Here we consider the role played by the magnetic dipole field on the deformation of the known pulsars and its consequences as regards the generation of GWs. In particular, we obtained the useful Eqs. (12) and (13), with which one can calculate $\varepsilon _{\mathrm{B}}$ and $\eta$ in terms of I, M, R, $\kappa$ and the observable quantities P and $\dot{P}$, and distances to the Earth. Moreover, the amplitudes of GWs can be readily calculated.

Regarding the GWs generated by the pulsars, our calculations show that the amplitudes are extremely small, as a result the prospect for their detection, even for aLIGO, AdV and the planned ET, would be pessimistic. This conclusion is obviously dependent on the mechanism that generates the ellipticity. If there is some other mechanism that could generate substantially larger ellipticities, the prospects for the detection of GWs emitted by the pulsars of Table 1 could be much less pessimistic.

Appendix

Table 1 presents the periods (P), their first derivatives ($\dot{P}$), and the estimated distances (d) from Earth of 1964 pulsars drawn from the ATNF Pulsar Catalog (http://www.atnf.csiro.au/people/pulsar/psrcat/). Another selection criterion is that the pulsars must have only an unique measured value for $\dot{P}$. Also presented are values of $\eta$, $\varepsilon$ and h calculated from the appropriate equations, which can be found in Sect. 3.

Table 1 P, $\dot{P}$ and d for pulsars drawn from the ATNF catalog, with an unique measured value for $\dot{P}$, and the corresponding $\varepsilon$, $\eta$ and h for $\kappa = 10$