1 Introduction

The observed cosmic acceleration at late time is one of the most important mysteries in the universe [1,2,3]. This phenomenon may be explained by introducing an unknown form of energy to govern the dynamics of the late-time universe [4, 5]. For the simplest case, this unknown form of energy, dubbed dark energy, is supposed to be in the form of evolving scalar fields. In general, viable dark energy models should have a mechanism to alleviate the coincidence problem, which is the problem why the energy density of dark energy and matter are comparable in magnitude at present although they evolve independently throughout the whole evolution of the universe [6,7,8]. A possible assumption for alleviating the coincidence problem is based on the introduction of an interaction between dark energy and dark matter. Various phenomenological forms of the interaction between dark energy and dark matter have been proposed and investigated in the literature [9,10,11,12]. Interestingly, it has recently been shown that models of dark energy in which an interaction between dark energy and dark matter is assumed can satisfy the bound on the Hubble parameter at redshift 2.34 from BOSS data, while the \(\Lambda \)CDM model predicts too large Hubble parameter at this redshift [13].

In addition to the phenomenological models of the interaction between dark energy and dark matter, the models of the interaction between dark energy and dark matter can be constructed from the frame transformation of the theory of gravity. Applying the conformal transformation to some classes of scalar–tensor theories, one obtains the coupling terms between dark energy and dark matter in the Einstein frame in which the gravity action takes the Einstein–Hilbert form [14,15,16]. The cosmological consequences of the interaction between dark energy and dark matter due to the conformal transformation have been investigated in [17, 18]. However, in order to transform general scalar–tensor theories to Einstein frame, we need transformations that are more general than the conformal transformation. It has been shown that subclasses of the GLPV theory which is the generalization of the Horndeski theory can be transformed to the Einstein frame using the disformal transformation defined as [19,20,21]

$$\begin{aligned} \bar{g}_{\mu \nu } = C(\phi )g_{\mu \nu } + D(\phi ,X)\phi _{,\mu }\phi _{,\nu }, \end{aligned}$$
(1)

where subscript \({}_,\) denotes partial derivatives, and \(X = - \frac{1}{2}\partial _\mu \phi \partial ^\mu \phi \) is the kinetic energy of scalar field. Here, the conformal coefficient C depend only on scalar field \(\phi \), while the disformal coefficient D can depend both on \(\phi \) and its kinetic term X. In the case where D depends only on the scalar field, the above transformation provides relations among some pieces of Lagrangian in the Horndeski theory, but cannot generate a piece of the GLPV Lagrangian from the Horndeski theory [22]. However, it has been shown that if C also depends on X, the application of the transformation to GLPV action can generate terms that do not belong to the GLPV theory [20] and therefore these terms might be a cause of the Ostrogradski instabilities in the theories. Nevertheless, according to the discussion in [23], the Ostrogradski instabilities can be eliminated by hidden constraints in some cases.

The cosmological consequences of the interaction between dark energy and dark matter due to the disformal transformation, called disformal coupling between dark energy and dark matter, has been studied in various aspects for the case where the conformal and disformal coefficients depend on the field \(\phi \) only. It has been shown in [24] that the disformal coupling between dark energy and dark matter leads to a new stable fixed point compared with the case of conformal coupling, and the cosmological parameters at this fixed point can satisfy the observational bounds. The metric singularity of the new fixed point found in [24] presents the phantom behavior in the Jordan frame [25]. The influences of the disformal coupling on the observational quantities such as the CMB and matter power spectra have been investigated in [26,27,28]. In this work, we study the disformal coupling between dark energy and dark matter for more general case where the disformal coefficients depends on both \(\phi \) and its kinetic terms X. The physical motivation for such disformal coupling is related to the frame transformation among the general scalar–tensor theories presented above. Our aims are to study how the kinetic-dependent disformal coupling influences the evolution of the universe at late time by finding and analyzing the physically relevant fixed points of the model, rather than search for all possible fixed points of the model. We will show in the following sections that there are features arising only for the case where the disformal coefficient depends on both \(\phi \) and X.

In Sect. 2, the evolution equations for dark energy and dark matter with disformal coupling are presented in the covariant form. The autonomous equations for this model of dark energy are computed in Sect. 3, and the evolution of the late-time universe is studies using the dynamical analysis in Sect. 4. The conclusions are given in Sect. 5.

2 Disformal coupling between dark energy and dark matter

In this section, we derive the disformal coupling between scalar field and matter arising from the general disformal transformation defined in Eq. (1). From the metric in Eq. (1), we have

$$\begin{aligned} \bar{g}^{\mu \nu } = \frac{1}{C}g^{\mu \nu } - \frac{D \phi ^{,\mu }\phi ^{,\nu }}{C^2 - 2CDX} . \end{aligned}$$
(2)

In order to study coupling between dark energy and dark matter due to disformal transformation, we suppose that the field \(\phi \) in the disformal transformation plays a role of dark energy, and therefore the interaction between dark energy and dark matter can occur when the Lagrangian of dark matter depends on metric \(\bar{g}_{\mu \nu }\) defined in Eq. (1). Thus we write the action for gravity in terms of metric \(g_{\mu \nu }\) and write the action for the dark matter in terms of \(\bar{g}_{\mu \nu }\) as

$$\begin{aligned} S&=\int \mathrm{d}^4x \left\{ \sqrt{-g} \left[ \frac{1}{2}R + P(\phi ,X)+ \mathscr {L}_\mathcal{M}(g_{\mu \nu }) \right] \right. \nonumber \\&\quad \left. + \sqrt{ -\bar{g}}\mathscr {L}_{c}(\bar{g}_{\mu \nu }, \psi , \psi _{,\mu })\phantom {\frac{1}{2}}\right\} \end{aligned}$$
(3)

where we have set \(1/\sqrt{8\pi G} = 1\), \(P(\phi ,X) \equiv X - V(\phi )\) is the Lagrangian of the scalar field, \(V(\phi )\) is the potential of the scalar field, \(\mathscr {L}_{c}\) is the Lagrangian of dark matter and \(\mathscr {L}_\mathcal{M}\) is the Lagrangian of ordinary matter including baryon and radiation. Varying this action with respect to \(g_{\alpha \beta }\), we get

$$\begin{aligned} G^{\alpha \beta } = T^{\alpha \beta }_\phi + T^{\alpha \beta }_{c}+ T^{\alpha \beta }_\mathcal{M}, \end{aligned}$$
(4)

where \(G^{\alpha \beta }\) is the Einstein tensor computed from \(g_{\mu \nu }\), and the energy momentum tensor for scalar field and matter are defined in the unbarred frame as

$$\begin{aligned} T^{\mu \nu }_{\phi }&\equiv \frac{2}{\sqrt{-g}}\frac{\delta (\sqrt{-g}P(\phi ,X))}{\delta g_{\mu \nu }},\quad T^{\mu \nu }_{\mathcal{M}} \equiv \frac{2}{\sqrt{-g}} \frac{\delta (\sqrt{-g} \mathscr {L}_\mathcal{M})}{\delta g_{\mu \nu }}, \end{aligned}$$
(5)
$$\begin{aligned} T^{\mu \nu }_{{c}}&\equiv \frac{2}{\sqrt{-g}}\frac{\delta \left( \sqrt{-\bar{g}}\mathscr {L}_{{c}}\right) }{\delta g_{\mu \nu }}\, . \end{aligned}$$
(6)

Using these definitions of the energy momentum tensor and the conservation of the energy momentum tensor of ordinary matter, we have \(\nabla _\alpha (T^{\alpha \beta }_\phi + T^{\alpha \beta }_{{c}}) =0\) due to \(\nabla _\alpha G^{\alpha \beta }=0\). However, we see that the energy momentum tensors of dark energy and dark matter do not separately conserve because the Lagrangian of dark matter depends on field \(\phi \). On the other hand, since \(\bar{g}_{\alpha \beta }\) does not depend on \(\psi \), the energy momentum tensor of dark matter is conserved in the barred frame such as

$$\begin{aligned} \bar{\nabla }_\alpha \bar{T}^{\alpha \beta }_{c}=0, \end{aligned}$$
(7)

where \(\bar{\nabla }_\alpha \) is defined from barred metric, and the energy momentum tensor in the barred frame is related to that in the unbarred frame defined in Eq. (6) as

$$\begin{aligned} T^{\alpha \beta }_{c}&= \frac{\sqrt{-\bar{g}}}{\sqrt{-g}}\, \frac{\delta \bar{g}_{\rho \sigma }}{\delta g_{\alpha \beta }}\, \frac{2}{\sqrt{-\bar{g}}} \frac{\delta \left( \sqrt{-\bar{g}}\mathscr {L}_{{c}}\right) }{\delta \bar{g}_{\rho \sigma }} \nonumber \\&= \frac{\sqrt{-\bar{g}}}{\sqrt{-g}}\frac{\delta \bar{g}_{\rho \sigma }}{\delta g_{\alpha \beta }}\bar{T}^{\rho \sigma }_{c}. \end{aligned}$$
(8)

To compute the interaction terms between scalar field and dark matter, we vary the action with respect to \(\phi \) as

$$\begin{aligned} \delta S = \underbrace{\int \mathrm{d}x^4 \sqrt{-g} \frac{\delta P}{\delta \phi }\delta \phi }_{S_\phi } + \underbrace{\int \mathrm{d}^4x \frac{\delta (\sqrt{-\bar{g}} \mathscr {L}_{{c}})}{\delta \phi }\delta \phi }_{S_{c}} = 0. \end{aligned}$$
(9)

One can show that

$$\begin{aligned} S_\phi = \int \mathrm{d}^4x \sqrt{-g}\left( \phi ^{,\mu }_{;\mu } - V_{,\phi } \right) \delta \phi , \end{aligned}$$
(10)

where \({}_;\) denotes the covariant derivative and \(V_{,\phi } = \partial V / \partial \phi \), and

$$\begin{aligned} S_{c}= & {} \int \mathrm{d}^4x \frac{\delta (\sqrt{-\bar{g}} \mathscr {L}_{{c}})}{\delta \bar{g}_{\alpha \beta }}\frac{\delta \bar{g}_{\alpha \beta }}{\delta \phi }\delta \phi \nonumber \\= & {} \int \mathrm{d}^4x \left\{ \frac{\sqrt{-\bar{g}}}{2} \left[ \bar{T}^{\alpha \beta }_{c}\left( C_{,\phi }g_{\alpha \beta } + D_{,\phi }\phi _{,\alpha }\phi _{,\beta }\right) \right] \right. \nonumber \\&-\sqrt{-g}\nabla _\beta \left( \frac{\sqrt{-\bar{g}}}{\sqrt{-g}} \bar{T}^{\alpha \beta }_{c}D \phi _{,\alpha }\right) \nonumber \\&\left. + \frac{\sqrt{-g}}{2} \nabla _\omega \left[ \phi ^{,\omega } \frac{\sqrt{-\bar{g}}}{\sqrt{-g}} \bar{T}^{\alpha \beta }_{c}\left( D_{,X}\phi _{,\alpha }\phi _{,\beta }\right) \right] \right\} \,\delta \phi . \end{aligned}$$
(11)

Combining Eq. (10) with the above equation, we obtain the evolution equation for the scalar field \(\phi \),

$$\begin{aligned} \phi ^{,\alpha }_{;\alpha } - V_{,\phi }= & {} \nabla _\beta \left( \frac{\sqrt{-\bar{g}}}{\sqrt{-g}} \bar{T}^{\alpha \beta }_{c}D \phi _{,\alpha }\right) \nonumber \\&- \frac{1}{2} \frac{\sqrt{-\bar{g}}}{\sqrt{-g}} \bar{T}^{\alpha \beta }_{c}\left( C_{,\phi }g_{\alpha \beta } + D_{,\phi }\phi _{,\alpha }\phi _{,\beta }\right) \nonumber \\&- \frac{1}{2} \nabla _\omega \left[ \phi ^{,\omega } \frac{\sqrt{-\bar{g}}}{\sqrt{-g}}\bar{T}^{\alpha \beta }_{c}D_{,X}\phi _{,\alpha }\phi _{,\beta }\right] \equiv Q. \nonumber \\ \end{aligned}$$
(12)

Multiplying the above equation by \(\phi ^{,\lambda }\), we get

$$\begin{aligned} Q\phi ^{,\lambda } = \nabla _\alpha T^{\alpha \lambda }_\phi = - \nabla _\alpha T^{\alpha \lambda }_{c}. \end{aligned}$$
(13)

In order to write the barred quantities in the interaction term Q in terms of unbarred quantities, we write Eq. (8) as

$$\begin{aligned} T^{\alpha \beta }_{c}= \left( C \delta ^\alpha _\rho \delta ^\beta _\sigma - \frac{1}{2} D_{,X}\phi ^{,\alpha }\phi ^{,\beta }\phi _{,\rho }\phi _{,\sigma }\right) \mathrm{J}\bar{T}^{\rho \sigma }_{c}, \end{aligned}$$
(14)

where \(\mathrm{J}\equiv \sqrt{-\bar{g}} / \sqrt{-g}\). Hence, we get

$$\begin{aligned} T_{c}= & {} g_{\alpha \beta } T^{\alpha \beta }_{c}= \mathrm{J}C g_{\rho \sigma } \bar{T}^{\rho \sigma }_{c}+ \mathrm{J}D_{,X}X \phi _{,\rho }\phi _{,\sigma }\bar{T}^{\rho \sigma }_{c}, \end{aligned}$$
(15)
$$\begin{aligned} T_{m \mathrm{p}}\equiv & {} \phi _{,\alpha }\phi _{,\beta } T^{\alpha \beta }_{c}= \mathrm{J}\left( C - 2 D_{,X}X^2\right) \phi _{,\rho }\phi _{,\sigma } \bar{T}^{\rho \sigma }_{c}, \end{aligned}$$
(16)

and therefore

$$\begin{aligned}&g_{\alpha \beta }\bar{T}^{\alpha \beta }_{c}= \frac{C T_{c}- D_{, X} X \left( T_{m \mathrm{p}}+ 2 T_{c}X \right) }{C J \left( C - 2 D_{, X} X^2 \right) }, \end{aligned}$$
(17)
$$\begin{aligned}&\phi _{,\alpha }\phi _{,\beta }\bar{T}^{\alpha \beta }_{c}= \frac{T_{m \mathrm{p}}}{J \left( C - 2 D_{, X} X^2 \right) }. \end{aligned}$$
(18)

These relations yield

$$\begin{aligned} \bar{T}^{\alpha \beta }_{c}=\frac{T^{\alpha \beta }_{c}}{C \mathrm{J}} + \frac{D_{, X} \phi {}^{,\alpha } \phi {}^{,\beta }}{2 C \mathrm{J}(C - 2 D_{, X} X^2)}T_{m \mathrm{p}}. \end{aligned}$$
(19)

Inserting Eqs. (17), (18) and (19) into Eq. (12) we can write Q as

$$\begin{aligned} FQ= & {} C [-2 D F_1 F_{\text {1,} \phi } + C F_1 (- D_{, \phi } + F_{\text {2,} X \phi }) + D_{, X} (C_{, \phi } F_1 \nonumber \\&-\,\, 2 F_{\text {1,} \phi } F_2) X ] T_{m \mathrm{p}}- C C_{, \phi } F_1 (C - 2 D_{, X} X^2) T_{c}\nonumber \\&-\,\, C D_{, X} F_1 F_2 T_{m \mathrm{p}}\Box \phi + 2 C D F_1^2 \Theta _1 + 2 C D_{, X} F_1^2 \Theta _2 \nonumber \\&+\,\, 2 C D F_1^2 \Theta _3 - C D_{, X} F_1 F_2 \Theta _4 - C (D_{,\text {XX}} F_1 F_2 \nonumber \\&-\,\, D_{, X} F_{\text {1,X}} F_2 + D_{, X} F_1 F_{\text {2,X}}) T_{m \mathrm{p}}\Theta _5, \end{aligned}$$
(20)

where \(F_1 \equiv C - 2 D_{,X} X^2\),   \(F_2 \equiv C + 2 D X\),   \(F \equiv 2 C^2 F_1^2\) and

$$\begin{aligned} \Theta _1= & {} \phi _{;\alpha \beta } T^{\alpha \beta }_{c}, \Theta _2 = \phi _{,\alpha } X_{,\beta } T^{\alpha \beta }_{c}, \Theta _3 = \phi _{,\alpha } \nabla _\beta T^{\alpha \beta }_{c}, \end{aligned}$$
(21)
$$\begin{aligned} \Theta _4= & {} \phi ^{,\alpha } \nabla _\alpha T_{m \mathrm{p}}, \Theta _5 = \phi ^{,\alpha } X_{,\alpha }. \end{aligned}$$
(22)

The form of this interaction terms can reduce to that in [26, 28] when \(\lambda _3 = 0\).

3 Dynamical equations

3.1 Evolution equations for the FLRW universe

We now compute the evolution equations for all matter components in the spatially flat FLRW universe. Using the perfect fluid model for radiation and matter as well as the FLRW line element in the form

$$\begin{aligned} \mathrm{d}s^2 = a^2(\tau ) \left( - \mathrm{d}\tau ^2 + \delta _{ij}\mathrm{d}x^i \mathrm{d}x^j\right) , \end{aligned}$$
(23)

the component (00) of Eq. (4) yields

$$\begin{aligned} \mathcal{H}^2 \equiv \left( \frac{a'}{a}\right) ^2 = \frac{1}{3} \left[ a^2\left( \rho _r + \rho _b + \rho _c\right) + \frac{1}{2} (\phi ')^2 + a^2V(\phi )\right] , \end{aligned}$$
(24)

where a prime denotes the derivative with respect to conformal time \(\tau \); \(\rho _r\), \(\rho _b\) and \(\rho _c\) are the energy density of radiation, baryon and dark matter, respectively. Furthermore, the interaction term Q in Eq. (20) becomes

$$\begin{aligned} FQ= & {} 2 C \phi ' \rho _c' F_1 \bigl (D F_1 + D_{, X} F_2 X\bigr ) + a^2 C \rho _c [-4 F_{\text {1,} \phi } X \bigl (D F_1 \nonumber \\&+ \,\,D_{, X} F_2 X\bigr ) + C F_1 \bigl (C_{, \phi } + 2 (- D_{, \phi } + F_{\text {2,} X \phi }) X\bigr )] \nonumber \\&+\,\, 4 C \phi ' \mathcal{H}\rho _c [D F_1^2 - X \bigl (D_{, \text {XX}} F_1 F_2 X\nonumber \\&+ \,\,D_{, X} (F_1^2 - F_{\text {1,X}} F_2 X + F_1 F_{\text {2,X}} X)\bigr )] \nonumber \\&+\,\, 2 C \phi '' \rho _c [D F_1^2 + X \bigl (2 D_{, \text {XX}} F_1 F_2 X \nonumber \\&+ \,\,D_{, X} (2 F_1^2 + 3 F_1 F_2 - 2 F_{\text {1,X}} F_2 X + 2 F_1 F_{\text {2,X}} X)\bigr )]. \nonumber \\ \end{aligned}$$
(25)

From now on, we will use \(X \equiv (\phi ')^2 / (2 a^2)\). Inserting this expression for the interaction terms into Eq. (13), we can write \(\rho _c'\) as

$$\begin{aligned} F_c\rho _c'= & {} a^2 C \phi ' \rho _c \Big [-4 F_{\text {1,} \phi } X (D F_1 + D_{, X} F_2 X) + C F_1 \big (C_{, \phi } \nonumber \\&+ \,\,2 ( - D_{, \phi } + F_{\text {2,} X \phi }) X \big )\Big ] + 2 C \phi '' \phi ' \rho _c \Big [D F_1^2 \nonumber \\&+\,\, X \big (2 D_{, \text {XX}} F_1 F_2 X + D_{, X} (2 F_1^2 + 3 F_1 F_2 - 2 F_{\text {1,X}} F_2 X \nonumber \\&+\,\, 2 F_1 F_{\text {2,X}} X)\big )\Big ] - 2 C \mathcal{H}\rho _c \Big [3 a^2 C F_1^2+ 4 a^2 X \Big (- D F_1^2 \nonumber \\&+\,\, X \big (D_{, \text {XX}} F_1 F_2 X + D_{, X} (F_1^2 - F_{\text {1,X}} F_2 X + F_1 F_{\text {2,X}} X)\big )\Big )\Big ] \nonumber \\ \end{aligned}$$
(26)

where \(F_c \equiv 2 a^2 C F_1 [C F_1 - 2 X (D F_1 + D_{, X} F_2 X)]\). Substituting this expression for \(\rho _c'\) into Eq. (25) and using Eq. (12), we get

$$\begin{aligned}&\phi '' + 2 \mathcal{H}\phi ' + V_{,\phi }a^2 = F_\phi ^{-1} \rho _c \Bigl \{ 6 \phi ' \mathcal{H}\bigl (F_1^2 F_d + F_1 F_2 F_{\text {d,X}} X \nonumber \\&\quad - 2 D_{, X} F_{\text {d3}} X^2\bigr ) + a^2 C \rho _c \bigl (- C_{, \phi } F_1 + 2 (D_{, \phi } F_1 - F_1 F_{\text {2,} X \phi } \nonumber \\&\quad + 2 F_{\text {1,} \phi } F_{\text {d1}}) X\bigr ) + 2 a^2 V_{, \phi } \bigl (F_1^2 F_d + F_1 F_2 F_{\text {d,X}} X \nonumber \\&\quad - 2 D_{, X} F_{\text {d3}} X^2\bigr )\Bigr \}\equiv - Q_0, \end{aligned}$$
(27)

where

$$\begin{aligned} F_\phi= & {} 2 \big [C F_1 (F_1 - 2 F_{\text {d1}} X) + \rho _c (F_1^2 F_d + F_1 F_2 F_{\text {d,X}} X \nonumber \\&- 2 D_{, X} F_{\text {d3}} X^2)\big ] \end{aligned}$$
(28)

and

$$\begin{aligned} F_d\equiv & {} D + 2 X D_{,X}, \qquad \quad \quad F_{d1} \equiv D + D_{,X} X, \nonumber \\ F_{d2}\equiv & {} D F_{1,X} + D_{,X}X F_{2,X}, \quad F_{d3} \equiv F_{1,X}F_2 - F_{2,X} F_1.\nonumber \\ \end{aligned}$$
(29)

The evolution equations for \(\rho _r\) and \(\rho _b\) can be computed from the conservation of their energy yielding

$$\begin{aligned} \rho _r' = - 4\mathcal{H}\rho _r, \qquad \rho _b' = - 3\mathcal{H}\rho _b. \end{aligned}$$
(30)

3.2 Autonomous equations

In order to study the evolution of the universe for the disformal coupled model of dark energy, we analyze solutions for the evolution equations presented in the previous section using dynamical analysis. For concreteness, we derive the autonomous equations using the conformal coupling, disformal coupling and the scalar field potential of the form

$$\begin{aligned} C = C_0 \mathrm{e}^{\lambda _1 \phi }, \quad D = M^{-4 - 4 \lambda _3} \mathrm{e}^{\lambda _2 \phi } X^{\lambda _3}, \quad V = M_v^4 \mathrm{e}^{\lambda _4\phi }, \end{aligned}$$
(31)

where \(\lambda _1\), \(\lambda _2\), \(\lambda _3\), \(\lambda _4\) and \(C_0\) are the dimensionless constant parameters, while M and \(M_v\) are the constant parameters with dimension of mass. Here, we extend the analysis in the literature by supposing that the disformal coefficient D also depends on the kinetic term X through \(X^{\lambda _3}\) which is the simplest extension. Using the following dimensionless variables:

$$\begin{aligned} \Omega _c\equiv & {} \frac{a^2\rho _c}{3 \mathcal{H}^{2}}, \quad \Omega _r \equiv \frac{a^2\rho _r}{3 \mathcal{H}^{2}}, \quad \Omega _b \equiv \frac{a^2\rho _b}{3 \mathcal{H}^{2}}, \nonumber \\ x_1^2\equiv & {} \frac{\phi '^2}{6 \mathcal{H}^{2}}, \quad x_2 \equiv \frac{a^2 V}{3 \mathcal{H}^{2}}, \quad x_3 \equiv \frac{D \mathcal{H}^{2}}{a^2 C}, \end{aligned}$$
(32)

we can write Eqs. (27) and (30) in the form of autonomous equations as

$$\begin{aligned} \frac{\mathrm{d} x_1}{\mathrm{d} N}= & {} \frac{1}{q} \{ x_1 (\Omega _r + 3 x_1^2 - 3 x_2 +1) \big [18 \lambda _3 x_1^2 x_3^2 \big ((3 \lambda _3+1) x_1^2 \nonumber \\&-\,\, (\lambda _3+1) (\Omega _b + \Omega _r + x_2 - 1)\big ) + 3 x_3 \big (- 2 \lambda _3^2 (\Omega _b + \Omega _r \nonumber \\&+\,\, x_1^2 + x_2 - 1) - (3 \lambda _3+1) (\Omega _b + \Omega _r + 3 x_1^2 + x_2 - 1)\big )\nonumber \\&+\,\, 1\big ] - 2 \big (\sqrt{3/2} \lambda _4 x_2 + 2 x_1\big ) \big [18 \lambda _3 x_1^2 x_3^2 \big ((3 \lambda _3 + 1) x_1^2 \nonumber \\&-\,\, (\lambda _3 + 1) (\Omega _b + \Omega _r + x_2 - 1)\big ) + 3 x_3 \big (- 2 \lambda _3^2 (\Omega _b + \Omega _r \nonumber \\&+\,\, x_1^2 + x_2 - 1) - (3 \lambda _3 + 1) (\Omega _b + \Omega _r + 3 x_1^2 + x_2 - 1)\big ) \nonumber \\&+\,\, 1\big ] -\sqrt{3/2} \big [6 x_3 \big (\lambda _3 (6 x_3 x_1^2 + 2) + 1\big ) \big (- \lambda _2 x_1^2 \nonumber \\&+\,\, \sqrt{6} (\lambda _3 + 1) x_1 + (\lambda _3 + 1) \lambda _4 x_2 \big )+ \lambda _1 \big (6 (3 \lambda _3 + 2) x_1^2 x_3 \nonumber \\&- \,\,1\big )\big ](\Omega _b + \Omega _r + x_1^2 + x_2 - 1)\}, \end{aligned}$$
(33)
$$\begin{aligned} \frac{\mathrm{d} x_2}{\mathrm{d} N}= & {} x_2 \big (\Omega _r + \sqrt{6} \lambda _4 x_1 + 3 x_1^2-3 x_2 + 3\big ), \end{aligned}$$
(34)
$$\begin{aligned} \frac{\mathrm{d} x_3}{\mathrm{d} N}= & {} - x_3 [3 \lambda _3 + (\lambda _3+ 1) \Omega _r - 2 \frac{\lambda _3}{x_1}\frac{\mathrm{d} x_1}{\mathrm{d} N} + 3 (\lambda _3 + 1) x_1^2 \nonumber \\&+ \,\,\sqrt{6} (\lambda _1 - \lambda _2) x_1-3 (\lambda _3 + 1) x_2+3], \end{aligned}$$
(35)
$$\begin{aligned} \frac{d \Omega _b}{\mathrm{d} N}= & {} \Omega _b (\Omega _r + 3 x_1^2 -3 x_2), \end{aligned}$$
(36)
$$\begin{aligned} \frac{d \Omega _r}{\mathrm{d} N}= & {} \Omega _r \left( \Omega _r + 3 x_1^2-3 x_2-1\right) , \end{aligned}$$
(37)

where \(N \equiv \ln a\) and

$$\begin{aligned} q\equiv & {} 2 [18 \lambda _3 x_1^2 x_3^2 ((3 \lambda _3 + 1) x_1^2 - (\lambda _3 + 1) (\Omega _b + \Omega _r + x_2 - 1)) \nonumber \\&+\, 3 x_3 (- 2 \lambda _3^2 (\Omega _b + \Omega _r \,{+}\,x_1^2\,{+}\,x_2-1)-(3 \lambda _3 \,{+}\, 1) (\Omega _b \,{+}\, \Omega _r \nonumber \\&+\, 3 x_1^2 + x_2 - 1)) + 1]. \end{aligned}$$
(38)

The evolution of the universe is completely described by these autonomous equations and the constraint equation which is obtained from Eq. (24) as

$$\begin{aligned} 1= x_1^2 + x_2 + \Omega _c + \Omega _b + \Omega _r. \end{aligned}$$
(39)

In order to derive the above autonomous equations, we also use

$$\begin{aligned} \frac{1}{\mathcal{H}^2} \frac{\mathrm{d} \mathcal{H}}{\mathrm{d} \tau } = \frac{1}{2} \left( 3 x_2 - 3 x_1^2 - 1 - \Omega _r\right) , \end{aligned}$$
(40)

which can be obtained by differentiating the constraint equation with respect to N. From the above equation, we see that

$$\begin{aligned} \frac{\mathrm{d}^2 a}{\mathrm{d}t^2} = \frac{\mathcal{H}^2}{2 a} \left( 3 x_2 - 3 x_1^2 - 1 - \Omega _r\right) , \end{aligned}$$
(41)

where t is the cosmic time.

4 Dynamical analysis

Here, we concentrate on dynamics of the universe at late time, so that we ignore the contribution from radiation density in the autonomous equations. Moreover, we are mainly interested in the physical fixed points that correspond to the acceleration of the universe at late time.

The fixed points of the autonomous equations can be obtained by setting the LHS of Eqs. (33)–(36) to zero and solving the resulting polynomial equations for \(x_1, x_2, x_3\) and \(\Omega _b\). The obtained solutions are the fixed points of the system denoted by variables with subscript \({}_f\), e.g., \(x_{1f}, x_{2f}\) and \(x_{3f}\) are the fixed points for \(x_1, x_2\) and \(x_3\), respectively. It follows from Eqs. (41) and (36) that the fixed points which correspond to the acceleration of the universe can exist if \(x_{2f}\ne 0\) and \(\Omega _{b\, f} = 0\). When \(x_{2f}\ne 0\), Eq. (34) gives the following relation for the fixed points:

$$\begin{aligned} x_{2f}= 1 + \sqrt{\frac{2}{3}} \lambda _4 x_{1f}+ x_{1f}^2. \end{aligned}$$
(42)

Inserting this relation into Eq. (35), assuming that \(x_{1f}\ne 0\) and using the fact that both \(\mathrm{d} x_3 / dN\) and \(\mathrm{d} x_1 / dN\) vanish at fixed point, we get

$$\begin{aligned} 0 = \sqrt{6} \left( -\lambda _1 + \lambda _2 + \left( \lambda _3 + 1\right) \lambda _4\right) x_{1f}x_{3f}. \end{aligned}$$
(43)

Applying Eqs. (42) and (43) to Eq. (33), we can compute the fixed points for the case where both \(x_{1f}\) and \(x_{2f}\) do not vanish. This case corresponds to the scaling solution which will be analyzed in detail in Sect. 4.2.

We note that the relation in Eq. (43) is derived by supposing \(x_{1f}\ne 0\). In the case \(x_{1f}= 0\), Eq. (42) gives \(x_{2f}= 1\), i.e., this fixed point is the potential dominated solution. We will consider this case in detail in the next section.

4.1 Potential dominated solution

The potential dominated solution corresponds to the fixed point \((x_{1f}, x_{2f}) = (0,1)\). Substituting this fixed point into Eq. (33) and setting \(\Omega _b = 0\), we get \(\lambda _4 = 0\) at the fixed point. Setting \(\lambda _4 = 0\), Eq. (33) yields

$$\begin{aligned} \lim _{x_{1f}\rightarrow 0} \left( \frac{1}{x_{1f}} \left. \frac{\mathrm{d} x_1}{\mathrm{d} N}\right| _{x_1 = x_{1f}, x_2 = x_{2f}, \Omega _b = 0} \right) = - 3. \end{aligned}$$
(44)

Substituting this relation into Eq. (35), we obtain

$$\begin{aligned} -6 \lambda _3 x_{3f}= 0. \end{aligned}$$
(45)

This implies that the fixed point that corresponds to the potential dominated solution occurs in two situations. The first is the situation where the disformal coefficient is much smaller than the conformal coefficient, i.e., \(x_{3f}= 0\). The second is the situation where the disformal coefficient do not depend on X, i.e., \(\lambda _3 = 0\). This result can easily be understood by noting that the field \(\phi \) is nearly constant in time within the potential dominated regime, so that the ratio of disformal coefficient to conformal coefficient nearly vanish if the disformal coefficient depends on kinetic term of the scalar field. Performing the usual stability analysis, one can show that the fixed point for the potential dominated solution is stable for \(\lambda _3 \ge 0\).

4.2 Scaling and field dominated solutions

We now consider the case where both \(x_{1f}\) and \(x_{2f}\) do not vanish. In our consideration, \(x_{1f}^2 + x_{2f}\le 1\), i.e., \(\Omega _c \ge 0\) at the fixed points, so that these fixed points correspond to scaling and field dominated solutions.

According to Eq. (43), the existence of the fixed points requires \(x_{3f}= 0\) or

$$\begin{aligned} \lambda _2 = \lambda _1 - \left( \lambda _3 + 1\right) \lambda _4. \end{aligned}$$
(46)

Since \(x_{3f}= 0\) implies that disformal coefficient vanishes at the fixed point, this fixed point is the conformal scaling solution. Hence, the case \(x_{3f}\ne 0\) corresponds to the disformal scaling solutions, in which the condition given in Eq. (46) is required for the existence of fixed points. We will consider these fixed point in the following sections.

4.2.1 Conformal scaling solutions

Substituting Eq. (42) into Eq. (33) and then setting \(x_{3f}= 0\), we obtain the following fixed points:

$$\begin{aligned} \left( x_{1f},x_{2f},x_{3f}\right)= & {} \left( -\frac{\lambda _4}{\sqrt{6}}, 1 - \frac{\lambda _4^2}{6},0\right) , \end{aligned}$$
(47)
$$\begin{aligned} \left( x_{1f},x_{2f},x_{3f}\right)= & {} \left( \frac{\sqrt{6}}{\lambda _1 - 2 \lambda _4}, \frac{\lambda _1^2-2 \lambda _4 \lambda _1+6}{\left( \lambda _1-2 \lambda _4\right) {}^2},0\right) . \end{aligned}$$
(48)

The first fixed point is actually the scalar field dominated solution because \(x_{1f}^2 + x_{2f}= 1\), while the second fixed point is the scaling solution. Since \(\Omega _b\) always vanishes at the fixed point in our consideration, we will perform stability analysis by linearizing only Eqs. (33)–(35). The inclusion of the evolution equation for the baryon density given in Eq. (36) will give rise to additional eigenvalue, \(\mu = 3 x_{1f}^2 -3 x_{2f}\), which is negative for the fixed points corresponding to accelerating universe. To simplify our analysis, we will write the eigenvalues of the fixed points in terms of the density parameter \(\Omega _{d}\) and equation of state parameter \(w_{d}\) of dark energy at fixed point. In terms of the dynamical variables defined in Eq. (32), the quantities \(\Omega _{d}\) and \(w_{d}\) at fixed point can be written as

$$\begin{aligned} \Omega _{df}= x_{1f}^2 + x_{2f}, \qquad w_{df}= \frac{x_{1f}^2 - x_{2f}}{x_{1f}^2 + x_{2f}}, \end{aligned}$$
(49)

where \(\Omega _{df}\) and \(w_{df}\) are the value of \(\Omega _{d}\) and \(w_{d}\) at fixed points, respectively. Inserting the fixed points from Eqs. (47) and (48) into the above equations, we, respectively, get

$$\begin{aligned}&\lambda _4 = \mp \sqrt{3(1 + w_{df})}\,, \text{ for } \text{ the } \text{ fixed } \text{ points } \text{ in } \text{ Eq. } \text{(47) }\,, \end{aligned}$$
(50)
$$\begin{aligned}&\left. \begin{array}{l} \lambda _1 = \mp \frac{2 w_{df}\sqrt{3\Omega _{df}} }{\sqrt{1 + w_{df}}}\,, \\ \lambda _4 = \mp \frac{\sqrt{3} \left( 1 + w_{df}\Omega _{df}\right) }{\sqrt{(1 + w_{df})\Omega _{df}}}\,, \end{array} \right\} \text{ for } \text{ the } \text{ fixed } \text{ points } \text{ in } \text{ Eq. } \text{(48) }\,. \nonumber \\ \end{aligned}$$
(51)

The eigenvalues \(\mathbf {\mu } \equiv (\mu _1,\mu _2,\mu _3)\) for the fixed points in Eqs. (47) and (48) are, respectively, given by

$$\begin{aligned} \mathbf {\mu }= & {} \Big (- 3 (\lambda _3 + 1) \gamma _{f}\mp \sqrt{3\gamma _{f}} (\lambda _1 - \lambda _2), \nonumber \\&- \frac{3}{2} (1 - w_{df}), 3 w_{df}\pm \frac{1}{2} \sqrt{3\gamma _{f}} \lambda _1 \Big )\,, \end{aligned}$$
(52)
$$\begin{aligned} \mathbf {\mu }= & {} \Big (-6 + 3 (1 - \lambda _3) (1 + w_{df}\Omega _{df}) \pm \lambda _2 \sqrt{3 \gamma _{f}\Omega _{df}}, \nonumber \\&- \frac{3}{4} \Big (1 - w_{df}\Omega _{df}+ \frac{A}{\sqrt{\gamma _{f}}}\Big ),\nonumber \\&-\, \frac{3}{4} \Big (1 - w_{df}\Omega _{df}- \frac{A}{\sqrt{\gamma _{f}}}\Big )\Big )\,, \end{aligned}$$
(53)

where \(\gamma _{f}\equiv 1 + w_{df}\) and

$$\begin{aligned} A \equiv&\big [\left( 1 - w_{df}\right) - 2 \left( 1 - \Omega _{df}\right) \left( 4 - 5 w_{df}\right) + \gamma _{f}w_{df}^2 \Omega _{df}^2 \nonumber \\&- 2 w_{df}^2\Omega _{df}\big ]^{1/2}. \end{aligned}$$
(54)

The stabilities of the fixed points in Eqs. (47) and (48) have already been discussed in the literature [17, 29], so that we will not consider in detail here. However, we would like to check whether the values for parameters \(\lambda _4, \lambda _3, \lambda _2, \lambda _1\) can imply the evolution of the universe at late time using the dynamical analysis. Before considering more complicate fixed points in the next sections, let us start with the potential dominated solution discussed in Sect. 4.1 and conformal scaling solutions given in Eqs. (47) and (48). In the calculation for the conformal scaling solutions, we suppose that \(x_{1f}\ne 0\), so that \(w_{df}> -1\) and therefore \(\lambda _4 = 0\) is not allowed in Eqs. (50) and (51). This implies that the universe will evolve towards the potential dominated solution, corresponding to the De Sitter expansion, at late time if \(\lambda _4 = 0\) and \(\lambda _3 \ge 0\).

In the case \(\lambda _4 < 0\), the universe evolves towards the stable fixed point \((w_{d},\Omega _{d}) = (w_{df},1)\) if \(\lambda _1 < - 6 w_{df}/ \sqrt{3\gamma _{f}}\) and \(\lambda _3\) as well as \(\lambda _2\) are suitably chosen, e.g. \(\lambda _3 \sim \lambda _2 \sim \mathcal{O}(1)\). Similarly, for the case \(\lambda _4 > 0\), the universe will evolve towards the stable fixed point \((w_{d},\Omega _{d}) = (w_{df},1)\) if \(\lambda _1 > 6 w_{df}/ \sqrt{3\gamma _{f}}\). Here, \(w_{df}\) can be specified by \(\lambda _4\) through Eq. (50). However, if \(\lambda _4\) and \(\lambda _1\) satisfy Eq. (51) and \(\lambda _3\) as well as \(\lambda _2\) are suitably chosen, the universe will reach the stable fixed point \((w_{d}, \Omega _{d}) = (w_{df}, \Omega _{df})\) at late time, where \(w_{df}\) and \(\Omega _{df}\) are related to \(\lambda _1\) and \(\lambda _4\) through Eq. (51). We note that if we set \(\lambda _1, \lambda _2, \lambda _3\) and \(\lambda _4\) such that Eq. (46) is satisfied, the first eigenvalue in Eqs. (52) and (53) will be zero. Consequently, one can show that these fixed points are saddle points, and therefore the universe will finally evolve towards the disformal scaling solutions discussed in the next section. Hence, in this section, we will consider only the cases where the relation in Eq. (46) is not satisfied.

It is interesting to check whether the fixed points in Eqs. (47) and (48) can be stable for the same value of \(\lambda _1, \lambda _2, \lambda _3\) and \(\lambda _4\), i.e., the universe has two possible stable fixed points for the same value of parameters. Let us suppose that \(w_{df}\) for the fixed point in Eq. (47) is \(w_{df}{}_1\), so that Eq. (50) gives \(\lambda _4 = \mp \sqrt{3(1 + w_{df}{}_1)}\). We then set \((w_{df}, \Omega _{df}) = (w_{df}{}_2, \Omega _{df}{}_2)\) for the fixed point in Eq. (48), and use Eq. (51) to show that

$$\begin{aligned} \lambda _4 = \mp \frac{\sqrt{3} (1 + w_{df}{}_2 \Omega _{df}{}_2)}{\sqrt{(1 + w_{df}{}_2) \Omega _{df}{}_2}} \nonumber , \end{aligned}$$

for this fixed point. In the case where \(\lambda _4\) computed from both fixed points are the same, we can write \(\Omega _{df}{}_2\) in terms of \(w_{df}{}_1\) and \(w_{df}{}_2\) as

$$\begin{aligned} \Omega _{df}{}_2&= \Big [1 + w_{df}{}_1 - w_{df}{}_2 + w_{df}{}_1 w_{df}{}_2 \nonumber \\&\quad \pm \Big ( (1 + w_{df}{}_1) (1 + w_{df}{}_2) (w_{df}{}_1 w_{df}{}_2 + w_{df}{}_1 \nonumber \\&\quad - 3 w_{df}{}_2 + 1) \Big )^{1/2} \Big ] / (2 w_{df}{}_2^2). \end{aligned}$$
(55)

Applying a simple numerical calculation to the above equation, it can be checked that both values of \(\Omega _{df}{}_2\) are unphysical unless \(-0.99 \le w_{df}{}_2 < w_{df}{}_1 \le 1\). Hence, if this condition on \(w_{df}{}_1\) and \(w_{df}{}_2\) is satisfied and \(\lambda _1\) as well as \(\lambda _4\) satisfy Eq. (51), the universe will evolve towards the fixed point \((w_{df}, \Omega _{df}) = (w_{df}{}_2, \Omega _{df}{}_2)\) because this fixed point is stable. The universe will not evolve to fixed point given in Eq. (47) because this fixed point becomes unstable in this situation. To show that the fixed point in Eq.  (47) is unstable in this case, we compute \(\lambda _1\) from Eq. (51) by setting \((w_{d},\Omega _{d}) = (w_{df}{}_2, \Omega _{df}{}_2)\) and then insert the result into the third eigenvalue in Eq. (52). Therefore we get

$$\begin{aligned} 3 w_{df}{}_1 - \frac{3 w_{df}{}_2 \sqrt{\Omega _{df}{}_2(1 + w_{df}{}_1)}}{\sqrt{1+ w_{df}{}_2}} > 0, \end{aligned}$$
(56)

for the case \(-0.99 \le w_{df}{}_2 < w_{df}{}_1 \le 1\), \(\Omega _{df}{}_2\) satisfies Eq. (55) and \(0< \Omega _{df}{}_2 < 1\). Nevertheless, if \(\lambda _1\) and \(\lambda _4\) do not satisfy Eq. (51), Eq. (56) is not valid and hence the universe can evolve to the stable fixed point \((w_{d}, \Omega _{d}) = (w_{df}, 1)\) associated with Eq. (47).

4.2.2 Disformal scaling solutions

In the case where the relation in Eq. (46) is satisfied, the fixed points at which the disformal coefficient does not vanish, i.e., \(x_{3f}\ne 0\), can exist. Hence, these fixed points correspond to the disformal scaling solutions. However, since the LHS of Eq. (35) vanishes due to the condition in Eq. (46) for this case, Eq. (35) does not provide relation among \(x_{1f}\), \(x_{2f}\) or \(x_{3f}\). Therefore, we have only two relations among \(x_{1f}\), \(x_{2f}\) and \(x_{3f}\) obtained from Eqs. (33) and (34). This suggests that we cannot solve the relations among \(x_{1f}\), \(x_{2f}\) and \(x_{3f}\) to write these fixed points completely in terms of the parameters of the model. Hence, the values for one of the fixed point \(x_{1f}\), \(x_{2f}\) or \(x_{3f}\) can be chosen independently of the parameters of the model in our dynamical analysis. To ensure that the chosen values of \(x_{1f}\), \(x_{2f}\) or \(x_{3f}\) are in agreement with the observational bounds, we write \(x_{1f}\) and \(\lambda _4\) in terms of \(w_{df}\) and \(\Omega _{df}\) by inserting Eq. (42) into Eq. (49) and solving the resulting equations as

$$\begin{aligned} x_{1f}= \pm \frac{\sqrt{(1 + w_{df})\Omega _{df}}}{\sqrt{2}}, \quad \lambda _4 = \mp \frac{\sqrt{3} \left( 1 + w_{df}\Omega _{df}\right) }{\sqrt{(1 + w_{df})\Omega _{df}} }. \end{aligned}$$
(57)

This implies that we can choose \(x_{1f}\) and \(\lambda _4\) by fixing \(w_{df}\) and \(\Omega _{df}\). Substituting these relations into Eq. (42), we obtain

$$\begin{aligned} x_{2f}= \frac{1}{2} \left( 1 - w_{df}\right) \Omega _{df}. \end{aligned}$$
(58)

Since the above equation is computed from Eq. (42), this equation is a consequence of the vanishing of the LHS of Eq. (34).

Substituting relations in Eqs. (46) and (42) into Eq. (33), we obtain the polynomial equation which has degree 2 in \(x_{3f}\) and degree 6 in \(x_{1f}\). Since it is not easy to solve this equation for \(x_{1f}\), which lies inside the physical phase space, we instead solve this equation for \(x_{3f}\), and we write \(x_{1f}\) and \(\lambda _4\) in the solutions in terms of \(w_{df}, \Omega _{df}\) using Eq. (57) as

$$\begin{aligned} x_{3f}{}_1= & {} \frac{1}{3 \lambda _3 \Omega _{df}(1 + w_{df}) }, \end{aligned}$$
(59)
$$\begin{aligned} x_{3f}{}_2= & {} \Big [ 6 w_{df}\sqrt{\Omega _{df}} \pm \lambda _1 \sqrt{3 (1 + w_{df})}\Big ] / \Big [ 3 (1 + w_{df}) \Omega _{df}\nonumber \\&\times \big (6 (2 \lambda _3 + 1) w_{df}\sqrt{\Omega _{df}} \pm \lambda _1 \sqrt{3 (1 + w_{df})}\big ) \Big ] \end{aligned}$$
(60)

where \(x_{3f}{}_1\) and \(x_{3f}{}_2\) are the solutions for the polynomial equation of the fixed points. From the above calculations, we conclude that there are two classes of the fixed points for the disformal scaling solutions shown in Table 1.

Table 1 The fixed points for the disformal scaling solutions. For these fixed points, the parameters \(\lambda _1\) and \(\lambda _3\) are arbitrary, while \(\lambda _2\) and \(\lambda _4\) are replaced by Eqs. (46) and (57), respectively
Full size table

It follows from Eq. (59) that \(x_{3f}{}_1 \rightarrow \infty \) when \(\lambda _3 = 0\), implying that class I of fixed points does not exist for the case where the disformal coefficient does not depend on the kinetic terms of scalar field. It can be checked that, for the case \(\lambda _3 = 0\), the fixed points belonging to class II are the fixed points discussed in [24]. According the result in [24], one of the eigenvalues for each fixed points in class II is zero for the case where \(\lambda _3 = 0\). Hence, to simplify our analysis, we check whether the fixed points in the two classes have zero eigenvalue. We compute the metric \(M_{ij} \equiv \partial E_i / \partial x_j\), where the indices i and j run from 1 to 3 and \(E_i\) is the RHS of Eqs. (33)–(35), respectively. Evaluating this matrix at the fixed points, we get

$$\begin{aligned} \det M= & {} \frac{\partial E_1}{\partial x_3} \left[ 3 (\lambda _3 + 1) \big (\sqrt{6} \lambda _4 + 6 x_{1f}\big ) x_{1f}x_{2f}\right. \nonumber \\&+\,\, \big (9 (\lambda _3 + 1) x_{1f}^2 + 2 \sqrt{6} (\lambda _1 - \lambda _2) x_{1f}\nonumber \\&-\,\,3 (\lambda _3 + 1) (x_{2f}- 1)\big ) \big (\sqrt{6} \lambda _4 x_{1f}+ 3 x_{1f}^2 - 6 x_{2f}\nonumber \\&\left. + \,\,3\big )\phantom {3 (\lambda _3 + 1) \big (\sqrt{6} \lambda _4 + 6 x_{1f}\big )}\right] x_{3f}. \end{aligned}$$
(61)

Inserting the fixed points in Table 1 into this matrix, we get \(\det M = 0\) for all fixed points which suggests that one of the eigenvalues for each fixed points vanishes. Therefore, to determine the stability of the fixed points, we have to go beyond linear analysis. However, as discussed above for the case of disformal solution, we have only two relations among \(x_{1f}\), \(x_{2f}\) and \(x_{3f}\) which are not sufficient for writing the fixed points completely in terms of the parameters of the model. Hence, is interesting to check whether the constraint equation given in Eq. (46) can imply the constraint equation for the dynamical variables \(x_1\), \(x_2\) and \(x_3\). Using the relation in Eq. (46) and the definitions of \(x_1, x_2\) and \(x_3\), we get

$$\begin{aligned} x_{3f}= \frac{1}{3 C_0}\left( \frac{M_v}{M}\right) ^{4 + 4\lambda _3} \frac{x_{1f}^{2 \lambda _3}}{x_{2f}^{1 + \lambda _3}} = r_0 \frac{x_{1f}^{2 \lambda _3}}{x_{2f}^{1 + \lambda _3}}, \end{aligned}$$
(62)

where \(r_0\) is a constant which controls the magnitude of \(x_3\) for given \(x_1\) and \(x_2\). Hence, the third relation among \(x_{1f}\), \(x_{2f}\) and \(x_{3f}\) can be constructed from the constraint given in Eq. (46) by introducing other constant parameter \(r_0\). The above constraint equation suggests that, for a given \(r_0\), \(x_3\) can be computed from \(x_1\) and \(x_2\), so that the dimension of the phase space is reduced [24]. Substituting this relation and the relation in Eq. (42) into Eq. (33), we obtain polynomial equation degree \(6 + 4 \lambda _3\) of \(x_{1f}\). Similar to the previous analysis, instead of solve this equation for \(x_{1f}\), we solve this equation for \(r_0\), so that we get two expressions for \(r_0\):

$$\begin{aligned} r_0= & {} r_{01} = \frac{1}{6 \lambda _3} \left( \frac{1 - w_{df}}{1 + w_{df}}\right) ^{\lambda _3 + 1}, \end{aligned}$$
(63)
$$\begin{aligned} r_0= & {} r_{0\pm } = \frac{1}{2 \sqrt{3}} \left( \frac{1 - w_{df}}{1 + w_{df}}\right) ^{\lambda _3 + 1}\nonumber \\&\times \frac{\lambda _1 \sqrt{1 + w_{df}} \pm 2w_{df}\sqrt{3\Omega _{df}}}{\lambda _1 \sqrt{3(1+ w_{df})} \pm 6 \left( 2 \lambda _3+1\right) \sqrt{\Omega _{df}} w_{df}}. \end{aligned}$$
(64)

Moreover, we also use the relations in Eq. (57) to write the above expressions in terms of \(w_{df}\) and \(\Omega _{df}\). The above relations suggest that for any given \(w_{df}\), \(\Omega _{df}\) and the parameters of the model, the LHS of Eq. (35) vanishes (a fixed point exists) if \(r_0\) satisfies the above expressions. Here, \(x_{1f}\) and \(\lambda _4\) are presented in terms of \(w_{df}\) and \(\Omega _{df}\), therefore the different values of \(w_{df}\) and \(\Omega _{df}\) corresponds to different values of \(x_{1f}\), \(\lambda _4\) as well as \(x_{2f}\) (according to Eq. (58)). In terms of \(r_0\), the fixed points in Table 1 now can be presented in Table 2.

Table 2 The fixed points for the disformal scaling solutions. For these fixed points, the parameters \(\lambda _1\) and \(\lambda _3\) are arbitrary, while \(\lambda _2\), \(\lambda _4\) and \(r_0\) are replaced by Eqs. (46), (57) and (63)–(64), respectively
Full size table

It can be checked that the fixed points in class II reduce to the fixed points in [24] when \(\lambda _3 = 0\). Since the analytic expressions for the above fixed points are complicate, we perform the stability analysis using numerical calculation and show the region of the cosmological parameters at fixed point \((w_{df}, \Omega _{df})\) in which the fixed point is stable in Figs. 1, 2, 3 and 4. In our consideration, \(\lambda _4\), \(x_{1f}\) and \(x_{2f}\) can be computed from \(w_{df}\) and \(\Omega _{df}\), while \(\lambda _2\) and \(r_0\) can be computed from \(w_{df}\), \(\Omega _{df}\), \(\lambda _1\) and \(\lambda _3\). Therefore, the stability of the fixed points for the disformal scaling cases can be explored by plotting the stability regions of the fixed points in the \(w_{df}\)–\(\Omega _{df}\) plane for various values of \(\lambda _1\) and \(\lambda _3\).

Fig. 1
figure 1

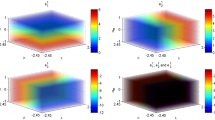
Regions I, II and III represent the regions in which the fixed point \(\mathrm{II}^+\) is a saddle point for the cases where the values of \((\lambda _3,\lambda _1)\) are (0, 2), (0, 5) and (0, 10), respectively. The fixed point is stable outside these regions. Note that region II totally overlaps with a part of region III, and region I totally overlaps with a part of region II

Full size image
Fig. 2
figure 2

In the upper (lower) panel, regions I, II and III represent the regions in which the fixed point \(\mathrm{II}^+\) (\(\mathrm{II}^-\)) is a saddle point for the cases where the values of \((\lambda _3,\lambda _1)\) are (1, 1), (1, 5) and (5, 1), respectively. The fixed point is stable outside these regions

Full size image

Let us first consider the case \(\lambda _3 = 0\). It is clear that this case is not allowed for the fixed points in class I. The numerical investigation shows that the fixed point \(\mathrm{II}^-\) is stable for a wide range of \(\lambda _1\) when \(-1< w_{df}< 0\) and \(0< \Omega _{df}< 1\). However, it follows from Fig. 1 that the parameters region in which the fixed point \(\mathrm{II}^+\) is saddle increases area with increasing \(\lambda _1\). The fixed point \(\mathrm{II}^+\) can become a saddle point within the region \(w_{df}\in (-0.99, -0.97)\) and \(\Omega _{df}\in [0.7,1)\) until \(\lambda _1 \gg 1\) and \(\lambda _3 \gg 1\).

We now turn to the case \(\lambda _3 > 1\). It follows from Fig. 2 that, for the fixed points in class II, the area of the saddle region in the \(w_{df}\)–\(\Omega _{df}\) plane increases when \(\lambda _3\) or \(\lambda _1\) increases. Similar to the case \(\lambda _3 = 0\), the fixed points in class II can become a saddle points within the region \(w_{df}\in (-0.99, -0.97)\) and \(\Omega _{df}\in [0.7,1)\) unless \(\lambda _1 \gg 1\).

The fixed points in class I are saddle points for the whole region of \(-1< w_{df}< 0\) and \(0< \Omega _{df}< 1\) when \(\lambda _1 = 1\) and \(\lambda _3 = 1\). However, according to Fig. 3, these fixed points become stable within some regions in the \(w_{df}\)–\(\Omega _{df}\) plane when \(\lambda _1\) or \(\lambda _3\) increases. For this class, the fixed points can be stable within the region \(w_{df}\in (-0.99, -0.97)\) and \(\Omega _{df}\in [0.7,1)\) if \(\lambda _1\) is sufficiently large, i.e., the slope of the conformal coefficient is large.

Fig. 3
figure 3

In the upper panel, regions I and II denote the stable regions for the fixed point \(\mathrm{I}^+\) for the cases where the values of \((\lambda _3,\lambda _1)\) are (1, 100) and (20, 1), respectively. In the lower panel, regions I and II denote the stable regions for the fixed point \(\mathrm{I}^-\) for the cases where the values of \((\lambda _3,\lambda _1)\) are (1, 500) and (20, 1), respectively. The fixed point is saddle outside these regions

Full size image
Fig. 4
figure 4

The plots of \(E_{w_{df}}\) as a function of \(w_{df}\) for the fixed points in the class \(\mathrm{II}^+\) (upper panel) and \(\mathrm{II}^-\) (lower panel). In the upper panel, lines 1–7 represent the case where \((\lambda _1, \lambda _3) =\) (1,1), (1,1), (5,1), (10,1), (5,5), (1,5) and (1,20), respectively. For line 2, \(r_0\) and \(\lambda _4\) are computed by setting \(w_{df}= -0.98\) and \(\Omega _{df}= 0.9\), while these parameters are computed by setting \(w_{df}= -0.99\) and \(\Omega _{df}= 0.9\) for the other lines. In the lower panel, lines 1–3 represents the case where \((\lambda _1, \lambda _3) =\) (1,1), (5,5) and (5,5), respectively. For this panel, \(r_0\) and \(\lambda _4\) are computed by setting \(w_{df}= -0.99\) and \(\Omega _{df}= 0.9\)

Full size image

We now consider whether the same value of parameters \(\lambda _1, \lambda _2, \lambda _3\) and \(\lambda _4\) can lead to different stable fixed point at late time. Since the fixed points in class I do not support \(\lambda _3 = 0\), we consider the case where \(\lambda _3 = 0\) for the fixed points in class II. In the case where \(\lambda _3 = 0\), Eq. (64) becomes

$$\begin{aligned} r_{0\pm } = \frac{1}{6} \frac{1 - w_{df}}{1 + w_{df}}. \end{aligned}$$
(65)

This shows that, for a given value of \(r_0\), or equivalently \(x_{3f}\), the above equation can be satisfied by single value of \(w_{df}\). Inserting the value of \(w_{df}\) computed from Eq. (65) into Eq. (57), we see that the values of \(\Omega _{df}\) that satisfy Eq. (57) for a fixed value of \(\lambda _4\) are given by

$$\begin{aligned} \sqrt{\Omega _{df}} = \left\{ \begin{array}{ll} \frac{- \lambda _4\sqrt{1 + w_{df}} \pm \sqrt{(1 + w_{df})\lambda _4^2 - 12 w_{df}}}{2 \sqrt{3} w_{df}} &{} \text{ for } \text{ negative }\, \lambda _4 \\ - \frac{- \lambda _4\sqrt{1 + w_{df}} \pm \sqrt{(1 + w_{df})\lambda _4^2 - 12 w_{df}}}{2 \sqrt{3} w_{df}} &{} \text{ for } \text{ possitive }\, \lambda _4 \\ \frac{\sqrt{3}}{|\lambda _4|} &{} \text{ for }\quad w_{df}= 0. \\ \end{array}\right. \end{aligned}$$
(66)

This equation shows that \(\Omega _{df}\) takes a single value for a given \(\lambda _4\) if \(w_{df}= 0\). However, if \(w_{df}\ne 0\), there are two possible values of \(\Omega _{df}\) for a given \(\lambda _4\). When \(-1< w_{df}< 0\) and \(\lambda _4\) is a real number, it follows from the above equation that, for a given value of \(\lambda _4\) and \(w_{df}\), one possible value of \(\sqrt{\Omega _{df}}\) is positive, while the another is negative. For \(0< w_{df}< 1\), the numerical evaluation of Eq. (66) shows that if the values of \(\lambda _4\) and \(w_{df}\) are chosen such as the first value of \(\Omega _{df}\) lies within the range (0, 1), the second value of \(\Omega _{df}\) will be larger than unity. According to these analysis, only single fixed point lies inside the physical phase space for a given value of \(\lambda _1, \lambda _3,\lambda _4\) and \(r_0\) when \(\lambda _3 = 0\).

In the cases where \(\lambda _3 \ne 0\) and \(-1< w_{df}< 1\), Eq. (63) suggests that \(w_{df}\) takes a single value for a given real value of \(r_0\) and \(\lambda _3\). Using a similar analysis to the case where \(\lambda _3 = 0\), we conclude that the fixed points \((w_{df}, \Omega _{df})\) belonging to class I take single physically relevant value for a given value of \(\lambda _1, \lambda _3, \lambda _4\) and \(r_0\).

The situation changes when we consider the fixed points in the class II. It can be checked that, for given values of \(r_0\) and the other parameters, Eq. (64) is satisfied by several values of \(w_{df}\) and \(\Omega _{df}\). The relation between \(w_{df}\) and the parameters of the model can be computed by combining Eq. (64) with Eq. (57), so that we get

$$\begin{aligned} E_{w_{df}}= & {} \sqrt{3} \Big [(1 - w_{df})^{2 + 2\lambda _3} \big (12 w_{df}+ \lambda _1^2 (1 + w_{df})\nonumber \\&- 2 \lambda _1 \lambda _4 (1 + w_{df})\big ) + 36 r_0^2 \left( 1 + w_{df}\right) ^{2 + 2 \lambda _3} \nonumber \\&\times \Big (12 (1 + 2 \lambda _3)^2 w_{df}+ \lambda _1^2 (1 + w_{df}) \nonumber \\&- 2 \lambda _1 \lambda _4 (1 + 2\lambda _3) (1 + w_{df})\Big ) - 12 r_0 \left( 1 - w_{df}^2\right) ^{1 + \lambda _3} \nonumber \\&\times \Big (\lambda _1^2 (1 + w_{df}) - 2\lambda _1 \lambda _4 (1 + \lambda _3) (1 + w_{df})\nonumber \\&+ \,\,12 w_{df}(1 + 2 \lambda _3 )\Big )\Big ] = 0 . \end{aligned}$$
(67)

To compute values of \(w_{df}\) that satisfy the above equation for a given value of \(\lambda _1,\lambda _3,\lambda _4\) and \(r_0\), we perform the following analysis. We first use Eqs. (64) and (57) to compute \(\lambda _4\) and \(r_0\) for selected value of \(\lambda _1, \lambda _3, w_{df}\) and \(\Omega _{df}\). Since the disformal fixed point exists when the energy density of baryon can be neglected compared with the energy density of dark matter, this fixed point should be reached in the future. Hence, the value of \(w_{df}\) and \(\Omega _{df}\) are chosen such that the present value of \(w_d\) and \(\Omega _d\) can be in agreement with the observational bounds. We then substitute the computed value of \(\lambda _4\) and \(r_0\) as well as the selected value of \(\lambda _1\) and \(\lambda _3\) into Eq. (67). It is clear that the value of \(w_{df}\) that is used to compute \(\lambda _4\) and \(r_0\) is the solution of the resulting equation. In the following consideration, we will see that there is another solution for this equation corresponding to the stable physically relevant fixed point. This implies that there are two stable physically relevant fixed points for the same value of the parameters of the model.

For illustration, we plot Eq. (67) in Fig. 4 for the case where \(r_0\) and \(\lambda _4\) are computed from \(w_{df}= w_{df}^* = -0.99\), \(-0.98\) and \(\Omega _{df}= \Omega _{df}^* = 0.9\). From the plots, we see that in addition to the obvious solution \(w_{df}= w_{df}^*\), Eq. (67) also has a solution in a range \(w_{df}= w_{df}^s\in (-0.98, 0.15)\). In the cases where \(\lambda _1 \sim \mathcal{O}(1)\) and \(\lambda _3 \sim \mathcal{O}(1)\), the plots show that this solution lies within the ranges \(w_{df}^s \in (0,0.15)\) and \(w_{df}^s \in (-0.98,0)\) for the fixed points in the classes \(\mathrm{II}^-\) and \(\mathrm{II}^+\), respectively. The value of \(\Omega _{df}\) associated with \(w_{df}^s\) can be obtained by inserting \(w_{df}^s\) into Eq. (57). For the ranges of parameters considered in Fig. 4, the values of \(\Omega _{df}\) lies within the range (0, 1). Applying the above stability analysis to the two fixed points associated with the zero points of \(E_{w_{df}}\) in Fig. 4, we find that both of the fixed points are stable fixed points. These results indicate that in the case where \(\lambda _3 > 0\), the fixed point \(\mathrm{II}^+\) (an also \(\mathrm{II}^-\)) can take two different physically relevant values for the same value of the parameters of the model, and the fixed point is stable at these values.

Fig. 5
figure 5

The evolution of \(\Omega _{c}\) and \(w_{d}\). Lines 3–6 represent the case where the initial conditions are setting such that the initial value of \(w_{d}= w_{df}^*, -0.89, - 0.79\) and \(-0.69\), respectively. The first and second lines represent the evolution of \(\Omega _{c}\) for the case where the initial conditions for \(w_{d}\) are equal to that for line 3 and 4, respectively. Note that the evolution of \(\Omega _{c}\) is nearly the same for the case where the initial values of \(w_{d}\) are \(-0.89, -0.79\) and \(-0.69\)

Full size image

It follows from Fig. 4 that, for the fixed point \(\mathrm{II}^+\), the solution \(w_{df}^s\) for \(E_{w_{df}} = 0\) shifts to the lower value when \(\lambda _1\) increases, and shifts to the larger value when \(\lambda _3\) increases. According to our numerical investigation, we also find that \(w_{df}^s\) gets closer to 0 as \(\lambda _3\) gets larger, but \(w_{df}^s\) will not exist when \(\lambda _1 \gtrsim 30\). This means that the fixed point \(\mathrm{II}^+\) can take only one physically relevant value for a given value of the parameters when \(\lambda _1 \gtrsim 30\). From Fig. 4, we see that, for the fixed point \(\mathrm{II}^-\), the solution \(w_{df}^s\) shifts towards 0 when \(\lambda _3\) increases. From the detail of the numerical analysis for fixed point \(\mathrm{II}^-\), we find that \(\Omega _{df}\) associated with \(w_{df}^s\) becomes larger than unity when \(\lambda _1 \gtrsim 1\). Nevertheless, the value of \(\Omega _{df}\) can be reduce by enhancing the value of \(\lambda _3\), e.g., \(\Omega _{df}< 1\) for \(\lambda _1 = \lambda _3 = 5\). For both \(\mathrm{II}^+\) and \(\mathrm{II}^-\) fixed points, the solution \(w_{df}^s\) does not exist if \(\Omega _{df}^* \gtrsim 0.9\). Based on the above analysis, we conclude that the fixed point associated with \(w_{df}^s\) will not exist if \(\lambda _1\) is sufficiently larger than unity or the values of \(r_0\) and \(\lambda _4\) correspond to \(\Omega _{df}^* \gtrsim 0.9\).

We now study the situation in which the different fixed points with the same value of the parameters of the model can be reached. In order to perform, we solve Eqs. (33)–(36) numerically by setting the present value of \(\Omega _{c}, \Omega _b, \Omega _r, \Omega _d\) and \(w_d\) to be \(0.27, 0.03, 10^{-4}, 0.7 - 10^{-4}\) and \(-0.99\), respectively. For illustration, we plot in Fig. 5 the evolution of \(\Omega _{c}\) and \(w_{d}\) for the case where \(\lambda _1 = \lambda _3 = 1\) and \(r_0, \lambda _4\) are computed from \((w_{df},\Omega _{df}) = (w_{df}^*,\Omega _{df}^*) = (-0.99,0.9)\). From the figure, we see that if the initial conditions are chosen such that the initial value of \(w_{d}\) is significantly larger than \(w_{df}^*\), the universe will evolve towards the fixed point associated to the solution \(w_{df}^s\) in Fig. 4. Unfortunately, the present value of \(w_{d}\) may lie outside the observational bounds if the universe evolves towards this fixed point. Hence, the existence of the solution \(w_{df}^s\) seems to be a problem, which can be avoided by setting \(\lambda _1\) to be sufficiently larger than unity or setting the value of \(r_0\) and \(\lambda _4\) to be matched with \(\Omega _{df}^* \gtrsim 0.9\). We stress that these conclusions are based on the situation where \(\lambda _3 > 0\) and \(\lambda _1 > 0\).

5 Conclusions

In this work, we study the dynamics of the universe at late time for the model in which dark energy directly interacts with dark matter through disformal coupling. When the disformal coefficient depends on the kinetic terms of scalar field, there exist two classes of fixed points which can describe the acceleration of the universe in addition to that found in literature. The fixed points in the first class are saddle points unless \(\lambda _1\) is sufficiently larger than unity, and it exists only for the case where the disformal coefficient depends on the kinetic terms of scalar field. The fixed points in the second class can be stable within the parameter ranges that correspond to the accelerating universe.

In the case where the disformal coefficient depends only on the scalar field, the fixed points in the second class become the fixed points that found in the literature. Interestingly, in the case where the disformal coefficient also depends on the kinetic terms of scalar field, the stable fixed points in the second class can take different physically relevant values for the same value of the parameters of the model. For the case where \(\lambda _1 \sim \lambda _3 \sim 1\) and the values of \(r_0\) and \(\lambda _4\) are set such that the fixed point can occur at \(0.9 \gtrsim \Omega _{df}\gtrsim 0.7\) and \(w_{df}\sim -0.99\), the universe will evolve towards the fixed point \((w_{d}, \Omega _{d}) = (w_{df},\Omega _{df})\) if the initial value of \(w_{d}\) is close to \(w_{df}\). Nevertheless, if the initial value of \(w_{d}\) is sufficiently larger than \(w_{df}\), the universe will evolve towards another value of the fixed point at which the present value of \(w_{d}\) may not be in agreement with the observational bounds. The existence of two different values of the fixed point for the same value of the parameters can be avoided if \(\lambda _1\) is sufficiently larger than unity, or the values of \(r_0\) and \(\lambda _4\) are set from the fixed point \(w_{df}\sim -0.99\) and \(\Omega _{df}\gtrsim 0.9\).