Abstract
We test the holographic relation between the vacuum expectation values of gauge invariant operators in \({\mathcal {N}} = 6\) U\(_k(N)\times \mathrm{U}_{-k}(N)\) mass-deformed ABJM theory and the LLM geometries with \({\mathbb {Z}}_k\) orbifold in 11-dimensional supergravity. To do so, we apply the Kaluza–Klein reduction to construct a 4-dimensional gravity theory and implement the holographic renormalization procedure. We obtain an exact holographic relation for the vacuum expectation values of the chiral primary operator with conformal dimension \(\Delta = 1\), which is given by \(\langle {\mathcal {O}}^{(\Delta =1)}\rangle = N^{\frac{3}{2}} \, f_{(\Delta =1)}\), for large N and \(k=1\). Here the factor \(f_{(\Delta )}\) is independent of N. Our results involve an infinite number of exact dual relations for all possible supersymmetric Higgs vacua and so provide a non-trivial test of gauge/gravity duality away from the conformal fixed point. We extend our results to the case of \(k\ne 1\) for LLM geometries represented by rectangular-shaped Young diagrams. We also discuss the exact mapping of the gauge/gravity at finite N for classical supersymmetric vacuum solutions in field theory side and corresponding classical solutions in gravity side.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the context of the AdS/CFT correspondence [1,2,3,4], it was conjectured that the string/M theory on AdS\(_{d+1}\times {\mathcal {X}}\) with a compact manifold \({\mathcal {X}}\) is dual to d-dimensional conformal field theory (CFT). The conjecture was soon extended to quantum field theories (QFTs) which can be obtained from the CFTs at the Ultraviolet (UV) fixed point by adding relevant operators to the action or considering vacua where the conformal symmetry is broken. Then the dual geometries for those QFTs are asymptotic to AdS\(_{d+1}\times {\mathcal {X}}\). Due to computational difficulties on both sides, most of the efforts to test the duality were focused on the large N limit of the QFT, N being the rank of the gauge group.
In this letter, we analyze a model which shows a supporting evidence for an exact dual relation away from the conformal fixed point in the large N limit. We consider the \({\mathcal {N}}=6\) \(\mathrm{U}_{k}(N)\times \mathrm{U}_{-k}(N)\) Aharony–Bergman–Jafferis–Maldacena (ABJM) theory with Chern–Simons level k [5], as the CFT at the UV fixed point. The ABJM theory allows the supersymmetry preserving mass deformation and the deformed theory (mABJM) [6, 7] has discrete Higgs vacua as represented by the Gomis, Rodriguez-Gomez, Van Raamsdonk, Verlinde (GRVV) matrices [7]. It was known that the vacua of the mABJM theory have one-to-one correspondence [8, 9] with the half BPS Lin–Lunin–Maldacena (LLM) geometries [10, 11] with \({\mathbb {Z}}_k\) orbifold having SO(2,1)\(\times \)SO(4)/\({\mathbb {Z}}_k\times \)SO(4)/\({\mathbb {Z}}_k\) isometry in 11-dimensions [9, 12]. Since the mABJM theory is obtained by a relevant deformation from the ABJM theory at the UV fixed point, the dual geometry should be asymptotically AdS\(_4\times S^7/{\mathbb {Z}}_k\).
Here we test the above gauge/gravity duality. On the field theory side, we calculate the vacuum expectation values (VEVs) of the chiral primary operator (CPO) with conformal dimension \(\Delta =1\) for all possible supersymmetric vacua of the mABJM theory with any k. In gravity side, we implement the Kaluza–Klein (KK) reduction on \(S^7\) and construct 4-dimensional quadratic action from 11-dimensional supergravity on the AdS\(_4\times S^7\) background. Applying the holographic renormalization method [13,14,15], we obtain an exact holographic relation for the VEVs of the CPO with \(\Delta =1\), which is given by \(\langle {\mathcal {O}}^{(\Delta =1)}\rangle = N^{\frac{3}{2}} \, f_{(\Delta =1)}\). Here we consider \(k=1\) case and \(f_{(\Delta )}\) is a function of the conformal dimension and also depends on some parameters of LLM solutions [11]. This result is extended to \(k > 1\) for specific types of LLM solutions. From our results, we notice that the VEVs of CPOs obtained from the classical supersymmetric vacuum solutions at finite N (\({\ge }2\)) are read from classical supersymmetric solutions in dual gravity theory.
2 Discrete Higgs vacua and dual geometries
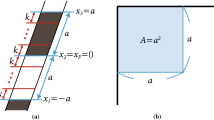
The SU(4) global symmetry of the ABJM theory is broken to \(\mathrm{SU(2)} \times \mathrm{SU(2)}\times \mathrm{U}(1)\) symmetry under the supersymmetry preserving mass deformation [6, 7]. To make manifest the broken symmetry, we split the scalar fields into \(Y^A = (Z^a, W^{\dagger a})\), where \(A = 1,2,3,4\) and \(a = 1,2\). Then the Higgs vacua of the mABJM theory are represented as direct sums of irreducible \(n\times (n+1)\) GRVV matrices [7], \(\mathcal{M}_a^{(n)}\) with the occupation number \(N_n\), and their Hermitian conjugates \((n+1)\times n\) matrices \(\bar{\mathcal{M}}_a^{(n)}\) with \(N_n'\) [9]. (See also [16, 17] for the vacuum solutions.) Since \(Z^a\) and \(W^{\dagger a}\) are \(N\times N\) matrices, we have two constraints, \(\sum _{n=0}^\infty \left( n + \frac{1}{2} \right) \left( N_n + N_n'\right) = N\) and \(\sum _{n=0}^\infty N_n = \sum _{n=0}^\infty N_n'\). In addition, in order to have supersymmetric vacua the range of the occupation numbers should be \(0\le N_n,\, N_n' \le k\) [8, 9]. As a result, the supersymmetric vacua of the mABJM theory are completely classified in terms of the occupation numbers, \(\{ N_n,\, N_n'\}\).
The LLM geometry with \({\mathbb {Z}}_k\) orbifold is determined by the two functions Z and V,
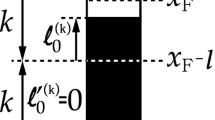
where \(\tilde{x}\) and \(\tilde{y}\) are 11-dimensional coordinates, the \(\tilde{x}_i\) are the positions of boundaries of black and white strips in the droplet picture [11], and \(N_\mathrm{B} \) is the number of finite black droplets. Due to the quantization condition of the 4-form flux, the difference between the consecutive \(\tilde{x}_i\) is quantized as \(\tilde{x}_{i+1} - \tilde{x}_i = 2\pi l_\mathrm{P}^3 \mu _0 {\mathbb {Z}}\) with the Planck length \(l_\mathrm{P}\) and the mass parameter \(\mu _0\). This implies that all possible LLM geometries are parametrized by the quantized \(\tilde{x}_i\). For the asymptotic expansion of the LLM geometries, it is convenient to introduce new parameters [18],
where A is the area in the Young-diagram picture in the LLM solution, defined as
Here \(\{ l_n, \,l_n\}\) are set of parameters classifying the LLM geometries in the droplet picture. See [9] for the details. There is one-to-one correspondence between \(\{l_n, l_n'\}\) and the occupation numbers \(\{N_n, N_n'\}\) in the vacua of the mABJM theory [9].
3 Kaluza–Klein holography
In order to implement the KK holography method [19,20,21], we consider asymptotic expansion of the LLM geometries with \({\mathbb {Z}}_k\) orbifold and regard the deviation from \(\mathrm{AdS}_4\times S^7/{\mathbb {Z}}_k\) geometry as solutions to perturbed equations of motion in 11-dimensional supergravity on such background. According to the dictionary of the gauge/gravity duality [3, 4], the deviations in asymptotic limit encode the information of VEVs of CPOs [22] in the mABJM theory.
Our purpose in this letter is to compare quantitatively the VEVs of CPOs in the mABJM theory with the corresponding asymptotic coefficients of KK scalar fields, based on the KK holographic procedure [19,20,21]. Since the elements of the GRVV matrices are real numbers, one can compute the VEVs of CPOs in terms of numerical values and compare them with the corresponding coefficients of the KK scalars in gravity side. The number of supersymmetric vacua is numerous for a given N and thus large number of non-trivial tests can be carried out.
More precisely, the VEV of CPO with conformal dimension \(\Delta \) is proportional to the coefficient of \(z^\Delta \)-term in the asymptotic expansion of the dual scalar field on the gravity side [19], where z represents the coordinate in holographic direction. When we restrict our interest to the CPOs with low conformal dimensions, it is sufficient to consider the dual LLM geometry near the asymptotic limit.
In particular, the VEVs of CPO with \(\Delta =1\) are holographically determined by the solutions of the linearized supergravity equations of motion on the AdS\(_4\times S^7/{\mathbb {Z}}_k\) background. In this case, diagonalized gauge invariant fields in 11-dimensions can be identified with 4-dimensional gravity fields without non-trivial field redefinitions. However, for \(\Delta \ge 2\), nonlinear terms in the equations of motion are not negligible and non-trivial field redefinitions in the construction of the 4-dimensional gravity theory are necessary [19]. In this letter we focus on the CPO with \(\Delta = 1\) and leave our study of CPOs with \(\Delta \ge 2\) as future work.
3.1 Field theory side
The CPO with conformal dimension \(\Delta \) in the ABJM theory is
where the coefficients, \(C_{A_1,\ldots ,A_{\Delta }}^{B_1,\ldots ,B_{\Delta }}\), are symmetric in upper as well as lower indices and traceless over one upper and one lower indices. The CPO in (3.1) is written by reflecting the global SU(4) symmetry of the ABJM theory. On the other hand, in the mABJM theory the CPO should reflect the SU(2)\(\times \)SU(2)\(\times \)U(1) global symmetry, of which the explicit form will be given later.
For a given vacuum, the complex scalar fields near the vacuum are written as \(Y^A(x) = Y_0^A + \hat{Y}^A\), where the \(Y_0^A\) \((A=1,2,3,4)\) are the vacuum solutions represented by GRVV matrices [7], and the \(\hat{Y}^A\) are field operators. Then the VEV of a CPO with dimension \(\Delta \) for a specific vacuum in the mABJM theory is given by
where \(\langle \cdots \rangle _m\) and \(\langle \cdots \rangle _0\) denote the VEVs in the mABJM theory and the ABJM theory, respectively. The \(\frac{1}{N}\)-corrections come from the contributions of multi-trace terms [23,24,25]. Here we note that quantum corrections of scalar fields are absent due to the high supersymmetry of the mABJM theory. The smallest amount of supersymmetry which protects R-charges of BPS operators in 3-dimensional Chern–Simons matter theories is \({\mathcal {N}} = 3\) [26]. In our case, however, the vacua in the mABJM theory preserve the \({\mathcal {N}} = 6\) supersymmetries [8, 9]. The second term in the above equation is a one point function in a conformal field theory and is vanishing. Therefore, in the large N limit we have
The vacua parametrized by the occupation numbers \(\{N_n,\, N_n'\}\) of the GRVV matrices are composed of \(N\times N\) matrices having numerical matrix components. Therefore, the resulting VEV \(\langle {\mathcal {O}}^{(\Delta )}\rangle _{0} \) is a numerical value for a given N. We compare the specific value of VEV with the corresponding asymptotic coefficient in gravity side.
3.2 Gravity side
We start with the \(k=1\) case and write the fluctuations of 11-dimensional supergravity fields on the AdS\(_4\times S^7\) background as
where \(g^{0}_{pq}\) and \(F^{0}_{pqrs}\) represent the background geometry. To construct the 4-dimensional gravity theory, we implement KK reduction on \(S^7\). This reduction involves the expansion of the fluctuations in (3.4) in terms of \(S^7\) spherical harmonics. The expansion is generally expressed in terms of scalar, vector, and tensor spherical harmonics. However, the dual gravity fields of the CPO with \(\Delta =1\) are built purely from the coefficients of the scalar spherical harmonics. Here the truncated expansion involving only the scalar spherical harmonics is given,
where \(I_1\) is non-negative integer, x denotes the AdS\({}_4\) coordinates, y the \(S^7\) coordinates, and we divide the 11-dimensional indices \(p,q,\ldots \) into the indices of AdS\(_4\), \(\mu , \nu ,\ldots ,\) and those of \(S^7\), \(a,b,\ldots .\) The notation (ab) is for symmetrized traceless combination, while the notation \([ab\cdots ]\) is for anti-symmetrization among the indices, \(a,b,\ldots .\) The scalar spherical harmonic \(Y^{I_1}\) is determined by the eigenvalue equation,
where \(L = (32\pi ^2 k N)^{1/6} l_\mathrm{P}\) is the radius of \(S^7\). The expansion (3.5) follows the convention of [19, 27]. See also [28, 29] for the linearized equations of motion on AdS\(_4\times S^7\) background in the de Donder gauge.
Plugging (3.5) into the linearized equations of motion on the \(\mathrm{AdS}_4\times S^7\) background and collecting relevant equations of motion, we obtain two diagonalized equations for KK scalar fields in 4-dimensions (see [30] for details),
where
with gauge invariant combinations,
In the subsequent discussion, we will expand the LLM solution as in (3.4) and read the corresponding values of \(\Phi ^{I_1}\) and \(\Psi ^{I_1}\).
4 Exact holography
In mABJM theory, the CPO defined in (3.1) is constrained by the \(\mathrm{SU(2)}\times \mathrm{SU(2)}\times \mathrm{U}(1)\) global symmetry. In particular for the \(\Delta = 1\) case, we have [30]
where the overall numerical factor is determined by the normalization condition, \(C_{A_1,\ldots ,A_{\Delta }}^{(I)B_1,\ldots ,B_{\Delta }}C_{B_1, \ldots ,B_{\Delta }}^{(J)A_1,\ldots ,A_{\Delta }}+ (\text {c.c.})= \delta ^{IJ}\). We have verified that all CPOs with \(\Delta =1\) except for \({\mathcal {O}}^{(1)}\) in (4.1) have vanishing VEVs for all supersymmetric vacua of the mABJM theory.
Plugging (4.1) into (3.3) and expressing the vacuum solutions in terms of the GRVV matrices, we obtain
Here \(\mu \) is the mass parameter in the mABJM theory and has the relation \(\mu = 4\mu _0\) with the mass parameter \(\mu _0\) in the LLM geometries.
The LLM geometries near the asymptotic limit can be regarded as AdS\(_4\times S^7/{\mathbb {Z}}_k\) plus small fluctuations. Though the gauge conditions of the LLM solutions in 11-dimensional supergravity are not clear, the 4-dimensional fields \(\Phi ^{I_1}\) and \(\Psi ^{I_1}\) in (3.8) are gauge invariant and can be read from the asymptotic expansions. According to the holographic dictionary, asymptotic coefficients of \(\Phi ^{I_1}\) and \(\Psi ^{I_1}\) encode the VEVs of the corresponding CPOs in the mABJM theory.
Warp factors in the LLM geometries [11] are completely fixed by Z and V in (2.1), which are functions of \(\tilde{x}\) and \(\tilde{y}\). To implement the holographic renormalization procedure [13,14,15], we should rewrite the LLM solution in terms of the Fefferman–Graham (FG) coordinate system,
where z is the holographic direction and \(\tau \) is one of the \(S^7\) coordinates in the asymptotic limit. Here the warp factors \(g_i(z,\tau )\), \(i=1,2,3,4\), are defined as
where \(G_{tt}\), \(G_{xx}\), \(G_{\theta \theta }\), and \(G_{\tilde{\theta }\tilde{\theta }}\) with polar coordinates \(\rho \) and \(\xi \) are the warp factors in the LLM solutions [11]. For the detailed expressions of the LLM solution, see also [30]. For a general droplet parametrized by the \(C_i\) in (2.2), the asymptotic expansion of these warp factors gives
with \(\beta _3 = 2 C_1^3 - 3 C_1 C_2 + C_3\). From the asymptotic expansion of the warp factors and a similar expansion for the 4-form flux [30], one can read the fluctuations in (3.4), which will later be used in the construction of the modes \(\Phi ^{I_1}\) and \(\Psi ^{I_1}\).
We need to express the LLM geometries in terms of the spherical harmonics on \(S^7\). Since the geometries have SO(4)\(\times \)SO(4) isometry, they can be appropriately expressed in terms of the spherical harmonics having the same isometry. The scalar spherical harmonics on \(S^7\) are defined by the eigenvalue equation (3.6). In \(\mu _0 z\rightarrow 0\) limit the warp factors in (4.3) depend only on the \(\tau \) coordinate, and thus the appropriate spherical harmonics are the solutions of (3.6) which also depends only on \(\tau \) coordinate. One obtains two kinds of such solutions represented by the hypergeometric function \(_2F_1(a,b,c;\tau ^2)\), which correspond to those with \( I_1= 4i\) and \(I_1= 4i +2\) (\(i=0,1,2,\ldots \)). The first few nonvanishing \(Y^{I_1}\) are given by
where we used the normalization \(\frac{3}{\pi ^4}\int Y^{I_1}Y^{J_1} = \frac{3 I_1! \delta ^{I_1 J_1}}{ 2^{I_1-1} (I_1 + 3)!}\).
According to the dictionary of gauge/gravity duality, the mass of the scalar mode is related to the conformal dimension \(\Delta \) of the corresponding operator. In the AdS\(_4\)/CFT\(_3\) correspondence the relation is
From (3.7) we see that the masses of the 4-dimensional scalar modes have the form \(m^2 = n(n-6)/L^2\) with \(n= I_1 + 12\) for \(\Phi ^{I_1}\) and \(n= I_1\) for \(\Psi ^{I_1}\), respectively. So the relation (4.7) is rewritten as \(n(n-6) = 4\Delta (\Delta -3)\). From this relation the scalar mode \(\Phi ^{I_1}\) satisfying the relation \((I_1+12) (I_1+6) = 4\Delta ( \Delta -3)\) cannot be the dual scalar field of the CPO with \(\Delta = 1\). On the other hand, we notice that the field \(\Psi ^{I_1}\) satisfies the relation \(I_1(I_1-6) = 4\Delta (\Delta -3)\), which implies \(\Delta = \frac{I_1}{2}\). We naturally expect that the dual scalar field for the CPO with \(\Delta =1\) in (4.1) is nothing but \(\Psi ^{I_1}\) in (3.8) with \(I_1=2\).
By writing the asymptotic expansion of the LLM geometries (4.5) in terms of the scalar spherical harmonics (4.6), we obtain the asymptotic behavior of the 4-dimensional scalar modes, \(\Phi ^{I_1}\) and \(\Psi ^{I_1}\) with \(I_1=2\),
According to the holographic renormalization procedure for the scalar action on the AdS\(_4\) background, we have
where \({\mathbb N}\) is a numerical number depending on the normalization of the scalar \(\Psi ^{I_1=2}\), \(\psi ^{(1)}\) is the coefficient of the radial coordinate z in the expansion of the scalar mode, and \(\lambda \) is the ’t Hooft coupling constant defined as \(\lambda = N/k\) in ABJM theory. The overall coefficient \(N^2/\sqrt{\lambda }\) in (4.9) comes from the behavior of the 4-dimensional Newtonian constant, \(\frac{1}{G_4}\sim \frac{N^2}{\sqrt{\lambda }}\), in the large N limit. In the case \(k=1\), the overall normalization in (4.9) is reduced to \(N^{\frac{3}{2}}\). Actually the \(N^{3/2}\)-dependence in the right-hand side of (4.9) is a peculiar behavior of the normalization factor in holographic dual relation for the M2-brane theory [5, 31, 32]. The numerical factor \({\mathbb N}\) in (4.9) depends on the conventions of fields in the gauge theory and the gravity theory. By identifying the occupation number of vacua in the mABJM theory with the discrete torsion in the LLM geometries [9], i.e.,
the normalization factor \({\mathbb N}\) is fixed.
Comparing the values in (4.2) in \(k=1\) field theory with the corresponding values of \(\beta _3\) in gravity side, we obtain an exact holographic relation in the large N limit,
with the numerical normalization factor \({\mathbb N} = -\frac{\sqrt{2} }{144\pi }\). In the Young-diagram picture of the LLM geometries, \(\beta _3\) has no dependence on N and depends only on the shape of Young diagrams and is independent of the size of the diagram. To prove the holographic relation (4.11), we used Eqs. (4.2) and (4.10), and the following identity:
where \(\tilde{C}_p \equiv A^{\frac{p}{2}} C_p\), A being the area of the Young diagram in (2.2). For details, see also [30].
We also obtain the normalization factor \({\mathbb N}\) for \(k\ne 1\) with \(N_\mathrm{B} = 1\). In the Young-diagram picture, this corresponds to the rectangular-shaped diagrams. For this case the exact dual relation is given by
where \(\tilde{N} = A/k\) and \(\lambda = N/k\) is ’t Hooft coupling constant in the ABJM theory. In the large N limit, \(\tilde{N}\) approaches N and the overall factor \(N^2/\sqrt{\lambda }\) in (4.9) appears. For \(k=1\), the holographic relation (4.12) reduces to the result in (4.11).
We obtained Eqs. (4.11) and (4.12) in the large N limit. As we see in (3.2), to obtain the VEVs of CPOs in finite N, we need to take into account the 1 / N-corrections, which correspond to quantum corrections in field theory side. However, we notice that without considering the quantum corrections in calculations of VEVs of CPO with \(\Delta = 1\) the gauge/gravity relations (4.11) and (4.12) are satisfied even at the finite N (\({\ge } 2\)) exactly. This fact suggests that the VEVs of CPOs obtained from the classical supersymmetric vacuum solutions at finite N are read from classical supersymmetric solutions in dual gravity theory.
5 Conclusion
In this letter, we carried out the KK reduction and the holographic renormalization procedure for the mABJM theory and the LLM geometry in 11-dimensional supergravity. By calculating the VEVs of CPO with \(\Delta =1\) in field theory side and the corresponding asymptotic coefficients in gravity side, we found a supporting evidence for an exact gauge/gravity duality with \(k=1\) in the large N limit. We could test the duality since discrete Higgs vacua exist in the mABJM theory and they correspond one-to-one with the LLM geometries. We also extended the exact holographic relation to the case of any k for LLM geometries represented by rectangular-shaped Young diagrams.
It seems that the Higgs vacua of the mABJM theory are parametrized by the VEVs of CPOs and those are nonrenormalizable due to the high supersymmetry. This is similar to the case of the Coulomb branch in large N limit in \({\mathcal {N}}=4\) super Yang–Mills theory [19, 20]. Though our quantitative results for the gauge/gravity correspondence involve infinite examples, we need to accumulate more analytic evidence for CPOs with \(\Delta \) (\({\ge } 2\)) and k (\({\ge } 1\)) to define supersymmetric vacua. One should also test the dictionary of the gauge/gravity duality for one point functions of vector and tensor fields. For instance, it is important to verify that one point functions of the energy-momentum tensor vanish for all possible supersymmetric vacua, since the mABJM theory is a supersymmetric theory. We leave these issues for future study.
One necessary condition of the supergravity approximation in AdS/CFT correspondence is the large N limit. It was reported recently that the dual gravity limit of the ABJM theory is broken down at the sub-leading order of N in one-loop quantum correction in the supergravity theory [33]. This result indicates that though we can calculate the 1 / N-corrections in (3.2) in the field theory side, finding the corresponding results in 11-dimensional supergravity is non-trivial. That is, quantum corrections in supergravity may not give corresponding 1 / N-corrections. Therefore, obtaining meaningful results in ABJM theory in terms of the gauge/gravity at finite N is very limited.
On the other hand, we noticed that when we insert the classical supersymmetric vacuum solutions only into the CPO with \(\Delta = 1\), i.e., without considering the quantum corrections, the dual relations (4.11) and (4.12) are satisfied at the finite N (\({\ge } 2\)) exactly. Though we need to consider quantum corrections for finite N seriously, we think that this observation may give some intuition for the understanding of the gauge/gravity duality. We need more investigation in this direction.
Recently, it was reported that the mABJM theory on \(S^3\) has no gravity dual for the mass parameter larger than a critical value [34] (see also [35,36,37]). Though the setup is different from ours, which is the mABJM theory on R\(^{2,1}\), it is also intriguing to investigate the large mass region for our case. It seems promising to pursue this issue since the LLM geometries have no singularity over the whole transverse region.
References
J.M. Maldacena, The large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 38, 1113 (1999)
J.M. Maldacena, Adv. Theor. Math. Phys. 2, 231 (1998). arXiv:hep-th/9711200
S.S. Gubser, I.R. Klebanov, A.M. Polyakov, Gauge theory correlators from noncritical string theory. Phys. Lett. B 428, 105 (1998). arXiv:hep-th/9802109
E. Witten, Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 2, 253 (1998)
O. Aharony, O. Bergman, D.L. Jafferis, J. Maldacena, N = 6 superconformal Chern–Simons-matter theories, M2-branes and their gravity duals. JHEP 0810, 091 (2008). arXiv:0806.1218 [hep-th]
K. Hosomichi, K.M. Lee, S. Lee, S. Lee, J. Park, N = 5, 6 superconformal Chern–Simons theories and M2-branes on orbifolds. JHEP 0809, 002 (2008). arXiv:0806.4977 [hep-th]
J. Gomis, D. Rodriguez-Gomez, M. Van Raamsdonk, H. Verlinde, A massive study of M2-brane proposals. JHEP 0809, 113 (2008). arXiv:0807.1074 [hep-th]
H.C. Kim, S. Kim, Supersymmetric vacua of mass-deformed M2-brane theory. Nucl. Phys. B 839, 96 (2010). arXiv:1001.3153 [hep-th]
S. Cheon, H.C. Kim, S. Kim, Holography of mass-deformed M2-branes, p 48. arXiv:1101.1101 [hep-th]
I. Bena, N.P. Warner, A harmonic family of dielectric flow solutions with maximal supersymmetry. JHEP 0412, 021 (2004). arXiv:hep-th/0406145
H. Lin, O. Lunin, J.M. Maldacena, Bubbling AdS space and 1/2 BPS geometries. JHEP 0410, 025 (2004). arXiv:hep-th/0409174
R. Auzzi, S.P. Kumar, Non-abelian vortices at weak and strong coupling in mass deformed ABJM theory. JHEP 0910, 071 (2009). arXiv:0906.2366 [hep-th]
M. Henningson, K. Skenderis, The holographic Weyl anomaly. JHEP 9807, 023 (1998). arXiv:hep-th/9806087
V. Balasubramanian, P. Kraus, A stress tensor for anti-de Sitter gravity. Commun. Math. Phys. 208, 413 (1999). arXiv:hep-th/9902121
S. de Haro, S.N. Solodukhin, K. Skenderis, Holographic reconstruction of space-time and renormalization in the AdS/CFT correspondence. Commun. Math. Phys. 217, 595 (2001). arXiv:hep-th/0002230
K.K. Kim, O.K. Kwon, C. Park, H. Shin, Renormalized entanglement entropy flow in mass-deformed ABJM theory. Phys. Rev. D 90(4), 046006 (2014). arXiv:1404.1044 [hep-th]
K.K. Kim, O.K. Kwon, C. Park, H. Shin, Holographic entanglement entropy of mass-deformed Aharony–Bergman–Jafferis–Maldacena theory. Phys. Rev. D 90(12), 126003 (2014). arXiv:1407.6511 [hep-th]
C. Kim, K.K. Kim, O.K. Kwon, Holographic entanglement entropy of anisotropic minimal surfaces in LLM geometries. Phys. Lett. B 759, 395 (2016). arXiv:1605.00849 [hep-th]
K. Skenderis, M. Taylor, Kaluza–Klein holography. JHEP 0605, 057 (2006). arXiv:hep-th/0603016
K. Skenderis, M. Taylor, Holographic Coulomb branch vevs. JHEP 0608, 001 (2006). arXiv:hep-th/0604169
K. Skenderis, M. Taylor, Anatomy of bubbling solutions. JHEP 0709, 019 (2007). arXiv:0706.0216 [hep-th]
I.R. Klebanov, E. Witten, AdS/CFT correspondence and symmetry breaking. Nucl. Phys. B 556, 89 (1999). arXiv:hep-th/9905104
E. Witten, Multitrace operators, boundary conditions, and AdS/CFT correspondence, p 13. arXiv:hep-th/0112258
M. Berkooz, A. Sever, A. Shomer, ‘Double trace’ deformations, boundary conditions and space-time singularities. JHEP 0205, 034 (2002). arXiv:hep-th/0112264
S.S. Gubser, I.R. Klebanov, A Universal result on central charges in the presence of double trace deformations. Nucl. Phys. B 656, 23 (2003). arXiv:hep-th/0212138
M.K. Benna, I.R. Klebanov, T. Klose, Charges of monopole operators in Chern–Simons Yang–Mills theory. JHEP 1001, 110 (2010). arXiv:0906.3008 [hep-th]
H.J. Kim, L.J. Romans, P. van Nieuwenhuizen, The mass spectrum of chiral N = 2 D = 10 supergravity on S**5. Phys. Rev. D 32, 389 (1985)
B. Biran, A. Casher, F. Englert, M. Rooman, P. Spindel, The fluctuating seven sphere in eleven-dimensional supergravity. Phys. Lett. B 134, 179 (1984)
A. Casher, F. Englert, H. Nicolai, M. Rooman, The mass spectrum of supergravity on the round seven sphere. Nucl. Phys. B 243, 173 (1984)
D. Jang, Y. Kim, O.K. Kwon, D.D. Tolla, Mass-deformed ABJM theory and LLM geometries: exact holography, p 44. arXiv:1612.05066 [hep-th]
I.R. Klebanov, A.A. Tseytlin, Entropy of near extremal black p-branes. Nucl. Phys. B 475, 164 (1996). arXiv:hep-th/9604089
N. Drukker, M. Marino, P. Putrov, From weak to strong coupling in ABJM theory. Commun. Math. Phys. 306, 511 (2011). arXiv:1007.3837 [hep-th]
J.T. Liu, W. Zhao, One-loop supergravity on \({\rm AdS}_4\times S^7/{{\mathbb{Z}}}_k\) and comparison with ABJM theory. JHEP 1611, 099 (2016). arXiv:1609.02558 [hep-th]
T. Nosaka, K. Shimizu, S. Terashima, Mass deformed ABJM theory on three sphere in large N limit. JHEP 1703, 121 (2017). arXiv:1608.02654 [hep-th]
L. Anderson, K. Zarembo, Quantum phase transitions in mass-deformed ABJM matrix model. JHEP 1409, 021 (2014). arXiv:1406.3366 [hep-th]
L. Anderson, J.G. Russo, ABJM theory with mass and FI deformations and quantum phase transitions. JHEP 1505, 064 (2015). arXiv:1502.06828 [hep-th]
T. Nosaka, K. Shimizu, S. Terashima, Large N behavior of mass deformed ABJM theory. JHEP 1603, 063 (2016). arXiv:1512.00249 [hep-th]
Acknowledgements
We would like to thank Changrim Ahn, Loriano Bonora, Kyung Kiu Kim, and Chanyong Park for helpful discussions. This work was supported by the National Research Foundation of Korea (NRF) grant with the Grant Number NRF-2014R1A1A2057066 and NRF-2016R1D1A1B03931090 (Y.K.) and NRF-2014R1A1A2059761 (O.K.).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3.
About this article
Cite this article
Jang, D., Kim, Y., Kwon, OK. et al. Exact holography of the mass-deformed M2-brane theory. Eur. Phys. J. C 77, 342 (2017). https://doi.org/10.1140/epjc/s10052-017-4909-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-017-4909-3