Study on the radiative decays of $h_c$ via intermediate meson loops model

Abstract

Recently, the BESIII Collaboration reported two new decay processes: $h_c(1P)\rightarrow \gamma \eta$ and $\gamma \eta ^\prime$. Inspired by this measurement, we propose to study the radiative decays of $h_c$ via intermediate charmed meson loops in an effective Lagrangian approach. With the acceptable cutoff parameter range, the calculated branching ratios of $h_c(1P)\rightarrow \gamma \eta$ and $\gamma \eta ^\prime$ are of the orders of $10^{-4}$ to $10^{-3}$ and $10^{-3}$ to $10^{-2}$, respectively. The ratio $R_{h_c}= \mathcal {B}( h_c\rightarrow \gamma \eta )/\mathcal {B}( h_c\rightarrow \gamma \eta ^\prime )$ can reproduce the experimental measurements with the commonly acceptable $\alpha$ range. This ratio provide us with some information on the $\eta$–$\eta ^\prime$ mixing, which may be helpful for us to test the SU(3)-flavor symmetries in QCD.

1 Introduction

The properties of charmonium states and their related theoretical ideas and methods which is based on theory of Quantum Chromodynamics (QCD) have already produced a lot of knowledge [1] since the first charmonium state $J/\psi$ was observed in 1974 [2,3,4]. All the charmonium states below $D\bar{D}$ threshold have been observed experimentally and can be well described by potential models [5]. Among these states, the P-wave spin-singlet state $h_c(^1P_1)$ is the last charmonium state below the $D\bar{D}$ threshold that was confirmed experimentally. In 1992, the E760 Collaboration at Fermi Lab first established this state in the $p\bar{p}$ annihilation. Since the quantum numbers of $h_c$ is $J^{PC}=1^{+-}$, it cannot be produced in $e^+e^-$ annihilation directly. As a result, there are only a few decay modes of $h_c$ observed experimentally. The dominant decay mode of $h_c$ is E1 radiative transition and the branching ratio of $h_c\rightarrow \gamma \eta _{c}$ is about $(51 \pm 6)\%$ [6, 7]. The hadronic decay $h_c\rightarrow 2(\pi ^+\pi ^-) \pi ^0$ has a branching ratio $(2.2^{+0.8}_{-0.7})\%$ [8], while the branching ratio of hadronic decay $h_c\rightarrow 3(\pi ^+\pi ^-) \pi ^0$ only has an upper limit <2.9% [8]. Accordingly, there are not many theoretical studies of $h_c$. The $h_c$ production addressed by a hadron collider [9], by $e^+e^-$ annihilation [10] and by the B factory [11,12,13] are investigated. In Ref. [14], the authors studied the $O(\alpha _{s}v^{2})$ corrections to the decays of $h_{c}$ in non-relativistic QCD. In Ref. [15], Guo et al. applied the NREFT to study the isospin violation mechanisms of $\psi ^\prime \rightarrow h_c\pi ^0$. Liu and Zhao in Ref. [16] studied the helicity selection rule evading mechanism of the process $h_c$ decaying to baryon–anti-baryon pairs with effective Lagrangian approach. Recently, Zhu and Dai in Ref. [17] studied the $\eta$ and $\eta ^\prime$ production in the radiative $h_c$ decay with a light-cone factorization approach.

Since $h_c$ has negative C parity, it very likely decays into a photon plus a pseudoscalar meson, such as $\eta _c$, $\eta$ and $\eta ^\prime$. Very recently, based on the $4.48\times 10^8$ $\psi ^\prime$ events collected with the BESIII detector operating at the BEPCII storage ring, the BESIII Collaboration firstly observed the radiative decay processes $h_c \rightarrow \gamma \eta$ and $\gamma \eta ^\prime$ with a statistical significance of $4.0\sigma$ and $8.0\sigma$, respectively [18]. The measured branching fractions of $h_{c}\rightarrow \gamma \eta$ and $\gamma \eta ^\prime$ are $(4.7\pm 1.5\pm 1.4)\times 10^{-4}$ and $(1.52\pm 0.27\pm 0.29)\times 10^{-3}$, respectively, where the first errors are statistical and the second errors are systematic uncertainties. These two decay modes may be useful for providing constraints to theoretical models in the charmonium region. The ratio between them can also be used to study the $\eta$–$\eta ^\prime$ mixing [19], which is important to test SU(3)-flavor symmetries in QCD.

In this work, we will investigate the radiative decays $h_{c}\rightarrow \gamma \eta (\gamma \eta ^\prime )$ via the intermediate meson loop (IML) model in an effective Lagrangian approach(ELA). The IML transition is regarded as an important nonperturbative transition mechanisms which has a long history [20,21,22,23] and recently are widely used to study the production and decays of ordinary and exotic states [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54]. The paper is organized as follows: After the introduction in Sect. 1, we will present calculation of the radiative decays $h_{c}\rightarrow \gamma \eta (\gamma \eta ^\prime )$ via the intermediate charmed meson loop and give some relevant formulas in Sect. 2. In Sect. 3, the numerical results are presented. A brief summary will be given in Sect. 4.

2 The radiative decays of $h_c$

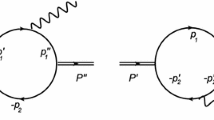
Generally speaking, we should include all the possible intermediate meson exchange loops in the calculation. In reality, the breakdown of the local quark–hadron duality allows us to pick up the leading contributions as a reasonable approximation [20, 21]. The coupling between $h_c$ and $D^{(*)} {\bar{D}}^{(*)}$ is an S-wave, so we consider the intermediate charmed meson exchange loops as the leading contributions. At the hadronic level, as shown in Fig. 1, the initial state $h_c$ dissolves into two charmed mesons which are off-shell and originate from the coupled channel effects. Then these two virtual charmed mesons turn into a final photon and an $\eta (\eta ^\prime )$ meson by exchanging the charmed meson.

In order to calculate the contributions from the charmed meson loops in Fig. 1, we need the leading-order effective Lagrangians for the couplings. Based on the heavy quark symmetry [55, 56], the Lagrangian for the P-wave charmonia at leading order is

$$\begin{aligned} \mathcal {L}=ig_1Tr[P_{c{\bar{c}}}^\mu {\bar{H}}_{2i}\gamma _\mu {\bar{H} }_{1i}]+h.c., \end{aligned}$$

(1)

where the spin multiplets for these four P-wave charmonium states are expressed as

$$\begin{aligned} P_{c{\bar{c}}}^\mu= & {} \frac{1 + \not v}{2} \left( \chi _{c2}^{\mu \alpha }\gamma _\alpha +\frac{1}{{\sqrt{2}}}\varepsilon ^{\mu \nu \alpha \beta }v_\alpha \gamma _\beta \chi _{c1\nu }\right. \nonumber \\&+\left. \frac{1}{{\sqrt{3}}}( \gamma ^\mu -v^\mu ) \chi _{c0}+h_c^\mu \gamma _5 \right) \frac{1-\not v}{2}, \end{aligned}$$

(2)

with $v^\mu$ being the four-velocity of the multiplets.

Fig. 1

The hadron-level diagrams for $h_c \rightarrow \gamma \eta$ and $\gamma \eta ^\prime$ via charged intermediate charmed meson loops. Similar diagrams for neutral and strange intermediate charmed meson loops

The charmed and anti-charmed meson triplets read

$$\begin{aligned}&H_{1i} = \frac{1+\not v}{2} \left[ \mathcal{D}_{i}^{*\mu }\gamma _{\mu }-\mathcal{D}_{i}\gamma _{5}\right] , \end{aligned}$$

(3)

$$\begin{aligned}&H_{2i} =\left[ {\bar{ \mathcal{D}}}_{i}^{*\mu }\gamma _{\mu }- {\bar{\mathcal{D}} }_{i}\gamma _{5}\right] \frac{1-\not v}{2}, \end{aligned}$$

(4)

$$\begin{aligned}&{\bar{H}}_{1i,2i}=\gamma ^0 H_{1i,2i}^\dag \gamma ^0, \end{aligned}$$

(5)

where $\mathcal{D}$ and $\mathcal{D}^{*}$ denote the pseudoscalar and vector charmed meson fields, respectively, i.e. $\mathcal{D}^{( *) }=\left( D^{0(*) },D^{+( *) },D_{s}^{+( *) }\right)$. $v^\mu$ is the four-velocity of the charmed mesons. $\varepsilon _{\mu \nu \alpha \beta }$ is the antisymmetric Levi-Civita tensor and $\varepsilon _{0123}=+1$.

Consequently, the relevant effective Lagrangian for $h_c$ reads

$$\begin{aligned} \mathcal {L}_{h_c \mathcal{D}^{( *) }\mathcal{D}^{( *) }}= & {} g_{h_c \mathcal{D}^*\mathcal{D} }h_c^\mu \left( \mathcal{D} {\bar{\mathcal{D}}}_\mu ^*+ \mathcal{D}_\mu ^*{\bar{ \mathcal D}} \right) \nonumber \\&+ig_{h_c \mathcal{D}^*\mathcal{D}^*}\varepsilon _{\mu \nu \alpha \beta }\partial ^{\mu }h_c^\nu \mathcal{D}^{*\alpha }{\bar{\mathcal{D}}}^{*\beta }, \end{aligned}$$

(6)

where the coupling constants will be determined later.

The effective Lagrangian for the light pseudoscalar meson coupled to a charm mesons pair can be constructed based on the heavy quark limit and chiral symmetry [55,56,57],

$$\begin{aligned} {\mathcal L}_{\mathcal{D}^{(*)}\mathcal{D}^{(*)} {\mathcal P}}= & {} -ig_{\mathcal{D}^{*}\mathcal{D} {\mathcal P}}\left( \mathcal{D}^i \partial ^\mu {\mathcal P}_{ij} \mathcal{D}_\mu ^{*j\dagger }-\mathcal{D}_\mu ^{*i}\partial ^\mu {\mathcal P}_{ij} \mathcal{D}^{j \dag }\right) \nonumber \\&+\frac{1}{2}g_{\mathcal{D}^*D^*{\mathcal P}}\varepsilon _{\mu \nu \alpha \beta }\mathcal{D}_i^{*\mu }\partial ^\nu {\mathcal P} {\overset{ \leftrightarrow }{\partial }}{\!^{\alpha }} \mathcal{D}_j^{*\beta \dag }, \end{aligned}$$

(7)

where ${\mathcal P}$ is for $3\times 3$ matrices for the pseudoscalar octet, i.e.,

$$\begin{aligned} \mathcal {P}= & {} \left( \begin{array}{ccc} \frac{\pi ^0}{\sqrt{2}}+\frac{\eta \cos \alpha _P+\eta ^\prime \sin \alpha _P}{ \sqrt{2}} &{} \pi ^+ &{} K^+ \\ \pi ^- &{} -\frac{\pi ^0}{\sqrt{2}}+\frac{ \eta \cos \alpha _P + \eta ^\prime \sin \alpha _P}{\sqrt{2}} &{} K^0 \\ K^- &{} {\bar{K}}^0 &{} - \eta \sin \alpha _P + \eta ^\prime {\cos \alpha _P} \end{array} \right) . \end{aligned}$$

(8)

The physical states $\eta$ and $\eta ^\prime$ are the linear combinations of $n{\bar{n}} = ({u\bar{u}} + {d\bar{d}})/\sqrt{2}$ and $s\bar{s}$ and they are taken to be of the following form:

$$\begin{aligned} |\eta \rangle= & {} \cos \alpha _P|n\bar{n}\rangle -\sin \alpha _P |s\bar{s} \rangle \, \nonumber \\ |\eta ^\prime \rangle= & {} \sin \alpha _P |n\bar{n}\rangle + \cos \alpha _P |s\bar{s} \rangle , \end{aligned}$$

(9)

where $\alpha _P \simeq \theta _P + \arctan \sqrt{2}$. The empirical value for the pseudoscalar mixing angle $\theta _P$ should be in the range $-24.6^\circ$ to $-11.5^\circ$ [58]. In this work, we will take $\theta _P = -19.3^\circ$ [59] and $-14.4^\circ$ [60], respectively. The coupling constants will be determined in the next section.

In order to calculate these two radiative decay processes, the effective Langrangian containing the interaction of photon are also needed. If we implement the minimal substitution $\partial ^{\mu }\rightarrow \partial ^\mu +ieA^\mu$ for the free scalar and massive vector fields, then we can obtain the relevant Lagrangians [61, 62],

$$\begin{aligned} \mathcal {L}_{DD\gamma }= & {} ieA_{\mu }D^{-}{\overset{\leftrightarrow }{ \partial }}{\!^{\mu }}D^{+}+ieA_{\mu }D_{s}^{-}{\overset{\leftrightarrow }{ \partial }}{\!^{\mu }}D_{s}^{+}\, , \end{aligned}$$

(10)

$$\begin{aligned} \mathcal {L}_{D^{*}D^{*}\gamma }= & {} ieA_{\mu }\left[ g^{\alpha \beta }D_{\alpha }^{*-}{\overset{\leftrightarrow }{\partial }}{\!^{\mu }} D_{\beta }^{*+}+g^{\mu \beta }D_{\alpha }^{*-}\partial ^{\alpha }D_{\beta }^{*+}\right. \nonumber \\&\left. \qquad \qquad -g^{\mu \alpha }\partial ^{\beta }D_{\alpha }^{*-}D_{\beta }^{*+} \phantom {\frac{1}{2}}\right] \nonumber \\&+ ieA_{\mu }\left[ g^{\alpha \beta }D_{s\alpha }^{*-}{\overset{ \leftrightarrow }{\partial }}{\!^{\mu }}D_{s\beta }^{*+}+g^{\mu \beta }D_{s\alpha }^{*-}\partial ^{\alpha }D_{s\beta }^{*+}\right. \nonumber \\&\left. \qquad \qquad -g^{\mu \alpha }\partial ^{\beta }D_{s\alpha }^{*-}D_{s\beta }^{*+} \phantom {\frac{1}{2}} \right] , \end{aligned}$$

(11)

where $A\overleftrightarrow \partial _\mu B=A \partial _\mu B-(\partial _\mu A)B$, $F_{\mu \nu }=\partial _\mu A_\nu -\partial _\nu A_\mu$, and $M_{\mu \nu }=\partial _\mu M_\nu -\partial _\nu M_\mu$. Note that the neutral interactions vanish. The interaction of $D^*D\gamma$ has the following form [63, 64]:

$$\begin{aligned} \mathcal {L}_{D^{*}D\gamma }= & {} \frac{e}{4}\varepsilon ^{\mu \nu \alpha \beta }F_{\mu \nu }[g_{D^{*+}D^{+}\gamma }D_{\alpha \beta }^{*+}D^+ + g_{D^{*0}D^0\gamma }D_{\alpha \beta }^{*0}D^0\nonumber \\&+ g_{D_s^{*+}D_s^+\gamma } D_{s\alpha \beta }^{*+}D_{s}^{+}]+h.c.. \end{aligned}$$

(12)

With the above Lagrangians, we can write out the explicit transition amplitudes of $h_c(p_1) \rightarrow [D^{(*)}(q_1) {\bar{D}}^{(*)}(q_3)] D^{(*)}(q_2) \rightarrow \gamma (p_2) \eta ^{(\prime )}(p_3)$ shown in Fig. 1,

$$\begin{aligned} \mathcal {M}^{(a)}= & {} \int \frac{d^4q_2}{( 2\pi )^4} [ g_{h_cD^*D}\epsilon _{1\mu }] [ e\epsilon _{2 \theta }( q_2^\theta -q_1^\theta )] [ -g_{D^*D\eta }p_{3\rho }] \nonumber \\&\times \frac{i}{q_1^2-m_1^2} \frac{i}{q_2^2-m_2^2} \frac{i( -g^{\mu \rho }+q_3^\mu q_3^\rho /m_3^2) }{ q_3^2-m_3^2}\mathcal {F}( m_2,q_2^2) , \end{aligned}$$

(13)

$$\begin{aligned} \mathcal {M}^{( b) }= & {} \int \frac{d^4q_2}{( 2\pi )^4} [ g_{h_cD^*D}\epsilon _{1\mu }] [ eg_{D^{*+}D^+\gamma }\varepsilon _{\theta \phi \kappa \lambda }p_2^\theta \epsilon _2^\phi q_2^\kappa ]\nonumber \\&\times [ -g_{D^*D^*\eta }\varepsilon _{\rho \tau \sigma \xi }p_3^\tau q_3^\sigma ]\times \frac{i}{q_1^2-m_1^2} \nonumber \\&\times \frac{i( -g^{\lambda \rho }+q_2^{\lambda }q_2^\rho /m_2^2)}{q_2^2-m_2^2}\frac{i(-g^{\mu \xi }+q_3^\mu q_3^\xi /m_3^2) }{q_3^2-m_3^2}\mathcal {F} ( m_2,q_2^2), \end{aligned}$$

(14)

$$\begin{aligned} \mathcal {M}^{( c) }= & {} \int \frac{d^4q_2}{( 2\pi )^4} [ g_{h_cD^*D}\epsilon _{1\mu }] [ e\epsilon _2^\theta [ g_{\kappa \lambda }( q_{2\theta }-q_{1\theta }) \nonumber \\&+g_{\theta \lambda }q_{2\kappa }-g_{\theta \kappa }q_{1\lambda }] ] [ g_{D^*D\eta }p_{3\rho }]\nonumber \\&\times \frac{i(-g^{\mu \kappa }+q_1^\mu q_1^{\kappa }/m_1^2)}{ q_1^2-m_1^2}\nonumber \\&\times \frac{i(-g^{\lambda \rho }+q_2^\lambda q_2^\rho /m_2^2)}{q_2^2-m_2^2}\frac{i}{q_3^2-m_3^2}\mathcal {F} ( m_2,q_2^2) , \end{aligned}$$

(15)

$$\begin{aligned} \mathcal {M}^{( d) }= & {} \int \frac{d^4q_2}{( 2\pi )^4} \left[ g_{h_cD^*D^*}\varepsilon _{\mu \nu \alpha \beta }p_1^\mu \epsilon _1^\nu \right] \nonumber \\&\times [ eg_{D^{*+}D^+\gamma }\varepsilon _{\theta \phi \kappa \lambda }p_2^\theta \epsilon _2^\phi q_1^\kappa ] [-ig_{D^*D\eta }p_{3\rho }] \nonumber \\&\times \frac{i(-g^{\beta \lambda }+q_1^\beta q_1^\lambda /m_1^2)}{q_1^2-m_1^2}\frac{i}{q_2^2-m_2^2}\nonumber \\&\times \frac{ i\left( -g^{\alpha \rho }+q_3^\alpha q_3^\rho /m_3^{2}\right) }{ q_3^2-m_3^2}\mathcal {F}\left( m_2,q_2^2 \right) , \end{aligned}$$

(16)

$$\begin{aligned} \mathcal {M}^{( e) }= & {} \int \frac{d^4q_2}{( 2\pi )^4} \left[ g_{h_cD^*D^*}\varepsilon _{\mu \nu \alpha \beta }p_1^\mu \epsilon _1^\nu \right] \nonumber \\&\times \left[ e\epsilon _2^\theta \left[ g_{\kappa \lambda }\left( q_{2\theta } -q_{1\theta } \right) +g_{\theta \lambda }q_{2\kappa } -g_{\theta \kappa }q_{1\lambda } \right] \right] \nonumber \\&\times [-g_{D^*D^*\eta }\varepsilon _{\rho \tau \sigma \xi }p_3^\tau q_3^\sigma ] \nonumber \\&\times \frac{i(-g^{\beta \kappa }+q_1^\beta q_1^\kappa /m_1^2)}{q_1^2-m_1^2}\frac{i(-g^{\lambda \rho }+q_2^{\lambda }q_2^\rho /m_2^2)}{q_2^2-m_2^2} \nonumber \\&\times \frac{i(-g^{\alpha \xi }+q_3^\alpha q_3^\xi /m_3^2)}{ q_3^2-m_3^2}\mathcal {F}\left( m_2,q_2^2\right) \, , \end{aligned}$$

(17)

where $p_1$, $p_2$ and $p_3$ are the four-momenta of the initial state $h_c$, final state photon and $\eta (\eta ^{\prime })$, respectively. $\varepsilon _1$ and $\varepsilon _2$ are the polarization vector of $h_c$ and photon, respectively. $q_1$, $q_3$ and $q_2$ are the four-momenta of the charmed meson connecting $h_c$ and photon, the charmed meson connecting $h_c$ and $\eta (\eta ^{\prime })$, and the exchanged charmed meson, respectively.

In the triangle diagram of Fig. 1, the exchanged charmed mesons are off-shell. To compensate the off-shell effect and to regularize the divergence [65,66,67], we introduce a monopole form factor,

$$\begin{aligned} \mathcal {F}\left( m_2,q_2^{2}\right) =\frac{\Lambda ^2-m_2^2}{ \Lambda ^2-q_2^2}, \end{aligned}$$

(18)

where $q_2$ and $m_2$ are the momentum and mass of the exchanged charmed meson, respectively. The parameter $\Lambda \equiv m_2+\alpha \Lambda _{\mathrm{QCD}}$ and the QCD energy scale $\Lambda _{\mathrm{QCD}} = 220 \mathrm {MeV}$. The determination of this dimensionless parameter $\alpha$ depends on the specific process, which is usually of order one.

Fig. 2

(Color online). a The $\alpha$-dependence of the branching ratios of $h_c\rightarrow \gamma \eta$ (solid line) and $\gamma \eta ^\prime$ (dashed line), respectively. The $\eta$–$\eta ^\prime$ mixing angle $\theta _P=-19.3^\circ$ is from Ref. [59]. b The $\alpha$-dependence of the branching ratios of $h_c\rightarrow \gamma \eta$ (solid line) and $\gamma \eta ^\prime$ (dashed line), respectively. The $\eta$–$\eta ^\prime$ mixing angle $\theta _P=-14.4^\circ$ from Ref. [60]

3 Numerical results

The coupling constants $g_{h_c\mathcal{D}^*\mathcal{D}}$ and $g_{h_c\mathcal{D}^*\mathcal{D}^*}$ are determined as

$$\begin{aligned} g_{h_c\mathcal{D}^*\mathcal{D}}=-2g_{1}\sqrt{m_{h_c}m_\mathcal{D} m_{\mathcal{D}^*}} , \quad g_{h_c\mathcal{D}^{*}\mathcal{D}^{*}}=2g_{1}\frac{m_{\mathcal{D}^*}}{\sqrt{m_{h_c}}}, \end{aligned}$$

(19)

with $g_{1}=-\sqrt{m_{\chi _{c0}}/3}/f_{\chi _{c0}}$, where $m_{\chi _{c0}}$ and $f_{\chi _{c0}}=510\pm 40$ $\mathrm {MeV}$ are the mass and decay constant of $\chi _{c0}$, respectively [55].

In the heavy quark and chiral limits, the charmed meson couplings to pseudoscalar mesons have the following [57]:

$$\begin{aligned} g_{\mathcal{D}^*\mathcal{D}\mathcal {P}}=\frac{2g}{f_\pi }\sqrt{m_\mathcal{D} m_{\mathcal{D}^*}}, \quad g_{\mathcal{D}^*\mathcal{D}^*\mathcal {P}}=\frac{g_{D^*D\mathcal {P}}}{ \sqrt{m_\mathcal{D}m_{\mathcal{D}^*}}}, \end{aligned}$$

(20)

where $g=0.59,$ $f_\pi =132$ $\mathrm {MeV}$ are adopted.

With the help of the measured experimental total width of $D^{*+}$ and the branching ratio of $D^{*+}\rightarrow D^{+}\gamma$ [58], we determine the coupling constant: $g_{D^{*+}D^+\gamma }=0.5\, \mathrm {GeV}^{-1}$. Since the $D^{*0}$ and $D_s^{*\pm }$ total widths are kept unknown, we adopt the values $g_{D^{* 0}D^0\gamma } \simeq 2.0\, \mathrm {GeV}^{-1}$ [68] and $g_{D_{s}^{*}D_{s}\gamma }=-0.3\pm 0.1\, \mathrm {GeV}^{-1}$[69].

In Fig. 2a, we plot the $\alpha$ dependence of the branching ratios of $h_c\rightarrow \gamma \eta$ (solid line) and $h_c\rightarrow \gamma \eta ^\prime$ (dashed line) with $\theta _p=-19.3^\circ$, respectively. We also zoom into details of the figure with a narrower range $\alpha =0.2$–0.3 in order to show the best fit of the $\alpha$ parameter. As shown in this figure, there is no cusp structure in the curve, which is because the mass of $h_c$ lies below the intermediate $D{\bar{D}}^*$ threshold. The $\alpha$ dependence of the branching ratios are not drastically sensitive with the commonly accepted $\alpha$ range. For the process $h_c\rightarrow \gamma \eta$, our calculated branching ratios can reproduce the experimental data [18] at $\alpha =0.27\pm 0.06$. For $h_c\rightarrow \gamma \eta ^\prime$; the results are consistent with the experimental measurements with $\alpha =0.24\pm 0.03$. At the same cutoff parameter $\alpha$, the calculated branching ratios of $h_c\rightarrow \gamma \eta ^\prime$ are about one order of magnitude larger than that of $h_c\rightarrow \gamma \eta$, which is mainly attributed to the $\eta$–$\eta ^\prime$ mixing shown in Eq. (9). In Fig. 2b, with $\theta _P=-14.4^\circ$, we plot the $\alpha$ dependence of the branching ratios of $h_c\rightarrow \gamma \eta$ (solid line) and $h_c\rightarrow \gamma \eta ^\prime$ (dashed line), respectively. We also zoom into details of the figure with a narrower range, $\alpha =0.15$–0.35, in order to show the best fit of the $\alpha$ parameter. The behavior is similar to that of Fig. 2a. With $\theta _P=-14.4^\circ$, the branching ratios of $h_c\rightarrow \gamma \eta$ and $\gamma \eta ^\prime$ can reproduce the experimental data with $\alpha =0.188_{-0.048}^{+0.038}$ and $0.26_{-0.03}^{+0.02}$, respectively. The errors for $\alpha$ are asymmetric. This asymmetry comes from a fact that the $\alpha$ dependence of the $\mathcal{B} (h_c \rightarrow \gamma \eta (\eta ^\prime ))$ is nonlinear.

Fig. 3

(Color online). a The branching ratios of $h_c\rightarrow \gamma \eta$ (solid line) and $h_c\rightarrow \gamma \eta ^{\prime }$ (dashed line) in terms of the $\eta$–$\eta ^\prime$ mixing angle with $\alpha =0.3$. b The branching ratios of $h_c\rightarrow \gamma \eta$ (solid line) and $h_c\rightarrow \gamma \eta ^{\prime }$ (dashed line) in terms of the $\eta$–$\eta ^\prime$ mixing angle with $\alpha =0.5$

In order to illustrate the impact of the mixing angle, in Fig. 3a, b, we present the branching ratios in terms of the $\eta$–$\eta ^\prime$ mixing angle with $\alpha =0.3$ (solid line) and 0.5 (dashed line), respectively. In the case $\alpha =0.3$, when the mixing angle $\alpha _P$ increases, the branching ratios of $h_c \rightarrow \gamma \eta$ increase, while the branching ratios of $h_c \rightarrow \gamma \eta ^\prime$ decrease. This behavior suggests how the mixing angle influences our calculated results to some extent. A similar behavior appears in the case $\alpha =0.5$.

As is well known, the $\eta$–$\eta ^\prime$ mixing is a long-standing question in the literature. This mixing angle plays an important role in physical processes involving the $\eta$ and $\eta ^\prime$ mesons. In Ref. [18], the BESIII Collaboration measured the branching fraction ratio $R_{h_c}= [\mathcal {B}( h_c\rightarrow \gamma \eta )/\mathcal {B}( h_c\rightarrow \gamma \eta ^\prime )] = [30.7\pm 11.3(\mathrm{stat})\pm 8.7(\mathrm{sys})]\%$. This ratio $R_{h_c}$ can be used to study the $\eta$–$\eta ^\prime$ mixing [19], which is important to test SU(3)-flavor symmetries in QCD. In Fig. 4, we plot the $\alpha$ dependence of the ratio $R_{h_c}$ with $\theta _P=-19.3^\circ$ (solid line) and $-14.4^\circ$ (dashed line), respectively. As shown from this figure, the calculated ratio $R_{h_c}$ can reproduce the experimental measurements at the commonly acceptable $\alpha$ range for $\theta _P=-19.3^\circ$. With $\theta _P=-14.4^\circ$, the calculated ratio $R_{h_c}$ is slightly larger than the experimental value. Furthermore, this ratio is less sensitive to the cutoff parameter $\alpha$, which is because the involved loops are the same. When we take the ratio, the coupling vertices are canceled out, so the ratio reflects the open threshold effects through the intermediate charmed meson loops and the mixing angle between $\eta$ and $\eta ^\prime$ to some extent. In Fig. 5, we plot the $\eta$–$\eta ^\prime$ mixing angle dependence of the ratios $R_{h_c}$ at $\alpha =0.3$ (solid line) and 1.0 (dashed line), respectively. This ratio changes very little when increasing the cutoff parameter $\alpha$; as a result, it can be used to probe the $\eta$–$\eta ^\prime$ mixing. In our study, at $\alpha =0.3$, our results are consistent with the experimental measurements in the range $\alpha _P=(36.7^{ +2.1}_{-2.3})^\circ$, which corresponds to $\theta _P=(-18.0^{+2.3}_{-2.1})^\circ$. In the case $\alpha =1.0$, we can reproduce the experimental data in the range $\alpha _P=(36.2^{+2.2}_{-2.4})^\circ$, which corresponds to $\theta _P=(-18.5^{+2.4}_{-2.2})^\circ$. So our calculations can give a strong constraint on the $\eta$–$\eta ^\prime$ mixing angle and we expect more precise measurements on this ratio, which may help us constrain this mixing angle.

Fig. 4

(Color online). The $\alpha$-dependence of the ratios $R_{h_c}$ with $\eta$–$\eta ^\prime$ mixing angle $\theta _P=-19.3^\circ$ (solid line) and $\theta _P=-14.4^\circ$ (dashed line), respectively

Fig. 5

The ratios $R_{h_c}$ in terms of the $\eta$–$\eta ^\prime$ mixing angle with $\alpha =0.3$ (solid line) and $\alpha =1.0$ (dashed line)

The $\eta$–$\eta ^\prime$ mixing angle can neither be calculated from first principles in QCD nor measured from experiments directly. There are a lot of studies on this subject using different methods [70,71,72,73,74] and different processes, including various decay processes involving the light pseudoscalar mesons. For example, in Ref. [60], the KLOE Collaboration updated the $\eta$–$\eta ^\prime$ mixing angle value by fitting their measurement $R_\phi = BR(\phi \rightarrow \gamma \eta )/BR(\phi \rightarrow \gamma \eta ^\prime )$ together with several other decay channels. From the fit they extract the $\eta$–$\eta ^\prime$ mixing angle $\theta _P=(-14.4 \pm 0.6)^\circ$. In Ref. [75], the authors studied the $\eta$–$\eta ^\prime$ mixing up to next-to-next-to-leading order in U(3) chiral perturbation theory in the light of recent lattice simulations and phenomenological inputs. Within the framework of the effective Lagrangian approach, the authors perform a thorough analysis of the $J/\psi \rightarrow VP$, $J/\psi \rightarrow \gamma P$ together with a few other processes to investigate this mixing problem [76]. In the future, more decay processes involving the light pseudoscalar mesons and more precise experimental measurements maybe will provide a unique method to study the $\eta$–$\eta ^\prime$ mixing effects deeply.

4 Summary

In this work, we investigate the radiative decay processes $h_c \rightarrow \gamma \eta$ and $\gamma \eta ^\prime$ via an intermediate meson loop model in an effective Lagrangian approach. Our results show that the obtained branching ratios are not drastically sensitive to the cutoff parameter $\alpha$ to some extent. The calculated branching ratios of $h_c\rightarrow \gamma \eta$ are typically of the order of $10^{-4}$ to $10^{-3}$, while for $h_c\rightarrow \gamma \eta ^\prime$, the branching ratios are of the order of $10^{-3}$ to $10^{-2}$ in the same cutoff range. The study of these two decay channels, especially their ratio $R_{h_c}$, can provide us some information on the $\eta$–$\eta ^\prime$ mixing, which may be helpful for us to test SU(3)-flavor symmetries in QCD. The BESIII detector will collect $3\times 10^9$ $\psi ^\prime$ events [77], which will provide a unique method to study the $\eta$–$\eta ^\prime$ mixing effects deeply.