Estimating nonlinear effects in forward dijet production in ultra-peripheral heavy ion collisions at the LHC

Abstract

Using the framework that interpolates between the leading power limit of the color glass condensate and the high energy (or $k_{T}$) factorization we calculate the direct component of the forward dijet production in ultra-peripheral $\mathrm {Pb}$–$\mathrm {Pb}$ collisions at CM energy $5.1\,\mathrm {TeV}$ per nucleon pair. The formalism is applicable when the average transverse momentum of the dijet system $P_{T}$ is much bigger than the saturation scale $Q_{s}$, $P_{T}\gg Q_{s}$, while the imbalance of the dijet system can be arbitrary. The cross section is uniquely sensitive to the Weizsäcker–Williams (WW) unintegrated gluon distribution, which is far less known from experimental data than the most common dipole gluon distribution appearing in inclusive small-x processes. We have calculated cross sections and nuclear modification ratios using WW gluon distribution obtained from the dipole gluon density through the Gaussian approximation. The dipole gluon distribution used to get WW was fitted to the inclusive HERA data with the nonlinear extension of unified BFKL + DGLAP evolution equation. The saturation effects are visible but rather weak for realistic $p_{T}$ cut on the dijet system, reaching about 20% with the cut as low as $6\,\mathrm {GeV}$. We find that the LO collinear factorization with nuclear leading-twist shadowing predicts quite similar effects.

1 Introduction

High energy collisions of heavy ions provide a unique opportunity to investigate the quark–gluon plasma regime of QCD. In addition, they also offer a more direct insight into dense initial nucleus states. Relativistic nuclei are in fact very strong sources of electromagnetic fields, thus when they collide at large impact parameters it is possible to study photon–nucleus interactions. Such ultra-peripheral heavy ion collisions (UPC) can be investigated using the current LHC setup, and there are plenty of unique possibilities to explore various aspects of nuclear physics [1] and the small-x regime [2]. In particular, photon–nucleus interactions can shed some light on certain aspects of the small-x physics, principally the saturation phenomenon [3].

In the present work we will be focused on the dijet production in UPC in the kinematic configuration which probes relatively small values of x. The purpose of this analysis is twofold. First, we give predictions within a framework which incorporates a nonlinear gluon saturation phenomenon. For certain differential cross sections we will also give predictions using the collinear factorization with the leading-twist nuclear shadowing [4, 5]. Second, the dijet configurations in $\gamma A$ collisions are sensitive to subtle QCD effects related to gluon distributions appearing in saturation formalism; we describe this situation in some more details later below. Thus, the second goal is to check if UPC can shed some light on that subject. A previous study in a similar context for the Electron Ion Collider was done in [6] using a slightly different formulation.

One of the aspects of jet production in hadron–hadron collisions (for recent review see [7]) is that factorization theorem does not work for observables sensitive to transverse momenta of partons, like azimuthal correlations. More precisely, the transverse momentum dependent (TMD) parton densities are not universal [8, 9]. This shows up as a process dependence of Wilson line structure in the operators entering the definitions of leading-twist TMD parton distribution functions. On the other hand, the non-operator approaches like the DDT formula [10] provide a way to access such observables in the leading logarithmic approximation. The TMD factorizations are much stronger as they hold up to leading power. In addition, the operator definitions of TMD gluon distributions are valid also for small values of x and in general the non-universality still holds. This is in particular true in the saturation regime. In the color glass condensate (CGC) effective theory [11], which models the saturation phenomenon, the non-universality appears as a proliferation of color averages of many Wilson line operators. These correlators in principle parametrize non-perturbative physics, playing a similar role to parton distributions. In fact, there is a connection to the TMD factorization: for dijet production it has been shown that the leading power limit of the CGC formulas corresponds to the TMD expressions, provided that the CGC color averages are replaced by the hadronic matrix elements [12]. Moreover, it appears that there are two fundamental objects describing the hadronic target. On the TMD factorization side, there are two TMD gluon distributions, having the most elementary Wilson line structure (see also [13]). The first one is

$$\begin{aligned} xG_{1}\left( x,k_{T}\right)= & {} 2\int \frac{\mathrm{d}\xi ^{-}\mathrm{d}^{2}\xi _{T}}{(2\pi )^{3}P^{+}}\, e^{ixP^{+}\xi ^{-}-i\mathbf {k}_{T}\cdot \mathbf {\xi }_{T}} \nonumber \\&\times \,\left\langle P\right| \text {Tr}\left\{ F^{+i}\left( \xi ^{-},\xi _{T}\right) U^{\left[ +\right] \dagger }F^{+i}\left( 0\right) U^{\left[ +\right] }\right\} \left| P\right\rangle ,\nonumber \\ \end{aligned}$$

(1)

where $F^{\mu \nu }\left( x\right)$ are gluon strength tensors in fundamental representation and $U^{\left[ +\right] }$ is the Wilson line joining the space-time points $\xi$ and 0 through the $+\infty$. The trace is over the fundamental color space. The second TMD gluon distribution is

$$\begin{aligned} xG_{2}\left( x,k_{T}\right)= & {} 2\int \frac{\mathrm{d}\xi ^{-}\mathrm{d}^{2}\xi _{T}}{(2\pi )^{3}P^{+}}\, e^{ixP^{+}\xi ^{-}-i\mathbf {k}_{T}\cdot \mathbf {\xi }_{T}}\nonumber \\&\times \left\langle P\right| \text {Tr}\left\{ F^{+i}\left( \xi ^{-},\xi _{T}\right) U^{\left[ -\right] \dagger }F^{+i}\left( 0\right) U^{\left[ +\right] }\right\} \left| P\right\rangle ,\nonumber \\ \end{aligned}$$

(2)

where $U^{\left[ -\right] }$ is the Wilson line that goes from $\xi$ to 0 via $-\infty$. The appearance of the form of the gauge links $U^{\left[ \pm \right] }$ is related to the kind of collinear gluons that are resummed: $U^{\left[ +\right] }$ represents the final state interactions, while $U^{\left[ -\right] }$ the initial state interactions. In the case of $xG_{1}$ one can get rid of the Wilson lines by a suitable choice of gauge (and boundary condition at $+\infty$ for transverse gauge field components) giving a gluon number density interpretation to that distribution. On the CGC side, those two gluon distributions appear in two different contexts. The $xG_{1}$ appears in the McLerran–Venugopalan (MV) model [14] as the gluon number density calculated in the semi-classical approximation, thus it is often named the Weizsäcker–Williams (WW) gluon distribution. The $xG_{2}$ appears as a Fourier transform of the forward dipole amplitude on the nucleus, thus it is named the ‘dipole’ gluon distribution. In general, these are two independent quantities, but they can be related in a certain approximation; see Eq. (11). It is interesting that most ‘simple’ QCD processes like inclusive DIS, semi-inclusive DIS or Drell–Yan all probe the dipole gluon distribution. Thus, this gluon distribution is quite well constrained from the data. It is not the case for the WW gluon distribution which has been only calculated from models. However, it has been shown in [12] that the WW gluon distribution can be probed when more complicated final states are considered, in particular dijets in $\gamma A$ and pA collisions. The dihadron correlations in pA collisions were used to test these unintegrated gluon distributions within the saturation framework [15, 16]. The advantage of $\gamma A$ collisions is that in the close to back-to-back dijet configuration the WW gluon is probed directly. Note that the A-dependent Sudakov broadening of imbalance is present in the DGLAP formalism; see [17] for the study of this effect in the massive neutral gauge boson production. The study of this effect for dijet production is beyond the scope of this paper.

Although in the present work we focus mainly on the nonlinear saturation phenomena, the nuclear effects are not restricted to saturation alone. In fact, before the onset of saturation the nuclear shadowing may be significant. It is a leading-twist effect since the suppression of gluons is encoded in the collinear PDFs within the collinear factorization approach [5]. Large gluon shadowing consistent with prediction of [5] was reported in the coherent $J/\Psi$ photoproduction of $\mathrm {Pb}$. For example the shadowing for $x=10^{-3}$, $Q^2 \sim 3\, \mathrm {GeV}^2$ was found to be $\approx 0.6$, for the recent discussion and extensive list of references see [18] (for $J/\Psi$ production in CGC see [19,20,21]). In the present work we estimate both effects, the leading-twist nuclear shadowing and the saturation, for selected jet observables. The question whether and how these should be combined remains open and is beyond the scope of this paper.

We are considering the limit when typical transverse momenta are much larger than $Q_s$. In the limit $k_t \lesssim Q_s$ production of leading particles/jets may be suppressed very strongly. This effect may be responsible for the large suppression of the forward pion production in $d-Au$ collisions at BNL, for the summary and references see chapter 8 of Ref. [5]. How fast these effects die out at $k_t > Q_s$ still has to be investigated.

In the small-x literature the gluon distributions with transverse momentum dependence are typically called unintegrated gluon distributions (UGDs). We shall follow this standard terminology, keeping in mind the following issues. First, the name UGD would suggest that integrating it over $k_T$ one gets a collinear gluon PDF. There is no proof of that statement within QCD. There are theoretical difficulties with such a relation, connected to the proper formulation of factorization in the case with transverse momentum dependence; see for example [22]. Second, the collinear parton densities are obtained from the DGLAP equations (up to NNLO order) whereas the unintegrated gluon distributions are usually obtained from the evolution which includes resummation of large logarithms $\ln 1/x$. Thus the two types of distributions are typically obtained in the different regimes. In the nucleus case for instance, at present no UGD exists which could lead to the gluon distribution incorporating the leading-twist shadowing. This, however, does not mean that the latter is inherently incompatible with all approaches using UGDs. In principle, one could construct a framework in which the leading-twist shadowing gluon distribution could be obtained from the UGDs provided they account for diffractive states and the appropriate resummation of collinear and small x logarithms would be performed in both cases.

From the above review it is clear that the study of dijets in UPC collision is of great importance for better understanding of the WW gluon distribution in the small x regime. One of the goals of this work is to investigate whether the present LHC kinematics can give a restriction of that distribution. This is done, by a direct calculation of the cross sections and nuclear modification factors for various observables taking into account existing information on WW gluon distribution.

The work is organized as follows. In Sect. 2 we describe the framework and ingredients necessary to compute the process of interest within the saturation regime. Next, in Sect. 3 we give detailed description of the unintegrated gluon distribution functions, kinematic cuts and actual implementation of the formalism. The results of numerical simulations are given in Sect. 4. Finally, we give a brief summary in Sect. 5.

2 Factorization formula for the dijet cross section in UPC

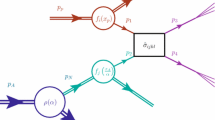
In the standard approach to ultra-peripheral collisions one factorizes the cross section into the quasi-real photon flux $\mathrm{d}N_{\gamma }/\mathrm{d}x_{\gamma }$ and the photon–nucleus cross section $\mathrm{d}\sigma _{\gamma A\rightarrow 2\,\text {jet}+X}$ [1]

$$\begin{aligned} \mathrm{d}\sigma _{AA\rightarrow 2\,\text {jet}+X}^{\mathrm {UPC}}=\int \mathrm{d}x_{\gamma }\,\frac{\mathrm{d}N_{\gamma }}{\mathrm{d}x_{\gamma }}\, \mathrm{d}\sigma _{\gamma A\rightarrow 2\,\text {jet}+X}, \end{aligned}$$

(3)

where $x_{\gamma }$ is the fraction of the heavy ion longitudinal momentum carried by the photon. The photon flux is given by the Weizsäcker–Williams approximation,

$$\begin{aligned} \frac{\mathrm{d}N_{\gamma }}{\mathrm{d}x_{\gamma }}=\frac{2Z^{2}\alpha }{\pi x_{\gamma }}\left[ \zeta K_{0}\left( \zeta \right) K_{1}\left( \zeta \right) -\frac{\zeta ^{2}}{2}\left( K_{1}^{2}\left( \zeta \right) -K_{0}^{2}\left( \zeta \right) \right) \right] , \end{aligned}$$

(4)

with Z being the charge of the ion, $\alpha =1/137$ is the electromagnetic coupling constant and $K_{0}$, $K_{1}$ are the modified Bessel functions. Their argument is $\zeta =x_{\gamma }R_{A}\sqrt{S}/\gamma$, where S is the CM energy squared, $\gamma$ is the Lorentz factor and $R_{A}$ is the nucleus radius.

We are interested in the $\gamma A\rightarrow 2\,\text {jet}+X$ process under the following assumptions: (i) The nucleus is probed at sufficiently small longitudinal momentum fraction $x_{A}$ so that the saturation formalism applies. In reality, as we show later, $x_A$ can reach values of order $\sim 10^{-3}$ (this would require $p_T$ of the jet down to $10 \; \mathrm{GeV}$) so that we probably venture outside the applicability domain of the saturation formalism. (ii) We focus on the kinematic region where $x_{A}<x_{\gamma }$, which implies that we look for a forward dijet configuration along the photon direction. A comment is in order here. Unlike for the pA collisions within the hybrid approach [23] this restriction is not absolutely necessary for $\gamma A$ collisions. The only restriction is that $x_A$ has to be small enough. Allowing for the full rapidity coverage will, however, unnecessarily make the $x_A$ spectrum broader towards the larger values (see Fig. 3). Moreover, restricting to forward jets may allow in the future to combine the present results with the resolved component of the cross section. (iii) The average transverse momentum of the dijet system $P_{T}=\left( p_{T1}+p_{T2}\right) /2$ is much bigger than the saturation scale $Q_{s}$, $P_{T}\gg Q_{s}$, and sets the hard scale of the process: $\mu \sim P_{T}$. iv) The transverse imbalance of the dijets $k_{T}=\left| \mathbf {p}_{T1}+\mathbf {p}_{T2}\right|$ can be anything allowed by the kinematics – this implies that the non-leading power corrections have to be taken into account.

Let us now describe the approach satisfying the above requirements (the justification will be given later in this section). It is a straightforward analog (in fact much simpler) of the formalism of [24] for dijets in pA collisions. The following factorization formula for the $\gamma A\rightarrow 2\,\text {jet}+X$ process will be used:

$$\begin{aligned} \mathrm{d}\sigma _{\gamma A\rightarrow 2\,\text {jet}+X}= & {} \sum _{\left\{ q,\overline{q}\right\} }\int \frac{\mathrm{d}x_{A}}{x_{A}}\int \mathrm{d}^{2}k_{T}\, \nonumber \\&\times \,x_{A}G_{1}\left( x_{A},k_{T}\right) \, \mathrm{d}\sigma _{\gamma g^{*}\rightarrow q\overline{q}}\left( x_{A},k_{T}\right) , \end{aligned}$$

(5)

where $xG_{1}$ is the Weizsäcker–Williams UGD function. The partonic cross section $d\sigma _{\gamma g^{*}\rightarrow q\overline{q}}$ is calculated using the LO amplitude for the process $\gamma g^{*}\rightarrow q\overline{q}$, where $g^{*}$ denotes the off-shell gluon. In the high energy approximation the momentum of the gluon has only one longitudinal component, parallel to the parent hadron. That is, taking the momentum of the nucleus to be $p_{A}$, the momentum of $g^{*}$ is $k_{A}^{\mu }=x_{A}p_{A}^{\mu }+k_{T}^{\mu }$, where $p_{A}^{\mu }=\left( 1,0,0,-1\right) \sqrt{S}/2$ and $k_{T}^{\mu }=\left( 0,k_{T}^{1},k_{T}^{2},0\right)$. The gluon spinor index is projected on the vector $p_{A}$. It can be shown that such amplitude is gauge invariant [25]. In practical calculations we used the helicity amplitudes calculated from the program described in [26] extended to quarks. The two-particle phase space is included in $d\sigma _{\gamma g^{*}\rightarrow q\overline{q}}$ and is constructed with the exact momentum conservation and taking into account the transverse momentum $k_T$ of the gluon. Let us note that in Eq. (5) there is no hard scale dependence in $xG_1$. In fact, in the saturation formalism the evolution with the hard scale is not typically present. This is primarily because the formalism is normally used for small hard scales, of the order of the saturation scale. In our case, however, the hard scale is set by the jet transverse momenta and may be large. Thus, it is important to include the resummation of the Sudakov logarithms in the calculation. Our method is described at the end of this section.

Let us now justify the present approach. We shall show that Eq. (5) coincides with known results in two regimes: in the linear regime with large dijet imbalance $k_{T}\sim P_{T}\gg Q_{s}$ and in the saturation regime with small imbalance $P_{T}\gg k_{T}\sim Q_{s}$.

Let us start with the first regime. The formula (5) is superficially identical to the high energy factorization (HEF) formalism [25, 27,28,29,30,31,32,33] for heavy quark pair production in inclusive DIS. Namely, in the latter the same phase space and off-shell matrix element is used. Consider now the limit $k_{T}\sim P_{T}\gg Q_{s}$ adequate to the HEF regime of applicability. It can be shown that, for large $k_T$, both $xG_{1}$ and $xG_{2}$ have the same asymptotics [13] (this is in fact true for many other TMD gluon distributions one can define at small x; see [34]). Therefore, in the linear HEF regime there is just one universal UGD (as long as there is no hard scale dependence). This justifies Eq. (5) in the regime $k_{T}\sim P_{T}\gg Q_{s}$.

Let us now consider another region of interest, i.e. $P_{T}\gg k_{T}\sim Q_{s}$. In that region the saturation effects cannot be neglected, but the power corrections $\mathcal {O}\left( k_{T}/P_{T}\right)$ can. Therefore, as proposed in [12] let us first consider the CGC regime, $k_{T}\sim P_{T}\sim Q_{s}$, and take the leading power limit of the corresponding formulas. In CGC picture the situation for two-particle production gets more complicated comparing to inclusive production due to a more complicated color flow in the dense nuclear matter. The relevant formula reads [12]

$$\begin{aligned}&\frac{\mathrm{d}\sigma _{\gamma A\rightarrow 2\,\text {jets}}}{\mathrm{d}^{3}p_{1}\mathrm{d}^{3}p_{2}}=\sum _{\left\{ q,\overline{q}\right\} }N_{c}\,\alpha \,e_{q}^{2}\,\delta \left( x_{B}p_{B}^{-}-p_{1}^{-}-p_{2}^{-}\right) \nonumber \\&\int \frac{\mathrm{d}^{2}x_{1T}}{\left( 2\pi \right) ^{2}}\frac{\mathrm{d}^{2}x'_{1T}}{\left( 2\pi \right) ^{2}}\frac{\mathrm{d}^{2}x_{2T}}{\left( 2\pi \right) ^{2}}\frac{\mathrm{d}^{2}x'_{2T}}{\left( 2\pi \right) ^{2}}\, e^{-i\mathbf {p}_{1T}\cdot \left( \mathbf {x}_{1T}-\mathbf {x}'_{1T}\right) }e^{-i\mathbf {p}_{2T}\cdot \left( \mathbf {x}_{2T}-\mathbf {x}'_{2T}\right) } \nonumber \\&\quad \times \psi _{\alpha \beta }^{\lambda }\left( \mathbf {x}_{1T}-\mathbf {x}_{2T}\right) \psi _{\lambda }^{\alpha \beta *} \left( \mathbf {x}'_{1T}-\mathbf {x}'_{2T}\right) \Big \{ 1 -S_{x_{g}}^{\left( 2\right) }\left( \mathbf {x}_{1T},\mathbf {x}_{2T}\right) \nonumber \\&\quad -S_{x_{g}}^{\left( 2\right) }\left( \mathbf {x}'_{2T},\mathbf {x}'_{1T}\right) + S_{x_{g}}^{\left( 4\right) }\left( \mathbf {x}_{1T},\mathbf {x}_{2T};\mathbf {x}'_{2T},\mathbf {x}'_{1T}\right) \Big \}, \end{aligned}$$

(6)

where $\psi _{\alpha \beta }^{\lambda }$ is the wave function of the $q\overline{q}$ dipole originating in photon with transverse polarization $\lambda =1,2$ (see e.g. [12] for the precise form) and the $S^{\left( i\right) }$ terms describe the interaction of the dipole with the color nucleus field. They are given by the correlators of Wilson lines

$$\begin{aligned} U\left( \mathbf {x}_{T}\right) =\mathcal {P}\exp \left\{ ig\int _{-\infty }^{+\infty }\mathrm{d}x^{-}A_{a}^{+}\left( x^{-},\mathbf {x}_{T}\right) t^{a}\right\} \end{aligned}$$

(7)

with $t^{a}$ being the color generator in the fundamental representation:

$$\begin{aligned}&S_{x_{g}}^{\left( 2\right) }\left( \mathbf {x}_{1T},\mathbf {x}_{2T}\right) =\frac{1}{N_{c}}\,\left\langle \mathrm {Tr}\, U\left( \mathbf {x}_{1T}\right) U^{\dagger }\left( \mathbf {x}_{2T}\right) \right\rangle _{x_{g}},\end{aligned}$$

(8)

$$\begin{aligned}&S_{x_{g}}^{\left( 4\right) }\left( \mathbf {x}_{1T},\mathbf {x}_{2T};\mathbf {x}'_{2T},\mathbf {x}'_{1T}\right) \nonumber \\&\quad =\frac{1}{N_{c}}\,\left\langle \mathrm {Tr}\, U\left( \mathbf {x}_{1T}\right) U^{\dagger }\left( \mathbf {x}'_{1T}\right) U\left( \mathbf {x}'_{2T}\right) U^{\dagger }\left( \mathbf {x}{}_{2T}\right) \right\rangle _{x_{g}}. \end{aligned}$$

(9)

The operation $\left\langle .\right\rangle _{x_{g}}$ represents the averaging over the distributions of color sources with $x_{g}$ being the smallest x probed; see e.g. [11] for details. Taking the leading power limit one gets [12]

$$\begin{aligned} \frac{\mathrm{d}\sigma _{\gamma A\rightarrow 2\,\text {jets}}}{\mathrm{d}^{2}k_{T}}=\sum _{\left\{ q,\overline{q}\right\} }\int \frac{\mathrm{d}x_{A}}{x_{A}}\, x_{A}G_{1}\left( x_{A},k_{T}\right) \mathrm{d}\sigma _{\gamma g\rightarrow q\overline{q}}\left( x_{A}\right) , \end{aligned}$$

(10)

where the fraction $x_g$ was identified with $x_A$ and the CGC average of the appearing bilocal operator

$$\begin{aligned} F^{+i}\left( \xi _{1}^{-},\xi _{1T}\right) U^{\left[ +\right] \dagger }F^{+i}\left( \xi _{2}^{-},\xi _{2T}\right) U^{\left[ +\right] } \end{aligned}$$

was identified with the hadronic matrix element $\left\langle .\right\rangle _{x_{g}}\longleftrightarrow \left\langle P\left| .\right| P\right\rangle /\left\langle P|P\right\rangle$ so that there appears the exact definition of the Weizsäcker–Williams UGD $xG_{1}$ as given in Eq. (1). Let us note that the hard cross section in Eq. (10) is calculated on-shell in accordance with the leading-twist limit. Comparing Eqs. (5) and (10), we see that the latter is recovered by neglecting the power corrections in $d\sigma _{\gamma g^{*}\rightarrow q\overline{q}}$ in Eq. (5), thus in the regime $P_{T}\gg k_{T}\sim Q_{s}$ they coincide.

To summarize, the factorization formula (5) for the $P_{T}\gg Q_{s}$ regime coincides with HEF when $k_{T}\sim P_{T}$ and with the leading power limit of CGC when $k_{T}\sim Q_{s}$. For $k_{T}$ between those limiting values it provides a smooth interpolation given by the off-shell matrix element and exact kinematics.

Let us note that, if the process under consideration were inclusive single jet production, Eq. (5) would change. In that case, the dipole gluon distribution $xG_2$ would appear instead of $xG_1$ [35,36,37,38].

As already mentioned, there is an issue related to Eqs. (5) or (10). Namely for $P_T\gg k_T$ the hard scale evolution is important and there should be some sort of the Sudakov form factor resumming large logarithms of the form $\log \left( k_{T}/P_{T}\right)$. In the correlation regime of Eq. (10), it is rather simple – the Sudakov form factor multiplies the r.h.s. This was applied in [6] in the context of dihadron correlations at EIC. On more general ground, in the saturation formalism a comprehensive study was done in [39]. In our study, which, as discussed, goes beyond the leading power, we shall follow a different path. As we describe in the next section, the formalism of Eq. (5) is particularly convenient to implement in a simple Monte Carlo program which is capable of generating complete kinematics, with full final state four momenta, and with unit weight when necessary. Knowing the weights of particular events in a sample one can estimate the Sudakov effect by a suitable modification of the weights applying the Sudakov probability. From that point of view it is independent of the saturation and can be applied for any sample of events. In what follows we shall refer to this approach as the Sudakov resummation model. In short, the model takes a weight $w_{i}\left( k_{T},P_{T}\right)$ for an event i (we suppress other weight variables for brevity) and modifies it by a surviving probability $\mathcal {P}\left( k_{T},P_{T}\right)$ of the gluon with transverse momentum $k_{T}$ which initiated the event. This probability is related to the Sudakov form factor. It is assumed that the gluons that do not survive at the scale $k_{T}$ appear at the scale $P_{T}$, so that the model does not change the total cross section. See [40] for details.

3 The framework for the unintegrated gluon distribution function

The complete direct components of the UPC cross section (3) have been implemented in the LxJet Monte Carlo program [41] based on foam algorithm [42]. It was previously used to calculate some jet observables within HEF (and beyond) in pp and pA collisions, including forward-central and forward–forward dijets [40, 43], three-jet production [44], $Z_{0}$+jet production [45], UGD fits [46] and recently forward–forward dijets [47] using the approach of [24]. The Sudakov resummation model is an independent plugin and is applied on the top of the generated and stored events.

The crucial ingredient of Eq. (5) is the WW UGD. As discussed in the introduction, there are no existing experimental constraints for this gluon. Thus, in the present work we shall follow [47] and use the WW distribution obtained from the dipole UGD using the Gaussian approximation

$$\begin{aligned} \nabla _{k_{T}}^{2}G_{1}\left( x,k_{T}\right)= & {} \frac{4\pi ^{2}}{N_{c}S_{\bot }(x)}\,\int \frac{d^{2}q_{T}}{q_{T}^{2}}\,\frac{\alpha _{s}(k_T^2)}{\left( \mathbf {k}_{T}-\mathbf {q}_{T}\right) ^{2}}\, \nonumber \\&xG_{2}\left( x,q_{T}\right) G_{2}\left( x,\left| \mathbf {k}_{T}-\mathbf {q}_{T}\right| \right) , \end{aligned}$$

(11)

where $S_{\perp }(x)$ is the effective transverse area of the target. The Balitsky–Kovchegov (BK) evolution equation [48, 49] is typically used to evaluate the dipole gluon distribution in the presence of saturation. In order to include subleading effects that may be important at non-asymptotic x we have used a more involved Kwiecinski–Martin–Stasto equation [50] with the nonlinear term [51] (below we set $xG_{2}\left( x,k_{T}\right) \equiv \mathcal {F}\left( x,k_{T}^{2}\right)$ for brevity):

$$\begin{aligned}&\mathcal {F}\left( x,k_{T}^{2}\right) \nonumber \\&\quad =\mathcal {F}_{0}\left( x,k_{T}^{2}\right) +\frac{\alpha _{s}(k_T^2)N_{c}}{\pi }\int _{x}^{1}\frac{\mathrm{d}z}{z}\int _{k_{T\,0}^{2}}^{\infty }\frac{\mathrm{d}q_{T}^{2}}{q_{T}^{2}} \nonumber \\&\qquad \times \, \Bigg \{ \frac{q_{T}^{2}\mathcal {F}\left( \frac{x}{z},q_{T}^{2}\right) \theta \left( \frac{k_{T}^{2}}{z}-q_{T}^{2}\right) -k_{T}^{2}\mathcal {F}\left( \frac{x}{z},k_{T}^{2}\right) }{\left| q_{T}^{2}-k_{T}^{2}\right| } \nonumber \\&\qquad +\,\frac{k_{T}^{2}\mathcal {F}\left( \frac{x}{z},k_{T}^{2}\right) }{\sqrt{4q_{T}^{4}+k_{T}^{4}}}\Bigg \} +\frac{\alpha _{s}(k_T^2)}{2\pi k_{T}^{2}}\int _{x}^{1}\mathrm{d}z \,\Bigg \{ \left( P_{gg}\left( z\right) -\frac{2N_{c}}{z}\right) \nonumber \\&\qquad \times \, \int _{k_{T\,0}^{2}}^{k_{T}^{2}}\mathrm{d}q_{T}^{2}\mathcal {F}\left( \frac{x}{z},q_{T}^{2}\right) +zP_{gq}\left( z\right) \Sigma \left( \frac{x}{z},k_{T}^{2}\right) \Bigg \} \nonumber \\&\qquad -\,\mathrm{d}\frac{2\alpha _{s}^{2}(k_T^2)}{R^{2}}\left\{ \left[ \int _{k_{T}^{2}}^{\infty }\frac{\mathrm{d}q_{T}^{2}}{q_{T}^{2}}\mathcal {F}\left( x,q_{T}^{2}\right) \right] ^{2} \right. \nonumber \\&\left. \qquad +\,\mathcal {F}\left( x,k_{T}^{2}\right) \int _{k_{T}^{2}}^{\infty }\frac{\mathrm{d}q_{T}^{2}}{q_{T}^{2}}\,\ln \left( \frac{q_{T}^{2}}{k_{T}^{2}}\right) \mathcal {F}\left( x,q_{T}^{2}\right) \right\} , \end{aligned}$$

(12)

Fig. 1

The Weizsacker–Williams (WW) unintegrated gluon distributions for proton and lead obtained from the KS dipole distributions [52]. The top row compares the WW distribution for lead with the dipole distribution for two values of x. The middle row shows the WW distributions for proton and lead as a function of $k_T$ for two values of x. Finally, the bottom row shows the WW distributions for proton and lead as a function of x for two values of $k_T$

where $\Sigma \left( x,k_{T}\right)$ is the accompanying singlet sea quark distribution and R has the interpretation of the target radius (more precisely, it appears from the integration of the impact parameter dependent gluon distribution assuming the uniform distribution of gluons). The parameter d, $0<d\le 1$ is set to $d=1$ for proton and can be varied for nucleus to study theoretical uncertainty. This equation accounts for DGLAP corrections, and a kinematic constraint along the BFKL ladder and running strong coupling constant. Due to all these (formally) subleading corrections this equation has been proven to be useful in modeling more exclusive final states. The actual initial condition $\mathcal {F}_{0}$ has been fitted to the inclusive DIS HERA [52]. In what follows we shall name this set of UGD KS (Kutak–Sapeta). Also, the parameter R had to be fitted giving $R\approx 2.4\,\mathrm {GeV}^{-1}$. The set for a nucleus (actually the UGD per nucleon) is obtained by changing the proton R parameter according to the simple Woods–Saxon prescription $R_{A}=A^{1/3}R$ where A is the mass number. The nonlinear term in (12) is enhanced then by $dA^{1/3}$ resulting in much stronger saturation effects than in the proton case (for $d=1$). In [47] except $d=1$ for nucleus, also the values $d=\left\{ 0.5,0.75\right\}$ have been used to study the dependence of the results on the strength of the nonlinear term. In the present work, the set with $d=0.5$, corresponding to weaker saturation will be used. As evident from Eq. (12) the saturation effects will become important whenever the nonlinear term will be of the same order as the linear term. Thus one can characterize the strength of the nonlinear effects by the parameter defined as the ratio of these two terms, which is proportional to the average gluon density per unit area, that is, a saturation scale. We choose $d=0.5$ to ensure that the saturation scale in the case of scattering off $\mathrm {Pb}$ is about 3 times larger than in the case of scattering off the proton. This choice is consistent with the ratio of average gluon density in $\mathrm {Pb}$ and proton for $x\sim 10^{-3} \div 10^{-4}$ and with account of the leading-twist nuclear shadowing, cf. Fig. 100, of [5]. The saturation scale for Pb for this value of x is about $Q^2_\mathrm{sat}\sim 2 \div 3\, \mathrm {GeV}^2$, to be compared with $Q^2_\mathrm{sat} \le 1\, \mathrm {GeV}^2$ for the proton case.

For the $\mathrm {Pb}$ nucleus the Woods–Saxon formula with the correction resulting from the d parameter gives $R_{\mathrm {Pb}}\approx 20.1\, \mathrm {GeV}^{-1}$. Keep in mind, however, that this number is only loosely related to the true nuclear radius (in the sense that it is a radius within the interpretation of the model of Eq. (12)).

Table 1 The kinematic cuts used in the numerical calculations of the dijet cross section in the ultra-peripheral $\mathrm {Pb}-\mathrm {Pb}$ collisions

Fig. 2

The longitudinal fractions probed within the kinematic cuts for different $p_{T}$ cuts: top left $p_{T0}=25\,\mathrm {GeV}$, top right $p_{T0}=10\,\mathrm {GeV}$, bottom left $p_{T0}=6\,\mathrm {GeV}$. In bottom right plot we show the distribution of collision energy of $\gamma A$ system

Finally, the $xG_{1}$ distributions for proton and lead were obtained from the KS gluon $\mathcal {F}$ through Eq. (11), using the method presented in detail in [47]. We note, in particular, that in our procedure of calculating the WW KS distributions, $xG_{1}$, we used the running coupling and x-dependent transverse target area. The x dependence of S(x) was adjusted to ensure that the impact parameter dipole amplitude reaches unity as expected in the black disk limit. The resulting distributions are shown in Fig. 1. Let us note that even for $x\sim 10^{-2}$ the nonlinear effects are still present in that model. This is one of the differences with respect to the leading-twist shadowing model and will be visible in the physical observables.

The kinematic setup is chosen as follows. We set the CM energy per nucleon to $\sqrt{S}=5.1\,\mathrm {TeV}$ and require two jets in the rapidity window $0<y_{1},y_{2}<5$ in the photon direction. The two-jet requirement is ensured by the jet algorithm of the anti-$k_t$-type [53], which in the case of our two-particle final state boils down to the condition $\sqrt{\Delta \phi ^{2}+\Delta y^{2}}>r$, where we choose the jet radius $r=0.5$. Note that, although it is a LO calculation, the jet algorithm is necessary, because the final states are in general not back-to-back, due to the transverse momentum of the off-shell gluon. The minimal $p_{T}$ of the jets is dictated by the longitudinal fractions x we want to probe. Obviously, there is a competition between the experimentally possible jet reconstruction and x small enough to see any saturation effects. In the case of UPC, although the CM energies of $\gamma$–A system are large, the photons cannot have too large longitudinal momenta as above around $x\simeq 0.03$ the flux becomes exponentially vanishing. This considerably limits the x fractions on the nucleus side, unless one goes to really small $p_{T}$. In our study we have considered $p_{T}$ cuts of 25, 10, and 6 $\mathrm {GeV}$. As discussed in the next section with this setup one can probe x down to $10^{-3}$ at the current energy. The setup is summarized in Table 1.

Fig. 3

The longitudinal fractions probed when the symmetric rapidity cuts $-5.0< y_1,y_2 < 5.0$ are applied. The left plot is for the $p_{T}$ cut $p_{T0}=25\,\mathrm {GeV}$, the right one for $p_{T0}=6\,\mathrm {GeV}$

4 Numerical results

We start by determining the longitudinal fractions x of the photon and the gluon that can be effectively probed within our cuts. In Fig. 2 we show differential cross sections in the longitudinal fractions for various $p_{T}$ cuts. We see that for $p_{T0}=25\,\mathrm {GeV}$ the gluon longitudinal momentum fraction $x_A$ is probed only slightly below $10^{-2}$, while for $p_{T0}=10\,\mathrm {GeV}$ the process probes $x_A$ easily around $10^{-3}$. With the smallest cut tested $p_{T0}=6\,\mathrm {GeV}$ one can go below $10^{-3}$. We also show the distribution of the $\gamma A$ CM energy, which reaches $1.2\,\mathrm {TeV}$. If we did not restrict the calculation to the forward jets, the $x_A$ fractions probed in the nucleus would have much broader distribution entering the relatively large x, which is an unwanted feature in the present approach. This is illustrated in Fig. 3 for two different $p_T$ cuts. All the distributions discussed above are shown without the Sudakov effect, as its impact on these spectra is very weak.

In Fig. 4 we present the differential cross sections in the jet $p_{T}$. In the present formalism the jets in general do not have equal $p_{T}$ thus we order them, $p_{T1}>p_{T2}>p_{T0}$, and show separate plots for leading and subleading jet spectra. For comparison we also calculate the same observable from the LO collinear factorization with nuclear PDFs implementing the leading-twist nuclear shadowing [4]. In the LO collinear factorization both jets have equal $p_{T}$. Interestingly their spectra are very close to the subleading jet spectrum of the present approach. The error bands are constructed by varying the hard scale by the factor of two with respect to the central value. The two bottom plots in Fig. 4 show the effect of the Sudakov resummation model. It has a significant effect on the subleading jet spectrum making its slope bigger. The error bands are bigger with resummation because the appearing hard scale can be varied as well and the results are sensitive to that scale.

In Fig. 5 we gather the information on the $p_{T}$ spectra and the probed longitudinal fractions in the nucleus $x_A$ in one 2D plot (for leading and subleading jets) to summarize the phase space coverage.

Fig. 4

Transverse momentum spectra for leading (left column) and subleading (right column) jets. The bottom row shows the effect of the Sudakov resummation model. For comparison we show the results from the LO collinear factorization using nuclear PDFs with the leading-twist shadowing (no additional effects are included in this LO calculation thus the spectra for leading and subleading jet are identical)

Fig. 5

Phase space coverage in $p_{T}$ and the longitudinal fraction $\log x$ probed in the nucleus for leading (left) and subleading (right) jets

One of the most interesting observables in the context of the small-x physics are azimuthal correlations, i.e. the differential cross sections as a function of the azimuthal angle between the two jets $\Delta \phi$. In Fig. 6 we calculate this observable for various $p_{T}$ cuts. The small kinks for $\Delta \phi$ about 0.5 are due to the jet algorithm. Namely, when the incoming gluon has non-zero $k_T$ there is an additional singularity, as the $k_T$ acts like an additional parton. Here, this singularity is regulated by the jet algorithm. The Sudakov resummation model (right plot of Fig. 6) flushes the $\Delta \phi \sim \pi$ events towards the smaller values of $\Delta \phi$, as expected.

Fig. 6

Differential cross sections in the azimuthal angle between the jets with (right) and without (left) Sudakov resummation model

Let us now switch to discussion of the nuclear effects. We shall study the nuclear modification ratios defined as

$$\begin{aligned} R_{\gamma A}=\frac{\mathrm{d}\sigma _{AA}^{UPC}}{A\mathrm{d}\sigma _{Ap}^{UPC}}, \end{aligned}$$

(13)

that is, the photon flux in both numerator and denominator originates from a nucleus. Let us start with $R_{\gamma A}$ as a function of the jet $p_{T}$ (Fig. 7) for the lowest $p_{T}$ cut studied. The maximal suppression is about 20% and it slowly decreases with increasing $p_{T}$. The suppression of around 5–10% is present through a wide range of $p_{T}$, especially for the subleading jet. We have compared the saturation model calculation to the leading-twist shadowing model and observe very similar suppression, which, however, vanishes much faster with increasing $p_{T}$. This is most pronounced for the subleading jet. Another difference is the slope of the $p_T$ spectrum for the leading jet in the small $p_T$ region. The suppression factor is also shown in the 2D plot on the $p_{T1}$–$p_{T2}$ plane and as a function of the ratio $p_{T1}/p_{T2}$ (Fig. 8). When the Sudakov resummation is applied the spectra change slightly. The suppression of $R_{\gamma A}$ becomes a little bit smaller. As a result the nuclear ratio approaches the unity faster for the leading jet spectrum. For the subleading jet the suppression also slightly decreases, but it seems to increase for larger $p_{T}$, although the calculation has large fluctuations there (the calculation is done close to the edge of the UGD grids here, so the real uncertainties are much bigger than presented). We note that all $R_{\gamma A}$ functions in $p_T$, both for leading and subleading jet should approach unity for large $p_T$ (see also the discussion of x dependence at the end of this section).

In Fig. 9 we present the $R_{\gamma A}$ as a function of $\Delta \phi$ for different $p_{T}$ cuts. Again, the maximal suppression of around 20% is clearly visible for $6\,\mathrm {GeV}$ $p_{T}$ cut. For the most realistic $p_{T}$ cut of $25\,\mathrm {GeV}$, which is not shown in the plot, the suppression was around 10%, but the curve had a non-monotonic shape which was due to the grid effects, as for that $p_{T}$ cut the $xG_{1}$ UGD is probed at relatively large, close to the edge of the fitted parameter space. The saturation effects are most visible close to back-to-back region (i.e. the leading-twist region) and quickly vanish with decrease of $\Delta \phi$. The spectra show a few percent of enhancement below $\Delta \phi \sim 2.8$, but this is a numerical effect hidden in the UGD grids. The situation slightly changes when the Sudakov resummation model is used, as seen in the bottom row of Fig. 9. The suppression is spread over a slightly larger region of $\Delta \phi$ and the artificial enhancement is gone.

Fig. 7

Nuclear modification ratio defined in Eq. (13) as a function of the transverse momentum spectra for leading (left column) and subleading (right column) jets. The bottom row show the effect of the Sudakov resummation model applied to the generated events. For comparison we show the results from the LO collinear factorization using nuclear PDFs with ‘leading-twist’ shadowing

Fig. 8

Nuclear modification ratio defined in Eq. (13) in the $p_{T1}-p_{T2}$ plane (left) and as a function of the $p_{T1}/p_{T2}$ ratio (right)

Fig. 9

Nuclear modification ratio defined in Eq. (13) as a function of the azimuthal angle between the jets with (right) and without (left) Sudakov resummation model

Fig. 10

Nuclear modification ratio defined in Eq. (13) as a function of the rapidity of the jet without (left) and with (right) the Sudakov resummation model. The bottom plot shows the nuclear modification ratio as a function of the longitudinal fraction $x_A$ probed in the nucleus for the $p_T$ cut $10\,\mathrm {GeV}$

Finally, for completeness, in Fig. 10 we show the suppression as a function of rapidity (these spectra are the same for leading and subleading jets). The curves slowly fall off with increase of the jet rapidity, as one could expect. After applying the Sudakov resummation, the spectra almost do not change, but the error bands become significantly bigger. For the $25\,\mathrm {GeV}$ $p_{T}$ cut the spectrum rises, but, again, this is the region that involves quite large x, for which the UGD grids are not trustworthy. It is interesting to note that close to central jet production, i.e. at rather large $x_A$, there is an initial suppression of around 10% (we note, however, that there is a finite bin width of 0.25 unit, so this statement should be taken in the average sense). This is also clearly visible when we plot the nuclear modification ratio as a function of the longitudinal fraction $x_A$ probed in the nucleus (Fig. 10 bottom). For definiteness, we plot the result for the $p_T$ cut of $10\,\mathrm {GeV}$. We compare the tendency of the saturation formalism used in the present work with the leading-twist shadowing. The calculation with saturation gives a suppression about 10% over the wide range of x: from $10^{-3}$ up to $10^{-2}$. For larger x (not shown) there are large fluctuations as we approach the edge of the phase space, but the ratio seems to be closer to unity. For the leading-twist shadowing the ratio approaches the unity much faster (around $10^{-2}$).

5 Summary

In this work we have investigated potential saturation effects in dijet production in ultra-peripheral heavy ion collisions at the LHC, for the $5.1\,\mathrm {TeV}$ CM energy per nucleon. The quasi-real photons are unique probes of the nucleus, as within the saturation formalism the Weizsäcker–Williams (WW) unintegrated gluon distribution is directly involved in the dijet production process. The WW distribution has an interpretation of the gluon number density, unlike other similar quantities that appear at small x.

In our work we used the ITMD formalism similar to the one used in [24, 47] for pA scattering. For sufficiently large jet $p_{T}$ it interpolates between the leading power limit of CGC formulas and the high energy $k_{T}$-factorization. The former is the back-to-back region of dijet imbalance and dominates the cross section. This is also the region where the saturation effects are strong. The latter is the region of very large imbalance, where the linear effects are dominant. There are number of advantages to this formulation:

• The formalism has a form of $k_{T}$-factorization which involves a convolution of unintegrated gluon distribution and off-shell matrix element. On phenomenology side, the usage of unintegrated gluon distributions is more convenient than using correlators of Wilson lines. Gluon distributions can be more easily supplemented with additional effects.

• It involves full momentum conservation for produced final states, taking into account the transverse momentum of the incoming gluons. This allows for a construction of Monte Carlo generators based on the formalism.

• Formalism is simple compared to the full CGC calculation, yet catching its essential features. When using the McLerran–Venugopalan model to obtain the WW gluon distribution, the present formulation should give identical results to CGC for $\Delta \phi \sim 0$ and $\Delta \phi \sim \pi$ for large $p_T$ jets. They could differ in the intermediate region, but taking into account general properties of $\Delta \phi$ distributions they cannot differ too much. The $p_T$ spectra should also be similar for large $p_T$.

In numerical computations we have used the unintegrated gluon distributions which evolve according to the nonlinear equation with subleading BFKL effects like energy conservation, running $\alpha _s$ and DGLAP correction. They were fitted to the inclusive proton HERA data (for nucleus the nonlinear term was scaled according to the Woods–Saxon formula) [52]. By definition these are the dipole unintegrated gluon distributions. The Weizsäcker–Williams gluons were obtained using the Gaussian approximation known in CGC following the procedure described in [47].

The results can be summarized as follows. The suppression due to the saturation effects is around 20% at most, for the smallest $p_{T}$ cutoff of the dijet transverse momenta. This is because the probed longitudinal fractions x are not very small. In addition, for the $p_{T}$ spectra, the saturation effects and the leading-twist shadowing look qualitatively similar. Thus, it would be rather difficult to distinguish between predictions of considered approaches. Nevertheless, it would be promising to focus on two main differences. The first difference is the slope of the $p_T$ spectra for $R_{\gamma A}$ in the small $p_T$ region (Fig. 7). The $p_T$ spectrum for the leading jet is much steeper for the saturation formalism. The second difference is the slope of the x spectra for $R_{\gamma A}$, i.e. how fast the nuclear effects vanish with increase of x (see Fig. 10 bottom). For the leading-twist nuclear shadowing this happens around $10^{-2}$, while for the saturation formalism with the WW gluon distribution used here it is a bigger value, very close to the edge of the phase space, so that we were unable to determine the exact value.

The question whether one should combine both mechanisms (and whether this is possible) remains open. In general, the predicted nuclear effects – regardless of the source – seem to be big enough to be seen in the data. Finally we note that the effect discussed strongly depends on the centrality of the $\gamma A$ collisions. So the study of the imbalance of jets as a function of centrality appears to be a promising strategy for exploring the effects discussed in this paper.