Nucleon structure functions in noncommutative space-time

Abstract

In the context of noncommutative space-time we investigate the nucleon structure functions which play an important role in identifying the internal structure of nucleons. We use the corrected vertices and employ new vertices that appear in two approaches of noncommutativity and calculate the proton structure functions in terms of the noncommutative tensor $\theta _{\mu \nu }$. To check our results we plot the nucleon structure function (NSF), $F_2(x)$, and compare it with experimental data and the results from the GRV, GJR and CT10 parametrization models. We show that with the new vertex that arises the noncommutativity correction will lead to a better consistency between theoretical results and experimental data for the NSF. This consistency will be better for small values of the Bjorken variable x. To indicate and confirm the validity of our calculations we also act conversely. We obtain a lower bound for the numerical values of $\Lambda _{\mathrm{NC}}$ scale which correspond to recent reports.

1 Introduction

Lepton–nucleon deep inelastic scattering (DIS) is an important tool to investigate nucleons and their constituents. Nucleon structure functions are the physical quantities for this purpose. Many phenomenological models have been established to investigate the structure functions of nucleons [1,2,3,4,5,6,7,8] but there is, however, a small deviation between the experimental data and the models’ predictions. On the other hand it is possible to investigate new physics, such as noncommutative (NC) space-time, in the DIS processes.

The motivation to consider noncommutative field theory (NCFT) leads back to string theory, where it was shown that in the presence of a constant background field the end points of an open string have noncommutative space-time (NCST) properties [9, 10].

The energy scale of NCST ($\Lambda _{\mathrm{NC}}$) has a wide range. This range results from different models and includes similar vertices. Different results for numerical values of $\Lambda _{\mathrm{NC}}$ from different models with similar vertices are due to the different employed experiments in the related analyzing process. These experiments include low energy as well as precise high energy collider experiments and finally sidereal and astrophysical events [11]. The description of them is as follows:

• At low energy experiments, for instance the Lamb shift in hydrogen [12], the magnetic moment of muon [13,14,15], atomic clock measurements [16] and Lorentz violation by clock comparison test [17] have already been studied in the presence of NCST. In three body bound states, the experimental data for a helium atom put an upper bound on the magnitude of the parameter of noncommutativity, $\theta _{\mathrm{NC}}$ [18].

• At high energy collider experiments we refer for example to forbidden decays in the standard model (SM), such as $Z\rightarrow \gamma \gamma$ [19], top quark decays [20,21,22] and Compton scattering [23] which has been investigated in the NCST. In the experiment that has been done by the OPAL collaboration, the NC bound from $e^- e^+$ scattering at 95% CL is $\Lambda _{\mathrm{NC}}> 141 GeV$ [24].

• Astrophysics and cosmological bounds on the NCST have also been explored in various processes, such as energy loss via $\gamma \rightarrow \bar{\nu }\nu$ in stellar clusters [25], effects of $\gamma \rightarrow \bar{\nu }\nu$ in primordial nucleosynthesis [26] and ultra high energy astrophysical neutrinos [27].

As we have mentioned and according to articles that have been cited, the bound on $\Lambda _{\mathrm{NC}}$ is strongly model dependent. For collider scattering experiments it is about a few TeV.

Some of the collider searches about the NCST can be qualified, considering some significant references. In Ref. [28] NC effects in several $2\rightarrow 2$ processes in $e^- e^+$ collisions such as Moller and Bhabha scattering, pair annihilation and $\gamma \gamma \rightarrow \gamma \gamma$ scattering are investigated. As a result, an NC scale of about 1TeV is extracted at high energy linear colliders. The pair production of the neutral electroweak gauge boson is studied at the LHC [29] and it is shown that under conservative assumptions, the NC bound is $\Lambda _{\mathrm{NC}}\ge 1 TeV$. Also pair production of a charged gauge boson at the LHC [30] exhibits a clear deviation for the azimuthal distribution from the SM at $\Lambda _{\mathrm{NC}}= 700\,\mathrm{GeV}$. The NC effect for the Drell–Yan process at the LHC has been taken into account in [31], and consequently a related scale is explored, such as $\Lambda _{\mathrm{NC}}\ge 0.4\,\mathrm{TeV}$.

Two approaches have been suggested to construct a noncommutative standard model (NCSM) [32, 33]. Using these approaches, the Feynman rules have been derived in [34,35,36,37], which have been used to address the phenomenological aspects of NCSM [38,39,40,41,42,43,44,45,46,47,48,49,50]. The significant features of the NCSM are that there are not only NC corrections for the existing vertices, that they are used to calculate the DIS processes; but they also contain new gauge boson interactions, which may cause some corrections in a leading order approximation of perturbative QCD. Here we would like to employ the NC corrections and the new raised interactions to address some phenomenology of electron–proton scattering.

The organization of this paper is as follows: In Sect. 2 we make a brief remarks about NCSM. In Sect. 3 the electron–proton DIS is computed in two approaches of the NCSM. In Sect. 4 we take into account the amended parton distributions, based on the NCSM approaches, to extract the nucleon structure function, using GRV, GJR and CT10 parametrization models [51,52,53]. Finally we will summarize our results and give our conclusion in Sect. 5.

2 Noncommutative standard model

Noncommutative theory leads to a commutation relation between the space-time coordinates

$$\begin{aligned}{}[\,{\hat{x}^\mu },\,{\hat{x}^\nu }] = i{\theta ^{\mu \nu }}, \end{aligned}$$

(1)

where hatted quantities are hermitian operators and ${\theta ^{\mu \nu }}$ is a real, constant and asymmetrical tensor. A simple way to construct the NCFT is the Weyl–Moyal star product [54, 55]

$$\begin{aligned} (f * g)(x) = {\left. {\exp \left( \frac{1}{2}i{\theta ^{\mu \nu }}\,\frac{\partial }{{\partial {x^\mu }}}\frac{\partial }{{\partial {y^\nu }}}\right) f(x)\,g(y)} \right| _{y \rightarrow x}} . \end{aligned}$$

(2)

Substituting the star product with the usual multiplication between conventional fields will lead to the NCFT. The star product has no effect on the integral of the quadratic term, i.e $\int {{d^4}x f*g}=\int {{d^4}x fg}$. Thus the propagators are equal in both the NCSM and the SM [54, 55]. This mechanism causes some difficulties such as charge quantization (which restricts the charges of matter fields to 0, $\pm 1$ [56, 57]) and the definition of the gauge group tensor product [58].

There are suggested two approaches in order to resolve these problems. The first one is built from an U(n) gauge group, which is a larger group with respect to the symmetry groups of the standard model. On this basis, two Higgs mechanisms lead to a reduction to the standard model group [32] (we call this approach an unexpanded approach). The second one is based on the Seiberg–Witten map [9, 10]. This gauge group is like the one of the standard model: non-commutative fields are expanded in terms of commutative ones (we call it an expanded approach) [33].

It is obvious that to assume a preferred direction leads to a violation of Lorentz invariance. Also it has been shown that the noncommutative field theories are not unitary for ${\theta ^{\mu 0}} \ne 0$. Therefore, for observable measurements we should take ${\theta ^{\mu 0}} = 0$ [59].

As previously mentioned, Feynman rules have been derived in both approaches [34,35,36,37]. All vertices contain NC corrections. In addition, there are some new interactions. For example, for the electromagnetic interaction between lepton and proton, there are corrections in $l \gamma l$ and $q \gamma q$ as lepton and quark vertices. In the SM, a photon does not interact with neutral particles like neutrino, gluon etc., but these interactions would exist in NCFT. Therefore one of the new and outstanding vertices is the photon–gluon interaction. Photon–fermion and photon–gluon vertices can be described briefly in different approaches:

• In the expanded approach:

  • 1. The photon–fermion vertex will be given by the expression [34]

    $$\begin{aligned}&\mathrm{ie} {Q_f}\left[ {{\gamma _\mu } - \frac{i}{2}{q^\nu }\left( {({\theta _{\mu \nu }}{\gamma _\rho } + {\theta _{\nu \rho }}{\gamma _\mu } + {\theta _{\rho \mu }}{\gamma _\nu })p_{in}^\rho - {\theta _{\mu \nu }}{m_f}} \right) } \right] \nonumber \\&\quad = i\,e{Q_f}{\gamma _\mu } +\frac{1}{2}e{Q_f} \left[ ({p_{out}}.\theta .{p_{in}}) {\gamma _\mu }\right. \nonumber \\&\qquad \left. - ({p_{out}}.{\theta _\mu })({{\not \!p}_{in}} - {m_f}) - ({{\not \!p}_{out}} - {m_f})({\theta _\mu }.{p_{in}})\right] . \end{aligned}$$

    (3)

  • 2. The photon–gluon vertex is given by [35]

    $$\begin{aligned} - 2\,e\,{\mathop {\mathrm Sin}\nolimits } 2{\theta _w}{K_{\gamma gg}}{\Theta _3}((\mu ,q),(\nu ,p),(\rho ,p')){\delta ^{ab}}, \end{aligned}$$

    (4)

    where ${K_{\gamma gg}}$ is the coupling constant of the theory. We assign to it three numerical values: -0.098, 0.197 and -0.396 [60, 61]. In Eq. (4), $\Theta _3$ is given by

    $$\begin{aligned}&{\Theta _3}((\mu ,{k_1}),(\nu ,{k_2}),(\rho ,{k_3})) = - ({k_1}.\theta .{k_2}) \nonumber \\&\quad \times \left[ {{({k_1} - {k_2})}^\rho }{g^{\mu \nu }} + {{({k_2} - {k_3})}^\mu }{g^{\nu \rho }}+ {{({k_3} - {k_1})}^\nu }{g^{\rho \mu }}\right] \nonumber \\&\quad - {\theta ^{\mu \nu }}\left[ {k_1^\rho ({k_2}.\,{k_3}) - k_2^\rho ({k_1}.\,{k_3})} \right] - {\theta ^{\nu \rho }}\left[ k_2^\mu ({k_3}.\,{k_1}) \right. \nonumber \\&\quad \left. - k_3^\mu ({k_2}.\,{k_1})\right] - {\theta ^{\rho \mu }}\left[ {k_3^\nu ({k_1}.\,{k_2}) - k_1^\nu ({k_3}.\,{k_2})} \right] \nonumber \\&\quad + ({\theta ^\mu }.\,{k_2})\left[ {{g^{\nu \rho }}k_3^2 - k_3^\nu k_3^\rho } \right] + ({\theta ^\mu }.\,{k_3})\left[ {{g^{\nu \rho }}k_2^2 - k_2^\nu k_2^\rho } \right] \nonumber \\&\quad + ({\theta ^\nu }.\,{k_3})\left[ {{g^{\mu \rho }}k_1^2 - k_1^\mu k_1^\rho } \right] + ({\theta ^\nu }.\,{k_1})\left[ {{g^{\mu \rho }}k_3^2 - k_3^\mu k_3^\rho } \right] \nonumber \\&\quad + ({\theta ^\rho }.\,{k_1})\left[ {{g^{\mu \nu }}k_2^2 - k_2^\mu k_2^\nu } \right] + ({\theta ^\rho }.\,{k_2})\left[ {{g^{\mu \nu }}k_1^2 - k_1^\mu k_1^\nu } \right] ,\nonumber \\ \end{aligned}$$

    (5)

    which is called the three-gauge boson vertex function [35].

• In the unexpanded approach [36]:

  • 1. The photon–fermion vertex is represented as

    $$\begin{aligned} - ie\;\exp \left( \frac{i}{2}k.\theta .q\right) {\gamma ^\mu }. \end{aligned}$$

    (6)

  • 2. The photon–gluon vertex has the following representation:

    $$\begin{aligned}&e\;{\delta _{ab}}\underbrace{({g_{\mu \nu }}{{(q - p)}_\rho } + {g_{\nu \rho }}{{(p + p')}_\mu } - {g_{\rho \mu }}{{(p' + q)}_\nu })\mathfrak {R}}_{{I^{\mu \nu \rho }}} \\&where\nonumber \\&\mathfrak {R}= - \frac{2}{3}\sin (\frac{1}{2}q.\theta .p). \nonumber \end{aligned}$$

    (7)

Considering the condition ${\theta ^{\mu 0}} = 0$ the following useful identities will be obtained:

$$\begin{aligned} A.\theta .B \equiv {A_\mu }{\theta ^{\mu \nu }}{B_\nu } = \mathbf {\theta }.\,(\mathbf {A} \times \mathbf {B}), \end{aligned}$$

(8)

$$\begin{aligned} A.\,\theta .\,\theta .\,B = {A_\mu }{\theta ^{\mu \nu }}\theta _\nu ^\beta {B_\beta } = {\left| {\mathbf {\theta }} \right| ^2}(\mathbf {A}.\,\mathbf {B}) - (\mathbf {A}.\,\mathbf {\theta })(\mathbf {B}.\mathbf {\theta }). \end{aligned}$$

(9)

3 Electron–proton scattering in noncommutative space-tame

Deep inelastic electron–proton scattering is a prevalent method to probe the proton. The electron–proton cross section in the laboratory system is given by [62, 63]

$$\begin{aligned} \frac{{\mathrm{d}\sigma }}{{\mathrm{d}{Q^2}\,\mathrm{d}\nu }}= & {} \frac{{{\alpha ^2}\pi }}{{4{E^2}\,{{\sin }^4}(\varphi /2)}}\frac{1}{{EE'}} \nonumber \\&\times [2{W_1}\,{\sin ^2}(\varphi /2) + {W_2}\,{\cos ^2}(\varphi /2)], \end{aligned}$$

(10)

where $\varphi$, E and $E'$ are the scattering angle and the energy of the incident and scattered electrons, respectively. The $W_1$ and $W_2$ functions characterize the structure of the proton. In the electron–parton elastic scattering, partons (quarks and gluons) are assumed to be point-like particles. To determine the structure functions, the usual method is to consider an electron which is scattered by quarks. For this purpose one can calculate the partonic cross section. The result would be multiplied by parton distributions. Finally, we need to integrate over the momentum fraction of each parton. In this paper we use this method in our calculations. We will now calculate the electron–parton scattering in two approaches of the NCFT, where both the photon–quark and the photon–gluon interactions are considered.

3.1 Parton model in expanded approach of NCSM

In the NCSM we follow the same method as in the usual space-time, with the exception that the electron–quark scattering is corrected in the NCST. Additionally we consider electron–gluon scattering in our calculations. So we should take into account the two individual contributions which we referred to before.

Corrected vertex contribution: At first we calculate the electron-quark scattering with respect to the given vertex in Eq. (3). In the laboratory system the corrected vertex could be written as:

$$\begin{aligned} \mathrm{ie}_{i}{g_e}{\gamma _\mu } + \frac{1}{2}{e_i}{g_e}\underbrace{\left[ { - (p'.\,{\theta _\mu })(\not \!p - m)} \right] }_{{C_\mu }} \end{aligned}$$

(11)

where $e_i$ is the charge of the ith quark. After doing some algebra (see Appendix A) the average of the squared invariant amplitude for electron–quark scattering in the expanded approach is obtained. We have

$$\begin{aligned} \left\langle {{{\left| \mathcal {M} \right| }^2}} \right\rangle= & {} \frac{1}{4}{\left( \frac{{{e_i}g_e^2}}{{{q^2}}}\right) ^2} Tr[\,{\gamma ^\mu }\,(\not k + {m_e})\,{\gamma ^\nu }(\not k' + {m_e})] \nonumber \\&Tr[\,{\gamma _\mu }\,(\not \!p + {m_q})\,{\gamma _\nu }(\not \!p' + {m_q})] \nonumber \\&- \frac{i}{8}{\left( \frac{e_i g_e^2}{q^2}\right) ^2}Tr[\,{\gamma ^\mu }\,(\not k + {m_e})\,{\gamma ^\nu }(\not k' + {m_e})] \nonumber \\&Tr[\,{\gamma _\mu }\,(\not \!p + {m_q})\,{C_\nu }(\not \!p' + {m_q})] \nonumber \\&- \frac{i}{8}{\left( \frac{e_i g_e^2}{q^2}\right) ^2}Tr[\,{\gamma ^\mu }\,(\not k + {m_e})\,{\gamma ^\nu }(\not k' + {m_e})] \nonumber \\&Tr[\,{C_\mu }\,(\not \!p + {m_q})\,{\gamma _\nu }(\not \!p' + {m_q})] \nonumber \\&+\frac{1}{16}{\left( \frac{e_i g_e^2}{q^2}\right) ^2}Tr[\,{\gamma ^\mu }\,(\not k + {m_e})\,{\gamma ^\nu }(\not k' + {m_e})] \nonumber \\&Tr[\,{C_\mu }\,(\not \!p + {m_q})\,{C _\nu }(\not \!p' + {m_q})]. \end{aligned}$$

(12)

In this equation the first term corresponds to the result of the calculation in the usual space-time with relic terms arising from NCST. One can easily show by the trace theorem that the terms containing the NC parameter, either of first order or of second order with respect to $\theta$ would vanish. Therefore, in this case the nucleon structure functions do not receive any correction from the NCST up to order of $\theta ^2$, and we have

$$\begin{aligned} M{W_1}({Q^2},\nu ) = \frac{1}{2}\sum \limits _i {e_i^2\,{q_i}(x)} \equiv {F_1}(x), \end{aligned}$$

(13)

$$\begin{aligned} \nu {W_2}({Q^2},\nu ) = \sum \limits _i {e_i^2\,x\,{q_i}(x)} \equiv {F_2}(x). \end{aligned}$$

(14)

New vertex contribution: Now we consider electron–gluon scattering in the expanded NCST. The photon–gluon vertex (see Eq. (4)), considering the $N = - 2\,\,{\mathop {\mathrm Sin}\nolimits } 2{\theta _w}{K_{\gamma gg}}$ is written

$$\begin{aligned} {g_e}N\,\Theta {\delta ^{ab}} \end{aligned}$$

(15)

where for simplification we omit the index 3 in $\Theta$ while we kept it before (see Eq. (3)). In the laboratory system and using the identity given by Eq. (8) the $\Theta$ quantity can be written

$$\begin{aligned}&\Theta ((\mu ,q),(\nu ,p),(\rho ,p')) \nonumber \\&\quad = - \theta ^{\mu \nu }\left[ - {q^\rho }({p^2}+ q.p)+ {p^\rho }({q^2} + q.p) \right] \nonumber \\&\qquad - {\theta ^{\nu \rho }}\left[ { - {p^\mu }{q^2} + {q^\mu }(q.p)} \right] + {\theta ^{\rho \mu }}\left[ {{p^\nu }(q.p) - {q^\nu }{p^2}} \right] \nonumber \\&\qquad - ({\theta ^\mu }.\,q)\left[ {{g^{\nu \rho }}{p^2} - {p^\nu }{p^\rho }} \right] + ({\theta ^\rho }.\,q)\left[ {{g^{\mu \nu }}{p^2} - {p^\mu }{p^\nu }} \right] \nonumber \\&\qquad + ({\theta ^\nu }.\,q)\left[ {{g^{\mu \rho }}({p^2} + 2q.p) - ({p^\mu }{p^\rho } + {p^\mu }{q^\rho } + {q^\mu }{p^\rho })} \right] .\nonumber \\ \end{aligned}$$

(16)

Fig. 1

A schematic graph for electron–gluon scattering

Considering Fig. 1 the invariant amplitude for the electron–gluon scattering can be calculated. By substituting the gluon vertex (see Eq. (15)) in the expression for the invariant amplitude, we find

$$\begin{aligned} {-i\mathcal {M}}= & {} [\bar{u(k')}(i{g_e}{\gamma ^\lambda })u(k)]\left[ \frac{{ - i{g_{\lambda \mu }}}}{{{q^2}}}\right] \nonumber \\&\times \; [{\varepsilon ^* _{2\nu }}{c_{1}^{*} }\,\,{g_e}N\,{\Theta ^{\mu \nu \rho }}\,{\delta ^{c_{1}c_{2}}}{\varepsilon _{3\rho }}c_{2}] \end{aligned}$$

(17)

where $\varepsilon _{i}$ is denoting the gluon polarization and $c_i$ is the color factor of the gluon. The symbol $\delta$ implies that color changing does not occur for the gluon. This is due to the fact that in the photon–gluon interaction, the photon is a colorless identity. Nevertheless we should take into account the contributions of all gluons since the gluons can appear in eight color states.

The scattering amplitude in Eq. (17) is proportional to $\theta$. To calculate the structure functions we need the square of this quantity, ${|\mathcal {M}|}^{2}$. Therefore the final result for the gluon–photon interaction as a NCST effect would initially appear at order $\theta ^2$. Following the required calculations the corrected parts of the structure function can be obtained (see Appendix A):

$$\begin{aligned} M{W_1}({Q^2},\nu ) = \frac{{{M^2}b(x)}}{{{Q^2}}}x\,g(x) \equiv {F_1}(x), \end{aligned}$$

(18)

$$\begin{aligned} \nu {W_2}({Q^2},\nu ) = a(x)\,x\,g(x) \equiv {F_2}(x), \end{aligned}$$

(19)

where

$$\begin{aligned} a(x)= & {} \frac{{{N^2}{\theta ^2}}}{{2}}\left( - 12xM{E^3} - 6{x^2}{M^2}{E^2} + 12{E^2}{Q^2}\right. \nonumber \\&- 5{x^2}{M^2}{Q^2} + 40xM{E^2}E' + 16{x^2}{M^2}EE' \nonumber \\&- 22EE'{Q^2} - 40xME{{E'}^2} - 6{x^2}{M^2}{{E'}^2} \nonumber \\&\left. + 12{{E'}^2}{Q^2} + 12xM{{E'}^3}+ 6{Q^4}\right) \end{aligned}$$

(20)

and

$$\begin{aligned} b(x)= & {} \frac{{{N^2}{\theta ^2}}}{{2}}\left( - 8{E^4} - 8{{E'}^4} + 4xM{E^3} + 2{x^2}{M^2}{E^2} \right. \nonumber \\&\quad \quad \left. + 24xME{{E'}^2} + 4{x^2}{M^2}{Q^2} - 24xM{E^2}E'\right. \nonumber \\&\quad \quad \left. - 6{x^2}{M^2}EE'- 4EE'{Q^2} + 2{x^2}{M^2}{{E'}^2}\right. \nonumber \\&\quad \quad - \left. 4xM{{E'}^3} + \frac{{11{Q^4}}}{4}\right) .\nonumber \\ \end{aligned}$$

(21)

Here $Q^2=-q^2$ and q is the momentum transferred by the photon, M is the mass of the proton and the other parameters are defined by

$$\begin{aligned} \nu = \frac{{{Q^2}}}{{2Mx}}, \end{aligned}$$

(22)

$$\begin{aligned} E = \frac{\nu }{y} = \frac{{{Q^2}}}{{2Mxy}}, \end{aligned}$$

(23)

$$\begin{aligned} E' = E - \frac{{{Q^2}}}{{2Mx}}. \end{aligned}$$

(24)

$\theta ^2$ is the square of $\mathbf {\theta }$ and the energy scale ($\Lambda _{\mathrm{NC}}$) for the NCST is given by

$$\begin{aligned} \left| \mathbf {\theta }\right| = \frac{1}{{{\Lambda _{\mathrm{NC}} ^2}}}. \end{aligned}$$

(25)

The final result for the nucleon structure function can be obtained by adding the gluon effect to the rest of the contributions. We get the following results:

$$\begin{aligned} M{W_1}({Q^2},\nu ) = \frac{1}{2}\sum \limits _i {e_i^2\,{q_i}(x)} + \frac{{{M^2}b(x)}}{{{Q^2}}}x\,g(x) \equiv {F_1}(x), \end{aligned}$$

(26)

$$\begin{aligned} \nu {W_2}({Q^2},\nu ) = \sum \limits _i {e_i^2\,x\,{q_i}(x)} + a(x)\,x\,g(x) \equiv {F_2}(x), \end{aligned}$$

(27)

where $q_i$ and $g_i$ are the distribution functions of the quarks and gluon, respectively.

In the following section, we will use Eq. (27) to indicate the effect of the gluon distribution to modify the proton structure function, resulting from the NC modification.

3.2 Parton model in unexpanded approach of NCST

In the unexpanded approach the calculations are like the ones in the expanded approach, except that we should use the vertex given by Eqs. (6) and (7).

Corrected vertex contribution: By replacing the photon–electron corrected vertex into the leptonic tensor, $L^{\mu \nu }$, this tensor will appear as

$$\begin{aligned} {L^{\mu \nu }}= & {} \frac{1}{2}\sum \limits _{\,Spins} {[\bar{u}(k'){\gamma ^\mu }{e^{\frac{i}{2}k.\theta .q}}\;u(k)]{{[\bar{u}(k'){\gamma ^\nu }{e^{\frac{i}{2}k.\theta .q}}u(k)]}^ * }} \nonumber \\= & {} \frac{1}{2}\sum \limits _{\,Spins} {\bar{u}(k'){\gamma ^\mu }{e^{\frac{i}{2}k.\theta .q}}\;u(k)\,\bar{u}(k){\gamma ^\nu }{e^{ - \frac{i}{2}k.\theta .q}}u(k')} \nonumber \\= & {} \frac{1}{2}\sum \limits _{\,Spins} {\bar{u}(k'){\gamma ^\mu }\;u(k)\bar{u}(k){\gamma ^\nu }u(k')}. \end{aligned}$$

(28)

It is obvious that no correction arises from the NCST in the leptonic tensor. Consequently one can show that there is no correction in the partonic sector.

New vertex contribution: Starting from Eq. (8), following the calculation listed in Appendix A for electron–gluon scattering in the expanded NC, using the definition $H = \frac{4}{{9}} - \frac{2}{{9}}\frac{{{M^2}}}{{{Q^2}}}$, one obtains

$$\begin{aligned} M{W_1}({Q^2},\nu ) = H\,g(x){\sin ^2}\left( \frac{1}{2}q.\theta .p\right) \equiv {F_1}(x), \end{aligned}$$

(29)

$$\begin{aligned} \nu {W_2}({Q^2},\nu ) = \frac{5}{{9}}x\,g(x){\sin ^2}\left( \frac{1}{2}q.\theta .p\right) \equiv {F_2}(x). \end{aligned}$$

(30)

Since our calculations are in the laboratory system and are according to Eq. (8), in this case we also do not have any gluon contribution. Therefore, the unexpanded approach of the NC does not have any effect on the nucleon structure functions in the laboratory system and consequently the structure functions would be as in the usual space-time, given by Eqs. (13) and (14).

4 Results and discussions

In Sect. 3 the correction of the NCST has been calculated up to leading order in terms of the NC parameter, $\theta$. The NC correction to the structure function, in the expanded approach, is just coming from electron–gluon scattering and, as we mentioned before, it contains the $\theta ^2$ term at the leading order of the approximation.

The modified structure functions of nucleon are given by Eqs. (26) and (27). The two nucleon structure functions $F_1(x)$ and $F_2(x)$ at the parton level for the spin 1/2 particles are not independent from each other, considering the Callan–Gross relation $F_2(x)=2x F_1(x)$. Therefore at the leading order approximation and in the usual space-time, it is sufficient to take into account one of these structure functions; preferably the $F_2(x)$ one. This is why most experimental data are relating to the $F_2 (x)$ rather than the $F_1(x)$ structure function. In the NC space-time, the Callan–Gross relation would not exist, though in the NCST it is not unexpected, due to the contribution of the photon–gluon interaction in calculations.

By writing Eq. (27) in terms of constituent quarks and gluon distributions we will have the following result for the proton structure function:

$$\begin{aligned} {F_2}(x)= & {} {\left( {\frac{2}{3}} \right) ^2}\left[ {x{u_v}(x) + 2x\,\bar{u}(x)} \right] + {\left( { - \frac{1}{3}} \right) ^2}\left[ x{d_v}(x)\right. \nonumber \\&\left. + 2x\,\bar{d}(x) \right] + {\left( { - \frac{1}{3}} \right) ^2}\left[ {2x\,s(x)} \right] + a(x)\,x\,g(x),\nonumber \\ \end{aligned}$$

(31)

where u(x), d(x), s(x) and g(x) denote the quark and gluon distribution functions. The final term comes from our calculations in the NCST. The factor a(x) (see Eq. (20)) contains the parameters of NCST like $\theta$ and $K_{\gamma gg}$ and the usual parameters like the energies of the incident and scattered electron (E and $E'$), the transferred momentum(q as $Q^2=-q^2$), the proton mass (M) and the momentum fraction carried by each parton (x).

Fig. 2

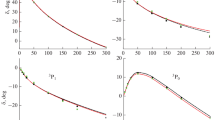
Our results for the modified nucleon structure function (NSF), $F_2(x)$, at $Q^2=3.5\;\mathrm{GeV}^2$, $4.5\;\mathrm{GeV}^2$ and $650\;\mathrm{GeV}^2$, which are compared with the available experimental data  [64] and the normal GRV parametrization model  [51]. Here “GRV-Im.” indicates our results for the modified NSF, using the GRV model. “GRV-Uim.” denotes the normal NSF in the GRV model

We have depicted the modified nucleon structure function ($F_2(x)$) in Fig. 2 by substituting Eqs. (22), (23) and (24) in Eq. (20). The values of $Q^2$ and y have been chosen so as to correspond to the available range of experimental data. The results have been compared with available experimental data [64] and the prediction of the GRV parametrization model at the LO approximation [51]. The reason for employing this approximation going back to the reality is that we intend to indicate the effect of the gluon distribution more dominantly in NC space-time, while we know that in normal space-time, the gluon distribution would not exist in the LO approximation. To indicate the theoretical uncertainty in the standard model prediction for the structure function $F_2(x)$, we also use the GJR and CT10 parametrization models [52, 53] and find the results for the modified nucleon structure function. We present here the results for these models in the modified and normal cases. For instance in Fig. 3 the results for the nucleon structure function, arising from the normal cases and the modified models, are compared with each other and also with the available experimental data. As we would expect, the theoretical uncertainty, using different parametrization models, is very low and we get a firm conclusion for the validity of the modified models, considering the NC effect.

To plot the $F_2(x)$ we need two NC parameters, $\Lambda _{\mathrm{NC}}$ and $K_{\gamma gg}$. Good fits for $F_2$ with experimental data are obtained for the approved amounts of the energy scale $\Lambda _{\mathrm{NC}}$. Figures 2 and 3 indicate the good compatibility with the experimental data, especially for small values of the Bjorken x variable where we expect the effect of new physics to be more relevant. As has been mentioned above, in the literature there is no specific value for the NC scale. Collider scattering experiments could be proper evidence to search NCST effects because they are very sensitive to NC signals. The usual bound from these experiments is $\Lambda _{\mathrm{NC}}\sim 1$ TeV. The present work is also implemented for collider scattering experiments to find the modified structure functions of the nucleons in NCST. So we have also employed this range, which is prevalent in such processes.

Fig. 3

Nucleon structure function (NSF), $F_2(x)$, at $Q^2= 650\;GeV^2$, compared with the available experimental data [64], using the GRV, CT10 and GJR models. Here “Im.” indicates our results for the modified NSF (up panel), and “Uim.” denotes the normal NSF (down panel), using the three mentioned models

Following the procedure which was described in the expanded approach, one finds three numerical values for the $K_{\gamma gg}$ parameter, which are −0.098, 0.197 and −0.396, respectively [60, 61]. The results for all three values of $K_{\gamma gg}$ are similar. Therefore we have just presented the results coming from the numerical values of the parameters and scales which are tabulated in Table 1. As can be seen from Table 1, the numerical value for the NC scale is changing by variation of $Q^2$. For example for fixed $K_{\gamma gg}$, a goodness fitting is provided at $\Lambda _{\mathrm{NC}}= 830\; \mathrm{GeV}$ for $Q^2=3.5\; \mathrm{GeV}^2$, while for the $Q^2=650\; \mathrm{GeV}^2$ case, the $\Lambda _{\mathrm{NC}}$ scale is equal to $2200\;\mathrm{GeV}$. The $\Lambda _{\mathrm{NC}}$ also depends on the measure of the $K_{\gamma gg}$ parameter. According to Table 2 for a fixed $Q^2$, the value of $\Lambda _{\mathrm{NC}}$ increases when the magnitude of $K_{\gamma gg}$ increases. For instance, at fixed $Q^2$ for $K_{\gamma gg}=-0.098$ we will get $\Lambda _{\mathrm{NC}}=2200\; \mathrm{GeV}$ and it is $4400\;\mathrm{GeV}$ for $K_{\gamma gg}=-0.396$. The numerical values for the NC scale, using the GJR and CT10 parametrization models, are of the same order as the ones in Tables 1 and 2, with a similar behavior when the squared transfer momentum is varying.

To see the stability of results with respect to different values of $K_{\gamma gg}$ parameter, we depict in Fig. 4 the $F_2(x)$ structure function at $Q^2=650\; \mathrm{GeV}^2$, using three numerical values for the $K_{\gamma gg}$ parameter with $\Lambda _{\mathrm{NC}}=4000\; \mathrm{GeV}$. As can be seen, there is sufficient stability for the nucleon structure function with respect to variation of the $K_{\gamma gg}$ parameter.

We also investigate the effect of $Q^2$ variation on the structure function $F_2(x)$. In Fig. 5 we plot the modified $F_2(x)$ at $x=0.000161$, using three different values for $K_{\gamma gg}$ values. It shows again that the differentiation between SM prediction and NCST modification would occur at large $Q^2$ values.

Table 1 $\Lambda _{\mathrm{NC}}$ variations with squared transfer momentum for a fixed $K_{\gamma gg} = -0.098$

Table 2 $\Lambda _{\mathrm{NC}}$ variations with parameter $K_{\gamma gg}$ for a fixed $Q^2=650 (\mathrm{GeV})^2$

To confirm the validity of our obtained results we can act conversely and concentrate to extract the energy scale, $\Lambda _{\mathrm{NC}}$. We then need to consider Eq. (31), while the energy scale, $\Lambda _{\mathrm{NC}}$, is unknown. At fixed $K_{\gamma gg}$ parameter, using the available experimental data for the $F_2(x)$ structure function, we are able to obtain the lower bound of $\Lambda _{\mathrm{NC}}$ (for more details, see Appendix B). We get

• For $K_{\gamma gg}=-0.098$: $\Lambda _{\mathrm{NC}}\ge 430\; GeV,$

• For $K_{\gamma gg}=0.197$: $\Lambda _{\mathrm{NC}}\ge 610\; GeV,$

• For $K_{\gamma gg}=-0.396$: $\Lambda _{\mathrm{NC}}\ge 860\; GeV.$

However, in obtaining the above numerical values for $\Lambda _{\mathrm{NC}}$ scale we use the GRV model, but similar results will appear when we employ the GJR and CT10 models. To have confirmation on the validity of our calculations, we once again go back to the Drell–Yan process, which plays an important role for investigating the structure function of the nucleon and in testing the parton model. Analyzing these processes at the NCST will yield $\Lambda _{\mathrm{NC}}\ge 0.4\;\mathrm{TeV}$ [31], which is compatible with our result.

Fig. 4

Our results for the modified nucleon structure function (NSF), $F_2(x)$, versus Bjorken x variable at $Q^2=650\;GeV^2$, using three different numerical values for the $K_{\gamma gg}$ parameter which are compared with the available experimental data [64] and the normal GRV parametrization model [51]. The plots relate to $\Lambda _{\mathrm{NC}} = 4000\; GeV$. Here “GRV-Im.” indicates our results for the modified NSF, using the GRV model. “GRV-Uim.” denotes the normal NSF in the GRV model

Fig. 5

Our results for the modified nucleon structure function (NSF) , $F_2(x)$, at $x=0.000161$, versus $Q^2$ variable, using three different values of $the K_{\gamma gg}$ parameter, which are compared with the available experimental data [64] and the normal GRV parametrization model [51]. The plots relate to $\Lambda _{\mathrm{NC}} = 1300\;\mathrm{GeV}$. Here “GRV-Im.” indicates our results for the modified NSF, using GRV model. The “GRV-Uim.” denotes the normal NSF in the GRV model

5 Conclusion

We have considered the effect of NCST on the proton structure functions. There are two approaches to construct the usable NC theory. In both approaches, all present vertices are modified by the NC parameter $\theta _{\mu \nu }$. In this case, in addition to the usual interactions, some new interactions would also appear. We have applied two new corrections and two new interactions, one for each approach, to calculate the structure functions of proton. Three of the four corrections do not have any effect but a new interaction from an expanded approach contributes to the nucleon structure function. As can be seen, the obtained results for the improved proton structure function, $F_2(x)$, are in better compatibility with the available experimental data rather than the results coming from the normal GRV, CT10 and GJR parametrization models, specially at small values of the Bjorken x variable, which is related to the high energy region. Also the order of magnitude of the NC energy scale that we have, using the NCSM approach, corresponds with the expected range of the other predictions.

Here we consider the special case when the tensor component $\theta _{\mu 0}$ is zero. Therefore laboratory rotation does not have any effect on the result. To investigate the effect of the Earth rotation one can calculate the case for $\theta _{\mu 0}\ne 0$, which we hope to address in the future.

On the other hand, the current results can be extended to the higher order approximation, but these effects are expected to be very small and might be ignorable with respect to a lower approximation order.

The results which we got in NC space-time include automatically the Lorentz violation. The calculations in which we impose by hand the Lorentz invariance, can be done [65] and we will do so in our further research activity.

In non-minimal NCSM, the Z boson is also coupled to gluons and it could modify the $F_2(x)$ structure function. However, the main contribution for the $F_2(x)$ is arising out of the electromagnetic interaction. In this case the portion of weak interaction is negligible. Weak interactions have specially been used to compute the $xF_3(x)$ structure function where the parity violation occurs. We will report about this issue in the near future as a separated research project.

Appendices

Appendix A

Here we perform in detail the required calculations for the electron–quark and electron–gluon scattering in the expanded NC. Similar calculations can be done for unexpanded NC.

Electron–quark scattering: Employing the Feynman rules like the ones for Fig. 1 we will be able to obtain the required results up to leading order, considering the NC parameter. Since propagators are not affected by NC corrections, just vertices should be written in NC space-time. According to the photon–fermion vertex in the laboratory system (see Eq. (11)) the invariant amplitude reads

$$\begin{aligned} {-i\mathcal {M}}= & {} [\bar{u}(k')(i{g_e}{\gamma ^\mu })u(k)][\frac{{ - i{g_{\mu \nu }}}}{{{q^2}}}][\bar{u}(p')(i{e_i}{g_e}{\gamma ^\nu })u(p)] \nonumber \\&+\, [\bar{u}(k')(i{g_e}{\gamma ^\mu })u(k)][\frac{{ - i{g_{\mu \nu }}}}{{{q^2}}}]\nonumber \\&\times \, [\bar{u}(p')(\frac{1}{2}{e_i}{g_e}{C^\nu })u(p)]. \end{aligned}$$

(32)

After some simplification we have

$$\begin{aligned} {-\mathcal {M}}= & {} \frac{{{e_i}g_e^2}}{{{q^2}}}[\bar{u}(k'){\gamma ^\mu }u(k)][\bar{u}(p'){\gamma _\mu }u(p)] \nonumber \\&- i\frac{{{e_i}g_e^2}}{{2{q^2}}}[\bar{u}(k'){\gamma ^\mu }u(k)][\bar{u}(p'){C_\mu }u(p)]. \end{aligned}$$

(33)

Then, for the squared invariant amplitude, we get

$$\begin{aligned} \begin{array}{l} {{\left| \mathcal {M} \right| ^2}} = {(\frac{{{e_i}g_e^2}}{{{q^2}}})^2}[\bar{u}(k'){\gamma ^\mu }u(k)][\bar{u}(p'){\gamma _\mu }u(p)]{[\bar{u}(k'){\gamma ^\nu }u(k)]^\dag }\\ {[\bar{u}(p'){\gamma _\nu }u(p)]^\dag }+ \frac{i}{2}{(\frac{{{e_i}g_e^2}}{{{q^2}}})^2}[\bar{u}(k'){\gamma ^\mu }u(k)][\bar{u}(p'){\gamma _\mu }u(p)]\\ {[\bar{u}(k'){\gamma ^\nu }u(k)]^\dag }{[\bar{u}(p'){C_\nu }u(p)]^\dag } - \frac{i}{2}{(\frac{{{e_i}g_e^2}}{{{q^2}}})^2}{[\bar{u}(k'){\gamma ^\mu }u(k)]}\\ {[\bar{u}(p'){C_\mu }u(p)]}{[\bar{u}(k'){\gamma ^\nu }u(k)]^\dag }{[\bar{u}(p'){\gamma _\nu }u(p)]^\dag } +\frac{1}{4}(\frac{e_i g_e^2}{q^2})^2 \\ {[\bar{u}(k'){\gamma ^\mu }u(k)]}{[\bar{u}(p'){C_\mu }u(p)]}{[\bar{u}(k'){\gamma ^\nu }u(k)]^\dag }{[\bar{u}(p'){C _\nu }u(p)]^\dag }. \end{array} \end{aligned}$$

(34)

We remember that for two $4\times 4$ ${\Gamma _1}$ and ${\Gamma _2}$ matrices Casimir’s trick will lead to

$$\begin{aligned}&\sum \limits _{all\;spins} {[\bar{u}(a){\Gamma _1}u(b)]{{[\bar{u}(a){\Gamma _2}u(b)]}^\dag }} \nonumber \\&\quad = Tr[\,{\Gamma _1}\,({\not \!p_b} + {m_b})\,{\bar{\Gamma }_2}({\not \!p_a} + {m_a})]\;. \end{aligned}$$

(35)

According to the definition of ${\bar{\Gamma }_2} = {\gamma ^0}\Gamma _2^\dag \,{\gamma ^0}$ , we have ${\gamma ^0}{C^{\nu \dag }}\,{\gamma ^0} = - {C^\nu }$, ${\gamma ^0}{\gamma ^{\nu \dag }}\,{\gamma ^0} = {\gamma ^\nu }$. Now by taking average over the initial spin states and a sum over the final spin states and using the Casimir trick we arrive at Eq. (12).

Electron–gluon scattering: To do the required calculations, we consider Fig. 1 and proceed to address the square of invariant amplitude in Eq. (17). Then doing the average over initial spins states and summing over the final spin states and then the gluon polarization states

$$\begin{aligned} \sum {{\varepsilon _\mu }\varepsilon _\nu ^ * } \rightarrow - {g_{\mu \nu }}, \end{aligned}$$

(36)

and we have color algebra

$$\begin{aligned} \sum \limits _{{c_1}{c_2}} {{\delta ^{{c_1}{c_2}}}{\delta _{{c_1}{c_2}}}} = \sum \limits _{{c_1} = 1}^8 {{\delta ^{{c_1}{c_1}}}} = 8; \end{aligned}$$

(37)

we will get the following result:

$$\begin{aligned} \begin{array}{l} \left\langle {{\left| \mathcal {M} \right| }^2} \right\rangle = \frac{16{N^2}g_e^4}{q^4}\left[ \theta ^2\left( k.k'\,(p^2+q^2)(-p^2 q^2+(q.p)^2)\right. \right. \\ \left. \left. -q^2q.p\,(k.pk'.q+k.qk'.p)+q^4 k.p\,k'.p+k.q\,k'.q\,(q.p)^2\right. \right. \\ \left. \left. -k.k'\, q.p\, (p^2 q^2-(q.p)^2)\right) -p^4 k.\theta .q\, k'.\theta .q+k.\theta .\theta .q \right. \\ \left. \times (q^2p^2\,k'.(q+p))+k.\theta .\theta . k'(p^2+(p+q)^2)(p^2q^2\right. \\ \left. -(p.q)^2)-q.\theta \theta .q\left( p^2\,k.k'(\frac{p^2}{2}+2q^2+3q.p)+k.pk'.p\right. \right. \\ \left. \left. (2p^2+q^2+2p.q)+(k.qk'.p+k.p\,k'.q)(p^2+2p.q)\right) \right. \\ \left. -p^2k.qk'.q +k'.\theta .\theta . q \left( (q^2\,p^2-2(q.p)^2)k.(p+q)\right) \right. \\ \left. \left. +(p^2\,k.q+q^2\,k.p)\,q.p\right) \right] . \end{array} \end{aligned}$$

(38)

In Eq. (38) we neglected the electron mass. We note that since there are not more than two gluon legs, the incident gluon is like the outgoing gluon. Mathematically, the Kronecker delta function confirms this reality. On the other hand since gluons are appearing in eight color states, we should consider the color factor in our calculation, which can be done using Eq. (37). Now to simplify the above equation, by taking $\alpha$, $\beta$, $\gamma$ as the angles between the $\mathbf {k}$, $\mathbf {k}'$, $\mathbf {k} \times \mathbf {k}'$ and $\mathbf {\theta }$ directions, respectively, in the laboratory system and using Eqs. (8) and (9) we get

$$\begin{aligned} k.\,\theta .\,\theta .\,k = {E^2}|\mathbf {\theta }{|^2}{\sin ^2}\alpha , \end{aligned}$$

(39)

$$\begin{aligned} k'.\,\theta .\,\theta .\,k' = {E'^2}|\mathbf {\theta }{|^2}{\sin ^2}\beta , \end{aligned}$$

(40)

$$\begin{aligned} k.\,\theta .\,\theta .\,k' = E\,E'|\mathbf {\theta }{|^2}(\cos \varphi - \cos \beta \cos \alpha ), \end{aligned}$$

(41)

$$\begin{aligned} k.\,\theta .\,k' = E\,E'|\mathbf {\theta }|\sin \varphi \cos \gamma . \end{aligned}$$

(42)

Then by taking the average over $\alpha$, $\beta$ and $\gamma$, Eq. (38) will lead to

$$\begin{aligned} \left\langle {{{\left| \mathcal {M} \right| }^2}} \right\rangle = \frac{{8{N^2}g_e^4}}{{{q^4}}}{\theta ^2}EE'm_{eff}^2\left[ {a'{{\cos }^2}(\frac{\varphi }{2}) + b'{{\sin }^2}(\frac{\varphi }{2})} \right] , \end{aligned}$$

(43)

where

$$\begin{aligned} a'= & {} - 12{m_{eff}}{E^3} - 6m_{eff}^2{E^2} + 12{E^2}{Q^2} - 5m_{eff}^2{Q^2} \nonumber \\&+6{Q^4} + 40{m_{eff}}{E^2}E' + 16m_{eff}^2EE' - 40{m_{eff}}E{{E'}^2} \nonumber \\&- 22EE'{Q^2}- 6m_{eff}^2{{E'}^2} + 12{{E'}^2}{Q^2} + 12{m_{eff}}{{E'}^3}, \end{aligned}$$

(44)

$$\begin{aligned} b'= & {} - 8{E^4} - 8{{E'}^4} + 4{m_{eff}}{E^3} + 2m_{eff}^2{E^2} \nonumber \\&+ 4m_{eff}^2{Q^2} - 24{m_{eff}}{E^2}E' - 6m_{eff}^2EE' \nonumber \\&- 4EE'{Q^2} + 24{m_{eff}}E{{E'}^2} + 2m_{eff}^2{{E'}^2} \nonumber \\&+ \frac{{11{Q^4}}}{4} - 4{m_{eff}}{{E'}^3}. \end{aligned}$$

(45)

Here ${m_{eff}}$ is the zeroth component of the four-momentum for the gluon. By substituting Eq. (43) into

$$\begin{aligned} \begin{array}{l} \mathrm{d}\sigma = \frac{1}{{(2E)(2m)}}\frac{{\left\langle {{{\left| \mathcal {M} \right| }^2}} \right\rangle }}{{4{\pi ^2}}}\frac{{{d^3}k'}}{{2E'}}\frac{{{d^3}p'}}{{2{{p'}_0}}}{\delta ^{(4)}}(p + k - p' - k')\\ \quad \;\; = \frac{1}{{4mE}}\frac{{\left\langle {{{\left| \mathcal {M} \right| }^2}} \right\rangle }}{{4{\pi ^2}}}\frac{1}{2}E'dE'\mathrm{d}\Omega \frac{{{d^3}p'}}{{2{{p'}_0}}}{\delta ^{(4)}}(p + k - p' - k'). \end{array} \end{aligned}$$

(46)

Now we use

$$\begin{aligned} \int {\frac{{{d^3}p'}}{{2{{p'}_0}}}{\delta ^{(4)}}(p + q - p')} = \frac{1}{{2m}}\delta (\nu + \frac{{{q^2}}}{{2m}}), \end{aligned}$$

(47)

where in laboratory system we have

$$\begin{aligned} d(\cos \varphi )dE' = \frac{1}{{2EE'}}\mathrm{d}{Q^2}\mathrm{d}\nu . \end{aligned}$$

(48)

Thus, we obtain

$$\begin{aligned} \frac{{\mathrm{d}\sigma }}{{\mathrm{d}{Q^2}\mathrm{d}\nu }}= & {} \frac{{\pi {\alpha ^2}}}{{4{E^2}{{\sin }^4}(\frac{\varphi }{2})}}\frac{1}{{EE'}} \nonumber \\&\times \; \left[ {a\,{{\cos }^2}(\frac{\varphi }{2}) + b{{\sin }^2}(\frac{\varphi }{2})} \right] \delta \left( \nu - \frac{{{Q^2}}}{{2{m_{eff}}}}\right) .\nonumber \\ \end{aligned}$$

(49)

Here $a = \frac{{{N^2}{\theta ^2}}}{{2}}a'$ and $b = \frac{{{N^2}{\theta ^2}}}{{2}}b'$. Now, by comparing Eqs. (49) and (10) we determine the gluon contributions to the nucleon structure function, which are denoted by $w_1^{\mathrm{gluon}}$ and $w_2^{\mathrm{gluon}}$, respectively:

$$\begin{aligned} w_1^{\mathrm{gluon}} = \frac{b}{2}\delta \left( \nu - \frac{{{Q^2}}}{{2M\,{x_g}}}\right) , \end{aligned}$$

(50)

$$\begin{aligned} w_2^{\mathrm{gluon}} = a\,\delta \left( \nu - \frac{{{Q^2}}}{{2M\,{x_g}}}\right) , \end{aligned}$$

(51)

in which we use ${m_{eff}} = {x_g}M$. Here ${x_g}$ is the fraction of the momentum of the nucleon which is carried by the gluon. To obtain the nucleon structure function which results from the electron–gluon scattering it is necessary to multiply $w_1^{\mathrm{gluon}}$ and $w_2^{\mathrm{gluon}}$ by $g({x_g})$, as the probability function, to find the gluon which is carrying the fraction of the nucleon’s momentum. Then integrating with respect to ${x_g}$ the result will be

Table 3 Sample numerical values for the $\Lambda _{\mathrm{NC}}$ scale in the $2.7< Q^2< 20000\;\mathrm{GeV}^2$ range at different values of the parameter $K_{\gamma gg}$

$$\begin{aligned} {W_1}({Q^2},\nu )= & {} \int \limits _0^1 {d{x_g}g({x_g})w_1^{\mathrm{gluon}}} \nonumber \\= & {} \int \limits _0^1 {d{x_g}g({x_g})\frac{{b({x_g})}}{2}\delta \left( \nu - \frac{{{Q^2}}}{{2M{x_g}}}\right) } \nonumber \\= & {} \int \limits _0^1 {d{x_g}g({x_g})\frac{{b({x_g})}}{2}\frac{{{x_g}}}{\nu }\delta ({x_g} - x)} \nonumber \\= & {} \frac{{b(x)}}{2}\frac{x}{\nu }g(x) = \frac{{b(x)}}{M}\frac{{{M^2}x}}{{{Q^2}}}g(x), \end{aligned}$$

(52)

$$\begin{aligned} {W_2}({Q^2},\nu )= & {} \int \limits _0^1 {d{x_g}g({x_g})w_2^{\mathrm{gluon}}} \nonumber \\= & {} \int \limits _0^1 {d{x_g}g({x_g})\,a({x_g})\,\delta \left( \nu - \frac{{{Q^2}}}{{2M{x_g}}}\right) } \nonumber \\= & {} \int \limits _0^1 {d{x_g}g({x_g})\,a({x_g})\frac{{{x_g}}}{\nu }\delta ({x_g} - x)} \nonumber \\= & {} \frac{1}{\nu }a(x)\,x\,g(x), \end{aligned}$$

(53)

where Eqs. (18) and (19), as the corrected portion of the structure function, come from the gluon–photon interaction.

Appendix B

We use Eq. (31) to find the lower bound for $\Lambda _{\mathrm{NC}}$ where the a(x) term in this equation is given by Eq. (20). By substituting numerical values for E and E$'$ which can be obtained in terms of the variables x and y (see Eqs. (22), (23) and (24)), and finally using the $Q^2$ value in Eq. (20), the a term in Eq. (31) is calculable. Now, we replace the numerical value for the $F_2(x)$ experimental data together with the numerical values for parton densities at the specified x-variable. These are quoted from the GRV parametrization model  [51]. Thus, we are able to extract the value of the $\Lambda _{\mathrm{NC}}$ scale.

Consequently, using different numerical values for the $K_{\gamma gg}$ parameter, three values are obtained for $\Lambda _{\mathrm{NC}}$. Some sample results are listed by Table 3 in the $2.7< Q^2< 20000\;\mathrm{GeV}^2$ range. As can be seen from this table, the value of $\Lambda _{\mathrm{NC}}$ changes by the variation of $Q^2$. Our purpose is to determine the lowest bound of $\Lambda _{\mathrm{NC}}$. Looking carefully at this table we see this value occurs at $Q^2=3.5\;\mathrm{GeV}^2$ for $x=0.008$, which is not identical for the different values of the $K_{\gamma gg}$ parameter. We determine the lowest bounds for the $\Lambda _{\mathrm{NC}}$ scale in Table 3 at different amounts of the $K_{\gamma gg}$ parameter, using the underlined representation.