1 Introduction

After the discovery of the Higgs like scalar at 126 GeV [1, 2], the fine tuning problem of the Higgs mass, originating from its large radiative correction, has become a pressing issue within the framework of various proposals beyond standard model physics. Among various extra dimensional models [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25] the ADD [3,4,5] and the RS [14, 15] model drew special attention as regards this problem. In particular, the RS [14, 15] model keeps the Higgs mass well within the acceptable upper bound without invoking any hierarchical parameters in the theory. The phenomenology that follows in such a beyond standard model (BSM) physics [26,27,28,29,30,31] is crucially dependent on the stable value of the radius modulus of the model which determines the various parameters in the 4-dimensional effective theory of the model. However, the issue of stabilizing the modulus, consistent with the requirement of the solution of gauge hierarchy problem, was proposed by Goldberger and Wise [32] by invoking an additional scalar field in the bulk. By choosing the appropriate boundary values of this scalar at the two orbifold fixed points they could obtain the appropriate value for the warp factor. Subsequently the RS model was generalized with curved 3-branes, in particular with a de Sitter (DS) and anti-de Sitter (ADS) 3-brane sitting at the orbifold fixed points [33]. The phenomenological implications of this have also been discussed in [33, 34]. Here, we demonstrate that, for the de Sitter 3-brane, a positive value of the brane vacuum energy can naturally lead to a modulus potential which has a metastable minimum. The value of the corresponding radius modulus depends on the brane cosmological constant and can be tuned to address the gauge hierarchy and stability issue concomitantly. Thus, we do not require any external bulk scalar to achieve modulus stabilization. In this context it may be mentioned that Csaki et al. [35] explored how the 3-brane matters namely matter on either of the two branes or in bulk may contribute to Hubble expansion on the brane. They showed in such a scenario how the Hubble expansion equation on the brane comes with the correct signature only after assuming a stabilizing mechanism for the modulus. In our work we demonstrate how the modulus stabilization can be achieved in the presence of brane vacuum energy without introducing any other bulk scalar potential.

2 A brief survey of warp geometry in non-flat 3-branes

RS model is formulated in a 5-dimensional anti-de Sitter bulk space-time where the extra dimension is compactified in a \(\mathrm M^4 \times S^1/Z_2\) manifold. In the RS model two 3-branes are placed at the two orbifold fixed points, which are assumed to be flat such that the cosmological constant induced on the visible brane is zero. It has been shown that an appropriate tuning between the brane tension and the bulk induced cosmological constant on the brane can exactly cancel the resulting effective cosmological constant on the brane to make it flat [36]. However, a slight imbalance between these may lead to positive or negative brane vacuum energy, which leads to warped geometry models with non-flat 3-branes.

A generalized version of the RS model with non-flat 3-branes was addressed in [33] where a more general warp factor was derived and the correlation between the extra dimensional modulus and brane cosmological constant was discussed in the light of the gauge hierarchy problem.

The metric ansatz in the generalized-RS scenario, satisfying the 5-d Einstein equations with a negative bulk cosmological constant is [33]

$$\begin{aligned} {\mathrm{d}s}^2=e^{-2A(r_c \phi )}g_{\mu \nu } {\mathrm{d}x}^{\mu }{\mathrm{d}x}^{\nu } + r_c ^2 {\mathrm{d}\phi }^2. \end{aligned}$$
(1)

This results in the 4-d Einstein equations,

$$\begin{aligned} ^4 G_{\mu \nu } - g_{\mu \nu }e^{-2A}[-6 A'^2 +3 A'']=-\frac{\Lambda }{4M^3}g_{\mu \nu }e^{-2A}, \end{aligned}$$
(2)

while the component of the equation along the extra dimension is

$$\begin{aligned} -\frac{1}{2}e^{2A} ~ ^4 R+6A'^2=-\frac{\Lambda }{4M^3} \end{aligned}$$
(3)

along with the boundary conditions

$$\begin{aligned}{}[A'(y)]_i=\frac{\epsilon _i}{24M^3}V_i. \end{aligned}$$
(4)

Here, \(\Lambda \) is the bulk cosmological constant, R the bulk Ricci scalar and \(V_i\) the brane tension on the ith brane, where \(i=\mathrm{vis(hid)}\) is for visible (hidden) branes, respectively, and \(\epsilon _{\mathrm{hid}}=-\epsilon _{\mathrm{vis}}=1\).

On solving Eqs. (2) and (3) one obtains the equations

$$\begin{aligned} 6A'^2=\frac{\Lambda }{4M^3} + 2\Omega e^{2A} \end{aligned}$$
(5)

and

$$\begin{aligned} 3 A''=\Omega e^{2A} \end{aligned}$$
(6)

where \(\Omega \) represents the effective cosmological constant induced on the brane.

Although \(\Lambda < 0\) (AdS bulk), \(\Omega \) can be both positive and negative (\(\Omega <0\) for AdS and \(\Omega >0\) for DS space-times, respectively).

3 de Sitter Brane

When \(\Omega >0\) the solution of Eqs. (5) and (6) gives the generalized warp factor as

$$\begin{aligned} e^{-A}=\omega \mathrm{sinh}\left( \mathrm{ln}\frac{c_2}{\omega }-kr_c |\phi |\right) , \end{aligned}$$
(7)

where \(\omega =\frac{\Omega }{3k^2}\) and \(c_2=1+\sqrt{1+\omega ^2}\).

On equating the ratio of the Higgs mass and the Planck mass to the warp factor at the visible brane,

$$\begin{aligned} \frac{m}{m_0}=10^{-16}=e^{-A}=\omega \mathrm{sinh}\left( \mathrm{ln}\frac{c_2}{\omega }-kr_c \pi \right) , \end{aligned}$$
(8)

one obtains

$$\begin{aligned} e^{-kr_c \pi }=\frac{10^{-16}}{c_2}\left[ 1 + \sqrt{1+\omega ^2 10^{32}}\right] . \end{aligned}$$
(9)

It is important to note here that \(e^{-kr_c \pi }\) assumes a definite solution for every value of \(\omega \). The value of the present day cosmological constant \(\Omega \sim 10^{-124}\) (in Planck units) yields \(kr_c \pi \sim 16 \mathrm{ln } 10\), which in turn produces the required warping of the Higgs mass on the visible brane as in the RS scenario.

4 Anti-de Sitter Brane

When \(\Omega < 0\) the solution of Eqs. (5) and (6) yields the generalized warp factor

$$\begin{aligned} e^{-A}=\omega \mathrm{cosh}\left( \mathrm{ln}\frac{\omega }{c_1}+kr_c |\phi |\right) , \end{aligned}$$
(10)

where \(\omega =-\frac{\Omega }{3k^2}\) and \(c_1=1+\sqrt{1-\omega ^2}\).

Once again to solve the gauge hierarchy problem, the ratio of the Higgs mass m to the Planck mass \(m_0\) at the visible brane, i.e., \(\phi =\pi \), yields

$$\begin{aligned} \frac{m}{m_0}=10^{-16}=e^{-A}=\omega \mathrm{cosh}\left( \mathrm{ln}\frac{\omega }{c_1}+kr_c \pi \right) , \end{aligned}$$
(11)

which implies that

$$\begin{aligned} e^{-kr_c \pi }=\frac{10^{-16}}{c_1}\left[ 1 \pm \sqrt{1-\omega ^2 10^{32}}\right] . \end{aligned}$$
(12)

This leads to \(\omega ^2 \le 10^{-32}\), thereby establishing a constraint on the upper limit of \(\omega \). It is quite clear from Eq. (9) that \(e^{-kr_c \pi }\) has two solutions for every allowed value of \(\omega \) except for \(\omega ^2 = 10^{-32}\), and both values give rise to the necessary warping.

Thus the generalized RS scenario [33] incorporates the effects of the brane cosmological constant on the warp factor and also successfully addresses the gauge hierarchy problem such that the Higgs mass on the visible brane is appropriately warped to the TeV scale. The fact that the cosmological constant can assume such small values and yet address the hierarchy issue implies that the gauge hierarchy problem and the cosmological fine tuning problem are interlinked.

5 Modulus potential in a curved brane scenario

In the generalized RS scenario [33], \(r_c\) represents the distance between the two branes. However, \(r_c\) is assumed to have a stable non-zero value in both cases. The mechanism of generating this stable value is not addressed in this model. Hence, the next step would be to treat the distance between the two branes as a 4-dimensional field, the so called radion field or the modular field, T(x), whose vacuum expectation value would be \(r_c\). An appropriate mechanism is now required to stabilize the modulus to its vacuum expectation value by generating a potential term for the modulus in the effective 4-dimensional Lagrangian. Goldberger and Wise [32] introduced a bulk scalar field in the RS [14, 15] Lagrangian, which in turn generated a 4-dimensional potential for \(r_c\). The parameters of this potential are dependent on the newly introduced terms in the action and could be adjusted such that the minimum of the potential settles at the value of \(r_c\) to generate the required warping. Goldberger and Wise [32], in their analysis assumed flat 3-branes as in the original RS [14, 15] scenario and neglected any possible back-reaction of the stabilizing bulk scalar on the background metric. Motivated by the non-flat warped geometry scenario [33], as discussed in the previous section, we now explore the possibility of stabilizing the modulus \(r_c\), without invoking any external scalar field. In this work, we investigate the stability of the radion field from a modular potential which may be generated due to the non-flat character of the 3-branes at the orbifold boundaries.

The metric ansatz we consider is the following:

$$\begin{aligned} {\mathrm{d}s}^2=e^{-2A(x_\mu ,\phi )}g_{\mu \nu } {\mathrm{d}x}^{\mu }{\mathrm{d}x}^{\nu } + T(x)^2 {\mathrm{d}\phi }^2, \end{aligned}$$
(13)

which satisfies the Einstein equations obtained from the action

$$\begin{aligned}&S=S_{\mathrm{gravity}}+S_{\mathrm{vis}}+S_{\mathrm{hid}}\end{aligned}$$
(14)
$$\begin{aligned}&S_{\mathrm{gravity}}=\int _{-\infty } ^{\infty } \mathrm{d}^4x \int _{-\pi } ^{\pi } \mathrm{d}\phi \sqrt{-G}(2M^3 R - \Lambda ),\end{aligned}$$
(15)
$$\begin{aligned}&S_{\mathrm{vis}}=\int _{-\infty }^{\infty } \mathrm{d}^4x \sqrt{-g_{\mathrm{vis}}} (L_{\mathrm{vis}} -V_{\mathrm{vis}}) ,\end{aligned}$$
(16)
$$\begin{aligned}&S_{\mathrm{hid}}=\int _{-\infty }^{\infty } \mathrm{d}^4x \sqrt{-g_{\mathrm{hid}}}(L_{\mathrm{hid}} -V_{\mathrm{hid}}). \end{aligned}$$
(17)

5.1 Case A: de Sitter 3-branes

In this section we consider de Sitter 3-branes for which the generalized warp factor is given by

$$\begin{aligned} e^{-A}=\omega \mathrm{sinh}\left( \mathrm{ln} \frac{c_2}{\omega } - k|\phi |T(x)\right) . \end{aligned}$$
(18)

Considering the above form of the warp factor, the first term of Eq. (15) becomes

$$\begin{aligned} S_{\mathrm{gravity}}^{(1)}= & {} -2M^3\int \mathrm{d}^4x \int _{-\pi }^{\pi } \mathrm{d}\phi ~ \sqrt{-g} e^{-2A} \left[ T(x)~ {^4}R \right. \\&+\;8k^2e^{-2A} T(x) +12k^2e^{-2A} T(x)\mathrm{coth}^2 \\&\times \;\left( \mathrm{ln} \frac{c_2}{\omega }-kT(x)|\phi |\right) \\&+\;6k|\phi | T(x),^\alpha T(x),_\alpha \mathrm{coth}\left( \mathrm{ln} \frac{c_2}{\omega } - kT(x)|\phi |\right) \\&-\;6k^2|\phi |^2 T(x) T(x),^{\alpha }T(x),_{\alpha }\mathrm{coth}^2 \\&\left. \times \;\left( \mathrm{ln} \frac{c_2}{\omega } - kT(x)|\phi |\right) \right] , \end{aligned}$$

while the second term gives

$$\begin{aligned} S_{\mathrm{gravity}}^{(2)}= -\int \mathrm{d}^4 x \int _{-\pi }^{\pi } e^{-4A} \sqrt{-g} ~ \Lambda . \end{aligned}$$
(19)

The effective action, which is obtained by integrating over the higher dimension, is

$$\begin{aligned} ^4S = \int \mathrm{d}^4 x (^4S_{(1)} +^4S_{(2)} +^4S_{(3)}) \end{aligned}$$
(20)

where

$$\begin{aligned} ^4 S_{(1)}= & {} -2M^3 \int \mathrm{d}^4 x \sqrt{-g} ^4R\left[ \frac{c_2 ^2}{4k}+\frac{\omega ^2}{k}\mathrm{ln}\frac{\Phi }{f} \right. \nonumber \\&\left. +\;\frac{\omega ^4}{4 k c_2^2}\frac{f^2}{\Phi ^2}-\frac{\omega ^4}{4kc_2^2}-\frac{c_2 ^2\Phi ^2}{4kf^2}\right] \end{aligned}$$
(21)
$$\begin{aligned} ^4 S_{(2)}= & {} \int \mathrm{d}^4 x \sqrt{-g} \left[ \phantom {\frac{\partial ^\mu \Phi \partial ^\mu \Phi }{\Phi ^ 4}}- \frac{1}{2}\partial _\mu \Phi \partial ^\mu \Phi - 4 \frac{M^3}{k}\omega ^2 \right. \nonumber \\&\left. \times \;\left( \frac{1}{\Phi ^2}\mathrm{ln}\frac{\Phi }{f}\right) \partial _\mu \Phi \partial ^\mu \Phi + \frac{3M^3}{k}\frac{\omega ^4}{c_2 ^2}f^2 \frac{\partial ^\mu \Phi \partial ^\mu \Phi }{\Phi ^ 4}\right] \end{aligned}$$
(22)
$$\begin{aligned} ^4 S_{3}= & {} -2M^3 \int \mathrm{d}^4 x \sqrt{-g} [V(\Phi )]. \end{aligned}$$
(23)

Here, \(\Phi = fe^{-kT(x)\pi }\) and \(f=\sqrt{\frac{6M^3c_1^2}{k}}\). \(^4 S_{(1)}\) is the contribution to the effective action from pure gravity and gravity coupled with the modular field T(x). \(^4 S_{(2)}\) is the kinetic term of the effective action and \(^4 S_{(3)}\) is the contribution to the effective action purely from the modulus, which in turn generates the modular potential.

The modular potential \(V(\Phi )\) is given by

$$\begin{aligned} V(\Phi )= & {} \left[ 6k\omega ^4 \mathrm{ln} \frac{\Phi }{f} -3k\omega ^4 +2k\frac{\omega ^6}{c_2 ^2}\frac{f^2}{\Phi ^2}+2k\omega ^2 c_2 ^2 -\frac{1}{2}k\frac{\omega ^8}{c_2 ^4} \right. \nonumber \\&-\;\frac{1}{2}kc_2 ^4 \frac{\Phi ^4}{f^4}-3k\omega ^4\left( \frac{\omega ^2}{c_2 ^2 - \omega ^2}+\frac{c_2 ^2 \Phi ^2}{ \omega ^2 f^2-c_2 ^2 \Phi ^2 +}\right) \nonumber \\&+\;\frac{2k \omega ^6}{ c_2 ^2-\omega ^2}\left( \frac{\omega ^2}{c_2^2}+\frac{c_2^2}{\omega ^2}\right) +\frac{2kc_2 ^2 \omega ^4 \Phi ^2}{ \omega ^2 f^2-c_2 ^2 \Phi ^2} \nonumber \\&\times \;\left( \frac{\omega ^2 f^2}{c_2 ^2 \Phi ^2} + \frac{c_2 ^2 \Phi ^2}{\omega ^2 f^2}\right) -\frac{1}{2}\frac{k \omega ^6}{c_2 ^2-\omega ^2}\left( \frac{\omega ^4}{c_2 ^4}+\frac{c_2 ^4}{\omega ^4}\right) \nonumber \\&\left. -\;\frac{1}{2}\frac{k c_2 ^2 \omega ^4 \Phi ^2}{\omega ^2 f^2-c_2 ^2 \Phi ^2}\left( \frac{\omega ^4 f^4}{c_2 ^4\Phi ^4}+\frac{c_2^4\Phi ^4}{\omega ^4 f^4}\right) \right] . \end{aligned}$$
(24)

It may be seen that in the limit \(\omega \rightarrow 0\), we retrieve the gravity-radion action as derived in Goldberger and Wise [37]. Clearly, the presence of \(\omega \) generates a potential term for the modular field \(\Phi \).

Fig. 1
figure 1

Modular potential for the DS brane for \(\omega =10^{-5}\)

Full size image
Fig. 2
figure 2

First derivative of the modular potential for the DS brane for \(\omega =10^{-5}\)

Full size image

To obtain the minimum of the potential, we find that its first derivative with respect to \(\frac{\Phi }{f}\) is

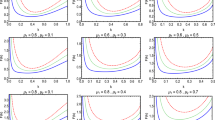
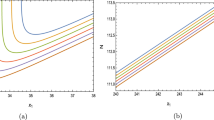
$$\begin{aligned} \frac{\mathrm{d}V(\Phi /f)}{\mathrm{d}(\Phi /f)}=6M^3k\omega ^2 c_2 ^2\left[ \frac{\omega ^4 f^3}{c_2 ^4 \Phi ^3} +\frac{\Phi }{f}-\frac{2\omega ^2 f}{c_2^2 \Phi }\right] . \end{aligned}$$
(25)

From Eq. (28) it is clear that the first derivative of the potential vanishes when \(\frac{\Phi }{f} \rightarrow \frac{\omega }{c_2}\). The potential and its first derivative for \(\omega =10^{-5}\) are illustrated in Figs. 1 and 2, respectively.

From Figs. 1 and 2 it is evident that the potential attains a metastable minimum, \(\frac{\Phi }{f}=e^{-kT(x)\pi }\rightarrow \frac{\omega }{c_2}\). One should note that, from the form of the warp factor given in Eq. (18), \(\frac{\Phi }{f}< \frac{\omega }{c_2}\) is not possible. Hence, we consider \(\frac{\Phi }{f}=\frac{\omega }{c_2}+\epsilon \) where \(\epsilon<<\frac{\omega }{c_2}\). Using this in Eq. (18) and neglecting higher order terms for \(\epsilon \) we obtain \(e^{-A} \simeq c_2 \epsilon \). Adjusting the value of \(\epsilon \sim 10^{-16}\) we find that a proper resolution to the gauge hierarchy problem can be achieved.

5.2 Case B: Anti-de Sitter 3 brane

Here, we assume that the 3-branes are AdS branes. In such a scenario, the generalized warp factor is given by

$$\begin{aligned} e^{-A}=\omega \mathrm{cosh}\left( \mathrm{ln} \frac{\omega }{c_1} + k|\phi |T(x)\right) . \end{aligned}$$
(26)

Under such circumstances

$$\begin{aligned} S_{\mathrm{gravity}}^{(1)}= & {} -2M^3\int \mathrm{d}^4x \int _{-\pi }^{\pi } \mathrm{d}\phi ~ \sqrt{-g} e^{-2A} \Biggl [T(x)~ {^4}R \\&+\;8k^2e^{-2A} T(x) +12k^2e^{-2A} T(x)\mathrm{tanh}^2 \\&\times \;\left( \mathrm{ln} \frac{\omega }{c_1}+kT(x)|\phi |\right) -6k|\phi | T(x),^\alpha T(x),_\alpha \\&\times \;\mathrm{tanh}\left( \mathrm{ln} \frac{\omega }{c_1} + kT(x)|\phi |\right) \\&-6k^2|\phi |^2 T(x) T(x),^{\alpha }T(x),_{\alpha }) \\&\times \;\mathrm{tanh}^2\left( \mathrm{ln} \frac{\omega }{c_1} + kT(x)|\phi |\right) \Biggr ] \end{aligned}$$

and

$$\begin{aligned} S_{\mathrm{gravity}}^{(2)}= -\int \mathrm{d}^4 x \int _{-\pi }^{\pi } e^{-4A} \sqrt{-g} ~ \Lambda . \end{aligned}$$
(27)

The contribution to \(S_{\mathrm{gravity}}^{(1)}\) from the brane boundaries is the same as in the RS scenario.

The effective action for the AdS branes is

$$\begin{aligned} ^4S = \int \mathrm{d}^4 x (^4S_{(1)} +^4S_{(2)} +^4S_{(3)}) \end{aligned}$$
(28)

where, defining as before, \(\Phi = fe^{-kT(x)\pi }\),

$$\begin{aligned} ^4 S_{(1)}= & {} -2M^3 \int \mathrm{d}^4 x \sqrt{-g} ^4R\left[ \frac{c_1 ^2}{4k}-\frac{\omega ^2}{k}\mathrm{ln}\frac{\Phi }{f} \right. \nonumber \\&+\left. \;\frac{\omega ^4}{4 k c_1^2}\frac{f^2}{\Phi ^2}-\frac{\omega ^4}{4kc_1^2}-\frac{c_1 ^2\Phi ^2}{4kf^2}\right] ,\end{aligned}$$
(29)
$$\begin{aligned} ^4 S_{(2)}= & {} \int \mathrm{d}^4 x \sqrt{-g} \Biggl [- \frac{1}{2}\partial _\mu \Phi \partial ^\mu \Phi + 4 \frac{M^3}{k}\omega ^2 \nonumber \\&\times \;\left( \frac{1}{\Phi ^2}\mathrm{ln}\frac{\Phi }{f}\right) \partial _\mu \Phi \partial ^\mu \Phi +\frac{3M^3}{k}\frac{\omega ^4}{c_1 ^2}f^2 \frac{\partial ^\mu \Phi \partial ^\mu \Phi }{\Phi ^ 4}\Biggr ],\end{aligned}$$
(30)
$$\begin{aligned} ^4 S_{3}= & {} -2M^3 \int \mathrm{d}^4 x \sqrt{-g} [V(\Phi )] \end{aligned}$$
(31)

where \(V(\Phi )\) is the modular potential given by

$$\begin{aligned} V(\Phi )= & {} \left[ -6k\omega ^4 ln \frac{\Phi }{f} -3k\omega ^4 -2k\frac{\omega ^6}{c_1 ^2}\frac{f^2}{\Phi ^2}-2k\omega ^2 c_1 ^2\right. \nonumber \\&-\;\frac{1}{2}k\frac{\omega ^8}{c_1 ^4}-\frac{1}{2}kc_1 ^4 \frac{\Phi ^4}{f^4}3k\omega ^4\left( \frac{\omega ^2}{c_1 ^2 + \omega ^2}+\frac{c_1 ^2 \Phi ^2}{c_1 ^2 \Phi ^2 + \omega ^2 f^2}\right) \nonumber \\&+\;\frac{2k \omega ^6}{\omega ^2 + c_1 ^2}\left( \frac{\omega ^2}{c_1 ^2}+\frac{c_1 ^2}{\omega ^2}\right) +\frac{2kc_1 ^2 \omega ^4 \Phi ^2}{c_1 ^2 \Phi ^2 + \omega ^2 f^2} \nonumber \\&\times \;\left( \frac{\omega ^2 f^2}{c_1 ^2 \Phi ^2} + \frac{c_1 ^2 \Phi ^2}{\omega ^2 f^2}\right) \frac{1}{2}\frac{k \omega ^6}{\omega ^2 + c_1 ^2}\left( \frac{\omega ^4}{c_1 ^4}+\frac{c_1 ^4}{\omega ^4}\right) \nonumber \\&\left. +\frac{1}{2}\frac{k c_1 ^2 \omega ^4 \Phi ^2}{c_1 ^2 \Phi ^2+\omega ^2 f^2}\left( \frac{\omega ^4 f^4}{c_1 ^4\Phi ^4}+\frac{c_1 ^4\Phi ^4}{\omega ^4 f^4}\right) \right] . \end{aligned}$$
(32)

To solve for the critical points of this potential, we find that its first derivative with respect to \(\frac{\Phi }{f}\) is

$$\begin{aligned} \frac{\mathrm{d}V(\Phi /f)}{\mathrm{d}(\Phi /f)}=6M^3k\omega ^2 c_1 ^2\left[ \frac{\omega ^4 f^3}{c_1 ^4 \Phi ^3} +\frac{\Phi }{f}+\frac{2\omega ^2 f}{c_1^2 \Phi }\right] \end{aligned}$$
(33)

From Eq. (33) it is clear that the first derivative of the potential has no zero crossing. The potential does not have any minimum. The potential and its first derivative for \(\omega =10^{-20}\) are shown in Figs. 3 and 4 respectively. From the aforementioned figures it is quite evident that in the scenario of AdS 3-branes, the modular potential does not have any turning points. Thus, in this situation stability cannot be attained. However, the resolution to the gauge hierarchy problem is independent of the radion field stabilization. Hence, in this scenario, the gauge hierarchy problem can be addressed as discussed in Sect. 2, although the stability of the modular field cannot be achieved.

Fig. 3
figure 3

Modular potential for the ADS brane for \(\omega =10^{-20}\)

Full size image
Fig. 4
figure 4

First derivative of the modular potential for the ADS brane for \(\omega =10^{-20}\)

Full size image

6 Summary and conclusion

In this work, we explore the possibility of stabilizing the extra dimensional modulus in the context of warped non-flat branes, without introducing any extra bulk scalar field. We show that the non-flat maximally symmetric brane automatically gives rise to a stable braneworld model when the brane cosmological constant is positive; in other words, it is de Sitter in character.

In the current work, we include the dynamics of the modular field in the context of warped geometry in a curved 3-brane scenario that naturally incorporates the effect of the brane cosmological constant on modular stability. We find that the presence of the brane cosmological constant naturally generates a potential energy term for the modulus field in the Lagrangian of the effective action and no external scalar field is required to stabilize the modulus.

We further show that if the branes are anti-de Sitter, then the radion potential which arises self-consistently due to the presence of the brane vacuum energy, does not have any turning points (Figs. 3 and 4) and hence modular stabilization cannot be achieved in such a scenario. However, the resolution to the gauge hierarchy problem which is independent of modular stabilization can always be attained. This is discussed in Sect. 3. On the other hand, if the 3-branes are de Sitter branes, then the modular potential has a metastable minimum at which the radion field is stabilized (see Figs. 1 and 2). The value of this minimum depends on the brane vacuum energy and by tuning the brane cosmological constant appropriately the gauge hierarchy problem can be resolved at the minimum of this potential. Thus, the stabilization of the modular field and the resolution to the gauge hierarchy problem in the context of non-flat 3-branes in a warped brane world scenario can all be addressed concomitantly. The fact that we live presently in a de Sitter universe with a tiny cosmological constant therefore can account for the stability of the modulus and points towards a stable braneworld description of our universe.