1 Introduction

Today’s astrophysical measurements reveal that the Universe is experiencing an accelerated expansion phase [1,2,3,4,5,6,7,8,9,10,11]. These sets of observational data have driven the quest for convincing theoretical explanations of such a phenomenon. Among the various proposed models, the most popular one is the theory of general relativity (GR) modified by a cosmological constant term \(\Lambda \), which is called “the concordance” or \(\Lambda \) CDM model [12]. In this model, it is assumed that the \(\Lambda \) term may take over the recent eras of the dynamical evolution of the Universe after domination of what is called “Dark Matter” (DM), of which the interactions are still somewhat obscure. Observational data have discovered that at least \(70\%\) of the total energy budget of the Universe is in the form of the so-called “Dark Energy” (DE), which is regarded as a cosmic medium with unusual properties attributed to cosmological constant effects. These data show that the \(\Lambda \) CDM model is in good shape [13,14,15]. In spite of its fine agreement with the observation data, there are two major concerns in this context; the first one is referred to as “the cosmological constant problem” which asks the question of the origin and the great disagreement between theoretical and expected values of the cosmological constant [16,17,18]. The other problem deals with this puzzlement of why we happen to live in a special era of evolution of cosmos where the contribution of \(\Lambda \), DM and the baryonic matter are of the same order. This is pointed out as “cosmic coincidence problem” in the literature.

These issues have motived people to seek for some other theoretical foundations or at least apply some modifications to the assumed \(\Lambda \) CDM model. In this respect, cosmological scenarios with running \(\Lambda \) have been proposed. The first developments, in this context, have been made by Shapiro et al. [19,20,21,22]. They have shown that there is no sturdy evidence to indicate that the cosmological constant is running or not. This fact encourages one to investigate cosmological scenarios within different theoretical backgrounds that admit running cosmological parameters. Up to now, different running cosmological constant models have been proposed, among which we can quote a time dependent cosmological constant motivated by quantum field theory [22,23,24], a running vacuum in the context of supergravity [25], \(\Lambda \)(t) cosmology induced by Elko fields [26], running cosmological constant via covariant/non-covariant parametrization [27] and some more [28,29,30].

In this paper we work on a particular subclass of \(f(\mathsf{R},\mathsf{T})\) gravity, in which \(\mathsf{R}\) and \(\mathsf{T}\) are the Ricci scalar and the trace of EMT, respectively. Firstly, this model was introduced by Harko et al. [31] and later has been widely investigated in [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51]. In the background of \(f(\mathsf{R},\mathsf{T})\) gravity, we have investigated a linear combination of the Ricci scalar and an arbitrary function of the trace of EMT, i.e., \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\Lambda (\mathsf{T})\). In this model, the Einstein gravity has been modified by a minimally coupled “trace-dependent” cosmological constant. One may find some efforts made to elaborate on the cosmological features of \(\Lambda (\mathsf{T})\) CDM in the literature. The idea of a running cosmological constant, \(\Lambda (\mathsf{T})\), probably dates back to the paper of Poplawski [52]. He found that \(\Lambda (\mathsf{T})\) gravity will reduce to Palatini \(f(\mathsf{R})\) gravity when the pressure of the fluid is neglected. Besides, he concluded that cosmological data are consistent with \(\Lambda (\mathsf{T})\) gravity without any knowledge about the functionality of \(\Lambda (\mathsf{T})\) parameter. In [53], Bianchi Type-V cosmological solutions have been derived.Footnote 1 The locally rotationally symmetric (LRS) Bianchi type-I cosmological models have been considered in [55]. In most work on \(\Lambda (\mathsf{T})\) gravity, the EMT is forced to be conserved. With this assumption, the authors of [37, 40] have shown that these types of models lead to an accelerated expansion era with an undesirable present value for the EoS parameter.

Up to now, cosmological consequences of the violation of the EMT conservation have not been studied properly. It may be a good idea to consider the minimally coupled part of the \(f(\mathsf{R},\mathsf{T})\) model as a running cosmological constant and inspect its cosmological solutions. As we shall see, when the conservation of EMT is allowed to be violated, it would result in a DE era which is accompanied by an observationally allowed present value for the EoS parameter. Specifically, such a model mimics a de Sitter solution. Interestingly, a similar DE solution has been reported in [56], which arises from the violation of EMT conservation. The authors of [56] have pointed out that violation of EMT conservation can be predicted by modified quantum mechanical models or by models that utilize the causal set approach to quantum gravity.Footnote 2 In our analysis, we have applied the dynamical system approach and employed a useful method to parametrize the \(\Lambda (\mathsf{T})\) function. In this method we have presented a way to determine whether or not a given model might lead to a stable late time solution.

The present paper has been organized as follows: In Sect. 2, the field equation of \(f(\mathsf{R},\mathsf{T})\) gravity has been reviewed. Besides, the relevant dimensionless parameters which will be used in the construction of subsequent equations are introduced. A discussion of the EMT conservation will be given as well. In Sect. 3, we discuss the late time solutions of the only conserved \(f(\mathsf{R},\mathsf{T})\) model. In this case, some issues have already been illustrated, however, we present some other features. Section 4 is devoted to a description of the mentioned method. In Sect. 5, we consider models in which the \(\Lambda (\mathsf{T})\) function shows a power-law behavior. These models will be investigated independently. Finally, in Sect. 6 we summarize our results.

2 Field equations of \(f(\mathsf{R},\mathsf{T})\) gravity

In this section, we present the field equations of \(f(\mathsf{R},\mathsf{T})\) modified gravity (MG) and discuss the conservation of EMT. We assume that a pressure-less fluid (DM along with baryonic matter) and ultra-relativistic matter are present. The action of \(f(\mathsf{R},\mathsf{T})\) gravity can then be written as

$$\begin{aligned} S=\int \sqrt{-g} \mathrm{d}^{4} x \left[ \frac{1}{2\kappa ^{2}} f\left( \mathsf{R}, \mathsf{T}^{\text {(p, u)}}\right) +\mathsf{L}^{\text {(total)}} \right] , \end{aligned}$$
(1)

where we have defined the Lagrangian of the total matter as

$$\begin{aligned} \mathsf{L}^{\text {(total)}}\equiv \mathsf{L}^{\text {(p)}}+\mathsf{L}^{\text {(u)}}. \end{aligned}$$
(2)

In the above definitions, we have used \(\mathsf{R}\) and \(\mathsf{T}^{\text {(p, u)}}\equiv g^{\mu \nu } \mathsf{T}^{\text {(p, u)}}_{\mu \nu }\) as the Ricci curvature scalar and the trace of EMT of pressure-less and ultra-relativistic fluids (for which we get these matters as the total matter content of the Universe), respectively. The letters “\(\mathrm{p}\)” and “\(\mathrm{u}\)” indicate the pressure-less and ultra-relativistic fluids and g is the determinant of the metric, \(\kappa ^{2}\equiv 8 \pi G\) is the gravitational coupling constant, and we set \(c=1\). Since the ultra-relativistic fluid has a traceless EMT i.e., \(\mathsf{T}^{(\mathrm{u})}=0\), we have \(\mathsf{T}^{\text {(p, u)}}=\mathsf{T}^{\text {(p)}}+\mathsf{T}^{\text {(u)}}=\mathsf{T}^{\text {(p)}}\equiv \mathsf{T}\). Hereupon, we will drop the letter “p” from the trace of the pressure-less matter for simplicity.Footnote 3 The EMT \(\mathsf{T}_{\mu \nu }^{\text {(p, u)}}\) is defined as the Euler–Lagrange expression of the Lagrangian of the total matter, i.e.,

$$\begin{aligned} \mathsf{T}_{\mu \nu }^{\text {(p, u)}}\equiv -\frac{2}{\sqrt{-g}} \frac{\delta \left[ \sqrt{-g}(\mathsf{L}^{\text {(p)}}+\mathsf{L}^{\text {(u)}}) \right] }{\delta g^{\mu \nu }}. \end{aligned}$$
(3)

The field equations for \(f(\mathsf{R},\mathsf{T})\) gravity can be obtained [31]:

$$\begin{aligned}&F(\mathsf{R},\mathsf{T}) \mathsf{R}_{\mu \nu }-\frac{1}{2} f(\mathsf{R},\mathsf{T}) g_{\mu \nu }+\Big ( g_{\mu \nu } \square -\triangledown _{\mu } \triangledown _{\nu }\Big )F(\mathsf{R},\mathsf{T})\nonumber \\&\quad =\Big (8\pi G-{\mathcal F}(\mathsf{R},\mathsf{T})\Big )\mathsf{T}_{\mu \nu }^{\text {(p, u)}}-\mathcal {F}(\mathsf{R},\mathsf{T})\mathbf {\Theta _{\mu \nu }^{\text {(p, u)}}}, \end{aligned}$$
(4)

where

$$\begin{aligned} \mathbf {\Theta _{\mu \nu }^{\text {(p, u)}}}\equiv g^{\alpha \beta }\frac{\delta \mathsf{T}_{\alpha \beta }^{\text {(p, u)}}}{\delta g^{\mu \nu }}, \end{aligned}$$
(5)

and for the sake of convenience, we have defined the following functions as derivatives with respect to the trace \(\mathsf{T}\) and the Ricci curvature scalar \(\mathsf{R}\):

$$\begin{aligned} {\mathcal F}(\mathsf{R},\mathsf{T}) \equiv \frac{\partial f(\mathsf{R},\mathsf{T})}{\partial \mathsf{T}}\quad \text{ and }\quad F(\mathsf{R},\mathsf{T}) \equiv \frac{\partial f(\mathsf{R},\mathsf{T})}{\partial \mathsf{R}}. \end{aligned}$$
(6)

We consider a spatially flat, homogeneous and isotropic Universe, which is described by the Friedmann–Lemaître–Robertson–Walker (FLRW) metric:

$$\begin{aligned} \mathrm{d}s^{2}=-\mathrm{d}t^{2}+a^{2}(t) \left( \mathrm{d}r^{2}+r^{2}\mathrm{d}\Omega ^2\right) , \end{aligned}$$
(7)

where a(t) denotes the scale factor of the Universe. Therefore, the field equation (4), by assuming the metric (7), leads to

$$\begin{aligned}&3H^{2}F(\mathsf{R},\mathsf{T})+\frac{1}{2} \left( f(\mathsf{R},\mathsf{T})-F(\mathsf{R},\mathsf{T})\mathsf{R}\right) +3\dot{F}(\mathsf{R},\mathsf{T})H\nonumber \\&\quad =\left( 8 \pi G +{\mathcal F} (\mathsf{R},\mathsf{T})\right) \rho ^{\text {(p)}}+8 \pi G\rho ^{\text {(u)}}, \end{aligned}$$
(8)

as the modified Friedmann equation, and

$$\begin{aligned}&2F(\mathsf{R},\mathsf{T}) \dot{H}+\ddot{F} (\mathsf{R},\mathsf{T})-\dot{F} (\mathsf{R},\mathsf{T}) H\nonumber \\&\quad =-\left( 8 \pi G+{\mathcal F} (\mathsf{R},\mathsf{T})\right) \rho ^{\text {(p)}}-\frac{32}{3} \pi G\rho ^{\text {(u)}}, \end{aligned}$$
(9)

as the modified Raychaudhuri equation. In Eqs. (8) and (9), H indicates the Hubble parameter. Hereafter, we work on the Lagrangians which include minimal coupling between the trace of EMT and the Ricci scalar, i.e.,

$$\begin{aligned} f(\mathsf{R},\mathsf{T})=g(\mathsf{R})+\beta \Lambda (-\mathsf{T}), \end{aligned}$$
(10)

where \(\beta \) can control the strength of the coupling. Since, for the pressure-less matter we have \(\mathsf{T}^\mathrm{{(p)}}=-\rho ^\mathrm{{(p)}}\), in order to avoid ambiguity due to the negative sign, we work hereafter with the \(\Lambda (-\mathsf{T})\) function. In fact, to guarantee that \(\Lambda (\mathsf{T})\) is always a real-valued function, we consider \(\Lambda (-\mathsf{T})\) instead. For this class of \(f(\mathsf{R},\mathsf{T})\) models we have \(\mathcal {F}(\mathsf{R}, \mathsf{T})=-\beta \Lambda '(-\mathsf{T})\) Footnote 4 and \(F(\mathsf{R}, \mathsf{T})=g'(\mathsf{R})\). The field equations (8) and (9) can then be rewritten as

$$\begin{aligned}&1+\frac{g}{6H^{2} g'} +\beta \frac{\Lambda }{6 H^{2} g'}-\frac{\mathsf{R}}{6 H^{2}} + \frac{\dot{g'}}{H g'}\nonumber \\&\quad = \frac{8 \pi G \rho ^{\text {(p)}}}{3H^{2} g'}-\beta \frac{\Lambda ' \rho ^{\text {(p)}}}{3H^{2} g'}+\frac{8 \pi G \rho ^{\text {(u)}}}{3H^{2} g'} \end{aligned}$$
(11)

and

$$\begin{aligned}&2\frac{\dot{H}}{H^{2}}+\frac{\ddot{g'}}{H^{2} g'} -\frac{\dot{g'}}{H g'}\nonumber \\&\quad = -\frac{8\pi G \rho ^{\text {(p)}}}{H^{2} g'}+\beta \frac{\Lambda ' \rho ^{\text {(p)}}}{H^{2} g'} -\frac{32\pi G \rho ^{\text {(u)}}}{3H^{2} g'}, \end{aligned}$$
(12)

where the arguments have been dropped for convenience. In order to construct the dynamical system for the field equations (11) and (12), it is helpful to define a few dimensionless variables and parameters by

$$\begin{aligned}&x_{1}\equiv -\frac{\dot{g}(\mathsf{R})}{H g(\mathsf{R})},\end{aligned}$$
(13)
$$\begin{aligned}&x_{2}\equiv -\frac{g(\mathsf{R})}{6 H^{2} g'(\mathsf{R})},\end{aligned}$$
(14)
$$\begin{aligned}&x_{3}\equiv \frac{\mathsf{R}}{6 H^{2}}=\frac{\dot{H}}{H^{2}}+2,\end{aligned}$$
(15)
$$\begin{aligned}&x_{4}\equiv \frac{\kappa ^{2} \Lambda (-\mathsf{T})}{3H^{2} g(\mathsf{R})},\end{aligned}$$
(16)
$$\begin{aligned}&x_{5}\equiv -\frac{\kappa ^{2}\mathsf{T} \Lambda '(-\mathsf{T})}{3H^{2} g(\mathsf{R})},\end{aligned}$$
(17)
$$\begin{aligned}&\Omega ^{\text {(u)}}\equiv \frac{\kappa ^{2} \rho ^{\text {(rad)}}}{3 H^{2} g(\mathsf{R})},\end{aligned}$$
(18)
$$\begin{aligned}&\Omega ^{\text {(p)}}\equiv \frac{\kappa ^{2} \rho ^{\text {(p)}}}{3 H^{2} g(\mathsf{R})}, \end{aligned}$$
(19)

where we have used Ricci scalar, \(\mathsf{R}=6(\dot{H}+2H^2)\) for metric (7), within the definition of (15). Moreover, we use the following definitions:

$$\begin{aligned} n\equiv & {} -\frac{\mathsf{T} \Lambda ''(-\mathsf{T})}{\Lambda ' (-\mathsf{T})},\end{aligned}$$
(20)
$$\begin{aligned} s\equiv & {} -\frac{\mathsf{T}\Lambda '(-\mathsf{T})}{\Lambda (-\mathsf{T})}=\frac{x_{5}}{x_{4}}. \end{aligned}$$
(21)

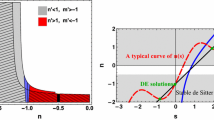
In general, eliminating \(\mathsf{T}\) from (20) and (21) yields \(n=n(s)\). Describing the models with \(n=n(s)\) instead of \(\Lambda (-\mathsf{T})\), can be suitable in dynamical system analysis. In the following subsections we discuss the consequences of conservation/non-conservation of EMT, which in turn, results in a key equation that helps us to study the dynamical evolution of the models. We classify minimally coupled models as those that respect EMT conservation and those that do not.

2.1 Models which obey the conservation of EMT

In this subsection, we present the results that come from considering the EMT conservation. If we apply the Bianchi identity to the field Eq. (4) and assume that the conservation of EMT holds for pressure-less and ultra-relativistic fluids, independently, we get

$$\begin{aligned}&\dot{\rho }^{(\text {p})}+3H\rho ^{(\text {p})}=0,\end{aligned}$$
(22)
$$\begin{aligned}&\dot{\rho }^{(\text {u})}+4H\rho ^{(\text {u})}=0. \end{aligned}$$
(23)

We then find the following constraint for the pressure-less fluidFootnote 5:

$$\begin{aligned} \dot{h}'=\frac{3}{2}Hh'. \end{aligned}$$
(24)

After straightforward but lengthy algebra, we arrive at a specific form for \(\Lambda (-\mathsf{T})\), as follows:

$$\begin{aligned} \Lambda (-\mathsf{T})=C_{1}\sqrt{-\mathsf{T}}+C_{2}, \end{aligned}$$
(25)

where \(C_{1}\) and \(C_{2}\) are constants of integration. It means that solution (25) is the only subclass of \(f(\mathsf{R},\mathsf{T})\) theories of gravity with minimal coupling that respect the conservation of EMT. For this solution we obtain \(x_{5}=x_{4}/2\), which reduces the space constructed from the variables of the theory.

2.2 Models which violate the conservation of EMT

These models do not generally respect conservation laws (22) and (23). Applying the Bianchi identity to the field Eq. (4) leads to the following equation between the function \(\mathcal {F}(\mathsf{R},\mathsf{T})\), the EMT and its trace:

$$\begin{aligned}&\kappa ^{2}\bigtriangledown ^{\mu }\mathsf{T}^\mathrm{(u)}_{\mu \nu }+(\kappa ^{2} +\mathcal {F}^\mathrm{(p)})\bigtriangledown ^{\mu }\mathsf{T}^\mathrm{(p)}_{\mu \nu }+\frac{1}{2}\mathcal {F}^\mathrm{(p)}\bigtriangledown _{\mu }\mathsf{T}^\mathrm{(p)}\nonumber \\&\quad +\mathsf{T}^\mathrm{(p)}_{\mu \nu }\bigtriangledown ^{\mu }\mathcal {F}^\mathrm{(p)}-\nabla _{\nu }(p^\mathrm{(p)}\mathcal {F}^\mathrm{(p)})=0, \end{aligned}$$
(26)

where the argument of \(\mathcal {F}(\mathsf{R},\mathsf{T})\) has been dropped for abbreviation. Notice that in the above equation, we have used \(\mathcal {F}^\mathrm{(p)}\) in the corresponding terms of pressure-less fluid, since only \(\mathsf{T}^{\mathrm{(p)}}\) would appear in the argument of \(\mathcal {F}(\mathsf{R},\mathsf{T})\); we further note that the function \(\mathcal {F}\) and its derivative are zero for the ultra-relativistic fluids. Equation (26) has a specific form such that we can consider the evolution of two fluids separately, i.e., we can write

$$\begin{aligned}&(\kappa ^{2}+\mathcal {F})\bigtriangledown ^{\mu }\mathsf{T}^\mathrm{(p)}_{\mu \nu }+ \frac{1}{2}\mathcal {F}^\mathrm{(p)}\bigtriangledown _{\mu }\mathsf{T}^\mathrm{(p)}+\mathsf{T}^\mathrm{(p)}_{\mu \nu }\bigtriangledown ^{\mu }\mathcal {F}^\mathrm{(p)}=0,\end{aligned}$$
(27)
$$\begin{aligned}&\bigtriangledown ^{\mu }\mathsf{T}^{\mathrm{(u)}}_{\mu \nu }=0, \end{aligned}$$
(28)

where \(p^\mathrm{(p)}=0\) has been used. From Eq. (28) we can deduce that in the minimal form of \(f(\mathsf{R},\mathsf{T})\) gravity, the conservation of EMT for ultra-relativistic fluid, i.e., Eq. (23) can be always assumed, at least, as long as mutual interactions are not taken into account. Therefore, regarding the choice (10) for \(f(\mathsf{R},\mathsf{T})\) function, we can rewrite Eq. (27) as

$$\begin{aligned} \left( \kappa ^{2} -\frac{3\beta }{2}\Lambda '+\beta \Lambda ''\mathsf{T}\right) \dot{\mathsf{T}}+3H\mathsf{T}\left( \kappa ^{2} -\beta \Lambda '\right) =0, \end{aligned}$$
(29)

where we have used \(\rho ^\mathrm{(p)}=-\mathsf{T}\). Once the function \(\Lambda (-\mathsf{T})\) is determined, the dependency of \(-\mathsf{T}\) and thus \(\rho ^{(\mathrm{p})}\) on the scale factor can be calculated. More precisely, Eq. (29) can be simplified as

$$\begin{aligned} \int _{\mathsf{T}_{0}}^{-\mathsf{T}} \frac{\kappa ^{2}-\frac{3\beta }{2}\Lambda '+ \beta \Lambda ''\mathsf{T}}{\mathsf{T}\left( \kappa ^{2} -\beta \Lambda '\right) }\mathrm{d}T=-3\int _{a_{0}}^{a} \mathrm{d}(\ln a), \end{aligned}$$
(30)

where \(\mathsf{T}_{0}\) and \(a_{0}\) denote the present values for the scale factor and EMT trace. Note that, in general, the integral on the left hand side of Eq. (30) may not be simply solved. Moreover, after the integration process, it may not be possible to clearly write the density as a function of scale factor. Let us choose the functionality of \(\Lambda \) parameter as \(\Lambda (-\mathsf{T})=\chi ^{2} (-\mathsf{T})^{\alpha }\), whence we obtain

$$\begin{aligned} \left[ \frac{\left( \rho -\alpha \beta \rho ^{\alpha }\right) ^{2 \alpha -1}}{\rho }\right] ^{\frac{1}{2 (\alpha -1)}}=Ca^{-3}, \end{aligned}$$
(31)

where C is a constant of integration. In this case, for later application, let us rewrite Eq. (29) in terms of the pressure-less fluid density in the following form:

$$\begin{aligned} \dot{\rho }^\mathrm{{(p)}}=-3H\frac{1 -\alpha \beta {\rho ^\mathrm{{(p)}}} ^{\alpha -1}}{1-\alpha \left( \alpha +\frac{1}{2}\right) \beta {\rho ^\mathrm{{(p)}}}^{\alpha -1}}\rho ^\mathrm{{(p)}}, \end{aligned}$$
(32)

or correspondingly, eliminating time gives

$$\begin{aligned}&\left[ 1-\alpha \left( \alpha +\frac{1}{2}\right) \beta {\rho ^\mathrm{{(p)}}}^{\alpha -1}\right] \frac{\mathrm{d}\rho ^\mathrm{{(p)}}(a)}{da}\nonumber \\&\quad +3\left( 1-\alpha \beta {\rho ^\mathrm{{(p)}}} ^{\alpha -1}\right) \frac{\rho ^\mathrm{{(p)}}(a)}{a}=0. \end{aligned}$$
(33)

In Sect. 3 we present an overview of the cosmological implications of the only conserved models, i.e., the models with \(\Lambda (-\mathsf{T})=\kappa ^{2}\sqrt{-\mathsf{T}}\). The dynamical system representation of this case has been considered in [40]. However, in this section we review the corresponding cosmological consequences of this case to complete our discussion. Moreover, we will present new details that have not been considered before. In Sect. 4 we consider cosmological behavior of models of type \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \Lambda (-\mathsf{T})\) for a general \(\Lambda (-\mathsf{T})\) function via the dynamical system approach. We will see that relaxing the EMT conservation which gives Eq. (29), leads to some interesting features; DE solutions will be achieved. In Sect. 5 we study the models with \(\Lambda (-\mathsf{T})=\chi ^{2} (-\mathsf{T})^{\alpha }\) when the EMT conservation has not been considered. Among non-conserved models there are two special cases that the equivalent dynamical system cannot be constructed properly. More precisely, as we will see the process of recasting the field equations into equivalent dynamical system would breaks down for cases with \(\alpha =1\) and \(\alpha =-1/2\). In Sects. 5.1 and 5.2 we will consider these cases algebraically.

3 Conserved \(\Lambda (\mathsf{T}) \mathsf{CDM}\) model in phase space

In this section we present a brief review on the cosmological solutions of the only case that respect the EMT conservation. The EMT conservation leads to the constraint Eq. (24) which gives Eq. (25) for \(\Lambda \) parameter, as the only solution. To illustrate late time effects of the extra term \(\sqrt{-\mathsf{T}}\), we put aside the ultra-relativistic fluid. Therefore, field equations (8) and (9) for the model \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \kappa ^{2}\sqrt{-\mathsf{T}}\) will take the following form:

$$\begin{aligned} 3H^{2}= & {} \kappa ^{2}\left( \rho ^\mathrm{{(p)}} -\beta {\rho ^\mathrm{{(p)}}}^{\frac{1}{2}}\right) ,\end{aligned}$$
(34)
$$\begin{aligned} 2\dot{H}= & {} \kappa ^{2}\left( -\rho ^\mathrm{{(p)}} +\frac{\beta }{2}{\rho ^\mathrm{{(p)}}}^{\frac{1}{2}}\right) . \end{aligned}$$
(35)

The energy conservation yields solution (22) for which the solution is given by \(\rho ^\mathrm{{(p)}}=\rho ^\mathrm{{(p)}}_{0}a^{-3}\), where we have set \(\rho ^\mathrm{{(p)}}(a=1)\equiv \rho ^\mathrm{{(p)}}_{0}\). We can check that differentiating Eq. (34) with respect to time together with using \(\dot{\rho }^\mathrm{{(p)}}=-3H\rho ^\mathrm{{(p)}}\) gives Eq. (35). This means that solutions of equation (34) would satisfy Eq. (35). Equation (34) can then be solved to give

$$\begin{aligned} a_{\alpha =\frac{1}{2}}(t)=\left( \frac{3 }{256}\right) ^{1/3}\left[ \sqrt{\Omega _{0}^\mathrm{{(p)}}}H_0 t \left( 8 \sqrt{3}-3 \beta t\right) \right] ^{2/3}, \end{aligned}$$
(36)

where we have set \(\kappa ^{2}=1\) and \(a(t=0)=0\). We can also check that solution (36) reduces to the standard matter dominated era solution for \(\beta =0\) and \(\Omega _{0}^\mathrm{{(p)}}=1\). From solution (36), the age of Universe can be calculated as

$$\begin{aligned} t_{0}^\mathrm{{(\pm )}}=\frac{4 }{\sqrt{3} \beta }\left[ 1\pm \left( 1-\frac{\beta }{\sqrt{3\Omega _{0}^\mathrm{{(p)}}}H_0} \right) ^{\frac{1}{2}}\right] , \end{aligned}$$
(37)

where \(t_{0}^\mathrm{{(+)}}\) shows the solution with positive sign and \(t_{0}^\mathrm{{(-)}}\) the solution with negative sign between the two terms in brackets. We suppose that \(\beta =b H_{0}\) where b is a constant, therefore we have

$$\begin{aligned} t_{0}^\mathrm{{(\pm )}}=\frac{4\times 9.8 }{\sqrt{3} b H_{0}}\left[ 1\pm \left( 1-\frac{b}{\sqrt{3\Omega _{0}^\mathrm{{(p)}}}}\right) ^{\frac{1}{2}}\right] ~~\text{ Gyear }. \end{aligned}$$
(38)

In the MG theories we can define an effective EoS parameter as \(w^\mathrm{{(eff)}}\equiv -1-2\dot{H}/3H^{2}\). For the conserved \(\Lambda (\mathsf{T}) \mathsf{CDM}\) model, using Eqs. (34) and (35) along with the solution (36) leads to the following solution for the effective EoS:

$$\begin{aligned} w^\mathrm{{(eff)}}=-\frac{1}{2}+\frac{8}{ b \text {t} \left( 3 b \text {t}-8 \sqrt{3}\right) +16}. \end{aligned}$$
(39)

As can be seen, this solution goes to zero for early times and to \(-1/2\) in the late times. Besides, we can obtain the fluid density for this case using \(\rho ^\mathrm{{(p)}}=\rho ^\mathrm{{(p)}}_{0}a^{-3}\), however, in this case the scale factor follows the form given in (36). In Fig. 1, we have drawn the related plots for cosmological parameters discussed above. The upper left plot presents the age of Universe for both positive and negative solutions obtained in (38). In this plot the orange line denotes the age of Universe for \(t_{0}^\mathrm{{(+)}}\) and the green one indicates \(t_{0}^\mathrm{{(-)}}\). We have plotted the rest of the diagrams for \(b=\pm 0.9\). For the purpose of comparison, we have employed a black line for the scale factor of the standard pressure-less fluid dominated era, i.e. \(a^{(\mathrm{sp})}\), for which \(a(t)\sim t^{2/3}\) holds.

Fig. 1
figure 1

Cosmological quantities for the model \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \kappa ^{2}\sqrt{-\mathsf{T}}\) when only pressure-less fluid is present. In the above plots we have used \(b\equiv \beta /H_{0}\). Upper left panel Two solutions for the age of Universe. Lower left panel The effective EoS parameter for \(b=-0.9\) is denoted by a red line. Upper right panel The scale factor of Universe for the same value of b (\(a^\mathrm{{sp}}\) shows the scale factor of standard matter era). Lower right panel The behavior of matter density parameter for the same value of b

Full size image

For reconstructing the dynamical system representation of Eqs. (34) and (35) we can use the dimensionless variables (16)–(19) (remember that in this case we have \(x_{5}=x_{4}\)/2). In terms of these variables we obtain

$$\begin{aligned}&\Omega ^{(\mathrm {p})}+\Omega ^{(\mathrm {u})}+\Omega ^{(\mathrm {\mathsf{DE}})}=1,\end{aligned}$$
(40)
$$\begin{aligned}&\frac{\mathrm{d} \Omega ^{(\mathrm {u})}}{\mathrm{d}t}=\Omega ^{(\mathrm {u})} \left( -\frac{3 \Omega ^{(\mathsf {DE})}}{2}+\Omega ^{(\mathrm {u})}-1\right) ,\end{aligned}$$
(41)
$$\begin{aligned}&\frac{\mathrm{d} \Omega ^{(\mathrm {\mathsf{DE}})}}{\mathrm{d}t}=\Omega ^{(\mathrm {\mathsf{DE}})}\left[ \frac{3 (1-\Omega ^{(\mathrm {\mathsf{DE}})})}{2}+\Omega ^{(\mathrm {u})}\right] , \end{aligned}$$
(42)

where we have redefined \(\Omega ^{(\mathrm {\mathsf{DE}})}\equiv -\beta x_{4}\). Note that since \(x_{4}\) is always positive [see the definition of (16)], it restricts the allowed values of \(\beta \) to negative values, in order that \(\Omega ^{(\mathrm {\mathsf{DE}})}\) stays positive. The fixed points of this dynamical system are presented in Table 1. Also, we have drawn in Fig. 2, the phase portrait of this model in the \((\Omega ^\mathrm{{(u)}},\Omega ^\mathrm{{(\mathsf{DE})}})\) plane.

Table 1 The fixed point solutions of \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \kappa ^{2}\sqrt{-\mathsf{T}}\) gravity
Full size table
Fig. 2
figure 2

Phase portrait of \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \kappa ^{2}\sqrt{-\mathsf{T}}\) gravity. The abbreviations “u-matter”, “p-matter” and “DM” have been used for specifying the ultra-relativistic, pressure-less and DE dominated eras, respectively

Full size image

4 Late time cosmological solutions of \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \Lambda (-\mathsf{T})\) gravity

In this section we investigate the late time cosmological solutions of a specific class of models of the form \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\Lambda (-\mathsf{T})\). This family of models can be interesting as they make a minor modification to GR. In fact we can interpret these types of models as a \(\Lambda (\mathsf{T})\) CDM theory, which implies a matter density dependent cosmological constant. Our aim here is to consider late time solutions only, hence we do not include the ultra-relativistic fluid. To reconstruct Eqs. (11) and (12) in terms of a closed dynamical system for \(g(\mathsf{R})=\mathsf{R}\), we use the definitions (16), (17), (20) and (21). The last two ones play the role of a (kind of) parametrizationFootnote 6 in determining the functionality of \(\Lambda (-\mathsf{T})\). This parametrization can be suitable at least for some well-defined models. Generally, eliminating the trace \(\mathsf{T}\) between the definitions (20) and (21) leaves us with a relation between the n and s parameters, which results in a function n(s). In fact, each \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \Lambda (-\mathsf{T})\) model can be specified by a function n(s). Models with constant s and n shall be considered in Sect. 5. Equations (11), (12) and (29) can be rewritten in terms of the dimensionless variables as follows:

$$\begin{aligned}&\Omega ^{(\mathrm {p})}-\beta x_{5}-\frac{\beta }{2}x_{4}=1,\end{aligned}$$
(43)
$$\begin{aligned}&\frac{2\dot{H}}{3H^{2}}=-1-\frac{\beta }{2}x_{4},\end{aligned}$$
(44)
$$\begin{aligned}&\frac{\dot{\rho }^{(\mathrm {p})}}{3H\rho ^{(\mathrm {p})}}=-\frac{1+\frac{\beta }{2}x_{4}}{1+\frac{\beta }{2}x_{4}-\beta (n+\frac{1}{2})x_{5}}. \end{aligned}$$
(45)

From the definition for effective EoS parameter and Eq. (44) we get

$$\begin{aligned} w^{(\mathrm {eff})}=\frac{\beta }{2}x_{4}. \end{aligned}$$
(46)

Using Eqs. (43)–(45) the following autonomous differential equations can be obtained:

$$\begin{aligned}&\frac{\mathrm{d}x_{4}}{\mathrm{d}N}=-3x_{5}\frac{1+\frac{\beta }{2}x_{4}}{1+\frac{\beta }{2}x_{4}- \beta \left( n+\frac{1}{2}\right) x_{5}}+3x_{4}\left( 1+\frac{\beta }{2} x_{4}\right) ,\end{aligned}$$
(47)
$$\begin{aligned}&\frac{\mathrm{d}x_{5}}{\mathrm{d}N}=-3x_{5}\left( 1+\frac{\beta }{2}x_{4}\right) \frac{n-\beta \left( \frac{x_{4}}{2}-\left( n+\frac{1}{2}\right) x_{5}\right) }{1+\frac{\beta }{2}x_{4}-\beta \left( n+\frac{1}{2}\right) x_{5}}. \end{aligned}$$
(48)

The above system admits three fixed points with the properties we have listed in Table 2.

Table 2 The fixed point solutions of \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \Lambda (-\mathsf{T})\) gravity
Full size table

Table 2 shows that its elements depend on the value of parameter n, generally. Note that the DE density parameter is defined so that the relation \(\Omega ^{(\mathrm {p})}+\Omega ^{(\mathrm {\mathsf{DE}})}=1\) holds and \(n'\equiv dn/ds\) at the fixed point. From Table 2 we observe that there is two type of DE solutions; \(P^{{(\mathsf{DE})}}_{1}\), of which the effective EoS parameter depends on n and \(P^{{(\mathsf{DE})}}_{2}\) for which \(\Omega ^{(\mathrm {p})}\) and thus \(\Omega ^{(\mathrm {\mathsf{DE}})}\) also depend on this parameter. Therefore, only some specific models can give rise to an accelerated expansion solution in the late times. Especially, to be consistent with the observational measurements, the value of n parameter can be much more confined. One of the eigenvalues of \(P^{{(\mathsf{DE})}}_{2}\) is zero, which shows that it is a non-hyperbolic critical point and its stability properties cannot be determined by linear approximation techniques. Hence, we focus on the solution characterizing the fixed point \(P^{{(\mathsf{DE})}}_{1}\).

The fixed points shown in Table 2 are solutions of the system \(\mathrm{d}x_{4}/\mathrm{d}N=0,~\mathrm{d}x_{5}/\mathrm{d}N=0\). From this fact we can conclude that, for any arbitrary function, namely, \(f(x_{4},x_{5})\) we must have \(\mathrm{d}f(x_{4},x_{5})/\mathrm{d}N=0\) at the equilibrium points. Hence, for the parameter \(s=s(x_{4},x_{5})\) we obtain

$$\begin{aligned} \frac{\mathrm{d}s}{\mathrm{d}N}=3s(s-n(s)-1)=0. \end{aligned}$$
(49)

Therefore, all solutions originating from the presence of the function \(\Lambda (-\mathsf{T})\) must satisfy the conditions \(s=0\) or \(n(s)=s-1\). As can be seen, the latter condition holds for the fixed points \(P^{{(\mathsf{DE})}}_{1}\) (for which we have \(x_{5}/x_{4}=n+1=s\)) and for the point \(P^{{(\mathsf{DE})}}_{2}\), the constraint equation \(x_{5}=sx_{4}=-2(n+1)/\beta \) must hold. The matter fixed point is related to the geometrical sector of the Lagrangian, i.e., \(\mathsf{R}\), and therefore it is not necessary to satisfy the conditions \(s=0\) or \(n(s)=s-1\). Specifying a function \(\Lambda (-\mathsf{T})\) with the corresponding n parameter, the condition \(n(s)=s-1\) leads to an algebraic equation with possible \(s_{i}\) roots.Footnote 7 Among them, we only pick out those which exhibit DE properties. Briefly speaking, there may be some \(s_{i}\) solutions for which the DE fixed points (or at least one) may pass necessary conditions so that a stable late time solution for the underlying model could be achieved. We note that the functions n(s) and \(n'(s)\) are calculated for these \(s_{i}\) solutions. True cosmological solutions are those that include an unstable DM fixed point which is connected to a stable DE one. Therefore, discarding the fixed point \(P^{{(\mathsf{DE})}}_{2}\) (owing to a vanishing eigenvalue), we seek conditions for the stability of other points. The stability properties of \(P^{{(\mathsf{DE})}}_{1}\) and \(P^{{(\mathsf{DM})}}\) are determined as follows:

$$\begin{aligned}&P^{{(\mathsf{DE})}}_{1}\quad \text{ is } \text{ stable } \text{ provided }\quad \left\{ \begin{array}{ll} \text{ for }~n'<1 &{} -\frac{3}{2}<n<-1,\\ \text{ and } \text{ for }~n>1 &{} -1<n<0, \end{array} \right. \end{aligned}$$
(50)
$$\begin{aligned}&P^{{(\mathsf{DM})}}\quad \text{ is } \text{ unstable } \text{ provided }\quad \left\{ \begin{array}{ll} \text{ for }~n'<1 &{} n<\frac{1-n'}{n'},\\ \text{ and } \text{ for }~n>1 &{} n<0. \end{array} \right. \end{aligned}$$
(51)

As a result, in order to have the allowed DM and DE solutions, it suffices that conditions (50) be satisfied. To complete this section, we explore the discussed method for two specific models. In the next section, we discuss the cosmological solutions for models with a power-law \(\Lambda (-\mathsf{T})\) function.

  • Models with \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+a(-\mathsf{T})^{\alpha }+b(-\mathsf{T})^{-\beta }\) where \(\alpha>0,~\beta >0\). In this case we obtain

    $$\begin{aligned}&n(s)=\alpha -\beta \left( 1-\frac{\alpha }{s}\right) -1,\end{aligned}$$
    (52)
    $$\begin{aligned}&n'(s)=-\frac{\alpha \beta }{s^2}, \end{aligned}$$
    (53)

    where the equation \(n(s)=s-1\) for (52) gives rise to the solutions \(s_{1}=\alpha \) and \(s_{2}=-\beta \). Therefore, a true cosmological solution can be achieved provided that the following conditions hold:

    $$\begin{aligned}&n'(s_{1})=-\frac{\beta }{\alpha }>1,\quad -\frac{1}{2}<\alpha <0,\end{aligned}$$
    (54)
    $$\begin{aligned}&n'(s_{1})=-\frac{\beta }{\alpha }<1,\quad 0<\alpha <1,\end{aligned}$$
    (55)
    $$\begin{aligned}&n'(s_{2})=-\frac{\alpha }{\beta }>1,\quad 0<\beta <\frac{1}{2},\end{aligned}$$
    (56)
    $$\begin{aligned}&n'(s_{2})=-\frac{\alpha }{\beta }<1,\quad s-1<\beta <0. \end{aligned}$$
    (57)

  • Models with \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+a{(-\mathsf{T})}^{\alpha } \exp ^{b(-\mathsf{T})^{\gamma }}\) for which we get

    $$\begin{aligned}&n(s)=\gamma \left( 1 -\frac{\alpha }{s}\right) +s-1,\end{aligned}$$
    (58)
    $$\begin{aligned}&n'(s)=\frac{\alpha \gamma }{s^2}+1. \end{aligned}$$
    (59)

    The only solution for the equation \(n(s)=s-1\) is \(s_{*}=\alpha \) which leads to \(n'(s_{*})=1 +\gamma /\alpha \). Hence, the conditions for a true cosmological solution read

    $$\begin{aligned}&n'(s_{*})=\frac{\alpha +\gamma }{\alpha }>1,\quad -\frac{1}{2}<\alpha <0,\end{aligned}$$
    (60)
    $$\begin{aligned}&n'(s_{*})=\frac{\alpha +\gamma }{\alpha }<1,\quad 0<\alpha <1. \end{aligned}$$
    (61)

5 Late time solutions for models with power-law \(\Lambda (-\mathsf{T})\) function

In this section, we consider a class of models of type \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \kappa ^2 (-\mathsf{T})^{\alpha }\), which violate the EMT conservation. We will investigate these types of models as dynamical systems as before. We then study, via considering the equilibrium points, the cosmological solutions provided by these models. However, for two values of \(\alpha \), the dynamical system approach does not work, thereby encouraging us to study these specific cases algebraically. In Sects. 5.1 and 5.2 we will study these specific cases and in Sect. 5.3 we deal with the general form of \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \kappa ^2 (-\mathsf{T})^{\alpha }\) gravity.

5.1 Models of type \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \kappa ^2 (-\mathsf{T})^{\alpha }\) with \(\alpha =1\)

For \(\alpha =1\), Eq. (33) reduces to the following equation:

$$\begin{aligned} \left( 1-\frac{3 \beta }{2}\right) \frac{\mathrm{d}\rho ^\mathrm{{(p)}} (a)}{\mathrm{d}a}+\frac{3 (1-\beta ) \rho ^\mathrm{{(p)}} (a)}{a}=0, \end{aligned}$$
(62)

for which the solution is given by

$$\begin{aligned} \rho ^\mathrm{{(p)}}(a)=\rho ^\mathrm{{(p)}}_{0} a^{\frac{6 (\beta -1)}{2-3\beta }}. \end{aligned}$$
(63)

For \(\beta =0\), the above solution leads to the standard form for DM energy density and behaves as \(a^{2}\) for large values of \(\beta \) parameter. In case in which \(\beta =1\) we have \(\rho ^\mathrm{{(p)}} (a)=\rho ^\mathrm{{(p)}}_{0}\). Moreover, for \(\alpha =1\), modified Friedman Eqs. (8) and (9) lead to

$$\begin{aligned}&3H^{2}=\kappa ^{2} \left( 1-\frac{3 \beta }{2}\right) \rho ^\mathrm{{(p)}},\end{aligned}$$
(64)
$$\begin{aligned}&2\dot{H}=\kappa ^{2}(\beta -1) \rho ^\mathrm{{(p)}}. \end{aligned}$$
(65)

Inserting the solution (63) into Eq. (64) and solving the resultant equation, we get the scale factor as a function of time, as

$$\begin{aligned} a_{\alpha =1} (t)=\left( \frac{3}{2}\right) ^{\frac{2-3 \beta }{6(1- \beta )}} \left[ \frac{3(1-\beta ) \sqrt{\Omega _{0}^{p}} H_{0}t}{\sqrt{2-3 \beta }}\right] ^{\frac{2-3 \beta }{3 (1-\beta )}}. \end{aligned}$$
(66)

This solution is valid only for \(\beta <2/3\) and it leads to the standard form for the pressure-less matter dominated era for \(\beta =0\). We can also check that the solutions (63) and (66) satisfy Eq. (65). Applying the definition given for effective EoS on Eqs. (64) and (65) we see that these types of models correspond to a constant value, \(w^\mathrm{{(eff)}}=\beta /(2-3\beta )\), which for \(\beta <2/3\) gives \(w^\mathrm{{(eff)}}>-1/3\). However, there is a special case; Eqs. (63), (64) and (65) yield a de Sitter solution for \(\beta =1\). As a result, power-law models with \(\alpha =1\) result in a single decelerated expanding cosmological state for the Universe (at all times) without ever passing through a pressure-less matter dominated era. However, these models predict a single de Sitter state as well.

5.2 Models of type \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \kappa ^2 (-\mathsf{T})^{\alpha }\) with \(\alpha =-1/2\)

In this case we have \(-\frac{3}{2}\Lambda '+ \Lambda ''\mathsf{T}=0\); thus Eq. (33) reduces to the following simple form:

$$\begin{aligned} \frac{\mathrm{d}\rho ^{(\mathrm {p})}(a)}{\mathrm{d}a}+3\left( \frac{1}{2}\beta {\rho ^{(\mathrm {p})}}^{-3/2}(a)+1\right) \frac{\rho ^{(\mathrm {p})}(a)}{a}=0, \end{aligned}$$
(67)

which has the following solution for the matter density in terms of the scale factor:

$$\begin{aligned} \rho ^{(\mathrm {p})} (a)=2^{-2/3}\left( \frac{\beta +2{\rho ^{(\mathrm {p})}_{0}}^{3/2}}{a^{9/2}} -\beta \right) ^{2/3}, \end{aligned}$$
(68)

where we have set \(\rho ^{(\mathrm {p})}(a=1)\equiv \rho _{0}\). This solution in the early times where \(a\rightarrow 0\) behaves as \(a^{-3}\) and in the late times where \(a\rightarrow \infty \), as \((-\beta /2)^{2/3}\). The Friedman equations can then be obtained:

$$\begin{aligned}&3H^{2}=\kappa ^{2} \rho ^{(\mathrm {p})},\end{aligned}$$
(69)
$$\begin{aligned}&2\dot{H}=-\kappa ^{2}\left( \rho ^{(\mathrm {p})}+\frac{\beta }{2} {\rho ^{(\mathrm {p})}}^{-1/2}\right) . \end{aligned}$$
(70)

As can be seen, the first modified Friedman equation reduces to its standard form (i.e., its form in GR), and for this reason writing down the equations as a physically consistent dynamical system breaks down. Exact solutions of Eq. (69) with energy density of DM given by (68) cannot be obtained explicitly. Nevertheless, we can obtain the early and late time solutions, being given by

$$\begin{aligned}&a_{\alpha =-1/2}^{(\mathrm {early})}(t)\approx \left( \frac{27}{256} \right) ^{1/9}\left[ \beta +2(3H_{0}^{2}\Omega _{0}^\mathrm{{(p)}})^{3/2} \right] ^{2/9}t^{2/3},\end{aligned}$$
(71)
$$\begin{aligned}&a_{\alpha =-1/2}^{(\mathrm {late})}(t)\approx e^{\frac{1}{6} \root 3 \of {-\beta } \left( 2^{2/3} \sqrt{3} t-\frac{4}{(\beta +2)^{\frac{1}{3}}}\right) }. \end{aligned}$$
(72)

From the solution (71) we see that the term in square brackets reduces to the standard form for pressure-less matter, i.e., \((3H_{0}^{2}/2)^{2/3}\), once we set \(\beta =0\). The above solutions have been obtained so that in the present time they would be equal to unity. The solution (72) shows that in the late times, we have a de Sitter solution for \(-2<\beta <0\) (notice that for the late time solution, i.e., \((-\beta /2)^{2/3}\), Eqs. (69) and (70) give \(H=constant\) and \(\dot{H}=0\), respectively). In the left panel of Fig. 3 we have plotted the scale factor for three cases; a numerical diagram has been drawn from Eqs. (69) for (68) in purple color, an asymptotic curve in the late times, i.e. the solution (72) in brown color, and the scale factor for the standard pressure-less dominated era in blue, for comparison. We used \(\beta =-1\) and \(\rho _{0}^\mathrm{{(p)}}=1\) for plotting purpose. In the right panel of Fig. 3, we have presented the effective EoS for the same values of parameters \(\beta \) and \(\rho _{0}^\mathrm{{(p)}}\). These diagrams show that in the model \(f(\mathsf{R},\mathsf{T})=\mathsf{R}-\kappa ^{2} (-\mathsf{T})^{-1/2}\), the Universe could experience an accelerated expansion in the late times, when only a pressure-less fluid is present. It is interesting to note that the unusual interaction between the only cosmological fluid and curvature of space-time, which leads to the violation of EMT conservation, has the consequence of a late de Sitter epoch in the evolution of the Universe.

Fig. 3
figure 3

Some cosmological parameters for power-law model with \(\alpha =-1/2\). Left panel Numerical solution of the scale factor in purple, approximate solution in brown and solution for the standard matter dominated era in blue. Right panel The evolution of effective EoS parameter

Full size image

5.3 Models of type: \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \kappa ^2 (-\mathsf{T})^{\alpha }\) (\(\alpha \ne 1,-1/2\))

In Sects. 5.1 and 5.2 we have considered cosmological implications of two specific models that could not be analyzed by the dynamical system approach. In the present subsection we will provide a comprehensive study of these models via this approach. We will see that unlike the conserved case, there is, however, a de Sitter solution in the case of non-conserved models. For those models in which \(f(\mathsf{R},\mathsf{T})=\mathsf{R} + \beta \Lambda (-\mathsf{T})\), the field equations (8) and (9) reduce to the following equations:

$$\begin{aligned}&3H^{2}=-\kappa ^{2}\left( \mathsf{T}^{\text {(p)}}-\beta h'\mathsf{T}^{\text {(p)}}+\frac{\beta }{2}h-\rho ^\mathrm{{(u)}}\right) ,\end{aligned}$$
(73)
$$\begin{aligned}&2\dot{H}=\kappa ^{2}\left( \mathsf{T}^{\text {(p)}}-\beta h'\mathsf{T}^{\text {(p)}}-\frac{4}{3}\rho ^{\text {(u)}}\right) . \end{aligned}$$
(74)

Substituting \(\Lambda (-\mathsf{T})=\kappa ^{2} (-\mathsf{T})^{\alpha }\) into Eqs. (73) and (74) using (29) leads to

$$\begin{aligned}&3H^{2}=\kappa ^{2}\left[ \rho ^{\text {(p)}}-\beta \left( \alpha +\frac{1}{2}\right) {\rho ^\mathrm{{(p)}}}^{\alpha }+\rho ^\mathrm{{(u)}} \right] ,\end{aligned}$$
(75)
$$\begin{aligned}&2\dot{H}=\kappa ^{2}\left( -\rho ^{\text {(p)}}+\beta \alpha {\rho ^\mathrm{{(p)}}}^{\alpha }-\frac{4}{3}\rho ^{\text {(u)}} \right) ,\end{aligned}$$
(76)
$$\begin{aligned}&\dot{\rho }^\mathrm{{(p)}}=-3H\frac{1-\beta \alpha {\rho ^\mathrm{{(p)}}}^{\alpha -1}}{1-\beta \alpha \left( \alpha +\frac{1}{2}\right) {\rho ^\mathrm{{(p)}}}^{\alpha -1}} \rho ^{\text {(p)}}. \end{aligned}$$
(77)

As can be seen, Eqs. (75) and (76) reduce to Eqs. (64) and (65) for \(\alpha =1\) and in the case of \(\alpha =-1/2\), these equations reduce to (69) and (70) in the absence of ultra-relativistic fluid. Using the definitions (16), (18) and (19), the above equations can be rewritten as

$$\begin{aligned}&\Omega ^\mathrm{{(p)}}-\beta \left( \alpha +\frac{1}{2}\right) x_{4}+\Omega ^\mathrm{{(u)}}=1,\end{aligned}$$
(78)
$$\begin{aligned}&\frac{2\dot{H}}{3H^{2}}=-1-\frac{\beta }{2}x_{4} -\frac{1}{3}\Omega ^\mathrm{{(u)}},\end{aligned}$$
(79)
$$\begin{aligned}&\dot{\rho }^\mathrm{{(p)}}=-3H\frac{1+\frac{\beta }{2} x_{4}}{1+\beta (1-\alpha )\left( \alpha +\frac{1}{2}\right) x_{4}}\rho ^\mathrm{{(p)}}. \end{aligned}$$
(80)

Finally, the dimensionless evolutionary equations for variables \(\Omega ^\mathrm{{(u)}}\) and \(x_{4}\) are obtained:

$$\begin{aligned}&\frac{\mathrm{d}\Omega ^\mathrm{{(u)}}}{\mathrm{d}N}=\Omega ^\mathrm{{(u)}} \left( -1+\frac{3\beta }{2}x_{4}+\Omega ^\mathrm{{(u)}} \right) ,\end{aligned}$$
(81)
$$\begin{aligned}&\frac{\mathrm{d}x_{4}}{\mathrm{d}N}=x_{4}\left\{ \frac{3(1-\alpha ) \left( 1+\frac{\beta }{2}x_{4}\right) \left[ 1+\beta \left( \alpha +\frac{1}{2}\right) x_{4}\right] }{1+\beta (1-\alpha ) \left( \alpha +\frac{1}{2}\right) x_{4}}+ \Omega ^\mathrm{{(u)}}\right\} . \end{aligned}$$
(82)

Note that in the case of the power-law dependency, we have \(x_{5}=x_{4}/2\), which demands a slightly different system of equations with respect to a general \(\Lambda (-\mathsf{T})\) function. As can be seen, Eq. (82) implies no DE solution for \(\alpha =1\). We cannot also interpret a DE model from it for \(\alpha =-1/2\), since Eq. (78) does not include a DE term. Moreover, one can check that Eqs. (78), (81) and (82) reduce to Eqs. (40), (41) and (42) for \(\alpha =1/2\) and \(\beta =-1\). Also, we can obtain the effective EoS from Eq. (79) as follows:

$$\begin{aligned} w^\mathrm{{(eff)}}=\frac{\beta }{2}x_{4}+\frac{1}{3}\Omega ^\mathrm{{(u)}}. \end{aligned}$$
(83)

The fixed point solutions of the system (81) and (82) are calculated in Table 3.

Table 3 The fixed point solutions for \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \kappa ^{2} (-\mathsf{T})^{\alpha }\) gravity with radiation
Full size table

Defining \(\Omega ^\mathrm{{(\mathsf{DE})}}\equiv -\beta \left( \alpha +\frac{1}{2}\right) x_{4}\), provided that \(\Omega ^\mathrm{{(p)}}+\Omega ^\mathrm{{(\mathsf{DE})}}+\Omega ^\mathrm{{(u)}}=1\), the fixed point \(P^{{(\mathsf{DE})}}\) can be accounted as a DE solution for which we have \(\Omega ^\mathrm{{(\mathsf{DE})}}=1\). The condition for accelerated expansion, \(w^{\text {(eff)}}<-1/3\) is satisfied only for \(-\frac{1}{2}<\alpha <1\). It is interesting to note that only for \(-\frac{1}{2}<\alpha <1\) both eigenvalues become negative, simultaneously. Therefore, in non-conserved class of models of the type \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \kappa ^2 (-\mathsf{T})^{\alpha }\), there is a stable solution for late times with the following properties:

$$\begin{aligned}&P^{{(\mathsf{DE})}}=\left( \Omega ^\mathrm{{(u)}}=0, \Omega ^\mathrm{{(p)}}=0, \Omega ^\mathrm{{(\mathsf{DE})}}=1\right) ,\nonumber \\&w^{\text {(eff)}}<-1/3,\quad \text{ for }\quad -\frac{1}{2}<\alpha <1. \end{aligned}$$
(84)

It is noteworthy that, for \(\alpha \rightarrow 0^{\pm }\), we have \(w_{\mathrm{eff}}\rightarrow -1\) so that we can get a DE solution with observationally accepted values of the EoS parameter. Planck 2015 measurements show that the Universe is undergoing an accelerated expansion driven by DE for which the present values of the EoS parameter lie in the interval \(-1.051<w^\mathrm{{\mathsf{DE}}}_{0}<-0.961\) [58]. This fact imposes a constraint on the \(\alpha \) parameter: \(-0.024\lesssim \alpha \lesssim 0.020\). In addition to the existence of a DE fixed point, there are unstable solutions which indicate domination of the ultra-relativistic and pressure-less fluids, i.e., the points \(P^{\text {(u)}}\) and \(P^{\text {(p)}}\), respectively. Two other solutions are \(Px_{1}\) and \(Px_{2}\), which are not physically interesting, since they do not correspond to dominant cosmological epochs.Footnote 8 Nevertheless, \(Px_{1}\) can be a late time solution for small values of \(\alpha \). Table 3 shows that the fixed point \(Px_{1}\) is a stable one for small values of \(\alpha \). Therefore, depending on the value of \(\alpha \), each of these solutions may be the late time solution. To show the two possibilities, we have plotted in Fig. 4 the phase space diagrams for the values \(\alpha =0.02\) and \(\alpha =-0.02\). The red solid circle denotes the fixed point \(P^{{(\mathsf{DE})}}\), the green one indicates \(Px_{1}\), the purple solid circle shows \(P^\mathrm{{(p)}}\), the cyan one indicates \(P^\mathrm{{(u)}}\) and the orange solid circle shows \(Px_{2}\). The diagrams show that physically interesting trajectories begin from \(P^\mathrm{{(u)}}\), pass along \(P^\mathrm{{(p)}}\) and then terminate at either \(P^\mathrm{{(\mathsf{DE})}}\) or \(Px_{1}\). Figure 4 also shows that, for \(\alpha <0\), the fixed point \(Px_{1}\) is for the late time solutions and for \(\alpha >0 \) the solution \(P^\mathrm{{(\mathsf{DE})}}\) would be chosen. These points will overlap for \(\alpha =0\), that is, the GR model plus a cosmological constant, known as the celebrated \(\Lambda \mathsf{CDM}\) model. The fixed point \(Px_{2}\) coincides with the fixed point \(P^{\text {(u)}}\) for \(\alpha =4/3\), otherwise it is physically meaningless. The fixed point \(Px_{2}\) is always unstable, that is, the functions \(f(\alpha )\) and \(g(\alpha )\) never get the same negative sign or pure imaginary values. In Fig. 4 the diagrams for the evolution of the matter density parameters and the effective EoS parameter are plotted for \(\alpha =0.02\), as well.

Fig. 4
figure 4

Cosmological quantities for models \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta (-\mathsf{T})^{\alpha }\). Upper panels the matter density parameters and the effective EoS for \(\alpha =0.02\) and initial values \(\Omega ^\mathrm{{(\mathsf{DE})}}_{i}=9.7\times 10^{-23}\) and \(\Omega ^\mathrm{{(u)}}_{i}=0.999\). Lower panels phase space portraits for two indicated values of \(\alpha \). Red and green trajectories show the possible physically justified solutions and black trajectories suffer from either lacking matter dominated or radiation dominated eras

Full size image

6 Conclusion

In this work we have investigated the cosmological consequences of violation of EMT conservation for a class of \(f(\mathsf{R},\mathsf{T})\) theories of gravity. We have considered both the ultra-relativistic fluid and DM in a spatially flat, homogeneous and isotropic background given by the FLRW metric. We have studied models of type \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \Lambda (-\mathsf{T})\) which we call minimally coupled \(f(\mathsf{R},\mathsf{T})\) models. A specific model can be considered, a \(\Lambda (\mathsf{T})\mathsf{CDM}\) model which allows for a density dependency for the cosmological constant. Firstly, we have presented the field equations of \(f(\mathsf{R},\mathsf{T})\) gravity and defined some dimensionless variables. We also classified the minimal models to those that respect the conservation of EMT and those that do not. The former models have been considered elsewhere, however, to complete our study, we have briefly reviewed their cosmological solutions through the dynamical system approach. Some new results have been obtained as well. We have algebraically showed that these types of models cannot be accepted, since they have a late time solution with an undesirable EoS parameter. Their EoS parameter varies from zero to \(-1/2\), which is not observationally confirmed. Thus, considering the EMT conservation, GR theory modified by a minimal \(\Lambda (-\mathsf{T})\) function has still the problem of incompatibility with recent observational outcomes. The latter models do not respect the conservation of EMT, for which a modified version of DM density conservation has been obtained. We have shown that, in the minimal models of \(f(\mathsf{R},\mathsf{T})\) gravity, it is always possible to consider the evolution of ultra-relativistic fluid and DM independent of each other, as long as interactions are turned off. Therefore, only a modification in the behavior of DM density can provide a different cosmological scenario, at least in the late time epochs.

To consider the cosmological consequences of the violation of EMT conservation, we presented a general method to formulate the dynamical system equations for generic minimally coupled models. We have defined two dimensionless n and s parameters constructed out of the \(\Lambda (-\mathsf{T})\) function and its derivatives and showed that the resulted autonomous equations will depend upon these parameters. As a result, we have obtained a set of closed equations of which the solutions, and hence the stability properties of them, will be controlled by these parameters. We have discussed that, at least for well-behaving models, we can parametrize \(\Lambda (-\mathsf{T})\) function in terms of a function n(s). We illustrated that all fixed points originating from the \(\Lambda (-\mathsf{T})\) function must lie on the line \(n=s-1\). In other words, for every function n(s) all fixed point solutions must occur at the location where the n(s) curve intersects with the line \(n=s-1\). The fixed points, representing the ultra-relativistic and pressure-less matter domination, are not subject to the above discussion as they are solutions of GR. Briefly speaking, this method shows that there generally exist two fixed point solutions which represent accelerated expansion/DE era in the late times. We have applied the method to inspect two models specified by \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+a(-\mathsf{T})^{\alpha }+b(-\mathsf{T})^{-\beta }\) and \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+a{(-\mathsf{T})}^{\alpha } \exp ^{b(-\mathsf{T})^{\gamma }}\) and discussed the validity of their solutions.

As a special case that cannot be explained by the above technique, we investigated the cosmological behavior of models with \(\Lambda (-\mathsf{T})=\kappa ^{2} (-\mathsf{T})^{\alpha }\). In this case, we included the ultra-relativistic fluid and discussed the late time solutions. We found that there are two different DE solutions of which the properties depend on the constant \(\alpha \). Nevertheless, each \(f(\mathsf{R},\mathsf{T})=\mathsf{R}+\beta \Lambda (-\mathsf{T})\) model accepts only one solution, by which, accordingly, such types of \(f(\mathsf{R},\mathsf{T})\) functions can be classified as two different models. We have argued that observationally consistent models may be constructed by small values of \(\alpha \). For example, Planck 2015 measurements have shown that if we believe in DE as one of the ingredients of the Universe which is presently driving the observed accelerated expansion, its EoS parameter must lie within \(-1.051<w_{0}^{(\mathsf{DE})}<-0.961\). This fact restricts us to accept \(-0.024<\alpha <0.02\). We have shown that, for the two specific models with \(\alpha =1\) and \(\alpha =1/2\), the dynamical system approach does not work, due to the structure of the related equations. Algebraic treatments showed that the former model, in general, indicates a single decelerating late time cosmological era. However, there is an exact single de Sitter solution, as well. For the determined values of \(\alpha \) and \(\beta \) parameters, we obtained a constant value for the EoS parameter with a specific value lying within the range \(w_{\alpha =1}>-1/3\). The latter case gives a proper solution including a connected matter and DE dominated eras. This model accepts a de Sitter solution in the late times. Finally, we would like to end this article by highlighting the importance of examining the observable signals of MG theories, in order to test the physical validity of the resulted models. If experiments confirm that a modified version of GR can explain observations better than the original version, the results could shed light on some fundamental cosmological questions. Modified gravity theories have been utilized successfully to account for galaxy cluster masses [59], the velocity field of DM and galaxies [60], the cosmic shear data [61], the rotation curves of galaxies [62, 63], velocity dispersions of satellite galaxies [64], and globular clusters [65]. These theories have also been used to propose an explanation for the Bullet Cluster [66] without resorting to nonbaryonic DM; see also [67] and the references therein. However, among the MG theories that have been proposed so far, Rastall’s gravity touches one of the cornerstones of GR, i.e., the conservation of EMT [68] and, interestingly, this issue has been entered within the context of MG theories [69, 70]. While in the present work, we have studied cosmological consequences of violation of EMT in the framework of \(f(\mathsf{R},\mathsf{T})\) gravity theory, it is of utmost importance to seek for observational evidence (such as the gold sample supernova type Ia data [71], SNLS supernova type Ia data set [72] and X-ray galaxy clusters analysis [73]) that could distinguish between the resulting models from this theory and GR. However, observational features of this theory need to be carried out with more scrutiny and dealing with this issue is beyond the scope of the present paper.