SL(2, Z) invariant rotating (m, n) strings in $AdS_3\times S^3$ with mixed flux

Abstract

We study rigidly rotating and pulsating (m, n) strings in $AdS_3 \times S^3$ with mixed three form flux. The $AdS_3 \times S^3$ background with mixed three form flux is obtained in the near horizon limit of SL(2, Z)-transformed solution, corresponding to the bound state of NS5-branes and fundamental strings. We study the probe (m, n)-string in this background by solving the manifest SL(2, Z)-covariant form of the action. We find the dyonic giant magnon and single spike solutions corresponding to the equations of motion of a probe string in this background and find various relationships among the conserved charges. We further study a class of pulsating (m, n) string in $AdS_3$ with mixed three form flux.

1 Introduction

Integrability in string theory has been proved to be one of the most useful techniques in studying the string spectrum in various semisymmetric superspaces [1].¹ The appearance of integrability on both sides of the AdS/CFT correspondence [3,4,5] has led to tremendous progress in the study of string theory. In this context, type IIB superstring theory on $AdS_5\times S^5$ has been shown to be described as supercoset sigma model [6]. The appearance of integrability via the appearance of hidden charges was first exploited in [7]. With the realization that the counting of gauge invariant operators on the gauge theory side can be elegantly formulated in terms of an integrable spin chain, it has been established that integrability played an important role on both sides of the duality, since the dual string theory is integrable in the semiclassical limit. In this connection, a special limit was put forth in which both sides of the duality were analyzed in great detail. In particular, the spectrum on the field theory side was shown to consist of elementary excitations, the so-called magnons which carry momentum p along the finitely or infinitely long spin chain. On the string theory side, the dual string state derived from the rigidly rotating string in the $\mathcal{R}\times S^3$ appears to give the same dispersion relation between the string energy (E) and the angular momentum (J) in the large ’t Hooft limit and is known as the giant magnon [8]. A more general kind of rotating strings, known as spiky strings, are dual to higher twist operators, also presented in [9]. It was further argued that they both fall into the category of special class of general rotating string solutions [10] on the sphere [11]. In addition to the rigidly rotating strings, the spinning and pulsating strings have also been shown to have an exact correspondence with some dual operators in the gauge theory [12]. The pulsating string was introduced first in [13]. Compared to the rigidly rotating strings, the folded and the pulsating strings were less studied even though the pulsating-rotating solutions offer better stability than the non-pulsating solutions [14]. These solutions are time-dependent as opposed to the usual rigidly rotating string solutions. They are expected to be dual to highly excited states in terms of operators [13].

Long ago, Schwarz [15] has constructed an SL(2, Z) multiplet of string-like solutions in type IIB string theory starting from the fundamental string solution. It is well known that the equations of motion of type IIB supergravity theory are invariant under an SL(2, R) group. This suggests the possibility to generate new supergravity solutions by applying this rotation to known solutions such as string-like as well as five-brane solutions. A discrete subgroup SL(2, Z) of this SL(2, R) group has been conjectured later to be the exact symmetry group of the type IIB string theory based on the fact that there are no fractional string or D-brane charges. The SL(2, Z) transformed solution of the bound state of Q5 NS5-branes and Q1 fundamental strings (F-strings) is characterized by charges with respect to RR and NS–NS two forms. In the near horizon limit of this solution, we obtain the $AdS_3 \times S^3$ background with mixed three form fluxes with integer charges. It has also been recently shown that the SL(2, Z)-transformation and the near horizon limit commute. This allows one to map the (m, n)-string in $AdS_3 \times S^3$ background with mixed three form fluxes to $(m',n')$-string in an $AdS_3 \times S^3$ background with NS–NS two form flux. Recently in a series of papers [16,17,18] the superstring theory on $AdS_3 \times S^3 \times T_4$ supported by a combination of RR and NS–NS three form fluxes (with parameter of the NS–NS three form q ) has been investigated in detail. The world-sheet theory interpolates between the pure RR flux model $(q = 0)$ and the pure NS–NS flux model $(q = 1)$.² The theory has been shown to be integrable and for a generic value of the parameter q the corresponding tree-level S-matrix for massive BMN-type excitations has been computed. Further computations along the lines of a rotating and pulsating string have been studied, for example, in [20,21,22,23,24,25,26,27,28,29]. In view of the study of superstrings in an $AdS_3\times S^3$ background with mixed flux, it is interesting to investigate further the rotating (m, n) string in an $AdS_3\times S^3$ background with mixed three form fluxes. This problem can be mapped to $(m', n')$ string in an $AdS_3\times S^3$ background with NS–NS two form flux by using the symmetries of the intersecting brane background itself. The rest of the paper is organized as follows. In Sect. 2, we study (m, n)-string in an $AdS_3 \times S^3$ background with mixed three form fluxes after mapping it to the simpler $(m',n')$-string in an $AdS_3 \times S^3$ background with NS–NS two form flux. In Sect. 3, we solve the corresponding equations of motion in the single angular momentum case where we find solutions that correspond to spike and giant magnon. Section 4 is devoted to the study of the rotating string with two angular momenta and we present the relations among various conserved charges. In Sect. 5, we discuss the pulsating strings in AdS$_3$ background with mixed three form flux. In Sect. 6, we conclude and present our outlook.

2 Rotating (m, n)-string in $AdS_3\times S^3$ with mixed flux

We begin this section with a review of the construction of $AdS_3\times S^3$ background with mixed three form fluxes that was performed recently in [30]. The starting point is the $AdS_3\times S^3$ background with NS–NS two form³

$$\begin{aligned} \begin{aligned}&\mathrm{d}s^2 =L^2[\mathrm{d}s^2_{\widetilde{AdS}_3}+\mathrm{d}s^2_{\Omega ^3}] \ , \\&H=2L^2 (\tilde{\epsilon }_{AdS_3}+\epsilon _{S^3}) \ , \quad L^2=r^2_5 \ , \\&e^{-2\Phi _\mathrm{NS}}=\frac{1}{g_s^2}\frac{r_1^2}{r_5^2} \ , \quad r_1^2=\frac{16 \pi ^4 g_s^2 \alpha '^3 Q_1}{V_4} \ , \\&r^2_5=Q_5 \alpha ' , V_4=(2\pi )^4\alpha '^2 v, \end{aligned} \end{aligned}$$

(1)

where d$s^2_{\widetilde{AdS}_3}$ is the line element of $AdS_3$ space expressed in dimensionless variables. It is well known that the solution given in (1) is a solution of type IIB supergravity equations of motion. On the other hand, we also know that type IIB superstring theory possesses an SL(2, Z)-duality transformation that leaves the metric in the Einstein frame unchanged. In the case of two forms, it is convenient to introduce the vector $\mathbf {B}$ defined as

$$\begin{aligned} \mathbf {B}=\left( \begin{array}{cc} B \\ C^{(2)} \\ \end{array}\right) \end{aligned}$$

(2)

where B and $C^{(2)}$ are NS–NS and RR two forms, respectively. The vector $\mathbf {B}$ transforms under an SL(2, Z) transformation as

$$\begin{aligned} \hat{\mathbf {B}}=(\Lambda ^T)^{-1} \mathbf {B}\ , \end{aligned}$$

(3)

where

$$\begin{aligned} \Lambda =\left( \begin{array}{c@{\quad }c} a &{} b \\ c &{} d \\ \end{array}\right) \ , \quad \mathrm {det}\Lambda =1 \ , \end{aligned}$$

(4)

and where a, b, c, d are integers. Type IIB theory also has two scalar fields $\chi$ and $\Phi$, where the dilaton $\Phi$ is in the NS–NS sector while $\chi$ belongs to the RR sector. It is convenient to combine these fields into a complex field $\tau =\chi +ie^{-\Phi }$ and introduce the following matrix:

$$\begin{aligned} \mathcal {M}= & {} e^\Phi \left( \begin{array}{c@{\quad }c} \tau \tau ^* &{} \chi \\ \chi &{} 1 \\ \end{array}\right) =e^\Phi \left( \begin{array}{c@{\quad }c} \chi ^2+e^{-2\Phi } &{} \chi \\ \chi &{} 1 \\ \end{array}\right) \ , \quad \nonumber \\&\mathrm {det}\mathcal {M}=1, \end{aligned}$$

(5)

which transforms under an SL(2, Z) transformation as

$$\begin{aligned} \hat{\mathcal {M}}=\Lambda \mathcal {M}\Lambda ^T \ , \end{aligned}$$

(6)

where $\Lambda$ is given in (4).

Then in order to find $AdS_3\times S^3$ background with mixed three form fluxes, we perform an SL(2, Z) transformation of the ansatz (1) and we obtain the line element in the form [30]

$$\begin{aligned} \mathrm{d}\bar{s}^2=\sqrt{\frac{c^2}{g_s^2}\frac{r_1^2}{r_5^2}+d^2} \left[ L^2[\mathrm{d}s^2_{\widetilde{AdS}_3}+\mathrm{d}s^2_{\Omega ^3}]+\mathrm{d}s_T^2\right] \ , \end{aligned}$$

(7)

where $\mathrm{d}s^2_T=\mathrm{d}x_6^2+\cdots +\mathrm{d}x_9^2$. We see that the new solution has the curvature radius $\bar{L}^2=\sqrt{\frac{c^2}{g_s^2}\frac{r_1^2}{r_5^2}+d^2}L^2= \frac{1}{g_s}\sqrt{c^2 r_1^2+d^2g_s^2 r^2_5}r_5$. Further, there are the following NS–NS and RR three forms:

$$\begin{aligned} \tilde{H}= & {} \mathrm{d}H=2\mathrm{d}L^2 (\tilde{\epsilon }_{AdS_3}+\epsilon _{S^3}) \ , \nonumber \\ \tilde{F}= & {} -bH= - 2bL^2 (\tilde{\epsilon }_{AdS_3}+\epsilon _{S^3}) \end{aligned}$$

(8)

and dilaton and zero form RR field as

$$\begin{aligned}&e^{-\tilde{\Phi }}= \frac{\sqrt{Q_1 Q_5 v}}{c^2 Q_1+d^2 Q_5 v}=\frac{1}{\hat{g}_s} \ , \nonumber \\&\tilde{\chi }= \frac{acQ_1+bdvQ_5}{c^2 Q_1+d^2 Q_5v}. \end{aligned}$$

(9)

Our goal is to study the dynamics of the probe (m, n)-string in this background.

To do this, we introduce the action for the (m, n)-string that has the form⁴

$$\begin{aligned}&S_{(m,n)}\nonumber \\&\quad =-T_{D1}\int \mathrm{d}\tau \mathrm{d}\sigma \sqrt{\mathbf {m}^T\mathcal {M}^{-1} \mathbf {m}}\sqrt{-\mathrm {det}g_{MN}\partial _\alpha x^M\partial _\beta x^N} \nonumber \\&\qquad +\,T_{D1}\int \mathrm{d}\tau \mathrm{d}\sigma \mathbf {m}^T \mathbf {B}_{MN}\partial _\tau x^M\partial _\sigma x^N \ , \end{aligned}$$

(10)

where

$$\begin{aligned} \mathbf {m}=\left( \begin{array}{cc} m \\ n \\ \end{array}\right) , \quad \mathbf {m}^T \mathcal {M}^{-1}\mathbf {m}=\mathbf {m}_i (\mathcal {M}^{-1})^{ij}\mathbf {m}_j \ , \mathbf {m}^T\mathbf {B}=\mathbf {m}_i \mathbf {B}^i,\nonumber \\ \end{aligned}$$

(11)

where m, n count the number of fundamental string (m) and D1-branes (n) and hence they have to be integers.

It is important that the action (10) is manifestly invariant under an SL(2, Z) transformation when $\mathbf {B}$ and $\mathcal {M}$ transform as in (2) and (6) and when $\mathbf {m}$ transforms as

$$\begin{aligned} \hat{\mathbf {m}}=\Lambda \mathbf {m}. \end{aligned}$$

(12)

Note that this action is expressed using the Einstein frame metric $g_{MN}$, which is related to the string frame metric $G_{MN}$ by the relation $g_{MN}=e^{-\Phi /2}G_{MN}$ where the Einstein frame metric is invariant under SL(2, Z)-transformations. Then it was shown in [30] that the (m, n)-string in a mixed $AdS_3\times S^3$ background with mixed three form fluxes can be mapped to an $(m',n')$-string in an $AdS_3\times S^3$ background with NS–NS three form flux. Explicitly, using the manifest covariance of the action (10) we obtain

$$\begin{aligned} S_{(m,n)}= & {} -T_{D1}\int \mathrm{d}\tau \mathrm{d}\sigma \sqrt{m'^2+n'^2e^{-2\Phi _\mathrm{NS}}}\nonumber \\&\times \,\sqrt{-\mathrm {det}(G_{MN}\partial _\alpha x^M\partial _\beta x^N)} \nonumber \\&+\,T_{D1}\int \mathrm{d}\tau \mathrm{d}\sigma m'B_{MN}\partial _\tau x^M\partial _\sigma x^N \ , \end{aligned}$$

(13)

where $G_{MN},B_{MN}$ and $\Phi ^\mathrm{NS}$ correspond to the background (1) and we used the fact that

$$\begin{aligned} \mathbf {m}^T \mathcal {M}^{-1}\mathbf {m}= & {} (\Lambda ^{-1} \mathbf {m})^T \mathcal {M}_\mathrm{NS}^{-1} (\Lambda ^{-1}\mathbf {m})\nonumber \\= & {} (m'^2+n'^2 e^{-2\Phi _\mathrm{NS}}) e^{\Phi _\mathrm{NS}} \end{aligned}$$

(14)

with

$$\begin{aligned} \mathbf {m}'=\left( \begin{array}{cc} m' \\ n'\\ \end{array}\right) =\left( \begin{array}{cc} dm -bn \\ -cm+an \\ \end{array}\right) . \end{aligned}$$

(15)

We see that we reduced the problem of the dynamics of the (m, n)-string in mixed $AdS_3\times S^3$ background to the much simpler analysis of $(m',n')$-string in pure NS–NS $AdS_3\times S^3$ background where the action is given in (13). On the other hand, this action is non-linear due to the presence of the square root of the determinant that makes the analysis of equations of motion rather awkward. For that reason it is useful to rewrite this action in Polyakov-like form when we introduce an auxiliary metric $\gamma _{\alpha \beta }$ and write the action $S_{(m,n)}$ into the form

$$\begin{aligned} S= & {} -\frac{\tau _{(m,n)}}{2}\int \mathrm{d}\tau \mathrm{d}\sigma \sqrt{-\gamma }\gamma ^{\alpha \beta } G_{\alpha \beta } \nonumber \\&+\,q_{(m,n)}\int \mathrm{d}\tau \mathrm{d}\sigma B_{MN} \partial _\tau x^M \partial _\sigma x^N \ , \end{aligned}$$

(16)

where

$$\begin{aligned} \tau _{(m,n)}= & {} T_{D1}\sqrt{m'^2+n'^2e^{-2\Phi _\mathrm{NS}}}, \nonumber \\ q_{(m,n)}= & {} T_{D1}m'=T_{D1}\mathbf {m}^T \mathbf {q}, \end{aligned}$$

(17)

where $\mathbf {q}=\left( \begin{array}{cc} d \\ -b \\ \end{array}\right)$ is the charge vector of $(d,-b)$-flux background. Note that we have also used the fact that $\Phi _\mathrm{NS}$ is constant for the background (1). To see an equivalence between (16) and Nambu–Goto form of the action, note that the equations of motion for $\gamma _{\alpha \beta }$ have the form

$$\begin{aligned} T_{\alpha \beta }= & {} -\frac{2}{\sqrt{-\gamma }} \frac{\delta S_{(m,n)}}{\delta \gamma ^{\alpha \beta }}=\tau _{(m,n)}[- \gamma _{\alpha \beta }\gamma ^{\gamma \delta }G_{\gamma \delta }+2G_{\alpha \beta }]\nonumber \\= & {} 0, \end{aligned}$$

(18)

which has clearly a solution $\gamma _{\alpha \beta }=G_{\alpha \beta }$. Inserting this solution into (16) we obtain the original action. In the following we use the Polyakov form of the action due to the manifest linearity of the theory. The equations of motion with respect to $\gamma$ have been already determined in (18), while the equations of motion with respect to $x^M$ can easily be determined from (16),

$$\begin{aligned}- & {} \frac{\tau _{(m,n)}}{2}\sqrt{-\gamma }\gamma ^{\alpha \beta }\partial _M G_{KL}\partial _\alpha x^K \partial _\beta x^L\nonumber \\&+\,\tau _{(m,n)}\partial _\alpha [\sqrt{-\gamma }\gamma ^{\alpha \beta }G_{MN} \partial _\beta x^N]\nonumber \\&+\,q_{(m,n)}H_{MNK}\partial _\tau x^N\partial _\sigma x^K=0 \ , \end{aligned}$$

(19)

where

$$\begin{aligned} H_{MNK}=\partial _M B_{NK}+\partial _N B_{KM}+\partial _K B_{MN}. \end{aligned}$$

(20)

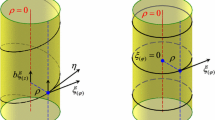
Our goal is to find solutions of the equations of motion derived above that correspond to giant magnon or single spike configurations. For that reason it is convenient to use the following explicit form of the background metric (1):

$$\begin{aligned} \mathrm{d}s^2= & {} L^2[-\cosh ^2\rho \mathrm{d}t^2+ \mathrm{d}\rho ^2+\sinh ^2\rho \mathrm{d}\phi ^2+\mathrm{d}\theta ^2\nonumber \\&+\,\sin ^2\theta \mathrm{d}\phi _1^2+\cos ^2\theta \mathrm{d}\phi ^2_2] , \nonumber \\ b_{t\phi }= & {} L^2\sinh ^2\rho , \quad b_{\phi _1\phi _2}=-L^2\cos ^2\theta , \end{aligned}$$

(21)

where we used ordinary symbols for coordinates instead of symbols with tilde used in (1) keeping in mind that all coordinates are dimensionless. Note that due to the fact that the action does not depend explicitly on $\phi ,\phi _1,\phi _2$ and t, the action is invariant under constant shifts,

$$\begin{aligned} t'(\sigma ^\alpha )= & {} t(\sigma ^\alpha )+\epsilon _t \ , \quad \phi '(\sigma ^\alpha )= \phi (\sigma ^\alpha )+\epsilon _\phi \ , \quad \phi '_{1,2}(\sigma ^\alpha )\nonumber \\= & {} \phi _{1,2}(\sigma ^\alpha )+\epsilon _{1,2}, \end{aligned}$$

(22)

where all the $\epsilon$ are constants. With the help of the standard Noether theorem we derive the following conserved currents:

$$\begin{aligned}&\mathcal {J}^\alpha _t=-\tau _{(m,n)}\sqrt{-\gamma }G_{tM}\partial _\beta x^M \gamma ^{\beta \alpha }+q_{(m,n)}B_{tN}\epsilon ^{\alpha \beta }\partial _\beta x^N \ , \nonumber \\&\mathcal {J}^\alpha _\phi =-\tau _{(m,n)}\sqrt{-\gamma }G_{\phi M}\partial _\beta x^M \gamma ^{\beta \alpha }+q_{(m,n)}B_{\phi N}\epsilon ^{\alpha \beta }\partial _\beta x^N \nonumber \\&\mathcal {J}^\alpha _{\phi _1,\phi _2}=-\tau _{(m,n)}\sqrt{-\gamma }G_{\phi _{1,2} M}\partial _\beta x^M \gamma ^{\beta \alpha }\nonumber \\&~~~~~~~~~~~~~~~~+\,q_{(m,n)}B_{\phi _{1,2} N}\epsilon ^{\alpha \beta }\partial _\beta x^N \end{aligned}$$

(23)

where $\epsilon ^{\tau \sigma }=-\epsilon ^{\sigma \tau }=1$. Note that these currents obey the relations

$$\begin{aligned} \partial _\alpha \mathcal {J}^\alpha _A=0 \ , A=t,\phi ,\phi _{1,2}. \end{aligned}$$

(24)

Using these relations we derive the following conserved charges:

$$\begin{aligned}&P_t=\int \mathrm{d}\sigma \left( -\tau _{(m,n)}\sqrt{-\gamma }G_{tt}\partial _\beta t \gamma ^{\beta \tau }+q_{(m,n)}B_{t\phi }\epsilon ^{\tau \sigma }\partial _\sigma \phi \right) ,\nonumber \\&J_\phi = \int \mathrm{d}\sigma \left( -\tau _{(m,n)}\sqrt{-\gamma }G_{\phi \phi }\partial _\beta \phi \gamma ^{\beta \tau }+q_{(m,n)}B_{\phi t}\epsilon ^{\tau \sigma }\partial _\sigma t \right) , \nonumber \\&\begin{aligned} J_{\phi _1}&= \int \mathrm{d}\sigma \left( -\tau _{(m,n)}\sqrt{-\gamma }G_{\phi _1 \phi _1}\partial _\beta \phi _1 \gamma ^{\beta \tau }\right. \\&\left. \quad +\,q_{(m,n)}B_{\phi _1\phi _2 }\epsilon ^{\tau \sigma }\partial _\sigma \phi _2 \right) ,\\ J_{\phi _2}&= \int \mathrm{d}\sigma \left( -\tau _{(m,n)}\sqrt{-\gamma }G_{\phi _2 \phi _2}\partial _\beta \phi _2 \gamma ^{\beta \tau }\right. \\&\quad \left. +\,q_{(m,n)}B_{\phi _2\phi _1 }\epsilon ^{\tau \sigma }\partial _\sigma \phi _1 \right) . \end{aligned} \end{aligned}$$

(25)

Now we try to solve the equations of motion explicitly when we consider the following ansatz:

$$\begin{aligned}&t=\gamma \tau , \quad \theta =\theta (y), \quad \phi _1=\omega _1\tau +g_1(y), \nonumber \\&\phi _2=\omega _2\tau +g_2(y), \end{aligned}$$

(26)

where y is a function of world-sheet coordinates $y = \alpha \sigma + \beta \tau$, together with $\rho =0$ and $\phi =0$. At the same time we impose the conformal gauge when $\gamma _{\tau \tau }=-1 \ , \gamma _{\sigma \sigma }=1 \ , \gamma _{\tau \sigma }=0$. In this case the components of the stress energy tensor have the form

$$\begin{aligned} T_{\tau \tau }= & {} T_{\sigma \sigma }=\tau _{(m,n)}[G_{\tau \tau }+G_{\sigma \sigma }]=0 \ , \nonumber \\ T_{\tau \sigma }= & {} 2\tau _{(m,n)}G_{\tau \sigma }=0 \ , \end{aligned}$$

(27)

where

$$\begin{aligned}&G_{\tau \tau }=\partial _\tau x^M \partial _\tau x^N G_{MN}=L^2[-\gamma ^2+ \beta ^2\theta '^2\nonumber \\&\qquad \qquad +\,(\omega _1+\beta {g'}_1)^2 \sin ^2\theta + (\omega _2+\beta {g'}_2)^2\cos ^2\theta ] \ , \nonumber \\&G_{\sigma \sigma }= \partial _\sigma x^M \partial _\sigma x^N G_{MN}= \alpha ^2L^2[\theta '^2+{g'}_1^2\sin ^2\theta \nonumber \\&\qquad \qquad +\,{g'}_2^2\cos ^2\theta ] \ , \nonumber \\&G_{\tau \sigma }=g_{\sigma \tau }=L^2[\alpha \beta \theta '^2 +\alpha (\omega _1+\,\beta {g'}_1){g'}_1\sin ^2\theta \nonumber \\&\qquad \qquad +\, \alpha (\omega _2+\beta {g'}_2){g'}_2\cos ^2\theta ]. \end{aligned}$$

(28)

The equation of motion for $\phi _1$ implies

$$\begin{aligned} g'_1 =\frac{1}{(\alpha ^2-\beta ^2)} \left( \frac{\Phi _1}{\sin ^2\theta }+\beta \omega _1- \frac{q_{(m,n)}}{\tau _{(m,n)}}\alpha \omega _2 \right) , \end{aligned}$$

(29)

where $\Phi _1=\mathrm {const}$. and $g_1'= \frac{\partial g_1}{\partial y}$

In the same way the equation of motion for $\phi _2$ implies

$$\begin{aligned} g'_2 =\frac{1}{(\alpha ^2-\beta ^2)} \left( \frac{\Phi _2}{\cos ^2\theta }+\beta \omega _2-\frac{q_{(m,n)}}{\tau _{(m,n)}}\alpha \omega _1 \right) . \end{aligned}$$

(30)

From these two equations we can see one important point: that the case of the single angular momentum, i.e., $\omega _2=0 \ , g_2=0$ is possible only when $q_{(m,n)}=0$ as follows from the equation of motion for $\phi _2$.

In order to find the equation of motion for $\theta$ we use the constraint $T_{\tau \tau }=0$ and we obtain

$$\begin{aligned}&-\,L^2\gamma ^2(\alpha ^2-\beta ^2)^2+L^2\sin ^2\theta \omega _1^2(\alpha ^2-\beta ^2)^2\nonumber \\&\quad +\, L^2\cos ^2\theta \omega _2^2(\alpha ^2-\beta ^2)^2\nonumber \\&\quad +\,L^2(\alpha ^2+\beta ^2)(\alpha ^2-\beta ^2)^2 \theta '^2+2L^2\beta \omega _1(\alpha ^2-\beta ^2)\nonumber \\&\quad \times \sin ^2\theta \left( \frac{\Phi _1}{\sin ^2\theta }+\,\beta \omega _1+\frac{q_{(m,n)}}{\tau _{(m,n)}}\alpha \omega _2 \right) \nonumber \\&\quad +\,2L^2\beta \omega _2(\alpha ^2-\beta ^2)\cos ^2\theta \left( \frac{\Phi _2}{\cos ^2\theta }+\beta \omega _2-\frac{q_{(m,n)}}{\tau _{(m,n)}}\alpha \omega _1 \right) \nonumber \\&\quad +\,L^2\sin ^2\theta (\alpha ^2+\beta ^2) \left( \frac{\Phi _1}{\sin ^2\theta }+\beta \omega _1+\frac{q_{(m,n)}}{\tau _{(m,n)}}\alpha \omega _2 \right) ^2 \nonumber \\&\quad +\,L^2\cos ^2\theta (\alpha ^2+\beta ^2) \left( \frac{\Phi _2}{\cos ^2\theta }+\beta \omega _2-\frac{q_{(m,n)}}{\tau _{(m,n)}}\alpha \omega _1 \right) ^2\nonumber \\&\quad =0. \end{aligned}$$

(31)

This equation simplifies considerably when we impose the boundary condition that, for $\theta \rightarrow \frac{\pi }{2} ,\ \theta '=0$. Since $\lim _{\theta \rightarrow \frac{\pi }{2}}\cos \theta =0$, we have to demand that $\Phi _2=0$ and the previous equation implies

$$\begin{aligned} \begin{aligned}&\!-\gamma ^2(\alpha ^2-\beta ^2)^2+\omega _1^2(\alpha ^2-\beta ^2)^2\\&\!\quad +\, 2\beta \omega _1(\alpha ^2-\beta ^2) \left( \Phi _1+\beta \omega _1-\frac{q_{(m,n)}}{\tau _{(m,n)}}\alpha \omega _2 \right) \\&\quad \!+\,(\alpha ^2+\beta ^2) \left( \Phi _1+\beta \omega _1-\frac{q_{(m,n)}}{\tau _{(m,n)}}\alpha \omega _2 \right) ^2 =0, \end{aligned} \end{aligned}$$

(32)

which can be solved for $\gamma$. Let us now consider the constraint $T_{\tau \sigma }=0$, which implies

$$\begin{aligned} G_{\tau \sigma }= & {} g_{\theta \theta }\alpha \beta \theta '^2\nonumber \\&+\,g_{\phi _1\phi _1}\alpha g'_1(\omega _1+ \beta g'_1)+g_{\phi _2\phi _2}\alpha g'_2(\omega _2+\beta g'_2)=0,\nonumber \\ \end{aligned}$$

(33)

which for $\theta =\pi /2, \theta '(\pi /2)=0$ implies

$$\begin{aligned} g'_1|_{\theta =\pi /2}(\omega _1+\beta g'_1|_{\theta =\pi /2})=0, \end{aligned}$$

(34)

and we have to analyze under which condition this equation is obeyed. The first possibility is that $g'_1|_{\theta =\pi /2}=0$ and using (29) we find that this is possible when

$$\begin{aligned} \Phi ^{I}_1=-\beta \omega _1\mathbf + \frac{q_{(m,n)}}{\tau _{(m,n)}}\alpha \omega _2 . \end{aligned}$$

(35)

The second possibility how to obey (33) is to demand that $\omega _1+\beta g'_1|_{\theta =\pi /2}=0$, which implies

$$\begin{aligned} \Phi ^{II}_1=-\frac{1}{\beta } \left( \alpha ^2\omega _1 -\beta \frac{q_{(m,n)}}{\tau _{(m,n)}}\alpha \omega _2 \right) . \end{aligned}$$

(36)

These two values of the constants $\Phi ^{I}_1,\Phi ^{II}_2$ determine whether we have a giant spike or a giant magnon solution. Before we proceed to the discussion of the general case with two angular momenta, we consider the simpler case of single angular momentum.

3 Single angular momentum

Let us now consider the case when $g'_2=0$ and $\omega _2=0$. As we argued previously this is possible on condition that $q_{(m,n)}=0$ too. In this case we have

$$\begin{aligned} g'_1=\frac{1}{(\alpha ^2-\beta ^2)} \left( \frac{\Phi _1}{\sin ^2\theta }+\beta \omega _1 \right) \ , \end{aligned}$$

(37)

while the constraint $T_{\tau \tau }=0$ takes the form

$$\begin{aligned}&-\,L^2\gamma ^2(\alpha ^2-\beta ^2)^2+L^2\sin ^2\theta \omega _1^2(\alpha ^2-\beta ^2)^2\nonumber \\&\quad +\,L^2(\alpha ^2+\beta ^2)(\alpha ^2-\beta ^2)^2 \theta '^2\nonumber \\&\quad +\,2L^2\beta \omega _1(\alpha ^2-\beta ^2)\sin ^2\theta \left( \frac{\Phi _1}{\sin ^2\theta }+\beta \omega _1 \right) \nonumber \\&\quad +\,L^2\sin ^2\theta (\alpha ^2+\beta ^2) \left( \frac{\Phi _1}{\sin ^2\theta }+\beta \omega _1 \right) ^2 =0 . \end{aligned}$$

(38)

If we impose again the condition that for $\theta =\frac{\pi }{2},\theta '=0$, we obtain the equation

$$\begin{aligned}&-\,\gamma ^2(\alpha ^2-\beta ^2)^2+\omega _1^2(\alpha ^2-\beta ^2)^2 + 2\beta \omega _1(\alpha ^2-\beta ^2)\nonumber \\&\quad \times \, (\Phi _1+\beta \omega _1)+ (\alpha ^2+\beta ^2)(\Phi _1+\beta \omega _1)^2=0, \end{aligned}$$

(39)

which can be solved for $\gamma$. Further, the constraint $T_{\tau \sigma }=0$ has the form

$$\begin{aligned} G_{\tau \sigma }= g_{\theta \theta }\alpha \beta \theta '^2+g_{\phi _1\phi _1}\alpha g'_1(\omega _1+ \beta g'_1)=0, \end{aligned}$$

(40)

which for $\theta =\pi /2, \theta '(\pi /2)=0$ implies

$$\begin{aligned} g'_1|_{\theta =\pi /2}(\omega _1+\beta g'_1|_{\theta =\pi /2})=0, \end{aligned}$$

(41)

which can be solved for two values of $\Phi _1^{I,II}$,

$$\begin{aligned} \Phi ^{I}_1=-\beta \omega _1 \end{aligned}$$

(42)

and

$$\begin{aligned} \Phi ^{II}_1=-\frac{\alpha ^2}{\beta }\omega _1 . \end{aligned}$$

(43)

We begin with the first case.

3.1 Giant Magnon solution

We first consider the case with $\Phi ^{I}_1=-\beta \omega _1$. Equation (39) implies $\gamma =\omega _1$ ,while the constraint $T_{\tau \tau }=0$ gives the equation for $\theta '$

$$\begin{aligned} \theta '^2=\dfrac{\omega _1^2 \cos ^2\theta (\alpha ^2\sin ^2\theta -\beta ^2)}{(\alpha ^2-\beta ^2)^2\sin ^2\theta }. \end{aligned}$$

(44)

Using (25), we find the explicit form of the conserved charges,

$$\begin{aligned} P_t= & {} -2\kappa L^2 \tau _{(m,n)}\int {\mathrm{d}\theta \dfrac{(\alpha ^2-\beta ^2)\sin \theta }{\alpha \cos \theta \sqrt{\alpha ^2\sin ^2\theta -\beta ^2}}} \ , \nonumber \\ J_{\phi _1}= & {} 2\kappa L^2\tau _{(m,n)} \int {\mathrm{d}\theta \dfrac{\sin \theta }{\alpha \cos \theta }\sqrt{\alpha ^2\sin ^2\theta -\beta ^2}} \ , \end{aligned}$$

(45)

where $\kappa$ counts the number of spikes on the (m, n)-string world-volume. Both of these integrals diverge but the difference between $E=-P_t$ and $J_{\phi _1}$ is finite and is equal to

$$\begin{aligned} E-J_{\phi _1}= & {} 2\kappa \tau _{(m,n)} L^2\sqrt{1-\left( \frac{\beta }{\alpha }\right) ^2}\nonumber \\= & {} 2\kappa \tau _{(m,n)} L^2\sin \left( \dfrac{\triangle \phi _1}{2}\right) , \end{aligned}$$

(46)

where we introduced the difference angle $\phi _1$ defined as

$$\begin{aligned} \triangle \phi _1= & {} 2 \int _{\phi ^\mathrm{min}_1}^{\phi ^\mathrm{max}_1}\mathrm{d}\phi _1 =2\alpha \int _{\theta _\mathrm{min}}^{\theta ^{max}}{\dfrac{{g'}_1\mathrm{d}\theta }{\alpha \mid \theta '\mid }}\nonumber \\= & {} -2 \arccos \left( \frac{\beta }{\alpha }\right) . \end{aligned}$$

(47)

Note that (46) is the generalization of the giant magnon dispersion relation to the specific case of an (m, n)-string in $(d,-b)$-mixed flux background. More explicitly, the condition $q_{(m,n)}=T_{D1}m'=0$ implies that $dm=bn$ and $\tau _{(m,n)}=T_{D1}e^{-\Phi _\mathrm{NS}}n'=T_{D1}\frac{n}{d}e^{-\Phi _\mathrm{NS}}$. A special case is when $n'=1$, which corresponds to a (b, d)-string and we derive the giant magnon dispersion relation. Note that this is in agreement with the SL(2, Z)-covariance of Type IIB string theory, since the $(d,-b)$-flux background is derived from the (1, 0)-flux background by SL(2, Z)-rotation with the matrix $\Lambda =\left( \begin{array}{c@{\quad }c} a &{} b \\ c &{} d \\ \end{array}\right)$ where the NS–NS and RR two forms transform as

$$\begin{aligned} \left( \begin{array}{cc} B'\\ C'^{(2)} \\ \end{array}\right) =(\Lambda ^T)^{-1}\ \left( \begin{array}{cc} B\\ C^{(2)} \\ \end{array}\right) , \end{aligned}$$

(48)

while the (m, n)-string transforms as $\mathbf {m}'=\Lambda \mathbf {m}$, so that the (b, d)-string is an SL(2, Z) rotation of a D1-brane.

3.2 Spike solution

In the second case, we have $\Phi ^{II}_1=-\frac{\alpha ^2}{\beta }\omega _1$. Equation (39) gives $\gamma ^2=\frac{\alpha ^2}{\beta ^2}\omega _1^2$, while the constraint $T_{\tau \tau }=0$ implies the following differential equation for $\theta$:

$$\begin{aligned} \theta '^2=\dfrac{\alpha ^2\omega _1^2\cos ^2\theta (\beta ^2\sin ^2\theta -\alpha ^2)}{\beta ^2(\alpha ^2-\beta ^2)^2\sin ^2\theta }. \end{aligned}$$

(49)

It is easy to see that the energy is equal to

$$\begin{aligned} E=\dfrac{2\kappa L^2 \tau _{(m,n)}}{\alpha }\int {\mathrm{d}\theta \dfrac{(\alpha ^2-\beta ^2)\sin \theta }{\cos \theta \sqrt{\beta ^2\sin ^2\theta -\alpha ^2}}}, \end{aligned}$$

(50)

which is divergent. On the other hand note that $J_{\phi _1}$ is now finite and is equal to

$$\begin{aligned} J_{\phi _1}= & {} -2\kappa \tau _{(m,n)} L^2\cos \left( \frac{\alpha }{\beta }\right) . \end{aligned}$$

(51)

In order to find a finite dispersion relation, let us determine the angle difference,

$$\begin{aligned} \triangle \phi _1= & {} \frac{2}{\alpha } \int _{\theta _\mathrm{min}}^{\theta ^\mathrm{max}} {\mathrm{d}\theta \dfrac{\sqrt{(\beta ^2\sin ^2\theta -\alpha ^2)}}{\sin \theta \cos \theta }}, \end{aligned}$$

(52)

which is divergent. Then it is easy to find the following dispersion relation:

$$\begin{aligned} E+\kappa \tau _{(m,n)}L^2\triangle \phi _1 =2\kappa \tau _{(m,n)}L^2\left( \frac{\pi }{2}-\theta _1\right) . \end{aligned}$$

(53)

This is the dispersion relation corresponding to the single spike solution of the string.

4 Two angular momenta

In this section we consider athe more interesting case of two non-zero angular momenta. Recall that in Sect. 2 we determined that these solutions are characterized by the condition $\Phi _2=0$ and the two values of $\Phi _1$ given in (35) and (36). Let us begin with the first case.

4.1 First limiting case $\Phi ^{I}_1$

We begin with the first case with $\Phi ^{I}_1=-\beta \omega _1+\frac{q_{(m,n)}}{\tau _{(m,n)}}\alpha \omega _2$. Note that for this value of $\Phi ^I_1$, see Eq. (32), implies $\gamma =\omega _1$.

Using (31), we get the differential equation of $\theta$

$$\begin{aligned} \theta '^2= & {} \dfrac{\Omega ^2\cos ^2\theta }{(\alpha ^2-\beta ^2)^2\sin ^2\theta } [\sin ^2\theta -\sin ^2\theta _0 ] \ , \end{aligned}$$

(54)

where $\Omega ^2=\alpha ^2(1-\frac{q^2_{(m,n)}}{\tau ^2_{(m,n)}})(\omega _1^2-\omega _2^2)$ and $\sin \theta _0=\dfrac{(\beta \omega _1-\alpha \omega _2\frac{q_{(m,n)}}{\tau _{(m,n)}})}{\Omega }$.

The explicit form of the conserved charge E is

$$\begin{aligned} E=\dfrac{2\kappa \omega _1\tau _{(m,n)}L^2(\alpha ^2-\beta ^2)}{\alpha \Omega }\int {\dfrac{\mathrm{d}\theta \sin \theta }{\cos \theta \sqrt{\sin ^2\theta -\sin ^2\theta _0 }}},\nonumber \\ \end{aligned}$$

(55)

which is divergent. For the remaining conserved charges $J_{\phi _1}$ and $J_{\phi _2}$, we get

$$\begin{aligned} J_{\phi _1}= & {} \dfrac{2\kappa \omega _1\tau _{(m,n)} L^2}{\alpha \Omega }(\alpha ^2-\beta ^2) \int { \mathrm{d}\theta \dfrac{\sin \theta }{\cos \theta \sqrt{\sin ^2\theta -\sin ^2\theta _0}}}\nonumber \\&-\,\dfrac{2\kappa \alpha \omega _1\tau _{(m,n)} L^2}{\Omega } \left( 1-\frac{q^2_{(m,n)}}{\tau ^2_{(m,n)}}\right) \int { \mathrm{d}\theta \dfrac{\sin \theta \cos \theta }{\sqrt{\sin ^2\theta -\sin ^2\theta _0}}}\nonumber \\ \end{aligned}$$

(56)

and

$$\begin{aligned} J_{\phi _2}= & {} \dfrac{2\kappa \tau _{(m,n)} L^2\alpha \omega _2}{\Omega } \left( 1-\frac{q^2_{(m,n)}}{\tau ^2_{(m,n)}}\right) \int \mathrm{d}\theta { \dfrac{{\sin \theta \cos \theta }}{\sqrt{\sin ^2\theta -\sin ^2\theta _0}}} \nonumber \\&-\,{2\kappa \tau _{(m,n)} L^2\frac{q_{(m,n)}}{\tau _{(m,n)}}\sin \theta _0}\displaystyle \int \mathrm{d}\theta {\dfrac{\cos \theta }{\sin \theta \sqrt{\sin ^2\theta -\sin ^2\theta _0}}}\nonumber \\ \end{aligned}$$

(57)

and for the angle difference

$$\begin{aligned} \triangle \phi _1= & {} \dfrac{2(\alpha \omega _2\dfrac{q_{(m,n)}}{\tau _{(m,n)}}-\beta \omega _1)}{\Omega }\int {\dfrac{\mathrm{d}\theta \cos \theta }{\sin \theta \sqrt{\sin ^2\theta -\sin ^2\theta _0}}}\nonumber \\= & {} -2\sin \theta _0\int {\dfrac{\mathrm{d}\theta \cos \theta }{\sin \theta \sqrt{\sin ^2\theta -\sin ^2\theta _0}}}\nonumber \\= & {} -2\cos ^{-1}(\sin \theta _0). \end{aligned}$$

(58)

Collecting these results, we obtain the following dispersion relation:

$$\begin{aligned} \dfrac{E}{\omega _1}-\dfrac{J_{\phi _1}}{\omega _1} =\dfrac{J_{\phi _2}}{\omega _2}-\dfrac{\kappa q_{(m,n)}L^2\triangle \phi _1}{\omega _2}. \end{aligned}$$

(59)

Using the previous integral we evaluate the right side of the equation above and we obtain

$$\begin{aligned}&\frac{J_{\phi _2}-\kappa q_{(m,n)}L^2\triangle \phi _1}{\omega _2} = \frac{1}{\omega _1}\sqrt{(J_{\phi _2}-\kappa q_{(m,n)}L^2\triangle \phi _1)^2+ 4\kappa ^2\tau ^2_{(m,n)}L^4 \left( 1-\frac{q^2_{(m,n)}}{\tau ^2_{(m,n)}}\right) (1-\sin ^2\theta _0)}, \end{aligned}$$

(60)

and hence we derive the final form of the dispersion relation,

$$\begin{aligned} E-J_{\phi _1}= & {} \sqrt{(J_{\phi _2}-\kappa q_{(m,n)}L^2\triangle \phi _1)^2+ 4\kappa ^2\tau ^2_{(m,n)}L^4 \left( 1-\frac{q^2_{(m,n)}}{\tau ^2_{(m,n)}}\right) \sin ^2\frac{\triangle \phi _1}{2}} \nonumber \\= & {} \sqrt{(J_{\phi _2}-\kappa \mathbf {m}^T \mathbf {q}T_{D1}L^2\triangle \phi _1)^2+ 4\kappa ^2\mathbf {m}^T \mathcal {M}^{-1}\mathbf {m}e^{-\Phi _\mathrm{NS}}T_{D1}^2L^4 \left( 1-\frac{\mathbf {m}^T \mathbf {q}}{\mathbf {m}^T \mathcal {M}^{-1}\mathbf {m}e^{-\Phi _\mathrm{NS}}}\right) \sin ^2\frac{\triangle \phi _1}{2}}. \end{aligned}$$

(61)

This dispersion relation is the generalization of the dispersion relations derived in [18] and also in [21] to the case of an (m, n)-string in the $(d,-b)$-mixed flux background. We see that this dispersion relation is linear in $\triangle \phi _1$, which is identified with the world-sheet momentum p, which spoils the periodicity of this solution. On the other hand it is clear that this dispersion relation reduces to the usual giant magnon dispersion relation when $\mathbf {m}^T \mathbf {q}=0$ and also $n'=1$, which corresponds to the (b, d)-string in the $(d,-b)$-flux background and the dispersion relation has the form

$$\begin{aligned} E-J_{\phi _1}=\sqrt{J^2_{\phi _2}+4\kappa ^2 e^{-2\Phi _\mathrm{NS}}L^4T^2_{D1}\sin ^2\frac{\triangle \phi _1}{2}} , \end{aligned}$$

(62)

which again corresponds to the SL(2, Z)-rotation of the dispersion relation of the D1-brane in a pure NS–NS flux background. On the other hand it is interesting to analyze the dispersion relation when $n'=0$, which implies $q_{(m,n)}=\tau _{(m,n)}$, which corresponds to $m=\frac{an}{c}$. If we again consider the case when $m'=1$ we find that this corresponds to an (a, c)-string and we find that the dispersion relation has the form

$$\begin{aligned} E-J_{\phi _1}=J_{\phi _2}-\kappa T_{D1}L^2 \triangle \phi _1 . \end{aligned}$$

(63)

We interpret this solution as the bound state of $J_{\phi _2}$ elementary magnons so that for $J_{\phi _2}=1$ we obtain the massless dispersion relation

$$\begin{aligned} E-J_{\phi _1}=\epsilon =1-\kappa T_{D1}L^2\triangle _{\phi _1}, \end{aligned}$$

(64)

which has a nice physical interpretation. The (a, c)-string in a $(d,-b)$-flux background is defined by an SL(2, Z)-rotation of the fundamental string in a pure NS–NS flux background, where the matrix $\Lambda$ is given in (4). On the other hand we know that the fundamental string in $AdS_3\times S^3$ with NS–NS flux has an exact WZW conformal field theory description with a massless dispersion relation [18].

4.2 Second limiting case $\Phi ^{II}_1$

Now, we consider the second case with $\Phi ^{II}_1=-\frac{1}{\beta }(\alpha ^2\omega _1 -\beta \frac{q_{(m,n)}}{\tau _{(m,n)}}\alpha \omega _2)$. From (32) we again find $\gamma ^2=\dfrac{\alpha ^2}{\beta ^2}\omega _1^2$.

Using (31) we find that the differential equation for $\theta$ has the form

$$\begin{aligned} \theta '^2= & {} \dfrac{\Omega ^2\cos ^2\theta }{(\alpha ^2-\beta ^2)^2\sin ^2\theta }[\sin ^2\theta -\sin ^2\theta _0] \ , \end{aligned}$$

(65)

where $\Omega ^2=\alpha ^2\left( 1-\frac{q^2_{(m,n)}}{\tau ^2_{(m,n)}}\right) (\omega _1^2-\omega _2^2) \ , \quad \sin \theta _0=\frac{1}{\beta \Omega }\left( \alpha ^2\omega _1-\alpha \beta \omega _2\dfrac{q_{(m,n)}}{\tau _{(m,n)}}\right) .$

Using (65) we determine the following conserved charges:

$$\begin{aligned} E= & {} \dfrac{2\kappa \omega _1\tau _{(m,n)}L^2(\alpha ^2-\beta ^2)}{\beta \Omega }\int {\dfrac{\mathrm{d}\theta \sin \theta }{\cos \theta \sqrt{\sin ^2\theta -\sin ^2\theta _0}} } \ , \nonumber \\ J_1= & {} {-2\kappa \omega _1\tau _{(m,n)} L^2} \sqrt{\dfrac{1-\frac{q^2_{(m,n)}}{\tau ^2_{(m,n)}}}{\omega _1^2-\omega _2^2}}\cos \theta _0 \ , \nonumber \\ J_2= & {} {2\kappa \tau _{(m,n)} L^2\omega _2}\sqrt{\dfrac{1-\frac{q^2_{(m,n)}}{\tau ^2_{(m,n)}}}{\omega _1^2-\omega _2^2}} \cos \theta _0 -2n\tau L^2\frac{q_{(m,n)}}{\tau _{(m,n)}} (\frac{\pi }{2}-\theta _0) ,\nonumber \\ \end{aligned}$$

(66)

together with the angle difference

$$\begin{aligned} \triangle \phi _1= & {} -2\sin \theta _0\int _{\theta _{min}}^{\pi /2} \frac{\mathrm{d}\theta \cos \theta }{\sin \theta \sqrt{\sin ^2\theta -\sin ^2\theta _0}}\nonumber \\&-\,2\dfrac{\omega _1}{\beta \Omega }(\alpha ^2-\beta ^2)\int {\dfrac{\mathrm{d} \theta \sin \theta }{\cos \theta \sqrt{\sin ^2\theta -\sin ^2\theta _0}}}. \end{aligned}$$

(67)

From (66) and (67) we see that E and $\triangle \phi _1$ are both divergent but their combination is finite and is equal to

$$\begin{aligned} E+\kappa \tau _{(m,n)} L^2\triangle \phi _1= & {} 2\kappa \tau _{(m,n)} L^2 \left( \frac{\pi }{2 }-\theta _0 \right) . \end{aligned}$$

(68)

Further, the dispersion relation between the angular momenta can be written as

$$\begin{aligned} J_1=\sqrt{(2\kappa \tau _{(m,n)} L^2)^2(1-\frac{q^2_{(m,n)}}{\tau ^2_{(m,n)}})\sin ^2\dfrac{(\triangle \phi _1)_\mathrm{reg}}{2}+[J_2-\kappa \tau _{(m,n)} L^2\frac{q_{(m,n)}}{\tau _{(m,n)}}(\triangle \phi _1)_\mathrm{reg}]^2} \end{aligned}$$

(69)

where $(\triangle \phi _1)_\mathrm{reg}=-2\cos ^{-1}(\sin \theta _0)$. Note that (69) could be rewritten using the original variables $\mathbf {m}$ and $\mathcal {M}$ and we could discuss the various properties of this relation with the dependence on the values of the vector $\mathbf {m}$ exactly in the same way as in the previous section, but we will not repeat it here since the discussion would be exactly the same.

5 Pulsating (m, n)-string in $AdS_3$ with mixed flux

In this section we will analyze the pulsating (m, n)-string in mixed three form flux background. Recall that such a string has an action

$$\begin{aligned} S= & {} -\frac{\tau _{(m,n)}}{2}\int \mathrm{d}\tau \mathrm{d}\sigma \sqrt{-\gamma }\gamma ^{\alpha \beta } G_{\alpha \beta }+q_{(m,n)}\nonumber \\&\times \,\int \mathrm{d}\tau \mathrm{d}\sigma B_{MN} \partial _\tau x^M \partial _\sigma x^N \ , \end{aligned}$$

(70)

with the equation of motion for $x^M$

$$\begin{aligned}&-\frac{\tau _{(m,n)}}{2}\sqrt{-\gamma }\gamma ^{\alpha \beta }\partial _M G_{KL}\partial _\alpha x^K \partial _\beta x^L\nonumber \\&\quad +\,\tau _{(m,n)}\partial _\alpha [\sqrt{-\gamma }\gamma ^{\alpha \beta }G_{MN} \partial _\beta x^N]\nonumber \\&\quad +\,q_{(m,n)}H_{MNK}\partial _\tau x^N\partial _\sigma x^K=0 \ , \end{aligned}$$

(71)

and the equations of motion for $\gamma _{\alpha \beta }$

$$\begin{aligned} T_{\alpha \beta }=-\frac{2}{\sqrt{-\gamma }} \frac{\delta S_{(m,n)}}{\delta \gamma ^{\alpha \beta }}=\tau _{(m,n)}[- \gamma _{\alpha \beta }\gamma ^{\gamma \delta }G_{\gamma \delta }+2G_{\alpha \beta }]=0 .\nonumber \\ \end{aligned}$$

(72)

In order to find a pulsating (m, n)-string in $AdS_3$, we consider the following ansatz:

$$\begin{aligned} t = t(\tau ),\quad \rho = \rho (\tau ), \quad \phi = \kappa \sigma \end{aligned}$$

(73)

with $b_{t\phi }=L^2\sinh ^2\rho$. Then it is easy to find the form of the induced metric,

$$\begin{aligned} G_{\tau \tau }= & {} L^2(-\cosh ^2\rho \dot{t}^2+\dot{\rho }^2) \ , \quad G_{\sigma \sigma }= L^2 \kappa ^2 \sinh ^2\rho \ , \quad \nonumber \\&G_{\tau \sigma }=G_{\sigma \tau }=0 \ , \end{aligned}$$

(74)

so that (72) in the conformal gauge takes the form

$$\begin{aligned}&T_{\tau \tau }=T_{\sigma \sigma }= \tau _{(m,n)}L^2[-\cosh ^2\rho \dot{t}^2+\dot{\rho }^2+ \kappa ^2 \sinh ^2\rho ]=0 \ , \nonumber \\&T_{\tau \sigma }=2\tau _{(m,n)}G_{\tau \sigma }=0 . \end{aligned}$$

(75)

From (71) we find that the equation of motion for t has the very simple form

$$\begin{aligned}&L^2(\tau _{(m,n)} \dot{t}\cosh ^2\rho -\kappa q_{(m,n)}\sinh ^2\rho ) =\mathcal {E} . \end{aligned}$$

(76)

On the other hand the equation of motion for $\rho$ is more complicated and is equal to

$$\begin{aligned}&-\frac{\tau _{(m,n)}}{2}(-\partial _\rho G_{tt}\dot{t}^2+\kappa ^2\partial _\rho G_{\phi \phi })-L^2\tau _{(m,n)} \ddot{ \rho } \nonumber \\&\quad +\,2\kappa L^2 q_{(m,n)}\sinh \rho \cosh \rho \dot{t}=0 \ , \end{aligned}$$

(77)

while the equation of motion for $\phi$ implies

$$\begin{aligned} \kappa L^2\tau _{(m,n)}\sinh ^2\rho =A. \end{aligned}$$

(78)

Now using (76) we find that $P_t$ is equal to

$$\begin{aligned} P_t\!=\!-E= & {} -\int \mathrm{d}\sigma L^2 \left( \tau _{(m,n)}\cosh ^2\rho \dot{t}-\kappa q_{(m,n)}\sinh ^2\rho \right) =-2\pi \mathcal {E} .\nonumber \\ \end{aligned}$$

(79)

The second important quantity is the oscillation number that is associated with string motion along the $\rho$ direction,

$$\begin{aligned} N=\oint {\mathrm{d}\rho \Pi _{\rho }} \ , \end{aligned}$$

(80)

where $\Pi _\rho$ is the canonical momentum conjugate to $\rho$,

$$\begin{aligned} \Pi _\rho= & {} \tau _{(m,n)}L^2\dot{\rho }. \end{aligned}$$

(81)

Now using Eqs. (75) and (76) we obtain a differential equation for $\rho$ in the form

$$\begin{aligned} \dot{\rho }^2= & {} \dfrac{(\kappa q_{(m,n)}L^2\sinh ^2\rho +\mathcal {E})^2-\kappa ^2\tau ^2_{(m,n)} L^4\sinh ^2\rho \cosh ^2\rho }{\tau ^2_{(m,n)} L^4\cosh ^2\rho },\nonumber \\ \end{aligned}$$

(82)

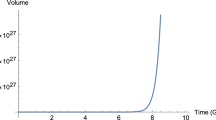
and hence the oscillation number N is equal to

$$\begin{aligned} N= & {} \oint \dfrac{\mathrm{d}\rho }{{\cosh \rho }} \nonumber \\&\times \,{\sqrt{(\kappa q_{(m,n)} L^2\sinh ^2\rho +\mathcal {E})^2-\kappa ^2\tau ^2_{(m,n)} L^4\sinh ^2\rho \cosh ^2\rho }}. \end{aligned}$$

Changing the variable $x=\sinh \rho$, we get

$$\begin{aligned} N= & {} \oint {\dfrac{\mathrm{d}x}{{1+x^2}} {\sqrt{(\kappa q_{(m,n)} L^2x^2+\mathcal {E})^2-\kappa ^2\tau ^2_{(m,n)} L^4x^2(1+x^2)}}} \nonumber \\= & {} \kappa L^2 \sqrt{\tau _{(m,n)}^2-q_{(m,n)}^2}\int _0^{\sqrt{R_+}}{\dfrac{\mathrm{d}x}{1+x^2}\sqrt{(R_+ -x^2)(x^2-R_-)}}\nonumber \\= & {} \kappa L^2 \sqrt{\tau _{(m,n)}^2-q_{(m,n)}^2}\dfrac{1}{\sqrt{-R_-}} \left[ R_- E\left( \dfrac{R_+}{R_-}\right) +(1+R_+) \right. \nonumber \\&\left. \qquad \times \left[ K\left( \dfrac{R_+}{R_-}\right) -(1+R_-)\Pi \left( -R_+,\dfrac{R_+}{R_-}\right) \right] \right] , \end{aligned}$$

(83)

where $R_+$ and $R_-$ are the roots of the quadratic equation in the square root with

$$\begin{aligned} R_{\pm }=\dfrac{2q_{(m,n)}\mathcal {E}-\kappa L^2 \tau ^2_{(m,n)} \pm \tau _{(m,n)}\sqrt{-4L^2\kappa q_{(m,n)}\mathcal {E}+4\mathcal {E}^2 +L^4 \kappa ^2 \tau ^2_{(m,n)}}}{2\kappa L^2 (\tau ^2_{(m,n)}-q^2_{(m,n)})}.\nonumber \\ \end{aligned}$$

(84)

In the short string limit

$$\begin{aligned} N= & {} \frac{\pi }{4 L^2 \kappa \tau _{(m,n)}} \mathcal {E}^2 +\frac{\pi q_{(m,n)} }{4 L^4 \kappa ^2 \tau ^3_{(m,n)}} \mathcal {E}^3-\frac{5\pi (-3q^2_{(m,n)} +\tau ^2_{(m,n)}) }{32 L^6 \kappa ^3 \tau ^5_{(m,n)}} \mathcal {E}^4\nonumber \\&-\,\frac{7 \pi q_{(m,n)} (-5q^2_{(m,n)}+3\tau ^2_{(m,n)}) }{32 L^8 \kappa ^4 \tau ^7_{(m,n)}}\mathcal {E}^5+O[\mathcal {E}]^6 . \end{aligned}$$

(85)

Reversing the above series, we have the expression for $\mathcal {E}$

$$\begin{aligned} \mathcal {E}= & {} \frac{2 \sqrt{L^2 \kappa \tau _{(m,n)}}}{\sqrt{\pi } }\sqrt{N}-\frac{2 q_{(m,n)} }{\pi \tau _{(m,n)}} N+\frac{5 (-q^2_{(m,n)}+\tau ^2_{(m,n)})}{2 \pi ^{3/2} \tau ^2_{(m,n)} \sqrt{L^2 \kappa \tau _{(m,n)}} } N^{3/2} \nonumber \\&+\,\frac{6 (-q^3_{(m,n)}+q_{(m,n)} \tau ^2_{(m,n)})}{L^2 \kappa \pi ^2 \tau ^4_{(m,n)}} N^2 + O[N]^{5/2}. \end{aligned}$$

(86)

Putting $m'=1$ and $n'=0$, we have the following expression:

$$\begin{aligned} N= & {} \frac{\pi }{4 L^2 \kappa T_{D1}}\mathcal {E}^2 +\frac{\pi }{4 L^4 \kappa ^2 T_{D1}^2}\mathcal {E}^3+\frac{5\pi }{16 L^6 \kappa ^3 T_{D1}^3}\mathcal {E}^4 \\&+\,\frac{7 \pi }{16 L^8 \kappa ^4 T_{D1}^4}\mathcal {E}^5+O[\mathcal {E}]^6, \end{aligned}$$

$$\begin{aligned} \mathcal {E}=\frac{2 \sqrt{L^2 \kappa T_{D1}}}{\sqrt{\pi } }\sqrt{N}-\frac{2 }{\pi } N + O[N]^{5/2}. \end{aligned}$$

(87)

The condition $n'=0$ implies that $cm=an$ and $\tau _{(m,n)}=T_{D1}m'=T_{D1}\frac{n}{c}$. Again putting $m'=1$, we get $m=a$ and $n=c$. So we note that the (a, c)-string in $(d,-b)$-flux background is the SL(2, Z) rotation of F-string and our result for the specific case $m'=1$ and $n'=0$ should match with [26].

6 Conclusion

In this paper, we have studied the rotating and pulsating (m, n)-type string in an $AdS_3 \times S^3$ background with mixed fluxes which has been obtained by taking the SL(2, Z) transformations of the usual $(F1-NS5)$ bound state followed by a near horizon geometry. We have applied an SL(2, Z) transformation on the (m, n)-probe string action and generated $(m',n')$-string action, where the $m'$ and $n'$ are the SL(2, Z) invariants. The giant magnon and its dyonic counterpart solutions have been obtained by solving relevant equations of motion of the probe string in the above background in the presence of NS–NS fluxes. We have shown various regularized dispersion relations among different conserved charges that the background admits. We have also checked that in the absence of probe D-string charges, the relations among various charges do match exactly with the F-string result. Furthermore, we have looked at an oscillating (m, n)-string in the background of $AdS_3$ with NS–NS flux. In the short string limit, we have obtained the energy of such a string in terms of the oscillation number. The work done in this paper can be extended in several ways. One of the interesting problems to consider is to study the pulsating and circular string solutions of an (m, n)-type string in $R\times S^3$ with the NS–NS flux turned on. A point to note, however, is that the pulsating and oscillating strings in $R\times S^3$ is qualitatively different from the $AdS_3$ case. It is left as a further example for future work. In the context of obtaining the mixed flux background, one of the backgrounds which one might look for is the $AdS_3 \times S^3 \times S^3 \times S^1$ with mixed flux. A way to do so would be to start with the NS1–$NS1'$–NS5–$NS5'$ intersecting brane solution of [32] and then apply the SL(2, Z) transformation followed by a rotation and check the commutativity of the these two operations. At present, it appears to be a nice idea to pursue further.