1 Introduction

The origins of the primary inflationary era [1,2,3,4], current accelerating phase of the universe expansion [5,6,7,8,9] as well as the dark matter problem [10,11,12] are some of the big puzzles in the standard model of cosmology. Our insufficient understanding of these problems leads the coincidence and fine-tuning problems [13,14,15,16]. In order to solve the above mentioned problems, some authors have been introduced a new type of energy-momentum source [17,18,19,20]. In another approach, physicist try to solve the above problems by modifying the Einstein field equations [21,22,23,24,25,26]. In this line, one may refer to the scalar-tensor gravity [27], vector–tensor theories [28], tensor–vector–scalar theories [29], quadratic gravity [30], Chern–Simons theories [31], massive gravity [32, 33] and Gauss–Bonnet theory [34], for a review see also [35]. Scalar-tensor (ST) theories of gravity are the simplest alternative to Einstein’s general theory of gravity (GR) and have a long history. The first attempts were done by Jordan [36, 37], Fierz [38], and Brans–Dicke [39]. These theories possess just one massless scalar field and have a constant coupling strength to matter fields. This work was generalized later to the theories in which the scalar field has a dynamic coupling to the matter fields and/or an arbitrary self-interaction in [40,41,42] as well as to the theory with multiple scalar fields [43]. In the vector–tensor theories of gravity, in addition to the metric tensor, the gravitational action is modified by adding a vector field that is non-minimally coupled to gravity. Studying these theories one is referred to the work by Will, Nordtvedt and Hellings [44,45,46]; see also [47, 48]. The tensor–vector–scalar theory is proposed by Bekenstein [49] where the standard Einstein tensor field of general relativity (GR) is coupled to a vector field as well as a scalar field, hence the theory is called by this name. This theory is a relativistic version of modified newtonian dynamics (MOND) [50] reproducing MOND in the weak field limit. The most important advantage to adopt tensor–vector–scalar theory refers to the explanation of many galactic and cosmological observations without the need for dark matter [51, 52]. The quadratic gravity theories are based on the idea of adding appropriate quadratic terms in the Riemann and Ricci tensors or the Ricci scalar inspired by the string or quantum gravity theories [53]. Chern–Simons gravity is the special case of the quadratic theories including only the parity-violating term \(^{*}RR={{^{*}R^{\alpha }}_{\beta }}^{\gamma \delta }{R^{\beta }}_{\alpha \delta \gamma }\) in which \({{^{*}R^{\alpha }}_{\beta }}^{\gamma \delta }=\frac{1}{2}\epsilon ^{\gamma \delta \rho \sigma }{R^{\alpha }}_{\beta \rho \sigma }\) [54]. Massive gravity theories are new attempts which attribute a mass to the putative graviton. The simplest work in this line and in a ghost-free manner suffers from the van Dam–Veltman–Zakharov (vDVZ) discontinuity problem [55, 56]. Due to the three additional helicity states for the massive spin-2 graviton, the limit of small graviton mass does not coincide with Einstein GR. For instance, the predicted perihelion advance violates the previous observational experiments. In order to resolve the vDVZ problem, a new model was introduced by Visser by considering a non-dynamical flat background metric [57]. Gauss–Bonnet theory is built on adding the quadratic combination of two Riemann tensors to the Einstein–Hilbert action in which it does not increase the differential order of the resulting equations of motion [58, 59]. In most of these modified theories, the energy-momentum source is described by a divergence-free tensor which couples to the geometry in a minimal way [21, 22]. However, it is worthwhile mentioning that this property of the energy-momentum tensor, which leads to the energy-momentum conservation law, is not obeyed by the particle production process [60,61,62,63,64]. Therefore, it is not unreasonable to consider a non-divergence-free energy-momentum tensor and look for a new gravitational theory. In this regard, Rastall firstly considered such kind of sources and introduced a modification to the Einstein field equations [23]. Also, there is another theory known as the curvature–matter theory of gravity [24,25,26], in which, similar to the Rastall theory, matter and geometry are coupled to each other in a non-minimal way, meaning that the ordinary energy-momentum conservation law is not valid. However, it is important to stress that all of the potential alternatives to the general theory of relativity must be viable. This means that they must be metric theories in order to be in agreement with the Einstein equivalence principle, which is today supported by a very strong empirical evidence, and that they must pass the solar system tests [35]. On the other hand, the recent starting of gravitational wave (GW) astronomy with the event GW150914, which is the first historical detection of GWs [65], could be fundamental for discriminating about various modified theories of gravity because some differences among such theories can be emphasized in the linearized theory of gravity and, in principle, can be found by GW experiments; see [66, 67] for details.

In this work, we proposed a generalized Rastall theory to show that a coupling between the geometry and matter fields helps us in providing a geometric interpretation for the dark energy and thus the current accelerating expansion phase of the universe. The main point in favor of the Rastall theory and its generalized version is that the usual conservation law on \(T_{\mu \nu }\) is tested only in the flat Minkowski spacetime or specifically in a gravitational weak field limit. Indeed, this theory reproduces a phenomenological way for distinguishing features of quantum effects in gravitational systems, i.e the violation of the classical conservation laws [24, 60, 68]. Also, one may find that the condition \({T^{\mu \nu }}_{;\mu }\ne 0\) is phenomenologically confirmed by the particle creation process in cosmology [61,62,63,64, 69,70,71,72,73]. One also may refer to [74] in favor of the viability of the original Rastall theory and our proposed generalization. In this work, it is shown that the restrictions on the Rastall parameter are of the order of \(\le \)1% with respect to the corresponding value of the general theory of relativity. In other words, the results in [74] are a confirmation that the Rastall theory and its generalization are viable theories, in the sense that the deviation of any extended theory of gravity from the standard general theory of relativity must be weak. Beside the current accelerating expansion phase of the universe, the radiation dominated era in this framework is also addressed. Moreover, we will show that the ability of the geometry to couple with the energy-momentum source may produce the primary inflationary era in our generalized version of the Rastall theory.

The paper is organized as follows. After reviewing the original Rastall theory in the next section, we address a generalization to this theory in the third section. Section 4 includes some general remarks on the constructed new theory in FRW universe. In Sect. 5, considering a flat FRW universe filled by a pressureless matter, we show that a non-minimal coupling between the geometry and the energy-momentum source may be considered as an origin for the dark energy and thus the current accelerated phase of the universe expansion. In Sect. 6, the radiation dominated era in our generalization of the Rastall theory is investigated. In Sect. 7, we study two methods to model the primary inflationary era of the universe in our formalism. Finally, Sect. 8 is devoted to the summary and concluding remarks.

2 A brief review on the Rastall theory

Based on the Rastall theory, the ordinary energy-momentum conservation law is not always available in the curved spacetime and therefore we should have [23]

$$\begin{aligned} T^{\mu \nu }_{\ \ ;\mu }=\lambda ^{\prime } R^{;\nu }, \end{aligned}$$
(1)

where R and \(\lambda ^{\prime }\) are the Ricci scalar of the spacetime and the Rastall constant parameter, respectively. In fact, \(\lambda ^{\prime }\) is a measure of the tendency of the geometry (matter fields) to couple with the matter fields (geometry) leading to the changes into the matter fields (geometry). This equation leads to the following field equations:

$$\begin{aligned} G_{\mu \nu }+\kappa ^{\prime }\lambda ^{\prime } g_{\mu \nu }R=\kappa ^{\prime } T_{\mu \nu }, \end{aligned}$$
(2)

which can finally be rewritten as

$$\begin{aligned} G_{\mu \nu }=\kappa ^{\prime } S_{\mu \nu }, \end{aligned}$$
(3)

where \(\kappa ^{\prime }\) is the Rastall gravitational coupling constant and \(S_{\mu \nu }\) is the effective energy-momentum tensor defined as

$$\begin{aligned} S_{\mu \nu }=T_{\mu \nu }-\frac{\kappa ^{\prime }\lambda ^{\prime } T}{4\kappa ^{\prime }\lambda ^{\prime }-1}g_{\mu \nu }. \end{aligned}$$
(4)

In fact, in this theory the matter fields and geometry are coupled to each other in a non-minimal way [23,24,25,26] and its compatibility with some observational data have firstly been shown by Al-Rawaf and Taha [75, 76]. Moreover, since the particle production process during the cosmos evolution does not respect the energy-momentum conservation law [60,61,62,63,64], the Rastall theory may be considered as a classical background formulation for this phenomenon [69]. Finally, we should mention that Eq. (2) implies that \(R(4\kappa ^{\prime }\lambda ^{\prime }-1)=\kappa ^{\prime } T\) where T is the trace of energy-momentum tensor. Therefore, because \(\lambda ^{\prime }\) is constant and the \(R(4\kappa ^{\prime }\lambda ^{\prime }-1)=\kappa ^{\prime } T\) condition applies to all spacetimes and energy-momentum sources, the \(\kappa ^{\prime }\lambda ^{\prime }=\frac{1}{4}\) case is not allowed [23]. More studies on the various aspects of this theory can be found in [74, 77,78,79,80,81,82,83,84,85,86,87,88,89,90].

3 The generalized Rastall theory with varying Rastall parameter

Basically, Rastall assumed that, for all of the spacetimes and energy-momentum sources, the ratio of the flow of the energy-momentum tensor (\(T^{\nu \mu }_{\ \ \ ;\mu }\)) to the Ricci scalar divergence (\(R^{;\nu }\)) is constant (\(\lambda ^{\prime }\)). It means that the evolutions of energy-momentum source and also the geometry do not affect this ratio. As an example, consider the matter dominated era in the universe history. The energy density of matter decreases during the universe expansion, but the mentioned ratio is a constant parameter in Rastall theory [75, 76] meaning that the coupling between energy-momentum source and geometry is constant, and that it is not affected by the evolution of the cosmic system. In fact, it is a very restricting condition to assume the evolution of system does not affect the mutual coupling. In addition, since the mutual coupling is a constant parameter in Rastall gravity, it did not continuously change during the universe evolution [69, 75, 76]. Indeed, since the cosmic evolution is a continuous process [13], it is a reasonable expectation that the mutual coupling between the energy-momentum sources and the geometry should be varying gradually and smoothly. Therefore, at least theoretically, it is not prohibited to generalize the Rastall theory as

$$\begin{aligned} T^{\mu \nu }_{\ \ \ ;\mu }=(\lambda R)^{;\nu }, \end{aligned}$$
(5)

leading to

$$\begin{aligned} (T_{\mu \nu }-g_{\mu \nu }\lambda R)^{;\nu }=0. \end{aligned}$$
(6)

Now, regarding the Bianchi identity, i.e. \(G_{\mu \nu }^{\ \ \ ;\nu }=0\), we obtain

$$\begin{aligned} G_{\mu \nu }=\kappa (T_{\mu \nu }-\lambda g_{\mu \nu }R), \end{aligned}$$
(7)

where \(\kappa \) is a constant and, finally, we obtain

$$\begin{aligned} G_{\mu \nu }+\kappa \lambda g_{\mu \nu }R=\kappa T_{\mu \nu }. \end{aligned}$$
(8)

Although this result looks like to the field equations of the original Rastall theory (2), here, \(\lambda \) is not generally constant. Just the same as \(\lambda ^{\prime }\) in the Rastall theory, \(\lambda \) is a measure for the strength of the coupling between the geometry to the matter fields. As is apparent, the Einstein field equations are recovered in the appropriate limit of \(\lambda =0\), a limit in which the matter fields and geometry are coupled to each other in a minimal way.

4 FRW metric and general remarks on the mutual non-minimal coupling between the geometry and matter fields

The line element of the FRW universe is written as

$$\begin{aligned} \mathrm{d}s^2=-\mathrm{d}t^2+a(t)^2\left[ \frac{\mathrm{d}r^2}{1-kr^2}+r^2(\mathrm{d}\theta ^2+\mathrm{sin}(\theta )^2\mathrm{d}\phi ^2)\right] ,\nonumber \\ \end{aligned}$$
(9)

where a(t) is the scale factor and \(k=-1,0,1\) is the curvature parameter corresponding to the open, flat and closed universes, respectively. If the universe is filled by an energy-momentum source with \(T^\mu _\nu =\mathrm{diag}(-\rho ,p,p,p)\) in which \(\rho \) and p are the energy density and pressure of the cosmic fluid, respectively, then using Eq. (8), the Friedmann equations in a flat FRW universe are given as

$$\begin{aligned} (12\kappa \lambda -3)H^2+6\kappa \lambda \dot{H}=-\kappa \rho \end{aligned}$$
(10)

and

$$\begin{aligned} (12\kappa \lambda -3)H^2+(6\kappa \lambda -2) \dot{H}=\kappa p. \end{aligned}$$
(11)

Here, \(H=\frac{\dot{a}}{a}\) denotes the Hubble parameter, and the dot sign indicates the derivative with respect to the cosmic time t. In this manner, from Eq. (5), one easily obtains

$$\begin{aligned} \frac{\mathrm{d}(\rho +\lambda R)}{\mathrm{d}t}+3H(\rho +p)=0, \end{aligned}$$
(12)

meaning that the \(\lambda R\) term is the energy density corresponding to the ability of geometry to couple with the energy-momentum sources in a non-minimal way (\(\lambda \ne 0\)). It is worthwhile mentioning here that, for an empty spacetime where \(\rho =p=0\), we should have \(\frac{\mathrm{d}(\lambda R)}{\mathrm{d}t}=0\). In addition, Eq. (12) can also be rewritten as

$$\begin{aligned} \rho +\rho _\mathrm{g}=-\int 3H(\rho +p)\mathrm{d}t, \end{aligned}$$
(13)

where \(\rho _\mathrm{g}\equiv \lambda R\). It is obvious that, in the absence of the ability of the geometry to couple with the energy-momentum sources in a non-minimal way (\(\lambda =0\)), the usual energy-momentum conservation law and the Einstein field equations can be recovered through Eqs. (8) and (12). In the following sections, we study the role of the non-minimal coupling between geometry and energy-momentum sources in the various expansion phases of the flat FRW universe.

5 Matter dominated era and an accelerating universe

Consider a flat FRW universe with the scale factor a filled by the pressureless dust matter fields. Using Eq. (8), one obtains the Friedmann equations,

$$\begin{aligned}&(12\kappa \lambda -3)H^2+6\kappa \lambda \dot{H}=-\kappa \rho _\mathrm{m},\end{aligned}$$
(14)
$$\begin{aligned}&(12\kappa \lambda -3)H^2+(6\kappa \lambda -2) \dot{H}=0, \end{aligned}$$
(15)

where \(\rho _\mathrm{m}\) denotes the energy density. It is clear that, in the \(\lambda \rightarrow 0\) limit, Eqs. (14) and (15) reduce to those of the matter dominated era in the standard cosmology [13]. In addition, Eq. (8) leads to \(R=-\frac{\kappa }{4\kappa \lambda -1}\rho _\mathrm{m}\) for a dust source requiring that we should have \(\kappa \lambda \ne \frac{1}{4}\) for \(\rho _\mathrm{m}\ne 0\) in agreement with Rastall’s original hypothesis [23]. For the deceleration parameter, defined as \(q=-1-\frac{\dot{H}}{H^2}\) [13], one can use Eq. (15) to obtain

$$\begin{aligned} q(z)=1+\frac{1}{6\kappa \lambda (z)-2}, \end{aligned}$$
(16)

where z denotes the redshift. It is obvious that the deceleration parameter of the matter dominated era in the Einstein regime (\(q=\frac{1}{2}\)) can be covered in the appropriate limit of \(\lambda =0\).

For a flat FRW universe filled by a pressureless matter, the continuity equation can be written as

$$\begin{aligned} \dot{\rho }_\mathrm{m}+3H\rho _\mathrm{m}=\frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\kappa \lambda }{4\kappa \lambda -1}\rho _\mathrm{m}\right) . \end{aligned}$$
(17)

If the pressureless source does not interact with geometry, then this equation is decomposed into the following equations:

$$\begin{aligned}&\dot{\rho }_\mathrm{m}+3H\rho _\mathrm{m}=0,\nonumber \\&\frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\kappa \lambda }{4\kappa \lambda -1}\rho _\mathrm{m}\right) =0, \end{aligned}$$
(18)

meaning that the ordinary energy-momentum conservation law is valid. Therefore, \(\lambda =0\) is a simple solution to the \(\frac{\mathrm{d}}{\mathrm{d}t}(\frac{\kappa \lambda }{4\kappa \lambda -1}\rho _\mathrm{m})=0\) equation leading to the ordinary Einstein field equations. Now, for a non-interacting universe, it is easy to check that Eq. (18) [or equally Eq. (17)] admits the following solution:

$$\begin{aligned}&\rho _\mathrm{m}=\rho _0 a^{-3},\nonumber \\&\lambda (a)=\frac{1}{4\kappa +\kappa C \rho _\mathrm{m}}=\frac{1}{4\kappa +\kappa \alpha a^{-3}}, \end{aligned}$$
(19)

where \(\rho _0\) and C are integration constants and thus \(\alpha =C\rho _0\) is a constant. It is obvious that we have \(\lambda =\frac{1}{4\kappa }\) in the absence of dust source, i.e for \(\rho _\mathrm{m}=0\). Here, we only considered a simple situation in which there is no energy exchange between the geometry and matter source. In this case, the existence of matter source only affects the ability and tendency of geometry to couple with energy source, and it does not lead to an energy exchange between the geometry and matter source, and thus a palpable mutual interaction between them. By a palpable interaction, we mean an interaction leading to a visible and measurable energy exchange between the components of system. Therefore, it seems that the non-minimal coupling between geometry and the matter source has some indirect, complex and non-local aspects hidden until now, a result in line with some previous work claiming that the probable non-local features of mutual relation between geometry and the energy sources may be considered as the origin for the dark sectors of the cosmos [91,92,93]. It is also useful to note that, even in the simplest case of (18), the properties of the geometry, including its curvature and \(\lambda \), are determined by the energy sources filling it. This is in agreement with the general relativity backbone, where the curvature of the geometry (as its property) is specified by the energy sources filling it. In a more realistic case, they may exchange energy with each other, and therefore, one cannot always decompose Eqs. (17) into  (18). Now, inserting Eqs. (32) into (14) and (15), respectively, and combining the results with each other, one reaches

$$\begin{aligned} H(a)=H_0\sqrt{\frac{a^3+\alpha }{a^3}}, \end{aligned}$$
(20)

where \(H_0=\frac{\kappa \rho _{0}}{3\alpha }\) is a constant. This equation indicates that, for the limits of \(a^3\ll \alpha \), we have \(H(a)\approx H_0\sqrt{\frac{\alpha }{a^3}}\) leading to \(a(t)=a_{0m}t^{\frac{2}{3}}\) with the integration constant \(a_{0m}=(\frac{9}{4}H^{2}_{0}\alpha )^{1/3}\), which exactly is the scale factor of the matter dominated era in the standard model of cosmology. Moreover, for the limit of \(a\gg 1\), we have \(H(a)\rightarrow H_0\) leading to \(a(t)=a_0\exp (H_0t)\) for the scale factor of the current accelerating expansion phase of the universe, in which \(a_0\) is a constant.

Now, combining \(1+z=a^{-1}\) with \(\lambda (a)=\frac{1}{4\kappa +\kappa \alpha a^{-3}}\) and inserting the result into Eq. (16), we obtain

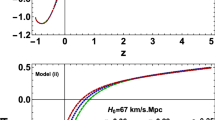
$$\begin{aligned} q(z)=\frac{\alpha (1+z)^3-2}{2(1+\alpha (1+z)^3)}. \end{aligned}$$
(21)

In order to describe the evolution of the universe from the matter dominated era to the current accelerating phase, the deceleration parameter q(z) should satisfy the three conditions as (i) \(q(z\rightarrow \infty )\rightarrow \frac{1}{2}\), (ii) \(q(z\approx 0.6)\rightarrow 0\) and (iii) \(q(z\rightarrow 0)\le -\frac{1}{2}\) [13]. Using Eq. (21), one can verify that the deceleration parameter of the matter dominated era of the standard cosmology (\(q=\frac{1}{2}\)) is obtainable in the \(\lambda \rightarrow 0\) limit or equivalently in the \(\alpha \rightarrow \infty \) limit. Moreover, at high redshift limit (\(z\rightarrow \infty \)) and independent of the \(\alpha \) parameter, we have \(q\rightarrow \frac{1}{2}\), which again addresses the matter dominated era. Therefore, the change of the pressureless matter density in our model is the same as that of the standard cosmology, i.e \(\rho _\mathrm{m}=\rho _0 a^{-3}\). Additionally, although the deceleration parameter in our model differs from that of the matter dominated era of the standard cosmology, this era is covered at the appropriate limit of \(z\rightarrow \infty \) in our model. Here, from Eq. (21), for \(-1<\alpha \le \frac{1}{2}\), we have \(q(z=0)\le -\frac{1}{2}\), which demonstrates the satisfaction of the third condition. In addition, since there is no divergence in the history of the evolution of the universe from the early matter dominated era to its current phase, q(z) should not diverge which requires that its denominator should not vanish for any non-negative amount of z. This requires \(0\le \alpha \le \frac{1}{2}\), which consequently leads to the total restricting range on the deceleration parameter as \(-1\le q(z=0)\le -\frac{1}{2}\).

Fig. 1
figure 1

Deceleration parameter q versus the redshift z for some values of \(\alpha \)

Full size image

For example, consider the case of \(q(z=0)=-0.55\) [94] which through Eq. (21) corresponds to \(\alpha =\frac{3}{7}\). Considering this value of the \(\alpha \) parameter, one can find that the \(q=0\) case is associated to the redshift \(z\simeq 0.67\) when the universe leaves its decelerating phase and enters to the accelerating phase. This result is in agreement with some observational evidence [95,96,97]. The deceleration parameter q(z) is plotted in Fig. 1 versus the redshift z for some values of the \(\alpha \) parameter. It is seen from the figure that, for small redshifts, representing the late time in the history of the universe, the deceleration parameter goes to negative values representing an accelerated expanding phase in our constructed model. As a result, a non-minimal coupling between the geometry and pressureless matter, which mainly consists of dark matter, may lead to a description for the dark energy, and therefore the current accelerating phase of the universe expansion.

Based on the above results, this mutual relation between geometry and the matter source suggests that this source and its enclosing cosmic horizon may achieve the thermodynamic equilibrium, a result which is in agreement with the recent study by Mimoso et al., focusing on the properties and criteria of a thermodynamic equilibrium between the cosmic horizon and the cosmic fluids in various cosmic eras [98].

6 Radiation dominated era and the curvature-radiation non-minimal coupling

For the flat FRW universe filled by a radiation source, the Friedmann equations are as follows:

$$\begin{aligned}&(12\kappa \lambda -3)H^2+6\kappa \lambda \dot{H}=-\kappa \rho _\mathrm{r},\end{aligned}$$
(22)
$$\begin{aligned}&(12\kappa \lambda -3)H^2+(6\kappa \lambda -2) \dot{H}= \frac{1}{3}\kappa \rho _\mathrm{r}, \end{aligned}$$
(23)

where \(\rho _\mathrm{r}\) is the energy density. Because the energy-momentum associated to radiation fields is a traceless source, i.e \(T=0\), by contracting Eq. (8), one finds \(R(4\kappa \lambda -1)=\kappa T\), which clearly for \(\kappa \lambda \ne \frac{1}{4}\) results in a null Ricci scalar for a radiation source, i.e. \(R=0\). Some simple calculations for the continuity equation and deceleration parameter also lead to

$$\begin{aligned}&\dot{\rho }_\mathrm{r}+4H\rho _\mathrm{r} =0,\nonumber \\&\rho _\mathrm{r}=\rho _{0r}a^{-4}, \end{aligned}$$
(24)

where \(\rho _{0r}\) is the integration constant, and

$$\begin{aligned} q(z)=1, \end{aligned}$$
(25)

respectively. In order to obtain the last equation, we combined Eqs. (22) and (23) with each other to get \(\frac{\dot{H}}{H^2}=-2\), a result which leads to \(a=a_0t^{\frac{1}{2}}\) for the scale factor where \(a_0\) is the integration constant, in agreement with the radiation dominated era of the standard cosmology [13]. Based on Eqs. (24) and (25), the density changes of the radiation source and the deceleration parameter of the radiation dominated era are the same as those of the standard cosmology meaning that the radiation dominated era in our model is the same as that of the standard cosmology. Indeed, since \(R=0\) in the radiation dominated era, independent of the value of \(\lambda \) parameter we have \((\lambda R)^{;\nu }=0\) meaning that the above results are independent of \(\lambda \) parameter. Now, we use the \(\rho _\mathrm{m}\rightarrow 0\) limit of the \(\lambda (a)\) relation obtained in Eq. (19), in order to find the value of \(\lambda \) which leads to \(\lambda =\frac{1}{4\kappa }\). It means that, since \(\lambda \) is a constant quantity, the geometry and radiation do not affect each other.

Indeed, since radiation is a traceless source, simple calculations lead to

$$\begin{aligned} \dot{\rho }_\mathrm{r}+4H\rho _\mathrm{r}+\dot{\rho }_\mathrm{m}+3H\rho _\mathrm{m}=\frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\kappa \lambda }{4\kappa \lambda -1}\rho _\mathrm{m}\right) , \end{aligned}$$
(26)

for the continuity equation in a universe filled by both radiation and dust. In the absence of any interaction between radiation, dust and geometry, this equation is decomposed to Eqs. (17) and (24) meaning that the \(\rho _\mathrm{r}=\rho _{0r}a^{-4}\), \(\rho _\mathrm{m}=\rho _0 a^{-3}\) and \(\lambda (\rho _\mathrm{m})=\frac{1}{4\kappa +\kappa C \rho _\mathrm{m}}\) solutions are also available in this case. Therefore, for \(\rho _\mathrm{m}=0\), we have \(\lambda =\frac{1}{4\kappa }\) meaning that the \(\lambda =\frac{1}{4\kappa }\) case is allowed in the radiation case. Inserting \(\lambda =\frac{1}{4\kappa }\) into either Eqs. (22) or (23) and combining the result with (24), we again obtain \(\frac{\dot{H}}{H^2}=-2\) leading to \(a=a_0t^{\frac{1}{2}}\) and thus \(R=0\). Here, we should mention that, since we have \(R=T=0\) in this era, the \(R(4\kappa \lambda -1)=\kappa T\) condition is available independent of the value of \(\lambda \) parameter. Indeed, unlike the Rastall theory, where the \(\lambda ^{\prime }=\frac{1}{4\kappa }\) case is not allowed [23], here, the \(\lambda =\frac{1}{4\kappa }\) case can be allowed. Therefore, although the geometry generally has the ability to couple with the energy-momentum source in a non-minimal way (\(\lambda =\mathrm{constant}\ne 0\)), since \(\lambda \) is constant, geometry and the radiation source do not affect each other. This means that the ordinary energy-momentum conservation law is respected by the radiation source as seen in (24).

Finally, we should mention that due to the fact that the radiation source does not coupled to the geometry in a non-minimal way, there is no energy flux between the geometry and radiation fields. This may be considered as the reason for the failure to achieve the thermodynamic equilibrium between the cosmic horizon and the radiation fields [98].

7 \(\lambda \) and the primary inflationary era

In this section, we address two methods to model the primary inflationary era in our formalism, and we also study the role and behavior of \(\lambda \) in these methods.

7.1 \(\lambda \) as the generator of the primary inflationary phase

Now, let us consider an empty flat FRW universe with its describing equations as

$$\begin{aligned} (12\kappa \lambda -3)H^2+6\kappa \lambda \dot{H}=0 \end{aligned}$$
(27)

and

$$\begin{aligned} (12\kappa \lambda -3)H^2+(6\kappa \lambda -2) \dot{H}=0. \end{aligned}$$
(28)

It is easy to check that both above equations are true only for \(\lambda =\frac{1}{4\kappa }=\mathrm{constant}\) and \(\dot{H}=0\). It is worthwhile mentioning that, as a desired result, the \(\lambda =\frac{1}{4\kappa }=\mathrm{constant}\) solution is in full agreement with the \(\rho _\mathrm{m}\rightarrow 0\) limit of the results obtained in Eqs. (19) and (26). Besides, since the spacetime is empty (\(T_{\mu \nu }=0\)), we should have \(\frac{\mathrm{d}(\lambda R)}{\mathrm{d}t}=0\), meaning that \(\lambda =\frac{\rho _\mathrm{g}}{R}\),where \(\rho _\mathrm{g}\equiv \psi \) is a constant. In addition, using the above equations, one sees that the \(\lambda =\frac{1}{4\kappa }=\mathrm{constant}\) and \(\dot{H}=0\) conditions lead to an exponential growth in the scale factor, i.e. \(a(t)=a_0\exp (H_0t)\) where \(a_0\) and \(H_0\) are the integration constants, with the non-vanishing Ricci scalar \(R=12H_0^2\), respectively. Now, combining the above results with each other, we obtain \(H_0=\sqrt{\frac{\kappa \psi }{3}}\). It is also obvious that, since \(\lambda \) and \(\rho _\mathrm{g}\) are constant, Eqs. (5) and (12) are met here and therefore, \(\psi \) is nothing but the integration constant in the RHS of Eq. (13). Indeed, we should remind the reader that, since Eq. (13) is the result of Eq. (5) and thus Eq. (12), the fulfillment of Eq. (5) [or equally (12)] is necessary and sufficient.

On the other hand, from Eq. (8), we know that \(R(4\kappa \lambda -1)=T\) which its right hand side vanishes due to the emptiness of the spacetime. Then, since the Ricci scalar does not vanish, i.e. \(R\ne 0\), we find that we should have \(\lambda =\frac{1}{4\kappa }\). This is in agreement with the previous mentioned results obtained from solving Eqs. (27) and (28), applying the \(\rho _\mathrm{m}\rightarrow 0\) limit to Eq. (19). Once again, we see that unlike the original Rastall theory, the case of \(\lambda =\frac{1}{4\kappa }\) may be allowed in this new formulation of the Rastall theory.

Therefore, the inflationary era may be supported in this model by a unique feature of the geometry which is the ability of the geometry to couple with the energy-momentum sources in a non-minimal way in agreement with this fact that \(\lambda =constant \ne 0\). In fact, the empty flat FRW spacetime is forced to expand exponentially by this ability. We should note that the absence of the energy-momentum source does not mean that the geometry does not have the ability of coupling to the energy-momentum sources. Indeed, in this case, the absence of an energy-momentum source only means that the geometry does not couple to anything. It is also worthwhile to mention that since \(T=0\) and \(\lambda \) is constant in both the radiation dominated and the primary inflationary phases, the obtained results about these eras may be generalizable to the original Rastall theory.

7.2 Energy extraction during the inflationary era

We saw that the ability and tendency of geometry to couple with the energy sources, in the non-minimal way, does not disappear, i.e. \(\lambda \ne 0\), in the absence of an energy-momentum source. In fact, this is a property of geometry which enforces the empty FRW spacetime to expand exponentially. Moreover, from Eq. (12), we found that the \(\lambda R=\rho _\mathrm{g}(\equiv \psi )\) term behaves as an energy density. Here, \(\psi \) is the energy density associated with the non-minimal coupling \(\lambda \), and therefore, we get \(E=\int \psi \mathrm{d}V=\frac{4\pi }{3}\psi a(t)^3V_0\) for the total energy of co-moving volume \(V_0\) corresponding to this coupling at any given time t. Finally, for the amount of the energy of the co-moving volume \(V_0\) specified from spacetime at time \(t+\delta t\), due its intrinsic property to couple with the energy-momentum sources in the non-minimal way, we have

$$\begin{aligned} E(t+\delta t)= & {} \frac{4\pi }{3}\psi a(t+\mathrm{d}t)^3V_0\nonumber \\\simeq & {} \frac{4\pi }{3}\psi a(t)^3V_0\exp \left( 3\sqrt{\frac{\kappa \psi }{3}}\delta t\right) , \end{aligned}$$
(29)

meaning that the released energy grows exponentially.

Therefore, in our formalism, the ability and tendency of geometry to couple with the energy-momentum sources enforces the universe to expand, and in fact, it is the backbone of the universe expansion and the energy production in the primary inflationary phase. Thus, this ability may also help us to provide a unified mechanism explaining the primary inflationary era as well as the current accelerating phase of the universe expansion.

7.3 Standard inflation and \(\lambda \)

In the previous subsection, we found that, even in the absence of an inflaton field, the tendency of geometry to couple with the energy-momentum sources may lead to an inflationary phase for the universe expansion and, consequently, the slow-rolling parameters do not appear in that scenario. It is useful to mention that there are also some inflationary models in which the slow-roll condition does not appear [99,100,101]. Here, we will show that the standard inflation scenario by implementing an inflaton field can also be valid in our formalism.

In order to achieve this goal, we consider a spatially homogeneous scalar field evolving in potential \(\mathcal {V}(\phi )\). Therefore, simple calculation yields \(\rho _\phi =\frac{1}{2}\dot{\phi }^2+\mathcal {V}(\phi )\) and \(p_\phi =\frac{1}{2}\dot{\phi }^2-\mathcal {V}(\phi )\) for the energy density and pressure of the inflaton field [13]. Now, the Friedmann equations in a flat FRW universe filled by the mentioned field are written as

$$\begin{aligned}&(12\kappa \lambda -3)H^2+6\kappa \lambda \dot{H}=-\kappa \rho _\phi ,\nonumber \\&(12\kappa \lambda -3)H^2+(6\kappa \lambda -2) \dot{H}=\kappa p_\phi , \end{aligned}$$
(30)

which finally lead to

$$\begin{aligned} \dot{H}= & {} -\frac{\kappa }{2}[\rho _\phi +p_\phi ], \end{aligned}$$
(31)

for the Raychaudhuri equation. In addition, in the same way as the matter dominated era, considering a simple situation in which there is no energy exchange between the energy-momentum source and geometry, we obtain \(\dot{\rho }_\phi +3H(\rho _\phi +p_\phi )=-\frac{\mathrm{d}(\lambda R)}{\mathrm{d}t}=0\), leading to

$$\begin{aligned}&\ddot{\phi }+\frac{\partial \mathcal {V}}{\partial \phi }+3H\dot{\phi }=0,\nonumber \\&\lambda =\frac{1}{4\kappa [1+\gamma ^{-1}(3p_\phi -\rho _\phi )]}, \end{aligned}$$
(32)

for the continuity equation in which \(\gamma ^{-1}\) is constant. Now, if \(\ddot{\phi }\) is negligible and \(\dot{\phi }^2\ll \mathcal {V}(\phi )\), then \(p_\phi \simeq -\rho _\phi \) and from Eqs. (31) and (32), we find that \(\dot{H}\simeq 0\) and \(\lambda (\phi )\simeq \frac{1}{4\kappa [1-4\gamma ^{-1}\mathcal {V}(\phi )]}\), respectively. In fact, when \(\ddot{\phi }\) is negligible, Eq. (32) helps us in getting \(\mathcal {V}^{\prime \prime }\simeq \frac{3\kappa }{2}\dot{\phi }^2\), leading to \(\eta \equiv \frac{2}{3\kappa }(\frac{\mathcal {V}^{\prime \prime }}{\mathcal {V}})\simeq \frac{\dot{\phi }^2}{\mathcal {V}}\). Therefore, during the inflation process, when the slow-roll approximation is valid, we have \(\eta \ll 1\) in agreement with the standard inflation hypothesis [13]. In this manner, inserting Eq. (32) into Eq. (30), one can easily obtain \(H^2\simeq \frac{\kappa }{3}[4\mathcal {V}-\gamma ]\) recovering the standard inflation results at the appropriate limit of \(\lambda \rightarrow 0\) (or equally \(\gamma \rightarrow 0\)). Moreover, since \(q=-1-\frac{\dot{H}}{H^2}\simeq -1\) at the time of inflation, we should have \(\epsilon \equiv -\frac{\dot{H}}{H^2}\ll 1\) [13]. Now, using Eqs. (31) and (32), one obtains \(\epsilon \simeq \frac{8}{\kappa }[\frac{\mathcal {V}^\prime }{4\mathcal {V}-\gamma }]^2\), where the prime sign stands for the derivative with respect to \(\phi \). It is interesting to note that if we define \(\tilde{V}(\phi )\equiv 4\mathcal {V}-\gamma \), then we have \(H^2\simeq \frac{\kappa }{3}\tilde{V}\) and \(\epsilon \simeq \frac{8}{\kappa }[\frac{\mathcal {V}^\prime }{4\mathcal {V}-\gamma }]^2=\frac{1}{2\kappa }(\frac{\frac{\partial \tilde{V}}{\partial \phi }}{\tilde{V}})^2\) similar to those of the standard inflation scenario [13]. Therefore, if the slow-roll approximation is valid, then a spatially homogeneous scalar field evolving in potential \(\mathcal {V}(\phi )\) can support the primary inflationary era in our formalism whenever the inflaton field (or equally \(\mathcal {V}(\phi )\)) satisfies the \(H^2\simeq \mathrm{constant}>0\), \(\epsilon <1\) and \(\eta \ll 1\) conditions. It is finally worth to mention that approaching the end of inflation, where \(\mathcal {V}(\phi )\rightarrow 0\), we have \(\lambda \rightarrow \frac{1}{4\kappa }\) revealing the consistency with our results in previous sections about the radiation dominated era.

8 Summary and concluding remarks

After referring to the Rastall theory, we addressed a generalization of this theory and studied some of its cosmological consequences. Based on our results, a non-minimal coupling between the geometry and a pressureless matter field may lead to a transition from the matter dominated era to the current accelerating phase, in agreement with some previous observations [95,96,97]. We only focused on the \(T^{\mu \nu }_{\ \ ;\mu }=0=-\frac{\mathrm{d}(\lambda R)}{\mathrm{d}t}\) solutions. In this case, a dust source, which satisfies the ordinary energy-momentum conservation law, is allowed, and as we have seen, the evolution of its energy density is the same as that of the standard cosmology. It should also be noted that although the same as the general relativity \(T^{\mu \nu }_{\ \ ;\mu }=0\) in our model, since \(\lambda \ne 0\), the Friedmann equations in our model differ from those of the standard cosmology. In addition, we found that, in our formalism, the evolution of the energy density in the radiation dominated era is the same as that of the standard cosmology. Indeed, we found that, during the radiation dominated era, \(\lambda \) remains a non-zero constant quantity, meaning that the evolution of the radiation source and the geometry do not affect the value of \(\lambda \).

Finally, we considered an empty flat FRW universe and realized that, even in the absence of an inflaton field, a primary inflationary era can be driven in this generalized version of Rastall theory when \(\lambda =\frac{1}{4\kappa }\). Therefore, our study shows that the ability and tendency of geometry to couple with the energy-momentum sources (\(\lambda \ne 0\)) may be the backbone of the primary inflationary era and the current accelerating phases of the universe expansion in a unified picture. Also, a scenario for a universe filled by an inflaton field in the context of the Rastall theory has been introduced. In this context, as the matter dominated era, we have only focused on simple case of \(T^{\mu \nu }_{\ \ ;\mu }=0=-\frac{\mathrm{d}(\lambda R)}{\mathrm{d}t}\) meaning that there is no energy exchange between geometry and the cosmic fluid. Once again, we should remind the reader that since \(\lambda \ne 0\), the Friedmann equations in our model differ from those of general relativity. It is seen that if the inflaton field meets the usual slow-roll conditions, then it can support an inflationary phase.