Observational constraints on f(T) gravity from varying fundamental constants

Abstract

We use observations related to the variation of fundamental constants, in order to impose constraints on the viable and most used f(T) gravity models. In particular, for the fine-structure constant we use direct measurements obtained by different spectrographic methods, while for the effective Newton constant we use a model-dependent reconstruction, using direct observational Hubble parameter data, in order to investigate its temporal evolution. We consider two f(T) models and we quantify their deviation from $\Lambda$CDM cosmology through a sole parameter. Our analysis reveals that this parameter can be slightly different from its $\Lambda$CDM value, however, the best-fit value is very close to the $\Lambda$CDM one. Hence, f(T) gravity is consistent with observations, nevertheless, as every modified gravity, it may exhibit only small deviations from $\Lambda$CDM cosmology, a feature that must be taken into account in any f(T) model-building.

1 Introduction

Modified gravity [1] is one of the two main roads one can follow in order to provide an explanation for the early and late-time universe acceleration (the second one in the introduction of the dark-energy concept [2, 3]). Furthermore, apart from the cosmological motivation, modified gravity has a theoretical motivation too, namely to improve the renormalizability properties of standard general relativity [4].

In constructing a gravitational modification, one usually starts from the Einstein–Hilbert action and extends it accordingly. Thus, one can obtain f(R) gravity [5], Gauss–Bonnet and f(G) gravity [6, 7], gravity with higher-order curvature invariants [8, 9], massive gravity [10] etc. Nevertheless, one could start from the equivalent, torsional formulation of gravity, namely from the Teleparallel Equivalent of General Relativity (TEGR) [11,12,13], in which the gravitational Lagrangian is the torsion scalar T, and construct various modifications, such as f(T) gravity [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] (see [30] for a review), teleparallel Gauss–Bonnet gravity [31, 32], gravity with higher-order torsion invariants [33], etc.

An important question in the above gravitational modifications is what are the forms of the involved unknown functions, and what are the allowed values of the various parameters. Excluding forms and parameter regimes that lead to obvious contradictions and problems, the main tool we have in order to provide further constraints is to use observational data. For the case of torsional gravity one can use solar system data [34,35,36,37], or cosmological observations from Supernovae type Ia, cosmic microwave background and baryonic acoustic oscillations [38,39,40,41].

On the other hand, in some modified cosmological scenarios one can obtain a variation of the fundamental constants, such as the fine-structure constant and the Newton constant. Such a possibility has been investigated in the literature since Dirac [42, 43] and Milne and Jordan [44,45,46,47] times. Later on, Brans and Dicke proposed the time variation of the Newton constant, driven by a dynamical scalar field coupled to curvature [48, 49], while Gamow triggered subsequent speculations on the possible variation of the fine-structure constant [50]. Similarly, in recent modified gravities, which involve extra degrees of freedom compared with general relativity, one may obtain such a variation of the fundamental constants [51,52,53,54,55,56,57,58,59,60,61,62,63]. However, since experiments and observations give strict bounds on these variations [64,65,66,67,68,69,70,71,72,73,74,75,76], one can use them in order to constrain the theories at hand.

In the present work we are interested in investigating the constraints on f(T) gravity by observations related to the variation of fundamental constants. In particular, since f(T) gravity predicts a variation of the fine-structure constant and the Newton constant, we will use the recent observational bounds of these variations in order to constrain the f(T) forms as well as the range of the involved parameters. The plan of the work is the following: In Sect. 2 we give a brief review of f(T) gravity and cosmology. In Sect. 3 we investigate the constraints on specific f(T) gravity models arising from the observational bounds of the fine-structure constant variation, while in Sect. 4 we study the corresponding constraints that arise from the observational bounds of the Newton constant variation. Finally, in Sect. 5 we summarize our results.

2 f(T) gravity and cosmology

In this section we provide a short review of f(T) gravity and cosmology. We use the tetrad fields $e^\mu _A$, which form an orthonormal base at each point of the tangent space of the underlying manifold $(\mathcal {M},g_{\mu \nu })$, where $g_{\mu \nu }=\eta _{A B} e^A_\mu e^B_\nu$ is the metric tensor defined on this manifold (we use Greek indices for the coordinate space and Latin indices for the tangent one). Furthermore, instead of the torsionless Levi-Civita connection which is used in the Einstein–Hilbert action, we use the curvatureless Weitzenböck connection $\overset{\mathbf {w}}{\Gamma }^\lambda _{\nu \mu }\equiv e^\lambda _A\, \partial _\mu e^A_\nu$ [13]. Hence, the gravitational field in such a formalism is described by the following torsion tensor:

$$\begin{aligned} T^\rho _{\mu \nu } \equiv e^\rho _A \left( \partial _\mu e^A_\nu - \partial _\nu e^A_\mu \right) . \end{aligned}$$

(1)

Subsequently, the Lagrangian of the teleparallel equivalent of general relativity, namely the torsion scalar T, is constructed by contractions of the torsion tensor as [13]

$$\begin{aligned} T\equiv \frac{1}{4} T^{\rho \mu \nu } T_{\rho \mu \nu } +\frac{1}{2}T^{\rho \mu \nu }T_{\nu \mu \rho } -T_{\rho \mu }{}^{\rho }T^{\nu \mu }{}_{\nu }\, \, . \end{aligned}$$

(2)

One may consider generalized theories in which the Lagrangian T is extended to an arbitrary function f(T), similarly to the f(R) extension of curvature-based gravity. In particular, such a gravitational action will read

$$\begin{aligned} {\mathcal S}_{gr} = \frac{1}{16\pi G_\mathrm{N}}\int \mathrm{d}^4x |e| f(T), \end{aligned}$$

(3)

where $e = \text {det}(e_{\mu }^A) = \sqrt{-g}$, and $G_\mathrm{N}$ is the Newton constant. Additionally, along the gravitational action (3) we consider the matter sector, and hence the total action writes as

$$\begin{aligned} \mathcal {S}&= \frac{1}{16\pi G_\mathrm{N}} \int \mathrm{d}^4 x\, |e|\, f(T) + \int \mathrm{d}^4 x\, \mathcal {L}_m (e^A_{\mu }, \Psi _M), \end{aligned}$$

(4)

where $\mathcal {L}_m (e^A_{\mu }, \Psi _M)$ is the total matter Lagrangian including the electromagnetic field. Finally, variation in terms of the tetrad fields give rise to the field equations as

$$\begin{aligned}&e^{-1}\partial _{\mu }(ee_A^{\rho }S_{\rho }{}^{\mu \nu })f_{T} -f_{T}e_{A}^{\lambda }T^{\rho }{}_{\mu \lambda }S_{\rho }{}^{\nu \mu }+\frac{1}{4} e_ { A } ^ { \nu }f({T}) \nonumber \\&\quad + e_A^{\rho }S_{\rho }{}^{\mu \nu }\partial _{\mu }({T})f_{TT} = 4\pi G_\mathrm{N}e_{A}^{\rho } {\mathcal {T}^{(m)}}_{\rho }{}^{\nu }, \end{aligned}$$

(5)

where $f_{T}=\partial f/\partial T$, $f_{TT}=\partial ^{2} f/\partial T^{2}$, and with ${\mathcal {T}^{(m)}}_{\rho }{}^{\nu }$ the total matter energy-momentum tensor. In the above equation we have inserted for convenience the “super-potential” tensor $S_\rho ^{\mu \nu } = \frac{1}{2} \left( K^{\mu \nu }_{\rho }+\delta ^\mu _\rho T^{\alpha \nu }_{\alpha }-\delta ^\nu _\rho T^{\alpha \mu }_{\alpha }\right)$, defined in terms of the co-torsion tensor $K^{\mu \nu }_{\rho }=-\frac{1}{2}\left( T^{\mu \nu }_{\rho } - T^{\nu \mu }_{\rho } - T_\rho ^{\mu \nu }\right)$. Applying f(T) gravity in a cosmological framework we consider a spatially flat FLRW universe with line element $ds^2= -dt^2 + a^2 (t) [dr^2 + r^2\, d \theta ^2 + \sin ^2 \theta \, d \phi ^2]$, which arises from the diagonal tetrad $e_{\mu }^A=\mathrm{diag}(1,a(t),a(t),a(t))$, with a(t) the scale factor. In this case, the field equations (5) become

$$\begin{aligned} H^2&= \frac{8 \pi G_\mathrm{N}}{3} \left( \rho + \rho _T \right) ,\end{aligned}$$

(6)

$$\begin{aligned} \dot{H}&= - 4 \pi G_\mathrm{N}\, \left[ \left( p+ p_T \right) + \left( \rho + \rho _T \right) \right] , \end{aligned}$$

(7)

where $\rho$ and p are, respectively, the total matter energy density and pressure, and where $\rho _T$, $p_T$ are the effective dark-energy density and the pressure of gravitational origin, given by

$$\begin{aligned} \rho _T&= \frac{1}{16 \pi G_\mathrm{N}}\, \left[ 2 T f_T - f (T) - T\right] ,\end{aligned}$$

(8)

$$\begin{aligned} p_T&= \frac{1}{16 \pi G_\mathrm{N}}\, \left[ 4 \dot{H}\, \left( 2T f_{TT} + f_T- 1\right) \right] - \rho _T~. \end{aligned}$$

(9)

In the above expressions we have used

$$\begin{aligned} T = - 6H^2, \end{aligned}$$

(10)

which arises straightforwardly from (2) in the FLRW universe. Finally, from Eqs. (8), (9) we can define the effective dark-energy equation of state (EoS) as

$$\begin{aligned} w = -1 - \frac{2 \dot{H}}{3 H^2}= -1 + \frac{2}{3}H(1+z) \frac{\mathrm{d}H}{\mathrm{d}z}, \end{aligned}$$

(11)

where as usual we use the redshift $z=\frac{a_0}{a}-1$, as the independent variable, and for simplicity we set $a_0=1$. Clearly, w has a dynamical nature.

In the following we focus on two well-studied, viable f(T) models, which correspond to a small deviation from $\Lambda$CDM cosmology, and which according to [38,39,40,41] are the ones that fit the observational data very efficiently.

• The first scenario is the power-law model (hereafter $f_{1}$CDM) introduced in [14], with

  $$\begin{aligned} f (T) = T + \theta \left( -T \right) ^{b}, \end{aligned}$$

  (12)

  where $\theta$, b are the two free model parameters, out of which only one is independent. Inserting this f(T) form into the first Friedmann equation (6) at present time, i.e. at redshift $z= 0$, one may derive that

  $$\begin{aligned} \theta =(6H_0^2)^{1-b}\left( \frac{1- \Omega _{m0}}{2b-1} \right) , \end{aligned}$$

  (13)

  where $\Omega _{m0}=\frac{8\pi G \rho _{m0}}{3H_0^2}$ is the corresponding density parameter at present. Hence, and using additionally that $\rho _{m}=\rho _{m0}(1+z)^{3}$, Eq. (6) for this model can be written as

  $$\begin{aligned} \frac{H^2(z)}{H_0^2} = \left( 1- \Omega _{m0}\right) \left[ \frac{H^2(z)}{H_0^2}\right] ^b + \Omega _{m0}(1+z)^3. \end{aligned}$$

  (14)

  Lastly, we mention that the above model for $b= 0$ reduces to $\Lambda$CDM cosmology, while for $b= 1/2$ it gives rise to the Dvali–Gabadadze–Porrati (DGP) model [77].

• The second scenario is the square-root-exponential (hereafter $f_{2}$CDM) of [15], with

  $$\begin{aligned} f(T)=T + \beta T_{0}(1-e^{-p\sqrt{T/T_{0}}}), \end{aligned}$$

  (15)

  in which $\beta$ and p the two free model parameters out of which only one is independent. Inserting this f(T) form into (6) at present time, one obtains

  $$\begin{aligned} \beta =\frac{1- \Omega _{m0}}{1-(1+p)e^{-p}}. \end{aligned}$$

  (16)

  Finally, the first Friedmann equation (6) for this model can be written as

  $$\begin{aligned}&\frac{H^2(z)}{H_0^2} + \frac{1-\Omega _{m0} }{1-(1+p)e^{-p}}\!\left\{ \left[ 1+ \frac{pH(z)}{H_0} \right] \, e^{-\frac{pH(z)}{H_0} }\!- \!1\right\} \nonumber \\&\quad = \Omega _{m0}\,(1+z)^3 . \end{aligned}$$

  (17)

  Lastly, note that this model reduces to $\Lambda$CDM cosmology for $p\rightarrow +\infty$. Hence, in the following, for this model it will be convenient to set $b\equiv 1/p$, and hence $\Lambda$CDM cosmology is obtained for $b \rightarrow 0^{+}$.

3 Observational constraints from fine-structure constant variation

In this section we will use observational data of the variation of the fine-structure constant $\alpha$, in order to constrain f(T) gravity. Let us first quantify the $\alpha$-variation in the framework of f(T) cosmology. In general, in a given theory the fine-structure constant is obtained using the coefficient of the electromagnetic Lagrangian. In the case of modified gravities, this coefficient generally depends on the new degrees of freedom of the theory [56,57,58,59,60,61,62,63, 78]. Even if one starts from the Jordan-frame formulation of a theory, with an uncoupled electromagnetic Lagrangian, and although the electromagnetic Lagrangian is conformally invariant, and it is not affected by conformal transformations between the Jordan and Einstein frames, thus it will acquire a dependence on the extra degree(s) of freedom due to quantum effects [79, 80]. In particular, if $\phi$ is the extra degree of freedom that arises from the conformal transformation $\tilde{g}_{\mu \nu } =\Omega ^2 g_{\mu \nu }$ from the Jordan to the Einstein frame, then quantum effects such as the presence of heavy fermions (note that this does not necessarily require new physics till the Planck scale) will induce a coupling of $\phi$ to photons, namely [79, 80]

$$\begin{aligned} S_{\mathrm{EM}}=-\frac{1}{g_{\mathrm{bare}}^2}\int \mathrm{d}^4x\sqrt{-g}B_F(\phi )F_{\mu \nu }F^{\mu \nu }, \end{aligned}$$

(18)

where $F_{\mu \nu }$ is the electromagnetic tensor, $g_{bare}$ the bare coupling constant, and

$$\begin{aligned} B_F(\phi )=1+\beta _\gamma \frac{\phi }{M_{\mathrm{pl}}}+\cdots , \end{aligned}$$

(19)

with $M_{\mathrm{pl}}=1/(8\pi G_\mathrm{N})$ the Planck mass and $\beta _\gamma =\mathcal{{O}}(1)$ a constant (we have assumed that $\beta _\gamma \phi \ll M_{\mathrm{pl}}$). Hence, the scalar coupling to the electromagnetic field will imply a dependence of the fine-structure constant of the form [78,79,80]

$$\begin{aligned} \frac{1}{\alpha _{\mathrm{E}}}=\frac{1}{\alpha _{\mathrm{J}}} B_F(\phi ), \end{aligned}$$

(20)

where the subscripts denote the Einstein and Jordan frames, respectively, or equivalently

$$\begin{aligned} \frac{\Delta \alpha }{\alpha }\equiv \frac{\alpha _{\mathrm{E}}-\alpha _{\mathrm{J}}}{\alpha _{\mathrm{J}}} =\frac{1}{ B_F(\phi )} -1. \end{aligned}$$

(21)

The above factor is in general time (i.e. redshift) dependent. Therefore, it proves convenient to normalize it in order to have $\Delta \alpha =0$ at present ($z=0$), which in the case where $B_F(z=0)\equiv B_{F0}\ne 1$ is obtained through a rescaling $F_{\mu \nu }\rightarrow \sqrt{ B_{F0}} F_{\mu \nu }$ and $B_F\rightarrow B_F/B_{F0}$. Thus, we result to

$$\begin{aligned} \frac{\Delta \alpha }{\alpha }=\frac{B_{F0}}{ B_F(\phi )} -1. \end{aligned}$$

(22)

Although the above procedure is straightforward in cases where a conformal transformation from the Jordan to the Einstein frame exists, it becomes more complicated for theories where such a transformation is not known. In case of f(T) gravity, it is well known that a conformal transformation does not exist in general, since transforming the metric as $\tilde{g}_{\mu \nu } =\Omega ^2 g_{\mu \nu }$, with $\Omega ^2=f_T$ a smooth non-vanishing function of spacetime coordinates, one obtains Einstein gravity plus a scalar field Lagrangian, plus the transformed matter Lagrangian, plus a non-vanishing term $2\Omega ^{-6}\tilde{\partial }^\mu \Omega ^2\tilde{T}^\rho _{\ \rho \mu }$ [81]. This additional term forbids the complete transformation to the Einstein frame, and hence in every application one has indeed to perform calculations in the more complicated Jordan one.

In order to avoid performing calculations in the Jordan frame we will make the reasonable assumption that $f(T)=T+\text {const}.+\text {corrections}$, which has been shown to be the case according to observations [34,35,36,37,38,39,40,41], and holds for the two forms considered in this work, namely (12) and (15), too. Hence, $\Omega ^2=1+\text {corrections}$, and then $\tilde{\partial }^\mu \Omega ^2$ is negligible, which implies that the above extra term can be neglected. In the end of our investigation, we will verify the validity of the above assumption. Thus, we can indeed obtain an approximate transformation to the Einstein frame, and in particular the introduced degree of freedom reads $\phi =-\sqrt{3}/f_T$ [81]. Hence, inserting this into (19) we acquire

$$\begin{aligned} B_F(\phi )=1-\frac{\sqrt{3}\beta _\gamma }{M_{\mathrm{pl}} f_T}+\cdots , \end{aligned}$$

(23)

and thus inserting into Eq. (22), we can easily extract the variation of the fine-structure constant as

$$\begin{aligned} \frac{\Delta \alpha }{\alpha } (z)= \frac{M_{\mathrm{pl}}f_{T0}-\sqrt{3}\beta _\gamma }{M_{\mathrm{pl}}f_T(z)-\sqrt{3}\beta _\gamma } - 1, \end{aligned}$$

(24)

where $f_{T0}= f_T (z= 0)$. Lastly, since $\beta _\gamma =\mathcal{{O}}(1)$, the above relation becomes

$$\begin{aligned} \frac{\Delta \alpha }{\alpha } (z)\approx \frac{f_{T0}}{f_T(z)} - 1. \end{aligned}$$

(25)

Hence, for a general f(T), the ratio $\Delta \alpha / \alpha$ indeed depends on z, through the $f_T(z)$ function (we recall that according to (10), $T(z)=-6H^2(z)$), while in the case of standard $\Lambda$CDM cosmology, where $f(T)=T+\Lambda$, $\Delta \alpha / \alpha$ becomes zero.

Table 1 Compilation of recent measurements of the fine-structure constant obtained by different spectrographic methods. For details in each case, see the corresponding references

In the following, we confront Eq. (25) with observations of the fine-structure constant variation, in order to impose constraints on f(T) gravity (it proves that the neglected term between (24) and (25) imposes an error of the order of $10^{-9}$ and hence our approximation is justified). We use direct measurements of the fine-structure constant that are obtained by different spectrographic methods, summarized in Table 1. Additionally, along with these data sets, and in order to diminish the degeneracy between the free parameters of the models, we use 580 Supernovae data (SNIa) from Union 2.1 compilation [88], as well as data from BAO observations, adopting the three measurements of A(z) obtained in [89], and using the covariance among these data given in [90].

In the following two subsections, we analyze two viable models, namely $f_1$CDM of (12) and $f_2$CDM of (15), separately.

3.1 Model $f_1$CDM: $f(T) = T + \theta \left( -T \right) ^{b}$

For the power-law $f_1$CDM model of (12), we easily acquire

$$\begin{aligned} f_T(z)&= 1- b\,\left( \frac{1-\Omega _{m0}}{2b-1} \right) \, \left[ \frac{H^2(z)}{H_0^2}\right] ^{(b-1)}, \end{aligned}$$

(26)

where we have used also (10). Inserting (26) into (25) we can derive the evolution of $\Delta \alpha / \alpha$ as

$$\begin{aligned} \frac{\Delta \alpha }{\alpha } (z) \approx \frac{\left[ 1- b\,\left( \frac{1-\Omega _{m0}}{2b-1} \right) \right] }{\left\{ 1- b\,\left( \frac{1-\Omega _{m0}}{2b-1} \right) \, \left[ \frac{H^2(z)}{H_0^2}\right] ^{(b-1)}\right\} }-1, \end{aligned}$$

(27)

where the ratio $H^2(z)/H_0^2$ is given by (14).

We mention that while analyzing the model for the data set of $\Delta \alpha / \alpha$ of Table 1, we have marginalized over $\Omega _{m0}$, and thus the statistical information focuses only on the parameter b. For the fittings $\Delta \alpha / \alpha$ $+$ SNIa and $\Delta \alpha / \alpha$ $+$ SNIa $+$ BAO, we have considered $\Omega _{m0}$ as a free parameter, and we have found that $\Omega _{m0} = 0.23 \pm 0.13$ (for $\Delta \alpha / \alpha$ $+$ SNIa) and $\Omega _{m0} = 0.293 \pm 0.023$ (for $\Delta \alpha / \alpha$ $+$ SNIa $+$ BAO) at 1$\sigma$ confidence level.

Fig. 1

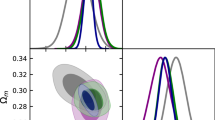
1$\sigma$ and 2$\sigma$ confidence regions for the $f_1$CDM power-law model of (12), obtained from the joint analysis $\Delta \alpha / \alpha$ $+$ SNIa $+$ BAO. The cross marks the best-fit value

Finally, in Fig. 1 we present the 68.27 and 95.45$\%$ confidence regions in the plane $\Omega _{m0} - b$, considering the observational data $\Delta \alpha / \alpha$ $+$ SNIa $+$ BAO. Note that these results are in qualitative agreement with those of different observational fittings [38,39,40], and show that $\Lambda$CDM cosmology (which is obtained for $b=0$) is inside the obtained region. In fact, one may notice from Table 2 that the reduced $\chi ^2$ for $\Delta \alpha / \alpha$ $+$ SNIa and $\Delta \alpha / \alpha$ $+$ SNIa $+$ BAO data are very close to 1, while for single data from $\Delta \alpha / \alpha$ its value slightly exceeds 1 although not significantly.

Table 2 Summary of the best-fit values of the parameter b of the $f_1$CDM power-law model of (12), for three different observational data sets with reduced $\chi ^2$: $\chi ^2_{\mathrm{min}}/\mathrm{d.o.f.}$ (d.o.f. stands for the “degrees of freedom”)

Additionally, in order to examine the late-time asymptotic behavior of the scenario at hand, in Fig. 2 we depict the evolution of the equation-of-state parameter given in (11), applying a reconstruction at 1$\sigma$ confidence level via error propagation using the joint analysis $\Delta \alpha / \alpha$ $+$ SNIa $+$ BAO. As we can see, w at late times acquires values very close to ‘$-1$’, as expected. For a more detailed investigation of the late-time asymptotics up to the far future one must apply the method of dynamical system analysis as it was done in [91,92,93], where it was thoroughly shown that the universe will end in a de Sitter phase.

Fig. 2

The evolution of the equation-of-state parameter given in (11), for the $f_1$CDM power-law model of (12), applying a reconstruction at 1$\sigma$ confidence level via error propagation using the joint analysis $\Delta \alpha / \alpha$ $+$ SNIa $+$ BAO

In summary, it is clear that $f_1$CDM model, under all the above three different combinations of statistical data sets, remains close to $\Lambda$CDM cosmology as expected. Lastly, note that this is a self-consistent verification for the validity of our assumption that $f(T)=T+\text {const}.+\text {corrections}$, which allowed us to work in the Einstein frame.

3.2 Model $f_2$CDM: $f(T)=T + \beta T_{0}(1-e^{-p\sqrt{T/T_{0}}})$

For the square-root-exponential $f_2$CDM model of (15), we easily obtain

$$\begin{aligned} f_T (z) = 1+ \frac{p}{2} \left[ \frac{1-\Omega _{m0}}{1-(1+p)\, e^{-p}}\right] \, \left[ \frac{ H_0}{H(z)} \right] e^{-\frac{pH(z)}{H_0}}.\nonumber \\ \end{aligned}$$

(28)

Inserting (28) into (25) we can derive the evolution of $\Delta \alpha / \alpha$ as

$$\begin{aligned} \frac{\Delta \alpha }{\alpha } (z) \approx \frac{\left\{ 1+ \frac{p}{2}\left[ \frac{1-\Omega _{m0}}{1-(1+p) e^{-p}}\right] e^{-p} \right\} }{\left\{ 1+ \frac{p}{2} \left[ \frac{1-\Omega _{m0}}{1-(1+p)\, e^{-p}}\right] \, \left[ \frac{ H_0}{H(z)} \right] e^{-\frac{pH(z)}{H_0}}\right\} } -1, \end{aligned}$$

(29)

where the ratio $H^2(z)/H_0^2$ is given by (17).

We mention that while analyzing the model for the data set of $\Delta \alpha / \alpha$ of Table 1, we have marginalized over $\Omega _{m0}$, and thus the statistical information focuses only on the parameter b. For the fittings $\Delta \alpha / \alpha +$ SNIa and $\Delta \alpha / \alpha + \mathrm{SNIa} + \mathrm{BAO}$ we have taken $\Omega _m$ as a free parameter, and we note that $\Omega _{m0} = 0.277 \pm 0.019$ (for $\Delta \alpha / \alpha$ $+$ SNIa) and $\Omega _{m0} = 0.283 \pm 0.016$ (for $\Delta \alpha / \alpha$ $+$ SNIa $+$ BAO) at 1$\sigma$ confidence level.

Fig. 3

1$\sigma$ and 2$\sigma$ confidence regions for the $f_2$CDM square-root-exponential model of (15), obtained from the joint analysis $\Delta \alpha / \alpha$ $+$ SNIa $+$ BAO. The cross marks the best-fit value

Finally, in Fig. 3 we present the 68.27$\%$ and 95.45$\%$ confidence regions in the plane $\Omega _{m0} - b$, considering the observational data $\Delta \alpha / \alpha$ $+$ SNIa $+$ BAO (we have taken $b \gtrsim 0.001$ in order to avoid divergences in the function H(z) at high redshifts). Note that these results are in qualitative agreement with those of different observational fittings [38,39,40], and show that $\Lambda$CDM cosmology (which is obtained for $b \rightarrow 0^{+}$) is inside the obtained region. Furthermore, and similarly to the $f_1$CDM model, from Table 3 we deduce that although the data from $\Delta \alpha / \alpha$ alone show a slightly deviating nature (reduced $\chi ^2= 1.1$) from $\Lambda$CDM scenario, but for $\Delta \alpha / \alpha$ $+$ SNIa and $\Delta \alpha / \alpha$ $+$ SNIa $+$ BAO data it is implied that the model is very close to $\Lambda$CDM cosmology. This is also a self-consistent verification for the validity of our assumption that $f(T)=T+\text {const}.+\text {corrections}$, which allowed us to work in the Einstein frame.

Table 3 Summary of the best-fit values of the parameter $b\equiv 1/p$ of the $f_2$CDM square-root-exponential model of (15), for three different observational data sets with reduced $\chi ^2$: $\chi ^2_{\mathrm{min}}/\mathrm{d.o.f.}$ (d.o.f. stands for “degrees of freedom”)

Lastly, in order to examine the late-time asymptotic behavior of $f_2$CDM model, in Fig. 4 we depict the evolution of the equation-of-state parameter given in (11), applying a reconstruction at 1$\sigma$ confidence level via error propagation using the joint analysis $\Delta \alpha / \alpha$ $+$ SNIa $+$ BAO, where one can see that w at late times acquires values very close to ‘$-1$’, as expected. Similarly to the previous model, for a more detailed investigation of the late-time asymptotics one must apply the method of dynamical system analysis [91,92,93], where it can thoroughly be shown that the universe will end in a de Sitter phase.

Fig. 4

The evolution of the equation-of-state parameter given in (11), for the $f_2$CDM square-root-exponential model of (15), applying a reconstruction at 1$\sigma$ confidence level via error propagation using the joint analysis $\Delta \alpha / \alpha$ $+$ SNIa $+$ BAO

4 Observational constraints from the Newton constant variation

Fig. 5

Results for the $f_1$CDM power-law model of (12). Left graph estimation of $G_{\mathrm{eff}}/G_\mathrm{N}$ as a function of the redshift, from 37 Hubble data points. Right graph reconstruction of $G_{\mathrm{eff}}/G_\mathrm{N}$ as a function of the redshift, from the observational Hubble parameter data, for b $\in [-0.01,0.01]$

In this section we will directly use the observational constraints imposed on f(T) models in order to examine the variation of the gravitational constant $G_\mathrm{N}$. Let us first quantify the $G_\mathrm{N}$-variation in the framework of f(T) cosmology. As is well known, a varying effective gravitational constant is one of the common features in many modified gravity theories [1]. In case of f(T) gravity, the effective Newton constant $G_{\mathrm{eff}}$ can be straightforwardly extracted as [40, 94]

$$\begin{aligned} G_{\mathrm{eff}} = \frac{G_\mathrm{N}}{f_T}. \end{aligned}$$

(30)

Hence, for the $f_1$CDM power-law model of (12), and using (26), we obtain

$$\begin{aligned} G_{\mathrm{eff}}(z) = \frac{G_\mathrm{N}}{1- b\,\left( \frac{1-\Omega _{m0}}{2b-1} \right) \, \left[ \frac{H^2(z)}{H_0^2}\right] ^{(b-1)}}, \end{aligned}$$

(31)

where the ratio $H^2(z)/H_0^2$ is given by (14) (clearly, for $b= 0$ we have $G_{\mathrm{eff}}(z)=G_\mathrm{N}=\text {const}.$). Similarly, for the $f_2$CDM square-root-exponential model of (15), and using (28), we acquire

$$\begin{aligned} G_{\mathrm{eff}}(z) = \frac{G_\mathrm{N}}{ 1+ \frac{p}{2} \left[ \frac{1-\Omega _{m0}}{1-(1+p)\, e^{-p}}\right] \, \left[ \frac{ H_0}{H(z)} \right] e^{-\frac{pH(z)}{H_0}}}, \end{aligned}$$

(32)

where the ratio $H^2(z)/H_0^2$ is given by (17) (clearly, for $b=1/p\rightarrow 0^+$ we have $G_{\mathrm{eff}}(z)=G_\mathrm{N}=\text {const}.$).

Let us now use the above expressions for $G_{\mathrm{eff}}(z)$ and confront them with the observational bounds of the Newton constant variation. We use observational Hubble parameter data in order to investigate the temporal evolution of the function $G_{\mathrm{eff}}(z)$, since such a compilation is usually used to constrain cosmological parameters, due to the fact that it is obtained from model-independent direct observations. We adopt 37 observational Hubble parameter data in the redshift range $0< z \le 2.36$, compiled in [95], out of which 27 data points are deduced from the differential age method, whereas 10 correspond to measures obtained from the radial baryonic acoustic oscillation method.

We apply the following methodology: Firstly, we estimate the error in the measurements associated with the function $G_{\mathrm{eff}}/G_\mathrm{N}$, for both models of (31) and (32), via the standard method of error propagation theory, namely

$$\begin{aligned}&\sigma ^2_{G_{\mathrm{eff}}/G_\mathrm{N}} = \left| \frac{\partial G_{\mathrm{eff}}/G_\mathrm{N}}{\partial H} \right| ^2 \sigma ^2_H + \left| \frac{\partial G_{\mathrm{eff}}/G_\mathrm{N}}{\partial b} \right| ^2 \sigma ^2_b \nonumber \\&\quad + \left| \frac{\partial G_{\mathrm{eff}}/G_\mathrm{N}}{\partial \Omega _m} \right| ^2 \sigma ^2_{\Omega _m}, \end{aligned}$$

(33)

and we fix the free parameters of the two models within the values obtained in the joint analysis of [41] and of Sect. 3 of the current work. Then the measurements of $G_{\mathrm{eff}}/G_\mathrm{N}$ are calculated directly for each redshift defined in the adopted compilation.

Fig. 6

Results for the $f_2$CDM square-root-exponential model of (15). Left graph estimation of $G_{\mathrm{eff}}/G_\mathrm{N}$ as a function of the redshift, from 37 Hubble data points. Right graph reconstruction of $G_{\mathrm{eff}}/G_\mathrm{N}$ as a function of the redshift, from the observational Hubble parameter data, for $b\equiv 1/p$ $\in [0,0.5]$

In the left graph of Fig. 5 we depict the 1$\sigma$ confidence-level estimation of the function $G_{\mathrm{eff}}(z)/G_\mathrm{N}$ from 37 Hubble data points, in the case of the $f_1$CDM power-law model of (12). Additionally, in the right graph of Fig. 5 we present the corresponding 1$\sigma$ confidence-level reconstruction of $G_{\mathrm{eff}}(z)/G_\mathrm{N}$ for b $\in [-0.01,0.01]$ from the observational Hubble parameter data. When we perform the analysis within the known range of the parameter b for this model (from [41] as well as from Fig. 1 above), we find that $G_{\mathrm{eff}}/G_\mathrm{N} \approx 1$. Nevertheless, a minor deviation is observed for the fixed value of $b = 0.01$ (see the left graph of Fig. 5). For instance, note that $G_{\mathrm{eff}}(z=0.07)/G_\mathrm{N} = 0.992 \pm 0.004$ and $G_{\mathrm{eff}}(z=2.36)/G_\mathrm{N} =0.99923 \pm 0.00005$, for the first and the last data points of the redshift interval [0, 2.36], respectively.

In Fig. 6 we present the corresponding graphs for the $f_2$CDM square-root-exponential model of (15). When we perform the analysis within the known range of the parameter $b\equiv 1/p$ for this model (from [41] as well as from Fig. 3 above), we find that $G_{\mathrm{eff}}/G_\mathrm{N} \approx 1$, similarly to the case of $f_1$CDM model.

In summary, from the analysis of this section, we verify the results of the previous section, namely that the parameter b, which quantifies the deviation of both $f_1$CDM and $f_2$CDM models from $\Lambda$CDM cosmology, is very close to zero. These results are in qualitative agreement with previous observational constraints on f(T) gravity, according to which only small deviations are allowed, with $\Lambda$CDM paradigm being inside the allowed region [34,35,36,37,38,39,40,41].

5 Conclusions

In the present work we have used observations related to the variation of fundamental constants, in order to impose constraints on the viable and most used f(T) gravity models. In particular, since f(T) gravity predicts a variation of the fine-structure constant, we used the recent observational bounds of this variation, from direct measurements obtained by different spectrographic methods, along with standard probes such as Supernovae type Ia and baryonic acoustic oscillations, in order to constrain the involved model parameters of two viable and well-used f(T) models.

For both the $f_1$CDM power-law model and the $f_2$CDM square-root-exponential model, we found that the parameter that quantifies the deviation from $\Lambda$CDM cosmology can be slightly different from its $\Lambda$CDM value, nevertheless the best-fit value is very close to the $\Lambda$CDM one. Additionally, since f(T) gravity predicts a varying effective gravitational constant, we quantified its temporal evolution with the use of the previously constrained model parameters. For both the $f_1$CDM and the $f_2$CDM models, we found that the deviation from $\Lambda$CDM cosmology is very close to zero.

These results are in qualitative agreement with previous observational constraints on f(T) gravity [38,39,40,41], however, they have been obtained through completely independent analysis. In summary, f(T) gravity is consistent with observations, and thus it can serve as a candidate for modified gravity, although, as every modified gravity, it may have only a small deviation from $\Lambda$CDM cosmology, a feature that must be taken into account in any f(T) model-building.