CMB anomalies and the effects of local features of the inflaton potential

Abstract

Recent analysis of the WMAP and Planck data have shown the presence of a dip and a bump in the spectrum of primordial perturbations at the scales $k=0.002$ Mpc${}^{-1}$ and $k=0.0035$ Mpc${}^{-1}$, respectively. We analyze for the first time the effects of a local feature in the inflaton potential to explain the observed deviations from scale invariance in the primordial spectrum. We perform a best-fit analysis of the cosmic microwave background (CMB) radiation temperature and polarization data. The effects of the features can improve the agreement with observational data respect to the featureless model. The best-fit local feature affects the primordial curvature spectrum mainly in the region of the bump, leaving the spectrum unaffected on other scales.

1 Introduction

There are important observational motivations to study modifications of the inflaton potential, like the observed deviations of the spectrum of primordial curvature perturbations from a power-law spectrum [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. In Refs. [1,2,3,4,5,6,7,8,9,10,11,12,13] the authors study the effects of analyzing the cosmic microwave background (CMB) radiation using a free function for the spectrum of primordial scalar perturbations, i.e., they do not consider the usual power-law spectrum predicted by most of the simplest inflationary models [14, 15, 22]. For example, the primordial spectrum can be parametrized with wavelets [4, 5], linear interpolation [6,7,8], interpolating spline functions [11,12,13], among other methods [1, 16].

Some interesting evidence of these deviations were given in [1, 16] where it was used a method based on a piecewise cubic Hermite interpolating polynomial (PCHIP) for the primordial power spectrum. This analysis showed that the spectrum of primordial perturbations can be approximated with a power law in the range of values $0.007 \text{ Mpc }^{-1}<k < 0.2 \text{ Mpc }^{-1}$, while in the range $0.001 \text{ Mpc }^{-1}<k < 0.0035 \text{ Mpc }^{-1}$ there are a dip and a bump at $k=0.002$ Mpc${}^{-1}$ and $k=0.0035$ Mpc${}^{-1}$, with a statistical significance of about $2\sigma$ and $1\sigma$, respectively. Similar results were reported in several other analyses [1,2,3, 14, 23,24,25,26,27,28,29,30,31,32,33,34] using different techniques and both the WMAP [35] and the Planck [36, 37] measurements. In this paper we study how local features of the inflaton potential can model this type of local glitches of the spectrum of primordial curvature perturbations. We also study the effects of these features on the primordial tensorial perturbation spectrum.

Features of the inflaton potential can affect the evolution of primordial curvature perturbations [1, 38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59] and consequently generate a variation in the amplitude of the spectrum and bispectrum [38,39,40,41,42,43,44,45,46, 56]. This can provide a better fit of the observational data in the regions where the spectrum shows some deviations from a power law [1,2,3, 40, 41, 43,44,45,46, 51, 52, 60,61,62]. In this paper we perform a best-fit analysis of the CMB radiation temperature and polarization [63] data and we study the effects of a local feature of the inflation potential which affects the primordial curvature spectrum in the region of the bump.

Fig. 1

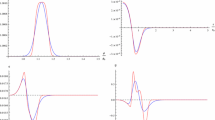
The numerically computed slow-roll parameters $\epsilon$ and $\eta$ around the feature time $t_0$ for $\lambda =-4\times 10^{-12}, \sigma =0.05$, and $k_0=1.2\times 10^{-3}$ (blue), $\lambda =-10^{-12}, \sigma =0.05$, and $k_0=1.3\times 10^{-3}$ (red), $\lambda =-10^{-11}, \sigma =0.04$, and $k_0=1.3\times 10^{-3}$ (green), and $\lambda =-1.5\times 10^{-11}, \sigma =0.04$, and $k_0=1.2\times 10^{-3}$ (orange). The dashed lines correspond to the featureless slow-roll parameters

2 Local features

We consider a single scalar field minimally coupled to gravity with a standard kinetic term according to the action

$$\begin{aligned} S = \int \mathrm{d}^4x \sqrt{-g} \left[ \frac{1}{2} M^2_{Pl} R - \frac{1}{2} g^{\mu \nu } \partial _\mu \phi \partial _\nu \phi -V(\phi ) \right] , \end{aligned}$$

(1)

where $M_{Pl} = (8\pi G)^{-1/2}$ is the reduced Planck mass and $g_{\mu \nu }$ is the flat FLRW metric. The Friedmann equation and the equation of motion of the inflaton are obtained from the variation of the action with respect to the metric and the scalar field, respectively,

$$\begin{aligned} H^2 \equiv \left( \frac{\dot{a}}{a}\right) ^2= \frac{1}{3 M^2_{Pl}}\left( \frac{1}{2} \dot{\phi }^2 + V(\phi ) \right) , \end{aligned}$$

(2)

$$\begin{aligned} \ddot{\phi }+ 3H\dot{\phi }+ \partial _{\phi }V = 0, \end{aligned}$$

(3)

where H is the Hubble parameter, and dots and $\partial _{\phi }$ denote derivatives with respect to time and scalar field, respectively. The slow-roll parameters are defined

$$\begin{aligned} \epsilon \equiv -\frac{\dot{H}}{H^2}, \quad \eta \equiv \frac{\dot{\epsilon }}{\epsilon H}. \end{aligned}$$

(4)

We consider a potential energy given by [39]

$$\begin{aligned} V(\phi )= & {} V_{0}(\phi ) + V_F(\phi ) , \end{aligned}$$

(5)

$$\begin{aligned} V_F(\phi )= & {} \lambda e^{-( \frac{\phi -\phi _0}{\sigma })^{2}} , \end{aligned}$$

(6)

where $V_{0}(\phi )$ is the featureless potential and $V_F$ corresponds to a step symmetrically dumped by an even power negative exponential factor. In this paper we will consider the case of a quadratic inflaton potential,

$$\begin{aligned} V_0(\phi )=\frac{1}{2} m^2 \phi ^2 . \end{aligned}$$

(7)

The tensor-to-scalar ratio for a monomial potential $\phi ^n$ is $r \approx 16 n /(4N_e + n)$, where $N_e$ is the number of e-folds before the end of inflation [14, 15]. In the case of quadratic inflation $r\approx 0.16$ for $N_e\approx 50$, which is not in good agreement with observational data. Our analysis confirms this when we fit data without the feature. We will show later that the effects of local features improve the agreement with CMB data but not enough to get a $\chi ^2$ as low as the one of other inflationary models with lower values of r.

This type of modification of the slow-roll potential is called a local feature (LF) [39] which differs from the branch feature (BF) [39, 56], since the potential is symmetric with respect to the location of the feature and it is only affected in a limited range of the scalar field value. Due to this the spectrum and bispectrum are only modified in a narrow range of scales, in contrast to the BF in which there are differences in the power spectrum between large and small scale which are absent in the case of LF. In some cases the step in the spectrum due to a BF can be very small, and the difference between large and small scale effects would not make BF observationally distinguishable from LF. Nevertheless in general the oscillation patterns produce in the spectrum by a single BF would be different because a single LF can be considered as the combination of two appropriate BF [39].

In this paper we use the local type effect of these features to model phenomenologically local glitches of the primordial scalar spectrum on the scales $k=0.002 \text{ Mpc }^{-1}$ and $k=0.0035 \text{ Mpc }^{-1}$ [1], and to study their effects on the primordial tensor spectrum, without affecting other scales.

Fig. 2

The power spectrum of primordial curvature perturbations $P_{\zeta }$ is plotted for $\lambda =-4\times 10^{-12}, \sigma =0.05$, and $k_0=1.2\times 10^{-3}$ (blue), $\lambda =-10^{-12}, \sigma =0.05$, and $k_0=1.3\times 10^{-3}$ (red), $\lambda =-10^{-11}, \sigma =0.04$, and $k_0=1.3\times 10^{-3}$ (green), and $\lambda =-1.5\times 10^{-11}, \sigma =0.04$, and $k_0=1.2\times 10^{-3}$ (orange). The dashed lines correspond to the featureless spectrum

Fig. 3

The power spectrum of primordial tensor perturbations $P_{h}$ is plotted for $\lambda =-4\times 10^{-12}, \sigma =0.05$, and $k_0=1.2\times 10^{-3}$ (blue), $\lambda =-10^{-12}, \sigma =0.05$, and $k_0=1.3\times 10^{-3}$ (red), $\lambda =-10^{-11}, \sigma =0.04$, and $k_0=1.3\times 10^{-3}$ (green), and $\lambda =-1.5\times 10^{-11}, \sigma =0.04$, and $k_0=1.2\times 10^{-3}$ (orange). The dashed lines correspond to the featureless spectrum. The plot on the right corresponds to a zoom of the left plot. As can be seen, the effects of the different features on the spectrum $P_h$ are rather small and the spectra of the models with features are difficult to distinguish from the featureless model spectrum

The effects of the feature on the slow-roll parameters are shown in Fig. 1, where we can see that there are oscillations of the slow-roll parameters around the feature time $t_0$, defined as $\phi _0=\phi (t_0)$ [39]. The magnitude of the potential modification is controlled by the parameter $\lambda$, as its effect is such that larger value of $\lambda$ give larger values of the slow-roll parameters. The size of the range of field values where the potential is affected by the feature is determined by the parameter $\sigma$ and the slow-roll parameters are smaller for larger $\sigma$. We define $k_0$ as the scale exiting the horizon at the feature time $t_0$, $k_0=-1/\tau _0$, where $\tau _0$ is the value of conformal time corresponding to $t_0$. Oscillations occur around $k_0$, and their location can be controlled by changing $\phi _0$. We adopt a system of units in which $c=\hbar =M_{Pl}=1$.

3 Spectrum of curvature tensor perturbations

In order to study the curvature perturbations we expand perturbatively the action with respect to the background FLRW solution. The second order action for scalar perturbations in the comoving gauge takes the form [64]

$$\begin{aligned} S_2= & {} \int \mathrm{d}t \mathrm{d}^3x\left[ a^3 \epsilon \dot{\zeta }^2-a\epsilon (\partial \zeta )^2 \right] . \end{aligned}$$

(8)

The equation for curvature perturbations $\zeta$ obtained from the Lagrange equations is

$$\begin{aligned} \frac{\partial }{\partial t}\left( a^3\epsilon \frac{\partial \zeta }{\partial t}\right) - a\epsilon \delta ^{ij} \frac{\partial ^2 \zeta }{\partial x^i\partial x^j}=0. \end{aligned}$$

(9)

Taking the Fourier transform and using conformal time $\mathrm{d}\tau \equiv \mathrm{d}t/a$ we get

$$\begin{aligned} \zeta ''_k + 2 \frac{z'}{z} \zeta '_k + k^2 \zeta _k = 0, \end{aligned}$$

(10)

where k is the comoving wave number, $z\equiv a\sqrt{2 \epsilon }$, and primes denote a derivative with respect to the conformal time. The two-point function of curvature perturbations is

$$\begin{aligned} \left\langle \hat{\zeta }(\vec {k}_1, t) \hat{\zeta }(\vec {k}_2, t) \right\rangle \equiv (2\pi )^3 \frac{2\pi ^2}{k^3} P_{\zeta }(k) \delta ^{(3)}(\vec {k}_1+\vec {k}_2) , \end{aligned}$$

(11)

where the power spectrum of curvature perturbations is defined as

$$\begin{aligned} P_{\zeta }(k) \equiv \frac{k^3}{2\pi ^2}|\zeta _k|^2 . \end{aligned}$$

(12)

The effects of the features on the primordial scalar spectrum are plotted in Fig. 2 for different values of the parameters $\lambda , \sigma$, and $k_0$ [39]. The spectrum of primordial curvature perturbations has oscillations around $k_0$, whose amplitude is larger for larger $\lambda$ since the latter controls the magnitude of the potential modification. The amplitude of the spectrum oscillations is larger for smaller $\sigma$, because in this case the change in the potential is more abrupt and consequently the slow-roll parameters are larger.

Fig. 4

The $D_l^{TT}=\ell (\ell +1) C_\ell ^{TT}/(2\pi )$ spectrum in units of $\mu K^2$ is plotted as a function of the multipole l. We compare the best fit obtained using the inflationary model without feature (red line) to the one obtained introducing the local feature (black line). In the lower panel we plot the relative difference with respect to the featureless case. The data points are from the 2015 Planck release [37]. The cosmological parameters used to compute the two spectra are reported in Table 1

The equation for tensor perturbations can be derived in a way similar to the case of scalar perturbations, giving

$$\begin{aligned} h''_k+2\frac{a'}{a} h'_k+k^2 h_k=0 , \end{aligned}$$

(13)

where again k is the comoving wave number. The power spectrum of tensor perturbations is obtained from the two-point function as

$$\begin{aligned} P_{h}(k) \equiv \frac{2k^3}{\pi ^2}|h_k|^2, \end{aligned}$$

(14)

from which the tensor-to-scalar ratio can be defined as the ratio between the spectrum of tensor and scalar perturbations as

$$\begin{aligned} r\equiv \frac{P_h}{P_{\zeta }} . \end{aligned}$$

(15)

The effects of the features on the primordial tensor spectrum are plotted in Fig. 3 for different values of the parameters $\lambda , \sigma$, and $k_0$. These effects are not very significant and in fact the observational data analysis we will present in the rest of the paper confirms that local features affect mainly the curvature spectrum.

Table 1 Constraints on the cosmological parameters and $\chi ^2$ for the model with and without feature. All the constraints are given at 1$\sigma$ confidence level. The lower limits on the feature parameters correspond to the limits we used as a prior. The best-fit values are the values inside curly brackets. We separately report the different contributions to the $\chi ^2$ (Planck low-$\ell$, Planck high-$\ell$ and from the priors on the nuisance parameters) and the total

4 Effects of local features on the CMB spectrum

In Fig. 4 we show the effects of local features on the temperature (TT) CMB spectrum. Since we are considering a feature of local type, as theoretically expected, the spectrum is not affected on scales sufficiently far from $k_0$. Branch features [39] could on the contrary also introduce a step in the power spectrum, modifying it also on scales far from $k_0$, and for this reason LF are more appropriate to model local deviations of the spectrum.

The main effects produced by the LF appear between $\ell =10$ and $\ell =100$ in the TT spectrum. They correspond to the wiggles of the primordial scalar fluctuations shown in Fig. 2. The class of LF we consider allows one to fit the small bump at $\ell \simeq 40$ better than the dip at $\ell \simeq 20$ in the CMB spectrum. The impact of the LF on the BB spectrum is much smaller, since, as discussed previously, the effect of the feature on the primordial tensorial perturbations spectrum is negligible.

Fig. 5

A comparison between the model with and without features is given for the parameters $H_0$, $\omega _b$, $\omega _c$, $\theta$, $\tau$ and $\ln (10^{10}A_s)$. All the results are obtained considering the Planck low-$\ell$+high$\ell$ data combination. As can be seen the effects of the feature on the estimation of these non-inflationary cosmological parameters is negligible

Fig. 6

The results of the data fitting analysis for the parameters $\lambda$, $\sigma$ and $k_0$ are shown for the model with local features

Fig. 7

The numerically computed spectrum of the primordial curvature fluctuations $P_{\zeta }$ and of the tensor perturbations $P_{h}$ are plotted for the best-fit values in Table 1: $\lambda =-1.12\times 10^{-12}, \sigma =0.053$, and $k_0=1.13\times 10^{-3}$ (blue). On the left, the red lines correspond to the best-fit reconstructed primordial power spectrum from Ref. [16]. The dashed lines correspond to the featureless spectrum

Fig. 8

The 1, 2 and 3$\sigma$ constraints obtained from observational data analysis are plotted for the primordial curvature perturbations spectrum for the model with local features. The spectrum for the featureless model is plotted with a red line

4.1 The observational data analysis method

To study the effects produced by local features on the CMB spectrum, we modified the Boltzmann code CAMB [65] that computes the theoretical spectra and the corresponding Markov chain monte carlo (MCMC) code CosmoMC [66] in order to use a non-standard power spectrum for the primordial curvature perturbations.

As a base model we considered the standard parameterization of the $\Lambda$CDM model for the evolution of the universe, which includes four parameters: the current energy density of baryons and of cold dark matter (CDM) $\Omega _b h^2$ and $\Omega _c h^2$, the ratio between the sound horizon and the angular diameter distance at decoupling $\theta$, and the optical depth to reionization $\tau$.

The parameterization of the primordial power spectra is modified to take into account the presence of the local feature. To see the effects of the feature, we compare the results obtained in the featureless model with the ones obtained when a local feature is added. The comparison of the effects of LF of different inflationary potentials is left for future studies.

The data sets that we use to test the LF are taken from the last release from the Planck Collaboration [37] for the temperature and E-mode polarization modes. We consider the temperature and polarization power spectra in the range $2\le \ell \le 29$ (low-$\ell$) and only the temperature power spectrum at higher multipoles, $30\le \ell \le 2500$ (high-$\ell$). Since the polarization spectra at high multipoles are still under discussion and some residual systematics were detected by the Planck Collaboration [67, 68], we do not include the full polarization spectra obtained by Planck. Moreover, we do not include the data on the BB spectrum as obtained from the Bicep2/Keck Collaboration [69], because the baseline inflationary model that we consider ($\phi ^2$) cannot reproduce the small amount of primordial tensor modes that are observed after cleaning the Bicep2/Keck data using the polarized dust emission obtained by the high frequency maps by Planck [70].

5 Results

The results of the data fitting analysis are reported in Table 1 and in Figs. 5, 6, 7 and 8.

In Table 1 we show the best-fit values written inside brackets and the 1$\sigma$ constraints of the parameters. It should be noted that the bounds we obtain are more stringent than the Planck ones because $n_s$ is not a free parameter. Fixing the value of scalar spectral index reduces the confidence ranges for the others parameters, and consequently our bounds are smaller. If we had left free the potential of the inflaton in a generic monomial form $V_0 \sim \phi ^n$, then we could have obtained larger bounds as in the Planck team analysis where $n_s$ is a free parameter. This could be done in a future work, but it goes beyond the scope of the present paper.

Comparing the results obtained with and without feature we can see that the presence of the LF has no impact on the background cosmological parameters. This is clear from the marginalized 1D and 2D plots in Fig. 5. The effect of the feature is evident around the location of the bump of the CMB temperature spectrum (see Fig. 4), and it corresponds to an improvement of the total $\chi ^2$. As reported in Table 1, the improvement comes from the $\chi ^2$ of the low-$\ell$ Planck likelihood. Our analysis cannot be compared with the Planck results [68, 70], we are assuming the $\phi ^2$ inflationary model instead of using a phenomenological approach with independent $n_s$ and r. Quadratic inflation corresponds to high values of r which are not in agreement with the Planck best-fit model obtained using $n_s$ and r as independent parameters. The effects of the feature improve the $\chi ^2$ with respect to the featureless $\phi ^2$ case, but this improvement is not large enough to make it competitive with other models. Nevertheless, the same LF could be applied to other inflationary scenarios to produce an analogous improvement of the $\chi ^2$. The analyses of the effects of the LF for inflationary models that are in better agreement with the observed CMB spectra are left for future studies.

In Fig. 6 we show the 1D marginalized posterior distributions and the correlations between the feature parameters. From the correlation plot between $\lambda$ and $k_0$ we can see that the size of the feature can be larger if the feature is located at a smaller wavemode $k_0$. This is because the CMB temperature spectrum does not allow any wiggles above $\ell \simeq 60$, thus limiting the amplitude of the feature. The 2D plots for the parameter $\sigma$ seem to show that there is no lower bound on it. This is not in tension with the 1$\sigma$ constraints on the $\sigma$ parameter reported in Table 1, because of volume effects that occur in the Bayesian marginalization procedure. The preference for a non-minimum value of $\sigma$ is mild, indeed there is no lower bound at 2$\sigma$ confidence level.

The constraints on the primordial scalar spectrum are shown in Figs. 7 and 8. In the left panel of Fig. 7 we compare the best-fit primordial power spectrum of scalar perturbations obtained in our analysis (blue) and the reconstructed one from Ref. [16]. The comparison underlines how a local feature can reproduce the behavior of the primordial spectrum, but further studies, which will be presented in some future work, on the feature potential are required in order to obtain a perfect agreement. The right panel of the same Fig. 7 shows that the effect of the feature is very small in the tensor spectrum. In Fig. 8 we plot the marginalized constraints on the primordial scalar spectrum. The 1, 2, and 3$\sigma$ bands refer to the model with LF, while the solid black line shows the corresponding best-fit spectrum, computed from the entire set of primordial spectra obtained from the MCMC scan. The red dashed line shows the spectrum obtained for the same cosmological parameters but without the feature. From the figures we can note that the effects that the LF brings about are more important for the scalar spectrum, while they are negligible for the tensor spectrum. For this reason, we do not show the same plot as for Fig. 8 for the tensor spectrum.

6 Conclusions

We have studied the effects of local features in the inflaton potential on the spectra of primordial curvature perturbations and their impact on the temperature anisotropies of the CMB. In order to study the effects on the CMB spectrum we have modified the CAMB and CosmoMC codes in order to use a non-standard power-law power spectrum for the primordial perturbations, to take into account the presence of the local feature. We have performed a best-fit analysis of CMB temperature and polarization data from Planck. We have found no significant effects on cosmological parameters related to the propagation of CMB photons after decoupling, while LF improve the fit of the CMB temperature and polarization data. We have also confirmed the theoretical expectation that local features do not affect the primordial power spectrum at scales far from the characteristic scale $k_0$, which leaves the horizon around the feature time.

In the future it will be interesting to analyze the effects of local features in order to explain other deviations of the CMB spectrum, such as for example the anomalies occurring around $l\approx 800$ [2]. It will also be important to study the effects of LF in inflationary models with different featureless $V_0$ potentials, and to compare them to the effects of branch features.