A new recipe for $\Lambda$CDM

Abstract

It is well known that a canonical scalar field is able to describe either dark matter or dark energy but not both. We demonstrate that a non-canonical scalar field can describe both dark matter and dark energy within a unified setting. We consider the simplest extension of the canonical Lagrangian ${\mathcal {L}} \propto X^\alpha - V(\phi )$ where $\alpha \ge 1$ and V is a sufficiently flat potential. In this case the kinetic term in the Lagrangian behaves just like a perfect fluid, whereas the potential term mimicks dark energy. For very large values, $\alpha \gg 1$, the equation of state of the kinetic term drops to zero and the universe expands as if filled with a mixture of dark matter and dark energy. The velocity of sound in this model and the associated gravitational clustering are sensitive to the value of $\alpha$. For very large values of $\alpha$ the clustering properties of our model resemble those of cold dark matter (CDM). But for smaller values of $\alpha$, gravitational clustering on small scales is suppressed, and our model has properties resembling those of warm dark matter (WDM). Therefore our non-canonical model has an interesting new property: its expansion history resembles $\Lambda$CDM, while its clustering properties are akin to those of either cold or warm dark matter.

1 Introduction

Ever since the discovery that high redshift type Ia supernovae supported an accelerating universe, concordance cosmology or $\Lambda$CDM, has come to dominate popular thinking. Although issues relating to the smallness of $\Lambda$ have given rise to several rival models of cosmic acceleration [1,2,3,4,5,6,7,8] there is no doubt that, despite some recent evidence to the contrary [9,10,11,12], $\Lambda$CDM agrees well with a large set of cosmological observations [13].

As its name suggests, $\Lambda$CDM consists of two components: the cosmological constant, $\Lambda$, and cold dark matter (CDM). Despite its enormous success in explaining observations, the origin of $\Lambda$ is not known. It may simply be a residual vacuum fluctuation, although quantum field theory usually predicts much larger values, and the cosmological constant problem remains unresolved. As concerns dark matter, mainstream thinking usually assumes it to be a non-baryonic relic of the big bang [14,15,16,17,18] but other explanations can also be found in the literature [19,20,21,22,23,24,25,26,27,28]. Furthermore, since $96\%$ of the content of the universe is of unknown origin, attempts have been made to describe both dark matter and dark energy within a unified setting. The Chaplygin gas (and its subsequent generalisation) belongs to this category of models, since its equation of state (EOS) behaves like pressureless dust at early times and like a $\Lambda$-term at late times [29,30,31]; also see [32]. Unfortunately the Chaplygin gas has problems with gravitational clustering and so falls short of describing the real universe [33,34,35,36,37,38,39].

In this paper we show that a unified description of dark matter and dark energy can emerge from non-canonical scalar fields; see [40,41,42] for earlier work in this direction. These fields possess an additional degree of freedom (encoded in the parameter $\alpha$) which allows a scalar field rolling along a flat potential to behave like a two component fluid consisting of an almost pressureless kinetic component (dark matter) and a cosmological constant. For large values of $\alpha$ the equation of state of the kinetic component drops to zero and the expansion of the universe is similar to $\Lambda$CDM. Non-canonical scalars cluster on small scales, thereby providing us with a realistic model of an accelerating universe consisting of dark matter and dark energy. For very large values of $\alpha$ the kinetic component clusters like cold dark matter, whereas for smaller $\alpha$ values, clustering in our model resembles warm dark matter.

2 Non-canonical scalars and $\Lambda$CDM

Perhaps the simplest generalisation of the canonical scalar field Lagrangian density

$$\begin{aligned} {\mathcal {L}}(X,\phi )=X-V(\phi ),\quad X = \frac{1}{2}{{\dot{\phi }}}^2 \end{aligned}$$

(1)

which preserves the second order nature of the field equations is the non-canonical Lagrangian [41, 43,44,45,46,47]

$$\begin{aligned} {\mathcal {L}}(X,\phi ) = X\left(\frac{X}{M^{4}}\right)^{\alpha -1} -V(\phi ), \end{aligned}$$

(2)

where M has dimensions of mass while $\alpha$ is dimensionless. When $\alpha = 1$ the k-essence Lagrangian (2) reduces to (1).

We shall be working in the spatially flat Friedmann–Robertson–Walker (FRW) universe

$$\begin{aligned} \mathrm{d}s^2 = \mathrm{d}t^2-a^{2}(t)\; [\mathrm{d}x^2 + \mathrm{d}y^2 + \mathrm{d}z^2], \end{aligned}$$

(3)

for which the energy–momentum tensor has the form

$$\begin{aligned} T^{\mu }_{\nu } = {\mathrm {diag}}(\rho _{{\phi }}, -p_{{\phi }}, - p_{{\phi }}, - p_{{\phi }}), \end{aligned}$$

(4)

where the energy density, $\rho _{{\phi }}$, and pressure, $p_{{\phi }}$, are given by

$$\begin{aligned} \rho _{{\phi }}= & {} \left(\frac{\partial {\mathcal {L}}}{\partial X}\right)\, (2\, X)- {\mathcal {L}},\end{aligned}$$

(5)

$$\begin{aligned} p_{{\phi }}= & {} {\mathcal {L}}. \end{aligned}$$

(6)

Substituting for ${\mathcal {L}}$ from (2) into (5) and (6) one gets

$$\begin{aligned} \begin{aligned} \rho _{{\phi }}&= \left(2\alpha -1\right)X\left(\frac{X}{M^{4}}\right)^{\alpha -1} +\; V(\phi ),\\ p_{{\phi }}&= X\left(\frac{X}{M^{4}}\right)^{\alpha -1} -\; V(\phi ), \end{aligned} \end{aligned}$$

(7)

which reduces to the canonical form $\rho _{{\phi }} = X + V$,  $p_{{\phi }} = X - V$ when $\alpha = 1$. The two Friedmann equations are

$$\begin{aligned} H^{2}= & {} \frac{8 \pi G}{3}\left[\left(2\alpha -1\right)X\left(\frac{X}{M^{4}}\right)^{\alpha -1} + V(\phi )\right],\end{aligned}$$

(8)

$$\begin{aligned} \frac{\ddot{a}}{a}= & {} -\frac{8 \pi G}{3}\left[\left(\alpha + 1\right)X\left(\frac{X}{M^{4}}\right)^{\alpha -1} -V(\phi )\right], \end{aligned}$$

(9)

where $\phi (t)$ satisfies the equation of motion

$$\begin{aligned} {\ddot{\phi }}+ \frac{3\, H{\dot{\phi }}}{2\alpha -1} + \left(\frac{V'(\phi )}{\alpha (2\alpha -1)}\right)\left(\frac{2\,M^{4}}{{\dot{\phi }}^{2}}\right)^{\alpha - 1} =0, \end{aligned}$$

(10)

which reduces to the standard canonical form ${\ddot{\phi }}+ 3\, H {\dot{\phi }} + V'(\phi ) = 0$ when $\alpha =1$.

Consider the equation of motion (10) for the simplest case when $V'$ is small and can be neglected in (10). Setting $V'\simeq 0$ in (10) one finds

$$\begin{aligned} {\ddot{\phi }} = -\frac{3\, H{\dot{\phi }}}{2\alpha -1}, \end{aligned}$$

(11)

which is easily integrated to give

$$\begin{aligned} {{\dot{\phi }}} \propto a^{-\frac{3}{2\alpha - 1}}, \end{aligned}$$

(12)

and which reduces to the canonical result, ${{\dot{\phi }}} \propto a^{-3}$, when $\alpha = 1$. Substituting for $X \equiv {{\dot{\phi }}}^2/2$ from (12) into (7) one readily finds

$$\begin{aligned} \rho _{{\phi }}= & {} \rho _X + V(\phi )\end{aligned}$$

(13)

$$\begin{aligned} p_{{\phi }}= & {} p_X - V(\phi ), \end{aligned}$$

(14)

with $\rho _X = \left(2\alpha -1\right)X(\frac{X}{M^{4}})^{\alpha -1} \equiv \rho _{0X} a^{-3(1+w)}$ and $p_X = w \rho _X$, where

$$\begin{aligned} w = \frac{p_X}{\rho _X} = \frac{1}{2\alpha -1}, \end{aligned}$$

(15)

is the equation of state (EOS) of the kinetic component of the scalar field. From (15) one notes that $w \ge 0$ for $\alpha \ge 1$, therefore models based solely on the kinetic term cannot describe cosmic acceleration, including the phantom regime recently reviewed in [48].

From (13) and (14) it follows that the non-canonical scalar field behaves like a mixture of two non-interacting perfect fluids: $\rho _X$ and $V(\phi )$, where the equation of state of $\rho _X$ is given by (15). Assuming for simplicity that $V(\phi ) = \Lambda /8\pi G$ one finds (after setting $8\pi G = 1$)

$$\begin{aligned} \rho _{{\phi }}= & {} \rho _X + \Lambda \end{aligned}$$

(16)

$$\begin{aligned} p_{{\phi }}= & {} p_X - \Lambda , \end{aligned}$$

(17)

substituting (16) into (8) gives

$$\begin{aligned} H(z) = H_0\left[\Omega _{0X} (1+z)^{3(1+w)} + \Omega _\Lambda \right]^{1/2} \end{aligned}$$

(18)

where $\Omega _{0X} = \frac{8\pi G\rho _{0X}}{3H_0^2}$ and w is described by (15).

From (15) and (18) we find that the expansion history is very sensitive to the value of the non-canonical parameter $\alpha$. For the canonical value $\alpha = 1$ the scalar field behaves like a mixture of ‘$\Lambda$ + stiff matter’. However, for $\alpha = 2$ the expansion history mimicks ‘$\Lambda$ $+$ radiation’. For the physically interesting case $\alpha \gg 1$, $w \rightarrow 0$ and $\rho _X \propto a^{-3}$, consequently (18) describes $\Lambda$CDM in this limit:

$$\begin{aligned} H(z) \simeq H_0[\Omega _{0m} (1+z)^3 + \Omega _\Lambda ]^{1/2},\quad \hbox {where }\Omega _{0m} {\equiv } \Omega _{0X}.\nonumber \\ \end{aligned}$$

(19)

Fig. 1

$\Delta H$ is plotted against the expansion factor, a, for $\alpha = 50,100,200,1000$ (top to bottom). Here $\Delta H = (H-H_{\Lambda CDM})/H_{\Lambda CDM}$ and $a=1$ corresponds to the present epoch

The equation of state of the scalar field, $w_\phi$, is given by

$$\begin{aligned} 1+ w_\phi (z) = (1+w) \left[1+\frac{\Omega _\Lambda }{\Omega _{0X}(1+z)^{3(1+w)}}\right]^{-1} \end{aligned}$$

(20)

where w is described by (15). We find that $w_\phi \simeq w$ when $z \gg 1$, while its current value is $w_{\phi ,0} = (1+w)[1+\frac{\Omega _\Lambda }{\Omega _{0X}}]^{-1}-1$. From (15) and (20) one finds that, for $\alpha \gg 1$, $w_\phi \simeq 0$ at $z \gg 1$, and $w_{\phi ,0} \simeq -\Omega _\Lambda$ at $z = 0$. Thus for large values of $\alpha$, the EOS of the scalar field smoothly interpolates between dust-like behaviour at high redshifts and a negative value at present.¹ In Fig. 1 we plot the fractional difference between the Hubble parameter H(z) in our model from $\Lambda$CDM for different values of the parameter $\alpha$ (but identical values of the matter density). One can see that for $\alpha \ge 10^3$ the deviation is less than $1\%$. Hence for such large values of $\alpha$ our model will be virtually indistinguishable from $\Lambda$CDM model by observables measuring background cosmology alone.

We have assumed thus far that $V(\phi )$ is a constant. This however need not necessarily be the case. It is important to note that $\Lambda$CDM-like expansion can also arise in the case of other potentials which are flat. The reason for this is simple. Our treatment above was based on the assumption that the last term in (10) was negligibly small compared to the remaining two terms, allowing the former to be neglected. This feature is shared by several flat potentials some of which are described below.

Fig. 2

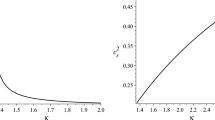
Left The equation of state for the scalar field $w_{\phi }$ as a function of scale factor for $V(\phi ) \sim \phi ^2$ (solid line). The dashed line is for equation of state described by (18) for $\Omega _{\Lambda } = 0.7$ and $\Omega _{0X} = 0.3$. We have set $\sigma _{i} = 10^{-6}$. Right The behaviour of the Om parameter. The solid and dashed lines represent the same models as in the left panel

• $V(\phi ) = \frac{1}{2}m^2\phi ^2$. In order to study this power-law potential, we first form an autonomous system of equations for our model. For Lagrangians of the form ${\mathcal {L}} = F(X) - V(\phi )$, De-Santiago et al. [49] have already constructed an autonomous system of equations involving the dimensionless variables

  $$\begin{aligned} \begin{aligned} x&= \frac{\sqrt{2XF_{X} -F}}{\sqrt{3}m_{pl}H},\\ y&= \frac{\sqrt{V}}{\sqrt{3}m_{pl}H},\\ w_{k}&= \frac{F}{2XF_{X}-F},\\ \sigma&= -\frac{m_{pl}}{\sqrt{3|\rho _{k}|}}\frac{\mathrm{d} \log V}{\mathrm{d}t}. \end{aligned} \end{aligned}$$

  (21)

  Applying these variables to our Lagrangian given by (2), we get

  $$\begin{aligned} w_{k}= & {} \frac{1}{\alpha -1},\nonumber \\ \Omega _{\phi }= & {} x^2 + y^2 = 1,\\ \gamma= & {} 1 + w_{\phi } = x^{2}(1+w_{k}).\nonumber \end{aligned}$$

  (22)

  For $\alpha \gg 1$, $w_{k} \sim 0$ and one can safely approximate $\gamma \sim x^2$. Using the formulation prescribed in De-Santiago et al. [49], we can now form an autonomous system of equations for $\gamma$ and $\sigma$:

  $$\begin{aligned} \gamma ^{\prime }= & {} 3\sigma (1-\gamma )\sqrt{\gamma } - 3\gamma (1-\gamma ),\nonumber \\ \sigma ^{\prime }= & {} - 3\sigma ^{2} \sqrt{\gamma }(\Gamma -1) + \frac{3}{2}\sigma (1-\sigma (1-\gamma )/\sqrt{\gamma }).\nonumber \\ \end{aligned}$$

  (23)

  Here ‘prime’ denotes derivative w.r.t. $\log a$ and $\Gamma = \frac{V V''(\phi )}{V'(\phi )^2}$, so that $\Gamma = \frac{1}{2}$ for $V = \frac{1}{2}m^2\phi ^2$. In order to solve this autonomous system, one requires initial conditions for $\gamma$ and $\sigma$. We set these at decoupling, $a \sim 10^{-3}$, assuming that initially the scalar field kinetic energy dominates over its potential energy, so that $w_{\phi } \sim \frac{1}{2\alpha -1}$. With $\alpha \gg 1$, we have $\gamma _{i} \sim 1$. Similarly one finds $\sigma _{i} \sim 0$ at decoupling. We set $\sigma _{i} = 10^{-6}$ for our subsequent calculations. (One should note that $w_{\phi }$ is not exactly equal to zero initially, due to the large but finite value of $\alpha$.) With these initial conditions, the autonomous system of equations in (20) is evolved from decoupling until today, and the resultant behaviour of the equation of state for the scalar field, $w_{\phi }$, is shown in Fig. 2 (left panel). We find that the behaviour of $w_{\phi }$ in our model is quite similar to that described by (18) for $\Lambda$CDM. Nevertheless, the two models are by no means identical. Indeed, the expansion history in both models can easily be distinguished by means of the Om diagnostic. The Om diagnostic [50]

  $$\begin{aligned} Om (a) = \frac{(H/H_{0})^2 - 1}{a^{-3} -1} \end{aligned}$$

  (24)

  has the interesting property that its value stays pegged to the current value of the density parameter, i.e. $Om(z) = \Omega _{0m}$, only in $\Lambda$CDM. In other models one expects $Om(z) \ne \Omega _{0m}$. The right panel of Fig. 2 shows the behaviour of Om in a $\Lambda$CDM model described by Eq. (18), with $w \simeq 0$ (dashed line). The same figure also shows the Om diagnostic for a dark matter-dark energy model described by the Lagrangian (2) with $V = \frac{1}{2} m^2\phi ^2$. Figure 2 clearly shows that the two potentials $V = \Lambda$ and $V = \frac{1}{2} m^2\phi ^2$ can be distinguished by their expansion histories, as encoded in the Om diagnostic. Thus the $m^2\phi ^2$ model has a time-dependent value of Om which is lower than that in $\Lambda$CDM. The Om diagnostic therefore emerges as a useful means of distinguishing between rival dark matter-dark energy models based on non-canonical scalars. One might add that future measurements of the expansion history are likely to determine Om to great precision, helping break near-degeneracies between rival dark energy models [51, 52].

• Finally, an interesting example of a piece-wise flat potential is the step potential

  $$\begin{aligned} V(\phi ) = A + B\tanh {\beta \phi } \end{aligned}$$

  (25)

  where $A+B = V_{\mathrm{{initial}}}$ and $A-B = V_\mathrm{final}$. For $V_{\mathrm{{initial}}} \simeq 10^{64}~\hbox {GeV}^4$, $V_{\mathrm{{final}}} \simeq 10^{-47}~\hbox {GeV}^4$ this potential would interpolate between inflation at early times, and dark energy at late times, and therefore might describe a model of quintessential inflation. We shall examine this possibility in greater detail in a companion paper.

Fig. 3

The scale-dependence of linear gravitational clustering is illustrated for a non-canonical model with $V(\phi ) = \Lambda /8\pi G$. The linear density contrast, $\delta$, is shown as a function of the expansion factor, a, for the non-canonical scalar field with $\alpha = 5\times 10^4, ~10^5, ~5\times 10^5$ and also for $\Lambda$CDM (bottom to top with $\Lambda$CDM at the top). Two scales are considered: $k = 0.01~\hbox {h}/\hbox {Mpc}$ (left) and $k = 0.1~\hbox {h}/\hbox {Mpc}$ (right)

To summarise, we have demonstrated that the two components of the non-canonical scalar field density, namely $\rho _X$ and $V(\phi )$ in (13), can play the dual role of dark matter and dark energy viz-a-viz the expansion history of the universe. In Fig. 2 we have shown how different non-canonical models of dark energy can be distinguished by means of the Om diagnostic. In order to deepen the parallel between a non-canonical scalar field and a unified treatment of dark matter and dark energy we also need to demonstrate that the field $\phi$ can cluster. In order to do this we first note that linearised scalar perturbations in a spatially flat FRW universe are described by the line element [53,54,55]

$$\begin{aligned} \mathrm{d}s^2= & {} (1+2\, A)\,\mathrm{d}t ^2 - 2\, a(t)\, (\partial _{i} B )\; \mathrm{d}t\; \mathrm{d}x^i\,\\&-\, a^{2}(t)\; [(1-2\, \psi )\; \delta _{ij}+ 2\, (\partial _{i}\, \partial _{j}E )]\, \mathrm{d}x^i\, \mathrm{d}x^j. \end{aligned}$$

The linearised Einstein equation $\delta G^{\mu }_{\;\nu } = \kappa \, \delta T^{\mu }_{\;\nu }$ together with the perturbation equation for the scalar field gives

$$\begin{aligned} {\mathcal {R}}_{k}'' + 2\left(\frac{z'}{z}\right){\mathcal {R}}_{k}' + c_{s}^{2}k^{2}{\mathcal {R}}_{k} = 0, \end{aligned}$$

(26)

where

$$\begin{aligned} z \equiv \frac{a\,(\rho _{{\phi }}+ p_{{\phi }})^{1/2}}{c_{s}H}, \end{aligned}$$

(27)

${\mathcal {R}}$ is the curvature perturbation

$$\begin{aligned} {\mathcal {R}} \equiv \psi + \left(\frac{H}{\dot{\phi }}\right)\delta \phi , \end{aligned}$$

(28)

and $\psi$, $\delta \phi$ correspond to the metric perturbation and the scalar field perturbation, respectively. The derivative in (26) is taken with respect to the conformal time, $\eta = \int \mathrm{d}t/a(t)$ and $c_s$ is the effective sound speed of perturbations in the scalar field [56]

$$\begin{aligned} c_s^{2} \equiv \left[\frac{\left({\partial {\mathcal {L}}}/{\partial X}\right)}{\left({\partial {\mathcal {L}}}/{\partial X}\right) + \left(2\, X\right)\, \left({\partial ^{2} {\mathcal {L}}}/{\partial X^{2}}\right)}\right]. \end{aligned}$$

(29)

Rewriting (26) in terms of the Mukhanov–Sasaki variable $u_{{k}} \equiv z\,{\mathcal {R}}_{k}$, one gets

$$\begin{aligned} u_{k}'' + \left(c_{s}^{2}k^{2} - \frac{z''}{z}\right)u_{k} = 0. \end{aligned}$$

(30)

The key to our understanding of gravitational clustering is provided by the sound speed. Substituting (2) into (29) we get

$$\begin{aligned} c_s^{2} = \frac{1}{2\,\alpha - 1}. \end{aligned}$$

(31)

We therefore find that the sound speed is a constant, and that, for $\alpha \gg 1$, $c_{S}^{2} \rightarrow 0$. In other words, when the value of the non-canonical parameter $\alpha$ is large, the sound speed vanishes, and the scalar field begins to behave like a pressureless fluid.

An important property of our model follows from (19) and (31), namely, when $\alpha \gg 1$, the background universe expands like $\Lambda$CDM, while its clustering properties could resemble those of cold dark matter or even warm dark matter. The non-canonical scalar therefore provides a unified prescription for dark matter and dark energy since both components are sourced by the same non-canonical scalar field. We elaborate on this issue below.

The evolution equation for the linear density contrast of the X-fluid in (13), namely $\delta = \frac{\rho _X - {\bar{\rho }_X}}{{\bar{\rho }_X}}$, evaluated on sub-horizon scales ($|\mathbf{k}| \gg H/c$), is given by [36]

$$\begin{aligned} \delta _k^{\prime \prime }= & {} - [2+ A - 3(2w-c_{s}^2)]\delta _k^{\prime } \nonumber \\&+\,\frac{3}{2}\Omega _{X}(1- 6 c_{s}^2 + 8w - 3w^2) \delta _k -{\left( \frac{k c_{s}}{aH}\right) ^2}\delta _k \end{aligned}$$

(32)

where w, the equation of state of the X-fluid, is described by (15), $\Omega _{X} = 8\pi G\rho _X/3H^2$, $A = \frac{(H^2)^{\prime }}{2H^2}$ and $^{\prime } \equiv \frac{\mathrm{d}}{\mathrm{d}\log a}$. We evolve this equation from the decoupling epoch ($a = 10^{-3}$) when it is reasonable to assume $\delta _k \sim a$ and $\frac{\mathrm{d}\delta _k}{\mathrm{d}a} \sim 1$. Our results are shown in Fig. 3 for two different scales, $k \,{=}\,0.01~\hbox {h}/\hbox {Mpc}, 0.1~\hbox {h}/\hbox {Mpc}$ in the context of a non-canonical model with $V(\phi ) = \Lambda /8\pi G$. We find that gravitational clustering in this model is scale-dependent. On very large scales $k \le 0.01~\hbox {h}/\hbox {Mpc}$, scalar field models with large values of $\alpha \ge 10^4$ display clustering identical to $\Lambda$CDM. However, on smaller scales $k \ge 0.1~\hbox {h}/\hbox {Mpc}$, the density contrast in our model is suppressed relative to $\Lambda$CDM even for $\alpha$ values as large as $10^5$, for which the background expansion is indistinguishable from $\Lambda$CDM, as demonstrated in Fig. 1. (The reader might like to note that similar results may be obtained if one models dark matter by a perfect fluid with $p=k\rho$, $0\le k \ll 1$, and adds it to the cosmological constant in the so-called standard model.)

We have thus demonstrated that our model is capable of mimicking the behaviour of a dark matter $+$ vacuum energy model both with respect to cosmological expansion and gravitational clustering. Another possibility provided by our model is that the non-canonical scalar comes as an add-on to dark matter (instead of replacing it). This is the usual procedure adopted by models such as quintessence, in which the matter part of the Lagrangian remains unchanged while dark energy is sourced by a potential such as $V \propto \phi ^{-\alpha }$. It is easy to see that the expansion history in such a model (consisting of conventional dark matter and a non-canonical scalar) is

$$\begin{aligned} H(z) = H_0[\Omega _{0m} (1+z)^3 + \Omega _{0X} (1+z)^{3(1+w)} + \Omega _\Lambda ]^{1/2}\nonumber \\ \end{aligned}$$

(33)

where the last two terms are sourced by the scalar field and w is described by (15).

The clustering properties of the non-canonical scalar are once more given by (31). The new model (33) therefore describes a universe filled with the cosmological constant and two kinds of dark matter: the first being the usual dark matter whereas, depending upon the value of $w \equiv c_s^2$, the second component, $\Omega _{0X}$, can behave like a hot, warm or cold dark matter component. This could have interesting cosmological consequences. For instance, as recently demonstrated in [57], a model with $\Omega _{0X} \ll \Omega _{0m}$ could help alleviate the tension faced by $\Lambda$CDM in simultaneously fitting CMB and weak lensing data. A subdominant component of dark matter, like the one discussed in this paper, could also seed early black hole formation, as discussed in [58].

3 Discussion

In this paper we have demonstrated that a single non-canonical scalar field can play the dual role of describing both dark matter and dark energy. To summarise, a non-canonical scalar field rolling along a flat potential has a kinetic energy which decreases rapidly with time and a potential energy which decreases much more slowly. For large values of the non-canonical parameter $\alpha$ in (2), the kinetic energy can play the role of dark matter while the potential energy behaves like dark energy. If $V(\phi ) = \Lambda /8\pi G$ then the expansion history of this model mimicks $\Lambda$CDM. Other (suitably flat) potentials give rise to a slightly different expansion history.

On its own this result, while surprising, is not unique. It is well known that, for a given expansion history, a(t), it is always possible to reconstruct the canonical scalar field potential $V(\phi )$ which will reproduce the expansion history precisely [59, 60]. Therefore, in principle, it is possible to obtain a potential which reproduces the $\Lambda$CDM expansion rate $a(t) \propto (\sinh {\frac{3}{2}\sqrt{\frac{\Lambda }{3}}t})^{2/3}$. However, the fact that (non-oscillating) canonical scalar fields do not cluster on sub-horizon scales, prevents this potential from providing one with a realistic portrayal of $\Lambda$CDM; also see [37].

The big advantage of non-canonical scalars arises from the fact that, for large values of the non-canonical parameter $\alpha$, the sound speed in (31) drops to zero. Therefore the non-canonical scalar field can cluster, in contrast to canonical models in which clustering is absent.

It is necessary to point out that properties similar to those possessed by our model have also appeared in other discussions of unification (of dark matter and dark energy). For instance in [40] Scherrer proposed a non-canonical model which had an expansion rate exactly like $\Lambda$CDM. Our model differs from [40] in two main respects:

• (i) The purely kinetic Lagrangian ${\mathcal {L}}(X)$ in [40] possesses an extremum in X about which it is expanded in a Taylor series. Our Lagrangian, on the other hand, has a power-law kinetic term with no extremum.

• (ii) The sound velocity in [40] drops off as $a^{-3}$ whereas in our model the sound velocity is a constant and is given by (31).

We therefore conclude that the whereas the expansion history in our model and in [40] is identical (corresponding to $\Lambda$CDM), the nature of gravitational clustering in these two models is rather different. Indeed, gravitational clustering in our model is scale-dependent, and is sensitive to the choice of $\alpha$.

Fig. 4

Perturbations, $\delta _k$, in the non-canonical scalar field model are shown at the present epoch. $\delta _k$ is plotted against k for $\alpha = 2\times 10^7, ~7\times 10^7, ~5\times 10^8$ (bottom to top, solid lines). Perturbations in warm dark matter consisting of a sterile neutrino with mass $= 0.5, 1, 3~\hbox {KeV}$ are also shown (bottom to top, dashed lines). The top most solid line corresponds to $\Lambda$CDM

In this context one should note that the value of $\alpha$ can never be infinitely large. Consider two models characterised by $\alpha _1$ and $\alpha _2$ where $1 \ll \alpha _1 \ll \alpha _2$. Since the Jeans length in our model is

$$\begin{aligned} \lambda _J \sim c_s/\sqrt{G\rho },\quad \hbox {where }c_s = \frac{1}{\sqrt{2\,\alpha - 1}}, \end{aligned}$$

(34)

it follows that the clustering properties of our field will be sensitive to the value of $\alpha$. Clearly gravitational clustering in the model with $\alpha _1$ will be inhibited on small scales relative to the model with $\alpha _2$. This property was illustrated by Fig. 3. It is interesting that a similar situation arises when dark matter is sourced by an oscillating massive canonical scalar field with mass m [21,22,23,24,25,26,27]. In this case, as shown in [24, 28], the Jeans length depends upon the scalar field mass as $\lambda _J \sim (G\rho )^{-1/4}\, \mathrm{m}^{-1/2}$. Ultra-light scalars are therefore able to suppress clustering on small scales, thereby providing one with a resolution to the substructure and cuspy core problems which plague standard cold dark matter.² One expects that a similar mechanism will operate in our model as well, with $\alpha$ playing the role of m. (A key distinction between the two models is that whereas the canonical scalar field needs to oscillate in order to describe dark matter, the non-canonical field does not oscillate but simply rolls along its flat potential.)

A useful analogy can also be drawn between clustering in our model and that in particle dark matter. Consider the case when a relic particle of mass m (such as a neutralino or a sterile neutrino) plays the role of dark matter. In this case perturbations on scales smaller than the free-streaming distance [14]

$$\begin{aligned} \lambda _\mathrm{fs} \sim 40~\hbox {Mpc} \left( \frac{m}{30~\mathrm{{eV}}}\right) ^{-1} \end{aligned}$$

(35)

are effectively erased during the relativistic motion of the particle.

A larger value of m in (35) leads to a smaller value of $\lambda _\mathrm{fs}$. Comparing (35) with (34) we find that the role of mass, in particle dark matter models, is played by the parameter $\alpha$ in our model. In other words, whereas very large values of $\alpha$ will make clustering in our model resemble cold dark matter, smaller values of $\alpha$ will make our model closer to warm dark matter. We demonstrate the similarity of our model with the sterile neutrino model for warm dark matter in Fig. 4. In this figure we show $\delta _k$ for our model, obtained by solving Eq. (25), and compare it with the density contrast in the warm dark matter model, as described in [61]; also see [62,63,64,65]. This figure clearly demonstrates that, for suitable values of $\alpha$, clustering in our model can be like cold or warm dark matter, even as its expansion history mimicks $\Lambda$CDM. The cosmological properties of our model will be examined in greater detail in a companion paper.³

Finally, we would like to draw attention to the following interesting property of the non-canonical scalar which follows from (12). If the value of $\alpha$ is large, then the velocity of the scalar field freezes to an almost constant value, i.e. for $\alpha \gg 1$, $X \rightarrow \hbox {constant}$. This is completely unlike the behaviour of a canonical scalar ($\alpha = 1$) for which ${{\dot{\phi }}} \propto a^{-3}$ if $V = \hbox {constant}$. In the canonical case the universe inflates once $V > X$, at which point since $a \propto e^{\int \sqrt{V} \mathrm{d}t}$ and ${{\dot{\phi }}} \propto a^{-3}$, the value of ${{\dot{\phi }}}$ rapidly drops to zero and the motion of the scalar field comes to an abrupt halt. Not so for the non-canonical scalar which can continue to roll along a flat potential even as the universe inflates.

This may have interesting consequences. It has been postulated [1,2,3,4,5,6,7, 66] that the vacuum energy is not unchanging but a dynamical quantity whose value changes abruptly during the course of a phase transition. Such behaviour is mimicked by the step-like potential (25). Since this potential is piece-wise flat, it can, in principle, describe a universe which inflates twice – once at early times, and then again at the current cosmological epoch. But for this to occur, the scalar field must continue to roll along V for a protracted time interval (corresponding to the age of the universe) and not stop in between (as in the canonical case). In the non-canonical context, for large values of $\alpha$, the kinetic term is almost a constant, which should allow the scalar field to roll along its potential as the latter cascades to lower values. Such a scenario may provide us with a model of quintessential inflation and this possibility will be examined in greater detail in a companion paper. (The reader is referred to [67] for a recent review of quintessential inflation.)